Harmonic Besov and Triebel–Lizorkin Spaces on the Ball

Abstract

Harmonic Besov and Triebel–Lizorkin spaces on the unit ball in ${\mathbb R}^d$ with full range of parameters are introduced and studied. It is shown that these spaces can be identified with respective Besov and Triebel–Lizorkin spaces of distributions on the sphere. Frames consisting of harmonic functions are also developed and frame characterization of the harmonic Besov and Triebel–Lizorkin spaces is established.

1 Introduction

The theory of Besov and Triebel–Lizorkin spaces $B^{sq}_p$ and $F^{sq}_p$ in the classical setting on ${\mathbb R}^d$ has been developed mainly by J. Peetre, H. Triebel, M. Frazier, and B. Jawerth, see [5–7, 19, 24, 25]. Besov and Triebel–Lizorkin spaces have also been developed in various other settings such as on the sphere [17], on the ball [13] and in the general framework of Dirichlet spaces [12].

The purpose of this article is to introduce and study the Besov and Triebel–Lizorkin spaces $B^{sq}_p(\mathscr {H})$, $F^{sq}_p(\mathscr {H})$ (with full range of parameters) consisting of harmonic functions on the unit ball $B^d$ in ${\mathbb R}^d$, $d>1$. The primary motivation for this undertaking is to fill up the existing void in the theory of spaces of harmonic functions and create a framework for future development.

The gist of our approach to spaces of harmonic functions U on $B^d$ is the representation of U in terms of solid spherical harmonics:

$$\begin{aligned} U(x) = \sum _{k=0}^\infty \sum _{\nu =1}^{N(k, d)} b_{k\nu }(U)|x|^kY_{k\nu }\Big (\frac{x}{|x|}\Big ), \quad |x|<1, \end{aligned}$$

(1.1)

where $\{Y_{k\nu }\}$ is an orthonormal basis for spherical harmonics on the unit sphere ${{\mathbb S}^{d-1}}$ and $\{b_{k\nu }(U)\}$ are the coefficients of U. Identity (1.1) and the likes in the sequel are extended by continuity for $x=(0,\dots ,0)$. The harmonic Besov and Triebel–Lizorkin spaces $B^{sq}_p(\mathscr {H})$ and $F^{sq}_p(\mathscr {H})$ are defined by means of the multiplier operator

$$\begin{aligned} J^\beta U(x) := \sum _{k=0}^\infty |x|^k(k+1)^{-\beta }\sum _{\nu =1}^{N(k, d)} b_{k\nu }(U)Y_{k\nu }\Big (\frac{x}{|x|}\Big ),\quad \beta \in {\mathbb R}. \end{aligned}$$

(1.2)

For example, $B^{sq}_p(\mathscr {H})$, $q<\infty$, is defined by the norm

$$\begin{aligned} \Vert U\Vert _{B^{sq}_p(\mathscr {H})} := \left( \int _0^1 (1-r)^{(\beta -s)q}\Vert J^{-\beta } U(r\cdot )\Vert _{L^p({{\mathbb S}^{d-1}})}^q \frac{\mathrm{d}r}{1-r}\right) ^{1/q}, \quad \beta >s. \end{aligned}$$

A similar idea has been used in [18] for the development of Besov and Triebel–Lizorkin spaces of analytic functions in the unit disc in the complex plane.

The Besov spaces $B^{sq}_p(\mathscr {H})$ for $s\in {\mathbb R}$ and $1\le p, q\le \infty$ have been introduced in [9, 10] for distributions f on the unit sphere ${{\mathbb S}^{d-1}}$ in ${\mathbb R}^d$ with (our notation) U being the Poisson integral of f under the name “Lipschitz spaces of distributions on the sphere” and some of their properties have been established. We consider them as spaces of harmonic function on $B^d$ instead.

Our basic tool is well localized kernels consisting of band limited functions on the sphere, that are readily available from [16, 17] and also from [11].

The first step in developing the harmonic Besov and Triebel–Lizorkin spaces on $B^d$ is to show that the growth of the coefficients $\{b_{k\nu }(U)\}$ of any function $U\in B^{sq}_p(\mathscr {H})$ or $U\in F^{sq}_p(\mathscr {H})$ is at most polynomial. The main result in this article asserts that the harmonic Besov and Triebel–Lizorkin spaces $B^{sq}_p(\mathscr {H})$ and $F^{sq}_p(\mathscr {H})$ can be identified with the Besov and Triebel–Lizorkin spaces $\mathcal {B}^{sq}_p({{\mathbb S}^{d-1}})$ and $\mathcal {F}^{sq}_p({{\mathbb S}^{d-1}})$ of distributions on ${{\mathbb S}^{d-1}}$, developed in [17]. This allows to mitigate between spaces of harmonic functions on $B^d$ and distributions/functions on ${{\mathbb S}^{d-1}}$. In particular, this enables us to develop frames consisting of harmonic functions on $B^d$ by harmonic extension of the existing spherical frame elements (needlets) from [17]. We use these frames to characterize the harmonic Besov and Triebel–Lizorkin spaces $B^{sq}_p(\mathscr {H})$ and $F^{sq}_p(\mathscr {H})$ by respective sequence spaces.

The analogue of our identification of harmonic Besov and Triebel–Lizorkin spaces on $B^d$ with respective spaces of distributions on ${{\mathbb S}^{d-1}}$ in the setting of ${\mathbb R}^{d+1}_+$ is essentially obtained by Triebel, see [25, Sect. 1.8.3] and the references therein.

The layout of the rest of this article is as follows. Section 2 contains some background material and basic facts that are used later in the paper. In Sect. 3 we consider harmonic functions on $B^d$ and distributions on ${{\mathbb S}^{d-1}}$ and their frame decomposition. Harmonic Besov and Triebel–Lizorkin spaces on $B^d$ are introduced in Sect. 4 and some of their basic properties are established. Also, the Besov and Triebel–Lizorkin spaces of distributions on ${{\mathbb S}^{d-1}}$ are recalled. The identification of harmonic Besov and Triebel–Lizorkin spaces on $B^d$ with Besov and Triebel–Lizorkin spaces of distributions on ${{\mathbb S}^{d-1}}$ is established in Sect. 5. The frame characterization of harmonic Besov and Triebel–Lizorkin spaces on $B^d$ is given in Sect. 6. In Sect. 7 we briefly discuss the identification of the harmonic Hardy space $\mathscr {H}^p$ on $B^d$ with the harmonic Triebel–Lizorkin space $F^{02}_p(\mathscr {H})$. In Sect. 8 we show how the results for harmonic spaces on $B^d$ can be transferred to harmonic spaces on ${\mathbb R}^d\setminus \overline{B^d}$ by means of the Kelvin transform. There is an appendix, where we place the proof of Peetre’s inequality for band limited functions on ${{\mathbb S}^{d-1}}$.

2 Background

Here we introduce some notation and collect well known technical results that will be used in the sequel.

2.1 Notation

In this article we use standard notation. Thus ${\mathbb R}^d$, $d>1$, stands for the d-dimensional Euclidean space. The inner product of $x,y\in {\mathbb R}^d$ is denoted by $x\cdot y$ and the Euclidean norm of x by $|x|:=\sqrt{x\cdot x}$. We denote $B(y,r):=\{x : |x-y|< r\}$. Then $B^d=B(0, 1)$. The unit sphere in ${\mathbb R}^d$ is ${{\mathbb S}^{d-1}}:=\{x : |x|=1\}$ and $\rho (x, y)$ will stand for the geodesic distance between $x, y\in {{\mathbb S}^{d-1}}$, that is, $\rho (x,y):=\arccos (x\cdot y)$.

The Lebesgue measure on ${{\mathbb S}^{d-1}}$ is denoted by $\sigma$ and $|E|:=\sigma (E)$ stands for the Lebesgue measurable of $E\subset {{\mathbb S}^{d-1}}$. In particular, $\omega _d:=\sigma ({{\mathbb S}^{d-1}})=2\pi ^{d/2}/\Gamma (d/2)$ is the measure of ${{\mathbb S}^{d-1}}$.

All functions we consider are complex-valued if it is not specified otherwise. The inner product of $f,g\in L^2({{\mathbb S}^{d-1}})$ is given by

$$\begin{aligned} \left\langle f,g\right\rangle := \int _{{{\mathbb S}^{d-1}}} f(y)\overline{g(y)}\,\mathrm{d}\sigma (y) \end{aligned}$$

(2.1)

and the nonstandard convolution of functions $F\in L^\infty [-1,1]$ and $g\in L^1({{\mathbb S}^{d-1}})$ is defined by

$$\begin{aligned} F*g(x):=\left\langle F(x\cdot \bullet ),\overline{g}\right\rangle =\int _{{{\mathbb S}^{d-1}}}F(x\cdot y)g(y) \mathrm{d}\sigma (y). \end{aligned}$$

(2.2)

We shall use the abbreviated notation $\Vert \cdot \Vert _p := \Vert \cdot \Vert _{L^p({{\mathbb S}^{d-1}})}$ for the $L^p$-norm on ${{\mathbb S}^{d-1}}$.

We shall denote by $G(x, \delta )$ the spherical cap (ball on ${{\mathbb S}^{d-1}}$) centered at $x\in {{\mathbb S}^{d-1}}$ of radius $\delta$, that is,

$$\begin{aligned} G(x, \delta ):=\{y\in {{\mathbb S}^{d-1}}: \rho (x, y) < \delta \}. \end{aligned}$$

(2.3)

Positive constants will be denoted by c, $c_1$, $c'$, $\dots$ and will be allowed to vary at every occurrence. The notation $a\sim b$ will stand for $c_1\le a/b\le c_2$. The constants will usually depend on some parameters that may or may not be indicated explicitly.

2.2 Spherical Harmonics

The solid spherical harmonics will be our main vehicle in dealing with harmonic functions on the unit ball $B^d$ in ${\mathbb R}^d$.

Denote by $\mathcal {H}_k$ the space of all spherical harmonics of degree $k$ on ${{\mathbb S}^{d-1}}$. As is well known the dimension of $\mathcal {H}_k$ is $N(k, d)= \frac{2k+d-2}{k}\left( {\begin{array}{c}k+d-3\\ k-1\end{array}}\right) \sim k^{d-1}$. Furthermore, the spaces $\mathcal {H}_k$, $k=0, 1, \dots$, are orthogonal and $L^2({{\mathbb S}^{d-1}}) =\bigoplus _{k\ge 0} \mathcal {H}_k$.

Let $\{Y_{k\nu }: \nu =1, \dots , N(k, d)\}$ be a real-valued orthonormal basis for $\mathcal {H}_k$. Then the kernel of the orthogonal projector onto $\mathcal {H}_k$ is given by

$$\begin{aligned} Z_k(x\cdot y) = \sum _{\nu =1}^{N(k, d)} Y_{k\nu }(x)Y_{k\nu }(y). \end{aligned}$$

(2.4)

As is well known

$$\begin{aligned} Z_k(x\cdot y)= \frac{k+\mu }{\mu \omega _d}\, C^{\mu }_k(x\cdot y), \quad \mu :=\frac{d-2}{2},~d>2. \end{aligned}$$

(2.5)

Here $C_k^{\mu }$ is the Gegenbauer (ultraspherical) polynomial of degree $k$ normalized by $C_k^{\mu }(1)= \left( {\begin{array}{c}k+ 2\mu -1\\ k\end{array}}\right)$; the polynomials $C_k^{\mu }$, $k\ge 0$, are orthogonal on $[-1, 1]$ with weight $w(t):= (1-t^2)^{\mu -1/2}$, see [23, p. 80, (4.7.1)]. In the case $d=2$ the kernel of the orthogonal projector onto $\mathcal {H}_k$ takes the form

$$\begin{aligned} Z_0(x\cdot y)=\frac{1}{2\pi },\quad Z_k(x\cdot y)=\frac{1}{\pi }T_k(x\cdot y),\quad k\ge 1, \end{aligned}$$

where $T_k$ is the kth degree Chebyshev polynomial of the first kind.

The set of all band-limited functions (i.e. spherical polynomials) on ${{\mathbb S}^{d-1}}$ of degree $\le N$ will be denoted by $\Pi _N$, i.e. $\Pi _N :=\bigoplus _{k=0}^N \mathcal {H}_k$.

The Poisson kernel on the unit ball $B^d$ is given by

$$\begin{aligned} P(y, x):=\sum _{k\ge 0}|x|^kZ_k\Big (\frac{x}{|x|}\cdot y\Big ) =\frac{1}{\omega _d}\frac{1-|x|^2}{|x-y|^d}, \quad |x| <1,\; y\in {{\mathbb S}^{d-1}}. \end{aligned}$$

(2.6)

We refer the reader to [15, 22] for the basics of spherical harmonics.

Kernels of the form

$$\begin{aligned} \Lambda _N(x\cdot y) := \sum _{k=0}^\infty \lambda (k/N)Z_k(x\cdot y), \quad x, y\in {{\mathbb S}^{d-1}}, \quad N\ge 1, \end{aligned}$$

(2.7)

where $\lambda \in C^\infty ({\mathbb R}_+)$ is compactly supported (${\mathbb R}_+:=[0, \infty )$), will play a key role in this article. Observe that in this case

$$\begin{aligned} \Lambda _N(u) := \sum _{k=0}^\infty \lambda (k/N)Z_k(u), \quad u\in [-1, 1], \end{aligned}$$

(2.8)

is simply an algebraic polynomial kernel. We shall utilize kernels of this sort, where $\lambda$ is an admissible $C^\infty$ function.

Definition 2.1

We say that a function $\lambda \in C^\infty ({\mathbb R}_+)$ is admissible of type (a) or (b) if $\lambda$ satisfies the conditions:

• (a) ${\text {supp}}\lambda \subset [0, 2]$ and $\lambda (u)=1$ for $u\in [0, 1]$ or

• (b) ${\text {supp}}\lambda \subset [1/4, 4]$.

Theorem 2.2

Let $\lambda$ be admissible and $\Vert \lambda ^{(m)}\Vert _\infty \le A$ for $0\le m\le K$. Then for any $N\ge 1$ the kernel $\Lambda _N$ from (2.7)–(2.8) obeys

$$\begin{aligned} |\Lambda _N^{(\nu )}(\cos \theta )| \le c A N^{d-1+2\nu }(1+N|\theta |)^{-K}, \quad |\theta |\le \pi , \; \nu \ge 0, \end{aligned}$$

(2.9)

and hence

$$\begin{aligned} |\Lambda _N^{(\nu )}(x\cdot y)| \le c A N^{d-1+2\nu }(1+N\rho (x, y))^{-K}, \quad x, y\in {{\mathbb S}^{d-1}}. \end{aligned}$$

(2.10)

Here the constant $c>0$ depends only on K, $\nu$, d. Furthermore, for $x, y, z\in {{\mathbb S}^{d-1}}$

$$\begin{aligned} |\Lambda _N(x\cdot z)-\Lambda _N(y\cdot z)| \le cA \frac{\rho (x, y) N^d}{(1+N\rho (x, z))^{K}}, \quad \hbox {if}\quad \rho (x, y) \le N^{-1}. \end{aligned}$$

(2.11)

For a proof, see [16, Theorem 3.5] and [17, Lemma 2.6], also [11, Theorem 5.1].

2.3 Maximal Inequality

Let $\mathcal {M}_t$ be the maximal operator, defined by

$$\begin{aligned} M_t f(x):=\sup _{G \ni x} \Big (\frac{1}{|G|}\int _G |f(y)|^t \mathrm{d}\sigma (y)\Big )^{1/t}, \quad t>0, \end{aligned}$$

(2.12)

where the $\sup$ is over all spherical caps $G=G(z,\delta )$ containing x (see (2.3)).

We shall use the Fefferman-Stein vector-valued maximal inequality (see [3, 21]): If $0<p<\infty$, $0<q\le \infty$, and $0< t < \min \{p, q\}$, then for any sequence of measurable functions $f_1, f_2, \dots$ on ${{\mathbb S}^{d-1}}$

$$\begin{aligned} \Big \Vert \Big ( \sum _{j=1}^{\infty } \left[ \mathcal {M}_t f_j(\cdot )\right] ^q \Big )^{1/q}\Big \Vert _{L^p} \le c \Big \Vert \Big ( \sum _{j=1}^{\infty }|f_j(\cdot )|^q \Big )^{1/q}\Big \Vert _{L^p}. \end{aligned}$$

(2.13)

This inequality is usually stated for $t=1$ under the condition $p, q >1$. Then the above version of the maximal inequality follows readily. A proof of (2.13) for $t=1$ is also given in [8, Theorem 1.2] from where it follows that the constant $c>0$ in (2.13) can be written the form $c=(c_1(d)\max \{p/t, (p/t-1)^{-1}\}\max \{1, (q/t-1)^{-1}\})^{1/t}$.

We shall also need the following integral version of the maximal inequality: Let p, q, t be as above. Then for any continuous function $F: [a,b)\times {{\mathbb S}^{d-1}}\rightarrow {\mathbb C}$ one has

$$\begin{aligned} \Big \Vert \Big ( \int _{a}^{b}\Big [\mathcal {M}_t(F(r,\cdot ))(\cdot )\Big ]^q \mathrm{d}r\Big )^{1/q}\Big \Vert _{L^p} \le c \Big \Vert \Big ( \int _{a}^{b}|F(r, \cdot )|^q \mathrm{d}r \Big )^{1/q}\Big \Vert _{L^p}, \end{aligned}$$

(2.14)

with the same constant $c>0$ as in (2.13). This inequality is an immediate consequence of (2.13) by discretization using Riemann sums and a limiting process.

The next lemma contains an analogue of Peetre’s inequality which involves the maximal operator $\mathcal {M}_t$ from (2.12).

Lemma 2.3

Let $t>0$ and $N\in {\mathbb N}$. Then there exists a constant $c>0$ depending only on t and d such that for any $g\in \Pi _N$

$$\begin{aligned} \sup _{y\in {{\mathbb S}^{d-1}}}\frac{|g(y)|}{(1+N\rho (x, y))^{(d-1)/t}} \le c\mathcal {M}_tg(x), \quad \forall x\in {{\mathbb S}^{d-1}}. \end{aligned}$$

(2.15)

Here $\mathcal {M}_t$ is the maximal operator from (2.12).

To streamline our presentation we place the proof of this lemma in the appendix.

We shall need the following simple

Lemma 2.4

For any $g\in L^1({{\mathbb S}^{d-1}})$ and $M > d-1$

$$\begin{aligned} \int _{{\mathbb S}^{d-1}}\frac{N^{d-1}|g(y)|}{(1+N\rho (x, y))^M}\, \mathrm{d}\sigma (y) \le c\mathcal {M}_1g(x), \quad \forall x\in {{\mathbb S}^{d-1}}, \forall N\in {\mathbb N}, \end{aligned}$$

(2.16)

where $\mathcal {M}_1$ is the maximal operator from (2.12) with $t=1$ and c depends only on d and M.

The proof of this lemma is straightforward and we omit it (for the idea see e.g. [21, (16) in Chapter II, Sect. 2.1]).

The following obvious inequality will also be needed: If $M> d-1$, then

$$\begin{aligned} \int _{{{\mathbb S}^{d-1}}} \frac{N^{d-1}}{(1+N\rho (x,y))^M}\mathrm{d}\sigma (y)\le c,\quad \forall x\in {{\mathbb S}^{d-1}},~\forall N\ge 1, \end{aligned}$$

(2.17)

where c depends only on d and M.

2.4 Useful inequalities

The following Nikolski-type inequality (see e.g. [2, Theorem 5.5.1]) will be used.

Lemma 2.5

If $0<q\le p\le \infty$, then for any $g\in \Pi _N$, $N\ge 1$,

$$\begin{aligned} \Vert g\Vert _{L^p({{\mathbb S}^{d-1}})} \le cN^{(d-1)(1/q-1/p)}\Vert g\Vert _{L^q({{\mathbb S}^{d-1}})}, \end{aligned}$$

(2.18)

where $c=c(d, p, q)$.

Two simple inequalities will be needed.

Lemma 2.6

• (a) If $\gamma , K>0$, then

  $$\begin{aligned} \int _0^1(1-r)^{\gamma -1}r^K \mathrm{d}r \le cK^{-\gamma }, \quad c=c(\gamma ). \end{aligned}$$

  (2.19)

• (b) If $\alpha , \gamma >0$ and $0<r<1$, then

  $$\begin{aligned} \sum _{\ell =0}^\infty r^{\alpha 2^\ell }2^{\ell \gamma } \le c(1-r)^{-\gamma }, \quad c=c(\alpha , \gamma ). \end{aligned}$$

  (2.20)

Proof

(a) Substituting $r=1-u/K$ in the integral in (2.19) we get

$$\begin{aligned} \int _0^1(1-r)^{\gamma -1}r^K \mathrm{d}r = K^{-\gamma }\int _0^K u^{\gamma -1}\Big (1-\frac{u}{K}\Big )^Kdu \le K^{-\gamma }\int _0^\infty u^{\gamma -1}e^{-u}du, \end{aligned}$$

implying (2.19) with $c=\Gamma (\gamma )$, $\Gamma$ being the $\Gamma$-function. Here for the last inequality we used the following obvious inequality $(1-u/K)^K \le e^{-u}$, whenever $0\le u\le K$.

(b) It is readily seen that

$$\begin{aligned} \sum _{\ell =0}^\infty r^{\alpha 2^\ell }2^{\ell \gamma } \le c\int _{1/2}^\infty r^{\alpha u}u^{\gamma -1}du = c\Big (\frac{r}{1-r}\Big )^\gamma \int _{\frac{1-r}{2r}}^\infty \left( r^{\frac{r}{1-r}}\right) ^{\alpha v} v^{\gamma -1} dv, \end{aligned}$$

where we applied the substitution $u=\frac{rv}{1-r}$. Evidently, $r^{\frac{r}{1-r}} \le 1/2$ whenever $1/2\le r<1$ and (2.20) follows. In the case when $0< r <1/2$ inequality (2.20) follows trivially from the case $r=1/2$. $\square$

3 Harmonic Functions on $B^d$ and Distributions on ${\mathbb {S}}^{d-1}$

The purpose of this article is to study harmonic functions on $B^d$, which are intimately related to their boundary values. The boundary values of harmonic functions are in general distributions. In this section, we clarify the relationship between harmonic functions on $B^d$ and their boundary value distributions on ${{\mathbb S}^{d-1}}$.

3.1 Harmonic Functions on $\varvec{B^d}$

Denote by $\mathscr {H}(B^d)$ the set of all harmonic functions on the unit ball in ${\mathbb R}^d$. The properties of spherical harmonics readily imply the following representation of any function $U\in \mathscr {H}(B^d)$:

$$\begin{aligned} U(x) = \sum _{k=0}^\infty \frac{|x|^k}{a^k} \int _{{\mathbb S}^{d-1}}U(a\eta )Z_k\Big (\frac{x}{|x|}\cdot \eta \Big ) \mathrm{d}\sigma (\eta ), \quad |x|<a, \; 0<a<1. \end{aligned}$$

(3.1)

Using the spherical harmonic basis functions (see (2.4)) this takes the form

$$\begin{aligned} U(x)&= \sum _{k=0}^\infty |x|^k\sum _{\nu =1}^{N(k, d)} \frac{1}{a^k}\int _{{\mathbb S}^{d-1}}U(a\eta )Y_{k\nu }(\eta ) \mathrm{d}\sigma (\eta )Y_{k\nu }\Big (\frac{x}{|x|}\Big ) \\&= \sum _{k=0}^\infty |x|^k\sum _{\nu =1}^{N(k, d)} b_{k\nu }(U)Y_{k\nu }\Big (\frac{x}{|x|}\Big ), \quad |x|<a.\nonumber \end{aligned}$$

(3.2)

Above the series converge absolutely and uniformly on every compact subset of B(0, a). It is an important observation that the coefficients

$$\begin{aligned} b_{k\nu }(U):= \frac{1}{a^k}\int _{{\mathbb S}^{d-1}}U(a\eta )Y_{k\nu }(\eta ) \mathrm{d}\sigma (\eta ) \end{aligned}$$

(3.3)

are independent of a for all $0<a<1$. This implies the representation

$$\begin{aligned} U(x) = \sum _{k=0}^\infty |x|^k\sum _{\nu =1}^{N(k, d)} b_{k\nu }(U)Y_{k\nu }\Big (\frac{x}{|x|}\Big ), \quad |x|<1, \end{aligned}$$

(3.4)

where the coefficients $b_{k\nu }(U)$ are from (3.3) and the convergence is absolute and uniform on every compact subset of $B^d$. In certain cases, it is convenient to write this representation in the form

$$\begin{aligned} U(r\xi ) = \sum _{k=0}^\infty r^k\sum _{\nu =1}^{N(k, d)} b_{k\nu }(U)Y_{k\nu }(\xi ), \quad 0\le r<1, \;\;\xi \in {{\mathbb S}^{d-1}}. \end{aligned}$$

(3.5)

Applying the Cauchy–Schwarz inequality, it follows by (3.3) that for any $0<a<1$

$$\begin{aligned} |b_{k\nu }(U)| \le a^{-k}\Vert U(a\cdot )\Vert _{L^2({{\mathbb S}^{d-1}})}, \quad \nu =1, \dots , N(k, d), \;\; k=0, 1, \dots , \end{aligned}$$

(3.6)

The topology on $\mathscr {H}(B^d)$ is naturally induced by the uniform convergence on all compact subsets of $B^d$. Clearly, $\mathscr {H}(B^d)$ is complete with respect to this topology.

We are interested in harmonic functions $U\in \mathscr {H}(B^d)$ with coefficients of at most polynomial growth:

$$\begin{aligned} |b_{k\nu }(U)| \le c(k+1)^\gamma , \quad \nu =1, \dots , N(k, d), \;\; k=0, 1, \dots , \end{aligned}$$

(3.7)

for some constants $\gamma , c>0$. As will be shown in Proposition 4.2 below the functions in the harmonic Besov and Triebel–Lizorkin spaces of interest to us will have this property.

The following basic lemma on harmonic functions will play an important role in what follows (see [4], Lemma 2, page 172):

Lemma 3.1

Suppose B is a ball in ${\mathbb R}^d$ with center $x\in {\mathbb R}^d$. Let U be a harmonic function on B that is continuous on the closure of B. Then for any $p>0$

$$\begin{aligned} |U(x)|^p \le c(p,d)\frac{1}{|B|}\int _B|U(y)|^p \mathrm{d}y. \end{aligned}$$

(3.8)

3.2 Distributions on $\varvec{{{\mathbb S}^{d-1}}}$

To define distributions on ${{\mathbb S}^{d-1}}$ we shall use as test functions the class $\mathcal {S}:= C^\infty ({{\mathbb S}^{d-1}})$ consisting of all functions $\phi$ on ${{\mathbb S}^{d-1}}$ such that

$$\begin{aligned} \Vert Z_k*\phi \Vert _2 \le c(\phi , m)(1+k)^{-m}, \;\; \forall k, m\ge 0. \end{aligned}$$

Recall that the convolution $Z_k*\phi$ is defined in (2.2). It will be convenient to define the topology on $\mathcal {S}$ by the sequence of norms

$$\begin{aligned} P_m(\phi ):= \sum _{k\ge 0}(k+1)^m \Vert Z_k*\phi \Vert _2 = \sum _{k\ge 0}(k+1)^m \Big (\sum _{\nu =1}^{N(k, d)} |\langle \phi , Y_{k\nu }\rangle |^2\Big )^{1/2}. \end{aligned}$$

(3.9)

Evidently, the topology on $\mathcal {S}$ can be equivalently defined by the seminorms

$$\begin{aligned} P_m^*(\phi ):= \Vert \Delta _0^m \phi \Vert _\infty , \quad m=0, 1, \dots , \end{aligned}$$

where $\Delta _0$ is the Laplace–Beltrami operator on ${{\mathbb S}^{d-1}}$. Furthermore, it can be defined by the seminorms

$$\begin{aligned} P_m^{**}(\phi ):= \sum _{|\alpha |=m}\Vert {\partial }^{\alpha } {\tilde{\phi }}\Vert _\infty , \quad m=0, 1, \dots , \end{aligned}$$

where $\tilde{\phi }(x):=\phi (x/|x|)$, see e.g. [20]. It is easy to see that $\mathcal {S}$ is complete in the topology of $\mathcal {S}$ defined above.

Observe that all $Y_{k\nu }\in \mathcal {S}$ and hence by (2.4) $Z_k(x\cdot y)\in \mathcal {S}$ as a function of x for every fixed y and as function of y for every fixed x.

The space $\mathcal {S}':=\mathcal {S}'({{\mathbb S}^{d-1}})$ of distributions on ${{\mathbb S}^{d-1}}$ is defined as the space of all continuous linear functionals on $\mathcal {S}$. The pairing of $f\in \mathcal {S}'$ and $\phi \in \mathcal {S}$ will be denoted by $\langle f, \phi \rangle := f(\overline{\phi })$, which is consistent with the inner product on $L^2({{\mathbb S}^{d-1}})$, see (2.1). More precisely, $\mathcal {S}'$ consists of all linear functionals f on $\mathcal {S}$ for which there exist constants $c>0$ and $m\in {\mathbb N}_0$ such that

$$\begin{aligned} |\langle f, \phi \rangle | \le c P_m(\phi ),\quad \forall \phi \in \mathcal {S}. \end{aligned}$$

(3.10)

For any $f\in \mathcal {S}'$ we define $Z_k*f$ by

$$\begin{aligned} Z_k*f(x) :=\langle f, \overline{Z_k(x\cdot \bullet )}\rangle =\langle f, Z_k(x\cdot \bullet )\rangle , \end{aligned}$$

(3.11)

where on the right f is acting on $\overline{Z_k(x\cdot y)}=Z_k(x\cdot y)$ as a function of y ($Z_k$ is real-valued). From (3.9) and (3.10) it follows that

$$\begin{aligned} |\langle f, Y_{k\nu }\rangle | \le c(k+1)^m,\quad \forall k\ge 0,\; \forall \nu =1, \dots , N(k, d), \end{aligned}$$

(3.12)

with c and m as in (3.10). Furthermore, $Z_k*f\in \mathcal {H}_k$ and

$$\begin{aligned} \Vert Z_k*f\Vert _2 \le c(k+1)^{m+(d-1)/2},\quad \forall k\ge 0, \end{aligned}$$

(3.13)

in light of (3.12) and (2.4). For more information about distributions on ${{\mathbb S}^{d-1}}$, see [17].

3.3 Convergence

We shall frequently use that

$$\begin{aligned} f=\sum _{k\ge 0} Z_k*f, \quad \forall f\in \mathcal {S}' \end{aligned}$$

(3.14)

with convergence in distributional sense. This follows readily by duality from the fact that $\phi =\sum _{k\ge 0} Z_k*\phi$ for every $\phi \in \mathcal {S}$ with convergence in the topology of $\mathcal {S}$.

By the same token, if $\lambda \in C^\infty ({\mathbb R}_+)$ is an admissible cutoff function of type (a) in the sense of Definition 2.1 and $\Lambda _N$ is the kernel from (2.7), then we have $f=\lim _{N\rightarrow \infty } \Lambda _N*f$ in $\mathcal {S}'$. This yields the following Littlewood-Paley decomposition of distributions: Let $\varphi \in C^\infty ({\mathbb R}_+)$ be an admissible function of type (b) such that ${\text {supp}}\varphi \subset [1/2, 2]$ and

$$\begin{aligned} \sum _{j=1}^\infty \varphi \big (2^{1-j}u\big )=1 \quad \hbox { for } u\in [1, \infty ). \end{aligned}$$

(3.15)

For the existence of such functions, see e.g. [17]. Set

$$\begin{aligned} \Phi _0 := Z_0=\omega _d^{-1} \quad \text{ and }\quad \Phi _j := \sum _{k=0}^\infty \varphi \Big (\frac{k}{2^{j-1}}\Big )Z_k, \quad j=1, 2, \dots . \end{aligned}$$

(3.16)

Then

$$\begin{aligned} f=\sum _{j\ge 0}\Phi _j*f \quad \hbox {for all }f\in \mathcal {S}' \hbox {(convergence in}\; \mathcal {S}'), \end{aligned}$$

(3.17)

see [17, Lemma 2.1].

The relationship between harmonic functions on $B^d$ and distributions on ${{\mathbb S}^{d-1}}$ is clarified by the following

Proposition 3.2

• (a) To any $U\in \mathscr {H}(B^d)$ represented by (3.4) (or (3.5)) with coefficients satisfying (3.7) there corresponds a distribution $f\in \mathcal {S}'$, $f=f_U$, (the boundary value function/distribution of U ) defined by

  $$\begin{aligned} f:= \sum _{k\ge 0}\sum _{\nu =1}^{N(k, d)} b_{k\nu }(U) Y_{k\nu } \quad \hbox {(convergence in }\mathcal {S}') \end{aligned}$$

  (3.18)

  with coefficients $b_{k\nu }(U)=\langle f, Y_{k\nu }\rangle$.

• (b) To any distribution $f\in \mathcal {S}'$ with coefficients $b_{k\nu }(f):=\langle f, Y_{k\nu }\rangle$ there corresponds a harmonic function $U\in \mathscr {H}(B^d)$, $U=U_f$, (the harmonic extension of f to $B^d)$ defined by

  $$\begin{aligned} U(x) = \sum _{k=0}^\infty |x|^k\sum _{\nu =1}^{N(k, d)} b_{k\nu }(f)Y_{k\nu }\Big (\frac{x}{|x|}\Big ), \quad |x|<1, \end{aligned}$$

  (3.19)

  with coefficients $b_{k\nu }(U)=b_{k\nu }(f)$ obeying (3.7), where the series converges uniformly on every compact subset of $B^d$.

• (c) For every $U\in \mathscr {H}(B^d)$ we have $U_{f_U} = U$ and for every $f\in \mathcal {S}'$ we have $f_{U_f} = f$.

Proof

(a) From the fact that the coefficients $b_{k\nu }(U)$ obey (3.7) it readily follows that the series in (3.18) converges in $\mathcal {S}'$. This and the orthogonality of $\{Y_{k\nu }\}$ lead to $\langle f, Y_{k\nu }\rangle = b_{k\nu }(U)$.

(b) If $f\in \mathcal {S}'$, then by (3.12) we have $|b_{k\nu }(f)| \le c(k+1)^m$ for some constants $c, m>0$, implying that the series in (3.19) converges uniformly on every compact subset of $B^d$ and $b_{k\nu }(U)=b_{k\nu }(f)$.

Claim (c) reflects the fact that in either case $b_{k\nu }(U)=b_{k\nu }(f)$.$\square$

3.4 Frame Decomposition of Distributions on $\varvec{{{\mathbb S}^{d-1}}}$

Here we recall the construction of a frame (needlets) on ${{\mathbb S}^{d-1}}$ whose elements are bandlimited functions. Note that the situation is more favorable in dimension $d=2$, where Meyer’s periodic wavelets (see [14]) form a basis with the desired properties.

The construction of needlets on ${{\mathbb S}^{d-1}}$, $d>2$, starts with the selection of a real-valued function $\lambda \in C^\infty ({\mathbb R}_+)$ with the properties: ${\text {supp}}\lambda \subset [1/2, 2]$, $\lambda \ge 0$, $\lambda (u)\ge c>0$ for $u\in [3/5, 5/3]$, and $\sum _{\nu =0}^\infty \lambda ^2(2^{-\nu }u) =1$ for $u\in [1, \infty )$. Define

$$\begin{aligned} \Lambda _0:=Z_0, \quad \hbox {and}\quad \Lambda _j:=\sum _{\nu =0}^\infty \lambda \Big (\frac{\nu }{2^{j-1}}\Big )Z_\nu , \quad j\ge 1. \end{aligned}$$

(3.20)

It is easy to see that $f=\sum _{j=0}^\infty \Lambda _j*\Lambda _j*f$ for every $f\in \mathcal {S}'$ (convergence in $\mathcal {S}'$).

The next step is to discretize $\Lambda _j*\Lambda _j$ for $j\ge 1$ by a cubature formula on ${{\mathbb S}^{d-1}}$. One constructs a cubature on ${{\mathbb S}^{d-1}}$ with nodes in $\mathcal {X}_j\subset {{\mathbb S}^{d-1}}$ consisting of $\le c2^{j(d-1)}$ almost uniformly distributed points on ${{\mathbb S}^{d-1}}$ and positive coefficients $\{w_\xi \}_{\xi \in \mathcal {X}_j}$ of size $w_\xi \sim 2^{-j(d-1)}$ such that

$$\begin{aligned} \int _{{\mathbb S}^{d-1}}f(x)\mathrm{d}\sigma (x)= \sum _{\xi \in \mathcal {X}_j} w_\xi f(\xi ) \end{aligned}$$

(3.21)

for all spherical harmonics of degree $\le 2^{j+1}$, see [17]. In fact, $\mathcal {X}_j$ can be selected as a maximal $\delta _j$-net on ${{\mathbb S}^{d-1}}$ with $\delta _j = \gamma 2^{-j}$, where $\gamma >0$ is a sufficiently small constant. Then it readily follows that there exists a disjoint partition $\{A_\xi \}_{\xi \in \mathcal {X}_j}$ of ${{\mathbb S}^{d-1}}$ consisting of measurable sets such that $G(\xi ,\delta _j/2)\subset A_\xi \subset G(\xi , \delta _j)$, $\xi \in \mathcal {X}_j$. In addition, set $\mathcal {X}_0:=\{e_1\}$ with $e_1:= (1, 0, \dots , 0)$, and $w_{e_1}:=\omega _d^{-1}$. From (3.21) it follows that

$$\begin{aligned} \Lambda _j*\Lambda _j(x\cdot y) =\int _{{\mathbb S}^{d-1}}\Lambda _j(x\cdot \eta )\Lambda _j(\eta \cdot y)\mathrm{d}\sigma (y) = \sum _{\xi \in \mathcal {X}_j} w_\xi \Lambda _j(\xi \cdot x)\Lambda _j(\xi \cdot y), \end{aligned}$$

which allows to discretize $f=\sum _{j=0}^\infty \Lambda _j*\Lambda _j*f$ and obtain

$$\begin{aligned} f=\sum _{j=0}^\infty \sum _{\xi \in \mathcal {X}_j}\langle f,\psi _\xi \rangle \psi _\xi , \quad \forall f\in \mathcal {S}' \quad \hbox {(convergence in } \mathcal {S}'). \end{aligned}$$

(3.22)

Here $\psi _\xi :=w_\xi ^{1/2}Z_0$, $\xi \in \mathcal {X}_0$, and

$$\begin{aligned} \psi _\xi (x):=w_\xi ^{1/2} \Lambda _j(\xi \cdot x), \quad \xi \in \mathcal {X}_j, \;j\ge 1. \end{aligned}$$

(3.23)

We set $\mathcal {X}:=\cup _{j\ge 0}\mathcal {X}_j$ assuming that equal points from different sets $\mathcal {X}_j$ are distinct points in $\mathcal {X}$ so that $\mathcal {X}$ can be used as an index set. This completes the construction of the system $\{\psi _\xi \}_{\xi \in \mathcal {X}}$. From above it readily follows that $\{\psi _\xi \}_{\xi \in \mathcal {X}}$ is a tight frame for $L^2({{\mathbb S}^{d-1}})$.

Observe that the frame elements $\{\psi _\xi \}$ are not only band limited, but also have excellent localization on ${{\mathbb S}^{d-1}}$. From the properties of $\lambda$ and Theorem 2.2 it follows that (see also [16, 17]) for any $M>0$ there exists a constant $c>0$ such that

$$\begin{aligned} |\psi _\xi (x)| \le c2^{j(d-1)/2}(1+2^j\rho (x, \xi ))^{-M}, \quad x\in {{\mathbb S}^{d-1}},\; \xi \in \mathcal {X}_j,\; j\ge 0. \end{aligned}$$

(3.24)

Moreover, as shown in [11, Theorem 5.1] the localization of $\psi _\xi$ can be improved to sub-exponential: For any ${\varepsilon }>0$ the cutoff function $\lambda$ above can be selected so that

$$\begin{aligned} |\psi _\xi (x)| \le c_12^{j(d-1)/2}\exp \big \{-c_2\big (2^j\rho (x, \xi )\big )^{1-{\varepsilon }}\big \}, \quad x\in {{\mathbb S}^{d-1}}, \; \xi \in \mathcal {X}_j,\; j\ge 0,\nonumber \\ \end{aligned}$$

(3.25)

where $c_1, c_2>0$ are constants depending on ${\varepsilon }$.

Note that for more flexibility it is possible to construct a pair of dual frames $\{\psi _\xi \}_{\xi \in \mathcal {X}}$, $\{\tilde{\psi }_\xi \}_{\xi \in \mathcal {X}}$ on ${{\mathbb S}^{d-1}}$, where each $\psi _\xi$ is defined as above with $\lambda$ being an arbitrary admissible complex-valued cutoff function of type (b), while $\tilde{\psi }_\xi$ is defined as above with $\tilde{\lambda }$ instead of $\lambda$ such that $\sum _{\nu \ge 0} \lambda (2^{-\nu }u)\overline{\tilde{\lambda }(2^{-\nu }u)}=1$ on $[1,\infty )$.

For more details and proofs, see [11, 17].

3.5 Frame Decomposition of Harmonic Functions on $\varvec{B^d}$

By harmonic extension of the needlets from Sect. 3.3 we next construct a decomposition system for harmonic functions in $\mathscr {H}(B^d)$. We define $\Psi _\xi (x):=w_\xi ^{1/2}Z_0=\omega _d^{-1/2}$, $\xi \in \mathcal {X}_0$, and for all $\xi \in \mathcal {X}_j$, $j\ge 1$, we set

$$\begin{aligned} \Psi _\xi (x) :=w_\xi ^{1/2}\sum _{\nu =0}^{2^j} \lambda \Big (\frac{\nu }{2^{j-1}}\Big )|x|^\nu Z_\nu \Big (\frac{x}{|x|}\cdot \xi \Big ), \quad x\in {\mathbb R}^d, \end{aligned}$$

(3.26)

where $\lambda$ is from the definition of needlets in (3.20). Observe that $\Psi _\xi (x)\big |_{|x|=1}$ is just the function $\psi _\xi$ from (3.23) and $\Psi _\xi \in \mathscr {H}(B^d)$, i.e. $\Psi _\xi$ is the harmonic extension of $\psi _\xi$ on $B^d$. We also define a natural dual to $\{\Psi _\xi \}_{\xi \in \mathcal {X}}$ by $\tilde{\Psi }_\xi := \Psi _\xi$ for $\xi \in \mathcal {X}_0$, and

$$\begin{aligned} \tilde{\Psi }_\xi (x) :=w_\xi ^{1/2}\sum _{\nu =0}^{2^j} \lambda \Big (\frac{\nu }{2^{j-1}}\Big )|x|^{-\nu } Z_\nu \Big (\frac{x}{|x|}\cdot \xi \Big ), \quad |x| > 0, \; \xi \in \mathcal {X}_j, \; j\ge 1.\nonumber \\ \end{aligned}$$

(3.27)

Note that $\tilde{\Psi }_\xi |_{{\mathbb S}^{d-1}}= \Psi _\xi |_{{\mathbb S}^{d-1}}=\psi _\xi$ and $\Psi _\xi$, $\tilde{\Psi }_\xi$ are real-valued.

Observe that if more flexibility is needed the cutoff functions $\lambda$ and $\tilde{\lambda }$ mentioned in Sect. 3.3 can be used in the construction of $\Psi _\xi$, $\tilde{\Psi }_\xi$.

We next record some basic properties of the system $\{\Psi _\xi \}_{\xi \in \mathcal {X}}$, $\{\tilde{\Psi }_\xi \}_{\xi \in \mathcal {X}}$.

Proposition 3.3

• (a) Each function $\Psi _\xi$, $\xi \in \mathcal {X}$, from (3.26) is harmonic on ${\mathbb R}^d$ and for each $\tilde{\Psi }_\xi$ from (3.27) the function $|x|^{2-d}\tilde{\Psi }_\xi (x)$ is harmonic on ${\mathbb R}^d\setminus \{0\}$.

• (b) Any $U\in \mathscr {H}(B^d)$ with coefficients obeying (3.7) is represented as

$$\begin{aligned} U= \sum _{\xi \in \mathcal {X}} <U, \tilde{\Psi }_\xi > \Psi _\xi , \end{aligned}$$

(3.28)

where the convergence is uniform on every compact subset of $B^d$ and the coefficients

$$\begin{aligned} < U, \tilde{\Psi }_\xi >:= \langle U(r\cdot ) , \tilde{\Psi }_\xi (r\cdot )\rangle =\int _{{\mathbb S}^{d-1}}U(r\eta )\tilde{\Psi }_\xi (r\eta ) \mathrm{d}\sigma (\eta ), \quad r\in (0, 1),\qquad \end{aligned}$$

(3.29)

do not depend on r. Furthermore, $< U, \tilde{\Psi }_\xi >= \langle f_U, \psi _\xi \rangle$ with $f_U$ being the boundary value distribution of U, defined in (3.18).

Proof

The validity of (a) is immediate from the theory of spherical harmonics as $|x|^{2-d}\tilde{\Psi }_\xi (x)$ is the Kelvin transform of $\Psi _\xi$.

To prove (b) we observe that by (3.22)

$$\begin{aligned} f_U=\sum _{\xi \in \mathcal {X}} \langle f_U, \psi _\xi \rangle \psi _\xi , \end{aligned}$$

where the convergence is in $\mathcal {S}'({{\mathbb S}^{d-1}})$. Hence, by harmonic extension

$$\begin{aligned} U(r\eta )=\sum _{\xi \in \mathcal {X}} \langle f_U, \psi _\xi \rangle \Psi _\xi (r\eta ). \end{aligned}$$

On the other hand, by the properties of $\{Z_k\}$ it readily follows that

$$\begin{aligned} \langle U(r\cdot ) , \tilde{\Psi }_\xi (r\cdot )\rangle = \langle f_U, \psi _\xi \rangle \end{aligned}$$

and this completes the proof.$\square$

4 Besov and Triebel–Lizorkin Spaces

We now center on Besov spaces $B^{s q}_p(\mathscr {H})$ and Triebel–Lizorkin spaces $F^{s q}_p(\mathscr {H})$ consisting of harmonic functions on the unit ball $B^d$. As will be shown these spaces can be identified with the Besov $\mathcal {B}^{sq}_p$ and Triebel–Lizorkin $\mathcal {F}^{sq}_p$ spaces of distributions on the unit sphere ${{\mathbb S}^{d-1}}$.

4.1 Harmonic Besov and Triebel–Lizorkin Spaces on $\varvec{B^d}$

For $U\in \mathscr {H}(B^d)$ and $\beta \in {\mathbb R}$ we define

$$\begin{aligned} J^\beta U(r\xi ) := \sum _{k=0}^\infty r^k(k+1)^{-\beta }\sum _{\nu =1}^{N(k, d)} b_{k\nu }(U)Y_{k\nu }(\xi ), \quad 0\le r<1, \;\;\xi \in {{\mathbb S}^{d-1}}.\qquad \end{aligned}$$

(4.1)

By (3.6) it follows that the above series converges absolutely and uniformly on every compact subset of $B^d$ and hence $J^\beta U$ is a well defined harmonic function on $B^d$.

Observe that if, for example, $f\in \mathcal {S}({{\mathbb S}^{d-1}})$, $U(r\xi ):=\int _{{\mathbb S}^{d-1}}P(y, r\xi )f(y)\mathrm{d}\sigma (y)$ is the Poisson integral of f, and $TU(r\xi ):= \frac{d}{\mathrm{d}r}(rU(r\xi ))$, then $J^{-m}U(r\xi )=T^mU(r\xi )$, $m \in {\mathbb N}$.

Definition 4.1

Let $s\in {\mathbb R}$, $0<q\le \infty$, and $\beta :=s+1$.

• (a) The harmonic Besov space $B^{sq}_p(\mathscr {H})$, $0<p\le \infty$, is defined as the set of all $U\in \mathscr {H}(B^d)$ such that

  $$\begin{aligned} \Vert U\Vert _{B^{sq}_p(\mathscr {H})} := \Big (\int _0^1 (1-r)^{(\beta -s)q}\Vert J^{-\beta } U(r\cdot )\Vert _{L^p({{\mathbb S}^{d-1}})}^q \frac{\mathrm{d}r}{1-r}\Big )^{1/q} <\infty \quad \hbox {if}\; q\ne \infty \end{aligned}$$

  and

  $$\begin{aligned} \Vert U\Vert _{B^{s\infty }_p(\mathscr {H})} := \sup _{0<r<1} (1-r)^{\beta -s}\Vert J^{-\beta } U(r\cdot )\Vert _{L^p({{\mathbb S}^{d-1}})} <\infty . \end{aligned}$$

• (b) The harmonic Triebel–Lizorkin space $F^{sq}_p(\mathscr {H})$, $0<p<\infty$, is defined as the set of all $U\in \mathscr {H}(B^d)$ such that

  

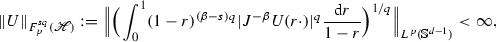
  if $q\ne \infty$, and

  $$\begin{aligned} \Vert U\Vert _{F^{s\infty }_p(\mathscr {H})} := \Big \Vert \sup _{0<r<1} (1-r)^{\beta -s}|J^{-\beta } U(r\cdot )|\Big \Vert _{L^p({{\mathbb S}^{d-1}})} <\infty . \end{aligned}$$

As will be shown, choosing an arbitrary $\beta >s$ above will result in equivalent quasi-norms for $B^{sq}_p(\mathscr {H})$ and $F^{sq}_p(\mathscr {H})$, respectively. The choice $\beta =s+1$ suppresses the dependence of the quasi-norm on $\beta$ and simplifies the notation.

Some other basic properties of the harmonic Besov and Triebel–Lizorkin spaces $B^{sq}_p(\mathscr {H})$ and $F^{sq}_p(\mathscr {H})$ are given in Proposition 4.4 below.

We next show that the harmonic functions U from $B^{sq}_p(\mathscr {H})$ and $F^{sq}_p(\mathscr {H})$ have coefficients of at most polynomial growth (see (3.7)).

Proposition 4.2

Let $s\in {\mathbb R}$, $0<p, q \le \infty$. Then there exist constants $\gamma , c>0$ such that for any $U\in B^{sq}_p(\mathscr {H})$

$$\begin{aligned} |b_{k\nu }(U)| \le c(k+1)^\gamma \Vert U\Vert _{B^{sq}_p}, \quad \nu =1, \dots , N(k, d), \;\; k=0, 1, \dots . \end{aligned}$$

(4.2)

The same estimate holds for any $U\in F^{sq}_p(\mathscr {H})$, $0<p<\infty$, with $\Vert U\Vert _{F^{sq}_p}$ in place of $\Vert U\Vert _{B^{sq}_p}$ on the right.

This proposition will follow from the next lemma that will play an important role in the sequel.

Lemma 4.3

Let $U\in \mathscr {H}(B^d)$ and formally denote

$$\begin{aligned} f:= \sum _{k\ge 0}\sum _{\nu =1}^{N(k, d)} b_{k\nu }(U) Y_{k\nu }, \end{aligned}$$

(4.3)

which simply means that $b_{k\nu }(f):=b_{k\nu }(U)$. Also, let the function $\varphi \in C^\infty ({\mathbb R}_+)$ and ${\text {supp}}\varphi \subset [1/2, 2]$. Write

$$\begin{aligned} \Phi _0*f := Z_0*f,\quad \Phi _j*f := \sum _{k=0}^{2^j}\varphi \Big (\frac{k}{2^{j-1}}\Big )Z_k*f~~\hbox {for}~~j\ge 1, \end{aligned}$$

(4.4)

where $Z_k*f:= \sum _{\nu =1}^{N(k, d)} b_{k\nu }(U) Y_{k\nu }$ and set

$$\begin{aligned} I_j:=[1-2^{-j}, 1-2^{-j-1}], \quad j\ge 0. \end{aligned}$$

(4.5)

Then for any $\beta \in {\mathbb R}$, $0<t<1$, and $j\ge 0$ we have

$$\begin{aligned} |\Phi _j*f(x)| \le c 2^{-j\beta }\Big (\mathcal {M}_1\Big (\int _{I_j} \big [\mathcal {M}_t(J^{-\beta } U(r\cdot ))(\cdot )\big ]^t \frac{\mathrm{d}r}{1-r}\Big )(x)\Big )^{1/t},\; \forall x\in {{\mathbb S}^{d-1}},\nonumber \\ \end{aligned}$$

(4.6)

where $\mathcal {M}_1$ and $\mathcal {M}_t$ are two versions of the maximal operator defined in (2.12) and $c>0$ is a constant depending only on $\varphi , d, \beta , t$. Moreover,

$$\begin{aligned} \Vert \Phi _j*f\Vert _p \le c2^{-j\beta }\Big \Vert \Big (\int _{I_j} |J^{-\beta } U(r\cdot )|^{t} \frac{\mathrm{d}r}{1-r}\Big )^{1/t}\Big \Vert _p \quad \text{ if }~~ t<p<\infty , \end{aligned}$$

(4.7)

$$\begin{aligned} \Vert \Phi _j*f\Vert _p \le c2^{-j\beta }\Big (\int _{I_j}\Vert J^{-\beta } U(r\cdot )\Vert _p^t \frac{\mathrm{d}r}{1-r}\Big )^{1/t} \quad \text{ if }~~ t<p\le \infty , \end{aligned}$$

(4.8)

with constants c depending only on $p, \varphi , d, \beta , t$.

Proof

Observe first that $\Phi _j*f$ and $Z_k*f$ are well defined on ${{\mathbb S}^{d-1}}$ because their definitions involve finite linear combinations of spherical harmonics.

Let first $j\ge 1$. From (4.4) we have for any $0<r<1$ and $\beta \in {\mathbb R}$

$$\begin{aligned} \Phi _j*f = \sum _{k\ge 0} \Big [\varphi \Big (\frac{k}{2^{j-1}}\Big )r^{-k}(k+1)^{-\beta }\Big ] r^{k}(k+1)^{\beta }Z_k*f. \end{aligned}$$

(4.9)

Denote

$$\begin{aligned} Q_{jr}(x\cdot y) := \sum _{k\ge 0} \varphi \Big (\frac{k}{2^{j-1}}\Big )r^{-k}(k+1)^{-\beta }Z_k(x\cdot y), \quad j\ge 1. \end{aligned}$$

(4.10)

Set $N:=2^{j-1}$ and consider the function $\lambda (u):= N^{-\beta }\varphi (u) r^{-Nu}(u+1/N)^{-\beta }$. Clearly, $Q_{jr}(x\cdot y) := \sum _{k\ge 0} \lambda (k/N)Z_k(x\cdot y)$ and ${\text {supp}}\lambda \subset [1/2, 2]$. It is easy to see that

$$\begin{aligned} \Vert \lambda ^{(m)}\Vert _\infty \le c r^{-3N}N^{-\beta } \quad \hbox {for} \;\; m\ge 0, \quad c=c(m,\varphi , \beta ). \end{aligned}$$

We now invoke Theorem 2.2 to conclude that for any $M>0$

$$\begin{aligned} |Q_{jr}(x\cdot y)| \le c\frac{2^{j(d-1)}r^{-2^{j+1}}2^{-j\beta }}{\big (1+2^j\rho (x, y)\big )^M}, \quad x, y\in {{\mathbb S}^{d-1}},\quad c=c(M, \varphi , \beta , d).\qquad \quad \end{aligned}$$

(4.11)

From (4.1) and (4.4) it follows that $J^{-\beta } U(r\xi ) = \sum _{k\ge 0}r^k (k+1)^\beta Z_k*f(\xi )$ and using (4.9) and (4.10) we get

$$\begin{aligned} \Phi _j*f = Q_{jr}*J^{-\beta } U(r\cdot ),\quad \forall r\in (0,1). \end{aligned}$$

(4.12)

Let $\mathcal {Y}_j$ be a maximal $\delta$-net on ${{\mathbb S}^{d-1}}$ with $\delta =2^{-j}$, and assume that $\{A_\xi \}_{\xi \in \mathcal {Y}_j}$ is a companion disjoint partition of ${{\mathbb S}^{d-1}}$ consisting of measurable sets such that $G(\xi , 2^{-j-1})\subset A_\xi \subset G(\xi , 2^{-j})$, $\xi \in \mathcal {Y}_j$ (see (2.3)).

Let $0<t<1$ and set $r_j:=1-3\cdot 2^{-j-2}$. Then

$$\begin{aligned} I_j:=\big [1-2^{-j}, 1-2^{-j-1}\big ] = \big [r_j-2^{-j-2}, r_j+2^{-j-2}\big ]. \end{aligned}$$

By (4.12) with $r=r_j$ and the fact that $0<t<1$ it follows that

$$\begin{aligned} |\Phi _j*f(x)|^t&= \Big |\int _{{\mathbb S}^{d-1}}Q_{jr_j}(x\cdot y)J^{-\beta } U(r_jy) \mathrm{d}\sigma (y)\Big |^t\\&\le \frac{c}{2^{j(d-1)t}}\sum _{\xi \in \mathcal {Y}_j} \sup _{y\in A_\xi }|Q_{jr_j}(x\cdot y)|^t \sup _{y\in A_\xi }|J^{-\beta } U(r_jy)|^t.\nonumber \end{aligned}$$

(4.13)

Applying Lemma 3.1 with $B=B(y,\sin 2^{-j-2})\subset I_j\times G(y,2^{-j-2})$ to the harmonic on $B^d$ function $J^{-\beta } U$ we get

$$\begin{aligned} |J^{-\beta } U(r_jy)|^t \le c2^{jd}\int _{I_j}\int _{G(y, 2^{-j-2})}|J^{-\beta } U(r\eta )|^t \mathrm{d}\sigma (\eta ) \mathrm{d}r, \quad \forall y\in A_\xi , \; \xi \in \mathcal {Y}_j.\nonumber \\ \end{aligned}$$

(4.14)

Therefore, for all $\vartheta \in A_\xi$ and $y\in A_\xi$

$$\begin{aligned} |J^{-\beta } U(r_jy)|^t&\le c\int _{I_j} \frac{1}{|G(\vartheta , 2^{-j+1})|} \int _{G(\vartheta , 2^{-j+1})}|J^{-\beta } U(r\eta )|^t \mathrm{d}\sigma (\eta ) \frac{\mathrm{d}r}{1-r} \nonumber \\&\le c\int _{I_j} \big [\mathcal {M}_t(J^{-\beta } U(r\cdot ))(\vartheta )\big ]^t \frac{\mathrm{d}r}{1-r}, \end{aligned}$$

(4.15)

where $\mathcal {M}_t$ is the maximal operator defined in (2.12). From (4.13), (4.11) with $r=r_j$, $r_j^{-2^{j+1}} \sim 1$, and (4.15) we infer

$$\begin{aligned} |\Phi _j&*f(x)|^t\nonumber \\&\le c\sum _{\xi \in \mathcal {Y}_j} \frac{2^{-j\beta t}}{(1+2^j\rho (x, \xi ))^{Mt}} \frac{1}{|A_\xi |} \int _{A_\xi }\int _{I_j} \big [\mathcal {M}_t(J^{-\beta } U(r\cdot ))(\vartheta )\big ]^t \frac{\mathrm{d}r}{1-r} \mathrm{d}\sigma (\vartheta ) \nonumber \\&\le c 2^{-j\beta t}2^{j(d-1)}\int _{{\mathbb S}^{d-1}}\frac{\int _{I_j} \big [\mathcal {M}_t(J^{-\beta } U(r\cdot ))(\vartheta )\big ]^t \frac{\mathrm{d}r}{1-r}}{(1+2^j\rho (x, \vartheta ))^{Mt}} \mathrm{d}\sigma (\vartheta ). \end{aligned}$$

(4.16)

Recall that estimate (4.11) hold for any $M>0$. We choose M so that $Mt\ge d$. Now, we apply Lemma 2.4 to (4.16) to obtain (4.6) in the case $j\ge 1$.

The case $j=0$ is simpler. Indeed, using Lemma 3.1 and bounding the Jacobian $r^{d-1}$ of the spherical change of variables from above by 1 we get

$$\begin{aligned} |\Phi _0*f(x)|^t&=|U(0)|^t=|J^{-\beta } U(0)|^t \le \frac{c}{|B(0, 2^{-1})|}\int _{B(0, 2^{-1})}|J^{-\beta } U(y)|^t \mathrm{d}y\\&\le c\int _0^{1/2} \frac{1}{|G(\vartheta , \pi )|} \int _{G(\vartheta , \pi )}|J^{-\beta } U(r\eta )|^t \mathrm{d}\sigma (\eta ) \frac{\mathrm{d}r}{1-r}\\&\le c\int _{I_0} \big [\mathcal {M}_t(J^{-\beta } U(r\cdot ))(\vartheta )\big ]^t \frac{\mathrm{d}r}{1-r} \end{aligned}$$

for all $\vartheta \in {{\mathbb S}^{d-1}}$. From the fact that the above inequalities are valid for all $\vartheta \in {{\mathbb S}^{d-1}}$ it follows that (4.6) holds in the case $j=0$.

In order to prove (4.7) we choose $t^\star \in (0,t)$ and then apply (4.6) with $t^\star$ in the place of t, the maximal inequality (2.13) for a single function with 1 and $p/t^\star$ in the place of t and p and Hölder’s inequality ($t/t^\star >1$) to obtain

$$\begin{aligned} \Vert \Phi _j*f\Vert _p&\le c2^{-j\beta }\Big \Vert \Big [\mathcal {M}_1\Big (\int _{I_j} \big [\mathcal {M}_{t^\star }(J^{-\beta } U(r\cdot ))(\cdot )\big ]^{t^\star } \frac{\mathrm{d}r}{1-r}\Big )(\cdot )\Big ]^{1/t^\star } \Big \Vert _p\nonumber \\&\le c2^{-j\beta }\Big \Vert \Big (\int _{I_j} \big [\mathcal {M}_{t^\star }(J^{-\beta } U(r\cdot ))(\cdot )\big ]^{t^\star } \frac{\mathrm{d}r}{1-r}\Big )^{1/t^\star } \Big \Vert _p \\&\le c2^{-j\beta }\Big \Vert \Big (\int _{I_j} \big [\mathcal {M}_{t^\star }(J^{-\beta } U(r\cdot ))(\cdot )\big ]^{t} \frac{\mathrm{d}r}{1-r}\Big )^{1/t} \Big \Vert _p.\nonumber \end{aligned}$$

(4.17)

Now applying the maximal inequality (2.14) with $t^\star$ and t in the place of t and q we obtain (4.7).

In turn (4.7) implies (4.8) for $p<\infty$ by applying the Minkowski inequality ($t<p$). Finally, (4.8) for $p=\infty$ follows immediately from (4.6) and the obvious property of the maximal operator $\mathcal {M}_t g (x)\le \Vert g\Vert _\infty$.$\square$

Proof of Proposition 4.2

(i) Let $U\in F^{sq}_p(\mathscr {H})$ and denote by $\{b_{k\nu }(U)\}$ the coefficients of U, defined in (3.3). Let the function $\varphi \in C^\infty ({\mathbb R}_+)$ be such that ${\text {supp}}\varphi \subset [1/2, 2]$ and $\varphi (u)=1$ for $u\in [2^{-1/2}, 2^{1/2}]$. Just as in (4.4) write

$$\begin{aligned} \Phi _0*f := Z_0*f,\quad \Phi _j*f := \sum _{k=0}^{2^j}\varphi \Big (\frac{k}{2^{j-1}}\Big )Z_k*f~~\hbox {for}~~j\ge 1, \end{aligned}$$

(4.18)

where $Z_k*f:= \sum _{\nu =1}^{N(k, d)} b_{k\nu }(U) Y_{k\nu }$.

Let $\beta >s$ and $0<t<\min \{1, p, q\}$. With these notations we use Lemma 4.3 to conclude that (4.7) is valid. Applying Hölder’s inequality ($q/t>1$) to (4.7) leads us to

$$\begin{aligned} \Vert \Phi _j*f\Vert _p&\le c2^{-j\beta }\Big \Vert \Big (\int _{I_j} |J^{-\beta } U(r\cdot )|^q \frac{\mathrm{d}r}{1-r}\Big )^{1/q}\Big \Vert _p \nonumber \\&\le c2^{-js}\Big \Vert \Big (\int _{I_j}(1-r)^{(\beta -s)q} |J^{-\beta } U(r\cdot )|^q \frac{\mathrm{d}r}{1-r}\Big )^{1/q}\Big \Vert _p \nonumber \\&\le c2^{-js}\Vert U\Vert _{F^{sq}_p}. \end{aligned}$$

(4.19)

Here we used that $1-r\sim 2^{-j}$ whenever $r\in I_j$.

Using Lemma 2.5 and (4.19) we obtain, for each $j\ge 1$ and $0<q\le \infty$,

$$\begin{aligned} \Vert \Phi _j*f\Vert _2 \le c2^{j(d-1)|1/p-1/2|}\Vert \Phi _j*f\Vert _p \le c2^{j[(d-1)|1/p-1/2|-s]}\Vert U\Vert _{F^{sq}_p} \end{aligned}$$

and

$$\begin{aligned} \Vert \Phi _j*f\Vert _2^2 =\sum _{k=0}^{2^j}\varphi \Big (\frac{k}{2^{j-1}}\Big )^2\sum _{\nu =1}^{N(k, d)} |b_{k\nu }(U)|^2 \ge \sum _{2^{j-3/2}\le k\le 2^{j-1/2}}\sum _{\nu =1}^{N(k, d)} |b_{k\nu }(U)|^2. \end{aligned}$$

The above and the fact that ${\mathbb N}\subset \cup _{j\ge 1}[2^{j-3/2}, 2^{j-1/2}]$ imply (4.2) for $k\ge 1$ with $\Vert U\Vert _{B^{sq}_p(\mathscr {H})}$ replaced by $\Vert U\Vert _{F^{sq}_p(\mathscr {H})}$. Also (4.2) for $k=0$ follows immediately from (4.19) with $j=0$. This proves Proposition 4.2 for Triebel–Lizorkin spaces.

(ii) We next prove (4.2) in the case when $U\in B^{sq}_p$. This proof will follow in the footsteps of the above proof. We shall borrow from above. Denote by $\{b_{k\nu }(U)\}$ the coefficients of U, defined in (3.3). We define $\Phi _j*f$ just as in (4.18).

Let $\beta >s$ and $0<t<\min \{1, p, q\}$. With these notations we use Lemma 4.3 to conclude that (4.8) is valid. Applying Hölder’s inequality ($q/t>1$) to (4.8) leads us to

$$\begin{aligned} \Vert \Phi _j*f\Vert _p&\le c2^{-j\beta }\Big (\int _{I_j} \Vert J^{-\beta } U(r\cdot )\Vert _p^q \frac{\mathrm{d}r}{1-r}\Big )^{1/q} \\&\le c2^{-js}\Big (\int _{I_j} (1-r)^{(\beta -s)q}\Vert J^{-\beta } U(r\cdot )\Vert _p^q \frac{\mathrm{d}r}{1-r}\Big )^{1/q} \le c2^{-js}\Vert U\Vert _{B^{sq}_p}. \end{aligned}$$

Here we used that $1-r\sim 2^{-j}$ whenever $r\in I_j$.

Further, we proceed just as in the proof of (4.2) in part (i).$\square$

In the next proposition we collect some basic properties of the harmonic Besov and Triebel–Lizorkin spaces.

Proposition 4.4

• (a) The harmonic Besov and Triebel–Lizorkin spaces $B^{sq}_p(\mathscr {H})$ and $F^{sq}_p(\mathscr {H})$ introduced by Definition 4.1 are independent of the selection of the parameter $\beta >s$.

• (b) The harmonic Besov and Triebel–Lizorkin spaces $B^{sq}_p(\mathscr {H})$ and $F^{sq}_p(\mathscr {H})$ are continuously embedded into $\mathscr {H}(B^d)$, that is, for any admissible parameters s, p, q and any compact $K\subset B^d$ there exists a constant $c>0$ such that

  $$\begin{aligned} \Vert U\Vert _{L^\infty (K)} \le c\Vert U\Vert _{B^{sq}_p}, \quad \forall U\in B^{sq}_p(\mathscr {H}) \end{aligned}$$

  (4.20)

and similarly for $U\in F^{sq}_p(\mathscr {H})$.

• (c) The spaces $B^{sq}_p(\mathscr {H})$ and $F^{sq}_p(\mathscr {H})$ are complete and hence they are quasi-Banach spaces (Banach spaces if $p, q\ge 1$ ).

Proof

Part (a) will follow from the identification of $B^{sq}_p(\mathscr {H})$ and $F^{sq}_p(\mathscr {H})$ with Besov and Triebel–Lizorkin spaces of distributions on ${{\mathbb S}^{d-1}}$, see Remark 5.3. Part (b) follows readily by Proposition 4.2. The completeness of the harmonic Besov and Triebel–Lizorkin spaces $B^{sq}_p(\mathscr {H})$ and $F^{sq}_p(\mathscr {H})$ follows by (b) and a standard argument using Fatou’s lemma. It also follows by the identification of $B^{sq}_p(\mathscr {H})$ and $F^{sq}_p(\mathscr {H})$ with Besov and Triebel–Lizorkin spaces on ${{\mathbb S}^{d-1}}$ and the completeness of the latter spaces.

$\square$

4.2 Besov and Triebel–Lizorkin Spaces on $\varvec{{{\mathbb S}^{d-1}}}$

To define Besov and Triebel–Lizorkin spaces on ${{\mathbb S}^{d-1}}$ we employ functions of the form (3.16).

Definition 4.5

Let $s\in {\mathbb R}$, $0<q\le \infty$ and $\varphi$ satisfy the conditions: $\varphi \in C^\infty ({\mathbb R}_+)$, ${\text {supp}}\varphi \subset [1/2, 2]$, and $|\varphi (u)|\ge c>0$ for $u\in [3/5, 5/3]$. For a distribution $f\in \mathcal {S}'$ set

$$\begin{aligned} \Phi _0*f = Z_0*f,\quad \Phi _j*f = \sum _{k\ge 0}\varphi \Big (\frac{k}{2^{j-1}}\Big )Z_k*f, ~ j\ge 1, \end{aligned}$$

(4.21)

where $Z_k*f$ is defined in (3.11).

• (a) The Besov space $\mathcal {B}^{sq}_p:=\mathcal {B}^{sq}_p({{\mathbb S}^{d-1}})$, $0<p\le \infty$, is defined as the set of all distributions $f\in \mathcal {S}'$ such that

  $$\begin{aligned} \Vert f\Vert _{\mathcal {B}^{s q}_p} := \Big (\sum _{j=0}^\infty \Big (2^{sj}\Vert \Phi _j*f\Vert _{L^p({{\mathbb S}^{d-1}})}\Big )^q\Big )^{1/q} < \infty , \end{aligned}$$

  (4.22)

  where the $\ell ^q$-norm is replaced by the sup-norm if $q=\infty$.

• (b) The Triebel–Lizorkin space $\mathcal {F}^{sq}_p:=\mathcal {F}^{sq}_p({{\mathbb S}^{d-1}})$, $0<p<\infty$, is defined as the set of all distributions $f\in \mathcal {S}'$ such that

$$\begin{aligned} \Vert f\Vert _{\mathcal {F}^{s q}_p} := \Big \Vert \Big (\sum _{j=0}^\infty \big (2^{sj}|\Phi _j*f(\cdot )|\big )^q\Big )^{1/q}\Big \Vert _{L^p({{\mathbb S}^{d-1}})} < \infty , \end{aligned}$$

(4.23)

where the $\ell ^q$-norm is replaced by the sup-norm if $q=\infty$.

Several remarks are in order:

• (a) The definitions of the Besov and Triebel–Lizorkin spaces above are independent of the particular selection of the function $\varphi$ with the required properties. Different $\varphi$’s produce equivalent quasi-norms and one may impose additional conditions on $\varphi$ if necessary.

• (b) The class $\mathcal {S}$ is continuously embedded in each of the spaces $\mathcal {B}^{sq}_p$ and $\mathcal {F}^{sq}_p$, that is, there exist constants $m\ge 0$ and $c>0$ depending only on s, p, q such that

  $$\begin{aligned} \Vert \phi \Vert _{\mathcal {B}^{sq}_p} \le cP_m(\phi ), \quad \forall \phi \in \mathcal {S}, \end{aligned}$$

  (4.24)

  and the same inequality holds with $\mathcal {B}^{sq}_p$ replaced by $\mathcal {F}^{sq}_p$.

• (c) The spaces $\mathcal {B}^{sq}_p$ and $\mathcal {F}^{sq}_p$ are continuously embedded in $\mathcal {S}'$, which means that for any $s\in {\mathbb R}$ and $0<p, q\le \infty$ there exist constants $c>0$ and $m\in {\mathbb N}_0$ such that

  $$\begin{aligned} |\langle f, \phi \rangle | \le c\Vert f\Vert _{\mathcal {B}^{sq}_p}P_m(\phi ), \quad \forall f\in \mathcal {B}^{sq}_p, \;\; \forall \phi \in \mathcal {S}, \end{aligned}$$

  (4.25)

  and similarly for the Triebel–Lizorkin spaces $\mathcal {F}^{sq}_p$.

• (d) The above readily implies that $\mathcal {B}^{sq}_p$ and $\mathcal {F}^{sq}_p$ are complete and hence they are quasi-Banach spaces (Banach spaces if $p, q\ge 1$).

For details and proofs, see [17].

5 Identification of harmonic Besov and Triebel–Lizorkin spaces

We now come to the main assertions in this article.

Theorem 5.1

Let $s\in {\mathbb R}$, $0<p < \infty$, $0<q\le \infty$. A harmonic function $U\in F^{s q}_p(\mathscr {H})$ if and only if its boundary value distribution $f=f_U$ defined by (3.18) belongs to $\mathcal {F}^{sq}_p({{\mathbb S}^{d-1}})$, moreover $\Vert U\Vert _{F^{s q}_p} \sim \Vert f\Vert _{\mathcal {F}^{s q}_p}$.

Theorem 5.2

Let $s\in {\mathbb R}$, $0<p, q\le \infty$. A harmonic function $U\in B^{s q}_p(\mathscr {H})$ if and only if its boundary value distribution $f=f_U$ belongs to $\mathcal {B}^{sq}_p({{\mathbb S}^{d-1}})$, moreover $\Vert U\Vert _{B^{s q}_p} \sim \Vert f\Vert _{\mathcal {B}^{s q}_p}$.

We start with the proof of Theorem 5.1, which is somewhat more involved than the proof of Theorem 5.2.

5.1 Proof of Theorem 5.1

(i) We first show that if $f=f_U\in \mathcal {F}^{sq}_p({{\mathbb S}^{d-1}})$ is the boundary distribution of a harmonic function $U\in \mathscr {H}(B^d)$ with $f_U$ defined in (3.18), then $U\in F^{sq}_p(\mathscr {H})$ and $\Vert U\Vert _{F^{sq}_p} \le c\Vert f\Vert _{\mathcal {F}^{sq}_q}$.

Let $\varphi \in C^\infty ({\mathbb R}_+)$ be such that ${\text {supp}}\varphi \subset [1/2, 2]$ and $\varphi$ satisfy (3.15). Define the kernels $\Phi _j$, $j=0, 1, \dots$, just as in (3.16). Also, choose $\tilde{\varphi }\in C^\infty ({\mathbb R}_+)$ so that ${\text {supp}}\tilde{\varphi }\subset [1/4, 4]$ and $\tilde{\varphi }(u)=1$ for $u\in [1/2, 2]$. Set

$$\begin{aligned} \tilde{Q}_{jr}(x\cdot y) := \sum _{k\ge 0}\tilde{\varphi }\Big (\frac{k}{2^{j-1}}\Big )r^k(k+1)^\beta Z_k(x\cdot y), \quad j\ge 1,\; 0<r<1. \end{aligned}$$

(5.1)

Denote briefly $N:=2^{j-1}$ and let $g(u):= N^\beta \tilde{\varphi }(u)r^{Nu}(u+1/N)^\beta$. Clearly, we have $\tilde{Q}_{jr}(x\cdot y) = \sum _{k\ge 0}g(k/N)Z_k(x\cdot y)$ and ${\text {supp}}g\subset [1/4, 4]$. It is readily seen that

$$\begin{aligned} \Vert g^{(m)}\Vert _\infty \le cr^{N/8}N^\beta \quad \hbox {for}~m\ge 0,\quad c=c(m, \tilde{\varphi }, \beta ). \end{aligned}$$

Then applying Theorem 2.2 we conclude that for any $M>0$

$$\begin{aligned} |\tilde{Q}_{jr}(x\cdot y)| \le c\frac{2^{j(d-1)}r^{2^{j-4}}2^{j\beta }}{\big (1+2^j\rho (x, y)\big )^M}, \quad \forall x, y\in {{\mathbb S}^{d-1}},\quad c=c(M, \tilde{\varphi }, \beta , d).\qquad \end{aligned}$$

(5.2)

From (3.15) and the fact that $\tilde{\varphi }(u)=1$ for $u\in {\text {supp}}\varphi$ we get for all $\xi \in {{\mathbb S}^{d-1}}$

$$\begin{aligned} J^{-\beta } U(r\xi )&= \sum _{k\ge 0}r^k (k+1)^\beta Z_k*f(\xi ) \nonumber \\&= Z_0*f(\xi ) +\sum _{j\ge 1} \sum _{k\ge 0} \tilde{\varphi }\Big (\frac{k}{2^{j-1}}\Big )r^k(k+1)^\beta \varphi \Big (\frac{k}{2^{j-1}}\Big )Z_k*f(\xi )\nonumber \\&= Z_0*f(\xi ) +\sum _{j\ge 1} \tilde{Q}_{jr}*\Phi _j*f(\xi ). \end{aligned}$$

(5.3)

Choose $0<t<\min \{p, q\}$. Clearly $\Phi _j*f\in \Pi _{2^{j+1}}$. Then by (5.2) with $M= (d-1)/t+ d$ and Lemma 2.3 it follows that

$$\begin{aligned} |\tilde{Q}_{jr}*\Phi _j&*f(x)|\nonumber \\&\le \! c r^{2^{j-4}}2^{j\beta } \int _{{\mathbb S}^{d-1}}\frac{2^{j(d-1)}|\Phi _j*f(y)|}{\big (1+2^j\rho (x, y)\big )^{(d-1)/t+d}}\mathrm{d}\sigma (y)\nonumber \\&\le \! c r^{2^{j-4}}2^{j\beta }\!\sup _{y\in {{\mathbb S}^{d-1}}}\frac{|\Phi _j*f(y)|}{\big (1+2^{j+1}\rho (x, y)\big )^{\frac{d-1}{t}}} \int _{{\mathbb S}^{d-1}}\frac{2^{j(d-1)}}{\big (1+2^j\rho (x, y)\big )^{d}}\mathrm{d}\sigma (y)\\&\le \! c r^{2^{j-4}}2^{j\beta } \mathcal {M}_t(\Phi _j*f)(x).\nonumber \end{aligned}$$

(5.4)

Here for the last inequality we used (2.17). Hence,

$$\begin{aligned} |J^{-\beta } U(r\xi )|\le |Z_0*f(\xi )| +c\sum _{j\ge 1} r^{2^{j-4}}2^{j\beta } \mathcal {M}_t(\Phi _j*f)(\xi ),\quad \forall \xi \in {{\mathbb S}^{d-1}},\nonumber \\ \end{aligned}$$

(5.5)

implying

$$\begin{aligned} \Vert U\Vert _{F^{sq}_p} \le c(\Vert Z_0*f\Vert _p+\mathcal {N})\le c(\Vert f\Vert _{\mathcal {F}^{sq}_p}+\mathcal {N}) \end{aligned}$$

with

$$\begin{aligned} \mathcal {N}:=\Big \Vert \Big (\int _0^1(1-r)^{(\beta -s)q} \Big (\sum _{j\ge 1} r^{2^{j-4}}2^{j\beta } \mathcal {M}_t(\Phi _j*f)(\cdot )\Big )^q \frac{\mathrm{d}r}{1-r}\Big )^{1/q}\Big \Vert _p. \end{aligned}$$

It remains to show that $\mathcal {N}\le c\Vert f\Vert _{\mathcal {F}^{sq}_p}$. Three cases are to be considered here.

Case 1: $0<q\le 1$. We have

$$\begin{aligned} \mathcal {N}&\le c\Big \Vert \Big (\int _0^1(1-r)^{(\beta -s)q} \sum _{j\ge 1} r^{2^{j-4}q}2^{j\beta q} \big [\mathcal {M}_t(\Phi _j*f)(\cdot )\big ]^q \frac{\mathrm{d}r}{1-r}\Big )^{1/q}\Big \Vert _p\\&=c\Big \Vert \Big (\sum _{j\ge 1} 2^{j\beta q} \big [\mathcal {M}_t(\Phi _j*f)(\cdot )\big ]^q \int _0^1(1-r)^{(\beta -s)q-1} r^{2^{j-4}q} \mathrm{d}r\Big )^{1/q}\Big \Vert _p \end{aligned}$$

and applying first inequality (2.19) and then the maximal inequality (2.13) we arrive at

$$\begin{aligned} \mathcal {N}&\le c\Big \Vert \Big (\sum _{j\ge 1} 2^{jsq} \big [\mathcal {M}_t(\Phi _j*f)(\cdot )\big ]^q\Big )^{1/q}\Big \Vert _p\\&\le c\Big \Vert \Big (\sum _{j\ge 1} 2^{jsq} |\Phi _j*f(\cdot )|^q\Big )^{1/q}\Big \Vert _p = c\Vert f\Vert _{\mathcal {F}^{sq}_p}. \end{aligned}$$

Case 2: $1<q<\infty$. We write

$$\begin{aligned}&\Big (\sum _{j\ge 1} r^{2^{j-4}}2^{j\beta } \mathcal {M}_t(\Phi _j*f)(\cdot )\Big )^q\\&\quad =\Big (\sum _{j\ge 1} \Big (r^{2^{j-4}}2^{j(\beta -s)}\Big )^{1-1/q} \Big (r^{2^{j-4}}\Big )^{1/q} 2^{j[s+(\beta -s)/q]} \mathcal {M}_t(\Phi _j*f)(\cdot )\Big )^q \end{aligned}$$

and applying Hölder’s inequality and (2.20) we get

$$\begin{aligned} \Big (\sum _{j\ge 1} r^{2^{j-4}}&2^{j\beta }\mathcal {M}_t(\Phi _j*f)(\cdot )\Big )^q\\&\le \Big (\sum _{j\ge 1} r^{2^{j-4}} 2^{j[s+(\beta -s)/q]q} \big [\mathcal {M}_t(\Phi _j*f)(\cdot )\big ]^q\Big ) \Big (\sum _{j\ge 1} r^{2^{j-4}}2^{j(\beta -s)}\Big )^{q-1}\\&\le c\sum _{j\ge 1} r^{2^{j-4}}(1-r)^{-(\beta -s)(q-1)} 2^{j(sq+\beta -s)} \big [\mathcal {M}_t(\Phi _j*f)(\cdot )\big ]^q. \end{aligned}$$

Therefore, using the above, (2.19), and the maximal inequality (2.13) we obtain

$$\begin{aligned} \mathcal {N}&\le c\Big \Vert \Big (\sum _{j\ge 1} 2^{j(sq+\beta -s)} \big [\mathcal {M}_t(\Phi _j*f)(\cdot )\big ]^q \int _0^1r^{2^{j-4}}(1-r)^{\beta -s-1}\mathrm{d}r\Big )^{1/q}\Big \Vert _p\\&\le c\Big \Vert \Big (\sum _{j\ge 1} 2^{jsq} \big [\mathcal {M}_t(\Phi _j*f)(\cdot )\big ]^q\Big )^{1/q}\Big \Vert _p\\&\le c\Big \Vert \Big (\sum _{j\ge 1} 2^{jsq} |\Phi _j*f(\cdot )|^q\Big )^{1/q}\Big \Vert _p \le c\Vert f\Vert _{\mathcal {F}^{sq}_p}. \end{aligned}$$

Case 3: $q=\infty$. We have

$$\begin{aligned} \mathcal {N}&=\Big \Vert \sup _{0<r<1} (1-r)^{\beta -s}\sum _{j\ge 1} r^{2^{j-4}}2^{j\beta } \mathcal {M}_t(\Phi _j*f)(\cdot )\Big \Vert _p\\&\le \Big \Vert \sup _{j\ge 1}2^{js}\mathcal {M}_t(\Phi _j*f)(\cdot ) \sup _{0<r<1} (1-r)^{\beta -s}\sum _{j\ge 1} r^{2^{j-4}}2^{j(\beta -s)}\Big \Vert _p\\&\le c\Big \Vert \sup _{j\ge 1}2^{js}\mathcal {M}_t(\Phi _j*f)(\cdot )\Big \Vert _p \le c\Big \Vert \sup _{j\ge 1}2^{js} |\Phi _j*f(\cdot )|\Big \Vert _p = c \Vert f\Vert _{\mathcal {F}^{s\infty }_p}. \end{aligned}$$

For the second inequality above we used (2.20) and for the third inequality we used the maximal inequality (2.13). The proof of the first part of the theorem is complete.

(ii) In this part, we show that if $U\in F^{s q}_p(\mathscr {H})$, then the boundary distribution $f\in \mathcal {S}'$ associated to U belongs to $\mathcal {F}^{sq}_p({{\mathbb S}^{d-1}})$ and $\Vert f\Vert _{\mathcal {F}^{sq}_p} \le c \Vert U\Vert _{F^{sq}_p}$. This proof relies on Lemma 4.3.

Following Proposition 3.2 we write

$$\begin{aligned} f:= \sum _{k\ge 0}\sum _{\nu =1}^{N(k, d)} b_{k\nu }(U) Y_{k\nu } = \sum _{k\ge 0} Z_k*f, \quad \hbox {(convergence in}\; \mathcal {S}') \end{aligned}$$

(5.6)

where $Z_k*f$ is defined in (3.11).

Let $\Phi _j$ and $\varphi$ be just as in the definition of Besov and Triebel–Lizorkin spaces on ${{\mathbb S}^{d-1}}$ (Definition 4.5 in Sect. 4.2), that is, $\Phi _j$ is defined by (4.21) with $\varphi \in C^\infty ({\mathbb R}_+)$, $|\varphi (u)|\ge c>0$ for $u\in [3/5, 5/3]$, and ${\text {supp}}\varphi \subset [1/2, 2]$.

Let $\beta >s$ and $0<t<\min \{1, p, q\}$. Lemma 4.3 yields for $j\ge 0$

$$\begin{aligned} |\Phi _j*f(x)| \le c 2^{-j\beta }\Big (\mathcal {M}_1\Big (\int _{I_j} \big [\mathcal {M}_t(J^{-\beta } U(r\cdot ))(\cdot )\big ]^t \frac{\mathrm{d}r}{1-r}\Big )(x)\Big )^{1/t}, \; \forall x\in {{\mathbb S}^{d-1}}.\nonumber \\ \end{aligned}$$

(5.7)

Now, we are prepared to estimate $\Vert f\Vert _{\mathcal {F}^{sq}_p}$. We consider two cases depending on whether $q<\infty$ or $q=\infty$.

Case 1: $q<\infty$. We obtain from (4.23) and (5.7)

$$\begin{aligned} \Vert f\Vert _{\mathcal {F}^{sq}_p}&\le c \Big \Vert \Big (\sum _{j\ge 0} 2^{-j(\beta -s)q}\Big (\mathcal {M}_1\Big (\int _{I_j} \big [\mathcal {M}_t(J^{-\beta } U(r\cdot ))(\cdot )\big ]^t \frac{\mathrm{d}r}{1-r}\Big )(\cdot )\Big )^{q/t}\Big )^{1/q}\Big \Vert _{L^p} \\&\le c \Big \Vert \Big (\sum _{j\ge 0} 2^{-j(\beta -s)q}\Big (\int _{I_j} \big [\mathcal {M}_t(J^{-\beta } U(r\cdot ))(\cdot )\big ]^t \frac{\mathrm{d}r}{1-r}\Big )^{q/t}\Big )^{1/q}\Big \Vert _{L^p}. \end{aligned}$$

Here we applied the maximal inequality (2.13) with 1, q / t and p / t in the place of t, q, p. Now, applying Hölder’s inequality ($q/t>1$) to $\int _{I_j} \cdots$ we get

$$\begin{aligned} \Vert f\Vert _{\mathcal {F}^{sq}_p}&\le c \Big \Vert \Big (\sum _{j\ge 0} 2^{-j(\beta -s)q}\int _{I_j} \big [\mathcal {M}_t(J^{-\beta } U(r\cdot ))(\cdot )\big ]^{q} \frac{\mathrm{d}r}{1-r}\Big )^{1/q}\Big \Vert _{L^p} \\&\le c \Big \Vert \Big (\int _0^1 (1-r)^{(\beta -s)q} \big [\mathcal {M}_t(J^{-\beta } U(r\cdot ))(\cdot )\big ]^{q} \frac{\mathrm{d}r}{1-r}\Big )^{1/q}\Big \Vert _{L^p}, \end{aligned}$$

where we used that $1-r\sim 2^{-j}$ for $r\in I_j$. At this point we apply the maximal inequality (2.14) and obtain

$$\begin{aligned} \Vert f\Vert _{\mathcal {F}^{sq}_p} \le c \Big \Vert \Big (\int _0^1 (1-r)^{(\beta -s)q} |J^{-\beta } U(r\cdot )|^q \frac{\mathrm{d}r}{1-r}\Big )^{1/q}\Big \Vert _{L^p} = c\Vert U\Vert _{F^{sq}_p}. \end{aligned}$$

Case 2: $q=\infty$. Using (5.7) we have

$$\begin{aligned} \Vert f\Vert _{\mathcal {F}^{s\infty }_p}&= \Vert \sup _{j\ge 0}2^{js}|\Phi _j*f(\cdot )|\Vert _p\\&\le c\Big \Vert \sup _{j\ge 0}2^{-j(\beta -s)} \Big [\mathcal {M}_1\Big (\int _{I_j} \big [\mathcal {M}_t(J^{-\beta } U(r\cdot ))(\cdot )\big ]^t \frac{\mathrm{d}r}{1-r}\Big )(\cdot )\Big ]^{1/t}\Big \Vert _p \\&\le c\Big \Vert \Big [\mathcal {M}_1 \Big (\sup _{j\ge 0}2^{-j(\beta -s)t} \int _{I_j} \big [\mathcal {M}_t(J^{-\beta } U(r\cdot ))(\cdot )\big ]^t \frac{\mathrm{d}r}{1-r}\Big )(\cdot )\Big ]^{1/t}\Big \Vert _p. \end{aligned}$$

Since $p/t>1$ we can apply the maximal inequality (2.13) for a single function to obtain

$$\begin{aligned} \Vert f\Vert _{\mathcal {F}^{s\infty }_p} \le c\Big \Vert \sup _{j\ge 0}2^{-j(\beta -s)} \Big (\int _{I_j} \big [\mathcal {M}_t(J^{-\beta } U(r\cdot ))(\cdot )\big ]^t \frac{\mathrm{d}r}{1-r}\Big )^{1/t}\Big \Vert _p. \end{aligned}$$

Applying Hölder’s inequality ($1/t>1$) to $\int _{I_j} \cdots$ we get

$$\begin{aligned} \Vert f\Vert _{\mathcal {F}^{s\infty }_p}&\le c\Big \Vert \sup _{j\ge 0}2^{-j(\beta -s)} \int _{I_j} \mathcal {M}_t(J^{-\beta } U(r\cdot ))(\cdot ) \frac{\mathrm{d}r}{1-r}\Big \Vert _p \\&\le c\Big \Vert \sup _{j\ge 0}2^{-j(\beta -s)} \sup _{r\in I_j} \mathcal {M}_t(J^{-\beta } U(r\cdot ))(\cdot )\Big \Vert _p \\&\le c\Big \Vert \sup _{0<r<1}(1-r)^{\beta -s}\mathcal {M}_t(J^{-\beta } U(r\cdot ))(\cdot )\Big \Vert _p \\&\le c\Big \Vert \mathcal {M}_t\big (\sup _{0<r<1}(1-r)^{\beta -s}|J^{-\beta } U(r\cdot )|\big )(\cdot )\Big \Vert _p. \end{aligned}$$

Applying again the maximal inequality (2.13) for a single function we arrive at

$$\begin{aligned} \Vert f\Vert _{\mathcal {F}^{s\infty }_p} \le c\Big \Vert \sup _{0<r<1}(1-r)^{\beta -s}|J^{-\beta } U(r\cdot )|\Big \Vert _p = c\Vert U\Vert _{F^{s\infty }_p}. \end{aligned}$$

The proof of Theorem 5.1 is complete. $\square$

5.2 Proof of Theorem 5.2

This proof will follow in the footsteps of the one for the Triebel–Lizorkin spaces (Sect. 5.1). We shall adhere to the notation there and only indicated the necessary changes.

(i) We first show that if $f\in \mathcal {B}^{sq}_p({{\mathbb S}^{d-1}})$ is the boundary distribution of a harmonic extension $U\in \mathscr {H}(B^d)$, i.e. $f=f_U$, then $U\in B^{sq}_p(\mathscr {H})$ and $\Vert U\Vert _{B^{sq}_p} \le c\Vert f\Vert _{\mathcal {B}^{sq}_q}$.

Let $\varphi \in C^\infty ({\mathbb R}_+)$ be such that ${\text {supp}}\varphi \subset [1/2, 2]$ and $\varphi$ satisfy (3.15). Define the kernels $\Phi _j$, $j=0, 1, \dots$, as in (3.16). Just as in the case of Triebel–Lizorkin spaces we have the representation

$$\begin{aligned} J^{-\beta } U(r\xi )= Z_0*f(\xi )+\sum _{j\ge 1} \tilde{Q}_{jr}*\Phi _j*f(\xi ),\quad \forall \xi \in {{\mathbb S}^{d-1}}, \end{aligned}$$

with $\tilde{Q}_{jr}$ from (5.1). Then by (5.4)

$$\begin{aligned} |\tilde{Q}_{jr}*\Phi _j*f(\xi )|\le c r^{2^{j-4}}2^{j\beta } \mathcal {M}_t(\Phi _j*f)(\xi ),\quad j\ge 1, \end{aligned}$$

for any $0<t<\min \{p,q\}$. Now, applying the maximal inequality (2.13) we infer for $p<\infty$

$$\begin{aligned} \Vert \tilde{Q}_{jr}*\Phi _j*f\Vert _p \le c r^{2^{j-4}}2^{j\beta }\Vert \Phi _j*f\Vert _p. \end{aligned}$$

For $p=\infty$ the above implication is immediate. Therefore, putting ${p^\star }:=\min \{1, p\}$ we have

$$\begin{aligned} \Vert J^{-\beta } U(r\cdot )\Vert _p^{{p^\star }} \le \Vert Z_0*f\Vert _p^{p^\star }+c \sum _{j\ge 1} r^{2^{j-4}{p^\star }}2^{j\beta {p^\star }} \Vert \Phi _j*f\Vert _p^{p^\star }. \end{aligned}$$

(5.8)

Assuming $q<\infty$, this yields

$$\begin{aligned} \Vert U\Vert _{B^{sq}_p} \le c(\Vert f\Vert _{\mathcal {B}^{sq}_p}+\mathcal {N}), \end{aligned}$$

$$\begin{aligned} \mathcal {N}:=\Big (\int _0^1(1-r)^{(\beta -s)q} \Big (\sum _{j\ge 1} r^{2^{j-4}{p^\star }}2^{j\beta {p^\star }} \Vert \Phi _j*f\Vert _p^{p^\star }\Big )^{q/{p^\star }} \frac{\mathrm{d}r}{1-r}\Big )^{1/q}. \end{aligned}$$

(5.9)

Three cases present themselves here.

Case 1: $0<q\le {p^\star }$. Using that $q/{p^\star }\le 1$ we get

$$\begin{aligned} \mathcal {N}^q&\le c \int _0^1(1-r)^{(\beta -s)q}\sum _{j\ge 1} r^{2^{j-4}q}2^{j\beta q} \Vert \Phi _j*f\Vert _p^q \frac{\mathrm{d}r}{1-r}\\&= c \sum _{j\ge 1} 2^{j\beta q} \Vert \Phi _j*f\Vert _p^q \int _0^1(1-r)^{(\beta -s)q-1}r^{2^{j-4}q}\mathrm{d}r. \end{aligned}$$

We now apply inequality (2.19) to obtain

$$\begin{aligned} \mathcal {N}^q \le c \sum _{j\ge 1} 2^{jsq} \Vert \Phi _j*f\Vert _p^q \le c\Vert f\Vert _{\mathcal {B}^{sq}_p}^q \end{aligned}$$

as desired.

Case 2: ${p^\star }<q<\infty$. Write

$$\begin{aligned}&\left( \sum _{j\ge 1} r^{2^{j-4}{p^\star }}2^{j\beta {p^\star }} \Vert \Phi _j*f\Vert _p^{p^\star }\right) ^{q/{p^\star }}\\&\quad = \left( \sum _{j\ge 1} \big (r^{2^{j-4}{p^\star }}2^{j(\beta -s){p^\star }}\big )^{1-\frac{{p^\star }}{q}} \big (r^{2^{j-4}{p^\star }}\big )^{\frac{{p^\star }}{q}} 2^{j\big [s+(\beta -s)\frac{{p^\star }}{q}\big ]{p^\star }} \Vert \Phi _j*f\Vert _p^{p^\star }\right) ^{q/{p^\star }}. \end{aligned}$$

Applying Hölder’s inequality (using that $q/{p^\star }>1$) we get

$$\begin{aligned}&\left( \sum _{j\ge 1} r^{2^{j-4}{p^\star }}2^{j\beta {p^\star }} \Vert \Phi _j*f\Vert _p^{p^\star }\right) ^{q/{p^\star }}\\&\quad \le \left( \sum _{j\ge 1} r^{2^{j-4}{p^\star }}2^{j\big [s+(\beta -s)\frac{{p^\star }}{q}\big ]q} \Vert \Phi _j*f\Vert _p^q\right) \left( \sum _{j\ge 1} r^{2^{j-4}{p^\star }}2^{j(\beta -s){p^\star }}\right) ^{q/{p^\star }-1}. \end{aligned}$$

Using inequality (2.20) we obtain

$$\begin{aligned} \left( \sum _{j\ge 1} r^{2^{j-4}{p^\star }}2^{j(\beta -s){p^\star }}\right) ^{q/{p^\star }-1} \le c (1-r)^{-(\beta -s)(q-{p^\star })}. \end{aligned}$$

Putting the above two estimates in (5.9) we get

$$\begin{aligned} \mathcal {N}^q&\le c \sum _{j\ge 1} 2^{j[sq+(\beta -s){p^\star }]}\Vert \Phi _j*f\Vert _p^q\\&\qquad \;\;\, \times \int _0^1(1-r)^{(\beta -s)q-1}(1-r)^{-(\beta -s)(q-{p^\star })} r^{2^{j-4}{p^\star }} \mathrm{d}r\\&\le c \sum _{j\ge 1} 2^{j[sq+(\beta -s){p^\star }]}\Vert \Phi _j*f\Vert _p^q \int _0^1(1-r)^{(\beta -s){p^\star }-1} r^{2^{j-4}{p^\star }} \mathrm{d}r. \end{aligned}$$

We apply inequality (2.19) to the above integral to obtain

$$\begin{aligned} \mathcal {N}^q&\le c \sum _{j\ge 1} 2^{j[sq+(\beta -s){p^\star }]} 2^{-j(\beta -s){p^\star }}\Vert \Phi _j*f\Vert _p^q\\&= c \sum _{j\ge 1} 2^{jsq}\Vert \Phi _j*f\Vert _p^q \le c\Vert f\Vert _{\mathcal {B}^{sq}_p}^q \end{aligned}$$

as desired.

Case 3: $q=\infty$. From (5.8) we obtain

$$\begin{aligned} \Vert U&\Vert _{B^{s\infty }_p}^{p^\star }\le \Vert Z_0*f\Vert _p^{p^\star }+c\sup _{0<r<1} (1-r)^{(\beta -s){p^\star }} \sum _{j\ge 1} r^{2^{j-4}{p^\star }}2^{j\beta {p^\star }} \Vert \Phi _j*f\Vert _p^{p^\star }\\&\le \Vert f\Vert _{\mathcal {B}^{s\infty }_p}^{p^\star }+c\left( \sup _{j\ge 1} 2^{sj}\Vert \Phi _j*f\Vert _p\right) ^{p^\star }\!\!\sup _{0<r<1} (1-r)^{(\beta -s){p^\star }}\sum _{j\ge 1} r^{2^{j-4}{p^\star }}2^{j(\beta -s){p^\star }}\\&\le \Vert f\Vert _{\mathcal {B}^{s\infty }_p}^{p^\star }+c\left( \sup _{j\ge 1} 2^{sj}\Vert \Phi _j*f\Vert _p\right) ^{p^\star }= c\Vert f\Vert _{\mathcal {B}^{s\infty }_p}^{p^\star }, \end{aligned}$$

where for the last inequality we used (2.19). This completes the proof of the first part of the theorem.

(ii) We next show that if $U\in B^{s q}_p(\mathscr {H})$, then the boundary distribution $f=f_U\in \mathcal {S}'$ associated to U belongs to $\mathcal {B}^{sq}_p({{\mathbb S}^{d-1}})$ and $\Vert f\Vert _{\mathcal {B}^{sq}_p} \le c \Vert U\Vert _{B^{sq}_p}$.

Let $\Phi _j$, $j=0, 1, \dots$, be just as in the definition of Besov and Triebel–Lizorkin spaces on ${{\mathbb S}^{d-1}}$ (Definition 4.5 in Sect. 4.2). Then inequality (4.8) holds for these $\Phi _j$’s and the function f from the hypothesis. This inequality coupled with the definition of $\Vert f\Vert _{\mathcal {B}^{sq}_p}$ in (4.23) leads to

$$\begin{aligned} \Vert f\Vert _{\mathcal {B}^{sq}_p}&\le c\left( \sum _{j\ge 0} 2^{-j(\beta -s)q}\Big (\int _{I_j} \Vert J^{-\beta } U(r\cdot )\Vert _p^{t} \frac{\mathrm{d}r}{1-r}\Big )^{q/t}\right) ^{1/q} \\&\le c\left( \sum _{j\ge 0} 2^{-j(\beta -s)q}\int _{I_j} \Vert J^{-\beta } U(r\cdot )\Vert _p^q \frac{\mathrm{d}r}{1-r}\right) ^{1/q} \\&\le c\left( \int _0^1 (1-r)^{(\beta -s)q} \Vert J^{-\beta } U(r\cdot )\Vert _p^q \frac{\mathrm{d}r}{1-r}\right) ^{1/q} = c \Vert U\Vert _{B^{sq}_p}. \end{aligned}$$

Here for the second inequality we applied Hölder’s inequality ($q/t>1$) to $\int _{I_j}\cdots$. The proof of Theorem 5.2 is complete. $\square$

Remark 5.3

Theorems 5.1 and 5.2 readily yield that the harmonic Triebel–Lizorkin and Besov space norms introduced in Definition 4.1 are equivalent for different $\beta >s$.

6 Frame Characterization of Harmonic Besov and Triebel–Lizorkin Spaces on $B^d$

Theorems 5.1 and 5.2 allow easily to transfer results on Besov and Triebel–Lizorkin spaces on ${{\mathbb S}^{d-1}}$ to harmonic Besov and Triebel–Lizorkin spaces on $B^d$. Here we record the frame characterization of harmonic Besov and Triebel–Lizorkin spaces on $B^d$ that follows by the respective results on ${{\mathbb S}^{d-1}}$ from [17].

We assume that $\{\Psi _\xi \}_{\xi \in \mathcal {X}}$ are the harmonic needlets and $\{\tilde{\Psi }_\xi \}_{\xi \in \mathcal {X}}$ is its dual frame, defined in (3.26)–(3.27). Recall that $\mathcal {X}:=\cup _{j\ge 0}\mathcal {X}_j$ contains the centers of localization of the needlets on ${{\mathbb S}^{d-1}}$ and $\{A_\xi \}_{\xi \in \mathcal {X}_j}$ ($j\ge 0$) is a disjoint partition of ${{\mathbb S}^{d-1}}$, defined in Sect. 3.3.

Definition 6.1

Let $s \in {\mathbb R}$, $0<p,q \le \infty$. The Besov sequence space ${\mathfrak b}^{s q}_p$ is defined as the set of all sequences of complex numbers $h=\{h_\xi \}_{\xi \in \mathcal {X}}$ such that

$$\begin{aligned} \Vert h\Vert _{{\mathfrak b}^{s q}_p} := \left( \sum _{j=0}^\infty \Big [2^{j(s + (d-1)/2 -(d-1)/p)}\Big (\sum _{\xi \in \mathcal {X}_j} |h_\xi |^p\Big )^{1/p}\Big ]^{q}\right) ^{1/q} <\infty \end{aligned}$$

(6.1)

with the usual modification when $p=\infty$ or $q=\infty$.

We introduce the operators:

Analysis operator $S_{\tilde{\Psi }}: U \mapsto \{<U, \tilde{\Psi }_\xi >\}_{\xi \in \mathcal {X}}$,

Synthesis operator $T_\Psi : \{h_\xi \}_{\xi \in \mathcal {X}} \mapsto \sum _{\xi \in \mathcal {X}}h_\xi \Psi _\xi$.

Theorem 6.2

Let $s \in {\mathbb R}$ and $0<p, q\le \infty$. Then the operators $S_{\tilde{\Psi }}: B_p^{s q} \rightarrow {\mathfrak b}_p^{s q}$ and $T_\Psi : {\mathfrak b}_p^{s q} \rightarrow B_p^{s q}$ are bounded, $T_\Psi \circ S_{\tilde{\Psi }}= \mathrm{Id}$ in $B_p^{s q}$. Consequently, a harmonic function $U \in B_p^{s q}$ if and only if $\{< U, \tilde{\Psi }_\xi >\}\in {\mathfrak b}_p^{s q}$ and

$$\begin{aligned} \Vert U\Vert _{B_p^{s q}} \!\sim \!\Vert \{< U, \tilde{\Psi }_\xi>\}\Vert _{{\mathfrak b}_p^{s q}} \!\sim \!\left( \sum _{j=0}^\infty \left[ 2^{s j}\Big (\sum _{\xi \in \mathcal {X}_j} \Vert < U, \tilde{\Psi }_\xi >\psi _\xi \Vert _{L^p({{\mathbb S}^{d-1}})}^p\Big )^{1/p}\right] ^{q}\right) ^{1/q}, \end{aligned}$$

where $< U, \tilde{\Psi }_\xi>$ is defined in (3.29).

In the following we adhere to the notation from above.

Definition 6.3

Let $s \in {\mathbb R}$, $0<p <\infty$, and $0<q\le \infty$. The Triebel–Lizorkin sequence space ${\mathfrak f}^{s q}_p$ is defined as the set of all sequences of complex numbers $h=\{h_\xi \}_{\xi \in \mathcal {X}}$ such that

$$\begin{aligned} \Vert h\Vert _{{\mathfrak f}^{s q}_p} := \left\| \left( \sum _{\xi \in \mathcal {X}} \Big [|A_\xi |^{-s/(d-1)-1/2} |h_\xi | {\mathbbm {1}}_{A_\xi }(\cdot )\Big ]^q\right) ^{1/q}\right\| _{L^p({{\mathbb S}^{d-1}})} <\infty , \end{aligned}$$

(6.2)

where ${\mathbbm {1}}_{A_\xi }$ stands for the characteristic function of $A_\xi$.

Theorem 6.4

Let $s \in {\mathbb R}$ and $0<p<\infty$, $0<q\le \infty$. Then the operators $S_{\tilde{\Psi }}: F_p^{s q} \rightarrow {\mathfrak f}_p^{s q}$ and $T_\Psi : {\mathfrak f}_p^{s q} \rightarrow F_p^{s q}$ are bounded, $T_\Psi \circ S_{\tilde{\Psi }}= \mathrm{Id}$ in $F_p^{s q}$. Consequently, a harmonic function $U \in F_p^{s q}$ if and only if $\{<U, \tilde{\Psi }_\xi >\}\in {\mathfrak f}_p^{s q}$ and

$$\begin{aligned} \Vert U\Vert _{F_p^{s q}} \sim \Vert \{< U, \tilde{\Psi }_\xi>\}\Vert _{{\mathfrak f}_p^{s q}} \sim \Big \Vert \Big (\sum _{j=0}^\infty 2^{sjq}\sum _{\xi \in \mathcal {X}_j} |<U, \tilde{\Psi }_\xi >\psi _\xi |^q\Big )^{1/q}\Big \Vert _{L^p({{\mathbb S}^{d-1}})}. \end{aligned}$$

Theorems 6.2 and 6.4 follow readily by Theorems 4.5 and 5.5 in [17] and Theorems 5.2 and 5.1 above. We omit the details.

7 Harmonic Hardy Spaces

Here we consider the harmonic Hardy spaces $\mathscr {H}^p(B^d)$ on the ball (usually denoted by $h^p(B^d)$), see e.g. [1, Chapter 6].

Definition 7.1

The space $\mathscr {H}^p :=\mathscr {H}^p(B^d)$, $1\le p\le \infty$, is defined as the set of all harmonic functions $U\in \mathscr {H}(B^d)$ such that

$$\begin{aligned} \Vert U\Vert _{\mathscr {H}^p} := \sup _{0\le r<1} \Vert U(r\cdot )\Vert _{L^p({{\mathbb S}^{d-1}})} <\infty . \end{aligned}$$

(7.1)

Proposition 4.3 in [17] and Theorem 5.1 imply the following identification of harmonic Hardy spaces:

Proposition 7.2

For $1<p<\infty$, we have

$$\begin{aligned} \mathscr {H}^p(B^d)\sim L^p({{\mathbb S}^{d-1}})\sim \mathcal {F}^{02}_p({{\mathbb S}^{d-1}})\sim F^{02}_p(\mathscr {H}) \quad \hbox {with equivalent norms.} \end{aligned}$$

(7.2)

More precisely, there exists a boundedly invertible linear map between any two of the above spaces.

Proof

Let

$$\begin{aligned} \mathcal {P}f(r\xi ):=\int _{{{\mathbb S}^{d-1}}} P(y, r\xi )f(y)\mathrm{d}\sigma (y) \quad \hbox {for} f\in L^p({{\mathbb S}^{d-1}}), 1<p<\infty , \end{aligned}$$

where $P(y, r\xi )$ is the Poisson kernel, defined in (2.6). As is well known (see e.g. [1, Theorem 6.13]) for any $U\in \mathscr {H}^p(B^d)$, $1<p<\infty$, there exists a function $f=f_U\in L^p({{\mathbb S}^{d-1}})$ such that $U=\mathcal {P}f$. As $P(y, r\xi )$ is a summability kernel on ${{\mathbb S}^{d-1}}$, we have $\Vert f(\cdot )-\mathcal {P}f(r\cdot )\Vert _p \rightarrow 0$ as $r\rightarrow 1-$ and $\Vert \mathcal {P}f(r\cdot )\Vert _p \le \Vert f\Vert _p$ for $0\le r <1$. Therefore, $\Vert U\Vert _{\mathscr {H}^p} = \Vert f\Vert _{L^p}$.

On the other hand, from the properties of the Poisson kernel it readily follows that if $f\in L^p({{\mathbb S}^{d-1}})$, $1<p<\infty$, then $\mathcal {P}f\in \mathscr {H}^p(B^d)$ and $f_{\mathcal {P}f} =f$, using the notation from above.

Therefore, $\mathcal {P}: L^p({{\mathbb S}^{d-1}})\rightarrow \mathscr {H}^p(B^d)$, $1<p<\infty$, is a linear isometric isomorphism, leading to the identification $\mathscr {H}^p(B^d)\sim L^p({{\mathbb S}^{d-1}})$ in (7.2).

The identification $L^p({{\mathbb S}^{d-1}})\sim \mathcal {F}^{02}_p({{\mathbb S}^{d-1}})$ is established in [17, Proposition 4.3] and $\mathcal {F}^{02}_p({{\mathbb S}^{d-1}})\sim F^{02}_p(\mathscr {H})$ follows by Theorem 5.1.$\square$

8 Harmonic Besov and Triebel–Lizorkin Spaces on $\mathbb {R}^d\setminus \overline{B^d}$

It is natural to consider the set $\mathscr {H}({\mathbb R}^d\setminus \overline{B^d})$ of all harmonic functions U on ${\mathbb R}^d\setminus \overline{B^d}$ such that $\lim _{|x|\rightarrow \infty }U(x) =0$ if $d>2$ or $\lim _{|x|\rightarrow \infty }U(x) = \mathrm{const.}$ if $d=2$. As is well known the Kelvin transform

$$\begin{aligned} KU(x):= |x|^{2-d}U(x/|x|^2) \end{aligned}$$

maps one-to-one $\mathscr {H}(B^d)$ onto $\mathscr {H}({\mathbb R}^d\setminus \overline{B^d})$ and $\mathscr {H}({\mathbb R}^d\setminus \overline{B^d})$ onto $\mathscr {H}(B^d)$. Consequently, every harmonic function $U\in \mathscr {H}({\mathbb R}^d\setminus \overline{B^d})$ has the representation

$$\begin{aligned} U(x) = \sum _{k=0}^\infty \frac{1}{|x|^{k+d-2}}\sum _{\nu =1}^{N(k, d)} b_{k\nu }(U)Y_{k\nu }\Big (\frac{x}{|x|}\Big ), \quad |x|>1, \end{aligned}$$

where $b_{k\nu }(U):= a^{k+d-2}\int _{{\mathbb S}^{d-1}}U(a\eta )Y_{k\nu }(\eta ) \mathrm{d}\sigma (\eta )$, $a>1$. Above the series converges absolutely and uniformly on every closed subset of ${\mathbb R}^d\setminus \overline{B^d}$.

In this setting the operator $J^\beta$ (see (4.1)) is defined by

$$\begin{aligned} J^\beta U(r\xi ) := \sum _{k=0}^\infty \frac{(k+1)^{-\beta }}{r^{k+d-2}} \sum _{\nu =1}^{N(k, d)} b_{k\nu }(U)Y_{k\nu }(\xi ), \quad r>1, \;\;\xi \in {{\mathbb S}^{d-1}}. \end{aligned}$$

Then the harmonic Besov space $B^{sq}_p(\mathscr {H})$, $s\in {\mathbb R}$, $0<p,q\le \infty$, on ${\mathbb R}^d\setminus \overline{B^d}$ is defined by the quasi-norm ($\beta :=s+1$)

$$\begin{aligned} \Vert U\Vert _{B^{sq}_p(\mathscr {H})} := \Big (\int _1^\infty (1-r^{-1})^{(\beta -s)q}\Vert J^{-\beta } U(r\cdot )\Vert _{L^p({{\mathbb S}^{d-1}})}^q \frac{\mathrm{d}r}{r(r-1)}\Big )^{1/q} \quad \hbox {if}\; q\ne \infty \end{aligned}$$

and by the usual modification of this norm when $q=\infty$.

Similarly, the harmonic Triebel–Lizorkin space $F^{sq}_p(\mathscr {H})$, $s\in {\mathbb R}$, $0<p <\infty$, $0<q\le \infty$, on ${\mathbb R}^d\setminus \overline{B^d}$ is defined by the quasi-norm ($\beta :=s+1$)

$$\begin{aligned} \Vert U\Vert _{F^{sq}_p(\mathscr {H})} := \Big \Vert \Big (\int _1^\infty (1-r^{-1})^{(\beta -s)q}|J^{-\beta } U(r\cdot )|^q \frac{\mathrm{d}r}{r(r-1)}\Big )^{1/q}\Big \Vert _{L^p({{\mathbb S}^{d-1}})} \quad \hbox {if}\; q\ne \infty \end{aligned}$$

and with the obvious modification if $q=\infty$.

It is readily seen that the Kelvin transform is an isometric isomorphism between the harmonic Besov spaces $B^{sq}_p(\mathscr {H})$ on $B^d$ and on ${\mathbb R}^d\setminus \overline{B^d}$ as well as between the harmonic Triebel–Lizorkin spaces $F^{sq}_p(\mathscr {H})$ on $B^d$ and on ${\mathbb R}^d\setminus \overline{B^d}$. Moreover, the Kelvin transform retains unchanged the boundary distributions in both cases. Therefore, the identifications established in Theorems 5.1 and 5.2 above are valid for the respective harmonic Besov and Triebel–Lizorkin spaces on ${\mathbb R}^d\setminus \overline{B^d}$ as well.

One also applies the Kelvin transform to the frames from Sect. 3.4 to construct a pair of dual frames $\{\Psi _\xi \}_{\xi \in \mathcal {X}}$, $\{\tilde{\Psi }_\xi \}_{\xi \in \mathcal {X}}$, where each frame element $\Psi _\xi$ is a harmonic function on ${\mathbb R}^d\setminus \overline{B^d}$. Then frame characterization of the harmonic Besov and Triebel–Lizorkin spaces on ${\mathbb R}^d\setminus \overline{B^d}$ follows easily by Theorems 6.2 and 6.4. We skip the details.

In sum, by virtue of the Kelvin transform one obtains analogues of all results in this article for harmonic functions on ${\mathbb R}^d\setminus \overline{B^d}$.

Appendix

1.1 Proof of Lemma 2.3

Assume $g\in \Pi _N$. Let $\lambda \in C^\infty ({\mathbb R}_+)$ be an admissible function of type (a) in the sense of Definition 2.1. Set

$$\begin{aligned} \Lambda _N(x\cdot y):=\sum _{k\ge 0} \lambda (k/N)Z_k(x\cdot y). \end{aligned}$$

Clearly, $\Lambda _N*g=g$ and by Theorem 2.2 for any $M>0$ there exists a constant $c>0$ such that for $x, y, z\in {{\mathbb S}^{d-1}}$

$$\begin{aligned} |\Lambda _N(x\cdot z) - \Lambda _N(y\cdot z)| \le \frac{c \rho (x, y)N^{d}}{(1+N\rho (x, z))^M}, \quad \hbox {if}\;\; \rho (x, y)\le N^{-1}. \end{aligned}$$

(9.1)

Fix $0<{\varepsilon }<1$. For $y\in {{\mathbb S}^{d-1}}$ we have

$$\begin{aligned} |g(y)| \le \inf _{u\in G(y, {\varepsilon }N^{-1})}|g(u)| + \sup _{u\in G(y, {\varepsilon }N^{-1})}|g(y)-g(u)| \end{aligned}$$

and hence

$$\begin{aligned} H(x)&:= \sup _{y\in {{\mathbb S}^{d-1}}}\frac{|g(y)|}{(1+N\rho (x, y))^{(d-1)/t}} \le \sup _{y\in {{\mathbb S}^{d-1}}}\frac{\inf _{u\in G(y, {\varepsilon }N^{-1})}|g(u)|}{(1+N\rho (x, y))^{(d-1)/t}}\\&\quad + \sup _{y\in {{\mathbb S}^{d-1}}}\frac{\sup _{u\in G(y, {\varepsilon }N^{-1})}|g(y)-g(u)|}{(1+N\rho (x, y))^{(d-1)/t}} =: H_1(x)+H_2(x). \end{aligned}$$

To estimate $H_1(x)$ we first note that

$$\begin{aligned} \inf _{u\in G(y, {\varepsilon }N^{-1})}|g(u)| \le \left( \frac{1}{|G(y, {\varepsilon }N^{-1})|}\int _{G(y, {\varepsilon }N^{-1})}|g(u)|^t \mathrm{d}\sigma (u)\right) ^{1/t}, \end{aligned}$$

implying

$$\begin{aligned} H_1(x)&\le \left( \frac{|G(x, \rho (x, y)+{\varepsilon }N^{-1})|}{|G(y, {\varepsilon }N^{-1})|(1+N\rho (x, y))^{d-1}}\right) ^{1/t}\nonumber \\&\quad \times \left( \frac{1}{|G(x, \rho (x, y)+{\varepsilon }N^{-1})|} \int _{G(y, {\varepsilon }N^{-1})}|g(u)|^t \mathrm{d}\sigma (u) \right) ^{1/t}. \end{aligned}$$

(9.2)

Since $G\big (x, \rho (x, y)+{\varepsilon }N^{-1}\big ) \subset G\big (y, 2\rho (x, y)+{\varepsilon }N^{-1}\big )$, we have

$$\begin{aligned} \big |G\big (x, \rho (x, y)+{\varepsilon }N^{-1}\big )\big |&\le \big |G\big (y, 2\rho (x, y)+{\varepsilon }N^{-1}\big )\big |\\&\le (2/{\varepsilon })^{d-1}(1+ N\rho (x, y))^{d-1}|G(y, {\varepsilon }N^{-1})|. \end{aligned}$$

We use the above in (9.2) and enlarge the region of integration in (9.2) from $B(y, {\varepsilon }N^{-1})$ to $G(x, \rho (x, y)+{\varepsilon }N^{-1})$ to bound $H_1(x)$ by

$$\begin{aligned}&c {\varepsilon }^{(-d+1)/t}\sup _{y\in {{\mathbb S}^{d-1}}} \left( \frac{1}{|G(x, \rho (x, y)+{\varepsilon }N^{-1})|} \int _{G(x, \rho (x, y)+{\varepsilon }N^{-1})} |g(u)|^t \mathrm{d}\sigma (u)\right) ^{1/t}\\&\qquad \le c {\varepsilon }^{(-d+1)/t} \mathcal {M}_tg(x). \end{aligned}$$

Therefore,

$$\begin{aligned} H_1(x) \le c {\varepsilon }^{(-d+1)/t} \mathcal {M}_tg(x). \end{aligned}$$

(9.3)

We now estimate $H_2(x)$. Using (9.1) we obtain

$$\begin{aligned} \sup _{u\in G(y, {\varepsilon }N^{-1})}|g(y)-g(u)|&\le \sup _{u\in G(y, {\varepsilon }N^{-1})} \int _{{\mathbb S}^{d-1}}|\Lambda _N(y\cdot z)- \Lambda _N(u\cdot z)||g(z)| \mathrm{d}\sigma (z)\\&\le c\sup _{u\in G(y, {\varepsilon }N^{-1})} \int _{{\mathbb S}^{d-1}}\frac{N^{d}\rho (y, u) |g(z)|}{(1+N\rho (y, z))^M} \mathrm{d}\sigma (z)\\&\le c{\varepsilon }\int _{{\mathbb S}^{d-1}}\frac{N^{d-1}|g(z)|}{(1+N\rho (y, z))^M} \mathrm{d}\sigma (z) \end{aligned}$$

and choosing $M := (d-1)/t+d$ we get

$$\begin{aligned} H_2(x) \le c {\varepsilon }\sup _{y\in {{\mathbb S}^{d-1}}} \int _{{\mathbb S}^{d-1}}\frac{N^{d-1}|g(z)|}{(1+N\rho (y, x))^{\frac{d-1}{t}}(1+N\rho (y, z))^{\frac{d-1}{t}+d}} \mathrm{d}\sigma (z). \end{aligned}$$

Clearly, $1+N\rho (x, z) \le (1+N\rho (y, x))(1+N\rho (y, z))$ and hence

$$\begin{aligned} H_2(x)&\le c {\varepsilon }\sup _{y\in {{\mathbb S}^{d-1}}} \int _{{\mathbb S}^{d-1}}\frac{N^{d-1}|g(z)|}{(1+N\rho (x, z))^{\frac{d-1}{t}}(1+N\rho (y, z))^{d}} \mathrm{d}\sigma (z)\\&\le c {\varepsilon }\sup _{z\in {{\mathbb S}^{d-1}}}\frac{|g(z)|}{(1+N\rho (x, z))^{\frac{d-1}{t}}} \sup _{y\in {{\mathbb S}^{d-1}}}\int _{{\mathbb S}^{d-1}}\frac{N^{d-1}}{(1+N\rho (y, z))^{d}} \mathrm{d}\sigma (z)\\&\le c' {\varepsilon }H(x), \end{aligned}$$

where for the last inequality we used (2.17). From this and (9.3) we infer

$$\begin{aligned} H(x) \le c {\varepsilon }^{(-d+1)/t} \mathcal {M}_t g(x) + c' {\varepsilon }H(x). \end{aligned}$$

Here the constants c and $c'$ are independent of ${\varepsilon }$. Consequently, choosing ${\varepsilon }$ so that $c' {\varepsilon }= 1/2$ and taking into account that $H(x)<\infty$ we obtain (2.15). $\square$