1 Introduction

In this paper we continue the study of the stability of solving the interior problem of tomography initiated in papers [1, 2, 5, 13]. The starting point of the study is the Gelfand–Graev formula [8], which converts the tomographic data into the finite Hilbert transform (FHT) of an unknown function f along a collection of lines. In what follows we pick one such line, call it the x-axis, and assume that the function to be reconstructed depends on a one-dimensional argument by restricting f to the x-axis.

Let \(I_1\) be the interval where f is supported, and \(I_2\) be the interval where the Hilbert transform of f can be computed using the Gelfand–Graev formula. The equation to be solved can be written in the form \(\left. {\mathcal {H}}_1 f=g\right| _{I_2}\), where \({\mathcal {H}}_1\) is the FHT that integrates over \(I_1\) and gives the result on \(I_2\), i.e. \({\mathcal {H}}_1: L^2(I_1)\rightarrow L^2(I_2)\). In the case of complete data, \(I_1\subset I_2\), and the classical FHT inversion formula reconstructs f in a stable fashion. In the case of interior problem (i.e., when the tomographic data are truncated), \(I_1\) is no longer a subset of \(I_2\), and the inversion problem becomes severely unstable. The approach employed in the papers mentioned above is based on a differential operator L that commutes with \({\mathcal {H}}_1\). The operator was obtained in [11, 12]. By using the commutation property \(L {\mathcal {H}}_1={\mathcal {H}}_1 L\) one can obtain the singular value decomposition of \({\mathcal {H}}_1\). Then the rate of decay of the singular values of \({\mathcal {H}}_1\) is the measure of instability of finding f.

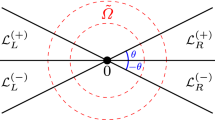
Depending on the type of tomographic data available, different relative positions of the intervals \(I_{1,2}\) are possible. The case when \(I_1\) and \(I_2\) are at a positive distance from each other is investigated in [13]. It is shown there that the spectrum of the operator \({\mathcal {H}}_1^*{\mathcal {H}}_1\) is discrete, and its eigenvalues \(\sigma _n\) go to zero exponentially fast as \(n\rightarrow \infty \). The case when \(I_1\) and \(I_2\) overlap is investigated in [1, 2]. It is shown that the spectrum of \({\mathcal {H}}_1^*{\mathcal {H}}_1\) is still discrete and has two accumulation points: 0 and 1. The eigenvalues of the operator can be enumerated in such a way that \(\sigma _n\rightarrow 0,\, n\rightarrow \infty \), and \(\sigma _n\rightarrow 1,\ n\rightarrow -\infty \), and in each case \(\sigma _n\) approach the limit exponentially fast. The only case that remained unanswered was when \(I_1\) and \(I_2\) touch each other. It was interesting to understand the nature of the spectrum of \({\mathcal {H}}_1\) and estimate how ill-posed it is to find f. Since this is a transitional case, it is clear that something special must be happening here. Thus, our problem can be formulated as follows. Given two adjacent intervals \(I_1=(a_1,0)\) and \(I_2=(0,a_2)\), study the instabily of reconstruction of an \(L^2(a_1,0)\) function f(x) knowing its FHT on \((0,a_2)\).

Fix two points \(a_{1,2}\) such that \(a_1 < 0 < a_2\) and consider two intervals

$$\begin{aligned} I_1:=(a_1,0),\quad I_2:=(0,a_2). \end{aligned}$$
(1.1)

Following [11, 12], define a differential operator

$$\begin{aligned} Lf(x)=(P f')'+Qf,\ P(x)=(x-a_1)x^2(x-a_2),\ Q(x)=2\left( x-\frac{a_1+a_2}{4}\right) ^2.\nonumber \\ \end{aligned}$$
(1.2)

Each of the intervals in (1.1) gives rise to a singular Sturm-Liouville problem (SLP). Using recent developments in the Titchmarsh–Weyl theory obtained in [4, 7], we show in this paper that the SLPs have only continuous spectrum and obtain two isometric transformations \(U_1\), \(U_2\), such that \(U_2{\mathcal {H}}_1 U_1^*\) is a multiplication operator with \(\sigma (\lambda )\), \(\lambda \ge (a_1^2+a_2^2)/8\) (see Theorem 3.1). Here \(\lambda \) is the spectral parameter. Then we show that \(\sigma (\lambda )\rightarrow 0\) as \(\lambda \rightarrow \infty \) exponentially fast (cf. (3.47)). This implies that the problem of finding f is severely ill-posed. We also obtain the leading asymptotic behavior of the kernels involved in the integral operators \(U_1\), \(U_2\) as \(\lambda \rightarrow \infty \). These are the functions \(\phi _{1,2}\) given in (3.19) and (3.36), respectively. When the intervals are symmetric, the operators \(U_1\), \(U_2\) are obtained explicitly in terms of hypergeometric functions (see Theorem 4.3). Obviously, the operator with the kernel \(1/(x-y)\) acting from \(L^2(-a,0)\rightarrow L^2(0,a)\) is naturally related to the operator with the kernel \(1/(x+y)\) acting from \(L^2(0,a)\rightarrow L^2(0,a)\). Thus our results extend those of [14], where, in particular, the diagonalization of the operator \(1/(x+y):\, L^2(0,\infty )\rightarrow L^2(0,\infty )\) is obtained. See also the paper [6], whether the diagonalization of the operator \(1/(x+y):\, L^2(0,\infty )\rightarrow L^2(0,\infty )\) is discussed in the context of inverting the Laplace transform.

The paper is organized as follows. In Sect. 2 we establish that the operator L in (1.2) commutes with the FHT defined on the two intervals (1.1). We also briefly summarize the Titchmarsh–Weyl theory for differential operators with two singular points obtained in [4, 7]. In Sect. 3 we diagonalize the FHT acting from \(L^2(a_1,0)\rightarrow L^2(0,a_2)\). In Sect. 4 we diagonalize the FHT in the case of symmetric intervals. In Sect. 5 we prove that L does not have discrete spectrum, and some auxiliary results are proven in Sects. 6 and 7.

2 Spectrum of the Commuting Differential Operator L

2.1 Commuting Differential Operator

Recall that the operator L is defined by (1.2). By considering Frobenius solutions to the equation \(Lf=\lambda f\) near \(x=a_1,0\), and \(a_2\) we conclude that

  • Near \(x=a_j,j=1,2\), there are two linearly independent solutions \(\phi _j(x)\) and \(\theta _j(x)=\phi _j(x)\ln (x-a_j)+\psi _j(x)\), where \(\phi _j\) and \(\psi _j\) are analytic near \(x=a_j\), and \(\psi _j(a_j)=0\);

  • Near \(x=0\) there are two linearly independent solutions

    $$\begin{aligned} y_{\pm }=x^{-\frac{1}{2}\pm i\mu }\psi _{\pm }(x) \end{aligned}$$
    (2.1)

    where

    $$\begin{aligned} \mu =\sqrt{ \frac{\lambda -\frac{(a_1+a_2)^2}{8}}{-a_1a_2}-\frac{1}{4}}, \end{aligned}$$
    (2.2)

    \(\psi _{\pm }(0)=1\), and \(\psi _{\pm }(z)\) are analytic in the disk \(|z|<\min \{|a_1|,a_2\}\).

Also, we see immediately that L is of the Limit Circle (LC) type at \(x=a_j,j=1,2\), and of the Limit Point (LP) type at \(x=0\). Consequently, no boundary condition is required at \(x=0\). The two SLPs mentioned in the introduction become

$$\begin{aligned} (P(x)f')'+Q(x)f=\lambda f,\ x\in I_j,\ P(x)f'(x)\rightarrow 0 \text { as }x\rightarrow a_j,\ j=1,2. \end{aligned}$$
(2.3)

Next we define two FHTs

$$\begin{aligned} ({\mathcal {H}}_j f)(z):=\frac{1}{\pi }\int _{I_j}\frac{f(x)}{x-z}dx,\ j=1,2. \end{aligned}$$
(2.4)

Lemma 2.1

Pick any \(f\in C^2(I_j)\), \(j=1,2\), such that f(x) is bounded as \(x\rightarrow a_j\), and

$$\begin{aligned} f(x)=o(|x|^{-1}),\ f'(x)=o(|x|^{-2}),\ x\rightarrow 0. \end{aligned}$$
(2.5)

Then one has:

$$\begin{aligned} ({\mathcal {H}}_j L f)(x)=(L{\mathcal {H}}_j f)(x)\text { if } \text {dist}(x,I_j)>0,\ j=1,2. \end{aligned}$$
(2.6)

Remark 2.2

Assumptions (2.5) are inspired by the properties (2.1), (2.2).

The proof of the lemma is based on integration by parts and is completely analogous to that of Proposition 2.1 in [11]. The only difference is that now the boundary terms at \(x=0\) vanish because (1.2) and (2.5) imply

$$\begin{aligned} P(x)f'(x)\rightarrow 0 \text { and } P'(x)f(x)\rightarrow 0\text { as } x\rightarrow 0. \end{aligned}$$
(2.7)

2.2 Basic Facts About Diagonalizing the Operator L

Consider the operator L acting on smooth functions defined on \(I_1\). Recall that L is of the LC type at \(a_1\), and of the LP type—at 0. Consider the Liouville transformation

$$\begin{aligned} t=\int _{a_1}^x\frac{ds}{\sqrt{-P(s)}},\ x\in I_1. \end{aligned}$$
(2.8)

The transformation (2.8) maps the interval \(I_1\) into the ray \((0,\infty )\). The inverse of the map defines \(x=x(t)\) as a function of t. Define

$$\begin{aligned} F(t):=\root 4 \of {-P(x)}y(x),\ q(t):=Q(x)+\left( \frac{(P'(x))^2}{16P(x)}-\frac{P''(x)}{4}\right) ,\ x=x(t), t>0.\nonumber \\ \end{aligned}$$
(2.9)

A standard computation shows that if f(x) solves the equation \(Lf=\lambda f\) on \(I_1\), then F(t) solves

$$\begin{aligned} F''(t)+(\lambda -q(t))F(t)=0,\ t>0. \end{aligned}$$
(2.10)

Note that \(q(t(x))\rightarrow (a_1^2+a_2^2)/8\) as \(x\rightarrow 0^-\) (and \(t\rightarrow \infty \)). It is easy to see that after subtracting the constant \((a_1^2+a_2^2)/8\) from q and shifting the spectral parameter accordingly, our potential q(t) satisfies the conditions (1.2)–(1.4) stated in [7]. In particular, in the terminology of [7], (2.10) falls under Case I with \(q_0=1/4\) (cf. (1.3), (1.4) in [7]). Thus the spectral theory developed in [7] can be applied to our equation.

Following [7], we need to find two solutions \(\Phi (t,\lambda ),\Theta (t,\lambda )\) to (2.10) with the following properties:

$$\begin{aligned}&\Phi (t,\lambda ),\Theta (t,\lambda )\in \mathbb R,\quad \forall t>0,\lambda \in \mathbb R, \nonumber \\&\Phi '(t,\lambda )\rightarrow 0 \text { as }t\rightarrow 0^+,\quad W_t(\Theta (t,\lambda ),\Phi (t,\lambda ))=1,\ t>0,\quad \forall \lambda \in \mathbb C; \nonumber \\&\lim _{t\rightarrow 0} W_t(\Theta (t,\lambda '),\Phi (t,\lambda ))=1,\quad \forall \lambda ,\lambda '\in \mathbb C. \end{aligned}$$
(2.11)

Let \(\phi (x,\lambda ),\theta (x,\lambda )\) be the solutions to \((L-\lambda )f=0\) on \(I_1\) that correspond to the solutions \(\Phi (t,\lambda ),\Theta (t,\lambda )\) to (2.10). As is well known, the Wronskians of the two pairs are related by

$$\begin{aligned} W_t(\Theta (t,\lambda ),\Phi (t,\lambda ))=-P(x)W_x(\theta (x,\lambda ),\phi (x,\lambda )). \end{aligned}$$
(2.12)

Hence, in terms of the solutions to the original equation, conditions (2.11) mean:

$$\begin{aligned}&\phi (x,\lambda ),\theta (x,\lambda )\in \mathbb R,\quad \forall x\in I_1,\lambda \in \mathbb R, \nonumber \\&P(x)\phi '(x,\lambda )\rightarrow 0 \text { as }x\rightarrow a_1^+,\quad (-P(x))W_x(\theta (x,\lambda ),\phi (x,\lambda ))=1,\ x\in I_1, \quad \forall \lambda \in \mathbb C; \nonumber \\&\lim _{x\rightarrow a_1^+} (-P(x))W_x(\theta (x,\lambda '),\phi (x,\lambda ))=1,\quad \forall \lambda ,\lambda '\in \mathbb C. \end{aligned}$$
(2.13)

Note that the first condition on the second line in (2.13) is equivalent to the requirement that \(\phi (x,\lambda )\) be bounded as \(x\rightarrow a_1\) (cf. Lemma 2.1). Once two solutions \(\phi (x,\lambda ),\theta (x,\lambda )\) that satisfy (2.13) have been found, we determine the Titchmarsh–Weyl m-function \(m(\lambda )\) from the requirement

$$\begin{aligned} \theta (x,\lambda )+m(\lambda )\phi (x,\lambda )\in L^2(I_1),\ \mathfrak {I}\lambda > 0. \end{aligned}$$
(2.14)

Then the m-function determines the spectral density by the formula

$$\begin{aligned} {\rho }(\lambda _2)-{\rho }(\lambda _1)=\lim _{u\rightarrow 0^+} \frac{1}{\pi }\int _{\lambda _1}^{\lambda _2} \mathfrak {I}m(s+iu)ds, \end{aligned}$$
(2.15)

where \(\lambda _1,\lambda _2\) are points of continuity of \({\rho }\). Define the operator \(U: L^2(I_1)\rightarrow L^2(\mathbb R,d{\rho })\) and its adjoint by the formulas:

$$\begin{aligned} (U f)(\lambda )=\int _{I_1} \phi (x,\lambda ) f(x)dx,\quad (U^* \tilde{f})(x)=\int _{\mathbb R} \phi (x,\lambda ) \tilde{f}(\lambda )d{\rho }(\lambda ). \end{aligned}$$
(2.16)

The Titchmarsh–Weyl theory asserts that (cf. [4, 7])

  • the operator U is an isometry: \(\Vert f\Vert _{L^2(I_1)}=\Vert U f\Vert _{ L^2(\mathbb R,d{\rho })}\);

  • U is unitary: \(U^{-1}=U^*\); and

  • U diagonalizes L: (\(U L U^{-1}\tilde{f})(\lambda )=\lambda \tilde{f}(\lambda )\) for a sufficiently “nice” f, i.e. for \(f\in D(L)\).

The interval \(I_2\) can be considered in a completely analogous fashion. The only difference is that the two Wronskians in (2.13) are multiplied by P(x) instead of \(-P(x)\). Thus, the analogue of (2.13) becomes

$$\begin{aligned}&\phi (x,\lambda ),\theta (x,\lambda )\in \mathbb R,\quad \forall x\in I_2,\lambda \in \mathbb R, \nonumber \\&P(x)\phi '(x,\lambda )\rightarrow 0 \text { as }x\rightarrow a_2^-,\quad P(x)W_x(\theta (x,\lambda ),\phi (x,\lambda ))=1,\ x\in I_2, \quad \forall \lambda \in \mathbb C; \nonumber \\&\lim _{x\rightarrow a_2^-} P(x)W_x(\theta (x,\lambda '),\phi (x,\lambda ))=1,\quad \forall \lambda ,\lambda '\in \mathbb C. \end{aligned}$$
(2.17)

3 General Case

From (1.2) we have

$$\begin{aligned}&x^2(x-a_1)(x-a_2)y''+[2x(x-a_1)(x-a_2)+x^2(2x-a_1-a_2)]y'\nonumber \\&\quad +[2(x-\frac{a_1+a_2}{4})^2-\lambda ] y=0. \end{aligned}$$
(3.1)

Our first goal is to obtain approximations as \(\lambda \rightarrow \infty \) to two linearly independent solutions to (3.1) that are valid on all \(I_1\) and \(I_2\). Consider first the interval \(I_1=(a_1,0)\). It was shown in [13] that in a neighborhood of \(x=a_1\) two solutions to (3.1) can be written in the form

$$\begin{aligned}&g_1(x)=J_0(2\sqrt{t})+t^{-1/4}O\left( \epsilon ^{1-\frac{2}{3}\delta }\right) ,\ g_2(x)=Y_0(2\sqrt{t})+t^{-1/4}O\left( \epsilon ^{1-\frac{2}{3}\delta }\right) , \nonumber \\&1\le t\le O\left( \epsilon ^{-\left( 1+\frac{2}{3}\delta \right) }\right) ,\ t:=\frac{\lambda (x-a_1)}{-P'(a_1)},\ \epsilon :=\lambda ^{-1/2},\ 0<\delta \ll 1. \end{aligned}$$
(3.2)

Thus, t is a rescaled variable defined near \(x=a_1\). The leading order terms of the WKB solutions to (3.1), valid away from \(x=a_1,0\), are given by

$$\begin{aligned} Y_1(x)&=(-P(x))^{-\frac{1}{4}}\left\{ \cos \left(\sqrt{\lambda }\int _{a_1}^x \frac{dt}{\sqrt{-P(t)}}-\frac{\pi }{4}\right) + O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right\} , \nonumber \\ Y_2(x)&=(-P(x))^{-\frac{1}{4}}\left\{ \sin \left(\sqrt{\lambda }\int _{a_1}^x \frac{dt}{\sqrt{-P(t)}}-\frac{\pi }{4}\right) + O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right\} , \nonumber \\ x&\in [a_1+O\left( \epsilon ^{1+2\delta }\right) ,-e^{-1/\sqrt{\epsilon }}]. \end{aligned}$$
(3.3)

Using the asymptotic formulae 8.451.1, 8.451.2 of [9] for the Bessel functions \(J_0(t),Y_0(t)\) as \(t\rightarrow \infty \), it was shown in [13] that

$$\begin{aligned} g_1(x)&=\frac{1}{c(\lambda )}\left\{ \left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) Y_1(x)+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) Y_2(x)\right\} , \nonumber \\ g_2(x)&=\frac{1}{c(\lambda )}\left\{ O\left( \epsilon ^{\frac{1}{2}-\delta }\right) Y_1(x)+\left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) Y_2(x)\right\} , \end{aligned}$$
(3.4)

and

$$\begin{aligned} g_1(x)&=\frac{\cos \left(\varphi (x;\lambda )-\frac{\pi }{4}\right)+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) }{c(\lambda )(-P(x))^{\frac{1}{4}}},\ g_2(x)=\frac{\sin \left(\varphi (x;\lambda )-\frac{\pi }{4}\right)+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) }{c(\lambda )(-P(x))^{\frac{1}{4}}}, \nonumber \\ x&\in [a_1+O\left( \epsilon ^{1+2\delta }\right) ,-e^{-1/\sqrt{\epsilon }}], \end{aligned}$$
(3.5)

where

$$\begin{aligned} \varphi (x;\lambda ):=\sqrt{\lambda }\int _{a_1}^x \frac{dt}{\sqrt{-P(t)}},\ c(\lambda ):=\lambda ^{1/4}\sqrt{\frac{\pi }{-P'(a_1)}}. \end{aligned}$$
(3.6)

In a neighborhood of \(x=0\) the leading order equation is

$$\begin{aligned} a_1a_2x^2y''+2a_1a_2xy'+\left[ \frac{(a_1+a_2)^2}{8}-\lambda \right] y=0. \end{aligned}$$
(3.7)

The characteristic roots are \(-\frac{1}{2}\pm i\mu \), where

$$\begin{aligned} \mu =\sqrt{ \frac{\lambda -\frac{(a_1+a_2)^2}{8}}{-a_1a_2}-\frac{1}{4}}=\sqrt{\frac{\lambda -\frac{a_1^2+a_2^2}{8}}{-a_1a_2}}= \sqrt{\frac{\lambda }{-a_1 a_2}}+O(\epsilon ),\ \lambda \rightarrow \infty . \end{aligned}$$
(3.8)

Thus, \(\mu \ge 0\) provided \(\lambda \ge \frac{a_1^2+a_2^2}{8}\). The corresponding solutions to (3.1) have the form

$$\begin{aligned} y_{\pm }(x)=(-x)^{-\frac{1}{2}\pm i\mu }\psi _{1,2}(x;\lambda ), \end{aligned}$$
(3.9)

where \(\psi _{1,2}(0;\lambda )=1\), and \(\psi _{1,2}(x;\lambda )\) are analytic in the disk \(|x|<\max \{|a_1|,a_2\}\).

To match the WKB solutions (3.3) with those given in (3.9) we use formula 2.266 of [9] to obtain

$$\begin{aligned} \frac{1}{(-P(x))^{\frac{1}{4}}}&=\frac{1+O(x)}{(-a_1 a_2)^{1/4}\sqrt{-x}}, \nonumber \\ \int _{a_1}^x \frac{dt}{\sqrt{-P(t)}}&=\frac{1}{\sqrt{-a_1 a_2}}\left. \ln \frac{2\sqrt{-a_1 a_2}\sqrt{(t-a_1)(a_2-t)}+(a_1+a_2)t-2a_1 a_2}{|t|}\right| _{a_1}^{x} \nonumber \\&=\frac{1}{\sqrt{-a_1 a_2}}\left. \ln \frac{[\sqrt{-a_1}\sqrt{a_2-t}+\sqrt{a_2}\sqrt{t-a_1}]^2}{|t|}\right| _{a_1}^{x} \nonumber \\&=-\frac{\ln (-x)+\kappa +O(x)}{\sqrt{-a_1 a_2}},\ x\rightarrow 0^-,\ \kappa :=\ln \frac{a_2-a_1}{-4a_1a_2}. \end{aligned}$$
(3.10)

Therefore,

$$\begin{aligned} \varphi (x;\lambda )=-(\mu +O(\epsilon ))(\ln (-x)+\kappa +O(x)). \end{aligned}$$
(3.11)

For convenience, instead of solutions (3.3) we will temporarily consider an equivalent pair \(Y_\pm \):

$$\begin{aligned} Y_+(x):=(Y_1(x)+i Y_2(x)) e^{i\pi /4},\ Y_-(x):=(Y_1(x)-i Y_2(x))e^{-i\pi /4}. \end{aligned}$$
(3.12)

Clearly,

$$\begin{aligned} Y_\pm (x)&=(-P(x))^{-\frac{1}{4}}\left\{ \exp (\pm i \varphi (x;\lambda )) + O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right\} , \nonumber \\ x&\in [a_1+O\left( \epsilon ^{1+2\delta }\right) ,-e^{-1/\sqrt{\epsilon }}]. \end{aligned}$$
(3.13)

According to the sentence following (7.6) (see Sect. 7 below), we will assume \(x\in [-c_2\epsilon ^2,-c_1\epsilon ^2]\), where \(0<c_1<c_2<1\). From (3.3), (3.6), and (3.11) we find

$$\begin{aligned}&(-x)^{1/2}Y_\pm (x;\lambda ) \nonumber \\&\quad = \frac{1+O(x)}{(-a_1 a_2)^{1/4} }[\exp (\pm i\varphi (x;\lambda ))+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) ] \nonumber \\&\quad =\frac{1+O(x)}{(-a_1 a_2)^{1/4} }[\exp (\mp i\mu (\ln (-x)+\kappa ))+O(\epsilon \ln (-x))+O(x/\epsilon )+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) ] \nonumber \\&\quad =\frac{\exp (\mp i\mu (\ln (-x)+\kappa ))+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) }{(-a_1 a_2)^{1/4}},\ x\in [-c_2\epsilon ^2,-c_1\epsilon ^2]. \end{aligned}$$
(3.14)

From (7.8),

$$\begin{aligned} (-x)^{1/2}y_\pm (x)=(-x)^{\pm i\mu }+O(\epsilon ),\ x\in [-c_2\epsilon ^2,-c_1\epsilon ^2]. \end{aligned}$$
(3.15)

Matching (3.14) and (3.15) shows

$$\begin{aligned} Y_\pm (x)=\frac{1}{(-a_1a_2)^{1/4}}\left\{ \exp (\mp i\mu \kappa )y_{\mp }(x)\left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) +\exp (\pm i\mu \kappa )y_{\pm }(x)O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right\} .\nonumber \\ \end{aligned}$$
(3.16)

Using (3.4), (3.12), and (3.16) yields

$$\begin{aligned} g_1(x;\lambda )=&\left( \frac{|a_1|^3}{a_2}\right) ^{1/4}\sqrt{\frac{a_2-a_1}{\pi }}\frac{1}{2\lambda ^{1/4}}\biggl \{e^{i\mu \kappa +i\frac{\pi }{4}} \left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) y_+(x;\lambda ) \nonumber \\&+e^{-i\mu \kappa -i\frac{\pi }{4}} \left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) y_-(x;\lambda )\biggr \},\nonumber \\ g_2(x;\lambda )=&\left( \frac{|a_1|^3}{a_2}\right) ^{1/4}\sqrt{\frac{a_2-a_1}{\pi }}\frac{1}{2i\lambda ^{1/4}}\biggl \{-e^{i\mu \kappa +i\frac{\pi }{4}} \left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) y_+(x;\lambda ) \nonumber \\&+e^{-i\mu \kappa -i\frac{\pi }{4}} \left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) y_-(x;\lambda )\biggr \}. \end{aligned}$$
(3.17)

Recall that t is defined according to (3.2). Using formula 8.478 of [9] it is easy to find that the Wronskian \(W_x\) of \(\pi Y_0(2\sqrt{t})\) and \(J_0(2\sqrt{t})\) (as functions of x) equals \(\frac{1}{a_1-x}\). Using the limit

$$\begin{aligned} \lim _{x\rightarrow a_1^+} (-P(x)) W_x(\pi Y_0(2\sqrt{t}), J_0(2\sqrt{t}))= -a_1^2(a_2-a_1), \end{aligned}$$
(3.18)

we obtain that properties (2.13) are satisfied if we set

$$\begin{aligned} \phi _1(x,\lambda ):=g_1(x),\ \theta _1(x,\lambda ):=-\pi g_2(x)/[a_1^2(a_2-a_1)]. \end{aligned}$$
(3.19)

Here and in what follows, the subscript ‘1’ in \(\phi _1,\theta _1,m_1\), and \(\rho _1\) means that these functions correspond to the interval \(I_1\). Condition (2.14) now implies that the m function needs to be selected so that the leading coefficients in front of the singularity \((-x)^{-\frac{1}{2}+i\mu }\) as \(x\rightarrow 0^-\) in \(\theta _1(x,\lambda )\) and \(m_1(\lambda )\phi _1(x,\lambda )\) are equal each other in magnitude and are of opposite signs. Using (3.17) and (3.19) we obtain

$$\begin{aligned} m_1(\lambda )=\frac{\pi i}{a_1^2(a_2-a_1)}\left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) . \end{aligned}$$
(3.20)

Equation (2.15) now immediately implies

$$\begin{aligned} \rho _1'(\lambda )=\frac{1}{a_1^2(a_2-a_1)}\left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) , \end{aligned}$$
(3.21)

which matches the case of \(a_2=-a_1=a\) considered in Sect. 4 for large \(\lambda \).

Next we consider the interval \(I_2\). The derivation of the spectral density is very similar, so we sketch here only the main formulas. The analogue of (3.2) becomes

$$\begin{aligned}&g_1(x)=J_0(2\sqrt{t})+t^{-1/4}O\left( \epsilon ^{1-\frac{2}{3}\delta }\right) ,\ g_2(x)=Y_0(2\sqrt{t})+t^{-1/4}O\left( \epsilon ^{1-\frac{2}{3}\delta }\right) , \nonumber \\&1\le t\le O\left( \epsilon ^{-\left( 1+\frac{2}{3}\delta \right) }\right) ,\ t:=\frac{\lambda (a_2-x)}{P'(a_2)},\ 0<\delta \ll 1. \end{aligned}$$
(3.22)

Thus, t is a rescaled variable defined near \(x=a_2\). The leading order terms of the WKB solutions, valid away from \(x=0,a_2\), are given by

$$\begin{aligned} Y_1(x)&=(-P(x))^{-\frac{1}{4}}\left\{ \cos \left(\sqrt{\lambda }\int ^{a_2}_x \frac{dt}{\sqrt{-P(t)}}-\frac{\pi }{4}\right) + O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right\} , \nonumber \\ Y_2(x)&=(-P(x))^{-\frac{1}{4}}\left\{ \sin \left(\sqrt{\lambda }\int ^{a_2}_x \frac{dt}{\sqrt{-P(t)}}-\frac{\pi }{4}\right) + O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right\} , \nonumber \\ x&\in [e^{-1/\sqrt{\epsilon }},a_2-O\left( \epsilon ^{1+2\delta }\right) ]. \end{aligned}$$
(3.23)

Matching \(g_{1,2}\) in (3.22) with \(Y_{1,2}\) in (3.23) gives (cf. [13])

$$\begin{aligned} g_1(x)&=\frac{1}{c(\lambda )}\left\{ \left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) Y_1(x)+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) Y_2(x)\right\} , \nonumber \\ g_2(x)&=\frac{1}{c(\lambda )}\left\{ O\left( \epsilon ^{\frac{1}{2}-\delta }\right) Y_1(x)+\left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) Y_2(x)\right\} , \end{aligned}$$
(3.24)

and

$$\begin{aligned} g_1(x)&=\frac{\cos \left(\varphi (x;\lambda )-\frac{\pi }{4}\right)+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) }{c(\lambda )(-P(x))^{\frac{1}{4}}},\ g_2(x)=\frac{\sin \left(\varphi (x;\lambda )-\frac{\pi }{4}\right)+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) }{c(\lambda )(-P(x))^{\frac{1}{4}}}, \nonumber \\ x&\in [e^{-1/\sqrt{\epsilon }},a_2-O\left( \epsilon ^{1+2\delta }\right) ], \end{aligned}$$
(3.25)

where

$$\begin{aligned} \varphi (x;\lambda ):=\sqrt{\lambda }\int ^{a_2}_x \frac{dt}{\sqrt{-P(t)}},\ c(\lambda ):=\lambda ^{1/4}\sqrt{\frac{\pi }{P'(a_2)}}. \end{aligned}$$
(3.26)

Analogously to (3.10) we have

$$\begin{aligned} \int ^{a_2}_x \frac{dt}{\sqrt{-P(t)}}&=-\frac{1}{\sqrt{-a_1 a_2}}\left. \ln \frac{[\sqrt{-a_1}\sqrt{a_2-t}+\sqrt{a_2}\sqrt{t-a_1}]^2}{|t|}\right| ^{a_2}_x \nonumber \\&=-\frac{\ln x+\kappa +O(x)}{\sqrt{-a_1 a_2}},\ x\rightarrow 0^+, \end{aligned}$$
(3.27)

where \(\kappa \) is the same as in (3.10). Therefore,

$$\begin{aligned} \varphi (x;\lambda )=-(\mu +O(\lambda ^{-1/2}))(\ln x+\kappa +O(x)). \end{aligned}$$
(3.28)

With the solutions \(Y_\pm \) defined according to (3.12) (using \(Y_{1,2}\) for the interval \(I_2\)), we have

$$\begin{aligned} Y_\pm (x)&=(-P(x))^{-\frac{1}{4}}\left\{ \exp (\pm i \varphi (x;\lambda )) + O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right\} , \nonumber \\ x&\in [e^{-1/\sqrt{\epsilon }},a_2-O\left( \epsilon ^{1+2\delta }\right) ]. \end{aligned}$$
(3.29)

Next we assume \(x\in [c_1\epsilon ^2,c_2\epsilon ^2]\), where \(0<c_1<c_2<1\). From (3.28) and (3.29) we find similarly to (3.14)

$$\begin{aligned} x^{1/2}Y_\pm (x;\lambda ) =\frac{\exp (\mp i\mu (\ln x+\kappa ))+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) }{(-a_1 a_2)^{1/4}},\ x\in [c_1\epsilon ^2,c_2\epsilon ^2]. \end{aligned}$$
(3.30)

The solutions analogous to (3.1) have the form

$$\begin{aligned} y_{\pm }(x)=x^{-\frac{1}{2}\pm i\mu }\psi _{1,2}(x;\lambda ), \end{aligned}$$
(3.31)

where \(\psi _{1,2}(0;\lambda )=1\), and \(\psi _{1,2}(x;\lambda )\) are analytic in the disk \(|x|<\max \{|a_1|,a_2\}\). Similarly to (3.15),

$$\begin{aligned} x^{1/2}y_\pm (x)=x^{\pm i\mu }+O(\epsilon ),\ x\in [c_1\epsilon ^2,c_2\epsilon ^2]. \end{aligned}$$
(3.32)

Matching (3.30) and (3.32) shows

$$\begin{aligned} Y_\pm (x)=\frac{1}{(-a_1a_2)^{1/4}}\left\{ \exp (\mp i\mu \kappa )y_{\mp }(x)\left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) +\exp (\pm i\mu \kappa )y_{\pm }(x)O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right\} .\nonumber \\ \end{aligned}$$
(3.33)

Combining (3.12), (3.24), (3.26), and (3.33) gives

$$\begin{aligned} g_1(x;\lambda )=&\left( \frac{a_2^3}{|a_1|}\right) ^{1/4}\sqrt{\frac{a_2-a_1}{\pi }}\frac{1}{2\lambda ^{1/4}}\biggl \{e^{i\mu \kappa +i\frac{\pi }{4}} \left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) y_+(x;\lambda ) \nonumber \\&+e^{-i\mu \kappa -i\frac{\pi }{4}} \left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) y_-(x;\lambda )\biggr \}, \nonumber \\ g_2(x;\lambda )=&\left( \frac{a_2^3}{|a_1|}\right) ^{1/4}\sqrt{\frac{a_2-a_1}{\pi }}\frac{1}{2i\lambda ^{1/4}}\biggl \{-e^{i\mu \kappa +i\frac{\pi }{4}} \left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) y_+(x;\lambda ) \nonumber \\&+e^{-i\mu \kappa -i\frac{\pi }{4}} \left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) y_-(x;\lambda )\biggr \}. \end{aligned}$$
(3.34)

With t defined according to (3.22), we have \(W_x(\pi Y_0(2\sqrt{t}), J_0(2\sqrt{t}))=1/(a_2-x)\). Thus

$$\begin{aligned} \lim _{x\rightarrow a_2^-} P(x) W_x(\pi Y_0(2\sqrt{t}), J_0(2\sqrt{t})) = -a_2^2(a_2-a_1), \end{aligned}$$
(3.35)

and properties (2.17) are satisfied by setting

$$\begin{aligned} \phi _2(x,\lambda ):=g_1(x),\ \theta _2(x,\lambda ):=-\pi g_2(x)/[a_2^2(a_2-a_1)]. \end{aligned}$$
(3.36)

From (2.14), (3.34), and (3.36) we obtain

$$\begin{aligned} m_2(\lambda )=\frac{\pi i}{a_2^2(a_2-a_1)}\left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) . \end{aligned}$$
(3.37)

Equation (2.15) now immediately implies

$$\begin{aligned} \rho _2'(\lambda )= \frac{1}{a_2^2(a_2-a_1)}\left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) . \end{aligned}$$
(3.38)

Now we can find the asymptotics of the diagonal representation of \({\mathcal {H}}\). Following (2.16) introduce the operators

$$\begin{aligned} (U_1 f)(\lambda )=\int _{I_1} \phi _1(x,\lambda ) f(x)dx,\quad (U_1^* \tilde{f})(x)=\int _{\mathbb R} \phi _1(x,\lambda ) \tilde{f}(\lambda )d{\rho }_1(\lambda ), \nonumber \\ (U_2 f)(\lambda )=\int _{I_2} \phi _2(x,\lambda ) f(x)dx,\quad (U_2^* \tilde{f})(x)=\int _{\mathbb R} \phi _2(x,\lambda ) \tilde{f}(\lambda )d{\rho }_2(\lambda ). \end{aligned}$$
(3.39)

The domain and range spaces of these four operators are defined similarly to Sect. 2.2.

Recall that \(\phi _{1,2}(x,\lambda )\) are solutions to \((L-\lambda )f=0\) on \(I_{1,2}\) that are bounded at \(a_{1,2}\), respectively. If \(\lambda \ge (a_1^2+a_2^2)/8\), \(\phi _{1,2}(x,\lambda )\) satisfy (3.31). Thus, \(\phi _{1,2}(x,\lambda )\) satisfy the assumptions of Lemma 2.1, and from (2.6)

$$\begin{aligned} \lambda {\mathcal {H}}_1\phi _1={\mathcal {H}}_1 L\phi _1=L{\mathcal {H}}_1\phi _1. \end{aligned}$$
(3.40)

Hence \({\mathcal {H}}_1\phi _1\) satisfies (3.1) on \(I_2\) and is bounded near \(a_2\). From the Frobenius theory it follows that there cannot be two linearly independent solutions to \((L-\lambda )f=0\) on \(I_2\) that are bounded at \(a_2\), so we conclude that \({\mathcal {H}}_1\phi _1=\nu (\lambda )\phi _2\) for some function \(\nu (\lambda )\). Obviously,

$$\begin{aligned} ({\mathcal {H}}_1 U_1^* \tilde{f})(\lambda )&=\int _{\mathbb R} ({\mathcal {H}}_1\phi _1(x,\lambda )) \tilde{f}(\lambda )d{\rho }_1(\lambda ) =\int _{\mathbb R} (\nu (\lambda )\phi _2(x,\lambda )) \tilde{f}(\lambda )d{\rho }_1(\lambda ) \nonumber \\&=\int _{\mathbb R} \left( \nu (\lambda )\frac{{\rho }'_1(\lambda )}{{\rho }'_2(\lambda )}\right) \phi _2(x,\lambda ) \tilde{f}(\lambda )d{\rho }_2(\lambda ), \end{aligned}$$
(3.41)

where \(\tilde{f}\in L^2(\mathbb R,d{\rho }_1)\). In Sect. 5 below we will show that L does not have discrete spectrum. It is also well-known that L has no continuous spectrum in the region \(\lambda <(a_1^2+a_2^2)/8\). Hence the integrals in (3.41) are actually over the interval \(\lambda \ge (a_1^2+a_2^2)/8\). The first equality in (3.41) holds because \({\mathcal {H}}_1:L^2(I_1)\rightarrow L^2(I_2)\) is continuous, and the kernel \(1/(x-y)\) is smooth on \(I_1\times I_2\). Hence

$$\begin{aligned} U_2{\mathcal {H}}_1 U_1^* =\nu (\lambda )\frac{{\rho }'_1(\lambda )}{{\rho }'_2(\lambda )}, \end{aligned}$$
(3.42)

To find \(\nu (\lambda )\) we use the well-known identity

$$\begin{aligned} \frac{1}{\pi }\int _{-\infty }^0 \frac{(-x)^{-\frac{1}{2}+i\mu }}{x-y} dx=-\frac{y^{-\frac{1}{2}+i\mu }}{\cosh (\mu \pi )},\ y>0,\ \mu \in \mathbb R. \end{aligned}$$
(3.43)

When the interval of integration is not all of \((-\infty ,0)\) and the integrand is not exactly \((-x)^{-\frac{1}{2}+i\mu }\), we can interpret (3.43) as a statement about the leading singularities. More precisely, if \({\mathcal {H}}_1\) acts on a function with the leading singularity \((-x)^{-\frac{1}{2}+i\mu }\), \(x\rightarrow 0^-\), the result is a function with the leading singularity \((-1/\cosh (\mu \pi ))y^{-\frac{1}{2}+i\mu }\), \(y\rightarrow 0^+\). Thus, from (3.17), (3.19) and (3.34), (3.36) we obtain

$$\begin{aligned} \nu (\lambda )= & {} -\frac{1}{\cosh (\mu \pi )}\left( \frac{|a_1|}{a_2^3}\right) ^{1/4}\left( \frac{|a_1|^3}{a_2}\right) ^{1/4}\left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) \nonumber \\= & {} \frac{a_1a_2}{\cosh (\mu \pi )}\left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) . \end{aligned}$$
(3.44)

Using now (3.21) and (3.38) finally gives

$$\begin{aligned} U_2{\mathcal {H}}_1 U_1^* =\frac{a_2^3}{a_1}\frac{1}{\cosh (\mu \pi )}\left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) . \end{aligned}$$
(3.45)

Define \(J:=[(a_1^2+a_2^2)/8,\infty )\). The results of this section combined with the results in [4, 7]) can be summarized in the following theorem.

Theorem 3.1

The operators \(U_j: L^2(I_j)\rightarrow L^2(J,{\rho }'_j)\) and \(U_j^*: L^2(J,{\rho }'_j)\rightarrow L^2(I_j)\), \(j=1,2\), defined in (3.39) are isometric transformations. Moreover, in the sense of operator equality on \( L^2(J,{\rho }'_1)\) one has

$$\begin{aligned} U_2{\mathcal {H}}_1 U_1^* =\sigma (\lambda ), \end{aligned}$$
(3.46)

where

$$\begin{aligned} \sigma (\lambda )=\frac{a_2^3}{a_1}\frac{1}{\cosh (\mu \pi )}\left( 1+O\left( \epsilon ^{\frac{1}{2}-\delta }\right) \right) ,\lambda \rightarrow \infty . \end{aligned}$$
(3.47)

4 Symmetric Case

In this section we consider the case of symmetric intervals, i.e. \(a_2=-a_1=a\). The polynomials P and Q are given by \(P=x^2(x^2-a^2)\) and \(Q(x)=2x^2\), and the differential equation in (3.1) becomes

$$\begin{aligned} (x^2(x^2-a^2)y')'+(2x^2-\lambda )y=0. \end{aligned}$$
(4.1)

Due to symmetry, if y(x) is a solution to (4.1), then so is \(y(-x)\).

4.1 Solution of \(Ly=\lambda y\)

The change of variables \(x=az\) reduces (4.1) to

$$\begin{aligned} z^2(z^2-1)y''+2z(2z^2-1)y'+ \left( 2z^2-\frac{\lambda }{a^2}\right) y=0. \end{aligned}$$
(4.2)

According to [10], 2.410, two linearly independent solutions of (4.2) are given by

$$\begin{aligned} y(z)=z^{-\frac{1}{2}\pm i\mu }\eta _{\pm } (z^2), \end{aligned}$$
(4.3)

where

$$\begin{aligned} \mu =\sqrt{\frac{\lambda }{a^2}-\frac{1}{4}}, ~\alpha =\frac{1}{4} \pm \frac{1}{2}i\mu ,~\beta =\frac{3}{4} \pm \frac{1}{2}i\mu , ~\gamma =1\pm i\mu , \end{aligned}$$
(4.4)

and \(\eta _\pm (\xi )\) are solutions of the hypergeometric equation

$$\begin{aligned} \xi (\xi -1){\eta ''}_\pm +[(\alpha +\beta +1)\xi -\gamma ]\eta '_\pm +\alpha \beta \eta _\pm =0 \end{aligned}$$
(4.5)

with the corresponding choice of the sign in \(\alpha ,\beta ,\gamma \). Sometimes, we will use notation \(\eta \) instead of \(\eta _+\).

Since we are interested in a solution \(\varphi (z)=\varphi (z,\lambda )\) of (4.2) that is analytic at \(z=1\), we reduce (4.5) to another hypergeometric equation

$$\begin{aligned} \zeta (\zeta -1){\eta ''}+[(\alpha +\beta +1)\zeta -(1+\alpha +\beta -\gamma )]\eta '+\alpha \beta \eta =0 \end{aligned}$$
(4.6)

by the change of variables \(\xi =1-\zeta \). Then

$$\begin{aligned} \varphi (z)=z^{-\frac{1}{2}+i\mu }F\left( \frac{1}{4} +\frac{ i\mu }{2},\frac{3}{4} +\frac{ i\mu }{2},1,1-z^2\right) . \end{aligned}$$
(4.7)

Using the transformation formula 15.3.6 from [3], the behavior of \(\varphi \) near \(z=0\) is given by

$$\begin{aligned} \varphi (z)= & {} \frac{\Gamma (-i\mu )}{\Gamma (\frac{1}{4} -\frac{ i\mu }{2})\Gamma (\frac{3}{4} -\frac{ i\mu }{2})} z^{-\frac{1}{2}+i\mu }F\left( \frac{1}{4} +\frac{ i\mu }{2},\frac{3}{4} +\frac{ i\mu }{2},1+i \mu ,z^2\right) \nonumber \\&+\frac{\Gamma (i\mu )}{\Gamma (\frac{1}{4} +\frac{ i\mu }{2})\Gamma (\frac{3}{4} +\frac{ i\mu }{2})} z^{-\frac{1}{2}-i\mu }F\left( \frac{1}{4} -\frac{ i\mu }{2},\frac{3}{4} -\frac{ i\mu }{2},1-i \mu ,z^2\right) \nonumber \\= & {} k f(z) + lg(z), \end{aligned}$$
(4.8)

where

$$\begin{aligned} f(z)= & {} z^{-\frac{1}{2}+i\mu }F\left( \frac{1}{4} +\frac{ i\mu }{2},\frac{3}{4} +\frac{ i\mu }{2},1+i \mu ,z^2\right) , \nonumber \\ g(z)= & {} z^{-\frac{1}{2}-i\mu }F\left( \frac{1}{4} -\frac{ i\mu }{2},\frac{3}{4} -\frac{ i\mu }{2},1-i \mu ,z^2\right) , \end{aligned}$$
(4.9)

and k, l are the corresponding prefactors.

It follows from (4.3), (4.4) that f(z),  g(z) themselves are solutions to (4.2) with \(f(z)=z^{-\frac{1}{2}+i\mu }\eta _+(z^2)\) and \(g(z)=z^{-\frac{1}{2}-i\mu }\eta _-(z^2)\). Moreover, in the case

$$\begin{aligned} \lambda \ge \frac{a^2}{4} \end{aligned}$$
(4.10)

we have \(l=\bar{k}\) and \(g(z)=\overline{f(z)}\) when \(z\in {\mathbb {R}}\). Thus, for these values of \(\lambda \) and z,

$$\begin{aligned} \varphi (z,\lambda )= kf(z)+\bar{k} \overline{f(\bar{z})}=2\mathfrak {R}[kf(z)]. \end{aligned}$$
(4.11)

It follows from (4.11) that \(\varphi (z,\lambda )\) is real for all \(z\in {\mathbb {R}}\) and \(\lambda \ge a^2/4\). Returning to the original variable \(x=az\), we obtain that

$$\begin{aligned} \phi (x,\lambda )=\left( \frac{x}{a}\right) ^{-\frac{1}{2}+i\mu }F\left(\frac{1}{4} +\frac{ i\mu }{2},\frac{3}{4} +\frac{ i\mu }{2},1,1-\left( \frac{x}{a}\right) ^2\right) \end{aligned}$$
(4.12)

is a real solution of (3.1) on (0, a) that is analytic at \(x=a\). It is clear that \(\phi (-x,\lambda )\) is also a solution, it is real on \((-a,0)\) and analytic at \(x=- a\).

Lemma 4.1

If \(\lambda \ge \frac{a^2}{4}\) then

$$\begin{aligned} |k|^2=\frac{\coth (\pi \mu )}{2\pi \mu }. \end{aligned}$$
(4.13)

Proof

Using (4.8), the Schwarz symmetry of \(\Gamma (z)\), and formulae 8.332.1, 8.332.4 of [9], we obtain

$$\begin{aligned} |k|^2=\dfrac{|\Gamma (-i\mu )|^2(\frac{1}{4}-\frac{i\mu }{2})(\frac{1}{4}+\frac{i\mu }{2})}{\Gamma (\frac{5}{4}-\frac{i\mu }{2})\Gamma (\frac{5}{4}+\frac{i\mu }{2})\Gamma (\frac{3}{4}-\frac{i\mu }{2})\Gamma (\frac{3}{4}+\frac{i\mu }{2})}=\frac{\coth (\pi \mu )}{2\pi \mu }. \end{aligned}$$
(4.14)

\(\square \)

4.2 Spectral Measure for \(Ly=\lambda y\) and Diagonalization of \({\mathcal {H}}_1\)

Following the approach in Sect. 3, in order to calculate the spectral measure \({\rho }(\lambda )\) we start with constructing a real-valued solution \( {\theta }(x,\lambda )\), which must be chosen so that the requirements (2.13) hold. Since \( {\theta }(x)= {\theta }(x,\lambda )\) must be linearly independent from \(\phi (x,\lambda )\), we choose \( {\theta }(x,\lambda )\) as the standard second linearly independent solution of the hypergeometric equation near \(x=a\), see [9], 9.153.2, which can be written as

$$\begin{aligned} {\theta }(x,\lambda )=\kappa \left[ \phi (x,\lambda )\ln \left( \frac{a^2-x^2}{a^2}\right) +\Psi \left( \frac{a^2-x^2}{a^2},\lambda \right) \right] , \end{aligned}$$
(4.15)

where \(\Psi (\frac{a^2-x^2}{a^2},\lambda )\) is the analytic (non-logarithmic) part of this second solution at \(x=\pm a\) and \(\Psi (0,\lambda )=0\). We will show below that \(\kappa \) is real and \(\Psi (\frac{a^2-x^2}{a^2},\lambda )\) is real-valued for all \(x\in {\mathbb {R}}\) and appropriate \(\lambda \).

Lemma 4.2

Set \(\kappa =-\frac{1}{2a^3}\). Let the functions \(\phi (x,\lambda )\) and \( {\theta }(x,\lambda )\) be defined by (4.12) and (4.15), respectively. Then the pair \(\phi (x,\lambda )\) and \( {\theta }(x,\lambda )\) satisfies all the requirements (2.13) on (0, a), and the pair \(\phi (-x,\lambda )\) and \( {\theta }(-x,\lambda )\) satisfies all the requirements (2.13) on \((-a,0)\).

Proof

We start with the interval (0, a). Clearly,

$$\begin{aligned} W_x:=W_x( {\theta }(x,\lambda ),\phi (x,\lambda ))&= \kappa \left| \begin{array}{ll} \phi \ln \frac{a^2-x^2}{a^2}+\Psi &{}\quad \phi \\ \phi '\ln \frac{a^2-x^2}{a^2}-\phi \frac{2x}{a^2-x^2}+\frac{d}{dx}\Psi &{}\quad \phi ' \end{array} \right| \nonumber \\&=\kappa \left( \phi '\Psi -\phi \frac{d}{dx}\Psi +\phi ^2\frac{2x}{a^2-x^2}\right) . \end{aligned}$$
(4.16)

Thus, using that \(\phi \) and \(\Psi \) are smooth near a, we obtain

$$\begin{aligned} 1=\lim _{x\rightarrow a^-} PW_x( {\theta },\phi )=-2a^3\kappa . \end{aligned}$$
(4.17)

Here we have used that \(\phi (a,\lambda )=1\), cf. (4.12). This shows that \(\kappa \) is real. By Abel’s theorem, \(P(x) W_x\) is constant, so the second condition in the second line of (2.13) is satisfied.

Since \(\phi \) is real-valued and \(P(x)W_x(\theta ,\phi )\equiv 1\) on (0, a), the Wronskian of \(\phi \) and \(\mathfrak {I}\theta \) is zero. Since \(\Psi (0,\lambda )=0\) and \(\phi (a,\lambda )=1\), we immediately conclude that \(\mathfrak {I}\Psi \equiv 0\).

Repeating now the calculations for \(W_x( {\theta }(x,\lambda '),\phi (x,\lambda ))\) and arguing similarly to (4.16)–(4.17), we obtain

$$\begin{aligned} \lim _{x\rightarrow a^-}P(x)W( {\theta }(x,\lambda '),\phi (x,\lambda ))=1 \end{aligned}$$
(4.18)

for any \(\lambda ,\lambda '\in {\mathbb {C}}\). Note that in this case the logarithmic terms will appear in the Wronskian, but they will not affect the limit in (4.18). Thus our choice of \(\kappa \) is correct, and all the requirements in (2.13) are satisfied.

Next we consider the interval \((-a,0)\). Analytic continuation of the solutions \( {\theta }(x,\lambda ),\phi (x,\lambda )\), \( \lambda \ge \frac{a^2}{4}\), from the interval (0, a) to the negative half-axis is no longer real-valued. Therefore, on the interval \((-a,0)\) we replace them by the real-valued solutions \( {\theta }(-x,\lambda ),\phi (-x,\lambda )\). It is straightforward to see that the Wronskian of these solutions is \(-\frac{1}{P(-x)}\). However the sign in front of P(x) in (2.13) is also changed to the opposite. Thus the pair \( {\theta }(-x,\lambda ),\phi (-x,\lambda )\) satisfies (2.17), and the lemma is proven. \(\square \)

We are interested in \(\mathfrak {I}m(\lambda )\), where \(\lambda \in {\mathbb {R}}\). Given the solutions \(\phi \) and \(\theta \) with the required properties, we can compute the spectral density \(\rho '(\lambda )\). Again, we start with the interval (0, a). We need \(\mathfrak {I}m(\lambda )\), where \(\lambda \in {\mathbb {R}}\). In the upper halfplane \(\mathfrak {I}\lambda >0\), the function \(m(\lambda )\) is defined by the requirement that \( {\theta }(x,\lambda )+m(\lambda )\phi (x,\lambda )\in L^2(0,a)\), and then \(m(\lambda )\) is analytically continued to the ray \(\lambda \ge \frac{a^2}{4}\).

If \(z\in {\mathbb {R}}\) and \(\mu >0\) then \(g(z)=\overline{f(\bar{z})}\), where f, g are linearly independent solutions of (4.2) defined by (4.9). Then, since \(\theta \) is real valued, there exists some \(l\in {\mathbb {C}}\) such that \(\theta = l f+\bar{l} \bar{f}\), where \(z=\frac{x}{a}\). Note that \(l=l(\mu )\) and \(\bar{l}=\bar{l}(\mu )\) are continuous functions of \(\mu \) that are complex conjugate when \(\mu >0\). Then, according to (4.9) and [3], 15.3.10, we have

$$\begin{aligned} {\theta }(x,\lambda )= & {} lf(x/a)+\bar{l}\,\overline{f(x/a)}\nonumber \\= & {} -2\mathfrak {R}\left[ l\frac{\Gamma (1+i\mu )}{\Gamma (\frac{1}{4} +\frac{ i\mu }{2})\Gamma (\frac{3}{4} +\frac{ i\mu }{2})}\right] \ln \frac{a^2-x^2}{a^2}+O(1),~~ x\rightarrow a^-.\qquad \quad \end{aligned}$$
(4.19)

Note that according to (4.8), \(\frac{\Gamma (1+i\mu )}{\Gamma (\frac{1}{4} +\frac{ i\mu }{2})\Gamma (\frac{3}{4} +\frac{ i\mu }{2})}=i\mu \bar{k}\). Comparing the logarithmic terms of (4.19) and (4.15), and using Lemma 4.2, we obtain

$$\begin{aligned} -[i\mu l\bar{k} + \overline{i\mu l\bar{k}}]=-\frac{1}{2a^3}~~~\mathrm{or}~~~\mathfrak {I}(l\bar{k})=-\frac{1}{4\mu a^3}. \end{aligned}$$
(4.20)

Let \(\mathfrak {I}\lambda >0\). According to (4.9), \(g (z) \in L^2(0,a)\) and \( f(z) \not \in L^2(0,a)\). So, the requirement that

$$\begin{aligned} {\theta }+m\phi =lf+\bar{l} g + m(kf+\bar{k}g)\in L^2(0,a) \end{aligned}$$
(4.21)

implies \(l+mk=0\) or \(m=-\frac{l}{k}= \frac{-l \bar{k}}{|k|^2}\). Taking into account the continuity of \(l=l(\mu )\), equation (4.20) and Lemma 4.1, we obtain

$$\begin{aligned} \mathfrak {I}m(\lambda )= \frac{- \mathfrak {I}(l\bar{k})}{ |k|^2}=\frac{1}{ 4a^3\mu |k|^2}=\frac{\pi \tanh (\pi \mu )}{2a^3}. \end{aligned}$$
(4.22)

For the interval \((-a,0)\) and \(\mathfrak {I}\lambda >0\), the function \(m(\lambda )\) is defined by the requirement that \( {\theta }(-x,\lambda )+m(\lambda )\phi (-x,\lambda )\in L^2(-a,0)\). Arguing analogously to (4.20)–(4.22), we obtain that the m-function given in (4.22) works for the interval \((-a,0)\) as well. Thus,

$$\begin{aligned} \rho '(\lambda )=\frac{\tanh (\pi \sqrt{\frac{\lambda }{a^2}-\frac{1}{4}})}{2a^3}, \end{aligned}$$
(4.23)

and the above holds for both intervals \((-a,0)\) and (0, a).

Using (4.8), we have

$$\begin{aligned} \phi _1(x)\sim&k(-x/a)^{-\frac{1}{2}+i\mu }+\bar{k}(-x/a)^{-\frac{1}{2}-i\mu },\ x\rightarrow 0^-, \nonumber \\ \phi _2(x)\sim&k(x/a)^{-\frac{1}{2}+i\mu }+\bar{k}(x/a)^{-\frac{1}{2}-i\mu },\ x\rightarrow 0^+. \end{aligned}$$
(4.24)

Observing that \(\rho _1'(\lambda )/\rho _2'(\lambda )\equiv 1\) (cf. (3.45)) and combining (4.24) with (3.43), we prove the following result.

Theorem 4.3

Let \(J := [a^2/4,\infty )\). Define the functions

$$\begin{aligned} \phi _2(x,\lambda )&:=\left( \frac{x}{a}\right) ^{-\frac{1}{2}+i\mu }F\left(\frac{1}{4} +\frac{ i\mu }{2},\frac{3}{4} +\frac{ i\mu }{2},1,1-\left( \frac{x}{a}\right) ^2\right); \nonumber \\ {\theta }_2(x,\lambda )&:=-\frac{1}{2a^3}\left[ \phi _2(x,\lambda )\ln \left( \frac{a^2-x^2}{a^2}\right) \!+\!\Psi \left( \frac{a^2-x^2}{a^2},\lambda \right) \right] ,0<x<a,\ \lambda \in J, \end{aligned}$$
(4.25)

and

$$\begin{aligned} \phi _1(x,\lambda ):=\phi _2(-x,\lambda ),\ {\theta }_1(x,\lambda ):= {\theta }_2(-x,\lambda ),\ -a<x<0,\ \lambda \in J. \end{aligned}$$
(4.26)

Here F is the hypergeometric function (see 15.1.1 in [3]), and \(\Psi \) is the analytic (non-logarithmic) part of the second solution in [9], 9.153.2. The operators \(U_j: L^2(I_j)\rightarrow L^2(J,{\rho }')\) and \(U_j^*: L^2(J,{\rho }')\rightarrow L^2(I_j)\), \(j=1,2\), defined in (3.39) are isometric transformations. Moreover, in the sense of operator equality on \( L^2(J,{\rho }')\) one has

$$\begin{aligned} U_2{\mathcal {H}}_1 U_1^* =\frac{a^2}{\cosh (\mu \pi )}. \end{aligned}$$
(4.27)

Lemma 4.4

One has

$$\begin{aligned} k \sim \frac{e^{i(\frac{\pi }{4}-\mu \ln 2)}}{\sqrt{2\pi \mu }}~~~~~\mathrm{as}~~~~~\mu \rightarrow +\infty . \end{aligned}$$
(4.28)

Proof

The result follows from (4.8) and formulae 8.335.1, 8328.2 in [9]. \(\square \)

Lemma 4.4 shows that the behavior of \(\phi _2(x;\lambda )\) as \(x\rightarrow 0^+\) in the symmetric case (cf. (4.24)) and in the general case (given by (3.34)) match up.

4.3 Large \(\lambda \) Asymptotics of \(\phi (z,\lambda )\) on \(I_2\)

In this subsection we calculate a uniform approximation of \(\phi (z,\lambda )\) on \(I_2\) as \(\lambda \rightarrow \infty \). First, we assume for simplicity that \(a=1\), so \(\varphi (x,\lambda )=\phi (z,\lambda )\) and \(x=z\) (cf. (4.8)). Using (4.8) and the integral representation given by formula 9.111 of [9], we obtain

$$\begin{aligned} \phi (z,\lambda )=\frac{2}{\sqrt{z}}\mathfrak {R}\left[z^{i\mu }\frac{\Gamma (1+i\mu )\Gamma (-i\mu )}{|\Gamma (\frac{1}{4} -\frac{ i\mu }{2})\Gamma (\frac{3}{4} -\frac{ i\mu }{2})|^2} \int _0^1e^{\frac{i\mu }{2}h(t)}r(t)dt\right], \end{aligned}$$
(4.29)

where

$$\begin{aligned} h(t)=\ln t+\ln (1-t)-\ln (1-z^2t),~~~r(t)=\frac{1}{[t(1-t)^3(1-z^2t)]^\frac{1}{4}}. \end{aligned}$$
(4.30)

According to Lemma 4.1, the constant prefactor of the intergral in (4.29) is \(\frac{i\coth \pi \mu }{2\pi }\). We use the stationary phase method to calculate the asymptotic behavior of the integral. The stationary point \(t_*\in (0,1)\) defined by \(h'(t_*)=0\) is calculated to be

$$\begin{aligned} t_*=\frac{1-\sqrt{1-z^2}}{z^2}= \frac{1}{1+\sqrt{1-z^2}}. \end{aligned}$$
(4.31)

We also have

$$\begin{aligned} 1-t_*= \frac{\sqrt{1-z^2}}{1+\sqrt{1-z^2}},~~~1-z^2t_*=\sqrt{1-z^2}, \end{aligned}$$
(4.32)

so that

$$\begin{aligned} h(t_*)= & {} -2\ln (1+\sqrt{1-z^2}),~~~ r(t_*)=\frac{1+\sqrt{1-z^2}}{\sqrt{1-z^2}}~~\mathrm{and}\nonumber \\ h''(t_*)= & {} -2\frac{(1+\sqrt{1-z^2})^2}{\sqrt{1-z^2}}. \end{aligned}$$
(4.33)

Applying the stationary phase method and then returning to the original scale (i.e., arbitrary a), we get

$$\begin{aligned} \phi (x,\lambda )=\frac{\sqrt{2}a}{\sqrt{\pi \mu }\sqrt{x}(a^2-x^2)^{\frac{1}{4}}}\cos \left(\mu \ln \frac{a+\sqrt{a^2-x^2}}{x}-\frac{\pi }{4}\right)+O(\mu ^{-1}), \end{aligned}$$
(4.34)

which is valid uniformly on compact subintervals of (0, a). Note that the asymptotics (4.34) in the symmetrical case matches the asymptotics (3.25) for \(\phi _2\) in the general case (cf. (3.25) and (3.36)). Recall that \(\lambda \) and \(\mu \) are related by (3.8).

5 Absence of Discrete Spectrum

In this section we prove that the two Sturm-Liouville problems defined in (2.3) have no discrete spectrum. We will consider only the case \(j=1\), with the other case being analogous. By assumption, if \(\lambda \) is an eigenvalue and f(x) is the corresponding eigenfunction, then f is bounded (and, hence analytic) near \(a_1\) and \(f\in L^2(I_1)\). From (3.8) and (3.9) it follows that if \(\lambda >(a_1^2+a_2^2)/8\), then neither of the solutions \(y_{\pm }(x)\) is in \(L^2(I_1)\). Hence \(f\in L^2(I_1)\) imples \(f\equiv 0\). If \(\lambda =(a_1^2+a_2^2)/8\), the solutions behave like \((-x)^{1/2}\) and \((-x)^{1/2}\ln (-x)\), so no linear combination of two such functions can be in \(L^2(I_1)\).

Suppose next that \(\lambda <(a_1^2+a_2^2)/8\). In this case the solutions of \((L-\lambda )f=0\) behave like \((-x)^{-\frac{1}{2}\pm q}\) as \(x\rightarrow 0^-\) for some \(q>0\). Clearly, only one of the solutions is in \(L^2\). Let f denote the solution which is in \(L^2\) and bounded near \(a_1\). Thus, \(f(x)\sim (-x)^{-\frac{1}{2}+q}\) as \(x\rightarrow 0^-\). We can assume \(f(a_1)\not =0\), since otherwise \(f\equiv 0\). Denote \(g:={\mathcal {H}}_1 f\). Using (2.6) we have

$$\begin{aligned} \lambda g=\lambda {\mathcal {H}}_1 f={\mathcal {H}}_1 L f=L{\mathcal {H}}_1 f=Lg. \end{aligned}$$
(5.1)

By the properties of the Hilbert transform, g has the same behavior at zero as f: \(g(y)\sim y^{-\frac{1}{2}+q}\) as \(y\rightarrow 0^+\). Since \(Lg=\lambda g\) on \(I_2\), we obtain that f and g are the same solutions up to a multiplicative factor, i.e.

$$\begin{aligned} ({\mathcal {H}}_1 f)(y)=kf(y),\ y\in I_2, \end{aligned}$$
(5.2)

where k is a constant. Using that \(f(a_1)\not =0\) and analytically continuing f from \(I_2\) into a neighborhood of \(a_1\), we see that f has a logarithmic singularity there. But this contradicts the assumption that f is analytic in a neighborhood of \(a_1\). Hence \(f\equiv 0\).

Remark 5.1

At first glance it follows from equation (3.43) that \({\mathcal {H}}_1\) preserves the ratio of the coefficients in front of the singularities \((-x)^{-\frac{1}{2}\pm i\mu }\) and, therefore, \({\mathcal {H}}_1\) converts a solution of \((L-\lambda )f=0\) on \(I_1\) into (the analytic continuation of) the same solution on \(I_2\). This would lead to a contradiction similar to the one obtained above. It is easy to check that f and \({\mathcal {H}}_1 f\) are, in fact, two different solutions. Indeed, analytic continuations of \((-x)^{-\frac{1}{2}\pm i\mu }\) from the negative half-axis to the positive half-axis can be written in the form \(c_{\pm }(-x)^{-\frac{1}{2}\pm i\mu }\), where \(c_+\not = c_-\). Hence the ratios of the coefficients in front of the singularities in f and \({\mathcal {H}}_1 f\) at zero are different.

6 Validity of the WKB Solutions

The goal of this section is to construct the WKB solution in a neighborhood of \(x=0\).

If Eq. (2.3) is written as a 2 by 2 system, then the transformation

$$\begin{aligned} Y=\mathrm{diag}\left( 1,\sqrt{\frac{\lambda }{-P}}\right) \tilde{Z} \end{aligned}$$
(6.1)

reduces it to

$$\begin{aligned} \epsilon \tilde{Z}'=\left( \begin{array}{l@{\quad }l} 0 &{} \frac{1}{\sqrt{-P}}\\ -\frac{1}{\sqrt{-P}}+\frac{\epsilon ^2Q}{\sqrt{-P}}&{} -\frac{\epsilon P'}{2P} \end{array} \right) \tilde{Z}, \end{aligned}$$
(6.2)

where \(\epsilon =\frac{1}{\sqrt{\lambda }}\). Using now

$$\begin{aligned} \tilde{Z}=\left( \begin{array}{c@{\quad }c} 1 &{}i\\ i&{} 1 \end{array} \right) Z, \end{aligned}$$
(6.3)

we reduce (6.2) to

$$\begin{aligned} \epsilon Z'=\left[ \left( \begin{array}{c@{\quad }c} \frac{i}{\sqrt{-P}} &{}0\\ 0&{} - \frac{i}{\sqrt{-P}} \end{array} \right) -\frac{\epsilon }{4} \left( \begin{array}{c@{\quad }c} \frac{P'}{P}+2i\epsilon \frac{Q}{\sqrt{-P}} &{} -i\frac{P'}{P} - 2\epsilon \frac{Q}{\sqrt{-P}} \\ i\frac{P'}{P}- 2\epsilon \frac{Q}{\sqrt{-P}} &{} \frac{P'}{P}-2i\epsilon \frac{Q}{\sqrt{-P}} \end{array} \right) \right] Z=AZ. \end{aligned}$$
(6.4)

Using the Pauli matrices

$$\begin{aligned} {\sigma }_1= \begin{pmatrix} 0 &{} 1\\ 1&{}0 \end{pmatrix},~~~ {\sigma }_2= \begin{pmatrix} 0 &{} -i\\ i&{}0 \end{pmatrix},~~~ {\sigma }_3= \begin{pmatrix} 1 &{} 0\\ 0&{}-1 \end{pmatrix}, \end{aligned}$$

we can write \( A=A_0+\epsilon A_1+\epsilon ^2A_2\),   where

$$\begin{aligned} A_0=\frac{i {\sigma }_3}{\sqrt{-P}},~A_1=-\frac{P'}{4P}(I+ {\sigma }_2),~A_2=\frac{Q}{2\sqrt{-P}}( {\sigma }_1-i {\sigma }_3). \end{aligned}$$
(6.5)

Now the transformation \(Z=(I+\epsilon U)X\), where \(U=\frac{P'}{8\sqrt{-P}} {\sigma }_1\), reduces (6.4) to \(\epsilon X'=\tilde{B}X\), where

$$\begin{aligned} \tilde{B}=A_0+\epsilon \mathrm{diag}A_1+\epsilon ^2B(\epsilon ) \end{aligned}$$
(6.6)

and \(B(\epsilon )\) is defined by the equation

$$\begin{aligned} (I+\epsilon U) B(\epsilon )=A_2(I+\epsilon U)+A_1U-U\mathrm{diag}A_1-U'. \end{aligned}$$
(6.7)

It is clear that \(B(\epsilon )\) is analytic near \(\epsilon =0\) provided \(\epsilon U\) is small. Direct calculation yields

$$\begin{aligned} B(0)=\left( -\frac{(P')^2}{32(-P)^\frac{3}{2}}-\frac{Q}{2\sqrt{-P}}\right) i {\sigma }_3+\left( \frac{2PP''-(P')^2}{16(-P)^\frac{3}{2}}+\frac{Q}{2\sqrt{-P}}\right) {\sigma }_1. \end{aligned}$$
(6.8)

Consider equation \(\epsilon X'=\tilde{B}X\) as a perturbation of the diagonal equation

$$\begin{aligned} \epsilon W'=(A_0+\epsilon \mathrm{diag}A_1)W, \end{aligned}$$
(6.9)

which has a solution

$$\begin{aligned} W=P^{-\frac{1}{4}}e^{{\frac{i}{\epsilon }}\int ^z\frac{d\zeta }{\sqrt{-P(\zeta )}} {\sigma }_3}. \end{aligned}$$
(6.10)

Looking now for a solution of \(\epsilon X'=\tilde{B}X\) in the form \(X=TW\), we obtain

$$\begin{aligned} \epsilon T'=\left[ A_0+\epsilon \mathrm{diag}A_1,T\right] +\epsilon ^2 BT = \left[ A_0,T\right] +\epsilon ^2 BT, \end{aligned}$$
(6.11)

where we have used the fact that \(\mathrm{diag}A_1\) commutes with any matrix T and matrix W is nondegenerate. Differential equation (6.11) can be written as the Volterra integral equation

$$\begin{aligned} T(x)=I+\epsilon \int ^x e^{\frac{i {\sigma }_3}{\epsilon }\int ^x_\zeta \frac{d\xi }{\sqrt{-P(\xi )}}}B(\zeta )T(\zeta ) e^{-\frac{i {\sigma }_3}{\epsilon }\int ^x_\zeta \frac{d\zeta }{\sqrt{-P(\zeta )}}}d\zeta =I+\mathcal {I}T, \end{aligned}$$
(6.12)

where different contours of integration with the same endpoint x will be selected (see below) for each entry of the matrix integrand. We denote this collection of contours by \(\tilde{\gamma }(x)\).

Fig. 1
figure 1

The map v(x) maps the complex x-plane (left) into the region of the complex v-plane, shown on the right. The point shown on \((a_1,0)\) is \(-e^{-\frac{1}{\sqrt{\epsilon }}}\)

Full size image

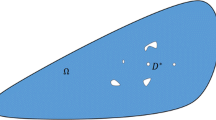
We will solve equation (6.12) by iterations in a certain region \(\Omega =\Omega (\epsilon )\) of the complex x plane that comes exponentially close to \(x=0\). In order to describe the region \(\Omega =\Omega (\epsilon )\) and contours \(\tilde{\gamma }(z)\) (and taking into account (3.10)), we use the conformal mapping

$$\begin{aligned} v(x)=\int ^x_{a_1}\frac{d\zeta }{\sqrt{-P(\zeta )}} \end{aligned}$$
(6.13)

that maps the upper half plane \(\mathfrak {I}x\ge 0\) into the semi-strip \(-\frac{\pi }{\sqrt{-a_1a_2}}\le \mathfrak {I}v\le 0\) and \(\mathfrak {R}v\le 0\) of the complex v plane, where \(v(a_1)=0\), \(v(a_2)=-\frac{i\pi }{\sqrt{-a_1a_2}}\) and \(v(0)=-\infty \), see Fig. 1. The lower half plane \(\mathfrak {I}x\ge 0\) is mapped into the complex conjugated semi-strip. Let us pick an arbitrary fixed point \(a_*\in (0,a_2)\), for example, \(a_*=a_2/2\). By \(\widehat{\Omega }=\widehat{\Omega }(\epsilon )\) we define the isosceles triangle with the base \([\overline{v(a_*)},v(a_*)]\) and the (third) vertex at \(v(-e^{-\frac{1}{\sqrt{\epsilon }}})\). According to (3.10),

$$\begin{aligned} v\left( -e^{-\frac{1}{\sqrt{\epsilon }}}\right) =-\epsilon ^{-\frac{1}{2}} +O(1) ~~~~~\mathrm{as}~~~\epsilon \rightarrow 0. \end{aligned}$$
(6.14)

Then \(\Omega \) is the preimage of \(\widehat{\Omega }\) under the map (6.13), which is schematically shown on Fig. 2. It contains the segment \([a_{**},-e^{-\frac{1}{\sqrt{\epsilon }}}]\), \(a_{**}\in (a_1,0)\), where \(v(a_{**})=\mathfrak {R}v(a_*)\). Contours \(\tilde{\gamma }_{1,1}(x)\), \(\tilde{\gamma }_{2,2}(x)\) are the preimages of the segments \([v(a_*),v(x)]\), \([\overline{v(a_*)},v(x)]\). The remaining two contours connect \(\frac{a_1}{2}\) and x.

Fig. 2
figure 2

The triangular region \(\widehat{\Omega }\). The preimage \(\Omega \) of \(\widehat{\Omega }\) is shown on the left. It has the shape of an oval with a part of its interior (another oval) removed. Given a point \(x\in \Omega \), the contours \(\tilde{\gamma }_{1,1}(x)\), \(\tilde{\gamma }_{2,2}(x)\), are the preimages of the segments \([v(a_*),v(x)]\), \([\overline{v(a_*)},v(x)]\), respectively. The latter are shown on the right. The unmarked points are \(-e^{-\frac{1}{\sqrt{\epsilon }}}\)—on the left, and its image \(v(-e^{-\frac{1}{\sqrt{\epsilon }}})\)—on the right

Full size image

Let \(\widehat{\Omega }_0\), \(\Omega _0\) denote the semi-strip \(|\mathfrak {I}v|\le \frac{\pi }{\sqrt{-a_1a_2}}\), \(\mathfrak {R}v\le v(a_*)\), and its preimage under the map (6.13), respectively. Note that \(\Omega _0\) contains both shores of the branchcut \([0,a_*]\), and \(\Omega (\epsilon )\subset \Omega _0\) for all small \(\epsilon >0\). Denote by \(\mathcal {B}\) the vector space of two by two matrix functions M(x), which are analytic in \(\Omega _0\) and bounded in \(\Omega (\epsilon )\). The vector space \(\mathcal {B}\) becomes a Banach space with the norm given by \(\sup _{x\in \Omega _0} \Vert M(x)\Vert \), where \(\Vert \cdot \Vert \) denotes a matrix norm.

The Volterra equation (6.12) can be written in the operator form as

$$\begin{aligned} T=(\mathrm{Id}-\mathcal {I})^{-1}I=\sum _{j=0}^\infty \mathcal {I}^jI. \end{aligned}$$
(6.15)

In order to show the convergence of the series in (6.15), we need to estimate the norm of \(\mathcal {I}\). In the variable v, the operator \(\mathcal {I}\) becomes

$$\begin{aligned} \mathcal {I}M=\epsilon \int _{\widehat{\gamma }(v)} e^{\frac{i {\sigma }_3}{\epsilon }(v-\xi ) }\tilde{B}(\xi ) M(\xi ) e^{-\frac{i {\sigma }_3}{\epsilon }(v-\xi )}d\xi , \end{aligned}$$
(6.16)

where \(\tilde{B}(\xi )=\left. \sqrt{-P(x)}B(x)\right| _{x=v^{-1}(\xi )}\). According to (6.6)–(6.8), the matrix \(\sqrt{-P(x)}B(x)\in \mathcal {B}\). Let \( \Vert \tilde{B}(x)\Vert =b\). It follows then from the construction of \(\mathcal {I}\) and (6.16) that

$$\begin{aligned} \Vert \mathcal {I}M \Vert \le 2b\epsilon ^\frac{1}{2}\Vert M\Vert . \end{aligned}$$
(6.17)

Thus, choosing \(\epsilon <\frac{1}{4b^2}\), we can guarantee the convergence of the series in (6.15), that is, the convergence of iterations to the solution of the Volterra equation (6.12).

According to the above argument, we have constructed a fundamental solution of the form

$$\begin{aligned} Y(x)= & {} \mathrm{diag}\left(1,\sqrt{\frac{\lambda }{-P}}\right)\left( \begin{array}{cc} 1 &{}i\\ i&{} 1 \end{array}\right) \left( I+\frac{\epsilon P'}{8\sqrt{-P}} {\sigma }_1\right) \nonumber \\&\times \left( I+O\big (\epsilon ^{\frac{1}{2}}\big )\right) (-P)^{-\frac{1}{4}}e^{{\frac{i}{\epsilon }}\int ^x_{a_1}\frac{d\zeta }{\sqrt{-P(\zeta )}} {\sigma }_3} \end{aligned}$$
(6.18)

on \(\Omega (\epsilon )\). Then, according to (3.8), (3.10), there exist two solution \(Y_\pm (x)\) of (2.3), given by

$$\begin{aligned} Y_\pm (x)= & {} (-P)^{-\frac{1}{4}}e^{\pm {\frac{i}{\epsilon }}\int ^x_{a_1}\frac{d\zeta }{\sqrt{-P(\zeta )}}}\Big (I+O\big (\epsilon ^{\frac{1}{2}}\big )\Big )\nonumber \\= & {} \frac{e^{\pm i\mu \kappa }}{(-a_1a_2)^\frac{1}{4}}(-x)^{-\frac{1}{2}\pm i\mu }(1+O\big (\epsilon ^\frac{1}{2}\big )+O(x)). \end{aligned}$$
(6.19)

7 Validity of the Inner Solutions

Here we prove an estimate for solutions (3.9), called inner solutions, on a small interval centered at \(x=0\). This estimate allows us to match the WKB and inner solutions.

Introducing \(y_1=f\), \(y_2=Pf'\), we can reduce the original equation (2.3) to the matrix equation

$$\begin{aligned} \tilde{Y}'=\left( \begin{array}{ll} 0 &{}\quad \frac{1}{P(x)}\\ \lambda -Q&{}\quad 0 \end{array} \right) \tilde{Y}, \end{aligned}$$
(7.1)

where the columns of the matrix \(\tilde{Y}\) are \((y_j,y'_j)\), \(j=1,2\), respectively. The shearing transformation

$$\begin{aligned} \tilde{Y}=\mathrm{diag}\big (1,\sqrt{\lambda }x\big ) Y \end{aligned}$$
(7.2)

reduces (7.1) to

$$\begin{aligned} Y'=&\left( \begin{array}{c@{\quad }c} 0 &{} \frac{\sqrt{\lambda }}{x(x-a_1)(x-a_2)}\\ \frac{\lambda -Q}{\sqrt{\lambda }x}&{} -\frac{1}{x} \end{array} \right) Y= \left( \frac{\tilde{B}}{x}+\tilde{M}\right) Y \nonumber \\ =&\left[ \frac{1}{x} \left( \begin{array}{c@{\quad }c} 0 &{}\frac{\sqrt{\lambda }}{a_1a_2}\\ \sqrt{\lambda }-\frac{(a_1+a_2)^2}{8 \sqrt{\lambda }}&{} - 1 \end{array} \right) + \left( \begin{array}{c@{\quad }c} 0 &{} \frac{\sqrt{\lambda }(a_1a+2-x)}{(x-a_1)(x-a_2)}\\ \frac{a_1+a_2-2x}{\sqrt{\lambda }x}&{} 0 \end{array} \right) \right] Y, \end{aligned}$$
(7.3)

where \(\tilde{B},\tilde{M}\) are the first and the second terms in the square brackets and \(M=M(x)\) is analytic at \(x=0\).

It is clear (and can be easily verified) that

$$\begin{aligned} \tilde{B}= & {} U\mathrm{diag}\left( -\frac{1}{2}+i\mu ,-\frac{1}{2}-i\mu \right) U^{-1},~~\mathrm{where}\nonumber \\ U= & {} \left( \begin{array}{c@{\quad }c} \frac{1}{a_1a_2} &{} \frac{1}{a_1a_2}\\ -\frac{1}{2\sqrt{\lambda }}+i\frac{\mu }{\sqrt{\lambda }}&{}-\frac{1}{2\sqrt{\lambda }}-i\frac{\mu }{\sqrt{\lambda }} \end{array} \right) , \end{aligned}$$
(7.4)

and \(\mu \) is given in (3.8). The change of variables \(Y=UZ\) reduces (7.3) to \(Z'=(\frac{ B}{x}+ M)Z\), where \(B=\mathrm{diag}(-\frac{1}{2}+i\mu ,-\frac{1}{2}-i\mu )\) and \(M=U^{-1}\tilde{B} U\). Another change of variables \(Z=TW\), where \(W=x^B\), gives

$$\begin{aligned} T'=\frac{1}{x} [i\mu {\sigma }_3,T]+MT, \end{aligned}$$
(7.5)

where, according to (7.1), (7.4), \(M=O(\sqrt{\lambda })\). As in Sect. 6, we replace the latter system with the Volterra equation

$$\begin{aligned} T(x)=I+x^{i\mu {\sigma }_3}\int ^x_0 \zeta ^{-i\mu {\sigma }_3} M(\zeta )T(\zeta )\zeta ^{i\mu {\sigma }_3} d\zeta x^{i\mu {\sigma }_3}=I+\mathcal {I}T. \end{aligned}$$
(7.6)

Since \(|x^{\pm i\mu }|=1 \) on \({\mathbb {R}}\setminus \{0\}\), we conclude that on the interval \(\tilde{J}=(-\lambda ^{-1},\lambda ^{-1})\subset {\mathbb {R}}\), the norm of the operator \(\mathcal {I}\) does not exceed \(O(\lambda ^{-\frac{1}{2}})\). Thus, we obtain

$$\begin{aligned} \tilde{Y}(x)=\mathrm{diag}(1,\sqrt{\lambda }x) U(I+O(\lambda ^{-\frac{1}{2}}))x^{-\frac{1}{2}I+i\mu {\sigma }_3} \end{aligned}$$
(7.7)

uniformly on \(\tilde{J}\). This immediately implies (see (3.9))

$$\begin{aligned} y_{\pm }=(-x)^{-\frac{1}{2}\pm i\mu }\Big (1+O\big (\lambda ^{-\frac{1}{2}}\big )\Big ) \end{aligned}$$
(7.8)

uniformly on \(\tilde{J}\). Since \(\tilde{J}\) has a common segment with \(\Omega \) for large \(\lambda \), we can match the WKB and the inner solutions there. Thus, comparing \(Y_\pm \) and \(y_\pm \) on \(\Omega (\epsilon )\), we conclude that

$$\begin{aligned} Y_\pm (x)= \frac{e^{\pm i\mu \kappa }}{(-a_1a_2)^\frac{1}{4}}y_\pm (x)\Big (1+O\big (\lambda ^{-\frac{1}{2}}\big )\Big ). \end{aligned}$$
(7.9)