Kakeya-Type Sets Over Cantor Sets of Directions in $\mathbb {R}^{d+1}$

Abstract

Given a Cantor-type subset $\Omega$ of a smooth curve in $\mathbb R^{d+1}$, we construct examples of sets that contain unit line segments with directions from $\Omega$ and exhibit analytical features similar to those of classical Kakeya sets of arbitrarily small $(d+1)$-dimensional Lebesgue measure. The construction is based on probabilistic methods relying on the tree structure of $\Omega$, and extends to higher dimensions an analogous planar result of Bateman and Katz (Math Res Lett 15(1):73–81, 2008). In contrast to the planar situation, a significant aspect of our analysis is the classification of intersecting tube tuples relative to their location, and the deduction of intersection probabilities of such tubes generated by a random mechanism. The existence of these Kakeya-type sets implies that the directional maximal operator associated with the direction set $\Omega$ is unbounded on $L^p(\mathbb {R}^{d+1})$ for all $1\le p<\infty$.

1 Introduction

1.1 Background

A Kakeya set (also called a Besicovitch set) in $\mathbb {R}^{d+1}$ is a set that contains a unit line segment in every direction. The study of such sets spans approximately a hundred years. The first major analytical result in this area, due to Besicovitch [5], shows that there exist Kakeya sets with Lebesgue measure zero. Over the past forty-plus years, dating back at least to the work of Fefferman [10], the study of Kakeya sets has been a simultaneously fruitful and vexing endeavor. On one hand its applications have been found in many deep and diverse corners of analysis, PDEs, additive combinatorics and number theory. On the other hand, certain fundamental questions concerning the size and dimensionality of such sets have eluded complete resolution.

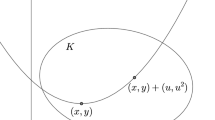
In order to obtain quantitative estimates for analytical purposes, it is often convenient to work with the $\delta$-neighborhood of a Kakeya set, rather than the set itself. Here $\delta$ is an arbitrarily small positive constant. The $\delta$-neighborhood of a Kakeya set is therefore an object that consists of many thin $\delta$-tubes. A $\delta$-tube is by definition a cylinder of unit axial length and spherical cross-section of radius $\delta$. The defining property of a zero measure Kakeya set dictates that the volume of its $\delta$-neighborhood goes to zero as $\delta \rightarrow 0$, while the sum total of the sizes of these tubes is roughly a positive absolute constant. Indeed, a common construction of thin Kakeya sets in the plane (see for example [23, Chap. 10]) relies on the following fact: given any $\epsilon > 0$, there exists an integer $N \ge 1$ and a collection of distinct $2^{-N}$-tubes, i.e., a family of $1 \times 2^{-N}$ rectangles, $\{ P_t : 1 \le t \le 2^{N}\}$ in $\mathbb R^{2}$ such that

$$\begin{aligned} \left| \bigcup _t P_t \right| < \epsilon , \text { and } \sum _{t} |\widetilde{P}_t| = 1. \end{aligned}$$

(1.1)

Here $|\cdot |$ denotes Lebesgue measure (in this case two-dimensional), and $\widetilde{P}_t$ denotes the “reach” of the tube $P_t$, namely the tube obtained by translating $P_t$ by two units in the positive direction along its axis. While it is not known that every Kakeya set in two or higher dimensions shares a similar feature, the ones that do have found repeated applications in analysis. Fundamental results have relied on the existence of such sets, for example the lack of differentiation for integral averages over parallelepipeds of arbitrary orientation, and the counterexample of the ball multiplier [23, Chap. 10]. The property described above continues to be the motivation for the Kakeya-type sets that we will study in the present paper.

Definition 1.1

For $d \ge 1$, we define a set of directions $\Omega$ to be a compact subset of $\mathbb R^{d+1}$. We say that a tube in $\mathbb R^{d+1}$ has orientation $\omega \in \Omega$ or a tube is oriented in direction $\omega$ if its axis is parallel to $\omega$. We say that $\Omega$ admits Kakeya-type sets if one can find a constant $C_0 \ge 1$ such that for any $N\ge 1$, there exists $\delta _N > 0$, $\delta _N \rightarrow 0$ as $N \rightarrow \infty$ and a collection of $\delta _N$-tubes $\{P_t^{(N)}\} \subseteq \mathbb R^{d+1}$ with orientations in $\Omega$ with the following property:

$$\begin{aligned} \text {if} \,\,\,E_N := \bigcup _t P_t^{(N)},\quad E_N^*(C_0) := \bigcup _t C_0P_t^{(N)},\,\,\text {then}\,\, \lim _{N\rightarrow \infty }\frac{|E^*_N(C_0)|}{|E_N|} = \infty . \end{aligned}$$

(1.2)

Here $|\cdot |$ denotes $(d+1)$-dimensional Lebesgue measure, and $C_0P_t^{(N)}$ denotes the tube with the same centre, orientation and cross-sectional radius as $P_t^{(N)}$, but $C_0$ times its length. We will refer to $\{ E_N : N \ge 1\}$ as sets of Kakeya-type.

Specifically in this paper, we will be concerned with certain subsets of a curve, either on the sphere $\mathbb S^d$, or equivalently on a hyperplane at unit distance from the origin, that admit Kakeya-type sets.

Kakeya and Kakeya-type sets of zero measure have intrinsic structural properties that continually prove useful in an analytical setting. The most important of these properties is arguably the so-called stickiness property, originally observed by Wolff [25]. Roughly speaking, if a Kakeya-type set is a collection of many overlapping line segments, then stickiness dictates that the map which sends a direction to the line segment in the set with that direction is almost Lipschitz, with respect to suitably defined metrics. Another way of expressing this is that if the origins of two overlapping $\delta$-tubes are positioned close together, then the angle between these thickened line segments must be small, resulting in the intersection taking place far away from the respective bases. This idea, which has been formalized in several different ways in the literature [13–15, 25], will play a central role in our results, as we will discuss in Sect. 6.

Geometric and analytic properties of Kakeya and Kakeya-type sets are often studied using a suitably chosen maximal operator. Conversely, certain blow-up behavior for such operators typically follow from the existence of such sets. We introduce two such well-studied operators for which the existence of Kakeya-type sets implies unboundedness.

Given a set of directions $\Omega$, consider the directional maximal operator $D_{\Omega }$ defined by

$$\begin{aligned} D_{\Omega }f(x) := \sup _{\omega \in \Omega }\sup _{h>0}\frac{1}{2h}\int _{-h}^{h} |f(x+\omega t)|dt, \end{aligned}$$

(1.3)

where $f:\mathbb {R}^{d+1}\rightarrow \mathbb {C}$ is a function that is locally integrable along lines. Also, for any locally integrable function f on $\mathbb R^{d+1}$, consider the Kakeya–Nikodym maximal operator $M_{\Omega }$ defined by

$$\begin{aligned} M_{\Omega }f(x) := \sup _{\omega \in \Omega }\sup _{\begin{array}{c} P\ni x\\ P\parallel \omega \end{array}} \frac{1}{|P|} \int _P |f(y)|dy, \end{aligned}$$

(1.4)

where the inner supremum is taken over all cylindrical tubes P containing the point x, oriented in the direction $\omega$. The tubes are taken to be of arbitrary length l and have circular cross-section of arbitrary radius r, with $r\le l$. If $\Omega$ is a set with nonempty interior, then due to the existence of Kakeya sets with $(d+1)$-dimensional Lebesgue measure zero [5], $D_{\Omega }$ and $M_{\Omega }$ are both unbounded as operators on $L^p(\mathbb {R}^{d+1})$ for all $1 \le p<\infty$. More generally, if $\Omega$ admits Kakeya-type sets, then these operators are unbounded on $L^p(\mathbb {R}^{d+1})$ for all $1 \le p<\infty$ (see Sect. 1.2 below).

The complementary case when $\Omega$ has empty interior has been studied extensively in the literature. It is easy to see that the operators in (1.3) and (1.4) exhibit a kind of monotonicity: if $\Omega \subset \Omega '$, then $D_{\Omega }f(x)\le D_{\Omega '}f(x)$ and $M_{\Omega }f(x)\le M_{\Omega '}f(x)$, for any suitable function f. Since these operators are unbounded when $\Omega '= \text { the unit sphere } \mathbb S^d$, treatment of the positive direction—identifying “small” sets of directions $\Omega$ for which these operators are bounded on some $L^p$—has garnered much attention [1, 2, 6, 20–22]. These types of results rely on classical techniques in $L^p$-theory, such as square function estimates, Littlewood-Paley theory and almost-orthogonality principles.

For a general dimension $d\ge 1$, Nagel et al. [20] showed that $D_{\Omega }$ is bounded on all $L^p(\mathbb R^{d+1})$, $1<p\le \infty$, when $\Omega = \{(v_i^{a_1},\ldots ,v_i^{a_{d+1}}) : i \ge 1\}$. Here $0<a_1<\cdots <a_{d+1}$ are fixed constants, and $\{ v_i : i \ge 1\}$ is a sequence obeying $0<v_{i+1}\le \lambda v_i$ for some lacunary constant $0<\lambda <1$. Carbery [6] showed that $D_{\Omega }$ is bounded on all $L^p(\mathbb R^{d+1})$, $1<p\le \infty$, in the special case when $\Omega$ is the set given by the $(d+1)$-fold Cartesian product of a geometric sequence, namely $\Omega = \{(r^{k_1},\ldots ,r^{k_{d+1}}) : k_1,\ldots ,k_{d+1}\in \mathbb {Z}^+\}$ for some $0<r<1$. Very recently, Parcet and Rogers [21] generalized an almost-orthogonality result of Alfonseca [1] to extend the boundedness of $D_{\Omega }$ on all $L^p(\mathbb R^{d+1})$, $1<p\le \infty$, for sets $\Omega$ that are lacunary of finite order, defined in a suitable sense. Building upon previous work of Alfonseca, Soria, and Vargas [2], Sjögren and Sjölin [22] and Nagel et al. [20], the recent result of Parcet and Rogers [21] recovers those of its predecessors.

Aside from this set of positive results with increasingly weak hypotheses, there has also been much development in the negative direction, pioneered by Bateman, Katz and Vargas [3, 4, 7, 8, 12, 24]. Of special significance to this article is the work of Bateman and Katz [4], where the authors establish that $D_{\Omega }$ is unbounded in $L^p(\mathbb R^2)$ for all $1 \le p < \infty$ if $\Omega = \{(\cos \theta , \sin \theta ): \theta \in \mathcal C_{1/3} \}$, where $\mathcal C_{1/3}$ is the Cantor middle-third set. A crowning success of the methodology of [4] combined with the aforementioned work in the positive direction (in particular [1]) is a result by Bateman [3] that gives a complete characterization of the $L^p$-boundedness of $D_{\Omega }$ and $M_{\Omega }$ in the plane, while also describing all direction sets $\Omega$ that admit planar sets of Kakeya-type. The distinctive feature of this latter body of work [3, 4] dealing with the negative point of view is the construction of counterexamples using a random mechanism that exploits the property of stickiness. We too adopt this approach to construct Kakeya-type sets in $\mathbb R^{d+1}$, $d \ge 2$ consisting of tubes whose orientations lie along certain subsets of a curve on the hyperplane $\{1\}\times \mathbb {R}^d$.

1.2 Results

As mentioned above, Bateman and Katz [4] establish the unboundedness of $D_{\Omega }$ and $M_{\Omega }$ on $L^p(\mathbb {R}^2)$, for all $p \in [1,\infty )$, when $\Omega = \{(\cos \theta , \sin \theta ) : \theta \in \mathcal C_{1/3} \}$ by constructing suitable Kakeya-type sets in the plane. In this paper, we extend their construction to the general $(d+1)$-dimensional setting. To this end, we first describe what we mean by a Cantor set of directions in $(d+1)$ dimensions.

Fix some integer $M\ge 3$. Construct an arbitrary Cantor-type subset of [0, 1) as follows.

• Partition [0, 1] into M subintervals of the form [a, b], all of equal length $M^{-1}$. Among these M subintervals, choose any two that are not adjacent (i.e., do not share a common endpoint); define $\mathcal {C}_M^{[1]}$ to be the union of these chosen subintervals, called first stage basic intervals.

• Partition each first stage basic interval into M further (second stage) subintervals of the form [a, b], all of equal length $M^{-2}$. Choose two non-adjacent second stage subintervals from each first stage basic one, and define $\mathcal {C}_M^{[2]}$ to be the union of the four chosen second stage (basic) intervals.

• Repeat this procedure ad infinitum, obtaining a nested, non-increasing sequence of sets. Denote the limiting set by $\mathcal {C}_M$:

  $$\begin{aligned} \mathcal {C}_M = \bigcap _{k=1}^{\infty } \mathcal {C}_M^{[k]}. \end{aligned}$$

  We call $\mathcal {C}_M$ a generalized Cantor-type set (with base M).

While conventional uniform Cantor sets, such as the Cantor middle-third set, are special cases of generalized Cantor-type sets, the latter may not in general look like the former. In particular, sets of the form $\mathcal C_M$ need not be self-similar, although the actual sequential selection criterion leading up to their definition will be largely irrelevant for the content of this article. It is well-known (see [9, Chap. 4]) that such sets have Hausdorff dimension at most $\log 2/\log M$. By choosing M large enough, we can thus construct generalized Cantor-type sets of arbitrarily small dimension.

In this paper, we prove the following.

Theorem 1.2

Let $\mathcal {C}_M\subset [0,1]$ be a generalized Cantor-type set described above. Let $\gamma : [0,1]\rightarrow \{1\} \times [-1,1]^d$ be an injective map that satisfies a bi-Lipschitz condition

$$\begin{aligned} \forall \ x,y,\ c|x-y| \le |\gamma (x)-\gamma (y)| \le C|x-y|, \end{aligned}$$

(1.5)

for some absolute constants $0 < c < 1 < C < \infty$. Set $\Omega = \{\gamma (t) : t\in \mathcal {C}_M\}$. Then

• (a) the set $\Omega$ admits Kakeya-type sets,

• (b) the operators $D_{\Omega }$ and $M_{\Omega }$ are unbounded on $L^p(\mathbb R^{d+1})$ for all $1 \le p < \infty$.

The condition in Theorem 1.2 that $\gamma$ satisfies a bi-Lipschitz condition can be weakened, but it will help in establishing some relevant geometry. Throughout this exposition, it is instructive to envision $\gamma$ as a smooth curve on the plane $x_1=1$, and we recommend the reader does this to aid in visualization. Our underlying direction set of interest $\Omega = \gamma (\mathcal {C}_M)$ is essentially a Cantor-type subset of this curve.

The main focus of this article, for reasons explained below, is on (a), not on (b). Indeed, the implication (a) $\implies$ (b) is well-known in the literature; let $f = \mathbf {1}_{E_N}$, where $E_N$ is as in (1.2), and let $P_t^{(N)} = P_t$ be one of the tubes that constitute $E_N$. If $x\in C_0 P_t$, then

$$\begin{aligned} M_{\Omega }f(x) \ge \frac{1}{|C_0 P_t|} \int _{C_0 P_t} f(y)dy. \end{aligned}$$

The integrand is pointwise bounded from below by $\mathbf {1}_{P_t}$; thus,

$$\begin{aligned} M_{\Omega }f(x) \ge \frac{1}{|C_0 P_t|} \int _{C_0 P_t} \mathbf {1}_{P_t}(y)dy = \frac{|P_t|}{|C_0 P_t|} = \frac{1}{C_0}. \end{aligned}$$

A similar conclusion holds for $D_{\Omega }f(x)$. Thus there exists a constant $c_0 = c_0(C_0) > 0$ such that

$$\begin{aligned} \min \bigl [ D_{\Omega }f(x), M_{\Omega }f(x) \bigr ] \ge c_0 \,\, \text { for } x \in E_N^{*}(C_0). \end{aligned}$$

(1.6)

This shows that

$$\begin{aligned} \min \bigl [ ||D_{\Omega }||_{p \rightarrow p}, ||M_{\Omega }||_{p \rightarrow p} \bigr ] \ge c_0 \left( \frac{|E_N^{*}(C_0)|}{|E_N|} \right) ^{\frac{1}{p}}, \,\, \text { which } \rightarrow \infty \text { if } 1 \le p < \infty . \end{aligned}$$

On the other hand, the condition (a) of Theorem 1.2 is not a priori strictly necessary in order to establish part (b) of the theorem. Suppose that $\{G_N : N \ge 1\}$ and $\{ \widetilde{G}_N : N \ge 1\}$ are two collections of sets with $|\widetilde{G}_N|/|G_N| \rightarrow \infty$, enjoying the additional property that for any point $x \in \widetilde{G}_N$, there exists a finite line segment originating at x and pointing in a direction of $\Omega$, which spends at least a fixed positive proportion of its length in $G_N$. By an easy adaptation of the argument in (1.6), the sequence of test functions $f_N = 1_{G_N}$ would then prove the claimed unboundedness of $D_{\Omega }$. Kakeya-type sets, if they exist, furnish one such family of test functions with $G_N = E_N$ and $\widetilde{G}_N = E_N^{*}$.

In [21], Parcet and Rogers construct, for certain examples of direction sets, families of sets $G_N$ that supply a different class of test functions sufficient to prove unboundedness of the associated directional maximal operators. The direction sets considered in [21] are different from those under examination here, and we are currently unaware if Theorem 1.2 (b) could be proved using a similar construction. A set as constructed in [21] is typically a Cartesian product of a planar Kakeya-type set with a cube, and as such not of Kakeya-type according to Definition 1.1. In particular, it consists of rectangular parallelepipeds with possibly different sidelengths, with these sides not necessarily pointing in a direction from the underlying direction set $\Omega$, although there are line segments with orientations from $\Omega$ contained within them. Further, in contrast with Definition 1.1, $\widetilde{G}_N$ need not be obtained by translating $G_N$ along its longest side. Our main goal is to prove Theorem 1.2 (a), which in turn would imply Theorem 1.2 (b) via the argument above. This requires us to understand several technical differences between the two-dimensional and higher-dimensional settings.

The reason for considering Kakeya-type sets in this paper is twofold. First, they appear as natural generalizations of a classical feature of planar Kakeya set constructions, as explained in (1.1). Studying higher-dimensional extensions of this phenomenon is of interest in its own right, and this article provides a concrete illustration of a sparse set of directions that gives rise to a similar phenomenon. Perhaps more importantly, we use the special direction sets in this paper as a device for introducing certain machinery whose scope reaches beyond these examples. In [16], we prove Theorem 1.2 for a much more general class of direction sets that include but could be far sparser than the Cantor-like sets described in this paper. In addition to the framework introduced in [4], the methods developed in the present article, specifically the investigation of root configurations and slope probabilities in Sects. 7 and 8 are central to the analysis in [16]. While the consideration of general direction sets in [16] necessarily involves substantial technical adjustments, many of the main ideas of that analysis can be conveyed in the simpler setting of the Cantor example that we treat here. As such, we recommend that the reader approach the current paper as a natural first step in the process of understanding properties of direction sets that give rise to unbounded directional and Kakeya–Nikodym maximal operators on $L^p(\mathbb {R}^{d+1})$.

2 Overview of the Proof of Theorem 1.2

2.1 Steps of the Proof and Layout

The basic structure of the proof is modeled on [4], with some important distinctions that we point out below. Our goal is to construct a family of tubes rooted on the hyperplane $\{0\} \times [0,1)^d$, the union of which will eventually give rise to the Kakeya-type set. The slopes of the constituent tubes will be assigned from $\Omega$ via a random mechanism involving stickiness akin to the one developed by Bateman and Katz [4]. The description of this random mechanism is in Sect. 6, with the required geometric and probabilistic background collected en route in Sects. 3, 4 and 5. The essential elements of the construction, barring the details of the slope assignment, have been laid out in Sect. 2.2 below. The main estimates leading to the proof of Theorem 1.2 are (2.5) and (2.6) in Proposition 2.1 in this section. Of these the first, a precise version of which is available in Proposition 6.4, provides a lower bound of $a_N= \sqrt{\log N}/N$ on the size of the part of the tubes lying near the root hyperplane. The second inequality, also quantified in Proposition 6.4, yields an upper bound of $b_N = 1/N$ for the portion away from it. The disparity in the relative sizes of these two parts is the desired conclusion of Theorem 1.2

The language of trees was a key element in the random construction of [3, 4]. We continue to adopt this language, introducing the relevant definitions in Sect. 4 and providing some detail on the connection between the geometry of $\Omega$ and a tree encoding it. Specifically, the notion of Bernoulli percolation on trees plays an important role in the proof of (2.6) with $b_N = 1/N$, as it did in the two-dimensional setting. The higher-dimensional structure of $\Omega$ does however result in minor changes to the argument, and the general percolation-theoretic facts necessary for handling (2.6) have been compiled in Sect. 5. Other probabilistic estimates specific to the random mechanism of Sect. 6 and central to the derivation of (2.5) are separately treated in Sect. 7. The proof is completed in Sects. 8 and 9.

Of the two estimates (2.5) and (2.6) necessary for the Kakeya-type construction, the first is the most significant contribution of this paper. A deterministic analogue of (2.5) was used in [3, 4], where a similar lower bound for the size of the Kakeya-type set was obtained for every slope assignment $\sigma$ in a certain measure space. The counting argument that led to this bound fails to produce the necessary estimate in higher dimensions and is replaced here by a probabilistic statement that suffices for our purposes. More precisely, the issue is the following. A large lower bound on a union of tubes follows if they do not have significant pairwise overlap among themselves; i.e., if the total size of pairwise intersections is small. In dimension two, a good upper bound on the size of this intersection was available uniformly in every sticky slope assignment. Although the argument that provided this bound is not transferable to general dimensions, it is still possible to obtain the desired bound with large probability. A probabilistic statement similar to but not as strong as (2.5) can be derived relatively easily via an estimate on the first moment of the total size of random pairwise intersections. Unfortunately, this is still not sharp enough to yield the disparity in the sizes of the tubes and their translated counterparts necessary to claim the existence of a Kakeya-type set. To strengthen the bound, we need a second moment estimate on the pairwise intersections. Both moment estimates share some common features; for instance,

• Euclidean distance relations between roots and slopes of two intersecting tubes,

• interplay of the above with the relative positions of the roots and slopes within the respective trees that they live in, which affects the slope assignments.

However, the technicalities are far greater for the second moment compared to the first. In particular, for the second moment we are naturally led to consider not just pairs, but triples and quadruples of tubes, and need to evaluate the probability of obtaining pairwise intersections among these. Not surprisingly, this probability depends on the structure of the root tuple within its ambient tree. It is the classification of these root configurations, computation of the relevant probabilities and their subsequent application to the estimation of expected intersections that we wish to highlight as the main contributions of this article.

2.2 Construction of a Kakeya-Type Set

We now choose some integer $M\ge 3$ and a generalized Cantor-type set $\mathcal {C}_M\subseteq [0,1)$ as described in Sect. 1.2, and fix these items for the remainder of the article. We also fix an injective map $\gamma : [0,1]\rightarrow \{1\} \times [-1,1]^d$ satisfying the bi-Lipschitz condition in (1.5). These objects then define a fixed set of directions $\Omega = \{\gamma (t) : t\in \mathcal {C}_M\} \subseteq \{1\} \times [-1,1]^d$.

Next, we define the thin tube-like objects that will comprise our Kakeya-type set. Fix an arbitrarily large integer $N\ge 1$, typically much bigger than M. Let $\{Q_t : t\in \mathbb {T}_N\}$, parametrized by the index set $\mathbb T_N$, be the collection of disjoint d-dimensional cubes of sidelength $M^{-N}$ generated by the lattice $M^{-N}\mathbb {Z}^d$ in the set $\{0\}\times [0,1)^d$. More specifically, each $Q_t$ is of the form

$$\begin{aligned} Q_t = \{0 \} \times \prod _{l=1}^d\left[ \frac{j_l}{M^N},\frac{j_{l}+1}{M^N}\right) , \end{aligned}$$

(2.1)

for some $\mathbf {j} = ( j_1,\ldots , j_d)\in \{0, 1, \ldots , M^N-1\}^d$, so that $\#(\mathbb {T}_N) = M^{Nd}$.

For technical reasons, we also define $\widetilde{Q}_t$ to be the $\kappa _d$-dilation of $Q_t$ about its center point, where $\kappa _d$ is a small, positive, dimension-dependent constant. The reason for this technicality, as well as possible values of $\kappa _d$, will soon emerge in the sequel, but for concreteness choosing $\kappa _d = d^{-d}$ will suffice.

Recall that the Nth iterate $\mathcal {C}^{[N]}_M$ of the Cantor construction is the union of $2^N$ disjoint intervals each of length $M^{-N}$. We choose a representative element of $\mathcal {C}_M$ from each of these intervals, calling the resulting finite collection $\mathcal {D}^{[N]}_M$. Clearly $\text {dist}(x, \mathcal {D}^{[N]}_M) \le M^{-N}$ for every $x \in \mathcal C_M$. Set

$$\begin{aligned} \Omega _N := \gamma \left( \mathcal {D}^{[N]}_M\right) , \end{aligned}$$

(2.2)

so that $\text {dist}(\omega ,\Omega _N) \le CM^{-N}$ for any $\omega \in \Omega$, with C as in (1.5).

For any $t \in \mathbb T_N$ and any $\omega \in \Omega _N$, we define

$$\begin{aligned} \mathcal P_{t, \omega } := \left\{ r + s \omega : r \in \widetilde{Q}_t, \; 0 \le s \le 10 C_0\right\} , \end{aligned}$$

(2.3)

where $C_0$ is a large constant to be determined shortly [for instance, $C_0 = d^d c^{-1}$ will work, with c as in (1.5)]. Thus the set $\mathcal P_{t, \omega }$ is a cylinder oriented along $\omega$. Its (vertical) cross-section in the plane $x_1=0$ is the cube $\widetilde{Q}_t$. We say that $\mathcal P_{t,\omega }$ is rooted at $Q_t$. While $\mathcal P_{t, \omega }$ is not strictly speaking a tube as defined in the introduction, the distinction is negligible, since $\mathcal P_{t, \omega }$ contains and is contained in constant multiples of $\delta$-tubes with $\delta = \kappa _d\cdot M^{-N}$. By a slight abuse of terminology but no loss of generality, we will henceforth refer to $\mathcal P_{t, \omega }$ as a tube.

If a slope assignment $\sigma {: }\,\mathbb {T}_N \rightarrow \Omega _N$ has been specified, we set $P_{t,\sigma } := \mathcal P_{t, \sigma (t)}$. Thus $\{P_{t, \sigma }{:}\, t \in \mathbb T_N \}$ is a family of tubes rooted at the elements of an $M^{-N}$-fine grid in $\{0\} \times [0,1)^d$, with essentially uniform length in t that is bounded above and below by fixed absolute constants. Two such tubes are illustrated in Fig. 1. For the remainder, we set

$$\begin{aligned} K_N(\sigma ) := \bigcup _{t\in \mathbb {T}_N} P_{t,\sigma }. \end{aligned}$$

(2.4)

Fig. 1

Two typical tubes $P_{t_1,\sigma }$ and $P_{t_2,\sigma }$ rooted, respectively at $t_1$ and $t_2$ in the $\{x_1=0\}$-coordinate plane

For a certain choice of slope assignment $\sigma$, this collection of tubes will be shown to generate a Kakeya-type set in the sense of Definition 1.1. This particular slope assignment will not be explicitly described, but rather inferred from the contents of the following proposition.

Proposition 2.1

For any $N\ge 1$, let $\Sigma _N$ be a finite collection of slope assignments from the lattice $\mathbb {T}_N$ to the direction set $\Omega _N$. Every $\sigma \in \Sigma _N$ generates a set $K_N(\sigma )$ as defined in (2.4). Denote the power set of $\Sigma _N$ by $\mathfrak {P}(\Sigma _N)$.

Suppose that $(\Sigma _N,\mathfrak {P}(\Sigma _N),\text {Pr})$ is a discrete probability space equipped with the probability measure $\mathrm{Pr}$, for which the random sets $K_N(\sigma )$ obey the following estimates:

$$\begin{aligned} \text {Pr}\left( \{\sigma : |K_N(\sigma )\cap [0,1]\times \mathbb {R}^d|\ge a_N\}\right) \ge \frac{3}{4}, \end{aligned}$$

(2.5)

and

$$\begin{aligned} \mathbb {E}_{\sigma }|K_N(\sigma )\cap [C_0,C_0+1]\times \mathbb {R}^d|\le b_N, \end{aligned}$$

(2.6)

where $C_0 \ge 1$ is a fixed constant, and $\{a_N\}$, $\{b_N\}$ are deterministic sequences satisfying

$$\begin{aligned} \frac{a_N}{b_N}\rightarrow \infty ,\quad \text {as}\quad N\rightarrow \infty . \end{aligned}$$

Then $\Omega$ admits Kakeya-type sets.

Proof

Fix any integer $N\ge 1$. Applying Markov’s Inequality to (2.6), we see that

$$\begin{aligned}&\text {Pr}\left( \{\sigma : |K_N(\sigma )\cap [C_0,C_0+1]\times \mathbb {R}^d|\ge 4b_N\}\right) \\&\quad \le \frac{\mathbb {E}_{\sigma } |K_N(\sigma )\cap [C_0,C_0+1]\times \mathbb {R}^d|}{4b_N} \le \frac{1}{4}, \end{aligned}$$

so,

$$\begin{aligned} \text {Pr}\left( \{\sigma : |K_N(\sigma )\cap [C_0,C_0+1]\times \mathbb {R}^d|\le 4b_N\}\right) \ge \frac{3}{4}. \end{aligned}$$

(2.7)

Combining this estimate with (2.5), we find that

$$\begin{aligned}&\text {Pr}\left( \bigl \{\sigma {:} |K_N(\sigma )\cap [0,1]\times \mathbb {R}^d|\ge a_N \bigr \}\bigcap \bigl \{ \sigma {:} |K_N(\sigma )\cap [C_0,C_0+1]\times \mathbb {R}^d| \le 4b_N \bigr \}\right) \\&\quad \ge \, \text {Pr}\left( \bigl \{|K_N(\sigma )\cap [0,1]\times \mathbb {R}^d|\ge a_N \bigr \} \right) \\&\qquad + \text {Pr}\left( \bigl \{ |K_N(\sigma )\cap [C_0,C_0+1]\times \mathbb {R}^d|\le 4b_N \bigr \}\right) -1 \\&\quad \ge \, \frac{3}{4} + \frac{3}{4} - 1 = \frac{1}{2}. \end{aligned}$$

We may therefore choose a particular $\sigma \in \Sigma _N$ for which the size estimates on $K_N(\sigma )$ given by (2.5) and (2.7) hold simultaneously. Set

$$\begin{aligned} E_N := K_N(\sigma )\cap [C_0,C_0+1] \times \mathbb {R}^d, \quad \text {so that} \quad E_N^{*} (2C_0+1)\supseteq K_N(\sigma )\cap [0,1]\times \mathbb {R}^d. \end{aligned}$$

Then $E_N$ is a union of $\delta$-tubes oriented along directions in $\Omega _N\subset \Omega$ for which

$$\begin{aligned} \frac{|E_N^{*}(2C_0+1)|}{|E_N|} \ge \frac{a_N}{4b_N} \rightarrow \infty ,\,\,\text {as}\,\,N\rightarrow \infty , \end{aligned}$$

by hypothesis. This shows that $\Omega$ admits Kakeya-type sets, per condition (1.2). $\square$

The conclusion of Proposition 2.1 proves part (a) of our Theorem 1.2. The implication (a) $\implies$ (b) has already been discussed in Sect. 1.2. The remainder of this paper is devoted to establishing a proper randomization over slope assignments $\Sigma _N$ that will then allow us to verify the hypotheses of Proposition 2.1 for suitable sequences $\{a_N\}$ and $\{b_N\}$. We return to a more concrete formulation of the required estimates in Proposition 6.4.

3 Geometric Facts

In this section, we will take the opportunity to establish some geometric facts about two intersecting tubes in Euclidean space. These facts will be used in several instances within the proof of Theorem 1.2. Nonetheless they are really general observations that are not limited to our specific arrangement or description of tubes (Fig. 2).

Fig. 2

A simple triangle is defined by two rooted tubes, $\mathcal {P}_{t_1,v_1}$ and $\mathcal {P}_{t_2,v_2}$, and any point p in their intersection

Lemma 3.1

For $v_1, v_2 \in \Omega _N$ and $t_1, t_2 \in \mathbb T_N$, $t_1 \ne t_2$, let $\mathcal P_{t_1, v_1}$ and $\mathcal P_{t_2, v_2}$ be the tubes defined as in (2.3). If there exists $p = (p_1, \ldots , p_{d+1}) \in \mathcal P_{t_1, v_1} \cap \mathcal P_{t_2, v_2}$, then the inequality

$$\begin{aligned} \bigl | \text {cen}(Q_{t_2}) - \text {cen}(Q_{t_1}) + p_1(v_2-v_1) \bigr | \le 2 \kappa _d \sqrt{d} M^{-N}, \end{aligned}$$

(3.1)

holds, where $\text {cen}(Q)$ denotes the centre of the cube Q.

Proof

The proof is described in the diagram below. If $p \in \mathcal P_{t_1, v_1} \cap \mathcal P_{t_2, v_2}$, then there exist $x_1 \in \widetilde{Q}_{t_1}$, $x_2 \in \widetilde{Q}_{t_2}$ such that $p = x_1 + p_1v_1 = x_2 + p_1 v_2$, i.e., $p_1(v_2-v_1) = x_1 - x_2$. The inequality (3.1) follows since $|x_i - \text {cen}(Q_{t_i})| \le \kappa _d \sqrt{d} M^{-N}$ for $i=1,2$. $\square$

The inequality in (3.1) provides a valuable tool whenever an intersection takes place. For the reader who would like to look ahead, the Lemma 3.1 will be used along with Corollary 3.2 to establish Lemma 8.5. The following Corollary 3.3 will be needed for the proofs of Lemmas 8.6 and 8.10.

Corollary 3.2

Under the hypotheses of Lemma 3.1 and for $\kappa _d > 0$ suitably small,

$$\begin{aligned} |p_1 (v_2- v_1)| \ge \kappa _d M^{-N}. \end{aligned}$$

(3.2)

Proof

Since $t_1 \ne t_2$, we must have $|\text {cen}(Q_{t_1}) - \text {cen}(Q_{t_2})| \ge M^{-N}$. Thus an intersection is possible only if

$$\begin{aligned} p_1|v_2-v_1| \ge |\text {cen}(Q_{t_2}) - \text {cen}(Q_{t_1})| - 2\kappa _d \sqrt{d} M^{-N} \ge (1 - 2\kappa _d \sqrt{d}) M^{-N} \ge \kappa _d M^{-N}, \end{aligned}$$

where the first inequality follows from (3.1) and the last inequality holds for an appropriate selection of $\kappa _d$. $\square$

Corollary 3.3

If $t_1 \in \mathbb T_N$, $v_1, v_2 \in \Omega _N$ and a cube $Q \subseteq \mathbb R^{d+1}$ of sidelength $C_1M^{-N}$ with sides parallel to the coordinate axes are given, then there exists at most $C_2 = C_2(C_1)$ choices of $t_2 \in \mathbb T_N$ such that $\mathcal P_{t_1, v_1} \cap \mathcal P_{t_2, v_2} \cap Q \ne \emptyset$.

Proof

As $p = (p_1, \ldots , p_{d+1})$ ranges in Q, $p_1$ ranges over an interval I of length $C_1 M^{-N}$. If $p \in \mathcal P_{t_1, v_1} \cap \mathcal P_{t_2, v_2} \cap Q$, the inequality (3.1) and the fact diam$(\Omega ) \le$ diam$(\{1\}\times [-1,1]^d) = 2 \sqrt{d}$ implies

$$\begin{aligned} \bigl | \text {cen}(Q_{t_2}) - \text {cen}(Q_{t_1}) + \text {cen}(I)(v_2-v_1) \bigr |&\le |(p_1-\text {cen}(I))(v_2-v_1)| + 2 \kappa _d \sqrt{d} M^{-N} \\&\le 2\sqrt{d} (C_1 + \kappa _d) M^{-N}, \end{aligned}$$

restricting $\text {cen}(Q_{t_2})$ to lie in a cube of sidelength $2\sqrt{d} (C_1 + \kappa _d) M^{-N}$ centred at $\text {cen}(Q_{t_1}) - \text {cen}(I) (v_2-v_1)$. Such a cube contains at most $C_2$ sub-cubes of the form (2.1), and the result follows. $\square$

While the above formulation of Corollary 3.3 is more convenient for later use, we point out that the intersection of tubes is not the important feature here. In fact, given $v\in \Omega _N$ and a cube Q one can show that there exist at most C choices of $t\in \mathcal {T}_N$ such that $\mathcal P_{t,v}\cap Q \ne \emptyset$. For purposes of our application, Q will always be $\mathcal P_{t_1,v_1}$ intersected with a slab of thickness $O(M^{-N})$ transverse to it.

A recurring theme in the proof of Theorem 1.2 is the identification of a criterion that ensures that a specified point lies in the Kakeya-type set $K_N(\sigma )$ defined in (2.4). With this in mind, we introduce for any $p = (p_1, p_2, \ldots , p_{d+1}) \in [0,10C_0] \times \mathbb R^d$ a set

$$\begin{aligned} \text {Poss}(p) := \bigl \{Q_t : t \in \mathbb T_N, \,\, \text {there exists}\,\, v \in \Omega _N\,\, \text {such that}\,\, p \in \mathcal P_{t, v} \bigr \}. \end{aligned}$$

(3.3)

This set captures all the possible $M^{-N}$-cubes of the form (2.1) in $\{0\} \times [0,1)^d$ such that a tube rooted at one of these cubes has the potential to contain p, provided it is given the correct orientation. Note that Poss(p) is independent of any slope assignment $\sigma$. Depending on the location of p, Poss(p) could be empty. This would be the case if p lies outside a large enough compact subset of $[0, 10C_0] \times \mathbb R^d$, for example. Even if Poss(p) is not empty, an arbitrary slope assignment $\sigma$ may not endow any $Q_t$ in Poss(p) with the correct orientation.

In the next lemma, we list a few easy properties of Poss(p) that will be helpful later, particularly during the proof of Lemma 9.3. Lemma 3.4 establishes the main intuition behind the Poss(p) set, as we give a more geometric description of Poss(p) in terms of an affine copy of the direction set $\Omega _N$. This is illustrated in Fig. 3 for a particular choice of directions $\Omega _N$.

Fig. 3

a depicts the cone generated by a second stage Cantor construction, $\Omega _2$, on the set of directions given by the curve $\{(1,t,t^2){:}\, 0\le t\le C\}$ in the $\{1\}\times \mathbb {R}^2$ plane. In b, a point $p = (p_1,p_2,p_3)$ has been fixed and the cone of directions has been projected backward from p onto the coordinate plane, $p-p_1\Omega _2$. The resulting Poss(p) set is thus given by all cubes $Q_t$, $t\in \mathbb {T}_N$ such that $\widetilde{Q}_t$ intersects a subset of the curve $\{(0,p_2-p_1t,p_3-p_1t^2) : 0\le t\le C\}$

Lemma 3.4

• (a) For any slope assignment $\sigma$,

  $$\begin{aligned} \bigl \{Q_t: t \in \mathbb T_N, p \in P_{t, \sigma } \bigr \} \subseteq \text {Poss}(p). \end{aligned}$$

• (b) For any $p \in [0,10C_0] \times \mathbb R^d$,

  $$\begin{aligned} \text {Poss}(p)&= \bigl \{Q_t : \widetilde{Q}_t \cap (p - p_1 \Omega _N) \ne \emptyset \bigr \} \end{aligned}$$

  (3.4)
  $$\begin{aligned}&\subseteq \{ Q_t : t \in \mathbb T_N, Q_t \cap (p - p_1 \Omega _N) \ne \emptyset \}. \end{aligned}$$

  (3.5)

  Note that the set in (3.4) could be empty, but the one in (3.5) is not.

Proof

If $p \in P_{t, \sigma }$, then $p \in \mathcal P_{t, \sigma (t)}$ with $\sigma (t)$ equal to some $v \in \Omega$. Thus $\mathcal P_{t,v}$ contains p and hence $Q_t \in \text {Poss}(p)$, proving part (a). For part (b), we observe that $p \in \mathcal P_{t,v}$ for some $v \in \Omega _N$ if and only if $p - p_1 v \in \widetilde{Q}_t$, i.e., $\widetilde{Q}_t \cap (p - p_1 \Omega _N) \ne \emptyset$. This proves the relation (3.4). The containment in (3.5) is obvious. $\square$

We will also need a bound on the cardinality of Poss(p) within a given cube, and on the cardinality of possible slopes that give rise to indistinguishable tubes passing through a given point. We now prescribe these. Lemmas 3.5 and 3.6 are not technically needed for the remainder, but can be viewed as steps toward establishing Lemma 3.7 which will prove critical throughout Sect. 9. Not surprisingly, the Cantor-like construction of $\Omega$ plays a role in all these estimates.

Lemma 3.5

Given $C_0, C_1 > 0$, there exists $C_2 = C_2(C_0, C_1, M, d) > 0$ with the following property. Let $p = (p_1, \ldots , p_{d+1}) \in (0,10C_0] \times \mathbb R^d$, and Q be any cube in $\{0\} \times [0,1)^d$ with sidelength in $[M^{-\ell }, M^{-\ell +1})$ for some $\ell \le N-1$. Then

$$\begin{aligned} \# \bigl \{Q_t : t \in \mathbb T_N, Q_t \cap Q \ne \emptyset , \, \text {dist}(Q_t, p-p_1 \Omega _N) \le C_1 M^{-N} \bigr \} \le C_2 2^{N - \ell }. \end{aligned}$$

(3.6)

Proof

Let $j \in \mathbb Z$ be the index such that $M^{-j} \le p_1 < M^{-j+1}$. By scaling, the left hand side of (3.6) is comparable to (i.e., bounded above and below by constant multiples of) the number of $p_1^{-1} M^{-N}$-separated points lying in

$$\begin{aligned} Q' := \bigl \{ x \in p_1^{-1}Q: \, \text {dist}(x, p_1^{-1}p - \Omega _N) \le C_1 p_1^{-1} M^{-N} \bigr \}.\end{aligned}$$

But $p_1^{-1} p - \Omega _N = (1, c) - \Omega _N$ is an image of $\Omega _N$ following an inversion and translation. This implies that there is a subset $\Omega _N'$ of $\Omega _N$, depending on p and $p_1^{-1}Q$ and with diameter $O(M^{j - \ell })$, such that $Q'$ is contained in a $O(M^{j-N})$-neighborhood of $-\Omega _N' + (1, c)$. The number of $M^{j-N}$-separated points in $Q'$ is comparable to that in $\Omega _N'$.

Suppose first that $j \le \ell$. If $\mathcal C' \subseteq \mathcal C_M^{[N]}$ is defined by the requirement $\Omega _N' = \gamma (\mathcal C')$, then (1.5) implies that diam$(\mathcal C') = O(M^{j-\ell })$. Thus $\mathcal C'$ is contained in at most O(1) intervals of length $M^{j-\ell }$ chosen at step $\ell -j$ in the Cantor-type construction. Each chosen interval at the kth stage gives rise to two chosen subintervals at the next stage, with their centres being separated by at least $M^{-k-1}$. So the number of $M^{j-N}$-separated points in $\mathcal C'$, and hence $\gamma (\mathcal C')$ is $O(2^{(N-j) - (\ell -j)}) = O(2^{N-\ell })$ as claimed. The case $j \ge \ell$ is even simpler, since the number of $M^{j-N}$-separated points in $\mathcal C'$ is trivially bounded by $2^{N-j} \le 2^{N-\ell }$. $\square$

Lemma 3.6

Fix $t \in \mathbb T_N$ and $p = (p_1, \ldots , p_{d+1}) \in [M^{-\ell }, M^{-\ell +1}] \times \mathbb R^d$, for some $0 \le \ell \ll N$. Let Q be a cube centred at p of sidelength $C_1 M^{-N}$. Then

$$\begin{aligned} \# \bigl \{ v \in \Omega _N : Q \cap \mathcal P_{t,v} \ne \emptyset \bigr \} \le C_2 2^\ell . \end{aligned}$$

Proof

If both $\mathcal P_{t,v}$ and $\mathcal P_{t,v'}$ have nonempty intersection with Q, then there exist $q = (q_1, \ldots , q_{d+1}), q' = (q_1', \ldots , q'_{d+1}) \in Q$ such that both $q - q_1v$ and $q' - q_1'v'$ land in $\widetilde{Q}_t$. Thus,

$$\begin{aligned} p_1 |v - v'|&\le |(q - p_1v) - (q' - p_1v')| + |q-q'| \\&\le |(q - q_1v) - (q' - q_1'v')| + |q_1-p_1||v| + |q_1'-p_1||v'| + |q-q'| \\&\le (\kappa _d \sqrt{d} + 10 C_1 \sqrt{d} )M^{-N}. \end{aligned}$$

In other words, $|v-v'| \le (10 C_1+ \kappa _d) \sqrt{d} M^{\ell -N}$. Recalling that $v = \gamma (\alpha )$ and $v' = \gamma (\alpha ')$ for some $\alpha , \alpha ' \in \mathcal D_M^{[N]}$, combining the last inequality with (1.5) implies that $|\alpha - \alpha '| \le C_2 M^{\ell -N}$. Thus there is a collection of at most O(1) chosen intervals at step $N - \ell$ of the Cantor-type construction which $\alpha$ (and hence $\alpha '$) can belong to. Since each interval gives rise to two chosen intervals at the next stage, the number of possible $\alpha$ and hence v is $O(2^{\ell })$. $\square$

A slight modification of the proof above yields a stronger conclusion, stated below, when p is far away from the root hyperplane. We will return to this result several times in the sequel (see for example Lemma 6.3 for a version of it in the language of trees), and make explicit use of it in Sect. 9, specifically in the proofs of Lemmas 9.1 and 9.2.

Lemma 3.7

There exists a constant $C_0 \ge 1$ with the following properties.

• (a) For any $p \in [C_0, C_0+1] \times \mathbb R^d$ and $t \in \mathbb T_N$, there exists at most one $v \in \Omega _N$ such that $p \in \mathcal P_{t,v}$. In other words, for every $Q_t$ in Poss(p), there is exactly one $\delta$-tube rooted at t that contains p.

• (b) For any p as in (a), and $Q_t$, $Q_{t'} \in$ Poss(p), let $v = \gamma (\alpha )$, $v' = \gamma (\alpha ')$ be the two unique slopes in $\Omega _N$ guaranteed by (a) such that $p \in \mathcal P_{t,v} \cap \mathcal P_{t',v'}$. If k is the largest integer such that $Q_t$ and $Q_{t'}$ are both contained in the same cube $Q \subseteq \{0\} \times [0,1)^d$ of sidelength $M^{-k}$ whose corners lie in $M^{-k} \mathbb Z^d$, then $\alpha$ and $\alpha '$ belong to the same kth stage basic interval in the Cantor construction.

Proof

• (a) Suppose $v, v' \in \Omega _N$ are such that $p \in \mathcal P_{t,v} \cap \mathcal P_{t,v'}$. Then $p - p_1 v$ and $p - p_1v'$ both lie in $\widetilde{Q}_t$, so that $p_1 |v-v'| \le \kappa _d \sqrt{d} M^{-N}$. Since $p_1 \ge C_0$ and (1.5) holds, we find that

  $$\begin{aligned} |\alpha - \alpha '| \le \frac{\kappa _d \sqrt{d}}{cC_0} M^{-N} < M^{-N}, \end{aligned}$$

  where the last inequality holds if $C_0$ is chosen large enough. Let us recall from the description of the Cantor-like construction in Sect. 1.2 that any two basic rth stage intervals are non-adjacent, and hence any two points in $\mathcal C_{M}$ lying in distinct basic rth stage intervals are separated by at least $M^{-r}$. Therefore the inequality above implies that both $\alpha$ and $\alpha '$ belong to the same basic Nth stage interval in $\mathcal C_M^{[N]}$. But $\mathcal D_M^{[N]}$ contains exactly one element from each such interval. So $\alpha = \alpha '$ and hence $v = v'$.

• (b) If $p \in \mathcal P_{t,v} \cap \mathcal P_{t',v'}$, then $p_1|v-v'| \le \text {diam}(\widetilde{Q}_t \cup \widetilde{Q}_{t'}) \le \text {diam}(Q) = \sqrt{d} M^{-k}$. Applying (1.5) again combined with $p_1 \ge C_0$, we find that $|\alpha - \alpha '| \le \frac{\sqrt{d}}{cC_0} M^{-k} < M^{-k},$ for $C_0$ chosen large enough. By the same property of the Cantor construction as used in (a), we obtain that $\alpha$ and $\alpha '$ lie in the same kth stage basic interval in $\mathcal C_M^{[k]}$. $\square$

4 Rooted, Labelled Trees

4.1 The Terminology of Trees

An undirected graph $\mathcal {G} := (\mathcal {V},\mathcal {E})$ is a pair, where $\mathcal {V}$ is a set of vertices and $\mathcal {E}$ is a symmetric, nonreflexive subset of $\mathcal {V}\times \mathcal {V}$, called the edge set. By symmetric, here we mean that the pair $(u,v)\in \mathcal {E}$ is unordered; i.e., the pair (u, v) is identical to the pair (v, u). By nonreflexive, we mean $\mathcal {E}$ does not contain the pair (v, v) for any $v\in \mathcal {V}$.

A path in a graph is a sequence of vertices such that each successive pair of vertices is a distinct edge in the graph. A finite path (with at least one edge) whose first and last vertices are the same is called a cycle. A graph is connected if for each pair of vertices $v\ne u$, there is a path in $\mathcal {G}$ containing v and u. We define a tree to be a connected undirected graph with no cycles.

All our trees will be of a specific structure. A rooted, labelled tree $\mathcal {T}$ is one whose vertex set is a nonempty collection of finite sequences of nonnegative integers such that if $\langle i_1,\ldots ,i_n\rangle \in \mathcal {T}$, then

• (i) for any k, $0\le k\le n$, $\langle i_1,\ldots ,i_k\rangle \in \mathcal {T}$, where $k=0$ corresponds to the empty sequence, and

• (ii) for every $j\in \{0,1,\ldots ,i_n\}$, we have $\langle i_1,\ldots ,i_{n-1},j\rangle \in \mathcal {T}$.

We say that $\langle i_1,\ldots , i_{n-1}\rangle$ is the parent of $\langle i_1,\ldots ,i_{n-1},j\rangle$ and that $\langle i_1,\ldots ,i_{n-1},j\rangle$ is the $(j+1)th$ child of $\langle i_1,\ldots ,i_{n-1}\rangle$. If u and v are two sequences in $\mathcal {T}$ such that u is a child of v, or a child’s child of v, or a child’s child’s child of v, etc., then we say that u is a descendant of v (or that v is an ancestor of u), and we write $u \subset v$ (see the remark below). If $u=\langle i_1,\ldots ,i_m\rangle \in \mathcal {T}$, $v = \langle j_1,\ldots ,j_n\rangle \in \mathcal {T}$, $m\le n$, and neither u nor v is a descendant of the other, then the youngest common ancestor of u and v is the vertex in $\mathcal {T}$ defined by

$$\begin{aligned} D(u,v) = D(v,u) := {\left\{ \begin{array}{ll} \emptyset , &{}\text { if }\,\, i_1\ne j_1\\ \langle i_1,\ldots ,i_k\rangle &{}\text { if }\,\, k = \max \{l{:}\, i_l=j_l\}. \end{array}\right. } \end{aligned}$$

(4.1)

One can similarly define the youngest common ancestor for any finite collection of vertices.

Remark At first glance, using the notation $u\subset v$ to denote when u is a descendant of v may seem counterintuitive, since u is a descendant of v precisely when v is a subsequence of u. However, we will soon be identifying vertices of rooted labelled trees with certain nested families of cubes in $\mathbb {R}^d$. Consequently, as will become apparent in the next two subsections, u will be a descendant of v precisely when the cube associated with u is contained within the cube associated with v.

We designate the empty sequence $\emptyset$ as the root of the tree $\mathcal {T}$. The sequence $\langle i_1,\ldots ,i_n\rangle$ should be thought of as the vertex in $\mathcal {T}$ that is the $(i_n+1)th$ child of the $(i_{n-1}+1)th$ child,$\ldots$, of the $(i_1+1)th$ child of the root. All unordered pairs of the form $(\langle i_1,\ldots ,i_{n-1}\rangle ,\langle i_1,\ldots ,i_{n-1},i_n\rangle )$ describe the edges of the tree $\mathcal {T}$. We say that the edge originates at the vertex $\langle i_1,\ldots ,i_{n-1}\rangle$ and that it terminates at the vertex $\langle i_1,\ldots ,i_{n-1},i_n\rangle$. Note that every vertex in the tree that is not the root is uniquely identified by the edge terminating at that vertex. Consequently, given an edge $e\in \mathcal {E}$, we define v(e) to be the vertex in $\mathcal {V}$ at which e terminates. The vertex $\langle i_1,\ldots ,i_n\rangle \in \mathcal {T}$ also prescribes a unique path, or ray, from the root to this vertex:

$$\begin{aligned} \emptyset \rightarrow \langle i_1\rangle \rightarrow \langle i_1,i_2\rangle \rightarrow \cdots \rightarrow \langle i_1,i_2,\ldots ,i_n\rangle . \end{aligned}$$

We let $\partial \mathcal {T}$ denote the collection of all rays in $\mathcal {T}$ of maximal (possibly infinite) length. For a fixed vertex $v = \langle i_1,\ldots ,i_m\rangle \in \mathcal {T}$, we also define the subtree (of $\mathcal {T}$) generated by the vertex v to be the maximal subtree of $\mathcal {T}$ with v as the root, i.e., it is the subtree

$$\begin{aligned} \{\langle i_1,\ldots ,i_m,j_1,\ldots ,j_k\rangle \in \mathcal {T}{:}\, k\ge 0\}. \end{aligned}$$

The height of the tree is taken to be the supremum of the lengths of all the sequences in the tree. Further, we define the height $h(\cdot )$, or level, of a vertex $\langle i_1,\ldots ,i_n\rangle$ in the tree to be n, the length of its identifying sequence. All vertices of height n are said to be members of the nth generation of the root, or interchangeably, of the tree. More explicitly, a member vertex of the nth generation has exactly n edges joining it to the root. The height of the root is always taken to be zero.

If $\mathcal {T}$ is a tree and $n\in \mathbb {Z}^+$, we write the truncation of $\mathcal {T}$ to its first n levels as $\mathcal {T}_n = \{\langle i_1,\ldots ,i_k\rangle \in \mathcal {T}{:}\, 0\le k\le n\}.$ This subtree is a tree of height at most n. A tree is called locally finite if its truncation to every level is finite, i.e., consists of finitely many vertices. All of our trees will have this property. In the remainder of this article, when we speak of a tree we will always mean a locally finite, rooted labelled tree, unless otherwise specified.

Roughly speaking, two trees are isomorphic if they have the same collection of rays. To make this precise we define a special kind of map between trees that will turn out to be very important for us later.

Definition 4.1

Let $\mathcal {T}_1$ and $\mathcal {T}_2$ be two trees with equal (possibly infinite) heights. Let $\sigma : \mathcal {T}_1\rightarrow \mathcal {T}_2$; we call $\sigma$ sticky if

• for all $v\in \mathcal {T}_1$, $h(v) = h(\sigma (v))$, and

• $u\subset v$ implies $\sigma (u)\subset \sigma (v)$ for all $u,v\in \mathcal {T}_1$.

We often say that $\sigma$ is sticky if it preserves heights and lineages.

A one-to-one and onto sticky map between two trees, whose inverse is then automatically sticky, is an isomorphism and the two trees are said to be isomorphic; we will write $\mathcal {T}_1 \cong \mathcal {T}_2$. Two isomorphic trees can be treated as essentially identical objects.

4.2 Encoding Bounded Subsets of the Unit Interval by Trees

The language of rooted labelled trees is especially convenient for representing bounded sets in Euclidean spaces. This connection is well-studied in the literature. We refer the interested reader to [19] for more information.

We start with $[0,1)\subset \mathbb {R}$. Fix any positive integer $M\ge 2$. We define an M-adic rational as a number of the form $i/M^k$ for some $i\in \mathbb {Z}$, $k\in \mathbb {Z}^+$, and an M-adic interval as $[i\cdot M^{-k},(i+1)\cdot M^{-k})$. For any nonnegative integer i and positive integer k such that $i<M^k$, there exists a unique representation

$$\begin{aligned} i = i_1M^{k-1} + i_2M^{k-2} + \cdots + i_{k-1}M + i_k, \end{aligned}$$

(4.2)

where the integers $i_1,\ldots ,i_k$ take values in $\mathbb {Z}_M := \{0,1,\ldots ,M-1\}$. These integers should be thought of as the “digits” of i with respect to its base M expansion. An easy consequence of (4.2) is that there is a one-to-one and onto correspondence between M-adic rationals in [0, 1) of the form $i/M^k$ and finite integer sequences $\langle i_1,\ldots ,i_k\rangle$ of length k with $i_j \in \mathbb {Z}_M$ for each j. Naturally then, we define the tree of infinite height

$$\begin{aligned} \mathcal {T}([0,1);M) = \{\langle i_1,\ldots ,i_k\rangle : k\ge 0,\ i_j\in \mathbb {Z}_M\}. \end{aligned}$$

(4.3)

The tree thus defined depends of course on the base M; however, if M is fixed, as it will be once we fix the direction set $\Omega = \gamma (\mathcal {C}_M)$ (see Sect. 1.2), we will omit its usage in our notation, denoting the tree $\mathcal {T}([0,1);M)$ by $\mathcal {T}([0,1))$ instead.

Identifying the root of the tree defined in (4.3) with the interval [0, 1) and the vertex $\langle i_1,\ldots ,i_k\rangle$ with the interval $[i\cdot M^{-k},(i+1)\cdot M^{-k})$, where i and $\langle i_1,\ldots ,i_k\rangle$ are related by (4.2), we observe that the vertices of $\mathcal {T}([0,1);M)$ at height k yield a partition of [0, 1) into M-adic subintervals of length $M^{-k}$. This tree has a self-similar structure: every vertex of $\mathcal {T}([0,1);M)$ has M children and the subtree generated by any vertex as the root is isomorphic to $\mathcal {T}([0,1);M)$. In the sequel, we will refer to such a tree as a full M-adic tree.

Any $x\in [0,1)$ can be realized as the intersection of a nested sequence of M-adic intervals, namely

$$\begin{aligned} \{x\} = \bigcap _{k=0}^{\infty }I_k(x), \end{aligned}$$

where $I_k(x) = [i_k(x)\cdot M^{-k},(i_k(x)+1)\cdot M^{-k})$. The point x should be visualized as the destination of the infinite ray

$$\begin{aligned} \emptyset \rightarrow \langle i_1(x)\rangle \rightarrow \langle i_1(x),i_2(x)\rangle \rightarrow \cdots \rightarrow \langle i_1(x),i_2(x),\ldots ,i_k(x)\rangle \rightarrow \cdots \end{aligned}$$

in $\mathcal {T}([0,1);M)$. Conversely, every infinite ray

$$\begin{aligned} \emptyset \rightarrow \langle i_1\rangle \rightarrow \langle i_1,i_2\rangle \rightarrow \langle i_1,i_2,i_3\rangle \cdots \end{aligned}$$

identifies a unique $x\in [0,1)$ given by the convergent sum

$$\begin{aligned} x = \sum _{j=1}^{\infty } \frac{i_j}{M^j}. \end{aligned}$$

Thus the tree $\mathcal {T}([0,1);M)$ can be identified with the interval [0, 1) exactly. Any subset $E\subseteq [0,1)$ is then given by a subtree $\mathcal {T}(E;M)$ of $\mathcal {T}([0,1);M)$ consisting of all infinite rays that identify some $x\in E$. As before, we will drop the notation for the base M in $\mathcal {T}(E;M)$ once this base has been fixed.

Any truncation of $\mathcal {T}(E;M)$, say up to height k, will be denoted by $\mathcal {T}_k(E;M)$ and should be visualized as a covering of E by M-adic intervals of length $M^{-k}$. More precisely, $\langle i_1,\ldots ,i_k\rangle \in \mathcal {T}_k(E;M)$ if and only if $E\cap [i\cdot M^{-k},(i+1)\cdot M^{-k})\ne \emptyset$, where i and $\langle i_1,\ldots ,i_k\rangle$ are related by (4.2).

We now state and prove a key structural result about our sets of interest, the generalized Cantor sets $\mathcal {C}_M$.

Proposition 4.2

Fix any integer $M\ge 3$. Define $\mathcal {C}_M$ as in Sect. 1.2. Then

$$\begin{aligned} \mathcal {T}(\mathcal {C}_M;M)\cong \mathcal {T}([0,1);2). \end{aligned}$$

That is, the M-adic tree representation of $\mathcal {C}_M$ is isomorphic to the full binary tree, illustrated in Fig. 4.

Fig. 4

A pictorial depiction of the isomorphism between a standard middle-thirds Cantor set and its representation as a full binary subtree of the full base $M=3$ tree

Proof

Denote $\mathcal {T} = \mathcal {T}(\mathcal {C}_M;M)$ and $\mathcal {T}' = \mathcal {T}([0,1);2)$. We must construct a bijective sticky map $\psi : \mathcal {T}\rightarrow \mathcal {T}'$. First, define $\psi (v_0) = v'_0$, where $v_0$ is the root of $\mathcal {T}$ and $v'_0$ is the root of $\mathcal {T}'$.

Now, for any $k\ge 1$, consider the vertex $\langle i_1,i_2,\ldots ,i_k\rangle \in \mathcal {T}$. We know that $i_j\in \mathbb {Z}_M$ for all j. Furthermore, for any fixed j, this vertex corresponds to a kth level subinterval of $\mathcal {C}_M^{[k]}$. Every such k-th level interval is replaced by exactly two arbitrary $(k+1)$-th level subintervals in the construction of $\mathcal {C}_M^{[k+1]}$. Therefore, there exists $N_1 := N_1(\langle i_1,\ldots ,i_k\rangle ),$ $N_2 := N_2(\langle i_1,\ldots ,i_k\rangle )\in \mathbb {Z}_M$, with $N_1<N_2$, such that $\langle i_1,\ldots ,i_k,i_{k+1}\rangle \in \mathcal {T}$ if and only if $i_{k+1}=N_1$ or $N_2$. Consequently, we define

$$\begin{aligned} \psi (\langle i_1,i_2,\ldots ,i_k\rangle ) = \langle l_1,l_2,\ldots ,l_k\rangle \in \mathcal {T}', \end{aligned}$$

(4.4)

where

$$\begin{aligned} l_{j+1} = {\left\{ \begin{array}{ll} 0 &{}\text { if } i_{j+1} = N_1(\langle i_1,\ldots ,i_j\rangle ),\\ 1 &{}\text { if } i_{j+1} = N_2(\langle i_1,\ldots ,i_j\rangle ). \end{array}\right. } \end{aligned}$$

The mapping $\psi$ is injective by construction and surjectivity follows from the binary selection of subintervals at each stage in the construction of $\mathcal {C}_M$. Moreover, $\psi$ is sticky by (4.4). $\square$

The following corollary is an easy consequence of the above and left to the reader.

Corollary 4.3

Recall the definition of $\mathcal D_M^{[N]}$ from Sect. 2.2. Then

$$\begin{aligned} \mathcal T_N(\mathcal D_M^{[N]};M) \cong \mathcal T_N([0,1);2). \end{aligned}$$

Proposition 4.2 and Corollary 4.3 guarantee that the tree encoding our set of directions will retain a certain binary structure. This fact will prove vital to establishing Theorem 1.2.

4.3 Encoding Higher-Dimensional Bounded Subsets of Euclidean Space by Trees

The approach to encoding a bounded subset of Euclidean space by a tree extends readily to higher dimensions. For any $\mathbf {i} = \langle j_1,\ldots ,j_d\rangle \in \mathbb {Z}^d$ such that $\mathbf {i}\cdot M^{-k}\in [0,1)^d$, we can apply (4.2) to each component of $\mathbf {i}$ to obtain

$$\begin{aligned} \frac{\mathbf {i}}{M^k} = \frac{\mathbf {i}_1}{M} + \frac{\mathbf {i}_2}{M^2} + \cdots + \frac{\mathbf {i}_k}{M^k}, \end{aligned}$$

with $\mathbf {i}_j\in \mathbb {Z}_M^d$ for all j. As before, we identify $\mathbf {i}$ with $\langle \mathbf {i}_1,\ldots ,\mathbf {i}_k\rangle$.

Let $\phi {:}\, \mathbb {Z}_M^d \rightarrow \{0,1,\ldots , M^d-1\}$ be an enumeration of $\mathbb {Z}_M^d$. Define the full $M^d$-adic tree

$$\begin{aligned} \mathcal {T}([0,1)^d;M,\phi ) = \left\{ \langle \phi (\mathbf {i}_1),\ldots ,\phi (\mathbf {i}_k)\rangle : k\ge 0,\ \mathbf {i}_j \in \mathbb {Z}_M^d\right\} . \end{aligned}$$

(4.5)

The collection of kth generation vertices of this tree may be thought of as the d-fold Cartesian product of the kth generation vertices of $\mathcal {T}([0,1);M)$. For our purposes, it will suffice to fix $\phi$ to be the lexicographic ordering, and so we will omit the notation for $\phi$ in (4.5), writing simply, and with a slight abuse of notation,

$$\begin{aligned} \mathcal {T}([0,1)^d;M) = \left\{ \langle \mathbf {i}_1,\ldots ,\mathbf {i}_k\rangle : k\ge 0,\ \mathbf {i}_j \in \mathbb {Z}_M^d\right\} . \end{aligned}$$

(4.6)

As before, we will refer to the tree in (4.6) by the notation $\mathcal {T}([0,1)^d)$ once the base M has been fixed.

By a direct generalization of our one-dimensional results, each vertex $\langle \mathbf {i}_1,\ldots ,\mathbf {i}_k\rangle$ of $\mathcal {T}([0,1)^d;M)$ at height k represents the unique M-adic cube in $[0,1)^d$ of sidelength $M^{-k}$, containing $\mathbf {i}\cdot M^{-k}$, of the form

$$\begin{aligned} \left[ \frac{j_1}{M^k},\frac{j_1+1}{M^k}\right) \times \cdots \times \left[ \frac{j_d}{M^k},\frac{j_d+1}{M^k}\right) . \end{aligned}$$

As in the one-dimensional setting, any $x\in [0,1)^d$ can be realized as the intersection of a nested sequence of M-adic cubes. Thus, we view the tree in (4.6) as an encoding of the set $[0,1)^d$ with respect to base M. As before, any subset $E\subseteq [0,1)^d$ then corresponds to a subtree of $\mathcal {T}([0,1)^d;M)$.

The connection between sets and trees encoding them leads to the following easy observations that we record for future use in Lemma 9.3.

Lemma 4.4

Let $\Omega _N$ be the set defined in (2.2).

• (a) Given $\Omega _N$, there is a constant $C_1 > 0$ (depending only on d and C, c from (1.5)) such that for any $1 \le k \le N$, the number of kth generation vertices in $\mathcal T_N(\Omega _N;M)$ is $\le C_1 2^k$.

• (b) For any compact set $\mathbb K \subseteq \mathbb R^{d+1}$, there exists a constant $C(\mathbb K) > 0$ with the following property. For any $x = (x_1, \cdots , x_{d+1}) \in \mathbb K$, and $1 \le k \le N$, the number of kth generation vertices in $\mathcal T_N(E(x);M)$ is $\le C(\mathbb K) 2^k$, where $E(x) := (x - x_1 \Omega _N) \cap \{0\} \times [0,1)^d$.

Proof

There are exactly $2^k$ basic intervals of level k that comprise $\mathcal C_M^{[k]}$. Under $\gamma$, each such basic interval maps into a set of diameter at most $CM^{-k}$. Since $\Omega _N = \gamma (\mathcal D_M^{[N]}) \subseteq \gamma (\mathcal C_M^{[k]})$, the number of kth generation vertices in $\mathcal T_N(\Omega _N;M)$, which is also the number of kth level M-adic cubes needed to cover $\Omega _N$, is at most $C_1 2^k$. This proves (a).

Let Q be any kth generation M-adic cube such that $Q \cap \Omega _N \ne \emptyset$. Then on one hand, $(x - x_1 Q) \cap (x - x_1 \Omega _N) \ne \emptyset$; on the other hand, the number of kth level M-adic cubes covering $(x - x_1 Q)$ is $\le C(\mathbb K)$, and part (b) follows. $\square$

Notation We end this section with a notational update. In light of the discussion above and for simplicity, we will henceforth identify a vertex $u = \langle i_1, i_2, \ldots , i_k \rangle \in \mathcal T([0,1)^d)$ with the corresponding cube $\{ 0\} \times u$ lying on the root hyperplane $\{ 0 \} \times [0,1)^d$. In this parlance, a vertex $t \in \mathcal T_N([0,1)^d)$ of height N is the same as a root cube $Q_t$ (or $\widetilde{Q}_t$) defined in (2.1), and the notation $t \subseteq u$ stands both for set containment as well as tree ancestry.

5 Electrical Circuits and Percolation on Trees

5.1 The Percolation Process Associated to a Tree

The proof of Theorem 1.2 will require consideration of a special probabilistic process on certain trees called a (bond) percolation. Imagine a liquid that is poured on top of some porous material. How will the liquid flow—or percolate—through the holes of the material? How likely is it that the liquid will flow from hole to hole in at least one uninterrupted path all the way to the bottom? The first question forms the intuition behind a formal percolation process, whereas the second question turns out to be of critical importance to the proof of Theorem 1.2; this idea plays a key role in establishing the planar analogue of that theorem in Bateman and Katz [4], and again in the more general framework of [3].

Although it is possible to speak of percolation processes in far more general terms (see [11]), we will only be concerned with a percolation process on a tree. Accordingly, given some tree $\mathcal {T}$ with vertex set $\mathcal {V}$ and edge set $\mathcal {E}$, we define an edge-dependent Bernoulli (bond) percolation process to be any collection of random variables $\{X_e : e\in \mathcal {E}\}$, where $X_e$ is Bernoulli$(p_e)$ with $p_e<1$. The parameter $p_e$ is called the survival probability of the edge e. We will always be concerned with a particular type of percolation on our trees: we define a standard Bernoulli(p) percolation to be one where the random variables $\{X_e : e\in \mathcal {E}\}$ are mutually independent and identically distributed Bernoulli(p) random variables, for some $p<1$. In fact, for our purposes, it will suffice to consider only standard Bernoulli$(\frac{1}{2})$ percolations.

Rather than imagining a tree with a percolation process as the behaviour of a liquid acted upon by gravity in a porous material, it will be useful to think of the percolation process as acting more directly on the mathematical object of the tree itself. Given some percolation process on a tree $\mathcal {T}$, we will think of the event $\{X_e=0\}$ as the event that we remove the edge e from the edge set $\mathcal {E}$, and the event $\{X_e=1\}$ as the event that we retain this edge; denote the random set of retained edges by $\mathcal {E}^*$. Notice that with this interpretation, after percolation there is no guarantee that $\mathcal {E}^*$, the subset of edges that remain after percolation, defines a subtree of $\mathcal {T}$. In fact, it can be quite likely that the subgraph that remains after percolation is a union of many disconnected subgraphs of $\mathcal {T}$.

For a given edge $e\in \mathcal {E}$, we think of $p = \text {Pr}(X_e=1)$ as the probability that we retain this edge after percolation. The probability that at least one uninterrupted path remains from the root of the tree to its bottommost level is given by the survival probability of the corresponding percolation process. More explicitly, given a percolation on a tree $\mathcal {T}$, the survival probability after percolation is the probability that the random variables associated to all edges of at least one ray in $\mathcal {T}$ take the value 1, i.e.,

$$\begin{aligned} \text {Pr}\left( \text {survival after percolation on } \mathcal {T}\right) := \text {Pr}\left( \bigcup _{R\in \partial \mathcal {T}}\bigcap _{e\in \mathcal {E}\cap R} \{X_e=1\}\right) . \end{aligned}$$

(5.1)

Estimation of this probability will prove to be a valuable tool in the proof of Theorem 1.2. This estimation will require reimagining a tree as an electrical network.

5.2 Trees as Electrical Networks

Formally, an electrical network is a particular kind of weighted graph. The weights of the edges are called conductances and their reciprocals are called resistances. In his seminal works on the subject, Lyons visualizes percolation on a tree as a certain electrical network. In [17], he lays the groundwork for this correspondence. While his results hold in great generality, we describe his results in the context of standard Bernoulli percolation on a locally finite, rooted labelled tree only. We briefly review the concepts relevant to our application here.

A percolation process on the truncation of any given tree $\mathcal {T}$ is naturally associated to a particular electrical network. To see this, we truncate the tree $\mathcal {T}$ at height N and place the positive node of a battery at the root of $\mathcal {T}_N$. Then, for every ray in $\partial \mathcal {T}_N$, there is a unique terminating vertex; we connect each of these vertices to the negative node of the battery. A resistor is placed on every edge e of $\mathcal {T}_N$ with resistance $R_e$ defined by

$$\begin{aligned} \frac{1}{R_e} = \frac{1}{1-p_e}\prod _{\emptyset \subset v(e^\prime )\subseteq v(e)} p_{e^\prime }. \end{aligned}$$

(5.2)

Notice that the resistance for the edge e is essentially the reciprocal of the probability that a path remains from the root of the tree to the vertex v(e) after percolation. For standard Bernoulli$(\frac{1}{2})$ percolation, we have

$$\begin{aligned} R_e = 2^{h(v(e))-1}. \end{aligned}$$

(5.3)

One fact that will prove useful for us later is that connecting any two vertices at a given height by an ideal conductor (i.e., one with zero resistance) only decreases the overall resistance of the circuit. This will allow us to more easily estimate the total resistance of a generic tree.

Proposition 5.1

Let $\mathcal {T}_N$ be a truncated tree of height N with corresponding electrical network generated by a standard Bernoulli$(\frac{1}{2})$ percolation process. Suppose at height $k<N$ we connect two vertices by a conductor with zero resistance. Then the resulting electrical network has a total resistance no greater than that of the original network.

Proof

Let u and v be the two vertices at height k that we will connect with an ideal conductor. Let $R_1$ denote the resistance between u and D(u, v), the youngest common ancestor of u and v; let $R_2$ denote the resistance between v and D(u, v). Let $R_3$ denote the total resistance of the subtree of $\mathcal {T}_N$ generated by the root u and let $R_4$ denote the total resistance of the subtree of $\mathcal {T}_N$ generated by the root v. These four connections define a subnetwork of our tree, depicted in Fig. 5a. The connection of u and v by an ideal conductor, as pictured in Fig. 5b, can only change the total resistance of this subnetwork, as that action leaves all other connections unaltered. It therefore suffices to prove that the total resistance of the subnetwork comprised of the resistors $R_1$, $R_2$, $R_3$ and $R_4$ can only decrease if u and v are joined by an ideal conductor.

In the original subnetwork, the resistors $R_1$ and $R_3$ are in series, as are the resistors $R_2$ and $R_4$. These pairs of resistors are also in parallel with each other. Thus, we calculate the total resistance of this subnetwork, $R_{\text {original}}$:

$$\begin{aligned} R_{\text {original}}&= \left( \frac{1}{R_1+R_3} + \frac{1}{R_2+R_4}\right) ^{-1}\nonumber \\&= \frac{(R_1+R_3)(R_2+R_4)}{R_1+R_2+R_3+R_4}. \end{aligned}$$

(5.4)

After connecting vertices u and v by an ideal conductor, the structure of our subnetwork is inverted as follows. The resistors $R_1$ and $R_2$ are in parallel, as are the resistors $R_3$ and $R_4$, and these pairs of resistors are also in series with each other. Therefore, we calculate the new total resistance of this subnetwork, $R_{\text {new}}$, as

$$\begin{aligned} R_{\text {new}}&= \left( \frac{1}{R_1} + \frac{1}{R_2}\right) ^{-1} + \left( \frac{1}{R_3} + \frac{1}{R_4}\right) ^{-1}\nonumber \\&= \frac{R_1R_2(R_3+R_4) + R_3R_4(R_1+R_2)}{(R_1+R_2)(R_3+R_4)}. \end{aligned}$$

(5.5)

We claim that (5.4) is greater than or equal to (5.5). To see this, simply cross-multiply these expressions. After cancellation of common terms, our claim reduces to

$$\begin{aligned} R_1^2R_4^2 + R_2^2R_3^2 \ge 2R_1R_2R_3R_4. \end{aligned}$$

But this is trivially satisfied since $(a-b)^2\ge 0$ for any real numbers a and b. $\square$

Fig. 5

a The original subnetwork with the resistors $R_1$, $R_3$ and $R_2$, $R_4$ in series; b the new subnetwork obtained by connecting vertices u and v by an ideal conductor

5.3 Estimating the Survival Probability After Percolation

We now present Lyons’ pivotal result linking the total resistance of an electrical network and the survival probability under the associated percolation process.

Theorem 5.2

(Lyons, Theorem 2.1 of [18]) Let $\mathcal {T}$ be a tree with mutually associated percolation process and electrical network, and let $R(\mathcal {T})$ denote the total resistance of this network. If the percolation is Bernoulli, then

$$\begin{aligned} \frac{1}{1+R(\mathcal {T})} \le \text {Pr}(\mathcal {T}) \le \frac{2}{1+R(\mathcal {T})}, \end{aligned}$$

where $\text {Pr}(\mathcal {T})$ denotes the survival probability after percolation on $\mathcal {T}$.

We will not require the full strength of this theorem. A reasonable upper bound on the survival probability coupled with the result of Proposition 5.1 will suffice for our applications. For completeness, we state and prove a sufficient simpler version of Theorem 5.2 as essentially formulated by Bateman and Katz [4].

Proposition 5.3

Let $M\ge 2$ and let $\mathcal {T}$ be a subtree of a full M-adic tree. Let $R(\mathcal {T})$ and $\text {Pr}(\mathcal {T})$ be as in Theorem 5.2. Then under Bernoulli percolation, we have

$$\begin{aligned} \text {Pr}(\mathcal {T}) \le \frac{2}{1+R(\mathcal {T})}. \end{aligned}$$

(5.6)

Proof

We will only focus on the case when $R(\mathcal T) \ge 1$, since otherwise (5.6) holds trivially. We prove this by induction on the height of the tree N. When $N=0$, then (5.6) is trivially satisfied. Now suppose that up to height $N-1$, we have

$$\begin{aligned} \text {Pr}(\mathcal {T}) \le \frac{2}{1+R(\mathcal {T})}. \end{aligned}$$

Suppose $\mathcal {T}$ is of height N. We can view the tree $\mathcal {T}$ as its root together with at most M edges connecting the root to the subtrees $\mathcal {T}_1,\ldots ,\mathcal {T}_M$ of height $N-1$ generated by the terminating vertices of these edges. If there are $k < M$ edges originating from the root, then we take $M-k$ of these subtrees to be empty. Note that by the induction hypothesis, (5.6) holds for each $\mathcal T_j$. To simplify notation, we denote

$$\begin{aligned} \text {Pr}(\mathcal {T}_j) = P_j\text { and }R(\mathcal {T}_j) = R_j, \end{aligned}$$

taking $P_j=0$ and $R_j=\infty$ if $\mathcal {T}_j$ is empty.

Using independence and recasting $\text {Pr}(\mathcal {T})$ as one minus the probability of not surviving after percolation on $\mathcal {T}$, we have the formula:

$$\begin{aligned} \text {Pr}(\mathcal {T}) = 1 - \prod _{k=1}^M\left( 1 - \frac{1}{2} P_k\right) . \end{aligned}$$

Note that the function $F(x_1,\ldots ,x_M) = 1 - (1-x_1/2)(1-x_2/2)\cdots (1-x_M/2)$ is monotone increasing in each variable on $[0,2]^M$. Now define

$$\begin{aligned} Q_j := \frac{2}{1+R_j}. \end{aligned}$$

Since resistances are nonnegative, we know that $Q_j\le 2$ for all j. Therefore,

$$\begin{aligned} \text {Pr}(\mathcal {T})&= F(P_1,\ldots ,P_M)\\&\le F(Q_1,\ldots ,Q_M)\\&\le \frac{1}{2} \sum _{k=1}^M Q_k. \end{aligned}$$

Here, the first inequality follows by monotonicity and the induction hypothesis. Plugging in the definition of $Q_k$, we find that

$$\begin{aligned} \text {Pr}(\mathcal {T}) \le \sum _{k=1}^M \frac{1}{1+R_k}. \end{aligned}$$

But since each resistor $R_j$ is in parallel, we know that

$$\begin{aligned} \frac{1}{R(\mathcal {T})} = \sum _{k=1}^M\frac{1}{1 + R_k}. \end{aligned}$$

Combining this formula with the previous inequality and recalling that $R(\mathcal T) \ge 1$, we have

$$\begin{aligned} \text {Pr}(\mathcal {T}) \le \frac{1}{R(\mathcal {T})} \le \frac{2}{1+R(\mathcal {T})}, \end{aligned}$$

as required. $\square$

6 The Random Mechanism and the Property of Stickiness

As discussed in the introduction of this paper, the construction of a Kakeya-type set with orientations given by $\Omega$ will require a certain random mechanism. We now describe this mechanism in detail.

In order to assign a slope $\sigma (\cdot )$ to the tubes $P_{t,\sigma }:= \mathcal P_{t, \sigma (t)}$ given by (2.3), we want to define a collection of random variables $\{X_{\langle i_1,\ldots , i_k\rangle }{:}\, \langle i_1,\ldots ,i_k\rangle \in \mathcal {T}([0,1)^d)\}$, one on each edge of the tree used to identify the roots of these tubes. The tree $\mathcal {T}_1( [0,1)^d)$ consists of all first generation edges of $\mathcal {T}([0,1)^d)$. It has exactly $M^d$ many edges and we place (independently) a Bernoulli$(\frac{1}{2})$ random variable on each edge: $X_{\langle 0\rangle }, X_{\langle 1\rangle },\ldots ,X_{\langle M^d-1\rangle }$. Now, the tree $\mathcal {T}_2( [0,1)^d)$ consists of all first and second generation edges of $\mathcal {T}([0,1)^d)$. It has $M^d+M^{2d}$ many edges and we place (independently) a new Bernoulli$(\frac{1}{2})$ random variable on each of the $M^{2d}$ second generation edges. We label these $X_{\langle i_1,i_2\rangle }$ where $0\le i_1,i_2<M^d$. We proceed in this way, eventually assigning an ordered collection of independent Bernoulli$(\frac{1}{2})$ random variables to the tree $\mathcal {T}_N([0,1)^d)$:

$$\begin{aligned} \mathbb {X}_N := \left\{ X_{\langle i_1,\ldots ,i_k\rangle } : \langle i_1,\ldots ,i_k\rangle \in \mathcal {T}_N([0,1)^d),\ 1\le k\le N\right\} , \end{aligned}$$

where $X_{\langle i_1,\ldots ,i_k\rangle }$ is assigned to the unique edge identifying $\langle i_1, i_2, \ldots , i_k\rangle$, namely the edge joining $\langle i_1, i_2, \ldots , i_{k-1} \rangle$ to $\langle i_1,i_2,\ldots ,i_k\rangle$. Each realization of $\mathbb X_N$ is a finite ordered collection of cardinality $M^d + M^{2d} + \cdots + M^{Nd}$ with entries either 0 or 1.

We will now establish that every realization of the random variable $\mathbb {X}_N$ defines a sticky map between the truncated position tree $\mathcal {T}_N([0,1)^d)$ and the truncated binary tree $\mathcal {T}_N([0,1);2)$, as defined in Definition 4.1. Fix a particular realization $\mathbb {X}_N = \mathbf x = \{ x_{\langle i_1, \ldots , i_k\rangle }\}$. Define a map $\tau _{\mathbf x} : \mathcal {T}_N([0,1)^d)\rightarrow \mathcal {T}_N([0,1);2)$, where

$$\begin{aligned} \tau _{\mathbf x}(\langle i_1,i_2,\ldots ,i_k\rangle ) = \left\langle x_{\langle i_1\rangle },x_{\langle i_1,i_2\rangle },\ldots , x_{\langle i_1,i_2,\ldots ,i_k\rangle }\right\rangle . \end{aligned}$$

(6.1)

We then have the following key proposition.

Proposition 6.1

The map $\tau _{\mathbf x}$ just defined is sticky for every realization $\mathbf x$ of $\mathbb X_N$. Conversely, any sticky map $\tau$ between $\mathcal {T}_N([0,1)^d)$ and $\mathcal {T}_N([0,1); 2)$ can be written as $\tau = \tau _{\mathbf x}$ for some realization $\mathbf x$ of $\mathbb X_N$.

Proof

Recalling Definition 4.1, we need to verify that $\tau _{\mathbf x}$ preserves heights and lineages. By (6.1), any finite sequence $v = \langle i_1, i_2, \ldots , i_k \rangle$ in $\mathcal T([0,1)^d)$ is mapped to a sequence of the same length in $\mathcal T([0,1);2)$. Therefore $h(v) = h(\tau _{\mathbf x}(v))$ for every $v \in \mathcal T([0,1)^d)$.

Next suppose $u\supset v$. Then $u = \langle i_1,\ldots ,i_{h(u)}\rangle$, with $h(u) \le k$. So again by (6.1),

$$\begin{aligned} \tau _{\mathbf x}(u) = \left\langle x_{\langle i_1\rangle },\ldots ,x_{\langle i_1,\ldots ,i_{h(u)}\rangle }\right\rangle \supset \left\langle x_{\langle i_1\rangle },\ldots ,x_{\langle i_1,\ldots ,i_{h(u)}\rangle },\ldots ,x_{\langle i_1,\ldots ,i_k\rangle }\right\rangle = \tau _{\mathbf x}(v). \end{aligned}$$

Thus, $\tau _{\mathbf x}$ preserves lineages, establishing the first claim in Proposition 6.1.

For the second, fix a sticky map $\tau : \mathcal {T}_N([0,1)^d) \rightarrow \mathcal {T}_N([0,1); 2)$. Define $x_{\langle i_1 \rangle } := \tau (\langle i_1 \rangle )$, $x_{\langle i_1, i_2\rangle } := \pi _2 \circ \tau (\langle i_1, i_2 \rangle )$, and in general

$$\begin{aligned} x_{\langle i_1, \ldots , i_k\rangle } := \pi _k \circ \tau (\langle i_1, i_2, \ldots , i_k \rangle ), \quad k \ge 1, \end{aligned}$$

where $\pi _k$ denotes the projection map whose image is the kth coordinate of the input sequence. The collection $\mathbf x = \{x_{\langle i_1, i_2, \ldots , i_k\rangle } \}$ is the unique realization of $\mathbb X_N$ that verifies the second claim. $\square$

6.1 Slope Assignment Algorithm

Recall from Sects. 1.2 and 2.2 that $\Omega := \gamma (\mathcal C_M)$ and $\Omega _N := \gamma (\mathcal D_{M}^{[N]})$, where $\mathcal C_M$ is the generalized Cantor-type set and $\mathcal D_M^{[N]}$ a finitary version of it. In order to exploit the binary structure of the trees $\mathcal {T}(\mathcal {C}_M) := \mathcal {T}(\mathcal {C}_M;M)$ and $\mathcal {T}(\mathcal {D}^{[N]}_M) := \mathcal {T}(\mathcal {D}^{[N]}_M;M)$ advanced in Proposition 4.2 and Corollary 4.3, we need to map traditional binary sequences onto the subsequences of $\{0,\ldots ,M-1\}^{\infty }$ defined by $\mathcal {C}_M$ or $\mathcal D_{M}^{[N]}$.

Proposition 6.2

Every sticky map $\tau$ as in (6.1) that maps $\mathcal {T}_N([0,1)^d;M)$ to $\mathcal {T}_N([0,1);2)$ induces a natural mapping $\sigma = \sigma _{\tau }$ from $\mathcal {T}_N([0,1)^d)$ into $\Omega _N$. The maps $\sigma _\tau$ obey a uniform Lipschitz-type condition: for any $t, t' \in \mathcal T_N([0,1)^d)$, $t \ne t'$,

$$\begin{aligned} \bigl | \sigma _{\tau }(t) - \sigma _{\tau }(t') \bigr | \le CM^{-h(D(\tau (t),\tau (t')))}, \end{aligned}$$

(6.2)

where C is as in (1.5).

Remark While the choice of $\mathcal D_M^{[N]}$ for a given $\mathcal C_M^{[N]}$ is not unique, the mapping $\tau \mapsto \sigma _{\tau }$ is unique given a specific choice. Moreover, if $\mathcal D_M^{[N]}$ and $\overline{\mathcal D}_M^{[N]}$ are two selections of finitary direction sets at scale $M^{-N}$, then the corresponding maps $\sigma _{\tau }$ and $\overline{\sigma }_{\tau }$ must obey

$$\begin{aligned} \bigl |\sigma _{\tau }(v) - \overline{\sigma }_{\tau }(v)\bigr | \le C M^{-h(v)} \,\,\text { for every } v \in \mathcal T_N([0,1)^d), \end{aligned}$$

(6.3)

where C is as in (1.5). Thus given $\tau$, the slope in $\Omega$ that is assigned by $\sigma _{\tau }$ to an M-adic cube in $\{0\} \times [0,1)^d$ of sidelength $M^{-N}$ is unique up to an error of $O(M^{-N})$. As a consequence $P_{t, \sigma _\tau }$ and $P_{t, \overline{\sigma }_{\tau }}$ are comparable, in the sense that each is contained in a $O(M^{-N})$-thickening of the other.

Proof

There are two links that allow passage of $\tau$ to $\sigma$. The first of these is the isomorphism $\psi$ constructed in Proposition 4.2 that maps $\mathcal T(\mathcal C_M;M)$ onto $\mathcal T([0,1);2)$. Under this isomorphism, the pre-image of any k-long sequence of 0’s and 1’s is a vertex w of height k in $\mathcal T(\mathcal C_M;M)$, in other words one of the $2^k$ chosen M-adic intervals of length $M^{-k}$ that constitute $\mathcal C_M^{[k]}$. The second link is a mapping $\Phi : \mathcal T_N(\mathcal C_M;M) \rightarrow \mathcal D_M^{[N]}$ that sends every vertex w to a point in $\mathcal C_M \cap w$, where, per our notational agreement at the end of Sect. 4, we have also let w denote the particular M-adic interval that it identifies. While the choice of the image point, i.e., $\mathcal D_{M}^{[N]}$ is not unique, any two candidates $\Phi$, $\overline{\Phi }$ satisfy

$$\begin{aligned} |\Phi (w) - \overline{\Phi }(w) \bigr | \le \text {diam}(w) = M^{-h(w)} \,\, \text { for every } w \in \mathcal T_N(\mathcal C_M;M). \end{aligned}$$

(6.4)

We are now ready to describe the assignment $\tau \mapsto \sigma = \sigma _{\tau }$. Given a sticky map $\tau :\mathcal T_N([0,1)^d;M) \rightarrow \mathcal T_N([0,1);2)$ such that

$$\begin{aligned} \tau (\langle i_1, i_2, \ldots , i_k \rangle ) = \langle X_{\langle i_1\rangle }, \ldots , X_{\langle i_1, i_2, \cdots , i_k\rangle }\rangle , \end{aligned}$$

the transformed random variable

$$\begin{aligned} Y_{\langle i_1,i_2\ldots ,i_k\rangle } := \gamma \circ \Phi \circ \psi ^{-1} \left( \langle X_{\langle i_1\rangle }, X_{\langle i_1,i_2\rangle },\ldots , X_{\langle i_1,i_2,\ldots ,i_k\rangle }\rangle \right) \end{aligned}$$

associates a random direction in $\Omega _N = \gamma (\mathcal {D}^{[N]}_M)$ to the sequence $t = \langle i_1,\ldots ,i_k\rangle$ identified with a unique vertex $t \in \mathcal {T}_N([0,1)^d)$. Thus, defining

$$\begin{aligned} \sigma := \gamma \circ \Phi \circ \psi ^{-1} \circ \tau \end{aligned}$$

(6.5)

gives the appropriate (random) mapping claimed by the proposition. The weak Lipschitz condition (6.2) is verified as follows,

$$\begin{aligned} \bigl | \sigma _{\tau }(t) - \sigma _{\tau }(t') \bigr |&= \bigl |\gamma \circ \Phi \circ \psi ^{-1} \circ \tau (t) - \gamma \circ \Phi \circ \psi ^{-1} \circ \tau (t') \bigr | \\&\le C \bigl | \Phi \circ \psi ^{-1} \circ \tau (t) - \Phi \circ \psi ^{-1} \circ \tau (t') \bigr | \\&\le C M^{-h(D(\psi ^{-1} \circ \tau (t), \psi ^{-1} \circ \tau (t')))} \\&= C M^{-h(D(\tau (t), \tau (t')))}. \end{aligned}$$

Here the first inequality follows from (1.5), the second from the definition of $\Phi$. The third step uses the fact that $\psi$ is an isomorphism, so that $h(D(\tau (t),\tau (t'))) = h(D(\psi ^{-1} \circ \tau (t), \psi ^{-1} \circ \tau (t')))$. Finally, any non-uniqueness in the definition of $\sigma$ comes from $\Phi$, hence (6.3) follows from (6.4) and (1.5). $\square$

The stickiness of the maps $\tau _{\mathbf x}$ is built into their definition (6.1). The reader may be interested in observing that there is a naturally sticky map already introduced in this article, which should be viewed as the inspiration for the construction of $\tau$ and $\sigma _{\tau }$. We refer to the geometric content of Lemma 3.7, which in the language of trees has a particularly succinct reformulation. We record this below.

Lemma 6.3

For $C_0$ obeying the requirement of Lemma 3.7 and $p \in [C_0, C_0+1] \times \mathbb R^d$, let Poss(p) be as in (3.3). Let $\Phi$ and $\psi$ be the maps used in Proposition 6.2. Then the map $t \mapsto \beta (t)$ which maps every $t \in \text {Poss}(p)$ to the unique $\beta (t) \in [0,1)$ such that

$$\begin{aligned} p \in \mathcal P_{t, v(t)} \quad \text {where} \quad v(t) = \gamma \circ \Phi \circ \psi ^{-1} \circ \beta (t), \end{aligned}$$

(6.6)

extends as a well-defined sticky map from $\mathcal T_N(\text {Poss}(p);M)$ to $\mathcal T_N([0,1);2)$.

Proof

By Lemma 3.7(a), there exists for every $t \in \text {Poss}(p)$ a unique $v(t) \in \Omega _N$ such that $p \in \mathcal P_{t, v(t)}$. Let us therefore define for $1 \le k \le N$,

$$\begin{aligned} \beta (\pi _1(t), \ldots , \pi _k(t)) = (\pi _1 \circ \beta (t), \ldots , \pi _k \circ \beta (t)) \end{aligned}$$

(6.7)

where $\beta (t)$ is as in (6.6) and as always $\pi _k$ denotes the projection to the kth coordinate of an input sequence. More precisely, $\pi _k(t)$ represents the unique kth level M-adic cube that contains t. Similarly $\pi _k(\beta (t))$ is the kth component of the N-long binary sequence that identifies $\beta (t)$. The function $\beta$ defined in (6.7) maps $\mathcal T_N(\text {Poss}(p);M)$ to $\mathcal T_N([0,1);2)$, and agrees with $\beta$ as in (6.6) if $k=N$.

To check that the map is consistently defined, we pick $t \ne t'$ in Poss(p) with $u = D(t,t')$ and aim to show that $\beta (\pi _1(t), \ldots , \pi _k(t)) = \beta (\pi _1(t'), \ldots , \pi _k(t'))$ for all k such that $k \le h(u)$. But by definition (6.6), v(t) and $v(t')$ have the property that $p \in \mathcal P_{t,v(t)} \cap \mathcal P_{t',v(t')}$. Hence Lemma 3.7(b) asserts that $\alpha (t) = \gamma ^{-1}(v(t))$ and $\alpha (t') = \gamma ^{-1}(v(t'))$ share the same basic interval at step h(u) of the Cantor construction. Thus $\beta (t) = \psi \circ \Phi ^{-1} \circ \alpha (t)$ and $\beta (t') = \psi \circ \Phi ^{-1} \circ \alpha (t')$ have a common ancestor in $\mathcal T_N([0,1);2)$ at height h(u), and hence $\pi _k(\beta (t)) = \pi _k(\beta (t'))$ for all $k \le h(u)$, as claimed. Preservation of heights and lineages is a consequence of the definition (6.7), and stickiness follows. $\square$

6.2 Construction of Kakeya-Type Sets Revisited

As $\tau$ ranges over all sticky maps $\tau _{\mathbf x}{:}\, \mathcal T_N([0,1)^d) \rightarrow \mathcal T_N([0,1);2)$ with $\mathbf x \in \mathbb X_N$, we now have for every vertex $t \in \mathcal {T}_N([0,1)^d)$ with $h(t)=N$ a random sticky slope assignment $\sigma (t) \in \Omega _N$ defined as above. For all such t, this generates a randomly oriented tube $P_{t,\sigma }$ given by (2.3) rooted at the M-adic cube $Q_t$ identified by t, with sidelength $\kappa _d\cdot M^{-N}$ in the $x_1=0$ plane. We may rewrite the collection of such tubes from (2.4) as

$$\begin{aligned} K_N(\sigma ) := \bigcup \limits _{\begin{array}{c} t\in \mathcal {T}_N\left( [0,1)^d\right) \\ h(t) = N \end{array}} P_{t,\sigma }. \end{aligned}$$

(6.8)

On average, a random collection of tubes with the above described sticky slope assignment will comprise a Kakeya-type set, as per (1.2). Specifically, we will show in the next section that the following proposition holds. In view of Proposition 2.1, this will suffice to prove Theorem 1.2.

Proposition 6.4

Suppose $(\Sigma _N,\mathfrak {P}(\Sigma _N),\text {Pr})$ is the probability space of sticky maps described above, equipped with the uniform probability measure. For every $\sigma \in \Sigma _N$, there exists a set $K_N(\sigma )$ as defined in (6.8), with tubes oriented in directions from $\Omega _N = \gamma (\mathcal D^{[N]}_M)$. Then these random sets obey the hypotheses of Proposition 2.1 with

$$\begin{aligned} a_N = c_M\frac{\sqrt{\log N}}{N} \qquad \text { and } \qquad b_N = \frac{C_M}{N} , \end{aligned}$$

(6.9)

where $c_M$ and $C_M$ are fixed positive constants depending only on M and d. The content of Proposition 2.1 allows us to conclude that $\Omega$ admits Kakeya-type sets.

7 Slope Probabilities and Root Configurations

Having established the randomization method for assigning slopes to tubes, we are now in a position to apply this toward the estimation of probabilities of certain events that will be of interest in the next section. Roughly speaking, we wish to compute conditional probabilities that one or more cubes on the root hyperplane are assigned prescribed slopes, provided similar information is available for other cubes.

Lemma 7.1

Let us fix $v_1, v_2 \in \Omega _N$, so that $v_1 = \gamma (\alpha _1)$ and $v_2 = \gamma (\alpha _2)$ for unique $\alpha _1, \alpha _2 \in \mathcal D_M^{[N]}$. We also fix $t_1, t_2 \in \mathcal T_N([0,1)^d)$, $h(t_1) = h(t_2) = N$, $t_1 \ne t_2$. Let us denote by $u \in \mathcal T_N([0,1)^d)$ and $\alpha \in \mathcal T_N(\mathcal D_M^{[N]})$ the youngest common ancestors of $(t_1, t_2)$ and $(\alpha _1, \alpha _2)$ respectively, i.e., $u = D(t_1, t_2)$, $\alpha = D(\alpha _1, \alpha _2)$. Then

$$\begin{aligned} \text {Pr}\bigl (\sigma (t_2)=v_2 \bigl | \sigma (t_1)=v_1\bigr ) = {\left\{ \begin{array}{ll} 2^{-(N-h(u))} &{}\quad \text {if}\,\, h(u) \le h(\alpha ), \\ 0 &{}\quad \text {otherwise.} \end{array}\right. } \end{aligned}$$

(7.1)

Proof

Keeping in mind the slope assignment as described in (6.5), and the stickiness of the map $\tau$ as given in Proposition 6.1, the proof can be summarized as in Fig. 6. Since $t_1$ and $t_2$ must map to $v_1 = \gamma (\alpha _1)$ and $v_2 = \gamma (\alpha _2)$ under $\sigma = \sigma _{\tau }$, the sticky map $\psi ^{-1} \circ \tau$ must map $t_1$ and $t_2$ to the Nth stage basic intervals in the Cantor construction containing $\alpha _1$ and $\alpha _2$ respectively. Since sticky maps preserve heights and lineages, we must have $h(\alpha ) \ge h(u)$. Assuming this, we simply count the number of distinct edges on the ray defining $t_2$ that are not common with $t_1$. The map $\tau$ generating $\sigma = \sigma _{\tau }$ is defined by a binary choice on every edge in $\mathcal {T}_N([0,1)^d)$, and the rays given by $t_1$ and $t_2$ agree on their first h(u) edges, so we have exactly $N-h(u)$ binary choices to make. This is precisely (7.1).

More explicitly, if $t_1 = \langle i_1, i_2, \ldots , i_N \rangle$ and $t_2 = \langle j_1, \ldots , j_N \rangle$, then

$$\begin{aligned} \langle i_1, \ldots , i_{h(u)} \rangle = \langle j_1, \ldots , j_{h(u)} \rangle . \end{aligned}$$

(7.2)

The event of interest may therefore be recast as

$$\begin{aligned} \bigl \{ \sigma (t_2)&= v_2 \bigl | \sigma (t_1) = v_1 \bigr \} \\&= \Bigl \{ \tau (j_1, \ldots , j_N) = \psi \circ \Phi ^{-1} (\alpha _2) \Bigl | \tau (i_1, \ldots , i_N) = \psi \circ \Phi ^{-1} (\alpha _1)\Bigr \}\\&= \Bigl \{ \langle X_{\langle j_1\rangle }, \ldots , X_{\langle j_1, \ldots , j_N\rangle } \rangle = \psi \circ \Phi ^{-1} (\alpha _2) \Bigl | \langle X_{\langle i_1\rangle }, \ldots , X_{\langle i_1, \ldots , i_N\rangle } \rangle = \psi \circ \Phi ^{-1} (\alpha _1) \Bigr \}\\&= \Bigl \{ X_{\langle j_1, \ldots , j_k \rangle } = \pi _k \circ \psi \circ \Phi ^{-1}(\alpha _2) \text { for } h(u) + 1 \le k \le N \Bigr \}, \end{aligned}$$

where $\pi _k$ denotes the kth component of the input sequence. At the second step above we have used (6.1) and Proposition 6.2, and the third step uses (7.2). The last event then amounts to the agreement of two $(N-h(u))$-long binary sequences, with an independent, 1/2 chance of agreement at each sequential component. The probability of such an event is $2^{-(N-h(u))}$, as claimed. $\square$

Fig. 6

Diagram of the sticky assignment between the two rays defining $t_1,t_2\in \mathcal {T}_N([0,1)^d)$ and the two rays defining their assigned slopes $\alpha _1,\alpha _2\in \mathcal {D}^{[N]}_M$. The bold edges defining $t_1$ are fixed to map to the corresponding bold edges at the same height defining $\alpha _1$. This leaves a binary choice to be made at each of the dotted edges along the path between $D(t_1,t_2)$ and $t_2$. We see that $t_2$ is assigned the slope $v_2$ under $\sigma$ if and only if these dotted edges are assigned via $\Phi \circ \psi ^{-1}\circ \tau$ to the dotted edges on the ray defining $\alpha _2$

The same idea can be iterated to compute more general probabilities. To exclude configurations that are not compatible with stickiness, let us agree to call a collection

$$\begin{aligned} \{(t, \alpha _t) : t \in A, \; h(t) = h(\alpha _t) = N \} \subseteq \mathcal T_N([0,1)^d) \times \mathcal D_M^{[N]} \end{aligned}$$

(7.3)

of point-slope combinations sticky-admissible if there exists a sticky map $\tau$ such that $\psi ^{-1} \circ \tau$ maps t to $\alpha _t$ for every $t \in A$. Notice that existence of a sticky $\tau$ imposes certain consistency requirements on a sticky-admissible collection (7.3); for example $h(D(\alpha _t, \alpha _{t'})) \ge h(D(t,t'))$, and more generally $h(D(\alpha _t : t \in A')) \ge h(D(A'))$ for any finite subset $A' \subseteq A$.

For sticky-admissible configurations, we summarize the main conditional probability of interest, leaving the proof to the interested reader.

Lemma 7.2

Let A and B be finite disjoint collections of vertices in $\mathcal T_N([0,1)^d)$ of height N. Then for any choice of slopes $\{ v_t = \gamma (\alpha _t) : t \in A \cup B\} \subseteq \Omega _N$ such that the collection $\{(t, \alpha _t) : t \in A \cup B \}$ is sticky-admissible, the following equation holds:

$$\begin{aligned} \text {Pr} \bigl (\sigma (t) = v_t \text { for all } t \in B \; \big | \; \sigma (t) = v_t \text { for all } t \in A \bigr ) = \left( \frac{1}{2}\right) ^{k(A,B)}, \end{aligned}$$

where k(A, B) is the number of distinct edges in the tree identifying B that are not common with the tree identifying A. If $\{(t,\alpha _t) : t\in A\cup B\}$ is not sticky-admissible, then the probability is zero.

7.1 Four Point Root Configurations

For the remainder of this section, we focus on some special events of the form dealt with in Lemma 7.2 that will be critical to the proof of (2.5). In all these cases of interest we will have $\#(A), \#(B) \le 2$. As is reasonable to expect, the configuration of the root cubes within the tree $\mathcal T_N([0,1)^d)$ plays a role in determining k(A, B). While there is a large number of possible configurations, we isolate certain structures that will turn out to be generic enough for our purposes. Loosely speaking, the classification of configurations with $A=\{t_1,t_1'\}$, $B=\{t_2,t_2'\}$ is based on certain algorithms used to compute k(A, B). For type 1 configurations (defined below), k(A, B) will depend on $u=D(t_1,t_2)$ and $u'=D(t_1',t_2')$; for type 2 configurations, u and $u'$ will be the same and we will need an additional vertex $u_1=D(t_1,t_1')$, after a possible permutation, to compute k(A, B).

Definition 7.3

Let $\mathbb I = \{(t_1, t_2); (t_1', t_2')\}$ be an ordered tuple of four distinct points in $\mathcal T_N([0,1)^d)$ of height N such that

$$\begin{aligned} h(u) \le h(u') \quad \text { where } u = D(t_1, t_2), \; u' = D(t_1', t_2'). \end{aligned}$$

(7.4)

We say that $\mathbb I$ is in type 1 configuration if exactly one of the following conditions is satisfied:

• (a) either $u \cap u' = \emptyset$, or

• (b) $u' \subsetneq u$, or

• (c) $u = u' = D(t_i, t_j')$ for all $i, j = 1,2$

If $\mathbb I$ satisfying (7.4) is not of type 1, we call it of type 2. An ordered tuple $\mathbb I$ not satisfying the inequality in (7.4) is said to be of type $j = 1, 2$ if $\mathbb I' = \{(t_1', t_2'); (t_1, t_2) \}$ is of the same type.

The different structural possibilities are listed in Fig. 7.

Fig. 7

All possible four point configurations of type 1, up to permutations

The advantage of a type 1 configuration is that, in addition to being overwhelmingly popular, it allows (up to permutations) an easy computation of the quantity k(A, B) described in Lemma 7.2 if $\#(A) = \#(B) = 2$, $A \cup B = \{ t_1, t_1', t_2, t_2' \}$ and $\#(A \cap \{ t_1, t_2\}) = \#(B \cap \{ t_1, t_2\}) = 1$.

Lemma 7.4

Let $\mathbb I = \{(t_1, t_2) ; (t_1', t_2')\}$ obeying (7.4) be in type 1 configuration. Let $v_i = \gamma (\alpha _i)$, $v_i' = \gamma (\alpha _i')$, $i = 1,2$, be (not necessarily distinct) points in $\Omega _N$. Then there exist two permutations $\{i_1, i_2\}$ and $\{ j_1, j_2\}$ of $\{1,2\}$ such that

$$\begin{aligned} \text {Pr} \bigl ( \sigma (t_{i_2}) = v_{i_2}, \sigma (t'_{j_2}) = v'_{j_2} \bigl | \sigma (t_{i_1}) = v_{i_1}, \sigma (t'_{j_1}) = v'_{j_1} \bigr ) = \left( \frac{1}{2} \right) ^{2N - h(u) - h(u')}. \end{aligned}$$

provided the collection $\{(t_i, \alpha _i), (t_i', \alpha _i') ; i=1,2\}$ is sticky-admissible. If the admissibility requirement is not met, then the probability is zero.

Proof

The proof is best illustrated by referring to the above diagram, Fig. 7. If $u \cap u' = \emptyset$, then any two permutations will satisfy the conclusion of the lemma, Fig. 7a. In particular, choosing $i_1 = j_1 = 1$, $i_2 = j_2 = 2$, we see that the number of edges in $B = \{ t_2, t_2 '\}$ not shared by $A = \{ t_1, t_1' \}$ is $k(A,B) = (N - h(u)) + (N - h(u')) = 2N - h(u) - h(u')$. The same argument applies if $u = u' = D(t_i, t_j')$ for all $i, j = 1,2$, Fig. 7b.

We turn to the remaining case where $u' \subsetneq u$. Here there are several possiblities for the relative positions of $t_1, t_2$. Suppose first that there is no vertex w on the ray joining u and $u'$ with $h(u) < h(w) < h(u')$ such that w is an ancestor of $t_1$ or $t_2$. This means that the rays of $t_1$, $t_2$ and $u'$ follow disjoint paths starting from u, so any choice of permutation suffices, Fig. 7c. Suppose next that there is a vertex w on the ray joining u and $u'$ with $h(u) < h(w) < h(u')$ such that w is an ancestor of exactly one of $t_1, t_2$, but no descendant of w on this path is an ancestor of either $t_1$ or $t_2$, Fig. 7d. In this case, we choose $t_{i_1}$ to be the unique element of $\{t_1, t_2\}$ whose ancestor is w. Note that the ray for $t_{i_2}$ must have split off from u in this case. Any permutation of $\{ t_1', t_2'\}$ will then give rise to the desired estimate. If neither of the previous two cases hold, then exactly one of $\{ t_1, t_2 \}$, say $t_{i_1}$, is a descendant of $u'$. If $u' = D(t_{i_1}, t_j')$ for both $j=1,2$, then again any permutation of $\{ t_1', t_2' \}$ works, Fig. 7e. Thus the only remaining scenario is where there exists exactly one element in $\{ t_1', t_2' \}$, call it $t_{j_1}'$, such that $h(D(t_{i_1}, t_{j_1}')) > h(u')$. In this case, we choose $A = \{t_{i_1}, t_{j_1}' \}$ and $B = \{t_{i_2}, t_{j_2}' \}$, Fig. 7f. All cases now result in $k(A,B) = 2N - h(u) - h(u')$, completing the proof. $\square$

Lemma 7.5

Let $\mathbb I = \{(t_1, t_2) ; (t_1', t_2') \}$ obeying (7.4) be in type 2 configuration. Then there exist permutations $\{i_1, i_2 \}$ and $\{ j_1, j_2\}$ of $\{1, 2\}$ for which we have the relations

$$\begin{aligned}&u_1 \subseteq u, \; u_2 \subsetneq u \text { with } h(u) \le h(u_1) \le h(u_2), \; \text { where } \\&u_1 = D(t_{i_1}, t_{j_1}'), \; u_2 = D(t_{i_2}, t_{j_2}'), \end{aligned}$$

and for which the following equality holds:

$$\begin{aligned} \text {Pr}\bigl (\sigma (t_{i_1})=v_{i_1}, \sigma (t_{j_1}') = v_{j_1}' \; \bigl | \; \sigma (t_{i_2})=v_{i_2}, \sigma (t_{j_2}') = v_{j_2}'\bigr ) = \left( \frac{1}{2} \right) ^{2N - h(u) - h(u_1)} \end{aligned}$$

for any choice of slopes $v_1, v_1', v_2, v_2' \in \Omega _N$ for which $\{(t_i, \alpha _i), (t_i', \alpha _i'); i=1,2\}$ is sticky-admissible.

Fig. 8

All possible four point configurations of type 2, up to permutations

Proof

Since $\mathbb I$ is of type 2, we know that $u=u'$, and hence all pairwise youngest common ancestors of $\{ t_1, t_1', t_2, t_2' \}$ must lie within u, but that there exist $i, j \in \{1,2\}$ such that $h(D(t_i, t_j')) > h(u)$. Let us set $(i_2, j_2)$ to be a tuple for which $h(D(t_{i_2}, t_{j_2}'))$ is maximal. The height inequalities and containment relations are now obvious, and Fig. 8 shows that $k(A,B) = (N - h(u)) + (N - h(u_1))$ if $A = \{t_{i_2}, t_{j_2}' \}$ and $B = \{ t_{i_1}, t_{j_1}'\}$. $\square$

7.2 Three Point Root Configurations

The arguments in the previous section simplify considerably when there are three root cubes instead of four. Since the proofs here are essentially identical to those presented in Lemmas 7.4 and 7.5, we simply record the necessary facts with the accompanying diagram of Fig. 9, leaving their verification to the interested reader.

Definition 7.6

Let $\mathbb I = \{(t_1, t_2); (t_1, t_2') \}$ be an ordered tuple of three distinct points in $\mathcal T_N([0,1)^d)$ of height N such that $h(u) \le h(u')$, where $u = D(t_1, t_2)$, $u' = D(t_1, t_2')$. We say that $\mathbb I$ is in type 1 configuration if exactly one of the following two conditions holds:

• (a) $u' \subsetneq u$, or

• (b) $u = u' = D(t_2, t_2')$.

Else $\mathbb I$ is of type 2, in which case one necessarily has $u = u'$ and $u_2 = D(t_2, t_2')$ obeys $u_2 \subsetneq u$. If $h(u) > h(u')$, then the type $\mathbb I$ is the same as that of $\mathbb I' = \{ (t_1, t_2'); (t_1, t_2) \}$.

Fig. 9

Structural possibilities for three point root configurations

Lemma 7.7

Let $\mathbb I = \{(t_1, t_2); (t_1, t_2') \}$ be any three-point configuration with $h(u) \le h(u')$ in the notation of Definition 7.6, and let $v_1 = \gamma (\alpha _1)$, $v_2 = \gamma (\alpha _2)$ $v_2' = \gamma (\alpha _2')$ be slopes in $\Omega _N$. Then

$$\begin{aligned} \text {Pr}\bigl (\sigma (t_2) = v_2, \; \sigma (t_2') = v_2' \bigl | \sigma (t_1) = v_1 \bigr ) = {\left\{ \begin{array}{ll} \left( \frac{1}{2}\right) ^{2N-h(u) - h(u')} &{}\quad if \,\,\mathbb \,\,I\,\, is \,\,of \,\,type 1, \\ \left( \frac{1}{2}\right) ^{2N-h(u) - h(u_2)} &{} \quad if \,\,\mathbb \,\,I \,\,is\,\, of\,\, type 2, \end{array}\right. } \end{aligned}$$

provided the point-slope combination $\{(t_1, \alpha _1), (t_2, \alpha _2), (t_2', \alpha _2') \}$ is sticky-admissible.

8 Proposition 6.4: Proof of the Lower Bound (2.5)

If a collection of many thin tubes is to have a large volume, then it is sensible to expect that the intersection of most pairs of tubes should be small. The following measure-theoretic lemma of Bateman and Katz [4] quantifies this phenomenon generally.

Lemma 8.1

[4, Proposition 2, p. 75] Suppose $(X,\mathcal {A},\mu )$ is a measure space and $A_1,\ldots ,A_n\in \mathcal {A}$ are sets with $\mu (A_j) = \alpha$ for every j. If

$$\begin{aligned} \sum _{i=1}^n\sum _{j=1}^n\mu (A_i\cap A_j) \le L, \end{aligned}$$

then

$$\begin{aligned} \mu \left( \bigcup _{i=1}^n A_i\right) \ge \frac{\alpha ^2 n^2}{16L}. \end{aligned}$$

We defer the proof of this fact to Refs. [3] or [4]. Using it, we reduce the derivation of inequality (2.5) with the $a_N$ specified in (6.9) via the following lemma. Throughout this subsection, all probability statements are understood to take place on the probability space $(\Sigma _N,\mathfrak {P}(\Sigma _N),\text {Pr})$ identified in Proposition 6.4.

Proposition 8.2

Fix integers N and R with $N \gg M$ and $N - \frac{1}{10}\log _M N \le R \le N - 10$. Define $P^{*}_{t, \sigma , R}$ to be the portion of $P_{t, \sigma }$ contained in the vertical slab $[M^{R-N}, M^{R+1-N}] \times \mathbb R^d$. Then

$$\begin{aligned} \mathbb E_{\sigma } \left[ \sum _{t_1 \ne t_2} \left| P^{*}_{t_1, \sigma , R} \cap P^{*}_{t_2, \sigma , R}\right| \right] \lesssim N M^{-2N + 2R}, \end{aligned}$$

(8.1)

where the implicit constant depends only on M and d.

If one can show that with large probability and for all R specified in Proposition 8.2, the quantity $\sum _{t_1 \ne t_2} \big | P^{*}_{t_1, \sigma , R} \cap P^{*}_{t_2, \sigma , R}\bigr |$ is bounded above by the right hand side of (8.1), then Lemma 8.1 would imply (2.5) with $a_N = \sqrt{\log N}/N$. Unfortunately, (8.1) only shows this on average for every R, and hence is too weak a statement to permit such a conclusion. However, with some additional work we are able to upgrade the statement in Proposition 8.2 to a second moment estimate, given below. While still not as strong as the statement mentioned above, this suffices for our purposes with a smaller choice of $a_N$.

Proposition 8.3

Under the same hypotheses as Proposition 8.2, there exists a constant $C_{M,d} > 0$ such that

$$\begin{aligned} \mathbb E_{\sigma } \left[ \left( \sum _{t_1 \ne t_2} \left| P^{*}_{t_1, \sigma , R} \cap P^{*}_{t_2, \sigma , R}\right| \right) ^2\right] \le C_{M,d}^2 \Bigl (N M^{-2N + 2R} \Bigr )^2. \end{aligned}$$

(8.2)

Corollary 8.4

Proposition 8.3 implies (2.5) with $a_N$ as in (6.9).

Proof

Fix a small constant $c_1 > 0$ such that $2c_1 < \frac{1}{10}$. Then the range of R satisfied by the inequalities $c_1 \log N \le N - R \le 2c_1 \log N$ obeys the hypothesis of Proposition 8.2. This choice is not strictly necessary but simplifies the following calculation somewhat. By Chebyshev’s inequality, (8.2) implies that there exists a large constant $C_{M,d} > 0$ such that for every R in this range,

$$\begin{aligned}&\text {Pr} \Bigl ( \Bigl \{ \sigma : \sum _{t_1 \ne t_2} \bigl | P^{*}_{t_1, \sigma , R} \cap P^{*}_{t_2, \sigma , R}\bigr | \ge 2C_{M,d} N \sqrt{\log N} M^{-2N + 2R} \Bigr \} \Bigr ) \\&\quad \le \, \frac{\mathbb E_{\sigma } \Bigl [ \Bigl (\sum _{t_1 \ne t_2} \left| P^{*}_{t_1, \sigma , R} \cap P^{*}_{t_2, \sigma , R}\right| \Bigr )^2\Bigr ]}{\bigl (2C_{M,d} N \sqrt{\log N} M^{-2N + 2R} \bigr )^2}\\&\quad \le \, \frac{1}{4 \log N}. \end{aligned}$$

Therefore,

$$\begin{aligned}&\text {Pr} \left( \bigcup _{N -R = c_1 \log N}^{2c_1 \log N}\left\{ \sigma : \sum _{t_1 \ne t_2} \left| P^{*}_{t_1, \sigma , R} \cap P^{*}_{t_2, \sigma , R}\right| \ge C_{M,d} N \sqrt{\log N} M^{-2N + 2R} \right\} \right) \\&\quad \le \, \frac{c_1 \log N}{4 \log N} < \frac{1}{4}. \end{aligned}$$

In other words, for a class of $\sigma$ with probability at least $\frac{3}{4}$,

$$\begin{aligned} \sum _{t_1 \ne t_2} \bigl | P^{*}_{t_1, \sigma , R} \cap P^{*}_{t_2, \sigma , R}\bigr | \le C_{M,d} N \sqrt{\log N} M^{-2N + 2R} \end{aligned}$$

for every $N - R \in \bigl [c_1 \log N, 2c_1 \log N \bigr ]$. For such $\sigma$ and the chosen range of R, we apply Lemma 8.1 with $A_t = P^{*}_{t, \sigma , R}$, $n = M^{Nd}$, for which $\alpha = C_d M^{R-N} M^{-Nd}$, and

$$\begin{aligned} \sum _{t_1, t_2} \bigl | P^{*}_{t_1, \sigma , R} \cap P^{*}_{t_2, \sigma , R}\bigr |&= \left[ \sum _{t_1=t_2} + \sum _{t_1 \ne t_2} \right] \bigl | P^{*}_{t_1, \sigma , R} \cap P^{*}_{t_2, \sigma , R}\bigr |\\&\le \alpha n + C_{M,d} N \sqrt{\log N} M^{-2N + 2R} \\&\lesssim M^{R-N} + N \sqrt{\log N} M^{-2N + 2R} \\&\lesssim N \sqrt{\log N} M^{-2N + 2R} =: L. \end{aligned}$$

The last step above uses the specified range of R. Lemma 8.1 now yields that

$$\begin{aligned} \Bigl | \bigcup _{t} P^{*}_{t, \sigma , R} \Bigr | \gtrsim \frac{(M^{R-N})^2}{L} \sim \frac{1}{N \sqrt{\log N}} \end{aligned}$$

for every $N - R \in \bigl [c_1\log N, 2c_1 \log N \bigr ]$. Since $\{\cup _t P^{*}_{t, \sigma , R} : R \ge 0\}$ is a disjoint collection, we obtain

$$\begin{aligned} \bigl | K_N(\sigma ) \cap [0,1] \times \mathbb R^d \bigr | \ge \sum _{R = N - 2c_1\log N}^{N - c_1 \log N} \Bigl | \bigcup _{t} P^{*}_{t, \sigma , R} \Bigr | \gtrsim \log N \frac{1}{N \sqrt{\log N}} = a_N, \end{aligned}$$

which is the desired conclusion (2.5). $\square$

8.1 Proof of Proposition 8.2

Thus, we are charged with proving Proposition 8.3. We will prove Proposition 8.2 first, since it involves many of the same ideas as in the proof of the main proposition, but in a simpler setting. We will need to take advantage of several geometric facts, counting arguments and probability estimates prepared in Sects. 3 and 7 that will be described shortly. For now, we prescribe the main issues in establishing the bound in (8.1).

Proof

Given N and R as in the statement of the proposition, we decompose the slab $[M^{R-N}, M^{R+1-N}] \times \mathbb R^d$ into thinner slices $Z_k$, where

$$\begin{aligned} Z_k:= \left[ \frac{k}{M^N}, \frac{k+1}{M^N}\right] \times \mathbb R^d, \quad M^R \le k \le M^{R+1}-1. \end{aligned}$$

Setting $P_{t, \sigma , k} := P_{t, \sigma } \cap Z_k$, we observe that $P^{*}_{t, \sigma , R}$ is an essentially disjoint union of $\{ P_{t, \sigma , k}\}$. Since $P^{*}_{t, \sigma , R}$ is transverse to $Z_k$, we arrive at the estimate

$$\begin{aligned} \sum _{t_1 \ne t_2} \left| P^{*}_{t_1, \sigma , R} \cap P^{*}_{t_2, \sigma , R}\right|&= \sum _{M^R \le k < M^{R+1}} \sum _{t_1 \ne t_2} \left| P_{t_1, \sigma , k} \cap P_{t_2, \sigma , k} \right| \nonumber \\&\lesssim M^{-(d+1)N} \sum _{M^R \le k < M^{R+1}} \sum _{t_1 \ne t_2} T_{t_1 t_2} (k) \end{aligned}$$

(8.3)

$$\begin{aligned}&\lesssim M^{-(d+1)N} \sum _{M^R \le k < M^{R+1}} \sum _{\begin{array}{c} u \in \mathcal T_N([0,1)^d) \\ h(u) < N \end{array}} \sum _{(t_1, t_2) \in \mathcal S_u} T_{t_1 t_2}(k), \end{aligned}$$

(8.4)

where $T_{t_1t_2}(k)$ is a random variable that equals one if $P_{t_1, \sigma , k} \cap P_{t_2, \sigma , k} \ne \emptyset$, and is zero otherwise. At the last step in the above string of inequalities, we have further stratified the sum in $(t_1, t_2)$ in terms of their youngest common ancestor $u = D(t_1, t_2)$ in the tree $\mathcal T_N([0,1)^d)$, with the index set $\mathcal S_u$ of the innermost sum being defined by

$$\begin{aligned} \mathcal S_u := \left\{ (t_1, t_2) : t_1, t_2 \in \mathcal T_N([0,1)^d), \; h(t_1) = h(t_2) = N, \; D(t_1, t_2) = u \right\} . \end{aligned}$$

We will prove below in Lemma 8.8 that

$$\begin{aligned} \mathbb E_{\sigma } \Bigl [ \sum _{(t_1, t_2) \in \mathcal S_u} T_{t_1 t_2}(k) \Bigr ] \lesssim M^{R-N} M^{-d h(u) + Nd} = M^{R - d h(u) + N(d-1)}. \end{aligned}$$

(8.5)

Plugging this expected count into the last step of (8.4) and simplifying, we obtain

$$\begin{aligned} \mathbb E_{\sigma } \Bigl [\sum _{t_1 \ne t_2} \left| P^{*}_{t_1, \sigma , R} \cap P^{*}_{t_2, \sigma , R}\right| \Bigr ]&\lesssim \sum _{M^R \le k < M^{R+1}-1} M^{R-2N} \sum _{\begin{array}{c} u \in \mathcal T_N([0,1)^d) \\ h(u) < N \end{array}} M^{-dh(u)} \\&\lesssim \sum _{M^R \le k < M^{R+1}-1} M^{R-2N} N \lesssim NM^{2R-2N}, \end{aligned}$$

which is the estimate claimed by Proposition 8.2. At the penultimate step, we have used the fact that there are $M^{dr}$ vertices u in $\mathcal T_N([0,1)^d)$ of height r, resulting in

$$\begin{aligned} \sum _u M^{-d h(u)} = \sum _{0 \le r < N} M^{-dr} M^{dr} = N. \end{aligned}$$

(8.6)

$\square$

8.2 Proof of Proposition 8.3

Proof

To establish (8.2), we take a similar route, with some extra care in summing over the (now more numerous) indices. Squaring the expression in (8.3), we obtain

$$\begin{aligned} \left[ \sum _{t_1 \ne t_2} \left| P^{*}_{t_1, \sigma , R} \cap P^{*}_{t_2, \sigma , R}\right| \right] ^2&\le M^{-2(d+1)N}\sum _{k,k' \in [M^R, M^{R+1})} \sum _{\begin{array}{c} t_1 \ne t_2 \\ t_1' \ne t_2' \end{array}} T_{t_1t_2}(k) T_{t_1' t_2'}(k') \\&\le \mathfrak S_2 + \mathfrak S_3 + \mathfrak S_4, \end{aligned}$$

where the index i in $\mathfrak S_i$ corresponds to the number of distinct points in the tuple $\{(t_1, t_2); (t_1', t_2')\}$. More precisely, for $i=2,3,4$,

$$\begin{aligned} \mathfrak S_i&:= M^{-2(d+1)N} \sum _{k,k'} \sum _{\mathbb I \in \mathfrak I_i} T_{t_1t_2}(k) T_{t_1't_2'}(k'), \quad \text { where } \end{aligned}$$

(8.7)

$$\begin{aligned} \mathfrak I_i&:= \left\{ \mathbb I = \{(t_1, t_2); (t_1', t_2')\} \Biggl | \begin{array}{ll} &{} t_j, t_j' \in \mathcal T_N([0,1)^d), h(t_j) = h(t_j') =N \; \forall j=1,2, \\ &{}t_1 \ne t_2, \; t_1' \ne t_2', \; \#(\{t_1, t_1', t_2, t_2'\}) = i \end{array} \right\} . \end{aligned}$$

The main contribution to the left hand side of (8.2) will be from $\mathbb E_{\sigma }(\mathfrak S_4)$, and we will discuss its estimation in detail. The other terms, whose treatment will be briefly sketched, will turn out to be of smaller size.

We decompose $\mathfrak I_4 = \mathfrak I_{41} \cup \mathfrak I_{42}$, where $\mathfrak I_{4j}$ is the collection of 4-tuples of distinct points $\{(t_1, t_2); (t_1', t_2')\}$ that are in configuration of type $j=1,2$, as explained in Definition 7.3. This results in a corresponding decomposition $\mathfrak S_4 = \mathfrak S_{41} + \mathfrak S_{42}$. For $\mathfrak S_{41}$, we further stratify the sum in terms of $u = D(t_1, t_2)$ and $u' = D(t_1', t_2')$, where we may assume without loss of generality that $h(u) \le h(u')$. Thus,

$$\begin{aligned} \mathbb E_{\sigma } \bigl (\mathfrak S_{41} \bigr )&= \sum _{k,k'}\sum _{\begin{array}{c} u,u' \in \mathcal T_N([0,1)^d) \\ h(u) \le h(u') < N \end{array}} \mathbb E_{\sigma } \bigl (\mathfrak S_{41}(u,u'; k, k') \bigr )\quad \text { where } \\ \mathfrak S_{41}(u,u';k,k')&:= M^{-2(d+1)N}\sum _{\mathbb I \in \mathfrak I_{41}(u,u')} T_{t_1t_2}(k) T_{t_1't_2'}(k'), \text { and }\nonumber \\ \mathfrak I_{41}(u,u')&:= \{\mathbb I \in \mathfrak I_{41} : u= D(t_1, t_2), u' = D(t_1', t_2') \}.\nonumber \end{aligned}$$

(8.8)

In Lemma 8.9 below, we will show that

$$\begin{aligned} \mathbb E_{\sigma } \bigl [ \mathfrak S_{41}(u,u';k,k') \bigr ]&\lesssim M^{-2(d+1)N} M^{2R-d (h(u) + h(u')) + 2N(d-1)} \nonumber \\&= M^{2R - 4N-d(h(u) + h(u'))}. \end{aligned}$$

(8.9)

Inserting this back into (8.8), we now follow the same summation steps that led to (8.1) from (8.5). Specifically, applying (8.6) twice, we obtain

$$\begin{aligned} \mathbb E_{\sigma } (\mathfrak S_{41})&\lesssim M^{2R - 4N} \sum _{k,k'} \sum _{u,u'} M^{-d(h(u) + h(u'))} \\&\lesssim \sum _{k,k'} N^2 M^{2R-4N} \lesssim N^2 M^{4R-4N}, \end{aligned}$$

which is the right hand side of (8.2).

Next we turn to $\mathfrak S_{42}$. Motivated by the configuration type, and after permutations of $\{ t_1, t_2 \}$ and of $\{t_1', t_2' \}$ if necessary (so that the conclusion of Lemma 7.5 holds), we stratify this sum in terms of $u = u' = D(t_1, t_2) = D(t_1', t_2')$, $u_1 = D(t_1, t_1')$, $u_2 = D(t_2, t_2')$, writing

$$\begin{aligned} \mathfrak S_{42}&= \sum _{k,k'} \sum _{ \begin{array}{c} u, u_1, u_2 \in \mathcal T_N([0,1)^d) \\ u_1, u_2 \subseteq u \end{array}} \mathfrak S_{42}(u,u_1, u_2; k,k'), \text { where } \nonumber \\ \mathfrak S_{42}(u,u_1, u_2; k,k')&:= M^{-2(d+1)N} \sum _{\mathbb I \in \mathfrak I_{42}(u,u_1, u_2)} T_{t_1t_2}(k) T_{t_1't_2'}(k'), \text { and } \nonumber \\ \mathfrak I_{42}(u,u_1, u_2)&:= \left\{ \mathbb I \in \mathfrak I_{42} \left| \begin{array}{l} u = D(t_1, t_2) = D(t_1' t_2'), \; \\ u_1 = D(t_1, t_1'), \; u_2 = D(t_2, t_2') \end{array} \right. \right\} \end{aligned}$$

(8.10)

for given $u_1, u_2 \subseteq u$ with $h(u) \le h(u_1) \le h(u_2)$. For such $u, u_1, u_2$, we will prove in Lemma 8.10 below that

$$\begin{aligned} \mathbb E_{\sigma } \bigl ( \mathfrak S_{42}(u,u_1, u_2; k,k') \bigr ) \lesssim M^{-2N-2d h(u_2)}. \end{aligned}$$

(8.11)

Accepting this estimate for the time being, we complete the estimation of $\mathbb E_{\sigma }(\mathfrak S_{42})$ as follows,

$$\begin{aligned} \mathbb E_{\sigma }(\mathfrak S_{42})\lesssim & {} \sum _{k,k'} \sum _{u, u_1, u_2} M^{-2N-2d h(u_2)} \nonumber \\&\lesssim M^{-2N} \sum _{k,k'} \sum _u \sum _{u_2 \subseteq u} M^{-2d h(u_2)} \sum _{ \begin{array}{c} u_1 \subseteq u \\ h(u_1) \le h(u_2) \end{array}} 1 \nonumber \\\lesssim & {} M^{-2N} \sum _{k,k'} \sum _u \sum _{u_2 \subseteq u} M^{-2d h(u_2)} \Bigl [ M^{d(h(u_2) - h(u))}\Bigr ]\\\lesssim & {} M^{-2N} \sum _{k,k'} \sum _u M^{-d h(u)} \sum _{u_2 \subseteq u} M^{-dh(u_2)} \nonumber \end{aligned}$$

(8.12)

$$\begin{aligned}\lesssim & {} NM^{-2N} \sum _{k,k'} \sum _u M^{-2dh(u)} \end{aligned}$$

(8.13)

$$\begin{aligned}\lesssim & {} N M^{2R-2N}. \end{aligned}$$

(8.14)

For the range $N-R \le \frac{1}{2}\log _M N$ assured by Proposition 8.3, the last quantity above is smaller than $(N M^{2R-2N})^2$. The string of inequalities displayed above involve repeated applications of the fact used to prove (8.6), namely that there are $M^{dj - dh(u)}$ cubes of sidelength $M^{-j}$ contained in u. Thus the estimates

$$\begin{aligned} \sum _{\begin{array}{c} u_1 \subseteq u \\ h(u_1) \le h(u_2) \end{array}} 1&\lesssim \sum _{j = h(u)}^{h(u_2)} M^{d(j-h(u))} \lesssim M^{d(h(u_2) - h(u))}, \\ \sum _{u_2 \subseteq u} M^{-d h(u_2)}&\lesssim \sum _{N \ge j \ge h(u)} M^{-dj} M^{d(j-h(u))} \lesssim NM^{-dh(u)}, \text { and } \\ \sum _{u} M^{-2d h(u)}&= \sum _{j = 0}^N M^{dj} M^{-2dj} = \sum _{j=0}^N M^{-dj} \lesssim 1 \end{aligned}$$

were used in (8.12) (8.13) and (8.14) respectively, completing the estimation of $\mathbb E(\mathfrak S_4)$.

Arguments similar to and in fact simpler than those above lead to the following estimates for $\mathbb E(\mathfrak S_3)$ and $\mathbb E(\mathfrak S_2)$, where $\mathfrak S_3$ and $\mathfrak S_2$ are as defined in (8.7):

$$\begin{aligned} \mathbb E(\mathfrak S_3)&= \mathbb E(\mathfrak S_{31}) + \mathbb E(\mathfrak S_{32}) \nonumber \\&\lesssim N M^{3R-3N} + M^{3R-3N} \lesssim NM^{3R-3N}, \text { and } \end{aligned}$$

(8.15)

$$\begin{aligned} \mathbb E(\mathfrak S_2)&\lesssim N M^{3R-(d+3)N}. \end{aligned}$$

(8.16)

Here without loss of generality and after a permutation if necessary, we have assumed that $\mathbb I = \{(t_1, t_2); (t_1, t_2') \}\in \mathfrak I_3$, with $h(D(t_1, t_2)) \le h(D(t_1, t_2'))$. The subsum $\mathfrak S_{3i}$ then corresponds to tuples $\mathbb I$ that are in type i configuration in the sense of Definition 7.6. There is only one possible configuration of pairs in $\mathfrak I_2$. The derivation of the expectation estimates (8.15) and (8.16) closely follow the estimation of $\mathfrak S_4$, with appropriate adjustments in the probability counts; for instance, (8.15) uses Lemma 7.7 and (8.16) uses Lemma 7.1. To avoid repetition, we leave the details of (8.15) and (8.16) to the reader, noting that the right hand term in each case is dominated by $(NM^{2R-2N})^2$ by our conditions on R. $\square$

8.3 Expected Intersection Counts

It remains to establish (8.5), (8.9) and (8.11). The necessary steps for this are laid out in the following sequence of lemmas. Unless otherwise stated, we will be using the notation introduced in the proofs of Propositions 8.2 and 8.3.

Lemma 8.5

Fix $Z_k$. Let us define $\mathcal A_u = \mathcal A_u(k)$ to be the (deterministic) collection of all $t_1 \in \mathcal T_N([0,1)^d)$, $h(t_1) = N$ that are contained in the cube u and whose distance from the boundary of some child of u is $\lesssim kM^{-N - h(u)}$ (Fig. 10).

For $t_1 \in \mathcal A_u$, let $\mathcal B_{t_1} = \mathcal B_{t_1}(k)$ denote the (also deterministic) collection of $t_2 \in \mathcal T_N([0,1)^d)$ with $h(t_2) = N$ and $D(t_1,t_2) = u$ such that the distance between the centres of $t_1$ and $t_2$ is $\lesssim kM^{-N - h(u)}$.

• (a) Then for any slope assignment $\sigma$, the random variable $T_{t_1t_2}(k) = 0$ unless $t_1 \in \mathcal A_{u}$ and $t_2 \in \mathcal B_{t_1}$. In other words,

  $$\begin{aligned} \sum _{(t_1, t_2) \in \mathcal S_u} T_{t_1t_2}(k)&= \sum _{t_1 \in \mathcal A_u} \sum _{t_2 \in \mathcal B_{t_1}} T_{t_1t_2}(k), \text { so that } \nonumber \\ \mathbb E_{\sigma } \left[ \sum _{(t_1, t_2) \in \mathcal S_u} T_{t_1t_2}(k) \right]&= \sum _{t_1 \in \mathcal A_u} \mathbb E_{\sigma } \left[ \sum _{t_2 \in \mathcal B_{t_1}} T_{t_1t_2}(k) \right] . \end{aligned}$$

  (8.17)

• (b) The description of $\mathcal A_u$ yields the following bound on its cardinality:

  $$\begin{aligned} \# (\mathcal A_u)\lesssim \Bigl (\frac{k}{M^N}\Bigr ) M^{d(N-h(u))} \lesssim M^{R-dh(u) + (d-1)N}. \end{aligned}$$

Fig. 10

A diagram of $\mathcal A_u$ when $d = 2$, $M = 3$. Here the largest square is u. The thatched area depicts $\mathcal A_u$. The finest squares are the root cubes contained in $\mathcal A_u$

Proof

We observe that $T_{t_1t_2}(k) = 1$ if and only if there exists a point $p = (p_1, \ldots , p_{d+1}) \in Z_k$ and $v_1, v_2 \in \Omega _N$ such that $p \in \mathcal P_{t_1, v_1} \cap \mathcal P_{t_2, v_2}$, and $\sigma (t_1) = v_1$, $\sigma (t_2) = v_2$. By Lemma 3.1, this implies that

$$\begin{aligned} |\text {cen}(t_1) - \text {cen}(t_2) + p_1(\sigma (t_1) - \sigma (t_2))| \le 2\kappa _d \sqrt{d} M^{-N}, \end{aligned}$$

(8.18)

where $\text {cen}(t_i)$ denotes the centre of the cube $t_i$. For $p \in Z_k$, (8.18) yields

$$\begin{aligned} |\text {cen}(t_1) - \text {cen}(t_2)|&\le p_1|\sigma (t_1) - \sigma (t_2)| + 2\kappa _d \sqrt{d} M^{-N} \lesssim p_1|\sigma (t_1) - \sigma (t_2)| \nonumber \\&\lesssim \Bigl (\frac{k+1}{M^N} \Bigr ) |\sigma (t_1) - \sigma (t_2)| \lesssim \Bigl (\frac{k}{M^N}\Bigr ) M^{-h(D(\tau (t_1), \tau (t_2) ))} \nonumber \\&\lesssim k M^{-N-h(u)}. \end{aligned}$$

(8.19)

The second inequality in the steps above follows from Corollary 3.2, the third from the definition of $Z_k$ and the fourth from the property (6.2) of the slope assignment. Here $\tau$ is the unique sticky map that generates $\sigma$, as specified in Proposition 6.2. Since $\tau$ preserves heights and lineages, $h(D(\tau (t_1), \tau (t_2))) \ge h(D(t_1, t_2)) = h(u)$, and the last step follows.

The inequality in (8.19) implies that $T_{t_1t_2}(k)= 0$ unless $t_2 \in \mathcal B_{t_1}$. Further, $t_1, t_2$ lie in distinct children of u, so $t_1$ must satisfy

$$\begin{aligned} \text {dist}(t_1, \partial u') \lesssim \frac{k}{M^N} M^{-h(u)} \quad \text { for some child u' of { u}}, \end{aligned}$$

to allow for the existence of some $t_2$ obeying (8.19). This means $t_1 \in \mathcal A_u$, proving (a).

For (b) we observe that u has $M^d$ children. The Lebesgue measure of the set

$$\begin{aligned} \bigcup _{u'} \Bigl \{ x \in u' : \text {dist}(x, \partial u') \lesssim kM^{-N-h(u)}, u' \text { is a child of } u \Bigr \} \end{aligned}$$

(8.20)

is therefore $\lesssim (M^d) kM^{-N-h(u)} M^{-(d-1)h(u)}$. The cardinality of $\mathcal A_u$ is comparable to the number of $M^{-N}$-separated points in the set (8.20), and (b) follows. $\square$

Our next task is to make further reductions to the expression on the right hand side of (8.17) that will enable us to invoke the probability estimates from Sect. 7. To this end, let us fix $Z_k$, $t_1 \in \mathcal A_u(k)$, $v_1 = \gamma (\alpha _1) \in \Omega _N$, and define a collection of point-slope pairs

$$\begin{aligned} \mathcal E_u(t_1, v_1; k) := \left\{ (t_2, v_2) \left| \begin{aligned}&t_2 \in \mathcal T_N([0,1)^d) \cap \mathcal B_{t_1}, \; v_2 = \gamma (\alpha _2) \in \Omega _N, \\&\; h(t_2) = h(\alpha _2) = N, \; u = D(t_1, t_2), \\&\mathcal P_{t_1, v_1} \cap \mathcal P_{t_2, v_2} \cap Z_k \ne \emptyset , \; h(D(\alpha _1, \alpha _2)) \ge h(u) \end{aligned} \right. \right\} . \end{aligned}$$

(8.21)

Thus $\mathcal E_u(t_1, v_1; k)$ is non-random as well. The significance of this collection is clarified in the next lemma.

Lemma 8.6

For $(t_2, v_2) \in \mathcal E_u(t_1, v_1;k)$ described as in (8.21), define a random variable $\overline{T}_{t_2v_2}(t_1, v_1;k)$ as follows:

$$\begin{aligned} \overline{T}_{t_2v_2}(t_1, v_1;k) := {\left\{ \begin{array}{ll} 1 &{}\quad \text {if } \sigma (t_2) = v_2, \\ 0 &{}\quad \text {otherwise. } \end{array}\right. } \end{aligned}$$

(8.22)

• (a) The random variables $T_{t_1t_2}(k)$ and $\overline{T}_{t_2v_2}(t_1, v_1;k)$ are related as follows: given $\sigma (t_1) = v_1$,

  $$\begin{aligned} T_{t_1t_2}(k) = \sup \bigl \{\overline{T}_{t_2v_2}(t_1, v_1;k) : (t_2, v_2) \in \mathcal E_u(t_1, v_1;k) \bigr \}. \end{aligned}$$

  (8.23)

  In particular under the same conditional hypothesis $\sigma (t_1) = v_1$, one obtains the bound

  $$\begin{aligned} T_{t_1t_2}(k) \le \sum _{ \begin{array}{c} v_2 \in \Omega _N \\ (t_2, v_2) \in \mathcal E_u(t_1, v_1;k) \end{array}} \overline{T}_{t_2v_2}(t_1, v_1;k), \end{aligned}$$

  (8.24)

  which in turn implies

  $$\begin{aligned} \mathbb E_{\sigma } \left[ \sum _{t_2 \in \mathcal B_{t_1}} T_{t_1t_2}(k) \Bigl | \sigma (t_1) = v_1 \right] \le \sum _{(t_2, v_2) \in \mathcal E_u(t_1, v_1;k)} \text {Pr}(\sigma (t_2) = v_2 \bigl | \sigma (t_1) = v_1\bigr ). \end{aligned}$$

  (8.25)

• (b) The cardinality of $\mathcal E_u(t_1, v_1; k)$ is $\lesssim 2^{N-h(u)}$.

Proof

We already know from Lemma 8.5 that $T_{t_1t_2}(k) = 0$ unless $t_2 \in \mathcal B_{t_1}$. Further, if $\sigma (t_1) = v_1$ is known, then it is clear that $T_{t_1t_2} (k) = 1$ if and only if there exists $v_2 \in \Omega _N$ such that $\mathcal P_{t_1, v_1} \cap \mathcal P_{t_2, v_2} \cap Z_k \ne \emptyset$ and $\sigma (t_2) = v_2$. But this means that the sticky map $\tau$ that generates $\sigma$ must map $t_2$ to the N-long binary sequence that identifies $\alpha _2$. Stickiness dictates that $h(D(\alpha _1, \alpha _2)) = h(D(\tau (t_1), \tau (t_2)))\ge h(D(t_1, t_2)) = h(u)$, explaining the constraints that define $\mathcal E_u(t_1, v_1;k)$. Rephrasing the discussion above, given $\sigma (t_1) = v_1$, the event $T_{t_1t_2}(k) = 1$ holds if and only if there exists $v_2 \in \Omega _N$ such that $(t_2, v_2) \in \mathcal E_u(t_1, v_1;k)$ and $\sigma (t_2) = v_2$. This is the identity claimed in (8.23) of part (a). The bound in (8.24) follows easily from (8.23) since the supremum is dominated by the sum. The final estimate (8.25) in part (a) follows by taking conditional expectation of both sides of (8.24), and observing that $\mathbb E_{\sigma }(\overline{T}_{t_2v_2}(t_1, v_1;k) |\sigma (t_1) = v_1) = \text {Pr}(\sigma (t_2) = v_2 \bigl | \sigma (t_1) = v_1\bigr )$.

We turn to (b). If $v_2 \in \Omega _N$ is fixed, then it follows from Corollary 3.3 (taking Q in that corollary to be the cube of sidelength $O(M^{-N})$ containing $\mathcal P_{t_1, v_1} \cap Z_k$) that there exist at most a constant number of choices of $t_2$ such that $(t_2, v_2) \in \mathcal E_u(t_1, v_1;k)$. But by Corollary 4.3 the number of points $\alpha _2 \in \mathcal D_M^{[N]}$ (and hence slopes $v_2 \in \Omega _N$) that obey $h(D(\alpha _1, \alpha _2)) \ge h(u)$ is no more than $2^{N - h(u)}$, proving the claim. $\square$

The same argument above applied twice yields the following conclusion, the verification of which is left to the reader.

Corollary 8.7

Given $t_1 \in \mathcal A_u(k)$, $t_1' \in \mathcal A_{u'}(k')$, $v_1, v_1' \in \Omega _N$, define $\mathcal E_u(t_1, v_1;k)$ and $\mathcal E_{u'}(t_1', v_1';k')$ as in (8.21) and the random variables $\overline{T}_{t_2v_2}(t_1, v_1;k)$, $\overline{T}_{t_2'v_2'}(t_1', v_1';k')$ as in (8.22). Then given $\sigma (t_1) = v_1$ and $\sigma (t_1') = v_1'$,

$$\begin{aligned} \sum _{\begin{array}{c} t_2 \in \mathcal B_{t_1} \\ t_2' \in \mathcal B_{t_1'} \end{array}} T_{t_1t_2}(k) T_{t_1't_2'}(k') \le \overset{*}{\sum } \overline{T}_{t_2v_2}(t_1, v_1;k) \overline{T}_{t_2'v_2'}(t_1', v_1';k'), \end{aligned}$$

where the notation $\overset{*}{\sum }$ represents the sum over all indices $\{(t_2, v_2); (t_2', v_2')\} \in \mathcal E_u(t_1,v_1; k) \times \mathcal E_{u'}(t_1',v_1'; k')$.

We are now ready to establish the key estimates in the proofs of Propositions 8.2 and 8.3.

Lemma 8.8

The estimate in (8.5) holds.

Proof

We combine the steps outlined in Lemmas 8.5, 8.6 and 7.1. By Lemma 8.5(a),

$$\begin{aligned} \mathbb E_{\sigma } \left[ \sum _{(t_1, t_2) \in \mathcal S_u} T_{t_1t_2}(k)\right]&= \sum _{t_1 \in \mathcal A_u} \mathbb E_{\sigma } \left[ \sum _{t_2 \in \mathcal B_{t_1}} T_{t_1t_2}(k)\right] \nonumber \\&= \sum _{t_1 \in \mathcal A_u} \mathbb E_{v_1} \mathbb E_{\sigma } \left[ \sum _{t_2 \in \mathcal B_{t_1}} T_{t_1t_2}(k) \left| \sigma (t_1) = v_1 \right. \right] . \end{aligned}$$

(8.26)

Applying (8.25) from Lemma 8.6 followed by Lemma 7.1, we find that the inner expectation above obeys the bound

$$\begin{aligned} \mathbb E_{\sigma } \left[ \sum _{t_2 \in \mathcal B_{t_1}} T_{t_1t_2}(k) \bigl | \sigma (t_1) = v_1 \right]&\le \sum _{(t_2,v_2) \in \mathcal E_u(t_1, v_1; k)} \text {Pr}(\sigma (t_2) = v_2 | \sigma (t_1) = v_1 ) \\&\le \#(\mathcal E_u(t_1, v_1;k)) \times \underbrace{2^{-N + h(u)}}_{\text {Lemma 7.1}} \\&\lesssim \underbrace{2^{N- h(u)}}_{\text {Lemma 8.6(b)}} \times 2^{-N+h(u)} \lesssim 1, \end{aligned}$$

uniformly in $v_1$. Inserting this back into (8.26), we arrive at

$$\begin{aligned} \mathbb E_{\sigma } \left[ \sum _{(t_1, t_2) \in \mathcal S_u} T_{t_1t_2}(k)\right] \lesssim \#(\mathcal A_u), \end{aligned}$$

which according to Lemma 8.5(b) is the bound claimed in (8.5). $\square$

Lemma 8.9

The estimate in (8.9) holds.

Proof

The proof of (8.9) shares many similarities with that of Lemma 8.8, except that there are now two copies of each of the objects appearing in the proof of (8.5) and the probability estimate comes from Lemma 7.4 instead of Lemma 7.1. We outline the main steps below.

In view of Lemma 7.4 and after a permutation of $(t_1, t_2)$ and of $(t_1', t_2')$ if necessary, we may assume that for every $\mathbb I = \{(t_1, t_2); (t_1', t_2') \} \in \mathfrak I_{41}(u,u')$,

$$\begin{aligned} \text {Pr}\bigl ( \sigma (t_2) = v_2, \; \sigma (t_2') = v_2' | \sigma (t_1) = v_1, \; \sigma (t_1') = v_1' \bigr ) = \left( \frac{1}{2} \right) ^{2N - h(u) - h(u')}. \end{aligned}$$

(8.27)

Now,

$$\begin{aligned}&\mathbb E_{\sigma } \bigl ( \mathfrak S_{41}(u,u'; k,k')\bigr ) \\&\quad \le \, M^{-2(d+1)N}\mathbb E_{\sigma }\left[ \sum _{\mathbb I \in \mathfrak I_{41}(u,u')} T_{t_1t_2}(k) T_{t_1't_2'}(k')\right] \\&\quad = M^{-2(d+1)N}\sum _{ \begin{array}{c} t_1 \in \mathcal A_u(k) \\ t_1' \in \mathcal A_{u'}(k') \end{array}} \mathbb E_{v_1, v_1'} \mathbb E_{\sigma } \left[ \sum _{ \begin{array}{c} t_2 \in \mathcal B_{t_1} \\ t_2' \in \mathcal B_{t_1'} \end{array}} T_{t_1t_2}(k) T_{t_1't_2'}(k') \Bigl | \sigma (t_1) = v_1, \sigma (t_1') = v_1' \right] \\&\quad \lesssim \,M^{-2(d+1)N}\underbrace{\left( \frac{kk'}{M^{2N}} M^{d(2N-h(u) - h(u'))}\right) }_{\#(t_1, t_1') \text { from Lemma } 8.5} \lesssim M^{2R-4N - d(h(u) + h(u'))}, \end{aligned}$$

since according to Corollary 8.7

$$\begin{aligned}&\mathbb E_{\sigma } \left[ \sum _{ \begin{array}{c} (t_2, t_2') \in \mathcal B_{t_1} \times \mathcal B_{t_1'} \end{array}} T_{t_1t_2}(k) T_{t_1't_2'}(k') \Bigl |\sigma (t_1) = v_1, \sigma (t_1') = v_1' \right] \\&\quad \le \,\mathbb E_{\sigma } \Bigl [\sum ^{*} \overline{T}_{t_2 v_2}(t_1, v_1;k) \overline{T}_{t_2', v_2'}(t_1', v_1';k') \Bigl | \sigma (t_1) = v_1, \; \sigma (t_1') = v_1'\Bigr ]\\&\quad \lesssim \,\sum ^{*} \text {Pr}(\sigma (t_2) = v_2, \; \sigma (t_2') = v_2'\; | \; \sigma (t_1) = v_1, \sigma (t_1') = v_1' ) \\&\quad \lesssim \,\underbrace{{(2^{N- h(u)})}}_{\#(\mathcal E_{u}(t_1, v_1;k))} \, \times \, \underbrace{{(2^{N- h(u')})}}_{\#(\mathcal E_{u'}(t_1', v_1';k'))} \, \times \, \underbrace{{(2^{-2N+h(u)+h(u')})}}_{{8.27}~\text {via Lemma} ~7.4} \\&\quad \lesssim \,1, \quad \text { uniformly in } v_1, v_1'. \end{aligned}$$

The proof is therefore complete. $\square$

Lemma 8.10

The estimate in (8.11) holds.

Proof

The proof of (8.11) is similar to (8.9), and in certain respects simpler. But the configuration type dictates that we set up a different class $\mathcal E^{*}$ of point-slope tuples that will play a role analogous to $\mathcal E_u(t_1, v_1; k)$ in the preceding lemmas. Recall the structure of a type 2 configuration from Fig. 8 and the definition of $\mathfrak I_{42}(u,u_1, u_2)$ from (8.10). Given root cubes $t_2, t_2'$, and $u, u_1, u_2 \in \mathcal T_N([0,1)^d)$ with the property that

$$\begin{aligned} u_1 \subseteq u,\; u_2 \subsetneq u, \quad u_2 = D(t_2, t_2'), \quad h(u) \le h(u_1) \le h(u_2) \le N = h(t_2) = h(t_2'), \end{aligned}$$

and slopes $v_2 = \gamma (\alpha _2)$, $v_2' = \gamma (\alpha _2') \in \Omega _N$, we define $\mathcal E^{*}$ (depending on all these objects) to be the following collection of root-slope tuples:

$$\begin{aligned} \mathcal E^{*} := \left\{ \{(t_1, v_1);(t_1', v_1')\} \left| \begin{aligned}&\mathbb I = \{(t_1, t_2);(t_1', t_2') \} \in \mathfrak I_{42}(u, u_1, u_2), \\&v_1 = \gamma (\alpha _1), \; v_1' = \gamma (\alpha _1') \text { for some } \alpha _1, \alpha _1' \in \mathcal D_M^{[N]}, \\&\mathcal P_{t_1, v_1} \cap \mathcal P_{t_2, v_2} \cap Z_k \ne \emptyset , \; \mathcal P_{t_1', v_1'} \cap \mathcal P_{t_2', v_2'} \cap Z_{k'} \ne \emptyset , \\&\{(t_i, \alpha _i), (t_i', \alpha _i') : i=1, 2 \} \text { is sticky-admissible }. \end{aligned} \right. \right\} \end{aligned}$$

(8.28)

The relevance of $\mathcal E^{*}$ is this: if $\sigma (t_2) = v_2$ and $\sigma (t_2') = v_2'$ are given, then $T_{t_1t_2}(k) T_{t_1't_2'}(k') = 0$ unless there exist $v_1, v_1' \in \Omega _N$ with $\{(t_1, v_1);(t_1', v_1') \} \in \mathcal E^{*}$ and $\sigma (t_1) = v_1$, $\sigma (t_1') = v_1'$.

We first set about obtaining a bound on the size of $\mathcal E^{*}$ that we will need momentarily. Stickiness dictates that $h(D(\alpha _1, \alpha _2)) \ge h(u)$, and that $\alpha _1$ is an Nth level descendant of $\alpha$, the ancestor of $\alpha _2$ at height h(u). Thus the number of possible $\alpha _1$ (and hence $v_1$) is $\le 2^{N-h(u)}$, by Corollary 4.3. Again by stickiness, $h(D(\alpha _1, \alpha _1')) \ge h(u_1)$, so for a given $\alpha _1$, the number of $\alpha _1'$ (hence $v_1'$) is no more than the number of possible descendants of $\alpha ^{*}$, the ancestor of $\alpha _1$ at height $h(u_1)$. This number is thus $\le 2^{N-h(u_1)}$. Once $v_1, v_1'$ have been fixed (recall that $v_2, v_2', t_2, t_2'$ are already fixed), it follows from Corollary 3.3 that the number of $t_1, t_1'$ obeying the intersection conditions in (8.28) is $\lesssim 1$. Combining these, we arrive at the following bound on the cardinality of $\mathcal E^{*}$:

$$\begin{aligned} \#(\mathcal E^{*}) \lesssim \bigl (2^{N-h(u)} \bigr ) \bigl ( 2^{N-h(u_1)}\bigr ) = 2^{2N - h(u) - h(u_1)}. \end{aligned}$$

(8.29)

We use this bound on the size of $\mathcal E^{*}$ to estimate a conditional expectation, essentially the same way as in the previous two lemmas.

$$\begin{aligned}&\mathbb E_{\sigma } \left[ \sum _{ \begin{array}{c} t_1, t_1' \\ \mathbb I \in \mathfrak I_{42}(u, u_1, u_2) \end{array}} T_{t_1t_2}(k) T_{t_1't_2'}(k') \bigl | \sigma (t_2) = v_2, \sigma (t_2') = v_2' \right] \nonumber \\&\quad =\, \sum _{\mathcal E^{*}}\text {Pr}(\sigma (t_1) = v_1, \sigma (t_1') = v_1' | \sigma (t_2) = v_2, \sigma (t_2') = v_2' ) \nonumber \\&\quad \lesssim \, \#(\mathcal E^{*}) \left( \frac{1}{2}\right) ^{2N - h(u) - h(u_1)} \lesssim 1, \end{aligned}$$

(8.30)

where the last step follows by combining Lemma 7.5 with (8.29). As a result, we obtain

$$\begin{aligned}&\mathbb E_{\sigma }\bigl (\mathfrak S_{42}(u,u_1, u_2; k, k') \bigr ) \\&\quad =\, M^{-2(d+1)N} \mathbb E_{\sigma } \left[ \sum _{\mathbb I \in \mathfrak I_{42}(u,u_1, u_2)} T_{t_1t_2}(k) T_{t_1't_2'}(k') \right] \\&\quad \le \, M^{-2(d+1)N} \sum _{t_2, t_2' \subseteq u_2} \mathbb E_{v_2, v_2'} \mathbb E_{\sigma } \left[ \sum _{ \begin{array}{c} t_1, t_1' \\ \mathbb I \in \mathfrak I_{42}(u, u_1, u_2) \end{array}} T_{t_1t_2}(k) T_{t_1't_2'}(k') \bigl | \sigma (t_2) = v_2, \sigma (t_2') = v_2' \right] \\&\quad \lesssim \, M^{-2(d+1)N} \sum _{t_2, t_2' \subseteq u_2} 1 \\&\quad \lesssim \, M^{-2(d+1)N}\bigl ( M^{-dh(u_2) + Nd}\bigr )^2, \end{aligned}$$

where the estimate from (8.30) has been inserted in the third step above. The final expression is the bound claimed in (8.11). $\square$

9 Proposition 6.4: Proof of the Upper Bound (2.6)

Using the theory developed in Sect. 5, we can establish inequality (2.6) with $b_N = C_M/N$ as in Proposition 6.4 with relative ease. For $x\in \mathbb {R}^{d+1}$, we write $x = (x_1,\overline{x})$, where $\overline{x} = (x_2,\ldots ,x_{d+1})$. Since the Kakeya-type set defined by (6.8) is contained in the parallelepiped $[C_0, C_0 + 1] \times [-2C_0,2C_0]^d$ , we may write

$$\begin{aligned}&\mathbb {E}_{\sigma }\left| K_N(\sigma )\cap [C_0,C_0+1]\times \mathbb {R}^d\right| = \mathbb E_{\sigma }\left( \int _{C_0}^{C_0+1}\int _{[-2C_0,2C_0]^d} \mathbf{1}_{K_N(\sigma )}(x_1,\overline{x})d\overline{x}dx_1\right) \nonumber \\&\quad = \,\int _{C_0}^{C_0+1}\int _{[-2C_0,2C_0]^d} \mathbb E_{\sigma }\left( \mathbf{1}_{K_N(\sigma )}(x_1,\overline{x}) \right) \, d\overline{x}dx_1 \nonumber \\&\quad =\, \int _{C_0}^{C_0+1}\int _{[-2C_0,2C_0]^d}\text {Pr}(x)\ d\overline{x}dx_1, \end{aligned}$$

(9.1)

where $\text {Pr}(x)$ denotes the probability that the point $(x_1,\overline{x})$ is contained in the set $K_N(\sigma )$. To establish inequality (2.6) then, it suffices to show that this probability is bounded by a constant multiple of 1 / N, the constant being uniform in $x \in [C_0,C_0+1]\times \mathbb {R}^{d}$.

Let us recall the definition of Poss(x) from (3.3). We would like to define a certain percolation process on the tree $\mathcal {T}_N(\text {Poss}(x))$ whose probability of survival can majorize $\text {Pr}(x)$. By Lemma 3.7(a), there corresponds to every $t \in$ Poss(x) exactly one $v(t) \in \Omega _N$ such that $\mathcal P_{t, v(t)}$ contains x. Let us also recall that $v(t) = \gamma (\alpha (t))$ for some $\alpha (t) \in \mathcal D_M^{[N]}$. By Corollary 4.3, $\alpha (t)$ is uniquely identified by $\beta (t) := \psi (\alpha (t))$, which is a deterministic sequence of length N with entries 0 or 1. Here $\psi$ is the tree isomorphism described in Lemma 4.2.

Given a slope assignment $\sigma = \sigma _{\tau }$ generated by a sticky map $\tau : \mathcal T_N([0,1)^d) \rightarrow \mathcal T_N([0,1);2)$ as defined in Proposition 6.2 and a vertex $t = \langle i_1, \ldots , i_N \rangle \in \mathcal T_N(\text {Poss}(x))$ with $h(t) = N$, we assign a value of 0 or 1 to each edge of the ray identifying t as follows. Let e be the edge identified by the vertex $\langle i_1, i_2, \ldots , i_k \rangle$. Set

$$\begin{aligned} Y_e := \Biggl \{ \begin{array}{ll} 1 &{}\quad \text {if }\, \pi _k(\tau (t)) = \pi _k(\beta (t)), \\ 0 &{}\quad \text {if }\, \pi _k(\tau (t)) \ne \pi _k(\beta (t)). \end{array} \end{aligned}$$

(9.2)

To clarify the notation above, recall that both $\tau (t)$ and $\beta (t)$ are N-long binary sequences, and $\pi _k$ denotes the kth component of the input. Though the definition of $Y_e$ suggests a potential conflict for different choices of t, our next lemma confirms that this is not the case.

Lemma 9.1

The description in (9.2) is consistent in t, i.e., it assigns a uniquely defined binary random variable $Y_e$ to each edge of $\mathcal T_N(\text {Poss}(x))$. The collection $\{ Y_e \}$ is independent and identically distributed as Bernoulli$(\frac{1}{2})$ random variables.

Proof

Let $t, t' \in \mathcal T_N(\text {Poss}(x))$, $h(t) = h(t') = N$. Set $u = D(t,t')$, the youngest common ancestor of t and $t'$. In order to verify consistency, we need to ascertain that for every edge e in $\mathcal T_N(\text {Poss}(x))$ leading up to u and for every sticky map $\tau$, the prescription (9.2) yields the same value of $Y_e$ whether we use t or $t'$. Rephrasing this, it suffices to establish that

$$\begin{aligned} \pi _k(\tau (t)) = \pi _k(\tau (t')) \quad \text { and } \quad \pi _k(\beta (t)) = \pi _k(\beta (t')) \quad \text { for all } 0 \le k \le h(u). \end{aligned}$$

(9.3)

Both equalities are consequences of the height and lineage-preserving property of sticky maps, by virtue of which

$$\begin{aligned} h(D(t,t')) \le \min \bigl [ h(D(\tau (t), \tau (t'))), h(D(\beta (t), \beta (t')))\bigr ]. \end{aligned}$$

Of these, stickiness of $\tau$ has been proven in Proposition 6.1. The unambiguous definition and stickiness of $\beta$ has been verified in Lemma 6.3.

For the remainder, we recall from Sect. 6 (see the discussion preceding Proposition 6.1) that for $t = \langle i_1, i_2, \ldots , i_N \rangle$, the projection $\pi _k(\tau (t)) = X_{\langle i_1, \ldots , i_k \rangle }$ is a Bernoulli$(\frac{1}{2})$ random variable, so Pr$(Y_e = 1) = \frac{1}{2}$. Further the random variables $Y_e$ associated with distinct edges e in $\mathcal T_N(\text {Poss}(x))$ are determined by distinct Bernoulli random variables of the form $X_{\langle i_1, \ldots , i_k \rangle }$. The stated independence of the latter collection implies the same for the former. $\square$

Thus the collection $\mathbb {Y}_N = \{Y_e\}_{e\in \mathcal {E}}$ defines a Bernoulli percolation on $\mathcal {T}_N(\text {Poss}(x))$, where $\mathcal {E}$ is the edge set of $\mathcal {T}_N(\text {Poss}(x))$. As described in Sect. 5.1, the event $\{Y_e=0\}$ corresponds to the removal of the edge e from $\mathcal {E}$, and the event $\{Y_e=1\}$ corresponds to retaining this edge.

Lemma 9.2

Let $\text {Pr}(x) = \text {Pr}\{\tau : x \in K_N(\sigma _{\tau }) \}$ be as in (9.1), and $\{Y_e \}$ as in (9.2).

• (a) For any $x \in [C_0, C_0+1] \times \mathbb R^d$, the event $\{ \tau : x \in K_N(\sigma _{\tau })\}$ is contained in

  $$\begin{aligned} \{\tau : \exists \text { a full-length ray in } \mathcal T_N(\text {Poss}(x)) \text { that survives percolation via } \{ Y_e \}\}. \end{aligned}$$

  (9.4)

• (b) As a result,

  $$\begin{aligned} \text {Pr}(x) \le \text {Pr}\bigl (\text {survival after percolation on } \mathcal {T}_N(\text {Poss}(x))\bigr ). \end{aligned}$$

Proof

It is clear that $x \in K_N(\sigma _{\tau })$ if and only if there exists $t \in \text {Poss}(x)$ such that $\sigma _{\tau }(t) = v(t)$, where v(t) is the unique slope in $\Omega _N$ prescribed by Lemma 3.7(a) for which $x \in \mathcal P_{t, v(t)}$. In other words, we have

$$\begin{aligned} \begin{array}{ll} \{ \tau : x \in K_N(\sigma _{\tau }) \} &{}= \bigcup \{\sigma (t)= v(t) : t\in \text {Poss}(x)\} \\ &{}= \bigcup \{ \tau (t) = \beta (t) : t\in \text {Poss}(x)\}, \end{array} \end{aligned}$$

(9.5)

where the last step follows from the preceding one by unraveling the string of bijective mappings $\gamma ^{-1}$, $\Phi ^{-1}$ and $\psi$ (described in Proposition 6.2) that leads from $\sigma (t)$ to $\tau (t)$, and which incidentally also generates $\beta (t) = \langle j_1, \ldots , j_N \rangle \in \mathcal T([0,1);2)$ from v(t). Since t is identified by some sequence $\langle i_1,i_2,\ldots , i_N\rangle$, we have its associated random binary sequence

$$\begin{aligned} \tau (t) = \langle X_{\langle i_1\rangle },X_{\langle i_1,i_2\rangle }, \ldots ,X_{\langle i_1,i_2,\ldots ,i_N\rangle }\rangle \in \mathcal T_N([0,1);2). \end{aligned}$$

Using this, we can rewrite (9.5) as follows:

$$\begin{aligned}&\bigcup _{t\in \text {Poss}(x)}\{\sigma (t)=v(t)\}\nonumber \\&\quad =\, \bigcup _{t\in \text {Poss}(x)} \bigl \{\langle X_{\langle i_1\rangle },X_{\langle i_1,i_2\rangle }, \ldots ,X_{\langle i_1,i_2,\ldots ,i_N\rangle }\rangle = \langle j_1,j_2,\ldots ,j_N\rangle \bigr \}\nonumber \\&\quad =\, \bigcup _{t\in \text {Poss}(x)}\bigcap _{k=1}^N\{X_{\langle i_1,\ldots ,i_k\rangle } = j_k\} \nonumber \\&\quad = \,\bigcup _{\mathcal {R} \leftrightarrow \langle i_1, \ldots , i_N \rangle \in \partial \mathcal {T}}\bigcap _{e \leftrightarrow \langle i_1,\ldots ,i_k\rangle \in \mathcal {E}\cap \mathcal {R}}\{X_{\langle i_1,\ldots ,i_k\rangle } - j_k = 0\} \nonumber \\&\quad =\,\bigcup _{\mathcal {R}\in \partial \mathcal {T}}\bigcap _{e \in \mathcal E \cap \mathcal R} \{Y_e = 1\}. \end{aligned}$$

(9.6)

In the above steps we have set $\mathcal {T} := \mathcal {T}_N(\text {Poss}(x))$ for brevity and let $\mathcal {E}$ be the edge set of $\mathcal {T}$. The last step uses (9.2), and the final event is the same as the one in (9.4). Using (9.6), we have

$$\begin{aligned} \text {Pr}(x)&\le \text {Pr}\left( \bigcup _{\mathcal {R}\in \partial \mathcal {T}}\bigcap _{e \in \mathcal E \cap \mathcal R} \{Y_e = 1\} \right) . \end{aligned}$$

(9.7)

This last expression is obviously equivalent to the right hand side of (5.1), verifying the second part of the lemma. $\square$

Our next task is therefore to estimate the survival probability of $\mathcal T_N(\text {Poss}(x))$ under Bernoulli$(\frac{1}{2})$ percolation. For this purpose and in view of the discussion in Sect. 5.3, we should visualize $\mathcal T_N(\text {Poss}(x))$ as an electrical circuit, the resistance of an edge terminating at a vertex of height k being $2^{k-1}$, per equation (5.2). Let us denote by $R(\text {Poss}(x))$ the resistance of the entire circuit. In light of the theorem of Lyons, restated in the form of Proposition 5.3, it suffices to establish the following lemma.

Lemma 9.3

With the resistance of $\text {Poss}(x)$ defined as above, we have

$$\begin{aligned} R(\text {Poss}(x)) \gtrsim N. \end{aligned}$$

(9.8)

Proof

We begin by constructing a different electrical network from the one naturally associated to our tree $\text {Poss}(x)$. For every $k\ge 1$, we connect all vertices at height k by an ideal conductor to make one node $V_k$, as in Fig. 11. Call this new circuit E.

The resistance of E cannot be greater than the resistance of the original circuit, by Proposition 5.1. Now fix k, $1\le k\le N$, and let $R_k$ denote the resistance between $V_{k-1}$ and $V_k$. The number of edges between $V_{k-1}$ and $V_k$ is equal to the number $N_k$ of kth generation vertices in $\mathcal T_N(\text {Poss}(x))$. Recalling the containment (3.5) from Lemma 3.4, we find that $N_k$ is bounded above by $\overline{N}_k$, the number of kth level vertices in $\mathcal T_N(\{0\} \times [0,1)^d \cap (x-x_1 \Omega _N))$. By Lemma 4.4(b), $\overline{N}_k \lesssim 2^{k}$, where the implicit constant is uniform in $x \in [C_0, C_0+1] \times [-2C_0, 2C_0]^d$. Thus,

$$\begin{aligned} \frac{1}{R_k} = \sum _{1}^{N_k} \frac{1}{2^{k-1}} = \frac{N_k}{2^{k-1}}\lesssim \frac{\overline{N}_k}{2^k} \lesssim 1, \end{aligned}$$

and this holds for any $1\le k\le N$. Since the resistors $\{R_k\}_{k=1}^N$ are in series, $R(\text {Poss}(x)) \ge R(E) = \sum _{k=1}^{N} R_k \gtrsim N$, establishing inequality (9.8). $\square$

Fig. 11

A diagram of the circuit E for a typical $\text {Poss}(x)$. Each resistor at height k from the root $V_0$ has resistance ${\sim }2^k$. The total resistance between $V_{k-1}$ and $V_k$ is denoted by $R_k$

Combining Lemmas 9.2 and 9.3 with Proposition 5.3 gives us the desired bound of $\lesssim 1/N$ on (9.1). This completes the proof of inequality (2.6), and so too Proposition 6.4.