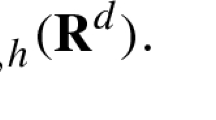Sharpness of Complex Interpolation on $\alpha$-Modulation Spaces

Abstract

In this paper, we solve a long standing problem on the modulation spaces, $\alpha$-modulation spaces and Besov spaces. We establish sharp conditions for the complex interpolation between these function spaces. We show that no $\alpha$-modulation space $M_{p,q}^{s,\alpha }$ can be regarded as the interpolation space between $M_{p_1,q_1}^{s_1,\alpha _1}$ and $M_{p_2,q_2}^{s_2,\alpha _2}$, unless $\alpha _1$ is equal to $\alpha _2$, essentially. Especially, our results show that the $\alpha$-modulation spaces can not be obtained by complex interpolation between modulation spaces and Besov spaces.

1 Introduction

The modulation spaces $M_{p,q}^{s}$ were introduced by Feichtinger [10] in 1983 using the short-time Fourier transform. His initial motivation was to use a different space from the $L^{p}$ to measure the smoothness of a function. Since their introduction, it became increasingly clear that the modulation spaces are quite natural and useful for the studying time-frequency behavior of functions and that they play a significant role in harmonic analysis and partial differential equations. Particularly, these spaces and their applications received extensive studies in the last 10 years. For instance, the reader may see [1, 2, 7, 10, 11, 16, 20–22] and the references therein.

The definition of classical Besov spaces $B_{p,q}^{s}$ is based on a dyadic decomposition of the frequency space, while the definition of modulation spaces is based on the unit square decomposition of the frequency space (uniform frequency decomposition). Thus, it is natural to build a bridge connecting modulation spaces and Besov spaces. To this end, under the guidance of Feichtinger, in his PhD thesis Gröbner introduced the $\alpha$-modulation space $M_{p,q}^{s,\alpha }$ , which form a family of intermediate spaces between these two types of spaces. The parameter $\alpha$ controls the ’mixture’ between both kinds of spaces. Gröbner used the general framework of decomposition spaces considered by Feichtinger and Gröbner in [8] and [9] to build the $\alpha$-modulation spaces. Borup and Nielsen [4] and Fornasier [12] constructed Banach frames for $\alpha$-modulation spaces in the multivariate setting. Borup and Nielsen [5, 6] also discussed, in the framework of $\alpha$-modulation spaces, the boundedness of certain pseudo-differential operators with symbols in the Hörmander class.

The modulation spaces arise as special $\alpha$-modulation spaces in the case $\alpha =0$, and the (inhomogeneous) Besov space $B_{p,q}^s$ can be regarded as the limit case of $M_{p,q}^{s,\alpha }$ as $\alpha \rightarrow 1$ (see [13]). So, for the sake of convenience, we can view the Besov spaces as special $\alpha$-modulation spaces and use $M_{p,q}^{s,1}$ to denote the inhomogeneous Besov space $B_{p,q}^s$. The interested reader should also consult the recent paper [15], which contains a more comprehensive study of $\alpha$-modulation spaces.

As we mentioned above, the $\alpha$-modulation space $M_{p,q}^{s,\alpha }$ plays the role of an intermediate space between the spaces $M_{p,q}^{s}$ and $B_{p,q}^{s}$. One may ask how it plays, or in what sense, as an intermediate space. For instance, in [23] it was shown that, from the view as the action of certain unimodular Fourier multipliers, the $\alpha$-modulation space is an intermediate function space between modulation space and Besov space. But this intuition is false in some other cases. Thus, one motivation of this paper is to explore this fact in the sense of complex interpolation.

A natural long standing question on modulation, $\alpha$-modulation and Besov spaces is: Can we obtain the $\alpha$-modulation spaces by interpolation between certain modulation spaces and Besov spaces? More specifically, if $s=(1-\alpha )s_0+\alpha s_1$, can we conclude

$$\begin{aligned} M_{p,q}^{s,\alpha }=[M_{p,q}^{s_1,0}, M_{p,q}^{s_2,1}]_{\alpha }\,? \end{aligned}$$

(1.1)

Here $\left[ X,Y\right] _{\theta }$ denotes the complex interpolation space of exponent $\theta$ ($0<\theta <1$) between X and Y (see [3]).

In [15], the authors pointed out that the answer of the question is negative in some special cases. The main technique used in [15] is based on the fact that, for two $\alpha$-modulation spaces $M_{p_1,q_1}^{s_1,\alpha _1}$ and $M_{p_2,q_2}^{s_2,\alpha _2}$ which are multiplication algebras, the complex interpolation spaces of $M_{p_1,q_1}^{s_1,\alpha _1}$ and $M_{p_2,q_2}^{s_2,\alpha _2}$ are also multiplication algebras. This method, which deeply depends on the multiplication algebra property of $\alpha$-modulation spaces, leads to some unnatural constrains that seemingly can not be diminished. The algebra property seems not to be the most suitable tool for characterizing the complex interpolation between $\alpha$-modulation spaces.

Instead, in our proof, the solution is obtained by taking full advantage of the properties of complex interpolation. Actually, in this paper we give a complete answer in a more general sense. We construct some specific functions and operators to test the operator interpolation inequalities, making the arguments more clear and efficient. As a consequence, we show that no $\alpha$-modulation space can be regarded as the interpolation space between $M_{p_1,q_1}^{s_1,\alpha _1}$ and $M_{p_2,q_2}^{s_2,\alpha _2}$, unless $\alpha _1$ is equal to $\alpha _2$, essentially. Also, our conclusion gives the solution of the question mentioned above.

It is known that the theory of complex interpolation is a powerful tool in the study of linear and multi-linear operators on function spaces. In order to obtain the boundedness of a linear or multi-linear operator between certain function spaces, we only need to obtain its boundedness on endpoint spaces. Then boundedness on the full range of function spaces (interpolation spaces) can be easily obtained by complex interpolation. In view of this motivation, establishing a theory of complex interpolation for the $\alpha$-modulation spaces seems worthwhile. We notice that the known results imply $[M_{p_1, q_1}^{s_1, \alpha }, M_{p_2, q_2}^{s_2, \alpha }]_{\theta }=M_{p_{\theta }, q_{\theta }}^{s_{\theta }, \alpha }$ for $\theta \in (0,1)$. This indicates that the complex interpolation theory indeed works for the $\alpha$-modulation spaces if $\alpha$ is fixed. But the situation becomes complicated for the modulation spaces of different $\alpha$. To clarify this matter, on the analogy of the known results, one might wonder whether $[M_{p_1, q_1}^{s_1, \alpha _1}, M_{p_2, q_2}^{s_2, \alpha _2}]_{\theta }=M_{p_{\theta }, q_{\theta }}^{s_{\theta }, \alpha _{\theta }}$ holds for $\theta \in (0,1)$, where $\alpha _{\theta }=(1-\theta )\alpha _1+\theta \alpha _2.$ First, we ask if the interpolation space between $M_{p_{1},q_{1}}^{s_{1},\alpha _{1}}$ and $M_{p_{2},q_{2}}^{s_{2},\alpha _{2}}$ exists if $\alpha _{1}\ne \alpha _{2}.$ Second, even if the interpolation space between $M_{p_{1},q_{1}}^{s_{1},\alpha _{1}}$ and $M_{p_{2},q_{2}}^{s_{2},\alpha _{2}}$ exists, for instance it is a certain $\alpha$-modulation space, we do not know if $M_{p_{\theta },q_{\theta }}^{s_{\theta },\alpha _{\theta }}$ is just the right interpolation space. For these reasons, to approach our aim, we will not consider directly the discrimination of $[M_{p_{1},q_{1}}^{s_{1},\alpha _{1}},M_{p_{2},q_{2}}^{s_{2},\alpha _{2}}]_{\theta }=M_{p_{\theta },q_{\theta }}^{s_{\theta },\alpha _{\theta }},$ but try to find conditions on the pairs $(p_{1},p_{2}),(q_{1},q_{2}),(s_{1},s_{2})$ and $(\alpha _{1},\alpha _{2}),$ for which $[M_{p_{1},q_{1}}^{s_{1},\alpha _{1}},M_{p_{2},q_{2}}^{s_{2},\alpha _{2}}]_{\theta }$ is an $\alpha$-modulation space.

In the spirit of the abstract complex interpolation theory for Quasi-Banach spaces, we know that the complex interpolation space $[M_{p_1, q_1}^{s_1, \alpha _1}, M_{p_2, q_2}^{s_2, \alpha _2}]_{\theta }$ is well-defined for arbitrary values of the parameters, even for $\alpha _1 \ne \alpha _2$. However, under the condition $\alpha _1 \ne \alpha _2$, we will show that, for any $\theta \in (0,1)$, the interpolation space $[M_{p_1, q_1}^{s_1, \alpha _1}, M_{p_2, q_2}^{s_2, \alpha _2}]_{\theta }$ is not any $\alpha$-modulation space. To achieve our target, for three $\alpha$-modulation spaces $M_{p_1, q_1}^{s_1, \alpha _1}$, $M_{p_2, q_2}^{s_2, \alpha _2}$ and $M_{p, q}^{s, \alpha }$ to be checked, we will assume towards a contradiction that $[M_{p_{1},q_{1}}^{s_{1},\alpha _{1}},M_{p_{2},q_{2}}^{s_{2},\alpha _{2}}]_{\theta }=M_{p,q}^{s,\alpha }$ holds and choose a known triplet of complex interpolation spaces $Y_1, Y_2$ and $Y_{\theta }$ satisfying $[Y_1,Y_2]_{\theta }=Y_{\theta }$.

By choosing a suitable operator T, we use the general property of interpolation spaces to obtain

$$\begin{aligned} \left\| T| {M_{p, q}^{s, \alpha }\rightarrow [Y_1,Y_2]_{\theta }}\right\| \lesssim \left\| T| {M_{p_1, q_1}^{s_1, \alpha _1}\rightarrow Y_1}\right\| ^{1-\theta }\left\| T| {M_{p_2, q_2}^{s_2, \alpha _2}\rightarrow Y_2}\right\| ^{\theta } \end{aligned}$$

(1.2)

and

$$\begin{aligned} \left\| T| {[Y_1,Y_2]_{\theta }\rightarrow M_{p, q}^{s, \alpha }}\right\| \lesssim \left\| T| {Y_1\rightarrow M_{p_1, q_1}^{s_1, \alpha _1}}\right\| ^{1-\theta }\left\| T| {Y_2\rightarrow M_{p_2, q_2}^{s_2, \alpha _2}}\right\| ^{\theta }. \end{aligned}$$

(1.3)

Theoretically, as long as we collect enough known complex interpolation triplets and operators, the information of $\alpha$-modulation spaces to be checked can be characterized in full. This will yield stronger criteria for disproving the identity $[M_{p_{1},q_{1}}^{s_{1},\alpha _{1}},M_{p_{2},q_{2}}^{s_{2},\alpha _{2}}]_{\theta }=M_{p,q}^{s,\alpha }$. So, the rest of the work is to establish suitable tools for achieving the goal mentioned above.

We use

$$\begin{aligned} \mathcal {M}=\{M_{p,q}^{s,\alpha }: \; p,q\in (0, \infty ], s\in \mathbb {R}, \alpha \in [0,1] \} \end{aligned}$$

(1.4)

to denote the set of all $\alpha$-modulation spaces.

Now, we state our main theorems.

Theorem 1.1

(Banach case) Let $1\le p_i, q_i\le \infty$, $s_i\in \mathbb {R}$, $\alpha _i \in [0,1]$ for $i=1,2$. Then

$$\begin{aligned} \left[ M_{p_1,q_1}^{s_1,\alpha _1},M_{p_2,q_2}^{s_2,\alpha _2}\right] _{\theta }\in \mathcal {M} \end{aligned}$$

(1.5)

for some $\theta \in (0,1)$, if and only if

$$\begin{aligned} \alpha _1=\alpha _2 \qquad \text {or} \qquad p_1=q_1=2 \qquad \text {or} \qquad p_2=q_2=2. \end{aligned}$$

(1.6)

Moreover, we have

$$\begin{aligned} \left[ M_{p_1,q_1}^{s_1,\alpha _1},M_{p_2,q_2}^{s_2,\alpha _2}\right] _{\theta } = {\left\{ \begin{array}{ll} M_{p_{\theta },q_{\theta }}^{s_{\theta },\alpha },\; &{}\text {if}\; \alpha _1=\alpha _2=\alpha , \\ M_{p_{\theta },q_{\theta }}^{s_{\theta },\alpha _{2}},\; &{}\text {if}\; p_1=q_1=2, \\ M_{p_{\theta },q_{\theta }}^{s_{\theta },\alpha _{1}},\; &{}\text {if}\; p_2=q_2=2, \\ H^{s_{\theta }},\; &{}\text {if}\; p_1=q_1=p_2=q_2=2, \end{array}\right. } \end{aligned}$$

(1.7)

where

$$\begin{aligned} \frac{1}{p_{\theta }}=\frac{1-\theta }{p_1}+\frac{\theta }{p_2},\;\frac{1}{q_{\theta }}=\frac{1-\theta }{q_1}+ \frac{\theta }{q_2}, \; s_{\theta }=(1-\theta )s_1+\theta s_2. \end{aligned}$$

(1.8)

Theorem 1.2

(Quasi-Banach case) Let $0<p,q\le \infty$, $s_i\in \mathbb {R}$, $\alpha _i \in [0,1]$ for $i=1,2$. Then

$$\begin{aligned} \left[ M_{p,q}^{s_1,\alpha _1},M_{p,q}^{s_2,\alpha _2}\right] _{\theta }\in \mathcal {M} \end{aligned}$$

(1.9)

for some $\theta \in (0,1)$, if and only if

$$\begin{aligned} \alpha _1=\alpha _2 \qquad \qquad \text {or} \qquad \qquad p=q=2. \end{aligned}$$

(1.10)

Moreover, we have

$$\begin{aligned} \left[ M_{p,q}^{s_1,\alpha _1},M_{p,q}^{s_2,\alpha _2}\right] _{\theta } = {\left\{ \begin{array}{ll} M_{p,q}^{s_{\theta },\alpha },\;&{}\text {if}\;\alpha _1=\alpha _2=\alpha ,\\ H^{s_{\theta }},\;&{}\text {if}\;p=q=2, \end{array}\right. } \end{aligned}$$

(1.11)

where $s_{\theta }=(1-\theta )s_1+\theta s_2$.

Remark 1.3

In Theorem 1.1, the constrains $p_i, q_i\ge 1$ are convenient for us to use the dual method. If $p_i<1$ or $q_i<1$, then the dual method does not work in most cases. Heuristically, this indicates that we may not be able to catch enough information about p from it’s dual $p'$ in the case $p<1$. So, we have to establish more delicate estimates to make up for the loss of duality. We handle this situation in Theorem 1.2 based on the restrictive conditions $p_1=p_2$ and $q_1=q_2.$ However, we believe that the additional assumption in Theorem 1.1 or Theorem 1.2 can be eliminated. In other words, it is our conjecture that the results in Theorem 1.1 remain true when $0<p_{i},q_{i}\le \infty .$

The organization of this paper is as follows. In Sect. 2, we introduce some notations and definitions that will be used throughout this paper. We recall the definitions of $\alpha$-modulation spaces and Besov spaces and collect some of their properties that will be used later on. We also present some basic results about the technique of complex interpolation which will be our main tools in the proof. In Sect. 3, we establish some relations among $p_i, q_i, s_i$, under the assumption that the convexity inequality associated with certain $\alpha$-modulation spaces holds for all Schwartz functions. These estimates are the key for the discrimination of the complex interpolation in Theorem 1.1. In Sect. 4, we establish some additional estimates for the proof of Theorem 1.2. These estimates allow us to obtain a new proof for the sharpness of embeddings between $\alpha$-modulation spaces. We complete the proof of our main theorems in Sect. 5. Since the assumptions in our theorems are fairly weak, we must first obtain some priori estimates, then the estimates obtained in Sects. 3 and 4 can be used for further determination of the parameters. In combination with the positive results of complex interpolation for $\alpha$-modulation spaces, we obtain the sufficient and necessary conditions and complete our proofs.

2 Preliminary

We recall some notations. Let C be a positive constant that may depend on $n,p_i,q_i,s_i,\alpha _i$, where $i=1, 2.$ The notation $X\lesssim Y$ denotes the statement $X\le CY$. The notation $X\sim Y$ means the statement $X\lesssim Y \lesssim X$, and the notation $X\simeq Y$ denotes the statement $X=CY$. We write $a\wedge b=\min \{a,b \}$, $a\vee b=\max \{a, b\}.$ For a multi-index $k=(k_1,k_2,...,k_n)\in \mathbb {Z}^{n}$, we denote $|k|_{\infty }: =\max _{i=1,2...n}|k_i|$, and $\langle k\rangle : =(1+|k|^{2})^{\frac{1}{2}}.$ The translation operator is defined by $T_xf(t)=f(t-x)$, $t, x\in \mathbb {R}^n$. For any $p\in (0, \infty ]$, we denote by $p'$ the dual number of p, i.e.,

$$\begin{aligned} p'= {\left\{ \begin{array}{ll} \frac{p}{p-1}, &{}1<p\le \infty , \\ \infty , &{}0<p\le 1. \end{array}\right. } \end{aligned}$$

(2.1)

Let $\mathscr {S}:= \mathscr {S}(\mathbb {R}^{n})$ be the set of all Schwartz functions and $\mathscr {S}':=\mathscr {S}'(\mathbb {R}^{n})$ be the space of all tempered distributions. We define the Fourier transform $\mathscr {F}f$ and the inverse Fourier transform $\mathscr {F}^{-1}f$ of $f\in \mathscr {S}(\mathbb {R}^{n})$ by

$$\begin{aligned} \mathscr {F}f(\xi )=\widehat{f}(\xi )=\int _{\mathbb {R}^{n}}f(x)e^{-2\pi ix\cdot \xi }dx, \mathscr {F}^{-1}f(x)=\widehat{f}(-x)=\int _{\mathbb {R}^{n}}f(\xi )e^{2\pi ix\cdot \xi }d\xi . \end{aligned}$$

We use $L^{p}(\mathbb {R}^n)$, to denote the Banach space (or Quasi-Banach space when $0<p\le 1)$ of measurable functions $f:\mathbb {R}^n \rightarrow \mathbb {C}$ whose norm (or Quasi-norm)

$$\begin{aligned} \Vert f\Vert _{L^{p}(\mathbb {R}^n)}:= \left( \int _{\mathbb {R}^n}|f(x)|^{p}dx\right) ^{\frac{1}{p}} \end{aligned}$$

(2.2)

is finite, with the usual modification when $p=\infty$.

We recall some definitions and properties of the function spaces to be discussed in this paper. For the convenience of doing calculations pertaining to $\alpha$-modulation spaces, we give the definition of $\alpha$-modulation spaces based on decomposition methods, without introducing them in full generality. Now, we give the partition of unity on frequency space for $\alpha \in [0,1)$. We suppose that $c>0$ and $C>0$ are two appropriate constants, and choose a Schwartz function sequence $\{\eta _k^{\alpha }\}_{k\in \mathbb {Z}^n}$ satisfying

$$\begin{aligned} {\left\{ \begin{array}{ll} |\eta _k^{\alpha }(\xi )|\ge 1, \;\text {if}\;|\xi -\langle k\rangle ^{\frac{\alpha }{1-\alpha }}k|<c\langle k\rangle ^{\frac{\alpha }{1-\alpha }};\\ \mathbf {supp}\eta _k^{\alpha }\subset \{\xi : |\xi -\langle k\rangle ^{\frac{\alpha }{1-\alpha }}k|<C\langle k\rangle ^{\frac{\alpha }{1-\alpha }}\};\\ \sum _{k\in \mathbb {Z}^{n}}\eta _k^{\alpha }(\xi )\equiv 1, \forall \xi \in \mathbb {R}^{n};\\ |\partial ^{\gamma }\eta _k^{\alpha }(\xi )|\le C_{\alpha }\langle k\rangle ^{-\frac{\alpha |\gamma |}{1-\alpha }} , \forall \xi \in \mathbb {R}^{n}, \gamma \in (\mathbb {Z}^{+}\cup \{0\})^{n}. \end{array}\right. } \end{aligned}$$

(2.3)

Then $\{\eta _{k}^{\alpha }(\xi )\}_{k\in \mathbb {Z}^{n}}$ constitutes a smooth partition of unity on $\mathbb {R}^{n}$. The frequency decomposition operators associated with above function sequence can be defined by

$$\begin{aligned} \Box _{k}^{\alpha }:= \mathscr {F}^{-1}\eta _{k}^{\alpha }\mathscr {F} \end{aligned}$$

(2.4)

for $k\in \mathbb {Z}^{n}$. Let $0< p,q \le \infty$, $s\in \mathbb {R}$, $\alpha \in [0,1)$. The $\alpha$-modulation space associated with the above decomposition is defined by

$$\begin{aligned} M_{p,q}^{s,\alpha }(\mathbb {R}^n)=\left\{ f\in \mathscr {S}'(\mathbb {R}^{n}): \Vert f\Vert _{M_{p,q}^{s,\alpha }(\mathbb {R}^n)} =\Bigg ( \sum _{k\in \mathbb {Z}^{n}}\langle k\rangle ^{\frac{sq}{1-\alpha }}\Vert \Box _k^{\alpha } f\Vert _{L^p}^{q}\right) ^\frac{1}{q}<\infty \Bigg \} \end{aligned}$$

with the usual modification when $q=\infty$. For simplicity, we denote $M_{p,q}^s=M_{p,q}^{s,0}$ and $\eta _k(\xi )=\eta _k^0(\xi )$.

Remark 2.1

We recall that the above definition is independent of the choice of exact $\eta _k^{\alpha }$ (see [15]). Also, for sufficiently small $\delta >0$, one can construct a function sequence $\{\eta _{k}^{\alpha }(\xi )\}_{k\in \mathbb {Z}^{n}}$ such that $\eta _k^{\alpha }(\xi )=1$ and $\eta _k^{\alpha }(\xi )\eta _l^{\alpha }(\xi )=0$ if $k\ne l$, when $\xi$ lies in the ball $B(\langle k\rangle ^{\frac{\alpha }{ 1-\alpha }}k,\langle k\rangle ^{\frac{\alpha }{ 1-\alpha }}\delta )$ (see [4, 12, 14]).

Next we introduce the dyadic decomposition of $\mathbb {R}^n$. Let $\varphi$ be a smooth bump function supported in the ball $\{\xi : |\xi |<\frac{3}{2}\}$ which is equal to 1 on the ball $\{\xi : |\xi |\le \frac{4}{3}\}$. Denote

$$\begin{aligned} \psi (\xi )=\varphi (\xi )-\varphi (2\xi ), \end{aligned}$$

(2.5)

and a function sequence

$$\begin{aligned} {\left\{ \begin{array}{ll} \psi _j(\xi )=\psi (2^{-j}\xi ),\;j\in \mathbb {N} \\ \psi _0(\xi )=1-\sum _{j\in \mathbb {N}}\psi _j(\xi )=\varphi (\xi ). \end{array}\right. } \end{aligned}$$

(2.6)

For integers $j\in \mathbb {N}\cup \{0\}$, we define the Littlewood-Paley operators

$$\begin{aligned} \widehat{\Delta _jf}(\xi )=\psi _j(\xi )\widehat{f}(\xi ). \end{aligned}$$

(2.7)

Let $0< p,q\le \infty$, $s\in \mathbb {R}$. For $f\in \mathscr {S}'$ we set

$$\begin{aligned} \Vert f\Vert _{B_{p,q}^s}=\left( \sum _{j=0}^{\infty }2^{jsq}\Vert \Delta _jf\Vert _{L^p}^q \right) ^{1/q} \end{aligned}$$

(2.8)

with the usual modification when $q=\infty$. The (inhomogeneous) Besov space is the space of all tempered distributions f for which the quantity $\Vert f\Vert _{B_{p,q}^s}$ is finite.

Remark 2.2

As for the $\alpha$-modulation space, the definition of Besov space is independent of the choice of the bump functions $\varphi$. So one can choose an appropriate $\varphi$ as one needs. Also, one can easily verify that the function sequence $\{\psi _j\}_{j\in \{0\}\bigcup \mathbb {N}}$ satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathbf {supp}\psi \subset \{\xi \in \mathbb {R}^n: \frac{2}{3}\le |\xi |\le \frac{3}{2}\}; \\ \psi _0(\xi )=1\;\text {and},\;\psi _0(\xi )\psi _l(\xi )=0,\;\xi \in B(0,\delta ); \\ \psi _j(\xi )=1\;\text {and}\;\psi _j(\xi )\psi _l(\xi )=0,\;2^j-2^j\delta \le |\xi | \le 2^j+2^j\delta ,\;l\ne j, \end{array}\right. } \end{aligned}$$

(2.9)

for $l,j\in \mathbb {N}$, where $\delta =1/4$.

We list some basic properties about $\alpha$-modulation spaces.

Lemma 2.3

(see [13, 15]) Let $0< p_i, q_i\le \infty$, $s_i\in \mathbb {R}$ for $i=1,2$, $\alpha \in [0,1]$. Then we have

$$\begin{aligned}{}[M_{p_1, q_1}^{s_1, \alpha }, M_{p_2, q_2}^{s_2, \alpha }]_{\theta }=M_{p_{\theta }, q_{\theta }}^{s_{\theta }, \alpha } \end{aligned}$$

(2.10)

for $\theta \in (0,1)$, where

$$\begin{aligned} \frac{1}{p_{\theta }}=\frac{1-\theta }{p_{1}}+\frac{\theta }{p_{2}}, \;\frac{1}{q_{\theta }}=\frac{1-\theta }{q_{1}}+\frac{\theta }{q_{2}}, \;s_{\theta }=(1-\theta )s_{1}+\theta s_{2}. \end{aligned}$$

Lemma 2.4

(see [15]) $M_{2,2}^{s, \alpha }(\mathbb {R}^n)=H^s(\mathbb {R}^n)$ with equivalent norms. Here $H^s(\mathbb {R}^n)$ denotes the Sobolev space of order s.

We also need the following proposition which will be used in our proof.

Proposition 2.5

(Dual method for $\alpha$ modulation spaces) Suppose $0<p,q\le \infty$. Let $f\in \mathscr {S}$ and define

$$\begin{aligned} T_f(\varphi )=\langle \varphi , f \rangle \end{aligned}$$

(2.11)

for $\varphi \in \mathscr {S}'$. Then $T_f$ is a bounded linear functional on $M_{p,q}^{s,\alpha }$, and

$$\begin{aligned} \Vert T_f\Vert _{\big ( M_{p,q}^{s,\alpha } \big )^*}\sim \Vert f\Vert _{M_{p',q'}^{-s+n\alpha (\frac{1}{1\wedge p}-1),\alpha }}. \end{aligned}$$

(2.12)

The only thing we must point out is that this proposition works also in the endpoint case $p=\infty$ or $q=\infty$. One can verify this proposition by the same method used in determining the dual spaces of $\alpha$-modulation spaces (see [15]). We omit the details here, but refer the reader to [15] for a further discussion.

We recall some basic results about complex interpolation. The following well-known results are the main reason why complex interpolation plays an important role for proving boundedness of linear operators. For a proof of the following result, see [15, Proposition 2.11] and the references therein.

Lemma 2.6

(Operator interpolation for complex interpolation) Let $(X_1, X_2)$ and $(Y_1,Y_2)$ be two compatible couples of Quasi Banach spaces, $\theta \in (0,1).$ If a linear operator T belongs to $L(X_1,Y_1)\cap L(X_2,Y_2)$, then we have

$$\begin{aligned} \left\| T|\; {[X_1,X_2]_{\theta }\rightarrow [Y_1,Y_2]_{\theta }}\right\| \le \left\| T|\; {X_1\rightarrow Y_1}\right\| ^{1-\theta }\left\| T|\; {X_2\rightarrow Y_2}\right\| ^{\theta }. \end{aligned}$$

(2.13)

Taking $X_1=X_2=\mathbb {C}$ or $Y_1=Y_2=\mathbb {C}$, one can easily verify two direct corollaries from the above Lemma 2.6.

Lemma 2.7

(Convexity Inequality) Let $(X_1, X_2)$ be a compatible couple of Quasi Banach spaces. For every $\theta \in (0,1)$, we have

$$\begin{aligned} \Vert f\Vert _{[X_1,X_2]_{\theta }}\le \Vert f\Vert ^{1-\theta }_{X_1}\Vert f\Vert ^{\theta }_{X_2} \end{aligned}$$

(2.14)

for $f\in X_1\cap X_2$.

Lemma 2.8

(Dual Convexity Inequality) Let $(X_1, X_2)$ be a compatible couple of Quasi Banach spaces. Let T be a linear functional defined in $X_1$ and $X_2$. Then for every $\theta \in (0,1)$, we have

$$\begin{aligned} \Vert T\Vert _{[X_1,X_2]^{*}_{\theta }}\le \Vert T\Vert ^{1-\theta }_{X_1^{*}}\Vert T\Vert ^{\theta }_{X_2^{*}} \end{aligned}$$

(2.15)

for $T\in X_1^{*}\cap X_2^{*}$.

3 The Convexity Inequality

In this section, we deduce some estimates about the indices $p_i,q_i$ under the assumption that the convexity inequality $\Vert f\Vert _{M_{p,q}^{s,\alpha }}\lesssim \Vert f\Vert ^{1-\theta }_{M_{p_1,q_1}^{s_1,\alpha _1}}\Vert f\Vert ^{\theta }_{M_{p_2,q_2}^{s_2,\alpha _2}}$ holds for all Schwartz functions f. If $M_{p,q}^{s,\alpha }$ is the complex interpolation space between $M_{p_1,q_1}^{s_1,\alpha _1}$ and $M_{p_2,q_2}^{s_2,\alpha _2}$, the convexity inequality follows. We construct some specific functions to test the convexity inequality and obtain some relationship among the parameters.

For $\alpha \in (0,1)$, $j\in \{0\}\cup \mathbb {N}$, denote

$$\begin{aligned} \Gamma _j^{\alpha ,1}=\{l\in \mathbb {Z}^n:\;\Delta _j\circ \Box _l^{\alpha }\ne 0 \}. \end{aligned}$$

(3.1)

For $\alpha _1, \alpha _2 \in (0,1)$, $k\in \mathbb {Z}^n$, we denote

$$\begin{aligned} \Gamma _k^{\alpha _1,\alpha _2}=\{l\in \mathbb {Z}^n:\;\Box _k^{\alpha _2}\circ \Box _l^{\alpha _1}\ne 0 \}. \end{aligned}$$

(3.2)

By the above definition, we deduce $\langle l\rangle ^{\frac{1}{1-\alpha _1}}\sim \langle k\rangle ^{\frac{1}{1-\alpha _2}}$ for $l\in \Gamma _k^{\alpha _1, \alpha _2}$. We also have $\Gamma _k^{\alpha _1, \alpha _2}\sim \langle k\rangle ^{\frac{n(\alpha _2-\alpha _1)}{1-\alpha _2}}$ for $\alpha _1\le \alpha _2$, $\Gamma _k^{\alpha _1, \alpha _2}\sim 1$ for $\alpha _1\ge \alpha _2$.

For $f\in \mathscr {S}$ with compact Fourier support and $\widehat{f}(\xi )=1$ in a open subset of $\mathbb {R}^n$, we denote

$$\begin{aligned} \Gamma _f^{\alpha }=\{k\in \mathbb {Z}^n:\;\Box _k^{\alpha }f\ne 0 \},\; \widetilde{\Gamma _f^{\alpha }}=\{k\in \mathbb {Z}^n:\;\Box _k^{\alpha }f=\mathscr {F}^{-1}\eta _k^{\alpha } \}. \end{aligned}$$

(3.3)

For $g\in \mathscr {S}$ with compact support and $g(x)=1$ in a open subset of $\mathbb {R}^n$, we denote

$$\begin{aligned} \mathbf {supp}g=\overline{\{x\in \mathbb {R}^n: g(x)\ne 0 \}},\;\widetilde{\mathbf {supp}g}=\{x\in \mathbb {R}^n: g(x)=1 \}. \end{aligned}$$

(3.4)

We recall a convolution lemma which will be used frequently in this paper.

Lemma 3.1

(Convolution in $L^{p}$ with $p<1,$ see Proposition 2.1 in [15]) Let $0<p<1$ , $x_0\in \mathbb {R}^n$, $r>0$. Suppose $f, g\in L^p$ with Fourier support in $B(x_0, r)$. Then

$$\begin{aligned} \Vert f*g\Vert _{L^p}\lesssim r^{n(1/p-1)}\Vert f\Vert _{L^p}\Vert g\Vert _{L^p}. \end{aligned}$$

(3.5)

Lemma 3.2

Suppose $0< p_i,q_i\le \infty$, $s_i\in \mathbb {R}$, $\alpha _i \in [0,1]$ for $i=1,2$. We assume $\alpha _1<\alpha _2$. For fixed $\theta \in (0,1)$, we denote

$$\begin{aligned} \frac{1}{p}=\frac{1-\theta }{p_1}+\frac{\theta }{p_2},\;\frac{1}{q}=\frac{1-\theta }{q_1}+ \frac{\theta }{q_2}, \; s=(1-\theta )s_1+\theta s_2 \end{aligned}$$

(3.6)

For any $\alpha \in [0,1]$, if the convexity inequality

$$\begin{aligned} \Vert f\Vert _{M_{p,q}^{s,\alpha }}\lesssim \Vert f\Vert ^{1-\theta }_{M_{p_1,q_1}^{s_1,\alpha _1}}\Vert f\Vert ^{\theta }_{M_{p_2,q_2}^{s_2,\alpha _2}} \end{aligned}$$

(3.7)

holds for all $f\in \mathscr {S}$, then we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{1}{p_1}+\frac{1}{q_1}\ge 1,\;\frac{1}{p_1}\le \frac{1}{q_1},\;&{}\text {if}\; \alpha >\alpha _1,\\ \frac{1}{p_2}+\frac{1}{q_2}\le 1,\;\frac{1}{p_2}\ge \frac{1}{q_2},\;&{}\text {if}\; \alpha =\alpha _1,\\ \frac{1}{p}+\frac{1}{q}\le 1,\;\frac{1}{p}\ge \frac{1}{q},\;&{}\text {if}\; \alpha <\alpha _1. \end{array}\right. } \end{aligned}$$

(3.8)

Proof

We only show the proof for the case $\alpha _1<\alpha _2<1$, since the proofs of the other cases are similar. For the sake of simplicity, we write $M=M_{p,q}^{s,\alpha }$ and $M_i=M_{p_i,q_i}^{s_i,\alpha _i}$ for $i=1,2$ in this proof. Let f be a smooth function with small Fourier support near the origin such that $\mathbf {supp}\widehat{f_k^{\alpha }}\subset \widetilde{\mathbf {supp}\eta _k^{\alpha }}$ for every $k\in \mathbb {Z}^n, \alpha \in [0,1]$, where we denote

$$\begin{aligned} \widehat{f_k^{\alpha }}=\widehat{f}\left( \frac{\xi -\langle k\rangle ^{\frac{\alpha }{1-\alpha }}k}{\langle k\rangle ^{\frac{\alpha }{1-\alpha }}}\right) . \end{aligned}$$

(3.9)

We divide the proof into several cases.

Case 1: $\alpha \in (\alpha _1, \alpha _2)$.

For each $k\in \mathbb {Z}^n$, we choose $j\in \{0\}\cup \mathbb {Z}^{+}$ such that $\langle k\rangle ^{\frac{1}{1-\alpha }}\sim 2^j$.

Firstly, a direct calculation yields

$$\begin{aligned} {\left\{ \begin{array}{ll} \Vert f_k^{\alpha }\Vert _{M}\sim 2^{js}\Vert f_k^{\alpha }\Vert _{L^{p}}\sim 2^{js}2^{jn\alpha (1-1/p)}, \\ \Vert f_k^{\alpha }\Vert _{M_2}\sim 2^{js_2}\Vert f_k^{\alpha }\Vert _{L^{p_2}}\sim 2^{js_2}2^{jn\alpha (1-1/p_2)}. \end{array}\right. } \end{aligned}$$

(3.10)

To estimate $\Vert f_k^{\alpha }\Vert _{M_1}$, we use Young’s inequality for $p_1\ge 1$ or Lemma 3.1 for $p_1<1$ to deduce

$$\begin{aligned} \Vert \Box _l^{\alpha _1} f_k^{\alpha }\Vert _{L^{p_1}}&= \Vert (\mathscr {F}^{-1}\eta _l^{\alpha _1})*f_k^{\alpha }\Vert _{L^{p_1}} \nonumber \\&\lesssim 2^{jn\alpha (1/(p_1\wedge 1)-1)}\Vert f_k^{\alpha }\Vert _{L^{p_1 \wedge 1}}\Vert \mathscr {F}^{-1}\eta _l^{\alpha _1}\Vert _{L^{p_1}} \nonumber \\&\lesssim \Vert \mathscr {F}^{-1}\eta _l^{\alpha _1}\Vert _{L^{p_1}} \nonumber \\&\lesssim 2^{jn\alpha _1 (1-1/p_1)}. \end{aligned}$$

(3.11)

Noting that

$$\begin{aligned} |\Gamma _{f_k^{\alpha }}^{\alpha _1}|\sim 2^{jn(\alpha -\alpha _1)} \end{aligned}$$

(3.12)

and

$$\begin{aligned} \langle l\rangle ^{\frac{1}{1-\alpha _1}}\sim 2^j \end{aligned}$$

(3.13)

for $l\in \Gamma _{f_k^{\alpha }}^{\alpha _1}$, we have

$$\begin{aligned} \Vert f_k^{\alpha }\Vert _{M_1}&= \bigg (\sum _{l\in \mathbb {Z}^n}\langle l\rangle ^{\frac{s_1 q_1}{1-\alpha _1}}\Vert \Box _l^{\alpha _1} f_k^{\alpha }\Vert ^{q_1}_{L^{p_1}}\bigg )^{\frac{1}{q_1}} \nonumber \\&\lesssim 2^{js_1}2^{jn\alpha _1 (1-1/p_1)} 2^{jn(\alpha -\alpha _1)/q_1}. \end{aligned}$$

(3.14)

The convexity inequality

$$\begin{aligned} \Vert f_{{k}}\Vert _{M}\lesssim \Vert f_{{k}}\Vert ^{1-\theta }_{M_1}\Vert f_{{k}}\Vert ^{\theta }_{M_2} \end{aligned}$$

(3.15)

then yields that

$$\begin{aligned} 2^{js}2^{jn\alpha (1-1/p)} \lesssim \left( 2^{js_1}2^{jn\alpha _1 (1-1/p_1)} 2^{jn(\alpha -\alpha _1)/q_1}\right) ^{1-\theta } \left( 2^{js_2}2^{jn\alpha (1-1/p_2)}\right) ^{\theta } \end{aligned}$$

(3.16)

as $j\rightarrow \infty$, which implies

$$\begin{aligned} s&+n\alpha (1-1/p)\le (1-\theta )\left( s_1+n\alpha _1(1-1/p_1)+n(\alpha -\alpha _1)/q_1\right) \nonumber \\&+\theta \left( s_2+n\alpha (1-1/p_2)\right) . \end{aligned}$$

(3.17)

Recalling

$$\begin{aligned} \frac{1}{p}=\frac{1-\theta }{p_1}+\frac{\theta }{p_2}, \; s=(1-\theta )s_1+\theta s_2, \end{aligned}$$

we have

$$\begin{aligned} n(\alpha -\alpha _1)(1-\theta )(1-1/p_1)\le n(\alpha -\alpha _1)(1-\theta )/q_1. \end{aligned}$$

(3.18)

Hence

$$\begin{aligned} 1-1/p_1\le 1/q_1, \end{aligned}$$

(3.19)

and we obtain

$$\begin{aligned} \frac{1}{p_1}+\frac{1}{q_1}\ge 1. \end{aligned}$$

(3.20)

Secondly, we set

$$\begin{aligned} F_{k,N}=\sum _{l\in \Gamma _k^{\alpha _1,\alpha }}T_{Nl}f_l^{\alpha _1}. \end{aligned}$$

(3.21)

Here $T_{Nl}$ denotes the translation operator: $T_{Nl}f(x)=f(x-Nl)$.

Obviously for $l\in \Gamma _k^{\alpha _1,\alpha }$, we have

$$\begin{aligned} \Box _l^{\alpha _1}F_{k,N}=T_{Nl}f_l^{\alpha _1}, \end{aligned}$$

(3.22)

and

$$\begin{aligned} \Vert \Box _l^{\alpha _1}F_{k,N}\Vert _{L_{p_1}}=\Vert T_{Nl}f_l^{\alpha _1}\Vert _{L^{p_1}}=\Vert f_l^{\alpha _1}\Vert _{L^{p_1}}\sim 2^{jn\alpha _1(1-1/p_1)}. \end{aligned}$$

(3.23)

So

$$\begin{aligned} \begin{aligned} \Vert F_{k,N}\Vert _{M_1}&=\bigg (\sum _{l\in \Gamma _k^{\alpha _1,\alpha }}\langle l\rangle ^{\frac{s_1q_1}{1-\alpha _1}}\Vert \Box _l^{\alpha _1}F_{k,N}\Vert ^{q_1}_{L_{p_1}}\bigg )^{\frac{1}{q_1}} \\&\sim 2^{js_1}2^{jn\alpha _1(1-1/p_1)}|\Gamma _k^{\alpha _1,\alpha }|^{1/q_1} \\&\sim 2^{js_1}2^{jn\alpha _1(1-1/p_1)}2^{jn(\alpha -\alpha _1)/q_1}. \end{aligned} \end{aligned}$$

(3.24)

On the other hand, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \Vert F_{k,N}\Vert _{M}\sim 2^{js}\Vert F_{k,N}\Vert _{L^p}, \\ \Vert F_{k,N}\Vert _{M_2} \sim 2^{js_2}\Vert F_{k,N}\Vert _{L^{p_2}}. \end{array}\right. } \end{aligned}$$

(3.25)

By the almost orthogonality of $\{T_{Nl}f_l^{\alpha _1}\}_{l\in \Gamma _k^{\alpha _1,\alpha } }$ as $N\rightarrow \infty$, we deduce that

$$\begin{aligned} \lim _{N\rightarrow \infty }\int _{\mathbb {R}^n}|F_{k,N}|^pdx= & {} \lim _{N\rightarrow \infty }\int _{\mathbb {R}^n}\Big |\sum _{l\in \Gamma _k^{\alpha _1,\alpha }}T_{Nl}f_l^{\alpha _1}\Big |^pdx =\lim _{N\rightarrow \infty }\sum _{l\in \Gamma _k^{\alpha _1,\alpha }}\int _{\mathbb {R}^n}|T_{Nl}f_l^{\alpha _1}|^pdx \\= & {} \sum _{l\in \Gamma _k^{\alpha _1,\alpha }}\int _{\mathbb {R}^n}|f_l^{\alpha _1}|^pdx \sim 2^{jn\alpha _1(p-1)}|\Gamma _k^{\alpha _1,\alpha }| \\&\sim 2^{jn\alpha _1(p-1)}2^{jn(\alpha -\alpha _1)}. \end{aligned}$$

With a small modification when $p=\infty$, we obtain

$$\begin{aligned} \lim _{N\rightarrow \infty }\Vert F_{k,N}\Vert _{L^p}=2^{jn\alpha _1(1-1/p)}2^{jn(\alpha -\alpha _1)/p} \end{aligned}$$

(3.26)

for $p\in (0, \infty ]$. So

$$\begin{aligned} {\left\{ \begin{array}{ll} \Vert F_{k,N}\Vert _{M}\sim 2^{js}2^{jn\alpha _1(1-1/p)}2^{jn(\alpha -\alpha _1)/p}, \\ \Vert F_{k,N}\Vert _{M_2} \sim 2^{js_2}2^{jn\alpha _1(1-1/p_2)}2^{jn(\alpha -\alpha _1)/p_2} \end{array}\right. } \end{aligned}$$

(3.27)

as $N \rightarrow \infty$. Letting N tend to infinity in the convexity inequality

$$\begin{aligned} \Vert F_{k,N}\Vert _{M}\lesssim \Vert F_{k,N}\Vert ^{1-\theta }_{M_1}\Vert F_{k,N}\Vert ^{\theta }_{M_2}, \end{aligned}$$

(3.28)

we deduce that

$$\begin{aligned}&\quad 2^{js}2^{jn\alpha _1(1-1/p)}2^{jn(\alpha -\alpha _1)/p} \nonumber \\&\lesssim \left( 2^{js_1}2^{jn\alpha _1(1-1/p_1)}2^{jn(\alpha -\alpha _1)/q_1}\right) ^{1-\theta } \left( 2^{js_2}2^{jn\alpha _1(1-1/p_2)}2^{jn(\alpha -\alpha _1)/p_2}\right) ^{\theta } \end{aligned}$$

(3.29)

as $j \rightarrow \infty$. Recalling

we obtain

$$\begin{aligned} (\alpha -\alpha _1)/p\le (1-\theta )(\alpha -\alpha _1)/q_1+\theta (\alpha -\alpha _1)/p_2, \end{aligned}$$

(3.30)

which yields

$$\begin{aligned} (1-\theta )(\alpha -\alpha _1)/p_1\le (1-\theta )(\alpha -\alpha _1)/q_1, \end{aligned}$$

(3.31)

and

$$\begin{aligned} 1/p_1\le 1/q_1. \end{aligned}$$

(3.32)

Case 2: $\alpha \ge \alpha _2$.

For each $k\in \mathbb {Z}^n$, we choose $j\in \{0\}\cup \mathbb {Z}^{+}$ such that $\langle k\rangle ^{\frac{1}{1-\alpha _2}}\sim 2^j$.

Firstly, a direct calculation yields

$$\begin{aligned} {\left\{ \begin{array}{ll} \Vert f_k^{\alpha _2}\Vert _{M}\sim 2^{js}\Vert f_k^{\alpha _2}\Vert _{L^{p}}\sim 2^{js}2^{jn\alpha _2 (1-1/p)}, \\ \Vert f_k^{\alpha _2}\Vert _{M_2}\sim 2^{js_2}\Vert f_k^{\alpha _2}\Vert _{L^{p_2}}\sim 2^{js_2}2^{jn\alpha _2 (1-1/p_2)}. \end{array}\right. } \end{aligned}$$

(3.33)

To estimate $\Vert f_k^{\alpha _2}\Vert _{M_1}$, we have

$$\begin{aligned} \Vert \Box _l^{\alpha _1} f_k^{\alpha _2}\Vert _{L^{p_1}} \lesssim \Vert \mathscr {F}^{-1}\eta _l^{\alpha _1}\Vert _{L^{p_1}}\lesssim 2^{jn\alpha _1 (1-1/p_1)}. \end{aligned}$$

(3.34)

Noting that

$$\begin{aligned} |\Gamma _{f_k^{\alpha _2}}^{\alpha _1}|\sim 2^{jn(\alpha _2-\alpha _1)} \end{aligned}$$

(3.35)

and

$$\begin{aligned} \langle l\rangle ^{\frac{1}{1-\alpha _1}}\sim 2^j \end{aligned}$$

(3.36)

for $l\in \Gamma _{f_k^{\alpha _2}}^{\alpha _1}$, we have

$$\begin{aligned} \Vert f_k^{\alpha _2}\Vert _{M_1}&= \left( \sum _{l\in \mathbb {Z}^n}\langle l\rangle ^{\frac{s_1 q_1}{1-\alpha _1}}\Vert \Box _l^{\alpha _1} f_k^{\alpha _2}\Vert ^{q_1}_{L^{p_1}}\right) ^{\frac{1}{q_1}} \nonumber \\&\lesssim 2^{js_1}2^{jn\alpha _1 (1-1/p_1)} 2^{jn(\alpha _2-\alpha _1)/q_1}. \end{aligned}$$

(3.37)

The convexity inequality

$$\begin{aligned} \Vert f_k^{\alpha _2}\Vert _{M}\lesssim \Vert f_k^{\alpha _2}\Vert ^{1-\theta }_{M_1}\Vert f_k^{\alpha _2}\Vert ^{\theta }_{M_2} \end{aligned}$$

(3.38)

then yields that

$$\begin{aligned} 2^{js}2^{jn\alpha _2 (1-1/p)} \lesssim \left( 2^{js_1}2^{jn\alpha _1 (1-1/p_1)} 2^{jn(\alpha _2-\alpha _1)/q_1}\right) ^{1-\theta } \left( 2^{js_2}2^{jn\alpha _2 (1-1/p_2)}\right) ^{\theta } \end{aligned}$$

as $j\rightarrow \infty$, which implies that

$$\begin{aligned} s+n\alpha _2(1-1/p)&\le (1-\theta )\left( s_1+n\alpha _1(1-1/p_1)\right. \\&\quad \left. +n(\alpha _2-\alpha _1)/q_1\right) +\theta \left( s_2+n\alpha _2(1-1/p_2)\right) . \end{aligned}$$

Recalling

$$\begin{aligned} \frac{1}{p}=\frac{1-\theta }{p_1}+\frac{\theta }{p_2}, \; s=(1-\theta )s_1+\theta s_2, \end{aligned}$$

we have

$$\begin{aligned} n(\alpha _2-\alpha _1)(1-\theta )(1-1/p_1)\le n(\alpha _2-\alpha _1)(1-\theta )/q_1. \end{aligned}$$

(3.39)

Hence, we obtain

$$\begin{aligned} 1-1/p_1\le 1/q_1, \end{aligned}$$

(3.40)

that is,

$$\begin{aligned} \frac{1}{p_1}+\frac{1}{q_1}\ge 1. \end{aligned}$$

(3.41)

Secondly, we set

$$\begin{aligned} F_{k,N}=\sum _{l\in \Gamma _k^{\alpha _1,\alpha _2}}T_{Nl}f_l^{\alpha _1}. \end{aligned}$$

(3.42)

Obviously for $l\in \Gamma _k^{\alpha _1,\alpha _2}$, we have

$$\begin{aligned} \Box _l^{\alpha _1}F_{k,N}=T_{Nl}f_l^{\alpha _1}, \end{aligned}$$

(3.43)

and

$$\begin{aligned} \Vert \Box _l^{\alpha _1}F_{k,N}\Vert _{L_{p_1}}=\Vert T_{Nl}f_l^{\alpha _1}\Vert _{L^{p_1}}=\Vert f_l^{\alpha _1}\Vert _{L^{p_1}}\sim 2^{jn\alpha _1(1-1/p_1)}. \end{aligned}$$

(3.44)

So

$$\begin{aligned} \begin{aligned} \Vert F_{k,N}\Vert _{M_1}&=\Bigg (\sum _{l\in \Gamma _k^{\alpha _1,\alpha _2}}\langle l\rangle ^{\frac{s_1q_1}{1-\alpha _1}}\Vert \Box _l^{\alpha _1}F_{k,N}\Vert ^{q_1}_{L_{p_1}}\Bigg )^{\frac{1}{q_1}} \\&\sim 2^{js_1}2^{jn\alpha _1(1-1/p_1)}|\Gamma _k^{\alpha _1,\alpha _2}|^{1/q_1} \\&\sim 2^{js_1}2^{jn\alpha _1(1-1/p_1)}2^{jn(\alpha _2-\alpha _1)/q_1}. \end{aligned} \end{aligned}$$

(3.45)

On the other hand, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \Vert F_{k,N}\Vert _{M}\sim 2^{js}\Vert F_{k,N}\Vert _{L^p} \\ \Vert F_{k,N}\Vert _{M_2} \sim 2^{js_2}\Vert F_{k,N}\Vert _{L^{p_2}}. \end{array}\right. } \end{aligned}$$

(3.46)

By an orthogonality argument as above, we have that

$$\begin{aligned} {\left\{ \begin{array}{ll} \Vert F_{k,N}\Vert _{M}\sim 2^{js}2^{jn\alpha _1(1-1/p)}2^{jn(\alpha _2-\alpha _1)/p} \\ \Vert F_{k,N}\Vert _{M_2} \sim 2^{js_2}2^{jn\alpha _1(1-1/p_2)}2^{jn(\alpha _2-\alpha _1)/p_2} \end{array}\right. } \end{aligned}$$

(3.47)

as $N \rightarrow \infty$. Letting N tend to infinity in the convexity inequality

$$\begin{aligned} \Vert F_{k,N}\Vert _{M}\lesssim \Vert F_{k,N}\Vert ^{1-\theta }_{M_1}\Vert F_{k,N}\Vert ^{\theta }_{M_2}, \end{aligned}$$

(3.48)

we deduce that

$$\begin{aligned}&2^{js}2^{jn\alpha _1(1-1/p)}2^{jn(\alpha _2-\alpha _1)/p} \nonumber \\&\quad \lesssim \left( 2^{js_1}2^{jn\alpha _1(1-1/p_1)}2^{jn(\alpha _2-\alpha _1)/q_1}\right) ^{1-\theta } \left( 2^{js_2}2^{jn\alpha _1(1-1/p_2)}2^{jn(\alpha _2-\alpha _1)/p_2}\right) ^{\theta } \end{aligned}$$

(3.49)

as $j \rightarrow \infty$. Recalling

$$\begin{aligned} \frac{1}{p}=\frac{1-\theta }{p_1}+\frac{\theta }{p_2}, \; s=(1-\theta )s_1+\theta s_2, \end{aligned}$$

we obtain

$$\begin{aligned} (\alpha _2-\alpha _1)/p\le (1-\theta )(\alpha _2-\alpha _1)/q_1+\theta (\alpha _2-\alpha _1)/p_2, \end{aligned}$$

(3.50)

and

$$\begin{aligned} (1-\theta )(\alpha _2-\alpha _1)/p_1\le (1-\theta )(\alpha _2-\alpha _1)/q_1. \end{aligned}$$

(3.51)

So it follows

$$\begin{aligned} 1/p_1\le 1/q_1. \end{aligned}$$

(3.52)

Case 3: $\alpha =\alpha _1$.

For each $k\in \mathbb {Z}^n$, we choose $j\in \{0\}\cup \mathbb {Z}^{+}$ such that $\langle k\rangle ^{\frac{1}{1-\alpha _2}}\sim 2^j$.

Firstly, direct calculations give that

$$\begin{aligned} \begin{aligned} \Vert f_k^{\alpha _2}\Vert _{M}=\left( \sum _{l\in \mathbb {Z}^n}\langle l\rangle ^{\frac{s q}{1-\alpha }}\Vert \Box _l^{\alpha } f_k^{\alpha _2}\Vert ^{q}_{L^{p}}\right) ^{\frac{1}{q}}&\gtrsim \Bigg (\sum _{l\in \widetilde{\Gamma _{f_k^{\alpha _2}}^{\alpha }}}\langle l\rangle ^{\frac{s q}{1-\alpha }}\Vert \mathscr {F}^{-1}\eta _l^{\alpha }\Vert ^{q}_{L^{p}}\Bigg )^{\frac{1}{q}} \\&\gtrsim 2^{js}2^{j\alpha n(1-1/p)}2^{j(\alpha _2-\alpha )n/q}, \end{aligned} \end{aligned}$$

(3.53)

$$\begin{aligned} \Vert f_k^{\alpha _2}\Vert _{M_1}=\left( \sum _{l\in \mathbb {Z}^n}\langle l\rangle ^{\frac{s_1 q_1}{1-\alpha _1}}\Vert \Box _l^{\alpha _1} f_k^{\alpha _2}\Vert ^{q_1}_{L^{p_1}}\right) ^{\frac{1}{q_1}}\lesssim & {} \Bigg (\sum _{l\in \Gamma _{f_k^{\alpha _2}}^{\alpha }}\langle l\rangle ^{\frac{s_1 q_1}{1-\alpha }}\Vert \mathscr {F}^{-1}\eta _l^{\alpha }\Vert ^{q_1}_{L^{p_1}}\Bigg )^{\frac{1}{q_1}} \nonumber \\\lesssim & {} 2^{js_1}2^{j\alpha n(1-1/p_1)}2^{j(\alpha _2-\alpha )n/q_1},\nonumber \\ \end{aligned}$$

(3.54)

and

$$\begin{aligned} \Vert f_k^{\alpha _2}\Vert _{M_2}\sim 2^{js_2}\Vert f_k^{\alpha _2}\Vert _{L^{p_2}} \sim 2^{js_2}2^{j\alpha _2 n(1-1/p_2)}. \end{aligned}$$

(3.55)

The convexity inequality

$$\begin{aligned} \Vert f_k^{\alpha _2}\Vert _{M}\lesssim \Vert f_k^{\alpha _2}\Vert ^{1-\theta }_{M_1}\Vert f_k^{\alpha _2}\Vert ^{\theta }_{M_2} \end{aligned}$$

(3.56)

then yields that

$$\begin{aligned}&2^{js}2^{j\alpha n(1-1/p)}2^{j(\alpha _2-\alpha )n/q}\\&\quad \lesssim \left( 2^{js_1}2^{j\alpha n(1-1/p_1)}2^{j(\alpha _2-\alpha )n/q_1}\right) ^{1-\theta } \left( 2^{js_2}2^{j\alpha _2 n(1-1/p_2)}\right) ^{\theta } \end{aligned}$$

as $j\rightarrow \infty$, which implies

$$\begin{aligned} \theta (\alpha -\alpha _2)(1-1/p_2)+\theta (\alpha _2-\alpha )/q_2\le 0. \end{aligned}$$

(3.57)

So

$$\begin{aligned} \frac{1}{p_2}+\frac{1}{q_2}\le 1. \end{aligned}$$

(3.58)

Secondly, we set

$$\begin{aligned} F_{k,N}=\sum _{l\in \Gamma _k^{\alpha ,\alpha _2}}T_{Nl}f_l^{\alpha }. \end{aligned}$$

(3.59)

Obviously for $l\in \Gamma _k^{\alpha ,\alpha _2}$, we have

$$\begin{aligned} \Box _l^{\alpha _1}F_{k,N}=T_{Nl}f_l^{\alpha }, \end{aligned}$$

(3.60)

and

$$\begin{aligned} \Vert \Box _l^{\alpha _1}F_{k,N}\Vert _{L_{p_1}}=\Vert T_{Nl}f_l^{\alpha }\Vert _{L^{p_1}}=\Vert f_l^{\alpha }\Vert _{L^{p_1}}\sim 2^{jn\alpha (1-1/p_1)}. \end{aligned}$$

(3.61)

So

$$\begin{aligned} \begin{aligned} \Vert F_{k,N}\Vert _{M_1}&=\left( \sum _{l\in \Gamma _k^{\alpha ,\alpha _2}}\langle l\rangle ^{\frac{s_1q_1}{1-\alpha _1}}\Vert \Box _l^{\alpha _1}F_{k,N}\Vert ^{q_1}_{L_{p_1}}\right) ^{\frac{1}{q_1}} \\&\sim 2^{js_1}2^{jn\alpha (1-1/p_1)}|\Gamma _k^{\alpha ,\alpha _2}|^{1/q_1} \\&\sim 2^{js_1}2^{jn\alpha (1-1/p_1)}2^{jn(\alpha _2-\alpha )/q_1}. \end{aligned} \end{aligned}$$

(3.62)

Similarly, we have

$$\begin{aligned} \Vert F_{k,N}\Vert _{M}\sim 2^{js}2^{jn\alpha (1-1/p)}2^{jn(\alpha _2-\alpha )/q}. \end{aligned}$$

(3.63)

On the other hand, we have

$$\begin{aligned} \Vert F_{k,N}\Vert _{M_2} \sim 2^{js_2}\Vert F_{k,N}\Vert _{L^{p_2}}. \end{aligned}$$

(3.64)

By an orthogonality argument as above, we have that

$$\begin{aligned} \Vert F_{k,N}\Vert _{M_2} \sim 2^{js_2}2^{jn\alpha (1-1/p_2)}2^{jn(\alpha _2-\alpha )/p_2} \end{aligned}$$

(3.65)

as $N \rightarrow \infty$. Letting N tend to infinity in the convexity inequality

$$\begin{aligned} \Vert F_{k,N}\Vert _{M}\lesssim \Vert F_{k,N}\Vert ^{1-\theta }_{M_1}\Vert F_{k,N}\Vert ^{\theta }_{M_2}, \end{aligned}$$

(3.66)

we deduce that

$$\begin{aligned} \begin{aligned}&2^{js}2^{jn\alpha (1-1/p)}2^{jn(\alpha _2-\alpha )/q} \\&\quad \lesssim \left( 2^{js_1}2^{jn\alpha (1-1/p_1)}2^{jn(\alpha _2-\alpha )/q_1}\right) ^{1-\theta } \left( 2^{js_2}2^{jn\alpha (1-1/p_2)}2^{jn(\alpha _2-\alpha )/p_2}\right) ^{\theta }\qquad \end{aligned} \end{aligned}$$

(3.67)

as $j \rightarrow \infty$. We obtain

$$\begin{aligned} 1/q_2\le 1/p_2. \end{aligned}$$

(3.68)

Case 4: $\alpha <\alpha _1$.

For $k\in \mathbb {Z}^n$, we choose $j\in \{0\}\cup \mathbb {Z}^{+}$ such that $\langle k\rangle ^{\frac{1}{1-\alpha _1}}\sim 2^j$.

Firstly, a direct calculation yields

$$\begin{aligned} {\left\{ \begin{array}{ll} \Vert f_k^{\alpha _1}\Vert _{M_1}\sim 2^{js_1}\Vert f_k^{\alpha _1}\Vert _{L^{p_1}}\sim 2^{js_1}2^{jn\alpha _1 (1-1/p_1)} \\ \Vert f_k^{\alpha _1}\Vert _{M_2}\sim 2^{js_2}\Vert f_k^{\alpha _1}\Vert _{L^{p_2}}\sim 2^{js_2}2^{jn\alpha _1 (1-1/p_2)}. \end{array}\right. } \end{aligned}$$

(3.69)

To estimate $\Vert f_k^{\alpha _1}\Vert _{M}$, we have

$$\begin{aligned} \begin{aligned} \Vert f_k^{\alpha _1}\Vert _{M}&= \left( \sum _{l\in \mathbb {Z}^n}\langle l\rangle ^{\frac{s q}{1-\alpha }}\Vert \Box _l^{\alpha } f_k^{\alpha _1}\Vert ^{q}_{L^{p}}\right) ^{\frac{1}{q}} \gtrsim \bigg (\sum _{l\in \widetilde{\Gamma _{f_k^{\alpha _1}}^{\alpha }}}\langle l\rangle ^{\frac{s q}{1-\alpha }}\Vert \mathscr {F}^{-1}\eta _l^{\alpha }\Vert ^{q}_{L^{p}}\bigg )^{\frac{1}{q}} \qquad \\&\gtrsim 2^{js}2^{jn\alpha (1-1/p)} 2^{jn(\alpha _1-\alpha )/q}. \end{aligned} \end{aligned}$$

(3.70)

The convexity inequality

$$\begin{aligned} \Vert f_k^{\alpha _1}\Vert _{M}\lesssim \Vert f_k^{\alpha _1}\Vert ^{1-\theta }_{M_1}\Vert f_k^{\alpha _1}\Vert ^{\theta }_{M_2} \end{aligned}$$

(3.71)

then yields that

$$\begin{aligned} 2^{js}2^{jn\alpha (1-1/p)} 2^{jn(\alpha _1-\alpha )/q} \lesssim \left( 2^{js_1}2^{jn\alpha _1 (1-1/p_1)}\right) ^{1-\theta } \left( 2^{js_2}2^{jn\alpha _1 (1-1/p_2)}\right) ^{\theta } \end{aligned}$$

(3.72)

as $j\rightarrow \infty$, which implies

$$\begin{aligned} (\alpha _1-\alpha )/q\le (\alpha _1-\alpha )(1-1/p). \end{aligned}$$

(3.73)

So we obtain

$$\begin{aligned} \frac{1}{p}+\frac{1}{q}\le 1. \end{aligned}$$

(3.74)

Secondly, we set

$$\begin{aligned} F_{k,N}=\sum _{l\in \Gamma _k^{\alpha ,\alpha _1}}T_{Nl}f_l^{\alpha }. \end{aligned}$$

(3.75)

Obviously for $l\in \Gamma _k^{\alpha ,\alpha _1}$, we have

$$\begin{aligned} \Box _l^{\alpha }F_{k,N}=T_{Nl}f_l^{\alpha }, \end{aligned}$$

(3.76)

and

$$\begin{aligned} \Vert \Box _l^{\alpha }F_{k,N}\Vert _{L_{p}}=\Vert T_{Nl}f_l^{\alpha }\Vert _{L^{p}}=\Vert f_l^{\alpha }\Vert _{L^{p}}\sim 2^{jn\alpha (1-1/p)}. \end{aligned}$$

(3.77)

So

$$\begin{aligned} \begin{aligned} \Vert F_{k,N}\Vert _{M}&=\Bigg (\sum _{l\in \Gamma _k^{\alpha ,\alpha _1}}\langle l\rangle ^{\frac{sq}{1-\alpha }}\Vert \Box _l^{\alpha }F_{k,N}\Vert ^{q}_{L_{p}}\Bigg )^{\frac{1}{q}} \\&\sim 2^{js}2^{jn\alpha (1-1/p)}|\Gamma _k^{\alpha ,\alpha _1}|^{1/q} \\&\sim 2^{js}2^{jn\alpha (1-1/p)}2^{jn(\alpha _1-\alpha )/q}. \end{aligned} \end{aligned}$$

(3.78)

On the other hand, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \Vert F_{k,N}\Vert _{M_1}\sim 2^{js_1}\Vert F_{k,N}\Vert _{L^{p_1}} \\ \Vert F_{k,N}\Vert _{M_2} \sim 2^{js_2}\Vert F_{k,N}\Vert _{L^{p_2}}. \end{array}\right. } \end{aligned}$$

(3.79)

By an orthogonality argument as above, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \Vert F_{k,N}\Vert _{M_1}\sim 2^{js_1}2^{jn\alpha (1-1/p_1)}2^{jn(\alpha _1-\alpha )/p_1} \\ \Vert F_{k,N}\Vert _{M_2} \sim 2^{js_2}2^{jn\alpha (1-1/p_2)}2^{jn(\alpha _1-\alpha )/p_2} \end{array}\right. } \end{aligned}$$

(3.80)

as $N \rightarrow \infty$. Letting N tend to infinity in the convexity inequality

$$\begin{aligned} \Vert F_{k,N}\Vert _{M}\lesssim \Vert F_{k,N}\Vert ^{1-\theta }_{M_1}\Vert F_{k,N}\Vert ^{\theta }_{M_2}, \end{aligned}$$

(3.81)

we deduce that

$$\begin{aligned} \begin{aligned}&2^{js}2^{jn\alpha (1-1/p)}2^{jn(\alpha _1-\alpha )/q} \\&\quad \lesssim \left( 2^{js_1}2^{jn\alpha (1-1/p_1)}2^{jn(\alpha _1-\alpha )/p_1}\right) ^{1-\theta } \left( 2^{js_2}2^{jn\alpha (1-1/p_2)}2^{jn(\alpha _1-\alpha )/p_2}\right) ^{\theta }\qquad \end{aligned} \end{aligned}$$

(3.82)

as $j \rightarrow \infty$. Thus we obtain

$$\begin{aligned} (\alpha _1-\alpha )/q\le (\alpha _1-\alpha )/p. \end{aligned}$$

(3.83)

The desired inequality

$$\begin{aligned} 1/q\le 1/p \end{aligned}$$

(3.84)

follows. $\square$

4 Additional Operator Norm Estimates

As we mentioned before, duality arguments are often not applicable in the context of Quasi-Banach spaces. So the key point for the discrimination of complex interpolation is how to regain the information without the full duality. To this end, in this section we bring some additional known complex interpolation spaces into the operator interpolation inequalities (2.13). Our purpose is to establish some asymptotic estimates for certain operators between the additional spaces and our target spaces. As a corollary, we give a direct proof for the sharpness of embedding between $\alpha$-modulation spaces (see [15] for an alternative proof).

Lemma 4.1

(Additional operator norm estimates) Let $0<p,q\le \infty$, $s_i\in \mathbb {R}$, $\alpha _i \in [0,1]$ for $i=1,2$. We have

$$\begin{aligned} \left\| \Box _k^{\alpha _1\vee \alpha _2}|\;M_{p,q}^{s_1,\alpha _1}\rightarrow M_{p,q}^{s_2,\alpha _2}\right\| \sim \langle k\rangle ^{\frac{(s_2-s_1)+\big (0\vee [n(\alpha _2-\alpha _1)(1/p-1/q)]\vee [n(\alpha _2-\alpha _1)(1-1/p-1/q)]\big )}{1-(\alpha _1\vee \alpha _2)}}, \end{aligned}$$

(4.1)

for $\alpha _1\vee \alpha _2<1$, $k\in \mathbb {Z}^n$, and

$$\begin{aligned} \left\| \Delta _j|\;M_{p,q}^{s_1,\alpha _1}\rightarrow M_{p,q}^{s_2,\alpha _2}\right\| \sim 2^{j\left[ (s_2-s_1)+\big (0\vee [n(\alpha _2-\alpha _1)(1/p-1/q)]\vee [n(\alpha _2-\alpha _1)(1-1/p-1/q)]\big )\right] }, \end{aligned}$$

(4.2)

for $\alpha _1\vee \alpha _2=1$, $j\in \{0\}\cup \mathbb {Z}^{+}$.

Proof

We only give the proof for the case $\alpha _1<\alpha _2=1$, which will be used in the proof of Theorem 1.2. The other cases can be handled similarly. For instance, in the case $\alpha _1<\alpha _2<1$, one can repeat the following process by replacing $\Delta _j$ with $\Box _k^{\alpha _2}$.

In the case $\alpha _1<\alpha _2=1$, we need to show

$$\begin{aligned} \left\| \Delta _j|\;M_{p,q}^{s_1,\alpha _1}\rightarrow B_{p,q}^{s_2}\right\| \sim 2^{j\left[ (s_2-s_1)+\big (0\vee [n(1-\alpha _1)(1/p-1/q)]\vee [n(1-\alpha _1)(1-1/p-1/q)]\big )\right] }. \end{aligned}$$

(4.3)

For Lower Bound Estimates. We only need to construct some special functions to test the operator inequalities. Take a smooth function f whose Fourier transform $\widehat{f}$ has small support near the origin such that $\mathbf {supp}\widehat{f_k^{\alpha }}\subset \widetilde{\mathbf {supp}\eta _k^{\alpha }}$ for every $k\in \mathbb {Z}^n, \alpha \in [0,1]$, where we denote

$$\begin{aligned} \widehat{f_k^{\alpha }}=\widehat{f}(\frac{\xi -\langle k\rangle ^{\frac{\alpha }{1-\alpha }}k}{\langle k\rangle ^{\frac{\alpha }{1-\alpha }}}). \end{aligned}$$

(4.4)

Firstly, we have

$$\begin{aligned} \left\| \Delta _j|\;M_{p,q}^{s_1,\alpha _1}\rightarrow B_{p,q}^{s_2}\right\| \gtrsim \frac{\Vert \Delta _j f_k^0\Vert _{B_{p,q}^{s_2}}}{\Vert f_k^0\Vert _{M_{p,q}^{s_1,\alpha _1}}} \sim \frac{2^{js_2}\Vert f_k^0\Vert _{L^p}}{2^{js_1}\Vert f_k^0\Vert _{L^p}} \gtrsim 2^{j(s_2-s_1)} \end{aligned}$$

(4.5)

for some suitable $k\in \mathbb {Z}^n$ such that $\langle k\rangle \sim 2^j$.

Next, we choose a smooth function h whose Fourier transform has sufficiently small support near the origin, such that $\widehat{h_{j}}(\xi )=\widehat{h}(\frac{\xi }{2^{j}})$ satisfies

$$\begin{aligned} \mathbf {supp}\widehat{h_j} \subset \widetilde{\mathbf {supp}}\psi _{j}. \end{aligned}$$

(4.6)

A direct calculation yields that

$$\begin{aligned} \Vert \Delta _jh_j\Vert _{B_{p,q}^{s_2}}=\Vert h_j\Vert _{B_{p,q}^{s_2}}\sim 2^{js_2}\Vert h_j\Vert _{L^p}\sim 2^{j(s_2+n(1-1/p))} \end{aligned}$$

(4.7)

and

$$\begin{aligned} \begin{aligned} \Vert h_j\Vert _{M_{p,q}^{s_1,\alpha _1}}=\left( \sum _{l\in \mathbb {Z}^n}\langle l\rangle ^{\frac{s_1 q}{1-\alpha _1}}\Vert \Box ^{\alpha _1}_l h_j\Vert ^{q}_{L^{p}}\right) ^{\frac{1}{q}}&\lesssim \bigg (\sum _{l\in \Gamma _{h_j}^{\alpha _1}}\langle l\rangle ^{\frac{s_1 q}{1-\alpha _1}}\Vert \mathscr {F}^{-1}\eta _l^{\alpha _1}\Vert ^{q}_{L^{p}}\bigg )^{\frac{1}{q}} \\&\lesssim 2^{js_1}2^{j\alpha _1 n(1-1/p)}2^{j(1-\alpha _1)n/q}. \end{aligned} \end{aligned}$$

(4.8)

So we have

$$\begin{aligned} \begin{aligned} \left\| \Delta _j|\;M_{p,q}^{s_1,\alpha _1}\rightarrow B_{p,q}^{s_2}\right\| \gtrsim \frac{\Vert \Delta _j h_j\Vert _{B_{p,q}^{s_2}}}{\Vert h_j\Vert _{M_{p,q}^{s_1,\alpha _1}}}&\gtrsim \frac{2^{j(s_2+n(1-1/p))}}{2^{js_1}2^{j\alpha _1 n(1-1/p)}2^{j(1-\alpha _1)n/q}} \\&= 2^{j\left( s_2-s_1+n(1-\alpha _1)(1-1/p-1/q)\right) }. \end{aligned} \end{aligned}$$

(4.9)

Finally, let

$$\begin{aligned} F_{j,N}=\sum _{l\in \Gamma _j^{\alpha _1,1}}T_{Nl}f_l^{\alpha _1}, \end{aligned}$$

(4.10)

where $T_{Nl}$ denotes the translation operator: $T_{Nl}f(x)=f(x-Nl)$. Using the same method as in the proof of Lemma 3.2, we have

$$\begin{aligned} \begin{aligned} \Vert F_{j,N}\Vert _{M_{p,q}^{s_1,\alpha _1}}&=\left( \sum _{l\in \Gamma _j^{\alpha _1,1}}\langle l\rangle ^{\frac{s_1q}{1-\alpha _1}}\Vert \Box _l^{\alpha _1}F_{j,N}\Vert ^{q}_{L^{p}}\right) ^{\frac{1}{q}} \\&\sim 2^{js_1}2^{jn\alpha _1(1-1/p)}|\Gamma _j^{\alpha _1,1}|^{1/q} \\&\sim 2^{js_1}2^{jn\alpha _1(1-1/p)}2^{jn(1-\alpha _1)/q}. \end{aligned} \end{aligned}$$

(4.11)

Also, we have that

$$\begin{aligned} \Vert \Delta _jF_{j,N}\Vert _{B_{p,q}^{s_2}}\lesssim \Vert F_{j,N}\Vert _{B_{p,q}^{s_2}}\sim 2^{js_2}\Vert F_{j,N}\Vert _{L^p}\sim 2^{js_2}2^{jn\alpha _1(1-1/p)}2^{jn(1-\alpha _1)/p} \end{aligned}$$

(4.12)

as $N \rightarrow \infty$. So by definition of the operator norm,

$$\begin{aligned} \left\| \Delta _j|\;M_{p,q}^{s_1,\alpha _1}\rightarrow B_{p,q}^{s_2}\right\|\gtrsim & {} \lim _{N\rightarrow \infty }\frac{\Vert \Delta _j F_{j,N}\Vert _{B_{p,q}^{s_2}}}{\Vert F_{j,N}\Vert _{M_{p,q}^{s_1,\alpha _1}}} \sim \frac{2^{js_2}2^{jn\alpha _1(1-1/p)}2^{jn(1-\alpha _1)/p}}{2^{js_1}2^{jn\alpha _1(1-1/p)}2^{jn(1-\alpha _1)/q}} \nonumber \\\gtrsim & {} 2^{j(s_2-s_1)}2^{jn(1-\alpha _1)(1/p-1/q)}.\nonumber \\ \end{aligned}$$

(4.13)

Now, we have the lower bound

$$\begin{aligned} \left\| \Delta _j|\;M_{p,q}^{s_1,\alpha _1}\rightarrow B_{p,q}^{s_2}\right\| \gtrsim 2^{j\left[ (s_2-s_1)+\big (0\vee [n(1-\alpha _1)(1/p-1/q)]\vee [n(1-\alpha _1)(1-1/p-1/q)]\big )\right] }. \end{aligned}$$

(4.14)

For Upper Bound Estimates. We only handle the following cases, then the other cases can be deduced by an easy interpolation argument.

Case 1. $p=q=2$.

$$\begin{aligned} \Vert \Delta _jf\Vert _{B_{2,2}^{s_2}}\sim 2^{js_2}\Vert \Delta _jf\Vert _{L^2}\sim 2^{j(s_2-s_1)}\Vert \Delta _jf\Vert _{M_{2,2}^{s_1,\alpha _1}}\lesssim 2^{j(s_2-s_1)}\Vert f\Vert _{M_{2,2}^{s_1,\alpha _1}}. \end{aligned}$$

(4.15)

Moreover, in this case we may write

$$\begin{aligned} 2^{j(s_2-s_1)}=2^{j\left( s_2-s_1+n(1-\alpha _1)(1/p-1/q)\right) }=2^{j\left( s_2-s_1+n(1-\alpha _1)(1-1/p-1/q)\right) }. \end{aligned}$$

(4.16)

Case 2. $p=\infty , q\le 1$.

$$\begin{aligned} \Vert \Delta _jf\Vert _{B_{\infty ,q}^{s_2}}\sim 2^{js_2}\Vert \Delta _jf\Vert _{L^{\infty }}&= 2^{js_2}\Big \Vert \sum _{l\in \Gamma _j^{\alpha _1,1}}\Box _l^{\alpha _1}\Delta _jf\Big \Vert _{L^{\infty }} \lesssim 2^{js_2}\sum _{l\in \Gamma _j^{\alpha _1,1}}\Vert \Box _l^{\alpha _1}f\Vert _{L^{\infty }} \\&\lesssim 2^{js_2}\left( \sum _{l\in \Gamma _j^{\alpha _1,1}}\Vert \Box _l^{\alpha _1}f\Vert ^q_{L^{\infty }}\right) ^{1/q} \lesssim 2^{j(s_2-s_1)}\Vert f\Vert _{M_{\infty ,q}^{\alpha _1,s_1}}. \end{aligned}$$

Moreover, for $p=\infty$ and $q=1,$ we can write,

$$\begin{aligned} 2^{j(s_2-s_1)}=2^{j\left( s_2-s_1+n(1-\alpha _1)(1-1/p-1/q)\right) }. \end{aligned}$$

(4.17)

Case 3. $p=q\le 1$.

$$\begin{aligned} \Vert \Delta _jf\Vert _{B_{p,q}^{s_2}}\sim 2^{js_2}\Vert \Delta _jf\Vert _{L^{p}}= & {} 2^{js_2}\Vert \sum _{l\in \Gamma _j^{\alpha _1,1}}\Box _l^{\alpha _1}\Delta _jf\Vert _{L^p} \lesssim 2^{js_2}\left( \sum _{l\in \Gamma _j^{\alpha _1,1}}\Vert \Box _l^{\alpha _1}f\Vert ^p_{L^p}\right) ^{1/p} \\= & {} 2^{js_2}\left( \sum _{l\in \Gamma _j^{\alpha _1,1}}\Vert \Box _l^{\alpha _1}f\Vert ^q_{L^p}\right) ^{1/q} \lesssim 2^{j(s_2-s_1)}\Vert f\Vert _{M_{p,q}^{\alpha _1,s_1}}. \end{aligned}$$

Moreover, in this case we have

$$\begin{aligned} 2^{j(s_2-s_1)}=2^{j\left( s_2-s_1+n(1-\alpha _1)(1/p-1/q)\right) }. \end{aligned}$$

(4.18)

Case 4. $p=q=\infty$.

$$\begin{aligned} \Vert \Delta _jf\Vert _{B_{\infty ,\infty }^{s_2}}\sim 2^{js_2}\Vert \Delta _jf\Vert _{L^{\infty }}= & {} 2^{js_2}\Big \Vert \sum _{l\in \Gamma _j^{\alpha _1,1}}\Box _l^{\alpha _1}\Delta _jf\Big \Vert _{L^{\infty }} \nonumber \\\lesssim & {} 2^{js_2}\sum _{l\in \Gamma _j^{\alpha _1,1}}\Vert \Box _l^{\alpha _1}f\Vert _{L^{\infty }} \nonumber \\\lesssim & {} 2^{js_2}|\Gamma _j^{\alpha _1,1}| \sup _{l\in \Gamma _j^{\alpha _1,1}}\Vert \Box _l^{\alpha _1}f\Vert _{L^{\infty }} \nonumber \\\lesssim & {} 2^{j(s_2-s_1)}2^{jn(1-\alpha _1)}\Vert f\Vert _{M_{\infty ,\infty }^{\alpha _1,s_1}}. \end{aligned}$$

(4.19)

Moreover, we have

$$\begin{aligned} 2^{j(s_2-s_1)}2^{jn(1-\alpha _1)}=2^{j(s_2-s_1)}2^{jn(1-\alpha _1)(1-1/p-1/q)} \end{aligned}$$

(4.20)

in this case.

Case 5. $p=2$, $q=\infty$.

$$\begin{aligned} \begin{aligned} \Vert \Delta _jf\Vert _{B_{2,\infty }^{s_2}}\sim 2^{js_2}\Vert \Delta _jf\Vert _{L^2}&\sim 2^{js_2}\Vert \Delta _jf\Vert _{M_{2,2}^{0,\alpha _1}} \\&\lesssim 2^{js_2}\left( \sum _{l\in \Gamma _j^{\alpha _1,1}}\Vert \Box _l^{\alpha _1}f\Vert ^2_{L^2}\right) ^{1/2} \\&\lesssim 2^{js_2}|\Gamma _j^{\alpha _1,1}|^{1/2} \sup _{l\in \Gamma _j^{\alpha _1,1}}\Vert \Box _l^{\alpha _1}f\Vert _{L^2} \\&\lesssim 2^{j(s_2-s_1)}2^{jn(1-\alpha _1)(1/2)}\Vert f\Vert _{M_{2,\infty }^{\alpha _1,s_1}}. \end{aligned} \end{aligned}$$

(4.21)

Moreover, we have

$$\begin{aligned} 2^{j(s_2-s_1)}2^{jn(1-\alpha _1)(1/2)}=2^{j\left( s_2-s_1+n(1-\alpha _1)(1/p-1/q)\right) }=2^{j\left( s_2-s_1+n(1-\alpha _1)(1-1/p-1/q)\right) } \end{aligned}$$

in this case.

Case 6. $p\le 1$, $q=\infty$.

$$\begin{aligned} \begin{aligned} \Vert \Delta _jf\Vert _{B_{p,\infty }^{s_2}}\sim 2^{js_2}\Vert \Delta _jf\Vert _{L^p}&= 2^{js_2}\Vert \sum _{l\in \Gamma _j^{\alpha _1,1}}\Box _l^{\alpha _1}\Delta _jf\Vert _{L^p} \\&\lesssim 2^{js_2}\left( \sum _{l\in \Gamma _j^{\alpha _1,1}}\Vert \Box _l^{\alpha _1}f\Vert ^p_{L^p}\right) ^{1/p} \\&\lesssim 2^{js_2}|\Gamma _j^{\alpha _1,1}|^{1/p} \sup _{l\in \Gamma _j^{\alpha _1,1}}\Vert \Box _l^{\alpha _1}f\Vert _{L^p} \\&\lesssim 2^{j(s_2-s_1)}2^{jn(1-\alpha _1)(1/p)}\Vert f\Vert _{M_{p,\infty }^{\alpha _1,s_1}}. \end{aligned} \end{aligned}$$

(4.22)

Moreover, we have

$$\begin{aligned} 2^{j(s_2-s_1)}2^{jn(1-\alpha _1)(1/p)}=2^{j\left( s_2-s_1+n(1-\alpha _1)(1/p-1/q)\right) } \end{aligned}$$

(4.23)

in this case. $\square$

In order to characterize the existence of embeddings between $\alpha$-modulation spaces, we only need to establish the following proposition, which can be viewed as a mild characterization of embedding.

Proposition 4.2

(Mild characterization for the embedding between $\alpha$-modulation spaces) Let $0<p,q\le \infty$, $s_i\in \mathbb {R}$, $\alpha _i \in [0,1]$ for $i=1,2$. Then the embedding relationship

$$\begin{aligned} M_{p,q}^{s_1,\alpha _1} \subset M_{p,q}^{s_2,\alpha _2} \end{aligned}$$

(4.24)

holds if and only if

$$\begin{aligned} \sup _{k\in \mathbb {Z}^n}\left\| \Box _k^{\alpha _1\vee \alpha _2}|\;M_{p,q}^{s_1,\alpha _1}\rightarrow M_{p,q}^{s_2,\alpha _2}\right\| \lesssim 1 \end{aligned}$$

(4.25)

for $\alpha _1\vee \alpha _2<1$, and

$$\begin{aligned} \sup _{j\in \{0\}\cup \mathbb {Z}^{+}}\left\| \Delta _j|\;M_{p,q}^{s_1,\alpha _1}\rightarrow M_{p,q}^{s_2,\alpha _2}\right\| \lesssim 1 \end{aligned}$$

(4.26)

for $\alpha _1\vee \alpha _2=1$.

Proof

We only give the proof for the case $\alpha _1, \alpha _2 < 1$, since the proofs of other cases are similar.

Case 1: $\alpha _1\le \alpha _2$.

If the embedding $M_{p,q}^{s_1,\alpha _1} \subset M_{p,q}^{s_2,\alpha _2}$ holds, we have

$$\begin{aligned} \Vert \Box _k^{\alpha _2}f\Vert _{M_{p,q}^{s_2,\alpha _2}}\lesssim \Vert \Box _k^{\alpha _2}f\Vert _{M_{p,q}^{s_1,\alpha _1}}\lesssim \Vert f\Vert _{M_{p,q}^{s_1,\alpha _1}}. \end{aligned}$$

(4.27)

On the other hand, if $\sup _{k\in \mathbb {Z}^n}\left\| \Box _k^{\alpha _2}|\;M_{p,q}^{s_1,\alpha _1}\rightarrow M_{p,q}^{s_2,\alpha _2}\right\| \lesssim 1$ holds, we deduce

$$\begin{aligned} \begin{aligned} \langle k\rangle ^{\frac{s_2}{1-\alpha _2}}\Vert \Box _k^{\alpha _2}f\Vert _{L^p}&\sim \Vert \Box _k^{\alpha _2}f\Vert _{M_{p,q}^{s_2,\alpha _2}} \\&= \Vert \Box _k^{\alpha _2}\sum _{l\in \Gamma _k^{\alpha _2,\alpha _2}}\Box _l^{\alpha _2}f\Vert _{M_{p,q}^{s_2,\alpha _2}} \\&\lesssim \Vert \sum _{l\in \Gamma _k^{\alpha _2,\alpha _2}}\Box _l^{\alpha _2}f\Vert _{M_{p,q}^{s_1,\alpha _1}} \\&\lesssim \left( \sum _{l\in \Gamma _k^{\alpha _2,\alpha _2}}\sum _{m\in \Gamma _l^{\alpha _1,\alpha _2}}\langle m\rangle ^{\frac{s_1q}{1-\alpha _1}}\Vert \Box _m^{\alpha _1}f\Vert ^q_{L^p}\right) ^{1/q}. \end{aligned} \end{aligned}$$

(4.28)

Observing that $|\Gamma _m^{\alpha _2,\alpha _1}|\lesssim 1$ and $|\Gamma _l^{\alpha _2,\alpha _2}|\lesssim 1$, we obtain

$$\begin{aligned} \Vert f\Vert _{M_{p,q}^{s_2,\alpha _2}}= & {} \left( \sum _{k\in \mathbb {Z}^n}\langle k\rangle ^{\frac{s_2q}{1-\alpha _2}}\Vert \Box _k^{\alpha _2}f\Vert ^q_{L^p}\right) ^{1/q} \nonumber \\\lesssim & {} \left( \sum _{k\in \mathbb {Z}^n}\sum _{l\in \Gamma _k^{\alpha _2,\alpha _2}}\sum _{m\in \Gamma _l^{\alpha _1,\alpha _2}}\langle m\rangle ^{\frac{s_1q}{1-\alpha _1}}\Vert \Box _m^{\alpha _1}f\Vert ^q_{L^p}\right) ^{1/q} \nonumber \\= & {} \left( \sum _{m\in \mathbb {Z}^n}\sum _{l\in \Gamma _m^{\alpha _2,\alpha _1}}\sum _{k\in \Gamma _l^{\alpha _2,\alpha _2}}\langle m\rangle ^{\frac{s_1q}{1-\alpha _1}}\Vert \Box _m^{\alpha _1}f\Vert ^q_{L^p}\right) ^{1/q} \nonumber \\\lesssim & {} \left( \sum _{m\in \mathbb {Z}^n}\langle m\rangle ^{\frac{s_1q}{1-\alpha _1}}\Vert \Box _m^{\alpha _1}f\Vert ^q_{L^p}\right) ^{1/q}=\Vert f\Vert _{M_{p,q}^{s_1,\alpha _1}}. \end{aligned}$$

(4.29)

Case 2: $\alpha _2\le \alpha _1$.

If the embedding $M_{p,q}^{s_1,\alpha _1} \subset M_{p,q}^{s_2,\alpha _2}$ holds, we have

$$\begin{aligned} \Vert \Box _k^{\alpha _1}f\Vert _{M_{p,q}^{s_2,\alpha _2}}\lesssim \Vert \Box _k^{\alpha _1}f\Vert _{M_{p,q}^{s_1,\alpha _1}}\lesssim \Vert f\Vert _{M_{p,q}^{s_1,\alpha _1}}. \end{aligned}$$

(4.30)

On the other hand, if $\sup _{k\in \mathbb {Z}^n}\left\| \Box _k^{\alpha _1}|\;M_{p,q}^{s_1,\alpha _1}\rightarrow M_{p,q}^{s_2,\alpha _2}\right\| \lesssim 1$ holds, we use $|\Gamma _k^{\alpha _1, \alpha _2}|\lesssim 1$ to deduce deduce

$$\begin{aligned} \begin{aligned} \Vert f\Vert _{M_{p,q}^{s_2,\alpha _2}}&= \left( \sum _{k\in \mathbb {Z}^n}\langle k\rangle ^{\frac{s_2q}{1-\alpha _2}}\Vert \Box _k^{\alpha _2}f\Vert ^q_{L^p}\right) ^{1/q} \\&\lesssim \left( \sum _{k\in \mathbb {Z}^n}\langle k\rangle ^{\frac{s_2q}{ 1-\alpha _2}}\sum _{l\in \Gamma _k^{\alpha _1,\alpha _2}}\Vert \Box _l^{\alpha _1}\Box _k^{\alpha _2}f\Vert ^q_{L^p} \right) ^{1/q} \\&\sim \left( \sum _{l\in \mathbb {Z}^n}\sum _{k\in \Gamma _l^{\alpha _2,\alpha _1}}\langle k\rangle ^{\frac{s_2q}{1-\alpha _2} }\Vert \Box _k^{\alpha _2}\Box _l^{\alpha _1}f\Vert ^q_{L^p}\right) ^{1/q} \\&\sim \left( \sum _{l\in \mathbb {Z}^n}\Vert \Box _l^{\alpha _1}f\Vert ^q_{M_{p,q}^{s_2,\alpha _2}}\right) ^{1/q}. \end{aligned} \end{aligned}$$

(4.31)

Then

$$\begin{aligned} \Vert f\Vert _{M_{p,q}^{s_2,\alpha _2}}\lesssim & {} \left( \sum _{k\in \mathbb {Z}^n}\Vert \Box _k^{\alpha _1}f\Vert ^q_{M_{p,q}^{s_2,\alpha _2}}\right) ^{1/q} \nonumber \\= & {} \left( \sum _{k\in \mathbb {Z}^n}\Vert \Box _k^{\alpha _1}\sum _{l\in \Gamma _k^{\alpha _1,\alpha _1}}\Box _l^{\alpha _1}f\Vert ^q_{M_{p,q}^{s_2,\alpha _2}}\right) ^{1/q} \nonumber \\\lesssim & {} \left( \sum _{k\in \mathbb {Z}^n}\Vert \sum _{l\in \Gamma _k^{\alpha _1,\alpha _1}}\Box _l^{\alpha _1}f\Vert ^q_{M_{p,q}^{s_1,\alpha _1}}\right) ^{1/q} \nonumber \\\lesssim & {} \left( \sum _{k\in \mathbb {Z}^n}\sum _{l\in \Gamma _k^{\alpha _1,\alpha _1}}\langle l\rangle ^{\frac{s_1q}{1-\alpha _1}}\Vert \Box _l^{\alpha _1}f\Vert ^q_{L^p}\right) ^{1/q} \nonumber \\= & {} \left( \sum _{l\in \mathbb {Z}^n}\sum _{k\in \Gamma _l^{\alpha _1,\alpha _1}}\langle l\rangle ^{\frac{s_1q}{1-\alpha _1}}\Vert \Box _l^{\alpha _1}f\Vert ^q_{L^p}\right) ^{1/q} \lesssim \Vert f\Vert _{M_{p,q}^{s_1,\alpha _1}}, \end{aligned}$$

(4.32)

where the last inequality holds for the reason that $|\Gamma _k^{\alpha _1,\alpha _1}|\lesssim 1$. $\square$

Combining Lemma 4.1 and Proposition 4.2, we obtain the following corollary.

Corollary 4.3

(see Theorems 4.1, 4.2 in [15]) Let $0<p,q\le \infty$, $s_i\in \mathbb {R}$, $\alpha _i \in [0,1]$ for $i=1,2$. Then

$$\begin{aligned} M_{p,q}^{s_1,\alpha _1} \subset M_{p,q}^{s_2,\alpha _2} \end{aligned}$$

(4.33)

holds if and only if

$$\begin{aligned} s_2+\big (0\vee [n(\alpha _2-\alpha _1)(1/p-1/q)]\vee [n(\alpha _2-\alpha _1)(1-1/p-1/q)]\big )\le s_1. \end{aligned}$$

We remark that the embedding results between $\alpha _1$-modulation and $\alpha _2$-modulation spaces go back to Gröbner’s thesis [13] in which he considered the case $1\le p, q\le \infty$. In [18], Toft and Wahlberg then obtained some partial sufficient conditions, as well as some partial necessary conditions for such embedding. Finally, Wang and Han gave a complete characterization [15]. Embeddings between modulation and Besov spaces are considered in [17] and [19].

5 Proof of Theorems 1.1 and 1.2

5.1 Proof of Theorem 1.1

In this subsection, we suppose $1\le p_i,q_i\le \infty$, $s_i\in \mathbb {R}$, $\alpha _i \in [0,1]$ for $i=1,2$. For a fixed $\theta \in (0,1)$, if

$$\begin{aligned} \left[ M_{p_1,q_1}^{s_1,\alpha _1},M_{p_2,q_2}^{s_2,\alpha _2}\right] _{\theta }\in \mathcal {M}, \end{aligned}$$

(5.1)

then there exists a $\alpha$-modulation space $M_{p,q}^{s,\alpha }$ such that

$$\begin{aligned} \left[ M_{p_1,q_1}^{s_1,\alpha _1},M_{p_2,q_2}^{s_2,\alpha _2}\right] _{\theta }=M_{p,q}^{s,\alpha }, \end{aligned}$$

(5.2)

where $p, q\in (0,\infty ]$, $s\in \mathbb {R}$, $\alpha \in [0,1].$ We first make some priori estimates to determine the values of p, q and s.

Step 1: Priori estimates for p, q, s.

For fixed $p_i, q_i, s_i$ under the assumption of Theorem 1.1, we denote

$$\begin{aligned} \frac{1}{p_{\theta }}=\frac{1-\theta }{p_1}+\frac{\theta }{p_2},\;\frac{1}{q_{\theta }}=\frac{1-\theta }{q_1}+ \frac{\theta }{q_2}, \; s_{\theta } =(1-\theta )s_1+\theta s_2 . \end{aligned}$$

We want to check that

$$\begin{aligned} p=p_{\theta }, q=q_{\theta } ,s=s_{\theta } \end{aligned}$$

(5.3)

under the assumption

$$\begin{aligned} \left[ M_{p_1,q_1}^{s_1,\alpha _1},M_{p_2,q_2}^{s_2,\alpha _2}\right] _{\theta }=M_{p,q}^{s,\alpha } \end{aligned}$$

(5.4)

for some $\theta \in (0,1)$.

By the convexity inequality, we have

$$\begin{aligned} \Vert f\Vert _{M_{p,q}^{s,\alpha }}\lesssim \Vert f\Vert ^{1-\theta }_{M_{p_1,q_1}^{s_1,\alpha _1}}\Vert f\Vert ^{\theta }_{M_{p_2,q_2}^{s_2,\alpha _2}} \end{aligned}$$

(5.5)

for all $f\in \mathscr {S}(\mathbb {R}^n)\subset M_{p_1,q_1}^{s_1,\alpha _1}\cap M_{p_2,q_2}^{s_2,\alpha _2}.$ On the other hand, take $f\in \mathscr {S}(\mathbb {R}^n)$, and define

$$\begin{aligned} T_f(\varphi )=\langle \varphi , f \rangle \end{aligned}$$

(5.6)

for $\varphi \in \mathscr {S}'$. Then $T_f$ is a bounded linear functional on $M_{p_1,q_1}^{s_1,\alpha _1}$, $M_{p_2,q_2}^{s_2,\alpha _2}$ and $M_{p,q}^{s,\alpha }$. We use Proposition 2.5 and Lemma 2.8 to deduce that

$$\begin{aligned} \Vert f\Vert _{M_{p',q'}^{-s,\alpha }}\lesssim \Vert f\Vert ^{1-\theta }_{M_{p'_1,q'_1}^{-s_1,\alpha _1}}\Vert f\Vert ^{\theta }_{M_{p'_2,q'_2}^{-s_2,\alpha _2}} \end{aligned}$$

(5.7)

for $p \ge 1.$

Proving $p=p_{\theta }$. Take a smooth function h whose Fourier transform $\widehat{h}$ has small compact support with $\widehat{h}(\xi )=1$ near the origin, such that

$$\begin{aligned} \mathbf {supp}\widehat{h}\subset \widetilde{\mathbf {supp}}\eta _{0}^{\alpha } \end{aligned}$$

(5.8)

for any $\alpha \in [0,1]$. Let

$$\begin{aligned} \widehat{h_{\lambda }}(\xi )=\widehat{h}(\frac{\xi }{\lambda }) \end{aligned}$$

(5.9)

for $\lambda \in (0,1)$. We use (5.5) to deduce

$$\begin{aligned} \Vert h_{\lambda }\Vert _{L^{p}}\lesssim \Vert h_{\lambda }\Vert ^{1-\theta }_{L^{p_1}}\Vert h_{\lambda }\Vert ^{\theta }_{L^{p_2}}. \end{aligned}$$

(5.10)

We then have

$$\begin{aligned} \lambda ^{n(1-\frac{1}{p})}\lesssim \lambda ^{n(1-\frac{1}{p_1})(1-\theta )}\lambda ^{n(1-\frac{1}{p_2})(\theta )} \end{aligned}$$

(5.11)

as $\lambda \downarrow 0$. This yields

$$\begin{aligned} \frac{1}{p} \le \frac{1-\theta }{p_1}+\frac{\theta }{p_2}=\frac{1}{p_{\theta }} \le 1, \end{aligned}$$

(5.12)

and hence $p \ge p_{\theta }\ge 1$. Using (5.7), a dual argument then yields that

$$\begin{aligned} \lambda ^{n(1-\frac{1}{p'})}\lesssim \lambda ^{n(1-\frac{1}{p'_1})(1-\theta )}\lambda ^{n(1-\frac{1}{p'_2})(\theta )} \end{aligned}$$

(5.13)

as $\lambda \rightarrow 0$. So

$$\begin{aligned} \frac{1}{p} \ge \frac{1}{p_{\theta }}, \end{aligned}$$

(5.14)

and then

$$\begin{aligned} p=p_{\theta }. \end{aligned}$$

(5.15)

Proving $s=s_{\theta }$. Take h to be the same function as above. For $j\in \mathbb {N}$, define $h_j(x)=e^{2\pi i \langle \rho _j,x \rangle }h(x)$ for an arbitrary $\rho _j \in \mathbb {R}^n$, such that

$$\begin{aligned} |\rho _j| \sim 2^j \end{aligned}$$

(5.16)

and

$$\begin{aligned} \mathbf {supp}\widehat{h_j} \subset \widetilde{\mathbf {supp}}\eta _{k_j}^{\alpha }, \widetilde{\mathbf {supp}}\eta _{k_{1,j}}^{\alpha _1}, \widetilde{\mathbf {supp}}\eta _{k_{2,j}}^{\alpha _2} \end{aligned}$$

(5.17)

for some suitable $k_j, k_{1,j}, k_{2,j}\in \mathbb {Z}^n$. Clearly, we have

$$\begin{aligned} \langle k_j\rangle ^{\frac{1}{1-\alpha }} \sim \langle k_{1,j}\rangle ^{\frac{1}{1-\alpha _1}} \sim \langle k_{2,j}\rangle ^{\frac{1}{1-\alpha _2}} \sim 2^j. \end{aligned}$$

(5.18)

We use inequality (5.5) to deduce

$$\begin{aligned} \Vert h_j\Vert _{M_{p,q}^{s,\alpha }}\lesssim \Vert h_j\Vert ^{1-\theta }_{M_{p_1,q_1}^{s_1,\alpha _1}}\Vert h_j\Vert ^{\theta }_{M_{p_2,q_2}^{s_2,\alpha _2}}. \end{aligned}$$

(5.19)

A direct calculation (using $p=p_\theta$) now yields

$$\begin{aligned} 2^{js}\lesssim 2^{(1-\theta )js_1}2^{\theta js_2}=2^{js_{\theta }} \end{aligned}$$

(5.20)

as $j\rightarrow \infty$. Then $s\le s_{\theta }$ follows. Using a dual argument as in Step 1, we obtain $s=s_{\theta }$.

Proving $q=q_{\theta }$. Let $h_j$ be the functions as above. We denote

$$\begin{aligned} T_j(f)=h_j*f \end{aligned}$$

(5.21)

and

$$\begin{aligned} \mathscr {T}_N=\sum _{j=1}^N T_j \end{aligned}$$

(5.22)

for $N \in \mathbb {N}.$ Recall the complex interpolation of modulation spaces

$$\begin{aligned} \left[ M_{p_1,q_1}^{s_1}, M_{p_2,q_2}^{s_2}\right] _{\theta }=M_{p_{\theta }, q_{\theta }}^{s_{\theta }}. \end{aligned}$$

(5.23)

Using Lemma 2.6, we have

$$\begin{aligned} \Vert \mathscr {T}_N|\;{M_{p_{\theta }, q_{\theta }}^{s_{\theta }}\rightarrow M_{p_{\theta },q}^{s_{\theta },\alpha }}\Vert \lesssim \Vert \mathscr {T}_N|\;{M_{p_1,q_1}^{s_1}\rightarrow M_{p_1,q_1}^{s_1,\alpha _1}\Vert }^{1-\theta } \Vert \mathscr {T}_N|\;{M_{p_2,q_2}^{s_2}\rightarrow M_{p_2,q_2}^{s_2,\alpha _2}\Vert }^{\theta } \end{aligned}$$

and

$$\begin{aligned} \Vert \mathscr {T}_N|\;{M_{p_{\theta },q}^{s_{\theta },\alpha }\rightarrow M_{p_{\theta }, q_{\theta }}^{s_{\theta }}}\Vert \lesssim \Vert \mathscr {T}_N|\;{M_{p_1,q_1}^{s_1,\alpha _1}\rightarrow M_{p_1,q_1}^{s_1}\Vert }^{1-\theta } \Vert \mathscr {T}_N|\;{M_{p_2,q_2}^{s_2,\alpha _2}\rightarrow M_{p_2,q_2}^{s_2}\Vert }^{\theta }. \end{aligned}$$

Because of $p_1, p_2\ge 1$, one can verify that

$$\begin{aligned} \Vert \mathscr {T}_N|\;{M_{p_1,q_1}^{s_1}\rightarrow M_{p_1,q_1}^{s_1,\alpha _1}}\Vert \sim \Vert \mathscr {T}_N|\;{M_{p_2,q_2}^{s_2}\rightarrow M_{p_2,q_2}^{s_2,\alpha _2}}\Vert \sim 1 \end{aligned}$$

(5.24)

and

$$\begin{aligned} \Vert \mathscr {T}_N|\;{M_{p_1,q_1}^{s_1,\alpha _1}\rightarrow M_{p_1,q_1}^{s_1}}\Vert \sim \Vert \mathscr {T}_N|\;{M_{p_2,q_2}^{s_2,\alpha _2}\rightarrow M_{p_2,q_2}^{s_2}}\Vert \sim 1 \end{aligned}$$

(5.25)

for all $N \in \mathbb {N}$. So

$$\begin{aligned} \Vert \mathscr {T}_N|\;{M_{p_{\theta }, q_{\theta }}^{s_{\theta }}\rightarrow M_{p_{\theta },q}^{s_{\theta },\alpha }}\Vert \lesssim 1 \end{aligned}$$

(5.26)

and

$$\begin{aligned} \Vert \mathscr {T}_N|\;{M_{p_{\theta },q}^{s_{\theta },\alpha }\rightarrow M_{p_{\theta }, q_{\theta }}^{s_{\theta }}}\Vert \lesssim 1 \end{aligned}$$

(5.27)

for all N. These inequalities imply

$$\begin{aligned} l^{q_{\theta }}\subset l^{q} \end{aligned}$$

(5.28)

and

$$\begin{aligned} l^{q}\subset l^{q_{\theta }}. \end{aligned}$$

(5.29)

However, the above two embedding relationships are true if and only if $q=q_{\theta }$.

Step 2: Dual argument. From the previous discussion, we know

$$\begin{aligned} p=p_{\theta }, q=q_{\theta } ,s=s_{\theta }. \end{aligned}$$

(5.30)

So we obtain

$$\begin{aligned} \Vert f\Vert _{M_{p_{\theta },q_{\theta }}^{s_{\theta },\alpha }}\lesssim \Vert f\Vert ^{1-\theta }_{M_{p_1,q_1}^{s_1,\alpha _1}}\Vert f\Vert ^{\theta }_{M_{p_2,q_2}^{s_2,\alpha _2}} \end{aligned}$$

(5.31)

and

$$\begin{aligned} \Vert f\Vert _{M_{p'_{\theta },q'_{\theta }}^{-s_{\theta },\alpha }}\lesssim \Vert f\Vert ^{1-\theta }_{M_{p'_1,q'_1}^{-s_1,\alpha _1}}\Vert f\Vert ^{\theta }_{M_{p'_2,q'_2}^{-s_2,\alpha _2}} \end{aligned}$$

(5.32)

for all $f\in \mathscr {S}$. We use Lemma 3.2 to deduce that

$$\begin{aligned} {\left\{ \begin{array}{ll} p_1=q_1=2,\;&{}\text {if}\; \alpha >\alpha _1,\\ p_2=q_2=2,\;&{}\text {if}\; \alpha =\alpha _1,\\ p_{\theta }=q_{\theta }=2,\;&{}\text {if}\; \alpha <\alpha _1. \end{array}\right. } \end{aligned}$$

(5.33)

Step 3: Completion of proof for Theorem 1.1. The proof for $\alpha _1=\alpha _2$ is trivial. By symmetry of $\alpha _1$ and $\alpha _2$, it suffices to consider the case $\alpha _1<\alpha _2$. We divide this proof into several cases.

Case 1: $\alpha <\alpha _1$. We have $p_{\theta }=q_{\theta }=2$, so

$$\begin{aligned} \left[ M_{p_1,q_1}^{s_1,\alpha _1},M_{p_2,q_2}^{s_2,\alpha _2}\right] _{\theta }=M_{p_{\theta },q_{\theta }}^{s,\alpha }=M_{2,2}^{s,\alpha _1}=M_{2,2}^{s,\alpha _2}. \end{aligned}$$

(5.34)

By the argument in the previous subsection, we have

$$\begin{aligned} p_1=q_1=p_2=q_2=2. \end{aligned}$$

(5.35)

Hence we have

$$\begin{aligned} \left[ M_{p_1,q_1}^{s_1,\alpha _1},M_{p_2,q_2}^{s_2,\alpha _2}\right] _{\theta }=\left[ M_{2,2}^{s_1,\alpha _1},M_{2,2}^{s_2,\alpha _2}\right] _{\theta } =\left[ H^{s_1}, H^{s_2}\right] _{\theta }=H^{s_{\theta }}. \end{aligned}$$

(5.36)

Case 2: $\alpha =\alpha _1$. We have $p_2=q_2=2$. Thus

$$\begin{aligned} \left[ M_{p_1,q_1}^{s_1,\alpha _1},M_{p_2,q_2}^{s_2,\alpha _2}\right] _{\theta }=\left[ M_{p_1,q_1}^{s_1,\alpha _1},M_{2,2}^{s_2,\alpha _1}\right] _{\theta } =M_{p_{\theta },q_{\theta }}^{s_{\theta },\alpha _1}. \end{aligned}$$

(5.37)

Case 3: $\alpha >\alpha _1$, $\alpha \ne \alpha _2$. We have $p_1=q_1=2$. Thus

$$\begin{aligned} \left[ M_{p_1,q_1}^{s_1,\alpha _1},M_{p_2,q_2}^{s_2,\alpha _2}\right] _{\theta }=\left[ M_{2,2}^{s_1,\alpha },M_{p_2,q_2}^{s_2,\alpha _2}\right] _{\theta }. \end{aligned}$$

(5.38)

Since

$$\begin{aligned} \left[ M_{p_1,q_1}^{s_1,\alpha _1},M_{p_2,q_2}^{s_2,\alpha _2}\right] _{\theta } =M_{p_{\theta },q_{\theta }}^{s_{\theta },\alpha }, \end{aligned}$$

we have

$$\begin{aligned} \left[ M_{2,2}^{s_1,\alpha },M_{p_2,q_2}^{s_2,\alpha _2}\right] _{\theta } =M_{p_{\theta },q_{\theta }}^{s_{\theta },\alpha }. \end{aligned}$$

which is in Case 2, so we have

$$\begin{aligned} p_2=q_2=2, \end{aligned}$$

(5.39)

and

$$\begin{aligned} \left[ M_{p_1,q_1}^{s_1,\alpha _1},M_{p_2,q_2}^{s_2,\alpha _2}\right] _{\theta }=\left[ M_{2,2}^{s_1,\alpha _1},M_{2,2}^{s_2,\alpha _2}\right] _{\theta } =\left[ H^{s_1}, H^{s_2}\right] _{\theta }=H^{s_{\theta }}. \end{aligned}$$

(5.40)

Case 4: $\alpha =\alpha _2$. We have $p_1=q_1=2$. Thus we obtain

$$\begin{aligned} \left[ M_{p_1,q_1}^{s_1,\alpha _1},M_{p_2,q_2}^{s_2,\alpha _2}\right] _{\theta }=\left[ M_{2,2}^{s_1,\alpha _2},M_{p_2,q_2}^{s_2,\alpha _2}\right] _{\theta } =M_{p_{\theta },q_{\theta }}^{s_{\theta },\alpha _2}. \end{aligned}$$

(5.41)

5.2 Proof of Theorem 1.2

In this subsection, we suppose $0< p, q\le \infty$, $s_i\in \mathbb {R}$, $\alpha _i \in [0,1]$ for $i=1,2$. For $\alpha _1=\alpha _2$, the claim is trivial, so that we can assume $\alpha _1\ne \alpha _2$. By symmetry, we can furthermore assume $\alpha _1<\alpha _2$, which implies $\alpha _{\theta }<1$.

For a fixed $\theta \in (0,1)$, if

$$\begin{aligned} \left[ M_{p,q}^{s_1,\alpha _1},M_{p,q}^{s_2,\alpha _2}\right] _{\theta }\in \mathcal {M}, \end{aligned}$$

(5.42)

then there exists a modulation space $M_{\tilde{p},\tilde{q}}^{s,\alpha }$ such that

$$\begin{aligned} \left[ M_{p,q}^{s_1,\alpha _1},M_{p,q}^{s_2,\alpha _2}\right] _{\theta }=M_{\tilde{p},\tilde{q}}^{s,\alpha }, \end{aligned}$$

(5.43)

where $\tilde{p}, \tilde{q}\in (0,\infty ]$, $s\in \mathbb {R}$, $\alpha \in [0,1].$

Take a smooth function h whose Fourier transform $\widehat{h}$ has small compact support with $\widehat{h}(\xi )=1$ near the origin. Denote $T_h(f)=h*f$. One can easily verify that

$$\begin{aligned} T_h: M_{p,q}^{s_1,\alpha _1}\rightarrow M_{p,q}^{s_1,0}, \qquad T_h: M_{p,q}^{s_2,\alpha _2}\rightarrow M_{p,q}^{s_2,0}, \end{aligned}$$

(5.44)

and

$$\begin{aligned} T_h: M_{p,q}^{s_1,0}\rightarrow M_{p,q}^{s_1,\alpha _1}, \qquad T_h: M_{p,q}^{s_2,0}\rightarrow M_{p,q}^{s_2,\alpha _2}. \end{aligned}$$

(5.45)

By the operator interpolation inequality (Lemma 2.6), we deduce that

$$\begin{aligned} T_h: M_{\tilde{p},\tilde{q}}^{s,\alpha }\rightarrow M_{p,q}^{s_{\theta },0} \qquad \text {and}\qquad T_h: M_{p,q}^{s_{\theta },0}\rightarrow M_{\tilde{p},\tilde{q}}^{s,\alpha }. \end{aligned}$$

(5.46)

Let g be a smooth function with compact support near the origin, $g_{\lambda }(\xi )=g(\frac{\xi }{\lambda })$. For sufficiently small $\lambda$, we have

$$\begin{aligned} T_h(g_{\lambda })=g_{\lambda }, \ \Vert g_{\lambda }\Vert _{M_{\tilde{p},\tilde{q}}^{s,\alpha }}=\Vert g_{\lambda }\Vert _{L^{\tilde{p}}},\ \Vert g_{\lambda }\Vert _{M_{p,q}^{s_{\theta },0}}=\Vert g_{\lambda }\Vert _{L^p}. \end{aligned}$$

(5.47)

Hence (5.46) implies

$$\begin{aligned} \Vert g_{\lambda }\Vert _{L^p}\lesssim \Vert g_{\lambda }\Vert _{L^{\tilde{p}}},\ \Vert g_{\lambda }\Vert _{L^{\tilde{p}}}\lesssim \Vert g_{\lambda }\Vert _{L^p}. \end{aligned}$$

(5.48)

Letting $\lambda \downarrow 0$, we conclude $1/p\le 1/\tilde{p}$ and $1/\tilde{p}\le 1/p.$ So we have $\tilde{p}=p$.

In this subsection, since p might be smaller than 1, the dual convexity inequality (5.7) is replaced by

$$\begin{aligned} \Vert f\Vert _{M_{p',\tilde{q}'}^{-s+n\alpha (\frac{1}{1\wedge p}-1),\alpha }} \lesssim \Vert f\Vert ^{1-\theta }_{M_{p',q'}^{-s_1+n\alpha _1 (\frac{1}{1\wedge p}-1),\alpha _1}} \Vert f\Vert ^{\theta }_{M_{p',q'}^{-s_2+n\alpha _2 (\frac{1}{1\wedge p}-1),\alpha _2}}. \end{aligned}$$

(5.49)

In the case that $p<1$, the dual form of Lemma 3.2 is not applicable without an a priori estimate on $\alpha$, even in the process of determining s. Additionally, by checking the proof, one can find that the method for obtaining priori estimates in the last subsection does not work in the case $p<1$. The main difficulty is that we are not able to determine the values of $\tilde{q}, s, \alpha$ individually as we did in the last subsection. It seems that we need to handle all the indices simultaneously.

We denote

$$\begin{aligned} s_{\theta }=(1-\theta )s_1+\theta s_2, \alpha _{\theta }=(1-\theta )\alpha _1+\theta \alpha _2. \end{aligned}$$

By Theorem 1.1, we only need to handle the case for $p<1$ or $q<1$. We divide the proof into three cases.

Case 1: $p<1, \frac{1}{p}>\frac{1}{q}$.

By Lemma 4.1, we have

(5.50)

We now use Lemma 2.6 to deduce that

$$\begin{aligned} \Vert \Delta _j|\; B_{p,q}^0\rightarrow M_{p,\tilde{q}}^{s,\alpha }\Vert \lesssim \Vert \Delta _j|\; B_{p,q}^0\rightarrow M_{p,q}^{s_1,\alpha _1}\Vert ^{1-\theta } \Vert \Delta _j|\; B_{p,q}^0\rightarrow M_{p,q}^{s_2,\alpha _2}\Vert ^{\theta }, \end{aligned}$$

(5.51)

which implies

$$\begin{aligned} 2^{js}2^{jn(1-\alpha )(1/p+1/\tilde{q}-1)}\lesssim 2^{js_{\theta }}2^{jn(1-\alpha _{\theta })(1/p+1/q-1)}. \end{aligned}$$

(5.52)

Letting $j\rightarrow \infty$, we obtain

$$\begin{aligned} s+n(1-\alpha )(1/p+1/\tilde{q}-1)\le s_{\theta }+n(1-\alpha _{\theta })(1/p+1/q-1). \end{aligned}$$

(5.53)

On the other hand, we use Lemma 4.1 to deduce

(5.54)

and

$$\begin{aligned} \Vert \Delta _j|\; M_{p,\tilde{q}}^{s,\alpha }\rightarrow B_{p,q}^0\Vert \sim {\left\{ \begin{array}{ll} 2^{-js}2^{jn(1-\alpha )(1/p-1/\tilde{q})}, &{}\frac{1}{p}>\frac{1}{\tilde{q}}, \\ 2^{-js}, &{}\frac{1}{p}\le \frac{1}{\tilde{q}}. \end{array}\right. } \end{aligned}$$

(5.55)

Using the operator interpolation inequality, one can deduce that

$$\begin{aligned} \Vert \Delta _j|\; M_{p,\tilde{q}}^{s,\alpha }\rightarrow B_{p,q}^0\Vert \lesssim \Vert \Delta _j|\; M_{p,q}^{s_1,\alpha _1}\rightarrow B_{p,q}^0\Vert ^{1-\theta } \Vert \Delta _j|\; M_{p,q}^{s_2,\alpha _2}\rightarrow B_{p,q}^0\Vert ^{\theta }, \end{aligned}$$

(5.56)

which implies

$$\begin{aligned} -s+n(1-\alpha )(1/p-1/\tilde{q}) \le -s_{\theta }+n(1-\alpha _{\theta })(1/p-1/q). \end{aligned}$$

(5.57)

Addition of (5.53) and (5.57) yields

$$\begin{aligned} n(1-\alpha )(2/p-1)\le n(1-\alpha _{\theta })(2/p-1). \end{aligned}$$

(5.58)

So we have

$$\begin{aligned} \alpha \ge \alpha _{\theta }. \end{aligned}$$

(5.59)

On the other hand, by the same method as in the last subsection (see the section “Proving $s=s_{\theta }$”), we can use

$$\begin{aligned} \Vert f\Vert _{M_{p,\tilde{q}}^{s,\alpha }} \lesssim \Vert f\Vert ^{1-\theta }_{M_{p,q}^{s_1,\alpha _1}} \Vert f\Vert ^{\theta }_{M_{p,q}^{s_2,\alpha _2}} \end{aligned}$$

(5.60)

and

$$\begin{aligned} \Vert f\Vert _{M_{p',\tilde{q}'}^{-s+n\alpha (\frac{1}{1\wedge p}-1),\alpha }} \lesssim \Vert f\Vert ^{1-\theta }_{M_{p',q'}^{-s_1+n\alpha _1 (\frac{1}{1\wedge p}-1),\alpha _1}} \Vert f\Vert ^{\theta }_{M_{p',q'}^{-s_2+n\alpha _2 (\frac{1}{1\wedge p}-1),\alpha _2}} \end{aligned}$$

(5.61)

to deduce

$$\begin{aligned} s\le s_{\theta } \end{aligned}$$

(5.62)

and

$$\begin{aligned} -s+n\alpha (1/p-1) \le -s_{\theta }+n\alpha _{\theta }(1/p-1). \end{aligned}$$

(5.63)

Adding the above two inequalities (5.62) and (5.63), we conclude

$$\begin{aligned} \alpha (1/p-1)\le \alpha _{\theta }(1/p-1) \end{aligned}$$

(5.64)

which implies $\alpha \le \alpha _{\theta }$. So we have $\alpha =\alpha _{\theta }$. Putting $\alpha =\alpha _{\theta }$ into (5.63), we deduce $s\ge s_{\theta }$. So we have $s=s_{\theta }$.

Finally, we put $\alpha = \alpha _{\theta }$, $s=s_{\theta }$ into (5.53) and (5.57) and deduce $\tilde{q}=q.$ Now, we have verified

$$\begin{aligned} \left[ M_{p,q}^{s_1,\alpha _1},M_{p,q}^{s_2,\alpha _2}\right] _{\theta }=M_{p,q}^{s_{\theta },\alpha _{\theta }}. \end{aligned}$$

(5.65)

Lemma 3.2 (together with $\alpha =\alpha _\theta \in (\alpha _1,\alpha _2)$) immediately yields $1/p\le 1/q$, which contradicts the assumption $1/p> 1/q$. We complete the proof for this case.

Case 2: $p<1, \frac{1}{p}\le \frac{1}{q}$.

As in Case 1, one can deduce $s\le s_{\theta }$ and $\alpha \le \alpha _{\theta }$. Using Lemma 4.1, we have

$$\begin{aligned} \Vert \Delta _j|\; M_{p,q}^{s_1,\alpha _1}\rightarrow B_{p,q}^0\Vert \sim 2^{-js_1} \end{aligned}$$

(5.66)

and

$$\begin{aligned} \Vert \Delta _j|\; M_{p,q}^{s_2,\alpha _2}\rightarrow B_{p,q}^0\Vert \sim 2^{-js_2}. \end{aligned}$$

(5.67)

Then we use the operator interpolation inequality to deduce

$$\begin{aligned} \Vert \Delta _j|\; M_{p,\tilde{q}}^{s,\alpha }\rightarrow B_{p,q}^0\Vert \lesssim 2^{-js_{\theta }}. \end{aligned}$$

(5.68)

However, Lemma 4.1 implies

$$\begin{aligned} \Vert \Delta _j|\; M_{p,\tilde{q}}^{s,\alpha }\rightarrow B_{p,q}^0\Vert \sim {\left\{ \begin{array}{ll} 2^{-js}2^{jn(1-\alpha )(1/p-1/\tilde{q})}, &{}\frac{1}{p}>\frac{1}{\tilde{q}}, \\ 2^{-js}, &{}\frac{1}{p}\le \frac{1}{\tilde{q}}. \end{array}\right. } \end{aligned}$$

(5.69)

So, we have

$$\begin{aligned} -s \le -s+n(1-\alpha )\max \{0, 1/p-1/\tilde{q}\}\le -s_{\theta }, \end{aligned}$$

(5.70)

which implies $s\ge s_{\theta }$. Recalling the fact $s\le s_{\theta }$, we conclude $s=s_{\theta }.$

Additionally, by Corollary 4.3, one can deduce the embedding

$$\begin{aligned} M_{p,q}^{s_1,\alpha _1}\subset B_{p,q}^{s_1},\; M_{p,q}^{s_2,\alpha _2}\subset B_{p,q}^{s_2}. \end{aligned}$$

(5.71)

Then, we use Lemma 2.6 to deduce

$$\begin{aligned} M_{p,\tilde{q}}^{s_{\theta },\alpha }\subset B_{p,q}^{s_{\theta }}. \end{aligned}$$

(5.72)

This implies

$$\begin{aligned} l^{\tilde{q}}\subset l^q, \end{aligned}$$

(5.73)

and hence $1/q\le 1/\tilde{q}$.

On the other hand, we use Lemma 4.1 to deduce that

$$\begin{aligned} {\begin{matrix} \Vert \Delta _j|\; B_{p,q}^0\rightarrow M_{p,q}^{s_1,\alpha _1}\Vert &{}\sim 2^{js_1}2^{jn(1-\alpha _1)(1/p+1/q-1)}, \\ \Vert \Delta _j|\; B_{p,q}^0\rightarrow M_{p,q}^{s_2,\alpha _2}\Vert &{}\sim 2^{js_2}2^{jn(1-\alpha _2)(1/p+1/q-1)}, \\ \Vert \Delta _j|\; B_{p,q}^0\rightarrow M_{p,\tilde{q}}^{s_{\theta },\alpha }\Vert &{}\sim 2^{js}2^{jn(1-\alpha )(1/p+1/\tilde{q}-1)}. \end{matrix}} \end{aligned}$$

(5.74)

As in Case 1, we use Lemma 2.6 (and the fact $s=s_\theta$ shown above) to deduce

$$\begin{aligned} s_{\theta }+n(1-\alpha )(1/p+1/\tilde{q}-1)\le s_{\theta }+n(1-\alpha _{\theta })(1/p+1/q-1), \end{aligned}$$

(5.75)

which implies

$$\begin{aligned} n(1-\alpha )(1/p+1/\tilde{q}-1)\le n(1-\alpha _{\theta })(1/p+1/q-1). \end{aligned}$$

(5.76)

Recalling $\alpha \le \alpha _{\theta }<1$, one can deduce

$$\begin{aligned} n(1-\alpha )(1/p+1/\tilde{q}-1)\le n(1-\alpha )(1/p+1/q-1) \end{aligned}$$

(5.77)

which implies $1/\tilde{q}\le 1/q.$ So we have $\tilde{q}=q.$ Putting $\tilde{q}=q$ into (5.76), we get

$$\begin{aligned} n(1-\alpha )(1/p+1/q-1)\le n(1-\alpha _{\theta })(1/p+1/q-1) \end{aligned}$$

(5.78)

which implies $\alpha \ge \alpha _{\theta }.$ Recalling $\alpha \le \alpha _{\theta }$ again, we conclude $\alpha = \alpha _{\theta }.$

Now, we have verified that

$$\begin{aligned} \left[ M_{p,q}^{s_1,\alpha _1},M_{p,q}^{s_2,\alpha _2}\right] _{\theta }=M_{p,q}^{s_{\theta },\alpha _{\theta }}. \end{aligned}$$

(5.79)

We use Lemma 3.2 in the dual convexity inequality

$$\begin{aligned} \Vert f\Vert _{M_{p',q'}^{-s_{\theta }+n\alpha _{\theta } (\frac{1}{1\wedge p}-1),\alpha _{\theta }}} \lesssim \Vert f\Vert ^{1-\theta }_{M_{p',q'}^{-s_1+n\alpha _1 (\frac{1}{1\wedge p}-1),\alpha _1}} \Vert f\Vert ^{\theta }_{M_{p',q'}^{-s_2+n\alpha _2 (\frac{1}{1\wedge p}-1),\alpha _2}} \end{aligned}$$

(5.80)

to deduce

$$\begin{aligned} \frac{1}{p'}+\frac{1}{q'}\ge 1, \end{aligned}$$

(5.81)

which contradicts the identity $p'=q'=\infty$. This completes the proof for the present case.

Case 3: $p\ge 1, q<1$.

By the same method used in the proof of Theorem 1.1, one can verify the relationship

$$\begin{aligned} \tilde{p}=p,\;\tilde{q}=q,\;s_{\theta }=s. \end{aligned}$$

(5.82)

Then we have

$$\begin{aligned} \left[ M_{p,q}^{s_1,\alpha _1},M_{p,q}^{s_2,\alpha _2}\right] _{\theta }=M_{p,q}^{s_{\theta },\alpha }. \end{aligned}$$

(5.83)

If $\alpha \le \alpha _1$, we use Lemma 3.2 to deduce $p\le q$, which contradicts to $q<1\le p.$

If $\alpha > \alpha _1$, we use Lemma 3.2 in the dual convexity inequality

$$\begin{aligned} \Vert f\Vert _{M_{p',q'}^{-s_{\theta }+n\alpha (\frac{1}{1\wedge p}-1),\alpha }} \lesssim \Vert f\Vert ^{1-\theta }_{M_{p',q'}^{-s_1+n\alpha _1 (\frac{1}{1\wedge p}-1),\alpha _1}} \Vert f\Vert ^{\theta }_{M_{p',q'}^{-s_2+n\alpha _2 (\frac{1}{1\wedge p}-1),\alpha _2}} \end{aligned}$$

(5.84)

to deduce

$$\begin{aligned} \frac{1}{p'}+\frac{1}{q'}\ge 1,\; \frac{1}{p'}\le \frac{1}{q'}, \end{aligned}$$

(5.85)

which also contradicts to the assumption in this case. This completes the proof. $\square$