1 Introduction

We first recall that for a bandwidth \(c>0,\) the infinite countable set of the eigenfunctions of the finite Fourier transform \({\displaystyle \mathcal F_c,}\) defined on \(L^2(-1,1)\) by \({\displaystyle \mathcal F_c f(x)=\int _{-1}^1 e^{icxy} f(y)\, dy,}\) are known as the prolate spheroidal wave functions (PSWFs). They have been extensively studied in the literature, since the pioneer work on the subject of Slepian and co-workers, see [11, 15, 16]. The interest in the PSWFs is essentially due to their wide range of applications in different scientific research area such as signal processing, physics, applied mathematics, see for example [7–9, 18]. Recently, in [19], the authors have given a generalization of the PSWFs by considering the eigenfunctions of the special case of the weighted Fourier transform \(\mathcal F_c^{(\alpha )},\) defined by \({\displaystyle \mathcal F_c^{(\alpha )} f(x)=\int _{-1}^1 e^{icxy} f(y)\,(1-y^2)^{\alpha }\, dy,\, \alpha > -1.}\) Note that although, the extra weight function \(\omega _{\alpha }(x) = (1-x^2)^{\alpha },\) generates new computational complications, the resulting eigenfunctions have some advantages over the classical PSWFs. In this paper, we first give some useful analytic and local estimates of a more general Jacobi-type PSWFs. This is done by using special spectral techniques from the theory of Sturm–Liouville operators applied to the following Jacobi perturbed differential operator, defined on \(C^2([-1,1])\) by

$$\begin{aligned} \mathcal L^{(\alpha ,\beta )}_c \varphi (x)&= (1-x^2)\varphi ''(x)+((\beta -\alpha )-(\alpha +\beta +2)x)\varphi '(x) - c^2 x^2 \varphi (x)\nonumber \\&= \mathcal L_0 \varphi (x)-c^2 x^2 \varphi (x). \end{aligned}$$
(1)

Note that in the limiting case \(c=0,\) the eigenfunctions of the previous differential operator are reduced to the Jacobi polynomials \(P_k^{(\alpha ,\beta )}.\) Moreover, in the special case \(c>0,\) \(\alpha =\beta =0,\) these eigenfunctions correspond to the classical Slepian PSWFs. Moreover, in the case where \(\alpha =\beta >-1,\) it has been shown in [19] that the finite weighted Fourier transform \(\mathcal F_c^{(\alpha )}\) commutes with \(\mathcal L^{(\alpha ,\alpha )}_c.\) Hence, both operators have the same eigenfunctions, called generalized prolate spheroidal wave functions (GPSWFs) and simply denoted by \(\psi ^{(\alpha )}_{n,c},\, n\ge 0.\) They are solutions of the following integral equation

$$\begin{aligned} \mathcal F_c^{(\alpha )} \psi ^{(\alpha )}_{n,c} (x) = \int _{-1}^{1} e^{icxy} \psi ^{(\alpha )}_{n,c}(y) \omega _{\alpha }(y)\, dy =\mu _{n}^{(\alpha )}(c) \psi ^{(\alpha )}_{n,c}(x),\quad |x|\le 1. \end{aligned}$$
(2)

Here, \(\mu _{n}^{(\alpha )}(c)\) is the eigenvalue of the integral operator \(\mathcal F_c^{(\alpha )},\) associated with the eigenfunction \( \psi ^{(\alpha )}_{n,c}.\)

The important part of this work is devoted to the study of the GPSWFs, that is \(\alpha =\beta .\) In particular, we give their analytic extensions to the whole real line. As a consequence, we obtain an explicit and practical formula (in terms of a ratio of two fast converging series) for computing the eigenvalues \(\mu _n^{(\alpha )}(c).\) Note that the behaviour as well as the decay rate of these eigenvalues, play a crucial role in most applications of the GPSWFs. In [19], by using an heuristic asymptotic analysis, the authors have given an asymptotic super-exponential decay rate of the \(|\mu _n^{(\alpha )}(c)|.\) In the second part of this work, we prove that for any \(\alpha \ge 0,\) the super-exponential decay rate of \(|\mu _n^{(\alpha )}(c)|\) starts holding from the plunge region around \({\displaystyle n = \frac{2c}{\pi }.}\) The proof of this result is based on the characterization of the GPSWFs as solutions of a generalized energy maximization problem, over a restricted Paley–Wiener space \(B_c^{(\alpha )},\) given by

$$\begin{aligned} B_c^{(\alpha )}=\{ f\in L^2(\mathbb R),\,\, \text{ Support } \widehat{f}\subset [-c,c],\,\, \widehat{f} \in L^2((-c,c),\omega _{-\alpha }\left( \frac{\cdot }{c}\right) ). \} \end{aligned}$$

Here, \(\widehat{f}\) denotes the Fourier transform of \(f\in L^2(\mathbb R),\) defined by

$$\begin{aligned} \widehat{f}(\xi )= \lim _{A\rightarrow +\infty }\int _{-A}^A e^{-ix \xi } f(x)\, dx,\quad \xi \in \mathbb R . \end{aligned}$$

More precisely, for a real number \(\alpha >-1,\) let \(J_{\alpha }\) denote the Bessel function of the first type and order \(\alpha \) and consider the self-adjoint compact operator \({\displaystyle \mathcal Q_c^{\alpha }=\frac{c}{2\pi } \mathcal F_c^{{\alpha }^*} \circ \mathcal F_c^{\alpha },}\) defined on \(L^2{(I, \omega _{\alpha })},\, I=[-1,1]\) by

$$\begin{aligned} \mathcal Q_c^{\alpha } g (x)= & {} \int _{-1}^1 \frac{c}{2 \pi }\mathcal K_{\alpha }(c(x-y)) g(y) \omega _{\alpha }(y) \, dy, \quad \nonumber \\ \mathcal K_{\alpha }(x)= & {} \sqrt{\pi } 2^{\alpha +1/2}\Gamma (\alpha +1) \frac{J_{\alpha +1/2}(x)}{x^{\alpha +1/2}}. \end{aligned}$$
(3)

By rewriting the energy maximization problem in term of the previous integral operator, one gets a characterization of the eigenvalues \({\displaystyle \lambda _n^{(\alpha )}(c)= \frac{c}{2\pi } |\mu _n^{(\alpha )}(c)|^2}\) of \(\mathcal Q_c^{\alpha }\) as a countable sequence generated by the energy problem. From this, we conclude that the \(\lambda _n^{(\alpha )}(c)\) decay with respect to the parameter \(\alpha ,\) that is for \(c>0,\) and any \(n\in \mathbb N,\)

$$\begin{aligned} 0 < \lambda _n^{(\alpha )}(c) \le \lambda _n^{(\alpha ')}(c) < 1,\quad \forall \, \alpha \ge \alpha ' \ge 0. \end{aligned}$$

Hence, by using the precise behaviour as well as the sharp decay rate of the \(\lambda _n^{(0)}(c),\) given in [6], one gets a similar behaviour and decay rate for the \((\lambda _n^{(\alpha )}(c))_n,\) for any \(\alpha \ge 0.\)

This work is organized as follows. In Sect. 2, we give some mathematical preliminaries on Jacobi polynomials and their finite weighted Fourier transform. Also, we describe the Bouwkamp method for the Jacobi series expansion of the eigenfunctions \(\psi _{n,c}^{(\alpha ,\beta )}\) of the differential operator \(\mathcal L_c^{(\alpha ,\beta )}.\) Then, we give some explicit and local estimates of these eigenfunctions. These estimates will be particularly useful in the subsequent study of the GPSWFs, given by Sects. 3 and 4. In Sect. 3, we first give an improvement as well as a new kind of decay rate of the Gegenbauer’s series expansion coefficients of the GPSWFs \(\psi _{n,c}^{(\alpha )}.\) Then, we give the analytic extension of the GPSWFs to the whole real line, as well as an explicit and practical formula (as a ratio of two fast converging series) for the accurate computation of the eigenvalues \(\mu _n^{(\alpha )}(c)\) and consequently of \(\lambda _n^{(\alpha )}(c).\) In Sect. 4, we characterize the GPSWFs as solutions of a generalized energy maximization problem and we prove the monotonicity of the \(\lambda _n^{(\alpha )}(c)\) with respect to the parameter \(\alpha .\) Moreover, we show that the GPSWFs are well adapted for the approximation of the classical c-band-limited as well as almost c-band-limited functions. Finally, in Sect. 5, we provide the reader with numerical examples that illustrate the different results of this work.

Notations and normalizations: The following notations will be frequently used in this work,

$$\begin{aligned} \omega _{\alpha ,\beta }(y)=(1-y)^{\alpha }(1+y)^{\beta },\,\, \quad \omega _{\alpha }(y)= (1-y^2)^{\alpha }, \,\, I=[-1,1]. \end{aligned}$$

Moreover, the eigenfunctions \(\psi _{n,c}^{(\alpha ,\beta )}\) and the GPSWFs \(\psi _{n,c}^{(\alpha )}\) are normalized so that

$$\begin{aligned} \int _{-1}^1 \left( \psi _{n,c}^{(\alpha ,\beta )}(t)\right) ^2 \, \omega _{\alpha ,\beta }(t)\, dt =1,\quad \int _{-1}^1 \left( \psi _{n,c}^{(\alpha )}(t)\right) ^2 \, \omega _{\alpha }(t)\, dt =1. \end{aligned}$$

2 Eigenfunctions of a Perturbed Jacobi Differential Operator

In this section, we give a description of the series expansion of the eigenfunctions \(\psi _{n,c}^{(\alpha ,\beta )}(x)\) of \(\mathcal L_c^{(\alpha ,\beta )},\) given by (1) and with respect to the basis of normalized Jacobi polynomials \(\mathcal B=\{{\widetilde{P}}^{(\alpha ,\beta )}_k,\, k\ge 0\}.\) Also, we give some properties as well as local estimates of \(\psi _{n,c}^{(\alpha ,\beta )}(x),\) generalizing some of those given in [3, 5] in the special case \(\alpha =\beta =0.\) For this purpose, we need the following mathematical preliminaries.

2.1 Mathematical Preliminaries

We first recall that for two real numbers \(\alpha , \beta >-1,\) the Jacobi polynomials \(P^{(\alpha ,\beta )}_k\) are given by the following three term recursion formula

$$\begin{aligned} P^{(\alpha ,\beta )}_{k+1}(x)= (A_k x + B_k)P^{(\alpha ,\beta )}_{k}(x) -C_k P^{(\alpha ,\beta )}_{k-1}(x),\quad x\in [-1,1]. \end{aligned}$$
(4)

with \(P^{(\alpha ,\beta )}_0(x)=1,\quad P^{(\alpha ,\beta )}_1(x)=\frac{1}{2}(\alpha +\beta +2)x +\frac{1}{2}(\alpha +\beta ).\) Here,

$$\begin{aligned} A_k= & {} \frac{(2k+\alpha +\beta +1)(2k+\alpha +\beta +2)}{2 (k+1)(k+\alpha +\beta +1)},\nonumber \\ B_k= & {} \frac{(\alpha ^2-\beta ^2)(2k+\alpha +\beta +1)}{2(k+1)(k+\alpha +\beta +1)(2k+\alpha +\beta )}\nonumber \\ C_k= & {} \frac{(k+\alpha )(k+\beta )(2k+\alpha +\beta +2)}{(k+1)(k+\alpha +\beta +1)(2k+\alpha +\beta )}. \end{aligned}$$
(5)

In the sequel, we let \({\widetilde{P}}^{(\alpha ,\beta )}_k\) denote the normalized Jacobi polynomial of degree k so that

$$\begin{aligned} \Vert {\widetilde{P}}^{(\alpha ,\beta )}_k \Vert ^2_{L^2_{\omega _{\alpha ,\beta }(I)}}=\int _{-1}^1 ({\widetilde{P}}^{(\alpha ,\beta )}_k(y))^2 \omega _{\alpha ,\beta }(y)\, dy =1.\end{aligned}$$

It is well known that in this case, we have

$$\begin{aligned} {\widetilde{P}}^{(\alpha ,\beta )}_{k}(x)= \frac{1}{\sqrt{h_k}}P^{(\alpha ,\beta )}_k(x),\quad h_k=\frac{2^{\alpha +\beta +1}\Gamma (k+\alpha +1)\Gamma (k+\beta +1)}{k!(2k+\alpha +\beta +1)\Gamma (k+\alpha +\beta +1)}. \end{aligned}$$
(6)

Straightforward computations give us the following useful identities

$$\begin{aligned} {\widetilde{P}}^{(\alpha ,\beta )}_{k+1}(x)= (a_k x + b_k){\widetilde{P}}^{(\alpha ,\beta )}_{k}(x) -c_k {\widetilde{P}}^{(\alpha ,\beta )}_{k-1}(x), \end{aligned}$$
(7)
$$\begin{aligned} a_k=\sqrt{\frac{h_{k}}{h_{k+1}}} A_k,\quad b_k=\sqrt{\frac{h_{k}}{h_{k+1}}} B_k,\quad c_k=\sqrt{\frac{h_{k-1}}{h_{k+1}}} C_k. \end{aligned}$$
(8)
$$\begin{aligned} x^2 {\widetilde{P}}^{(\alpha ,\beta )}_k(x)= & {} \frac{1}{a_k a_{k+1}}{\widetilde{P}}^{(\alpha ,\beta )}_{k+2}(x)-\Big (\frac{b_{k+1}}{a_k a_{k+1}}+\frac{b_k}{a_k^2}\Big ){\widetilde{P}}^{(\alpha ,\beta )}_{k+1}(x)\nonumber \\&+\Big (\frac{c_{k+1}}{a_k a_{k+1}}+\frac{b_k^2}{a_k^2} +\frac{c_k}{a_k a_{k-1}}\Big ){\widetilde{P}}^{(\alpha ,\beta )}_k(x)\nonumber \\&-\Big (\frac{c_k b_k}{a_k^2}+\frac{c_k b_{k-1}}{a_k a_{k-1}}\Big ){\widetilde{P}}^{(\alpha ,\beta )}_{k-1}(x) + \frac{c_k c_{k-1}}{a_k a_{k-1}}{\widetilde{P}}^{(\alpha ,\beta )}_{k-2}(x) \end{aligned}$$
(9)

The explicit expressions and bounds of the different moments of the weight function \(\omega _{\alpha ,\beta }\) as well as of the Jacobi polynomials \({\widetilde{P}}^{(\alpha ,\beta )}_k\) will be frequently needed in this work. For this purpose, we first recall the following useful inequalities for the Gamma function, see [2],

$$\begin{aligned} \sqrt{2e} \left( \frac{x+1/2}{e}\right) ^{x+1/2}\le \Gamma (x+1)\le \sqrt{2\pi } \left( \frac{x+1/2}{e}\right) ^{x+1/2},\quad x>0. \end{aligned}$$
(10)

Next, for an integer \(k\ge 0,\) let

$$\begin{aligned} I_k^{\alpha ,\beta }=\int _{-1}^1 y^{k}\omega _{\alpha ,\beta }(y)\, dy \end{aligned}$$
(11)

be the kth moment of \(\omega _{\alpha ,\beta }.\) To get an upper bound for \(I_k^{\alpha ,\beta },\) we may assume that \(\alpha \ge \beta .\) In this case, we have

$$\begin{aligned} I_k^{\alpha ,\beta }= & {} \int _0^1 y^{k} (1-y)^{\alpha }(1+y)^{\beta }\, dy + \int _0^1 y^{k} (1-y)^{\beta }(1+y)^{\alpha }\, dy\nonumber \\\le & {} \int _0^1 y^{k} (1-y^2)^{\alpha }\, dy + 2^{\alpha -\beta } \int _0^1 y^{k} (1-y^2)^{\beta }\, dy \le \frac{1}{2} \left( B(k/2+1/2,\alpha +1)\right. \nonumber \\&\left. +2^{\alpha -\beta } B(k/2+1/2,\beta +1)\right) . \end{aligned}$$
(12)

Here, \(B(\cdot ,\cdot )\) is the Beta function given by \({\displaystyle B(x,y)=\frac{\Gamma (x) \Gamma (y)}{\Gamma (x+y)},\, x, y >0.}\) Moreover, by using (10), taking into account that for any real number \(a>-1,\) the function

$$\begin{aligned} \varphi (x)= \left( 1+\frac{a}{x}\right) ^{a+x}, \quad x\ge 1 \end{aligned}$$
(13)

is decreasing on \([1,\infty )\) to \(e^a\) and by using some straightforward computations, one gets

$$\begin{aligned} I_k^{\alpha ,\beta }\le \frac{1}{2}\sqrt{\frac{\pi }{e}}\frac{2^{1+\beta }}{k^{1+\beta }} \left( \Gamma (1+\alpha )+2^{\alpha -\beta }\Gamma (1+\beta )\right) ,\quad \alpha \ge \beta . \end{aligned}$$

Consequently, for any real numbers \(\alpha ,\beta >-1,\) we have

$$\begin{aligned} I_k^{\alpha ,\beta } \le \frac{C_{\alpha ,\beta }}{k^{1+\min (\alpha ,\beta )}},\quad \forall \, \alpha , \beta > -1,\qquad C_{\alpha ,\beta }=\left( 2^{\alpha }+2^{\beta }\right) \sqrt{\frac{\pi }{e}}\Gamma (1+\max (\alpha ,\beta )). \end{aligned}$$
(14)

In the special case where \(\alpha =\beta ,\) and by using the parity of \(\omega _{\alpha }(y)=(1-y^2)^{\alpha }\) as well as the previous bound, one gets

$$\begin{aligned} I_{2k+1}^{\alpha ,\alpha }=0,\quad I_{2k}^{\alpha ,\alpha } = B(k+1/2,\alpha +1)\le \sqrt{\frac{\pi }{e}}\frac{\Gamma (\alpha +1)}{k^{1+\alpha }}. \end{aligned}$$
(15)

Also, note that for given integers \(k\ge n\ge 0,\) and by using the Rodrigues formula for the Jacobi polynomials, one gets the following formula for the kth moments of \({\widetilde{P}}^{(\alpha ,\beta )}_n,\) with \(k\ge n,\)

$$\begin{aligned} M_{k,n}\!=\!\int _{-1}^1 x^k {\widetilde{P}}^{(\alpha ,\beta )}_n(x)\omega _{\alpha ,\beta }(x)\, dx \!=\!\frac{1}{2^n\sqrt{h_n}}{k\atopwithdelims ()n}\int _{-1}^1 x^{k-n}(1-x)^{n+\alpha }(1+x)^{n+\beta }\, dx. \end{aligned}$$
(16)

In particular, if \(\alpha =\beta ,\) one gets

$$\begin{aligned} M_{k,n}= & {} \int _{-1}^1 x^k {\widetilde{P}}_n^{(\alpha ,\alpha )}(x)\omega _{\alpha }(x)\, dx\nonumber \\= & {} \left\{ \begin{array}{ll} 0 &{} \text{ if } k< n \text{ or } k-n \text{ is } \text{ odd }\\ \frac{{k\atopwithdelims ()n}}{2^n\sqrt{h_n}} B\left( \frac{k-n+1}{2},n+\alpha +1\right) &{} \text{ otherwise. } \end{array}\right. \end{aligned}$$
(17)

On the other hand, it is interesting to note that the weighted finite Fourier transform of Jacobi polynomial is given by the following explicit expression, see [13, p. 456],

$$\begin{aligned} \int _{-1}^{1} e^{ixy} P_k^{(\alpha , \beta )}(y) \omega _{\alpha ,\beta }(y)\, dy= & {} \frac{(ix)^k e^{ix}}{k!}2^{k+\alpha +\beta +1}B(k+\alpha +1,k+\beta +1) _1 \nonumber \\&\times \,F_1(k+\alpha +1,2k+\alpha +\beta +2,-2ix),\qquad \end{aligned}$$
(18)

where B(x, y) is the Beta function and \(_1 F_1(a,b,c)\) is the Kummer’s function. It is well known, see [13, p. 326] that the Kummer’s function has the following integral representation

$$\begin{aligned} _1F_1(a,b;z)=\frac{1}{B(a,b)}\int _0^1 e^{zt}t^{a-1}(1-t)^{b-a-1}dt,\quad z\in \mathbb C,\quad \mathcal Re(b)> \mathcal Re(a)>0. \end{aligned}$$
(19)

2.2 Computation and First Properties of the Eigenfunctions of \(\mathcal L_c^{(\alpha ,\beta )}\)

In this paragraph, we first describe the Bouwkamp method for the computation of the bounded eigenfunctions and the corresponding eigenvalues of the operator \(\mathcal L_c^{(\alpha ,\beta )},\) given by (1). Then, we give some general properties of these eigenfunctions. Note that Bouwkamp method can be briefly described as the representation of a perturbed version of classical orthogonal polynomials differential operator. This representation is done by the use of the original classical orthogonal polynomials. In our case, we consider the Jacobi orthonormal basis of \(L^2(I,\omega _{\alpha ,\beta }),\) given by \(\mathcal B^{\alpha ,\beta }=\{ {\widetilde{P}}^{(\alpha ,\beta )}_k(x),\, k\ge 0\}.\) Then, thanks to this method, the computation of the bounded eigenfunctions \(\psi ^{(\alpha ,\beta )}_{n,c}\) of \(\mathcal L_c^{(\alpha ,\beta )}\) and their associated eigenvalues \(\chi _n(c)\) is reduced to the computation of the eigenvectors and the associated eigenvalues of the infinite order matrix representation of \(\mathcal L_c^{(\alpha ,\beta )}\) with respect to the basis \(\mathcal B^{\alpha ,\beta }.\) It is interesting to note that only a finite number of the main diagonals of this representation matrix are not identically zeros. To the best of our knowledge, Niven, was the first to use this method in the early 1880s, see [12].

Note that since \(\psi ^{(\alpha ,\beta )}_{n,c}\in L^2(I, \omega _{\alpha ,\beta }),\) then its series expansion with respect to the basis \(\mathcal B^{\alpha ,\beta }\) is given by

$$\begin{aligned} \psi ^{(\alpha ,\beta )}_{n,c}(x) =\sum _{k\ge 0} \beta _k^n {\widetilde{P}}^{(\alpha ,\beta )}_k (x),\quad x\in [-1,1]. \end{aligned}$$
(20)

By combining (20) and the facts that

$$\begin{aligned} -\mathcal L_c^{(\alpha ,\beta )} \psi ^{(\alpha ,\beta )}_{n,c}(x)= & {} \chi _n(c) \psi ^{(\alpha ,\beta )}_{n,c}(x),\quad -\mathcal L_0^{(\alpha ,\beta )} {\widetilde{P}}^{(\alpha ,\beta )}_k(x)= \chi _k(0){\widetilde{P}}^{(\alpha ,\beta )}_k(x),\\ \chi _k(0)= & {} k(k+\alpha +\beta +1), \end{aligned}$$

one can easily check that the expansion coefficients \((\beta _k^n)_{k\ge 0},\, n\ge 0\) and the eigenvalues \((\chi _n(c))_{n\ge 0}\) are given by the following infinite order eigensystem

$$\begin{aligned} \mathbf D^{\alpha ,\beta } \cdot \mathbf B_n = \chi _n(c)\, \mathbf B_n,\quad \mathbf D^{\alpha ,\beta } = \left[ d_{i,j}\right] _{i,j\ge 0},\quad \mathbf B_n = [\beta _k^n, k\ge 0]^T. \end{aligned}$$
(21)

Here, \(\mathbf D^{\alpha ,\beta }\) is a 5-diagonals matrix representation of the operator \(-\mathcal L_c^{(\alpha ,\beta )}\) with coefficients given by

$$\begin{aligned} d_{i,i-2}= & {} d_{i,i-2} = c^2\frac{1}{a_{i-1}a_{i-2}},\quad d_{i,i-1}=-c^2\left( \frac{b_i}{a_ia_{i-1}}+\frac{b_{i-1}}{a_{i-1}^2}\right) \nonumber \\ d_{i,i}= & {} i(i+\alpha +\beta +1)+c^2\left( \frac{c_{i+1}}{a_i a_{i+1}}-\frac{b_i^2}{a_i^2}+\frac{c_{i}}{a_i a_{i-1}}\right) ,\nonumber \\ d_{i,i+1}= & {} c^2\left( \frac{c_{i+1} b_{i+1}}{a_{i+1}^2}+\frac{c_{i+1} b_i}{a_{i+1} a_i}\right) , \quad d_{i,j}= 0,\quad \text{ if } |j-i|\ge 3. \end{aligned}$$
(22)

We recall that the coefficients \(a_i, b_i, c_i\) are given by (5) and (8). In the special case where \(\alpha =\beta ,\) we have \(b_i=0,\) so that the previous eigensystem is reduced to a symmetric tri-diagonal system. In this case, for a fixed integer \(n\ge 0,\) the sequence \((\beta _k^n)_{k\ge 0}\) satisfies the following eigensystem

$$\begin{aligned}&c^2\frac{1}{a_{k+2}a_{k+1}} \beta _{k+2}^n + \left( k (k+2\alpha +1)+c^2 \left( \frac{c_{k+1}}{a_k a_{k+1}}+\frac{c_{k}}{a_k a_{k-1}}\right) \right) \beta _k^n \nonumber \\&\quad +c^2\frac{1}{a_{k}a_{k-1}} \beta _{k-2}^n = \chi _n(c) \beta _k^n. \end{aligned}$$
(23)

An expanded form of this system is given by

$$\begin{aligned}&\frac{\sqrt{(k+1)(k+2)(k+2\alpha +1)(k+2\alpha +2)}}{(2k+2\alpha +3)\sqrt{(2k+2\alpha +5)(2k+2\alpha +1)}} c^2 \beta _{k+2}^n + \big (k(k+2\alpha +1)\nonumber \\&\quad +c^2 \frac{2k(k+2\alpha +1)+2\alpha -1}{(2k+2\alpha +3)(2k+2\alpha -1)} \big ) \beta _k^n\nonumber \\&\quad +\frac{\sqrt{k(k-1)(k+2\alpha )(k+2\alpha -1)}}{(2k+2\alpha -1)\sqrt{(2k+2\alpha +1)(2k+2\alpha -3)}} c^2 \beta _{k-2}^n= \chi _n(c) \beta _k^n, \quad k\ge 0.\qquad \quad \end{aligned}$$
(24)

The following proposition provides us with some properties of the eigenfunctions \(\psi ^{(\alpha ,\beta )}_{n,c}(x)\) and eigenvalues \(\chi _n(c),\) generalizing some known properties for Jacobi polynomials.

Proposition 1

For given real numbers \(c>0,\) \(\alpha , \beta > -1,\) let \(\psi _{n,c}^{(\alpha ,\beta )}\) be the nth eigenfunction associated with \(\mathcal L_c^{(\alpha ,\beta )},\) and normalized so that \(\Vert \psi _{n,c}^{(\alpha ,\beta )}\Vert _{L^2(I,\omega _{\alpha ,\beta })}=1.\) Then we have

  • \((P_1)\) The set \(\mathcal B=\{ \psi _{n,c}^{(\alpha ,\beta )},\, n\ge 0 \}\) is an orthonormal basis of \(L^2(I,\omega _{\alpha ,\beta }).\)

  • \((P_2)\) If \(\psi _{n,c}^{(\beta ,\alpha )}\) is the nth normalized eigenfunction of \(\mathcal L_c^{(\beta ,\alpha )},\) then \(\psi _{n,c}^{(\alpha ,\beta )}\) and \(\psi _{n,c}^{(\beta ,\alpha )}\) are associated to the same eigenvalue \(\chi _n(c).\) Moreover, they are related to each others by the following rule

    $$\begin{aligned} \psi _{n,c}^{(\alpha ,\beta )}(-x)= (-1)^n \psi _{n,c}^{(\beta ,\alpha )}(x),\quad x\in \mathbb R. \end{aligned}$$
    (25)

Proof

Property \((P_1)\) follows from the general spectral theory of Sturm–Liouville operators. To prove \((P_2),\) we use the following well known property for Jacobi polynomials, see [17, p. 59]

$$\begin{aligned} P_k^{(\alpha ,\beta )}(-x)=(-1)^k P_k^{(\beta ,\alpha )}(x). \end{aligned}$$
(26)

Let \(\mathbf D^{(\alpha ,\beta )}=[d_{i,j}]_{i,j\ge 0}\) and \(\mathbf D^{(\beta ,\alpha )}=[{\widetilde{d}}_{i,j}]_{i,j\ge 0}\) be the matrix representation of \(-\mathcal L_c^{(\alpha ,\beta )}\) and \(-\mathcal L_c^{(\beta ,\alpha )}\) with respect to the basis of Jacobi polynomials \({\widetilde{P}}^{(\alpha ,\beta )}_k\) and \({\widetilde{P}}_k^{(\beta ,\alpha )},\) respectively. Then from (4) and (22), one gets

$$\begin{aligned} {\widetilde{d}}_{i,i+k}= (-1)^ d_{i,i+k},\quad -2\le k\le 2,\quad i\ge 0 \quad \text{ and }\quad {\widetilde{d}}_{i,j}=0,\quad \text{ if } |i-j|\ge 3. \end{aligned}$$
(27)

Let \(\mathbf B_n = [\beta _k^n, k \ge 0]^T\) and \(\widetilde{\mathbf B}_n = [\widetilde{\beta }_k^n, k\ge 0]^T =[(-1)^k \beta _k^n, k\ge 0]^T. \) Since \(\mathbf D^{(\alpha ,\beta )} \mathbf B_n = \chi _n(c) \mathbf B_n,\) then by using (27), it is easy to see that \(\mathbf D^{(\beta ,\alpha )} \widetilde{\mathbf B}_n = \chi _n(c) \mathbf B_n.\) This means that \(\psi _{n,c}^{(\alpha ,\beta )}\) and \(\psi _{n,c}^{(\beta ,\alpha )}\) are associated to the same eigenvalue \(\chi _n(c).\) Moreover, the series expansion of \(\psi _{n,c}^{(\beta ,\alpha )}\) in the basis \( \{\widetilde{P}_k^{(\beta ,\alpha )},\,\, k\ge 0\}\) is obtained from the series expansion of \(\psi _{n,c}^{(\alpha ,\beta )},\) as follows

$$\begin{aligned} \psi _{n,c}^{(\beta ,\alpha )}(x)= c_n \sum _{k=0}^{\infty } (-1)^k \beta _k^n {\widetilde{P}}_k^{(\beta ,\alpha )}(x), \end{aligned}$$
(28)

for some constant \(c_n.\) By combining (26) and the previous equality, one concludes that \(\psi _{n,c}^{(\alpha ,\beta )}(-x)= c_n \psi _{n,c}^{(\beta ,\alpha )}(x).\) Moreover, since \(\Vert \psi _{n,c}^{(\alpha ,\beta )}\Vert _{L^2(I,\omega _{\alpha ,\beta })}=\Vert \psi _{n,c}^{(\beta ,\alpha )}\Vert _{L^2(I,\omega _{\beta ,\alpha })}=1\) and since \(\psi _{n,c}^{(\alpha ,\alpha )}\) has the same parity as n,  see [19], then \(c_n=(-1)^n.\) This concludes the proof of (25). \(\square \)

Also, we should mention that the \((n+1)\)th eigenvalue \(\chi _n(c)\) satisfies the following classical inequalities,

$$\begin{aligned} n (n+\alpha +\beta +1) \le \chi _n(c) \le n (n+\alpha +\beta +1) +c^2,\quad \forall n\ge 0. \end{aligned}$$
(29)

To get the previous upper bound, we consider the following Sturm–Liouville form of \(-\mathcal L_c^{(\alpha ,\beta )},\)

$$\begin{aligned} - \mathcal L_c^{(\alpha ,\beta )} (f)(x)&=\, - \frac{d}{dx}\left[ \omega _{\alpha ,\beta }(x) (1-x^2) f'(x)\right] +c^2 x^2 \omega _{\alpha ,\beta }(x) \\ \nonumber&=\, - \mathcal L_0^{(\alpha ,\beta )} (f)(x) +c^2 x^2 \omega _{\alpha ,\beta }(x). \end{aligned}$$
(30)

Then, from the well known Poincaré Min–Max characterization of the eigenvalue of a self-adjoint operator, applied to the operator \(-\mathcal L_c^{(\alpha ,\beta )}, \) one gets

$$\begin{aligned} \chi _n(c)= & {} \min _{ \text{ dim } H =n} \,\, \max _{u\in H, \Vert u\Vert =1} \int _{-1}^1 \left( -\mathcal L_0^{(\alpha ,\beta )}(u)(x) u(x) +c^2 x^2 (u(x))^2 \right) \omega _{\alpha ,\beta }(x)\, dx \\\le & {} \min _{ \text{ dim } H =n} \,\, \max _{u\in H, \Vert u\Vert =1} \int _{-1}^1 -\mathcal L_0^{(\alpha ,\beta )}(u)(x) u(x) \omega _{\alpha ,\beta }(x)\, dx +c^2 \Vert u\Vert ^2\\\le & {} \chi _n(0)+ c^2= n(n+\alpha +\beta +1)+c^2. \end{aligned}$$

Next, to get a lower bound, it suffices to see that the self-adjoint operator \(-\mathcal L_c^{(\alpha ,\beta )}-(-\mathcal L_0^{(\alpha ,\beta )})= c^2 x^2\) is a positive operator, which implies that \(\chi _n(c)\ge \chi _n(0).\)

2.3 Local Estimates of the Eigenfunctions of \(\mathcal L_c^{(\alpha ,\beta )}\)

In this paragraph, we give various explicit and local estimates of the \(\psi _{n,c}^{(\alpha ,\beta )}.\) These estimates will be needed to prove some of the results of Sect. 3 and 4 of this work. We should mention that in the literature, only few references have studied the problem of the explicit estimates of the classical PSWFs and their eigenvalues \(\chi _n(c),\) see [3, 5, 14]. The following proposition provides us with explicit local bounds of \(\psi _{n,c}^{(\alpha ,\beta )},\) generalizing a similar result given in [3] for the special case \(\alpha =\beta =0.\)

Proposition 2

For real numbers \(c>0,\, \alpha , \beta > -1,\) with \(\alpha +\beta +1 \ge 0.\) Let \(n\in \mathbb N\) be such \(q= c^2/\chi _n(c) <1.\) Then we have

$$\begin{aligned}&\sup _{t\in [0,1]} (1-t^2) \omega _{\alpha ,\beta }(t) \left( \left| \psi _{n,c}^{(\alpha ,\beta )}(t)\right| ^2+ \frac{1-t^2}{(1-q t^2)\chi _n(c)}\left| (\psi _{n,c}^{(\alpha ,\beta )})'(t)\right| ^2\right) \nonumber \\&\quad \le 2(1+\max (\alpha ,\beta )). \end{aligned}$$
(31)

Moreover, if \(\alpha =\beta ,\) then we have

$$\begin{aligned} \sup _{t\in [-1,1]} (1-t^2) \omega _{\alpha }(t) \left( \left| \psi _{n,c}^{(\alpha )}(t)\right| ^2+ \frac{1-t^2}{(1-q t^2)\chi _n(c)}\left| (\psi _{n,c}^{(\alpha )})'(t)\right| ^2\right) \le 1+\alpha . \end{aligned}$$
(32)

Proof

The proof uses a classical technique for the local estimates of the eigenfunctions of a Sturm–Liouville operator. In our case, we first note that by using property \((P_2)\) of Proposition 1, it suffices to consider the case \(\alpha \ge \beta ,\) since the case \(\beta \ge \alpha ,\) follows from the equality (25). Next, consider the auxiliary function, defined on [0, 1] by

$$\begin{aligned} Z_n(t)= \left( \psi _{n,c}^{(\alpha ,\beta )}(t)\right) ^2+ \frac{1-t^2}{\chi _n(c) (1-q t^2)}\left( \left( \psi _{n,c}^{(\alpha ,\beta )}\right) '\right) ^2(t). \end{aligned}$$

Since \( \psi _{n,c}^{(\alpha ,\beta )}\) is the eigenfunction of the operator \(-\mathcal L^{(\alpha ,\beta )}_c\) associated with the eigenvalue \(\chi _n(c),\) then straightforward computations give us

$$\begin{aligned} Z_n'(t)= \frac{2 ((\psi _{n,c}^{(\alpha ,\beta )})')^2(t)}{\chi _n(c) (1-q t^2)}\left( (\alpha -\beta )+(1+\alpha +\beta ) t + qt \frac{1-t^2}{1-q t^2}\right) . \end{aligned}$$
(33)

Since \(0\le q\le 1,\) \(\alpha -\beta \ge 0\) and \(\alpha +\beta +1\ge 0,\) then it is easy to see that

$$\begin{aligned} Z_n'(t)\ge 0,\quad \forall \,\, t\in [0,1]. \end{aligned}$$

Next, we consider a second auxiliary function, given by

$$\begin{aligned} K_n(t)= (1-t^2) \omega _{\alpha ,\beta }(t) Z_n(t),\quad t\in [0,1]. \end{aligned}$$

Then, by using (33), one can easily check that there exists a positive valued function \(A(\cdot )\) on \([-1,1]\) with

$$\begin{aligned} K_n'(t)= & {} \omega _{\alpha ,\beta }(t)\left( -2 t +(\beta -\alpha )-(\alpha +\beta )t\right) Z_n(t)+ (1-t^2)\omega _{\alpha ,\beta }(t) Z'_n(t)\\= & {} \left( -2 t +(\beta -\alpha )-(\alpha +\beta )t\right) \omega _{\alpha ,\beta }(t) \left( \psi _{n,c}^{(\alpha ,\beta )}\right) ^2(t)+ A(t)\left( \psi _{n,c}^{(\alpha ,\beta )})'\right) ^2(t)\\\ge & {} \left( (\beta -\alpha )-(2+\alpha +\beta )t\right) \omega _{\alpha ,\beta }(t) \left( \psi _{n,c}^{(\alpha ,\beta )}\right) ^2(t). \end{aligned}$$

Finally, since \(K_n(1)=0\) and since \({\displaystyle \int _{-1}^1 \left( \psi _{n,c}^{(\alpha ,\beta )}\right) ^2(t) \, \omega _{\alpha ,\beta }(t)\, dt =1,}\) then by using the last inequality, one gets

$$\begin{aligned} K_n(t)-K_n(1)=K_n(t)\le & {} \max _{t\in [0,1]} \left( (\alpha -\beta )+(2+\alpha +\beta )t\right) \\&\times \int _{0}^1 \left( \psi _{n,c}^{(\alpha ,\beta )}\right) ^2(t) \, \omega _{\alpha ,\beta }(t)\, dt \le 2(1+\alpha ). \end{aligned}$$

Finally, if \(\beta =\alpha ,\) then from the parity of \(\psi _{n,c}^{(\alpha )}(t),\) we have \(\displaystyle \int _{0}^1 \left( \psi _{n,c}^{(\alpha )}\right) ^2(t) \, \omega _{\alpha }(t)\, dt=1/2,\) which means that the previous upper bound is replaced by \(1+\alpha .\) This concludes the proof of the proposition. \(\square \)

The following proposition provides us with an estimate of the maximum of the \(\psi _{n,c}^{(\alpha ,\beta )}\) inside the interval I.

Proposition 3

Let \(c>0,\) and \(\alpha \ge \beta \) with \(\alpha +\beta \ge -1,\) then for any positive integer n with \(q=c^2/\chi _n(c)\le 1,\) we have

$$\begin{aligned} \sup _{x\in [0,1]} |\psi _{n,c}^{(\alpha ,\beta )}(x)|=|\psi _{n,c}^{(\alpha ,\beta )}(1)|\le C_{\alpha } (\chi _n(c))^{\frac{1+\alpha }{2}},\quad C_{\alpha }= \frac{2^{1+\max (\alpha ,0)}}{\sqrt{3+\alpha }}\Big (\frac{1+\alpha }{3+\alpha } \Big )^{1+\frac{\alpha }{2}} \end{aligned}$$
(34)

Moreover, if \(\alpha =\beta ,\) then we have

$$\begin{aligned} \sup _{x\in [-1,1]} |\psi _{n,c}^{(\alpha )}(x)|=|\psi _{n,c}^{(\alpha )}(1)|\le \frac{C_{\alpha }}{\sqrt{2}} (\chi _n(c))^{\frac{1+\alpha }{2}}. \end{aligned}$$
(35)

Proof

We first recall that the auxiliary function \(Z_n\) given by :

$$\begin{aligned} Z_n(x)= \left( \psi _{n,c}^{(\alpha ,\beta )}(x)\right) ^2+ \frac{1-x^2}{\chi _n(c) (1-q x^2)}\left( \left( \psi _{n,c}^{(\alpha ,\beta )}\right) '\right) ^2(x) \end{aligned}$$

is increasing over [0,1] whenever \(q=c^2/\chi _n(c)\le 1,\) \(\alpha \ge \beta \) and \(\alpha +\beta +1 \ge 0.\) Hence, we have

$$\begin{aligned} {\displaystyle \sup _{x\in [0,1]} Z_n(x)= Z_n(1)= \left( \psi _{n,c}^{(\alpha ,\beta )}(x)\right) ^2} \end{aligned}$$

which implies that

$$\begin{aligned} \sup _{x\in [0,1]}|\psi _{n,c}^{(\alpha ,\beta )}(x)|=|\psi _{n,c}^{(\alpha ,\beta )}(1)|,\quad \forall n\in \mathbb N, \text{ with } q\le 1. \end{aligned}$$
(36)

Moreover, if \(\alpha =\beta \) then from the parity of \(\psi _{n,c}^{(\alpha )},\) one gets

$$\begin{aligned} \sup _{x\in [-1,1]}|\psi _{n,c}^{(\alpha )}(x)|=|\psi _{n,c}^{(\alpha )}(1)|,\quad \forall n\in \mathbb N, \text{ with } q\le 1. \end{aligned}$$
(37)

Next, we show how to get the upper bounds of \( |\psi _{n,c}^{(\alpha ,\beta )} (1)| \) and \( |\psi _{n,c}^{(\alpha )} (1)|. \) To alleviate notation, we simply denote \(\psi _{n,c}^{(\alpha ,\beta )}\) by \(\psi _{n,c}\) and \(\chi _n(c)\) by \(\chi _n.\) Also, without loss of generality, we may assume that \(\psi _{n,c}(1)>0.\) Since

$$\begin{aligned} (\psi _{n,c}'(x) (1-x^2) \omega _{\alpha ,\beta }(x))'=-\chi _n(c) \omega _{\alpha ,\beta }(x)(1-qx^2) \psi _{n,c} (x), \end{aligned}$$
(38)

then

$$\begin{aligned} \psi _{n,c}'(x)= & {} \frac{\chi _n}{(1-x^2) \omega _{\alpha ,\beta }(x)} \int _x^1 \omega _{\alpha ,\beta }(t)(1-qt^2) \psi _{n,c} (t) dt\\\le & {} \frac{\chi _n}{(1-x^2)}(1-qx^2)(1-x) \psi _{n,c}(1) = \chi _n(1-qx^2) \psi _{n,c}(1). \end{aligned}$$

Hence,

$$\begin{aligned} \psi _{n,c}(1)-\psi _{n,c}(x) \le \chi _n Q_q(x) \psi _{n,c}(1),\qquad Q_q(x)=(1-qx^2)(1-x^2). \end{aligned}$$
(39)

Next, let \(x_n\in [0,1]\) be such that \( Q_q(x_n)= \frac{a}{\chi _n},\) where the constant a to be fixed later on. By substituting x with \(x_n\) in (39) and by using (31), one gets

$$\begin{aligned} \psi _{n,c}(1) \le \frac{1}{1-a} \psi _{n,c}(x_n) \le \frac{1}{(1-a)}\sqrt{2(1+\alpha )}\left( \frac{1}{Q_q(x_n)\omega _{\alpha ,\beta }(x_n)}\right) ^{1/2}. \end{aligned}$$

That is

$$\begin{aligned} \psi _{n,c}(1) \le \frac{\sqrt{2(1+\alpha )}}{a^{1/2}(1-a)}\frac{\chi _n^{1/2}}{\sqrt{\omega _{\alpha ,\beta }(x_n)}} \end{aligned}$$
(40)

Note that the admissible solution of \( Q_q(x_n)=\frac{a}{\chi _n}\) is given by \( x_n=\left( \frac{(q+1)-\sqrt{(q-1)^2+\frac{4aq}{\chi _n}}}{2q} \right) ^{1/2}.\) Consequently,

$$\begin{aligned} \frac{1-\frac{a}{\chi _n}}{1+\sqrt{\frac{aq}{\chi _n}}}\le x_n = \left( \frac{2(1-\frac{a}{\chi _n})}{q+1+(1-q)\sqrt{1+\frac{4aq}{\chi _n(q-1)^2}}} \right) ^{\frac{1}{2}}\le \Big (1-\frac{a}{\chi _n}\Big )^{\frac{1}{2}}\le 1-\frac{a}{2\chi _n}. \end{aligned}$$

It is easy to see that in this case, we have

$$\begin{aligned} \frac{a}{2\chi _n} \le 1-x_n \le \frac{a}{\chi _n}\left( 1+\sqrt{\frac{\chi _n}{a}}\right) . \end{aligned}$$

Consequently, by using the first inequality when \(\alpha \ge 0\) and the second inequality when \(-1/2\le \alpha <0,\) one gets

$$\begin{aligned} \frac{1}{\sqrt{\omega _{\alpha ,\beta }(x_n)}} \le \left\{ \begin{array}{ll} \left( \frac{\chi _n}{2 a}\right) ^{\alpha /2} 2^{-\beta /2} \le \sqrt{2} \left( \frac{\chi _n}{a}\right) ^{\alpha /2} &{} \text{ if } -1/2\le \alpha <0\\ &{} \\ \left( \frac{2\chi _n}{a}\right) ^{\alpha /2} \frac{1}{(1+x_n)^{\beta /2}} \le 2^{\alpha +1/2}\left( \frac{\chi _n}{a}\right) ^{\alpha /2}&{} \text{ if } \alpha \ge 0. \end{array}\right. \end{aligned}$$
(41)

Hence, by combining (40) and (41), one gets

$$\begin{aligned} \psi _{n,c}^{(\alpha ,\beta )}(1) \le \frac{2^{1+\max (\alpha ,0)}\sqrt{(1+\alpha )}}{a^{(1+\alpha )/2}(1-a)}\chi _n^{\frac{1+\alpha }{2}}. \end{aligned}$$
(42)

Since the maximum of \( a^{\gamma }(1-a) \) is attained at \( a= \frac{\gamma }{1+\gamma } \) then for \(\gamma =\frac{1+\alpha }{2},\) one gets (34). Finally, (35) follows from the parity of \(\psi _{n,c}^{(\alpha )}\) and (32). \(\square \)

Remark 1

The techniques used for the proof of inequality (40) are similar to those used in [3] to prove a similar inequality, restricted to the special case \(\alpha =\beta =0.\) Nonetheless, the general setting of the previous proposition requires handling the new quantity \(\sqrt{\omega _{\alpha ,\beta }(x_n)}\) that generates extra difficulties to obtain the local estimates (34) and (35).

3 Generalized Prolate Spheroidal Wave Functions: Computations and Analytic Extension

In the sequel, we restrict ourselves to the case \(\alpha =\beta > -1.\) In the first part of this section, we further improve the super-exponential decay rate of the GPSWFs expansion coefficients \((\beta _k^n)_k,\) that has been given in given in [19]. Then, we show that for sufficiently large values of n and up a certain order \(K_n,\) all the coefficients \(\beta _k^n,\, 0\le k\le K_n\) are positive. As a consequence of this positivity result and the previous fast decay of the \(\beta _k^n,\) we show that in the case where \(\alpha =\beta ,\) the expansion coefficients \((\beta _k^n)_k\) are essentially concentrated around \(k=n.\) In the second part of this section, we give the analytic extension of the GPSWFs, together with an explicit expression for the eigenvalues \(\mu _n^{(\alpha )}(c)\) as a ratio of two fast convergent series.

3.1 Computation and Analytic Extension of the GPSWFs

We first note that in the interesting special case where \(\alpha =\beta ,\) formula (18) is simplified in a significant manner. This is given by the following lemma.

Proposition 4

Let \(\alpha > -1,\) then we have

$$\begin{aligned} \int _{-1}^{1} e^{ixy} P_k^{(\alpha , \alpha )}(y) \omega _{\alpha }(y)\, dy= i^k \sqrt{\pi } \left( \frac{2}{x}\right) ^{\alpha +1/2} \frac{\Gamma (k+\alpha +1)}{\Gamma (k+1)}J_{k+\alpha +1/2}(x),\quad \! x\!\in \! \mathbb R. \end{aligned}$$
(43)

Here, \(J_{a}\) denotes the Bessel function of the first kind and order \(\alpha .\)

Proof

It is well known, see for example [1, p. 200], that if \(a > -1\) and \(z= - 2 i x,\,\, x\in \mathbb R,\) then we have,

$$\begin{aligned} _1F_1(a +1/2,2 a +1; -2ix)= \Gamma (a+1)\left( \frac{2}{x}\right) ^{a} e^{-ix} J_{a}(x). \end{aligned}$$
(44)

By combining (18) and the previous equality with \(a=k+\alpha +1/2,\) one gets

$$\begin{aligned}&\mathcal F_1^{\alpha }(P_k^{(\alpha , \alpha )})(x)=\int _{-1}^{1} e^{ixy} P_k^{(\alpha , \alpha )}(y) \omega _{\alpha }(y)\, dy \nonumber \\&\quad = \frac{(i x)^k2^{2k+3\alpha +3/2} }{x^{k+\alpha +1/2}} \frac{\Gamma (k+\alpha +3/2)}{\Gamma (k+1)} B(k+\alpha +1,k+\alpha +1) J_{k+\alpha +1/2}(x).\qquad \quad \end{aligned}$$
(45)

Moreover, by using the following identities of Beta and Gamma functions,

$$\begin{aligned} B(x,y)=\frac{\Gamma (x) \Gamma (y)}{\Gamma (x+y)},\quad \Gamma (x+1)=x\Gamma (x),\quad \Gamma (b)\Gamma (b+1/2)=\sqrt{\pi } \frac{\Gamma (2b)}{2^{2b-1}}, \end{aligned}$$

one gets

$$\begin{aligned}&\mathcal F_1^{\alpha } P_k^{(\alpha , \alpha )}(x)\\&\quad = i^k \frac{2^{2k+3\alpha +3/2}}{(x)^{\alpha +1/2}} (k+\alpha +1/2) \frac{\Gamma (k+\alpha +1)}{\Gamma (k+1)}\frac{\Gamma (k+\alpha +1)\Gamma (k+\alpha +1/2)}{\Gamma (2k+2\alpha +2)}J_{k+\alpha +1/2}(x)\\&\quad = i^k\frac{\Gamma (k+\alpha +1)}{\Gamma (k+1)}\frac{2^{2k+3\alpha +3/2}}{(cx)^{\alpha +1/2}}\frac{k+\alpha +1/2}{2k+2\alpha +1} \frac{\Gamma (k+\alpha +1)\Gamma (k+\alpha +1/2)}{\Gamma (2k+2\alpha +1)}J_{k+\alpha +1/2}(x)\\&\quad =i^k \sqrt{\pi } \left( \frac{2}{x}\right) ^{\alpha +1/2} \frac{\Gamma (k+\alpha +1)}{\Gamma (k+1)}J_{k+\alpha +1/2}( x),\quad x\in \mathbb R. \end{aligned}$$

\(\square \)

Remark 2

In the special case \(\alpha =0,\) the equality (43) is reduced to the well known classical finite Fourier transform of Legendre function, see for example [1, p. 343].

As a first consequence of the previous proposition, one gets a simple and straightforward proof of the following result that has been already given by Lemma 3.4 in [19] and with different kind of proof.

Corollary 1

Under the above notations, for any real numbers \(c>0\) and \(\alpha >-1,\) we have

$$\begin{aligned} \beta _k^n= & {} \int _{-1}^1 {\widetilde{P}}_k^{(\alpha ,\alpha )}(y) \psi _{n,c}^{(\alpha )}(y) \omega _{\alpha }(y)\, dy\nonumber \\= & {} \frac{2\sqrt{\pi } i^k}{\mu _n^{(\alpha )}(c) \sqrt{h_k}}\left( 1+(-1)^{n+k}\right) \int _0^1 \frac{J_{k+\alpha +\frac{1}{2}}(ct)}{(ct)^{\alpha +\frac{1}{2}}} \psi _{n,c}^{(\alpha )}(t) \omega _{\alpha }(t)\, dt. \end{aligned}$$
(46)

Proof

Just write

$$\begin{aligned} \beta _k^n= & {} \frac{1}{\mu _n^{(\alpha )}(c)}\int _{-1}^1 {\widetilde{P}}_k^{(\alpha ,\alpha )}(y) \left( \int _{-1}^1 e^{icty} \psi _{n,c}^{(\alpha )}(t) \omega _{\alpha }(t)\, dt \right) \omega _{\alpha }(y)\, dy\\= & {} \frac{\sqrt{\pi } i^k}{\mu _n^{(\alpha )}(c) \sqrt{h_k}} \int _{-1}^1 \frac{J_{k+\alpha +\frac{1}{2}}(ct)}{(ct)^{\alpha +\frac{1}{2}}} \psi _{n,c}^{(\alpha )}(t) \omega _{\alpha }(t)\, dt. \end{aligned}$$

To conclude, it suffices to write the previous integral as \(\int _{-1}^1 = \int _{0}^1 + \int _{-1}^0\) and use the facts that the function \(\psi _{n,c}^{(\alpha )}\) and \({\displaystyle t\mapsto \frac{J_{k+\alpha +\frac{1}{2}}(ct)}{(ct)^{\alpha +\frac{1}{2}}}}\) has the same parity as n and k,  respectively. \(\square \)

A decay rate of the expansion coefficients is given by the following proposition that improves the result given by Theorem 3.4 in [19].

Proposition 5

For given real numbers \(c>0,\, \, \alpha >- 1\) and integers \(k,n \in \mathbb N,\) let

$$\begin{aligned} {\displaystyle \beta _{k}^{n}=\int _{-1}^{1} {\widetilde{P}}_k^{(\alpha ,\alpha )}(x) \; \psi ^{(\alpha )}_{n,c}(x)\, \omega _{\alpha }(x) dx.} \end{aligned}$$

Then, we have

$$\begin{aligned} |\beta _k^n|\le \frac{C_{\alpha }}{|\mu _n^{(\alpha )}(c)|}\frac{1}{k^{1+\alpha /2} }\frac{1}{2^k} \left( \frac{ec}{2k+1}\right) ^k, \end{aligned}$$
(47)

where \({ C_{\alpha }=\frac{\pi ^{7/4} \sqrt{\Gamma (1+\alpha )}(3/2)^{3/4}(3/2+2\alpha )^{3/4+\alpha }}{2^{\alpha +1}e^{\alpha +5/4}}.}\)

Proof

By using the expression of \(\beta _k^n\) and by combining (2) and (18), one gets

$$\begin{aligned} \beta _k^n= & {} \frac{1}{\mu _n^{(\alpha )}(c)}\int _{-1}^{1}\int _{-1}^{1}{\widetilde{P}}^{(\alpha ,\beta )}_{k}(x) \left( \int _{-1}^1 e^{icxy} \psi _{n,c}(y) \omega _{\alpha }(y) \, dy\right) \omega _{\alpha }(x)\, dx\\= & {} \frac{1}{\mu _n(c)}\int _{-1}^{1}\left( \int _{-1}^{1} e^{icxy}{\widetilde{P}}^{(\alpha ,\beta )}_{k}(x) \omega _{\alpha }(x)\, dx\right) \psi _{n,c}^{(\alpha )}(y) \omega _{\alpha }(y)\, dy\\= & {} \frac{1}{\mu _n^{(\alpha )}(c)}\int _{-1}^{1} \frac{(icy)^ke^{icy}}{k! \sqrt{h_k}}2^{k+2\alpha +1}B(k+\alpha +1,k+\alpha +1)\cdot \\&\qquad \qquad \qquad _1F_1(k+\alpha +1,2k+2\alpha +2;-2icy)\psi _n(y)\, \omega _{\alpha }(y)\, dy. \end{aligned}$$

On the other hand, from the integral representation of Kummer’s function given by (19), one gets

$$\begin{aligned}&|_1F_1(k+\alpha +1,2k+2\alpha +2;-2icy)|\\&\quad =\,\frac{\Gamma (2k+2\alpha +2)}{\Gamma (k+\alpha +1)^2} \left| \int _0^1 e^{-2icyt}t^{k+\alpha }(1-t)^{k+\alpha }dt\right| \\&\quad \le \, \frac{1}{B(k+\alpha +1,k+\alpha +1)}\left| \int _0^1 e^{-2icyt}t^{k+\alpha }(1-t)^{k+\alpha }dt\right| \\&\quad \le \,\frac{B(k+\alpha +1,k+\alpha +1)}{B(k+\alpha +1,k+\alpha +1)}=1. \end{aligned}$$

Consequently, we have

$$\begin{aligned} |\beta _k^n|\le & {} \frac{B(k+\alpha +1,k+\alpha +1)}{|\mu _n^{(\alpha )}(c)|}\frac{c^k 2^{k+2\alpha +1}}{k! \sqrt{h_k}} \left( \int _{-1}^1 (\psi _{n,c}^{(\alpha )})^2(y) \omega _{\alpha }(y)\, dy \right) ^{1/2}\nonumber \\&\times \left( \int _{-1}^1 y^{2k}\omega _{\alpha }(y)\, dy\right) ^{1/2} \nonumber \\\le & {} \frac{B(k+\alpha +1,k+\alpha +1)}{|\mu _n^{(\alpha )}(c)|}\frac{c^k 2^{k+3/2(\alpha +\alpha +1)}}{k! \sqrt{h_k}} \sqrt{I_{2k}^{\alpha ,\alpha }}. \end{aligned}$$
(48)

Note that from (10), we have

$$\begin{aligned} \frac{c^k}{k!}=\frac{c^k}{\Gamma (k+1)}\le \frac{1}{\sqrt{2}}\frac{1}{\sqrt{2k+1}} \left( \frac{ec}{2k+1}\right) ^k. \end{aligned}$$
(49)

In a similar manner, we get the following upper bound and lower bound of the quantity \(B(k+\alpha +1,k+\alpha +1)\) and the normalization constant \(h_k,\) given as follows.

$$\begin{aligned} B(k+\alpha +1,k+\alpha +1)= & {} \frac{\Gamma (k+\alpha +1) ^2}{\Gamma (2k+2\alpha +2)} \le \frac{\sqrt{2}\pi }{2^{2k+2\alpha +1}}\frac{(2k\!+\!2\alpha \!+\!1)^{2k+2\alpha +1}}{(2k\!+\!2\alpha \!+\!3/2)^{2k+2\alpha +3/2}} \nonumber \\\le & {} \frac{\sqrt{2}\pi }{2^{2k+2\alpha +1}} \frac{1}{\sqrt{2k+2\alpha +3/2}} \end{aligned}$$
(50)

Also, by using (10), the decay of the function \(\varphi ,\) given by (13) as well some straightforward computations, one gets

$$\begin{aligned}&\frac{e}{\pi } \frac{(2e)^{2\alpha +1}}{(3/2)^{3/2}(3/2+2\alpha )^{3/2+2\alpha }}\frac{1}{2k+2\alpha +1}\le h_k \nonumber \\&\quad \le \frac{\pi }{e}\left( \frac{2}{e}\right) ^{2\alpha +1}\frac{(3/2)^{3/2}(3/2+2\alpha )^{3/2+2\alpha }}{2k+2\alpha +1}. \end{aligned}$$
(51)

Finally, by combining (15), (48), (49)–(51), one gets the desired result (47). \(\square \)

Remark 3

By using our notation, the decay rate of the \((\beta _k^n)_k,\) given by Theorem 3.4 of [19] can be written as \({\displaystyle \frac{C^{''}_{\alpha }}{|\mu _n^{(\alpha )}(c)|}\frac{1}{k^{1+\alpha /2} } \left( \frac{ec}{2k+1}\right) ^k,}\) for some constant \(C^{''}_{\alpha }.\) The previous proposition ensures that this decay is further improved by a factor of \(1/2^k.\)

The following theorem provides us with a second decay rate of the \((\beta _k^n)_{k\ge 0},\) valid for sufficiently large values of n and the values of \(0\le k < n\) not too close to n. We should mention that the techniques of the proof of this theorem, given in “Appendix: Proof of Theorem 1”, are inspired from those developed for the special case \(\alpha =0\) and given in a joint work of one of us [4].

Theorem 1

Let \(c>0,\) be a fixed positive real number. Then, for all positive integers n, k such that \(q=c^2/\chi _n \le 1\) and \(k(k+2\alpha +1)+C_{\alpha }\, c^2\le \chi _n(c)\), we have

$$\begin{aligned} |\beta _0^n|\le \sqrt{\frac{\Gamma (\alpha +3/2)}{\sqrt{\pi }\Gamma (\alpha +1)}} \sqrt{1+\alpha } |\mu _n^{(\alpha )}(c)|\quad \text{ and } \quad |\beta _k^n|\le C'_{\alpha } \Big ( \frac{2}{q}\Big )^k|\mu _n^{(\alpha )}(c)|. \end{aligned}$$
(52)

Here, \({\displaystyle C'_{\alpha } =\frac{2^{\alpha }(3/2)^{3/4}(3/2+2\alpha )^{3/4+\alpha }}{e^{2\alpha +3/2}}\sqrt{1+\alpha }}\) and \(C_{\alpha }= 2 M_{\alpha }+N_{\alpha }\) with

$$\begin{aligned} M_{\alpha }= & {} \max \Big ({1/4,\sqrt{\frac{2(2\alpha +2)}{(2\alpha +5)(2\alpha +3)^2}}}\Big ),\nonumber \\ N_{\alpha }= & {} \max \Big (\frac{3}{2\alpha +5}, \frac{1}{2}+\frac{|4\alpha ^2-1|}{(2\alpha +3)(2\alpha +7)}\Big ). \end{aligned}$$
(53)

3.2 Analytic Extension of the GPSWFs

In this paragraph, we give explicit formulae for the analytic extension of the GPSWFs to the whole real line, as well for computing the eigenvalues \(\mu _n^{(\alpha )}(c)\) associated with the weighted finite Fourier transform \(\mathcal F_c^{\alpha }.\) We first note that due to Eq. (2), the GPSWFs have analytic extension to \(\mathbb R.\) In fact, it is well known, see [17, p. 168], that if \(\alpha > -1,\) then

$$\begin{aligned} {\displaystyle \sup _{y\in [-1,1]} |{\widetilde{P}}^{(\alpha ,\beta )}_k(y)|= \le \frac{1}{\sqrt{h_k} B(k+1,\alpha +1)}\le M_{\alpha } k^{\alpha +1/2},} \end{aligned}$$

for some constant \(M_{\alpha }.\) Moreover, by using the super-exponential decay rate of the expansion coefficients \((\beta _k^n)_k\) combined with (2), (20) and (43), one gets

$$\begin{aligned} \psi _{n,c}^{(\alpha )}(x)= & {} \frac{\sqrt{\pi } 2^{\alpha +1/2}}{\mu _n^{(\alpha )}(c)} \sum _{k\ge 0} i^k \beta _k^n\, \frac{\Gamma (k+\alpha +1)}{\sqrt{h_k} k!} \frac{J_{k+\alpha +1/2}(c x)}{(cx)^{\alpha +1/2}},\quad \forall \, x\ne 0. \end{aligned}$$

Moreover, from the parity of the \(\psi _{n,c}^{(\alpha )},\) it is easy to see that \(\mu _n^{(\alpha )}(c)= i^n |\mu _n^{(\alpha )}(c)|,\) \(n\ge 0.\) Hence, by using the fact that the previous expansion coincides with the expansion (20) at \(x=1,\) one obtains the following analytic extension of the GPSWFs as well as an explicit formula for their associated eigenvalues \(\mu _n^{(\alpha )}(c),\)

$$\begin{aligned} \psi _{n,c}^{(\alpha )}(x)=\frac{\sqrt{\pi } 2^{\alpha +1/2}}{|\mu _n^{(\alpha )}(c)|} \sum _{k\ge 0} i^{k-n} \beta _k^n\, \frac{\Gamma (k+\alpha +1)}{\sqrt{h_k} k!} \frac{J_{k+\alpha +1/2}(c x)}{(cx)^{\alpha +1/2}},\quad \forall \, x\ne 0 \end{aligned}$$
(54)

with

$$\begin{aligned} \mu _n^{(\alpha )}(c)= i^n \sqrt{\pi }\left( \frac{2}{c}\right) ^{\alpha +1/2}\frac{\sum _{k\ge 0} i^{k-n} \beta _k^n\, \frac{\Gamma (k+\alpha +1)}{\sqrt{h_k} k!} {J_{k+\alpha +1/2}(c)}}{\sum _{k\ge 0} \frac{\beta _k^n}{\sqrt{h_k}\, B(k+\alpha ,k) }},\quad n\ge 0. \end{aligned}$$
(55)

We should mention that due to the facts that the coefficients \((\beta _k^n)_k\) are concentrated around \(k=n\) and decay super-exponentially, the previous formula is accurate and practical for computing the \(\mu _n^{(\alpha )}(c).\) Also, note that in [19], the authors have given some properties of the eigenvalues \(\mu _n^{(\alpha )}(c)\) (denoted by \(\lambda _n^{(\alpha )}(c)\) in [19]). In particular, by considering the operator \(\mathcal F_c^{\alpha }\) as a Hilbert–Schmidt operator acting on \(L^2(I, \omega _{\alpha }),\) it has been shown that

$$\begin{aligned} \sum _{n\ge 0} |\mu _n^{(\alpha )}(c)|^2=\Vert \mathcal F_c^{\alpha }\Vert _{HS}^2 = \left( \int _{-1}^1 \omega _{\alpha }(x)\, dx \right) ^2= \frac{\pi \Gamma ^2(1+\alpha )}{\Gamma ^2(\alpha +3/2)}. \end{aligned}$$

Here, \(\Vert \cdot \Vert _{HS}\) denotes the Hilbert–Schmidt norm. More importantly, in [19], the authors have noted that the \(\mu _n^{(\alpha )}(c)\) has an asymptotic super-exponential decay rate given by

$$\begin{aligned} |\mu _n^{(\alpha )}(c)| \approx \frac{e^{\alpha }}{4^{\alpha }}\sqrt{\frac{\pi e}{2n+2\alpha +3}}\left( \frac{ec}{4n+4\alpha +2}\right) ^n,\quad n \gg 1. \end{aligned}$$
(56)

4 GPSWFs as Solutions of an Energy Maximization Problem and Quality of Approximation

In the first part of this section, we show that in the case where \(\alpha \ge 0,\) the GPSWFs are solutions of an energy maximization problem over a generalized Paley–Wiener space and with respect to certain weighted norms. As important consequences of this characterization, we get a monotonicity result the sequence \({\displaystyle \lambda _n^{(\alpha )}(c)=\frac{c}{2\pi } |\mu _n^{(\alpha )}(c)|^2}\) with respect to the parameter \(\alpha .\) Moreover, by using the results of [6], one gets a better understanding of the behaviour and the super-exponential decay rate of the \((\lambda _n^{(\alpha )}(c))_{n\ge 0}.\) In the second part, we show that the GPSWFs are well adapted for the approximation of functions from the classical Paley–Wiener space \(B_c\) as well as of almost c-band-limited functions.

4.1 GPSWFs as Solutions of an Energy Maximization Problem and Consequences

We recall that the starting point of the theory of the classical PSWFs (corresponding to the GPSWFs with \(\alpha =0)\) is the solution of the following energy maximization problem, see [16]

$$\begin{aligned} f = \arg \max _{f \in B_c} \frac{\Vert f\Vert _{L^2(I)}^2}{\Vert f\Vert _{L^2(\mathbb R)}^2}=\arg \max _{f \in B_c} 2\pi \frac{\Vert f\Vert _{L^2(I)}^2}{\Vert \widehat{f}\Vert _{L^2(\mathbb R)}^2}, \end{aligned}$$
(57)

where \(B_c\) is the Paley–Wiener of c-band-limited functions given by

$$\begin{aligned} B_c=\{ f\in L^2(\mathbb R),\,\, \text{ Support } \widehat{f}\subseteq [-c,c]\}. \end{aligned}$$
(58)

More precisely, it has been shown in [16] that from \(B_c,\) \(\psi _{0,c}^{(0)} \) is the most concentrated function in \(I=[-1,1]\) with the largest energy concentration ratio \(0<\lambda _0^{(0)}(c)<1.\) Moreover, for any integer \(n\ge 1,\) \(\psi _{n,c}^{(0)} \) is the most concentrated function from \(B_c\) which is orthogonal to the previous \(\psi _{i,c}^{(0)},\, 0\le i\le n-1.\) The orthogonality is with respect to the two usual inner products of \(L^2(I)\) and \(L^2(\mathbb R).\) As it will be seen, the extension of the previous characterization of the PSWFs to the more general case of the GPSWFs provides us with a better understanding of the behaviour and the super-exponential decay rate of the eigenvalues \((\lambda _n^{(\alpha )}(c))_{n\ge 0}.\) For \(\alpha > 0,\) we define the restricted Paley–Wiener space of weighted c-band-limited functions by

$$\begin{aligned} B_c^{(\alpha )}=\{ f\in L^2(\mathbb R),\,\, \text{ Support } \widehat{f}\subseteq [-c,c],\, \, \widehat{f}\in L^2\big ((-c,c), \omega _{- \alpha }(\frac{\cdot }{c})\big )\}. \end{aligned}$$
(59)

Here, \(L^2\big ((-c,c), \omega _{- \alpha }(\frac{\cdot }{c})\big )\) is the weighted \(L^2(-c,c)\)-space with norm given by

$$\begin{aligned} \Vert f\Vert ^2_{L^2\big ((-c,c), \omega _{- \alpha }(\frac{\cdot }{c})\big )}= \int _{-c}^c |f(t)|^2 \omega _{-\alpha }\left( \frac{t}{c}\right) \, dt. \end{aligned}$$

Note that when \(\alpha =0,\) the restricted Paley–Wiener space \(B_c^{(0)}\) is reduced to the usual space \(B_c.\) Also, since for any \(\alpha \ge \alpha ',\) \(\widehat{f}\in L^2\big ((-c,c), \omega _{- \alpha '}(\frac{\cdot }{c})\big )\) implies that \(\widehat{f}\in L^2\big ((-c,c), \omega _{- \alpha }(\frac{\cdot }{c})\big )\) then one gets

$$\begin{aligned} B_c^{(\alpha )} \subseteq B_c^{(\alpha ')},\qquad \forall \, \alpha \ge \alpha ' \ge 0. \end{aligned}$$
(60)

Remark 4

We give an example of a function from a restricted Paley–Wiener space. If \(c>1,\) then it has been shown in [10] that the function

$$\begin{aligned}{\displaystyle \eta (x)= \frac{\sin (c x-x/2)}{x^4}\left( 2\sin \left( \frac{x}{2}\right) -x \cos \left( \frac{x}{2}\right) \right) ,\,\, x\in \mathbb R}\end{aligned}$$

is a c-band-limited function. Moreover, its Fourier transform is an even function given by

$$\begin{aligned} \widehat{\eta }(-\xi )=\widehat{\eta }(\xi )=\left\{ \begin{array}{ll} 1 &{} \text{ if } \xi \in [0,c-1]\\ f(\xi +2-c) &{} \text{ if } \xi \in [c-1,c]\\ 0 &{} \text{ if } \xi \ge c. \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} f(-x)=f(x)=\left\{ \begin{array}{ll} 1 &{} \text{ if } x \in [0,1]\\ -4+12 x - 9 x^2+2 x^3 &{} \text{ if } x \in [1,2]\\ 0 &{} \text{ if } x \ge 2. \end{array} \right. \end{aligned}$$

Since for \(\xi \in [c-1,c],\) \(\widehat{\eta }(\xi )= (2\xi -2c+3) (\xi -c)^2,\) then it is easy to see that \(\eta \) belongs to the restricted Paley–Wiener space \(B_c^{\alpha }\) for any \(0\le \alpha <5.\)

The generalized maximization problem is formulated as follows. We note that from (43) with \(k=0,\) one gets the finite Fourier transform of the weight function \(\omega _{\alpha },\) given by

$$\begin{aligned} \int _{-1}^1 e^{ixy} \omega _{\alpha }(y)\, dy = \sqrt{\pi } 2^{\alpha +1/2}\Gamma (\alpha +1) \frac{J_{\alpha +1/2}(x)}{x^{\alpha +1/2}}= \mathcal K_{\alpha }(x),\quad x\in \mathbb R. \end{aligned}$$
(61)

Next, if \(f\in B_c^{(\alpha )},\) then \(\widehat{f} (x)= g(x) \omega _{\alpha }\left( \frac{x}{c}\right) \) with some \({\displaystyle g\in L^2\big ((-c,c), \omega _{ \alpha }(\frac{\cdot }{c})\big ).}\) By using the inverse Fourier transform, one gets

$$\begin{aligned} \frac{\Vert f\Vert ^2_{L^2(I,\omega _{\alpha })}}{\Vert \widehat{f}\Vert ^2_{L^2(\omega _{-\alpha }(\frac{\cdot }{c}))}}= & {} \frac{1}{\Vert \widehat{f}\Vert ^2_{L^2(\omega _{-\alpha }(\frac{\cdot }{c}))}} \int _{-1}^1 f(t)\cdot \overline{f(t)} \omega _{\alpha }(t)\, dt \nonumber \\= & {} \frac{1}{\Vert \widehat{f}\Vert ^2_{L^2(\omega _{-\alpha }(\frac{\cdot }{c}))}} \frac{1}{4\pi ^2}\int _{-1}^1 \int _{-c}^c e^{it y}\widehat{f}(y) \, dy\cdot \int _{-c}^c e^{-it x} \overline{\widehat{f}(x)} \, dx \omega _{\alpha }(t)\, dt \nonumber \\= & {} \frac{1}{\Vert \widehat{f}\Vert ^2_{L^2(\omega _{-\alpha }(\frac{\cdot }{c}))}} \frac{1}{4\pi ^2}\int _{-c}^c \int _{-c}^c \left( \int _{-1}^1 e^{it(y-x)} \omega _{\alpha }(t)\, dt\right) \widehat{f}(y) \, dy\nonumber \\&\cdot \int _{-c}^c e^{-it x} \overline{\widehat{f}(x)} \, dx \omega _{\alpha }(t)\, dt \nonumber \\= & {} \frac{1}{\Vert \widehat{f}\Vert ^2_{L^2(\omega _{-\alpha }(\frac{\cdot }{c}))}} \frac{1}{4\pi ^2} \int _{-c}^c \int _{-c}^c \mathcal K_{\alpha }(y-x) g(y) \omega _{\alpha }\left( \frac{y}{c}\right) \, dy \cdot \overline{g(x)} \omega _{\alpha }\left( \frac{x}{c}\right) \, dx \nonumber \\= & {} \frac{1}{4\pi ^2} \frac{ {\displaystyle \int _{-c}^c \left[ \int _{-c}^c \mathcal K_{\alpha }(y-x) g(y) \omega _{\alpha }\left( \frac{y}{c}\right) \, dy \right] \cdot \overline{g(x)} \omega _{\alpha }\left( \frac{x}{c}\right) \, dx}}{{\displaystyle \int _{-c}^c g(x) \overline{g(x)} \omega _{\alpha }\left( \frac{x}{c}\right) \, dx}}. \end{aligned}$$
(62)

Here, \(\mathcal K_{\alpha }\) is as given by (61). Note that since the compact integral operator \(\mathcal Q^{\alpha }\) defined on \({\displaystyle L^2(\omega _{\alpha }(\frac{\cdot }{c}))}\) by

$$\begin{aligned} \mathcal Q^{\alpha } g(x) = \frac{1}{4\pi ^2} \int _{-c}^c \mathcal K_{\alpha }(y-x) g(y) \omega _{\alpha }\left( \frac{y}{c}\right) \, dy \end{aligned}$$

has a symmetric kernel, then it is well known that in this case, \({\displaystyle \max _{f\in B^{\alpha }_c} 2 \pi \frac{\Vert f\Vert ^2_{L^2_{\omega _{\alpha }}(I)}}{\Vert \widehat{f}\Vert ^2_{L^2(\omega _{-\alpha }(\frac{\cdot }{c}))}} }\) is attained at the eigenfunction of \(2\pi \mathcal Q^{\alpha },\) associated with the largest eigenvalue. Hence, by using a trivial change of variable and functions, the generalized energy maximization problem is reduced to the solution of the following eigenproblem

$$\begin{aligned} \mathcal Q_c^{(\alpha )} G (x) = \int _{-1}^1 \frac{c}{2 \pi }\mathcal K_{\alpha }(c(x-y)) G(y) \omega _{\alpha }(y) \, dy = \lambda G(x),\quad x\in [-1,1]. \end{aligned}$$
(63)

On the other hand, it has been shown in [19] that the kernel \(\mathcal K_{\alpha }(c(x-y))\) is nothing but the kernel of the composition operators \(\mathcal F_c^{{\alpha }*} \circ \mathcal F_c^{\alpha }.\) Hence, the operators \(\mathcal Q_c^{\alpha }\) and \(\mathcal F_c^{\alpha }\) have the same eigenfunctions, given by the GPSWFs, \(\psi _{n,c}^{(\alpha )},\) and associated to the respective eigenvalues \(\lambda _n^{(\alpha )},\) \(\mu _n^{(\alpha )}(c).\) These eigenvalues are related to each others by the following rule

$$\begin{aligned} \lambda _n^{(\alpha )}(c)= \frac{c}{2\pi } |\mu _n^{(\alpha )}(c)|^2,\quad n\ge 0. \end{aligned}$$
(64)

Since from (60), if \(0\le \alpha '\le \alpha ,\) then we have \(B_c^{(\alpha )} \subseteq B_c^{(\alpha ')}\) and since for \(f\in B_c^{(\alpha )},\) then we have

$$\begin{aligned} \Vert f\Vert ^2_{L^2(I,\omega _{\alpha })}\le \Vert f\Vert ^2_{L^2(I,\omega _{\alpha '})},\quad \Vert \widehat{f}\Vert ^2_{L^2(\omega _{- \alpha }(\frac{\cdot }{c}))} \ge \Vert \widehat{f}\Vert ^2_{L^2(\omega _{- \alpha '}(\frac{\cdot }{c}))}. \end{aligned}$$

Hence, we have

$$\begin{aligned} \lambda _0^{(\alpha )}(c)= & {} \sup _{f\in B_c^{(\alpha )}} \frac{\Vert f\Vert ^2_{L^2(I,\omega _{\alpha })}}{\Vert \widehat{f}\Vert ^2_{L^2(\omega _{- \alpha }(\frac{\cdot }{c}))}} \le \sup _{f\in B_c^{(\alpha )}} \frac{\Vert f\Vert ^2_{L^2(I,\omega _{\alpha '})}}{\Vert \widehat{f}\Vert ^2_{L^2(\omega _{- \alpha '}(\frac{\cdot }{c}))}}\le \sup _{f\in B_c^{(\alpha ')}} \frac{\Vert f\Vert ^2_{L^2(I,\omega _{\alpha '})}}{\Vert \widehat{f}\Vert ^2_{L^2(\omega _{- \alpha '}(\frac{\cdot }{c}))}}\nonumber \\= & {} \lambda _0^{(\alpha ')}(c). \end{aligned}$$

More generally, for an integer \(n\ge 1,\) let \(\psi _{0,c}^{(\alpha ')},\ldots ,\psi _{n-1,c}^{(\alpha ')}\) be the first most concentrated GPSWFs, associated with the respective eigenvalues \(\lambda _0^{(\alpha ')}(c)>\lambda _1^{(\alpha ')}(c)>\cdots >\lambda _{n-1}^{(\alpha ')}(c).\) Note that the previous strict inequalities are due to the fact that these eigenvalues are simple, see [19]. By combining the previous formulation of the energy maximization problem and the well known Min–Max principle for eigenvalues of compact operator, one concludes that if \(S_n,\, H_n\) stand for an arbitrary subspace of dimension n of \(B_c^{(\alpha )},\) and \(B_c^{(\alpha ')},\) respectively, then we have

$$\begin{aligned} \lambda _n^{(\alpha )}(c)= & {} \max _{S_n\subset B_c^{(\alpha )}} \min _{\psi \in S_n} \frac{\Vert \psi \Vert ^2_{L^2(I,\omega _{\alpha })}}{\Vert \widehat{\psi }\Vert ^2_{L^2(\omega _{- \alpha }(\frac{\cdot }{c}))}} \le \max _{S_n\subset B_c^{(\alpha ')}} \min _{\psi \in S_n} \frac{\Vert \psi \Vert ^2_{L^2(I, \omega _{\alpha '}))}}{\Vert \widehat{\psi }\Vert ^2_{L^2(\omega _{- \alpha '}(\frac{\cdot }{c}))}}\\\le & {} \max _{H_n\subset B_c^{(\alpha ')}} \min _{\psi \in H_n} \frac{\Vert \psi \Vert ^2_{L^2(I,\omega _{\alpha '})}}{\Vert \widehat{\psi }\Vert ^2_{L^2(\omega _{- \alpha '}(\frac{\cdot }{c}))}} = \lambda _n^{(\alpha ')}(c). \end{aligned}$$

We have just proved the following theorem giving the monotony of the eigenvalues \(\lambda _n^{(\alpha )}(c)\) with respect to the parameter \(\alpha .\)

Theorem 2

For a given real number \(c>0,\) and an integer \(n\ge 0,\) we have

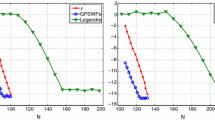
$$\begin{aligned} \lambda _n^{(\alpha )}(c) \le \lambda _n^{(\alpha ')}(c),\quad \forall \, \alpha \ge \alpha ' \ge 0. \end{aligned}$$
(65)

It is important to mention that a super-exponential decay rate of the sequence \((\lambda _n^{(\alpha )}(c))_n\) as well as an estimate of the location of the plunge region, where the fast decay starts are important consequences of the previous proposition. These two results follow directly from the results given in [6], where an explicit formula for estimating the \(\lambda _n^{(0)}(c)\) has been developed. This explicit formula enjoys with a surprising accuracy as soon as n reaches or goes beyond the plunge region around the value \(n_c = \frac{2c}{\pi }.\) Also, it proves that the exact asymptotic super-exponential decay rate is given by the quantity \({\displaystyle e^{-2n \log \left( \frac{4 n}{ec}\right) }.}\) From the previous theorem with \(\alpha '=0,\) one concludes that for any \(\alpha >0,\) the sequence \((\lambda _n^{(\alpha )}(c))_n\) has a super-exponential decay rate, bounded above by the decay rate of \((\lambda _n^{(0)}(c))_n.\) Moreover, the fast decay of these \((\lambda _n^{(\alpha )}(c))_n\) starts around \(n_c = \frac{2c}{\pi }.\) In the numerical results section, we give different tests that illustrate these precise behaviours of \((\lambda _n^{(\alpha )}(c))_n.\)

4.2 Approximation of Band-Limited Functions by the GPSWFs

In this paragraph, we first show that when restricted to the interval I,  the GPSWFs \(\psi _{n,c}^{(\alpha )}\) are well adapted for the approximation of functions from the usual Paley–Wiener space \(B_c.\) As a result, we check that the GPSWFs are also well adapted for the approximation of almost band-limited functions. This type of functions have been defined in [11] as follows.

Definition 1

Let \(\Omega =[-c, c],\) then a function f is said to be \(\epsilon _{\Omega }\)-band-limited in \(\Omega \) if

$$\begin{aligned} \frac{1}{2\pi }\int _{|\xi |> c} |\widehat{f}(\xi )|^2\, d\xi \le \epsilon _{\Omega }^2. \end{aligned}$$

Proposition 6

Let \(c>0,\,\, \alpha \ge 0\) be two real numbers and let \(f\in B_c.\) For any positive integer \(N> \frac{2c}{\pi },\) let

$$\begin{aligned} S_N(f)(x) = \sum _{k=0}^{N} <f,\psi _{k,c}^{(\alpha )}>_{L^2(I,\omega _{\alpha })} \psi _{k,c}^{(\alpha )}(x). \end{aligned}$$

Then, we have

$$\begin{aligned} \left( \int _{-1}^{1}|f(t)- S_N f(t)|^2 \omega _{\alpha }(t) dt\right) ^{1/2}\le C_1 \sqrt{\lambda _N^{(\alpha )}(c)}\, (\chi _N(c))^{(1+\alpha )/2}\, \Vert f\Vert _{L^2(\mathbb R)}, \end{aligned}$$
(66)

and

$$\begin{aligned} \sup _{x\in [-1,1]}|f(x)- S_N f(x)|\le C_1 \sqrt{\lambda _N^{(\alpha )}(c)}\, (\chi _N(c))^{1+\alpha /2}\, \Vert f\Vert _{L^2(\mathbb R)}. \end{aligned}$$
(67)

for some uniform constant \(C_1\) depending only on \(\alpha .\)

Proof

We first note that since \(\mathcal B=\{\psi _{n,c}^{(\alpha )},\,\, n\ge 0\}\) is an orthonormal basis of \(L^2(I,\omega _{\alpha }),\) and since \(\chi _I f\in L^2(I),\) where \(\chi _I\) denotes the characteristic function, then we have

$$\begin{aligned} f(x)= \sum _{k\ge 0} <f,\psi _{k,c}^{(\alpha )}>_{L^2(I,\omega _{\alpha })} \psi _{k,c}^{(\alpha )}(x),\quad a.e.\,\, x\in I. \end{aligned}$$
(68)

On the other hand, since \(f\in B_c,\) then \(f\in \mathcal C^{\infty }(\mathbb R)\cap L^2(\mathbb R).\) In particular, from the inverse Fourier transform, and by using the fact that \(f\in B_c,\) we have

$$\begin{aligned} f(x)= & {} \frac{1}{2\pi } \int _{\mathbb R} e^{i x y}\widehat{f}(y) dy=\frac{1}{2\pi } \int _{-c}^c e^{i x y}\widehat{f}(y) dy=\frac{c}{2\pi }\int _{-1}^1 e^{ictx} \widehat{f}(ct) \, dt,\nonumber \\&\quad \forall \, x\in [-1,1]. \end{aligned}$$
(69)

Consequently, for any integer \(k\ge 0,\) we have

$$\begin{aligned} |\langle f,\psi _{k,c}^{(\alpha )} \rangle _{L^2(I,\omega _{\alpha })}|= & {} \left| \int _{-1}^1 f(x) \psi _{k,c}^{(\alpha )}(x) \omega _{\alpha }(x)\, dx\right| \nonumber \\= & {} \frac{c}{2\pi }\left| \int _{-1}^1\left( \int _{-1}^1 e^{ictx} \widehat{f}(ct) \, dt\right) \psi _{n,c}^{(\alpha )}(x) \omega _{\alpha }(x)\, dx\right| \nonumber \\= & {} \frac{c}{2\pi } \left| \int _{-1}^1 \widehat{f}(ct) \left( \int _{-1}^1 e^{ictx} \psi _{k,c}^{(\alpha )}(x) \omega _{\alpha }(x)\, dx\right) \, dt\right| \nonumber \\= & {} \frac{c}{2\pi }\, |\mu _k^{(\alpha )}(c)| \left| \int _{-1}^1 \widehat{f}(ct) \psi _{n,c}^{(\alpha )}(t)\, dt\right| \nonumber \\\le & {} |\mu _k^{(\alpha )}(c)| \frac{c}{2\pi } \sup _{t\in [-1,1]}|\psi _{n,c}^{(\alpha )}(t)| \left( \int _{-1}^1 |\widehat{f}(ct)|^2\, dt\right) ^{1/2} \nonumber \\\le & {} \frac{C_{\alpha }}{\sqrt{2}} \sqrt{\frac{c}{2\pi }} |\mu _k^{(\alpha )}(c)| (\chi _k(c))^{(1+\alpha )/2} \Vert f\Vert _{L^2(\mathbb R)}\nonumber \\= & {} \frac{C_{\alpha }}{\sqrt{2}} \sqrt{\lambda _N^{(\alpha )}(c)}\, (\chi _N(c))^{(1+\alpha )/2}\, \Vert f\Vert _{L^2(\mathbb R)}. \end{aligned}$$
(70)

Here, \(C_{\alpha }\) is as given by (34). The last inequality follows from Plancherel formula and the bound over I of \(|\psi _{n,c}^{(\alpha )}(t)|,\) we have given in (35). On the other hand, by using the previous inequality, together with the super-exponential decay rate of the \(|\mu _n^{(\alpha )}(c)|,\) given by (56), as well as the Parseval’s equality

$$\begin{aligned} {\displaystyle \Vert f-S_Nf\Vert ^2_{L^2(I,\omega _{\alpha })}=\sum _{k\ge N+1}|\langle f,\psi _{k,c}^{(\alpha )}\rangle _{L^2(I,\omega _{\alpha })}|^2}, \end{aligned}$$

one can easily get (66). Finally, to get (67), it suffices to combine the previous inequality, (56) as well as the upper bound of \(|\psi _{n,c}^{(\alpha )}(t)|.\) \(\square \)

As a consequence of the previous result, we have the following corollary concerning the quality of approximation of almost band-limited functions by the GPSWFs.

Corollary 2

Let \(f\in L^2(\mathbb R)\) be an \(\epsilon _{\Omega }\)-band-limited in \(\Omega =[-c, +c]\) and let \(\alpha \ge 0,\) then for any positive integer \(N \ge \frac{2c}{\pi },\) we have

$$\begin{aligned} \left( \int _{-1}^{1}|f(t)- S_N f(t)|^2 \omega _{\alpha }(t) dt \right) ^{1/2}\le \epsilon _{\Omega }+C_1 \sqrt{\lambda _N^{(\alpha )}(c)}\, (\chi _N(c))^{(1+\alpha )/2}\, \Vert f\Vert _{L^2(\mathbb R)} \end{aligned}$$
(71)

where the constant \(C_1\) depends only on \(\alpha .\)

Proof

It suffices to consider the band-limiting operator \(\pi _{\Omega }\) defined by:

$$\begin{aligned} \pi _{\Omega }(f)(x)=\frac{1}{2\pi }\int _{\Omega } e^{i x \omega }\widehat{f}(\omega )\, d\omega . \end{aligned}$$

Since \(\pi _{\Omega } f \in B_c,\) \(\Vert (f-\pi _{\Omega } f)- S_N(f-\pi _{\Omega } f)\Vert _{L^2(I)}\le \Vert f-\pi _{\Omega }\Vert _{L^2(\mathbb R)}\le \epsilon _{\Omega }\) and \(\Vert \pi _{\Omega } f \Vert _{L^2(\mathbb R)}\le \Vert f \Vert _{L^2(\mathbb R)},\) then by applying the result of the previous proposition to \(\pi _{\Omega } f,\) one gets

$$\begin{aligned} \Vert f- S_N(f)\Vert _{L^2(I,\omega _{\alpha })}\le & {} \Vert (f-\pi _{\Omega } f)- S_N (f-\pi _{\Omega } f)\Vert _{L^2(I,\omega _{\alpha })}\\&+ \Vert \pi _{\Omega } f- S_N (\pi _{\Omega } f)\Vert _{L^2_{\omega _{\alpha }(I)}} \\\le & {} \epsilon _{\Omega }+ C_1 \sqrt{\lambda _N^{(\alpha )}(c)}\, (\chi _N(c))^{(1+\alpha )/2}\, \Vert \pi _{\Omega } f\Vert _{L^2(\mathbb R)} \\\le & {} \epsilon _{\Omega }+ C_1 \sqrt{\lambda _N^{(\alpha )}(c)}\, (\chi _N(c))^{(1+\alpha )/2} \, \Vert f\Vert _{L^2(\mathbb R)}. \end{aligned}$$

5 Numerical Results

In this section, we give three examples that illustrate the different results of this work. The first example deals with the computation and the analytic extension of the GPSWFs.

Example 1

In this example, we give different numerical tests that illustrate the construction scheme of the GPSWFs \(\psi _{n,c}^{(\alpha )}.\) For this purpose, we have considered the values \(\alpha =0.5\) and \(c=5\pi .\) Then, we have computed the different Jacobi expansion coefficients via the scheme of Sect. 2, by solving the eigensystem (21), truncated to the order \(N=90.\) Figure 1a show the graphs of the \(\psi _{n,c}^{(\alpha )}\) for the different values of \(n=0, 5, 15.\) Note that these graphs illustrate some of the provided properties of the \(\psi _{n,c}^{(\alpha )}.\) Also, we have used formula (68) and computed the analytic extensions of the previous GPSWFs. The graphs of these extensions are given by Fig. 1b, c. Note that as predicted by the characterisation of the GPSWFs as solutions of the energy maximization problem, for the values of \(n\le 2c\pi ,\) the \(\psi _{n,c}^{(\alpha )}\) are concentrated on I,  whereas for \(n> 2c/\pi ,\) they are concentrated on \(\mathbb R\setminus I.\)

Fig. 1
figure 1

a Graphs of \(\psi _{n,c}^{\alpha }\) with \(c=5\pi \) and \(\alpha =0.5,\) b, c graphs of some analytic extensions of the \(\psi _{n,c}^{\alpha }\)

Full size image

Example 2

In this example, we illustrate the important result given by Theorem 2, concerning the monotonicity with respect to the parameter \(\alpha \) of the sequence \({\displaystyle \lambda _n^{(\alpha )}(c)=\frac{c}{2\pi } |\mu _n^{(\alpha )}(c)|^2.}\) For this purpose, we have used formula (55) and computed highly accurate values of \(\mu _n^{(\alpha )}(c)\) and consequently of \(\lambda _n^{(\alpha )}(c)\) with \(c=10 \pi \) and with different values of \(\alpha =0,\, 0.5,\, 1.5.\) Note that as predicted by Theorem 2, the sequence \(\lambda _n^{(\alpha )}(c)\) is decreasing with respect to \(\alpha .\) The graphs of the \(\lambda _n^{(\alpha )}(c)\) as well as \(\log (\lambda _n^{(\alpha )}(c)) \) are given by Fig. 2a, b, respectively.

Fig. 2
figure 2

a Graphs of the \(\lambda _n^{(\alpha )}(c)\) for \(c=10\pi , \alpha =1.5\) (circles), \(\alpha =0.5\) (boxes) and \(\alpha =0\) (crosses), b graphs of \(\log (\lambda _n^{(\alpha )}(c))\)

Full size image

Example 3

In this last example, we illustrate the quality of approximation over I of band-limited and almost band-limited functions, by the GPSWFs. For this purpose, we have first considered the value of \(\alpha =0.5\) and the c-band-limited function \({\displaystyle f(x)=\frac{\sin (cx)}{cx}}\) with \(c=50.\) By computing the projections \(S_N(f),\) with \(N=32\) and \(N=40,\) we found that

$$\begin{aligned}&\sup _{x\in [-1,1]}|f(x)-S_{32}(f)(x)|\approx 2.22 \times 10^{-2},\\&\sup _{x\in [-1,1]}|f(x)-S_{40}(f)(x)|\approx 4.80 \times 10^{-6}. \end{aligned}$$

As predicted by Proposition 6, the drastic improvement in the previous approximation errors is due to the fact that the second value of \(N=40\) lies after the plunge region of the eigenvalues \(\lambda _n^{(\alpha )}(c),\) which is not the case for the first value of \(N=32.\)

Next, to illustrate the approximation of almost band-limited functions by the GPSWFs, we have considered the Weierstrass function

$$\begin{aligned} W_s(x)= \sum _{k\ge 0} \frac{\cos (2^{k}x)}{2^{ks}},\quad -1\le x\le 1. \end{aligned}$$
(72)

It is well known that \(W_s \in H^{s-\epsilon }(I),\,\forall \epsilon < s,\, s >0.\) One may consider \(W_s\) as a restriction over I of a function \(W\in H^{s-\epsilon }(\mathbb R).\) Note that if \(f\in H^s(\mathbb {R})\) with \(s>0\), then

$$\begin{aligned} \int _{|\xi |> c}|\widehat{f}(\xi )|^2\,\text{ d }\xi \le \int _{|\xi |> c}\frac{(1+|\xi |)^{2s}}{(1+|\xi |)^{2s}}|\widehat{f}(\xi )|^2\,\text{ d }\xi \le \frac{1}{(1+c)^{2s}} {\left\| {f}\right\| }_{H^s(\mathbb R)}^2. \end{aligned}$$

That is f is \(\frac{1}{(1+c)^{s}}{\left\| {f}\right\| }_{H^s}\)-almost band-limited to \([-c,c]\). Note that in [4], we have used the previous function to illustrate the quality of approximation by the classical PSWFs. In this example, we push forward this quality of approximation to the GPSWFs. For this purpose, we have considered the value of \(\alpha =0.5\) and the two couples of \((c,N)=(50,60), (100, 90).\) Then we have computed the associated projection \(S_N(W_s),\) for the value of \(s=1.\) Note that thanks to (43), the different expansion coefficients \({\displaystyle C_n(W_s)=\int _{-1}^1 W_s(y) \psi _{n,c}^{(\alpha )}(y) \omega _{\alpha }(y)\, dy}\) are computed exactly. In fact since \(W_s\) is an even function, and from the Jacobi series expansion of \(\psi _{n,c}^{(\alpha )},\) the computation of the \(C_n(W_s)\) is restricted to the even indexed coefficients and consequently to the computation of the different inner products with Jacobi polynomials of even degrees. More precisely, we have

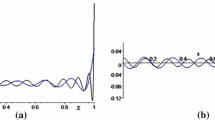
$$\begin{aligned} C_{2 m}(W_s)= & {} \sum _{l\ge 0} \beta _{2 l}^{2m} \sum _{k\ge 0}\frac{1}{2^{ks}}\int _{-1}^1 \cos (2^{k}x) {\widetilde{P}}_{2l}^{(\alpha ,\alpha )}(y)\, \omega _{\alpha }(y)\, dy\\= & {} \sqrt{\pi } 2^{\alpha +1/2} \sum _{l\ge 0} (-1)^l \beta _{2 l}^{2m} \frac{\Gamma (2l+\alpha +1)}{\sqrt{h_{2l}} (2l)!} \sum _{k\ge 0} 2^{-k(s+\alpha +1/2)} J_{2l+\alpha +1/2}(2^k). \end{aligned}$$

The graph of \(W_1\) is given by Fig. 3a, whereas the graphs of the approximation errors \(W_1(x)-S_N(W_1)(x)\) corresponding to the two couples \((c,N)=(50,60), (100, 90)\) are given by Fig. 3b, c, respectively. Note that as predicted by the theoretical results of Sect. 4, the approximation error decreases as \(c^{-s},\) whenever the truncation order N lies beyond the plunge of the \((\lambda _n^{(\alpha )}(c))_n.\) In this case, the extra error factor given by \(\sqrt{\lambda _N^{(\alpha )}(c)} \chi _N^{1/2+\alpha }\) can be neglected comparing the factor \(c^{-s}.\)

Fig. 3
figure 3

a Graph of the Weierstarss function \(W_1(x)\), b graph of the approximation error \(W_1(x)- S_N(W_1)(x)\) with \(\alpha =0.5, (c,N)=(50,60),\) c same as b with \((c,N)=(100,90)\)

Full size image