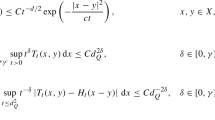Abstract
We study the boundary behavior of discrete monogenic functions, i.e. null-solutions of a discrete Dirac operator, in the upper and lower half space. Calculating the Fourier symbol of the boundary operator we construct the corresponding discrete Hilbert transforms, the projection operators arising from them, and discuss the notion of discrete Hardy spaces. Hereby, we focus on the 3D-case with the generalization to the n-dimensional case being straightforward.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Hardy spaces are an important tool in harmonic analysis. Originally developed for problems in Complex Analysis they were extended to other structures in almost any conceivable way [8, 15, 20]. This interest is due to one principal fact: elements of a Hardy space can be identified with boundary values of analytic functions (see, e.g., [10] for the case of Clifford analysis). This identification was the keystone for the work of Li et al. [15] and it is explained in detailed in [17]. The idea can be summarized as follows: one studies the boundary behaviour of null-solutions to the Dirac operator by analyzing the behaviour of the Fourier multipliers of the correspondent boundary operators. This approach was also used by Mitrea in [18].
Parallel to these developments, in the last decade one can observe an increasing interest in obtaining discrete counterparts for continuous structures. Since this interest is mainly driven by applications in physics one is compelled to address the discrete Dirac operator which stands as a discrete counterpart to the continuous Dirac operator. This operator was constructed in different contexts and by different methods for several times in the past (c.f. [6, 9, 14, 22], among others). Depending on their construction these discrete Dirac operators have different properties and even factorize different second order difference operators. As one would expect from the continuous case (where the classic Dirac operator factorizes the Laplacian) there is one particular operator which is more interesting from the practical point of view than all others. In the case of a higher dimensional grid, i.e. \(\mathbb {Z}^n\), it would be the star Laplacian. But here a major problem arises. Any factorization of the star Laplacian requires both forward and backward difference operators. This, in turn, requires a splitting of the usual Euclidean basis [6, 9, 11].
Nevertheless, first steps in the direction of a function theory for this kind of Dirac operator have already been made with a general Cauchy formula, Fischer decomposition, and polynomial solutions (see [1, 4, 12]). But here resides another problem: the fundamental solution of the Dirac operator, the so-called discrete Cauchy kernel, is known only via a Fourier integral which severely limits its applicability from the analytic point of view. For instance, in [7, 11–13] the authors use the discrete fundamental solution to construct discrete boundary integral operators for a discrete version of the boundary element method similar to Ryabenkij [19]. Since the discrete fundamental solution is only known as a numerical approximation the results could be given only in the form that when the discrete integral equation over the boundary is solvable then the corresponding discrete potentials provide a solution to the corresponding difference equation. No direct characterization of the boundary values could be given. But that is what we are interested in: characterizations of null-solutions of the discrete Dirac operator based on its discrete boundary values, as in the continuous case. This problem is not only affected by the expression of the fundamental solution, but also by the construction of the Dirac operator (which involves forward and backward differences) and by the discrete boundary itself. In difference to the continuous case a discrete boundary contains three layers, two for the inner boundary and two for the outer boundary. This means that, for instance, a discrete Cauchy integral formula for the inner domain will require function values from both layers of inner boundary. A detailed exposition of this effect is given in Sect. 3.
To obtain characterizations of boundary values of discrete monogenic functions and corresponding Hardy spaces we need to study the equation over the boundary. However, this presents an additional difficulty since in the discrete case there is no limit process to the boundary, that is to say, no traditional trace operator exists. This, combined with the lack of an explicit closed expression for the Cauchy kernel makes such a study quite difficult. Nevertheless, we will show that it is possible to get the symbol of the boundary operator in Fourier domain. For an easier understanding we will restrict ourselves to the case of \(d=3\) with the remark that the formulae and results are valid in any dimension.
The paper is organized as follows. In Sect. 2 we recall some basic facts about discrete Dirac operators, their underlying algebraic structure, and their fundamental solution which will be needed in the sequel. Also, for the sake of readership, we include in there a short description of the main results obtained in this paper. In Sect. 3, we discuss discrete Borel–Pompeiu and Cauchy formulae and introduce the discrete Cauchy transform. Although this section is essentially expository in its nature it contains the framework for discussing discrete boundary values in the next sections. In Sect. 4 we discuss the characterization of discrete boundary values by studying the discrete symbol of the operator arising from the corresponding boundary equation. This allows us to obtain conditions for a function to be a boundary value of a discrete monogenic function in the upper and in the lower half plane. We present these conditions both in terms of component functions and of the function itself. Based on those conditions, we obtain the corresponding Hilbert transforms (in the sense that they mimic the traditional Hilbert transform as an operator which squares to the identity). This allows us to get the projection operators (classically known as Plemelj or Hardy projections), Hardy spaces, and a decomposition theorem for \(l_p\)-functions on the boundary.
In the last section we show the convergence of our formulae, i.e. that when the lattice constant goes to zero we recover the classic formulae of the continuous case.
2 Preliminaries and Main Results
Let us start with some basic facts of discrete function theory. Without loss of generality we restrict ourselves to the (for practical applications) most important case \(d=3,\) with the remark that the results continue to hold in higher dimensions with no relevant changes.
For the grid \(h\mathbb {Z}^{3},\) with orthonormal basis \(e_k\), \(k=1, 2, 3,\) where \(h>0\) denotes the lattice constant (mesh size), we define the standard forward and backward differences \(\partial _{h}^{\pm j}\) as
for \(hm = h (m_1e_1+m_2e_2+m_3 e_3) \in h{\mathbb {Z}}^3.\) As stated in the introduction we want to use a discrete Dirac operator which factorizes the star-Laplacian \(\Delta _h.\) To get such an operator we follow the idea of [1, 6]. We split each basis element \(e_k, k=1,2,3,\) into two basis elements \(e_k^+\) and \(e_k^-, k=1,2,3,\) i.e., \(e_k=e_k^{+}+e_k^-, k=1,2,3,\) corresponding to the forward and backward directions. Let us remark that there is some freedom in the choice of such a basis. Special choices can be found in [2, 7, 11]. Here we choose the one satisfying the following relations:
where \(\delta _{jk}\) is the Kronecker delta. When allowing for complex coefficients, the basis elements \(\{ e_1, e_2, e_3 \}\) generate the complexified Clifford algebra \(\mathbb {C}_3= \mathbb {C} \otimes _{\mathbb {R}} \mathbb {R}_{0,3}.\) Also, the module is no longer preserved under multiplication. In fact, we have only the estimate (see [3])
Furthermore, we consider functions defined on \((\emptyset \not =) G \subset h\mathbb {Z}^{3}\) and taking values in \(\mathbb {C}_3.\) Properties like \(l_{p}\)-summability (\(1\le p<\infty \)) and so on, are defined for a \(\mathbb {C}_3\)-valued function by being ascribed to each component. The corresponding spaces are denoted, respectively, by \(l_{p}\left( G,\mathbb {C}_3\right) ,(1\le p<+\infty )\) and so on.
The discrete Dirac operator \(D^{+-}\) and its adjoint operator \(D^{-+}\) are given by
Both operators factorize the star-Laplacian
i.e.,
We remark that the factorization of the star-Laplacian requires \((e_j^+)^2 = (e_j^-)^2 =0\) as per reference [1].
For more details we refer the reader to the literature, e.g. [1, 4, 6, 11, 12].
2.1 Main Results
In this subsection we present our main results. A problem in the discrete versus continuous setting for boundary value problems is that in the first one it is required the values on two boundary layers while only one is enough in the second case. This is a direct consequence of having two difference operators (forward and backward differences) instead of a single derivative. It also has an indirect consequence of making it hard to characterize Hardy spaces in the discrete setting.
We begin by presenting Theorems 2.1 and 2.3, where the boundary value of discrete monogenic functions in the upper, resp. lower, lattice is characterized in terms of their behaviour in the Fourier domain, as well as their corollaries, which provided us with closed formulae for the symbols of the discrete Hilbert transforms in the upper, resp. the lower, lattice.
Theorem 2.1
Let \(f\in l_p(h\mathbb {Z}^2,\mathbb {C}_3)\) given by \(f=f_1+e^+_3f_2+e^-_3f_3+e^+_3e^-_3f_4\), with \({f_i : h{\mathbb {Z}}^2 \rightarrow \mathbb {C}_2, i=1, 2, 3,4.}\) Then \(f\) is the boundary value of a discrete monogenic function in the discrete upper half plane if and only if its discrete 2D-Fourier transform \(F = \mathcal {F}_h f,\) with
satisfies the system
Here, \(\underline{d}^{2}=\frac{4}{h^{2}}\sum \limits ^{2}_{j=1}\sin ^{2}\left( \frac{\xi _{j}h}{2}\right) \) and \(\widetilde{\underline{\xi }}_{-}=\sum \limits ^2_{j=1} {e_j^+\xi _{-j}^D+e_j^-\xi _{+j}^D}\) denote the symbols of 2-dimensional Laplace operator (restricted to the grid \(h{\mathbb {Z}}^2\)) and of the 2-dimensional Dirac operator \(D^{-+},\) respectively.
Corollary 2.2
Let \(f\in l_p(h\mathbb {Z}^2,\mathbb {C}_3)\) be a boundary value of a discrete monogenic function in the upper half space. Then its 2D-Fourier transform \(F = \mathcal {F}_h f,\) satisfies the equation
Theorem 2.3
Let \(f\in l_p(h\mathbb {Z}^2,\mathbb {C}_3)\) given by \(f=f_1+e^+_3f_2+e^-_3f_3+e^+_3e^-_3f_4\), with \({f_i : h{\mathbb {Z}}^2 \rightarrow \mathbb {C}_2, i=1, 2, 3,4.}\) Then \(f\) is the boundary value of a discrete monogenic function in the discrete lower half plane if and only if its 2D-Fourier transform \(F = \mathcal {F}_h f,\) with
satisfies the system
Corollary 2.4
Let \(f\in l_p(h\mathbb {Z}^2,\mathbb {C}_3)\) be a boundary value of a discrete monogenic function in the lower half space. Then its 2D-Fourier transform \(F = \mathcal {F}_h f,\) satisfies the equation
Finally, in Theorem 2.5 we introduce the operators \(A^+, A^-,\) which reconstruct the boundary data in the \(0-\)layer from the knowledge of boundary data in the \(1-\)layer, resp. \(-1-\)layer, thus giving the complete boundary data of a function in the upper, resp. lower, discrete Hardy space.
Theorem 2.5
An arbitrary function \(f\in l_p(\mathbb {Z}^2,\mathbb {C}_3)\) can be decomposed into a pair of functions \(P_+f\) and \(Q_+f\) where \(P_+f\in h_p^+\), i.e. it can be extended to the zero layer via its action in the Fourier domain by
with \(F^{+,1}(\underline{\xi })=\mathcal {F}_h f(\underline{\xi },1)\) and this pair \((F^{+,0}, F^{+,1})\) fulfills (23). In the same way an arbitrary function \(f\in l_p(\mathbb {Z}^2,\mathbb {C}_3)\) can be decomposed into a pair of functions \(P_-f\) and \(Q_-f\) where \(P_-f\in h_p^-\), i.e. it can be extended to the zero layer via its action in the Fourier domain by
with \(F^{-,-1}(\underline{\xi })=\mathcal {F}_h f(\underline{\xi },-1)\) fulfills (24).
2.2 Some Remarks on the Fundamental Solution
In this section we present some basic facts on discrete fundamental solutions which will be required in the sequel. We start with a fundamental solution of the discrete Dirac operator and its properties.
Definition 2.6
The function \(E^{-+}_h : h\mathbb {Z}^{3} \rightarrow {\mathbb {C}}_3\) is the discrete fundamental solution of \(D^{-+}_h\) if it satisfies
on \(h{\mathbb {Z}}^3,\) where \(\delta _h\) denotes the discrete Dirac function given by
There are several methods for constructing fundamental solutions. Here, we establish the fundamental solution by means of its symbol in the Fourier domain. We recall the discrete Fourier transform of \( u \in l_{p}\left( h\mathbb {Z}^3,\mathbb {C}_3\right) , 1\le p<+\infty , \)
where \( \langle mh,\xi \rangle =h \sum \limits ^3_{j=1}m_j \xi _j.\) Its inverse is given by \({\mathcal {F}}_h^{-1}=R_h \mathcal {F},\) where \(\mathcal {F}\) is the (standard) continuous Fourier transform
applied to functions \(f\) with \(\mathrm{supp} ( f)\in \left[ -\frac{\pi }{h},\frac{\pi }{h}\right] ^3\). Hereby, \(R_h\) denotes its restriction to the lattice \(h\mathbb {Z}^3.\)
Let us recall the known symbols for the forward and backward differences \(\partial _{h}^{\pm j},\) namely \(\xi _{\pm j}^D=\mp h^{-1}\left( 1-e^{\mp ih\xi _j}\right) ,\) as well as the symbol for the star-Laplacian, i.e., \(\mathcal {F}_h(-\Delta h u)(\xi )=d^2{\mathcal {F}}_h u(\xi ),\) where
Therefore, we have \({\mathcal {F}}_h (D_h^{-+} u )(\xi )=\left( \sum \limits ^{3}_{j=1}e^{+}_{j}\xi _{-j}^D+e^{-}_{j}\xi _{+j}^D\right) \mathcal {F}_h u(\xi ) \) so that \(D^{-+}\) has symbol
In consequence, the fundamental solution \(E^{-+}\) is given by
Moreover, we remark that \(\lim \limits _{h\rightarrow 0}\frac{\widetilde{\xi }_-}{d^2}=\frac{-i\xi }{|\xi |^2},\) the symbol of the right inverse of the continuous Dirac operator [11, 17].
Lemma 2.7
The fundamental solution \(E^{-+}\) satisfies
Proof
Statement (i) is obvious. For the proof of (ii) we recall that the fundamental solution of the discrete Dirac operator is given by
Since \(\widetilde{\xi }_{-}=\sum \limits ^3_{j=1}e^+_j\xi ^D_{-j}+e^-_j\xi ^D_{+j}e_j,\) with \(e_j = e^+_j+e^-_j,\) and \(\xi = \sum \limits ^3_{j=1}(e^+_j+e^-_j)\xi _j,\) we get
so that we can estimate the fundamental solution by the sum of the following two integrals
By the following theorem, adapted to dimension \(d=3\) (see [11, 21])
Let \(p_1, p_2\) be two positive integers with \(p_2 < p_1 +3.\) For \(N >0\) let \(\kappa _N\) denote the set of functions of the form \(T(\zeta ) = \frac{T_1(\zeta )}{T_2(\zeta )}, ~0 \not =\zeta \in [-\pi ,\pi ]^3,\) where \(T_j(\zeta )\) denotes trigonometric polynomials \(T_j(\zeta ) = \sum _{m \in {\mathbb {Z}}^3} t_{j,m} e^{i \langle m, \zeta \rangle }, j=1,2\) satisfying to
-
(i)
there exist homogeneous polynomials \(P_j(\zeta )\) of degree \(p_j,\) such that \(T_j(\zeta ) = P_j(\zeta ) + o(|\zeta |^{p_j})\) when \(\zeta \rightarrow 0,\) \(j=1,2;\)
-
(ii)
\(|T_2(\zeta )| \ge \frac{1}{N} |\zeta |^{p_2}\) for \(\zeta \in [-\pi , \pi ]^3;\)
-
(iii)
\(|t_{j, m}| \le N, \quad t_{j, m} = 0, ~|m|>N.\)
Then, it exists a constant \(M >0\) such that for all \(m \in {\mathbb {Z}}^3\) and \(T \in \kappa _N,\) it holds
As the integrals in (8) fulfilled the above conditions with the change of variables \(\zeta = h \xi \) and \(p_1=p_2=2\) in the first case, \(p_1=1\) and \(p_2=2\) in the second case, we obtain
Thus, the fundamental solution belongs to \(l_{p} (\mathbb {Z}^{3},\mathbb {C}_3 )\) for \(p > \frac{3}{2}.\) \(\square \)
For the convergence of the discrete fundamental solution to the continuous one we have the following fundamental lemma.
Lemma 2.8
Let \(E\) be the fundamental solution to the (continuous) Dirac operator in \(\mathbb {R}^3\). For any point \(mh\in h{\mathbb {Z}}^3,\) with \(m\not =0,\) there exists a constant \(C>0\) (independent on \(h\)), such that
Proof
The fundamental solution to the Dirac operator in the continuous case can be expressed via the Fourier transform as \(E=\mathcal {F}\left( \frac{-i\xi }{|\xi |^2}\right) .\) Hence, we have
By writing the above formula component-wisely (again, we use \(\widetilde{\xi }_{-}=\sum \limits ^3_{j=1}e^+_j\xi ^D_{-j}+e^-_j\xi ^D_{+j}e_j,\) with \(e_j = e^+_j+e^-_j,\) and \(\xi = \sum \limits ^3_{j=1}(e^+_j+e^-_j)\xi _j\)) we reduce the problem to the individual estimation of the following integrals for \(j=1,2,3\) ( c.f. also reference [11])
The first integral is the same as in (8) so that we get immediately
for a certain constant \(M>0\). The second and third integrals can be written in the following form
Integration by parts leads now to the desired result,
with the constant \(C_1>0\) being independent on \(h.\) The last estimate is true since the integrand of the first integral has an upper bound \(\frac{C_2}{|\xi _j|^2}\). Now, using \(|m|\le \sqrt{3}\max _j \{m_j\}\) we get
and, therefore,
with the constant \(C>0\) being independent on \(h.\) \(\square \)
Remark 2.9
The symbol of the discrete operator \(D^{+-}_{h}\) is given by
Therefore, its fundamental solution \(E^{+-}_h\) is given by
Moreover, for \(E_h^{+-}\) we have a convergence result similar to Lemma 2.8.
2.3 Discrete Stokes Formula
For our study we will need the discrete Stokes formula with respect to our Dirac operator both for functions defined on \(h\mathbb {Z}^3\) as well as for the case of the upper half lattice \(h\mathbb {Z}^3_{+},\) respectively.
In order to simplify notations we introduce the following conventions. First, we denote a point of the grid \({\mathbb {Z}}^3\) by \(n = (\underline{n} , n_3),\) where \(\underline{n} = (n_1,n_2)\in {\mathbb {Z}}^2.\) In consequence, the upper half lattice \(h\mathbb {Z}^3_{+}\) is defined by \(n_3>0.\) Second, whenever the mesh size \(h\) is fixed we shall abbreviate \(f(hn)\) to \(f(n).\)
Theorem 2.10
We have
for all function \(f,g\) such that the (infinite) series converge.
Proof
By definition of the discrete operators \(D_h^{+-}\) and \(D_h^{-+}\) and using \(n=(\underline{n}, n_3) = n_1e_1+n_2 e_2 +n_3e_3\) we have
\(\square \)
Replacing \(g\) in Theorem 2.10 by a translate of the fundamental solution, \(g= E_h^{-+}( \cdot -hm),\) for a fixed \(hm\in h{\mathbb {Z}}^3,\) the first sum becomes a discrete convolution between \({E_h^{-+}(\cdot -hm) D^{-+} = \delta _h(\cdot -hm)}\) and \(f\) and we get the following corollary.
Corollary 2.11
Let \(f\in l_{p}\left( h{\mathbb {Z}}^3,\mathbb {C}_3\right) \) with \({1\le p<3.}\) Then, we have
Furthermore, the following discrete unique continuation principle holds.
Corollary 2.12
If \(f \in l_p\left( h \mathbb {Z}^3,\mathbb {C}_3\right) , {1\le p<3,}\) is left monogenic with respect to the operator \(D_h^{+-}\), i.e., \(D_h^{+-} f=0\) in \(h\mathbb {Z}^3\), then
We now turn our attention to the case of the upper half lattice
In this case, we obtain the following Stokes’ theorem.
Theorem 2.13
We have
for all function \(f\) and \(g\) such that the series converge.
Proof
Starting from the definition of our operators \(D_h^{-+}\) and \(D_h^{+-}\) and again using the identification \(n=(\underline{n}, n_3) = n_1e_1+n_2 e_2 +n_3e_3\) we obtain
For the last term of the above equality, we get
so that we obtain
\(\square \)
A similar formula holds for the lower half lattice \(h{\mathbb {Z}}^3_- := \{h (\underline{n}, n_3), \underline{n} \in \mathbb {Z}^2, ~n_3 \in {\mathbb {Z}}_- \}.\) In fact,
so that the following theorem holds.
Theorem 2.14
We have
for all function \(f\) and \(g\) such that the above series converge.
3 Borel–Pompeiu and Cauchy Formulae for Upper and Lower Lattices
As in the continuous case the combination of the Stokes formula with translates of the fundamental solution provides the Borel–Pompeiu and Cauchy formulae on the desired domain. This will be used to define the discrete Cauchy transforms on the upper and lower half lattices \(h\mathbb {Z}^{3}_{\pm }.\)
We start with the Borel–Pompeiu formula for the upper lattice \(h{\mathbb {Z}}^3_+.\)
Theorem 3.1
Let \(E_h^{-+}\) be the discrete fundamental solution to operator \(D_h^{-+}.\) We have
for any discrete function \(f\) such that the series converge.
Proof
In our discrete Stokes formula (12) we replace \(g = E_h^{-+}(\cdot -hm),\) where \(m=(\underline{m}, m_3) \in \mathbb {Z}^3_+.\) This give us the discrete Borel–Pompeiu formula as follows
which leads to
\(\square \)
Remark 3.2
In fact there are several ways to construct a Borel–Pompeiu formula. The simplest and at the same time the one which requires the most work is by direct calculation. Another approach which uses the characteristic function appears in [1]. The final form of the Borel–Pompeiu formula depends also on the definition of the interior and the boundary of the domain.
Now, as a special case we obtain a discrete Cauchy formula.
Theorem 3.3
Let \(f\) be a discrete left monogenic function with respect to operator \(D^{+-}_h\), then the upper discrete Cauchy formula
holds under the condition that the involved series converge.
In the same way the lower discrete Cauchy formula can also be given by
A sufficient condition for the convergence of the series is \(f\in l_p(h\mathbb {Z}^3,\mathbb {C}_3),1\le p<\infty \). These Cauchy formulae allow us to introduce the following discrete Cauchy transforms.
Definition 3.4
For a discrete \(l_p\)-function \(f\), \(1\le p<+\infty \), defined on the boundary layers \((\underline{n}, 0), (\underline{n}, 1)\) with \(\underline{n} \in \mathbb {Z}^2,\) we define the upper Cauchy transform for \(m=(\underline{m}, m_3) \in \mathbb {Z}^3_+\) as
and for a discrete \(l_p\)-function \(f\), \(1\le p<\infty \), defined on the boundary layers \((\underline{n}, -1), (\underline{n}, 0)\) with \(\underline{n}\in \mathbb {Z}^2,\) we define the lower Cauchy transform at \(m = (\underline{m}, m_3) \in \mathbb {Z}^3_-\) by
From our discrete Cauchy formulae (16) and (17) we can see the dependence of monogenic functions on the values on boundary which consists of three different layers (two for each). This dependence appears also in our Cauchy transforms.
Theorem 3.5
Consider the upper and lower Cauchy transforms (18) and (19), respectively. Here, we have
Proof
We obtain property \((i)\) by application of Hölder’s inequality and the properties of the fundamental solution to operator \(D^{-+}_h.\) For the remaining properties, we prove only \((ii),\) the proof of \((iii)\) being similar.
We have for \(m_3>1\)
Taking into account that
and \(\partial _{h}^{-j} \left( E_h^{-+}(h(\cdot -m)) \right) = -(\partial _h^{+j}E^{-+})(h( \cdot -m)), \) for \(j=1,2,3,\) we have then
\(\square \)
From Theorem 3.3 we obtain a discrete equivalent of the boundary behaviour of a monogenic function. From Formula (16) we have for the boundary values (at the layer \(m_3=1\)) of a function which is discrete monogenic in the upper half plane
while from Formula (17) for the boundary values (\(m_3=-1\)) of a function which is discrete monogenic in the lower half plane we get
Additionally, we have for the values in the \(0\)-layer in case of a function which is monogenic in the (complete) upper half space
and
for a function which is monogenic in the (complete) lower half space.
4 Reconstruction on the Boundary Layers
From the last formulae in the previous section we can observe that the boundary condition involves function values not only in the \(0\)-layer, but also in the layers above and below. Now, this raises the question how far conditions (23) and (24) can be solved in the two upper, respectively two lower layers of the boundary? This will give us also the discrete equivalent of the Plemelj projections and the Hardy spaces.
Since our fundamental solution is only given as a Fourier integral we start our investigation by calculating the corresponding Fourier symbols.
Lemma 4.1
The Fourier symbols of the fundamental solution on the layers \(-1,0,1\) are given by
where \(\underline{d}^{2}=\frac{4}{h^{2}}\sum \limits ^{2}_{j=1}\sin ^{2}\left( \frac{\xi _{j}h}{2}\right) \) and \(\widetilde{\underline{\xi }}_{-}=\sum \limits ^2_{j=1} {e_j^+\xi _{-j}^D+e_j^-\xi _{+j}^D}\).
Proof
From Sect. 2 we know that the Fourier symbol of the fundamental solution \(E^{-+}_h(hn)\) for arbitrary \(n\in \mathbb {Z}^{3}\) is given by
with \(\widetilde{\xi }_-=\sum \limits ^3_{j=1} {e_j^+\xi _{-j}^D+e_j^-\xi _{+j}^D}.\) Now, for \(n_3\) fixed we apply the 2D discrete Fourier transform
where \(\underline{d}^{2}=\frac{4}{h^{2}}\sum \limits ^{2}_{j=1}\sin ^{2}\left( \frac{\xi _{j}h}{2}\right) \) and \(\widetilde{\underline{\xi }}_{-}=\sum \limits ^2_{j=1} {e_j^+\xi _{-j}^D+e_j^-\xi _{+j}^D},\widetilde{\underline{\xi }}_{3}=e_3^+\xi _{-3}^D+e_3^-\xi _{+3}^D\). We are interested in the Fourier symbol for \(n_3=-1,0,1\). To this end we need the following integrals
and
Now, for \(n_3=0\) we get
This results in
Furthermore, for the case \(n_3=1\) we have
Here, we get
Finally, the case \(n_3=-1\) being similar to the above case of \(n_3=1,\) we have that (27) holds. \(\square \)
Now, conditions (23) and (24) can be written as
as well as
on the Fourier side. The zero layer will not be very interesting for our investigation here. Nevertheless, for sake of completeness on the zero layer we have
respectively.
This allows us to write the terms (28) and (29) using the above lemma in Fourier domain. Here, we obtain
as well as
Again, for the zero layer we get
and
Now, to get conditions for our boundary values we need to study the solvability of equations (31) and (32). To simplify the presentation of our calculations we introduce the following abbreviations:
We would like to point out that \(C\) is a scalar operator while \(A\) and \(B\) are vector-valued operators. Since \(e_3^\pm \) act like projectors (\((e_3^\pm )^2=0\)!) and \(\mathbb {C}_3\) can be realized as \({\mathbb {C}}_3 = \mathbb {C}_2 \oplus e_3^+ \mathbb {C}_2 \oplus e_3^- \mathbb {C}_2\oplus e_3^+e_3^- \mathbb {C}_2,\) where \(\mathbb {C}_2\) is the complexified Clifford algebra spanned by \(\{ e^+_1,e^-_1,e^+_2,e^-_2 \},\) we can further decompose our functions into
where the components \(F^{+,0}_j, F^{-,0}_j, F^{+,1}_j,F^{-1}_j, j=1,2, 3, 4,\) take values in the subalgebra of \(\mathbb {C}_2.\)
Let us start with layer \(1\). Using the above decomposition we can write Condition (31) on the \(1-\)layer as
which leads to the following system
First of all, we observe that given the values of our function on the \(0-\)layer we can obtain its values on the \(1-\)layer as
Hereby, we remark that \((C+1)^{-1}\) exists, since \((C+1)=\left( \frac{h\underline{d}}{2\sqrt{4+h^{2}\underline{d}^{2}}}+\frac{1}{2}\right) =0\) is equivalent to \(4+h^{2}\underline{d}^{2}=h^{2}\underline{d}^{2}\).
But, more important, by eliminating \(F^{+,0}_2\) and \(F^{+,0}_1 - F^{+,0}_4\) we get the following conditions
for the function on the \(1-\)layer. This leads to the following characterization for a function to be a boundary value of a discrete monogenic function.
We now proceed with the proof of Theorem 2.1.
Proof
We only need to remark that \(C(C+1)-(A+B)B=\frac{1}{2}\left( \frac{h\underline{d}}{\sqrt{4+h^2\underline{d}^{2}}}-1\right) \). Moreover, in this case the values on the \(0-\)layer are given from (36) by
and the discrete monogenic function itself is obtained by applying the discrete upper Cauchy transform. \(\square \)
The condition in the previous theorem is given component-wise. But one would like to have an expression it in terms of the function itself. To obtain such a condition we remark that we have
By abbreviating \(\frac{\widetilde{\underline{\xi }}_{-}}{\underline{d}}\frac{h\underline{d}-\sqrt{4+h^2\underline{d}^{2}}}{2}:= G \) in Condition (2) we obtain \(F_1=-G^{-1}F_2\) and \(F_3=-G^{-1}\left( F_1-F_4\right) .\) Hence, we have
This results in
In the same way, from \(e_3^+F=e_3^+F_1+e_3^+e_3^-F_3\) and \(e_3^+e_3^-F=e_3^+e_3^-(F_1-F_4)-e_3^+F_2,\) together with Condition (2), we obtain
Here, we arrive at
Now, taking into account that \((e_3^+e_3^-+e_3^-e_3^+)F=-F\) we can sum up both terms and get
This allows us to get the desired characterization of a boundary value of a discrete monogenic function in terms of the function itself, thus proving Corollary 2.2.
Based on Corollary 2.2 we can introduce the operator
which satisfies \(H_+^2f=f\).
Now, let us take a look at the case of the lower half plane. For the \((-1)\)-layer and using our abbreviations we can write (32) as:
Again, we can obtain the values of the function on the \((-1)-\)layer in terms of its values on the \(0-\)layer.
as well as the condition for the function on the \((-1)-\)layer.
In the same way as in the case of the discrete upper half space we can obtain an equivalent description for the lower half space, as indicated in Theorem 2.3. In fact, from (39) we can obtain the values on the \(0-\)layer as
Similar to the case of the discrete upper half plane we would like to have a characterization of a boundary value of a discrete monogenic function in terms of the function itself. Let us start again with
Again, we use condition (3) together with the abbreviation \(\frac{\widetilde{\underline{\xi }}_{-}}{\underline{d}}\frac{h\underline{d}-\sqrt{4+h^2\underline{d}^{2}}}{2} := G\) to obtain \(F_1=GF_2\) and \(F_3=G\left( F_1-F_4\right) .\) This leads to
Here, we get
In the same way, from \(e_3^+F=e_3^+F_1+e_3^+e_3^-F_3\) and \(e_3^+e_3^-F=e_3^+e_3^-(F_1-F_4)-e_3^+F_2,\) we obtain
Hence, we have
Like in the case of the discrete upper half sphere we get
This proves Corollary 2.4. We can again point out that Equation 4 induces the following operator
which satisfies \(H^2_- f=f\).
Furthermore, we would like to remark that both Conditions (2) and (3) are linear. This motivates the following definition.
Definition 4.2
We define the upper discrete Hardy space \(h_p^+\) as the space of discrete functions \(f\in l_p(h\mathbb {Z}^2,\mathbb {C}_3)\) whose discrete 2D-Fourier transform fulfils system (2) and the lower discrete Hardy space \(h_p^-\) as the space of discrete functions \(f\in l_p(h\mathbb {Z}^2,\mathbb {C}_3)\) whose discrete 2D-Fourier transform fulfils system (3).
First of all it is obvious from the construction that the upper and lower discrete Hardy spaces are indeed spaces. The principal question at this point is: Does the decomposition of the continuous \(L_p\)-space into Hardy spaces still holds true in the discrete case?
We start by studying the intersection of the two spaces, i.e. \(h_p^+\cap h_p^-\). This means we are interested in what functions \(f\) have their discrete 2D-Fourier transform \(F=\mathcal {F}_h f\) fulfil both (37) and (41), i.e.
First of all, from the first and third equation we get
We remark that \(B^2+(C(C+1)-(A+B)B)^2\ne 0\) since \(h^2{\underline{d}}^2=(h \underline{d}-2)\sqrt{4+h^2{\underline{d}}^2}\) does not have any positive roots. This implies \(F_2=F_1=0.\)
Furthermore, from the second and fourth equations we obtain
which again implies \(F_3=F_4=0\). Therefore, we have \(h_p^+\cap h_p^- = \{ 0 \}.\) The question is now, what is \(P_+f+P_-f\)? Here we have:
Therefore, we get
Moreover, this equation can further be rewritten as
Notice that \(\sum _{k=1}^2\left[ e_k^+ \partial _h^{-k}+e_k^-\partial _h^{+k}\right] \) represents the discrete Dirac operator \(D^{-+}_h\) in 2D. When \(h\) goes to zero this term disappears.
Due to the properties of \(H_+\) and \(H_-\) we can introduce the Plemelj or Hardy projections \(P_+=\frac{1}{2}\left( I+ H_+ \right) \) and \(P_-=\frac{1}{2}\left( I+H_-\right) .\) From the previous constructions it is clear that \(f\in h_p^+\) is equivalent to say that \(P_+f=f,\) while \(f\in h_p^-\) means \(P_-f=f.\) We remark that the projectors \(P_+\) and \(P_-\) together with their respective projectors \(Q_+=I-P_+\) and \(Q_-=I-P_-\) provide two Hardy-type decompositions, one acting on the \(1\)-layer and the other on the \(-1\)-layer.
We now conclude this section with the proof of Theorem 2.5.
Proof
We begin with the remark that once the pair \((F^{+,0}, F^{+,1}),\) resp. \((F^{-,0}, F^{-,-1}),\) is obtained the decompositions are obvious by construction. For the individual construction of the pairs we need the extensions to the zero layer from the \(1\)-layer, resp. the \(-1\)-layer. We have for the \(1\)-layer
so that by \(e_3^-F^{+,0}=e_3^-\left( F^{+,0}_1-F^{+,0}_4\right) +e_3^-e_3^+F^{+,0}_2\) we get
that is
In a similar way, we have for the case of the lower lattice
which means that \(e^+_3F^{-, 0}=e^+_3F^{-, 0}_1+e^+_3e^-_3F^{-, 0}_3\) can be obtained by
that is to say,
\(\square \)
Furthermore, we get on the zero layer
which can be seen as the discrete equivalent of the usual jump condition in the continuous case.
5 Convergence Results
Finally, we are interested how far our discrete results correspond to the results in the continuous case. That means we need to study what happens if our lattice constant \(h\) goes to zero. Let us denote by \(C_\Gamma \) the continuous Cauchy transform
with \(E(x)\) being the fundamental solution to the Dirac operator \(D=\sum \limits ^3_{j=1}e_j\frac{\partial }{\partial _{x_j}} \) (c.f. [12]). For the convergence of our upper discrete Cauchy transform we have the following theorem. A similar theorem holds in case of the lower discrete Cauchy transform.
Theorem 5.1
If \(f\in L_p\left( \mathbb {R}^2,\mathbb {C}_3\right) \cap C^{\alpha }(\mathbb {R}^2, \mathbb {C}_3)\), \(0<\alpha \le 1, 1< p<+\infty \), then we get
for any point \(y\in \mathbb {Z}_+\) and \(C>0\) being a constant independent on \(h\) and \(f\).
Proof
Let us first remark that for functions \(f\in L_p\left( \mathbb {R}^2,\mathbb {C}_3\right) \cap C^{\alpha }(\mathbb {R}^2,\mathbb {C}_3)\), \(0<\alpha \le 1\), \(1< p<\infty \), we have \(\Vert f(\cdot h)\Vert _{p+2/\alpha }\le C\Vert f\Vert _{L_p}\). This is an easy adaptation of Lemma 3.1 in [7]. We will consider a fixed point \(y\) such that there exist for a given \(h\) an \(m_h\) with \(y=m_h h\) and \(y_3>1\). Now, let \(W(x)\) be a square with center \(x\) and edge length \(h\). Furthermore, let \(1/q+1/p=1\) and \(1/s+1/(p+2/\alpha )=1\) then we have
with \(c_1=2^{3/2}\). Now, Hölder’s inequality and Lemma 2.8 provides
as well as
The third term
can be modified to
We can estimate the first term using Hölders inequality:
For the second term we can use the Taylor expansion for the kernel:
The last term can be estimate in the same way as the third term. Since we have \(\Vert f\Vert _{{p+2/\alpha }}\le C\Vert f\Vert _{L_p}\) we get our result by joining all estimates together. \(\square \)
Since we have the convergence of our discrete Cauchy transforms to the continuous Cauchy transform the question remains how far (31) and (32) correspond to the classic continuous case when \(h \rightarrow 0\).
If we let \(h\rightarrow 0\) on both sides of terms (31) and (32), we get
as well as
Hereby, \(\widehat{f}^\pm (\underline{\xi },0)\) denote the limits of \(F^{\pm , \pm 1}(\underline{\xi }) = {\mathcal {F}}_h f^\pm (\underline{\xi },\pm 1h)\) when \(h\rightarrow 0\), as well as \(F^{\pm , 0}(\underline{\xi })= {\mathcal {F}}_h f^\pm (\underline{\xi },0).\) Therefore, we obtain
as well as
Now, if we remember our initial splitting of the Euclidean basis \(e_3=e_3^-+e_3^+\) with \(e_3^+e_3^-+e_3^-e_3^+=-1\), Equations (48) and (49) can be rewritten as
respectively. The last expressions are the Plemelj–Sokhotzki formulae for the half space in the continuous case [17].
References
Brackx, F., De Schepper, H., Sommen, F.: Discrete clifford analysis: a germ of function theory. In: Sabadini, I., et al. (eds.) Hypercomplex Analysis, pp. 37–53. Birkhäuser, Basel (2009)
Cerejeiras, P., Faustino, N., Vieira, N.: Numerical clifford analysis for nonlinear schrödinger problem. Numer. Methods Partial Differ. Equ. 24(4), 1181–1202 (2008)
Delanghe, R., Sommen, F., Soucek, V.: Clifford Algebra and Spinor-Valued Functions. Kluwer Academic, Dordrecht (1992)
De Ridder, H., De Schepper, H., Kähler, U., Sommen, F.: Discrete function theory based on skew weyl relations. Proc. Am. Math. Soc. 138(9), 3241–3256 (2010)
Faustino, N., Kähler, U.: Fischer decomposition for difference dirac operators. Adv. Appl. Clifford Algebras 17, 37–58 (2007)
Faustino, N., Kähler, U., Sommen, F.: Discrete dirac operators in clifford analysis. Adv. Appl. Clifford Algebras 17(3), 451–467 (2007)
Faustino, N., Gürlebeck, K., Hommel, A., Kähler, U.: Difference potentials for the navier–stokes equations in unbounded domains. J. Differ. Equ. Appl. 12(6), 577–595 (2006)
Folland, G.B., Stein, E.M.: Hardy Spaces on Homogeneous Groups. Princeton University Press, Princeton (1982)
Forgy, E., Schreiber, U.: Discrete Differential Geometry on Causal Graphs. arXiv:math-ph/0407005v1 (2004) (preprint)
Gilbert, J.E., Murray, M.: Clifford Algebras and Dirac Operators in Harmonic Analysis. Cambridge University Press, Cambridge (1991)
Gürlebeck, K., Hommel, A.: On finite difference Dirac operators and their fundamental solutions. Adv. Appl. Clifford Algebras 11(S2), 89–106 (2001)
Gürlebeck, K., Sprößig, W.: Quaternionic and Clifford calculus for physicists and engineers. Wiley, Chichester (1997)
Hommel, A.: Fundamentallösungen partieller Differentialoperatoren und die Lösung diskreter Randwertprobleme mit Hilfe von Differenzenpotentialen. PhD thesis, Bauhaus-Universitaät Weimar, Germany (1998)
Kanamori, I., Kawamoto, N.: Dirac-Kaehler fermion from clifford product with noncommutative differential form on a lattice. Int. J. Mod. Phys. A19, 695–736 (2004)
Li, C., McIntosh, A., Qian, T.: Clifford algebras, Fourier transforms, and singular convolution operators on Lipschitz surfaces. Rev. Mat. Iberoamericana 10, 665–721 (1994)
Lovasz, L.: Discrete Analytic Functions: An Exposition, Surveys in Differential Geometry, vol. IX, pp. 1–44. International Press, Somerville (2004)
McIntosh, A.: Clifford algebras, Fourier theory, singular integrals, and harmonic functions on Lipschitz domains. In: Ryan, J. (ed.) Clifford Algebras in Analysis and related Topics, pp. 33–88. CRC Press, Boca Raton (1996)
Mitrea, M.: Clifford Wavelets, Singular Integrals, and Hardy Spaces. Springer, Berlin (1994)
Ryabenskij, V.S.: The Method of Difference Potentials for Some Problems of Continuum Mechanics. Nauka, Moscow (1984). (Russian)
Stein, E.M., Weiss, G.: Introduction to Fourier Analysis on Euclidean Spaces. Princeton University Press, Princeton (1971)
Thomée, V.: Discrete interior Schauder estimates for elliptic difference operators. SIAM J. Numer. Anal. 5, 626–645 (1968)
Vaz, J.: Clifford-like calculus over lattices. Adv. Appl. Clifford Algebra 7(1), 37–70 (1997)
Acknowledgments
This work was supported by Portuguese funds through the CIDMA—Center for Research and Development in Mathematics and Applications, and the Portuguese Foundation for Science and Technology (“FCT-Fundação para a Ciência e a Tecnologia”), within project PEst-OE/MAT/UI4106/2014. The third author is the recipient of a Postdoctoral Foundation from FCT (Portugal) under Grant No. SFRH/BPD/74581/2010.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Chris Heil.
Rights and permissions
About this article
Cite this article
Cerejeiras, P., Kähler, U., Ku, M. et al. Discrete Hardy Spaces. J Fourier Anal Appl 20, 715–750 (2014). https://doi.org/10.1007/s00041-014-9331-8
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00041-014-9331-8