On Radii of Spheres Determined by Subsets of Euclidean Space

Abstract

In this paper the author considers the problem of how large the Hausdorff dimension of $E\subset \mathbb {R}^d$ needs to be in order to ensure that the radii set of $(d-1)$-dimensional spheres determined by $E$ has positive Lebesgue measure. The author also studies the question of how often can a neighborhood of a given radius repeat. There are two results obtained in this paper. First, by applying a general mechanism developed in Grafakos et al. (2013) for studying Falconer-type problems, the author proves that a neighborhood of a given radius cannot repeat more often than the statistical bound if $\dim _{{\mathcal H}}(E)>d-1+\frac{1}{d}$; In $\mathbb {R}^2$, the dimensional threshold is sharp. Second, by proving an intersection theorem, the author proves that for a.e $a\in \mathbb {R}^d$, the radii set of $(d-1)$-spheres with center $a$ determined by $E$ must have positive Lebesgue measure if $\dim _{{\mathcal H}}(E)>d-1$, which is a sharp bound for this problem.

1 Introduction

The classical Falconer distance conjecture states that if a set $E \subset {\mathbb {R}}^d$, $d \ge 2$, has Hausdorff dimension greater than $\frac{d}{2}$, then the one-dimensional Lebesgue measure ${\mathcal L}^1(\Delta (E))$ of its distance set,

$$\begin{aligned} \Delta (E):=\{|x-y|\in {\mathbb {R}}: x,y \in E\}, \end{aligned}$$

is positive, where $|\cdot |$ denotes the Euclidean distance. Falconer gave an example based on the integer lattice showing that the exponent $\frac{d}{2}$ is best possible. The best results currently known, culminating almost three decades of efforts by Falconer [3], Mattila [11], Bourgain [1], and others, are due to Wolff [15] for $d=2$ and Erdoǧan [2] for $d\ge 3$. They prove that ${\mathcal L}^1(\Delta (E))>0$ if

$$\begin{aligned} dim_{{\mathcal H}}(E)>\frac{d}{2}+\frac{1}{3}. \end{aligned}$$

It is natural to consider related problems, where distances determined by $E$ may be replaced by other geometric objects, such as triangles [5], volumes [6], angles [7], [8], and others. Generally, if

$$\begin{aligned} \Phi :(\mathbb {R}^d)^{k+1}\rightarrow \mathbb {R}^m \end{aligned}$$

for some $1\le m \le \left( {\begin{array}{c}d+1\\ 2\end{array}}\right)$, one can define a configuration set

$$\begin{aligned} \Delta _\Phi (E)=\{\Phi (x^1,\ldots , x^{k+1}):x^j\in E\} \end{aligned}$$

and ask how large $\dim _{{\mathcal H}}(E)$ needs to be to ensure $\mathcal {L}^m(\Delta _\Phi (E))>0$. For example, in the distance problem, $k=1, \Phi (x^1,x^2)=|x^1-x^2|$; in the volume problem, $k=d, \Phi (x^1,\ldots ,x^{d+1})=|\det (x^{d+1}-x^1,\ldots ,x^{d+1}-x^d)|$; in the angle problem, $k=1, \Phi (x^1,x^2)=\frac{x^1\cdot x^2}{|x^1||x^2|}$.

In this paper, the author considers the problem of the distribution of radii of spheres determined by $(d+1)$-tuples of points from $E$.

Definition 1.1

A sphere is said to be determined by a $(d+1)$-tuple $(x^1,\ldots ,x^{d+1})$ if it is the unique sphere passing through all the points $x^1,\ldots ,x^{d+1}$. A sphere is said to be determined by a set $E$ if it is determined by a $(d+1)$-tuple $(x^1,\ldots ,x^{d+1})\in E\times \cdots \times E$.

Let $R(x^1,\ldots , x^{d+1})$ be the radius of the unique $(d-1)$-dimensinal sphere determined by $(x^1,\ldots ,x^{d+1})$ and it equals $0$ if such a sphere does not exist or it is not unique. The author obtains two types of results. First, the author estimates how often a neighborhood of a given radius occurs, in the sense defined below. Second, the author finds the optimal dimension such that the Lebesgue measure of the set of radii is positive. The main geometric results are the following.

Theorem 1.2

Let $E\subset \mathbb {R}^d$ be compact and $\nu$ be a Frostman measure on $E$. Then $\dim _{{\mathcal H}}(E)>d-1+\frac{1}{d}$ implies

$$\begin{aligned} (\nu \times \cdots \times \nu )\left( \{(x^1,\ldots ,x^{d+1}):|R(x^1,\ldots ,x^{d+1})-t|<\epsilon \}\right) \lesssim \epsilon \end{aligned}$$

(1.1)

where the implicit constant is uniform in $t$ on any bounded set.

Moreover, $\dim _{{\mathcal H}}(E)>d-1+\frac{1}{d}$ implies

$$\begin{aligned} \mathcal {L}(R(E\times \cdots \times E))>0. \end{aligned}$$

When $d=2$, this result is sharp in the sense that (1.1) does not generally hold when $\dim _{{\mathcal H}}(E)<\frac{3}{2}$.

In contrast to the incidence result, using Mattila’s classical estimate on the dimension of intersections (see Theorem 5.1), one can see that

$$\begin{aligned} \dim _{{\mathcal H}}(E)>d-1\Longrightarrow R(E\times \cdots \times E)=\mathbb {R}^+. \end{aligned}$$

(1.2)

This is the optimal result because there is no unique $(d-1)$-dimensional sphere passing through $d+1$ points in a hyperplane. However, one can never get this bound by improving the incidence result above due to its sharpness.

The author also proves an intersection result where rotations and translations in Theorem 5.1 are replaced by dilations and translations (see Theorem 5.4). From this intersection theorem, one can conclude the following.

Theorem 1.3

Given $E\subset \mathbb {R}^d$ with $\dim _{{\mathcal H}}(E)>d-1$, then for a.e. $a\in \mathbb {R}^d$,

$$\begin{aligned} \mathcal {L}(\{r>0:E\text { determines } S^{d-1}_{a,r}\})>0, \end{aligned}$$

where $S^{d-1}_{a,r}$ is the $(d-1)$-dimensional sphere with center $a$ and radius $r$.

The bound $d-1$ is sharp because a hyperplane can never determine a $(d-1)$-dimensional sphere of finite radius.

Notation. Throughout the paper,

$X \lesssim Y$ means that there exists $C>0$ such that $X \le CY$.

$S^{d-1}=\{x\in \mathbb {R}^d:|x|=1\}.$

For $A\subset \mathbb {R}^d$, $A_{a,r}=\{rx+a:x\in A\}$.

For a measure $\mu$ on $\mathbb {R}^d$ and a function $q(x)$ on $\mathbb {R}^d$, $q_*\mu$ is the measure on $\mathbb {R}$ induced by $q(x)$, i.e. $\int _{\mathbb {R}} f\, d(q_*\mu )=\int _{\mathbb {R}^d} f\circ q\, d\mu$.

$\hat{\mu }(\xi )=\int e^{-2\pi i x\cdot \xi }\,d\mu (x)$ is the Fourier transform of measure $\mu$.

2 The Incidence Result

In [4], Grafakos et al. develop the following general mechanism to solve Falconer-type problems.

$\Phi$ is said to be translation invariant if it can be written as

$$\begin{aligned} \Phi _0(x^{k+1}-x^1,\ldots ,x^{k+1}-x^k). \end{aligned}$$

Theorem 2.1

(Grafakos et al. [4]) Suppose $\Phi$ is translation invariant and for some $\gamma >0$,

$$\begin{aligned} |\widehat{\mu _t}(-\xi ,\xi ,0,\ldots ,0)|&\lesssim (1+|\xi |)^{-\gamma },\nonumber \\ |\widehat{\mu _t}(0,\xi ,0,\ldots ,0)|&\lesssim (1+|\xi |)^{-\gamma },\\ |\widehat{\mu _t}(\xi ,0,0,\ldots ,0)|&\lesssim (1+|\xi |)^{-\gamma },\nonumber \end{aligned}$$

(2.1)

where $\mu _t$ is the natural measure on $\{u:\Phi _0(u)=t\}$ and the implicit constant is uniform in $t$ on any bounded set. Then $\dim _{{\mathcal H}}(E)>d-\frac{\gamma }{k}$ implies

$$\begin{aligned} (\nu \times \dots \times \nu )\left( \{(x^1,\dots ,x^{k+1}):|\Phi (x^1,\dots ,x^{k+1})-t|<\epsilon \}\right) \lesssim \epsilon ^m \end{aligned}$$

(2.2)

where $\nu$ is a Frostman measure on $E$ and the implicit constant is uniform in $t$ in any bounded set. It follows that the $m$-dimensional Lebesgue measure $\mathcal {L}^m(\Delta _\Phi (E))>0$.

3 Proof of Theorem 1.2

Since $R(x^1,\ldots ,x^{d+1})$ is translation invariant and it can be written as $R_0(x^{d+1}-x^1,\ldots ,x^{d+1}-x^d)$, by Theorem 2.1 it suffices to show that the three inequalities in (2.1) hold for the natural measure $\mu _1$ on $\{(u_0,\dots ,u_d)\in \mathbb {R}^d: R_0(u^1,\ldots ,u^d)=1\}$. Observe that

$$\begin{aligned}&\text {a } (d+1)\text {-tuple } (x^1,\ldots ,x^{d+1}) \text { determines a sphere of radius }1\\&\quad \Leftrightarrow (0, x^{d+1}-x^1,\ldots ,x^{d+1}-x^d) \text { determines a sphere of radius }\\&\qquad 1 \text { passing through the origin}\\&\quad \Leftrightarrow x^{d+1}-x^i\in a+S^{d-1} \text { for some } a\in S^{d-1}\\&\qquad \text { and } 0\ne x^{d+1}-x^i\ne x^{d+1}-x^j, \forall i\ne j. \end{aligned}$$

Hence

$$\begin{aligned}&\{(u^1,\ldots ,u^d):R_0(u^1,\ldots ,u^d)=1\}\nonumber \\&\quad =\{(\sigma _0+\sigma _1,\sigma _0+\sigma _2,\ldots ,\sigma _0+\sigma _d):\sigma _i\in S^{d-1}\}-N, \end{aligned}$$

(3.1)

where $N$ is a set of measure $0$.

Let $\psi$ be a smooth cut-off function which may vary from line to line. By changing variables as (3.1),

$$\begin{aligned} |\widehat{\mu _1}(\xi ,-\xi ,0,\ldots ,0)|&= \left| \int \limits _{\{u:R_0(u)=1\}} e^{-2\pi i u\cdot (\xi ,-\xi ,0,\ldots ,0)}\,du\right| \nonumber \\&= \left| \int \limits _{S^{d-1}}\dots \int \limits _{S^{d-1}} e^{-2\pi i\xi \cdot (\sigma _1-\sigma _2)} \psi \ d\sigma _0\dots d\sigma _d\right| \nonumber \\&\lesssim \left| \int \limits _{S^{d-1}}\int \limits _{S^{d-1}} e^{-2\pi i\xi \cdot (\sigma _1-\sigma _2)}\psi \ d\sigma _1\,d\sigma _2\right| \nonumber \\&= \left| \int \limits _{S^{d-1}} e^{-2\pi \xi \cdot \sigma _1}\left( \int \limits _{S^{d-1}} e^{2\pi i\xi \cdot \sigma _2}\psi \ d\sigma _2\right) d\sigma _1\right| \nonumber \\&= \left| \int \limits _{S^{d-1}} e^{-2\pi \xi \cdot \sigma _1} a(\xi ,\sigma _1)\,d\sigma _1\right| . \end{aligned}$$

(3.2)

By stationary phase (see, e.g. [13]), $|a(\xi ,\sigma _1)|\lesssim (1+|\xi |)^{-\frac{d-1}{2}}$ and

$$\begin{aligned} \left| \int \limits _{S^{d-1}} e^{-2\pi \xi \cdot \sigma _1}\left( (1+|\xi |)^{\frac{d-1}{2}}a(\xi ,\sigma _1)\right) d\sigma _1\right| \lesssim (1+|\xi |)^{-\frac{d-1}{2}}. \end{aligned}$$

(3.3)

Hence

$$\begin{aligned} |\widehat{\mu _1}(\xi ,-\xi ,0,\ldots ,0)|\lesssim (1+|\xi |)^{-(d-1)}. \end{aligned}$$

For $\widehat{\mu _1}(\xi ,0,\ldots ,0)$ and $\widehat{\mu _1}(0,\xi ,0,\ldots ,0)$, after changing variables as above,

$$\begin{aligned} \widehat{\mu _1}(\xi ,0,\ldots ,0)&= \int _{S^{d-1}}\dots \int \limits _{S^{d-1}} e^{-2\pi i\xi \cdot (\sigma _0+\sigma _1)} \psi \ d\sigma _0\dots d\sigma _d,\\ \widehat{\mu _1}(0,\xi ,0,\ldots ,0)&= \int \limits _{S^{d-1}}\dots \int \limits _{S^{d-1}} e^{-2\pi i\xi \cdot (\sigma _0+\sigma _2)} \psi \ d\sigma _0\dots d\sigma _d. \end{aligned}$$

By a similar argument,

$$\begin{aligned} |\widehat{\mu _1}(\xi ,0,\ldots ,0)|,\ |\widehat{\mu _1}(0,\xi ,0,\dots ,0)|\lesssim (1+|\xi |)^{-(d-1)}, \end{aligned}$$

which completes the proof of Theorem 1.2.

4 Sharpness of Theorem 1.2 in $\mathbb {R}^2$

When $d=2$, Theorem 1.2 says $\dim _{{\mathcal H}}(E)>\frac{3}{2}$ implies (2.2), more precisely

$$\begin{aligned} (\nu \times \nu \times \nu )\left( \{(x^1,x^2,x^3):|R(x^1,x^2,x^3)-t|<\epsilon \}\right) \lesssim \epsilon \end{aligned}$$

(4.1)

where $\nu$ is a Frostman measure on the compact set $E\subset \mathbb {R}^2$ and the implicit constant is uniform in $t$ on any bounded set. The following example motivated by Mattila [11] shows that $\frac{3}{2}$ is sharp for (4.1).

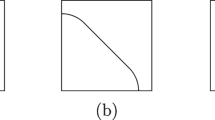
Without loss of generality, fix $t=100$. Let $C_\alpha \subset [0,1]$ denote the Cantor set of dimension $\alpha$ and $\nu$ denote the natural probability measure on $C_\alpha$. Let

$$\begin{aligned} E=\left( \bigcup _{k=-200}^{200}(C_\alpha +k)\right) \times [-200,200] \end{aligned}$$

(4.2)

and extend $\nu$ to $E$ in the natural way.

Let

$$\begin{aligned} S_a=\{(x,y)\in \mathbb {R}^2:0\le x\le 1, a\le y\le a+1\}. \end{aligned}$$

When $a\gg 1$, for all $x\in S_0, y\in S_a$, the vector $y-x$ is almost perpendicular to the $x$-axis. Therefore one can pick a $\sqrt{\epsilon }\times \epsilon$ rectangle in

$$\begin{aligned} \{z\in \mathbb {R}^2:|R(x,y,z)-100|<\epsilon \} \end{aligned}$$

such that its $\sqrt{\epsilon }$-edges are perpendicular to the $x$-axis. (see the figure above).

If $a$ varies continuously, the $\sqrt{\epsilon }\times \epsilon$ rectangle translates continuously. Then there exists an $a_0\in (a-2,a)$ such that one of the $\sqrt{\epsilon }$-edges lies on the line $x=n$ for some $n\in \mathbb {Z}$. By the construction of $E$, for all $x\in S_0, y\in S_{a_0}$,

$$\begin{aligned} \nu \left( \{z\in \mathbb {R}^2:|R(x,y,z)-100|<\epsilon \}\right) \gtrsim \epsilon ^{\frac{1}{2}}\cdot \epsilon ^\alpha =\epsilon ^{\frac{1}{2}+\alpha }. \end{aligned}$$

(4.3)

Hence

$$\begin{aligned} \begin{aligned}&(\nu \times \nu \times \nu )\left( \{(x,y,z):|R(x,y,z)-100|<\epsilon \}\right) \\&\quad \gtrsim (\nu \times \nu \times \nu )\left( \{(x,y,z):x\in S_0, y\in S_a, |R(x,y,z)-100|<\epsilon \}\right) \\&\quad \gtrsim \epsilon ^{\frac{1}{2}+\alpha }, \end{aligned} \end{aligned}$$

(4.4)

which implies that when $\alpha <\frac{1}{2}$, (4.1) fails.

It follows that for $\dim _{{\mathcal H}}(E)<\frac{3}{2}$, (4.1) is not generally true, which proves the sharpness arguement of Theorem 1.2.

Remark 4.1

The sharpness of (4.1) doesn’t mean $\frac{3}{2}$ is the best possible for the radii problem, but for the method used above, it cannot be, generally, improved.

Remark 4.2

The example above cannot show the sharpness in higher dimensions. For example, in $\mathbb {R}^3$, the rectangle one can pick will become a $\sqrt{\epsilon }\times \sqrt{\epsilon }\times \epsilon$ rectangle. For any set like $C_\alpha \times C_\beta \times C_\gamma$, the lower bound obtained for (2.2) is $\epsilon ^{\frac{\alpha }{2}+\frac{\beta }{2}+\gamma }$. In nontrivial cases (i.e. $\dim _{{\mathcal H}}(E)>2$) it is always true that $\frac{\alpha }{2}+\frac{\beta }{2}+\gamma >\frac{1}{2}(\alpha +\beta +\gamma )>1$, which does not contradict the upper bound. In fact, in many relavant problems, a similar example can show the sharpness in $d=2$ but fails in $d\ge 3$ (see, e.g. [5, 11]).

5 An Intersection Theorem

Given $A,B\subset \mathbb {R}^d$, the author considers the behavior of the intersection $A\cap T_\alpha (B)$, where $\{T_\alpha \}_\alpha$ is some family of transformations. Mattila ([10, 11]) proves a general intersection theorem for orthogonal transformations.

Theorem 5.1

(Mattila [10]) In $\mathbb {R}^d$, let $s,t>0, s+t>d$ and $t>\frac{d+1}{2}$. If $A,B\subset \mathbb {R}^d$ are Borel sets with $\mathcal {H}^s(A)>0,\mathcal {H}^t(B)>0$, then for $\theta _d$ almost all $g\in O(d)$,

$$\begin{aligned} \mathcal {L}(\{a\in \mathbb {R}^d:\dim _{{\mathcal H}}(A\cap (gB+a)\ge s+t-d\})>0, \end{aligned}$$

where $\theta _d$ is the Haar measure on $O(d)$.

There are also intersection theorems on larger transformation groups, e.g. similarities ([9, 10]).

Theorem 5.2

(Kahane [9]) Let $G$ be a closed subgroup of $GL(n,\mathbb {R})$ and let $\tau$ be a Haar measure on $G$. Let $E$ and $F$ be two $\sigma$-compact subsets of $\mathbb {R}^d$. Then for $\tau$-almost all $g\in G$ and $\epsilon >0$,

$$\begin{aligned} \mathcal {L}(\{a\in \mathbb {R}^d:\dim _{{\mathcal H}}(E\cap (gF+a))\ge \dim _{{\mathcal H}}(E)+\dim _{{\mathcal H}}(F)-d-\epsilon \})>0. \end{aligned}$$

From Theorem 5.1, it follows that when $d=2$, for every $r>0$, there exists some $a\in \mathbb {R}^2$ such that $\dim _{{\mathcal H}}(E\cap S_{a,r}^{d-1})\ge \dim _{{\mathcal H}}(E)-1>0$. Hence (1.2) holds for $d=2$. In higher dimensions it follows by the following lemma.

Lemma 5.3

Suppose $F\subset S^{d-1}\subset \mathbb {R}^d$ and $\dim _{{\mathcal H}}(F)>d-2$, then $F$ uniquely determines $S^{d-1}$, i.e. $S^{d-1}$ is the only sphere which can be determined by $F$.

Proof

It follows by induction. For $d=2$, it’s trivial because $F$ has at least three points.

Suppose it holds in $\mathbb {R}^{k-1}$. For $F\subset S^{k-1}\subset \mathbb {R}^k$ with $\dim _{{\mathcal H}}(F)>k-2$, there exists a hyperplane $P$ such that $\dim _{{\mathcal H}}(P\cap F)>k-3$ (see, e.g. [12]). Then $P\cap F$ determines the lower dimensional sphere $P\cap S^{k-1}$. Hence $F$ determines $S^{k-1}$ because there is at least one point in $F\backslash (P\cap F)$.

Note that all the intersection results above try to determine when the translation set has positive Lebesgue measure. The following theorem considers when the dilation set has positive Lebesgue measure.

Theorem 5.4

Suppose that $E\subset \mathbb {R}^d$ is compact with $\dim _{{\mathcal H}}(E)=s>1$ and $\Gamma \subset \mathbb {R}^d$ is a smooth hypersurface with nonzero Gaussian curvature. Then for a.e. $a\in \{z\in \mathbb {R}^d:E\subset \bigcup _{r\in \mathbb {R}}\Gamma _{z,r}\}$,

$$\begin{aligned} \mathcal {L}(\{r\in \mathbb {R}:\dim _{{\mathcal H}}(E\cap \Gamma _{a,r})\})\ge s-1\})>0 \end{aligned}$$

(5.1)

In particular, letting $\Gamma =S^{d-1}$, Theorem 1.3 follows from Theorem 5.4 and Lemma 5.3.

6 Proof of Theorem 5.4

Without loss of generality, one can assume that $\Gamma$ is bounded and on any line passing through the origin there is at most one point of $\Gamma$.

Let $\sigma$ denote the surface measure on $\Gamma$. Let $\{p_i\}$ be a partition of unity on $\Gamma$ such that in the support of each $p_i$, $\Gamma$ has a local coordinate system $u^i=(u_1^i,\dots ,u_{d-1}^i)$. Thus there is a well-defined coordinate system for the cone $C_i=\{rx: x\in \text {supp}\, p_i, r\in \mathbb {R}-\{0\}\}$. One can also extend $p_i$ to $C_i$ by setting $p_i(rx)=p_i(x), x\in \Gamma$. By changing variables $x=r\,x(u^i)+a$ on each $C_i+a$, it follows that

$$\begin{aligned} \begin{aligned} \int \limits _{\bigcup _r \Gamma _{a,r}}f(x)\,dx&=\sum _i\int \limits _{C_i+a}p_i(x-a)f(x)\,dx\\&=\sum _i\int \int \limits p_i(r\,x(u^i))f(r\,x(u^i)+a)|r|^{d-1}\phi _i(u^i)\,du^i\,dr\\&=\sum _i\int \limits _\mathbb {R}\int \limits _{\text {supp}\,p_i} p_i(x)f(rx+a)|r|^{d-1}\tilde{\phi }_i(x)\,d\sigma (x)\,dr\\&=\int _\mathbb {R}\int \limits _\Gamma f(rx+a)|r|^{d-1}\psi (x)\,d\sigma (x)\,dr, \end{aligned} \end{aligned}$$

(6.1)

where $\phi _i,\tilde{\phi }_i,\psi$ are smooth cut-off functions.

Since $\dim _{{\mathcal H}}(E)=s>1$, for every $\epsilon >0$, there exists a measure $\mu$ on $E$ such that the $(s-\epsilon )$-energy $I_{s-\epsilon }(\mu )<\infty$ (see, e.g. [12]). Let $q(x)=rx+a$. Define measures $\sigma _{a,r}$ on $\Gamma _{a,r}$ and $\mu _{a,r}$ on $E\cap \Gamma _{a,r}$ by

$$\begin{aligned} \begin{aligned} \sigma _{a,r}&=q_*(\psi \sigma ),\\ \mu _{a,r}&=\lim _{\delta \rightarrow 0}\mu *\rho _\delta \,d\sigma _{a,r}, \end{aligned} \end{aligned}$$

(6.2)

where $\rho _\delta (x)=\delta ^{-d}\rho (\frac{x}{\delta })$, $\rho \in C_0^\infty$ and $\int \rho =1$.

Let

$$\begin{aligned} g(r)={\left\{ \begin{array}{ll} |r|^{d-1}\Phi (r) &{} \quad \;\text {if}\ -1<r<1\\ \Phi (r) &{}\quad \;\text {otherwise} \end{array}\right. } \end{aligned}$$

(6.3)

where $\Phi \in L^1$ and $\Phi >0$ everywhere.

Lemma 6.1

Under notations above,

$$\begin{aligned} \int \int g(r)I_{s-1-\epsilon }(\mu _{a,r})\,dr\,da<\infty . \end{aligned}$$

(6.4)

Denote $\nu _{a,r}=\frac{g(r)^{\frac{1}{2}}\mu _{a,r}}{|r|^{d-1}\mu _{a,r}(\mathbb {R}^d)}$, $G_a=\{r\in \mathbb {R}:\mu _{a,r}(\mathbb {R}^d)>0\}$ and $H=\{z\in \mathbb {R}^d:E\subset \bigcup _{r\in \mathbb {R}}\Gamma _{z,r}\}$. From Lemma 6.1, $I_{s-1-\epsilon }(\mu _{a,r})<\infty$ for a.e. $(a,r)\in \mathbb {R}^d\times \mathbb {R}$. Then by (6.1), (6.2), for $a\in H$,

$$\begin{aligned} \begin{aligned} 1&=(\mu (E))^2\\&=\left( \lim _{\delta \rightarrow 0}\int \limits _{\bigcup _r\Gamma _{a,r}}\mu *\rho _\delta (x)\,dx\right) ^2\\&=\left( \lim _{\delta \rightarrow 0}\int \int \limits \mu *\rho _\delta (rx+a)|r|^{d-1}\psi (x)\,d\sigma (x)\,dr\right) ^2\\&=\left( \int \limits |r|^{d-1}\mu _{a,r}(\mathbb {R}^d) \,dr\right) ^2\\&=\left( \int \limits _{G_a}|r|^{d-1} \mu _{a,r}(\mathbb {R}^d)I_{s-1-\epsilon }^{-\frac{1}{2}}(\mu _{a,r})I_{s-1-\epsilon }^{\frac{1}{2}}(\mu _{a,r})\,dr\right) ^2\\&=\left( \int \limits _{G_a} I_{s-1-\epsilon }^{-\frac{1}{2}}(\nu _{a,r})g(r)^{\frac{1}{2}}I_{s-1-\epsilon }^{-\frac{1}{2}}(\mu _{a,r})\,dr\right) ^2\\&\le \int \limits _{G_a} I_{s-1-\epsilon }^{-1}(\nu _{a,r})\,dr \int \limits _{G_a} g(r)I_{s-1-\epsilon }(\mu _{a,r})\,dr. \end{aligned} \end{aligned}$$

(6.5)

Therefore,

$$\begin{aligned} \begin{aligned} \int \limits _{H}\left( \int \limits _{G_a} I_{s-1-\epsilon }^{-1}(\nu _{a,r})dr\right) ^{-1}da&\le \int \limits _H\int _{G_a} g(r)I_{s-1-\epsilon }(\mu _{a,r})\,dr\,da\\&\le \int \int \limits g(r)I_{s-1-\epsilon }(\mu _{a,r})\,dr\,da\\&<\infty . \end{aligned} \end{aligned}$$

(6.6)

It follows that for a.e. $a\in H$, $\int _{G_a} I_{s-1-\epsilon }^{-1}(\nu _{a,r})dr>0$. Hence for a.e. $a\in H$, $\mathcal {L}^1(G_a)>0$ and for a.e. $r\in G_a$, $I_{s-1-\epsilon }(\nu _{a,r})<\infty$. As a consequence, $\dim _{{\mathcal H}}(E\cap \Gamma _{a,r})\ge s-1-\epsilon$ for a.e. $r\in G_a$ (see, e.g. [12]). Since $G_a$ is independent of $\epsilon$, by choosing a sequence $\epsilon _j\rightarrow 0$, Theorem 5.4 follows.

7 Proof of Lemma 6.1

From the the well-known equality $I_\alpha (\mu )=c_{\alpha ,d}\int |\hat{\mu }(\xi )||\xi |^{-d+\alpha }\,d\xi$ (see, e.g. [12]) and Plancherel,

$$\begin{aligned} \begin{aligned}&\int \int g(r)I_{s-1-\epsilon }(\mu _{a,r})\,dr\,da\\&\quad =c_{\alpha ,d}\int \!\!\int \!\!\int g(r)\left| \hat{\mu }*\widehat{\sigma _{a,r}}(\xi )\right| ^2|\xi |^{-d-1+s-\epsilon }\,d\xi \,dr\,da\\&\quad =c_{\alpha ,d}\int \!\!\int \!\!\int g(r)\left| \int \hat{\mu }(\eta )\widehat{\psi \sigma }(r(\xi -\eta )) e^{-2\pi i a\cdot (\xi -\eta )}\,d\eta \right| ^2|\xi |^{-d-1+s-\epsilon }\,d\xi \,dr\,da\\&\quad =c_{\alpha ,d}\int \int \left( \int \left| \int \hat{\mu }(\eta )\widehat{\psi \sigma }(r(\xi -\eta )) e^{2\pi i a\cdot \eta }\,d\eta \right| ^2da\right) \ g(r)|\xi |^{-d-1+s-\epsilon }\,d\xi \,dr \\&\quad =c_{\alpha ,d}\int \int \left( \int \left| \hat{\mu }(a)\widehat{\psi \sigma }(r(\xi -a))\right| ^2da\right) g(r)|\xi |^{-d-1+s-\epsilon }\,d\xi \,dr\\&\quad =c_{\alpha ,d}\int \int \left( \int \left| \widehat{\psi \sigma }(r(\xi -a))\right| ^2g(r)\,dr\right) |\hat{\mu }(a)|^2|\xi |^{-d-1+s-\epsilon }\,da \,d\xi . \end{aligned} \end{aligned}$$

(7.1)

Since $\Gamma$ is smooth with nonzero Gaussian curvature everywhere, by stationary phase (see, e.g. [14]) and the construction of $g$ (see (6.3)),

$$\begin{aligned} \int |\widehat{\psi \sigma }(r(\xi -a))|^2g(r)\,dr\lesssim |\xi -a|^{-(d-1)}. \end{aligned}$$

Thus, to prove Lemma 6.1, it suffices to show

$$\begin{aligned} \int \int |\hat{\mu }(a)|^2|\xi -a|^{-(d-1)}|\xi |^{-d-1+s-\epsilon }\,da\,d\xi <\infty . \end{aligned}$$

(7.2)

For each $a\ne 0$, let $\xi =|a|\zeta$, then

$$\begin{aligned} \int |\xi -a|^{-(d-1)}|\xi |^{-d-1+s-\epsilon }\,d\xi =|a|^{-d+s-\epsilon }\int |\zeta -\frac{a}{|a|}|^{-(d-1)}|\zeta |^{-d-1+s-\epsilon }\,d\zeta . \end{aligned}$$

When $\epsilon$ is small, $1<s-\epsilon <d$, then $\int |\zeta -\frac{a}{|a|}|^{-(d-1)}|\zeta |^{-d-1+s-\epsilon }\,d\zeta <\infty$ uniformly because $\frac{a}{|a|}\in S^{d-1}$ which is compact. Hence

$$\begin{aligned} \begin{aligned} \int \int |\hat{\mu }(a)|^2|\xi -a|^{-(d-1)}|\xi |^{-d-1+s-\epsilon }\,da\,d\xi&\lesssim \int |\hat{\mu }(a)|^2|a|^{-d+s-\epsilon }\,da\\&<\infty , \end{aligned} \end{aligned}$$

(7.3)

which proves (7.2) and completes the proof of Lemma 6.1.