Near-Optimal Encoding for Sigma-Delta Quantization of Finite Frame Expansions

Abstract

In this paper we investigate encoding the bit-stream resulting from coarse Sigma-Delta quantization of finite frame expansions (i.e., overdetermined representations) of vectors. We show that for a wide range of finite-frames, including random frames and piecewise smooth frames, there exists a simple encoding algorithm—acting only on the Sigma-Delta bit stream—and an associated decoding algorithm that together yield an approximation error which decays exponentially in the number of bits used. The encoding strategy consists of applying a discrete random operator to the Sigma-Delta bit stream and assigning a binary codeword to the result. The reconstruction procedure is essentially linear and equivalent to solving a least squares minimization problem.

1 Introduction

In the modern era, the first step in signal processing consists of obtaining a digital representation of the signal of interest, i.e., quantizing it. This enables one to store, transmit, process, and analyze the signal via digital devices. Sigma-Delta (ΣΔ) quantization was proposed in the 1960’s as a quantization scheme for digitizing band-limited signals (see, e.g., [18]). Since then, and especially with the advent of very large scale integration (VLSI) technology, ΣΔ schemes have seen extensive use in the engineering community for analog-to-digital conversion of, for example, audio signals (cf. [25]). In the mathematical community, ΣΔ quantization has seen increasing interest since the work of Daubechies and DeVore [8]. In this paper, we are interested in efficiently encoding the bit-stream resulting from ΣΔ quantization of finite-frame expansions. Here one models the signal as an element in a finite dimensional space, and its samples as inner products with a spanning set of vectors. The goal is, using only the samples, to obtain a digital representation of the original signal that allows its high fidelity reconstruction.

1.1 Overview and Prior Work

For concreteness, let the vectors $\{\mathbf{f}_{i}\}_{i=1}^{N}\subset \mathbb {R}^{d}$ form a finite frame for $\mathbb {R}^{d}$. In other words, suppose there exist constants 0<A≤B<∞ such that the frame matrix $F\in \mathbb {R}^{N\times d}$ (with the vectors f _i as its rows) satisfies

$$A\Vert {\bf x}\Vert _2^2\leq\Vert F{\bf x}\Vert _2^2 \leq B\Vert {\bf x}\Vert _2^2 $$

for all $x\in \mathbb {R}^{d}$. Thus any full rank matrix is a frame matrix. In the context of data acquisition, finite frames are useful at modeling the sampling (i.e., measurement) process. In various applications, the measurement vector can be expressed as

$$ {\bf y}:=F{\bf x}\in \mathbb {R}^N . $$

(1)

For example, in imaging applications, “multiplex” systems (see, e.g., [6]) collect linear combinations of the pixels of interest, thus, their measurement vectors can be represented using (1). Such systems have been devised using coded apertures (see, e.g., [20]), as well as digital micro-mirror arrays (e.g., [10]). Indeed, by simply collecting more measurements than the ambient dimension of the image, as is often the case, and ensuring that F is full rank, we find ourselves in the finite frame setting. Similarly, systems that acquire finite dimensional signals using filter banks allow their measurement process to be modeled via (1). For a more in-depth treatment of finite frames and filter banks, see [11].

In order to allow digital storage and computer processing, including the recovery of ${\bf x}$, one must quantize the finite frame expansion (1). Quantizing the finite frame expansion of ${\bf x}$ consists of replacing the entries of the measurement vector ${\bf y}:=F{\bf x}\in \mathbb {R}^{N}$ with elements from a finite set. Giving these elements binary labels then enables digital storage and transmission of the quantized measurements. To be precise, let $\mathcal {A}\subset \mathbb {R}$ be a finite set (the quantization alphabet), and let $\mathcal{X}$ be a compact set in $\mathbb {R}^{d}$. A quantization scheme is a map

$${\mathcal {Q}}: F\mathcal{X} \mapsto \mathcal{A}^N $$

and a reconstruction scheme is an “inverse” map

$$\Delta: \mathcal{A}^N \mapsto \mathbb {R}^d. $$

Note that, depending on the practical application, one may require that the quantization schemes satisfy certain properties. For example, it is often preferred that the quantization scheme acts progressively on the measurements, i.e., as they arrive, to avoid storing too many analog quantities. Nevertheless, one seeks quantization and reconstruction schemes with approximation errors $\Vert {\bf x}- \Delta(\mathcal {Q}(F{\bf x}))\Vert _{2}$ that are as small as possible for all ${\bf x}\in\mathcal{X}$.

ΣΔ quantization schemes form an important class of such progressive quantizers, and there has been much work focusing on their application to the finite frame setting. In particular, the research on ΣΔ quantization of finite frame expansions has focused on the decay of the approximation error as a function of the number of measurements and has typically considered $\mathcal{X}=\mathcal{B}^{d}$, the Euclidean ball in $\mathbb {R}^{d}$. The work of Benedetto, Powell, and Yılmaz [4] first showed that the reconstruction error associated with 1st order ΣΔ quantization decays linearly in the number of measurements. Several results followed, improving on this linear error decay by using various combinations of specialized frames, higher order quantization schemes, and different reconstruction techniques. Blum et al. [5] showed that frames with certain smoothness properties allow for polynomial decay in the ΣΔ reconstruction error, provided appropriate alternative dual frames are used for reconstruction. Motivated by applications in compressed sensing, a similar result [16] was shown for random frames whose elements are Gaussian random variables. This was followed by the results of [21] and [22] showing that there exist (deterministic and random) frames for which higher order ΣΔ schemes yield approximation errors that behave like $e^{-c\sqrt{\frac {N}{d}}}$, where c is a constant. Specifically, in [21, 22] this root-exponential accuracy is achieved by carefully choosing the order of the scheme as a function of the oversampling rate N/d. For a more comprehensive review of ΣΔ schemes applied to finite frames, see [26].

While the above results progressively improved on the coding efficiency of ΣΔ quantization, it remains true that even the root-exponential performance $e^{-c\sqrt{\frac{N}{d}}}$ of [21, 22] is generally sub-optimal from an information theoretic perspective, including in the case where $\mathcal{X}=\mathcal {B}^{d}$. To be more precise, any quantization scheme tasked with encoding all possible points in $\mathcal{B}^{d}$ to within ϵ-accuracy must produce outputs which, in the case of an optimal encoder, each correspond to a unique subset of the unit ball having radius at most ϵ. Covering each of these subsets with a ball of radius at most ϵ then produces an ϵ-cover of $\mathcal{B}^{d}$. A simple volume argument now shows that covering $\mathcal{B}^{d}$ with balls of radius ϵ requires one to use at least $(\frac {1}{\epsilon} )^{d}$ such ϵ-balls.¹ Thus, quantizing $\mathcal{B}^{d}$ via an optimal map requires at least $d\ln{\frac {c}{\epsilon}}$ bits, or, viewed slightly differently: optimally quantizing $\mathcal{B}^{d}$ with b-bits yields an approximation error of the form $e^{-c \frac{b}{d}}$, where $c \in\mathbb{R}^{+}$ is a universal constant. Observing that the number of bits that result from a ΣΔ scheme is proportional to N and that the best known error rates are root-exponential in N, we conclude that ΣΔ schemes are sub-optimal.

This fact has been recognized in the mathematical literature on ΣΔ quantization. In particular, in the case where d=1 and the frame F is the N×1 repetition frame with F _i1=1 for all i∈[N], there has been research seeking upper bounds on the maximum number of possible ΣΔ bit-streams (cf. [2, 15, 17]). For example, [17] showed that asymptotically in N, the number of bit-streams is bounded by O(N ²) for first order single-bit ΣΔ schemes with certain initial conditions. This indicates that by losslessly encoding the possible ΣΔ bitstreams into codewords of length O(log(N)), one can achieve the desired exponential error rates. However, to do that one needs to identify the O(N ²) achievable sequences from among the 2^N potential ones, which to our knowledge is an unsolved problem. Moreover, to our knowledge, not much is known about the number of codewords generated by ΣΔ quantization in more general settings.

To help remedy this situation, this paper introduces a potentially lossy encoding stage, consisting of the map

$$\mathcal{E}: \mathcal{A}^N \mapsto{\mathcal{C}}, $$

where $\mathcal{C}$ is such that $|\mathcal{C}| \ll|\mathcal{A}^{N}|$. Consequently, $\log_{2}|\mathcal{C}|$ bits are sufficient for digitally representing the output of this encoder. To accommodate this additional encoding, the reconstruction is modified to approximate ${\bf x}$ directly from $\mathcal{C}$. Thus, we propose a decoder

$$\Delta: \mathcal{C} \mapsto \mathbb {R}^d, $$

where both the proposed decoder, Δ, and the proposed encoding map, $\mathcal{E}$, are linear, hence computationally efficient.

1.2 Contributions

For stable ΣΔ quantization schemes, we show that there exists an encoding scheme $\mathcal{E}$ acting on the output $\mathcal{Q}(F{\bf x})$ of the quantization, and a decoding scheme Δ, such that

$$ \left . \begin{array} {@{}l@{}} \displaystyle\epsilon_{\varSigma \Delta }:=\max_{{\bf x}\in\mathcal{B}^d} \bigl\Vert {\bf x}- \Delta \bigl( \mathcal{E} \bigl(\mathcal {Q}(F{\bf x}) \bigr) \bigr) \bigr\Vert _2 \leq CN^{-\alpha} \\ b_{\varSigma \Delta }:=\ln|\mathcal{C}| \leq C' d\ln N, \end{array} \right \}\quad{\implies}\quad \epsilon_{\varSigma \Delta } \leq\exp \biggl({-c \frac{b_{\varSigma \Delta }}{d}} \biggr). $$

where α, C, C′, and c are positive constants that depend on the ΣΔ scheme and d. More specifically:

• 1. We show that there exist frames (the Sobolev self-dual frames), for which encoding by random subsampling of the integrated ΣΔ bit-stream (and labeling the output) yields an essentially optimal rate-distortion tradeoff up to logarithmic factors of d.

• 2. We show that random Bernoulli matrices in $\mathbb {R}^{m\times d}$, with m≈d, are universal encoders. Provided one has a good frame for ΣΔ quantization, such Bernoulli matrices yield an optimal rate-distortion tradeoff, up to constants.

• 3. We show that in both cases above, the decoding can be done linearly and we provide an explicit expression for the decoder.

These contributions are made explicit in Theorems 3 and 4. Additionally, we note that ΣΔ schemes (see Sect. 2) act progressively on the samples ${\bf y}=F{\bf x}$, and do not require explicit knowledge of the frame that produced ${\bf y}$. Similarly, the Bernoulli encoding of the ΣΔ bit-stream does not require knowledge of the underlying frame. Nevertheless, and somewhat surprisingly, this encoding method allows the compression of the ΣΔ-bitstream in a near optimal manner. It also allows the decoding to be done linearly via an operator $\mathbb {R}^{m} \mapsto \mathbb {R}^{d}$, hence in time proportional to md, as opposed to time proportional to Nd needed (in general) for reconstructing a signal from its unencoded ΣΔ bitstream. One of the favorable properties of coarse ΣΔ quantization schemes is their robustness to certain errors that can arise in practice due to (for example) circuit imperfections (cf. [8]). Such imperfections can affect the elements that implement scalar quantization (i.e., assigning discrete values to continuous ones by toggling at a threshold), or multiplication. We remark that our methods for compressing the ΣΔ bit-stream inherit whatever robustness properties the original ΣΔ quantizer possesses. In other words, by compressing the bit-stream, we do not lose any of the desirable properties of ΣΔ quantization.

1.3 Organization

In Sect. 2, we introduce notation and provide a mathematical overview of ΣΔ quantization. We also state certain results on random matrices, in particular Johnson-Lindenstrauss embeddings, which will be useful in the remainder of the paper. In Sect. 3 we show that random subsampling of the discretely integrated ΣΔ bit-stream allows a linear decoder to achieve exponentially decaying reconstruction error, uniformly for all ${\bf x}\in\mathcal{B}^{d}$. This result pertains to a particular choice of frames, the Sobolev self-dual frames [21], and is contingent on using 1st order ΣΔ schemes. In Sect. 4 we instead use a Bernoulli matrix for reducing the dimensionality of the integrated ΣΔ-bit stream. Here, our result is more general and applies to stable ΣΔ schemes of arbitrary order, as well as to a large family of smooth and random frames. Finally, in Sect. 5 we illustrate our results with numerical experiments.

2 Preliminaries

Below we will denote the set $\{ 1, 2, \dots, n-1, n \} \subset\mathbb {N}$ by [n]. For any matrix $M \in\mathbb{R}^{m \times N}$ we will denote the jth column of M by ${\bf M}_{j} \in\mathbb{R}^{m}$. Furthermore, for a given subset $\mathcal{S} = \{ s_{1}, \dots, s_{n} \} \subset[N]$ with s ₁<s ₂<⋯<s _n , we will let $M_{\mathcal{S}} \in\mathbb{R}^{m \times n}$ denote the submatrix of M given by

$$M_{\mathcal{S}} := ( {\bf M}_{s_1} \cdots {\bf M}_{s_n} ). $$

The transpose of a matrix, $M \in\mathbb{R}^{m \times N}$, will be denoted by $M^{\rm T} \in\mathbb{R}^{N \times m}$, and the singular values of any matrix $M \in\mathbb{R}^{m \times N}$ will always be ordered as σ ₁(M)≥σ ₂(M)≥…≥σ _min(m,N)(M)≥0. We will denote the standard indicator function by

$$\delta_{i,j} := \left \{ \begin{array}{@{}l@{\quad}l@{}} 1 & \mathrm{if}~i=j\\ 0 & \mathrm{if}~i \neq j , \end{array} \right . $$

for $i,j \in\mathbb{N}$. Finally, given a frame matrix F, we define its Moore-Penrose pseudo-inverse to be F ^† :=(F ^T F)⁻¹ F ^T.

2.1 Sigma-Delta Quantization

Let $\mathcal{B}^{d}$ be the Euclidean unit ball in $\mathbb{R}^{d}$. Given ${\bf x} \in\mathcal{B}^{d}$, and a frame matrix $F \in\mathbb{R}^{N \times d}$, the simplest ΣΔ quantization scheme considered herein, in Sect. 3, is the single bit first order greedy scheme. Given ${\bf y}=F{\bf x}$, this scheme computes a vector ${\bf q} \in\{ -1, 1 \}^{N}$ via the following recursion with initial condition u ₀=0:

$$\begin{aligned} &q_i = \textrm{sign} ( y_i + u_{i-1} ), \end{aligned}$$

(2)

$$\begin{aligned} & u_i = y_i + u_{i-1} - q_i \end{aligned}$$

(3)

for all i∈[N]. To analyze this scheme as well as higher order schemes, it will be convenient to introduce the difference matrix, $D \in\mathbb{R}^{N \times N}$, given by

$$ D_{i,j} := \left \{ \begin{array}{@{}l@{\quad}l@{}} 1 & \textrm{if}~i=j\\ -1 & \textrm{if}~i = j+1\\ 0 & \textrm{otherwise}. \end{array} \right . $$

(4)

We may restate the relationships between ${\bf x}$, ${\bf u}$, and ${\bf q}$ resulting from the above scheme as

$$ D {\bf u} = F {\bf x} - {\bf q}. $$

(5)

Furthermore, a short induction argument shows that |u _i |≤1 for all i∈[N] provided that |y _i |≤1 for all i∈[N].

More generally, for a given alphabet $\mathcal {A}$ and $r \in\mathbb{Z}^{+}$ we may employ an rth-order ΣΔ quantization scheme with quantization rule $\rho: \mathbb{R}^{r+1} \mapsto\mathbb{R}$ and scalar quantizer $Q:\mathbb{R}\mapsto\mathcal{A}$. Such a scheme, with initial conditions u ₀=u ₋₁=⋯=u _1−r =0, computes ${\bf q}\in \mathcal {A}^{N}$ via the recursion

$$\begin{aligned} &q_i = Q \bigl(\rho(y_i,u_{i-1},u_{i-2}, \dots,u_{i-r}) \bigr), \end{aligned}$$

(6)

$$\begin{aligned} & u_i = y_i - q_i - \sum ^{r}_{j=1} {r \choose j} (-1)^j u_{i-j} \end{aligned}$$

(7)

for all i∈[N]. Here, the scalar quantizer Q is defined via its action

$$Q(v) = \operatorname*{arg\,min}_{q\in \mathcal {A}}|q-v|. $$

In this paper, we focus on midrise alphabets of the form

$$ \mathcal{A}^{\delta}_K=\bigl\{\pm (2n-1) \delta/2: n \in[K]\bigr\}, $$

(8)

where δ denotes the quantization step size. For example, when K=1, we have the 1-bit alphabet $\mathcal{A}_{1}^{\delta}=\{\pm\frac {\delta}{2} \}$. As before, we may restate the relationships between ${\bf x}$, ${\bf u}$, and ${\bf q}$ as

$$ D^r {\bf u} = F {\bf x} - {\bf q}. $$

(9)

As in the case of the first order scheme, we will ultimately need a bound on $\Vert {\bf u} \Vert _{\infty} := \max_{i \in[N]} |u_{i}|$ below. Hence, we restrict our attention to stable rth-order schemes. That is, rth-order schemes for which (6) and (7) are guaranteed to always produce vectors ${\bf u} \in\mathbb{R}^{N}$ having $\Vert {\bf u} \Vert _{\infty} \leq{C}_{\rho ,Q}(r)$ for all $N \in\mathbb{N}$, and ${\bf y} \in\mathbb{R}^{N}$ with $\Vert {\bf y}\Vert _{\infty}\leq1$. Moreover, for our definition of stability we require that $C_{\rho,Q}: \mathbb{N} \mapsto\mathbb{R}^{+}$ be entirely independent of both N and ${\bf y}$. Finally, it is important to note that stable rth-order ΣΔ schemes with C _ρ,Q (r)=O(r ^r) do indeed exist (see, e.g., [9, 14]), even when $\mathcal{A}$ is a 1-bit alphabet. In particular, we cite the following proposition [9] (cf. [21]).

Proposition 1

There exists a universal constant c>0 such that for any midrise quantization alphabet $\mathcal{A}=\mathcal{A}^{\delta}_{L}$, for any order $r\in\mathbb{N}$, and for all $\eta<\delta (L-\frac{1}{2} )$, there exists an rth order ΣΔ scheme which is stable for all input signals y with ∥y∥_∞≤η. It has

$$ \Vert u\Vert _\infty\leq c C^r r^r \frac{\delta}{2}, $$

(10)

where

$$C = \biggl( \biggl\lceil\frac{\pi^2}{(\cosh^{-1} \gamma)^2} \biggr\rceil\frac{e}{\pi} \biggr)\quad \mathit{and}\quad \gamma:=2L-\frac{2\eta}{\delta}. $$

In what follows we will need the singular value decomposition of D essentially computed by von Neumann in [27] (see also [21]). It is D=UΣV ^T, where

$$\begin{aligned} U_{i,j} =& \sqrt{\frac{2}{N + 1/2}} \cos \biggl( \frac{2(i-1/2)(N - j + 1/2) \pi}{2N + 1} \biggr), \end{aligned}$$

(11)

$$\begin{aligned} \varSigma_{i,j} =& \delta_{i,j}\sigma_j(D) = 2 \delta_{i,j} \cos \biggl( \frac{j \pi}{2N + 1} \biggr), \end{aligned}$$

(12)

and

$$ V_{i,j} = (-1)^{j+1} \sqrt{\frac{2}{N + 1/2}} \sin \biggl( \frac{2 i j}{2N + 1} \pi \biggr). $$

(13)

Note that the difference matrix, D, is full rank (e.g., see (12)). Thus, we may rearrange (5) to obtain

$$ {\bf u} = D^{-1}F{\bf x} - D^{-1}{\bf q}. $$

(14)

More generally, rearranging (9) tells us that

$$ {\bf u} = D^{-r}F{\bf x} - D^{-r}{\bf q} $$

(15)

for any rth-order scheme.

2.2 Johnson-Lindenstrauss Embeddings and Bounded Orthonormal Systems

We will utilize linear Johnson-Lindenstrauss embeddings [1, 3, 7, 13, 19, 23] of a given finite set $\mathcal{S} \subset\mathbb{R}^{N}$ into $\mathbb{R}^{m}$.

Definition 1

Let ϵ,p∈(0,1), and $\mathcal{S} \subset\mathbb{R}^{N}$ be finite. An m×N matrix M is a linear Johnson-Lindenstrauss embedding of $\mathcal{S}$ into $\mathbb{R}^{m}$ if the following holds with probability at least 1−p:

$$(1 - \epsilon) \Vert {\bf u} - {\bf v} \Vert _2^2 \leq \Vert M{\bf u} - M{\bf v} \Vert _2^2 \leq(1 + \epsilon) \Vert {\bf u} - {\bf v} \Vert _2^2 $$

for all ${\bf u},{\bf v} \in\mathcal{S}$. In this case we will say that M is a JL(N,m,ϵ,p)-embedding of $\mathcal{S}$ into $\mathbb{R}^{m}$.

We will say that a matrix B∈{−1,1}^m×N is a Bernoulli random matrix iff each of its entries is independently and identically distributed so that

$$\mathbb{P} [B_{i,j} = 1 ] = \mathbb{P} [B_{i,j} = -1 ]= \frac{1}{2} $$

for all i∈[m] and j∈[N]. The following theorem is proven in [1].

Theorem 1

Let $m, N \in\mathbb{N}$, $\mathcal{S} \subset\mathbb{R}^{N}$ finite, and ϵ,p∈(0,1). Let B∈{−1,1}^m×N be a Bernoulli random matrix, and set $\widetilde{B} = \frac{1}{\sqrt{m}}B$. Then, $\widetilde{B}$ will be a JL(N,m,ϵ,p)-embedding of $\mathcal{S}$ into $\mathbb{R}^{m}$ provided that $m \geq\frac{4 + 2 \log _{|\mathcal{S}|}(1/p)}{\epsilon^{2}/2 - \epsilon^{3}/3} \ln|\mathcal{S}|$.

Let $\mathcal{D} \subset\mathbb{R}^{n}$ be endowed with a probability measure μ. Further, let Ψ={ψ ₁,…,ψ _N } be an orthonormal set of real-valued functions on $\mathcal{D}$ so that

$$\int_{\mathcal{D}} \psi_i ({\bf t} ) \overline{ \psi_j ({\bf t})} d \mu ( {\bf t} ) = \delta_{i,j}. $$

We will refer to any such Ψ as an orthonormal system. More specifically, we utilize a particular type of orthonormal system:

Definition 2

We call Ψ={ψ ₁,…,ψ _N } a bounded orthonormal system with constant $K \in\mathbb{R}^{+}$ if

$$\Vert \psi_k \Vert _{\infty} := \sup_{{\bf t} \in \mathcal{D}} \bigl \vert \psi ( {\bf t} ) \bigr \vert \leq K\quad \mbox{for all}~k \in[N]. $$

For any orthonormal system, Ψ, on $\mathcal{D} \subset\mathbb {R}^{n}$ with probability measure μ, we may create an associated random sampling matrix, $R' \in\mathbb{R}^{m \times N}$, as follows: First, select m points ${\bf t}_{1}, \ldots, {\bf t}_{m} \in \mathcal{D}$ independently at random according to μ.² Then, form the matrix R′ by setting $R'_{i,j} := \psi_{j} ( {\bf t}_{i} )$ for each i∈[m] and j∈[N]. The following theorem concerning random sampling matrices created from bounded orthonormal systems is proven in [12].³

Theorem 2

Let $R' \in\mathbb{R}^{m \times N}$ be a random sampling matrix created from a bounded orthonormal system with constant K. Let $\mathcal{S} \subset[N]$ have cardinality $|\mathcal{S}| = d$, and set $\widetilde{R'} = \frac{1}{\sqrt{m}}R'$. Then, for ϵ∈(0,1), we will have

$$\sqrt{1 - \epsilon} \leq \sigma_d \bigl(\widetilde{R'}_{\mathcal{S}} \bigr) \leq \sigma_1 \bigl( \widetilde{R'}_{\mathcal{S}} \bigr) \leq \sqrt{1 + \epsilon} $$

with probability at least 1−p provided that m≥(8/3)K ² ϵ ⁻² dln(2d/p).

Note that Theorem 2 also applies to the special case where our orthonormal system, Ψ, consists of the N columns of a rescaled unitary matrix $U \in\mathbb{R}^{N \times N}$ (i.e., $\psi _{j} = \sqrt{N} {\bf U}_{j}$ for all j∈[N]). Here, $\mathcal{D} = [N] \subset\mathbb{R}$, $\psi_{j}(i) = \sqrt{N}U_{i,j}$ for all i,j∈[N], and μ is the discrete uniform measure on [N]. In this case we will consider the random sampling matrix, R′, for Ψ to be the product $\sqrt{N}RU$, where R∈{0,1}^m×N is a random matrix with exactly one nonzero entry per row (which is selected uniformly at random). We will refer to any such random matrix, R∈{0,1}^m×N, as a random selector matrix.

3 Exponential Accuracy for First Order Sigma-Delta via Random Sampling

In this section we will deal only with first order Sigma-Delta. Hence, given ${\bf x} \in\mathcal{B}^{d}$, the vectors ${\bf q}, {\bf u} \in \mathbb{R}^{N}$ will always be those resulting from (2) and (3) above. Our objective in this section is to demonstrate that a small set of sums of the bit stream produced by the first order scheme considered herein suffices to accurately encode the vector being quantized. Furthermore, and somewhat surprisingly, the number of sums we must keep in order to successfully approximate the quantized vector is entirely independent of N (though the reconstruction error depends on N). Proving this will require the following lemma.

Lemma 1

For every ${\bf x} \in\mathcal{B}^{d}$ we will have $D^{-1}{\bf q} \in \{ -N, \dots, N \}^{N} \subset\mathbb{Z}^{N}$.

Proof

Note that q _i ∈{−1,1} for all i∈[N] (see (2)). Furthermore, it is not difficult to check that

$$\bigl( D^{-1} \bigr)_{i,j} = \left \{ \begin{array}{@{}l@{\quad}l@{}} 1 & \textrm{if}~j \leq i\\ 0 & \textrm{otherwise}. \end{array} \right . $$

Thus, we have that $( D^{-1}{\bf q} )_{i} \in\{ -i, \dots, i \}$ for all i∈[N]. □

We are new equipped to prove the main theorem of this section.

Theorem 3

Let ϵ,p∈(0,1), and R∈{0,1}^m×N be a random selector matrix. Then, there exists a frame $F \in\mathbb{R}^{N \times d}$ such that

$$\bigl \Vert {\bf x} - \bigl(RD^{-1}F \bigr)^{\dagger} R D^{-1} {\bf q} \bigr \Vert _2 \leq\frac{ \sqrt{2} \pi}{\sqrt{1 - \epsilon}} \biggl( \frac {d^{\frac{3}{2}}}{N} \biggr) $$

for all ${\bf x} \in\mathcal{B}^{d} \subset\mathbb{R}^{d}$ with probability at least 1−p, provided that m≥(16/3)ϵ ⁻² d×ln(2d/p). Here, q is the output of the first order ΣΔ quantization scheme (2) and (3), applied to $F{\bf x}$. Furthermore, $R D^{-1} {\bf q}$ can always be encoded using b≤m(log₂ N+1) bits.

Proof

Let $U, \varSigma, V \in\mathbb{R}^{N \times N}$ be defined as in (11), (12), and (13), respectively. Define $F \in\mathbb{R}^{N \times d}$ to be the (renormalized) last d columns of U,

$$ F := \sqrt{\frac{N}{2d}} ( {\bf U}_{N-d+1} \cdots{\bf U}_N ). $$

(16)

We refer to the frame corresponding to F as the 1st order Sobolev self-dual frame. Denoting the ith row of F by ${\bf f}_{i} \in\mathbb{R}^{d}$, we note that (11) implies that

$$ \Vert {\bf y} \Vert _{\infty} = \Vert F {\bf x} \Vert _{\infty} \leq \max_{i \in[N]} \Vert {\bf f}_i \Vert _2 \Vert {\bf x} \Vert _2\leq\sqrt{ \frac{N}{2d}}\sqrt{\frac{2d}{N+1/2}} \cdot\Vert {\bf x} \Vert _2 \leq 1 $$

(17)

for all ${\bf x} \in\mathcal{B}^{d}$. Now, apply the random selector matrix, R, to (14) to obtain

$$ R{\bf u} = RD^{-1}F{\bf x} - RD^{-1}{\bf q}. $$

Since our goal is to obtain an upper bound on

$$ \bigl\Vert \bigl(RD^{-1}F\bigr)^\dagger R{\bf u}\bigr\Vert _2 = \bigl\Vert {\bf x} - \bigl(RD^{-1}F\bigr)^\dagger RD^{-1}{\bf q}\bigr\Vert _2 $$

(18)

and since ∥Ru∥₂ is easily controlled (see the discussion after (5)), it behooves us to study $RD^{-1}F \in\mathbb {R}^{m \times d}$. Observe that

$$ D^{-1}F = \sqrt{\frac{N}{2d}} V \varSigma^{-1} U^{\rm T} ( {\bf U}_{N-d+1} \cdots{\bf U}_N ) = \sqrt{ \frac{N}{2d}} \bigl( ({\bf V})_{N-d+1} \cdots({\bf V})_N \bigr) \widetilde{\varSigma}, $$

(19)

where $\widetilde{\varSigma} \in\mathbb{R}^{d \times d}$ has

$$\widetilde{\varSigma}_{i,j} ~=~ \frac{\delta_{i,j}}{\sigma_{N-d+j}(D)}. $$

Let $\mathcal{S} = \{ N-d+1, \dots, N \} \subset[N]$. Then,

$$RD^{-1}F ~=~ \sqrt{\frac{N}{2d}} R V_{\mathcal{S}} \widetilde{ \varSigma } ~=~ \sqrt{\frac{m}{2d}} \biggl( \frac{\sqrt{N} R V}{\sqrt{m}} \biggr)_{\mathcal{S}} \widetilde{\varSigma}. $$

Applying Theorem 2 now tells us that

$$ \sqrt{\frac{m}{2d}} \cdot\frac{\sqrt{1 - \epsilon}}{\sigma_{N-d+1}(D)} ~\leq~ \sigma_d \bigl( RD^{-1}F \bigr)~\leq~\sigma_1 \bigl( RD^{-1}F \bigr) ~\leq~ \sqrt{\frac{m}{2d}} \cdot \frac{\sqrt{1+ \epsilon }}{\sigma_{N}(D)} $$

(20)

with probability at least 1−p, provided that m≥(16/3)ϵ ⁻² dln(2d/p).

Whenever (20) holds we may approximate ${\bf x} \in \mathcal{B}^{d}$ by

$$\hat{\bf x} : = \bigl(RD^{-1}F \bigr)^{\dagger} R D^{-1} {\bf q}, $$

and then use (18) to estimate the approximation error as

$$\Vert {\bf x} - \hat{\bf x} \Vert _2 ~=~ \bigl \Vert \bigl(RD^{-1}F \bigr)^{\dagger} R {\bf u} \bigr \Vert _2 ~\leq~ \sqrt{\frac{2d}{m}} \cdot\frac{\sigma_{N-d+1}(D)}{\sqrt{1 - \epsilon}} \Vert R {\bf u} \Vert _2. $$

Using (12) and recalling that |u _i |≤1 for all i∈[N] since |y _i |≤1 for all i∈[N] (see (17)), we obtain

$$\begin{aligned} \Vert {\bf x} - \hat{\bf x} \Vert _2 \leq& \frac{2 \sqrt{2d}}{\sqrt{1 - \epsilon}} \cdot \cos \biggl( \frac{(N-d+1) \pi}{2N + 1} \biggr) \\ \leq& \frac{2 \sqrt{2d}}{\sqrt{1 - \epsilon}} \cdot \biggl(\frac{\pi}{2} - \frac{(N-d+1) \pi}{2N + 1} \biggr) \\ \leq& \frac{\sqrt{2}\pi}{\sqrt{1 - \epsilon}} \biggl( \frac{d^{\frac{3}{2}}}{N} \biggr). \end{aligned}$$

Finally, Lemma 1 tells us that $R D^{-1} {\bf q}$ can always be encoded using b≤m(log₂ N+1) bits. □

Remark 1

Theorem 3 provides the desired exponentially decaying rate-distortion bounds. In particular, by choosing the smallest integer m≥(16/3)ϵ ⁻² dln(2d/p), the rate is

$$\mathcal{R} = m ( \log_2 N + 1), $$

and the distortion is

$$\mathcal{D} = \frac{\sqrt{2} \pi d^{3/2}}{N\sqrt{1 - \epsilon}}. $$

Expressing the distortion in terms of the rate, we obtain

$$ \mathcal{D}(\mathcal{R}) = \frac{2 \sqrt{2} \pi d^{3/2}}{\sqrt{1 - \epsilon}} \cdot2^{-\mathcal{R}/m} = C_1(\epsilon) \cdot d^{3/2} \exp \biggl( - \frac{\mathcal{R}}{C_2(\epsilon) d \ln(2d/p)} \biggr). $$

(21)

Above, $C_{1}(\epsilon) = 2 \pi\cdot\sqrt{\frac{2}{1-\epsilon}}$ and $\frac{16}{3 \ln2 \cdot\epsilon^{2}} + \frac{1}{d \ln2 \cdot\ln (2d/p)} \geq C_{2}(\epsilon) \geq\frac{16}{3 \ln2 \cdot\epsilon^{2}}$.

Theorem 3 demonstrates that only O(logN)-bits must be saved and/or transmitted in order to achieve O(1/N)-accuracy (neglecting other dependencies). Moreover, from a practical point of view the use of random sampling matrices is appealing as they allow for the O(logN) bits to be computed “on the fly” and with minimal cost. However, the first order scheme we consider herein has deficiencies that merit additional consideration. Primarily, the first order scheme (2) and (3) must still be executed before its output bitstream can be compressed. Hence, utilizing the compressed sigma delta encoding described in this section has an O(N) “cost” associated with it (as the N-dimensional vector $F{\bf x}$ must be acquired and quantized). This cost may be prohibitive for some applications. Compared to the first order scheme we considered here, higher order schemes can allow the same reconstruction accuracy with a smaller number of measurements. Hence, we will consider results for higher order schemes (and more general frames) in the next section.

4 Exponential Accuracy for General Frames and Orders via Bernoulli Random Matrices

In this section we will deal with a more general class of stable rth-order Sigma-Delta schemes. Hence, given ${\bf x} \in \mathcal{B}^{d}$, the vectors ${\bf q}, {\bf u} \in\mathbb{R}^{N}$ will always be those resulting from (6) and (7) above. The main result of this section will require the following lemma, which is essentially proven in [3].

Lemma 2

Let ϵ,p∈(0,1), $\{ {\bf v}_{1}, \dots, {\bf v}_{d} \} \subset \mathbb{R}^{N}$, and B∈{−1,1}^m×N be a Bernoulli random matrix. Set $\widetilde{B} = \frac{1}{\sqrt{m}}B$. Then,

$$(1 - \epsilon) \Vert {\bf x } \Vert _2 \leq\Vert \widetilde{B} { \bf x} \Vert _2 \leq(1 + \epsilon) \Vert {\bf x} \Vert _2 $$

for all ${\bf x} \in\textrm{span} \{ {\bf v}_{1}, \dots, {\bf v}_{d} \}$ with probability at least 1−p, provided that

$$m \geq\frac{4 d \ln(12/ \epsilon) + 2 \ln(1/p)}{\epsilon^2/8 - \epsilon^3/24}. $$

Proof

Combine Theorem 1 with the proof of Lemma 5.1 and the subsequent discussion in [3]. □

In addition to considering more general rth-order quantization schemes, we will also consider a more general class of frames, $F \in \mathbb{R}^{N \times d}$. More specifically, we will allow any frame matrix which adheres to the following definition.

Definition 3

We will call a frame matrix $F \in\mathbb{R}^{N \times d}$ an (r,C,α)-frame if

• 1. $\Vert F{\bf x} \Vert _{\infty} \leq1$ for all ${\bf x} \in\mathcal {B}^{d}$, and

• 2. σ _d (D ^−r F)≥C⋅N ^α.

Roughly speaking, the first condition of Definition 3 ensures that the frame F is uniformly bounded, while the second condition can be interpreted as a type of smoothness requirement. We are now properly equipped to prove the main theorem of this section.

Theorem 4

Let ϵ,p∈(0,1), B∈{−1,1}^m×N be a Bernoulli random matrix, and $F \in\mathbb{R}^{N \times d}$ be an (r,C,α)-frame with $r \in\mathbb{N}$, α∈(1,∞), and $C \in\mathbb{R}^{+}$. Consider q, the quantization of $F{\bf x}$ via a stable rth-order scheme with alphabet $\mathcal {A}_{A}^{2\mu}$ and stability constant ${C}_{\rho,Q}(r) \in\mathbb{R}^{+}$ (see (6), (7), (8) and the subsequent discussion). Then, the following are true.

• (i) The reconstruction error (i.e., the distortion) satisfies

  $$\bigl \Vert {\bf x} - \bigl({B}D^{-r}F \bigr)^{\dagger} B D^{-r} {\bf q} \bigr \Vert _2 \leq \frac{{C}_{\rho,Q}(r) \cdot N^{1 - \alpha}}{C \cdot (1 - \epsilon)} $$

  for all ${\bf x} \in\mathcal{B}^{d} \subset\mathbb{R}^{d}$ with probability at least 1−p, provided that $m \geq\frac{4 d \ln(12/ \epsilon) + 2 \ln(1/p)}{\epsilon^{2}/8 - \epsilon^{3}/24}$.

• (ii) $B D^{-r} {\bf q}$ can always be encoded using b≤m[(r+1)log₂ N+log₂ A+1] bits.

Proof

Apply a Bernoulli random matrix, B∈{−1,1}^m×N, to (15) and then renormalize by m ^−1/2 to obtain

$$ \widetilde{B} {\bf u} = \widetilde{B}D^{-r}F{\bf x} - \widetilde {B}D^{-r}{\bf q}, $$

(22)

where $\widetilde{B} = \frac{1}{\sqrt{m}}B$. Considering $\widetilde {B}D^{-r}F \in\mathbb{R}^{m \times d}$, we note that Lemma 2 guarantees that $\widetilde{B}$ is an near-isometry on $\textrm{span} \{ D^{-r}{\bf F}_{1}, \dots, D^{-r}{\bf F}_{d} \}$. Thus,

$$ (1 - \epsilon) \cdot C \cdot N^{\alpha} \leq \sigma_d \bigl( \widetilde{B}D^{-r}F \bigr) $$

(23)

with probability at least 1−p, provided that $m \geq\frac{4 d \ln (12/ \epsilon) + 2 \ln(1/p)}{\epsilon^{2}/8 - \epsilon^{3}/24}$.

Given that (23) holds, we may approximate ${\bf x} \in \mathcal{B}^{d}$ using $B D^{-r} {\bf q} \in\mu\mathbb{Z}^{m}$ by

$$\hat{\bf x} : = \frac{1}{\sqrt{m}} \bigl(\widetilde{B}D^{-r}F \bigr)^{\dagger} B D^{-r} {\bf q} = \bigl(\widetilde{B}D^{-r}F \bigr)^{\dagger} \widetilde{B} D^{-r} {\bf q}, $$

and then use (22) to estimate the approximation error as

$$\Vert {\bf x} - \hat{\bf x} \Vert _2 = \bigl \Vert \bigl( \widetilde{B}D^{-r}F \bigr)^{\dagger} \widetilde{B} {\bf u} \bigr \Vert _2 = \bigl \Vert \bigl({B}D^{-r}F \bigr)^{\dagger} B {\bf u} \bigr \Vert _2 \leq \frac{N^{- \alpha}}{C \cdot(1 - \epsilon)} \Vert \widetilde{B} {\bf u} \Vert _2. $$

Noting that $\Vert {\bf u} \Vert _{\infty} \leq{C}_{\rho,Q}(r)$ since $\Vert F{\bf x} \Vert _{\infty} \leq1$ (by definition of (r,C,α)-frames), we obtain

$$\Vert {\bf x} - \hat{\bf x} \Vert _2 \leq \frac{N^{- \alpha}}{C \cdot(1 - \epsilon)} \Vert \widetilde{B} {\bf u} \Vert _2 \leq\frac {{C}_{\rho,Q}(r) \cdot N^{1 - \alpha}}{C \cdot(1 - \epsilon)}. $$

Finally, a short argument along the lines of Lemma 1 tells us that $B D^{-r} {\bf q} \in\mu\mathbb{Z}^{m}$ will always have $\Vert B D^{-r} {\bf q} \Vert _{\infty} \leq2 \mu A \cdot N^{r+1}$. Thus, $B D^{-r} {\bf q}$ can be encoded using b≤m[(r+1)log₂ N+log₂ A+1] bits. Note that μ does not influence the number of required bits. □

Remark 2

Theorem 4 also provides the desired exponentially decaying rate-distortion bounds. In particular, by choosing the smallest integer $m \geq\frac{4 d \ln(12/ \epsilon) + 2 \ln (1/p)}{\epsilon^{2}/8 - \epsilon^{3}/24}$, the rate is

$$\mathcal{R} = m \bigl[ (r+1) \log_2 N + \log_2 A + 1 \bigr], $$

and the distortion is

$$\mathcal{D} = \frac{{C}_{\rho,Q}(r) \cdot N^{1 - \alpha}}{C \cdot(1 - \epsilon)}. $$

Expressing the distortion in terms of the rate, we obtain

$$\begin{aligned} \mathcal{D}(\mathcal{R}) =& \frac{{C}_{\rho,Q}(r) \cdot(2A)^{(\alpha -1)/(r+1)}}{C \cdot(1 - \epsilon)} \cdot2^{-(\mathcal{R} (\alpha- 1)/m(r+1))} \\ \leq& \bar{C}_{\rho,Q}(A,\epsilon,\alpha,r) \cdot\exp \biggl( - \frac{\mathcal{R}}{d \cdot C_3(\epsilon,p)} \biggr). \end{aligned}$$

(24)

Above, $\bar{C}_{\rho,Q}(A,\epsilon,\alpha,r) = \frac{{C}_{\rho,Q}(r) \cdot(2A)^{(\alpha-1)/(r+1)}}{C \cdot(1 - \epsilon)}$ and $\frac{4 (r+1)\ln ( 12 / \epsilon p )}{\ln2 \cdot(\alpha-1) (\epsilon^{2}/8 - \epsilon^{3}/24)} + \frac{1}{d} \geq C_{3}(\epsilon,p) > 0$.

Remark 3

The choice of Bernoulli matrices in Theorem 4 is motivated by two properties. First, one can encode their action on the integrated ΣΔ bit-stream in a lossless manner. Second, Bernoulli matrices (of appropriate size) act as near isometries on $\textrm{span} \{ D^{-r}{\bf F}_{1}, \dots, D^{-r}{\bf F}_{d} \}$. In fact, any encoding matrix drawn from a distribution satisfying the above two properties would work for compressing the ΣΔ bit-stream. For example, [1] also studied other discrete random matrices (whose entries are ±1 with probability 1/6 each, and 0 with probability 2/3) and showed that they serve as Johnson-Lindenstrauss embeddings.

It is informative to compare the rate-distortion bounds resulting from Theorems 3 and 4 in the case of the first order Sigma-Delta scheme (and frame) considered by Theorem 3. If we define $F \in\mathbb{R}^{N \times d}$ as per (16) we can see, by considering (17) and (19), that it will be a $(1, d^{-3/2}(\sqrt{2} \pi)^{-1}, 3/2 )$-frame. Furthermore, the first order scheme considered by Theorem 3 has A=1 and C _ρ,Q (1)=1. Hence, we see that (24) becomes

$$\mathcal{D}(\mathcal{R}) = \frac{2^{3/4} \pi d^{3/2}}{1 - \epsilon} \cdot2^{-\mathcal{R} / 4m} \leq \frac{2^{3/4} \pi d^{3/2}}{1 - \epsilon} \cdot2^{-\mathcal{R} ( \frac{\epsilon^2 - \epsilon^3 / 3}{128 \cdot d \ln(12/ \epsilon) + 64 \ln(1/p)} )} $$

in this case. Comparing this expression to (21) we can see that the dependence on d has been improved (i.e., by a log factor) in the denominator of the exponent. However, we have sacrificed some computational simplicity for this improvement since $B D^{-1} {\bf q}$ will generally require more effort to compute then $RD^{-1}{\bf q}$ in practice.

Importantly, though, Theorem 4 also enables one to obtain near-optimal rate-distortion bounds. Moreover, fixing the desired distortion, fewer samples N may now be used than in Theorem 3 (hence less computation for quantization and encoding) via the use of higher order quantization schemes. As a result, we will be able to use (r,C,α)-frames having only $O(N^{\frac{1}{\alpha-1}})$ rows below while still achieving O(1/N) accuracy (ignoring dependences on other parameters such as d, etc.). This represents a clear improvement over the first order scheme we have considered so far for all α>2, provided such (r,C,α) frames exists. In the next section we will briefly survey some examples of currently known (r,C,α)-frames, for general $r \in\mathbb{N}$, which are suitable for use with the type of stable rth-order sigma delta schemes considered herein.

4.1 Examples of (r,C,α)-frames

In this section we briefly survey some (r,C,α)-frames that can by utilized in concert with Theorem 4 above.

Example 1

Sobolev self-dual frames [21]:

Our first example of a family of (r,C,α)-frames represents a generalization of the frame utilized by Theorem 3 to higher orders. Let $U_{D^{r}} = ( \mathbf{U}_{1} \cdots \mathbf{U}_{N} )$ be the matrix of left singular vectors of D ^r, corresponding to a decreasing arrangement of the singular values. Then, we refer to F _(r)=(U _N−d+1⋯U _N ) as the (rth-order) Sobolev self-dual frame. F _(r) is an (r,C,α)-frame with C=π ^−r(d+2r)^−r and α=r (see [21], Theorem 8).

For these frames, with fixed r, using the ΣΔ schemes of Proposition 1 and a Bernoulli encoding matrix, the exponent in the rate-distortion expression $\mathcal{D}(\mathcal{R})$ behaves like $-\frac{r-1}{r+1}\frac{\mathcal{R}}{d}$. Specifically, considering Example 1 with r=1 we see that (16), when unnormalized, is a (1,π ⁻¹(d+2)⁻¹,1)-frame instead of a $(1, d^{-3/2}(\sqrt{2} \pi)^{-1}, 3/2 )$-frame. Hence, the bound provided for the unscaled matrix by Example 1 with r=1 is weaker than the result for the rescaled matrix, whenever d is significantly smaller than N. What prevents us from rescaling F when r≥2 is that we have insufficient information regarding the left singular vectors of D ^r.

Example 2

Harmonic frames:

A harmonic frame, $F \in\mathbb{R}^{N \times d}$, is defined via the following related functions:

$$\begin{aligned} &F_0(t) = \frac{1}{\sqrt{2}}, \end{aligned}$$

(25)

$$\begin{aligned} &F_{2j-1}(t) = \cos(2 \pi j t),\quad j \geq1,\quad \textrm{and} \end{aligned}$$

(26)

$$\begin{aligned} &F_{2j}(t) =\sin(2 \pi j t),\quad j \geq1. \end{aligned}$$

(27)

We then define $F_{j,k} = \sqrt{\frac{2}{d}} \cdot F_{j'}(k/N)$, where $j' = j-d\operatorname{mod}2$ for all k∈[N] and $j \in[d+d\operatorname{mod}2]$. In addition to Sobolev self-dual frames, we note that harmonic frames also yield general (r,C,α)-frames. For sufficiently large N, a harmonic frame is an (r,C,α)-frame with $C= C_{1} e^{r/2} r^{-(r+C_{2})}$ and α=r+1/2 (see [21], Lemma 17). Here, C ₁ and C ₂ are constants that possibly depend on d. For this example, with fixed r, using the ΣΔ schemes of Proposition 1 and a Bernoulli encoding matrix, the exponent in the rate-distortion expression $\mathcal{D}(\mathcal{R})$ behaves like $-\frac{r-1/2}{r+1}\frac{\mathcal{R}}{d}$.

Example 3

Frames generated from piecewise-C ¹ uniformly sampled frame path:

Note that the example above is a special case of a smooth frame [5]. As one might expect, more general classes of smooth frames also yield (r,C,α)-frames. One such class of frames consists of those generated from piecewise-C ¹ uniformly sampled frame paths, as defined in [5]. For convenience, we reproduce the definition below.

Definition 4

A vector valued function $E: [0,1]\mapsto \mathbb {R}^{d}$ given by E(t)=[E ₁(t),E ₂(t),…,E _d (t)] is a piecewise-C ¹ uniformly sampled frame path if

• (1) for all n∈[d], $\mathbf{E}_{n}: [0,1] \mapsto\mathbb{R}$ is piecewise-C ¹,

• (2) the functions E _n are linearly independent, and

• (3) there exists an N ₀ such that for all N≥N ₀, the matrix F with entries F _ij =E _j (i/N) is a frame matrix.

In this case, we say that the frame F is generated from a piecewise-C ¹ uniformly sampled frame path.

For any piecewise-C ¹ uniformly sampled frame path, there is an $N_{0} \in\mathbb{N}$ such that for all N>N ₀, any frame generated from the frame path is an (r,C,α)-frame for some C (possibly depending on r and d) and α=r+1/2 (see [5], Theorem 5.4 and its proof). Here, again, with fixed r, using the ΣΔ schemes of Proposition 1 and a Bernoulli encoding matrix, the exponent in the rate-distortion expression $\mathcal{D}(\mathcal{R})$ behaves like $-\frac{r-1/2}{r+1}\frac{\mathcal{R}}{d}$. Example 3 deals with smooth frames of a fairly general type, albeit at the cost of less precision in specifying C. Perhaps more surprisingly, decidedly non-smooth frames also yield (r,C,α)-frames in general. In particular, we may utilize Bernoulli random matrices as both our bit stream compression operator, and our (r,C,α)-frame.

Example 4

Bernoulli and Sub-Gaussian frames:

Let γ∈[0,1]. Then, there exists constant c ₁ and c ₂, such that with probability exceeding $1-2e^{-c_{1} N^{1-\gamma}d^{\gamma}}$, a frame F whose entries are $\pm\frac{1}{\sqrt{d}}$ Bernoulli random variables is an (r,C,α)-frame, provided $N\geq(c_{2} r)^{\frac{1}{1-\gamma}} d$. Here C=d ^{−γ(r−1/2)−1/2} and α=1/2+γ(r−1/2). See [22, Proposition 4.1] for a proof.

In fact, Bernoulli frames are a special case of a more general class of frames whose entries are sub-Gaussian random variables. These more general types of random matrices also serve as (r,C,α)-frames.

Definition 5

If two random variables η and ξ satisfy P(|η|>t)≤KP(|ξ|>t) for some constant K and all t≥0 then we say that η is K-dominated by ξ.

Definition 6

We say that a matrix is sub-Gaussian with parameter c, mean μ, and variance σ ² if its entries are independent and e-dominated by a Gaussian random variable with parameter c, mean μ, variance σ ².

Let γ∈[0,1]. Then, there exists a constant c ₁>0 such that, with probability exceeding $1-3e^{-c_{1} N^{1-\gamma}d^{\gamma}}$, a random sub-Gaussian frame matrix F with mean zero, variance 1/N, and parameter c will be a (r,C,α)-frame whenever $\frac {N}{d}\geq(c_{2} r)^{\frac{1}{1-\gamma}}$ where c ₂ depends only on c. Here C=d ^{−γ(r−1/2)} and α=γ(r−1/2). See [22, Propositions 4.1 and 4.2] for a proof. Consequently, using the ΣΔ schemes of Proposition 1 together with a Bernoulli encoding matrix and a Sub-Gaussian frame results in the exponent of the rate-distortion expression, $\mathcal{D}(\mathcal{R})$, behaving like $-\frac{\gamma\cdot r-\frac{1}{2}(\gamma+2)}{r+1}\frac {\mathcal{R}}{d}$.

5 Numerical Experiments

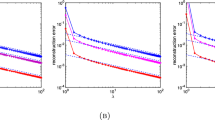
In this section we present numerical experiments to illustrate our results. To illustrate the results of Sect. 3, we first generate 5000 points uniformly from $\mathcal{B}^{d}$, with d=2,6,and 10. We then compute, for various N, the 1-bit 1st order greedy ΣΔ-quantization of $F{\bf x}$, where F is an N×d Sobolev self-dual frame. $RD^{-1}{\bf q}$, where R is an m×N random selector matrix with m=10d is then employed to recover an estimate $\hat{{\bf x}}= (RD^{-1}F)^{\dagger}RD^{-1}{\bf q}$ of ${\bf x}$. In Fig. 1 we plot (in log scale) the maximum and mean of $\Vert \hat{{\bf x}}-{\bf x}\Vert _{2}$ over the 5000 realizations of x versus the induced bit-rate.

Fig. 1

(left) The maximum and (right) mean ℓ ₂-norm error (in log₁₀ scale) plotted against the number of bits per dimension (b/d). Here we use a 1st order greedy ΣΔ scheme to quantize and a random selector matrix to encode

Our second experiment is similar (see Fig. 2), albeit we now use a third order 1-bit ΣΔ quantizer according to the schemes of [9] to quantize the harmonic frame expansion of vectors in $\mathcal{B}^{d}$, with d=2,6,and 10. Here, we use a d×m Bernoulli matrix, with m=5d to encode $BD^{-1}{\bf q}$ and subsequently obtain $\hat {{\bf x}}= (BD^{-1}F)^{\dagger}BD^{-1}{\bf q}$. As before, we plot the maximum and mean of $\Vert \hat{{\bf x}}-{\bf x}\Vert _{2}$ over the 5000 realizations of ${\bf x}$ versus the induced bit-rate.

Fig. 2

(left) The maximum and (right) mean ℓ ₂-norm error (in log₁₀ scale) plotted against the number of bits per dimension (b/d). Here we use a third order ΣΔ scheme to quantize and a Bernoulli matrix to encode

For our third experiment, we fix d=20 and use the ΣΔ schemes of [9] with r=1,2, and 3 to quantize the Bernoulli frame coefficients, and we use Bernoulli matrices with m=5d to encode. In Fig. 3 we show the maximum error versus the bit-rate. Note the different slopes corresponding to r=1,2,and 3. This observation is in agreement with the prediction (see the discussion around Example 4) that the exponent in the rate-distortion expression $\mathcal{D}(\mathcal {R})$ is a function of r.

Fig. 3

The maximum ℓ ₂-norm error (in log₁₀ scale) plotted against the number of bits per dimension (b/d). Here d=20 and ΣΔ schemes with r=1,2 and 3 are used to quantize the frame coefficients. A Bernoulli matrix is used for encoding