Abstract
Let ν be a countably additive vector measure defined on the Borel subsets  of a compact Hausdorff abelian group G. In this paper we define and study a vector valued Fourier transform and a vector valued convolution for functions which are (weakly) integrable with respect to ν. A form of the Riemann Lebesgue Lemma and a Uniqueness Theorem are established in this context. In order to study the vector valued convolution we discuss the invariance under reflection in G of these spaces of integrable functions. Finally we present a Young’s type inequality in this setting and several relevant examples, namely related with the vector measure associated to different important classical operators coming from Harmonic Analysis.
of a compact Hausdorff abelian group G. In this paper we define and study a vector valued Fourier transform and a vector valued convolution for functions which are (weakly) integrable with respect to ν. A form of the Riemann Lebesgue Lemma and a Uniqueness Theorem are established in this context. In order to study the vector valued convolution we discuss the invariance under reflection in G of these spaces of integrable functions. Finally we present a Young’s type inequality in this setting and several relevant examples, namely related with the vector measure associated to different important classical operators coming from Harmonic Analysis.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let G be a compact Hausdorff abelian group and \(m_{_{G}}\) its normalized Haar measure, defined on the Borel subsets  of G. Take X to be a complex Banach space,
of G. Take X to be a complex Banach space,  a (countably additive) vector measure and consider \(L^{1}_{w} (\nu)\), the space of weakly integrable functions with respect to ν. The main goal of this article is to introduce and study a vector valued Fourier transform and a vector valued convolution for (weakly) integrable functions with respect to a vector measure.
a (countably additive) vector measure and consider \(L^{1}_{w} (\nu)\), the space of weakly integrable functions with respect to ν. The main goal of this article is to introduce and study a vector valued Fourier transform and a vector valued convolution for (weakly) integrable functions with respect to a vector measure.
The paper consists of four sections. After this preliminary first section, in the second one we start by introducing the notion of vector valued Fourier transform. First for integrable functions with respect to ν (see Definition 2.1) and then for weakly integrable functions with respect to ν (see Definition 2.6). After giving some important examples we prove that a natural version of the Riemann-Lebesgue’s Lemma is not true in this setting. However, always assuming the vector measure ν is absolutely continuous with respect to \(m_{_{G}}\), we characterize those measures for which this important lemma is satisfied (see Theorem 2.5). We finish this section with a version of a Uniqueness Theorem (see Theorem 2.7 and Corollary 2.8).
The definition of the convolution, that is the main goal of the last section, takes us naturally to discuss the effect in the space \(L^{1}_{w} (\nu)\) of the reflection in G, given by R(t)=−t. This is done in section three, following the work of O. Delgado and P.J. Miana in [3], where they introduced the property of norm integral translation invariance for a vector measure  . Assuming ν has this property, they established that if \(f \in L^{1}_{w} (\nu)\) then \(f_{s} \in L^{1}_{w} (\nu)\) and \(\lVert{f_{s}}\rVert_{\nu } = \lVert{f}\rVert_{\nu}\); here f
s
=f(⋅−s), s∈G. Actually, it turns out that the development of O. Delgado and P.J. Miana in [3], can be done when we do not have an algebraic structure on G, but only an homeomorphism h:G→G with the corresponding property (see Definition 3.1 and Theorem 3.3). With our result we recover not only the translation invariant case but the reflection invariant case. In this section we also study the important case of vector measures associated to the convolution operator. Namely, it is well-known that the vector measure \(\nu_{\mu} (A) = \chi_{_{A}} * \mu\in L^{p} (G)\), where μ is a complex regular measure defined on
. Assuming ν has this property, they established that if \(f \in L^{1}_{w} (\nu)\) then \(f_{s} \in L^{1}_{w} (\nu)\) and \(\lVert{f_{s}}\rVert_{\nu } = \lVert{f}\rVert_{\nu}\); here f
s
=f(⋅−s), s∈G. Actually, it turns out that the development of O. Delgado and P.J. Miana in [3], can be done when we do not have an algebraic structure on G, but only an homeomorphism h:G→G with the corresponding property (see Definition 3.1 and Theorem 3.3). With our result we recover not only the translation invariant case but the reflection invariant case. In this section we also study the important case of vector measures associated to the convolution operator. Namely, it is well-known that the vector measure \(\nu_{\mu} (A) = \chi_{_{A}} * \mu\in L^{p} (G)\), where μ is a complex regular measure defined on  and 1≤p<∞, is always norm integral translation invariant. However, this is not the case for reflection invariance (see Example 3.6). Concerning this special vector valued measure, we prove that \(\widetilde{f}\in L^{1}_{w}(\nu_{\mu})\) when \(f \in L^{p}_{w}(\nu_{\mu})\) (have in mind that the vector measure ν depends on both μ and p). This is done in Theorem 3.7. By using the notion of vector measure scalarly
k-dominated by
\(m_{_{G}}\) (see Definition 3.8 and Theorem 3.9) we obtain a different proof of a well-known result that asserts that \(L^{1}(\nu_{\mu})=L^{1}_{w}(\nu_{\mu}) = L^{1} (G)\), with equivalent norms (see Corollary 3.10).
and 1≤p<∞, is always norm integral translation invariant. However, this is not the case for reflection invariance (see Example 3.6). Concerning this special vector valued measure, we prove that \(\widetilde{f}\in L^{1}_{w}(\nu_{\mu})\) when \(f \in L^{p}_{w}(\nu_{\mu})\) (have in mind that the vector measure ν depends on both μ and p). This is done in Theorem 3.7. By using the notion of vector measure scalarly
k-dominated by
\(m_{_{G}}\) (see Definition 3.8 and Theorem 3.9) we obtain a different proof of a well-known result that asserts that \(L^{1}(\nu_{\mu})=L^{1}_{w}(\nu_{\mu}) = L^{1} (G)\), with equivalent norms (see Corollary 3.10).
As we said before, in the last section we study a vector valued convolution for the case of weakly integrable functions (see Definition 4.1) and also for the case of integrable functions (see Definition 4.5). After some examples we establish several integration properties for both cases (see Theorem 4.8 and Theorem 4.10). In the last results of the paper we use the notions of the third section in order to prove the Young’s type inequality in this context. This is done in Corollaries 4.11, 4.12 and 4.13.
1.1 Notation and Preliminaries
Let G be a compact Hausdorff abelian group, let  be the σ-algebra consisting of the Borel sets of G and let \(m_{_{G}}\) be the normalized Haar measure of G, that is, the unique non-negative regular and translation-invariant measure such that \(m_{_{G}}(G)=1\). Recall that a complex continuous function γ defined on G is called a character if |γ(t)|=1 for all t∈G and γ(s+t)=γ(s)γ(t) for every s,t∈G. The set of all continuous characters of G is the dual group of
G and will be denoted by Γ. Note that Γ is discrete since G is compact. The reader is referred to [7, 12] for additional information on this subject. We denote by L
0(G) the space of classes (\(m_{_{G}}\)-a.e. equal functions being identified) of measurable functions defined on G, if 1≤p<∞ then L
p(G) is the subspace of L
0(G) such that \(\int_{G} |f|^{p}dm_{_{G}}<\infty\) and L
∞(G) is the subspace of functions in L
0(G) which are \(m_{_{G}}\)-a.e. bounded. Since the measure \(m_{_{G}}\) is finite we have L
∞(G)⊆L
p(G)⊆L
1(G) continuously. The Fourier transform of a function f∈L
1(G) is the function \(\widehat{f}:\varGamma\to \mathbb{C}\) given by
be the σ-algebra consisting of the Borel sets of G and let \(m_{_{G}}\) be the normalized Haar measure of G, that is, the unique non-negative regular and translation-invariant measure such that \(m_{_{G}}(G)=1\). Recall that a complex continuous function γ defined on G is called a character if |γ(t)|=1 for all t∈G and γ(s+t)=γ(s)γ(t) for every s,t∈G. The set of all continuous characters of G is the dual group of
G and will be denoted by Γ. Note that Γ is discrete since G is compact. The reader is referred to [7, 12] for additional information on this subject. We denote by L
0(G) the space of classes (\(m_{_{G}}\)-a.e. equal functions being identified) of measurable functions defined on G, if 1≤p<∞ then L
p(G) is the subspace of L
0(G) such that \(\int_{G} |f|^{p}dm_{_{G}}<\infty\) and L
∞(G) is the subspace of functions in L
0(G) which are \(m_{_{G}}\)-a.e. bounded. Since the measure \(m_{_{G}}\) is finite we have L
∞(G)⊆L
p(G)⊆L
1(G) continuously. The Fourier transform of a function f∈L
1(G) is the function \(\widehat{f}:\varGamma\to \mathbb{C}\) given by
Let s∈G. As usual, if f∈L 0(G) by f s we denote its translation, that is f s (t)=f(t−s) for each t∈G. Also by τ s we denote the map from L 0(G) into itself defined by τ s (f)=f s .
Let X be a complex Banach space, B
X
its closed unit ball and X′ the topological dual of X. Let 1≤p<∞. An scalarly measurable function f:G→X is said to be Dunford
p-integrable (or simply Dunford integrable when p=1) if 〈f,x′〉∈L
p(G) for all x′∈X′. The set consisting of classes of these functions will be denoted by \(L^{p}_{w}(G,X)\). For a function \(f\in L^{p}_{w}(G,X)\) the norm is defined by \(\|f\|_{L^{p}_{w}(G,X)} =\sup_{x'\in B_{X'}} (\int_{G} |\langle f,x'\rangle |^{p}dm_{_{G}})^{1/p}\). A Dunford p-integrable function f:G→X is said to be Pettis
p-integrable (or simply Pettis integrable when p=1) if for each  there is x
A
∈X satisfying \(\int_{A} \langle f,x'\rangle dm_{_{G}}=\langle x_{A},x'\rangle\), for all x′∈X′. The vector x
A
is unique and will be denoted by \((P)\int_{A} fdm_{_{G}}\). The set of classes of scalarly measurable functions which are Pettis p-integrable, endowed with the same norm as \(L^{p}_{w}(G,X)\), will be denoted by
there is x
A
∈X satisfying \(\int_{A} \langle f,x'\rangle dm_{_{G}}=\langle x_{A},x'\rangle\), for all x′∈X′. The vector x
A
is unique and will be denoted by \((P)\int_{A} fdm_{_{G}}\). The set of classes of scalarly measurable functions which are Pettis p-integrable, endowed with the same norm as \(L^{p}_{w}(G,X)\), will be denoted by  . For more information about Pettis integrability the reader is referred to [4, 10] and the nice survey [9, Chap. 12].
. For more information about Pettis integrability the reader is referred to [4, 10] and the nice survey [9, Chap. 12].
Let (Ω,Σ,μ) be a measure space and L 0(μ) the set consisting of classes (μ-a.e. equal functions being identified) of measurable functions. A Banach space E(μ)⊆L 0(μ) is called a Banach function space related to μ if L ∞(μ)⊆E(μ)⊆L 1(μ) and if f∈E(μ) and g∈L 0(μ) satisfies |g|≤|f| μ-a.e., then g∈E(μ) and ∥g∥ E(μ)≤∥f∥ E(μ). A Banach function space E(μ) is called order continuous if every increasing order bounded sequence in E(μ) converges in the norm of E(μ). The Köthe dual (or associate space) of E(μ) is the Banach function space related to μ defined by E(μ)×={g∈L 0(μ):fg∈L 1(μ),f∈E(μ)}, and endowed with the norm \(\|g\|_{E(\mu)^{\times}}=\sup_{f\in B_{E(\mu)}} \int_{\varOmega} |fg|d\mu, g\in E(\mu)^{\times}\). Recall that E(μ) is order continuous if and only if E(μ)× coincides with E(μ)′. In this case each x′∈E(μ)′ can be identified with a function g∈E(μ)× via the correspondence 〈f,x′〉=∫ Ω fgdμ for all f∈E(μ). For questions related to Banach function spaces see [13, Chap. 2].
Let  be a countably additive vector measure. A set
be a countably additive vector measure. A set  is called ν-null if ν(B)=0 for all
is called ν-null if ν(B)=0 for all  such that B⊆A. Given x′∈X′ let us denote by 〈ν,x′〉 the scalar measure defined by 〈ν,x′〉(A)=〈ν(A),x′〉 for each
such that B⊆A. Given x′∈X′ let us denote by 〈ν,x′〉 the scalar measure defined by 〈ν,x′〉(A)=〈ν(A),x′〉 for each  . The semivariation of ν is the non-negative set function
. The semivariation of ν is the non-negative set function  defined by \(\|\nu\|(A)=\sup_{x'\in B_{X'}} |\langle\nu,x'\rangle |(A)\),
defined by \(\|\nu\|(A)=\sup_{x'\in B_{X'}} |\langle\nu,x'\rangle |(A)\),  , where |〈ν,x′〉| is the variation of the measure 〈ν,x′〉. Recall that a set
, where |〈ν,x′〉| is the variation of the measure 〈ν,x′〉. Recall that a set  is ν-null if and only if ∥ν∥(A)=0. The vector measure ν is absolutely continuous with respect to a positive measure λ if λ(A)→0 implies that ∥ν∥(A)→0. As usual in this situation we write ν≪λ. In the case when λ is finite we have that ν≪λ if and only if any λ-null set is ν-null. A Rybakov control measure for ν is a finite positive measure μ satisfying ν≪μ and \(\mu= |\langle\nu,x'_{0}\rangle |\) for some \(x'_{0}\in X'\). This kind of measures always exist by the Rybakov Theorem (see [4, Theorem IX.2.2]). If μ is a Rybakov control measure for ν, note that μ and ν have the same null sets. Information on vector measures can be found in [4, Chaps. I and IX].
is ν-null if and only if ∥ν∥(A)=0. The vector measure ν is absolutely continuous with respect to a positive measure λ if λ(A)→0 implies that ∥ν∥(A)→0. As usual in this situation we write ν≪λ. In the case when λ is finite we have that ν≪λ if and only if any λ-null set is ν-null. A Rybakov control measure for ν is a finite positive measure μ satisfying ν≪μ and \(\mu= |\langle\nu,x'_{0}\rangle |\) for some \(x'_{0}\in X'\). This kind of measures always exist by the Rybakov Theorem (see [4, Theorem IX.2.2]). If μ is a Rybakov control measure for ν, note that μ and ν have the same null sets. Information on vector measures can be found in [4, Chaps. I and IX].
A measurable function f:G→ℂ is said to be weakly integrable with respect to the vector measure
ν if f∈L
1(|〈ν,x′〉|), for all x′∈X′. The subspace consisting of these functions will be denoted by \(L^{1}_{w}(\nu)\); this is a Banach space with the norm \(\|f\|_{\nu}=\sup_{x'\in B_{X'}} \int_{G} |f|d|\langle\nu ,x'\rangle|\), f∈L
1(ν). A weakly integrable function f:G→ℂ is said to be integrable with respect to
ν if for each  there is x
A
∈X such that ∫
A
fd〈ν,x′〉=〈x
A
,x′〉, for all x′∈X′. Again the vector x
A
is unique and it is denoted by ∫
A
fdν. The set consisting of classes (ν-a.e. equal functions being identified) of these functions will be denoted by L
1(ν). The integration operator
I
ν
:L
1(ν)→X is the linear and continuous function defined by I
ν
(f)=∫
G
fdν, for f∈L
1(ν). Given 1≤p<∞ we denote by L
p(ν) (resp. \(L^{p}_{w}(\nu)\)) the set of classes of measurable functions f:G→ℂ satisfying that |f|p∈L
1(ν) (resp. \(|f|^{p}\in L_{w}^{1}(\nu)\)). These vector spaces are complete when endowed with the norm \(\|f\|_{\nu,p}= \| |f|^{p} \|_{\nu}^{1/p}=\sup_{x'\in B_{X'}}(\int_{G} |f|^{p}d|\langle\nu,x'\rangle|)^{1/p}\). Note that the space L
∞(ν) consisting of classes of measurable functions which are ν-a.e. bounded, coincides with the space L
∞(μ), where μ is a Rybakov control measure for ν. For 1≤p<∞ the spaces L
p(ν) are order continuous Banach function spaces related to any Rybakov control measure for ν. Hence the set of simple functions
there is x
A
∈X such that ∫
A
fd〈ν,x′〉=〈x
A
,x′〉, for all x′∈X′. Again the vector x
A
is unique and it is denoted by ∫
A
fdν. The set consisting of classes (ν-a.e. equal functions being identified) of these functions will be denoted by L
1(ν). The integration operator
I
ν
:L
1(ν)→X is the linear and continuous function defined by I
ν
(f)=∫
G
fdν, for f∈L
1(ν). Given 1≤p<∞ we denote by L
p(ν) (resp. \(L^{p}_{w}(\nu)\)) the set of classes of measurable functions f:G→ℂ satisfying that |f|p∈L
1(ν) (resp. \(|f|^{p}\in L_{w}^{1}(\nu)\)). These vector spaces are complete when endowed with the norm \(\|f\|_{\nu,p}= \| |f|^{p} \|_{\nu}^{1/p}=\sup_{x'\in B_{X'}}(\int_{G} |f|^{p}d|\langle\nu,x'\rangle|)^{1/p}\). Note that the space L
∞(ν) consisting of classes of measurable functions which are ν-a.e. bounded, coincides with the space L
∞(μ), where μ is a Rybakov control measure for ν. For 1≤p<∞ the spaces L
p(ν) are order continuous Banach function spaces related to any Rybakov control measure for ν. Hence the set of simple functions  is dense in L
p(ν). For more information about integration of scalar functions with respect to vector measures see [11] and the references therein.
is dense in L
p(ν). For more information about integration of scalar functions with respect to vector measures see [11] and the references therein.
2 The Fourier Transform Associated to ν
Let G be a compact Hausdorff abelian group, X a complex Banach space and  a countably additive vector measure. Recall that if f∈L
1(ν) and ϕ∈L
∞(G) then fϕ∈L
1(ν). This allows us to give the following definition.
a countably additive vector measure. Recall that if f∈L
1(ν) and ϕ∈L
∞(G) then fϕ∈L
1(ν). This allows us to give the following definition.
Definition 2.1
The Fourier Transform of a function f∈L 1(ν) with respect to the vector measure ν is the vector valued function \(\widehat{f}^{\nu}:\varGamma\to X\) given by
Let us start with a general example using vector measures associated to operators that will be useful in the rest of the paper.
Example 2.2
Let \(E(m_{_{G}})\) be an order continuous Banach function space related to the Haar measure \(m_{_{G}}\) on a compact Hausdorff abelian group G. Let \(T:E(m_{_{G}})\to X\) be a bounded linear map, where X is a Banach space and consider the vector measure  associated to T, defined by \(\nu_{_{T}}(A)=T(\chi_{_{A}})\),
associated to T, defined by \(\nu_{_{T}}(A)=T(\chi_{_{A}})\),  . Then it is well-known (see for instance [11, Proposition 4.4]) that every function \(f\in E(m_{_{G}})\) is integrable with respect to \(\nu_{_{T}}\) and
. Then it is well-known (see for instance [11, Proposition 4.4]) that every function \(f\in E(m_{_{G}})\) is integrable with respect to \(\nu_{_{T}}\) and  . Hence, given \(f\in E(m_{_{G}})\) since \(f\overline{\gamma}\in E(m_{_{G}})\) for all γ∈Γ, we have
. Hence, given \(f\in E(m_{_{G}})\) since \(f\overline{\gamma}\in E(m_{_{G}})\) for all γ∈Γ, we have
In particular throughout this paper we work with the following important cases:
-
(1)
Given a complex regular measure μ defined on
 and 1≤p<∞ we consider the operator T
μ
:L
p(G)→L
p(G) given by T
μ
(f)=f∗μ for each f∈L
p(G), where
$$f*\mu(t)=\int_{G} f(t-s)d\mu(s), \quad t\in G. $$
and 1≤p<∞ we consider the operator T
μ
:L
p(G)→L
p(G) given by T
μ
(f)=f∗μ for each f∈L
p(G), where
$$f*\mu(t)=\int_{G} f(t-s)d\mu(s), \quad t\in G. $$Writing ν μ for \(\nu_{_{T_{\mu}}}\), the vector measure associated to T μ , formula (2.1) gives \(\widehat{f}^{\ \!\nu_{_{\mu}}}(\gamma)=f\overline{\gamma}*\mu, \ \gamma\in\varGamma\). For future references, note that \(\nu_{{{\mu }}} \ll m_{_{G}}\). In the particular case given by the compact Hausdorff abelian group \(\mathbb{T}= \{ x \in \mathbb{C}: |x| = 1 \}\) let us take \(x_{0} \in \mathbb{T}\) and define \(\mu=\delta_{x_{0}}\), the delta function centered at x 0. Notice that μ is a positive finite regular measure defined on
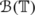 . In accordance, we will change our notation to that of multiplication. Hence we have \(\widehat{f}^{\ \! \nu_{_{\mu}}}(n)(t)=nf(t-x_{0}), \ n\in\mathbb{Z}, t\in\mathbb{T}\).
. In accordance, we will change our notation to that of multiplication. Hence we have \(\widehat{f}^{\ \! \nu_{_{\mu}}}(n)(t)=nf(t-x_{0}), \ n\in\mathbb{Z}, t\in\mathbb{T}\). -
(2)
Let us consider \(T={\rm id}\), the identity map from \(E(m_{_{G}})\) into itself. Then \(\widehat{f}^{\nu}(\gamma)=f\overline {\gamma}\) for all γ∈Γ.
-
(3)
Let 1≤p≤2 and p′ be its conjugate exponent, that is 1/p+1/p′=1. Let us consider now the vector measure associated to the Fourier transform
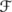 which, by the Hausdorff-Young inequality, satisfies
which, by the Hausdorff-Young inequality, satisfies 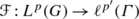 . Hence
. Hence  is given by
is given by
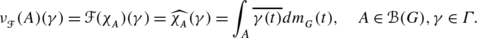
Therefore
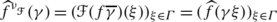 , γ∈Γ.
, γ∈Γ. -
(4)
Let 1≤p,q,r≤∞ and g∈L q(G) be such that 1/p+1/q=1/r. By Hölder’s inequality we can consider the multiplication operator M g :L p(G)→L r(G) given by M g (f)=fg. Hence for the vector measure associated to T g we have that \(\widehat{f}^{\nu_{M_{g}}}(\gamma)=fg\overline{\gamma}\), γ∈Γ. Note that the same result for 1<p<∞ can be obtained by using [11, Proposition 3.43 and Remark 3.44] (see also [2, 5]) and either M g :L p(ν)→L 1(ν) for \(g\in L^{p'}_{w}(\nu)\), or \(M_{g}:L_{w}^{p}(\nu)\to L^{1}(\nu)\) for g∈L p′(ν), or \(M_{g}:L_{w}^{p}(\nu)\to L_{w}^{1}(\nu)\) for \(g\in L^{p'}_{w}(\nu)\).
The first classical and important result concerning the Fourier transform is Riemann-Lebesgue’s Lemma. Note that for a given γ∈Γ one has
Therefore
Proposition 2.3
If
f∈L
1(ν), then
\(\widehat{f}^{\nu }\in\ell^{\infty}(\varGamma,X)\)
and
\(\|\widehat{f}^{\nu}\|_{\ell^{\infty}(\varGamma,X)} \leq\lVert {f}\rVert_{\nu }\). Hence the Fourier transform
 given by
given by
 , is a bounded linear operator.
, is a bounded linear operator.
However, the following simple example shows that \(\widehat{f}^{\nu}\) is not always in c 0(Γ,X), as it happens in the classical Riemann-Lebesgue’s Lemma.
Example 2.4
Let us consider the case (2) in Example 2.2. Recall that, in this case, \(E(m_{_{G}})\) is isometrically isomorphic to L 1(ν) (see for instance [11, Proposition 3.9]). Hence, since \(\widehat{f}^{\nu}(\gamma)=f\overline{\gamma}\) for all γ∈Γ,
When Γ is an infinite set, this shows that \(\widehat{f}^{\nu}\notin c_{0}(\varGamma,X)\).
If \(\nu\ll m_{_{G}}\) then the trigonometric polynomials on G are dense in L 1(ν) (see [3, Corollary 3.9]). This result allows us to characterize when a version of the Riemann-Lebesgue Lemma is satisfied in our setting.
Theorem 2.5
Assume that \(\nu\ll m_{_{G}}\). The following assertions are equivalent:
-
(a)
\(\widehat{f}^{\nu}\in c_{0}(\varGamma,X)\) for all f∈L 1(ν),
-
(b)
\(\widehat{\chi_{_{G}}}^{\nu}\in c_{0}(\varGamma,X)\).
Proof
Trivially (a) implies (b) so assume that (b) is satisfied and let us see (a). Fix ε>0. We have to show that the set \(\varGamma_{0}=\{\gamma\in\varGamma: \|\widehat{f}^{\nu}(\gamma)\|_{X}>\varepsilon\}\) is finite. Given f∈L 1(ν) let us take a trigonometric polynomial \(p=\sum_{j=1}^{n} \alpha_{j}\gamma_{j}\), where α j ∈ℂ∖{0}, γ j ∈Γ and j=1,…,n are such that ∥f−p∥ ν ≤ε/2. By Proposition 2.3 one has \(\|\widehat{f-p}^{\nu}(\gamma)\|_{X}\leq\|f-p\|_{\nu}\leq \varepsilon/2\), γ∈Γ. And by the assumption (b) for all j=1,…,n the sets
are finite. Let us see that
So take \(\gamma\notin\bigcup_{j=1}^{n} \varGamma_{j}\). Then
and also \(\|\widehat{f}^{\nu}(\gamma)\|_{X}\leq\|\widehat{f-p}^{\nu}(\gamma)\|_{X}+\|\widehat{p}^{\ \!\nu}(\gamma)\|_{X}\leq\varepsilon\). Consequently, Γ 0 is finite. □
Concerning the previous result we have the following open problem.
Open problem
Are there Banach spaces X for which the previous result holds for every X-valued measure? Are there natural subclasses of vector measures for which it holds? Are there classes of operators that transforms vector measures into vector measures for which the result holds?
We finish this section by defining a “Fourier transform” for \(f \in L^{1}_{w} (\nu)\). We will be able to do it under the requirement that the vector measure ν is absolutely continuous with respect to \(m_{_{G}}\). Then fixing x′∈X′ we have that \(\langle\nu,x'\rangle\ll |\langle\nu,x'\rangle|\ll \nu\ll m_{_{G}}\) and so we can consider the Radon-Nikodým derivative
Take now \(f\in L^{1}_{w}(\nu)\). Since \(\int_{G} |f|d|\langle\nu,x'\rangle|=\int_{G} |fh_{x'}|dm_{_{G}}\), then fh x′∈L 1(G). Hence we can define a “weak” Fourier transform as follows.
Definition 2.6
The Fourier Transform of a function \(f\in L^{1}_{w}(\nu)\) with respect to the vector measure ν is

As usual, L(Y,Z) stands here for the Banach space of all bounded linear operators going from the Banach space Y into the Banach space Z.
This transform is well defined since for all x′∈X′ one has

Clearly if f∈L 1(ν) (and \(\nu\ll m_{_{G}}\)) then

Our next result is a uniqueness theorem.
Theorem 2.7
Let
\(\nu\ll m_{_{G}}\). If
 for
\(f\in L^{1}_{w}(\nu)\)
then
f=0 in
\(L_{w}^{1}(\nu)\).
for
\(f\in L^{1}_{w}(\nu)\)
then
f=0 in
\(L_{w}^{1}(\nu)\).
Proof
Let x′∈X′. Since  then for all γ∈Γ,
then for all γ∈Γ,
This means that \(\widehat{fh_{x'}}(\gamma)=0\) for all γ∈Γ and so fh x′=0. Let \(\widetilde{G}=\{t\in G: h_{x'}(t)=0\}\). Note that
Therefore \(\widetilde{G}\) is ν-null. But on the other hand f=0 on \(G\setminus \widetilde{G}\) and so ∫ G |f|d|〈ν,x′〉|=0, for each x′∈X′. Hence f=0. □
Using (2.3) and Theorem 2.7 we obtain immediately the following.
Corollary 2.8
Let \(\nu\ll m_{_{G}}\). If \(\widehat{f}^{\ \!\!\nu}=0\) for f∈L 1(ν) then f=0 in L 1(ν).
From the case (1) in Example 2.2 and the above corollary we obtain directly the next result.
Example 2.9
Let μ be a complex regular measure defined on  . If f∈L
p(G), 1≤p<∞ and \(f\overline{\gamma}*\mu= 0\) for all γ∈Γ, then f=0.
. If f∈L
p(G), 1≤p<∞ and \(f\overline{\gamma}*\mu= 0\) for all γ∈Γ, then f=0.
3 Homeomorphism Invariant Spaces
Let G be a compact Hausdorff abelian group and \(m_{_{G}}\) its Haar measure. Then L
1(G) is norm translation invariant, that is if f∈L
1(G) then f
t
∈L
1(G) and \(\lVert{f}\rVert_{L^{1} (G)} = \lVert{f_{t}}\rVert_{L^{1} (G)}\), f∈L
1(G), t∈G. O. Delgado and P.J. Miana introduced the following property for a countably additive vector measure defined on  : ν
is said to be norm integral translation invariant if
\(\| I_{\nu} (\tau_{t}\phi) \|_{_{X}}= \|I_{\nu}(\phi) \|_{_{X}}\), for every simple function
: ν
is said to be norm integral translation invariant if
\(\| I_{\nu} (\tau_{t}\phi) \|_{_{X}}= \|I_{\nu}(\phi) \|_{_{X}}\), for every simple function
 and
t∈G. When this condition holds the spaces \(L_{w}^{1}(\nu)\) and L
1(ν) are norm translation invariant (see [3, Proposition 3.5]). Since we are dealing with G compact, its Haar measure is also reflection invariant, that is
and
t∈G. When this condition holds the spaces \(L_{w}^{1}(\nu)\) and L
1(ν) are norm translation invariant (see [3, Proposition 3.5]). Since we are dealing with G compact, its Haar measure is also reflection invariant, that is  . This implies that L
1(G) is norm reflection invariant, that is if f∈L
1(G) then \(\widetilde{f}\in L^{1} (G)\) and \(\lVert{f}\rVert_{L^{1} (G)} = \lVert{\widetilde{f}}\rVert_{L^{1} (G)}\), where \(\widetilde{f}\) is the function given by \(\widetilde{f}(t)=f(-t), t\in G\). We are now interested in this property for the spaces L
1(ν) and \(L^{1}_{w} (\nu)\). It turns out that the development of O. Delgado and P.J. Miana can be readily adapted to provide a solution for this question and, moreover, it can be done in a more general situation than that of G being a group.
. This implies that L
1(G) is norm reflection invariant, that is if f∈L
1(G) then \(\widetilde{f}\in L^{1} (G)\) and \(\lVert{f}\rVert_{L^{1} (G)} = \lVert{\widetilde{f}}\rVert_{L^{1} (G)}\), where \(\widetilde{f}\) is the function given by \(\widetilde{f}(t)=f(-t), t\in G\). We are now interested in this property for the spaces L
1(ν) and \(L^{1}_{w} (\nu)\). It turns out that the development of O. Delgado and P.J. Miana can be readily adapted to provide a solution for this question and, moreover, it can be done in a more general situation than that of G being a group.
Let K be a nonempty compact Hausdorff space,  be a (countably additive) vector measure and h:K→K an homeomorphism. Given a function f:K→ℂ, let f
h
:K→ℂ be defined by f
h
=f∘h
−1. If f is measurable, notice that f
h
is also measurable.
be a (countably additive) vector measure and h:K→K an homeomorphism. Given a function f:K→ℂ, let f
h
:K→ℂ be defined by f
h
=f∘h
−1. If f is measurable, notice that f
h
is also measurable.
Definition 3.1
The vector measure ν is said to be norm integral h-invariant if
for all  . The space \(L^{1}_{w}(\nu)\) (resp. L
1(ν)) is norm h-invariant if for each \(f\in L^{1}_{w}(\nu)\) (resp. f∈L
1(ν)) we have that \(f_{h} \in L^{1}_{w}(\nu)\) (resp. f
h
∈L
1(ν)) and ∥f
h
∥
ν
=∥f∥
ν
.
. The space \(L^{1}_{w}(\nu)\) (resp. L
1(ν)) is norm h-invariant if for each \(f\in L^{1}_{w}(\nu)\) (resp. f∈L
1(ν)) we have that \(f_{h} \in L^{1}_{w}(\nu)\) (resp. f
h
∈L
1(ν)) and ∥f
h
∥
ν
=∥f∥
ν
.
Lemma 3.2
If
ν
is norm integral
h-invariant and
\(\lVert{\nu }\rVert(A)= 0\)
for
 then
\(\lVert{\nu}\rVert (h(A)) = 0\).
then
\(\lVert{\nu}\rVert (h(A)) = 0\).
Proof
We will use the equivalent norm for L 1(ν) given by

First of all note that  . So, from (3.1) it follows that \(\lVert{\nu(h(D))}\rVert_{_{X}} = \lVert{\nu(D)}\rVert_{_{X}}\). Let
. So, from (3.1) it follows that \(\lVert{\nu(h(D))}\rVert_{_{X}} = \lVert{\nu(D)}\rVert_{_{X}}\). Let  be such that \(\lVert{\nu}\rVert (A) = 0\). Then
be such that \(\lVert{\nu}\rVert (A) = 0\). Then

This shows that  so ∥ν∥(h(A))=∥χ
h(A)∥
ν
=0. □
so ∥ν∥(h(A))=∥χ
h(A)∥
ν
=0. □
Note that the lemma above establishes that
is a well defined linear operator. The next theorem generalizes [3, Lemma 3.4 and Proposition 3.5]. It additionally indicates that the norm ⦀⋅⦀ is also preserved by the operator that carries f→f h . The first part of the proof is similar to that in [3], but we include it for the sake of completeness.
Theorem 3.3
If ν is norm integral h-invariant, then the spaces \(L^{1}_{w}(\nu)\) and L 1(ν) are norm h-invariant. Moreover,

Proof
Take  . Clearly \(T_{h}(\chi_{_{A}})=\chi_{_{h(A)}}\). Let
. Clearly \(T_{h}(\chi_{_{A}})=\chi_{_{h(A)}}\). Let  and define S
h
:X
ν
→X
ν
by S
h
(I
ν
(ϕ))=I
ν
(T
h
ϕ), for
and define S
h
:X
ν
→X
ν
by S
h
(I
ν
(ϕ))=I
ν
(T
h
ϕ), for  . Since ν is norm integral h-invariant, then S
h
is a well-defined isometry and
. Since ν is norm integral h-invariant, then S
h
is a well-defined isometry and

Fix x′∈X′ and consider \(y'_{h}=x'\circ S_{h} \in(X_{\nu})'\). By using Hahn-Banach’s Theorem we can find \(x'_{h}\in X'\) with \(\|x'_{h}\|=\|y'_{h}\|\leq\|x'\|\|S_{h}\|=\|x'\|\) such that \(x'_{h}=y'_{h}\) in X
ν
. From (3.5) we now obtain \(\langle\nu,x'_{h}\rangle(A)=\langle\nu, x'\rangle(h(A))\),  , and from this it is easy to check that
, and from this it is easy to check that  . Therefore
. Therefore

Take \(f\in L^{1}_{w}(\nu)\) and x′∈B
X′. Then there is  such that 0≤ϕ
n
↗|f| pointwise. Clearly 0≤T
h
ϕ
n
↗|T
h
f|=T
h
|f|, so applying the Monotone Convergence Theorem
such that 0≤ϕ
n
↗|f| pointwise. Clearly 0≤T
h
ϕ
n
↗|T
h
f|=T
h
|f|, so applying the Monotone Convergence Theorem

Since \(\|x'_{h}\|\leq\|x'\|\) we have that \(T_{h}f\in L^{1}_{w}(\nu)\) and ∥T
h
f∥
ν
≤∥f∥
ν
. Taking ϕ
h
instead of ϕ in (3.1) we find that the vector measure ν is also norm integral h
−1-invariant. Hence we also have that \(\| f \|_{\nu}= \|T_{h^{-1}}(T_{h}f)\| \leq \|T_{h}f\|_{\nu}\). Finally, take f∈L
1(ν) and let  be a sequence converging to f in L
1(ν). Since
be a sequence converging to f in L
1(ν). Since  and ∥T
h
ϕ
n
−T
h
f∥
ν
=∥ϕ
n
−f∥
ν
, then T
h
f∈L
1(ν). The continuity of I
ν
gives \(\|I_{\nu}(T_{h}f)\|_{_{X}}=\|I_{\nu}(f)\|_{_{X}}\). We will now prove (3.4). Take
and ∥T
h
ϕ
n
−T
h
f∥
ν
=∥ϕ
n
−f∥
ν
, then T
h
f∈L
1(ν). The continuity of I
ν
gives \(\|I_{\nu}(T_{h}f)\|_{_{X}}=\|I_{\nu}(f)\|_{_{X}}\). We will now prove (3.4). Take  and note that
and note that

Since ν is h-invariant, we have

Finally, the density of  in L
1(ν) together with the continuity of the map T
h
:L
1(ν)→L
1(ν) gives (3.4). □
in L
1(ν) together with the continuity of the map T
h
:L
1(ν)→L
1(ν) gives (3.4). □
In a topological group, besides translations, the reflection R(t)=−t,t∈G, is also a canonical homeomorphism. We are now interested in applying our development to this case. More concretely, we will say that ν is norm integral reflection invariant, if it is norm integral R-invariant. In the case when \(L^{1}_{w}(\nu)\) (resp. L 1(ν)) has an R-invariant norm we will say that \(L^{1}_{w}(\nu)\) (resp. L 1(ν)) is norm reflection invariant. Note that R −1=R and if f:G→ℂ, then \(\widetilde{f} (t) = f \circ R^{-1}\).
Corollary 3.4
Let G be a compact Hausdorff abelian group.
-
(a)
If ν is a norm integral translation invariant vector measure, then the spaces \(L^{1}_{w}(\nu)\) and L 1(ν) are norm translation invariant.
-
(b)
If ν is norm integral reflection invariant, then the spaces \(L^{1}_{w}(\nu)\) and L 1(ν) are norm reflection invariant.
Next, we give some examples.
Example 3.5
The following two vector measures are norm integral R-invariant.
-
(a)
Consider K=[−1,1] and take λ to be Lebesgue’s measure on
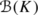 . Given 1≤p≤∞, let T:L
1(λ)→L
p(λ) be Volterra’s operator, that is, \(Tf (x) = \int_{0}^{x} f(s) ds\). Define ν to be \(\nu_{_{T}}\), the (countably additive) vector measure induced by T (recall that in this case I
ν
(f)=T(f), for all f∈L
1(ν)). Therefore for a given
. Given 1≤p≤∞, let T:L
1(λ)→L
p(λ) be Volterra’s operator, that is, \(Tf (x) = \int_{0}^{x} f(s) ds\). Define ν to be \(\nu_{_{T}}\), the (countably additive) vector measure induced by T (recall that in this case I
ν
(f)=T(f), for all f∈L
1(ν)). Therefore for a given  we have
$$ \bigl|I_\nu\phi_R (x)\bigr| = \biggl|\int _0^x \phi_R (s) ds \biggr| = \biggl|\int _0^x \phi(-s)ds \biggr| = \biggl|\int_0^{-x} \phi(s) ds \biggr| = \bigl|I_\nu\phi(-x)\bigr|. $$(3.6)
we have
$$ \bigl|I_\nu\phi_R (x)\bigr| = \biggl|\int _0^x \phi_R (s) ds \biggr| = \biggl|\int _0^x \phi(-s)ds \biggr| = \biggl|\int_0^{-x} \phi(s) ds \biggr| = \bigl|I_\nu\phi(-x)\bigr|. $$(3.6)Since λ is reflection invariant, this implies that \(\lVert {I_{\nu}\phi_{R}}\rVert_{L^{p}(K)} = \lVert{I_{\nu}\phi}\rVert_{L^{p}(K)}\) for 1≤p≤∞.
-
(b)
Let us consider the vector measure
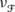 , associated to the Fourier transform studied in the case (3) in Example 2.2. Take
, associated to the Fourier transform studied in the case (3) in Example 2.2. Take 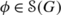 and γ∈Γ. By the reflection invariance of \(m_{_{G}}\) we have
and γ∈Γ. By the reflection invariance of \(m_{_{G}}\) we have
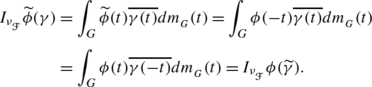
Since the correspondence \(\gamma\to\widetilde{\gamma}\) is a bijection on Γ, it follows from above that
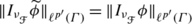 .
.
Example 3.6
We will now discuss the case of the vector measure considered in the case (1) in Example 2.2; as before we will denote it by ν μ .
-
(a)
As we said in the introduction, the vector measure ν μ is always norm integral translation invariant. If, in addition, μ is reflection invariant, we will next prove that ν is also norm integral reflection invariant. Notice \(T_{R} (f) = \widetilde{f}\) defines a linear isometry on L p(G). Let
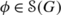 and t∈G. Then
$$g(t) = \bigl\lvert I_{\nu_{\mu}} \widetilde{\phi}(t) \bigr\rvert= \bigl\lvert \widetilde{ \phi} * \mu(t) \bigr\rvert= \biggl \vert \int_G \phi(s - t) d \mu(s) \biggr \vert .$$
and t∈G. Then
$$g(t) = \bigl\lvert I_{\nu_{\mu}} \widetilde{\phi}(t) \bigr\rvert= \bigl\lvert \widetilde{ \phi} * \mu(t) \bigr\rvert= \biggl \vert \int_G \phi(s - t) d \mu(s) \biggr \vert .$$On other side, since μ is reflection invariant, we have
$$h(t) \,{=}\, \bigl\lvert I_{\nu_{\mu}} \phi(t) \bigr\rvert\,{=}\, \bigl\lvert\phi* \mu(t) \bigr\rvert\,{=}\, \biggl \vert \int_G \phi(t - s) d \mu(s)\biggr \vert \,{=}\, \biggl \vert \int_G \phi(t + s) d \mu(s)\biggr \vert \,{=}\,\widetilde{g}(t). $$By the reflection invariance of the Haar measure, this implies that
$$\lVert{I_{\nu_{\mu}} \widetilde{\phi}}\rVert_{L^p (G)} = \lVert {g} \rVert_{L^p (G)} = \lVert{\widetilde{g}}\rVert_{L^p (G)} = \lVert{h} \rVert_{L^p (G)} = \lVert{I_{\nu_{\mu}} \phi}\rVert_{L^p (G)}. $$ -
(b)
However, the vector measure ν μ could be norm integral reflection invariant although μ is not reflection invariant. Namely, let us consider \(G=\mathbb{T}\), take \(x_{0} \in \mathbb{T}\) such that x 0≠±1 and define \(\mu=\delta_{x_{0}}\), the delta function centered at x 0. Next, we choose
 satisfying x
0∈A and \(x_{0}^{-1} \notin A\). Since μ(A)=1 and μ(A
−1)=0, the measure μ is not reflection invariant. Let
satisfying x
0∈A and \(x_{0}^{-1} \notin A\). Since μ(A)=1 and μ(A
−1)=0, the measure μ is not reflection invariant. Let  . Then
. Then
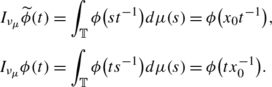
Since the norm in \(L^{p} (\mathbb{T})\) is invariant under both reflection and translation, from what we just established above we obtain \(\lVert{I_{\nu_{\mu}} \widetilde{\phi}}\rVert_{L^{p} (\mathbb{T})} = \lVert {\phi}\rVert_{L^{p} (\mathbb{T})} = \lVert{I_{\nu_{\mu}} \phi}\rVert_{L^{p} (\mathbb{T})}\). This shows that ν μ is norm integral reflection invariant.
-
(c)
We now present a vector measure ν μ that is not norm integral reflection invariant. Let us consider the measure \(\mu(s) = s d m_{_{\mathbb{T}}}(s)\) and notice it is regular. Take now as \(f: \mathbb{T}\rightarrow \mathbb{C}\) the continuous function defined by f(z)=z −1. Then
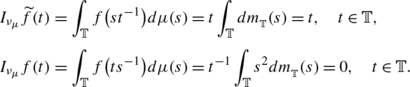
Since f∈L 1(ν μ ), it follows that ν μ is not norm integral reflection invariant.
We have just seen that a vector measure ν μ may not be norm integral reflection invariant. However, we have the following important result.
Theorem 3.7
Let 1≤p<∞. If \(f \in L^{p}_{w} ({\nu_{\mu}})\), then \(\widetilde{f}\in L^{1}_{w}({\nu_{\mu}})\) and there exists k>0 such that
Moreover, if f∈L p(ν μ ), then \(\widetilde{f}\in L^{1}({\nu_{\mu}})\).
Proof
We will start by proving there is a positive real number C such that

Since the vector measure ν
μ
is norm integral translation invariant, by Corollary 4.5 in [3] we have that L
p(ν
μ
)⊆L
p(G) and \(\lVert{f}\rVert_{L^{p} (G)} \leq\lVert{{\nu_{\mu}}}\rVert (G)^{-1/p} \lVert{f}\rVert_{{\nu _{\mu}},p}, \ f \in L^{p}({\nu_{\mu}})\). Take  . Then, by Minkowski’s inequality we find
. Then, by Minkowski’s inequality we find

with C=∥ν μ ∥(G)−1/p|μ|(G). This establishes (3.8). Let us now consider the norm ⦀⋅⦀ given in (3.2) and which is equivalent to that of L 1(ν μ ). Then (3.8) gives

Therefore

where k=4C=4∥ν
μ
∥(G)−1/p|μ|(G). Take  such that \(\lVert{{\nu_{\mu}}}\rVert(B) = 0\). Then, considering \(\phi= \chi_{_{B}} \) in (3.9) it follows that \(\lVert{\nu }\rVert(-B) = 0\). This shows that \(T_{R} f=\widetilde{f}\) is a well defined linear operator on L
0(ν
μ
). Consider \(f \in L^{p}_{w}({\nu_{\mu}})\) and take
such that \(\lVert{{\nu_{\mu}}}\rVert(B) = 0\). Then, considering \(\phi= \chi_{_{B}} \) in (3.9) it follows that \(\lVert{\nu }\rVert(-B) = 0\). This shows that \(T_{R} f=\widetilde{f}\) is a well defined linear operator on L
0(ν
μ
). Consider \(f \in L^{p}_{w}({\nu_{\mu}})\) and take  such that 0≤ϕ
n
↗|f|. Then \(0 \leq \widetilde{\phi}_{n} \nearrow \lvert \widetilde{f}\rvert\). Since both \(L^{p}_{w}({\nu_{\mu}})\) and \(L^{1}_{w}({\nu_{\mu}})\) have the Fatou property, we have \(\lVert{\phi_{n}}\rVert_{{\nu_{\mu}},p} \nearrow \lVert{f}\rVert_{{\nu_{\mu}},p}\) and also \(\lVert{\widetilde{\phi}_{n}}\rVert_{{\nu_{\mu}}} \nearrow\lVert{\widetilde{f}}\rVert_{{\nu_{\mu }}}\). On the other side, from (3.9) we obtain that \(\lVert{\widetilde{\phi}_{n}}\rVert_{{\nu _{\mu}}} \leq k \lVert{\phi_{n}}\rVert_{{\nu_{\mu}},p}\), n∈ℕ. Letting n→∞, we conclude that \(\widetilde{f}\in L^{1}_{w}({\nu_{\mu}})\) and \(\lVert{\widetilde{f}}\rVert_{{\nu _{\mu}}} \leq k \lVert{f}\rVert_{{\nu_{\mu}},p}\). Finally, let f∈L
p(ν
μ
) and consider a sequence
such that 0≤ϕ
n
↗|f|. Then \(0 \leq \widetilde{\phi}_{n} \nearrow \lvert \widetilde{f}\rvert\). Since both \(L^{p}_{w}({\nu_{\mu}})\) and \(L^{1}_{w}({\nu_{\mu}})\) have the Fatou property, we have \(\lVert{\phi_{n}}\rVert_{{\nu_{\mu}},p} \nearrow \lVert{f}\rVert_{{\nu_{\mu}},p}\) and also \(\lVert{\widetilde{\phi}_{n}}\rVert_{{\nu_{\mu}}} \nearrow\lVert{\widetilde{f}}\rVert_{{\nu_{\mu }}}\). On the other side, from (3.9) we obtain that \(\lVert{\widetilde{\phi}_{n}}\rVert_{{\nu _{\mu}}} \leq k \lVert{\phi_{n}}\rVert_{{\nu_{\mu}},p}\), n∈ℕ. Letting n→∞, we conclude that \(\widetilde{f}\in L^{1}_{w}({\nu_{\mu}})\) and \(\lVert{\widetilde{f}}\rVert_{{\nu _{\mu}}} \leq k \lVert{f}\rVert_{{\nu_{\mu}},p}\). Finally, let f∈L
p(ν
μ
) and consider a sequence  such that ϕ
n
→f in L
p(ν
μ
). From (3.7) it now follows that \(\widetilde{\phi}_{n} \rightarrow \widetilde{f}\) in \(L^{1}_{w}({\nu_{\mu}})\). Since each
such that ϕ
n
→f in L
p(ν
μ
). From (3.7) it now follows that \(\widetilde{\phi}_{n} \rightarrow \widetilde{f}\) in \(L^{1}_{w}({\nu_{\mu}})\). Since each  , we have that \(\widetilde{f}\in L^{1}({\nu_{\mu}})\). □
, we have that \(\widetilde{f}\in L^{1}({\nu_{\mu}})\). □
The above result gives special relevance to the case p=1. In this case we will obtain an alternative proof of the well-known result that \(L^{1}_{w}(\nu_{\mu}) =L^{1}(\nu_{\mu})= L^{1} (G)\) (see [11, Proposition 7.35 and Remark 7.36]).
Definition 3.8
Let k be a positive real number. A vector measure ν is k-scalarly bounded by
\(m_{_{G}}\), if \(|\langle\nu,x'\rangle|(A)\leq k m_{_{G}}(A)\) for all  and x′∈B
X′.
and x′∈B
X′.
In this situation, note that \(\nu\ll m_{_{G}}\).
Theorem 3.9
Let ν be a vector measure such that \(\nu \ll m_{_{G}}\) and, given x′∈X′, take h x′ as in (2.2). Then, the following assertions are equivalent:
-
(1)
ν is k-scalarly bounded by \(m_{_{G}}\),
-
(2)
\(\lVert{h_{x'}}\rVert_{L^{\infty}(G)} \leq k\) for all x′∈B X′,
-
(3)
\(L^{p}(G)\subseteq L^{p}_{w}(\nu)\) with \(\|f\|_{\nu,p}\leq k^{1/p} \|f\|_{L^{p}(G)}\) for all f∈L p(G) and 1≤p<∞.
-
(4)
\(L^{1}(G)\subseteq L^{1}_{w}(\nu)\) with \(\|f\|_{\nu}\leq k \|f\|_{L^{1}(G)}\) for all f∈L 1(G).
Proof
We start by proving that (1) implies (2). Given x′∈B
X′ and 
It follows that h x′∈L ∞(G) and \(\|h_{x'}\|_{L^{\infty}(G)}\leq k\). Assume now (2) and let us show (3). Given 1≤p<∞ and f∈L p(G) and x′∈B X′
and (3) follows. Clearly (3) implies (4) so finally let us prove that (4) implies (1). Fixing x′∈B X′ one has
so ν is k-scalarly bounded by \(m_{_{G}}\). □
Corollary 3.10
\(L^{1}_{w}(\nu_{\mu}) = L^{1}(\nu_{\mu})= L^{1} (G)\), with \(\lVert\,{\cdot}\,\rVert_{\nu_{\mu}}\) and \(\lVert\,{\cdot}\, \rVert_{L^{1} (G)}\) being equivalent norms.
Proof
First, we remark that \(m_{_{G}}\) and \(\lVert{\nu_{\mu}}\rVert\) have the same null sets ([3, Theorem 4.1]). Identifying \(x'\in B_{L^{1}(G)'}\) with g∈L ∞(G), it is easy to see that h x′=∫ G g(⋅+s)dμ(s). Therefore
Hence ν μ is k-scalarly bounded by \(m_{_{G}}\), with k=|μ|(G). It follows by Theorem 3.9(4) that \(L^{1}(G)\subseteq L^{1}_{w}(\nu_{\mu})\) and \(\|f\|_{\nu_{\mu}}\leq |\mu|(G) \|f\|_{L^{1}(G)}\), f∈L 1(G). On the other hand, [3, Corollary 4.5] indicates that \(L^{1}_{w}(\nu_{\mu}) \subseteq L^{1} (G)\) and \(\lVert{f}\rVert_{L^{1} (G)} \leq\|\nu_{\mu}\|(G)^{-1} \|f\|_{\nu_{\mu}}\), \(f \in L^{1}_{w}(\nu_{\mu})\). Finally, from \(L^{1}_{w}(\nu_{\mu}) = L^{1} (G)\) with equivalent norms, it follows that \(L^{1}_{w} (\nu_{\mu})\) is order continuous. This implies that \(L^{1}_{w}(\nu_{\mu}) = L^{1}(\nu_{\mu})\). □
4 Convolution Associated to ν
Let G be a compact Hausdorff abelian group, X a Banach space and  a countably additive vector measure satisfying \(\nu\ll m_{_{G}}\). In this section we will then introduce a convolution operator and a vector-valued convolution function (both associated to ν) and relate them with the Fourier transform studied in Sect. 3. Given x′∈X′ consider h
x′ as in (2.2) and take f∈L
1(G) and \(g\in L^{1}_{w}(\nu)\). Then gh
x′∈L
1(G) and so the classical Young’s Inequality implies that f∗(gh
x′)∈L
1(G) and \(\|f*(gh_{x'})\|_{L^{1}(G)}\leq\|f\|_{L^{1}(G)}\|gh_{x'}\|_{L^{1}(G)}\leq \|f\|_{L^{1}(G)}\|g\|_{\nu}\|x'\|\). This allows us to give the following definition.
a countably additive vector measure satisfying \(\nu\ll m_{_{G}}\). In this section we will then introduce a convolution operator and a vector-valued convolution function (both associated to ν) and relate them with the Fourier transform studied in Sect. 3. Given x′∈X′ consider h
x′ as in (2.2) and take f∈L
1(G) and \(g\in L^{1}_{w}(\nu)\). Then gh
x′∈L
1(G) and so the classical Young’s Inequality implies that f∗(gh
x′)∈L
1(G) and \(\|f*(gh_{x'})\|_{L^{1}(G)}\leq\|f\|_{L^{1}(G)}\|gh_{x'}\|_{L^{1}(G)}\leq \|f\|_{L^{1}(G)}\|g\|_{\nu}\|x'\|\). This allows us to give the following definition.
Definition 4.1
Let ν be a vector measure such that \(\nu\ll m_{_{G}}\). For f∈L 1(G) and \(g\in L^{1}_{w}(\nu)\) we define the convolution operator of f and g associated to ν, as the linear and continuous map f∗ ν g:X′→L 1(G) given by
Remark 4.2
Assume that the vector measure ν is norm integral translation invariant and \(\nu\ll m_{_{G}}\) and take 1≤p<∞. Then \(L^{p}_{w}(\nu)\subseteq L^{1}(G)\) (see [3, Sect. 3]). Therefore, in this situation Definition 4.1 makes also sense for f in \(L^{p}_{w}(\nu)\).
Theorem 4.3
Let ν be a norm integral translation invariant vector measure such that \(\nu\ll m_{_{G}}\) and f,g∈L 1(ν).
-
(a)
Then for all γ∈Γ and x′∈X′
$$ \widehat{f*_{\nu}g\bigl(x'\bigr)}(\gamma)=\bigl \langle\widehat{f}(\gamma )\widehat {g}^\nu(\gamma),x' \bigr\rangle. $$(4.1) -
(b)
If, in addition, ν is norm integral reflection invariant
$$ \bigl\langle f*_{\nu} g\bigl(x'\bigr),\phi\bigr \rangle=\biggl\langle\int_{G} (\widetilde {f}*\phi)gd\nu ,x'\biggr\rangle,\quad\phi\in L^\infty(G),\ x' \in X'. $$(4.2)
Proof
-
(a)
First of all note that for each x′∈X′ and γ∈Γ
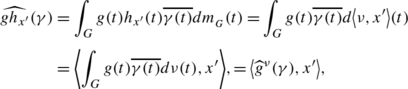
hence
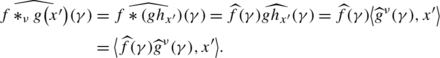
-
(b)
Let us take x′∈X′ and ϕ∈L ∞(G). Using Fubini’s Theorem
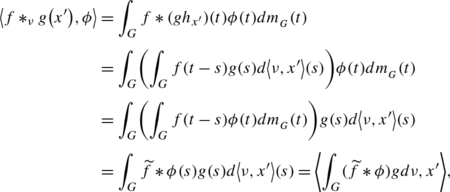
where the last equality is a consequence of the following fact: since \(\widetilde{f}\in L^{1}(\nu)\subseteq L^{1}(G)\) and ϕ∈L ∞(G) then the classical Young’s inequality gives that \(\widetilde{f}*\phi\in L^{\infty}(G)\).
□
Corollary 4.4
Let ν be a norm integral translation and reflection invariant vector measure such that \(\nu\ll m_{_{G}}\) and f,g∈L 1(ν). Then for all γ∈Γ
Proof
For γ∈Γ just take \(\phi=\overline{\gamma}\) in (4.2) and use (4.1). □
Following the classical case one can define the convolution of f and g with respect to ν in the following more natural way (for a similar definition in the setting of the bounded bilinear map see [1]).
Definition 4.5
Let f,g∈L 0(G). The convolution of f and g with respect to ν is the vector-valued function f∗ν g:G→X given by
provided that f(t−⋅)g∈L 1(ν) for \(m_{_{G}}\)-almost all t∈G.
Clearly in the case when \(\nu\ll m_{_{G}}\) we have that
for all x′∈X′ and f∈L 1(G), \(g\in L^{1}_{w}(\nu)\) satisfying f(t−⋅)g∈L 1(ν) for almost all t∈G.
We give now some examples. Recall that given an order continuous Banach function space \(E(m_{_{G}})\) and a Banach space X, an operator \(T:E(m_{_{G}})\to X\) is said to be \(m_{_{G}}\)-determined if the \(m_{_{G}}\)-null sets and the \(\nu_{_{T}}\)-null sets coincide (or equivalently if \(m_{_{G}}\) is a control measure for \(\nu_{_{T}}\) (see [11, Lemma 4.5])). This notion has been recently studied in [11, Chap. 4]. In particular multiplication operators, Fourier transform, translation operators and operators acting in L p(G) via convolution with measures are \(m_{_{G}}\)-determined (see respectively [11, Examples 4.7, 4.10, 4.17 and Remark 7.60]).
Example 4.6
With the notation of Example 2.2 if we assume that \(T:E(m_{_{G}})\to X\) is \(m_{_{G}}\)-determined, then we have that \(\nu_{_{T}}\ll m_{_{G}}\),
and
provided that f∈L 1(G), \(g\in L^{1}_{w}(\nu_{_{T}})\) satisfy \(f(t-\cdot)g\in E(m_{_{G}})\subseteq L^{1}(\nu_{_{T}})\) for almost all t∈G. According to (4.4) and (4.5) we have the following particular cases.
-
(a)
Consider the vector measure
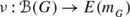 given by \(\nu(A)=\chi_{_{A}}\) and introduced in (2) of Example 2.2. Then for all t∈G and \(x'\in E(m_{_{G}})'\) (identified with a function \(h\in E(m_{_{G}})^{\times}\))
given by \(\nu(A)=\chi_{_{A}}\) and introduced in (2) of Example 2.2. Then for all t∈G and \(x'\in E(m_{_{G}})'\) (identified with a function \(h\in E(m_{_{G}})^{\times}\))
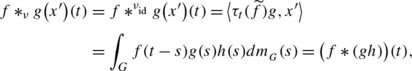
provided that f∈L 1(G), \(g\in L^{1}_{w}(\nu)\). If in addition f(t−⋅)g∈L 1(ν) for almost all t∈G we obtain \(f*^{\nu}g(t)=f*^{\nu_{_{\mathrm{id}}}}g(t)= \tau_{t}(\widetilde{f})g\).
-
(b)
If we consider the vector measure
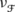 associated to the Fourier transform presented in (3) of Example 2.2 we have
associated to the Fourier transform presented in (3) of Example 2.2 we have
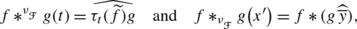
for all t∈G, f∈L 1(G) and
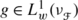 such that
such that 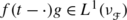 where x′∈(ℓ
p′(Γ))′ is identified with y∈ℓ
p(Γ).
where x′∈(ℓ
p′(Γ))′ is identified with y∈ℓ
p(Γ). -
(c)
Take finally the vector measure
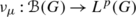 studied in (1) of Example 2.2. Then
$$f*^{\nu_{\mu}}g(t)=\bigl(\tau_{t}(\widetilde{f})g\bigr)*\mu \quad \mbox{and} \quad f*_{\nu_{\mu}}g\bigl(x'\bigr) (t)=\bigl\langle \bigl(\tau_{t}(\widetilde{f})g\bigr)*\mu ,h\bigr\rangle, $$
studied in (1) of Example 2.2. Then
$$f*^{\nu_{\mu}}g(t)=\bigl(\tau_{t}(\widetilde{f})g\bigr)*\mu \quad \mbox{and} \quad f*_{\nu_{\mu}}g\bigl(x'\bigr) (t)=\bigl\langle \bigl(\tau_{t}(\widetilde{f})g\bigr)*\mu ,h\bigr\rangle, $$for all t∈G, f∈L 1(G) and \(g\in L^{1}_{w}(\nu_{\mu})\) such that f(t−⋅)g∈L 1(ν μ ) and x′∈L p(G) is identified with the function h∈L p′(G).
Remark 4.7
In the previous example if the corresponding L p(ν) is both norm translation and reflection invariant, then given f∈L p(ν) we have that \(\tau_{t}(\widetilde{f})\in L^{p}(\nu)\) for all t∈G. Hence for all g∈L p′(ν) we obtain that f(t−⋅)g∈L 1(ν) for all t∈G.
In the following result we establish some integration properties for the vector-valued function f∗ν g.
Theorem 4.8
Assume \(\nu\ll m_{_{G}}\) and let f∈L 1(G). If \(g\in L^{1}_{w}(\nu)\) is such that f(t−⋅)g∈L 1(ν) for almost all t∈G, then f∗ν g is Dunford integrable and \(\|f*^{\nu}g\|_{L^{1}_{w}(G,X)}\leq \|f\|_{L^{1}(G)}\|g\|_{\nu}\). Moreover, if g∈L 1(ν) then f∗ν g is Pettis integrable and \((P)\int_{G}(f*^{\nu}g)dm_{_{G}}= (\int_{G} fdm_{_{G}}) (\int_{G} gd\nu )\).
Proof
Take x′∈B X′ and let h x′ be as in (2.2). Since \(g \in L^{1}_{w} (\nu)\), notice that gh x′∈L 1(G). Let ψ x′ be the (\(m_{_{G}}\)-a.e. defined) function ψ x′(t)=〈f∗ν g(t),x′〉,t∈G. Then
and so we conclude that ψ x′ is measurable. Next, using Fubini’s Theorem

Hence, f∗ν
g is Dunford integrable and we obtain the inequality. For the second part fix x′∈X′ and  . Since the correspondence \(s \rightarrow \int_{A} f(t -s) dm_{_{G}}(t)\) defines a bounded measurable function, we have
. Since the correspondence \(s \rightarrow \int_{A} f(t -s) dm_{_{G}}(t)\) defines a bounded measurable function, we have
and

□
Proposition 4.9
Let
ν
be a norm integral translation invariant vector measure such that
\(\nu\ll m_{_{G}}\)
and
f,g∈L
1(ν). If
 converges to
f
in
L
1(ν), then for each
x′∈X′ the sequence (〈ϕ
n
∗ν
g,x′〉)
n
converges to
f∗
ν
g(x′) in
L
1(G).
converges to
f
in
L
1(ν), then for each
x′∈X′ the sequence (〈ϕ
n
∗ν
g,x′〉)
n
converges to
f∗
ν
g(x′) in
L
1(G).
Proof
Fix x′∈X′. Using Fubini’s Theorem

□
In this last part of the paper we present various Young’s Theorems in our setting.
Theorem 4.10
Let ν be a vector measure such that \(\nu\ll m_{_{G}}, \ 1\leq p<\infty\) and \(g\in L_{w}^{1}(\nu)\).
-
(a)
Then f∗ ν g∈L(X′,L p(G)) and \(\|f*_{\nu} g\|_{ L(X',L^{p}(G))}\leq\|f\|_{L^{p}(G)}\|g\|_{\nu}\), for every f∈L p(G).
-
(b)
Assume that ν is also norm integral translation invariant. If \(f\in L_{w}^{p}(\nu)\), then \(f*_{\nu} g\in L(X',L_{w}^{p}(\nu))\) and \(\|f*_{\nu} g\|_{ L(X',L_{w}^{p}(\nu))}\leq\|f\|_{\nu,p}\|g\|_{\nu}\). Moreover, if f∈L p(ν) and g∈L 1(ν) then f∗ ν g∈L(X′,L p(ν)).
Proof
(a) Take x′∈B X′. Using Minkowski’s Inequality we have that

Hence f∗ ν g(x′)∈L p(G) for all x′∈B X′ and the inequality follows.
(b) Fix now x′∈B X′ and let us show that \(f*_{\nu} g(x')\in L^{p}_{w}(\nu)\). Take z′∈B X′. As in the previous case we use Minkowski’s Inequality together with the fact that ν is norm integral translation invariant to obtain

Hence \(f*_{\nu} g(x')\in L^{p}_{w}(\nu)\) for all x′∈B X′ and the inequality follows. Assume now that f∈L p(ν) and g∈L 1(ν) and take (ϕ n ) n and (ψ n ) n , sequences of simple functions converging to f and g in L p(ν) and L 1(ν) respectively. Clearly ϕ n ∈L ∞(G) and ψ n h x′∈L 1(G), so ϕ n ∗ ν ψ n (x′)=ϕ n ∗(ψ n h x′) is a bounded function and, in particular, belongs to L p(ν). On the other hand since \(f*_{\nu}g (x')\in L^{p}_{w}(\nu)\)

then f∗ ν g(x′)∈L p(ν), since L p(ν) is closed in \(L^{p}_{w}(\nu)\). Hence f∗ ν g∈L(X′,L p(ν)). □
Assuming that ν is not only norm integral translation invariant but also reflection invariant we obtain a natural extension of Theorem 4.10(b).
Corollary 4.11
Let ν be a norm integral translation and reflection invariant vector measure such that \(\nu\ll m_{_{G}}\) and 1≤p<∞. If \(f\in L^{p}_{w}(\nu)\) and \(g\in L^{q}_{w}(\nu)\) with 1≤q≤p′ then \(f*_{\nu} g\in L(X',L_{w}^{r}(\nu))\) with 1/p+1/q=1+1/r and \(\|f*_{\nu} g\|_{ L(X',L_{w}^{r}(\nu))}\leq\|f\|_{\nu,p}\|g\|_{\nu,q}\). Moreover if f∈L p(ν) and g∈L q(ν) then f∗ ν g∈L(X′,L r(ν)).
Proof
Let x′∈B X′. By Theorem 4.10(b) the linear map T f,x′(g)=f∗ ν g(x′) is a bounded application from \(L_{w}^{1}(\nu)\) into \(L_{w}^{p}(\nu)\) and \(\|T_{f,x'}\|_{L(L_{w}^{1}(\nu),L_{w}^{p}(\nu))}\leq\|f\|_{\nu,p}\). On the other hand, since ν is norm integral translation and reflection invariant, given \(g\in L_{w}^{p'}(\nu)\) then Hölder’s Inequality gives that for all t∈G

Hence, T f,x′ is also a bounded linear map from \(L_{w}^{p'}(\nu)\) into \(L^{\infty}(\nu)=L^{\infty}_{w}(\nu)\) and \(\|T_{f,x'}\|_{L(L_{w}^{p'}(\nu),L^{\infty}(\nu))}\leq\|f\|_{\nu,p}\). Then using a standard interpolation argument (see [6, Theorem 3.4]) the map T f,x′ is bounded from \(L_{w}^{q}(\nu)\) into \(L_{w}^{r}(\nu)\), where 1≤q≤p′ and 1/p+1/q=1+1/r, and we have

Therefore \(\|f*_{\nu}g(x')\|_{L^{r}_{w}(\nu)}=\|T_{f,x'}(g)\|_{L^{r}_{w}(\nu)}\leq \|f\|_{\nu,p}\|g\|_{\nu,q}\), so \(f*_{\nu}g(x')\in L^{r}_{w}(\nu)\) and the inequality follows. For the second part, again using Theorem 4.10(b) the map T f,x′ is now bounded from L 1(ν) into L p(ν). But since \(L^{\infty}(\nu)=L^{\infty}_{w}(\nu)\) then T f,x′ is also bounded from L p′(ν) into L ∞(ν) and the same interpolation theorem gives the result. □
We finish this paper by giving a generalization of Theorem 4.8.
Corollary 4.12
Let ν be a norm integral translation invariant vector measure such that \(\nu\ll m_{_{G}}\) and 1≤p<∞. Let \(f\in L^{p}_{w}(\nu)\) and \(g\in L^{1}_{w}(\nu)\) be such that f(t−⋅)g∈L 1(ν). Then f∗ν g is Dunford p-integrable and \(\|f*^{\nu} g\|_{ L^{p}_{w}(G,X)}\leq\|\nu\|(G)^{-1/p}\|f\|_{\nu,p}\| g\|_{\nu}\). Moreover if f∈L p(ν) and g∈L 1(ν) then f∗ ν g is Pettis p-integrable.
Proof
For the fist part just apply [3, Corollary 4.5], (4.3) and Theorem 4.10(b) to obtain, for each x′∈X′

Hence f∗ν g is Dunford p-integrable and the inequality follows. The second part is also a direct consequence of Theorem 4.10(b). □
With the same proof but applying now Corollary 4.11 we have the following final result.
Corollary 4.13
Let ν be a norm integral translation and reflection invariant vector measure such that \(\nu\ll m_{_{G}}\) and 1≤p<∞. Let \(f\in L^{p}_{w}(\nu)\) and \(g\in L^{q}_{w}(\nu)\) with 1≤q≤p′ such that f(t−⋅)g∈L 1(ν). Then f∗ν g is Dunford r-integrable with 1/p+1/q=1+1/r and \(\|f*^{\nu} g\|_{ L^{r}_{w}(G,X)}\leq\|\nu\|(G)^{-1/r}\|f\|_{\nu,p}\| g\|_{\nu,q}\). Moreover if f∈L p(ν) and g∈L q(ν) then f∗ ν g is Pettis r-integrable.
References
Blasco, O., Calabuig, J.M.: Fourier analysis with respect to bilinear maps. Acta Math. Sin. Engl. Ser. 25(4), 519–530 (2009)
del Campo, R., Fernández, A., Ferrando, I., Mayoral, F., Naranjo, F.: Multiplication operators on spaces on integrable functions with respect to a vector measure. J. Math. Anal. Appl. 343(1), 514–524 (2008)
Delgado, O., Miana, P.J.: Algebra structure for L p of a vector measure. J. Math. Anal. Appl. 358(2), 355–363 (2009)
Diestel, J., Uhl, J.J.: Vector Measures. Math. Surveys, vol. 15. Amer. Math. Soc., Providence (1977)
Ferrando, I., Galaz-Fontes, F.: Multiplication operators on vector measure Orlicz spaces. Indag. Math. 20(1), 57–71 (2009)
Fernández, A., Mayoral, F., Naranjo, F., Sánchez Pérez, E.A.: Complex interpolation of spaces of integrable functions with respect to a vector measure. Collect. Math. 61(3), 241–252 (2010)
Katznelson, Y.: An Introduction to Harmonic Analysis. Cambridge University Press, Cambridge (2004)
Mockenhaupt, G., Ricker, W.J.: Optimal extension of the Hausdorff-Young inequality. J. Reine Angew. Math. 620, 195–211 (2008)
Pap, E.: Handbook of Measure Theory. North-Holland/Elsevier, Amsterdam (2002)
Talagrand, M.: Pettis Integral and Measure Theory. Memoirs of the AMS, vol. 307 (1984)
Okada, S., Ricker, W., Sánchez Pérez, E.A.: Optimal Domain and Integral Extension of Operators acting in Function Spaces. Oper. Theory Adv. Appl., vol. 180. Birkhäuser, Basel (2008)
Rudin, W.: Fourier Analysis on Groups. Interscience, New York (1967)
Luxemburg, W.A.J., Zaanen, A.C.: Riesz Spaces I. North Holland, Amsterdam (1971)
Acknowledgements
J.M. Calabuig was supported by Ministerio de Economía y Competitividad and FEDER (project MTM2008-04594) and MEC “Jose Castillejo 2008”. E.A. Sánchez Pérez was supported by Ministerio de Economía y Competitividad and FEDER (project MTM2012-36740-c02-02). J.M. Calabuig and E.A. Sánchez Pérez were also supported by “Ayuda para Estancias de PDI de la UPV en centros de investigación de prestigio” (PAID-00-11).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Paul Butzer.
Rights and permissions
About this article
Cite this article
Calabuig, J.M., Galaz-Fontes, F., Navarrete, E.M. et al. Fourier Transform and Convolutions on L p of a Vector Measure on a Compact Hausdorff Abelian Group. J Fourier Anal Appl 19, 312–332 (2013). https://doi.org/10.1007/s00041-012-9252-3
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00041-012-9252-3
Keywords
- Countably additive vector measure
- Space of p-integrable functions
- Fourier transform
- Convolution
- Pettis integrability



 and 1≤p<∞ we consider the operator T
μ
:L
p(G)→L
p(G) given by T
μ
(f)=f∗μ for each f∈L
p(G), where
and 1≤p<∞ we consider the operator T
μ
:L
p(G)→L
p(G) given by T
μ
(f)=f∗μ for each f∈L
p(G), where
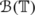 . In accordance, we will change our notation to that of multiplication. Hence we have
. In accordance, we will change our notation to that of multiplication. Hence we have 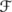 which, by the Hausdorff-Young inequality, satisfies
which, by the Hausdorff-Young inequality, satisfies 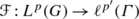 . Hence
. Hence  is given by
is given by
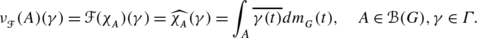
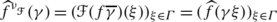 , γ∈Γ.
, γ∈Γ.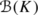 . Given 1≤p≤∞, let T:L
1(λ)→L
p(λ) be Volterra’s operator, that is,
. Given 1≤p≤∞, let T:L
1(λ)→L
p(λ) be Volterra’s operator, that is,  we have
we have
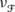 , associated to the Fourier transform studied in the case (3) in Example 2.2. Take
, associated to the Fourier transform studied in the case (3) in Example 2.2. Take 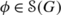 and γ∈Γ. By the reflection invariance of
and γ∈Γ. By the reflection invariance of 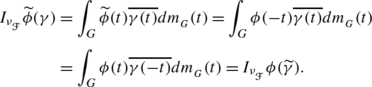
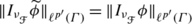 .
.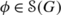 and t∈G. Then
and t∈G. Then
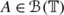 satisfying x
0∈A and
satisfying x
0∈A and  . Then
. Then
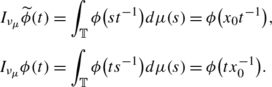
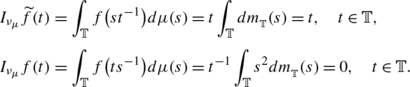
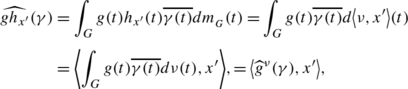
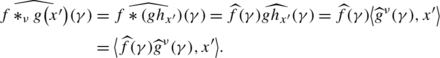
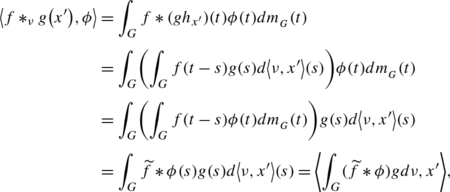
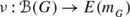 given by
given by 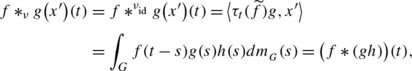
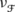 associated to the Fourier transform presented in (3) of Example 2.2 we have
associated to the Fourier transform presented in (3) of Example 2.2 we have
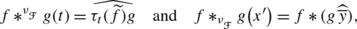
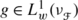 such that
such that 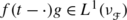 where x′∈(ℓ
p′(Γ))′ is identified with y∈ℓ
p(Γ).
where x′∈(ℓ
p′(Γ))′ is identified with y∈ℓ
p(Γ).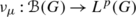 studied in (1) of Example 2.2. Then
studied in (1) of Example 2.2. Then