A Generalized Sampling Theorem for Stable Reconstructions in Arbitrary Bases

Abstract

We introduce a generalized framework for sampling and reconstruction in separable Hilbert spaces. Specifically, we establish that it is always possible to stably reconstruct a vector in an arbitrary Riesz basis from sufficiently many of its samples in any other Riesz basis. This framework can be viewed as an extension of the well-known consistent reconstruction technique (Eldar et al.). However, whilst the latter imposes stringent assumptions on the reconstruction basis, and may in practice be unstable, our framework allows for recovery in any (Riesz) basis in a manner that is completely stable.

Whilst the classical Shannon Sampling Theorem is a special case of our theorem, this framework allows us to exploit additional information about the approximated vector (or, in this case, function), for example sparsity or regularity, to design a reconstruction basis that is better suited. Examples are presented illustrating this procedure.

1 Introduction

The Shannon Sampling Theorem, or the Nyquist–Shannon Sampling Theorem as it is also called (we will refer to it as the NS-Sampling Theorem throughout the paper), is a mainstay in modern signal processing and has become one of the most important theorems in mathematics of information [32]. The list of applications of the theorem is long, and ranges from Magnetic Resonance Imaging (MRI) to sound engineering. We will in this paper address the question on whether or not the NS-Sampling Theorem can be improved. In particular, given the same set of information, can one design a reconstruction of a function that would be better than that provided by the NS-Sampling Theorem? The answer to such a question will obviously depend on the type of functions considered. However, suppose that we have some extra information about the functions to be reconstructed. One may, for example, have information about a basis that is particularly suited for such functions. Could this information be used to improve the reconstruction given by the NS-Sampling Theorem, even if it is based on the same sampling procedure? Although such a question has been posed before, and numerous extensions of the NS-Sampling Theorem have been developed [7, 8, 15, 16, 33], the generalization we introduce in this paper is, to the best of our knowledge, a novel approach for this problem.

The well known NS-Sampling Theorem [24, 26, 29, 30, 34] states that if

$$f = \mathcal{F}g, \quad g \in L^2(\mathbb{R}),$$

where $\mathcal{F}$ is the Fourier transform and supp(g)⊂[−T,T] for some T>0, then both f and g can be reconstructed from point samples of f. In particular, if $\epsilon\leq\frac{1}{2T}$ then

The quantity $\frac{1}{2T}$, which is the largest value of ϵ such that the theorem holds, is often referred to as the Nyquist rate [29]. In practice, when trying to reconstruct f or g, one will most likely not be able to access the infinite amount of information required, namely, {f(kϵ)} _k∈ℤ. Moreover, even if we had access to all samples, we are limited by both processing power and storage to taking only a finite number. Thus, a more realistic scenario is that one will be given a finite number of samples {f(kϵ)}_|k|≤N , for some N<∞, and seek to reconstruct f from these samples. The question is therefore: are the approximations

$$f_N(\cdot) = \sum_{k=-N}^{N}f(k\epsilon)\mathrm{sinc} \biggl(\frac{\cdot +k\epsilon}{\epsilon} \biggr), \qquad g_N(\cdot) = \epsilon\sum_{k=-N}^{N}f(k\epsilon)e^{2\pi\mathrm{i} \epsilon k\cdot}$$

optimal for f and g given the information {f(kϵ)}_|k|≤N ? To formalize this question consider the following. For N∈ℕ and ϵ>0, let

(1.1)

(C(ℝ) denotes the set of continuous functions on ℝ). Define the mappings (with a slight abuse of notation)

(1.2)

The question is, given a class of functions Θ⊂L ²(ℝ), could there exist mappings Ξ _N,ϵ,1:Ω _N,ϵ →L ²(ℝ) and Ξ _N,ϵ,2:Ω _N,ϵ →L ²(ℝ) such that

As we will see later, the answer to this question may very well be yes, and the problem is therefore to find such mappings Ξ _N,ϵ,1 and Ξ _N,ϵ,2.

As motivation for this work, consider the following reconstruction problem. Let g be defined by

$$g(t) = \begin{cases}1 & t \in[0,1/2)\\-1& t \in[1/2,1] \\0 & t \in\mathbb{R}\setminus[0,1].\end{cases} $$

This is the well-known Haar wavelet. Due to the discontinuity, there is no way one can exactly reconstruct this function with only finitely many function samples if one insists on using the mapping Λ _N,ϵ,2. We have visualized the reconstruction of g using Λ _N,ϵ,2 in Fig. 1. In addition to g not being reconstructed exactly, the approximation Λ _N,ϵ,2(g) is polluted by oscillations near the discontinuities of g. Such oscillations are indicative of the well-known Gibbs phenomenon in recovering discontinuous signals from samples of their Fourier transforms [23]. This phenomenon is a major hurdle in many applications, including image and signal processing. Its resolution has, and continues to be, the subject of significant inquiry [31].

Fig. 1

The figure shows Λ _N,ϵ,2(f) for $f = \mathcal {F}g$, N=500 and ϵ=0.5 (left) as well as g (right)

It is tempting to think, however, that one could construct a mapping Ξ _N,ϵ,2 that would yield a better result. Suppose for a moment that we do not know g, but we do have some extra information. In particular, suppose that we know that g∈Θ, where

$$ \Theta= \Biggl\{h \in L^2(\mathbb{R}): h = \sum _{k = 1}^M \beta_k\psi_k \Biggr\},$$

(1.3)

for some finite number M and where {ψ _k } are the Haar wavelets on the interval [0,1]. Could we, based on the extra knowledge of Θ, construct mappings Ξ _N,ϵ,1:Ω _N,ϵ →L ²(ℝ) and Ξ _N,ϵ,2:Ω _N,ϵ →L ²(ℝ) such that

Indeed, this is the case, and a consequence of our framework is that it is possible to find Ξ _N,ϵ,1 and Ξ _N,ϵ,2 such that

provided N is sufficiently large. In other words, one gets perfect reconstruction. Moreover, the reconstruction is done in a completely stable way.

The main tool for this task is a generalization of the NS-Sampling Theorem that allows reconstructions in arbitrary bases. Having said this, whilst the Shannon Sampling Theorem is our most frequent example, the framework we develop addresses the more abstract problem of recovering a vector (belonging to some separable Hilbert space $\mathcal{H}$) given a finite number of its samples with respect any Riesz basis of $\mathcal{H}$.

1.1 Organization of the Paper

We have organized the paper as follows. In Sect. 2 we introduce notation and idea of finite sections of infinite matrices, a concept that will be crucial throughout the paper. In Sect. 3 we discuss existing literature on this topic, including the work of Eldar et al. [13, 14, 33]. The main theorem is presented and proved in Sect. 4, where we also show the connection to the classical NS-Sampling Theorem. The error bounds in the generalized sampling theorem involve several important constants, which can be estimated numerically. We therefore devote Sect. 5 to discussions on how to compute crucial constants and functions that are useful for providing error estimates. Finally, in Sect. 6 we provide several examples to support the generalized sampling theorem and to justify our approach.

2 Background and Notation

Let i denote the imaginary unit. Define the Fourier transform $\mathcal{F}$ by

$$(\mathcal{F}f) (y) = \int_{\mathbb{R}^d} f(x) e^{-2\pi\mathrm{i} x\cdot y}\, dx,\quad f \in L^1\bigl(\mathbb{R}^d\bigr),$$

where, for vectors x,y∈ℝ^d, x⋅y=x ₁ y ₁+⋯+x _d y _d . Aside from the Hilbert space L ²(ℝ^d), we now introduce two other important Hilbert spaces: namely,

$$l^2(\mathbb{N}) = \biggl\{\alpha= \{\alpha_1,\alpha_2, \ldots\}: \sum_{k \in\mathbb{N}} \bigl|\alpha^2_k\bigr| < \infty \biggr\}$$

and

$$l^2(\mathbb{Z}) = \biggl\{\beta= \{\ldots\beta_{-1},\beta_0, \beta_{1} \ldots\}: \sum _{k \in\mathbb{Z}} \bigl|\beta^2_k\bigr| < \infty \biggr\},$$

with their obvious inner products. We will also consider abstract Hilbert spaces. In this case we will use the notation $\mathcal{H}$. Note that {e _j } _j∈ℕ and {e _j } _j∈ℤ will always denote the natural bases for l ²(ℕ) and l ²(ℤ) respectively. We may also use the notation $\mathcal{H}$ for both l ²(ℕ) and l ²(ℤ) (the meaning will be clear from the context). Throughout the paper, the symbol ⊗ will denote the standard tensor product on Hilbert spaces.

The concept of infinite matrices will be quite crucial to what follows, and also finite sections of such matrices. We will consider infinite matrices as operators from both l ²(ℕ) to l ²(ℤ) and l ²(ℕ) to l ²(ℕ). The set of bounded operators from a Hilbert space $\mathcal{H}_{1}$ to a Hilbert space $\mathcal{H}_{2}$ will be denoted by $\mathcal{B}(\mathcal{H}_{1},\mathcal{H}_{2})$. As infinite matrices are unsuitable for computations we must reduce any infinite matrix to a more tractable finite-dimensional object. The standard means in which to do this is via finite sections. In particular, let

For n∈ℕ, define P _n to be the projection onto span{e ₁,…,e _n } and, for odd m∈ℕ, let $\widetilde{P}_{m}$ be the projection onto $\mathrm{span}\{e_{-\frac{m-1}{2}},\ldots, e_{\frac{m-1}{2}}\}$. Then $\widetilde{P}_{m} U P_{n}$ may be interpreted as

an m×n section of U. Finally, the spectrum of any operator $T \in\mathcal{B}(\mathcal{H})$ will be denoted by σ(T).

3 Connection to Earlier Work

The idea of reconstructing signals in arbitrary bases is certainly not new and this topic has been subject to extensive investigations in the last several decades. The papers by Unser and Aldroubi [7, 33] have been very influential and these ideas have been generalized to arbitrary Hilbert spaces by Eldar [13, 14]. The abstract framework introduced by Eldar is very powerful because of its general nature. Our framework is based on similar generalizations, yet it incorporates several key distinctions, resulting in a number of advantages.

Before introducing this framework, let us first review some of the key concepts of [14]. Let $\mathcal{H}$ be a separable Hilbert space and let $f \in\mathcal{H}$ be an element we would like to reconstruct from some measurements. Suppose that we are given linearly independent sampling vectors {s _k } _k∈ℕ that span a subspace $\mathcal{S} \subset\mathcal{H}$ and form a Riesz basis, and assume that we can access the sampled inner products c _k =〈s _k ,f〉, k=1,2…. Suppose also that we are given linearly independent reconstruction vectors {w _k } _k∈ℕ that span a subspace $\mathcal{W} \subset \mathcal{H}$ and also form a Riesz basis. The task is to obtain a reconstruction $\tilde{f} \in\mathcal{W}$ based on the sampling data {c _k } _k∈ℕ. The natural choice, as suggested in [14], is

$$ \tilde{f} = W\bigl(S^*W\bigr)^{-1}S^*f,$$

(3.1)

where the so-called synthesis operators $S, W:l^{2}(\mathbb{N})\rightarrow\mathcal{H}$ are defined by

$$Sx = x_1s_1 + x_2s_2 + \cdots,\qquad Wy = y_1w_1 +y_2 w_2 +\cdots,$$

and their adjoints $S^{*}, W^{*}:\mathcal{H} \rightarrow l^{2}(\mathbb{N})$ are easily seen to be

$$S^*g = \bigl\{\langle s_1,g\rangle, \langle s_2,g\rangle, \ldots\bigr\}, \qquad W^*h = \bigl\{\langle w_1,h\rangle,\langle w_2,h\rangle\ldots\bigr\}.$$

Note that S ^∗ W will be invertible if and only if

$$\mathcal{H} = \mathcal{W} \oplus\mathcal{S}^{\perp}.$$

Equation (3.1) gives a very convenient and intuitive abstract formulation of the reconstruction. However, in practice we will never have the luxury of being able to acquire nor process the infinite amount of samples 〈s _k ,f〉, k=1,2…, needed to construct $\tilde{f}$. An important question to ask is therefore:

What if we are given only the first m∈ℕ samples 〈s _k ,f〉, k=1,…,m? In this case we cannot use (3.1). Thus, the question is, what can we do?

Fortunately, there is a simple finite-dimensional analogue to the infinite dimensional ideas discussed above. Suppose that we are given m∈ℕ linearly independent sampling vectors {s ₁,…,s _m } that span a subspace $\mathcal{S}_{m} \subset\mathcal{H}$, and assume that we can access the sampled inner products c _k =〈s _k ,f〉, k=1,…,m. Suppose also that we are given linearly independent reconstruction vectors {w ₁,…,w _m } that span a subspace $\mathcal{W}_{m} \subset \mathcal{H}$. The task is to construct an approximation $\tilde{f} \in\mathcal{W}_{m}$ to f based on the samples $\{c_{k}\}_{k=1}^{m}$. In particular, we are interested in finding coefficients $\{d_{k}\}_{k=1}^{m}$ (that are computed from the samples $\{c_{k}\}_{k=1}^{m}$) such that $\tilde{f} = \sum_{k=1}^{m} d_{k} w_{k}$. The reconstruction suggested in [12] is

$$ \tilde{f} = \sum_{k=1}^md_k w_k = W_m\bigl(S_m^*W_m\bigr)^{-1}S_m^*f,$$

(3.2)

where the operators $S_{m}, W_{m} : \mathbb{C}^{m} \rightarrow\mathcal{H}$ are defined by

$$ S_mx = x_1s_1+ \cdots +x_ms_m, \qquad W_my =y_1w_1 + \cdots+y_m w_m,$$

(3.3)

and their adjoints $S^{*}, W^{*}:\mathcal{H} \rightarrow\mathbb{C}^{m}$ are easily seen to be

$$S_m^*g = \bigl\{\langle s_1,g\rangle, \ldots, \langle s_m,g\rangle\bigr\}, \qquad W_m^*h = \bigl\{\langle w_1,h\rangle, \ldots, \langle w_m,h\rangle\bigr\}.$$

From this it is clear that we can express $S_{m}^{*}W_{m}: \mathbb{C}^{m}\rightarrow\mathbb{C}^{m}$ as the matrix

(3.4)

Also, $S_{m}^{*}W_{m}$ is invertible if and only if and ([12, Prop. 3])

$$ \mathcal{W}_m \cap\mathcal{S}_m^{\perp}= \{0\}.$$

(3.5)

Thus, to construct $\tilde{f}$ one simply solves a linear system of equations. The error can now conveniently be bounded from above and below by

$$\|f - P_{\mathcal{W}_m}f\| \leq\|f - \tilde{f}\| \leq\frac{1}{\cos (\theta_{\mathcal{W}_m\mathcal{S}_m})}\|f -P_{\mathcal{W}_m}f\|,$$

where $P_{\mathcal{W}_{m}}$ is the projection onto $\mathcal{W}_{m}$,

$$\cos(\theta_{\mathcal{W}_m\mathcal{S}_m}) = \mathrm{inf}\bigl\{\|P_{\mathcal {S}_m}g\|: g \in \mathcal{W}_m, \|g\| = 1\bigr\},$$

is the cosine of the angles between the subspaces $\mathcal{S}_{m}$ and $\mathcal{W}_{m}$ and $P_{\mathcal{S}_{m}}$ is the projection onto $\mathcal{S}_{m}$ [12].

Note that if $f \in\mathcal{W}_{m}$, then $\tilde{f} = f$ exactly—a feature known as perfect recovery. Another facet of this framework is so-called consistency: the samples $\langle s_{j},\tilde{f}\rangle$, j=1,…,m, of the approximation $\tilde{f}$ are identical to those of the original function f (indeed, $\tilde {f}$, as given by (3.2), can be equivalently defined as the unique element in $\mathcal{W}_{m}$ that is consistent with f).

Returning to this issue at hand, there are now several important questions to ask:

• (i) What if $\mathcal{W}_{m} \cap\mathcal{S}_{m}^{\perp} \neq\{0\}$ so that $S_{m}^{*}W_{m}$ is not invertible? It is very easy to construct theoretical examples such that $S_{m}^{*}W_{m}$ is not invertible. Moreover, as we will see below, such situations may very well occur in applications. In fact, $\mathcal{W}_{m} \cap\mathcal{S}_{m}^{\perp} = \{0\}$ is a rather strict condition. If we have that $\mathcal{W}_{m} \cap \mathcal{S}_{m}^{\perp} \neq\{0\}$ does that mean that is impossible to construct an approximation $\tilde{f}$ from the samples $S_{m}^{*}f$?

• (ii) What if $\|(S_{m}^{*}W_{m})^{-1}\|$ is large? The stability of the method must clearly depend on the quantity $\|(S_{m}^{*}W_{m})^{-1}\|$. Thus, even if $(S_{m}^{*}W_{m})^{-1}$ exists, one may not be able to use the method in practice as there will likely be increased sensitivity to both round-off error and noise.

Our framework is specifically designed to tackle these issues. But before we present our idea, let us consider some examples where the issues in (i) and (ii) will be present.

Example 3.1

As for (i), the simplest example is to let $\mathcal{H} = l^{2}(\mathbb {Z})$ and {e _j } _j∈ℤ be the natural basis (e _j is the infinite sequence with 1 in its j-th coordinate and zeros elsewhere). For m∈ℕ, let the sampling vectors $\{s_{k}\}_{k=-m}^{m}$ and the reconstruction vectors $\{w_{k}\}_{k=-m}^{m}$ be defined by s _k =e _k and w _k =e _k+1. Then, clearly, $\mathcal{W}_{m} \cap\mathcal{S}_{m}^{\perp} =\mathrm{span}\{e_{m+1}\}$.

Example 3.2

For an example of more practical interest, consider the following. For 0<ϵ≤1 let $\mathcal{H} = L^{2}([0,1/\epsilon])$, and, for odd m∈ℕ, define the sampling vectors

$$\{s_{\epsilon,k}\}_{k=-(m-1)/2}^{(m-1)/2}, \quad s_{\epsilon,k} =e^{-2\pi\mathrm{i}\epsilon k \cdot}\chi_{[0,1/\epsilon]},$$

(this is exactly the type of measurement vector that will be used if one models Magnetic Resonance Imaging) and let the reconstruction vectors $\{w_{k}\}_{k=1}^{m}$ denote the m first Haar wavelets on [0,1] (including the constant function, w ₁=χ _[0,1]). Let S _ϵ,m and W _m be as in (3.3), according to the sampling and reconstruction vectors just defined. A plot of $\|(S_{\epsilon,m}^{*}W_{m})^{-1}\|$ as a function of m and ϵ is given in Fig. 2. As we observe, for ϵ=1 only certain values of m yield stable reconstruction, whereas for the other values of ϵ the quantity $\|(S_{\epsilon,m}^{*}W_{m})^{-1}\|$ grows exponentially with m, making the problem severely ill-conditioned. Further computations suggest that $\|(S_{\epsilon,m}^{*}W_{m})^{-1}\|$ increases exponentially with m not just for these values of ϵ, but for all 0<ϵ<1.

Fig. 2

This figure shows $\log_{10}\|(S^{*}_{\epsilon,m}W_{m})^{-1}\|$ as a function of m and ϵ for m=1,2,…,100. The left plot corresponds to ϵ=1, whereas the right plot corresponds to ϵ=7/8 (circles), ϵ=1/2 (crosses) and ϵ=1/8 (diamonds)

Example 3.3

Another example can be made by replacing the Haar wavelet basis with the basis consisting of Legendre polynomials (orthogonal polynomials on [−1,1] with respect to the Euclidean inner product).

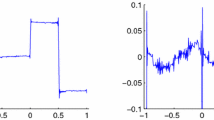
In Fig. 3 we plot the quantity $\| (S_{\epsilon,m}^{*}W_{m})^{-1} \|$. Unlike in the previous example, this quantity now grows exponentially and monotonically in m. Whilst this not only makes the method highly susceptible to round-off error and noise, it can also prevent convergence of the approximation $\tilde{f}$ (as m→∞). In essence, for convergence to occur, the error $\| f - P_{\mathcal{W}_{m}} f \|$ must decay more rapidly than the quantity $\| (S_{\epsilon,m}^{*} W_{m})^{-1} \|$ grows. Whenever this is not the case, convergence is not assured. To illustrate this shortcoming, in Fig. 3 we also plot the error $\| f -\tilde{f} \|$, where $f(x) =\frac{1}{1+16 x^{2}}$. The complex singularity at $x = \pm\frac{1}{4} \mathrm{i}$ limits the convergence rate of $\| f - P_{\mathcal{W}_{m}} f \|$ sufficiently so that $\tilde {f}$ does not converge to f. Note that this effect is well documented as occurring in a related reconstruction problem, where a function defined on [−1,1] is interpolated at m equidistant pointwise samples by a polynomial of degree m−1. This is the famous Runge phenomenon. The problem considered above (reconstruction from m Fourier samples) can be viewed as a continuous analogue of this phenomenon.

Fig. 3

The left figure shows $\log_{10}\|(S_{\epsilon,m}^{*}W_{m})^{-1}\|$ as a function of m for m=2,4,…,50 and $\epsilon= 1,\frac {7}{8},\frac{1}{2},\frac{1}{8}$ (squares, circles, crosses and diamonds respectively). The right figure shows $\log_{10}\| f - P_{\mathcal {W}_{m}} f \|$ (squares) and $\log_{10}\| f - \tilde{f} \|$ (circles) for m=2,4,6,…,100, where $f(x) = \frac{1}{1+16 x^{2}}$

Actually, the phenomenon illustrated in Examples 3.2 and 3.3 is not hard to explain if one looks at the problem from an operator-theoretical point of view. This is the topic of the next section.

3.1 Connections to the Finite Section Method

To illustrate the idea, let {s _k } _k∈ℕ and {w _k } _k∈ℕ be two sequences of linearly independent elements in a Hilbert space $\mathcal{H}$. Define the infinite matrix U by

(3.6)

Thus, by (3.4) the operator $S_{m}^{*}W_{m}$ is simply the m×m finite section of U. In particular

$$S_m^*W_m = P_mUP_m\vert_{P_m l^2(\mathbb{N})},$$

where $P_{m}UP_{m}\vert_{P_{m} l^{2}(\mathbb{N})}$ denotes the restriction of the operator P _m UP _m to the range of P _m (i.e. the m×m finite section of U). The finite section method has been studied extensively over the last several decades [9, 18, 19, 27]. It is well known that even if U is invertible then $P_{m}UP_{m}\vert_{P_{m} l^{2}(\mathbb{N})}$ may never be invertible for any m. In fact one must have rather strict conditions on U for $P_{m}UP_{m}\vert_{P_{m} l^{2}(\mathbb{N})}$ to be invertible with uniformly bounded inverse (such as positive self-adjointness, for example [27]). In addition, even if U:l ²(ℕ)→l ²(ℕ) is invertible and $P_{m}UP_{m}\vert_{P_{m} l^{2}(\mathbb{N})}$ is invertible for all m∈ℕ, it may be the case that, if

$$x=U^{-1}y, \quad x,y \in l^2(\mathbb{N}), \qquad x_m = (P_mUP_m\vert_{P_m l^2(\mathbb{N})})^{-1}P_my,$$

then

$$x_m \nrightarrow x, \quad m \rightarrow\infty.$$

Suppose that {s _k } _k∈ℕ and {w _k } _k∈ℕ are two Riesz bases for closed subspaces $\mathcal{S}$ and $\mathcal{W}$ of a separable Hilbert space $\mathcal{H}$. Define the operators $S, W:l^{2}(\mathbb{N}) \rightarrow\mathcal{H}$ by

$$ Sx = x_1s_1 +x_2s_2+ \cdots, \qquad Wy = y_1w_1 + y_2w_2+\cdots.$$

(3.7)

Suppose now that (S ^∗ W)⁻¹ exists. For m∈ℕ, let the spaces $\mathcal{S}_{m}, \mathcal{W}_{m}$ and operators $S_{m}, W_{m} : \mathbb{C}^{m}\rightarrow\mathcal{H}$ be defined as in Sect. 3 according to the vectors $\{s_{k}\}_{k=1}^{m}$ and $\{w_{k}\}_{k=1}^{m}$ respectively. As seen in the previous section, the following scenarios may well arise:

• (i) $\mathcal{W} \cap\mathcal{S}^{\perp} = \{0\}$, yet

  $$\mathcal{W}_m \cap\mathcal{S}^{\perp}_m \neq\{0\}, \quad\forall\, m \in\mathbb{N}.$$

• (ii) ∥(S ^∗ W)⁻¹∥<∞ and the inverse $(S_{m}^{*}W_{m})^{-1}$ exists for all m∈ℕ, but

  $$\bigl\|\bigl(S_m^*W_m\bigr)^{-1}\bigr\| \longrightarrow \infty, \quad m \rightarrow\infty.$$

• (iii) $(S_{m}^{*}W_{m})^{-1}$ exists for all m∈ℕ, however

  $$W_m\bigl(S_m^*W_m\bigr)^{-1}S_m^*f\nrightarrow f, \quad m \rightarrow\infty,$$

  for some $f \in\mathcal{W}$.

Thus, in order for us to have a completely general sampling theorem we must try to extend the framework described in this section in order to overcome the obstacles listed above.

4 The New Approach

4.1 The Idea

One would like to have a completely general sampling theory that can be described as follows:

• (i) We have a signal $f \in\mathcal{H}$ and a Riesz basis {w _k } _k∈ℕ that spans some closed subspace $\mathcal{W} \subset\mathcal{H}$, and

  $$f = \sum_{k=1}^{\infty} \beta_kw_k, \quad\beta_k \in\mathbb{C}.$$

  So $f \in\mathcal{W}$ (we may also typically have some information on the decay rate of the β _k s, however, this is not crucial for our theory).

• (ii) We have sampling vectors {s _k } _k∈ℕ that form a Riesz basis for a closed subspace $\mathcal{S} \subset\mathcal{H}$, (note that we may not have the luxury of choosing such sampling vectors as they may be specified by some particular model, as is the case in MRI) and we can access the sampling values {〈s _k ,f〉} _k∈ℕ.

Goal

Reconstruct the best possible approximation $\tilde{f} \in \mathcal{W}$ based on the finite subset $\{\langle s_{k},f\rangle\}_{k=1}^{m}$ of the sampling information {〈s _k ,f〉} _k∈ℕ.

We could have chosen m vectors {w ₁,…,w _m } and defined the operators S _m and W _m as in (3.3) (from {w ₁,…,w _m } and {s ₁,…,s _m }) and let $\tilde{f}$ be defined by (3.2). However, this may be impossible as $S_{m}^{*}W_{m}$ may not be invertible (or the inverse may have a very large norm), as discussed in Examples 3.2 and 3.3.

To deal with these issues we will launch an abstract sampling theorem that extends the ideas discussed above. To do so, we first notice that, since {s _j } and {w _j } are Riesz bases, there exist constants A,B,C,D>0 such that

(4.1)

Now let U be defined as in (3.6). Instead of dealing with $P_{m}UP_{m}\vert_{P_{m} l^{2}(\mathbb{N})} = S_{m}^{*}W_{m}$ we propose to choose n∈ℕ and compute the solution $\{\tilde{\beta}_{1},\ldots, \tilde{\beta}_{n}\}$ of the following equation:

(4.2)

provided a solution exists (later we will provide estimates on the size of n,m for (4.2) to have a unique solution). Finally we let

$$ \tilde{f} = \sum_{k=1}^n\tilde{\beta}_k w_k.$$

(4.3)

Note that, for n=m this is equivalent to (3.2), and thus we have simply extended the framework discussed in Sect. 3. However, for m>n this is no longer the case. As we later establish, allowing m to range independently of n is the key to the advantage possessed by this framework.

Before doing so, however, we first mention that the framework proposed above differs from that discussed previously in that it is inconsistent. Unlike (3.2), the samples $\langle s_{j},\tilde{f} \rangle$ do not coincide with those of the function f. Yet, as we shall now see, by dropping the requirement of consistency, we obtain a reconstruction which circumvents the aforementioned issues associated with (3.2).

4.2 The Abstract Sampling Theorem

The task is now to analyze the model in (4.2) by both establishing existence of $\tilde{f}$ and providing error bounds for $\|f-\tilde{f}\|$. We have

Theorem 4.1

Let $\mathcal{H}$ be a separable Hilbert space and $\mathcal{S}, \mathcal{W} \subset\mathcal{H}$ be closed subspaces such that $\mathcal{W} \cap\mathcal{S}^{\perp} = \{0\}$. Suppose that {s _k } _k∈ℕ and {w _k } _k∈ℕ are Riesz bases for $\mathcal{S}$ and $\mathcal{W}$ respectively with constants A,B,C,D>0. Suppose that

$$ f = \sum_{k\in\mathbb{N}} \beta_kw_k, \quad\beta= \{\beta_1, \beta_2,\ldots, \} \in l^2(\mathbb{N}).$$

(4.4)

Let n∈ℕ. Then there is an M∈ℕ (in particular $M = \min\{k: 0 \notin\sigma(P_{n}U^{*}P_{k}UP_{n} \lvert_{P_{n}\mathcal{H}}) \}$) such that, for all m≥M, the solution $\{\tilde{\beta}_{1},\ldots, \tilde{\beta}_{n}\}$ to (4.2) is unique. Also, if $\tilde{f}$ is as in (4.3), then

$$ \|f - \tilde{f}\|_{\mathcal{H}} \leq \sqrt{B}(1+K_{n,m})\bigl\|P_n^{\perp }\beta \bigr\|_{l^2(\mathbb{N})},$$

(4.5)

where

$$ K_{n,m} = \bigl \Vert \bigl(P_nU^*P_mUP_n\lvert_{P_n\mathcal {H}}\bigr)^{-1}P_nU^*P_mUP_n^{\perp}\bigr \Vert .$$

(4.6)

The theorem has an immediate corollary that is useful for estimating the error. We have

Corollary 4.2

With the same assumptions as in Theorem 4.1 and fixed n∈ℕ,

(4.7)

In addition, if U is an isometry (in particular, when {w _k } _k∈ℕ,{s _k } _k∈ℕ are orthonormal) then it follows that

$$K_{n,m} \longrightarrow0, \quad m \rightarrow\infty.$$

Proof of Theorem 4.1

Let U be as in as in (3.6). Then (4.4) yields the following infinite system of equations:

(4.8)

Note that U must be a bounded operator. Indeed, let S and W be as in (3.7). Since

$$\bigl\langle S^*W e_j,e_i \bigr\rangle= \langle s_i, w_j\rangle, \quad i,j \in \mathbb{N},$$

it follows that U=S ^∗ W. However, from (4.1) we find that both W and S are bounded as mappings from l ²(ℕ) onto $\mathcal{W}$ and $\mathcal{S}$ respectively, with $\|W\| \leq\sqrt{B}$, $\|S\| \leq\sqrt{D}$, thus yielding our claim. Note also that, by the assumption that $\mathcal{W} \cap\mathcal {S}^{\perp} = \{0\}$, (4.8) has a unique solution. Indeed, since $\mathcal{W} \cap\mathcal{S}^{\perp} =\{0\}$ and by the fact that {s _k } _k∈ℕ and {w _k } _k∈ℕ are Riesz bases, it follows that inf_∥x∥=1∥S ^∗ Wx∥≠0. Hence U must be injective.

Now let η _f ={〈s ₁,f〉,〈s ₁,f〉,…}. Then (4.8) gives us that

$$ P_nU^*P_m \eta_f =P_nU^*P_mU \bigl(P_n + P_n^{\perp}\bigr)\beta.$$

(4.9)

Suppose for a moment that we can show that there exists an M>0 such that $P_{n}U^{*}P_{m}UP_{n}\lvert_{P_{n}\mathcal{H}}$ is invertible for all m≥M. Hence, we may appeal to (4.9), whence

$$ \bigl(P_nU^*P_mUP_n\lvert_{P_n\mathcal{H}}\bigr)^{-1}P_nU^*P_m\eta_f = P_n\beta+ \bigl(P_nU^*P_mUP_n\lvert_{P_n\mathcal {H}}\bigr)^{-1}P_nU^*P_mUP_n^{\perp}\beta,$$

(4.10)

and therefore, by (4.9) and (4.1),

where

$$K_{n,m} = \bigl \Vert \bigl(P_nU^*P_mUP_n\lvert_{P_n\mathcal{H}}\bigr)^{-1} P_nU^*P_mUP_n^{\perp}\bigr \Vert .$$

Thus, (4.5) is established, provided we can show the following claim:

Claim

There exists an M>0 such that $P_{n}U^{*}P_{m}UP_{n}\lvert_{P_{n}\mathcal{H}}$ is invertible for all m≥M. Moreover,

$$\bigl \Vert \bigl(P_nU^*P_mUP_n\lvert_{P_n\mathcal{H}}\bigr)^{-1}\bigr \Vert \longrightarrow\bigl \Vert \bigl(P_nU^*UP_n\lvert_{P_n\mathcal{H}}\bigr)^{-1}\bigr \Vert \leq\bigl \Vert \bigl(U^*U\bigr)^{-1}\bigr \Vert , \quad m \rightarrow\infty.$$

To prove the claim, we first need to show that $P_{n}U^{*}UP_{n}\lvert_{P_{n}l^{2}(\mathbb{N})}$ is invertible for all n∈ℕ. To see this, let $\Theta: \mathcal {B}(l^{2}(\mathbb{N})) \rightarrow\mathbb{C}$ denote the numerical range. Note that U ^∗ U is self-adjoint and invertible. The latter implies that there is a neighborhood ω around zero such that σ(U ^∗ U)∩ω=∅ and the former implies that the numerical range Θ(U ^∗ U)∩ω=∅. Now the spectrum $\sigma(P_{n}U^{*}UP_{n}\lvert_{P_{n}l^{2}(\mathbb{N})})\subset\Theta(P_{n}U^{*}UP_{n}\lvert_{P_{n}l^{2}(\mathbb{N})}) \subset\Theta (U^{*}U)$. Thus,

$$\sigma\bigl(P_nU^*UP_n\lvert_{P_nl^2(\mathbb{N})}\bigr) \cap \omega= \emptyset, \quad\forall \, n \in\mathbb{N},$$

and therefore, $P_{n}U^{*}UP_{n}\lvert_{P_{n}l^{2}(\mathbb{N})}$ is always invertible. Now, make the following two observations

(4.11)

where the last series converges at least strongly (it converges in norm, but that is a part of the proof). The first is obvious. The second observation follows from the fact that P _m U→U strongly as m→∞. Note that

$$\|P_n\xi_j\|^2 = \langle P_n\xi_j, P_n\xi_j \rangle= \bigl\langle UP_n U^*e_j, e_j\bigr\rangle.$$

However, U ^∗ P _n U must be trace class since ran(P _n ) is finite-dimensional. Thus, by (4.2) we find that

(4.12)

Hence, the claim follows (the fact that $\Vert (P_{n}U^{*}UP_{n}\lvert_{P_{n}\mathcal{H}})^{-1}\Vert \leq \Vert (U^{*}U)^{-1}\Vert$ is clear from the observation that U ^∗ U is self-adjoint), and we are done. □

Proof of Corollary 4.2

Note that the claim in the proof of Theorem 4.1 yields the first part of (4.7), and the second part follows from the fact that U=S ^∗ W (where S,W are also defined in the proof of Theorem 4.1) and (4.1). Thus, we are now left with the task of showing that K _n,m →0 as m→∞ when U is an isometry. Note that the assertion will follow, by (4.6), if we can show that

$$\bigl \Vert P_nU^*P_mUP_n^{\perp}\bigr \Vert \longrightarrow0, \quad m \longrightarrow\infty.$$

However, this is straightforward, since a simple calculation yields

$$ \bigl \Vert P_nU^*P_mUP_n^{\perp}\bigr \Vert \leq \|U\|\bigl(\bigl\|P_nU^*P_m UP_n- P_nU^*UP_n\bigr\|\bigr)^{1/2},$$

(4.13)

which tends to zero by (4.12). To see why (4.13) is true, we start by using the fact that U is an isometry we have that

$$\bigl\|P_nU^*P^{\perp}_mUP_n\bigr\| =\bigl\|P_nU^*P_m UP_n - P_nU^*UP_n\bigr\|,$$

and therefore

$$ \bigl\|P^{\perp}_mUP_n\bigr\| \leq\bigl(\bigl\|P_nU^*P_m UP_n - P_nU^*UP_n\bigr\|\bigr)^{1/2}.$$

(4.14)

And, by again using the property that U is an isometry we have that

Hence, (4.13) follows from (4.14). □

Remark 4.3

Note that the trained eye of an operator theorist will immediately spot that the claim in the proof of Theorem 4.1 and Corollary 4.2 follows (with an easy reference to known convergence properties of finite rank operators in the strong operator topology) without the computations done in our exposition. However, we feel that the exposition illustrates ways of estimating bounds for

$$\bigl \Vert \bigl(P_nU^*P_mUP_n\lvert_{P_n\mathcal{H}} \bigr)^{-1}\bigr \Vert , \qquad\bigl \Vert P_nU^*P_mUP_n^{\perp}\bigr \Vert ,$$

which are crucial in order to obtain a bound for K _n,m . This is demonstrated in Sect. 5.

Remark 4.4

Note that S ^∗ W (and hence also U) is invertible if and only if $\mathcal{H} = \mathcal{W} \oplus\mathcal{S}^{\perp}$, which is equivalent to $\mathcal{W} \cap\mathcal{S}^{\perp} = \{0\}$ and $\mathcal{W}^{\perp} \cap\mathcal{S} = \{0\}$. This requirement is quite strong as we may very well have that $\mathcal{W} \neq\mathcal {H}$ and $\mathcal{S} = \mathcal{H}$ (e.g. Example 3.2 when ϵ<1). In this case we obviously have that $\mathcal{W}^{\perp} \cap\mathcal{S} \neq\{0\}$. However, as we saw in Theorem 4.1, as long as we have $f \in\mathcal{W}$ we only need injectivity of U, which is guaranteed when $\mathcal{W}\cap\mathcal{S}^{\perp} = \{0\}$.

If one wants to write our framework in the language used in Sect. 3, it is easy to see that our reconstruction can be written as

$$ \tilde{f} = W_n\bigl(W_n^*S_mS_m^*W_n\bigr)^{-1}W_n^*S_mS_m^*f,$$

(4.15)

where the operators $S_{m} : \mathbb{C}^{m} \rightarrow\mathcal{H}$ and $W_{n} : \mathbb{C}^{n} \rightarrow\mathcal{H}$ are defined as in (3.3), and S _m and W _n corresponds to the spaces

$$ \mathcal{S}_m = \mathrm{span}\{s_1,\ldots,s_m\}, \qquad\mathcal{W}_n = \mathrm{span}\{w_1,\ldots,w_n\},$$

(4.16)

where {w _k } _k∈ℕ and {s _k } _k∈ℕ are as in Theorem 4.1. In particular, we get the following corollary:

Corollary 4.5

Let $\mathcal{H}$ be a separable Hilbert space and $\mathcal{S}, \mathcal{W} \subset\mathcal{H}$ be closed subspaces such that $\mathcal{W} \cap\mathcal{S}^{\perp} = \{0\}$. Suppose that {s _k } _k∈ℕ and {w _k } _k∈ℕ are Riesz bases for $\mathcal{S}$ and $\mathcal{W}$ respectively. Then, for each n∈ℕ there is an M∈ℕ such that, for all m≥M, the mapping $W_{n}^{*}S_{m}S_{m}^{*}W_{n}:\mathbb {C}^{n} \rightarrow\mathbb{C}^{n}$ is invertible (with S _m and W _n defined as above). Moreover, if $\tilde{f}$ is as in (4.15), then

$$\bigl \Vert P_{\mathcal{W}_n}^{\perp}f \bigr \Vert _{\mathcal{H}} \leq \| f-\tilde{f}\|_{\mathcal{H}} \leq(1+ K_{n,m})\bigl \Vert P_{\mathcal {W}_n}^{\perp}f \bigr \Vert _{\mathcal{H}},$$

where $P_{\mathcal{W}_{n}}$ is the orthogonal projection onto $\mathcal {W}_{n}$, and

$$K_{n,m} = \bigl \Vert W_n\bigl(W_n^*S_mS_m^*W_n\bigr)^{-1}W_n^*S_mS_m^*P_{\mathcal {W}_n}^{\perp}\bigr \Vert .$$

Moreover, when {s _k } and {w _k } are orthonormal bases, then, for fixed n, C _n,m →0 as m→∞.

Proof

The fact that $W_{n}^{*}S_{m}S_{m}^{*}W_{n}:\mathbb{C}^{n} \rightarrow\mathbb{C}^{n}$ is invertible for large m follows from the observation that $\mathcal{W} \cap\mathcal{S}^{\perp} = \{0\}$ and the proof of Theorem 4.1, by noting that $S_{m}^{*}W_{n} = P_{m}UP_{n}$, where U is as in Theorem 4.1. Now observe that

(4.17)

Note also that $W^{*}_{n}W_{n}:\mathbb{C}^{n} \rightarrow\mathbb{C}^{n}$ is clearly invertible, since $\{w_{k}\}_{k =1}^{n}$ are linearly independent. Now (4.17) yields

$$W_n\bigl(W_n^*S_mS_m^*W_n\bigr)^{-1}W_n^*S_mS_m^*f =P_{\mathcal{W}_n}f + W_n\bigl(W_n^*S_mS_m^*W_n\bigr)^{-1}W_n^*S_mS_m^*P_{\mathcal{W}_n}^{\perp}f.$$

Thus,

$$\|f-\tilde{f}\|_{\mathcal{H}} \leq\bigl \Vert P_{\mathcal{W}_n}^{\perp}- W_n\bigl(W_n^*S_mS_m^*W_n\bigr)^{-1}W_n^*S_mS_m^*P_{\mathcal{W}_n}^{\perp}\bigr \Vert _{\mathcal{H}} \bigl \Vert P_{\mathcal{W}_n}^{\perp}f \bigr \Vert _{\mathcal{H}},$$

which gives the first part of the corollary. The second part follows from similar reasoning as in the proof of Corollary 4.2. □

Remark 4.6

The framework explained in Sect. 3 is equivalent to using the finite section method. Although this may work for certain bases, it will not in general (as Example 3.2 shows). Computing with infinite matrices can be a challenge since the qualities of any finite section may be very different from the original infinite matrix. The use of uneven sections (as we do in this paper) of infinite matrices seems to be the best way to combat these problems. This approach stems from [20] where the technique was used to solve a long standing open problem in computational spectral theory. The reader may consult [17, 21] for other examples of uneven section techniques.

When compared to the method of Eldar et al., the framework presented here has a number of important advantages:

• (i) It allows reconstructions in arbitrary bases and does not need extra assumptions as in (3.5).

• (ii) The conditions on m (as a function of n) for $P_{n}U^{*}P_{m}UP_{n}\lvert_{P_{n}\mathcal{H}}$ to be invertible (such that we have a unique solution) can be numerically computed. Moreover, bounds on the constant K _n,m can also be computed efficiently. This is the topic in Sect. 5.

• (iii) It is numerically stable: the matrix $A = P_{n} U^{*} P_{m} UP_{n} |_{P_{n} \mathcal{H}}$ has bounded inverse (Corollary 4.2) for all n and m sufficiently large.

• (iv) The approximation $\tilde{f}$ is quasi-optimal (in n). It converges at the same rate as the tail $\| P^{\perp}_{n} \beta\|_{l^{2}(\mathbb{N})}$, in contrast to (3.2) which converges more slowly whenever the parameter $\frac{1}{\cos( \theta_{\mathcal{W}_{m}\mathcal{S}_{m}})}$ grows with n=m.

As mentioned, this method is inconsistent. However, since {s _j } is a Riesz basis, we deduce that

$$\sum^{m}_{j=1} \bigl| \langle s_{j}, f - \tilde{f} \rangle\bigr|^2 \leq c \| f - \tilde{f}\|^2,$$

for some constant c>0. Hence, the departure from consistency (i.e. the left-hand side) is bounded by a constant multiple of the approximation error, and thus can also be bounded by $\| P^{\perp}_{n}\beta\|_{l^{2}(\mathbb{N})}$.

4.3 The Generalized (Nyquist–Shannon) Sampling Theorem

In this section, we apply the abstract sampling theorem (Theorem 4.1) to the classical sampling problem of recovering a function from samples of its Fourier transform. As we shall see, when considered in this way, the corresponding theorem, which we call the generalized (Nyquist–Shannon) Sampling Theorem, extends the classical Shannon theorem (which is a special case) by allow reconstructions in arbitrary bases.

Proposition 4.7

Let $\mathcal{F}$ denote the Fourier transform on L ²(ℝ^d). Suppose that {φ _j } _j∈ℕ is a Riesz basis with constants A,B (as in (4.1)) for a subspace $\mathcal{W} \subset L^{2}(\mathbb{R}^{d})$ such that there exists a T>0 with supp(φ _j )⊂[−T,T]^d for all j∈ℕ. For ϵ>0, let ρ:ℕ→(ϵℤ)^d be a bijection. Define the infinite matrix

Then, for $\epsilon\leq\frac{1}{2T}$, we have that U:l ²(ℕ)→l ²(ℕ) is bounded and invertible on its range with $\|U\| \leq\sqrt{\epsilon^{-d}B}$ and ∥(U ^∗ U)⁻¹∥≤ϵ ^d A ⁻¹ . Moreover, if {φ _j } _j∈ℕ is an orthonormal set, then ϵ ^d/2 U is an isometry.

Theorem 4.8

(The Generalized Sampling Theorem)

With the same setup as in Proposition 4.7, set

$$f = \mathcal{F}g, \quad g = \sum_{j=1}^{\infty}\beta_j \varphi_j \in L^2\bigl(\mathbb{R}^d\bigr),$$

and let P _n denote the projection onto span{e ₁,…,e _n }. Then, for every n∈ℕ there is an M∈ℕ such that, for all m≥M, the solution to

is unique. Also, if

$$\tilde{g} = \sum_{j=1}^{n}\tilde{\beta}_j \varphi_j, \qquad \tilde{f} = \sum _{j=1}^{n}\tilde{\beta}_j \mathcal{F}\varphi_j,$$

then

$$ \|g - \tilde{g} \|_{L^2(\mathbb{R}^d)} \leq\sqrt{B}(1+K_{n,m})\| P_n^{\perp}\beta\|_{l^2(\mathbb{N})}, \quad\beta= \{\beta_1, \beta_2, \ldots\},$$

(4.18)

and

$$ \|f - \tilde{f}\|_{L^{\infty}(\mathbb{R}^d)} \leq (2T)^{d/2} \sqrt {B}(1+K_{n,m})\|P_n^{\perp}\beta\|_{l^2(\mathbb{N})},$$

(4.19)

where K _n,m is given by (4.6) and satisfies (4.7). Moreover, when {φ _j } _j∈ℕ is an orthonormal set, we have

$$K_{n,m} \longrightarrow0, \quad m \rightarrow\infty,$$

for fixed n.

Proof of Proposition 4.7

Note that

$$u_{ij} = \int_{\mathbb{R}^d}\varphi_j(x) e^{-2\pi\mathrm{i} \rho(i)\cdot x}\, dx = \int_{[-T,T]^d}\varphi_j (x ) e^{-2\pi\mathrm{i} \rho(i)\cdot x}\, dx.$$

Since ρ:ℕ→(ϵℤ)^N is a bijection, it follows that the functions {x↦ϵ ^d/2 e ^{−2πiρ(i)⋅x}} _i∈ℕ form an orthonormal basis for L ²([−(2ϵ)⁻¹,(2ϵ)⁻¹]^d)⊃L ²([−T,T]^d). Let

$$\langle\cdot,\cdot\rangle= \overline{\langle\cdot,\cdot\rangle }_{L^2([-(2\epsilon)^{-1},(2\epsilon)^{-1}]^d)},$$

denote a new inner product on L ²([−(2ϵ)⁻¹,(2ϵ)⁻¹]^d). Thus, we are now in the setting of Theorem 4.1 and Corollary 4.2 with C=D=ϵ ^d. It follows by Theorem 4.1 and Corollary 4.2 that U is bounded and invertible on its range with $\|U\| \leq\sqrt{\epsilon^{-d}B}$ and ∥(U ^∗ U)⁻¹∥≤ϵ ^d A ⁻¹. Also, ϵ ^d/2 U is an isometry whenever A=B=1, in particular when {φ _k } _k∈ℕ is an orthonormal set. □

Proof of Theorem 4.8

Note that (4.18) now automatically follows from Theorem 4.1. To get (4.19) we simply observe that, by the definition of the Fourier transform and using the Cauchy–Schwarz inequality,

where the last inequality follows from the already established (4.18). Hence we are done with the first part of the theorem. To see that K _n,m →0 as m→∞ when {φ _j } _j∈ℕ is an orthonormal set, we observe that orthonormality yields A=B=1 and hence (since we already have established the values of C and D) ϵ ^d/2 U must be an isometry. The convergence to zero now follows from Theorem 4.1. □

Note that the bijection ρ:ℕ→(ϵℤ)^d is only important when d>1 to obtain an operator U:l ²(ℕ)→l ²(ℕ). However, when d=1, there is nothing preventing us from avoiding ρ and forming an operator U:l ²(ℕ)→l ²(ℤ) instead. The idea follows below. Let $\mathcal{F}$ denote the Fourier transform on L ²(ℝ), and let $f = \mathcal{F}g$ for some g∈L ²(ℝ). Suppose that {φ _j } _j∈ℕ is a Riesz basis for a closed subspace in L ²(ℝ) with constants A,B>0, such that there is a T>0 with supp(φ _j )⊂[−T,T] for all j∈ℕ. For ϵ>0, let

(4.20)

Thus, as argued in the proof of Theorem 4.8, $\widehat{U}\in\mathcal{B}(l^{2}(\mathbb{N}), l^{2}(\mathbb{Z}))$, provided $\epsilon\leq\frac{1}{2T}$. Next, let $P_{n} \in\mathcal{B}(l^{2}(\mathbb{N}))$ and, for odd m, $\tilde{P}_{m} \in\mathcal{B}(l^{2}(\mathbb{Z}))$ be the projections onto

$$\mathrm{span}\{e_1,\ldots, e_n\}, \qquad\mathrm{span}\{e_{-\frac {m-1}{2}},\ldots, e_{\frac{m-1}{2}}\}$$

respectively. Define $\{\tilde{\beta}_{1}, \ldots, \tilde{\beta}_{n}\}$ by (this is understood to be for sufficiently large m)

(4.21)

By exactly the same arguments as in the proof of Theorem 4.8, it follows that, if $g = \sum_{j=1}^{\infty} \beta_{j} \varphi_{j}$, $\tilde{g} = \sum_{j=1}^{n}\tilde{\beta}_{j} \varphi_{j}$, $f = \mathcal{F}g$ and $\tilde{f} = \sum_{j=1}^{n}\tilde{\beta}_{j}\mathcal{F} \varphi_{j}$, then

(4.22)

where K _n,m is as in (4.6).

Remark 4.9

Note that (as the proof of the next corollary will show) the classical NS-Sampling Theorem is just a special case of Theorem 4.8.

Corollary 4.10

Suppose that $f = \mathcal{F}g$ and supp(g)⊂[−T,T]. Then, for $0 < \epsilon\leq\frac{1}{2T}$ we have that

Proof

Define the basis {φ _j } _j∈ℕ for L ²([−(2ϵ)⁻¹,(2ϵ)⁻¹]) by

Letting $\widehat{U} = \{u_{k,l}\}_{k \in\mathbb{Z}, l \in\mathbb {N}}$, where $u_{k,l} = (\mathcal{F}\varphi_{l})(k\epsilon)$, an easy computation shows that

By choosing m=n in (4.21), we find that $\tilde{\beta}_{1} =\sqrt{\epsilon}f(0)$, $\tilde{\beta}_{2} = \sqrt{\epsilon}f(\epsilon)$, $\tilde{\beta}_{3} = \sqrt{\epsilon}f(-\epsilon)$, etc and that K _n,m =0 in (4.22). The corollary then follows from (4.22). □

Remark 4.11

Returning to the general case, recall the definition of Ω _N,ϵ from (1.1), the mappings Λ _N,ϵ,1, Λ _N,ϵ,2 from (1.2) and Θ from (1.3). Define Ξ _N,ϵ,1:Ω _N,ϵ →L ²(ℝ) and Ξ _N,ϵ,2:Ω _N,ϵ →L ²(ℝ) by

$$\Xi_{N,\epsilon,1}(f) = \sum_{j=1}^N\tilde{\beta}_j \mathcal{F}\varphi_j(\cdot), \qquad \Xi_{N,\epsilon,2}(f) = \sum_{j=1}^N\tilde{\beta}_j \varphi_j(\cdot),$$

where $\tilde{\beta}= \{\tilde{\beta}_{1}, \ldots, \tilde{\beta}_{N}\}$ is the solution to (4.21) with N=m. Then, for n>M (recall M from the definition of Θ (1.3)), and

$$m = m(\gamma) = \min\bigl\{k \in\mathbb{N}: \bigl\|\bigl(P_n\widehat{U}^*P_k\widehat{U}P_n\lvert_{P_n\mathcal{H}}\bigr)^{-1}\bigr\| \leq\epsilon\gamma\bigr\},\quad\gamma>1,$$

it follows that

Hence, under the aforementioned assumptions on m and n, both f and g are recovered exactly by this method, provided g∈Θ. Moreover, the reconstruction is done in a stable manner, where the stability depends only on the parameter γ.

To complete this section, let us sum up several of the key features of Theorem 4.8. First, whenever m is sufficiently large, the error incurred by $\tilde{g}$ is directly related to the properties of g with respect to the reconstruction basis. In particular, as noted above, g is reconstructed exactly under certain conditions. Second, for fixed n, by increasing m we can get arbitrarily close to the best approximation to g in the reconstruction basis whenever the reconstruction vectors are orthonormal (i.e. we get arbitrary close to the projection onto the first n elements in the reconstruction basis). Thus, provided an appropriate basis is known, this procedure allows for near-optimal recovery (getting the projection onto the first n elements in the reconstruction basis would of course be optimal). The main question that remains, however, is how to guarantee that the conditions of Theorem 4.8 are satisfied. This is the topic of the next section.

5 Norm Bounds

5.1 Determining m

Recall that the constant K _n,m in the error bound in Theorem 4.1 (recall also U from the same theorem) is given by

$$K_{n,m} = \bigl \Vert \bigl(P_nU^*P_mUP_n\lvert_{P_n\mathcal {H}}\bigr)^{-1}P_nU^*P_mUP_n^{\perp}\bigr \Vert .$$

It is therefore of utmost importance to estimate K _n,m . This can be done numerically. Note that we already have established bounds on ∥U∥ depending on the Riesz constants in (4.1) and since we obviously have that

$$K_{n,m} \leq\bigl\|\bigl(P_nU^*P_mUP_n\lvert_{P_n\mathcal{H}}\bigr)^{-1}\bigr\|\|U\|^2,$$

we only require an estimate for the quantity $\|(P_{n}U^{*}P_{m}UP_{n}\lvert_{P_{n}\mathcal{H}})^{-1}\|$.

Recall also from Theorem 4.1 that, if U is an isometry up to a constant, then K _n,m →0 as m→∞. In the rest of this section we will assume that U has this quality. In this case we are interested in the following problem: given n∈ℕ,θ∈ℝ₊, what is the smallest m∈ℕ such that K _n,m ≤θ? More formally, we wish to estimate the function $\Phi: \mathcal{U}(l^{2}(\mathbb{N})) \times\mathbb{N} \times\mathbb {R}_{+} \rightarrow\mathbb{N}$,

$$ \Phi(U,n,\theta) = \min \bigl\{m\in\mathbb{N}: \bigl \Vert \bigl(P_nU^*P_mUP_n\lvert_{P_n\mathcal{H}}\bigr)^{-1}P_nU^*P_mUP_n^{\perp }\bigr \Vert \leq\theta \bigr\},$$

(5.1)

where

$$\mathcal{U}\bigl(l^2(\mathbb{N})\bigr) = \bigl\{U \in\mathcal{B}\bigl(l^2(\mathbb {N})\bigr): U^*U = cI, c \in\mathbb{R}_+ \bigr\}.$$

Note that Φ is well defined for all θ∈ℝ₊, since we have established that K _n,m →0 as m→∞.

5.2 Computing Upper and Lower Bounds on K _n,m

The fact that $UP_{n}^{\perp}$ has infinite rank makes the computation of K _n,m a challenge. However, we may compute approximations from above and below. For M∈ℕ, define

Then, for L≥M,

Clearly, $K_{n,m} \leq \|U\| \widetilde{K}_{n,m}$ and, since P _M ξ→ξ as M→∞ for all $\xi\in\mathcal{H}$, and by the reasoning above, it follows that

$$K_{n,m,M} \leq K_{n,m} \leq\|U\| \widetilde{K}_{n,m},\qquad K_{n,m,M} \nearrow K_{n,m}, \quad M \rightarrow\infty.$$

Note that

$$\bigl(P_nU^*P_mUP_n\lvert_{P_n\mathcal{H}}\bigr)^{-1}P_nU^*P_mUP_n^{\perp}P_M:P_M \mathcal{H} \rightarrow P_n\mathcal{H}$$

has finite rank. Therefore we may easily compute K _n,m,M . In Fig. 4 we have computed K _n,m,M for different values of n,m,M. Note the rapid convergence in both examples.

Fig. 4

The figure shows K _n,m,M for n=75, m=350 and M=n+1,…,6000 (left) and K _n,m,M for n=100, m=400 and M=n+1,…,6000 (right) for the Haar wavelets on [0,1]

5.3 Wavelet Bases

Whilst in the general case Φ(U,n,θ) must be computed numerically, in certain cases we are able to derive explicit analytical bounds for this quantity. As an example, we now describe how to obtain bounds for bases consisting of compactly supported wavelets. Wavelets and their various generalizations present an extremely efficient means in which to represent functions (i.e. signals) [10, 11, 28]. Given their long list of applications, the development of wavelet-based reconstruction methods using the framework of this paper is naturally a topic of utmost importance.

Let us review the basic wavelet approach on how to create orthonormal subsets {φ _k } _k∈ℕ⊂L ²(ℝ) with the property that L ²([0,a])⊂cl(span{φ _k } _k∈ℕ) for some a>0. Suppose that we are given a mother wavelet ψ and a scaling function ϕ such that supp(ψ)=supp(ϕ)=[0,a] for some a≥1. The most obvious approach is to consider the following collection of functions:

$$\Omega_a = \bigl\{\phi_k, \psi_{j,k}: j \in \mathbb{Z}_+, k \in\mathbb{Z}, \mathrm{supp}(\phi_k)^o\cap[0,a] \neq\emptyset, \, \mathrm{supp}(\psi_{j,k})^o\cap[0,a] \neq\emptyset\bigr\},$$

where

$$\phi_k = \phi(\cdot- k), \qquad\psi_{j,k} =2^{\frac{j}{2}}\psi\bigl(2^j \cdot- k\bigr).$$

(The notation K ^o denotes the interior of a set K⊂ℝ.) Then we will have that

$$L^2\bigl([0,a]\bigr) \subset\mathrm{cl}\bigl(\mathrm{span}\{\varphi:\varphi\in \Omega_a\}\bigr) \subset L^2[-T,T],$$

where T>0 is such that [−T,T] contains the support of all functions in Ω _a . However, the inclusions may be proper (but not always, as is the case with the Haar wavelet.) It is easy to see that

Hence we get that

$$\Omega_a = \bigl\{\phi_k: |k| = 0,\ldots, \lceil a\rceil-1\bigr\} \cup\bigl\{\psi_{j,k}: j \in\mathbb{Z}_+, k \in \mathbb{Z}, -\lceil a\rceil+1 \leq k \leq2^j\lceil a\rceil-1\bigr\},$$

and we will order Ω _a as follows:

(5.2)

We will in this section be concerned with compactly supported wavelets and scaling functions satisfying

$$ \bigl|\mathcal{F}\phi(w)\bigr| \leq\frac{C}{|w|^p},\qquad\bigl|\mathcal{F}\psi(w)\bigr| \leq\frac{C}{|w|^p}, \quad\omega\in\mathbb{R}\setminus\{0\},$$

(5.3)

for some

$$C > 0, \quad p \in\mathbb{N}.$$

Before we state and prove bounds on Φ(U,n,θ) in this setting, let us for convenience recall the result from the proof of Theorem 4.1. In particular, we have that

$$ \bigl\|P_nU^*P_mUP_n - P_nU^*UP_n\bigr\| \leq \sum _{j=m+1}^\infty\bigl\langle U P_nU^*e_j, e_j\bigr\rangle, \quad m \rightarrow\infty.$$

(5.4)

Theorem 5.1

Suppose that {φ _l } _l∈ℕ is a collection of functions as in (5.2) such that supp(φ _l )⊂[−T,T] for all l∈ℕ and some T>0. Let U be defined as in Proposition 4.7 with $0 < \epsilon\leq \frac{1}{2T}$ and let the bijection ρ:ℕ→ϵℤ defined by ρ(1)=0,ρ(2)=ϵ,ρ(3)=−ϵ,ρ(4)=2ϵ,…. For θ>0,n∈ℕ define Φ(U,n,θ) as in (5.1). Then, if ϕ,ψ satisfy (5.3), we have that

where $f(\theta) = (\sqrt{1+4\theta^{2}} -1)^{2}/(4\theta^{2})$.

Proof

To estimate Φ(U,n,θ) we will determine bounds on

$$\Psi(U,n,\theta) = \min \bigl\{m \in\mathbb{N}: \bigl \Vert \bigl(P_nU^*P_mUP_n\lvert_{P_n\mathcal{H}}\bigr)^{-1}\bigr \Vert \bigl \Vert P_nU^*P_mUP_n^{\perp}\bigr \Vert \leq\theta \bigr\}.$$

Note that if r<1 and ∥P _n U ^∗ P _m UP _n −P _n U ^∗ UP _n ∥≤r, then

$$\bigl\|\bigl(P_nU^*P_mUP_n\lvert_{P_n\mathcal{H}}\bigr)^{-1}\bigr\|\leq\epsilon /(1-\epsilon r)$$

(recall that U ^∗ U=ϵ ⁻¹ I and that ϵ≤1). Also, recall (4.13), so that

$$\bigl \Vert \bigl(P_nU^*P_mUP_n\lvert_{P_n\mathcal{H}}\bigr)^{-1}\bigr \Vert \bigl \Vert P_nU^*P_mUP_n^{\perp}\bigr \Vert \leq \theta,$$

when r and m are chosen such that

$$\frac{\sqrt{\epsilon r}}{1-\epsilon r} \leq\theta,\qquad \bigl\|P_nU^*P_mUP_n - P_nU^*UP_n\bigr\| \leq r,$$

(note that $\|U\| = 1/\sqrt{\epsilon}$). In particular, it follows that

$$ \Psi(U,n,\theta) \leq\min\bigl\{m: \bigl\|P_nU^*P_mUP_n - P_nU^*UP_n\bigr\| \leq \epsilon^{-1}\bigl(\sqrt{1+4\theta^2} -1\bigr)^2/\bigl(4\theta^2\bigr) \bigr\}.$$

(5.5)

To get bounds on Ψ(U,n,θ) we will proceed as follows. Since ϕ,ψ have compact support, it follows that $\mathcal{F}\phi, \mathcal{F}\psi$ are bounded. Moreover, by assumption, we have that

$$\bigl|\mathcal{F}\phi(w)\bigr| \leq\frac{C}{|w|^p}, \qquad \bigl|\mathcal{F}\psi(w)\bigr| \leq \frac{C}{|w|^p}, \quad\omega\in\mathbb{R}\setminus\{0\}.$$

And hence, since

$$\mathcal{F}\psi_{j,k}(w) = e^{-2\pi\mathrm{i}2^{-j}kw}2^{\frac {-j}{2}}\mathcal{F}\psi\bigl(2^{-j}w\bigr),$$

we get that

$$ \bigl|\mathcal{F}\psi_{j,k}(w)\bigr| \leq2^{\frac{-j}{2}}\frac{C}{|2^{-j}w|^p}, \quad\omega\in\mathbb{R}.$$

(5.6)

By the definition of U it follows that

$$\sum_{j=m+1}^\infty\bigl\langle UP_n U^*e_j, e_j\bigr\rangle= \sum _{s=m+1}^{\infty}\sum_{t=1}^n\bigl|\mathcal{F}\varphi_t\bigl(\rho(s)\bigr)\bigr|^2.$$

And also, by (5.6) and (5.2) we have, for s>0,

thus we get that

(5.7)

Therefore, by using (5.4) we have just proved that

$$\bigl\|P_nU^*P_m UP_n - P_nU^*UP_n\bigr\| \leq\frac{4\epsilon^{-2p}\lceil a\rceil C^2}{m^{2p-1}} \biggl(1 + \frac{4^p n^{2p} -1}{4^p-1} \biggr),$$

and by inserting this bound into (5.5) we obtain

$$\Psi(U,n,\theta) \leq \biggl(\frac{4\epsilon^{1-2p}\lceil a \rceil C^2}{f(\theta)} \biggr)^{\frac{1}{2p-1}} \biggl(1+\biggl(\frac{4^p n^{2p}-1}{4^p-1} \biggr) \biggr)^{\frac{1}{2p-1}},$$

which obviously yields the asserted bound on Φ(U,n,θ). □

The theorem has an obvious corollary for smooth compactly supported wavelets.

Corollary 5.2

Suppose that we have the same setup as in Theorem 5.1, and suppose also that ϕ,ψ∈C ^p(ℝ) for some p∈ℕ. Then

$$\Phi(U,n,\theta) = \mathcal{O} \bigl(n^{\frac{2p}{2p-1}} \bigr), \quad n\rightarrow\infty.$$

5.4 A Pleasant Surprise

Note that if ψ is the Haar wavelet and ϕ=χ _[0,1] we have that

$$\bigl|\mathcal{F}\phi(w)\bigr| \leq\frac{2}{|w|}, \qquad \bigl|\mathcal{F}\psi(w)\bigr| \leq \frac{2}{|w|}, \quad\omega\in\mathbb{R}.$$

Thus, if we used the Haar wavelets on [0,1] as in Theorem 5.1 and used the technique in the proof of Theorem 5.1 we would get that

(5.8)

It is tempting to check numerically whether this bound is sharp or not. Let us denote the quantity in (5.8) by $\widetilde{\Psi}(U,n,\theta)$, and observe that this can easily be computed numerically. Figure 5 shows $\widetilde{\Psi}(U,n,\theta)$ for θ=1,2, where U is defined as in Proposition 4.7 with ϵ=0.5. Note that the numerical computation actually shows that

$$ \widetilde{\Psi}(U,n,\theta) = \mathcal{O} (n ),$$

(5.9)

which is indeed a very pleasant surprise. In fact, due to the ‘staircase growth shown in Fig. 5, the growth is actually better than what (5.9) suggests. The question is whether this is a particular quality of the Haar wavelet, or that one can expect similar behavior of other types of wavelets. The answer to this question will be the topic of future work.

Fig. 5

The figure shows sections of the graphs of $\widetilde{\Psi}(U,\cdot,1)$ (left) and $\widetilde{\Psi}(U,\cdot,2)$ (right) together with the functions (in black) x↦4.9x (left) and x↦4.55x. In this case U is formed by using the Haar wavelets on [0,1]

Note that Fig. 5 is interpreted as follows: provided m≥4.9n, for example, we can expect this method to reconstruct g to within an error of size $(1+\theta)\| P^{\top}_{n} \beta\|$, where θ=1 in this case. In other words, the error is only two times greater than the best approximation to g from the finite-dimensional space consisting of the first n Haar wavelets.

Having described how to determine conditions which guarantee existence of a reconstruction, in the next section we apply this approach to a number of example problems. First, however, it is instructive to confirm that these conditions do indeed guarantee stability of the reconstruction procedure. In Fig. 6 we plot $\|(\epsilon\hat{A})^{-1} \|$ against n (for ϵ=0.5), where $\hat{A}$ is formed via (4.21) using Haar wavelets with parameter m=⌈4.9n⌉. As we observe, the quantity remains bounded, indicating stability. Note the stark contrast to the severe instability documented in Fig. 2.

Fig. 6

The quantity $\| (\epsilon\hat{A})^{-1} \|$ against n=2,4,…,360

6 Examples

In this final section, we consider the application of the generalized sampling theorem to several examples.

6.1 Reconstruction from the Fourier Transform

In this example we consider the following problem. Let f∈L ²(ℝ) be such that

$$f = \mathcal{F}g, \quad\mathrm{supp}(g) \subset[-T,T].$$

We assume that we can access point samples of f, however, it is not f that is of interest to us, but rather g. This is a common problem in applications, in particular MRI. The NS Sampling Theorem assures us that we can recover g from point samples of f as follows:

$$g = \epsilon\sum_{n = -\infty}^{\infty}f(n\epsilon)\,e^{2\pi\mathrm {i} n\epsilon\cdot}, \quad\epsilon= \frac{1}{2T},$$

where the series converges in L ² norm. Note that the speed of convergence depends on how well g can be approximated by the functions e ^2πinϵ⋅, n∈ℤ. Suppose now that we consider the function

$$g(t) = \cos(2\pi t)\chi_{[0.5,1]}(t).$$

In this case, due to the discontinuity, forming

$$ g_N = \epsilon\sum _{n = -N}^{N}f(n\epsilon)\, e^{2\pi\mathrm{i}n\epsilon\cdot}, \quad \epsilon= \frac{1}{2}, \ N \in\mathbb{N},$$

(6.1)

may be less than ideal, since the convergence g _N →g as N→∞ may be slow.

This is, of course, not an issue if we can access all the samples {f(nϵ)} _n∈ℤ. However, such an assumption is infeasible in applications. Moreover, even if we had access to all samples, we are limited by both processing power and storage to taking only a finite number.

Suppose that we have a more realistic scenario: namely, we are given the finite collection of samples

$$ \eta_f = \bigl\{f(-N\epsilon), f\bigl((-N+1)\epsilon \bigr), \ldots, f\bigl((N-1)\epsilon\bigr), f(N\epsilon) \bigr\},$$

(6.2)

with N=900 and $\epsilon= \frac{1}{2}$. The task is now as follows: construct the best possible approximation to g based on the vector η _f . We can naturally form g _N as in (6.1). This approximation can be visualized in the diagrams in Fig. 7. Note the rather unpleasant Gibbs oscillations that occur, as discussed previously. The problem is simply that the set {e ^2πinϵ⋅} _n∈ℤ is not a good basis to express g in. Another basis to use may be the Haar wavelets {ψ _j } on [0,1] (we do not claim that this is the optimal basis, but at least one that may better capture the discontinuity of g). In particular, we may express g as

$$g = \sum_{j=1}^{\infty} \beta_j\psi_j, \quad\beta= \{\beta_1, \beta_2,\ldots\} \in l^2(\mathbb{N}).$$

We will now use the technique suggested in Theorem 4.8 to construct a better approximation to g based on exactly the same input information: namely, η _f in (6.2). Let $\widehat{U}$ be defined as in (4.20) with ϵ=1/2 and let n=500 and m=1801. In this case

Define $\tilde{\beta}= \{\tilde{\beta}_{1}, \ldots, \tilde{\beta}_{n}\}$ by (4.21), and let $\tilde{g}_{n,m} = \sum_{j=1}^{n}\tilde{\beta}_{j} \psi_{j}$. The function $\tilde{g}_{n,m}$ is visualized in Fig. 7. Although, the construction of g _N and $\tilde{g}_{n,m}$ required exactly the same amount of samples of f, it is clear from Fig. 7 that $\tilde{g}_{n,m}$ is favorable. In particular, approximating g by $\tilde{g}_{n,m}$ gives roughly four digits of accuracy. Moreover, had both n and m been increased, this value would have decreased. In contrast, the approximation g _N does not converge uniformly to g on [0,1].

Fig. 7

The upper figures show g _N (left), $\tilde{g}_{n,m}$ (middle) and g (right) on the interval [0,1]. The lower figures show g _N (left), $\tilde{g}_{n,m}$ (middle) and g (right) on the interval [0.47,0.57]

6.2 Reconstruction from Point Samples

In this example we consider the following problem. Let f∈L ²(ℝ) such that

$$f = \mathcal{F}g, \quad g(x) = \sum_{j=1}^K\alpha_j \psi_j(x) + \sin(2\pi x)\chi_{[0.3,0.6]}(x),$$

for K=400, where {ψ _j } are Haar wavelets on [0,1], and $\{\alpha_{j}\}_{j=1}^{K}$ are some arbitrarily chosen real coefficients in [0,10]. A section of the graph of f is displayed in Fig. 8. The NS Sampling Theorem yields that

$$f(t) = \sum_{k = -\infty}^{\infty} f \biggl(\frac{k}{2} \biggr) \mathrm{sinc}(2t-k),$$

where the series converges uniformly. Suppose that we can access the following pointwise samples of f:

$$\eta_f = \bigl\{f(-N\epsilon), f\bigl((-N+1)\epsilon\bigr), \ldots,f\bigl((N-1)\epsilon\bigr), f(N\epsilon) \bigr\},$$

with $\epsilon= \frac{1}{2}$ and N=600. The task is to reconstruct an approximation to f from the samples η _f in the best possible way. We may of course form

$$f_N(t) = \sum_{k = -N}^N f\biggl(\frac{k}{2} \biggr) \mathrm{sinc}(2t-k), \quad N = 600.$$

However, as Fig. 9 shows, this approximation is clearly less than ideal as f(t) is approximated poorly for large t. It is therefore tempting to try the reconstruction based on Theorem 4.8 and the Haar wavelets on [0,1] (one may of course try a different basis). In particular, let

$$\tilde{f} = \sum_{j=1}^n \tilde{\beta}_j \mathcal{F}\psi_j, \quad n = 500,$$

where

$$\widehat{A} \tilde{\beta}= P_n\widehat{U}^*P_m\eta_f, \quad\widehat{A} = P_n\widehat{U}^*P_m\widehat{U}P_n\lvert_{P_n\mathcal{H}},$$

with m=2N+1=1201 and $\widehat{U}$ is defined in (4.20) with ϵ=1/2. A section of the errors |f−f _N | and $|f - \tilde{f}|$ is shown in Fig. 9. In this case we have

In particular, the reconstruction $\tilde{f}$ is very stable. Figure 9 displays how our alternative reconstruction is favorable especially for large t. Note that with the same amount of sampling information the improvement is roughly by a factor of ten thousand.

Fig. 8

The figure shows Re(f) (left) and Im(f) (right) on the interval [−5000,5000]

Fig. 9

The figure shows the error |f−f _N | (left) and $|f - \tilde{f}|$ (right) on the interval [−5000,5000]

7 Concluding Remarks

The framework presented in this paper has been studied via the examples of Haar wavelets and Legendre polynomials. Whilst the general theory is now well developed, there remain many questions to answer within these examples. In particular,

• (i) What is the required scaling of m (in comparison to n) when the reconstruction basis consists of Legendre polynomials, and how well does the resulting method compare with more well-established approaches for overcoming the Gibbs phenomenon in Fourier series? Whilst there have been some previous investigations into this particular approach [22, 25], we feel that the framework presented in this paper, in particular the estimates proved in Theorem 4.1, are well suited for understanding this problem. We are currently investigating this possibility, and will present our results in future papers (see [2–5]).

• (ii) Whilst Haar wavelets have formed been the principal example in this paper, there is no need to restrict to this case. Indeed, Theorem 5.1 provides a first insight into using more sophisticated wavelet bases for reconstruction. Haar wavelets are extremely simple to work with, however the use of other wavelets presents a number of issues. In particular, it is first necessary to devise a means to compute the entries of the matrix U in a more general setting.

  In addition, within the case of the Haar wavelet, there remains at least one open problem. The computations in Sect. 5.1 suggest that n↦Φ(U,n,θ) is bounded by a linear function in this case, meaning that Theorem 5.1 is overly pessimistic. This must be proven. Moreover, it remains to be seen whether a similar phenomenon holds for other wavelet bases.

• (iii) The theory in this paper has concentrated on linear reconstruction techniques with full sampling. A natural question is whether one can apply non-linear techniques from compressed sensing to allow for subsampling. Note that, due to the infinite dimensionality of the problems considered here, the standard finite-dimensional techniques are not sufficient (see [1, 6]).