1 Introduction

In the 1960s, Italian mathematician Samuel Caputo put forward the concept of fractional calculus. Since then, fractional calculus has been widely used in physics, biology, economics, and other fields. Compared to integer-order systems, fractional-order (FO) systems [12, 18] are extensions of integer-order systems. It has all the characteristics of integer order models and special properties such as historical memory. Meanwhile, with the continuous deepening of research on FO systems, people have found that fractional calculus has a wider range of applications than integer calculus, as it can more accurately describe some complex systems. In [24], the robust fractional derivative estimation for partially unknown FO nonlinear systems under the influence of noise was studied. In [25], a new clustering region was designed to discuss the robustness of FO systems. In [15], through the use of FO control, we can better capture various complex parameters in the system, so that we can better monitor its complex physical behavior. In [9], a new FO function based on fuzzy control was designed to handle multiple position control directions and was suitable for interconnected systems. To reduce the distortion rate of the system, a FO model predictive control strategy with adaptive parameters was proposed in [8]. In [1], based on FO networks, a new stability criterion of LMI was proposed, and a novel feedback controller was formulated to make the FO system stable. Therefore, the study of FO systems is playing a significance role in the field of engineering.

In practical life, time-delay systems appear in various fields, and the time delay is often one of the sources of system instability and oscillation. For FO systems with time delays, some control strategies have been advanced in recent literature to ensure system robustness. In [6], the tracking problem of FO systems with parameter uncertainty was studied, and the finite-time robust stability criterion was obtained. In [13], a variable structure control based on an optimal FO selection strategy was proposed, which can improve the robustness of the system. In [26], based on Lyapunov theory, the global dissipation criterion was obtained for FO neural networks. For the FO delayed neural network in [10], sufficient conditions for two sets of event-triggered synchronization were gained. Unfortunately, some existing research may focus on linear systems [16]. The system studied in this article has time-varying delay and uncertainty, which makes the system more complex and puts higher requirements on controller design.

Sliding mode control (SMC) is a powerful robust control technique, which is famous for its anti-interference to external disturbances and parameter uncertainties. Its primary objective is to compel the system to converge to the desired sliding mode surface (SMS). The method of SMC is divided into two steps: the arrival process [19, 32] and the sliding process [11, 20, 28]. It is worth noting that SMC provides several key features, including quick speed response, high-performance, and anti-interference to disturbances. So far, the combination of FO time-delayed systems and SMC method has received widespread attention. In [32], a new SMC strategy was proposed, which can better improve transmission efficiency. In [21], a new controller based on integral SMS was designed to ensure that the generator can still achieve optimal speed despite interference. In [27], a new sensor fault detection technology has been proposed, which can calculate the error of the tracking signal to ensure system performance. In [3], a new integral SMS was raised to make sure the robustness of systems with Markov switching and Lévy noise. In [5], a new SMC strategy was proposed, which can quickly stabilize second-order objects with high accuracy. Therefore, it is significant to conduct comprehensive research on fractional-order sliding mode control (FOSMC). Regrettably, current research on sliding mode controllers is more focused on linear or time-varying systems [7], and there is less research on control problems for FO systems with time-varying delays. Therefore, the work of this article can provide new ideas and methods for the application of SMC in FO systems (see Fig. 1).

Asymptotic stability refers to whether a system can reach equilibrium when time approaches infinity under the action of a controller, which is often studied in many complex systems [2, 29, 31]. Fractional calculus can more accurately describe the behavior of some complex systems, and the introduction of delay terms can also comprehensively study the robustness of FO systems. Therefore, this paper mainly researches SMC for time-varying delays and uncertainty in FO systems. By designing appropriate SMS and SMC laws, FO systems can gradually approach the stable state of the system output after a while.

Based on the above discussion, we have discussed the FO systems with time-varying delays and uncertainties. Unlike existing research results, this paper has four contributions as follows:

  1. (1)

    For FO systems with time delay and uncertainties, an adaptive SMC law is designed that can automatically adjust control strategies based on the dynamic characteristics of the system to cope with external changes and uncertainties.

  2. (2)

    A new integral type SMS is introduced for the FO system, which adds an integral term to the SMS. This allows the system state to quickly converge from the initial value to SMS and can to some extent reduce system chattering. In addition, the accessibility of SMS was also analyzed.

  3. (3)

    \(\text {sgn} (s(t))\) is used instead of the non-continuous function \(\frac{s}{ | s |+ \sigma }\), which can significantly reduce the chattering phenomenon.

  4. (4)

    Compared to integer-order systems such as [7, 17], the modeling of SMC for FO systems with time delay and uncertainty is more complex, and the controller design process also requires the handling of fractional order operators and uncertainties in the system, which increases the complexity of theoretical proof.

Fig. 1
figure 1

SMC controller design

Full size image

2 Preliminaries

Consider a fractional-order system with uncertainties

$$\begin{aligned} D_{t }^{\alpha }\zeta (t)&= (Z+\varDelta Z) \zeta (t)+C\big (u(t)+r(\zeta (t),t)+i(\zeta (t-h(t)),t)\big )\nonumber \\&\quad +\,(Z_{d}+\varDelta Z_{d})\zeta (t-h(t)),\nonumber \\ \zeta (t)&= o(t), \quad t\in [-h_{m},0], \end{aligned}$$
(1)

where \(u(t)\in \mathbb {R}^{m} \) represents the control vector. \(\zeta (t)\in \mathbb {R}^{n} \) represents the state vector. \(Z_{} \in \mathbb {R}^{n\times n} \), \(Z_{d} \in \mathbb {R}^{n\times n}\), \(C\in \mathbb {R}^{n\times m} \). \(i(\zeta (t-h(t)),t)\in \mathbb {R} ^{m}\) and \(r(\zeta (t),t)\in \mathbb {R}^{m} \) are unknown nonlinear functions. h(t) is time delay and satisfies

$$\begin{aligned} 0\le h(t)\le h_{m}, 0\le \dot{ h}(t)\le d, \quad \forall t \ge 0, \end{aligned}$$
(2)

\(\zeta (t)= o (t)\) is initial value, which satisfies \(o (t)\in [-h_{m},0 ]\). \(\varDelta Z \) and \(\varDelta Z_{d} \) are uncertainty parameter matrices and meet the following conditions

$$\begin{aligned} {[} \varDelta Z ~ \varDelta Z_{d} ] = ED^{T} (t) [ M ~ N ], \end{aligned}$$
(3)

E, M, and N are both constant matrices and are known. D(t) represents time-varying and

$$\begin{aligned} D^{T} (t)D (t)\le I, \quad \forall t \ge 0. \end{aligned}$$
(4)

To prove the SMC method introduced in this paper, the following assumption and lemmas will be used.

Lemma 1

[22] Let R, U, and D(t) be appropriate matrices. If exists matrices \(P = P^{T}\), then

$$\begin{aligned} \begin{aligned}{} & {} P+RD(t)U+U^{T} D(t)^{T}R^{T}<0,\quad \forall D(t) \\{} & {} \mathrm{s.t.}\quad D(t)^{T} D(t)\le I, \end{aligned} \end{aligned}$$

if and only if \(\lambda >0\) satisfies

$$\begin{aligned} P+\lambda ^{-1} R^{T} R+\lambda U^{T} U<0. \end{aligned}$$

Lemma 2

[30] Let \(e\in \mathbb {R}^{n}\) and \( g\in \mathbb {R}^{n}\), and then

$$\begin{aligned} e^{T} g+g^{T} e\le \eta e^{T}e+ \eta ^{-1} g^{T}g, \end{aligned}$$

for any \(\eta >0\).

Lemma 3

[22] For a vector function \(\phi \): \([t_{1},t_{2}]\in \mathbb {R}^{n}\) and any positive definite matrix F, we have

$$\begin{aligned} \left( \int _{t_{1}}^{t_{2}} \varpi (s)ds\right) ^{T}F\left( \int _{t_{1}}^{t_{2}} \varpi (s)ds\right) \le (t_{2}-t_{1})\int _{t_{1}}^{t_{2}} \varpi ^{T} (s)F\varpi (s)ds. \end{aligned}$$

Lemma 4

[23] For a given symmetric matrix

$$\begin{aligned} \varXi =\begin{bmatrix} \varXi _{11} &{} \varXi _{12}\\ * &{} \varXi _{22} \end{bmatrix}, \end{aligned}$$

where \(\varXi _{11}\in \mathbb {R}^{m\times m}\), \(\varXi _{22}\in \mathbb {R}^{n\times m} \) and \(\varXi _{12}\in \mathbb {R}^{m\times n}\), the following conditions will be of equal value

$$\begin{aligned}&(1)~ \varXi<0,\\&(2)~ \varXi _{11}<0,\quad \varXi _{22}-\varXi _{12}^{T} \varXi _{11}^{-1}\varXi _{12}<0,\\&(3)~ \varXi _{22}<0,\quad \varXi _{11}-\varXi _{12} \varXi _{22}^{-1}\varXi _{12}^{T}<0. \end{aligned}$$

Lemma 5

[3] For any real vectors c and d, and there is a suitable dimension matrix P that satisfies \(P> 0\), the following inequality will be satisfied

$$\begin{aligned} c^{T}d+d^{T}c\le c^{T}Pc+d^{T}P^{-1}d. \end{aligned}$$

Assumption 1

\(r(\zeta (t),t)\) and \(i(\zeta (t-h(t)),t)\) are both nonlinear functions, which satisfy

$$\begin{aligned}&\Vert i(\zeta (t-h(t)),t) \Vert \le \rho \Vert \zeta (t-h(t))\Vert ,\\&\Vert r(\zeta (t),t) \Vert \le \xi \Vert \zeta (t) \Vert , \end{aligned}$$

where \(\alpha \) and \(\beta \) are positive constants.

3 Main Results

3.1 Switching Surface

The design of SMC generally involves two steps. The first step is to introduce the SMS function q(t), which could make sure the robustness of sliding mode dynamics. The second is to introduce appropriate SMC laws to force the system state onto a predefined SMS within a finite time. Firstly, we define an integral SMS s(t) in the following

$$\begin{aligned} s(t)= LD_{t}^{\alpha -1} \zeta (t)-\int _{0}^{t}L[ (Z+CK)\zeta (\tau )]d\tau . \end{aligned}$$
(5)

Among them, \(L\in \mathbb {R}^{m\times n} \) is selected, and \(K\in \mathbb {R}^{m\times n} \) is the controller gain matrix we designed, and LC is a nonsingular matrix.

Taking the derivative of (5), it has

$$\begin{aligned} \dot{s}(t)=LD^{\alpha }\zeta (t)-L(Z+CK)\zeta (t). \end{aligned}$$

When \(\dot{s}(t) = 0\), the equivalent controller is

$$\begin{aligned} u_{equ} (t)&= -i(\zeta (t-h(t)),t)-r(\zeta (t),t)+K\zeta (t)\nonumber \\&\quad -(LC)^{-1} L[\varDelta Z\zeta (t)+(Z_{d}+\varDelta Z_{d})\zeta (t-h(t))]. \end{aligned}$$
(6)

Furthermore, by substituting (6) into (1), we can obtain

$$\begin{aligned} D_{\alpha }^{t}\zeta (t)&= [Z+\varDelta Z-C(LC)^{-1}L\varDelta Z] \zeta (t)\nonumber \\&\quad +[Z_{d}+\varDelta Z_{d}-C(LC)^{-1}L(Z_{d}+\varDelta Z_{d})] \zeta \big (t-h(t)\big ). \end{aligned}$$
(7)

Remark 1

Compared to the SMC selected in [4], the SMS (5) contains an integral term. The integral SMS can ensure that the system only has one sliding mode stage by finding a suitable initial position, which avoids the shortcomings of traditional sliding modes in the approaching stage and ensures the robustness of the system. Therefore, the designed SMS has better anti-interference performance.

3.2 Stability Analysis

Subsequently, based on SMC, a dynamic equation for FO system is studied, which can be used to investigate the asymptotic stability of (1).

Theorem 1

Under Assumption 1. If there exist matrices \(G=G^{T}>0\), \(J>0\), and \(H>0\), and positive scalars \(\beta \), \(\epsilon _{1}\), \(\epsilon _{2}\), and \(\epsilon _{3}>0\), such that

$$\begin{aligned}&\begin{bmatrix} \varTheta _{11} &{}\varTheta _{12}&{} 0 &{} 0 &{} \varTheta _{15} &{}\varTheta _{16} &{}\varTheta _{17} &{}0 \\ * &{} \varTheta _{22} &{}0 &{}\varTheta _{24} &{}0 &{}0 &{} 0&{}0\\ *&{} * &{} \varTheta _{33} &{} 0 &{} 0 &{} 0 &{} 0&{}\varTheta _{38}\\ *&{} * &{} * &{}\varTheta _{44} &{}0 &{} 0 &{}0 &{}0\\ * &{} *&{} *&{} * &{} \varTheta _{55} &{} 0 &{}0&{} 0\\ * &{} * &{}* &{} * &{} * &{}\varTheta _{66} &{} 0&{}0\\ *&{} * &{} *&{} *&{} *&{} * &{}\varTheta _{77}&{}0\\ *&{} * &{} *&{} *&{} *&{} * &{}*&{}\varTheta _{88} \end{bmatrix}<0, \end{aligned}$$
(8)
$$\begin{aligned}&\begin{bmatrix} -G &{}GE \\ E^{T}G &{}-\epsilon _{3}I \end{bmatrix}<0, \end{aligned}$$
(9)

where \( \varTheta _{11}= GZ+Z^{T}G+\epsilon _{1}M^{T}M+2\beta +H+h_{m}J\), \( \varTheta _{22}= \epsilon _{2} N^{T}N-(1-d)H\), \( \varTheta _{33}=-\frac{J}{h_{m}}\), \( \varTheta _{44}=-G\), \( \varTheta _{55}=-C^{T}GC\), \( \varTheta _{66}=-\epsilon _{1}I\), \( \varTheta _{77}=-\epsilon _{2}I\), \( \varTheta _{88}=-\epsilon _{3}I\), \( \varTheta _{12}=GZ_{d}\), \( \varTheta _{24}= Z_{d}^{T}G\), \( \varTheta _{15}=\sqrt{2}GC\), \( \varTheta _{16}=GE\), \( \varTheta _{17}=GE\), \( \varTheta _{38}=GE\), then, by choosing \(L=C^{T}G\), the sliding mode motion dynamics (7) is asymptotically stable.

Proof

We choose the Lyapunov function as

$$\begin{aligned} V(t)= V_{1}(t)+V_{2}(t)+V_{3}(t), \end{aligned}$$
(10)

where

$$\begin{aligned} V_{1}(t)&=D^{\alpha -1} (\zeta ^{T} (t)G\zeta (t)),\end{aligned}$$
(11)
$$\begin{aligned} V_{2}(t)&=\int _{t-h(t)}^{t} (\zeta ^{T} (v)H\zeta (v))dv,\end{aligned}$$
(12)
$$\begin{aligned} V_{3}(t)&=\int _{-h(t)}^{t}\int _{t+\theta }^{t}(\zeta ^{T} (v)J\zeta (v))dvd\theta . \end{aligned}$$
(13)

Taking the derivative of (11), we can conclude

$$\begin{aligned} \dot{V}_{1}(t)&=D^{\alpha }_{t} (\zeta ^{T} (t)G\zeta (t))\nonumber \\&\le \zeta ^{T} (t) [ sym (G(Z+\varDelta Z-C(LC)^{-1}L \varDelta Z ))] \zeta (t)\nonumber \\&\quad +\,2\zeta ^{T} (t)G[Z_{d}+\varDelta Z_{d}-C(LC)^{-1}L \varDelta Z_{d} ]\zeta (t-h(t)) +2\kappa (t), \end{aligned}$$
(14)

where \(\kappa (t)=\sum _{k=1}^{\infty } \frac{\varGamma (1+\alpha )(D_{t}^{\alpha }\zeta (t) )^{T}GD_{t}^{\alpha -k }\zeta (t)}{\varGamma (1+k)\varGamma )(1-k+\alpha )} \).

Since the infinite term composed of fractional derivatives is a bounded set, \(\kappa (t)\) is bounded according to the definition in [14], and

$$\begin{aligned} \kappa (t)\le \iota \zeta (t)^{T} \zeta (t),\iota >0. \end{aligned}$$
(15)

From (12) and (13), we have

$$\begin{aligned} \dot{V}_{2}(t)&\le -(1-d)\zeta ^{T}(t-h(t))H\zeta (t-h(t))+\zeta ^{T} (t)H\zeta (t). \end{aligned}$$
(16)
$$\begin{aligned} \dot{V}_{3}(t)&\le h_{m} \zeta ^{T} (t)J\zeta (t)-\int _{t-h(t)}^{t} \zeta ^{T} (v)J\zeta (v)dv\nonumber \\&\le -\left( \int _{t-h(t)}^{t}\zeta (v)dv\right) ^{T}\frac{J}{h_{m}} \left( \int _{t-h(t)}^{t}\zeta (v)dv\right) + h_{m} \zeta ^{T} (t)J\zeta (t). \end{aligned}$$
(17)

According to Lemma 5 and \(L =C^{T} G\), one has

$$\begin{aligned}&-2\zeta ^{T}(t)GC(LC)^{-1} L\varDelta Z\zeta (t)\nonumber \\&\quad \le \zeta ^{T}(t)\varDelta Z^{T} G\varDelta Z\zeta (t)+\zeta ^{T}(t)GC (C^{T} GC)^{-1}C^{T} G\zeta (t), \end{aligned}$$
(18)
$$\begin{aligned}&-2\zeta ^{T}(t)GC(LC)^{-1} L( Z_{d}+\varDelta Z_{d})\zeta (t)\nonumber \\&\quad \le \zeta ^{T}(t)GC (C^{T} GC)^{-1}C^{T} G\zeta (t)+\zeta ^{T}(t-h(t))\nonumber \\&\qquad \times ( Z_{d}+\varDelta Z_{d})^{T} G ( Z_{d}+\varDelta Z_{d})\zeta (t-h(t)). \end{aligned}$$
(19)

According to Lemma 2, (3) and (4), it yields

$$\begin{aligned}&2\zeta ^{T}(t)G\varDelta Z\zeta (t) \le \epsilon _{1}\zeta ^{T}(t)M^{T}M\zeta (t)+ \epsilon _{1}^{-1} \zeta ^{T}(t)GEE^{T}G\zeta (t), \end{aligned}$$
(20)
$$\begin{aligned}&2\zeta ^{T}(t)G\varDelta Z_{d}\zeta (t-h(t)) \le \epsilon _{2}\zeta ^{T}(t-h(t))N^{T}N\zeta (t-h(t))\nonumber \\&\quad +\epsilon _{2}^{-1} \zeta ^{T}(t)GEE^{T}G\zeta (t). \end{aligned}$$
(21)

From (14) to (21) that

$$\begin{aligned} \dot{V}(t)\le \varsigma ^{T} (t)\varOmega _{i} \varsigma (t), \end{aligned}$$
(22)

where \(\varsigma ^{T}(t)=\begin{bmatrix} \zeta (t)^{T}&\zeta \big (t-h(t)\big )^{T}&\big ( \int _{t-h(t)}^{t} \zeta (v)dv\big )^{T} \end{bmatrix} \), and

$$\begin{aligned} \varOmega _{i} =\begin{bmatrix} \varSigma _{1i} &{} GZ_{d}&{}0 \\ *&{}\varSigma _{2i}&{}0\\ *&{}* &{} \varSigma _{3i} \end{bmatrix} \end{aligned}$$
(23)

with

$$\begin{aligned} \varSigma _{1i}&= GZ+Z^{T}G+\epsilon _{1}^{-1} GEE^{T}G+\epsilon _{1}M^{T}M\\&\quad +\,2GC(C^{T}GC)^{-1}C^{T}G+\varDelta Z^{T} G\varDelta Z+2\iota \\&\quad +\,\epsilon _{2}^{-1} GEE^{T}G+H+h_{m}J, \\ \varSigma _{2i}&=( Z_{d}+\varDelta Z_{d})^{T}G( Z_{d}+\varDelta Z_{d})+\epsilon _{2} N^{T}N-(1-d)H,\\ \varSigma _{3i}&=-\frac{J}{h_{m}}. \end{aligned}$$

In the following, by Schur complement and (3), \(\varOmega _{i}<0\) can be rewritten as

$$\begin{aligned}&\begin{bmatrix} \varTheta _{11} &{} 0 &{} 0 &{} 0 &{}0 &{}\varTheta _{15} &{}\varTheta _{16}&{}\varTheta _{17} \\ * &{} \varTheta _{22} &{}0 &{}0 &{}\varTheta _{24} &{}0 &{} 0&{}0\\ *&{} * &{} \varTheta _{33} &{} 0 &{} 0 &{} 0 &{} 0&{}0\\ *&{} * &{} * &{} -G &{}0 &{} 0 &{}0 &{}0\\ * &{} *&{} *&{} * &{} \varTheta _{44} &{} 0 &{}0&{}0 \\ * &{} * &{}* &{} * &{} * &{}\varTheta _{55} &{} 0&{}0\\ *&{} * &{} *&{} *&{} *&{} * &{}\varTheta _{66}&{}0\\ *&{} * &{} *&{} *&{} *&{} * &{}*&{}\varTheta _{77} \end{bmatrix}\nonumber \\&\quad +\,\varPi D(t)E+E^{T}D^{T}(t)\varPi ^{T}<0, \end{aligned}$$
(24)

where

$$\begin{aligned} \varPi&=\begin{bmatrix} M &{}0 &{} 0 &{} 0 &{} 0&{} 0 &{}0 &{}0 \\ 0 &{}N &{} 0 &{} 0 &{} 0&{} 0 &{}0 &{}0 \end{bmatrix},\\ E&=\begin{bmatrix} 0 &{}0 &{} 0 &{}E^{T}G&{} 0&{} 0 &{}0 &{}0\\ 0 &{}0 &{} 0 &{} 0 &{} E^{T}G&{} 0 &{}0 &{}0 \end{bmatrix},\\ D(t)&=\begin{bmatrix} D^{T}(t)&{}0 \\ 0&{}D^{T}(t) \end{bmatrix},\\ \varTheta _{11}&=GZ +Z^{T} G+2\iota +\epsilon _{1} M^{T}M,\\ \varTheta _{22}&=\epsilon _{2} N^{T}N. \end{aligned}$$

According to Lemma 1 and Schur complement, it can easy to conclude that (24) can be obtained by LMIs (8) and (9) when \(\epsilon _{3}>0\). Therefore, system (1) is asymptotic stable if \(\varOmega _{i}< 0\). This proof has been completed. \(\square \)

3.3 Reachability Analysis

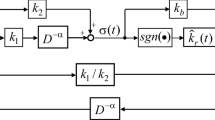
The accessibility of SMS (5) is ensured by designing a suitable adaptive SMC law as follows:

Theorem 2

For system (1) and its SMS function (5), \(L=C^{T}G\), G are solutions based on LMIs (8)–(9), then system (1) will be driven onto the designed SMS (5) by

$$\begin{aligned} u(t)=u_{ib} (t)+u_{ic} (t), \end{aligned}$$
(25)

with

$$\begin{aligned} u_{ib} (t)&=K\zeta (t)-(LC)^{-1}LZ_{d}\zeta (t-h(t)),\\ u_{ic} (t)&{=}{-}(LC)^{-1}\big ( \varepsilon {+}\hat{\xi }\left\| LC \right\| \left\| \zeta (t) \right\| {+} \hat{\rho }\left\| LC \right\| \times \left\| \zeta (t-h(t)) \right\| +\delta _{i} (t) \big ) {\text {sgn}}(s(t)), \end{aligned}$$

where \( \varepsilon >0 \), \(\delta _{i} (t)>0\) and

$$\begin{aligned} \delta _{i} (t)= \Vert LC \Vert ( \Vert M \zeta (t) \Vert + \Vert N\Vert \Vert \zeta (t-h(t)) \Vert ), \end{aligned}$$
(26)

constants \(\hat{\xi }\) and \(\hat{\rho }\) are unknown and can be estimated by the following equation,

$$\begin{aligned}&\tilde{\xi }(t)=\hat{\xi }-\xi , \dot{\hat{\xi }}=k_{1}\Vert s(t)\Vert \Vert LC\Vert \Vert \zeta (t)\Vert ,\nonumber \\&\tilde{\rho }(t)=\hat{\rho }-\rho , \dot{\hat{\rho }}=k_{2}\Vert s(t)\Vert \Vert LC\Vert \Vert \zeta (t-h(t))\Vert , \end{aligned}$$
(27)

\(k_{1}\) and \( k_{2} \) are both known positive constants.

Proof

The Lyapunov function is chosen

$$\begin{aligned} V_{SMC}=1/2(s^{T}(t)s(t)+k_{1}^{-1}\tilde{\xi }(t)^{2}+k_{2}^{-1}\tilde{\rho }(t)^{2}). \end{aligned}$$
(28)

Taking derivative of \(V_{SMC}\), we have

$$\begin{aligned} \dot{V}_{SMC}&=s^{T} (t)\dot{s} (t)+k_{1}^{-1}\tilde{\xi }(t)\dot{\tilde{\xi }}(t)+k_{2}^{-1}\tilde{\rho }(t)\dot{\tilde{\rho }}(t)\nonumber \\&=s^{T} (t)L\bigtriangleup Z\zeta (t)+s^{T} (t)L\bigtriangleup Z_{d}\zeta (t-h(t))\nonumber \\&\quad -s^{T} (t)\big ( \varepsilon +\hat{\xi }\left\| LC \right\| \left\| \zeta (t) \right\| + \hat{\rho }\left\| LC \right\| \nonumber \\&\quad \times \left\| \zeta (t-h(t)) \right\| +\delta _{i} (t) \big ) \text {sgn}(s(t))\nonumber \\&\quad +\,\tilde{\xi }(t)\Vert s(t)\Vert \Vert \zeta (t)\Vert +\tilde{\rho }(t)\Vert s(t)\Vert \Vert \zeta (t-h(t))\Vert \nonumber \\&\quad +s^{T} (t) LCf(t)+s^{T} (t) LCv(t). \end{aligned}$$
(29)

Based (27) and Assumption 1, it gets

$$\begin{aligned}&-s^{T} (t)\big (\hat{\xi }\left\| LC \right\| \left\| \zeta (t) \right\| + \hat{\rho }\left\| LC \right\| \left\| \zeta (t-h(t)) \right\| \big ) \text {sgn}(s(t))\nonumber \\&\quad +\,s^{T} (t) LC(f(t)+v(t))+\tilde{\xi }(t)\Vert s(t)\Vert \Vert LC\Vert \Vert \zeta (t)\Vert \nonumber \\&\quad +\tilde{\rho }(t)\Vert s(t)\Vert \Vert LC\Vert \Vert \zeta (t-h(t))\Vert \le 0. \end{aligned}$$
(30)

From (3), (4) and (30), it yields

$$\begin{aligned} \dot{V}_{SMC}&\le \Vert s(t)\Vert \Vert LE\Vert (\Vert M \zeta (t) \Vert + \Vert N \zeta (t-h(t)) \Vert )\nonumber \\&\quad - \,\varepsilon \Vert s(t)\Vert -\delta _{i} (t)\Vert s(t)\Vert -(\varepsilon +\delta _{i} (t)-\varLambda _{i})\Vert s(t)\Vert , \end{aligned}$$
(31)

where

$$\begin{aligned} \varLambda _{i}=\Vert LE\Vert \Vert M \zeta (t) \Vert +\Vert LE\Vert \Vert N \zeta (t-h(t)) \Vert . \end{aligned}$$
(32)

According to (26), we have

$$\begin{aligned} \dot{V}_{SMC}\le -\varepsilon \Vert s(t)\Vert<0 \quad \text {for} ~ \Vert s(t)\Vert \ne 0. \dot{V}_{SMC}\le -\varepsilon \Vert s(t)\Vert <0 \quad \text {with} ~ \Vert s(t)\Vert \ne 0. \end{aligned}$$
(33)

Based (27), we can obtain \(\dot{\tilde{\xi }}(t)\) and \(\dot{\tilde{\rho }}(t)\) are positive. Therefore, within a finite time \(t^{*}\), \(\tilde{\xi }(t)\) and \(\tilde{\rho }(t)\) exhibit positive values. Therefore, the following conditions can be obtained

$$\begin{aligned} \tilde{\xi }(t)\dot{\tilde{\xi }}(t)\ge 0,\quad \tilde{\rho }(t)\dot{\tilde{\rho }}(t)\ge 0, \quad \forall t\ge t^{*}. \end{aligned}$$

\(s^{T}(t)\dot{s}(t)<0\) can be obtained from (29) and (33), which verify the accessibility of SMS (5). \(\square \)

Remark 2

It is well known that the discontinuity of SMS is the main drawback of the SMC method, which leads to a chattering phenomenon during the control process. To avoid the chattering phenomenon, the following steps are provided: First, the SMS (5) is designed as an integral form. Second, a SMC law (25) is constructed by using the approach law method. Third, the continuous function \(\frac{s}{\left| s \right| +\sigma } \) replaces the non-continuous function \({\text {sgn}}(s(t))\). By using the above methods, the chattering phenomenon can be effectively suppressed.

4 Simulations

The feasibility of the introduced method is demonstrated by the following.

Example 1

Consider system (1) with \(\zeta (0)=[1,-1,-1]^{T}\), where \(h(t)=0.1*\sin (t)+1\), \(h_{m}=0.1\), \(d = 0.1\), \(\xi = 0.93\). The remaining parameters are chosen as

$$\begin{aligned} Z&=\begin{bmatrix} -2.5714 &{} 9&{}0\\ 1 &{}-1&{}1\\ 0&{}-14.28&{}0 \end{bmatrix},\quad Z_{d}=\begin{bmatrix} -0.8 &{}0&{} 1.5\\ 1.3 &{}-2.7&{}0\\ 1&{}-1&{}1 \end{bmatrix},\\ D(t)&=0.5*\sin (t),\quad C=\begin{bmatrix} 1 \\ -2 \\ 2 \end{bmatrix},\\ E&=\begin{bmatrix} 0.1 \\ 0.5 \\ 1 \end{bmatrix},\quad M=\begin{bmatrix} 1&2&0 \end{bmatrix},\quad N=\begin{bmatrix} 2.5&1.2&0.8 \end{bmatrix},\\ r(t)&=0.3\sin (t)(\zeta _{1}(t)+\zeta _{2}(t)+\zeta _{3}(t)),\\ i(t)&=0.5\sin (t)(\zeta _{1}(t-h(t))+\zeta _{2}(t-h(t))+\zeta _{3}(t-h(t))).. \end{aligned}$$

By solving LMIs (8) and (9) in Theorem 1, we can obtain

$$\begin{aligned} G&=\begin{bmatrix} 0.1140 &{}-0.0362 &{} -0.0070\\ -0.0362 &{} -0.0028 &{} -0.0127\\ -0.0070 &{} -0.0127 &{} 0.0207 \end{bmatrix},\\ H&=\begin{bmatrix} -1.1147 &{} -1.1077 &{} -0.3814\\ -1.1077 &{} -0.2287 &{} -0.1846\\ -0.3814 &{} -0.1846 &{} -0.3947 \end{bmatrix},\\ J&=\begin{bmatrix} 0.0740 &{} 0.1607 &{} 0.1947\\ 0.1607 &{} 0.1957 &{} 0.1959\\ 0.1947 &{} 0.1959 &{} 0.1948 \end{bmatrix}. \end{aligned}$$

\(\epsilon _{1}=0.0022\), \(\epsilon _{2}=0.0040\), \(\epsilon _{3}=0.0038\), and the gain matrices of SMC is \(K=\begin{bmatrix} -3 &{} -1&{}-2\\ \end{bmatrix}\).

After examination, all conditions in Theorems 1 and 2 can be satisfied. Thus, system (1) can be asymptotically stable by the adaptive SMC law.

Fig. 2
figure 2

State trajectories without controller

Full size image
Fig. 3
figure 3

State trajectories based SMC

Full size image
Fig. 4
figure 4

SMS control input in Example 1

Full size image
Fig. 5
figure 5

Sliding function s(t) in Example 1

Full size image

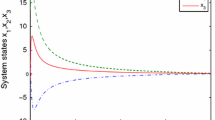
Figures 2, 4 and 5 illustrate the validity of main results. Among them, Figs. 2 and 3 show state trajectories of (1) without and with SMC controller. Figure 4 depicts the SMC input. It is not difficult to see from Fig. 2 that these system state variables are divergent. Figure 5 illustrates the reachability of the sliding function s(t) in finite-time. However, under the SMC law (25), all three state variables in the system will converge within 5 s and reach an equilibrium state.

Example 2

In this section, we provide an example based on the Chua’s circuit model proposed in [14] to demonstrate the effectiveness of the control method designed in this paper.

$$\begin{aligned} \left\{ \begin{aligned}&D_{t }^{\alpha }\zeta _{1}(t)=a\left[ \zeta _{2}(t)-m_{1}\zeta _{1}(t) \right] +f(\zeta _{1}(t))-c\zeta _{1}(t)(t-d) \\&D_{t}^{\alpha }\zeta _{2}(t)=\zeta _{1}(t)-\zeta _{2}(t)+\zeta _{3}(t)-c\zeta _{1}(t)(t-d) \\&D_{t }^{\alpha }\zeta _{3}(t)=-b\zeta _{2}(t)+c\left[ 2 \zeta _{1}(t-d)-\zeta _{3}(t-d)\right] \\ \end{aligned} \right. \end{aligned}$$
(34)

Among them, parameters of fractional-order systems are as follows: \(m_{0}=-\frac{1}{7} \), \(m_{1}=-\frac{2}{7} \), \(a=9\), \(b=14.28\), \(c=0.1\), \(f(\zeta _{1} (t) )=\frac{1}{2} [\left| \zeta _{1} (t)+1 \right| - \left| \zeta _{1} (t)-1 \right| ]\). Therefore,

$$\begin{aligned} Z&=\begin{bmatrix} -am_{1} &{} a &{} 0\\ 1 &{} -1 &{} 1\\ 0 &{}-b &{} 0 \end{bmatrix},\quad Z_{d} =\begin{bmatrix} -c &{} 0 &{} 0\\ -c &{} 0 &{} 0\\ -2c &{} 0 &{}-c \end{bmatrix},\\ D(t)&=0.5\sin (t),\quad C=\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix},\\ E&=\begin{bmatrix} 0.1 \\ 0.5 \\ 1 \end{bmatrix},\quad M=\begin{bmatrix} 1&2&0 \end{bmatrix},\quad N=\begin{bmatrix} 2.5&1.2&0.8 \end{bmatrix},\\ r(t)&=0.3\sin (t)(\zeta _{1}(t)+\zeta _{2}(t)+\zeta _{3}(t)),\\ i(t)&=0.5\sin (t)(\zeta _{1}(t-h(t))+\zeta _{2}(t-h(t))+\zeta _{3}(t-h(t))). \end{aligned}$$

Now solving LMIs (8) and (9), we obtain

$$\begin{aligned} G&=\begin{bmatrix} -0.7093 &{}0.1728 &{} -0.7776\\ 0.1728 &{} 0.2130 &{} -0.3239\\ -0.7776&{} -0.3239 &{} 0.3437 \end{bmatrix},\quad H=\begin{bmatrix} -8.3412 &{} -8.3412 &{} -8.3412\\ -8.3412 &{} -8.3412 &{} -8.3412\\ -8.3412 &{} -8.3412 &{} -8.3412 \end{bmatrix},\\ J&=\begin{bmatrix} 1.2355 &{} 1.2355 &{} 1.2355\\ 1.2355 &{} 1.2355 &{} 1.2355\\ 1.2355 &{} 1.2355 &{} 1.2355 \end{bmatrix}. \end{aligned}$$

\(\epsilon _{1}=0.0022\), \(\epsilon _{2}=0.0040\), \(\epsilon _{3}=0.0038\), and the gain matrix of SMC is \(K=\begin{bmatrix} -1 &{} 2&{}-3\\ \end{bmatrix}\).

Fig. 6
figure 6

State trajectories based SMC in Example 2

Full size image
Fig. 7
figure 7

SMS control input and sliding function s(t) with \(\frac{s}{\left| s \right| +\sigma } \) in Example 2

Full size image
Fig. 8
figure 8

SMS control input u(t) and sliding function s(t) with \({\text {sgn}}(s(t))\) in Example 2

Full size image

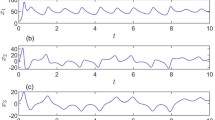
After examination, all conditions in Theorems 1 and 2 can be satisfied. Thus, system (34) can be asymptotically stable by the adaptive SMC law. Figures 6 and 7 illustrate the validity of main results. Among them, Fig. 6 shows state trajectories of (34) with SMC controller. Figure 7 depicts the SMC input and the reachability of the sliding function s(t) in finite-time.

In Example 2, when the continuous function \(\frac{s}{\left| s \right| +\sigma } \) in (25) is replaced by the signed function \({\text {sgn}}(s(t))\), Fig. 8 is obtained, which shows the control input u(t) and the sliding surface function s(t). From Fig. 8, it can be seen that there is a clear oscillation process in the state trajectory. Compared with Fig. 8, the continuous function \(\frac{s}{\left| s \right| +\sigma } \) used in Fig. 7 can significantly reduce the oscillation of the system, which indicates that the method proposed in this article is effective.

5 Conclusion

This paper introduces a novel dynamic model for FO systems with time delay and uncertainty. Firstly, a suitable integral-type SMS is designed, which can avoid the shortcomings of traditional sliding modes in the approaching stage and better ensure system performance. Secondly, under the guidance of the Lyapunov stability theory, it is not difficult to conclude that the FO system under SMC has asymptotic stability. Then, the adaptive SMC laws can force it to be driven to the designated SMS and avoid chattering during the sliding mode process. Finally, the effectiveness of the control technology is verified through an example.