A New Technique for the Reduced-Order Modelling of Linear Dynamic Systems and Design of Controller

Abstract

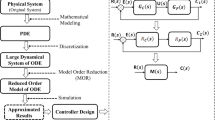
In this article, a new system diminution technique is proposed for the reduction in complexity and controller design of the higher-order models. This method is based on the Mihailov stability method which ensures the stability of the obtained simplified/micro-model if the higher-order plant is stable. In this technique, the reduced characteristic equation of the simplified plant is obtained by using the Mihailov stability technique and the reduced numerator equation is determined by using the improved Padé approximation technique. By using this reduced-order model, the PID controller is designed for the large-scale system. The accuracy and effectiveness of the proposed method are validated by comparing the step responses of the complete and lower-order models. The performance of the recommended technique is shown in terms of step responses and performance error indices. Three standard numerical systems are finally provided to validate the effectiveness and accuracy of the designed controller and the performance of the proposed model-order reduction technique.

1 Introduction

The study and synthesis of a large-scale model are a difficult work and lead to a continuous effort to simplify the complexity of the higher-order model. The higher-dimensional systems are exist in various fields of engineering and sciences such as aeronautic systems [31], jump systems [60, 67], control systems [6, 43], multilayer systems [59], electromagnetic systems [28], power systems [5], thermodynamics [9] and regulator problems [30]. The goal of a system diminution technique is to obtain a plant that is simpler than the actual system and retains the essential properties of the actual system. The model diminution of the complex system is a popular theme within the area of biological systems [55, 56], control systems [8, 34, 58], electromagnetic field [27, 66], mechanical engineering [12, 19, 20, 22, 24], power systems [25, 42, 43, 64], chemical engineering [7, 15], etc.

In the frequency domain, several system diminution technologies exist in the literature for the order diminution of the transfer function of the higher-order linear time invariant (LTI) dynamic models [2, 16, 18, 21, 46, 54, 65, 68]. Among these methods, the time moment matching technique [68] and Padé approximation approach [46] are the frequently used model diminution techniques, and these are suitable schemes for the matching of static responses of the microsystem and the original system [1, 40]. Sometimes these techniques fail to decrease the complexity of large-scale systems because these methods give unstable micro-models even though the original higher-order systems are stable [32, 37]. Routh stability scheme [16] is another commonly used method for the order diminution of higher-order plants, and it is a popular scheme for the matching of the transient responses of the higher-order plant and the lower-order system [1, 40]. This technique also has some limitations such as non-uniqueness (sometimes giving the same lower-order plant for the different large-scale models) and fails to retain the dominant poles of non-minimum phase complex system in its microsystem [36, 51].

Routh approximation is also another popular model reduction method for the diminution of higher-order linear systems in the frequency domain but it is limited for the complex system having strictly proper transfer function [18]. A stability equation scheme for the model reduction in minimum phase higher-order plant is described in [2] but it is not convenient for the non-minimum phase large-scale systems. In [21], the factor division algorithm is given for the approximation of large-scale systems into lower-order approximants. Sinha and Pal recommended the pole clustering scheme for the diminution of minimum and non-minimum large-scale models [54]. This technique also has some drawbacks such as it requires tuning factor for the matching of transient responses and gain adjustment factor for the matching of steady-state responses of the lower-order model with the large-scale plant. In the frequency domain, the Mihailov stability technique is one of the superior methods for the determination of denominator of the simplified plant [65]. In the Mihailov stability criterion method, the reduced model is always stable provided that the higher-order model must be stable. Because reduced denominator polynomial is obtained in such a way that the Mihailov frequency characteristic of the reduced system is matched with the characteristic of the original system hence if the original system is stable then the reduced model will also be stable.

In this article, a new system reduction technique is proposed for the simplification and design of a controller for the higher-order system. The proposed method retains the properties of the Mihailov stability criterion [65] and improved Padé approximation technique [53]. In this approach, the denominator polynomial is determined by the Mihailov stability technique, and the improved Padé approximation technique is applied for the evaluation of the numerator coefficients. The improved Padé approximation technique guarantees the preservation of initial few time moments and Markov parameters of the original system in the reduced model [53]. The proposed model reduction is simple and due to using of the Mihailov stability method, it ensures the stability of the lower-order plant for the stable original system. This method also ensures the preservation of time moments and Markov parameters because of using improved Padé approximation technique. The remaining paper is structured as in Sect. 2; the problem statement of the system reduction is given. The basic procedures of the proposed model reduction technique are described in Sect. 3. In Sect. 4, the new method for the design of a controller for the large-scale system is illustrated. In Sect. 5, three popular numerical examples are taken from the literature for the validation of proposed algorithms. The conclusion of the paper is given in Sect. 6.

2 Problem of Statement

Let us consider the transfer function $G\left( s \right)$ of a large-scale SISO LTI dynamic system, defined as follows:

$$ G\left( s \right) = \frac{N\left( s \right)}{D\left( s \right)} = \frac{{d_{0} + d_{1} s + \cdots + d_{n - 1} s^{n - 1} }}{{e_{0} + e_{1} s + e_{2} s^{2} + \cdots + e_{n} s^{n} }} $$

(1)

where $d_{0} , d_{1} \ldots d_{n - 1}$ and $e_{0} , e_{1} \ldots e_{n}$ are the known parameters. In model-order reduction, the main goal is to compute the unknown parameters of the transfer function of $r\text{th}$-order ($r < n$) reduced model defined as.

$$ R_{r} \left( s \right) = \frac{{Q_{r} \left( s \right)}}{{P_{r} \left( s \right)}} = \frac{{q_{0} + q_{1} s + q_{2} s^{2} + \cdots + q_{r - 1} s^{r - 1} }}{{p_{0} + p_{1} s + p_{2} s^{2} + \cdots + p_{r - 1} s^{r - 1} + p_{r} s^{r} }} $$

(2)

where $q_{0} , q_{1} \ldots q_{r - 1 }$ and $p_{0} , p_{1} \ldots p_{r}$ are unknown parameters.

3 Proposed System Reduction Technique

The proposed technique is illustrated in the following two steps

3.1 Determination of the Denominator Polynomial

The Mihailov stability criterion is used for the determination of denominator polynomial of the approximated reduced model. From (1), the denominator polynomial of the original system is written as

$$ D\left( s \right) = e_{0} + e_{1} s + e_{2} s^{2} + \cdots + e_{n} s^{n} $$

(3)

Putting $s = jw$ in (3) and isolating the real and imaginary parts as follows:

$$ \begin{aligned} D\left( s \right) & = e_{0} + e_{1} \left( {jw} \right) + e_{2} \left( {jw} \right)^{2} + \cdots e_{n} \left( {jw} \right)^{n} \\ & = \left( {e_{0} - e_{2} w^{2} + e_{4} w^{4} - \cdots e_{X} w^{X} } \right) + j\left( {e_{1} w - e_{3} w^{3} + e_{5} w^{5} - \cdots e_{Y} w^{Y} } \right) \\ & = \phi \left( w \right) + j\psi \left( w \right) \\ \end{aligned} $$

(4)

where

$$ \phi \left( w \right) = e_{0} - e_{2} w^{2} + e_{4} w^{4} - \cdots e_{X} w^{X} $$

(5)

$$ \psi \left( w \right) = e_{1} w - e_{3} w^{3} + e_{2} w^{5} - \cdots e_{Y} w^{Y} $$

(6)

$$ \left\{ {\begin{array}{*{20}l} {X = n - 1} \hfill \\ {Y = n } \hfill \\ \end{array} } \right.{\text{when}}\,n\,{\text{is}}\,{\text{even}} . $$

(7)

$$ \left\{ {\begin{array}{*{20}l} {X = n } \hfill \\ {Y = n - 1} \hfill \\ \end{array} } \right.{\text{when}} \,n\, {\text{is}}\,{\text{odd}} $$

(8)

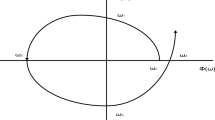
and $w$ is the angular frequency. The polynomials $\phi \left( w \right)$ and $\psi \left( w \right)$ are used for plotting Mihailov frequency characteristic of the higher-order plant in which $\phi \left( w \right)$ d $\psi \left( w \right)$ show horizontal axis and vertical axis, respectively, and $w$ varies from 0 to $\infty .$ For plotting the Mihailov frequency characteristic, set $\phi \left( w \right) = 0, \psi \left( w \right) = 0$, and it will give intersecting frequencies $w_{0} = 0, \pm w_{1} , \pm w_{2} , \ldots , \pm w_{n - 1} .$ For a stable system, the Mihailov characteristic starts from abscissa at $w = 0$ and intersects the vertical axis and horizontal axis alternatively as $w$ rises and the number of intersections is the same as the order of the transfer function of the higher-order plant. The reduced denominator polynomial is determined in such a way that its Mihailov frequency characteristic is approximately matched with the original system. From (2), the characteristic polynomial of the lower-order plant is written as

$$ P_{r} \left( s \right) = p_{0} + p_{1} s + p_{2} s^{2} + \cdots + p_{r - 1} s^{r - 1} + p_{r} s^{r} $$

(9)

Putting $s = jw$ in (9) and isolating the real and imaginary parts, it gives

$$ \begin{aligned} P_{r} \left( s \right) & = p_{0} + p_{1} \left( {jw} \right) + p_{2} \left( {jw} \right)^{2} + \cdots + p_{r - 1} \left( {jw} \right)^{r - 1} + p_{r} \left( {jw} \right)^{r} \\ & = \left( {p_{0} - p_{2} w^{2} + p_{4} w^{4} - \cdots p_{x} w^{x} } \right) + j\left( {p_{1} w - p_{3} w^{3} + p_{5} w^{5} - \cdots p_{y} w^{y} } \right) \\ & = \xi \left( w \right) + j\eta \left( w \right) \\ \end{aligned} $$

(10)

where

$$ \xi \left( w \right) = p_{0} - p_{2} w^{2} + p_{4} w^{4} - \cdots p_{x} w^{x} $$

(11)

$$ \eta \left( w \right) = p_{1} w - p_{3} w^{3} + p_{5} w^{5} - \cdots p_{y} w^{y} $$

(12)

$$ \left\{ {\begin{array}{*{20}l} {x = r - 1} \hfill \\ {y = r } \hfill \\ \end{array} } \right. {\text{when}}\,r\,{\text{is}}\,{\text{even}} $$

(13)

$$ \left\{ {\begin{array}{*{20}l} {x = r } \hfill \\ {y = r - 1} \hfill \\ \end{array} } \right.{\text{when}}\, r\,{\text{is}}\,{\text{odd}} $$

(14)

The Mihailov frequency characteristic of the reduced model is in the same manner as that of the large-scale system but it intersects $r$ times only. Hence, the poles of $\xi \left( w \right) = 0\,{\text{and}}\,\eta \left( w \right) = 0$ must be positive real and intersecting frequencies are the same as the higher-order model for the matching of input and output relationship and distributed along the $w$ axis alternatively.Consequently, the roots of (11) and (12) are the subset of the roots (5) and (6), and $\xi \left( w \right)$ and $\eta \left( w \right)$ can be written as

$$ \xi \left( w \right) = k_{1} \left( {w^{2} - w_{1}^{2} } \right)\left( {w^{2} - w_{3}^{2} } \right) \ldots $$

(15)

$$ \eta \left( w \right) = k_{2} w\left( {w^{2} - w_{2}^{2} } \right)\left( {w^{2} - w_{4}^{2} } \right) \ldots $$

(16)

where $k_{1}$ is obtained by using from $\phi \left( {jw_{0} } \right) = \xi \left( {jw_{0} } \right)$ and $k_{2}$ is obtained from $\psi \left( {jw_{1} } \right) = \eta \left( {jw_{1} } \right)$ or $\left( {d\psi /d\phi } \right)_{{w_{0} }} = \left( {d\eta /d\xi } \right)_{{w_{0} .}}$ After computing the characteristic equation of the lower-order model $P_{r} \left( {jw} \right) = \xi \left( w \right) + j\eta \left( w \right)$, replacing $jw = s$ and it will give $P_{r} \left( s \right) = p_{0} + p_{1} s + p_{2} s^{2} + \cdots + p_{r - 1} s^{r - 1} + p_{r} s^{r}$. Now, the improved Padé approximation method [53] is used for the determination of the numerator polynomial of the reduced model.

Remark 1

For the stable large-scale system, the reduced-order system will also be stable because both the models have approximately the same Mihailov frequency characteristic.

3.2 Determination of the Numerator Polynomial by Using an Improved Padé Approximation Algorithm

The transfer function (1) of the original model $G\left( s \right)$ can be written with regard to its power series expansion of $G\left( s \right)$ about $s = \infty$, i.e.

$$ \begin{aligned} G\left( s \right) & = M_{0} s^{ - 1} + M_{1} s^{ - 2} + \cdots + M_{2r} s^{ - 2r - 1} + \cdots \\ & = \mathop \sum \limits_{i = 0}^{\infty } M_{i} s^{ - i - 1} \\ \end{aligned} $$

(17)

The parameters $\left\{ {M_{i} :i = 1, \ldots , \infty } \right\}$ are called the Markov parameters of the system and “r” is the order of the reduced model. Similarly, $G\left( s \right)$ can also be written in the terms of its Taylor series expansion of $G\left( s \right)$ about $s = 0$; hence,

$$ \begin{aligned} G\left( s \right) & = c_{0} + c_{1} s + c_{2} s^{2} + \cdots + c_{2r} s^{2r} + \cdots \\ & = \mathop \sum \limits_{i = 0}^{\infty } c_{i} s^{i} \\ \end{aligned} $$

(18)

The parameters $\left\{ {c_{i} :i = 0, 1, 2, \ldots , \infty } \right\}$ are proportional to the system matching moments [46, 68].The numerator coefficients of rth-order reduced model are obtained by using improved Padé approximation technique. The improved Padé approximation method guarantees the preservation of the initial few time moments and Markov parameters [53] of the original system in the reduced-order system. The numerator polynomial coefficients are obtained as

$$ \begin{aligned} & q_{0} = c_{0} p_{0} \\ & q_{1} = c_{1} p_{0} + c_{0} p_{1} \\ & q_{2} = c_{2} p_{0} + c_{1} p_{1} + c_{0} p_{2} \\ & \vdots \\ & q_{\alpha - 1} = c_{\alpha - 1} p_{0} + c_{\alpha - 2} p_{1} + \cdots + c_{1} p_{\alpha - 2} + c_{0} p_{\alpha - 1} \\ & q_{r - \beta } = M_{\beta - 1} p_{r} + M_{\beta - 2} p_{r - 1} + \cdots + M_{1} p_{r - \beta + 2} + M_{0} p_{r - \beta + 1} \\ & q_{r - \beta + 1} = M_{\beta - 2} p_{r} + M_{\beta - 3} p_{r - 1} + \cdots + M_{1} p_{r - \beta + 3} + M_{0} p_{r - \beta + 2} \\ & \vdots \\ & q_{r - 2} = M_{1} p_{r} + M_{0} p_{r - 1} \\ & q_{r - 1} = M_{0} p_{r} \\ \end{aligned} $$

(19)

The unknown parameters ($q_{0} , q_{1} , q_{2} , \ldots , q_{r - 1} )$ of the numerator polynomial of the reduced model are calculated by solving the $\hbox{``}r\hbox{''}$ number of equations given in (19).

Remark 2

The numerator polynomial of the lower-order system is determined by using improved Padé approximation technique; due to this, the reduced model retains the properties of the improved Padé approximation method.

4 Design of PID Controller

The controller design and simulation of large-scale systems are lengthy and difficult tasks. As the complexity of the dynamic system increases, the simulation time and cost of the design of the controller increases proportionally. To circumvent these types of limitations, a “good” approximated model can be determined for the complex model, and the controller is designed by using this approximated plant. In case of a higher-dimensional model, large amounts of sensors are needed for sensing the state variables for the design of feedback controllers. Due to this, series controllers are appropriate over the feedback controllers.

In order to get the desired performance of the real-time dynamic system, a reference model $\left( {M(S)} \right)$ is formulated on the basis of given specification so that the closed-loop characteristic of the controlled plant with unity feedback is thoroughly matched with the characteristic of the computed reference model. The techniques of computing reference system from the desired specification in more details are given in [29, 61]. Consider a proportional–integral–derivative (PID) controller, which yields the desired closed-loop behaviour as

$$ G_{c} \left( s \right) = K_{p} + \frac{{K_{i} }}{s} + K_{d} s $$

(20)

For designing the PID controller by using the approximated system, the open-loop reference system $\left( {\tilde{M}\left( s \right)} \right)$ is calculated from the closed-loop reference system ($\left( {M(s)} \right)$

$$ \tilde{M}\left( s \right) = \frac{M\left( s \right)}{1 - M\left( s \right)} $$

(21)

The PID controller is designed so that the performance of an open-loop controlled system is the same as the performance of the open-loop reference system as

$$ G_{c} \left( s \right)G\left( s \right) = \tilde{M}\left( s \right) $$

(22)

$$ G_{c} \left( s \right) = \frac{{\tilde{M}\left( s \right)}}{G\left( s \right)} = \frac{{\mathop \sum \nolimits_{i = 0}^{2} e_{i} s^{i} }}{s} $$

(23)

where $e_{i} \left( {i = 0, 1, 2} \right)$ are the Taylor series coefficients about $s = 0,$ and determined by using moment generating algorithm [46, 68]. And $G\left( s \right)$ is the transfer function of the original system, it can also be replaced by an equivalent approximated model so that the mathematical computation and simulation time will be decreased. The unknown scalar constants of the PID controller are attained by comparing (20) and (23) as follows:

$$ K_{p} + \frac{{K_{i} }}{s} + K_{d} s = \frac{{e_{0} + e_{1} s + e_{2} s^{2} }}{s} $$

(24)

$$ \frac{{K_{i} + K_{p} s + K_{d} s^{2} }}{s} = \frac{{e_{0} + e_{1} s + e_{2} s^{2} }}{s} $$

(25)

Therefore, $K_{p} = e_{1} , K_{i} = e_{0} , K_{d} = e_{2} .$ After finding the scalar constants of the controller, the transfer function of the closed-loop plant can be written as

$$ G_{cl} \left( s \right) = \frac{{G_{c} \left( s \right)G\left( s \right)}}{{1 + G_{c} \left( s \right)G\left( s \right)}} $$

(26)

5 Simulation Results

In order to compare the proposed method with some other standard and recently proposed system reduction methods, the following performance error indices are computed [36, 50, 53].

$$ \left\{ {\begin{array}{*{20}l} { {\text{ISE}} = \mathop \smallint \limits_{0}^{\infty } \left[ {y\left( t \right) - y_{r} \left( t \right)} \right]^{2} {\text{d}}t } \hfill \\ {{\text{RISE}} = \mathop \smallint \limits_{0}^{\infty } \left[ {y\left( {t_{i} } \right) - y_{r} \left( t \right)} \right]^{2} {\text{d}}t/\mathop \smallint \limits_{0}^{\infty } \left[ {\hat{Y}\left( t \right)} \right]^{2} {\text{d}}t} \hfill \\ \end{array} } \right. $$

(27)

$$ \left\{ {\begin{array}{*{20}l} {{\text{IAE}} = \mathop \smallint \limits_{0}^{\infty } \left| {y\left( t \right) - y_{r} \left( t \right)} \right|{\text{d}}t } \hfill \\ {{\text{ITAE}} = \mathop \smallint \limits_{0}^{\infty } t\left| {y\left( t \right) - y_{r} \left( t \right)} \right|{\text{d}}t } \hfill \\ \end{array} } \right. $$

(28)

where $y\left( t \right)$ and $y_{r} \left( t \right)$ are the step responses of the higher-dimensional model and the simplified model.

Example 1

Consider the eighth-order transfer function of a flexible-missile control plant designed in [3]

$$ G\left( s \right) = \frac{{ - s^{6} + 3.06 \times 10^{2} s^{5} - 4.96 \times^{4} + 3.577 \times 10^{6} s^{3} - 6.303 \times 10^{7} s^{2} - 1.246 \times 10^{10} s + 5.906 \times 10^{11} }}{{s^{8} + 52.99s^{7} + 3.05 \times 10^{4} s^{6} + 1.375 \times 10^{6} s^{5} + 1.839 \times 10^{8} s^{4} + 5.232 \times 10^{9} s^{3} + 3.422 \times 10^{11} s^{2} + 2.823 \times 10^{12} s + 1.442 \times 10^{14} }} $$

(29)

For this system $c_{0} = 0.00409, M_{0} = 0$, and the characteristic equation of the original system is

$$ D\left( s \right) = s^{8} + 52.99s^{7} + 3.05 \times 10^{4} s^{6} + 1.375 \times 10^{6} s^{5} + 1.839 \times 10^{8} s^{4} + 5.232 \times 10^{9} s^{3} + 3.422 \times 10^{11} s^{2} + 2.823 \times 10^{12} s + 1.442 \times 10^{14} $$

(30)

The first step of the proposed method discussed in Sect. 3.1 is to obtain the real and imaginary parts of the denominator polynomial of the original system. For obtaining the real and imaginary parts substituting $s = jw$ in (30) and splitting the real part and imaginary part, it gives

$$ \begin{aligned} & \phi \left( w \right) = \left( {w^{2} - 591.1193} \right)\left( {w^{2} - 2491.5423} \right)\left( {w^{2} - 4220.8461} \right)\left( {w^{2} - 23196.4923} \right) \\ & \psi \left( w \right) = w\left( {w^{2} - 646.7532} \right)\left( {w^{2} - 3837.6991} \right)\left( {w^{2} - 21463.8398} \right) \\ \end{aligned} $$

In order to obtain the reduced denominator polynomial by the Mihailov stability method, first step is to assume the real and imaginary parts of the reduced polynomial which are having the same initial “r” characteristic roots as the original denominator polynomial have. For the second-order reduced system, real and imaginary parts are assumed as $\xi \left( w \right) = k_{1} \left( {w^{2} - 591.1193} \right)$ and $\eta \left( w \right) = k_{2} w .$ And, unknown parameters $k_{1}$ is calculated by using relation $\phi \left( {jw_{0} } \right) = \xi \left( {jw_{0} } \right)$ and $k_{2}$ is computed from $\psi \left( {jw_{1} } \right) = \eta \left( {jw_{1} } \right)$ and obtained as $k_{1} = - 2.4394 \times 10^{11}$ and $k_{2} = 1.9977 \times 10^{11}$. Thus, the characteristic equation of the second-order approximated model obtained by the Mihailov stability method is

$$ P_{2} \left( s \right) = 2.4394 \times 10^{11} s^{2} + 1.9977 \times 10^{11} s + 1.442 \times 10^{14} $$

(31)

By using the proposed method discussed in Sect. 3.2 (with $\alpha = 1, \beta = 1$), the second-order reduced plant is

$$ R_{2} \left( s \right) = \frac{{Q_{2} \left( s \right)}}{{P_{2} \left( s \right)}} = \frac{5.906}{{2.4394s^{2} + 1.9977s + 1442}} $$

(32)

The comparison of time responses of the actual model, simplified-order models evaluated by the proposed scheme and other standard methodologies are displayed in Fig. 1. From this comparison, it can be seen that the microsystem achieved by the recommended technique gives the closest approximation to the higher-order plant. Also, the quantitative analysis of the reduced-order systems determined by the recommended technique and other existing techniques in terms of performance indices ISE, RISE, IAE and ITAE values is shown in Table 1. It is clear from this table that the presented scheme is superior to some other standards methods because it is giving the least values of different error indices.

Fig. 1

Comparison of step responses of original system and reduced models

Table 1 Comparison of performance indices for the different system diminution techniques

Example 2

Consider a sixth-order system described by the following transfer function [13]

$$ G\left( s \right) = \frac{{s^{5} + 8s^{4} + 20s^{3} + 16s^{2} + 3s + 2}}{{s^{6} + 18.3s^{5} + 102.4s^{4} + 209.5s^{3} + 155.9s^{2} + 33.6s + 2}} $$

(33)

The characteristic equation of the original system is written as

$$ D\left( s \right) = s^{6} + 18.3s^{5} + 102.4s^{4} + 209.5s^{3} + 155.9s^{2} + 33.6s + 2 $$

(34)

Putting $s = jw$ in (34) and isolating the real part and imaginary part and it gives the following polynomials as

$$ \begin{aligned} & \phi \left( w \right) = - \left( {w^{2} - 0.0129} \right)\left( {w^{2} - 1.5327} \right)\left( {w^{2} - 100.8544} \right) \\ & \psi \left( w \right) = w\left( {w^{2} - 0.1627} \right)\left( {w^{2} - 11.2854} \right) \\ \end{aligned} $$

For the second-order reduced model, $\xi \left( w \right) = k_{1} \left( {w^{2} - 0.0129} \right), \eta \left( w \right) = k_{2} w\,{\text{and}}\;k_{1} = - 155.0388\;{\text{and}}\; k_{2} = 33.5652$. Hence, the characteristic equation of the second-order reduced system computed by the Mihailov stability criterion is

$$ P_{2} \left( s \right) = 155.0388s^{2} + 33.5652s + 2 $$

(35)

By using the proposed model reduction algorithm, the second-order reduced model is obtained as

$$ R_{2} \left( s \right) = \frac{{Q_{2} \left( s \right)}}{{P_{2} \left( s \right)}} = \frac{3s + 2}{{155.0388s^{2} + 33.5652s + 2}} $$

(36)

Figure 2 shows the time responses of the full-order model and reduced models obtained by the presented method and other standard methods. This figure reveals that the response of the obtained system by the proposed technique is much closer to the response of the full-order model. The quantitative comparison of the lower-order models computed by the proposed method and some other well-known methods in terms of ISE, RISE, IAE and ITAE values is tabulated in Table 2. It can be seen that the proposed method is giving the least values of the various performance indices. Hence, the proposed method is superior and comparable with some other standard system reduction methods.

Fig. 2

Qualitative comparison of system reduction methods in terms of the step response

Example 3

Consider the sixth-order regulator plant with its reference plant for the design of PID controller [57].

$$ G_{p} \left( s \right) = \frac{{2s^{5} + 3s^{4} + 16s^{3} + 20s^{2} + 8s + 1}}{{2s^{6} + 33.6s^{5} + 155.94s^{4} + 209.5s^{3} + 102.42s^{2} + 18.3s + 1}} $$

(37)

$$ M\left( s \right) = \frac{25}{{s^{2} + 20s + 25}} $$

(38)

The open-loop reference system is obtained as

$$ \tilde{M}\left( s \right) = \frac{M\left( s \right)}{1 - M\left( s \right)} = \frac{25}{{s\left( {s + 20} \right)}} $$

(39)

By using the complex model, the PID controller is determined as follows:

$$ G_{c} \left( s \right) = \frac{{\tilde{M}\left( s \right)}}{G\left( s \right)} = \frac{{e_{0} + e_{1} s + e_{2} s^{2} + \cdots }}{s} = \frac{{K_{i} + K_{p} s + K_{d} s^{2} }}{s} = \frac{{1.25 + 12.8125s - 0.6156s^{2} + \cdots }}{s} $$

(40)

Hence, $K_{p} = 12.8125,K_{i} = 1.25, K_{d} = - 0.6156$. By using this controller, the closed-loop system is computed as

$$ R_{cl} \left( s \right) = \frac{{G\left( s \right)G_{c} \left( s \right)}}{{1 + G\left( s \right)G_{c} \left( s \right)}} $$

(41)

The lower-order plant obtained by the proposed technique with ($\alpha = 2, \beta = 0$) is given follows:

$$ R_{2} \left( s \right) = \frac{5.934s + 1}{{101s^{2} + 16.23s + 1}} $$

(42)

By using the proposed lower-order plant, the PID controller is determined as follows:

$$ G_{cr} \left( s \right) = \frac{{\tilde{M}\left( s \right)}}{{R_{r} \left( s \right)}} = \frac{{e_{0} + e_{1} s + e_{2} s^{2} + \cdots }}{s} = \frac{{K_{i} + K_{p} s + K_{d} s^{2} }}{s} = \frac{{1.25 + 12.8125s + 49.2192s^{2} + \cdots }}{s} $$

(43)

Hence,$K_{p} = 12.8125, K_{i} = 1.25,\,{\text{and}}\,K_{d} = 49.2192$. The closed-loop transfer of the original system with the controller obtained by using the reduced model cab be computed by using the following equation:

$$ R_{cl} \left( s \right) = \frac{{G\left( s \right)G_{cr} \left( s \right)}}{{1 + G\left( s \right)G_{cr} \left( s \right)}} $$

(44)

Figure 3 shows the comparison of step responses of the reference model and the closed-loop model with PID controllers obtained by using the higher-order plant and the reduced-order plants. It can be seen that all the responses of the closed-loop plant with PID controllers are approximately matching with the reference model in both steady state and transient region. The time-domain specifications of the closed-loop system with controllers are given in Table 3. In this table, it is obvious that the time-domain specifications of the closed-loop plant with the controller calculated by using the original system are nearly the same as the time-domain specifications of the closed-loop system with the controller designed by using lower-order models. The design of the controller by using the approximated model is comparatively easy as the design of the controller by using the original full-order system. This table also reveals that the time-domain specifications of the closed-loop plant with the controllers are the same as the reference system.

Fig. 3

Comparison of step responses of the closed-loop systems

6 Conclusion and Future Scope

In this article, a new hybrid scheme for decreasing the order of the transfer function of the complex SISO systems is proposed. In this method, the denominator coefficients of the reduced model are determined by using the Mihailov stability criterion, while the numerator coefficients are calculated by using the improved Padé approximation method. This algorithm has been verified on the two standard numerical examples, and the time responses of the full-order model and the reduced-order plants are compared graphically in Figs. 1 and 2. The quantitative comparison in terms of various performance indices such as ISE, RISE, IAE and ITAE are tabulated in Tables 1 and 2. From the analysis, it has been summarized that the proposed scheme is simple and comparable with some other standard system diminution methods. This algorithm confirms the stability of the approximated plant if the higher-order plant is stable and exactly matching the steady-state value of the actual system. A new method for the design of the controller is also proposed. The controller design is done by using the large-scale system as well as the reduced models. The design of the controller by using reduced model is simple and easier than the design of the controller by using the original large-scale system. This design procedure is validated and verified in Fig. 3 and Table 3. In this contribution, the proposed works are implemented on the single input single output (SISO) LTI continuous systems and can also be extended for the large-scale multi-input multi-output (MIMO) and discrete systems.

Table 2 Comparison of proposed model system reduction method and some other model reduction methods

Table 3 Comparison of time-domain specification (in second) of closed-loop system with controller design by using the original system as well as various reduced models