1 Introduction

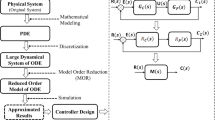
Analysis and design of controllers for achieving desired performance specification of a dynamical system can be carried out by obtaining a suitable mathematical model. Modeling of large-scale systems yields complex models which are difficult or even impossible to study due to computational, cost constraints or storage [18]. This problem is overwhelmed by replacing large-scale system into an equivalent reduced model. Therefore, system reduction methods producing reduced-order analyzable models are devised, while model diminution preserves certain features like transient response, static response and stability of the large-scale original model. However, the performance error indices need to be preferably small, and lower-order system computation should be efficient and numerically simple.

Nowadays, the applications of model order diminution are extended in the various fields of engineering and sciences. The application of system reduction in the field of chemical engineering for the identification of time-dependent parameters of the chemical vapor decomposition processes by using reduced-order models is discussed in [27]. The authors in [34] are focused on the model order diminution of power system with wind farm for the reduction in computational burden. As in [67], the work of this paper is focused on the tracking control of multi-spacecraft network with time-delay by using reduced-order modeling. In the field of electromagnetic, model order diminution is applied for the synthesis and study of large-scale electromagnetic systems [38, 41, 51]. In order to obtain the fast dynamic response behavior of the dynamical system, as industrial users and researcher attempt to design the controller, this design process is difficult for the large-scale dynamic system. The design of the controller becomes easy and simple by using reduced-order modeling as discussed in [8, 14, 15, 24]. Model order diminution is not only restricted for continuous and discrete time models but also extended in the Markov jump systems [10, 68]. The details about Markov jump systems can be found in the literature [6, 7, 65].

From last few decades, several techniques for system diminution of large-scale systems have been proposed in the frequency domain such as time moment matching [66], Padé approximation [53], Routh approximation [21], Routh Hurwitz [28], stability equation [5] and pole clustering [59]. These methods provide good approximation but also have some limitations. In order to overcome the limitations of these methods, various combined methods have been proposed [4, 23, 30, 33, 35, 43, 44, 48, 56, 58, 62]. In the last decade, several methods for the model order reduction in higher-order systems have been proposed in the time domain, such as aggregation method [1, 19], singular perturbation [25, 50], balanced realization [31, 39], Krylov subspace [2, 12], Arnoldi [9], Lanczos [13] and Hankel norm approximation method [29]. Typically, these methods offer good approximation but these methods have some limitations such as steady-state gain difference between the original plant and its approximant, failing to keep the stability of the original model and error bounds. However, balanced realization method retains stability of the lower-order system and provides a priori error bound [11, 22]. In order to overcome the limitations of these methods, several mixed techniques of model diminution have been given in [11, 20, 42, 64].

The pole clustering method discussed in [59] is widely used for the simplification of large-scale linear time-invariant (LTI) single as well as multivariable systems. This method ensures the preservation of stability, static and dynamic responses of original plant in the reduced model. However, this method has a drawback such as it requires extra mathematical computation for the determination of tuning factor and gain adjustment factor for the proper matching of time responses between reduced and original models. The determination of these factors increases the simulation time and extra storage memory. To overcome these limitations, several mixed methods have been proposed [33, 58, 62]. These mixed methods preserve only first dominant pole of the original plant. In order to overcome the drawback of pole clustering method and preservation of more than one dominant pole, a new model order diminution method is proposed in the paper. This new method is used for the simplification of large-scale single as well as multivariable systems and designing of controllers. The proposed method is based on the generalized pole clustering method and a simple mathematical technique discussed in the literature [26, 43]. The pole clustering method is a special case of the generalized pole clustering method. The reduced model obtained by the proposed scheme preserves the stability and steady-state gain of the original plant. The obtained reduced model is used for the design of compensator for the large-scale plant. The compensator is obtained by using a new method with the help of the obtained reduced model.

The remainder of this paper is structured as follows. Section 2 is focused on the main objective of the paper for the determination of reduced models of single and multivariable large-scale linear dynamic systems. In Sect. 3, a new model reduction method is discussed for the simplification of higher-order plants. The designing of the compensator for the large-scale systems by the new algorithm is discussed in Sect. 4. Section 5 shows the simulation examples to illustrate the benefits of the proposed method. Conclusions and future scopes of this paper are summarized in Sect. 6.

2 Statement of the Problem

Consider an \( n{\text{th}} \) order transfer function of large-scale stable systems

$$ G\left( s \right) = \frac{N\left( s \right)}{D\left( s \right)} = \frac{{d_{0} + d_{1} s + \cdots + d_{n - 1} s^{n - 1} }}{{e_{0} + e_{1} s + e_{2} s^{2} + \cdots + e_{n} s^{n} }} $$
(1)

The main goal of the paper is to reduce the computational cost in analysis and synthesis of large-scale dynamical plants (\( G\left( s \right) \)) by construction which do not lead to momentous harm in accuracy and yet reserve the fundamental features of the original model. The lower-dimensional system \( (R_{r} (s)) \) is defined as follows

$$ R_{r} \left( s \right) = \frac{{Q_{r} \left( s \right)}}{{P_{r} \left( s \right)}} = \frac{{q_{0} + q_{1} s + q_{2} s^{2} + \cdots + q_{r - 1} s^{r - 1} }}{{p_{0} + p_{1} s + p_{2} s^{2} + \cdots + p_{r - 1} s^{r - 1} + p_{r} s^{r} }} $$
(2)

Let the transfer function of large-scale multivariable system of the order “\( n \)” be

$$ \left[ {G\left( s \right)} \right] = \frac{1}{D\left( s \right)}\left[ {\begin{array}{*{20}c} {a_{11} \left( s \right)} & {a_{12} \left( s \right)} & \ldots & {a_{1u} \left( s \right)} \\ {a_{21} \left( s \right)} & {a_{22} \left( s \right)} & \ldots & {a_{2u} \left( s \right)} \\ \vdots & \vdots & \vdots & \vdots \\ {a_{v1} \left( s \right)} & {a_{v2} \left( s \right)} & \ldots & {a_{vu} \left( s \right)} \\ \end{array} } \right] $$
(3)
$$ = \left[ {g_{ij} \left( s \right)} \right]_{v \times u} $$
(4)

where \( i = 1, 2, 3, \ldots ,v;\; j = 1, 2, 3, \ldots ,u \), and u and v are the number of input and output variables, respectively. The \( g_{ij} \left( s \right) \) can be defined as

$$ g_{ij} \left( s \right) = \frac{{A_{ij} \left( s \right)}}{D\left( s \right)} $$
(5)

To realize the rth-order approximated model in the form of (6) from the original system, (3) is the objective of the paper such that it preserves the essential features of the original plant. The transfer matrix of the approximated multivariable model of the order “\( r \)” be

$$ \left[ {R_{r} \left( s \right)} \right] = \frac{1}{{P_{r} \left( s \right)}}\left[ {\begin{array}{*{20}c} {b_{11} \left( s \right)} & {b_{12} \left( s \right)} & \ldots & {b_{1u} \left( s \right)} \\ {b_{21} \left( s \right)} & {b_{22} \left( s \right)} & \ldots & {b_{2u} \left( s \right)} \\ \vdots & \vdots & \vdots & \vdots \\ {b_{v1} \left( s \right)} & {b_{v2} \left( s \right)} & \ldots & {b_{vu} \left( s \right)} \\ \end{array} } \right] $$
(6)
$$ = \left[ {r_{ij} \left( s \right)} \right]_{v \times u} $$
(7)

where \( i = 1, 2, 3, \ldots ,v; \;j = 1, 2, 3, \ldots ,u \). Hence, \( r_{ij} \left( s \right) \) can be represented as

$$ r_{ij} \left( s \right) = \frac{{B_{ij} \left( s \right)}}{{P_{r} \left( s \right)}} $$
(8)

The \( g_{ij} \left( s \right) \) and \( r_{ij} \left( s \right) \) are the various elements of the full-order and the lower-order transfer function matrices, respectively.

3 Proposed Method

The system reduction procedure for obtaining the rth-order approximated model is described in the following two steps:

3.1 Determination of Denominator Polynomial

The time and frequency behavior of any dynamic models depend upon the poles of the models. The poles which are far away from the imaginary axis of s-plane die out quickly in the time response and in several model reduction methods neglected directly for obtaining the reduced-order models [31, 45, 46]. The poles near to imaginary axis significantly affect the time response and are retained in the several reduction methods for computing the approximated reduced system [5, 21, 28, 35, 59]. For obtaining rth-order approximated model by pole clustering method, “r” numbers of clusters are required to compute. The poles of the original plant are placed in the clusters on the basis of the effectiveness of the poles. In order to place the poles in the clusters, following rules are followed

  1. 1.

    Separate clusters are made for real and complex poles.

  2. 2.

    Poles lying in the left and right half of s-plane are clustered separately.

  3. 3.

    Purely imaginary poles and poles at the origin of s-plane are retained in the approximated system.

3.1.1 Clustering of Real Poles

Consider the large-scale original system (1) in the pole-zero form as

$$ G_{p} \left( s \right) = \frac{N\left( s \right)}{D\left( s \right)} $$

where

$$ N\left( s \right) = \left( {s + z_{1} } \right)\left( {s + z_{2} } \right) \ldots \left( {s + z_{r - 1} } \right)\left( {s + z_{r} } \right)\left( {s + z_{r + 1} } \right) \ldots \left( {s + z_{2r - 1} } \right)\left( {s + z_{2r} } \right)\left( {s + z_{2r + 1} } \right) \ldots \left( {s + z_{n - 1} } \right) $$
(9)

and

$$ D\left( s \right) = \left( {s + p_{1} } \right)\left( {s + p_{2} } \right) \ldots \left( {s + p_{r - 1} } \right)\left( {s + p_{r} } \right)\left( {s + p_{r + 1} } \right) \ldots \left( {s + p_{2r - 1} } \right)\left( {s + p_{2r} } \right)\left( {s + p_{2r + 1} } \right) \ldots \left( {s + p_{n} } \right) $$
(10)

Assume the order of the approximated model is \( r (r < n) \) and for rth-order reduced model, \( r \) numbers of clusters are formulated. Arranging the poles lying in left half of s-plane in the ascending order of the magnitude

$$ {\text{Pole}}: - p_{1} , - p_{2} , \ldots , - p_{i} , \ldots , - p_{n} \quad \forall |p_{i} | < \left| {p_{i + 1} } \right| $$
(11)

The first pole is placed in the first cluster, second pole is placed in the second cluster similarly rth pole is placed in the rth cluster, \( \left( {r + 1} \right){\text{th}} \) pole is placed in the first cluster, \( \left( {r + 2} \right){\text{th }} \) pole is placed in the second cluster, similarly \( \left( {2r} \right){\text{th }} \) pole is placed in the rth cluster, and this procedure is continued up to the last pole. The main advantage of this algorithm is that it preserves \( \hbox{``}r\hbox{''} \) number of dominant poles of the original plant in the reduced model as compared to the existing pole clustering methods [26, 33, 58, 62] which preserve only one dominant pole. After placing the poles in the clusters, the cluster centers of the clusters are determined by using following algorithm

$$ c_{1} = - \left\{ {\left( {\left[ {\frac{1}{{\left| {p_{1} } \right|^{X} }}} \right] + \left[ {\frac{1}{{\left| {p_{r + 1} } \right|^{X} }}} \right] + \left[ {\frac{1}{{\left| {p_{2r + 1} } \right|^{X} }}} \right] + \cdots \left[ {\frac{1}{{\left| {p_{k} } \right|^{X} }}} \right]} \right)/k} \right\}^{{ - \left( {1/X} \right)}} $$
(12)
$$ c_{2} = - \left\{ {\left( {\left[ {\frac{1}{{\left| {p_{2} } \right|^{X} }}} \right] + \left[ {\frac{1}{{\left| {p_{r + 2} } \right|^{X} }}} \right] + \left[ {\frac{1}{{\left| {p_{2r + 2} } \right|^{X} }}} \right] + \cdots \left[ {\frac{1}{{\left| {p_{l} } \right|^{X} }}} \right]} \right)/l} \right\}^{{ - \left( {1/X} \right)}} $$
(13)
$$ \ldots \quad \ldots \quad \ldots \quad \ldots \quad \ldots $$
$$ c_{r} = - \left\{ {\left( {\left[ {\frac{1}{{\left| {p_{r} } \right|^{X} }}} \right] + \left[ {\frac{1}{{\left| {p_{2r} } \right|^{X} }}} \right] + \left[ {\frac{1}{{\left| {p_{3r} } \right|^{X} }}} \right] + \ldots \left[ {\frac{1}{{\left| {p_{m} } \right|^{X} }}} \right]} \right)/m} \right\}^{{ - \left( {1/X} \right)}} $$
(14)

where \( c_{1} , c_{2} , \ldots ,c_{r } \) are the cluster centers, \( X \) is the order of roots of the clusters, and its value will be any natural number depending upon the required accuracy in the approximated reduced model. And \( k, l \) and \( m \) are the total number of poles lying in the cluster-1, cluster-2 and cluster \( - r \), respectively, and the values of these variables may have same or different values, depending upon the poles of the original systems. After computing the cluster centers, the denominator polynomial of the reduced plant is obtained as follows

$$ P_{r} \left( s \right) = \left( {s - c_{1} } \right)\left( {s - c_{2} } \right) \ldots \left( {s - c_{r} } \right) $$
(15)

For the specific value of X, the cluster centers in (12–14) depend upon the poles which are near to the origin of s-plane. If the value of X is increasing from more than one, the cluster center is moving closer to the dominant pole of that cluster. Hence, it can be established that the cluster center depends upon the dominant pole of the cluster and its magnitude is closer to the dominant pole. From (12–14), it can be seen that when the value of X equals to one, the proposed technique of clustering becomes pole clustering technique of model reduction as described in [59]. Therefore, the pole clustering method is a special case of the proposed method.

3.1.2 Clustering of Complex Poles

In the determination of cluster centers of complex poles, the real and imaginary parts of the complex poles are determined separately by using algorithm as discussed for the real poles. If \( A_{i/2} \pm jB_{i/2 } \) are the cluster centers of complex poles for \( i = 1,2,3, \ldots ,r \), the denominator polynomial of the lower-order system is given as follows

$$ P_{r} \left( s \right) = \left( {s - A_{1} \pm jB_{1} } \right)\left( {s - A_{2} \pm jB_{2} } \right) \ldots \left( {s - A_{r/2} \pm jB_{r/2} } \right) $$
(16)

3.1.3 Clustering of Real and Complex Poles

The cluster centers for the real and complex poles are computed separately in the same way as discussed in the above procedure. The numbers of clusters for real and complex poles are decided on the basis of the order of the lower-order system. For the rth-order lower-order model suppose \( \alpha \) cluster centers are for real poles and \( \beta \) cluster centers are for complex poles, the denominator polynomial of the reduced system is

$$ P_{r} \left( s \right) = \mathop \prod \limits_{i = 1,j = 1}^{\alpha ,\beta /2} \left( {s - c_{i} } \right)\left( {s - A_{j} \pm jB_{j} } \right) | \alpha + \beta = r $$
(17)

3.2 Determination of the Numerator Polynomial of the Reduced Model

The numerator polynomial of the approximated system is determined by using a simple mathematical algorithm given in [26, 43, 45]. In this method, comparing the transfer function of the approximated model (2) with the transfer function of the large-scale plant (1) as follows

$$ \frac{{d_{0} + d_{1} s + \cdots + d_{n - 1} s^{n - 1} }}{{e_{0} + e_{1} s + e_{2} s^{2} + \cdots + e_{n} s^{n} }} = \frac{{q_{0} + q_{1} s + q_{2} s^{2} + \cdots + q_{r - 1} s^{r - 1} }}{{p_{0} + p_{1} s + p_{2} s^{2} + \cdots + p_{r - 1} s^{r - 1} + p_{r} s^{r} }} $$
(18)

After cross-multiplication of (18), equating the same powers of “\( s \)” from \( s^{0} \) to \( s^{r - 1 } \) on both sides it gives “r” number of equations.

$$ \left\{ {\begin{array}{*{20}l} {d_{0} p_{0} = e_{0} q_{0} } \hfill \\ {d_{0} p_{1} + d_{1} p_{0} = e_{0} q_{1} + e_{1} q_{0} } \hfill \\ {d_{0} p_{2} + d_{1} p_{1} + d_{2} p_{0} = e_{0} q_{2} + e_{1} q_{1} + e_{2} q_{0} } \hfill \\ \vdots \hfill \\ \end{array} } \right. $$
(19)

The coefficients \( (q_{0} , q_{1} , \ldots ,q_{r - 1} ) \) of the numerator polynomial are determined by solving \( \hbox{``}r\hbox{''} \) number of (19) in which the coefficients of the denominator characteristic \( (p_{0} + p_{1} s + p_{2} s^{2} + \cdots + p_{r - 1} s^{r - 1} + p_{r} s^{r} ) \) of the reduced plant are known. The proposed algorithm retains all the fundamental features of the pole clustering method with additional advantages as it does not require computation of gain adjustment and tuning factors and preserves “r” number of dominant poles.

4 Procedure for Design of Compensator

The design of controllers and simulation are a complicated task for the large-scale plants. As the order of the system increases, the complexity and cost of the controller design increase simultaneously. This difficulty can be solved if a “good” approximated reduced system is obtainable for the original large-scale model, and the design of the controller is carried out by using the reduced model. In case of a large-scale system, the enormous numbers of sensors are required for sensing the state variables of the systems for the design of feedback controllers. Due to this, series controllers are superior over the feedback controllers.

A reference plant \( (M(s)) \) is designed on the basis of the given specification of the large-scale systems for obtaining the desired performance such that the closed-loop operation of the controlled model with unity feedback is closely matched with the response of the reference plant. The procedure for obtaining the reference model from the given specification is given in [40, 60]. Let the transfer function of the compensator be given as follows

$$ G_{c} \left( s \right) = \frac{{K(1 + K_{1} s)}}{{s(1 + K_{2} s)}} $$
(20)

In order to design the compensator, first obtain the open-loop reference model \( \left( {\tilde{M}\left( s \right)} \right) \) from the given closed-loop reference system \( (M(s)) \)

$$ \tilde{M}\left( s \right) = \frac{M\left( s \right)}{1 - M\left( s \right)} $$
(21)

For finding the unknown parameters of the compensator, it is assumed that the response of the open-loop controlled model is matched with that of the open-loop reference model as

$$ G_{c} \left( s \right)G\left( s \right) = \tilde{M}\left( s \right) $$
(22)
$$ G_{c} \left( s \right) = \frac{{\tilde{M}\left( s \right)}}{G\left( s \right)} = \frac{{\mathop \sum \nolimits_{i = 0}^{2} e_{i} s^{i} }}{s} $$
(23)

where \( e_{i} \)\( \left( {i = 0, 1,2} \right) \) are the coefficients of the Taylor series expansion about \( s = 0, \) and these are obtained by using moment generating technique given in [46, 66]. And \( G\left( s \right) \) is the transfer function of the large-scale plant, it can also be replaced by a good approximated reduced-order system so that the mathematical computation and simulation time will be reduced in the design of compensator. The unknown parameters of the compensator can be obtained by comparing (20) and (23) as follows

$$ \frac{{K(1 + K_{1} s)}}{{s(1 + K_{2} s)}} = \frac{{e_{0} + e_{1} s + e_{2} s^{2} }}{s} $$
(24)

The compensator having the desired structure is determined by solving (24). After finding the parameters of the compensator, the closed-loop transfer function can be defined as follows

$$ G_{cl} \left( s \right) = \frac{{G_{c} \left( s \right)G\left( s \right)}}{{1 + G_{c} \left( s \right)G\left( s \right)}} $$
(25)

5 Illustrative Examples

In order to validate the performance of the proposed method, performance error indices like an integral of square error (ISE), integral of relative square error (RISE), integral of absolute error (IAE) and integral of time multiplied by absolute error (ITAE) are used in the paper. The following performance indices of lower-order plants are calculated, which are given as [43, 46, 56, 59]

$$ \left\{ {\begin{array}{*{20}l} {{\text{ISE}} = \mathop \smallint \limits_{0}^{\infty } \left[ {y\left( t \right) - y_{r} \left( t \right)} \right]^{2} {\text{d}}t } \hfill \\ {{\text{RISE}} = \mathop \smallint \limits_{0}^{\infty } \left[ {y\left( t \right) - y_{r} \left( t \right)} \right]^{2} {\text{d}}t/\mathop \smallint \limits_{0}^{\infty } \left[ {\hat{y}\left( t \right)} \right]^{2} {\text{d}}t} \hfill \\ \end{array} } \right. $$
(26)
$$ \left\{ {\begin{array}{*{20}l} {{\text{IAE}} = \mathop \smallint \limits_{0}^{\infty } \left| {y\left( t \right) - y_{r} \left( t \right)} \right|{\text{d}}t} \hfill \\ {{\text{ITAE}} = \mathop \smallint \limits_{0}^{\infty } t\left| {y\left( t \right) - y_{r} \left( t \right)} \right|{\text{d}}t} \hfill \\ \end{array} } \right. $$
(27)

where y(t) and yr(t) are the step responses of higher-order system and lower-order model, respectively, and \( \hat{y}(t) \) is the impulse response of the large-scale plant. The time domain analysis as rise time, peak time, maximum overshoot and settling time is used as performance to analyze the transient response of the closed-loop controlled plant when it is subjected to unit-step input and the validation of the obtained compensator.

Example 1

Consider an eighth-order standard system discussed in [28, 45, 46] which is given as

$$ G\left( s \right) = \frac{{35s^{7} + 1086s^{6} + 13285s^{5} + 82402s^{4} + 278376s^{3} + 511812s^{2} + 482964s + 194480}}{{s^{8} + 33s^{7} + 437s^{6} + 3017s^{5} + 11870s^{4} + 27470s^{3} + 37492s^{2} + 28880s + 9600}} $$
(28)

Poles: \( - 1, - 1 - 1j, - 1 + 1j, - 3, - 4, - 5, - 8, - 10. \)

The original system has one pair of complex pole, and it will be retained in the approximated reduced system. In order to obtain the fourth-order reduced system, the real poles are clustered into two clusters. For placing the poles into two clusters, first assemble the real poles in ascending order of their magnitude

  • Real poles: \( - 1, - 3, - 4, - 5, - 8, - 10 \)

The poles are clustered into two clusters as follows

  • Cluster-1 has poles: \( - 1, - 4, - 8 \)

  • Cluster-2 has poles: \( - 3, - 5, - 10. \)

The cluster centers of these clusters are obtained as follows

$$ c_{2p} = - \left\{ {\left( {\left[ {\frac{1}{{3^{X} }}} \right] + \left[ {\frac{1}{{5^{X} }}} \right] + \left[ {\frac{1}{{10^{X} }}} \right]} \right)/3} \right\}^{{ - \left( {1/X} \right)}} $$

By using above cluster centers, the denominator of the reduced model is obtained as

$$ D_{r} \left( s \right) = \left( {s + 1 \pm 1j} \right)\left( {s - c_{1p} } \right)\left( {s - c_{2p} } \right) $$
(29)

Taking different values of \( X \), the different denominator polynomials of the reduced plant will be obtained and after that the numerator polynomials are obtained by using a recently proposed simple mathematical algorithm described in Sect. 3.2. The lower-order system obtained by the proposed algorithm with \( X = 10 \) is

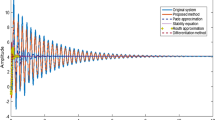
$$ R_{2} \left( s \right) = \frac{{31.1973s^{3} + 168.9203s^{2} + 252.5901s + 151.3297}}{{s^{4} + 6.462s^{3} + 14.66s^{2} + 16.39s + 7.47}} $$
(30)

From (29), it is clear that the obtained reduced plant is stable; hence, the proposed algorithm preserves the stability of the original plant. Figure 1 represents the step responses of the large-scale model, proposed reduced model and lower-order systems obtained by using various model reduction techniques. It is seen that the response of the proposed reduced model is thoroughly matched with the response of the original plant as compared to the other existing system reduction algorithms. Table 1 shows the effectiveness and superiority of the suggested algorithm by comparing with lower-order models obtained by existing techniques available in the literature. In this table, it is also seen that the proposed method is not giving the least performance indices when \( X = 5 \) but when \( X = 10 \) the proposed algorithm is giving least error indices as compared to other methods available in the literature. Hence, it can be concluded that for better performance indices and accuracy the value of \( X \) should be kept large value.

Fig. 1
figure 1

Qualitative comparison of proposed method with other standard methods in terms of step response

Full size image
Table 1 Comparison of various model reduction techniques on the basis of different performance error indices
Full size table

At X = 1, the proposed method becomes the pole clustering method [59] and the proposed algorithm is better than the pole clustering method because it is giving lower-performance error indices. The proposed approach is also superior to the pole clustering method since it does not require steady-state gain adjustment factor and tuning factor as required in the pole clustering method.

Example 2

Consider a sixth-order multivariable system which has been considered by several researchers [32, 36, 37, 43, 56, 63] and is described by the following transfer function

$$ \begin{aligned} G\left( s \right) & = \left[ {\begin{array}{*{20}l} {\frac{{2\left( {s + 5} \right)}}{{\left( {s + 1} \right)\left( {s + 10} \right)}}} \hfill & {\frac{{\left( {s + 4} \right)}}{{\left( {s + 2} \right)\left( {s + 5} \right)}}} \hfill \\ {\frac{{\left( {s + 10} \right)}}{{\left( {s + 1} \right)\left( {s + 20} \right)}}} \hfill & {\frac{{\left( {s + 6} \right)}}{{\left( {s + 2} \right)\left( {s + 3} \right)}}} \hfill \\ \end{array} } \right] \\ & = \frac{1}{D\left( s \right)}\left[ {\begin{array}{*{20}c} {A_{11} \left( s \right)} & {A_{12} \left( s \right)} \\ {A_{21} \left( s \right)} & {A_{22} \left( s \right)} \\ \end{array} } \right] \\ \end{aligned} $$
(31)

where

$$ \begin{aligned} D\left( s \right) & = \left( {s + 1} \right)\left( {s + 2} \right)\left( {s + 3} \right)\left( {s + 5} \right)\left( {s + 10} \right)\left( {s + 20} \right) \\ & = s^{6} + 41s^{5} + 571s^{4} + 3491s^{3} + 10060s^{2} + 13100s + 6000 \\ \end{aligned} $$

and

$$ \begin{aligned} A_{11} \left( s \right) & = 2s^{5} + 70s^{4} + 762s^{3} + 3610s^{2} + 7700s + 6000 \\ A_{12} \left( s \right) & = s^{5} + 38s^{4} + 459s^{3} + 2182s^{2} + 4160s + 2400 \\ A_{21} \left( s \right) & = s^{5} + 30s^{4} + 331s^{3} + 1650s^{2} + 3700s + 3000 \\ A_{22} \left( s \right) & = s^{5} + 42s^{4} + 601s^{3} + 3660s^{2} + 9100s + 6000 \\ \end{aligned} $$

The poles of the original system are \( p_{1} = - 1, p_{2} = - 2, p_{3} = - 3, p_{4} = - 5, p_{5} = - 10, p_{6} = - 20 \). The poles are grouped into two clusters as follows

  • Cluster-1 has poles: \( - 1, - 3, - 10 \)

  • Cluster-2 has poles: \( - 2, - 5, - 20. \)

The cluster centers are obtained by using (12)–(14) and the denominator polynomial of the reduced plant is obtained as

$$ D_{2} \left( s \right) = \left( {s - c_{1p} } \right)\left( {s - c_{2p} } \right) $$
(32)

The various denominator polynomials of the reduced system will be obtained after taking different values of \( X \). For the specific value of \( X \), the numerator coefficients are obtained by using the proposed algorithm as illustrated in Sect. 3.2. For \( X = 50, \) the transfer matrix of the reduced plant is obtained as:

$$ \left[ {R_{2} \left( s \right)} \right] = \frac{{\left[ {\begin{array}{*{20}l} {1.1858s + 2.0898} \hfill & {0.8505s + 0.8359} \hfill \\ {0.5406s + 1.0449} \hfill & {1.6734s + 2.0898} \hfill \\ \end{array} } \right]}}{{s^{2} + 3.0666s + 2.0898}} $$
(33)

The unit-step responses of the original and lower-order models are shown in Fig. 2, which indicate that the lower-order systems give good approximation. From which, it is clearly seen that the response of the lower-order model computed by the proposed technique is much closer to the original plant as compared to other techniques. A comparison of the presented technique with other existing techniques for a second-order lower-order system is given in Table 2. It can be observed in Table 2 that the proposed algorithm offers the lowest value of performance indices in comparison with some other existing system reduction methods. This table also shows that if \( X \) is taken \( 10 \), then the value of ISE of the proposed method is not least but when the value of \( X \) increased as \( X = 50 \) the proposed method is giving the least values of ISE. Therefore, for obtaining the better accuracy of the proposed technique the value of \( X \) can prefer more than one.

Fig. 2
figure 2

Qualitative analysis of proposed technique with other existing system diminution techniques

Full size image
Table 2 Comparison of various model diminution methods in terms of ISE
Full size table

Example 3

Consider the sixth-order stable practical open-loop helicopter engine including a fuel controller system taken from Prasad [47]

$$ G\left( s \right) = \frac{{248.05s^{4} + 1483.3s^{3} + 91931s^{2} + 468730s + 634950}}{{s^{6} + 26.24s^{5} + 1363.1s^{4} + 26803s^{3} + 326900s^{2} + 859170s + 52805 0}} $$
(34)

The input and output of the model are speed demand and propeller speed, respectively. Because of the elasticity of the propeller shaft, the time characteristic of the system exhibits unwanted oscillations. A simple critically damped reference system is given in [47] as

$$ M\left( s \right) = \frac{4}{{s^{2} + 4s + 4}} $$
(35)

The open-loop reference model is

$$ \tilde{M}\left( s \right) = \frac{M\left( s \right)}{1 - M\left( s \right)} = \frac{4}{{s\left( {s + 4} \right)}} $$
(36)

By using the original plant, the parameters of the controller are obtained as follows

$$ G_{c} \left( s \right) = \frac{{\tilde{M}\left( s \right)}}{G\left( s \right)} = \frac{{e_{0} + e_{1} s + e_{2} s^{2} }}{s} = \frac{{K(1 + K_{1} s)}}{{s(1 + K_{2} s)}} = \frac{{0.8316 + 0.5313s - 0.2841s^{2} }}{s} $$
(37)

Hence,

$$ K = 0.8316,\;K_{1} = 1.1735,\;K_{2} = 0.5347 $$
(38)

The closed-loop system with compensator is given in (39) in which compensator is obtained by using original plant.

$$ R_{cl} \left( s \right) = \frac{{G\left( s \right)G_{c} \left( s \right)}}{{1 + G\left( s \right)G_{c} \left( s \right)}} $$
(39)

The reduced-order model obtained by the proposed method with \( X = 50 \) is given as follows

$$ R_{2} \left( s \right) = \frac{0.6357s + 1.48}{{s^{2} + 3.042s + 2.056}} $$
(40)

By using the above reduced system, the compensator is obtained as follows

$$ G_{cr} \left( s \right) = \frac{{\tilde{M}\left( s \right)}}{{R_{r} \left( s \right)}} = \frac{{e_{0} + e_{1} s + e_{2} s^{2} }}{s} = \frac{{K(1 + K_{1} s)}}{{s(1 + K_{2} s)}} = \frac{{0.8316 + 0.5313s - 0.2841s^{2} }}{s} $$
(41)

Hence,

$$ K = 0.8316,\;K_{1} = 1.1735,\;K_{2} = 0.5347 $$
(42)

The closed-loop transfer of the original model with the compensator is given in (43) in which compensator is obtained by using proposed reduced model.

$$ R_{cl} \left( s \right) = \frac{{G\left( s \right)G_{cr} \left( s \right)}}{{1 + G\left( s \right)G_{cr} \left( s \right)}} $$
(43)

From (38), (42) and Table 3, it is clear that the compensator obtained by using large-scale original system is same as the compensator obtained by using proposed reduced model as compared to the reduced plants computed by some other standard model diminution methods. The design of compensator for large-scale system is a difficult task as compared to the design of compensator by using an equivalent reduced model. Hence, proposed model reduction method can be used for the design of compensator instead of design of compensator by using large-scale original system.

The comparison of time responses of the transfer functions of the closed-loop original plant with compensators is shown in Fig. 3. These compensators are obtained with the help of the large-scale original system and lower-order systems. The simulation result shows that the computed compensators perform well under both steady-state and transient responses. Clearly, the response of the closed-loop system with compensator computed by the reduced system obtained by proposed algorithm is much closer to that of the reference system compared with some other closed-loop systems. The time domain specifications of the closed-loop systems with compensators are tabulated in Table 3. From this table, it can be seen that the time domain specifications of the closed-loop system with the compensator obtained by using proposed lower-order systems are same with the specifications of the closed-loop plant with compensators design by using large-scale original system, and these specifications are also approximately matched with the specifications of desired reference model. Hence, the proposed method can be used for the design of compensator for obtaining the required performances of the dynamical systems.

Fig. 3
figure 3

Comparison of time responses of reference system and closed-loop system with compensator

Full size image
Table 3 Comparison of time domain specifications of closed-loop system with compensator
Full size table

6 Conclusion

The reduced-order approximants for linear, continuous time, SISO as well as MIMO plants are presented in this paper. It is determined from the idea of holding slow modes of the large-scale system in the lower-order denominator. The lower-order numerator is determined by using a simple mathematical algorithm described in the literature. To determine the accuracy, effectiveness and efficiency of the proposed reduced model, it is compared to approximants computed from the several existing recent and popular model reduction methods. From different time responses and various error indices, the proposed method shows the motivating benefits of simplicity of implementation, easy to program and the substantial advantage in execution time compared to the other existing techniques. Also, the stability of the approximant is always guaranteed when the original plant is stable and the best static and dynamic behavior fitting of the original system. And the reduced plant is used for the design of compensator, and by using this controller the proposed model gives the approximately same time domain specification as given by the reference model. From Table 3, it is also found that the compensator design by the original system is the same as the proposed reduced model and design of compensator is easier by using the reduced model. This method can also be extended for the large-scale interval and discrete time practical systems.