1 Introduction

Advances in CMOS technology necessarily involve a size reduction of the interconnects used in integrated circuits (ICs) [11], which are also required to operate at microwave frequencies (f) in current technologies [1, 3]. Thus, since the die size and the number of metal layers used for interconnection purposes is increased in today’s ICs, the aspect ratio of the interconnections becomes higher, whereas the spacing with other lines becomes smaller [10]. As a consequence, this scaling increases the series resistance of interconnects and thus the conductor losses [8, 22, 23], which yield signal degradation [12]. For this reason, the analysis of the negative impact of these losses must be accurately represented even considering that most of the interconnections are routed in a very complex way and operate at microwave frequencies [4, 21].

Generally, the metal layers used in IC technology are included for routing complicated circuits in compact spaces [17]. Therefore, an interconnection link composed of several traces may present different electrical characteristics along its length due to the variation on the proximity to the ground plane. In this regard, in order to determine the performance of a circuit, IC developers require the accurate determination of the fundamental parameters that allow for the representation of each segment composing a given link. These parameters are the characteristic impedance (\(Z_\mathrm{c})\) and the propagation constant (\(\gamma \)) [17, 24]. There are many approaches to obtain \(Z_\mathrm{c}\) and \(\gamma \); for instance, using full-wave structure simulators [15], closed-form formulas [2, 18], and measurement-based techniques [6, 13]. In all cases, the material properties of the structure, as well as the geometry of the interconnect, are considered to some extent. Bear in mind, however, that some of these methods may not be efficient for representing complicated circuits, whereas others over simplify the modeling by neglecting high-order effects occurring at high frequencies (i.e., skin and proximity effects, eddy currents, etc.) [26]. In this regard, several papers in the literature present contributions to explain the trend of the resistance (R) and the inductance (L) versus frequency curves associated with IC interconnects by analyzing the variation of the current flow distribution within the cross section of the traces [8, 22, 23]. Nevertheless, the available methods are limited in bandwidth since the current flow is only considered to vary following a single equation. Furthermore, there is a common practice to associate all the resistance and inductance to the signal trace, neglecting the variation of the current distribution within the ground plane. As a consequence, for wide frequency ranges, simplified models for the RLGC elements yield inaccurate results [14]. This aspect is particularly important when considering relatively long interconnects such as those used for global signal distribution networks. This is due to the fact that, for instance, underestimating the impact of effects associated with the series parasitic may create incorrect expectations about the performance of a link [19, 24]. In all cases, reliable models are necessary in order to understand and quantify the impact of high-order effects at microwave frequencies such as those introduced by the resistance and the inductance [5, 25]. In this work, a model and parameter extraction strategy is presented including skin and proximity effects, as well as the eddy current induced in the ground metal layers by the traveling electromagnetic waves. The model allows to accurately represent the performance of on-chip interconnects by considering the physically expected variation of the series parasitic with frequency.

2 Theoretical Framework

Figure 1 shows the stack-up defining the different metal layers within a generic IC. In this figure, the ground plane is located at the Metal-3 layer. This plane shields the upper interconnects from the silicon substrate, whereas the dielectric \(\hbox {SiO}_{2}\) layer establishes the separation of the ground plane from the interconnects on top. In general, the performance of the interconnect is strongly dependent on the properties of the materials: in this case, the metal, the \(\hbox {SiO}_{2}\) insulator, and the geometry of the structure. The latter is defined by the trace thickness t, the trace width w, the dielectric height h, and the ground plane thickness \(t_\mathrm{g}\) and width \(w_\mathrm{g}\).

Fig. 1
figure 1

Stack-up for a generic IC showing the different metal layers and illustrating the configuration of the electric and magnetic fields when a wave is propagating in TEM mode

Full size image

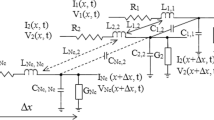
When a signal is propagating through an interconnect, the electric and magnetic fields are formed in the dielectric and conductor materials. For practical interconnects, most of the electromagnetic field is confined between the signal trace and the ground plane [9]; however, some of the field also interacts with the conductor materials forming the ground plane and even with the Si substrate. Hence, notice in Fig. 1 that the interaction of the magnetic field with the Metal-2 originates eddy current loops within this metal layer. Basically, this effect increases the conductor losses and the inductance in a transmission line [20, 27, 28]. A commonly used model to represent the eddy current effect in transmission lines was presented in [24] and illustrated in Fig. 2.

Fig. 2
figure 2

Equivalent circuit used to incorporate into the RLGC model the eddy current effect occurring in the ground plane of an interconnect. The model considers a homogeneous section presenting a length \(\Delta l\) much shorter than the wavelength of the propagating signal

Full size image

In Fig. 2, the elements represent the following per-unit-length parameters: \(R_\mathrm{s}\) is the resistance of the signal trace, \(R_\mathrm{g}\) is the resistance of the ground plane, and \(L_\mathrm{TL},C\), and G are the self-inductance, the capacitance, and the conductance of the transmission line, respectively. In this model, the parameters that account for the parasitic currents induced in the ground plane by the time-varying fields are \(L_\mathrm{eddy}\) and \(R_\mathrm{eddy}\), which are, respectively, the resistance and inductance associated with the eddy current loops in the ground plane and the Si substrate. Therefore, the equation that relates the R and L parameters in the conventional RLGC model to the model including the eddy current effects is [24]:

$$\begin{aligned} R+j\omega L=R_\mathrm{TL} +j\omega L_\mathrm{TL} +\frac{m^{2}\omega ^{2}}{R_\mathrm{eddy} +j\omega L_\mathrm{eddy} } \end{aligned}$$
(1)

which can be separated into real and imaginary parts to yield:

$$\begin{aligned} R+j\omega L=R_\mathrm{TL} +\frac{\omega ^{2}\left( {\frac{m^{2}}{R_\mathrm{eddy} }} \right) }{1+\omega ^{2}\left( {\frac{L_\mathrm{eddy} }{R_\mathrm{eddy} }} \right) ^{2}}+j\omega \left( {L_\mathrm{TL} +\frac{\omega ^{2}\left( {\frac{m^{2}}{R_\mathrm{eddy} }} \right) \left( {\frac{L_\mathrm{eddy} }{R_\mathrm{eddy} }} \right) }{1+\omega ^{2}\left( {\frac{L_\mathrm{eddy} }{R_\mathrm{eddy} }} \right) ^{2}}} \right) \end{aligned}$$
(2)

where \(R_\mathrm{TL}=R_\mathrm{s}+R_\mathrm{g}\). In (2), the resistance and inductance due to eddy current effects can be calculated by using the formulas proposed in [24]. For instance, \(R_\mathrm{eddy}\) is calculated by:

$$\begin{aligned} R_\mathrm{eddy} =R_\mathrm{DCe} +R_\mathrm{ACe} \end{aligned}$$
(3)

where \(R_\mathrm{DCe}\) is the series resistance component that is independent of frequency, \(R_\mathrm{ACe} =A\sqrt{f}\), and A weights the skin effect. On the other hand, \(L_\mathrm{eddy}\) has previously considered to be constant [20, 24, 27, 28]. Even though this latter assumption results in a simplified modeling approach that enables the easy determination of the associated parameters, severe errors may be introduced in simulation results, particularly when the phase is important. For this reason, in this work it is proposed an improved model where the frequency dependence of the inductance components is considered. For instance, for \(L_\mathrm{eddy}\), when the impact of the skin effect is taken into consideration it is possible to write [9]:

$$\begin{aligned} L_\mathrm{eddy} =L_\mathrm{e} +\frac{R_\mathrm{ACe} }{\omega }=L_\mathrm{e} +\frac{A}{2\pi \sqrt{f}} \end{aligned}$$
(4)

where the first term in the second member, \(L_\mathrm{e}\), is the inductance described in [24], whereas the second term can be defined as the inductance related to the skin effect. Notice that this term also involves the A parameter included in the resistance model in (3). Once these parameters are defined, it is necessary to identify the different variations that the R and L present depending on the impact of the skin effect on the effective area through which the current is flowing. In this paper, three frequency ranges are identified: low-, medium- and high-frequency ranges [8, 22, 23].

Fig. 3
figure 3

Conceptual depiction of the current distribution for different frequency ranges. Notice that this distribution not only modifies the resistance but also the inductance of the interconnect

Full size image

2.1 Low-Frequency Range

For the low-frequency range (Region I in Fig. 3), the current is flowing within the whole cross section of the signal strip and the ground plane. In this regard, the resistance at low frequencies can be calculated as the sum of the resistance of the signal strip (\(R_\mathrm{s})\) and that of the ground plane (\(R_\mathrm{g})\); this is:

$$\begin{aligned} R_{LF} =R_\mathrm{s0} +R_\mathrm{g0} \end{aligned}$$
(5)

For the case of the inductance, \(L_\mathrm{TL}\) of a planar and homogeneous TL is associated with the current loop formed along its length by the signal and ground paths. Thus, L is comprised by two parts: the internal (\(L_{\mathrm{int}})\) and the external inductance (\(L_{\mathrm{ext}})\) [9]. Based on this concept, a model based on current loops is used to represent the inductance [6]. In Fig. 3, three inductances connected in parallel \(L_{1}, L_{2}\), and \(L_{3} (L_{1}=L_{3}\) for a symmetrical TL) were used to represent the total inductance of the transmission line. Each one of these inductances is thus associated with a loop that exhibits an effective area depending mainly on the distribution of the current in the ground plane. Therefore, at low frequencies the outer inductance components (i.e., \(L_{1}\) and \(L_{3})\) are originated by a loop with larger transverse area than that corresponding to \(L_{2}\) since the associated current in the ground plane is farther from the signal trace. Thus, when the TL operates in Region I, it can be assumed that the current is homogeneously distributed across of the area of the signal trace and ground plane yielding a maximum value for the internal inductance since the current loops cover from the top of the signal trace to the bottom of the ground plane. In fact, the loops associated with \(L_{1}\) and \(L_{3}\) present a maximum area when the interconnect operates in this region. Hence, in this case, \(L_\mathrm{s}\) and \(L_\mathrm{g}\) present constant values \(L_\mathrm{s0}\) and \(L_\mathrm{g0}\), respectively, which can be calculated by:

$$\begin{aligned} L_{LF} =L_\mathrm{s0} +L_\mathrm{g0} =L_0 \end{aligned}$$
(6)

Bear in mind that at low frequencies the eddy current effect can be neglected due to the relative small magnitude when compared with the other inductance components. Hence, in this range the equivalent series impedance of the transmission line can be expressed as:

$$\begin{aligned} R_{LF} +j\omega L_{LF} \approx R_0 +j\omega L_0 \end{aligned}$$
(7)
Fig. 4
figure 4

Full-wave simulations showing the change in the current distribution at the bottom of the ground plane within Region III; notice that \(w_{a }> w_{b}\). The simulation was performed with w = 2 \(\upmu \hbox {m}, h = 1 \,\upmu \hbox {m}\), and \(t=t_\mathrm{g} = 1\,\upmu \hbox {m}\)

Full size image

2.2 Medium-Frequency Range

Figure 3 shows a sketch of the current distribution effects when the interconnect operates within the medium-frequency range, which occurs once the effective width of the cross section where the current is flowing within the ground plane starts decreasing as f increases. An equation that allows to determine the transition frequency from the low- to the medium-frequency range is [8]:

$$\begin{aligned} f_\mathrm{MF} =\frac{R^{\prime }_{p0} }{\mu }\left( {2.4+0.12\hbox {ln}\left( {1+\frac{w}{h}} \right) +0.1\hbox {ln}\left( {1+\frac{w_g }{h}} \right) } \right) \end{aligned}$$
(8)

where \(R{\prime }_{p0} =R_\mathrm{s0} R_\mathrm{g0} /\left( {R_\mathrm{s0} +R_\mathrm{g0} } \right) \) and \(\mu \) is the magnetic permeability of the surrounding media. In this case, when the Region II takes place, \(R_\mathrm{TL}\) is expected to increase with \(\sqrt{f}\) until the effective width of the interconnect reaches a minimum (\(w_{\mathrm{gmin}})\), which occurs when the current within the ground plane is confined just below the signal strip. In other words, within this region it is assumed that the width of the section where the current is flowing in the ground suffers no side reduction beyond \(w_{\mathrm{gmin}}\). Therefore, when only considering variations in the ground plane, it is expected that \(R_\mathrm{TL}\) remains approximately constant once fincreases beyond this point. However, a slight reduction in the effective area of the ground plane is observed when performing full-wave simulations as those presented in Fig. 4. Notice that the simulations show that the cross-sectional part of the ground plane when \(f_{\mathrm{gsat}}\) is reached is not rectangular. In fact, a different distribution of current in the ground is noticeable at two different frequencies \(f_{a}\) = 10 GHz and \(f_{b}\) = 20 GHz. Nevertheless, for practical purposes and considering this particular example, both frequencies belong to Region III since still a considerable amount of current is flowing at the bottom of the ground plane.

Now, once f increases up to a point where \(\delta > t_\mathrm{g}\), a reduction in the effective thickness of the ground plane is observed as f increases. This originates a confinement of the current concentration on top of the ground plane (see Region IV), proportionally increasing \(R_\mathrm{g }\) with \(\sqrt{f}\); thus, most of the current is confined to the upper section of the ground plane. An equation involving all these effects was proposed in [7] and presented below:

$$\begin{aligned} R_\mathrm{m} =R_\mathrm{s0} +R_g =R_{S0} +\frac{f}{k_1 f+k_2 \sqrt{f}+k_3 } \end{aligned}$$
(9)

where \(k_{1},k_{2}\), and \(k_{3}\) are constants related to the geometry of the ground plane, and the skin effect constants used to model the current distribution in the ground plane. On the other hand, as mentioned above, the inductance is modeled by current loops.

As f increases, the current in the ground plane is confined near below the signal line and reduces the transverse area of the loops associated with \(L_{1}\) and \(L_{3}\), which in turn reduces the total inductance in Region II. Once f rises up to a value so high that the interconnect is operating in Region III, the external inductance exhibits its minimum value, which remains constant from this frequency region on. Furthermore, the internal inductance remains approximately constant; however, a slight reduction of the current flow at the ground plane could occur as shown in Fig. 4. On the other hand, in Region IV, the skin effect modifies the effective thickness of the ground plane which reduces the equivalent inductance. A closed-form formula involving all the current distribution effects in the ground plane is [27]:

$$\begin{aligned} L_\mathrm{m} =L_\mathrm{extm} +\frac{1}{2\pi \left( {k_1 f+k_2 \sqrt{f}+k_3 } \right) } \end{aligned}$$
(10)

where \(L_\mathrm{extm} =L_\mathrm{s0} +L_{\mathrm{ext}} \), is the constant inductance in the medium-frequency range, \(L_\mathrm{s0}\) is the internal inductance of the signal trace, and \(L_{\mathrm{ext}}\) is the external inductance of the single-ended transmission line. In order to model the losses associated with the eddy current effects, consider that part of the magnetic field is forming current loops on metal layers adjacent to ground plane. In this regard, additional losses contributing to the series parasitic are included, \(R_\mathrm{eddy}\) and \(L_\mathrm{eddy}\). Notice that both parameters are frequency dependent. In this case, based on (3), \(R_\mathrm{eddy} =R_\mathrm{ACe} =A\sqrt{f}\), and (4), the terms in (2) are frequency dependent. Hence, combining these equations yields:

$$\begin{aligned} \frac{L_\mathrm{eddy} }{R_\mathrm{eddy} }=a_\mathrm{MF} \frac{1}{\sqrt{f}}+\frac{1}{f} \end{aligned}$$
(11)

and

$$\begin{aligned} \frac{m^{2}}{R_\mathrm{eddy} }=b_\mathrm{MF} \frac{1}{\sqrt{f}} \end{aligned}$$
(12)

where \(a_\mathrm{MF} =L_\mathrm{e} /A\) and \(b_\mathrm{MF} =m^{2}/A\). Thus replacing (11)–(12) into (2), an accurate expression for the equivalent series impedance of the transmission line within the medium-frequency range can be written including the eddy current effect; this is:

$$\begin{aligned} R_\mathrm{MF} +j\omega L_\mathrm{MF}= & {} R_\mathrm{m} +\frac{\omega ^{2}\left( {b_\mathrm{MF} \frac{1}{\sqrt{f}}} \right) }{1+\omega ^{2}\left( {a_\mathrm{MF} \frac{1}{\sqrt{f}}+\frac{1}{f}} \right) ^{2}}\nonumber \\&+j\omega \left( {L_\mathrm{m} +\frac{\omega ^{2}\left( {b_\mathrm{MF} \frac{1}{\sqrt{f}}} \right) \left( {a_\mathrm{MF} \frac{1}{\sqrt{f}}+\frac{1}{f}} \right) }{1+\omega ^{2}\left( {a_\mathrm{MF} \frac{1}{\sqrt{f}}+\frac{1}{f}} \right) ^{2}}} \right) \end{aligned}$$
(13)

2.3 High-Frequency Range

Once the frequency increases up to a point where the skin depth is comparable to the dimensions of the signal trace, the resistances and inductances associated with each conductor forming the transmission line become frequency dependent. This range is referred to as the high-frequency range (i.e., Region V) and becomes apparent at a minimum frequency calculated by means of [8]:

$$\begin{aligned} f_\mathrm{HF} =\frac{a}{\pi \mu \sigma t^{2}} \end{aligned}$$
(14)

where

$$\begin{aligned} a= & {} 0.8+0.48\hbox {ln}\left( {1+100\frac{t}{h}} \right) \hbox {ln}\left( {1+8\frac{h}{w}} \right) +0.6\left( {\frac{t}{w}} \right) ^{2}\left( {1+\frac{h}{w}} \right) \nonumber \\&-0.24\frac{\log _2 \left( {\frac{t}{h}} \right) }{1+\frac{w}{8h}}-0.24\left( {\log _2 \left( {\frac{w_g }{h}} \right) -5} \right) +0.002\frac{w_g }{h} \end{aligned}$$
(15)

where \(\sigma \) is the metal conductivity. In Region V, the area through which the current flows within the signal strip decreases with frequency. Therefore, the internal inductances associated with the signal and ground conductors vary with f. In this case, the expression used for modeling the resistance and inductance of planar transmission lines can be used [7], these are:

$$\begin{aligned} R_h \approx k_S \sqrt{f}+k_g \sqrt{f}=k_T \sqrt{f} \end{aligned}$$
(16)

and

$$\begin{aligned} L_h \approx \frac{k_S }{2\pi \sqrt{f}}+\frac{k_g }{2\pi \sqrt{f}}+L_\mathrm{ext} =\frac{k_T }{2\pi \sqrt{f}}+L_\mathrm{ext} \end{aligned}$$
(17)

where \(k_T =k_S +k_g,k_\mathrm{s}\) and \(k_\mathrm{g}\) are the skin effect constants for the signal strip and the ground plane, respectively. Similarly to medium-frequency range, additional losses introduced by the eddy current effects can be included. These losses are different from those corresponding to the low- and medium-frequency ranges because the fast time variation of the magnetic field now induces currents that can no longer be neglected. Thus, replacing (16) and (17) into (2), and based on similar relations as that expressed in (13), the total resistance and inductance including eddy current effects is calculated by:

$$\begin{aligned} R_\mathrm{HF} +j\omega L_\mathrm{HF}= & {} R_h +\frac{\omega ^{2}\left( {b_\mathrm{HF} \frac{1}{\sqrt{f}}} \right) }{1+\omega ^{2}\left( {a_\mathrm{HF} \frac{1}{\sqrt{f}}+\frac{1}{f}} \right) ^{2}}\nonumber \\&+j\omega \left( {L_h +\frac{\omega ^{2}\left( {b_\mathrm{HF} \frac{1}{\sqrt{f}}} \right) \left( {a_\mathrm{HF} \frac{1}{\sqrt{f}}+\frac{1}{f}} \right) }{1+\omega ^{2}\left( {a_\mathrm{HF} \frac{1}{\sqrt{f}}+\frac{1}{f}} \right) ^{2}}} \right) \end{aligned}$$
(18)

This completes the new modeling approach. The experimental validation is illustrated afterward.

3 Prototype and Measurements

Several microstrip lines with different lengths, widths, and dielectric thickness were designed and fabricated using a 0.35 \(\upmu \hbox {m}\) RF-CMOS manufacturing process. These lines were made of aluminum in the Metal-4 level with widths of 2 and 4 \(\upmu \hbox {m}\), and lengths of 400 and 1000 \(\upmu \hbox {m}\). For these structures, the ground plane was fabricated in the Metal-3 and Metal-1 layer levels, which yields that the height of the \(\hbox {SiO}_{2}\) dielectric is \(h = 1\,\upmu \hbox {m}\) and \(h= 3\,\upmu \hbox {m}\), respectively. For the lines with \(h= 1\,\upmu \hbox {m}\), the thickness of the ground plane is \(t_\mathrm{g} = 640 \hbox { nm}\), whereas for those with h = 3 \(\upmu \hbox {m}\) the metal thickness is \(t_\mathrm{g} = 665 \hbox { nm}\). In all cases, the signal trace presents a nominal thickness \(t= 925\) nm and the ground plane width is 300 \(\upmu \hbox {m}\).

Figure 5 shows photographs of the fabricated microstrip lines. Notice that ground-signal-ground (GSG) pad terminations were included in the design so that coplanar probes presenting a pitch of 150 \(\upmu \hbox {m}\) can be used for performing the corresponding S-parameter measurements. The experimental data were collected within the frequencies ranging from 0.01 to 40 GHz. For this purpose, a vector network analyzer (VNA) and GSG coplanar probes were used. The VNA was previously calibrated up to the probe tips by applying a line-reflect-match (LRM) algorithm and an impedance-standard-substrate (ISS) provided by the probe manufacturer. In addition, a line–line de-embedding procedure was applied to eliminate the parasitics introduced by the associated pad-to-line discontinuities [16].

Fig. 5
figure 5

Photographs showing the fabricated test structures at different interconnect levels: a Metal-3 (\(h = 1\,\upmu \hbox {m}\)), and b Metal-1 (\(h = 3\, \upmu \hbox {m}\))

Full size image
Fig. 6
figure 6

Experimental a R and b L versus f curves for an interconnect in the Metal-1 level; the extracted parameters are included in the figure

Full size image
Fig. 7
figure 7

Magnitude of a \(S_{11}\) and b \(S_{22}\) for an interconnect in Metal-1 level

Full size image
Fig. 8
figure 8

Experimental R and L versus f curves for the fabricated lines

Full size image

3.1 Results and Discussion

The experimental R and L versus frequency curves straightforwardly associated with the RLGC model can be obtained from the measured S-parameters by using: R = Re( \(\gamma Z_\mathrm{c})\) and L = Im(\(\gamma Z_\mathrm{c})/2 \pi f\). Afterward, the parameters associated with the proposed model were extracted for the different frequency ranges. Figure 6 presents the model–experiment correlation for the resistance (Fig. 6a) and inductance (Fig. 6b) of a microstrip transmission line with \(w = 4 \,\upmu \hbox {m}\) and \(t = 3\, \upmu \hbox {m}\), as well as the extracted parameters. Notice in this figure that the low- to medium-frequency transition was indicated after performing a calculation using (8) (\(f_\mathrm{MF} \approx \) 0.3 GHz). Thus, the parameters corresponding with the low-frequency range were extracted using data up to this frequency. On the other hand, the parameters corresponding to the medium-frequency range were calculated from \(f_\mathrm{MF }\hbox { to } f_\mathrm{HF}\). In this regard, (14) was applied, and the value of the starting frequency for the high-frequency range is 29 GHz. Finally, the parameters corresponding to the high-frequency range were obtained in a similar way but up to 40 GHz. Hence, when implementing the model for all the considered bandwidth, it was possible to represent with accuracy the resistance and the inductance in a consistent way.

A comparison of the proposal and the model proposed in [12] is presented in Fig. 7. For this purpose, the model parameters used in [24] were obtained by curve fitting. Additionally, the S-parameters were reconstructed using: \(G = \hbox {Re}({ \gamma /Z}_\mathrm{c})\) and \(C = \hbox {Im}({\gamma /Z}_\mathrm{c})/2\pi f\), and obtaining \(\gamma \) and \(Z_\mathrm{c}\) from the RLGC parameters [29]. In Fig. 7a, the magnitude of \(S_{11}\) is presented. Notice that both methods present similar accuracy. Nevertheless, the improved representation of the inductive term achieved by the proposal allowed to achieve better accuracy for the transmission parameter. This can be seen in Fig. 7b, where the magnitude of \(S_{21 }\)up to 40 GHz is illustrated. Notice the different curve trend exhibited by the curve obtained after applying the model proposed in [12]. This is due to the assumption of constant mutual inductance assumed in this previously reported approach. Therefore, a piecewise model allows highest accuracy instead the simplified one-region model because each section can be analyzed separately. This allows for an adequate representation of the current flow variation, which tends to change in each frequency section due to the effect of the eddy current loops in the ground plane.

Table 1 Extracted model parameters for R and L
Full size table

Figure 8 shows the corresponding model–experiment correlation for R and L up to 40 GHz for all the fabricated lines. As can be seen, an accurate representation of the experimental data was achieved. This also points out the fact that using the frequency transitions proposed in [8], an easy identification of the frequency ranges can be achieved.

Table 1 summarizes the obtained parameters for the fabricated lines. From Table 1, it is interesting to observe that each one of the extracted parameters presents a variation with geometry. As expected, \(R_\mathrm{s0}\) tends to increase as the signal trace width decreases. On the other hand, notice that this parameter presents a slight change with the dielectric thickness, which is also an expected result at low frequencies because the current flow remains almost constant in this frequency range. On the other hand, the parameters related with the variation of the current flow in the signal trace and the ground plane (i.e., \(k_{1}, k_{2}, k_{3}\), and \(k_{T})\) are dependent on the geometry of the structure. Notice that higher values are obtained in \(k_{2}\) and \(k_{T}\) with thin dielectric thickness, while \(k_{1}\) and \(k_{3 }\)are decreasing. Additionally, all the parameters describing the current variation take the higher value when the width of the conductor decreases. In this regard, if the width of the signal trace is reduced, the resistance and inductance are more sensitive to changes in the current distribution within the signal trace and ground plane because the area through which the current is flowing is small. Additionally, if the dielectric height is thin, highest electric field intensity is observed between the signal trace and the ground plane. In this case, the corresponding impact within the medium-frequency range decreases in comparison with the skin effect at the highest considered frequencies.

Additionally, the parameters associated with the eddy current effect (i.e., \(a_\mathrm{MF}, b_\mathrm{MF}\), \(a_\mathrm{HF}\) and \(b_\mathrm{HF})\), listed in the table, present higher values when the dielectric thickness increases because more intense magnetic field interacts with the metal layer below the ground plane. A similar result can be obtained when the width of the signal trace is reduced; if the width of the signal trace decreases, more magnetic flux impacts the metal layers below the ground plane, i.e., Metal-2 for the ground plane in Metal-3, and Si substrate for ground plane in Metal-1 (see Fig. 1).

Finally, it is important to point out the fact that the parameters used here can be used for the implementation of scalable models. In this regard, it is possible to perform the parameter extraction in order to predict series parasitic effects for structures belonging to a given technology by carefully designing a test chip including some geometries, using the models proposed here, and then using interpolation techniques.

4 Conclusions

This paper presents a continuous model divided by frequency sections that allows identifying the different operation regions affecting the frequency dependence of the series resistance and inductance of on-chip interconnects was carried out. The model allows incorporating the skin, proximity and eddy current effects into the interconnect model. Moreover, the models by frequency regions, allow for the representation of experimental data in a consistent way up to 40 GHz, and an accurate representation of the series resistance and parasitic inductance occurring in IC interconnects when guiding high-frequency signals.