Robust Fault Detection and Control for Continuous-Time Switched Systems with Average Dwell Time

Abstract

This paper is concerned with fault detection and control problem for continuous-time switched systems with average dwell time. Attention is focused on designing a fault detection observer and controller such that the impact of the unknown inputs and the faults on the system is minimized in the sense of $H_{\infty }$ norm. By employing multiple Lyapunov function and average dwell time techniques, a sufficient condition for the existence of such an observer and controller is exploited in terms of certain linear matrix inequalities. Finally, two illustrative examples are provided to show the effectiveness and applicability of the proposed results.

1 Introduction

Switched systems are a special class of hybrid systems. They are composed of a finite number of subsystems with switching rules supervising their interworking. Switched systems can be used to efficiently model many practical systems what motivates their study. In fact, practical systems are inherently multimodels needed to describe their behavior. In particular, chemical processes, transportation systems, industrial process control, intelligent vehicle, and many other plants meet this description [1, 2, 10]. Common Lyapunov function [17], multiple Lyapunov function, and average dwell time (ADT) techniques have been proposed to study switched systems. Hence, many problems are treated such as stability analysis, stabilization [5, 6], dynamic output feedback control [7, 27], $L_{2}$ gain and $H_{ \infty }$ control [25, 26], $H_{\infty }$ filter problem [19], and estimator design [16].

The fault detection (FD) in dynamic systems has been an active field of research during the past decades because of an increasing demand for higher safety and reliability standards [2, 22]. In particular, the fault detection and fault-tolerant control problems for switched systems have also attracted considerable attention [10, 18, 21]. The basic idea of the model-based approaches of FD is to use state observer or filter to construct a residual signal. On this basis, determine a residual evaluation function to compare with a predefined threshold. When the function has a value larger than the threshold, an alarm of faults is generated. On the other hand, it is well known that control inputs, unavoidable unknown inputs, and faults are coupled in many industrial systems. This fact can lead to potential sources of false alarm. This means that FD systems have to be robust to control inputs and unknown inputs and, at the same time, enhance the sensitivity to the faults [8]. Many approaches have been applied in FD area such as robust $H_{\infty }$ optimization scheme [14], $H_{\infty }$ filtering method [2], and minimum sensitivity realization [15].

In the last decade, average dwell time (ADT) technique was one of the most popular method to deal with many problems involving switched systems. The so-called average dwell time means that the average time interval between consecutive switching is no less than a specified constant. The motivation comes from that in practice, the switching frequency of most physical systems is limited and the system components cannot support too frequent switching [33]. Thus, it is meaningful to design the switching law satisfying an ADT constraint to meet control objectives. Recently, an enormous growth of interest in using the ADT approach to deal with FD and fault-tolerant control (FTC) problems is developed. In [33], the dwell time approach is used to investigate the robust control and fault detection problems by using the multiobjective optimization technique. In [22], the problem of robust fault detection filter design for continuous-time switched linear systems with state delays is formulated as an $H_{\infty }$ filtering problem. In [31] the problem of fault detection for switched systems under the asynchronous switching is investigated. The ADT is dependent on both state delay and switching delay of fault detection filters. In [23], the problem of output feedback stabilization with faulty actuators is studied based on the piecewise Lyapunov function method combined with the ADT.

In the present work, the fault detection problem is investigated for continuous-time switched linear systems by using the multiple Lyapunov function and average dwell time approach. A sufficient condition for the $H_{\infty }$ fault detection observer is exploited in the formation of LMI. Then, based on the obtained condition, a desired fault detection observer and controller are constructed. The main feature of the proposed results is the single-step design for observer-based $H_{\infty }$ controller and observer design problem, which overcomes the drawback induced by using two-step procedure. In addition, all the variables are put together in an augmented unknown one matrix to avoid the possibility to obtain some product terms between Lyapunov matrix $P_{i}$ and observer and controller matrices. Hence, the conservatism could be reduced by our proposed approach. A simulation example and an application to a pulse-width-modulation (PWM)-driven boost converter are given to show the effectiveness of the proposed method. The remainder paper is organized as follows. Section 2 deals with the problem statement, while some preliminary results are recalled in Sect. 3. Section 4 is devoted to give sufficient conditions building an observer and controller, these last are obtained by using multiple Lyapunov function and $H_{\infty }$ methods. To demonstrate the validity of the proposed approach, two examples are given in Sect. 5 that is followed by a conclusion in the last section.

Notations Standard notations are used in this paper. For a matrix A, $A^{T}$ denotes its transpose. $A > 0$ and $A < 0$ denote positive-definite and negative-definite matrices, respectively. The symbol $*$ within a matrix represents the symmetric entries. 0, $\mathbb {I}$ denote the null matrix and identity matrix with appropriate dimensions, respectively.

2 Problem Statement

Consider the following continuous-time switching system:

$$\begin{aligned} \left\{ \begin{aligned} \dot{x}(t)&=A_{\sigma (t)}x(t)+B_{\sigma (t)}u(t)+E_{\sigma (t)}d(t)+F_{\sigma (t)}f(t)\\ y(t)&=C_{\sigma (t)}x(t)+N_{\sigma (t)}d(t)+M_{\sigma (t)}f(t), \end{aligned}\right. \end{aligned}$$

(1)

where $x(t)\in \mathbb {R}^{n}$ is the state, $u(t)\in \mathbb {R}^{m}$ is the control input, $y(t)\in \mathbb {R}^{p}$ is the output, $d(t)\in \mathbb {R}^{g}$ is the unknown input vector (including disturbance, noise or structured model uncertainty), $f(t)\in \mathbb {R}^{q}$ is the fault and $\sigma \in \mathcal {I}=\left\{ 1,2,\ldots ,N\right\}$ is the switching signal that specifies which subsystem will be activated and N denotes the number of subsystems.

We assume the switching signal $\sigma (t)$ time-dependent, that is,

$$\begin{aligned} \sigma (t):\left\{ (t_{0}, \sigma (t_{0})), (t_{1}, \sigma (t_{1})),\ldots , (t_{k}, \sigma (t_{k})),\ldots ,|k=0,1,\ldots \right\} , \end{aligned}$$

where $t_{0}$ denotes the initial time, and $(t_{k}, \sigma (t_{k}))$ means that the $\sigma (t_{k})$th subsystem is activated during $t\in [t_{k},t_{k+1})$. k denotes the switching ordinal number. $A_{\sigma (t)}$, $B_{\sigma (t)}$, $C_{\sigma (t)}$, $E_{\sigma (t)}$, $F_{\sigma (t)}$, $N_{\sigma (t)}$, and $M_{\sigma (t)}$ are given constant matrices with appropriate dimensions for all $\sigma \in \mathcal {I}$. We denote matrices associated with $\sigma (t)=i$ by $A_{\sigma (t)}=A_{i}$, $B_{\sigma (t)}=B_{i}$, $C_{\sigma (t)}=C_{i}$, $E_{\sigma (t)}=E_{i}$, $F_{\sigma (t)}=F_{i}$, $N_{\sigma (t)}=N_{i}$ and $M_{\sigma (t)}=M_{i}$. Suppose that at the switching instants $t_k$, system (1) switches from the jth subsystem to the ith subsystem, thus $\sigma ( t_k^-) = j$, $\sigma (t_k^+) = \sigma (t_k) = i$.

In this paper, we are interested in the synthesis of an observer in order to detect faults when they occur in the switching system (1). Hence, consider the following switching observer:

$$\begin{aligned} \left\{ \begin{aligned} \dot{\hat{x}}(t)&=G_{\sigma (t)}\hat{x}(t)+L_{\sigma (t)}y(t)\\ \hat{y}(t)&=C_{\sigma (t)}\hat{x}(t), \end{aligned} \right. \end{aligned}$$

(2)

where $G_{\sigma (t)}\in \mathbb {R}^{n\times n}$, $L_{\sigma (t)}\in \mathbb {R}^{n\times p}$ are the observer matrices to be designed.

By using the following observer-based controller structure, the control can also be designed to stabilize the system in closed-loop despite the presence of perturbation and fault:

$$\begin{aligned} u(t)=K_{\sigma (t)}\hat{x}(t). \end{aligned}$$

(3)

The observer-based residual generator is defined by:

$$\begin{aligned} r(t)= & {} V_{\sigma (t)}(y(t)-\hat{y}(t)). \end{aligned}$$

(4)

Matrices $V_{i}$ and $K_{i}$ are also to be computed. By combining the above structures of the observer, the controller and the residual, and defining $e(t)={x}(t)-\hat{x}(t)$, the following augmented switched system is obtained:

$$\begin{aligned} \mathcal {S}: \left\{ \begin{aligned} \dot{\tilde{x}}(t)&=\tilde{A}_{i}\tilde{x}(t)+\tilde{B}_{i}\omega (t) \\ r(t)&=\tilde{C}_{i}\tilde{x}(t)+\tilde{D}_{i}\omega (t), \end{aligned} \right. \end{aligned}$$

(5)

where

$$\begin{aligned} \left\{ \begin{aligned}&\tilde{A}_{i}=\begin{bmatrix} A_{i}+B_{i}K_{i}&\quad -B_{i}K_{i}\\ A_{i}-L_{i}C_{i}+B_{i}K_{i}-G_{i}&\quad G_{i}-B_{i}K_{i}\end{bmatrix},\\&\tilde{B}_{i}=\begin{bmatrix} E_{i}&\quad F_{i}\\ E_{i}-L_{i}N_{i}&\quad F_{i}-L_{i}M_{i}\end{bmatrix} , \\&\tilde{C}_{i}=\begin{bmatrix} 0&V_{i}C_{i}\end{bmatrix}, \,\, \tilde{D}_{i}=\begin{bmatrix} V_{i}N_{i}&\quad V_{i}M_{i}\end{bmatrix}; \\&\tilde{x}(t)=\begin{bmatrix} x(t)\\ e(t)\end{bmatrix},\quad \omega (t)=\begin{bmatrix} d(t)\\ f(t)\end{bmatrix}. \end{aligned} \right. \end{aligned}$$

(6)

3 Preliminary Results

As used in the literature of fault detection [1, 22, 32], the identification of the fault f(t) is not necessary. One can use the following residual evaluation function:

$$\begin{aligned} J_{r}(T_e)=\left\| r(t)\right\| _{2}=\left( \int _{t_{0}}^{t_{0}+T_e}r^{T}(\tau )r(\tau )\mathrm{d}\tau \right) ^{1/2}, \end{aligned}$$

(7)

where $t_{0}$ denotes the initial evaluation time instant. $T_e$ is the evaluation time steps. The occurrence of faults can be detected by comparing $J_{r}(T_e)$ and $J_{th}$ according the following logic relationship:

$$\begin{aligned} J_{r}(T_e)\succ J_{th} \Rightarrow \hbox {Faults} \Rightarrow \hbox {Alarm} \\ J_{r}(T_e)\le J_{th} \Rightarrow \hbox {No Faults}. \end{aligned}$$

The threshold value can be calculated during the fault-free system operation as indicated in [8, 22]:

$$\begin{aligned} J_{th}=\underset{d(t)\in l_{2}[0,+\infty ), f(t)=0}{\sup }\left\| r(t)\right\| _{2}. \end{aligned}$$

(8)

Remark 1

For the fault detection problem, it is not necessary to estimate the fault. By considering the deviation of $J_{r}(T_e)$ between fault-free case and faulty case, we can decide whether or not the fault has occurred. Compared with the fault estimation methods [4, 9], the proposed technique reduces the requirement of a controller/observer and leads to less overall complexity in practice.

The technique of $H_{\infty }$ problem for the augmented switching system (5) with average dwell time consists in ensuring the asymptotic stability of the system for $\omega (t)=0$ while realizing the following condition under zero initial condition $\tilde{x}_{0}=0$, for any nonzero $\omega (t)\in \left[ 0,\infty \right)$ [24]:

$$\begin{aligned} \int _{t_{0}}^{\infty }e^{-\alpha s}r^{T}(s)r(s)\mathrm{d}s\le \gamma ^{2}\int _{t_{0}}^{\infty }\omega ^{T}(s)\omega (s)\mathrm{d}s. \end{aligned}$$

(9)

Remark 2

In the $H_{\infty }$ theory, the input $\omega (t)$ is assumed to be only bounded without any knowledge of its bound. In our case, $\omega (t)$ represents the fault f(t) and the perturbation d(t). No additional assumption is required on these inputs. The idea is to reduce the impact of this exogenous input $\omega (t)$ on the system by reducing as far as possible the scalars $\gamma$ defined by Eq. (9).

Before ending this section, we introduce the following definition and lemma.

Definition 1

[11] For any switching signal $\sigma (t)$ and any $t_{2}\succ t_{1}\succ 0$, let $N_{\sigma }(\tau ,t)$ denotes the number of switching of $\sigma (t)$ on an interval $(t_{1},t_{2})$. If

$$\begin{aligned} N_{\sigma }(\tau ,t)\le N_{0} + \frac{t_{2}-t_{1}}{\tau _{a}} \end{aligned}$$

(10)

holds for a given $N_{0}\ge 0$ and $\tau _{a}$, then the constant $\tau _{a}$ is called the average dwell time ADT and $N_{0}$ the chattering bound. $N_{0}$ must be at least two in the case of ADT switching [13], however, we can assume it to be zero for the simplicity of mathematical manipulation.

Lemma 1

[6]: If there exist function $\phi (t)$ and $\upsilon (t)$ satisfying

$$\begin{aligned} \dot{\phi }(t)\le -\zeta \phi (t)+\kappa \upsilon (t), \end{aligned}$$

then

$$\begin{aligned} \phi (t)\le e^{-\zeta (t-t_{0})}\phi (t_{0})+\kappa \int _{0}^{t-t_{0}}e^{-\zeta \tau }\upsilon (t-\tau )\mathrm{d}\tau . \end{aligned}$$

(11)

4 Main Results

As stated in the previous section, the problem of fault detection and control can be stated as designing a controller/observer unit such that the augmented system (5) is asymptotically stable and the $H_{\infty }$ performance index (9) is satisfied. The objective of this section is to obtain an LMI enabling to synthesize the switching observer together with its corresponding residual and controller. This will make possible fault detection and control of the continuous-time switching system under ADT constraint.

Theorem 1

Given constants $\alpha \succ 0$, $\gamma \succ 0$, $\epsilon _{i}\succ 0$, and $\mu \ge 1$, if there exist positive-definite matrices $\mathcal {P}_{i}$, and any matrices $G_{i}$, $L_{i}$, $K_{i}$ and $V_{i}$, for $i\in \mathcal {I}$ such that

$$\begin{aligned}&\begin{bmatrix} \psi _{i}+\alpha \mathcal {P}_{i}&\quad \mathcal {P}_{i}\tilde{B}_{i}&\quad \tilde{C}_{i}^{T}&\quad \Gamma _{i}^{T}\\ *&\quad -\gamma ^{2}\mathbb {I}&\quad \tilde{D}_{i}^{T}&\quad 0 \\ *&\quad *&\quad -\mathbb {I}&\quad 0 \\ *&\quad *&\quad *&\quad -\mathbb {I} \end{bmatrix}\prec 0\end{aligned}$$

(12)

$$\begin{aligned}&\mathcal {P}_{i}\le \mu P_{j},\,\ \forall (i,j)\in \mathcal {I}\times \mathcal {I},i\ne j \end{aligned}$$

(13)

then the system $\mathcal {S}$ is asymptotically stable with $H_{\infty }$ performance $\gamma$ for any switching signal with average dwell time satisfying

$$\begin{aligned} \tau _{a}\ge \tau ^{*}_{a}=\frac{\ln \mu }{\alpha }, \end{aligned}$$

(14)

where $\psi _{i}=\mathcal {A}_{i}^{T}\mathcal {P}_{i}+\mathcal {P}_{i}\mathcal {A}_{i}-\epsilon _{i}\mathcal {B}_{i}\mathcal {B}_{i}^{T}\mathcal {P}_{i}-\epsilon _{i}\mathcal {P}_{i}\mathcal {B}_{i}\mathcal {B}_{i}^{T}+\epsilon _{i}^{2}\mathcal {B}_{i}\mathcal {B}_{i}^{T}$

$$\begin{aligned} \mathcal {A}_{i}= & {} \begin{bmatrix} A_{i}&\quad 0 \\ A_{i}&\quad 0 \end{bmatrix} ; \quad \mathcal {B}_{i}=\begin{bmatrix} 0&\quad 0&\quad 0&\quad B_{i} \\ 0&\quad 0&\quad -\mathbb {I}&\quad B_{i} \end{bmatrix} ;\quad \\ \Gamma _{i}= & {} \mathcal B_{i}^{T}\mathcal {P}_{i}+\mathcal {K}_{i}\mathcal {C}_{i}; \mathcal {K}_{i}=\begin{bmatrix} G_{i}&\quad L_{i}&\quad 0&\quad 0 \\ K_{i}&\quad 0&\quad 0&\quad 0 \\ 0&\quad 0&\quad G_{i}&\quad L_{i} \\ 0&\quad \quad 0&\quad K_{i}&\quad 0 \end{bmatrix} ; \quad \mathcal {C}_{i}=\begin{bmatrix} 0&\quad \mathbb {I} \\ 0&\quad 0 \\ \mathbb {I}&\quad -\mathbb {I} \\ C_{i}&\quad 0 \end{bmatrix}. \end{aligned}$$

Proof

It is noted that $\tilde{A}_{i}=\mathcal {A}_{i}+\mathcal {B}_{i}\mathcal {K}_{i}\mathcal {C}_{i}$. The asymptotic stability of system $\mathcal {S}$ with $\omega (t)=0$ is firstly established.

For this, assume that condition (12) holds. From (12) and by Schur complement, the following inequality can be obtained:

$$\begin{aligned} \Lambda _{i}=\begin{bmatrix} \Sigma _{i}+\alpha \mathcal {P}_{i}+\tilde{C}_{i}^{T}\tilde{C}_{i}&\;\; \mathcal {P}_{i}\tilde{B}_{i}+\tilde{C}_{i}^{T}\tilde{D}_{i} \\ *&\;\; \tilde{D}_{i}^{T}\tilde{D}_{i}-\gamma ^{2}\mathbb {I} \end{bmatrix}\prec 0, \end{aligned}$$

(15)

where

$$\begin{aligned} \Sigma _{i}= & {} \mathcal {A}_{i}^{T}\mathcal {P}_{i}+\mathcal {P}_{i}\mathcal {A}_{i}-\epsilon _{i}\mathcal {B}_{i}\mathcal {B}_{i}^{T}\mathcal {P}_{i}-\epsilon _{i}\mathcal {P}_{i}\mathcal {B}_{i}\mathcal {B}_{i}^{T}+\epsilon _{i}^{2}\mathcal {B}_{i}\mathcal {B}_{i}^{T}\\ \nonumber&\quad +\left( \mathcal {B}_{i}^{T}\mathcal {P}_{i}\mathcal +\mathcal {K}_{i}\mathcal {C}_{i}\right) ^{T}\left( \mathcal {B}_{i}^{T}\mathcal {P}_{i}\mathcal +\mathcal {K}_{i} \mathcal {C}_{i}\right) . \end{aligned}$$

(16)

It is obvious that $\Lambda _{i}\prec 0$ implies the following inequality:

$$\begin{aligned} \Sigma _{i}+\alpha \mathcal {P}_{i}+\tilde{C}_{i}^{T}\tilde{C}_{i}\prec 0, \end{aligned}$$

(17)

which implies that

$$\begin{aligned} \mathcal {A}_{i}^{T}\mathcal {P}_{i}+\mathcal {P}_{i}\mathcal {A}_{i}-\mathcal {P}_{i}\mathcal {B}_{i}\mathcal {B}_{i}^{T}\mathcal {P}_{i}+\left( \mathcal {B}_{i}^{T}\mathcal {P}_{i}\mathcal +\mathcal {K}_{i}\mathcal {C}_{i}\right) ^{T}\left( \mathcal {B}_{i}^{T}\mathcal {P}_{i}\mathcal +\mathcal {K}_{i} \mathcal {C}_{i}\right) +\alpha \mathcal {P}_{i}\prec 0,\quad \end{aligned}$$

(18)

where the following relationship is used:

$$\begin{aligned} \mathcal {P}_{i}\mathcal {B}_{i}\mathcal {B}_{i}^{T}\mathcal {P}_{i}-\epsilon _{i}\mathcal {B}_{i}\mathcal {B}_{i}^{T}\mathcal {P}_{i}-\epsilon _{i}\mathcal {P}_{i}\mathcal {B}_{i}\mathcal {B}_{i}^{T}+\epsilon _{i}^{2}\mathcal {B}_{i}\mathcal {B}_{i}^{T}+\tilde{C}_{i}\tilde{C}_{i}^{T} \nonumber \\ =\left( \mathcal {P}_{i}\mathcal {B}_{i}-\epsilon _{i}\mathcal {B}_{i}\right) \left( \mathcal {B}_{i}^{T}\mathcal {P}_{i}-\epsilon _{i}\mathcal {B}_{i}^{T}\right) +\tilde{C}_{i}\tilde{C}_{i}^{T}\succ 0. \end{aligned}$$

(19)

Rewriting (18) yields

$$\begin{aligned} \left( \mathcal {A}_{i}+\mathcal {B}_{i}\mathcal {K}_{i}\mathcal {C}_{i}\right) ^{T}\mathcal {P}_{i}+\mathcal {P}_{i}\left( \mathcal {A}_{i}+\mathcal {B}_{i}\mathcal {K}_{i}\mathcal {C}_{i}\right) +\mathcal {C}_{i}^{T}\mathcal {K}_{i}^{T}\mathcal {K}_{i}\mathcal {C}_{i}+\alpha \mathcal {P}_{i}\prec 0, \end{aligned}$$

(20)

which implies that

$$\begin{aligned} (\mathcal {A}_{i}+\mathcal {B}_{i}\mathcal {K}_{i}\mathcal {C}_{i})^{T}\mathcal {P}_{i}+\mathcal {P}_{i}(\mathcal {A}_{i}+\mathcal {B}_{i}\mathcal {K}_{i}\mathcal {C}_{i})+\alpha \mathcal {P}_{i}\prec 0. \end{aligned}$$

(21)

Hence

$$\begin{aligned} \tilde{A}_{i}^{T}\mathcal {P}_{i}+\mathcal {P}_{i}\tilde{A}_{i}+\alpha \mathcal {P}_{i}\prec 0. \end{aligned}$$

(22)

Consider now the following Lyapunov function candidate:

$$\begin{aligned} V_{i}(t)=\tilde{x}^{T}(t)\mathcal {P}_{i}\tilde{x}(t), \end{aligned}$$

(23)

Then, along the trajectory of system (5), we have

$$\begin{aligned} \dot{V}_{i}(t)+\alpha V_{i}(t)= & {} \dot{\tilde{x}}^{T}(t)\mathcal {P}_{i}\tilde{x}(t)+\tilde{x}^{T}(t)\mathcal {P}_{i}\dot{\tilde{x}}(t)+\alpha \tilde{x}^{T}(t)\mathcal {P}_{i}\tilde{x}(t) \nonumber \\= & {} \tilde{x}^{T}(t)(\tilde{A}_{i}^{T}\mathcal {P}_{i}+\mathcal {P}_{i}\tilde{A}_{i}+\alpha \mathcal {P}_{i})\tilde{x}(t). \end{aligned}$$

(24)

Then, according to (22), we obtain

$$\begin{aligned} \dot{V}_{i}(t)+\alpha V_{i}(t)\le 0; \end{aligned}$$

(25)

it follows that

$$\begin{aligned} \dot{V}_{i}(t)\le -\alpha V_{i}(t). \end{aligned}$$

(26)

Let $t_{1},t_{2},\ldots ,t_{k},t_{k+1}\ldots$ denote the switching instants of $\sigma (t)$ over the interval $\left[ t_{0},t\right]$. Integrating inequality (26) from $t_{k}$ to $t_{k+1}$ gives

$$\begin{aligned} V_{i}(\tilde{x}(t_{k+1}))\le V_{i}(\tilde{x}(t_{k}))e^{-\alpha (t_{k+1}-t_{k})}. \end{aligned}$$

(27)

Thus, over the interval $\left[ t_{0},t\right)$ and according to (27) and (13), we have

$$\begin{aligned} V_{i}(\tilde{x}(t))\le & {} e^{-\alpha (t-t_{k})}V_{i}(\tilde{x}(t_{k})) \nonumber \\\le & {} \mu e^{-\alpha (t-t_{k})}V_{i-1}(\tilde{x}(t_{k}^{-})) \nonumber \\\le & {} \cdots \le \mu ^{N_{\sigma }(t_{0},t)}e^{-\alpha (t-t_{0})}V_{0}(\tilde{x}(t_{0})), \end{aligned}$$

(28)

where $t_{k}^{-}$ denotes the switching instant just before $t_{k}$. As the definition of the ADT, $N_{\sigma }(t_{0},t)\le N_{0}+(t-t_{0})/\tau _{a}$, (28) can be written as:

$$\begin{aligned} V_{i}(\tilde{x}(t))\le \mu ^{N_{0}}e^{-(\alpha -ln(\mu )/\tau _{a})(t-t_{0})}V_{0}(\tilde{x}(t_{0})). \end{aligned}$$

(29)

Therefore, if the average dwell time satisfies (14), we conclude that V(t) converges to zero as $t\rightarrow \infty$.

Then, the stability of system $\mathcal {S}$ is deduced.

The second part of the proof can be considered. For this, let any nonzero $\omega (t)\in \left[ 0,\infty \right)$ and zero initial condition $\tilde{x}(0)$. Consider the Lyapunov function candidate as in (23) and set $\Gamma (t)=-r^{T}(t)r(t)+\gamma ^{2}\omega ^{T}(t)\omega (t)$, one has

$$\begin{aligned} \dot{V_{i}}(t)+\alpha V_{i}(t)-\Gamma (t)=\eta ^{T}(t)\Pi _{i}\eta (t), \end{aligned}$$

(30)

where $\eta (t)=\begin{bmatrix}\tilde{x}(t) \\ \omega (t)\end{bmatrix}$ ,    $\Pi _{i}=\begin{bmatrix} \tilde{A}_{i}^{T}\mathcal {P}_{i}+\mathcal {P}_{i}\tilde{A}_{i}+\alpha \mathcal {P}_{i}+\tilde{C}_{i}^{T}\tilde{C}_{i}&\;\; \mathcal {P}_{i}\tilde{B}_{i}+\tilde{C}_{i}^{T}\tilde{D}_{i} \\ *&\;\;\tilde{D}_{i}^{T}\tilde{D}_{i}-\gamma ^{2}\mathbb {I}\end{bmatrix}$

To proof that $\Pi _{i}\prec 0$, we have

$$\begin{aligned} {\Sigma }_{i}-\left( \tilde{A}_{i}^{T}\mathcal {P}_{i}+\mathcal {P}_{i}\tilde{A}_{i}\right) =\mathcal {C}_{i}^{T}\mathcal {K}_{i}^{T}\mathcal {K}_{i}\mathcal {C}_{i}+\left( \mathcal {P}_{i}\mathcal {B}_{i}-\epsilon _{i}\mathcal {B}_{i}\right) \left( \mathcal {B}_{i}^{T}\mathcal {P}_{i}-\epsilon _{i}\mathcal {B}_{i}^{T}\right) \succ 0. \end{aligned}$$

Thus , $\Sigma _{i}\succ \tilde{A}_{i}^{T}\mathcal {P}_{i}+\mathcal {P}_{i}\tilde{A}_{i}$ which implies   $\Sigma _{i}+\tilde{C}_{i}^{T}\tilde{C}_{i}\succ \tilde{A}_{i}^{T}\mathcal {P}_{i}+\mathcal {P}_{i}\tilde{A}_{i}+\tilde{C}_{i}^{T}\tilde{C}_{i}$.

Therefore, ${\Pi }_{i}\prec \Lambda _{i}\prec 0$, and hence

$$\begin{aligned} \dot{V_{i}}(t)\le -\alpha V_{i}(t)+\Gamma (t). \end{aligned}$$

(31)

From Lemma 1, one has

$$\begin{aligned} V_{i}(t)\le e^{-\alpha (t-t_{k})}V_{i}(t_{k})+\int _{t_{k}}^{t}e^{-\alpha (t-s)}\Gamma (s)\mathrm{d}s. \end{aligned}$$

(32)

At the switching instants $t_{0}< t_{1}<t_{2}<\cdots t_{k}<t_{k+1}\cdots <t$ during $\left[ t_{0},t\right)$ and according to (32) and (13), we have the following developments:

$$\begin{aligned} V_{i}(t)\le & {} e^{-\alpha (t-t_{k})}V_{i}(t_{k})+\int _{t_{k}}^{t}e^{-\alpha (t-s)}\Gamma (s)\mathrm{d}s \nonumber \\\le & {} \mu e^{-\alpha (t-t_{k})}V_{i-1}(t_{k}^{-})+\int _{t_{k}}^{t}e^{-\alpha (t-s)}\Gamma (s)\mathrm{d}s \nonumber \\\le & {} \mu e^{-\alpha (t-t_{k-1})}V_{i-1}(t_{k-1})+\mu \int _{t_{k-1}}^{t_{k}}e^{-\alpha (t-s)}\Gamma (s)\mathrm{d}s+\int _{t_{k}}^{t}e^{-\alpha (t-s)}\Gamma (s)\mathrm{d}s \nonumber \\\le & {} \mu \mu e^{-\alpha (t-t_{k-1})}V_{i-2}(t_{k-1}^{-})+\mu \int _{t_{k-1}}^{t_{k}}e^{-\alpha (t-s)}\Gamma (s)\mathrm{d}s+\int _{t_{k}}^{t}e^{-\alpha (t-s)}\Gamma (s)\mathrm{d}s \nonumber \\\le & {} ...............\nonumber \\\le & {} \mu ^{N_{\sigma }(t_{0},t)} e^{-\alpha (t-t_{0})}V_{0}(t_{0})+\mu ^{N_{\sigma }(t_{0},t)}\int _{t_{0}}^{t_{1}}e^{-\alpha (t-s)}\Gamma (s)\mathrm{d}s\nonumber \\&+\cdots +\mu ^{N_{\sigma }(t_{k-1},t)}\int _{t_{k-1}}^{t_{k}}e^{-\alpha (t-s)}\Gamma (s)\mathrm{d}s+\mu ^{N_{\sigma }(t_{k},t)}\int _{t_{k}}^{t}e^{-\alpha (t-s)}\Gamma (s)\mathrm{d}s \nonumber \\= & {} \mu ^{N_{\sigma }(t_{0},t)} e^{-\alpha (t-t_{0})}V_{0}(t_{0})+\int _{t_{0}}^{t}\mu ^{N_{\sigma }(s,t)}e^{-\alpha (t-s)}\Gamma (s)\mathrm{d}s. \end{aligned}$$

(33)

Under zero initial condition, (33) implies

$$\begin{aligned}&\int _{t_{0}}^{t}e^{-\alpha (t-s)+{N_{\sigma }(s,t)}\ln \mu }r^{T}(s)r(s)\mathrm{d}s \nonumber \\&\quad \le \gamma ^{2}\int _{t_{0}}^{t}e^{-\alpha (t-s)+{N_{\sigma }(s,t)}\ln \mu }\omega ^{T}(s)\omega (s)\mathrm{d}s. \end{aligned}$$

(34)

Multiplying both sides of (34) by $e^{-{N_{\sigma }(0,t)}\ln \mu }$ yields

$$\begin{aligned}&\int _{t_{0}}^{t}e^{-\alpha (t-s)-{N_{\sigma }(0,s)}\ln \mu }r^{T}(s)r(s)\mathrm{d}s\nonumber \\&\quad \le \gamma ^{2}\int _{t_{0}}^{t}e^{-\alpha (t-s)-{N_{\sigma }(0,s)}\ln \mu }\omega ^{T}(s)\omega (s)\mathrm{d}s. \end{aligned}$$

(35)

Notice that $N_{\sigma }(0,s)\le s/\tau _{a}$ and $\tau _{a}\ge \frac{\ln \mu }{\alpha }$; we have $N_{\sigma }(0,s)\ln \mu \le \alpha s$.

Thus, (35) implies

$$\begin{aligned} \int _{t_{0}}^{t}e^{-\alpha (t-s)-\alpha s} r^{T}(s)r(s)\mathrm{d}s\le \gamma ^{2}\int _{t_{0}}^{t}e^{-\alpha (t-s)}\omega ^{T}(s)\omega (s)\mathrm{d}s. \end{aligned}$$

(36)

Integrating the above inequality from $t_{0}$ to $\infty$ yields (9). This completes the proof.

$\square$

Remark 3

The proposed design method in this paper provides strict LMIs in a single step which reduces redundancy in determination of the controller and observer gain matrices. Note that the number of variables to be determined in [22] is great than the ones used in our study. Besides, based on the use of Luenberger switching observer (2), the number of unknown matrices is lower in our case. In addition, it should be mentioned that the conservatism is reduced by regulating parameter $\epsilon _{i}$ where the more greater region is obtained for feasibility. This fact can be shown upon an example firstly studied in [22] leading to small $\gamma$ in our case (see Example 1).

Remark 4

It is worth noting that using the detection and control units into a single unit, leads to less complexity compared with the case of separate design. In addition, it reduces the delay of the communication between the system and the controller via communication channel. This means that our design approach presents more advantage in real-world applications than designed approaches of FD without control as in [2, 14, 22].

5 Examples

In this section, two examples are presented to illustrate the effectiveness of the proposed method. The first one is used for the comparison between the result of this paper and [22]. The second one is an application to a pulse-width-modulation (PWM)-driven boost converter.

Example 1

Consider the continuous-time switched system with two subsystems similar to the one studied in [22].

Mode 1:

$$\begin{aligned} A_{1}= & {} \left[ \begin{array}{l@{\quad }l} -3 &{} 2 \\ 1 &{} -6 \end{array}\right] ,\quad B_{1}=\left[ \begin{array}{l} 0 \\ 1 \end{array}\right] ,\quad C_{1}=\left[ \begin{array}{l@{\quad }l} 1&0 \end{array}\right] ,\quad E_{1}=\left[ \begin{array}{l} 0.3 \\ 0.5 \end{array}\right] ,\quad F_{1}=\left[ \begin{array}{l} 0.9 \\ 0.7 \end{array}\right] , \\ N_{1}= & {} 0.6, \, M_{1}=0.9. \end{aligned}$$

Mode 2:

$$\begin{aligned}&A_{2}=\left[ \begin{array}{ll} -2 &{} 1 \\ 3 &{} -9 \end{array}\right] ,\quad B_{2}=\left[ \begin{array}{ll} 1 \\ 0 \end{array}\right] ,\quad C_{2}=\left[ \begin{array}{ll} 1&0 \end{array}\right] ,\quad E_{2}=\left[ \begin{array}{ll} 0 \\ 0.1 \end{array}\right] ,\quad F_{2}=\left[ \begin{array}{ll} 1 \\ 0 \end{array}\right] , \\&N_{2}=0.9, \quad M_{2}=0.4. \end{aligned}$$

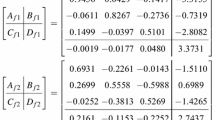
Given $\alpha =0.1$, $\mu =1.1$ and $\gamma =0.6$, based on Theorem 1, the observer, the controller and the residual with gain matrices are obtained as follows:

$$\begin{aligned}&G_{1}=\left[ \begin{array}{l@{\quad }l} -0.5606&{} 0.0191 \\ 0.1164 &{}-0.6857 \end{array}\right] , \quad L_{1}=\left[ \begin{array}{l}0.1566 \\ 0.2527 \end{array}\right] , \quad K_{1}=\left[ \begin{array}{l@{\quad }l} 0.0790&0.0467 \end{array}\right] ,\quad \\&V_{1}=0.3208 \\&G_{2}=\left[ \begin{array}{l@{\quad }l} -0.5831 &{} 0.2803 \\ 0.0274 &{} -0.5867\end{array}\right] , \quad L_{2}=\left[ \begin{array}{l}0.3497 \\ 0.0380\end{array}\right] , \quad K_{2}=\left[ \begin{array}{l@{\quad }l}0.1636&-0.2581 \end{array}\right] , \quad \\&V_{2}=0.3050. \end{aligned}$$

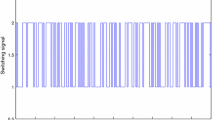
Then for the simulation purpose, we let the occurrence of the fault $f(t)=1$ from 40 to 60 s and $d(t)=\exp (-0.04t)\cos (0.3\pi t)$, the threshold value $J_{th}=0.9545$. The switching signal with average dwell time $\tau _{a}\ge \frac{\ln \mu }{\alpha }=0.9531$ is shown in Fig. 1. Figure 2 presents the residual signal while the evolution of the system states is shown in Fig. 4. From Fig. 3, $J_{r}(T_e)>J_{th}$ when $t=40$ s, which means that the fault f(t) can be immediately and effectively detected when it occurs under the disturbance input.

Fig. 1

The evolution of the switching signal $\sigma (t)$

Fig. 2

Residual signal r(t) when the fault occurs from 40 to 60 s

Fig. 3

The residual evaluation function $J_{r}(T_e)$

Fig. 4

State responses with input control

The comparison of Table 1 shows that the result of the proposed method in this paper is less conservative than the one of [22].

Example 2

In this example, a pulse-width-modulation (PWM)-driven boost converter, shown in Fig. 5, is given to illustrate the effectiveness of our design method. $e_{s}(t)$ is the source voltage, L is the inductance, C is the capacitance and R is the load resistance. The switch s(t) is controlled by a PWM device and can switch at most once time in each period T. As a typical circuit system, the converter is used to transform the source voltage into a higher voltage. This class of power converters has been modeled as switched systems. The differential equations for the boost converter are as follows [20, 29]:

Table 1 Comparison with the existing results

Fig. 5

Boost converter

$$\begin{aligned} {\dot{e}}_{c}(\tau )= & {} -\,\frac{1}{R{\hat{C}}}e_{c}(\tau )+(1-s(\tau ))\frac{1}{{\hat{C}}}i_{L}(\tau ),\end{aligned}$$

(37)

$$\begin{aligned} {\dot{i}}_{L}(\tau )= & {} -\,(1-s(\tau ))\frac{1}{{\hat{L}}}e_{c}(\tau )+s(\tau )\frac{1}{{\hat{L}}}, \end{aligned}$$

(38)

where $\tau =\frac{t}{T}$, ${\hat{L}}=\frac{L}{T}$ and ${\hat{C}}=\frac{C}{T}$.

Then, let $x={[}e_{c},i_{L}{]}^{T}$, so (37)–(38) can be formulated by:

$$\begin{aligned} {\dot{x}}(t) =A_{\sigma }x(t)+B_{\sigma }u(t), \sigma \in \left\{ 1,2\right\} . \end{aligned}$$

(39)

where

$$\begin{aligned} A_{1}=\left[ \begin{array}{l@{\quad }l} -\frac{1}{R{\hat{C}}}&{}\frac{1}{\hat{C}}\\ -\frac{1}{\hat{L}}&{} 0 \end{array}\right] ,\quad A_{2}=\left[ \begin{array}{l@{\quad }l} -\frac{1}{R{\hat{C}}}&{} 0\\ 0&{} 0\end{array}\right] ,\quad B_{1}=\left[ \begin{array}{l} 0 \\ 0 \end{array}\right] ,\quad B_{2}=\left[ \begin{array}{l} 0 \\ \frac{1}{\hat{L}}\end{array}\right] . \end{aligned}$$

According to the same normalization technique used in [5], matrices in (39) can be given by:

$$\begin{aligned} A_{1}=\left[ \begin{array}{l@{\quad }l} -1 &{} 1\\ -1&{} 0 \end{array}\right] ,\quad A_{2}=\left[ \begin{array}{l@{\quad }l} -1&{} 0\\ 0&{} 0\end{array}\right] ,\quad B_{1}=\left[ \begin{array}{l} 0 \\ 0 \end{array}\right] ,\quad B_{2}=\left[ \begin{array}{l} 0 \\ 1\end{array}\right] . \end{aligned}$$

We assume that the other system matrices are

$$\begin{aligned}&C_{1}=\left[ \begin{array}{l@{\quad }l} 0.1&-0.1\end{array}\right] , \quad E_{1}=\left[ \begin{array}{l} 0.1 \\ 0.2\end{array}\right] , \quad F_{1}=\left[ \begin{array}{l}-0.6 \\ 0.3\end{array}\right] ,\quad N_{1}=0.4 ,\,\ M_{1}=1.5 \\&C_{2}=\left[ \begin{array}{l@{\quad }l} 0.3&-0.4\end{array}\right] , \quad E_{2}=\left[ \begin{array}{l} 0.2 \\ 0.1\end{array}\right] , \quad F_{2}=\left[ \begin{array}{l}-0.8 \\ -0.3\end{array}\right] ,\quad N_{2}=-0.3 ,\,\ M_{2}=1.2. \end{aligned}$$

To demonstrate the effectiveness of the designed method, assume that the disturbance $d(t)=0.5\exp (-0.04t).\cos (0.05\pi t)$, and the fault is set up as:

$$\begin{aligned} f=\left\{ \begin{array}{l@{\quad }l} 1, &{} \quad 40\le t \le 60\\ 0, &{} \quad \text{ otherwise }. \end{array} \right. \end{aligned}$$

Fig. 6

The evolution of the switching signal $\sigma (t)$

Fig. 7

Residual signal r(t) when the fault occurs from 40 to 60 s

Given $\alpha =0.1$, $\mu =1.1$ and $\gamma =1.2$, by solving the conditions in Theorem 1, we can obtain the observer, residual and the corresponding stabilizing controller as follows:

$$\begin{aligned} G_{1}= & {} \left[ \begin{array}{l@{\quad }l} -0.2746 &{} 0.0986\\ -0.2747 &{} -0.4835 \end{array}\right] , \; G_{2}=\left[ \begin{array}{l@{\quad }l} -0.4045 &{} 0.0098\\ 0.4864 &{} -0.7272 \end{array}\right] ,\; L_{1}=\left[ \begin{array}{l} -3.4359\\ -4.4436 \end{array}\right] ,\\ L_{2}= & {} \left[ \begin{array}{l} 0.2256\\ -2.1329 \end{array}\right] , \quad K_{1}= \left[ \begin{array}{l@{\quad }l} -0.6425&-0.0110 \end{array}\right] , \quad K_{2}= \left[ \begin{array}{l@{\quad }l} 0.0321&-0.1646 \end{array}\right] ,\\ V_{1}= & {} 0.2206, \quad V_{2}=0.1260. \end{aligned}$$

The minimal average dwell time $\tau _{a}^*=0.9531$ is given by (14). The switching signal is shown in Fig. 6, which is generated by choosing an average dwell time $\tau _{a}=3.46$. The generated residual r(t) is shown in Fig. 7. The threshold can be determined as $J_{th}=1$ for $t=30$ s. Figure 8 shows the evolution of residual evaluation function $J_{r}(T_e)$, in which the solid line is fault-free case, while the dashed line is the faulty case f(t). The evolution of state trajectories is plotted in Fig. 9, showing that the stability is maintained in the presence of fault.

Fig. 8

The residual evaluation function $J_{r}(T_e)$

Fig. 9

State responses with input control

6 Conclusion

In this paper, the fault detection and control problem for continuous-time switched systems with average dwell time constraint has been investigated. The controller-based observer has been designed to maintain asymptotic stability of the faulty switching system and can be considered as a passive fault-tolerant control. This technique uses a new method assembling in a compact form all the variables in one augmented matrix. The obtained conditions have been worked out in a simple way to obtain new LMIs, and the desired observer/controller matrices can be constructed easily through the solution of LMIs. Finally, two illustrative examples are provided to show the effectiveness and applicability of the proposed results.