Adaptive Fuzzy Observer-Based Fault-Tolerant Control for Takagi–Sugeno Descriptor Nonlinear Systems with Time Delay

Abstract

This paper investigates the problems of state/fault estimation and active fault-tolerant control (AFTC) design for time-delay descriptor fuzzy systems subject to external disturbances and actuator faults. Using Takagi–Sugeno fuzzy models, an adaptive fuzzy observer is proposed to achieve system state and actuator fault estimation simultaneously. According to Lyapunov functional method, design and analysis conditions of the resulting closed-loop delayed descriptor system are formulated in terms of linear matrices inequalities (LMIs). Observer and controller gains are computed by solving a set of LMIs in only one step and then used to both estimate the unmeasured states and actuator faults in AFTC context. Numerical examples are provided to show the merit and the conservativeness of the proposed approach in comparison with the existing methods by considering various types of actuator faults.

1 Introduction

Actuator, sensor or plant failures may totally modify the system behavior by generating the instability and performance degradation of the control systems. Therefore, many researches on fault detection and isolation (FDI) have been extensively conducted during the last decades [16]. To ameliorate system performance efficiency and reliability, the issue of fault-tolerant control (FTC) has been more and more considered.

According to Blanke in [2] and [20], the objective of FTC is to preserve current performance and maintain stability conditions in the event of system component malfunctions. In the literature such as [7, 24], there are two classes of FTC: active and passive or reliable ones. The passive FTC (PFTC) tolerates only limited predetermined faults throughout the whole control process. The major drawback of this approach is that the fault tolerance capability could be very limited. In contrast to PFTC, the active FTC (AFTC) is generally constructed to treat the occurrence of system faults in real time. It is characterized by the use of an online FDI unit to preserve the stability and performance of the global system.

Generally speaking, the FTC allows to maintain a certain level of reliability, productivity and safety in most industrial systems and also to guarantee satisfactory performance not only during the normal operation but also in the presence of both sensor and actuator faults (see [22, 23, 29] and references therein).

Furthermore, it is well known that time delay can be a cause of instability for dynamical systems and performance degradation for control systems. So, this topic has received a substantial attention in the past years, and different design approaches have been proposed (see [11, 26] and references therein).

Recently, the TS fuzzy model-based control of descriptor fuzzy systems with time delay has been investigated for their interests in several engineering applications, such as constrained robot systems, circuit systems and chemical processes [8, 17].

Similar to the standard fuzzy systems with time delay, the results on stability analysis and stabilization of descriptor delayed systems can be classified into two categories: delay-independent criteria, which are applicable to delay of an arbitrary size [3, 25], and delay-dependent ones which include information about the size of delay [26]. It is known that the latter one results are usually less conservative than the former ones, especially when the size of delay is small [8, 30].

More recently, the active actuator FTC design problem of descriptor fuzzy systems has been investigated in [10] and [12]. However, the observer and controller design conditions are given in bilinear matrix inequality (BMI) form and then solved using a two-step algorithm. The present work improves the previous results in terms of conservatism reduction and computational complexity by formulating observer and fault-tolerant control design conditions in a set of linear matrices inequalities (LMIs) which can be solved on only one step using LMI Toolbox or Yalmip of MATLAB software [6]. Moreover, no tuning matrices are needed to solve the LMIs as required in [12].

By choosing an appropriate Lyapunov–Krasovskii functional, delay-dependent stability and stabilization conditions are developed to estimate time-varying faults, and an adaptive fuzzy observer is proposed to estimate both states system and actuator faults.

The purpose of this work is to develop a state/fault fuzzy observer-based FTC strategy of descriptor nonlinear delayed systems described by the T–S fuzzy models. Thus, using obtained fault information given by an adaptive fuzzy observer, a fault-tolerant controller is designed to compensate the effect of actuator faults [13, 21].

The rest of the paper is organized as follows. The second section introduces the structure of the T–S fuzzy descriptor system with state delay under actuator faults and the problem formulation. Section 3 holds the main result and gives LMI-based design conditions for the adaptive fuzzy observer-based fault-tolerant controller. A simulation examples are presented in Sect. 4 to compare and to show the validity of the suggested approach. Finally, Sect. 5 concludes this contribution.

Notations In this paper, a real symmetric positive definite matrix (respectively, negative definite matrix) is represented by $A > 0$ (respectively, $A < 0$). The notation $(*)$ corresponds to matrix block incited by symmetry, $\hbox {sym}(A)$ signifies $A+A^\mathrm{T}$, and $A^{\dag }$ represents the generalized inverse of A. $\lambda _\mathrm{max}(A)$ stands for the maximum eigenvalues of A. As well, $\Vert \cdot \Vert$ corresponds to the standard norm symbol, and $\forall$ denotes “for all.”

2 Problem Formulation

Consider a T–S fuzzy descriptor system with state delay described by a set of if-then rules, and each rule is a local linear representation of the nonlinear system. The ith rule of the system is given as follows.

Plant rule $i (i=1,2,\ldots ,r)$: If $\theta _{1}$ is  $\mu _{i1}$  and, $\cdots$, and $\theta _{p}$  is  $\mu _{ip}$, then

$$\begin{aligned} E\dot{x}{(t)}&=A_{i}x(t)+A_{hi}x(t-h)+B_iu(t)+Dd(t)+F_if_a(t)\nonumber \\ y(t)&=Cx(t)\nonumber \\ x(t)&=\varPhi (t), \quad \forall t \in [-\bar{h},0] \end{aligned}$$

(1)

where $\theta _{j}(x(t))$ are the premise variables which are assumed measurable, $\mu _{ij} (i=1,\ldots ,r, j=1,\ldots ,p)$ are the fuzzy sets which are characterized by the membership functions, r and p are the total number of if-then rules and the premise variables, respectively.

$x(t) \in \mathbb {R}^{n}$ is the state vector, $u(t) \in \mathbb {R}^{m}$ is the control input, $y(t)\in \mathbb {R}^{p}$ is the measured output, $d(t)\in \mathbb {R}^{\nu }$ is the external disturbance, $f_a(t)\in \mathbb {R}^{m}$ represents the actuator fault which can be constant or time-varying function, h is a constant delay satisfying $0 \leqslant h \leqslant \bar{h}$ and $\varPhi (t)$ is an initial condition.

Matrix $E \in \mathbb {R}^{n \times n}$ is assumed to be singular, and we suppose that $\mathrm{rank}(E)=q \le n$.

$A_{i}, A_{hi}, B_i, F_i$ and C are known real constant matrices of appropriate dimensions. It is supposed that matrices $F_i$ and $C_i$ are of full column rank and of full row rank, respectively.

By fuzzy blending, the overall fuzzy system is given as follows:

$$\begin{aligned} E\dot{x}{(t)}&= \sum \limits _{i = 1}^{r}{h_{i}(\theta (x(t)))[A_{i}x(t)+A_{hi}x(t-h)+B_iu(t)+Dd(t)+F_if_a(t)]} \nonumber \\ y(t)&=Cx(t) \end{aligned}$$

(2)

in which

$$\begin{aligned} \theta (x(t))= & {} [\theta _{1}(x(t)),\ldots ,\theta _{p}(x(t))]\\ h_{i}(\theta (x(t)))= & {} \frac{\nu _{i}(\theta (x(t)))}{\displaystyle \sum ^{r}_{i=1}\nu _{i}(\theta (x(t)))} ; \nu _{i}(\theta (x(t)))=\prod _{j=1}^{p}\mu _{ij}(\theta _i(x(t))) \end{aligned}$$

where $\mu _{ij}(\theta _i(x(t))$ is the grade of the membership of $\theta _i(x(t))$ in $\mu _{ij}$.

It is evident that $0\le h_{i}(\theta (x(t)))\le 1$ and $\displaystyle \sum ^{r}_{i=1}h_{i}(\theta (x(t)))=1$.

Then, for briefness we get $h_{i}$ to stand for $h_{i}(\theta (x(t)))$.

Before giving the design of the adaptive observer, six assumptions are assumed:

Assumption 1

[1]

$$\begin{aligned} \mathrm{rank} \left[ \begin{array}{c} E \\ C \end{array} \right] = n \end{aligned}$$

(3)

Assumption 2

[15] Triple matrix $(E, A_i, C)$ is R-detectable,

$$\begin{aligned} \mathrm{rank} \left[ \begin{array}{c} sE-A_i \\ C \end{array} \right] = n , \quad \forall s \in \mathbb {C}, Re(s) \ge 0, \quad \forall i=[1,\ldots ,r] \end{aligned}$$

(4)

Assumption 3

[14]

$$\begin{aligned} \mathrm{rank} \left[ \begin{array}{cc} E &{} D \\ C &{} 0 \end{array} \right] = n+\mathrm{rank}(D) \end{aligned}$$

(5)

Assumption 4

Fault $f_a(t)$ satisfies $\Vert f_a(t) \Vert \le \alpha _1$, and the derivative of $f_a(t)$ with respect to time is norm-bounded, i.e., $\Vert \dot{f}_a(t) \Vert \le f_{1\mathrm{max}}$ and $0 \le \alpha _1$, $f_{1\mathrm{max}} < \infty$.

Assumption 5

$$\begin{aligned} B_1=\cdots =B_r=B \end{aligned}$$

(6)

Assumption 6

$$\begin{aligned} \mathrm{rank}(B F_i)=\mathrm{rank}(B) , \quad \forall i \in [1,\ldots ,r] \end{aligned}$$

(7)

Remark 1

Referring to Assumption 6, there exists a nonzero matrix $\check{F}_i \in \mathbb {R}^{m \times m}$ such that $F_i=B \check{F}_i, \quad \forall i \in [1,\ldots ,r]$.

$$\begin{aligned} (I_n -B B^\dag )F_i=(I_n -B B^\dag )B \check{F}_i =0 , \quad \forall i \in [1,\ldots ,r] \end{aligned}$$

(8)

Two lemmas which are used in the proof are given as follows:

Lemma 1

[7] Given a symmetric positive definite matrix Q and a scalar $\mu \in \mathbb {R}^{+}$, we have the following inequality

$$\begin{aligned} 2x^\intercal y \le \frac{1}{\mu }x^\intercal Q x+\mu y^\intercal Q^{-1}y \end{aligned}$$

(9)

$x,y \in \mathbb {R}^{n}.$

Lemma 2

[8] Given a matrix R of appropriate dimension such that $R^\mathrm{T} \Pi R <0$, consider a negative definite matrix $\Pi < 0$, then $\exists \ \lambda > 0$ such that

$$\begin{aligned} R^\mathrm{T}\Pi R \le -\lambda (R+R^\mathrm{T})-\lambda ^{2} \Pi ^{-1} \end{aligned}$$

(10)

3 Main Results

3.1 Design of Adaptive Fuzzy Observer-Based Fault-Tolerant Controller

So as to estimate the state and the faults of system (2), we propose the following adaptive fuzzy observer design

$$\begin{aligned} \left\{ \begin{array}{ll}\dot{w}{(t)}&{}= \sum \limits _{i = 1}^{r}h_i[H_1 A_i \widehat{x}(t)+H_1 A_{hi} \widehat{x}(t-h)+H_1 B_iu(t) +L_{1i}(y(t)-\widehat{y}(t)) \\ &{}+L_{2i}(y(t-h)-\widehat{y}(t-h))+H_1 F_i\widehat{f}_a(t)] \\ \widehat{x}(t)&{}=w(t)+H_2 y(t)\\ e_{y}(t)&{}=y(t)-\widehat{y}(t)\\ \widehat{y}(t)&{}=C\widehat{x}(t)\\ \dot{\widehat{f}}_a(t)&{}=\Gamma \sum \limits _{i = 1}^{r}{ h_i N_{i}(\dot{e}_y(t)+\sigma e_y(t))} \end{array}\right. \end{aligned}$$

(11)

and the active fault-tolerant control is:

$$\begin{aligned} u(t)=-\sum ^{r}_{i=1}h_{i}K_{i}\widehat{x}(t)-B^\dag \sum ^{r}_{i=1}h_{i}F_i\widehat{f}_a(t) \end{aligned}$$

(12)

where $w(t) \in \mathbb {R}^{n}$ and $\widehat{x}(t) \in \mathbb {R}^{n}$ are the observer state and the estimated state vector, respectively. $\widehat{y}(t) \in \mathbb {R}^{p}$ and $\widehat{y}(t-h) \in \mathbb {R}^{p}$ are the estimated output vectors at the sampling time t and $t-h$, respectively. $e_y(t) \in \mathbb {R}^{p}$ is the output estimation error, $\widehat{f}_a(t) \in \mathbb {R}^{m}$ is the estimated of actuator fault $f_a(t)$, and $H_1,H_2,L_{1i},L_{2i}, N_{i}$ and $K_{i}$ are gain matrices with appropriate dimensions to be determined.

Under Assumption 1, there exist nonsingular matrices $H_1 \in \mathbf R ^{n\times n}$ and $H_2 \in \mathbf R ^{n\times m}$ such that in [5, 21]:

$$\begin{aligned} H_1 E + H_2 C = I_n \end{aligned}$$

(13)

The state and the fault estimation errors are given as follows :

$$\begin{aligned} e_x(t)=x(t)-\widehat{x}(t), \quad e_f(t)=f_a(t)-\widehat{f}_a(t) \end{aligned}$$

By taking into account (2), (11) and by using relation (13), state estimation error dynamic $e_x(t)$ and output estimation error $e_y(t)$ are given by:

$$\begin{aligned} \dot{e}_x(t)= & {} \sum ^{r}_{i=1}h_{i}[(H_1 A_i-L_{1i}C)e_x(t)+(H_1 A_{hi}-L_{2i}C)e_x(t-h)\nonumber \\&+H_1 F_ie_{f}(t)+H_1 Dd(t)] \end{aligned}$$

(14)

$$\begin{aligned} e_y(t)= & {} Ce_x(t) \end{aligned}$$

(15)

Using the same idea proposed in [4] and [19] concerning the disturbance–decoupling techniques, matrix $H_1$ is selected such that

$$\begin{aligned} H_1 D=0 \end{aligned}$$

(16)

Then, estimation error dynamic (14) can be simplified as:

$$\begin{aligned} \dot{e}_x(t)=\sum ^{r}_{i=1}h_{i}[(H_1 A_i-L_{1i}C)e_x(t)+(H_1 A_{hi}-L_{2i}C)e_x(t-h)+H_1 F_i e_{f}(t)] \end{aligned}$$

(17)

To find simultaneously matrices $H_1$ and $H_2$ from Eqs. (13) and (16), one can define the following augmented matrix:

$$\begin{aligned} \left[ \begin{array}{cc} H_1&H_2 \end{array} \right] \left[ \begin{array}{cc} E &{} D \\ C &{} 0 \end{array} \right] = \left[ \begin{array}{cc} I_n&0 \end{array} \right] \end{aligned}$$

(18)

Under Assumption 3, $H_1$ and $H_2$ can be expressed by the following system:

$$\begin{aligned} \left[ \begin{array}{cc} H_1&H_2 \end{array} \right] = \left[ \begin{array}{cc} I_n&0 \end{array} \right] \left[ \begin{array}{cc} E &{} D \\ C &{} 0 \end{array} \right] ^\dag \end{aligned}$$

(19)

In contrast to the constant fault giving in [28] and [27], here time-varying faults are considered. Then, it follows that $\dot{f}(t)\ne 0$. Consequently, the dynamic of fault estimation error is given by the following expression:

$$\begin{aligned} \dot{e}_f(t)=\dot{f}_a(t)-\dot{\widehat{f}}_a(t) \end{aligned}$$

(20)

Then,

$$\begin{aligned} \dot{e}_f(t)=\dot{f}_a(t)-\Gamma \sum \limits _{i = 1}^{r}{ h_i N_{i}(\dot{e}_y(t)+\sigma e_y(t))} \end{aligned}$$

(21)

Under Assumption 5 and Remark 1, the closed loop of the T–S Descriptor System without external disturbances becomes

$$\begin{aligned} E\dot{x}(t)= & {} \sum \limits _{i = 1}^{r} h_i[A_{i}x(t)-B K_{i}\widehat{x}(t)+A_{hi}x(t-h)+F_i f_a(t)\nonumber \\&+\,(I_n -B B^\dag ) F_i \widehat{f}_a(t)-F_i \widehat{f}_a(t)] \nonumber \\ E\dot{x}(t)= & {} \sum \limits _{i = 1}^{r}{ h_i[(A_{i}-B K_{i})x(t)+A_{hi}x(t-h)+B K_{i}e_x(t)+F_i e_f(t)]} \end{aligned}$$

(22)

3.2 Stability and Stabilization Analysis

Theorem 1

Considering system (22), under Assumptions 1, 2, 3 and 5, if there exist symmetric positive definite matrices $Q_1, Z_1$, $P_2, Q_2, Z_2$ and a positive definite matrices $P_1$ as well as $N_{i}, K_{i}$ and M such that $\forall i \in [1,\ldots ,r]$, the following conditions hold:

$$\begin{aligned}&E^\mathrm{T} P_1 = P_1^\mathrm{T}E \ge 0 \end{aligned}$$

(23)

$$\begin{aligned}&(H_1 F_i)^\mathrm{T} P_2 = N_{i} C \end{aligned}$$

(24)

$$\begin{aligned}&\phi _{i} < 0, \quad i=1,2,\ldots ,r \end{aligned}$$

(25)

then the adaptive fuzzy observer proposed in (11) and the FTC designed in (12) can realize that the state vector of overall system (22), the state estimation error and the fault estimation error are uniformly bounded.

where

$$\begin{aligned} \phi _{i}= \left[ \begin{array}{ccccccc} \varphi _{i}^{11} &{} \varphi _{i}^{12} &{} P_1^\mathrm{T} B K_{i} &{} 0 &{} P_1^\mathrm{T} F_i &{} 0 &{} \varphi _{i}^{17} \\ *&{} -(Q_1+E^\mathrm{T} Z_1 E) &{} 0 &{} 0 &{} 0 &{} 0 &{} A_h^\mathrm{T} P_1 \\ *&{} *&{} \varphi _{i}^{33} &{} \varphi _{i}^{34} &{} \varphi _{i}^{35} &{} \varphi _{i}^{36} &{} K_{i}^\mathrm{T} B^\mathrm{T} P_1 \\ *&{} *&{} *&{} -(Q_2+ Z_2) &{} \varphi _{i}^{45} &{} \varphi _{i}^{46} &{} 0 \\ *&{} *&{} *&{} *&{} \varphi _{i}^{55} &{} F_i^\mathrm{T} H_1^\mathrm{T} P_{2}^\mathrm{T} &{} F_i ^\mathrm{T} P_1 \\ *&{} *&{} *&{} *&{} *&{}\varphi ^{66} &{} 0 \\ *&{} *&{} *&{} *&{} *&{} *&{} \varphi ^{77} \\ \end{array} \right] \end{aligned}$$

(26)

in which

$$\begin{aligned} \varphi _{i}^{11}= & {} \mathrm{sym}(P_1^\mathrm{T} A_{i}-P_1^\mathrm{T} B K_{i})+Q_1-E^\mathrm{T} Z_1 E \\ \varphi _{i}^{12}= & {} P_1^\mathrm{T} A_{hi}+E^\mathrm{T} Z_1 E \\ \varphi _{i}^{17}= & {} (A_i-B K_{i})^\mathrm{T} P_1 \\ \varphi _{i}^{33}= & {} \mathrm{sym}(P_2 H_1 A_i-P_2 L_{1i} C)+Q_2-Z_2 \\ \varphi _{i}^{34}= & {} P_2(T A_{hi}-L_{2i} C)+Z_2 \\ \varphi _{i}^{35}= & {} -\frac{1}{\sigma }(A_{i}^\mathrm{T} H_1^\mathrm{T} P_2 - C^\mathrm{T} Y_{1i}^\mathrm{T})H_1 F_i \\ \varphi _{i}^{36}= & {} (H_1 A_{i}-L_{1i}C)^\mathrm{T} P_2 \\ \varphi _{i}^{45}= & {} -\frac{1}{\sigma }(A_{hi}^\mathrm{T} H_1^\mathrm{T} P_2 -C^\mathrm{T} Y_{2i}^\mathrm{T})H_1 F_i \\ \varphi _{i}^{46}= & {} (H_1 A_{hi}-L_{2i}C)^\mathrm{T} P_2 \\ \varphi _{i}^{55}= & {} -\frac{1}{\sigma }(H_1 F_{i})^\mathrm{T} P_2 (H_1 F_{i})+\frac{1}{\sigma \mu }M \\ \varphi ^{66}= & {} -P_2(h^2 Z_2)^{-1} P_2; \quad \varphi ^{77}=-P_1^\mathrm{T}(h^2 Z_1)^{-1} P_1 \\ \end{aligned}$$

Proof

See “Appendix A”.

Our objective now is to transform conditions in Theorem 1 in set of LMIs.

Theorem 2

Considering system (22), under Assumptions 1, 2, 3 and 5, if there exist symmetric positive definite matrices $\widetilde{Q}_1, \widetilde{Z}_1, X_2, Q_2, Z_2$ and a positive definite matrices $X_1$ as well as $N_{i} , Y_{1i}$, $Y_{2i} , M$ and $W_{i}$ such that $\forall i \in [1,\ldots ,r]$ the following conditions hold:

$$\begin{aligned} EX_{1}=X_1^\mathrm{T}E_{1}^\mathrm{T} \ge 0 \end{aligned}$$

(27)

Minimize $\eta > 0$ subject to [6]

$$\begin{aligned} \left[ \begin{array}{cc} \eta I_m &{} (H_1F_i)^\mathrm{T} X_2 - N_{i} C \\ *&{} \eta I_n \end{array} \right] > 0, \quad i=1,2,\ldots ,r \end{aligned}$$

(28)

$$\begin{aligned} \varXi _{i} < 0, \quad i=1,2,\ldots ,r \end{aligned}$$

(29)

where

$$\begin{aligned} \varXi _{i}= \left[ \begin{array}{cccc} \varXi _{i}^{11} &{} \varXi _{i}^{12} &{} \varXi _{i}^{13} &{} 0 \\ *&{} \varXi _{i}^{22} &{} \varXi _{i}^{23} &{} \lambda _3 I \\ *&{} *&{} \varXi _{i}^{33} &{} 0 \\ *&{} *&{} *&{} \varXi _{i}^{44} \\ \end{array} \right] \end{aligned}$$

(30)

then the adaptive fuzzy observer proposed in (11) and the FTC designed in (12) can realize that the state vector of overall system (22), the state estimation error and the fault estimation error are uniformly bounded.

In this case, the gains of the adaptive fuzzy observer and controller are, respectively, given by $L_{1i}= X_2^{-1} Y_{1i}$, $L_{2i}= X_2^{-1} Y_{2i}$ and $K_{i}= W_i X_1^{-1}$.

$$\begin{aligned} {\varXi _{i}^{11}}= & {} \left[ \begin{array}{ccccc} \mathrm{sym}(A_iX_1-B W_i) +\widetilde{Q}_1 - E \widetilde{Z}_1E^\mathrm{T} &{} A_{hi} X_1 +E \widetilde{Z}_1E^\mathrm{T} \\ *&{} -(\widetilde{Q}_1 + E \widetilde{Z}_1E^\mathrm{T}) \end{array} \right] \nonumber \\ {\varXi _{i}^{12}}= & {} \left[ \begin{array}{cccc} B W_i &{} 0 &{} F_i &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \end{array} \right] , \, {\varXi _{i}^{13}}=\left[ \begin{array}{c} (A_iX_1-B W_i)^\mathrm{T} \\ (A_{hi} X_1)^\mathrm{T} \end{array} \right] \\ {\varXi _{i}^{22}}= & {} \left[ \begin{array}{cc} -\lambda _3(X_1+X_1^\mathrm{T}) &{} 0 \\ *&{} -2\lambda _3 I \end{array} \right] , \, {\varXi _{i}^{23}}=\left[ \begin{array}{ccccc} (B W_i)^\mathrm{T} \\ 0 \\ F_i^\mathrm{T} \\ 0 \end{array} \right] \\ {\varXi _{i}^{33}}= & {} \left[ \begin{array}{c} -\lambda _2(X_1+X_1^\mathrm{T})+\lambda _2 ^2 h^2 \widetilde{Z}_1 \end{array} \right] \\ \end{aligned}$$

$$\begin{aligned} {\varXi _{i}^{44}}=\left[ \begin{array}{cccc} \mathrm{sym}(X_2 H_1 A_{i}-Y_{1i}C)+Q_2-Z_2 &{} X_2 H_1 A_{hi} - Y_{2i} C + Z_2 &{} -\frac{1}{\sigma }(A_{hi}^\mathrm{T} H_1^\mathrm{T} P_2 -C^\mathrm{T} Y_{2i}^\mathrm{T})H_1 F_i &{} (X_2 H_1 A_i - Y_{1i} C)^\mathrm{T} \\ *&{} -(Q_2+Z_2) &{} -\frac{1}{\sigma }(A_{hi}^\mathrm{T} H_1^\mathrm{T} P_2 -C^\mathrm{T} Y_{2i}^\mathrm{T})H_1 F_i &{} (X_2 H_1 A_{hi} - Y_{2i} C)^\mathrm{T} \\ *&{} *&{} -\frac{1}{\sigma }(H_1 F_{i})^\mathrm{T} P_2 (H_1 F_{i})+\frac{1}{\sigma \mu }M &{} (X_2 H_1 F_i)^\mathrm{T} \\ *&{} *&{} *&{} -2 \lambda _1 X_2+\lambda _1^2 h^2 Z_2 \end{array} \right] \end{aligned}$$

Proof

see “Appendix B”.

Remark 2

The actuator fault estimation for this class of systems is not fully investigated, and the problem is still open. In [12], the proposed result presents three drawbacks: The first one is that the result is delay independent. The second one is that the proposed LMI conditions require to choose some tuning matrices which need to be fixed beforehand. The third one is that the controller and observer design are the BMIs which are solved using a two-step algorithm.

4 Numerical Example

In this section, two examples are given to demonstrate the effectiveness of the proposed methods.

Example 1

As stated in Remark 2, to show the conservativeness of our approach a comparison with the result in [12] will be stated.

Consider the following T–S fuzzy descriptor system with time delay proposed in [8] and [18]

$$\begin{aligned} \left\{ \begin{aligned} E\dot{x}{(t)}&= \sum \limits _{i = 1}^{3}{ h_i[A_{i}x(t)+A_{hi}x(t-h)+B_iu(t)+Dd(t)]} \\ y(t)&=Cx(t)\\ \end{aligned} \right. \end{aligned}$$

(31)

where

$$\begin{aligned} E= & {} \left[ \begin{array}{ccc} 1&{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 \end{array} \right] ; \quad A_1=\left[ \begin{array}{ccc} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 1 &{} -6 &{} 0 \end{array} \right] ; \quad A_2=\left[ \begin{array}{ccc} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 1 &{} 0 &{}-6 \end{array} \right] ; \quad A_3=\left[ \begin{array}{ccc} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 1 &{} 0 &{} 0 \end{array} \right] \\ A_{hi}= & {} \left[ \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0.8 &{} 0 &{} 0 \end{array} \right] ;\quad B_{i}= \left[ \begin{array}{c} 0\\ 0 \\ 1 \end{array} \right] ;\quad D= \left[ \begin{array}{c} 1\\ 0\\ 1 \end{array} \right] ;\quad C=\left[ \begin{array}{ccc} 0 &{} 1 &{} 1\\ 1 &{} 0 &{} 0 \end{array} \right] ,\quad i=1,2,3 \end{aligned}$$

Applying Theorem 2, we get a feasible solution and we obtain the controller and observer gains as follows:

$$\begin{aligned} K_{1}= & {} \left[ \begin{array}{ccc} 3.2145&0.0920&3.4882 \end{array} \right] ,\quad K_{2}= \left[ \begin{array}{ccc} 3.7327&5.6808&-1.0278 \end{array} \right] ,\quad K_{3}= \left[ \begin{array}{ccc} 2.9409&4.3092&2.7649 \end{array} \right] \\ L_{11}= & {} \left[ \begin{array}{cc} 0.5832 &{} 0.8709 \\ 1.0490 &{} 0.5885 \\ -0.3761 &{} -0.3645 \end{array} \right] ,\quad L_{12}= \left[ \begin{array}{cc} 0.5997 &{} 0.8400 \\ 0.6547 &{} -0.2518 \\ 0.0338 &{} 0.5042 \end{array} \right] ,\quad L_{13}= \left[ \begin{array}{cc} 0.0911 &{} 0.7414 \\ 0.7329 &{} -0.0949 \\ -0.2118 &{} -0.1369 \end{array} \right] \\ L_{21}= & {} \left[ \begin{array}{cc} 0.6209 &{} 0.4146 \\ 0.0905 &{} -0.3693 \\ 0.5872 &{} 0.1145 \end{array} \right] ,\quad L_{22}= \left[ \begin{array}{cc} 0.6258 &{} 0.3519 \\ 0.5347 &{} 0.0940 \\ 0.1344 &{} -0.3350 \end{array} \right] ,\quad L_{23}= \left[ \begin{array}{cc} 0.1234 &{} 0.2435 \\ 0.4701 &{} 0.0217 \\ 0.4433 &{} -0.0174 \end{array} \right] \end{aligned}$$

Then, we apply Theorems 1 and 2 in [12], where delay-independent conditions have been developed, and we find an infeasible problem.

Example 2

In this section, we consider a truck–trailer system in [12, 28].

Considering the following dynamic model of the truck–trailer system,

$$\begin{aligned} \dot{x}_1{(t)}= & {} -a\frac{v\bar{t}}{L t_0}x_1(t)-(1-a)\frac{v\bar{t}}{L t_0}x_1(t-h)+\frac{v\bar{t}}{lt_0}u(t) \nonumber \\ \dot{x}_2{(t)}= & {} a\frac{v\bar{t}}{L t_0}x_1(t)+(1-a)\frac{v\bar{t}}{L t_0}x_1(t-h) \nonumber \\ \dot{x}_3{(t)}= & {} \frac{v\bar{t}}{t_0}\sin \left[ x_2(t)+a\frac{v\bar{t}}{2L}x_1(t)+(1-a) \frac{v\bar{t}}{2L}x_1(t-h)\right] \end{aligned}$$

(32)

Model parameters are: $a=0.7, l=2.8, L=5.5, v=-1$, $\bar{t}=2, t_0=0.5$ and $h=0.5$.

To have the T–S descriptor representation, the following state variable is introduced:

$$\begin{aligned} x_4(t)=x_2(t)-a\frac{v\bar{t}}{L t_0}x_1(t)-(1-a)\frac{v\bar{t}}{L t_0}x_1(t-h) \end{aligned}$$

(33)

The following fuzzy rules can be employed:

Rule 1: If $\theta (t)=x_2(t)+a\frac{v\bar{t}}{L t_0}x_1(t)+(1-a)\frac{v\bar{t}}{L t_0}x_1(t-h)$ is about 0, then

$$\begin{aligned} \left\{ \begin{aligned} E\dot{x}{(t)}&=A_{1}x(t)+A_{h1}x(t-h)+B_1u(t)+Dd(t) \\ y(t)&=Cx(t) \end{aligned} \right. \end{aligned}$$

Rule 2: If $\theta (t)=x_2(t)+a\frac{v\bar{t}}{L t_0}x_1(t)+(1-a)\frac{v\bar{t}}{L t_0}x_1(t-h)$ is about $\pi$ or $-\pi$, then

$$\begin{aligned} \left\{ \begin{aligned} E\dot{x}{(t)}&=A_{2}x(t)+A_{h2}x(t-h)+B_2u(t)+Dd(t) \\ y(t)&=Cx(t) \end{aligned} \right. \end{aligned}$$

where

$$\begin{aligned} E= & {} \left[ \begin{array}{cccc} 1&{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \end{array} \right] ;\quad A_1=\left[ \begin{array}{cccc} -a\frac{v\bar{t}}{L t_0}&{} 0 &{} 0 &{} 0 \\ a\frac{v\bar{t}}{L t_0} &{} 0 &{} 0 &{} 0 \\ -a\frac{v^2 \bar{t}^2}{2 L t_0} &{} \frac{v\bar{t}}{t_0} &{} 0 &{} 0 \\ -a\frac{v\bar{t}}{L t_0} &{} 1 &{} 0 &{} -1 \end{array} \right] ;\quad A_{h1}=\left[ \begin{array}{cccc} -(1-a)\frac{v\bar{t}}{L t_0}&{} 0 &{} 0 &{} 0 \\ (1-a)\frac{v\bar{t}}{L t_0} &{} 0 &{} 0 &{} 0 \\ (1-a)\frac{v^2 \bar{t}^2}{2 L t_0} &{} 0 &{} 0 &{} 0 \\ -(1-a)\frac{v\bar{t}}{L t_0} &{} 0 &{} 0 &{} 0 \end{array} \right] ;\\ B_{1}= & {} \left[ \begin{array}{cc} \frac{v\bar{t}}{l t_0} \\ 0 \\ 0 \\ 0 \end{array} \right] \\ A_2= & {} \left[ \begin{array}{cccc} -a\frac{v\bar{t}}{L t_0}&{} 0 &{} 0 &{} 0 \\ a\frac{v\bar{t}}{L t_0} &{} 0 &{} 0 &{} 0 \\ -a\frac{\varphi v^2 \bar{t}^2}{2 L t_0} &{} \frac{\varphi v\bar{t}}{t_0} &{} 0 &{} 0 \\ -a\frac{v\bar{t}}{L t_0} &{} 1 &{} 0 &{} -1 \end{array} \right] ;\quad A_{h1}=\left[ \begin{array}{cccc} -(1-a)\frac{v\bar{t}}{L t_0}&{} 0 &{} 0 &{} 0 \\ (1-a)\frac{v\bar{t}}{L t_0} &{} 0 &{} 0 &{} 0 \\ (1-a)\frac{\varphi v^2 \bar{t}^2}{2 L t_0} &{} 0 &{} 0 &{} 0 \\ -(1-a)\frac{v\bar{t}}{L t_0} &{} 0 &{} 0 &{} 0 \end{array} \right] ;\\ B_{2}= & {} \left[ \begin{array}{cc} \frac{v\bar{t}}{l t_0} \\ 0 \\ 0 \\ 0 \end{array} \right] ;\quad C=I_4 ;\quad D= \left[ \begin{array}{c} 0\\ 0\\ \frac{v\bar{t}}{t_0}\\ 0 \end{array} \right] \end{aligned}$$

we set $\varphi =\frac{10 t_0}{\pi }$ and $d(t)=\sin (\theta (t))-\theta (t)$

Consider now actuator faults, it is supposed that $F_1=B_1$ and $F_2=B_2$.

The membership functions for rules 1 and 2 are designed as follows:

$$\begin{aligned}&h_1(\theta (t))=\left( \frac{1}{1+exp(-3(\theta (t)+0.5\pi ))}\right) \nonumber \\&\quad \left( 1-\frac{1}{1+exp(-3(\theta (t)-0.5\pi ))}\right) , \; h_2(\theta (t))=1-h_1(\theta (t)) \end{aligned}$$

(34)

By solving (19), $H_1$ and $H_2$ can be given as follows

$$\begin{aligned}&H_1=\left[ \begin{array}{cccc} 0.5 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0.5 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \end{array} \right] ; H_2=\left[ \begin{array}{cccc} 0.5 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0.5 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right] \end{aligned}$$

By choosing the tuning parameter values as follows: $\lambda _1=2$, $\lambda _2=3, \lambda _3=3, \sigma =2, \mu =0.2, \Gamma =0.5$ and $\eta =0.01$.

Within MATLAB LMI Toolbox, we can solve the optimization problem of Theorem 2 and we obtain the following feasible solution:

$$\begin{aligned}&X_1= \left[ \begin{array}{cccc} 63.5299 &{} 9.2108 &{} -24.9982 &{} 0 \\ 9.2108 &{} 8.5007 &{} 17.5163 &{} 0 \\ -24.9982 &{} 17.5163 &{} 203.4188 &{} 0 \\ 27.2301 &{} 10.4030 &{} -8.4407 &{} 106.0576 \end{array} \right] ,\nonumber \\&\quad X_2= \left[ \begin{array}{cccc} 257.8177 &{} -0.1618 &{} 0.1288 &{} 0.0202 \\ -0.1618 &{} 169.4268 &{} 0.1317 &{} 0.0452 \\ 0.1288 &{} 0.1317 &{} 170.0010 &{} -0.0025 \\ 0.0202 &{} 0.0452 &{} -0.0025 &{} 170.0363 \end{array} \right] \end{aligned}$$

Fig. 1

State $x_1(t)$ and its estimated $\widehat{x}_1(t)$ with a time-varying fault $f_{a1}$

Fig. 2

State $x_2(t)$ and its estimated $\widehat{x}_2(t)$ with a time-varying fault $f_{a1}$

Fig. 3

State $x_3(t)$ and its estimated $\widehat{x}_3(t)$ with a time-varying fault $f_{a1}$

Let consider the first time-varying fault as follows:

$$\begin{aligned} f_{a1}(t)= \left\{ \begin{aligned}&0&t \le 4.5 \\&1.5&4.5< t \le 7 \\&0&7< t \le 10 \\&0.5+0.3\sin (7t)&10 < t \le 14 \\&0&t > 14 \end{aligned} \right. \end{aligned}$$

(35)

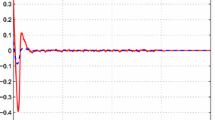
Simulation results of this example are illustrated in Figs. 1, 2, 3, 4, 5, 6, 7 and 8. It is quite clear to see that the adaptive observer proposed in this work can estimate system state and actuator faults (Fig. 9).

Fig. 4

State $x_4(t)$ and its estimated $\widehat{x}_4(t)$ with a time-varying fault $f_{a1}$

Fig. 5

Actuator fault $f_{a1}(t)$ and its estimated $\widehat{f}_{a1}(t)$

Fig. 6

State $x_1(t)$ and its estimated $\widehat{x}_1(t)$ with a time-varying fault $f_{a2}$

Fig. 7

State $x_2(t)$ and its estimated $\widehat{x}_2(t)$ with a time-varying fault $f_{a2}$

Fig. 8

State $x_3(t)$ and its estimated $\widehat{x}_3(t)$ with a time-varying fault $f_{a2}$

Fig. 9

State $x_4(t)$ and its estimated $\widehat{x}_4(t)$ with a time-varying fault $f_{a2}$

Fig. 10

Actuator fault $f_{a2}(t)$ and its estimated $\widehat{f}_{a2}(t)$

Consider now the second time-varying fault as follows:

$$\begin{aligned} f_{a2}(t)= \left\{ \begin{aligned}&0&t \le 7 \\&0.3(t-3)&7 < t \le 11 \\&0&t > 11 \end{aligned} \right. \end{aligned}$$

(36)

By referring to simulation results, it can be deduced that the use of the adaptive fuzzy observer-based fault-tolerant controller can rapidly recover the performance and the stability of the closed-loop system in the presence of time-varying fault which gives us a good estimation of the states and the actuator faults. As shown in Figs. 5 and 10, the two faults which are considered in this paper are rapidly and accurately estimated.

For the two examples of actuator faults, by choosing $\Gamma =0.5$ in the simulation example, the derivative of $f_{a1}(t)$ and $f_{a2}(t)$ over time are norm-bounded by $f_{11\mathrm{max}}=2.1$ and $f_{12\mathrm{max}}=0.3$, respectively. $\delta _1=\frac{\mu }{\sigma }f^2_{11\mathrm{max}}\lambda _\mathrm{max}(\Gamma ^{-1} M^{-1}\Gamma ^{-1})=0.0273$ and $\delta _2=\frac{\mu }{\sigma }f^2_{12\mathrm{max}}\lambda _\mathrm{max}(\Gamma ^{-1} M^{-1}\Gamma ^{-1})=5.5773.10^{-4}$ reduce the radius of the ball in which the estimation errors converge.

5 Conclusion

In this article, an adaptive fuzzy observer-based actuator fault-tolerant controller design for Takagi–Sugeno fuzzy descriptor system with time delay and external disturbances has been investigated. The proposed strategy allows to estimate simultaneously the system states and time-varying actuator faults. The delay-dependent stabilization conditions are presented in terms of LMIs which can be easily solved using MATLAB LMI Toolbox. A simulation results are given to show the effectiveness of the design method.

Appendices

Appendix A: Proof of Theorem 1

Consider the following Lyapunov–Krasovskii functional:

$$\begin{aligned} V(t)= & {} (Ex(t))^\mathrm{T} P_1 x(t) + \int _{t-h}^{t} x^\mathrm{T}(s)Q_1 x(s)\,\mathrm {d}s + e_x^\mathrm{T}(t)P_2 e_x(t) \nonumber \\&+ \int _{t-h}^{t} e_x^\mathrm{T}(s)Q_2 e_x(s)\,\mathrm {d}s \nonumber \\&+\, \frac{1}{\sigma } e_f^\mathrm{T}(t)\Gamma ^{-1} e_f(t) + h \int _{-h}^{0} \int _{t+\theta }^{t}(E\dot{x}(s))^\mathrm{T} Z_1 (E\dot{x}(s)) \,\mathrm {d}s\,\mathrm {d}\theta \nonumber \\&+\, h \int _{-h}^{0} \int _{t+\theta }^{t} \dot{e}_{x}^\mathrm{T}(s) Z_2 \dot{e}_x(s) \,\mathrm {d}s\,\mathrm {d}\theta \end{aligned}$$

(37)

The time derivative of V(t) is given by:

$$\begin{aligned} \dot{V}(t)= & {} (E\dot{x}(t))^\mathrm{T} P_1 x(t) + (Ex(t))^\mathrm{T} P_1 \dot{x}(t)+ x^\mathrm{T}(t)Q_1 x(t) \nonumber \\&-\, x^\mathrm{T}(t-h)Q_1 x(t-h) +2 \dot{e}_x^\mathrm{T}(t)P_2 e_x(t)\nonumber \\&+\, e_x^ T(t) Q_2 e_x(t)- e_x^ T(t-h) Q_2 e_x(t-h)+ \frac{2}{\sigma } e_f^\mathrm{T}(t) \Gamma ^{-1} \dot{e}_f(t) \nonumber \\&+\, h^2[(E\dot{x}(t))^\mathrm{T} Z_1 (E\dot{x}(s))]\nonumber \\&-\,h\int _{t-h}^{t}(E\dot{x}(s))^\mathrm{T} Z_1 (E\dot{x}(s)) \,\mathrm {d}s\ + h^2 [\dot{e}_{x}^\mathrm{T}(s) Z_2 \dot{e}_x(s)]\nonumber \\&-\,h\int _{t-h}^{t} \dot{e}_{x}^\mathrm{T}(s) Z_2 \dot{e}_x(s) \,\mathrm {d}s\ \end{aligned}$$

(38)

By using Lemma 1, we have:

$$\begin{aligned} \frac{2}{\sigma }e_f^\mathrm{T}(t)\Gamma ^{-1} \dot{f}_a(t)\leqslant & {} \frac{1}{\sigma \mu } e_f^\mathrm{T}(t)M e_f(t)+ \frac{\mu }{\sigma } \dot{f}_a^\mathrm{T}(t)\Gamma ^{-1} M^{-1}\Gamma ^{-1} \dot{f}_a(t) \nonumber \\ \frac{2}{\sigma }e_f^\mathrm{T}(t)\Gamma ^{-1} \dot{f}_a(t)\leqslant & {} \frac{1}{\sigma \mu } e_f^\mathrm{T}(t)M e_f(t)+ \delta \end{aligned}$$

(39)

where

$$\begin{aligned} \delta =\frac{\mu }{\sigma }f^2_{1\mathrm{max}} \lambda _\mathrm{max}(\Gamma ^{-1} M^{-1}\Gamma ^{-1}) \end{aligned}$$

(40)

By using (23) and substituting (22), (17) and (39) into Eq. (38), one can obtain:

$$\begin{aligned} \dot{V}(t)\le & {} x(t)^\mathrm{T} [P_1^\mathrm{T}(A_i-B K_{i})+(A_i^\mathrm{T}- K_{i}^\mathrm{T} B ^\mathrm{T})P_1 +Q_1] x(t) \nonumber \\&+\,2 x(t)^\mathrm{T} P_1^\mathrm{T} A_{hi}x(t-h)+2x(t)^\mathrm{T} P_1^\mathrm{T} B K_{i} e_x(t) + 2x(t)^\mathrm{T} P_1^\mathrm{T} F_i e_f(t) \nonumber \\&- x^\mathrm{T}(t-h)Q_1 x(t-h) + e_x^\mathrm{T}(t)[ P_2 (TA_i-L_{1i}C) \nonumber \\&+(TA_i-L_{1i}C)^\mathrm{T} P_2 + Q_2] e_x(t)+2e_x^\mathrm{T}(t)P_2(TA_{hi} -L_{2i} C) e_x(t-h)\nonumber \\&-\, e_x^ T(t-h) Q_2 e_x(t-h) + \frac{1}{\sigma \mu } e_f^\mathrm{T}(t)M e_f(t)+ \delta \nonumber \\&+\, h^2[(E\dot{x}(t))^\mathrm{T} Z_1 (E\dot{x}(s))] -h\int _{t-h}^{t}(E\dot{x}(s))^\mathrm{T} Z_1 (E\dot{x}(s)) \,\mathrm {d}s \nonumber \\&+\, h^2 [\dot{e}_{x}^\mathrm{T}(s) Z_2 \dot{e}_x(s)]-h\int _{t-h}^{t} \dot{e}_{x}^\mathrm{T}(s) Z_2 \dot{e}_x(s) \,\mathrm {d}s\ \end{aligned}$$

(41)

Applying Jessen’s inequality [9] to deal with the cross product items, we obtain

$$\begin{aligned}&-h\int _{t-h}^{t}(E\dot{x}(s))^\mathrm{T} Z_1 (E\dot{x}(s)) \,\mathrm {d}s\ \le \left[ \begin{array}{cc} Ex(t)\\ Ex(t-h) \end{array} \right] ^\mathrm{T} \left[ \begin{array}{cc} -Z_1 &{} Z_{1} \\ * &{} -Z_{1} \end{array} \right] \left[ \begin{array}{cc} Ex(t)\\ Ex(t-h) \end{array} \right] \nonumber \\ \end{aligned}$$

(42)

$$\begin{aligned}&\le \left[ \begin{array}{cc} x(t)\\ x(t-h) \end{array} \right] ^\mathrm{T} \left[ \begin{array}{cc} -E^\mathrm{T} Z_1 E &{} E^\mathrm{T} Z_{1} E \\ * &{} -E^\mathrm{T} Z_{1} E \end{array} \right] \left[ \begin{array}{cc} x(t)\\ x(t-h) \end{array} \right] \end{aligned}$$

(43)

$$\begin{aligned}&-h\int _{t-h}^{t} \dot{e}_{x}^\mathrm{T}(s) Z_2 \dot{e}_x(s) \,\mathrm {d}s\ \le \left[ \begin{array}{cc} e_x(t)\\ e_x(t-h) \end{array} \right] ^\mathrm{T} \left[ \begin{array}{cc} -Z_2 &{} Z_{2} \\ * &{} -Z_{2} \end{array} \right] \left[ \begin{array}{cc} e_x(t)\\ e_x(t-h) \end{array} \right] \end{aligned}$$

(44)

Noting the extended state vector as follows:

$$\begin{aligned} \xi (t)= \left[ \begin{array}{ccccc} x^\intercal (t)&x^\intercal (t-h)&e_x^\mathrm{T}(t)&e_x^\mathrm{T}(t-h)&e^\mathrm{T}_f(t) \end{array} \right] ^\mathrm{T} \end{aligned}$$

(45)

Then, we can write :

$$\begin{aligned} \dot{V}(t)\le \xi ^ T \phi _{i}^{11} \xi (t) + h^2[(E\dot{x}(t))^\mathrm{T} Z_1 (E\dot{x}(s))] + h^2 [\dot{e}_{x}^\mathrm{T}(s) Z_2 \dot{e}_x(s)]+\delta \end{aligned}$$

(46)

where

$$\begin{aligned} \phi _{i}^{11} =\left[ \begin{array}{ccccc} \varphi _{i}^{11} &{} \varphi _{i}^{12} &{} P_1^\mathrm{T} B K_{i} &{} 0 &{} P_1^\mathrm{T} F_i \\ *&{} -(Q_1+E^\mathrm{T} Z_1 E) &{} 0 &{} 0 &{} 0 \\ *&{} *&{} \varphi _{i}^{33} &{} \varphi _{i}^{34} &{} \varphi _{i}^{35} \\ *&{} *&{} *&{} -(Q_2+ Z_2) &{} \varphi _{i}^{45} \\ *&{} *&{} *&{} *&{} \varphi _{i}^{55} \end{array} \right] \end{aligned}$$

(47)

Denote

$$\begin{aligned} \phi _{i}=\left[ \begin{array}{ccc} \phi _{i}^{11} &{} \phi _{i}^{12} &{} \phi _{i}^{13} \\ *&{} -(h^2 P_2^{-1} Z_2 P_2^{-1})^{-1} &{} 0 \\ *&{} *&{} -(h^2 P_1^{-1} Z_1 P_1^{-T})^{-1} \\ \end{array} \right] \end{aligned}$$

(48)

where

$$\begin{aligned} ({\phi _{i}^{12}})^\mathrm{T}= & {} \left[ \begin{array}{ccccc} 0 &{} 0 &{} P_2 (T A_i-L_{1i} C) &{} P_2(T A_{hi}-L_{2i} C) &{} P_2(TF_i) \\ \end{array} \right] \\ ({\phi _{i}^{13}})^\mathrm{T}= & {} \left[ \begin{array}{ccccc} P_1^\mathrm{T}(A_i-B K_{i}) &{} P_1^\mathrm{T} A_{hi} &{} P_1^\mathrm{T} B K_{i} &{} 0 &{} P_1^\mathrm{T} F_i \\ \end{array} \right] \end{aligned}$$

By using Schur complement, inequality (25) is equivalent to $\xi ^ T \phi _{i}^{11} \xi (t) + h^2[(E\dot{x}(t))^\mathrm{T} Z_1 (E\dot{x}(s))] + h^2 [\dot{e}_{x}^\mathrm{T}(s) Z_2 \dot{e}_x(s)] < 0$.

If condition (25) holds, it follows from (41) that

$$\begin{aligned} \dot{V}(t) \le -\zeta \Vert \xi (t) \Vert ^2 + \delta \end{aligned}$$

(49)

where $\zeta =\lambda _\mathrm{min}(-\phi _i)$

It follows that $\dot{V}(t) \leqslant 0$ for $\zeta \Vert \xi (t) \Vert ^2 > \delta$, and according to Lyapunov stability theory, $\xi (t)$ will converge to a small set $\Psi = \{ \xi (t) / \Vert \xi (t) \Vert ^2 \le \frac{\delta }{\zeta } \}$ ; thus, $\xi (t)$ is uniformly bounded.

The proof is completed.

Appendix B: Proof of Theorem 2

We can write inequality (26) in this form

$$\begin{aligned} \varLambda _{i}=\left[ \begin{array}{ccc} \varLambda _{i}^{11} &{} \varLambda _{i}^{12} &{} \varLambda _{i}^{13} \\ *&{} \varLambda _{i}^{22} &{} \varLambda _{i}^{23} \\ *&{} *&{} \varLambda _{i}^{33} \\ \end{array} \right] < 0 \end{aligned}$$

(50)

where

$$\begin{aligned} \varLambda _{i}^{11}= & {} \left[ \begin{array}{cc} \mathrm{sym}(P_1^\mathrm{T} A_{i}-P_1^\mathrm{T} B K_{i})+Q_1-E^\mathrm{T} Z_1 E &{} P_1^\mathrm{T} A_{hi}+E^\mathrm{T} Z_1 E \\ *&{} -(Q_1+E^\mathrm{T} Z_1 E) \\ \end{array} \right] \\ \varLambda _{i}^{12}= & {} \left[ \begin{array}{cccc} P_1^\mathrm{T} B K_{i} &{} 0 &{} P_1^\mathrm{T} F_i &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] , \, \varLambda _{i}^{13}= \left[ \begin{array}{c} (A_i-B K_{i})^\mathrm{T} P_1 \\ A_{hi}^\mathrm{T} P_1 \end{array} \right] \end{aligned}$$

$$\begin{aligned} \varLambda _{i}^{22}= & {} \left[ \begin{array}{cccc} \mathrm{sym}(P_2 H_1 A_i-P_2 L_{1i} C) +Q_2-Z_2 &{} P_2(H_1 A_{hi}- L_{2i} C)+Z_2 &{} -\frac{1}{\sigma }(A_{hi}^\mathrm{T} H_1^\mathrm{T} P_2 - C^\mathrm{T} Y_{2i}^\mathrm{T})H_1 F_i &{} (H_1 A_{i}-L_{1i}C)^\mathrm{T} P_2 \\ *&{} -(Q_2+ Z_2) &{} -\frac{1}{\sigma }(A_{hi}^\mathrm{T} H_1^\mathrm{T} P_2 -C^\mathrm{T} Y_{2i}^\mathrm{T})H_1 F_i &{} (H_1 A_{hi}-L_{2i}C)^\mathrm{T} P_2 \\ *&{} *&{} -\frac{1}{\sigma }(H_1 F_{i})^\mathrm{T} P_2 (H_1 F_{i})+\frac{1}{\sigma \mu }M &{} (H_1 F_i)^\mathrm{T} P_2 \\ *&{} *&{} *&{} -P_2(h^2 Z_2)^{-1} P_2 \\ \end{array} \right] \\ \varLambda _{i}^{33}= & {} \left[ \begin{array}{c} -P_1^\mathrm{T}(h^2 Z_1)^{-1} P_1 \\ \end{array} \right] \end{aligned}$$

Consider the following symmetric matrix:

$$\begin{aligned} \mathbb {Z}= \left[ \begin{array}{ccc} \mathbb {Z}_{11} &{} 0 &{} 0\\ 0 &{} \mathbb {Z}_{22} &{} 0 \\ 0 &{} 0 &{} \mathbb {Z}_{33} \\ \end{array} \right] \end{aligned}$$

where $\mathbb {Z}_{11} =\hbox {diag}(P_1^{-T},P_1^{-T}), \mathbb {Z}_{22} = \hbox {diag}(P_1^{-T},I,I,I)$ and $\mathbb {Z}_{33} =P_1^{-T}$

We can transform inequality (50) by pre- and post-multiplying it by $\mathbb {Z}$, and we obtain this form:

$$\begin{aligned} \left[ \begin{array}{ccc} \mathbb {Z}_{11} \varLambda _{i}^{11} \mathbb {Z}_{11}^\mathrm{T} &{} \mathbb {Z}_{11} \varLambda _{i}^{12} \mathbb {Z}_{22}^\mathrm{T} &{} \mathbb {Z}_{11} \varLambda _{i}^{13} \mathbb {Z}_{33}^\mathrm{T}\\ *&{} \mathbb {Z}_{22} \varLambda _{i}^{22} \mathbb {Z}_{22}^\mathrm{T} &{} \mathbb {Z}_{22} \varLambda _{i}^{23} \mathbb {Z}_{33}^\mathrm{T} \\ *&{} *&{} \mathbb {Z}_{33} \varLambda _{i}^{33} \mathbb {Z}_{33}^\mathrm{T} \end{array} \right] <0 \end{aligned}$$

(51)

By using Lemma 2, we obtain the following inequalities:

$$\begin{aligned} -P_2(h^2 Z_2)^{-1} P_2\le & {} -2 \lambda _1 P_2+\lambda _1^2 h^2 Z_2 \end{aligned}$$

(52)

$$\begin{aligned} \mathbb {Z}_{33} \varLambda _{i}^{33} \mathbb {Z}_{33}^\mathrm{T}= & {} -P_1^{-T}(h^2 \widetilde{Z}_1)^{-1} P_1^{-1} \le -\lambda _2 (P_1^{-T}+P_1^{-1}) + \lambda _2^{2} h^2 \widetilde{Z}_1\qquad \quad \end{aligned}$$

(53)

$$\begin{aligned} \mathbb {Z}_{22} \varLambda _{i}^{22} \mathbb {Z}_{22}^\mathrm{T}\le & {} -\lambda _3 (\mathbb {Z}_{22}+\mathbb {Z}_{22}^\mathrm{T}) - \lambda _3^{2} (\varLambda _{i}^{22})^{-1} \end{aligned}$$

(54)

By applying Schur complement, we obtain the following inequality:

$$\begin{aligned} \left[ \begin{array}{cccc} \mathbb {Z}_{11} \varLambda _{i}^{11} \mathbb {Z}_{11}^\mathrm{T} &{} \mathbb {Z}_{11} \varLambda _{i}^{12} \mathbb {Z}_{22}^\mathrm{T} &{} \mathbb {Z}_{11} \varLambda _{i}^{13} \mathbb {X}_{33}^\mathrm{T} &{} 0 \\ * &{} -\lambda _3 (\mathbb {Z}_{22}+\mathbb {Z}_{22}^\mathrm{T})&{} \mathbb {Z}_{22} \varLambda _{i}^{23} \mathbb {Z}_{33}^\mathrm{T} &{} \lambda _3 I \\ * &{} * &{} \mathbb {Z}_{33} \varLambda _{i}^{33} \mathbb {Z}_{33}^\mathrm{T} &{} 0 \\ * &{} * &{} * &{} \varLambda _{i}^{22} \\ \end{array} \right] < 0 \end{aligned}$$

(55)

By posing $X_1=P_1^{-1}, X_2=P_2, \widetilde{Z}_1=P_1^{-1}Z_1 P_1^{-T}, \widetilde{Q}_1=P_1^{-T}Q_1 P_1^{-1}, Y_{1i}=P_2 L_{1i}, Y_{2i}=P_2 L_{2i}$ and $W_i=K_{i} P^{-1}_1$, we obtain inequality (30).

The proof is completed.