Thermocapillary migration of a compound drop inside a spherical cavity

Abstract

This study investigates the thermocapillary migration of a compound drop placed concentrically within a spherical cavity under the limit of vanishing Péclet and Reynolds number. The imposed temperature gradient, which is constant along the line connecting the centers of the drop and cavity, is the driving force for the migration of compound drop. The compound drop is assumed to translate with an unknown velocity to be determined using force-free conditions. The flow field in each phase of the drop and the continuous phase is governed by the Stokes equations, whereas the thermal problem in each phase is governed by the heat conduction equation. The hydrodynamic problem and the thermal problem are coupled through specific boundary conditions. A complete general solution of the Stokes equation is used to solve the hydrodynamic problem in each phase. The migration velocity of a compound drop inside a spherical cavity is presented for various values of the physical parameters involved such as viscosity ratio, thermal conductivity ratio, Marangoni number. It has been observed that the migration velocity which represents the rate of movement of compound drop due to thermocapillary effects, decreases as the ratio of the compound drop’s radius to the cavity radius increases. On the other hand, this velocity decreases with an increase in relative conductivity of the cavity wall and increases with Marangoni number at the interface of the compound drop. The analytical solution provides a closed-form expression for the migration velocity of the confined compound drop, and it is seen that the boundary effects play significant role in thermocapilary migration.

1 Introduction

When a drop of one liquid is suspended in an immiscible second liquid that exhibits a temperature gradient, it naturally migrates toward the warmer side. This movement occurs due to the interfacial tension gradient caused by temperature variations along the surface of the droplet. This intriguing phenomenon referred to as thermocapillary migration, holds significant importance in processes involving materials conducted under microgravity conditions,[1] as well as numerous other applications such as cosmetics [2], petroleum [3]. Compound drops, carrying nanoparticles, offer targeted drug delivery in nanomedicine. Encapsulating drugs within these drops boosts stability and enables precise, controlled release at specific body sites, reducing systemic side effects [4]. A simplified model of a spherical drop in a spherical cavity represents droplets in rock pores. Hydrodynamic interactions between the drop and pore walls influence viscous resistance and oil recovery efficiency. Recent research [5] used boundary collocation methods and provided numerical data on hydrodynamic drag forces contributing to our understanding of this process. In all these applications, the fluid particles guided by thermocapillary migration shift between different temperature zones within an environment where gravity plays a lesser role. Young et al.[6] were the first to have understood the thermocapillary migration of droplets when they observed the motion of a drop within a vertical liquid bridge positioned between the anvils of a micrometer. They generated a temperature gradient by heating the lower anvil to effectively reduce the upward buoyant motion of the drop and in some cases even directed them downward. Additionally, they developed a formula to calculate the migration velocity of a spherical droplet that is suspended in an unbounded fluid and subjected to a uniform temperature gradient under the conditions of small Marangoni and Reynolds numbers.

Subramanian [7] extended the research on thermocapillary migration of bubbles by incorporating nonzero convective heat transfer effects in the equations governing the temperature distribution. In a subsequent study, Haj-Hariri et al. [8] introduced the inclusion of inertia in the thermocapillary migration of fluid droplets and concluded that inertial effect causes the drop to deform into either a prolate spheroid or an oblate spheroid depending on the density ratio and other controlling parameters. Balasubramaniam and Chai [9] delved into the thermocapillary migration of a fluid sphere within confined pores, examining the impact on the motion of spherical fluid particles at low Marangoni numbers and nonzero Reynolds numbers, specifically analyzing the migration velocity of individual fluid particles. Chen et al. [10] utilized a boundary collocation method to investigate the thermocapillary mobility of a spherical drop moving along the central axis of an insulated circular tube. They observed a steady decrease in mobility with changes in the drop-to-tube radius ratio.

A spherical droplet moving within a spherical cavity serves as an idealized model for investigating droplet migration in media or microchannels composed of interconnected spherical pores. Lee and Keh [11] recently explored the thermocapillary migration of a fluid sphere within a spherical cavity, aligned along the line connecting their centers. They employed a hybrid analytical–numerical approach, which integrated a boundary collocation technique to obtain numerical results concerning droplet mobility. In an extension of their research, Lee and Keh [12] employed a semi-analytical method with boundary collocation to address the hydrodynamic drag force acting on the spherical droplet. Their findings indicated that, in specific droplet positions, the wall-corrected drag force typically increases with the viscosity ratio between the internal and external fluids. Furthermore, researchers [13] performed computations to solve for the thermocapillary migration of a fluid sphere within a spherical cavity, situated perpendicular to the line connecting their centers. This thorough investigation provided valuable insights into the intricate dynamics of droplet migration within such confined geometries, thereby advancing our understanding of thermocapillary phenomena in these settings.

The focus of this study is on the migration of a compound drop under the influence of a temperature gradient in a spherical cavity filled with viscous incompressible fluid. Compound drops, often referred to as double emulsions, are multi-component liquid systems comprising one or more droplets enclosed within another immiscible drop. Simulation and analysis done by Nguyen et al. [14] explained that during thermocapillary migration the inner droplet initially moves faster than the outer droplet. Both eventually reach the same speed, but their velocity patterns differ. Even though numerous studies have been performed on the thermocapillary migration of compound drops or bubbles, the thermocapillary migration of a compound drop in a concentric spherical cavity has not been investigated to date. Therefore, the proposed study aims to address this gap in the literature by investigating the thermocapillary migration of a compound drop placed concentrically in a spherical cavity with a uniform temperature gradient along the z-axis.

It also examines the influence of the thermal conductivity of the surrounding medium on the axially symmetric thermocapillary motion of the compound drop in the concentric cavity. We evaluate the migration velocity of the compound drop within the spherical cavity under the effect of a temperature gradient, noting that the boundary’s impact is slightly more pronounced in this axially symmetric migration. The presence of a rigid spherical boundary which is termed as a spherical cavity significantly affects the migration of the compound drop. By employing a complete general solution to Stokes equations, we provide closed-form expressions for velocity and pressure along with insights into the hydrodynamic forces experienced by the compound drop. The research explores normalized thermocapillary migration velocities relative to those in unbounded media and reveals that the migration velocity decreases as the ratio of the compound drop’s radius to the cavity radius grows. This study offers essential insights into confined fluid dynamics and heat transfer, with applications in various scientific and engineering domains.

2 Analysis

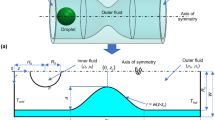
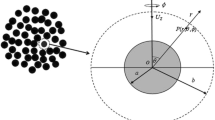
We consider a compound drop consisting of an inner drop referred to as droplet hereon, of radius $\epsilon a$ surrounded by an immiscible fluid envelope of radius a placed concentrically in a spherical cavity of radius b. For reference, the three phases involved in the problem are labeled in Fig. 1. The continuous phase in the cavity is denoted by Phase 1, the fluid envelope phase by Phase 2 and the droplet phase by Phase 3. The viscosities and thermal conductivities in the continuous phase in the spherical cavity and in each phase of compound drop are $\mu _1,~\mu _2~\text{ and }~\mu _3$ and $k_1,~k_2~\text{ and }~ k_3$, respectively. We use the spherical coordinate system $(r, \theta , \phi )$ with the origin attached at the center of the cavity. The capillary number $\mu _1 U_c/\sigma _{21}$ at the interface between Phase 2 and Phase 1 and the capillary number $\mu _2 U_c/\sigma _{32}$ between Phase 3 and Phase 2 are assumed to be very small so that the interfacial tensions $\sigma _{21}$ and $\sigma _{32}$ are sufficiently large to maintain the spherical shape of the compound drop, where $U_c$ is the characteristic velocity defined later in section 2.2. A linear temperature field $T_\infty (z)$ with uniform gradient $E_\infty e_z=\nabla T_\infty$ is imposed in the cavity surroundings far away from the compound drop, where ${\textbf {e}}_z$ is the unit vector in the z direction and $E_\infty$ is taken to be positive. Before deriving the thermocapillary migration it is necessary to obtain temperature and velocity distributions which are axisymmetric in all the phases within the cavity.

Fig. 1

A geometric representation of the problem

2.1 Thermal distribution

The equation describing the heat transfer in a steady fluid flow is governed by the conduction–convection equation which in dimensionless form is given as follows

$$\begin{aligned} Pe(\textbf{v}_j\cdot \nabla T_j)=\nabla ^2T_j,~~~j=1,2,3, \end{aligned}$$

(1)

where $Pe = \frac{U_c a}{\alpha }$ is the dimensionless Péclet number which provides a measure of the relative magnitude of the convection term in Eq. (1) compared with conduction, $\alpha$ is the thermal diffusivity, $\textbf{v}_j$ is the dimensionless fluid velocity, and $T_j$ is the dimensionless temperature. We have used the dimensionless variables $\tilde{{\textbf {v}}_j}={{\textbf {v}}_j}/{{U}}_c$ $\tilde{T_j}={T_j}/E_\infty a, \tilde{\nabla } =a \nabla , \tilde{r}=r/a$, with a being the radius of the compound drop and $U_c$ being the characteristic velocity defined in Sec. 2.2, to nondimensionalize Eq. (1). The symbol tilde has been dropped from Eq. (1) for convenience. Under the assumption of a negligibly small, Eq. (1) reduces to $\nabla ^2T_j=0$. In the present investigation; we assume that the heat transfer in the system of thermocapillary migration is governed by the conduction equation in each phase $j=1,2,3$ and the cavity surroundings. Thus, the temperature field in each phase j is governed by the following equations:

$$\begin{aligned} \nabla ^2T_1= & {} 0, ~~~~~~~~~1 \le r \le l, \end{aligned}$$

(2)

$$\begin{aligned} \nabla ^2 T_2= & {} 0, ~~~~~~~~~\epsilon \le r \le 1, \end{aligned}$$

(3)

$$\begin{aligned} \nabla ^2 T_3= & {} 0, ~~~~~~~~~0 < r\le \epsilon , \end{aligned}$$

(4)

and for the cavity surroundings

$$\begin{aligned} \nabla ^2T_w= & {} 0, ~~~~~~~~~r\ge l, \end{aligned}$$

(5)

where $l=b/a$ is the radii ratio of cavity-to-compound drop and

$$\begin{aligned} \nabla ^2 = \frac{1}{r^2} \frac{\partial }{\partial r} \left( r^2 \frac{\partial }{\partial r}\right) + \frac{1}{r^2 \sin \theta } \frac{\partial }{\partial \theta } \left( \sin \theta \frac{\partial }{\partial \theta }\right) + \frac{1}{r^2 \sin ^2 \theta } \frac{\partial ^2 }{\partial \phi ^2} \end{aligned}$$

is the Laplacian in spherical coordinate system.

The requirement of continuity of temperature and the normal heat flux on the liquid–liquid interfaces between the phases present in compound drop and the cavity wall imposes the following boundary conditions in addition to the requirement of the temperature in the cavity phase to agree with the imposed linear temperature field far from the compound drop. Thus, the boundary conditions can be expressed mathematically as follows:

$$\begin{aligned} T_w&=T_1, ~~~~~~~~~\nabla T_w \; .\; {\hat{n}}=k_{10}\nabla T_1 \; .\; {\hat{n}}, \; \;\; \; \text{ on } \quad r=l, \end{aligned}$$

(6)

$$\begin{aligned} T_1&=T_2,~~~~~~~~~ \nabla T_1 \; .\; {\hat{n}}=k_{21}\nabla T_2 \; .\; {\hat{n}}, \; \; \; \; \text{ on } \quad r=1, \end{aligned}$$

(7)

$$\begin{aligned} T_2&=T_3, ~~~~~~~~~\nabla T_2 \; .\; {\hat{n}}=k_{32}\nabla T_3 \; .\; {\hat{n}}, \; \; \; \; \text{ on } \quad r=\epsilon , \end{aligned}$$

(8)

$$\begin{aligned} r\rightarrow \infty , ~~~T_w \rightarrow T_\infty =T_0+z=T_0+ r \cos \theta , \end{aligned}$$

(9)

where $k_{10}=k_1/k_w,~k_{21}=k_2/k_1~\text{ and }~ k_{32}=k_3/k_2$ are the ratio of thermal conductivities in the cavity surroundings and each phase of the compound drop, respectively, and $T_0$ represents the undisturbed temperature at the center of the cavity. Since the temperature fields in each phase satisfy Laplace’s equation, the general expression for the thermal distribution in each phase can be expressed as the general solution of Laplace’s equations ensuring the regularity of the solution in each phase, as follows

$$\begin{aligned} T_w&=T_0+ r \cos \theta + \sum _{n=1}^\infty a_n r^{-(n+1)}P_n(\cos \theta ), ~\text{ for }~ r>l, \end{aligned}$$

(10)

$$\begin{aligned} T_1&=T_0+\sum _{n=1} ^\infty (b_n r^n+b_{n}^\prime r^{-(n+1)})P_n(\cos \theta ), ~\text{ for }~1< r<l, \end{aligned}$$

(11)

$$\begin{aligned} T_2&=T_0+\sum _{n=1} ^\infty (c_n r^n+c^\prime _n r^{-(n+1)}) P_n(\cos \theta ),~\text{ for }~ \epsilon<r<l, \end{aligned}$$

(12)

$$\begin{aligned} T_3&=T_0+\sum _{n=1} ^\infty d_n r^n P_n(\cos \theta ), ~\text{ for }~ r<\epsilon , \end{aligned}$$

(13)

where $P_n$ is the Legendre polynomial of degree n. The unknown coefficients $a_n,~ b_n,~b^\prime _n,~ c_n,~ c_n^\prime ,~ d_n$ appearing in Eq. (10)–(13) are obtained using the boundary conditions at the surface of droplet, drop and the cavity wall. It is important to note that due to the axial symmetry of the sphere, we exclusively consider solutions in (10)–(13) with only $\cos \theta$ and $\sin \theta$ terms and not the higher-order harmonics. The expressions of unknown coefficients are defined in Appendix (A.1).

2.2 Hydrodynamic distributions

In this subsection, we formulate the hydrodynamic problem in each phase where the flow fields are influenced by the temperature field obtained in the previous subsection. The steady fluid motion is governed by steady Navier–Stokes equation which is a nonlinear equation and in the absence of any body force, it is represented in dimensionless form as follows

$$\begin{aligned} Re(\textbf{v}_j \cdot \nabla \textbf{v}_j) =- \nabla p_j +\nabla ^2 {\textbf {v}}_j, ~~~~~~~~~~~ \nabla \cdot {\textbf {v}}_j=0,~~~~~~j=1,2,3, \end{aligned}$$

(14)

where ${\textbf {v}}_j, ~p_j$ are the fluid velocity, and pressure, respectively, in Phase j and $j=1,2,3$ corresponds to Phase 1, 2 and 3, respectively. We have used the dimensionless variables $\tilde{{\textbf {v}}_j}={{\textbf {v}}_j}/{{U}}_c, \tilde{\nabla } =a \nabla , \tilde{r}=r/a, (\tilde{p}_j, \tilde{\tau }_j) = a(p_j, \tau _j)/(\mu _j U_c)$, to nondimensionalize the governing equations in Phase j, $\mu _j$ is the coefficient of viscosity in phase j. The characteristic velocity is defined as ${U}_c = \dfrac{-(d\sigma _{21}/dT_1) |\nabla T_{\infty }|a}{\mu _{1}}$ and $d\sigma _{21}/dT_1$ is the rate of change of interfacial tension with temperature in Phase 1 and Phase 2. We have dropped the symbol tilde from Eqs. (14) for convenience. In Eq. (14), Re denotes the Reynolds number that characterizes the ratio of inertial to viscous force. In case of creeping flow, the viscous force dominates the inertial force and the Reynolds number is vanishingly small. Under this condition, i.e., $Re\rightarrow 0$, the Navier–Stokes equation given in Eq. (14) reduces to Stokes equation which is a linear equation. In the present study, the fluid flow corresponding to the hydrodynamic problem in each phase is governed by the Stokes equations and is given as follows

$$\begin{aligned} \nabla ^2 {\textbf {v}}_j=\nabla p_j, ~~~~~~~~~~~ \nabla \cdot {\textbf {v}}_j=0,~~~j=1,2,3. \end{aligned}$$

(15)

In general, the normal stress balance condition is used to determine the shape of a drop if the surface of the drop is deformed. This normal stress balance condition at a liquid–liquid interface in dimensionless form is given as

$$\begin{aligned}{}[(\tau -\lambda \hat{\tau })\cdot \hat{n}]\cdot \hat{n}=\frac{1}{Ca}(\nabla \cdot \hat{n}), \end{aligned}$$

(16)

where $\lambda$ is the internal-to-external viscosity ratio and Ca is the capillary number which represents the ratio of viscous forces, aim to deform the drop, to capillary forces, which aim to maintain its spherical shape. Equation (16) predicts the influence of the capillary number on drop deformation. When the drop’s shape is spherical, the capillary term on the right-hand side becomes a constant. Consequently, the left-hand side should also yield the same constant if the normal stress balance is to hold. However, in reality, the stress distribution across the surface of the drop is nonuniform, resulting in the stress difference being a function of position on the surface. For very small capillary numbers ($Ca<<1$), even a slight deviation from a spherical shape can lead to a significant variation in $(1/Ca)(\nabla \cdot \hat{n})$, which can counterbalance the stress variation across the drop’s surface. Thus, under such conditions, the drop tends to remain nearly spherical. The limit $Ca<<1$ indicates the dominance of interfacial tension effects, explaining the drop’s tendency to retain its spherical form. For more details, one may refer to [15]. Thus, for a spherical drop in the absence of thermal considerations the typical boundary conditions used at the liquid–liquid interface are : the no-penetration condition, continuity of tangential velocity and the continuity of tangential stress. These simplified conditions provide a clear framework for understanding the behavior of the fluids at the compound drop’s surface and the cavity wall. However, consideration of thermal gradient in the present investigation leads to an imbalance in the tangential stress due to variation in the surface tension, therefore, the following hydrodynamic boundary conditions are considered in the present study:

On $\quad r=l:$

$$\begin{aligned} {\textbf {v}}_{1}\cdot {\hat{n}}=0, ~~~~~~~~ {\textbf {v}}_{1}\cdot {\hat{t}}=0, \end{aligned}$$

(17)

On $\quad r=1 :$

$$\begin{aligned} {\textbf {v}}_{1}={\textbf {v}}_{2},~~~~~{\textbf {v}}_{1}\cdot {\hat{n}} = {\textbf {v}}_2 \cdot {\hat{n}} = {{\textbf {U}}}\cdot {\hat{n}} \end{aligned}$$

(18a)

$$\begin{aligned} \tau _{1\hat{n}\hat{t}} - \tau _{2\hat{n}\hat{t}} = - \bar{\nabla }_s \sigma _{21} \cdot \hat{t}, \end{aligned}$$

(18b)

On $\quad r= \epsilon :$

$$\begin{aligned} {\textbf {v}}_{2}={\textbf {v}}_{3},~~~~~ {\textbf {v}}_{2}\cdot {\hat{n}} = {\textbf {v}}_{3}\cdot {\hat{n}} = {\textbf {V}} \cdot {\hat{n}}, \end{aligned}$$

(19a)

$$\begin{aligned} \tau _{2\hat{n}\hat{t}} - \tau _{3\hat{n}\hat{t}} = -\bar{\nabla }_s \sigma _{32} \cdot \hat{t}, \end{aligned}$$

(19b)

where ${\hat{n}}, {\hat{t}}$ are the unit normal and the unit tangential vectors, respectively, and $\tau _{j}=\mu _{j}\left[ (\nabla {\textbf {v}}_{j})+(\nabla {\textbf {v}}_{j})^{T}\right]$, $j=1,2,3$ are the viscous stress tensors in Phase j, $\sigma _{21}$ and $\sigma _{32}$ are the surface tensions at the interface between Phase 2–Phase 1 and Phase 3–Phase 2, respectively, ${{\textbf {U}}} = U{\textbf {e}}_z$ is the migration velocity of the compound drop and ${{\textbf {V}}} = V{\textbf {e}}_z$ is the migration velocity of the droplet to be determined. We assume that the surface tensions at the interfaces depend linearly on the temperature, i.e., $\sigma _{21}=x_1-y_1 T_1$ and $\sigma _{32}=x_2-y_2 T_2$, where $x_i,y_i\ge 0~\text{ for }~i=1,2$ and hence $\sigma ^\prime _{21} = d \sigma _{21}/dT_1=-y_1<0,~\sigma ^\prime _{32} =d\sigma _{32}/dT_2=-y_2<0$, this shows the surface tension as a decreasing function of temperature, $\bar{\nabla }_s = \bar{\nabla }- \hat{n}(\hat{n}\cdot \bar{\nabla })$ is the surface gradient operator, and $\hat{n}$ is the unit normal. Thus, the jump in the shear stress takes the following form

$$\begin{aligned} \tau _{1\hat{n}\hat{t}} - \tau _{2\hat{n}\hat{t}}= & {} y_1 \bar{\nabla }_sT_1 \cdot \hat{t},\; \; \; \; \text{ On } \quad r=1, \\ \tau _{2\hat{n}\hat{t}} - \tau _{3\hat{n}\hat{t}}= & {} y_2\bar{\nabla }_sT_2\cdot \hat{t},\; \;\; \text{ On } \quad r=\epsilon . \end{aligned}$$

Here $T_1,\; T_2$ are the temperatures in Phase 1 and 2, respectively. We introduce the following dimensionless parameters

$$\begin{aligned} Ma_{1}= & {} \frac{y_1 T_sa}{\mu _1 U_c},\; {Ma}_{2}=\frac{y_2 T_s a}{\mu _2 U_c}~~~~~~\text{ Marangoni } \text{ numbers } \\ \lambda _{21}= & {} \frac{\mu _2}{\mu _1},~~~~~~~~~~\lambda _{32} =\frac{\mu _3}{\mu _2} ~~~~~~~~\text{ viscosity } \text{ ratio } \end{aligned}$$

where $T_s = a|\nabla T_{\infty }|$ is the space scale of the temperature, which transforms the jump in shear stress at the interface between Phase 1–Phase 2 and Phase 2–Phase 3 in the following form :

$$\begin{aligned} \tau _{1\hat{n}\hat{t}} - \lambda _{21} \tau _{2\hat{n}\hat{t}}&=Ma_{1} \bar{\nabla }_sT_1 \cdot \hat{t},\; \; \; \; \; \text{ On } \quad r=1, \end{aligned}$$

(20)

$$\begin{aligned} \tau _{2\hat{n}\hat{t}} -\lambda _{32} \tau _{3\hat{n}\hat{t}}&=Ma_{2} \bar{\nabla }_sT_2\cdot \hat{t},\; \;\; \; \; \text{ On } \quad r=\epsilon . \end{aligned}$$

(21)

2.2.1 Methodology :

The governing equations (15) with the help of boundary conditions (17), (18a), (19a) and (20)–(21) are solved in each phase. The boundary conditions (20) and (21) are satisfied since the temperature fields are known already due to the thermal distribution. We adopt a representation proposed by Palaniappan et al. [16] to express the velocity and pressure satisfying the Stokes equations, in terms of two scalars that are biharmonic and harmonic, respectively. This representation was later shown to be a complete general solution of the Stokes equations by Padmavathi et al. [17]. The notable advantage of employing this representation lies in its ability to transform the boundary value problem originally in vector form into a system of linear algebraic equations following the implementation of boundary conditions. Accordingly, the velocity and pressure fields in each phase can be represented as

$$\begin{aligned} {\textbf {v}}_j&=\nabla \times \nabla \times (\bar{{\textbf {r}}}\chi _j)+\nabla \times (\bar{{\textbf {r}}}\eta _j), \end{aligned}$$

(22)

$$\begin{aligned} p_j&=p_0+\frac{\partial }{\partial r}(\bar{{\textbf {r}}}\nabla ^2 \chi _j), \end{aligned}$$

(23)

where $\nabla ^4 \chi _j=0, \nabla ^2\eta _j=0$ and $p_0$ is a constant. It is worth noting that the far field representing the undisturbed flow can be characterized using the scalars $\chi ,~ \eta$ denoted as $\chi _0~ \text{ and }~ \eta _0$, respectively. These scalars $\chi _0, \eta _0$ in the current problem can be represented in series form as follows

$$\begin{aligned} \chi _0=\sum _{n=1} ^\infty \Big (A_{n1}^\prime r^n +B_{n1}^\prime r^{n+2}\Big ) s_n(\theta ,\phi ),~~~~~~~~~ \eta _0=0. \end{aligned}$$

(24)

where

$$\begin{aligned} s_n (\theta ,\phi )= & {} \sum _{m=0}^n P^m _n(\cos {\theta })\Big (A_{nm} \cos m\phi +B_{nm}\sin m\phi \Big ) \end{aligned}$$

are the spherical harmonics and $A_{nm}$ and $B_{nm}$ are the known constants; $P_n ^m$ is the associated Legendre polynomial of degree n and order m, respectively. The axisymmetric nature of the problem enables us to write the perturbed flow field in each phase due to the presence of the compound drop in terms of scalars in series form as follows :

$$\begin{aligned} \chi _j&=\sum _{n=1}^\infty \Big (A^\prime _{nj} r^n+B^\prime _{nj} r^{n+2}+C^\prime _{nj} r^{-(n+1)}+D_{nj} ^\prime r^{-(n-1)}\Big )s_n (\theta ,\phi ), \end{aligned}$$

(25)

$$\begin{aligned} \eta _j&=0, \end{aligned}$$

(26)

where $A^\prime _{nj},~B^\prime _{nj},~ C_{nj}^\prime ,~ D_{nj}^\prime$ for $j=1,2,3$ are the unknown coefficients with $C_{n3}^\prime = D_{n3}^\prime =0$ due to regularity condition inside the smaller drop $(r<\epsilon )$. These unknowns are determined by applying the hydrodynamic boundary conditions (17), (18a), (19a) and (20)–(21) along the surface of the drop and the cavity wall, respectively. Our objective is to compute the hydrodynamic drag exerted on the compound drop within the cavity and the droplet. It is found that only the coefficients $D^\prime _{11}~\text{ and }~D^\prime _{12}$ contribute to the evaluation of hydrodynamic drag on the compound drop and the droplet, respectively. Therefore, for brevity we provide only the coefficients $D^\prime _{11}~ \text{ and }~ D^\prime _{12}$ in Appendix (A.2).

2.3 Evaluation of hydrodynamic force

    The hydrodynamic force experienced by the compound drop and the droplet can be obtained by evaluating the following integral

$$\begin{aligned} \bar{D}_{j} =\mathop {\int \int }\limits _{S_j}(\tau _j \cdot \hat{n})\,dS_j,~~~~~j=1,2, \end{aligned}$$

(27)

where $S_j, j=1,2$ represents the surface of compound drop and the droplet, respectively, $\tau _j$ is the viscous stress tensor and $dS_j =r^2\sin \theta d\theta d\phi$ is the surface element. Evaluation of the integral given in Eq.(27) yields the following expression for drag force experienced by the compound drop and the droplet :

$$\begin{aligned} \bar{D}_1&= -8\pi ~ D_{11}^\prime ~ {\textbf {e}}_z, \end{aligned}$$

(28)

$$\begin{aligned} \bar{D}_2&= -8\pi ~D_{12}^\prime ~ {\textbf {e}}_z, \end{aligned}$$

(29)

where the unknown coefficients $D_{11}^\prime ~ \text{ and }~ D_{12}^\prime$ survive for $n=1$ and are presented in Appendix (A.2).

3 Results and discussion

3.1 Migration velocity

The migration velocity in the absence of gravity can be calculated by equating the net drag force on the compound drop and the droplet to zero when the flow is steady [18]. The use of the expressions for drag obtained in Eqs. (28)–(29) enable us to obtain the expression for the migration velocity under the assumption that the drop is freely suspended. Thus, equating Eqs.(28),(29) to zero yields the following expressions for the migration velocity of the drop and the droplet

$$\begin{aligned} {\textbf {U}}&= \Bigg ( \dfrac{Ma_1 X(Y_3Z_3-Y_4Z_2)+Ma_2 Y( Z_4Y_3-Y_5Z_2)}{Z_2Y_2-Z_1Y_3}\Bigg ){\textbf {e}}_z, \end{aligned}$$

(30)

$$\begin{aligned} {\textbf {V}}&= \Bigg (\dfrac{-1}{Z_2}(Z_1U + Ma_1 X Z_3 + Ma_2 Y Z_4)\Bigg ){\textbf {e}}_z, \end{aligned}$$

(31)

where $X,~Y,~Y_s,~s =2,..,5,~Z_m,~m=1,..,4$ are the functions of the physical parameters such as viscosity ratio, thermal conductivity ratio, Marangoni number, radius ratio, etc., and are presented in appendix. All the parameters involved in $X,Y,Y_s$ and $Z_m$, together affect the thermocapillary migration of the compound drop in a complicated way; we just provide a brief physical analysis with the aid of graphs. The migration velocities presented in Eqs. (30)–(31) are new to the literature. One may note that in the limiting case of $\epsilon \rightarrow 0$ the compound drop behaves like an isolated drop in a concentric spherical cavity and the normalized mobility of the compound drop due to the thermocapillary effect reduces to the following expression

$$\begin{aligned} \frac{{U}}{{U}_0}=\dfrac{3l^3(2+k_{21})(2+3\lambda _{21}) (l-1)^2 (2l^3+4l^2+6l+3)}{2\Big (2l^5+3\lambda _{21}l^5+3(l^5-\lambda _{21})\Big )\Big ((2+k_{21})(2+k_{10})l^3+2(1-k_{21})(1-k_{10})\Big )}, \end{aligned}$$

(32)

where ${U}_0$ is the migration velocity of an isolated drop due to thermocapillary effect in an unbounded medium. This result agrees with the expression for mobility obtained for a drop in a spherical cavity in the literature, under consideration of $l=1/\lambda$ (please see the equation on page 777 in [11] and Eq. (29) in [13]). It is worth mentioning here that as $\epsilon \rightarrow 1$ the droplet starts to migrate with the migration velocity of the compound drop, i.e., in the limiting case of $\epsilon \rightarrow 1$, $U=V$ and it reduces to

$$\begin{aligned} U = V&= \dfrac{3P l^3\Big (6 l^2 + 4 l^3 + 6 l + 4 + \lambda _{21} \lambda _{32} (4 l^3 + 3 l^2 - 3 l - 4) \Big ) }{Q\Big ( (l^3 - 1) ( 2 k_{10} + 2 k_{21} k_{32}) + k_{10} k_{21} k_{32} (2 + l^3) + 4 l^3 + 2\Big )},\, \end{aligned}$$

(33)

where

$$\begin{aligned} P&= M_{a1}\Big (9 - 25 l^2 + 16 l^5 + \lambda _{32}( 15 l^2 + 3 l^5 - 18 )\Big ) + M_{a2}\Big (-9 - 6 l^5 + \lambda _{21} (9 - 25 l^2 + 16 l^5)\Big ), \\ Q&= \lambda _{21} \lambda _{32}\Big ( 150 l^4 - 12 l^8 + 76 l^8 + 72 l^7 - 12 l^6 + 64 l^5 + 150 l^4 - 243 l - 17 l^2 - 204 + \lambda _{32}(108 l \\&\quad - 18 l^7 - 18 l^6 - 72 l^5 - 90 l^4 - 18 l^3 + 48 l^2 + 72) + \lambda _{21} \lambda _{32}( 28 l^8 + 21 l^7 - 21 l^6 + 112 l^5 + 105 l^4 \\ {}&\quad - 273 l^3 + 114 l^3 - 266 l^2 + 126 l + 168)\Big ) - \lambda _{32}(54 l + 36 + 24 l^5 + 54 l^2 + 24 l^8 + 36 l^7 + 36 l^3 + 36 l^6) \\ {}&\quad + 60 l^3 + 90 l^2 + 90 l + 60 l^6 + 60 l^7 + 40 l^8 + 40 l^5 + 60. \end{aligned}$$

Table 1 Numerical values of migration velocity U of a compound drop within a spherical cavity at arbitrary $a/b~~ \text{ and }~~ k_{10}$ and fixed parameters $\lambda _{21}=0.8,~ \lambda _{32}=1.2,~ \epsilon =0.4,~ Ma_1=10,~ Ma_2=5$, $k_{32}=0.6,~ k_{21}=0.5$

Fig. 2

Variation of migration velocity of a compound drop inside a spherical cavity, (A) versus a/b for various values of $\lambda _{32}$ by fixing other parameters as $\epsilon =0.2,~ k_{10}=1,~ k_{32}=1.9,~ k_{21}=0.5,~ \lambda _{21}=1.5,~ Ma_1=2,~ Ma_2=10$. (B) versus $k_{10}$ for arbitrary a/b at fixed values of $\epsilon =0.3,~ \lambda _{21}=1.2,~ \lambda _{32}=0.4,~ Ma_1=5,~ Ma_2=15,~ k_{32}=0.3,~ k_{21}=1.6$. (C) versus $Ma_1$ for different values of $\lambda _{21}$ and fixed parameters $a/b=0.5,~ \epsilon =0.2,~ \lambda _{32}=1.1,~ k_{10}=1,~ k_{21}=0.5,~ k_{32}=1.2,~ Ma_2=20$. (D) versus $Ma_2$ at different vales of a/b and fixed parameters $\epsilon =0.4,~ k_{10}=1,~ k_{21}=0.5,~ k_{32}=1.9,~ Ma_1=2,~ \lambda _{32}=6,~ \lambda _{21}=1.5$. (E) versus $\epsilon$ at different values of $k_{10}$ and fixed parameters $a/b=0.6,~ Ma_1=10,~ Ma_2=20,~ \lambda _{21}=1.3,~ \lambda _{32}=5,~ k_{21}=0.5$, $k_{32}=1$

The variation of migration velocity of the compound drop obtained in Eq. (30) is presented in Fig. 2. As expected, the migration velocity decreases as the gap between the compound drop surface and the cavity wall, which is the ratio a/b, increases. It can be further stated from Fig. 2A that an increase in the viscosity ratio between Phase 3 and Phase 2 causes a dip in the migration velocity. A higher value of viscosity ratio between Phase 3 and Phase 2 retards the motion of compound drop leading to a decay in the migration velocity. Figure 2B demonstrates the migration velocity versus $k_{10}$ at different values of a/b. It is found that the migration velocity decreases monotonically with an increase in $k_{10}$ or a decrease in the cavity wall conductivity $k_w$. This can be attributed to the fact that the applied constant temperature gradient $\nabla T_{\infty }$ in a drop-in cavity system increases with a decrease in $k_w$. An increase in the constant temperature gradient causes the temperature difference across the drop’s surface to decrease. This reduction in the surface temperature difference weakens the force that drives the drop’s movement due to temperature differences, leading to a decrease in the speed at which the drop moves. Variation of migration velocity versus $Ma_1$ for different values of viscosity ratio between Phase 2 and Phase 1, $\lambda _{21}$ is presented in Fig. 2C by keeping the other parameters fixed at $a/b=0.5,~ \epsilon =0.2,~ \lambda _{32}=1.1,~ k_{10}=1,~ k_{21}=0.5,~ k_{32}=1.2,~ Ma_2=20$. It is found that at a fixed value of $\lambda _{21}$ the migration velocity increases monotonically with the Marangoni number $Ma_1$. An increase in $Ma_1$ causes the dominance of thermocapillary effect over the viscous force. Viscous force retards the motion of the drop but dominance of thermocapillary effect as $Ma_1$ increases, overcomes the retardation and thus an increase in the migration velocity is observed. Note that it has been shown experimentally that the Marangoni number can be in the range of $5.4-810$ [19], and it has been further shown that the Marangoni number can be as high as $10^4$ and the experimental results agree with theoretical prediction of migration velocity for Marangoni number values up to 9600 [20]. In the present investigation, the Marangoni number values are taken up to 100. Figure 2D depicts the variation in migration velocity versus $Ma_2$ at different values of radius ratio a/b by keeping the other parameters fixed at $\epsilon =0.4,~ k_{10}=1,~ k_{21}=0.5,~ k_{32}=1.9,~ Ma_1=2,~ \lambda _{32}=6,~ \lambda _{21}=1.5$. It is found that at $Ma_2=0$, which is the Marangoni number at the interface between Phase 2 and Phase 3, the drop has a nonzero migration velocity at all values of a/b. This is due to consideration of a nonzero value of $Ma_1=2$ which assists in the migration of compound drop. As $Ma_2$ increases, the migration velocity decreases monotonically at all values of a/b and the compound drop slows down. Variation of the migration velocity of compound drop versus the radius $\epsilon$ of the droplet is presented in Fig. 2E for different values of $k_{10}$ by keeping the other parameters $a/b=0.6,~ Ma_1=10,~ Ma_2=20,~ \lambda _{21}=1.3,~ \lambda _{32}=5,~ k_{21}=0.5,~ k_{32}=1$ fixed. It may be observed that the droplet radius $\epsilon$ influences the migration velocity of compound drop significantly. A smaller $\epsilon$ value implies a higher migration velocity compared to a higher $\epsilon$ value. The migration velocity was further found to be a nonmonotonic function of $\epsilon$. This behavior may be attributed to the fact that migration velocity of compound drop decreases monotonically for $\epsilon <0.85$ and for $\epsilon >0.85$, the compound drop migrates with a higher velocity as compared to that of the droplet (please see Table 3 and 4 for comparison) and as $\epsilon \rightarrow 1$, the compound drop and the droplet move with the same velocity.

Fig. 3

Variation of migration velocity of a droplet within a drop placed concentrically in a spherical cavity (A) versus $\epsilon$ at different values of $k_{10}$ and fixed parameters $a/b=0.6$, $Ma_1=10$, $Ma_2=20$, $\lambda _{21}=1.3$, $\lambda _{32}=5$, $k_{21}=0.5$, $k_{32}=1.1$. (B) versus $\epsilon$ at different values of $k_{32}$ and other parameters $a/b=0.6$, $Ma_1=20$, $Ma_2=10$, $\lambda _{21}=3$, $\lambda _{32}=4.5$, $k_{21}=1.5$, $k_{10}=1$ fixed (C) versus $Ma_2$ at different values of $\epsilon$ and other parameters $a/b=0.4$, $k_{10}=1$, $k_{21}=0.5$, $k_{32}=1.9$, $\lambda _{21}=1.5$, $\lambda _{32}=6$, $Ma_1=20$ fixed

Figure 3A depicts the variation of migration velocity of the droplet versus its radius $\epsilon$ for different values of $k_{10}$ at fixed values of the parameters $a/b=0.6,~ Ma_1=10,~ Ma_2=20,~ \lambda _{21}=1.3,~ \lambda _{32}=5,~ k_{21}=0.5,~ k_{32}=1.1$; the fixed parameters are the same as considered for compound drop in Fig. 2E. Similar to the behavior of the migration velocity of compound drop, the migration velocity of droplet is found to be a nonmonotonic function of $\epsilon$ at all values of $k_{10}$, but the droplet moves faster than the compound drop. As $\epsilon$ increases, the migration velocity of the droplet decreases and reaches a minimum (as can be seen from Table 4 as well) which further starts to increase for $\epsilon >0.8$ in order to match with the migration velocity of the compound drop, since in the limiting case of $\epsilon \rightarrow 1$, the droplet migrates with a velocity equal to that of compound drop (see Eq. (33)). Figure 3B demonstrates the effects of variation in $\epsilon$ on the migration velocity of droplet for various values of $k_{32}$ and the fixed parameters $a/b=0.6,~ Ma_1=20,~ Ma_2=10,~ \lambda _{21}=3,~ \lambda _{32}=4.5,~ k_{21}=1.5,~ k_{32}=8$. In general the migration velocity decreases with $\epsilon$ at any value of $k_{32}$ and for $\epsilon$ values smaller than 0.85, the droplet with smaller $k_{32}$ values has higher migration velocity. However, this trend reverses as $\epsilon$ becomes greater than about 0.85 and the drop with a smaller $k_{32}$ value may move with a lower velocity. Figure 3C presents the effect of variation in $Ma_2$ on the migration velocity of droplet for different values of $\epsilon$ at fixed values of the parameters $a/b=0.4,~ k_{10}=1,~ k_{21}=0.5,~k_{32}=1.9,~ \lambda _{21}=1.5,~ \lambda _{32}=6,~ Ma_1=20$. It is found that the droplet’s migration velocity is monotonic increasing function of $Ma_2$, and a higher value of $Ma_2$ signifies the dominance of thermocapillary effect which assists the migration of droplet. It can be further observed that a smaller droplet migrates with ease than a droplet with higher radius $\epsilon$.

The numerical values of the migration velocity of compound drop in a spherical cavity are presented in Table 1 for various values of $k_{10}$ and a/b with fixed values of the parameters $\lambda _{21}=0.8,~ \lambda _{32}=1.2,~ \epsilon =0.4,~ Ma_1=10,~ Ma_2=5,~ k_{32}=0.6,~ k_{21}=0.5$. The migration velocity is observed to be a monotonic decreasing function of a/b which is expected since a smaller value of a/b represents the drop being away from the cavity wall which leads to a higher migration velocity compared to a higher value of a/b which reflects the drop being in the vicinity of the cavity wall. Table 2 presents the numerical values of the migration velocity of a compound drop for various values of $Ma_1$ and a/b at fixed values of the parameters $\lambda _{21}=1.8,~ \lambda _{32}=0.6,~ \epsilon =0.2,~ k_{10}=1,~ Ma_2=20,~ k_{32}=5,~ k_{21}=0.5$. In general, the migration velocity is found to be a monotonic decreasing function of a/b.

Table 2 Numerical values of the migration velocity U of a compound drop inside a spherical cavity at various $a/b~~ \text{ and }~~Ma_1$ and fixed parameters $\lambda _{21}=1.8,~ \lambda _{32}=0.6,~ \epsilon =0.2,~ k_{10}=1,~Ma_2=20,$ $k_{32}=5,~ k_{21}=0.5$

Table 3 Numerical values of the migration velocity U of a compound drop inside a spherical cavity at various $\epsilon ~ \text{ and }~ Ma_2$ and fixed parameters $a/b=0.7,~k_{10} =1.2,~ k_{21}=0.5,~ k_{32}=1.7,$ $\lambda _{21}=0.3,~ \lambda _{32}=0.6,~ Ma_1=100.$

Table 4 Numerical values of the migration velocity V of droplet within a drop placed concentrically in a spherical cavity at various $\epsilon ~ \text{ and }~ Ma_2$ and fixed parameters $a/b=0.7,~k_{10} =1.2,~ k_{21}=0.5,~ k_{32}=1.7,$ $\lambda _{21}=0.3,~ \lambda _{32}=0.6,~ Ma_1=100.$

Tables 3 and 4 present a comparison of the numerical values of the migration velocity U of compound drop with that of the droplet at various $\epsilon ~ \text{ and }~ Ma_2$ and fixed parameters $a/b=0.7,~k_{10} =1.2,~ k_{21}=0.5,~ k_{32}=1.7,$ $\lambda _{21}=0.3,~ \lambda _{32}=0.6,~ Ma_1=100.$ It can be seen from both the tables that the droplet migrates with a higher velocity than the compound drop. This trend continues till $\epsilon <0.6$, but for values $\epsilon \ge 0.6$, the compound drop migrates with a higher velocity than the droplet and it can be seen that as $\epsilon \rightarrow 1$, the compound drop and the droplet both move with the same migration velocity. In general, the migration velocity is found to be a nonmonotonic function of the droplet radius $\epsilon$ whereas a monotonic increasing function of $Ma_2$.

3.2 Heat source

Consider a heat source of strength $\xi$ located at ${\textbf {r}}_0=(0,0,h)$ placed in the thermal field where $h>a$ and the undisturbed uniform flow is along the z-axis. We can express the ambient temperature representing the undisturbed thermal field using the following equation

$$\begin{aligned} T_\infty (r,\theta , \phi )&=T_0+\frac{\xi }{|{\textbf {r}}-{\textbf {r}}_0|}. \end{aligned}$$

(34)

In order to compare the above-mentioned temperature with the ambient temperature $T_{\infty }=T_0+r\cos \theta$, we expand the ambient temperature $T_\infty$ given in Eq. (34) in positive powers of r to yield the following expression :

$$\begin{aligned} T_\infty (r,\theta , \phi )= T_0+\frac{\xi }{h} \sum _{n=1}^\infty \Big (\frac{r}{h}\Big )^n P_n(\cos \theta ). \end{aligned}$$

(35)

The above series converges in the domain $a < h$, and for the hydrodynamic problem, we choose the scalars $\chi _0,~ \eta _0$ as given in Eq. (24). The hydrodynamic force in this case is obtained in the following form:

$$\begin{aligned} \bar{D}_{hs}= & {} \dfrac{8\pi }{Z_2Y_1(l^2-2l+1)} \Bigg (U_{hs}(Y_2Z_2-Y_3Z_1)-\dfrac{Ma_1\xi X (Y_3Z_3-Y_4Z_2)}{h^2}\nonumber \\{} & {} - \dfrac{Ma_2\xi Y (Y_3Z_4-Y_5Z_2)}{h^2}\Bigg ){\textbf {e}}_z. \end{aligned}$$

(36)

The migration velocity of the compound drop in a cavity due to presence of a heat source is obtained as

$$\begin{aligned} {{\textbf {U}}}_{hs} = \dfrac{\xi }{h^2}\Bigg ( \dfrac{Ma_1 X(Y_3Z_3-Y_4Z_2)+Ma_2 Y( Z_4Y_3-Y_5Z_2)}{Z_2Y_2-Z_1Y_3}\Bigg ){\textbf {e}}_z, \end{aligned}$$

(37)

where $Y_s,~s=1..,5$ and $Z_i$, $i=1,2,3$ are the constants given in Appendix (A.2).

Fig. 4

Variation of migration velocity of a compound drop inside a cavity versus h (A) at arbitrary $\lambda _{21}$ by fixing $\xi =1$, $\epsilon =0.2$, $a/b=0.5$, $Ma_1=1$, $Ma_2 =2$, $\lambda _{32}=0.7$, $k_{10}=3.5$, $k_{21}=0.4$, $k_{32}=0.7$. (B) at different $Ma_1$ by fixing $\xi =1$, $a/b=0.5$, $\epsilon =0.4$, $Ma_2=4$, $\lambda _{21}=1.4$, $\lambda _{32} =0.9$, $k_{10} =3$, $k_{21} =0.2$, $k_{32} =0.3$

It can be inferred from Eq. (37) that the migration velocity is sensitive to the position h of the heat source. Figure 4A depicts the variation of migration velocity of compound drop versus h at different values of $\lambda _{21}$ by keeping the other parameters fixed at $\xi =1,~ \epsilon =0.2,~ a/b=0.5,~ Ma_1=1,~ Ma_2 =2,~ \lambda _{32}=0.7,~ k_{10}=3.5,~ k_{21}=0.4,~ k_{32}=0.7$. It may be observed from the figure that the migration velocity decreases monotonically with h at all values of $\lambda _{21}$; increase in $\lambda _{21}$ slows down the compound drop due to dominant viscous force. Effect of variation in h on the migration velocity of compound drop at different values of $Ma_1$ is presented in Fig. 4B at fixed values of the parameters $\xi =1,~ a/b=0.5,~ \epsilon =0.4,~ Ma_2=4,~ \lambda _{21}=1.4,~ \lambda _{32} =0.9,~ k_{10} =3,~ k_{21} =0.2,~ k_{32} =0.3$. The migration velocity is found to be a monotonic decreasing function of h at all values of $Ma_1$. Presence of heat source near the surface of compound drop affects the migration velocity, and as the position of heat source is changed to a position near the cavity wall, the migration velocity reduces by a considerable amount.

4 Conclusion

In this study, we have investigated the thermocapillary migration of a compound drop within a spherical cavity under the creeping flow conditions. The migration was driven by a constant temperature gradient along the centerline of the drop and cavity. The compound drop remained spherical due to the consideration of a very small capillary number, and its translation velocity was determined under force-free conditions. This study integrated the hydrodynamic and thermal aspects of a compound drop by using the Stokes equations for flow fields and the conduction equation for temperature fields, and derived closed-form expressions for velocity and pressure, allowing us to determine the hydrodynamic force acting on the compound drop. The key finding of the study was the migration velocity and its dependence over the various parameters involved. The migration velocity was found to be a decreasing function of the ratio of the compound drop’s radius to the cavity radius, and it increased with an increase in the Marangoni number $Ma_1$. It was also found that the radius $\epsilon$ of the droplet influences the migration velocity. The migration velocity was obtained in a particular case of presence of heat source in the fluid envelope, and it was found to be a monotonic decreasing function of the position h of the heat source. This research provided a closed-form expression for the migration velocity of the confined compound drop. Additionally, the study explained the effect of the presence of a heat source on the motion of a compound drop within the cavity in the context of uniform far field.

Appendix

1.1 Thermal distribution

$$\begin{aligned} a_1&= \dfrac{X_2l^3}{X_1},~~ b_1 = \dfrac{3}{X_1}\Big (2k_{21}l^3 + 2k_{32}l^3 + 4l^3 + 2\epsilon ^3l^3 + k_{21}k_{32}l^3 - 2\epsilon ^3k_{21}l^3 - 2\epsilon ^3k_{32}l^3 + 2\epsilon ^3k_{21} k_{32}l^3\Big ), \\ b_{1}^\prime&= \dfrac{-3}{X_1}\Big (2k_{21}l^3 - k_{32}l^3 - 2l^3 - \epsilon ^3l^3 + k_{21}k_{32}l^3 - 2\epsilon ^3k_{21}l^3 + \epsilon ^3 k_{32}l^3 + 2\epsilon ^3 k_{21}k_{32}l^3\Big ), \\ c_1&= \dfrac{9l^3(k_{32} + 2)}{X_1}, ~~~~~~~~~~~ c_{1}^\prime = \dfrac{-9\epsilon ^3l^3(k_{32} - 1)}{X_1}, ~~~~~~~~~~ d_1 = \dfrac{27l^3}{X_1}.\\ X_1&= 2k_{32} - 4k_{21} - 4k_{10} + 4k_{10}k_{21} - 2k_{10}k_{32} - 2k_{21}k_{32} - 2\epsilon ^3k_{10} + 4\epsilon ^3k_{21} - 2\epsilon ^3k_{32} + 4k_{10}l^3 + 4k_{21}l^3 \\ {}&\quad + 4k_{32}l^3 + 2\epsilon ^3 + 8l^3 + 4\epsilon ^3l^3 + 2k_{10}k_{21}l^3 + 2k_{10}k_{32}l^3 + 2k_{21}k_{32}l^3 + 2\epsilon ^3k_{10}l^3 - 4\epsilon ^3k_{21}l^3 \\ {}&\quad -4\epsilon ^3k_{32}l^3 + 2k_{10}k_{21}k_{32} - 4\epsilon ^3k_{10}k_{21} + 2\epsilon ^3k_{10}k_{32} - 4\epsilon ^3k_{21}k_{32} + 4\epsilon ^3k_{10}k_{21}k_{32} + k_{10}k_{21}k_{32}l^3 \\ {}&\quad - 2\epsilon ^3k_{10}k_{21}l^3 - 2\epsilon ^3k_{10}k_{32}l^3 + 4\epsilon ^3k_{21}k_{32}l^3 + 2\epsilon ^3k_{10}k_{21}k_{32}l^3 + 4,\\ X_2&= 4k_{10} - 2k_{21} + k_{32} + 2l^3\epsilon ^3 - 4k_{10}k_{21} + 2k_{10}k_{32} - k_{21}k_{32} - 4k_{10}l^3 + 2k_{21}l^3 + 2k_{32}l^3 \\ {}&\quad + 2k_{10}\epsilon ^3 + 2k_{21}\epsilon ^3 - k_{32}\epsilon ^3 + 4l^3 + \epsilon ^3 - 2k_{10}k_{21}l^3 - 2k_{10}k_{32}l^3 + k_{21}k_{32}l^3 + 4k_{10}k_{21}\epsilon ^3 \\ {}&\quad -2k_{10}k_{32}\epsilon ^3 - 2k_{21}k_{32}\epsilon ^3 - 2k_{10}l^3\epsilon ^3 - 2k_{21}l^3\epsilon ^3 - 2k_{32}l^3\epsilon ^3 - 2k_{10}k_{21}k_{32} - k_{10}k_{21}k_{32}l^3\\ {}&\quad - 4k_{10}k_{21}k_{32}\epsilon ^3 + 2k_{10}k_{21}l^3\epsilon ^3 + 2k_{10}k_{32}l^3\epsilon ^3 + 2k_{21}k_{32}l^3\epsilon ^3 - 2k_{10}k_{21}k_{32}l^3\epsilon ^3 + 2, \\ X&=\dfrac{9l^3(k_{32} - \epsilon ^3k_{32} + \epsilon ^3 + 2)}{X_1},~~~~~~~~~~ Y= \dfrac{27\epsilon ^4 l^3}{X_1}. \end{aligned}$$

1.2 Hydrodynamics distribution

$$\begin{aligned} D_{11}^\prime&= \dfrac{-(UY_2 + VY_3 + Ma_1 X Y_4 + Ma_2 Y Y_5)}{Y_1(l^2 - 2l + 1)}, \\ D_{12}^\prime&= \dfrac{1}{Y_1}(UZ_1 + Z_2 V + Ma_1 X Z_3+Ma_2 Y Z_4). \\ Y_1&= 6(1 - l)(12l - 12\epsilon - 8\lambda _{21} + 8\lambda _{32} - 18\epsilon l + 8\epsilon \lambda _{21} - 18\epsilon \lambda _{32} - 6l\lambda _{21} + 12l\lambda _{32} - 8\lambda _{21}\lambda _{32} \\ {}&\quad - 18\epsilon l^2 - 12\epsilon l^3 + 6\epsilon ^3 l + 18\epsilon ^5 l - 12\epsilon ^6 l + 18\epsilon ^8 l - 8\epsilon ^3\lambda _{21} + 8\epsilon ^5\lambda _{21} - 8\epsilon ^6\lambda _{21} + 8\epsilon ^8\lambda _{21} + 22\epsilon ^3\lambda _{32} \\ {}&\quad - 24\epsilon ^5\lambda _{32} + 36\epsilon ^6\lambda _{32} - 24\epsilon ^8\lambda _{32} + 6l^2\lambda _{21} + 8l^3\lambda _{21} + 12l^2\lambda _{32} + 8l^3\lambda _{32} + 4\epsilon ^3 + 12\epsilon ^5 8\epsilon ^6 + 12\epsilon ^8 \\ {}&\quad + 12l^2 + 8l^3 + 6\epsilon ^3 l^2 + 4\epsilon ^3 l^3 + 18\epsilon ^5 l^2 + 12\epsilon ^5 l^3 - 12\epsilon ^6 l^2 - 8\epsilon ^6 l^3 + 18\epsilon ^8 l^2 + 12\epsilon ^8 l^3 \\ {}&\quad + 6l^2\lambda _{21}\lambda _{32} + 8l^3\lambda _{21}\lambda _{32} + 6\epsilon ^3 l^2\lambda _{21} + 8\epsilon ^3 l^3\lambda _{21} - 6\epsilon ^5 l^2\lambda _{21} - 8\epsilon ^5 l^3\lambda _{21} + 6\epsilon ^6 l^2\lambda _{21} + 8\epsilon ^6 l^3\lambda _{21} \\ {}&\quad - 6\epsilon ^8 l^2\lambda _{21} - 8\epsilon ^8 l^3\lambda _{21} + 33\epsilon ^3 l^2\lambda _{32} + 22\epsilon ^3 l^3\lambda _{32} - 36\epsilon ^5 l^2\lambda _{32} - 24\epsilon ^5 l^3\lambda _{32} + 54\epsilon ^6 l^2\lambda _{32} + 36\epsilon ^6 l^3\lambda _{32} \\ {}&\quad - 36\epsilon ^8 l^2\lambda _{32} - 24\epsilon ^8 l^3\lambda _{32} + 6\epsilon l\lambda _{21} - 27\epsilon l\lambda _{32} + 12\epsilon \lambda _{21}\lambda _{32} - 6l\lambda _{21}\lambda _{32} - 6\epsilon l^2\lambda _{21} - 8\epsilon l^3\lambda _{21} \\ {}&\quad - 6\epsilon ^3 l\lambda _{21} + 6\epsilon ^5 l\lambda _{21} - 6\epsilon ^6 l\lambda _{21} + 6\epsilon ^8 l\lambda _{21} - 27\epsilon l^2\lambda _{32} - 18\epsilon l^3\lambda _{32} + 33\epsilon ^3 l\lambda _{32} - 36\epsilon ^5 l\lambda _{32} + 54\epsilon ^6 l\lambda _{32} \\ {}&\quad - 36\epsilon ^8 l\lambda _{32} - 4\epsilon ^3\lambda _{21}\lambda _{32} - 16\epsilon ^5\lambda _{21}\lambda _{32} + 16\epsilon ^6\lambda _{21}\lambda _{32} - 16\epsilon ^8\lambda _{21}\lambda _{32} + 9\epsilon l\lambda _{21}\lambda _{32} - 9\epsilon l^2\lambda _{21}\lambda _{32} \\ {}&\quad -12\epsilon l^3\lambda _{21}\lambda _{32} - 3\epsilon ^3 l\lambda _{21}\lambda _{32} - 12\epsilon ^5 l\lambda _{21}\lambda _{32} + 12\epsilon ^6 l\lambda _{21}\lambda _{32} - 12\epsilon ^8 l\lambda _{21}\lambda _{32} + 3\epsilon ^3 l^2\lambda _{21}\lambda _{32} \\ {}&\quad + 4\epsilon ^3 l^3\lambda _{21}\lambda _{32} + 12\epsilon ^5 l^2\lambda _{21}\lambda _{32} + 16\epsilon ^5 l^3\lambda _{21}\lambda _{32} - 12\epsilon ^6 l^2\lambda _{21}\lambda _{32} - 16\epsilon ^6 l^3\lambda _{21}\lambda _{32} + 12\epsilon ^8 l^2\lambda _{21}\lambda _{32} \\ {}&\quad +16\epsilon ^8 l^3\lambda _{21}\lambda _{32} + 8) \\ Y_2&= 3 l (12\lambda _{32} - 12\lambda _{21} - 18\epsilon + 18\epsilon \lambda _{21} - 27\epsilon \lambda _{32} - 12\lambda _{21}\lambda _{32} - 12\epsilon l^5 - 12\epsilon ^3\lambda _{21} + 12\epsilon ^5\lambda _{21} - 18\epsilon ^6\lambda _{21} \\ {}&\quad + 12\epsilon ^8\lambda _{21} + 33\epsilon ^3\lambda _{32} - 36\epsilon ^5\lambda _{32} + 54\epsilon ^6\lambda _{32} - 36\epsilon ^8\lambda _{32} + 12l^5\lambda _{21} + 8l^5\lambda _{32} + 6\epsilon ^3 + 18\epsilon ^5 \\ {}&\quad -12\epsilon ^6 + 18\epsilon ^8 + 8l^5 + 4\epsilon ^3l^5 + 12\epsilon ^5l^5 - 8\epsilon ^6l^5 + 12\epsilon ^8l^5 + 12l^5\lambda _{21}\lambda _{32} + 12\epsilon ^3l^5\lambda _{21} + 10\epsilon ^6l^2\lambda _{21} \\ {}&\quad - 12\epsilon ^5l^5\lambda _{21} + 8\epsilon ^6l^5\lambda _{21} - 12\epsilon ^8l^5\lambda _{21} + 22\epsilon ^3l^5\lambda _{32} - 24\epsilon ^5l^5\lambda _{32} + 36\epsilon ^6l^5\lambda _{32} - 24\epsilon ^8l^5\lambda _{32} \\ {}&\quad +27\epsilon \lambda _{21}\lambda _{32} - 10\epsilon l^2\lambda _{21} - 8\epsilon l^5\lambda _{21} - 18\epsilon l^5\lambda _{32} - 21\epsilon ^3\lambda _{21}\lambda _{32} - 24\epsilon ^5\lambda _{21}\lambda _{32} + 6\epsilon ^6\lambda _{21}\lambda _{32} \\ {}&\quad - 24\epsilon ^8\lambda _{21}\lambda _{32} - 15\epsilon l^2\lambda _{21}\lambda _{32} - 12\epsilon l^5\lambda _{21}\lambda _{32} + 25\epsilon ^3l^2\lambda _{21}\lambda _{32} - 4\epsilon ^3l^5\lambda _{21}\lambda _{32} + 30\epsilon ^6l^2\lambda _{21}\lambda _{32} \\ {}&\quad +24\epsilon ^5l^5\lambda _{21}\lambda _{32} - 36\epsilon ^6l^5\lambda _{21}\lambda _{32} + 24\epsilon ^8l^5\lambda _{21}\lambda _{32} + 12), \\ Y_3&= 3 l\epsilon \lambda _{21} (l - 1)^2 (2l^3 + 4l^2 + 6l + 3) (5\epsilon ^2\lambda _{32} - 3\lambda _{32} + 6\epsilon ^5\lambda _{32} + 2\epsilon ^5 - 2), \\ Y_4&= - l (l - 1)^2 (2l^3 + 4l^2 + 6l + 3) (4\lambda _{32} - 6\epsilon - 9\epsilon \lambda _{32} + 11\epsilon ^3\lambda _{32} - 12\epsilon ^5\lambda _{32} + 18\epsilon ^6\lambda _{32} \\ {}&\quad -12\epsilon ^8\lambda _{32} + 2\epsilon ^3 + 6\epsilon ^5 - 4\epsilon ^6 + 6\epsilon ^8 + 4), \\ Y_5&= -2 l \epsilon \lambda _{21} (l - 1)^2 (2l^3 + 4l^2 + 6l + 3) (5\epsilon ^5 - 5\epsilon ^3 + 5\epsilon ^2 - 1), \\ Z_1&= 3\epsilon (2l + 8\lambda _{21} - 12\lambda _{32} - 2l\lambda _{21} + 3l\lambda _{32} + 12\lambda _{21}\lambda _{32} + 6\epsilon ^{2}l - 12\epsilon ^{5}l - 8\epsilon ^{5}\lambda _{21} + 24\epsilon ^{5}\lambda _{32} \\ {}&\quad 12l^{2}\lambda _{21} - 2l^{3}\lambda _{21} + 8l^{4}\lambda _{21} + 18l^{2}\lambda _{32} + 18l^{3}\lambda _{32} + 18l^{4}\lambda _{32} - 12\epsilon ^{5} + 12l^{2} + 12l^{3} + 12l^{4} \\ {}&\quad + 12\epsilon ^{2}l^{2} + 8\epsilon ^{2}l^{3} + 4\epsilon ^{2}l^{4} - 12\epsilon ^{5}l^{2} - 2\epsilon ^{5}l^{3} + 8\epsilon ^{5}l^{4} - 18l^{2}\lambda _{21}\lambda _{32} - 3l^{3}\lambda _{21}\lambda _{32} + 12l^{4}\lambda _{21}\lambda _{32} \\ {}&\quad +12\epsilon ^{5}l^{2}\lambda _{21} + 2\epsilon ^{5}l^{3}\lambda _{21} - 8\epsilon ^{5}l^{4}\lambda _{21} - 24\epsilon ^{2}l^{2}\lambda _{32} - 16\epsilon ^{2}l^{3}\lambda _{32} - 8\epsilon ^{2}l^{4}\lambda _{32} + 24\epsilon ^{5}l^{2}\lambda _{32} + 4\epsilon ^{5}l^{3}\lambda _{32} \\ {}&\quad - 16\epsilon ^{5}l^{4}\lambda _{32} - 3l\lambda _{21}\lambda _{32} + 2\epsilon ^{5}l\lambda _{21} - 12\epsilon ^{2}l\lambda _{32} + 24\epsilon ^{5}l\lambda _{32} + 16\epsilon ^{5}\lambda _{21}\lambda _{32} - 4\epsilon ^{5}l\lambda _{21}\lambda _{32} \\ {}&\quad -24\epsilon ^{5}l^{2}\lambda _{21}\lambda _{32} - 4\epsilon ^{5}l^{3}\lambda _{21}\lambda _{32} + 16\epsilon ^{5}l^{4}\lambda _{21}\lambda _{32} - 8), \\ Z_2&= 3\epsilon (1 - l)(12l - 8\lambda _{21} + 12\lambda _{32} - 6l\lambda _{21} + 18l\lambda _{32} - 12\lambda _{21}\lambda _{32} + 18\epsilon ^{5}l + 8\epsilon ^{5}\lambda _{21} - 24\epsilon ^{5}\lambda _{32} + 6l^{2}\lambda _{21} \\ {}&\quad + 8l^{3}\lambda _{21} + 18l^{2}\lambda _{32} + 12l^{3}\lambda _{32} + 12\epsilon ^{5} + 12l^{2} + 8l^{3} + 18\epsilon ^{5}l^{2} + 12\epsilon ^{5}l^{3} + 9l^{2}\lambda _{21}\lambda _{32} + 12l^{3}\lambda _{21}\lambda _{32} \\ {}&\quad -6\epsilon ^{5}l^{2}\lambda _{21} - 8\epsilon ^{5}l^{3}\lambda _{21} - 36\epsilon ^{5}l^{2}\lambda _{32} - 24\epsilon ^{5}l^{3}\lambda _{32} - 9l\lambda _{21}\lambda _{32} + 6\epsilon ^{5}l\lambda _{21} - 36\epsilon ^{5}l\lambda _{32} - 16\epsilon ^{5}\lambda _{21}\lambda _{32} \\ {}&\quad - 12\epsilon ^{5}l\lambda _{21}\lambda _{32} + 12\epsilon ^{5}l^{2}\lambda _{21}\lambda _{32} + 16\epsilon ^{5}l^{3}\lambda _{21}\lambda _{32} + 8), \\ Z_3&=\epsilon (l-1)^2(4l^2+7l+4)(3\lambda _{32}-4\epsilon ^2\lambda _{32}+4\epsilon ^5\lambda _{32}+2\epsilon ^2-2\epsilon ^5 + 2), \\ Z_4&= 2\epsilon (l - 1)(6l - 4\lambda _{21} - 3l\lambda _{21} - 15l\epsilon ^3 + 3l^2\lambda _{21} + 4l^3\lambda _{21} - 10\epsilon ^3 + 6l^2 + 4l^3 - 15\epsilon ^3l^2 - 10\epsilon ^3l^3 + 4). \end{aligned}$$