Dynamics of a linear source epidemic system with diffusion and media impact

Abstract

This paper studies an impact of media epidemic system with diffusion and linear source. We first derive the uniform bounds of solutions to impact on media reaction diffusion system. Then, the basic reproduction number is calculated and the threshold dynamics of impact media reaction diffusion system is also given and the Kuratowski measure $\kappa$ of non-compactness is also considered. In addition, assume the spatial environment is homogeneous, it is shown that the unique endemic equilibrium of the system is global stability by constructing suitable Lyapunov function. Finally, we discuss the asymptotic profile of the system when the diffusion rate of the susceptible (infected) individuals for the system tends to zero or infinity. The main results show that the activities of infected individuals can only be at low risk, and then the virus eventually will be extinct, that is, to control the entry of viruses from abroad and increase the detection of domestic viruses. Finally, some numerical simulations are worked out to confirm the results obtained in this paper.

1 Introduction

In recent decades, environmental heterogeneity and individual mobility have played an important role in our lives. More and more scholars have interest considered the dynamical behaviors of the epidemic model with diffusion process because it is more practical than the traditional ordinary differential epidemic model. Research shows that the expansion of the reactive diffusion system as an infectious disease model and environmental heterogeneity have an important impact on the process of disease transmission [1,2,3,4,5,6,7].

The main contributions of [8] concern the existence, uniqueness and asymptotic dynamical behaviors of equilibrium of reaction–diffusion SIS epidemic system as the diffusion rate of the susceptible (infected) individuals tends to zero or infinity. In 2007, Allen et al. also studied a discrete reaction–diffusion SIS epidemic system in [9]. In 2008, in order to understand the spatial heterogeneity of the environment and the influence of individual movement on the persistence and extinction of the disease, the spatial SIS reaction diffusion system was studied in [8], in the subsequent works [10,11,12]. In 2012, when considering the spread and recovery rate of the disease is assumed to be spatial heterogeneity, temporally periodic, and the total population is constant, Peng et al. [13] studied the global stability and the asymptotic dynamical behaviors of the positive steady state. Method based on [8], Refs. [14, 15] investigated the dynamical behaviors and asymptotic profiles of steady states of the reaction diffusion SIS epidemic system. These main results showed that advection can help speed up the elimination of disease. In 2016, when considering population activity and standard morbidity are the two main infection mechanisms that simulate the spread of infectious diseases. Spatial heterogeneity plays an important role in the spread of infectious diseases. Wu and Zou [16] established a spread model that stimulates and promotes disease dynamics. In addition, Deng and Wu [17] studied a susceptible–infected–susceptible reaction–diffusion system with spatially heterogeneous disease transmission and recovery rates. In 2017, Kuto and coworkers [18] showed that the concentration profile of endemic equilibrium of a reaction–diffusion–advection susceptible–infected–susceptible epidemic system. Meanwhile, Ref. [19] considered the asymptotic profiles of the endemic equilibrium to a mass action infection mechanism diffusive SIS epidemic model. In [20, 21], spontaneous factors were mentioned by Hill et al., which can also have influence on the disease transmission. Therefore, in 2018, Tong and Lei in [22] extended the reaction–diffusion SIS epidemic system [8] to incorporate the effect of spontaneous infection by adding a term whereby uninfected individuals become infected at a rate. When considering the disease transmission and recovery rates is spatially heterogeneous, in 2019, Song et al. [23] proposed a susceptible-exposed-infected-recovered-susceptible (SEIRS) reaction–diffusion system. The main results reveal the importance of the movement of the exposed and recovered individuals in disease dynamics. In 2020, a diffusive susceptible–infected–susceptible epidemic system with logistic source and spontaneous infection in a heterogeneous environment was considered in [24]. The results show that varying total individuals and spontaneous infection can enhance persistence of infectious disease.

In fact, media coverage of health related events has become so important that several surveillance systems now rely on active trolling of Internet news media and blogs to detect emerging disease threats. The effect of media in infectious disease spread has long been under investigation. Therefore, in 2007, Liu and coworkers have been studied a media/psychological impact of epidemic system [25]. Subsequently, in 2008, a three-dimensional compartmental model with impact of media was gave in [26] and under a certain threshold quantity and then discussed the disease-free equilibrium of the model is globally asymptotically stable. Further, it is shown that a unique endemic equilibrium appears and a Hopf bifurcation can occur which causes oscillatory phenomena. Meanwhile, when considering the impact of media coverage on the control of spreading of emerging or reemerging infectious diseases in a given population, Cui et al. [27] considered a SIS infection model incorporating media coverage and it also gave the dynamic results of the system. When considering an effect of media-induced social distancing on disease transmission, in 2011, Cui et al. [28] studied an impact of epidemic system. They carried out a global qualitative analysis of system, it is shown that the typical threshold behavior holds, with solutions either tending to an equilibrium without disease, or the system being persistent and solutions converging to an endemic equilibrium.

Recently, Sun and Cui [29] introduced a saturated incidence rate of reaction–diffusion SIS epidemic model with linear source in spatially heterogeneous environments. Furthermore, when considering the heterogeneous environment, Suo and Li studied a linear source of diffusive SIS epidemic system with incidence function $\frac{SI}{c+S+I}$ in [30]. On the other hand, the work in [8, 9, 14, 24, 29,30,31,32] has shown that, in certain circumstances, the incidence functions $\frac{SI}{S+I}$, $\frac{SI}{1+I}$ and $\frac{SI}{c+S+I}$ used in models [24, 29, 30] may not be appropriate to describe the transmission process of disease, instead an alternate incidence function should be $e^{-\alpha I}$(see [26, 33]), where the positive number $\alpha$ stands for reflecting the impact of media coverage to the rate of contact transmission. Motivated by these works, in 2014, the authors [33] took the media coverage factors in a Filippov epidemics system. They extend the existing systems by incorporating a piecewise continuous transmission rate to describe that the media coverage exhibits its effect once the number of infected individuals exceeds a certain critical level. In 2015, a media impact of SIHR epidemic system has been investigated [34]. This system also describes the dynamics of media reports by considering how media is influenced by the disease statistics. Meanwhile, Xiao et al. [35] proposed a media impact switched off almost as the epidemic peaked, and then the authors given media coverage significantly delayed the epidemic’s peak and decreased the severity of the outbreak. In 2016, Yan et al. [39] studied a novel system to examine the implication for transmission dynamic behaviors of these correlations. The system incorporated the media impact function into the intensity of infection, and enhanced the traditional epidemic SEIR system with the addition of media dynamics. In 2020, Ding et al. [40] proposed a stochastic SIQR epidemic system incorporating media coverage. In 2021, the authors [41] asked the following questions: How do social media and individual behaviors affect epidemic transmission and control?

Although the news report is not the most important factor for the transmission of the infectious disease [36,37,38, 44, 45], it still is a very important topic and leads to many researchers that can be taken care of seriously. When there are a large number of infected populations cases, the news report may be bringing about cause the panic of the society. And then, it can to certain extent reduce the chance and possibility of contact and transmission between healthy and susceptible populations each other, and to better control and quickly prevent the transmission of the infectious disease. Motivated by the above discussions, the main purpose of this manuscript is to perform the dynamic analysis of an impact of media reaction diffusion SIS epidemic system with linear source in spatially heterogeneous environment. In the current work, many reaction diffusion epidemic models have been developed, including [3, 8, 9, 12,13,14, 29,30,31,32, 32]. Nevertheless, in this paper, we design an impact of media diffusion epidemic system with linear source and the incidence rate is assumed to be in the form $e^{-\alpha (x)I}$. The main contributions of this manuscript include three points:

• 1. We first study an impact of media diffusion epidemic system. The overall solution for the existence of the model and the uniformly boundedness of the solution are studied.

• 2. We calculate the basic reproduction number by [8] and the threshold dynamics of impact media reaction–diffusion system is also given and the Kuratowski measure $\kappa$ of non-compactness is considered. In addition, assume the spatial environment is homogeneous, it is shown that the unique endemic equilibrium of impact media SIS epidemic reaction–diffusion system is global stability by constructing suitable Lyapunov function.

• 3. We discuss the asymptotic profile property of system if the diffusion rate of system tends to zero or infinity. The main results show that if the ratio $\frac{\Lambda (x)}{m(x)}$ is smaller, the activities of infected individuals can only be at low risk, and then the virus eventually will be extinct, that is, to control the entry of viruses from abroad and increase the detection of domestic viruses.

We briefly outline the structure of this paper. The model description and uniform bounds of system (2.1) are derived in Sect. 2. After that, the threshold dynamics of system and the existence of the equilibriums for system are considered and the Kuratowski measure $\kappa$ of non-compactness is investigated in Sect. 3. Section 4 is devoted to the global asymptotic stability of the equilibrium for (2.1) when functions $\Lambda (x), m(x), \beta (x)$, $\alpha (x)$ and ${\overline{\gamma }}(x)$ are constants. Then, the asymptotic profile of system is also analyzed when $d_{1}$ or $d_{2}$ tends to zero or infinity in Sect. 5. Some numerical simulations are worked out to confirm the results obtained in Sect. 6. At last, a brief discussion of the obtained results and further research directions are given in Sect. 7.

2 Model description and uniform boundedness

2.1 Model description

With the rapid development of information, in the early days of disease outbreaks, more people can understand the transmission mechanism of infectious diseases and relevant disease prevention knowledge through TV, the Internet and other media, which can effectively control diseases. The higher the efficiency of media dissemination, the faster people can access various aspects of information. For example, in areas where infectious diseases are prevalent, the faster prevention and control measures can be taken through media dissemination and the more effective it is to reduce the contact between viruses and humans. Therefore, in-depth research on disease transmission models related to media coverage is of great practical significance for infectious disease prevention and control. Media communication plays a very important role in the outbreak of novel coronavirus. The main strategy for preventing virus outbreaks is to isolate individuals from items and individuals carrying the virus. During the quarantine period, the information reported and disseminated on online platforms is almost the only information available to the isolated population. If people can learn about the virus without leaving their homes, it can help them control their behavior and actively participate in prevention and control during the epidemic. Simply put, thanks to media communication, people can have a good understanding and perception of infectious diseases, which enables them to control their behavior, actively take protective measures, greatly reduce the number of infections and thus improve the effectiveness of disease prevention and control. In this paper, we consider the following an impact of media reaction diffusive SIS system with linear source

$$\begin{aligned} \left\{ \begin{aligned}&S_{t}=d_{1}\Delta S+\Lambda (x)-m(x)S-\beta (x) S Ie^{-\alpha (x) I}+{\overline{\gamma }}(x) I,&(x,t)\in \Omega \times (0,+\infty ),\\ {}&I_{t}=d_{2}\Delta I+ \beta (x) S Ie^{-\alpha (x) I}-{\overline{\gamma }}(x)I,&(x,t)\in \Omega \times (0,+\infty ),\\ {}&\frac{\partial S}{ \partial n}=\frac{ \partial I}{\partial n}=0,&x\in \partial \Omega ,\\ {}&S(x,0)=S_{0}(x),I(x,0)=I_{0}(x),&x\in \Omega , \end{aligned}\right. \end{aligned}$$

(2.1)

where S(x, t) is the density of susceptible individuals and I(x, t) represents the density of infected individuals. $d_{1}$ is positive constant measuring the motility of susceptible individuals and $d_{2}$ stands for positive constant measuring the motility of infected individuals. $\beta (x)$ stands for the rate of disease transmission. $\Lambda (x)-m(x)S$ is linear source function. $\Lambda (x)$ represents the input rate function of susceptible individuals abroad. ${\overline{\gamma }}(x)$ represents the rates of disease recovery. m(x) is the input rate function of susceptible individuals in the territory. The continuous functions $\beta (x)$ and ${\overline{\gamma }}(x)$ stand for positive Hölder functions on habitat region $\Omega$. The region $\Omega \subset {\mathbb {R}}^{N}(N>1)$ is bounded with smooth $\partial \Omega$, and the homogeneous Neumann boundary conditions mean that no individual flux crosses $\partial \Omega$. Here, we use the function $\alpha (x)$ stands for the reflect the impact of media coverage to the contact transmission rate. One may refer to [27, 29] and the references therein. We are assumed that the positive functions $\Lambda (x),\beta (x), {\overline{\gamma }}(x), m(x),\alpha (x)$ are Hölder continuous over region $\Omega$.

Obviously, the $SIe^{-\alpha (x) I}$ is a Lipschitz function. The solution S(x, t) and the solution I(x, t) are continuous in ${\mathbb {R}}_{+}\times {\mathbb {R}}_{+}$. In our manuscript, we assumed that initial values $S_{0}(x)$ and $I_{0}(x)$ are nonnegative continuous functions on region $\Omega$. More detailed explanations on the parameters can be found in [3, 11, 12], and the references therein.

2.2 Uniform boundedness

Observe that, the standard theory for parabolic equations, and the initial value $(S_{0}(x),I_{0}(x))$, guarantees that diffusive SIS system (2.1) has a unique classical solution such that $(S,I)\in C^{2,1}(x,t)).$ Further, using the strong maximum principle and combining with the Hopf boundary lemma, we know that the system still maintains the positiveness with the positive initial value $(S_{0},I_{0})$ for all $t>0$ and variable $x\in \Omega$.

Next, the uniform bound of diffusive SIS model (2.1) is discussed. To this end, our analysis has two cases: in one case, some special cases are obtained by using explicit L-estimates. In the other case, the general case is also derived by using the implicit $L^{\infty }$-estimates. In the future, suppose any given function ${\mathscr {G}}$ is continuous, and for notational convenience, we set

$$\begin{aligned} {\mathscr {G}}_{*} = \max _{x\in \Omega }{\mathscr {G}} (x)~~~\textrm{and}~~~ {\mathscr {G}}^{*} = \min _{x\in \Omega } {\mathscr {G}}(x)\end{aligned}$$

(2.2)

for function ${\mathscr {G}}(x) = \Lambda (x), m(x), \beta (x), {\overline{\gamma }}(x),\alpha (x)$.

Proposition 2.1

Suppose that $d_{1} = d_{2}$, $(S_{0}(x), I_{0}(x))$ is initial value, for any solution (S, I) of Eq. (2.1), then there is

$$\begin{aligned} S+I\le \max \left\{ \frac{\Lambda }{{\mathscr {B}}}, S_{0}(x)+(1+\epsilon _{0}) I_{ 0}(x)\right\} , \forall x \in \Omega , ~\mathrm{~for}~t\ge 0, \end{aligned}$$

(2.3)

where ${\mathscr {B}}=\frac{\epsilon _{0}{\overline{\gamma }}(x)}{1+\epsilon _{0}}$, $\epsilon _{0}=\frac{m(x)-{\overline{\gamma }}(x)-\frac{\beta (x)}{\alpha (x) e}+\sqrt{\Delta }}{\frac{2\beta (x)}{\alpha (x)e}}$,$\Delta =({\overline{\gamma }}(x)-\alpha (x))^{2}+(\frac{2\beta (x)}{\alpha (x)e})^{2}+\frac{2\beta (x)}{\alpha (x)e}({\overline{\gamma }}(x)+m(x))$.

Proof

For calculation convenience, we assume that diffusion rate $d_{1}=d_{2}=1.$ Set

$$\begin{aligned} u=S+(1+\epsilon _{0})I.\end{aligned}$$

(2.4)

From (2.4), S and I are equations of system (2.1), then

$$\begin{aligned} \begin{aligned} u_{t}-\Delta u=\Lambda (x)-m(x)S+\epsilon _{0}\beta (x) S Ie^{-\alpha (x) I}-\epsilon _{0} {\overline{\gamma }}(x)I.\end{aligned} \end{aligned}$$

(2.5)

Observe that Eq. (2.5) contains a inhomogeneous term $\epsilon _{0}\beta (x)Ie^{-\alpha (x) I}$, in order to better study the maximum value of this inhomogeneous term, we set

$$\begin{aligned} {\mathscr {F}}(I):=\epsilon _{0}\beta (x)Ie^{-\alpha (x) I}.\end{aligned}$$

(2.6)

Simultaneously taking the derivative of I on both sides of the formula (2.6), we arrive at

$$\begin{aligned} \frac{\partial {\mathscr {F}}}{\partial I}=\epsilon _{0}\beta (x)e^{-\alpha (x) I}-I\epsilon _{0}\beta (x) \alpha (x)e^{-\alpha (x) I}.\end{aligned}$$

(2.7)

Let ${\mathscr {F}}_{I}'(I)=0$, as it is easily seen, $I=\frac{1}{\alpha (x)}$. Further, for $I\in [0,\frac{1}{\alpha (x)}]$ we have ${\mathscr {F}}_{I}'(I)>0$, which implies that the function ${\mathscr {F}}$ is monotonically increasing depending $I>0$ in $I\in [0,\frac{1}{\alpha (x)}]$. In addition, for $I\in [\frac{1}{\alpha (x)},+\infty )$ we have ${\mathscr {F}}'(I)<0$, which implies that the function ${\mathscr {F}}$ is monotonically decreasing depending $I>0$ in $[\frac{1}{\alpha (x)},+\infty )$.

Recall that Eq. (2.5), based on the above property of inhomogeneous terms $\epsilon _{0}\beta (x)Ie^{-\alpha (x) I}$, we have the following inequality

$$\begin{aligned} u_{t}-\Delta u\leqslant \Lambda (x)-{\mathscr {B}}(S+(1+\epsilon _{0})I),\end{aligned}$$

(2.8)

where ${\mathscr {B}}=\frac{\epsilon _{0}{\overline{\gamma }}(x)}{1+\epsilon _{0}}$. Then, from $(1+\epsilon _{0})(m(x)-\beta (x) \frac{\epsilon _{0}}{\alpha (x)}e^{-1})= \epsilon _{0}{\overline{\gamma }}(x)$, we have

$$\begin{aligned} \epsilon _{0}=\frac{m(x)-{\overline{\gamma }}(x)-\frac{\beta (x)}{\alpha (x) e}+\sqrt{\Delta }}{\frac{2\beta (x)}{\alpha (x)e}},\Delta =({\overline{\gamma }}(x)-\alpha (x))^{2}+(\frac{2\beta (x)}{\alpha (x)e})^{2}+\frac{2\beta (x)}{\alpha (x)e}({\overline{\gamma }}(x)+m(x)).\end{aligned}$$

(2.9)

Therefore, we need the preset of $\epsilon _{0}$ to be greater than zero. According to our notation, that is, there exists positive number $\epsilon _{0}$ if and only if

$$\begin{aligned} \epsilon _{0}> \min _{x\in \Omega }{\epsilon _{0}}:=\frac{m^{*}-{\overline{\gamma }}_{*}-\frac{\beta _{*}}{\alpha ^{*} e}+\sqrt{\Delta ^{*}}}{\frac{2\beta _{*}}{\alpha ^{*}e}}>0,\Delta ^{*}=(\frac{2\beta ^{*}}{\alpha _{*}e})^{2}+\frac{2\beta ^{*}}{\alpha _{*}e}({\overline{\gamma }}^{*}+m^{*}).\end{aligned}$$

(2.10)

Observe that $u=S+(1+\epsilon _{0})I$ is sub-solution of system (2.1) and $\max \left\{ \frac{\Lambda }{{\mathscr {B}}}, S_{0}+(1+\epsilon _{0})I_{0}\right\}$ is sub-solution of system (2.1), and then the initial boundary value problem is given as follows:

$$\begin{aligned} \left\{ \begin{aligned}&S_{t}=d_{1}\Delta S+\Lambda (x)-m(x)S-\frac{\beta (x) S I}{e^{\alpha (x) I}}+{\overline{\gamma }}(x) I,&(x,t)\in \Omega \times (0,+\infty ),\\ {}&I_{t}=d_{2}\Delta I+ \frac{\beta (x) S I}{e^{\alpha (x) I}}-{\overline{\gamma }}(x) I,&(x,t)\in \Omega \times (0,+\infty ),\\ {}&\frac{ \partial S}{ \partial n}=\frac{ \partial I}{ \partial n}=0,&x\in \partial \Omega ,\\ {}&u_{0}(x)=S_{0}(x)+(1+\epsilon _{0})I_{0}(x),&x\in \Omega . \end{aligned}\right. \end{aligned}$$

(2.11)

Consequently, using the comparison principle, for $t \ge 0$, we give the following estimate

$$\begin{aligned}S+ I \le \max \left\{ \frac{\Lambda }{{\mathscr {B}}}, S_{0}(x) + (1 + \epsilon _{0}) I_{ 0} (x)\right\} , \forall x \in \Omega .\end{aligned}$$

The proof is complete. $\square$

Next, we derive some basic facts of positively invariant set for system (2.1) by using invariant region.

Proposition 2.2

Suppose that $m_{*}{\mathscr {C}}-\Lambda ^{*}-\beta ^{*} {\mathscr {C}}\frac{1}{\alpha _{*} e}>0$, for $\forall k>0$ such that $\frac{1}{\alpha _{*} {\mathscr {C}}}\ln \left( \frac{\beta ^{*} {\mathscr {C}}}{{\overline{\gamma }}_{*}}\right)<k<\frac{m_{*}{\mathscr {C}}-\Lambda ^{*}-\beta ^{*} {\mathscr {C}}\frac{1}{\alpha _{*} } e^{-1}}{{\overline{\gamma }}^{*}{\mathscr {C}}},$ then (S, I) of Eq. (2.1) satisfies $S<{\mathscr {C}},I<k{\mathscr {C}},$ where ${\mathscr {C}}=\max \left\{ S_{0},\frac{I_{0}}{k},\frac{\Lambda _{*}}{m^{*}}+1\right\}$.

Proof

To establish Proposition 2.2, based on the choice of k, since [42] (or refer to [43] ), we employ the invariant region theory to build the upper bounds of solutions. Then, a region has been assumed as

$$\begin{aligned}{\mathscr {X}}_{+}=(S_{1},I_{1})\times (S_{2},I_{2})\end{aligned}$$

such that (S, I) of system (2.1) for all variable x belongs to region $\Omega$ and time $t\in [0,+\infty )$ locates to region ${\mathscr {X}}_{+}$. In other words, the vector field of system (2.1)

$$\begin{aligned}\left( \Lambda (x)-m(x)S-\frac{\beta (x)SI}{e^{\alpha (x) I}}+{\overline{\gamma }}(x) I,\frac{\beta (x)SI}{e^{\alpha (x) I}}-{\overline{\gamma }}(x)I\right) \end{aligned}$$

points inward on the region ${\mathscr {X}}_{+}$. Thus, there exists a invariant rectangle, or equivalently, the boundary of region ${\mathscr {X}}_{+}$, which implies that (S, I) of system (2.1) will stay in ${\mathscr {X}}_{+}$. For convenience, set

$$\begin{aligned} \left\{ \begin{aligned}&{\mathscr {F}}_{1}(S,I)=\Lambda (x)-m(x)S-\frac{\beta (x) S I}{e^{\alpha (x) I}}+{\overline{\gamma }}(x) I,\\ {}&{\mathscr {F}}_{2}(S,I)=\frac{\beta (x) S I}{e^{\alpha (x) I}}-{\overline{\gamma }}(x) I.\end{aligned}\right. \end{aligned}$$

(2.12)

We choose $S_{1} =I_{1}= 0, S_{2}={\mathscr {C}}$ and $I_{2}= k{\mathscr {C}}$. Obviously, the positive initial value $S_{0}(x) \leqslant {\mathscr {C}}$ and $I_{0}(x) \leqslant k{\mathscr {C}}$ for all variable $x \in {\mathscr {X}}_{+}$. Thus, from (2.12), we show that

$$\begin{aligned} \left\{ \begin{aligned}&{\mathscr {F}}_{1}(0,I)\ge 0,&\forall I\in [0,k{\mathscr {C}}],\\ {}&{\mathscr {F}}_{1}({\mathscr {C}},I)\le 0,&\forall I\in [0,k{\mathscr {C}}],\\ {}&{\mathscr {F}}_{2}(S,0)\ge 0,&\forall S\in [0,{\mathscr {C}}],\\ {}&{\mathscr {F}}_{2}(S,k{\mathscr {C}})\le 0,&\forall S\in [0,{\mathscr {C}}],\end{aligned}\right. \end{aligned}$$

(2.13)

where ${\mathscr {F}}_{1}(0,I)=\Lambda (x)+{\overline{\gamma }} (x)I,{\mathscr {F}}_{1}({\mathscr {C}},I)=\Lambda (x)-m(x){\mathscr {C}}-\frac{\beta (x) {\mathscr {C}} I}{e^{\alpha (x) I}}+{\overline{\gamma }}(x) I,{\mathscr {F}}_{2}(S,0)=0,{\mathscr {F}}_{2}(S,k{\mathscr {C}})=\beta (x)S k{\mathscr {C}}e^{-\alpha (x) k{\mathscr {C}}}-{\overline{\gamma }}(x) k{\mathscr {C}}$.

In order to obtain (2.13), observe that the first and third of (2.13) are held. Next, we can check that the other two inequalities are met.

According to the solution S, for all the solution $S \in [0,{\mathscr {C}}]$, and for all the solution $I \in [0,k{\mathscr {C}}]$, we obtain

$$\begin{aligned} {\mathscr {F}}_{1}(0,I)=\Lambda (x)+{\overline{\gamma }}(x) I\geqslant 0.\end{aligned}$$

(2.14)

From (2.13), we need to verify that the following conditions are true, that is,

$$\begin{aligned} {\mathscr {F}}_{1}({\mathscr {C}},I)=\Lambda (x)-m(x){\mathscr {C}}-\frac{\beta (x) {\mathscr {C}}}{e^{\alpha (x) I}}I+{\overline{\gamma }}(x) I\le 0. \end{aligned}$$

(2.15)

Take the derivative of the above formula (2.15), which is written as

$$\begin{aligned} \frac{\partial }{\partial I}{\mathscr {F}}_{1}({\mathscr {C}},I) =-\beta (x) {\mathscr {C}} e^{-\alpha (x) I}+\alpha (x)\beta (x) I {\mathscr {C}} e^{-\alpha (x) I}+{\overline{\gamma }}(x). \end{aligned}$$

(2.16)

For convenience, let

$$\begin{aligned} {\mathscr {H}}_{0}(I):=\frac{\partial }{\partial I}{\mathscr {F}}_{1}({\mathscr {C}},I) =\frac{-\beta (x) {\mathscr {C}}+\alpha (x)\beta (x) I {\mathscr {C}}+{\overline{\gamma }}(x) e^{\alpha (x) I}}{ e^{\alpha (x) I}}, \end{aligned}$$

(2.17)

observe that the polynomial of (2.17) can be represented by

$$\begin{aligned} {\mathscr {H}}(I):=\alpha (x)\beta (x){\mathscr {C}} I +e^{\alpha (x) I}{\overline{\gamma }}(x)-\beta (x) {\mathscr {C}}.\end{aligned}$$

(2.18)

Take the derivative of I on both sides of (2.18), which is written as

$$\begin{aligned}\frac{\partial {\mathscr {H}}}{\partial I}:=\alpha (x)\beta (x){\mathscr {C}} +\alpha (x){\overline{\gamma }}(x)e^{\alpha (x) I}>0.\end{aligned}$$

If exist, based on the definition of the Lambert W function and solving the above equation with respect to I (refer to [33]), there exists $I_{1}=\zeta$, such that ${\mathscr {H}}(\zeta )=0$, we have

$$\begin{aligned} {\mathscr {H}}(0)<0~~\textrm{and}~~{\mathscr {H}}(k{\mathscr {C}})>0.\end{aligned}$$

(2.19)

We know that if $I\in (0,\zeta )$, we have ${\mathscr {F}}_{1}'({\mathscr {C}},I)<0$. If $I>\zeta$, we have ${\mathscr {F}}_{1}'({\mathscr {C}},I)>0$. That is, there exists $I=\zeta$ such that function ${\mathscr {F}}_{1}({\mathscr {C}},\zeta )$ is min value.

If not, we know that ${\mathscr {H}}\ge 0$ holds. To sum up, we only need to meet the following conditions

$$\begin{aligned} {\mathscr {F}}_{1}({\mathscr {C}},k{\mathscr {C}})\le 0 ~~~\textrm{and} ~~~{\mathscr {F}}_{1}({\mathscr {C}},0)\le 0, \end{aligned}$$

then, we have

$$\begin{aligned} {\mathscr {F}}_{1}({\mathscr {C}},0)= & {} \Lambda (x)-m(x){\mathscr {C}}\le 0,\end{aligned}$$

(2.20)

$$\begin{aligned} {\mathscr {F}}_{1}({\mathscr {C}},k{\mathscr {C}})= & {} \Lambda (x)-m(x){\mathscr {C}}-\beta (x) {\mathscr {C}} k{\mathscr {C}}e^{-\alpha (x) k{\mathscr {C}}}+{\overline{\gamma }}(x) k{\mathscr {C}}<0 \end{aligned}$$

(2.21)

and

$$\begin{aligned} {\mathscr {F}}_{1}({\mathscr {C}},\zeta )=\Lambda (x)-m(x){\mathscr {C}}-\beta (x) {\mathscr {C}} \zeta e^{-\alpha (x) \zeta }+{\overline{\gamma }}(x) \zeta <0. \end{aligned}$$

(2.22)

From Eq. (2.22), we obtain the following inequality

$$\begin{aligned} \Lambda (x)-{\mathscr {C}}m(x)-\frac{\beta (x) {\mathscr {C}}}{ e^{\alpha (x) \zeta }} \zeta +{\overline{\gamma }}(x) \zeta <\Lambda (x)-{\mathscr {C}}m(x)+ e^{-1}\frac{\beta (x) {\mathscr {C}}}{\alpha (x) }+{\overline{\gamma }}(x) k{\mathscr {C}}. \end{aligned}$$

By Eq. (2.13), we claim that

$$\begin{aligned}\Lambda (x)-{\mathscr {C}}m(x)+ e^{-1}\frac{\beta (x){\mathscr {C}}}{\alpha (x) }+{\mathscr {C}}k{\overline{\gamma }}(x)<0.\end{aligned}$$

Combining Eq. (2.20) with Eq. (2.22), we lead to the following conditions

$$\begin{aligned}\Lambda (x)<m(x){\mathscr {C}} \end{aligned}$$

and

$$\begin{aligned} k\le \frac{{\mathscr {C}}m(x)-\frac{\beta (x) {\mathscr {C}}}{\alpha (x) }e^{-1}-\Lambda (x)}{{\overline{\gamma }}(x){\mathscr {C}}}\le \frac{{\mathscr {C}}m_{*}-\Lambda ^{*}-\frac{\beta ^{*} {\mathscr {C}}}{\alpha _{*} } e^{-1}}{{\overline{\gamma }}^{*}{\mathscr {C}}}.\end{aligned}$$

Thus, the second equation of system (2.13) holds.

Next, observe that the third and fourth equations of system (2.13) can be written as we claim that

$$\begin{aligned} {\mathscr {F}}_{2}(S,0)=\beta (x) S e^{-\alpha (x) I}I-{\overline{\gamma }}(x) I\ge 0 \end{aligned}$$

and

$$\begin{aligned} {\mathscr {F}}_{2}(S,k{\mathscr {C}})=\frac{\beta (x) S k{\mathscr {C}}}{e^{\alpha (x) k{\mathscr {C}}}}-{\overline{\gamma }}(x) k{\mathscr {C}}\le 0. \end{aligned}$$

Observe that

$$\begin{aligned}{\mathscr {F}}_{2}(S,k{\mathscr {C}})\le {\mathscr {F}}_{2}({\mathscr {C}},k{\mathscr {C}})=\beta (x) {\mathscr {C}}^{2} ke^{-\alpha (x) k{\mathscr {C}}}-{\overline{\gamma }}(x) k{\mathscr {C}}\le 0, \end{aligned}$$

thus it gives us $k\ge \frac{1}{\alpha (x) {\mathscr {C}}}\ln \left( \frac{\beta (x) {\mathscr {C}}}{{\overline{\gamma }}(x)}\right) .$

Overall, if the following inequality

$$\begin{aligned} k\ge \frac{1}{\alpha (x){\mathscr {C}}}\ln \left( \frac{\beta (x) {\mathscr {C}}}{{\overline{\gamma }}(x)}\right)>\frac{1}{\alpha _{*}{\mathscr {C}}}\ln \left( \frac{\beta ^{*} {\mathscr {C}}}{{\overline{\gamma }}_{*}}\right) ,{\mathscr {C}}>\frac{\Lambda (x)}{m(x)}>\frac{\Lambda ^{*}}{m_{*}},\end{aligned}$$

(2.23)

which implies that ${\mathscr {X}}_{+}$ is a rectangle of system (2.1) in the first quadrant ${\mathbb {R}}_{+}$. The proof is completed.$\square$

2.3 Implicit bounds of system (2.1)

We now study the uniform bounds of system (2.1) by using $L^{p}$ theorem, then the following Lemma is given.

Lemma 2.1

There exists ${\mathscr {M}}^{**}>0$ independent of the positive initial value $(S_{0},I_{0})$, and there is some large time ${\mathcal {T}}$ such that

$$\begin{aligned} ||S(x,t)||_{L^{\infty }(\Omega )}+ ||I(x,t)||_{L^{\infty }(\Omega )}<{\mathscr {M}}^{**},\forall t>{\mathcal {T}}.\end{aligned}$$

(2.24)

Proof

To establish this Lemma 2.1, the following assertion needs to be proven.

For $\forall k>0$, there exists a ${\mathscr {M}}^{**}={\mathscr {M}}(k)>0$ independent of the positive initial value ($S_{0},I_{0})$ and there is some large time ${\mathcal {T}}$ such that

$$\begin{aligned} ||S(x,t)||_{L^{\infty }(\Omega )}+ ||I(x,t)||_{L^{\infty }(\Omega )}<{\mathscr {M}}^{**},\forall t>{\mathcal {T}}.\end{aligned}$$

(2.25)

We can prove that system (2.24) is true by using mathematical induction method.

(i). For convenience, we first define

$$\begin{aligned} v(t)=\mathop {\int }\limits _{\Omega }[S+(1+\varepsilon _{0})I]\textrm{d}t.\end{aligned}$$

(2.26)

The mathematical induction method will be used to derive Eq. (2.26).

Taking $k=1$, from (2.1), we have

$$\begin{aligned}\begin{aligned}\frac{ \textrm{d}v(t)}{ \textrm{d}t}=\mathop {\int }\limits _{\Omega } \Lambda (x)\textrm{d}x-\mathop {\int }\limits _{\Omega } m(x)S\textrm{d}x +\mathop {\int }\limits _{\Omega }\varepsilon _{0}\beta (x) Se^{-\alpha (x) I}I \textrm{d}x-\mathop {\int }\limits _{\Omega }\varepsilon _{0}{\overline{\gamma }} (x)I \textrm{d}x,\end{aligned}\end{aligned}$$

then we have $Ie^{-\alpha (x) I}\le \frac{1}{\alpha (x)} e^{-1}$ using inequality and

$$\begin{aligned}\begin{aligned} \frac{\textrm{d}v(t)}{\textrm{d}t}&\le \mathop {\int }\limits _{\Omega } \Lambda (x)\textrm{d}x-\mathop {\int }\limits _{\Omega } \left[ \frac{m(x)S\alpha (x)-\varepsilon _{0}\beta (x)Se^{-1}-\varepsilon _{0}{\overline{\gamma }}(x) I\alpha (x)}{\alpha (x)}\right] \textrm{d}x\\&\le \Lambda (x)|\Omega |-\mathop {\int }\limits _{\Omega } m^{*}S \textrm{d}x+\varepsilon _{0}\mathop {\int }\limits _{\Omega }\left( \frac{\beta _{*} S e^{-1}}{\alpha ^{*}}\right) \textrm{d}x-\varepsilon _{0}\mathop {\int }\limits _{\Omega }{\overline{\gamma }}^{*} I\textrm{d}x\\ {}&\le \Lambda (x)|\Omega |-(m^{*}- \frac{\varepsilon _{0}\beta _{*}}{\alpha ^{*}} e^{-1})\mathop {\int }\limits _{\Omega } S\textrm{d}x-\varepsilon _{0}{\overline{\gamma }}^{*}\mathop {\int }\limits _{\Omega } I\textrm{d}x\\ {}&=\Lambda (x)|\Omega |-(m^{*}-\frac{\varepsilon _{0}\beta _{*}}{\alpha ^{*}} e^{-1})\mathop {\int }\limits _{\Omega } S\textrm{d}x -\frac{\varepsilon _{0}{\overline{\gamma }}^{*}}{1+\varepsilon _{0}}(1+\varepsilon _{0})\mathop {\int }\limits _{\Omega } I\textrm{d}x\\ {}&= \Lambda (x)|\Omega |-{\mathscr {D}}\mathop {\int }\limits _{\Omega } S\textrm{d}x-{\mathscr {D}}(1+\varepsilon _{0})\mathop {\int }\limits _{\Omega } I\textrm{d}x.\end{aligned}\end{aligned}$$

We set${\mathscr {D}}:=\frac{\varepsilon _{0}{\overline{\gamma }}^{*}}{1+\varepsilon _{0}}=\left( m^{*}- \frac{\varepsilon _{0}\beta _{*}}{\alpha ^{*}} e^{-1}\right) ,$ where $\varepsilon _{0}=\frac{\alpha ^{*}m^{*}e-\beta _{*}-{\overline{\gamma }}^{*}\alpha ^{*}e+\sqrt{\Delta }}{2\beta _{*}}.$ $\Delta =(\beta _{*}+{\overline{\gamma }}^{*}\alpha ^{*}e-m^{*}\alpha ^{*}e)^{2}+4\alpha ^{*}\beta _{*} m e$. Then, we finally obtain

$$\begin{aligned} v(t)\le \frac{|\Omega | \Lambda _{*}(1-e^{-{\mathscr {D}}t})}{{\mathscr {D}}}+v(0)e^{-{\mathscr {D}} t}.\end{aligned}$$

(2.27)

Employing Lemma 2.1 of [9], combining the positiveness of the solution S with the solution I of (2.25), further, from (2.27), we obtain

$$\begin{aligned}\limsup _{t\rightarrow +\infty }v(t)\le \frac{ \Lambda _{*}|\Omega |}{{\mathscr {D}}},\end{aligned}$$

which is independent of the positive initial value $(S_{0}(x), I_{0}(x))$.

(ii) For $k-1$, assume that the inequality (2.24) is valid.

So it is next shown that (2.24) holds for the integer k. Multiplying both ends of the first equation of S in (2.1) by the variable $S^{k-1}$ and integrating from region $\Omega$, then we immediately obtain

$$\begin{aligned}\begin{aligned} \frac{1}{k }\frac{\textrm{d}}{\textrm{d}t} \mathop {\int }\limits _{\Omega } S^{k} \textrm{d}x&= -d_{1}(k-1) \mathop {\int }\limits _{\Omega } S^{k-2} |\nabla S|^{2} \textrm{d}x\\&\quad +\mathop {\int }\limits _{\Omega }[ \Lambda (x)-m(x)S) S^{k-1}-\beta (x) e^{-\alpha (x) I}I S^{k} + {\overline{\gamma }}(x) IS^{k-1}] \textrm{d}x.\end{aligned}\end{aligned}$$

Similarly, multiply both ends of the solution I-equation in (2.1) by the variable $I^{k-1}$ and integrate from region $\Omega$

$$\begin{aligned}\begin{aligned}\frac{1}{k }\frac{\textrm{d}}{\textrm{d}t} \mathop {\int }\limits _{\Omega }I^{k} \textrm{d}x&=- d_{2} (k-1) \mathop {\int }\limits _{\Omega }I^{k-2} |\nabla I|^{2 }\textrm{d}x+\mathop {\int }\limits _{\Omega }\beta (x) S e^{-\alpha (x) I}I^{k} \textrm{d}x-\mathop {\int }\limits _{\Omega }{\overline{\gamma }}(x) I^{k} \textrm{d}x.\end{aligned}\end{aligned}$$

On account of the above two equalities, we can get from (2.24) with the integer k replaced by the integer $k-1$ that

$$\begin{aligned}\begin{aligned}\frac{1}{k }\frac{\textrm{d}}{\textrm{d}t} \mathop {\int }\limits _{\Omega }(I^{k}&+S^{k})\textrm{d}x + (k-1) \mathop {\int }\limits _{\Omega }d_{2}I^{k-2} |\nabla I|^{2}+d_{1}S^{k-2} |\nabla S|^{2}\textrm{d}x\\&= \mathop {\int }\limits _{\Omega } [ \Lambda (x)S^{k-1}-m(x)S^{k} + \beta (x) e^{-\alpha (x) I}SI^{k}+ {\overline{\gamma }}(x) IS^{k-1}-{\overline{\gamma }}(x) I^{k}-\beta (x)e^{-\alpha (x)I}IS^{k}] \textrm{d}x.\end{aligned}\end{aligned}$$

Recall that $Ie^{-\alpha I}\le \frac{1}{\alpha } e^{-1}$, we have

$$\begin{aligned}\begin{aligned}\frac{1}{k }\frac{\textrm{d}}{\textrm{d}t} \mathop {\int }\limits _{\Omega }&(I^{k}+S^{k}) \textrm{d}x + (k-1) \mathop {\int }\limits _{\Omega }d_{2}I^{k-2} |\nabla I|^{2}+d_{1}S^{k-2} |\nabla S|^{2} \textrm{d}x\\ {}&\le \mathop {\int }\limits _{\Omega } [ \Lambda (x)S^{k-1}-m(x)S^{k}+\beta (x) \frac{1}{\alpha (x)} e^{-1}SI^{k-1}+ {\overline{\gamma }}(x) IS^{k-1}-{\overline{\gamma }}(x) I^{k}] \textrm{d}x.\end{aligned}\end{aligned}$$

Recall that Young’s inequality (see [3]) with $\epsilon$ will be used

$$\begin{aligned} ab \leqslant \epsilon a^{p} + C(\epsilon )b^{q},\end{aligned}$$

(2.28)

where $a, b, \epsilon >0, C(\epsilon )=\frac{1}{q} (\epsilon p)^{-\frac{q}{p}}, 1<p, q<\infty$ and $\frac{1}{p}+\frac{1}{q}=1$, then

$$\begin{aligned}&\frac{1}{k }\frac{ \textrm{d}}{\textrm{d}t}\mathop {\int }\limits _{\Omega }(I^{k}+S^{k}) \textrm{d}x +(k-1) \mathop {\int }\limits _{\Omega }d_{2}I^{k-2} |\nabla I|^{2}+d_{1}S^{k-2} |\nabla S|^{2} \textrm{d}x\nonumber \\&\quad \le \mathop {\int }\limits _{\Omega } [ (\Lambda (x)S^{k-1}-m(x)S^{k}) + \beta (x) \frac{1}{\alpha (x)} e^{-1}(\epsilon ' I^{k} + C_{1} (\epsilon ', k) S^{k})\nonumber \\&\qquad + {\overline{\gamma }}(x) (\epsilon ' I^{k} + C_{2} (\epsilon ', k) S^{k})-{\overline{\gamma }}(x) I^{k}] \textrm{d}x\nonumber \\&\quad = \mathop {\int }\limits _{\Omega } \Lambda (x)S^{k-1}\textrm{d}x-\mathop {\int }\limits _{\Omega }\left[ m(x)-\beta (x) \frac{1}{\alpha (x)} e^{-1} C_{1} (\epsilon ', k) - {\overline{\gamma }}(x)C_{2} (\epsilon ', k)\right] S^{k} \textrm{d}x\nonumber \\ {}&\qquad -\mathop {\int }\limits _{\Omega }\left[ {\overline{\gamma }}(x)-\frac{\beta (x) e^{-1}\epsilon ' }{\alpha (x)}-{\overline{\gamma }}(x) \epsilon ' \right] I^{k} \textrm{d}x\nonumber \\ {}&\quad \le \mathop {\int }\limits _{\Omega } \Lambda (x)S^{k-1}\textrm{d}x-\mathop {\int }\limits _{\Omega }\left[ m(x)-\beta (x) \frac{1}{\alpha (x)} e^{-1}\max \{ C_{1} (\epsilon ', k)\}- {\overline{\gamma }}(x)\max \{C_{2} (\epsilon ', k)\}\right] S^{k} \textrm{d}x\nonumber \\ {}&\qquad -\mathop {\int }\limits _{\Omega }\left[ \frac{{\overline{\gamma }}(x)\alpha (x)-\beta (x) e^{-1}\epsilon '}{\alpha (x)}- {\overline{\gamma }}(x) \epsilon ' \right] I^{k} \textrm{d}x, \end{aligned}$$

(2.29)

where $k, \epsilon '>0$, the positive constants $C_{1}(\epsilon ', k)$ and $C_{2}(\epsilon ', k)$ are determined by using Young’s inequality with $\epsilon '$ in (2.28).

Take $\epsilon ' >0$ such that

$$\begin{aligned} m(x)> \frac{\beta (x)}{\alpha (x)} e^{-1}\max \{ C_{1} (\epsilon ', k)\}+ {\overline{\gamma }}(x)\max \{C_{2} (\epsilon ', k)\},{\overline{\gamma }}(x)> \frac{ \beta (x)e^{-1}}{\alpha (x)}\epsilon '+{\overline{\gamma }}(x) \epsilon '. \end{aligned}$$

Thus, combining (2.29) with the induction hypothesis infers that

$$\begin{aligned} \frac{1}{k }\frac{ \textrm{d}}{ \textrm{d}t} \mathop {\int }\limits _{\Omega }(I^{k}+S^{k}) \textrm{d}x \le -D \mathop {\int }\limits _{\Omega }(I^{k}+S^{k}) \textrm{d}x + M_{1}, \forall t\ge 0, \end{aligned}$$

where

$$\begin{aligned} D=\min \left\{ m(x)- \frac{\beta (x)}{\alpha (x)} e^{-1}\max \{ C_{1} (\epsilon ', k)\}- {\overline{\gamma }}(x)\max \{C_{2} (\epsilon ', k)\},\left( \frac{{\overline{\gamma }}(x)\alpha (x)- \beta (x) e^{-1}\epsilon '}{\alpha (x)}- {\overline{\gamma }}(x) \epsilon ' \right) \right\} . \end{aligned}$$

Then, we end up with

$$\begin{aligned} \mathop {\int }\limits _{\Omega }(I^{k}+S^{k})\textrm{d}x \le e^{-kDt} \mathop {\int }\limits _{\Omega }(I_{0}^{k}+S_{0}^{k})\textrm{d}x + \frac{M_{1}}{D}(1-e^{-kDt}), \forall t\ge 0,\end{aligned}$$

where $M_{1}>0$ for large time t.

Thus, Eq. (2.24) holds. As we have seen, based on (i), (ii) and applying Lemma 2.1 of [3] to (2.1), we have (2.24). The proof is complete.$\square$

3 Threshold dynamics of system (2.1)

This part, our aim is to establish in an elementary manner the threshold dynamics of system (2.1) and mainly properties of the basic reproduction number (B.R.N.). Based on the uniform bounds of system (2.1), as in [3], the B.R.N. ${\mathcal {R}}$ of system (2.1) is defined by

$$\begin{aligned} {\mathcal {R}}=\sup _{0\ne \varphi \in H^{1}\Omega }\frac{\mathop {\int }\limits _{\Omega } \frac{\beta (x) \Lambda (x)}{m(x)}\varphi ^{2}\textrm{d}x}{\mathop {\int }\limits _{\Omega }d_{2}|\nabla \varphi |^{2}+{\overline{\gamma }}(x)\varphi ^{2}\textrm{d}x}.\end{aligned}$$

(3.1)

In fact, from [16], we also give the basic reproduction number of our paper, and is defined as ${\mathcal {R}}$. It shows that ${\mathcal {R}}$ is independent of $d_{1}$.

In addition, we know that the elliptic problem

$$\begin{aligned} -d_{1}\Delta S=\Lambda (x)-m(x)S,\textrm{variable}~x\in \Omega ;\frac{\partial S}{\partial n}=0,\textrm{variable}~x\in \partial \Omega \end{aligned}$$

(3.2)

exists a unique solution $S^{*}(x)>0$. Obviously, (2.1) admits a disease-free equilibrium (D.F.E.) $(S^{*}(x),0)$. By the expression of ${\mathcal {R}}$, and further discussion to similarity as [3], a proposition is given below.

Proposition 3.1

The following assertions hold.

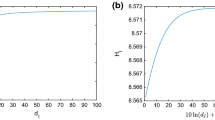
• 1. The function ${\mathcal {R}}$ of $d_{2}$ is a monotone decreasing; we have ${\mathcal {R}} \rightarrow \max \left\{ \frac{\beta (x) \Lambda (x)}{m(x)}{\overline{\gamma }}(x)^{-1}: x \in \Omega \right\}$ as $d_{2}\rightarrow 0$ and ${\mathcal {R}}\rightarrow \frac{\mathop {\int }\limits _{\Omega }\frac{\beta (x) \Lambda (x)}{m(x)}\textrm{d}x}{\mathop {\int }\limits _{\Omega } {\overline{\gamma }}(x) \textrm{d}x} ~~\textrm{as}~~d_{2} \rightarrow \infty .$

• 2. If the inequality $\mathop {\int }\limits _{\Omega }\frac{\beta (x)\Lambda (x)}{m(x)}\textrm{d}x<\mathop {\int }\limits _{\Omega }{\overline{\gamma }}(x) \textrm{d}x$ holds. Then, there exists a ${\hat{d}}_{2}>0$ such that ${\mathcal {R}}>1$ if ${\hat{d}}_{2}>d_{2}$; and ${\mathcal {R}}<1$ if ${\hat{d}}_{2}<d_{2}$.

• 3. If the inequality $\mathop {\int }\limits _{\Omega }\frac{\beta (x)\Lambda (x)}{m(x)}\textrm{d}x>\mathop {\int }\limits _{\Omega }{\overline{\gamma }}(x) \textrm{d}x$ holds. Then, ${\mathcal {R}}> 1$ for all $d_{2}$.

To study the global stability of the disease-free equilibrium in the cases when one of the diffusion rates is positive and the other is zero, we introduce the Kuratowski measure $\kappa$ of non-compactness. Define $\kappa ({\tilde{B}}):=\inf \{r>0: {\tilde{B}} \text{ has } \text{ a } \text{ finite } \text{ cover } \text{ of } \text{ diameter } <r\}$ for any bounded set ${\tilde{B}}$.

Let ${\overline{\Phi }}(t): \Sigma ^{+} \rightarrow \Sigma ^{+}$ denote the semiflow generated by Eq. (2.1). The following result allows us to deal with the non-compactness of ${\overline{\Phi }}$ when the diffusion rate $d_{2}=0$.

Lemma 3.1

If the diffusion rate $d_{1}>0$ and $d_{2}=0$, then ${\overline{\Phi }}(t):\Sigma ^{+} \rightarrow \Sigma ^{+}, t \ge 0$ is a $\kappa$-contraction on ${\mathscr {Y}}^{+}$in the sense that $\kappa ({\overline{\Phi }}(t) {\tilde{B}}) \le e^{-{\overline{\gamma }}^{*}} t \kappa ({\tilde{B}})$ for any bounded set ${\tilde{B}} \subset {\mathscr {Y}}^{+}$, where $0<e^{-{\overline{\gamma }}^{*} t}<1$.

Proof

First, we rewrite Eq. (2.1) with the diffusion rate $d_{2}=0$ and $E_{0}=(S^{*}(x), 0)$ as

$$\begin{aligned} \left( \begin{array}{c} S_{t}-d_{1} \Delta S \\ I_{t} \end{array}\right) =\left( \begin{array}{cc} -m(x) &{} -\beta (x)S^{*}(x)+{\overline{\gamma }}(x) \\ 0 &{} \beta (x)S^{*}(x)- {\overline{\gamma }}(x) \end{array}\right) \left( \begin{array}{l} S \\ I \end{array}\right) +\left( \begin{array}{l} {\mathscr {A}}_{1}(x, S, I) \\ {\mathscr {A}}_{2}(x, S, I) \end{array}\right) , \end{aligned}$$

(3.3)

where $\left( {\mathscr {A}}_{1}(x, S, I), {\mathscr {A}}_{2}(x, S, I)\right) ^{\textrm{T}}$ denote the nonlinear terms of Eq. (2.1). For any ${\hat{\phi }}(x)=\left( {\hat{\phi }}_{1}(x), {\hat{\phi }}_{2}(x)\right) \in \Sigma ^{+}$, the semiflow associated with Eq. (3.3) with initial condition

$$\begin{aligned} S(x, 0)={\hat{\phi }}_{1}(x), \quad I(x, 0)={\hat{\phi }}_{2}(x), \quad x \in \Omega \end{aligned}$$

is defined by

$$\begin{aligned} {\overline{\Phi }}(t) {\hat{\phi }}=(S(x, t, {\hat{\phi }}), I(x, t, {\hat{\phi }})), \quad \forall {\hat{\phi }} \in \Sigma ^{+}, t \ge 0 . \end{aligned}$$

We know that the solution $I(x, t, {\hat{\phi }})$ satisfies

$$\begin{aligned} \left\{ \begin{aligned}&I_{t} =[\beta (x)S^{*}(x)- {\overline{\gamma }}(x)] I(x, t, {\hat{\phi }})+{\mathscr {A}}_{2}(x, S, I), \quad&t>0, x \in \Omega , \\&I(x, 0) ={\hat{\phi }}_{2}(x), \quad&x \in \Omega . \end{aligned}\right. \end{aligned}$$

(3.4)

Note that the second equation $I_{t}$ also satisfies

$$\begin{aligned} \begin{aligned} I_{t}&=\beta (x) S Ie^{-\alpha (x) I}-{\overline{\gamma }}(x)I \le -{\overline{\gamma }}(x) I(x, t, {\hat{\phi }})+\frac{\beta _{*} S}{\alpha ^{*} e} \end{aligned} \end{aligned}$$

for $t>0, x \in \Omega$. Then, we have

$$\begin{aligned} I(x, t, {\hat{\phi }})=\breve{T}_{2}(t) {\hat{\phi }}_{2}+\mathop {\int }\limits _{0}^{t} \breve{T}_{2}(t-s) {\mathscr {A}}_{2}(x, S(x, s, {\hat{\phi }}), I(x, s, {\hat{\phi }})) \textrm{d} s, \end{aligned}$$

(3.5)

where the map $\breve{T}_{2}(t): C({\bar{\Omega }}, {\mathbb {R}}) \rightarrow C({\bar{\Omega }}, {\mathbb {R}})$ is given by $\breve{T}_{2}(t)=e^{[\beta (x)S^{*}(x)- {\overline{\gamma }}(x)] t}$. Next, define the first operator

$$\begin{aligned} {\mathscr {L}}(t){\hat{\phi }}=\left( 0, \breve{T}_{2}(t) {\hat{\phi }}_{2}\right) \end{aligned}$$

and the second operator

$$\begin{aligned} {\mathscr {N}}(t) {\hat{\phi }}=\left( S(x, t, {\hat{\phi }}), \mathop {\int }\limits _{0}^{t} \breve{T}_{2}(t-s) {\mathscr {A}}_{2}(x, S(x, s, {\hat{\phi }}), I(x, s, {\hat{\phi }})) \textrm{d} s\right) , \quad \forall {\hat{\phi }} \in \Sigma ^{+}. \end{aligned}$$

Note that

$$\begin{aligned} \begin{aligned} {\mathscr {L}}(t) {\hat{\phi }}&\le \left( 0, e^{-{\overline{\gamma }}^{*} t} {\hat{\phi }}_{2}\right) , \\ {\mathscr {N}}(t){\hat{\phi }}&\le \left( S(x, t, {\hat{\phi }}), \mathop {\int }\limits _{0}^{t} e^{-{\overline{\gamma }}_{*}(t-s)} \frac{\beta ^{*} }{\alpha ^{*} e}S(x, s, {\hat{\phi }}) \textrm{d} s\right) , \quad \forall {\hat{\phi }} \in \Sigma ^{+} . \end{aligned} \end{aligned}$$

(3.6)

Then, we have

$$\begin{aligned} {\overline{\Phi }}(t) {\hat{\phi }}={\mathscr {L}}(t) {\hat{\phi }}+{\mathscr {N}}(t){\hat{\phi }}, \quad \forall {\hat{\phi }} \in \Sigma ^{+}, t \ge 0 . \end{aligned}$$

We define the map $\breve{T}_{1}(t): C({\bar{\Omega }}, {\mathbb {R}}) \rightarrow C({\bar{\Omega }}, {\mathbb {R}})$ as the $C_{0}$ semigroup associated with $d_{1} \Delta -{\overline{\gamma }}$. By the compactness of $\breve{T}_{1}(t)$, from Eqs. (3.5) and (3.6), we know that ${\mathscr {N}}(t): \Sigma ^{+} \rightarrow \Sigma ^{+}$ is compact for each time $t>0$ and thus $\kappa ({\mathscr {N}}(t) {\tilde{B}})=0$ for any ${\tilde{B}} \subset \Sigma ^{+}$ and time $t>0$. In view of

$$\begin{aligned} \Vert {\mathscr {L}}(t) {\hat{\phi }}\Vert \le \left\| e^{-{\overline{\gamma }}(x) t} {\hat{\phi }}_{2}\right\| \le e^{-{\overline{\gamma }}^{*} t}\Vert {\hat{\phi }}\Vert , \end{aligned}$$

one obtains $\Vert {\mathscr {L}}(t)\Vert \le e^{-{\overline{\gamma }}^{*} t}, \quad \forall t>0.$

Therefore, for any $B \subset \Sigma ^{+}$, one has

$$\begin{aligned} \kappa ({\overline{\Phi }}(t) {\tilde{B}}) \le \kappa ({\mathscr {L}}(t) {\tilde{B}})+\kappa ({\mathscr {N}}(t) {\tilde{B}}) \le \Vert {\mathscr {L}}(t)\Vert \kappa ({\tilde{B}})+0 \le e^{-{\overline{\gamma }}^{*} t} \kappa ({\tilde{B}}), \quad \forall t>0, \end{aligned}$$

(3.7)

and $0<e^{-{\overline{\gamma }}^{*} t}<1$. Thus, ${\overline{\Phi }}(t): \Sigma ^{+} \rightarrow \Sigma ^{+}, t \ge 0$ is a $\kappa$-contraction of order $e^{-{\overline{\gamma }}^{*} t}$ on $\Sigma ^{+}$.$\square$

Similarly, we can obtain the following result for the case when the diffusion rate $d_{1}=0$.

Lemma 3.2

If the diffusion rate $d_{1}=0$ and $d_{2}>0$, then the map ${\overline{\Phi }}(t): \Sigma ^{+} \rightarrow \Sigma ^{+}, t\ge 0$ is a $\kappa$-contraction on region $\Sigma ^{+}$ in the sense that $\kappa (\Phi (t) {\tilde{B}}) \le e^{-m^{*} t} \kappa ({\tilde{B}})$ for any ${\tilde{B}} \subset \Sigma ^{+}$.

Proof

Let $u:=S-S^{*}(x)$, Eq. (2.1) is rewritten with the diffusion rate $d_{1}=0$ as

$$\begin{aligned} \begin{aligned} u_{t}&=\Lambda (x)-m(x)(u+S^{*}(x))-\beta (x) (u+S^{*}(x)) Ie^{-\alpha (x) I}+{\overline{\gamma }}(x) I\\ {}&=\Lambda (x)-m(x)u-\beta (x) u Ie^{-\alpha (x) I}+{\overline{\gamma }}(x) I -m(x)S^{*}(x)-\beta (x) S^{*}(x) Ie^{-\alpha (x) I}, \\ I_{t}-d_{2} \Delta I&= \beta (x) (u+S^{*}(x)) Ie^{-\alpha (x) I}-{\overline{\gamma }}(x) I \end{aligned} \end{aligned}$$

with $u(x, 0) \ge -S^{*}(x), I(x, 0) \ge 0, x \in \Omega$. We define $\breve{T}_{1}(t)=e^{-m(x) t}$ and $T_{2}(t): C({\bar{\Omega }}, {\mathbb {R}}) \rightarrow C({\bar{\Omega }}, {\mathbb {R}})$ as the $C_{0}$ semigroup associated with the diffusion rate $d_{2} \Delta -{\overline{\gamma }}$. Define a linear operator ${\mathcal {L}}(t){\hat{\phi }}=\left( \breve{T}_{1}(t) {\hat{\phi }}_{1}, 0\right)$ and a nonlinear operator

$$\begin{aligned} {\mathcal {N}}(t) {\hat{\phi }}=\left( \mathop {\int }\limits _{0}^{t} \breve{T}_{1}(t-s) {\mathscr {M}}(x, u(x, s, {\hat{\phi }}), I(x, s, \phi )) \textrm{d} s, I(x, t, {\hat{\phi }})\right) , \end{aligned}$$

where ${\mathscr {M}}(x, u, I)=\Lambda (x)-\beta (x) u Ie^{-\alpha (x) I}+{\overline{\gamma }}(x) I -m(x)S^{*}(x)-\beta (x) S^{*}(x) Ie^{-\alpha (x) I} \le \Lambda (x)+{\overline{\gamma }}(x) I -m(x)S^{*}(x)-\beta (x) S^{*}(x) Ie^{-\alpha (x) I}.$

Note that

$$\begin{aligned} \Vert {\mathcal {N}}(t) {\hat{\phi }}\Vert \le \max \left( \mathop {\int }\limits _{0}^{t} \beta _{*}\Vert u(x, s, {\hat{\phi }})\Vert \Vert I(x, s, {\hat{\phi }})\Vert \textrm{d} s,\Vert I(x, t, {\hat{\phi }})\Vert \right) , \end{aligned}$$

(3.8)

then

$$\begin{aligned} u(x, t, {\hat{\phi }})=\breve{T}_{1}(t) {\hat{\phi }}_{1}+\mathop {\int }\limits _{0}^{t} \breve{T}_{1}(t-s) {\mathscr {M}}(x, u(x, s, {\hat{\phi }}), I(x, s, {\hat{\phi }})) \textrm{d} s \end{aligned}$$

(3.9)

and

$$\begin{aligned} {\overline{\Phi }}(t) {\hat{\phi }}={\mathcal {K}}(t) {\hat{\phi }}+{\mathcal {N}}(t) {\hat{\phi }}, \quad \forall {\hat{\phi }} \in \Sigma ^{+}, t \ge 0. \end{aligned}$$

By the compactness of $\breve{T}_{2}(t)$, it follows from Eq. (3.8) and Eq. (3.9) that ${\mathcal {N}}(t): \Sigma ^{+} \rightarrow \Sigma ^{+}$ is compact for each time $t>0$, and thus $\kappa ({\mathcal {N}}(t) {\tilde{B}})=0$ for any ${\tilde{B}} \subset \Sigma ^{+}$ and time $t>0$. In view of

$$\begin{aligned} \Vert {\mathcal {K}}(t) {\hat{\phi }}\Vert \le \left\| e^{-m(x)t} {\hat{\phi }}_{1}\right\| \le e^{-m^{*} t}\Vert {\hat{\phi }}\Vert , \end{aligned}$$

we get

$$\begin{aligned} \Vert {\mathcal {K}}(t)\Vert \le e^{-m(x) t}, \quad \forall t>0. \end{aligned}$$

Hence, for ${\tilde{B}} \subset \Sigma ^{+}$ one gives

$$\begin{aligned} \kappa ({\overline{\Phi }}(t) {\tilde{B}}) \le \kappa ({\mathcal {K}}(t) {\tilde{B}})+\kappa ({\mathcal {N}}(t) {\tilde{B}}) \le \Vert {\mathcal {K}}(t)\Vert \kappa ({\tilde{B}})+0 \le e^{-m^{*} t} \kappa ({\tilde{B}})<\kappa ({\tilde{B}}) . \end{aligned}$$

Therefore, ${\overline{\Phi }}(t): \Sigma ^{+} \rightarrow \Sigma ^{+}, t \ge 0$ is a $\kappa$-contraction of order $e^{-m^{*}t}$ on region $\Sigma ^{+}$.$\square$

Next, we can consider the threshold type dynamical behaviors of system (2.1); it shows that if ${\mathcal {R}}<1$, the disease of system is eliminated. If ${\mathcal {R}}>1$, then the disease of system is persists. One has Theorems 3.1 and 3.2.

Theorem 3.1

If ${\mathcal {R}}<1$, then the disease-free equilibrium of system (2.1) is globally asymptotically stable.

Proof

Observe that ${\mathcal {R}}<1$, then, by Lemma 2.3 in [3] and [8], we know that $1-{\mathcal {R}}$ has the same sign as the principal eigenvalue ${\hat{\lambda }}$. ${\hat{\lambda }}$ satisfies the following the principal eigenvalue:

$$\begin{aligned} -d_{2}\Delta \psi +{\overline{\gamma }}(x)\psi -\frac{\beta (x)\Lambda (x)}{m(x)}\psi =\lambda \psi ,{~\mathrm for~variable~}x\in \Omega ;{~\mathrm and~}\frac{\partial \psi }{\partial n}=0,{~\mathrm for~variable~}x\in \partial \Omega .\qquad \end{aligned}$$

(3.10)

So ${\hat{\lambda }}> 0$. Meanwhile, employing the proof of [3] again, we obtain

$$\begin{aligned}\mathrm{~the~solution~}I(x,t)\rightarrow 0,\mathrm{uniformly ~~on~~region} ~\Omega ~~~\textrm{as} ~~~t\rightarrow \infty .\end{aligned}$$

Next, we will prove that the solution $S(x,t)\rightarrow {\mathcal {S}}^{*}(x)$ uniformly on as $t\rightarrow +\infty$.

Considering any small positive number $\epsilon$ independent of initial values, there exists time $t_{0}>0$ such that the solution satisfies $0\leqslant I\leqslant \epsilon$ for all variable x belong to region $\Omega , t>t_{0}$.

Note that S-equation of (2.1), we can easily know that the solution S is a super-solution to

$$\begin{aligned} \left\{ \begin{aligned}&B_{t}-d_{1}\Delta B=-m^{*}B+\left[ \Lambda (x)-\frac{\beta ^{*}\epsilon }{\alpha _{*}}\right] ,&x\in \Omega ,t\in (t_{0},+\infty ),\\ {}&B(x,t_{0})=S(x,t_{0}),x\in \Omega ,&\frac{ \partial B}{ \partial n}=0,x\in \partial \Omega , \end{aligned}\right. \end{aligned}$$

(3.11)

and a sub-solution to

$$\begin{aligned} \left\{ \begin{aligned}&B_{t}-d_{1}\Delta B=-m_{*}B+[\Lambda (x)+{\overline{\gamma }}^{*}\epsilon ],&x\in \Omega ,t\in (t_{0},+\infty ),\\ {}&B(x,t_{0})=S(x,t_{0}),&x\in \Omega ,\\ {}&\frac{ \partial B}{ \partial n}=0,&x\in \partial \Omega . \end{aligned}\right. \end{aligned}$$

(3.12)

Denote $B_{1}$ by the solutions of Eq. (3.11) and $B_{2}$ and by the solutions of Eq. (3.12), using comparison principle, then gives

$$\begin{aligned}B_{2}\le S(x,t)\le B_{1},\textrm{variable}~x\in \partial \Omega .\end{aligned}$$

In fact, we have

$$\begin{aligned}B_{1}\rightarrow {\mathcal {S}}^{*}_{+}(\epsilon ,x) ~ \textrm{and}~B_{2}\rightarrow {\mathcal {S}}^{*}_{-}(\epsilon ,x)~~ \mathrm{uniformly ~~on~~region}~~\Omega ~~~\mathrm{as~time} ~~~t\rightarrow \infty ,\end{aligned}$$

respectively. In addition, according to the unique solution of (3.11) and (3.12), we can easily obtain that ${\mathcal {S}}^{*}_{-}(\epsilon ,x)$ tends to ${\mathcal {S}}^{*}(x)$ and ${\mathcal {S}}^{*}_{+}(\epsilon ,x)$ tends to ${\mathcal {S}}^{*}(x)$ uniformly on region $\Omega$ as $\epsilon \rightarrow 0;$ hence, since the arbitrariness $\epsilon$, our analysis implies that

$$\begin{aligned}S(x,t)\rightarrow {\mathcal {S}}^{*}(x) ~~ \mathrm{uniformly ~~on~~region}~~\Omega ~{ \mathrm as~ time~} t\rightarrow +\infty .\end{aligned}$$

In addition, we know by Lemma 3.2 that $\phi (t)$ is $\kappa$-contracting on ${\mathscr {Y}}^{+}.$ Therefore, $\phi (t): {\mathscr {Y}} +\rightarrow {\mathscr {Y}}^{+}, t>0$ admits a connected global attractor that attracts each bounded set in ${\mathscr {Y}} +.$ Theorem 3.1 is proved.$\square$

Theorem 3.2

If ${\mathcal {R}}>1$, there exists a number $\delta _{*}$, then $(S, I )=(u_{1},u_{2})$ of system starting from positive initial value $(S_{0}, I_{0})$ satisfies $\liminf _{t\rightarrow \infty } u_{i}(x, t)\ge \delta _{*}$ uniformly for all variable x belong to $\Omega$, it shows that the disease of (2.1) persists uniformly; furthermore, system (2.1) exists at least one E.E.

Proof

Let ${\mathscr {X}}_{0}:= \{\phi = (\phi _{1}, \phi _{2}) \in {\mathscr {X}}_{+}: \phi _{2}(x)\ne 0 \},$ and $\partial {\mathscr {X}}_{0}:= {\mathscr {X}}_{+}{\setminus } {\mathscr {X}}_{0} = \{\phi = (\phi _{1}, \phi _{2} \in {\mathscr {X}}_{+}: \phi _{2}(x)=0 \}$, with this setting, ${\mathscr {X}}_{+} = {\mathscr {X}}_{0}\cup \partial {\mathscr {X}}_{0}$ with ${\mathscr {X}}_{0}$ being relatively open in ${\mathscr {X}}_{+}$. Let $M\partial := \{\phi \in \partial {\mathscr {X}}_{0}:\Phi (t)\phi \in \partial {\mathscr {X}}_{0}, t> 0\}$, where $\phi (t): {\mathscr {X}}_{+} \rightarrow {\mathscr {X}}_{+}$ be the semiflow generated by (2.1). To establish Theorem 3.2, we are concerned with the following three claims.

Claim 1. We claim that ${\mathscr {X}}_{0}$ is positively invariant with respect to $\Phi (t)$, that is, $\Phi (t){\mathscr {X}}_{0} \subseteq {\mathscr {X}}_{0}$ for all $t > 0.$

Let $(S_{0},I_{0}) \in {\mathscr {X}}_{0}$, observe that the solution $I_{0}(x)\ne 0$. From the second equation of (2.1), we have $I_{t}>d_{2}\Delta I-{\overline{\gamma }}(x)I$, and then we consider the solution I of system is an upper solution of the problem

$$\begin{aligned} \left\{ \begin{aligned}&z_{t}=d_{2}\Delta z-{\overline{\gamma }}(x) z,&x\in \Omega ,t\in (0,+\infty ),\\ {}&\frac{\partial z}{\partial n}=0,\\ {}&{\hat{z}}(x,0)=z(x,0)=z_{0}. \end{aligned}\right. \end{aligned}$$

(3.13)

From (3.13), using the maximum principle, we note that $I_{0}(x)\ne 0$, then $z(x, t)>0 ~\mathrm{for~ all}~\textrm{variable}~ x \in \Omega ~\mathrm{and~time}~t> 0;$ furthermore, by using the comparison principle, one obtains

$$\begin{aligned} I(x, t)>z(x, t)~\mathrm{for~ all}~\textrm{variable}~~x \in \Omega ~\mathrm{and~time }~t\in (0,+\infty ). \end{aligned}$$

Hence, $\Phi (t)u_{0} \in {\mathscr {X}}_{0}$.

Claim 2. We claim that the $\omega$ limit set $\omega (\varphi )$ of $\varphi$ is the singleton $\{Q_{0}\}$ for every $\varphi \in M\partial$. Suppose $I(x, t; \varphi )=0$, furthermore,

$$\begin{aligned}S(x, t; \varphi ) \rightarrow \frac{\Lambda (x)}{m(x)}~ \mathrm{uniformly~ for} ~x \in \Omega .\end{aligned}$$

But, based on the I-equation of (2.1), we know that there is a positive solution I(x, t) starting from the positive initial value $\varphi =(S_{0},I_{0})$, which contradicts with $\varphi \in M\partial$. As easy seen, we have the solution $I(x, t; \varphi ) =0$ for all time $t>t_{0}.$ Thus, $S(x, t; \varphi ) \rightarrow \frac{\Lambda (x)}{m(x)}$ uniformly for variable $x \in \Omega$.

Claim 3. We claim that $Q_{0}$ of system (2.1) is a uniform weak repeller, or equivalent, there has been a $\delta >0$ such that $\limsup \limits _{t\rightarrow \infty } || \Phi (t)\phi - Q_{0}||> \delta$ for all $\phi \in {\mathscr {X}}_{0}$.

For the claim 3, to contrary, if not, then for any $\delta >0,$ $\limsup \limits _{t\rightarrow \infty } ||\Phi (t)\phi - Q_{0}||< \delta$. In other words, there exists a time $t_{1} > 0$ such that the solution $S(x, t, \varphi )>-\delta$ and $I(x, t, \varphi )<\delta$ for all time $t\in (t_{1},+\infty )$.

We consider the upper solution $I(x, t; \varphi )$ of system (2.1) as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\partial y_{2}}{\partial t}=d_{2}\Delta y_{2}+\beta (x)\left( \frac{\Lambda (x)}{m(x)}-\delta \right) y_{2}e^{-\alpha (x) y_{2}}-{\overline{\gamma }}(x) y_{2},&x\in \Omega ,t\in (t_{1},+\infty ),\\ {}&\frac{ \partial y_{2}}{ \partial n}=0,&x\in \partial \Omega ,\\ {}&y_{2}(x,t_{1})=\psi _{2}(x)&x\in \Omega \end{aligned}\right. \end{aligned}$$

(3.14)

with $\psi _{2}\le I(x,t_{1})$. Denote the principal eigenvalue by ${\mathscr {K}}^{0}_{\delta }$, and consider its eigenvalue problem as follows:

$$\begin{aligned} \left\{ \begin{aligned}&d_{2}\Delta \phi -{\overline{\gamma }}(x)\phi +\beta (x)\left( \frac{\Lambda (x)}{m(x)}-\delta \right) e^{-\alpha (x) \phi }\phi ={\mathscr {K}}^{0}\phi ,&x\in \Omega ,t\in (t_{1},+\infty ),\\ {}&\frac{ \partial \phi }{ \partial n}=0,&x\in \partial \Omega . \end{aligned}\right. \end{aligned}$$

(3.15)

Thus, we choose a sufficiently small positive number $\delta$ such that ${\mathscr {K}}^{0}_{\delta } > 0$ if ${\mathcal {R}}_{0} > 1$, it is shown that ${\mathscr {K}}^{0}_{\delta }$ is continuous in $\delta$. Using Lemma 2.3 of [3], furthermore, we can consider eigenvalue problem as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\lambda \psi _{2}=d_{2}\Delta \psi _{2}+ \beta (x)\left( \frac{\Lambda (x)}{m(x)}-\delta \right) e^{-\alpha (x) \psi _{2}}\psi _{2}-{\overline{\gamma }}(x)\psi _{2},&x\in \Omega ,t\in (t_{1},+\infty ),\\ {}&\frac{ \partial \psi _{2}}{ \partial n}=0,&x\in \partial \Omega , \end{aligned}\right. \end{aligned}$$

(3.16)

which implies that the principal eigenvalue ${\mathscr {K}}^{0}_{\delta }$ is associated with positive eigenvector $\psi ^{*}_{2}$. To this end, we take a sufficiently small positive number $\alpha$ such that $\alpha \psi ^{*}_{2}<I(x, t_{1};\varphi ).$ Let $I(x, t_{1})=\alpha \psi ^{*}_{2}$ be the initial data of system (3.16), then a unique solution of the linear system (3.15) is given as

$$\begin{aligned} y_{2}(x, t; \varphi ) = \alpha \psi ^{*}_{2} e^{{\mathscr {K}}^{0} (t-t_{1})}.\end{aligned}$$

Using the comparison principle, we can obtain $I(x, t; \varphi )>y_{2}(x, t;\varphi )~\textrm{on}~ \Omega \times [t_{1},+\infty )$, it implies that when $t \rightarrow +\infty$, namely, $I(x, t; \varphi )\rightarrow +\infty ,$ which is a contradiction with Lemma 2.1. We can choose a continuous function $\rho : {\mathscr {X}}_{+} \rightarrow [0,+\infty )$ by

$$\begin{aligned}\rho (\varphi ) =\min _{x\in \Omega }\varphi _{2}(x), \varphi \in {\mathscr {X}}_{+},\end{aligned}$$

where $\varphi _{2}= I$, thus, $\rho ^{-1}(0,+\infty )\subseteq {\mathscr {X}}_{0}$. We have two cases: one case $\rho (\varphi )=0$ and $\varphi \in {\mathscr {X}}_{0}$, the other case $\rho (\varphi )> 0$, and then $\rho (\Phi (t)\phi )>0$.

Thus, by using semiflow definition, we know that the generalized distance function $\rho$ is a semiflow $\Phi (t): {\mathscr {X}}_{+} \rightarrow {\mathscr {X}}_{+}$. To this end, it shows that any forward orbit of $\Phi (t)$ in $M\partial$ will tend to $Q_{0}$ of system (2.1), and then there exists the stable subset $W_{s}(Q_{0})$ of $Q_{0}$ such that $W_{s}(Q_{0}) \bigcap {\mathscr {X}}_{0}=\emptyset$.

Further, we consider that $Q_{0}$ is an isolated invariant set in domain ${\mathscr {X}}_{+}$ and there are no sets of $Q_{0}$ form in domain $\partial {\mathscr {X}}_{0}$. Recall that Theorem 3 in [20], we know that there is a positive number $\delta _{1}$ such that $\{\min \{\rho (\psi )\}: \psi \in \omega (\varphi )\}>\delta _{1}~\mathrm{for ~any}~ \psi \in {\mathscr {X}}_{0}$, that is, for $\forall \varphi \in {\mathscr {X}}_{0}$, we obtain

$$\begin{aligned}\liminf _{t\rightarrow \infty }I(t, x, \varphi )>\delta _{1}.\end{aligned}$$

Observe that Lemma 2.1, we can choose a ${\mathscr {M}}^{**}>0$ and time $t_{2}$ such that $I(t, x, \varphi )<M^{**}~~\textrm{for}~\forall ~t>t_{2},~\forall x \in \Omega .$ By S-equation of (2.1), for $~t> t_{2}, x\in \Omega$, we have

$$\begin{aligned}S_{t}> d_{1}\Delta S+\Lambda ^{*}-(m_{*}+\beta _{*}{\mathscr {M}}^{**})S.\end{aligned}$$

Using the comparison principle, we can obtain

$$\begin{aligned}\liminf _{t\rightarrow \infty }S(x, t,\varphi )\ge \delta _{2}:= \frac{\Lambda ^{*}}{m_{*}+ \beta _{*}{\mathscr {M}}^{**}},\end{aligned}$$

where $\delta _{*}=\min \{\delta _{1}, \delta _{2}\}$. To this end, the uniform persistence is proved. Based on Theorem 4.7 in [11], we know that (2.1) admits at least a E.E. in ${\mathscr {X}}_{0}$. Theorem 3.1 is proved.$\square$

4 Global dynamics of the endemic equilibrium

We now explore the global dynamics of system (2.1), and consider that the coefficient functions $\Lambda (x), \beta (x), {\overline{\gamma }}(x),\alpha (x), m(x)$ are the positive constants $\Lambda , \beta , {\overline{\gamma }},\alpha , m$, then we have

$$\begin{aligned} \left\{ \begin{aligned}&S_{t}-d_{1}\Delta S=\Lambda -mS-\frac{\beta S }{e^{\alpha I}}I+{\overline{\gamma }} I,&(x,t)\in \Omega \times (0,+\infty ),\\ {}&I_{t}-d_{2}\Delta I=\frac{\beta S}{e^{\alpha I}} I-{\overline{\gamma }} I,&(x,t)\in \Omega \times (0,+\infty ),\\ {}&\frac{ \partial S}{ \partial n}=\frac{ \partial I}{ \partial n}=0,&x\in \partial \Omega ,\\ {}&S(x,0)=S_{0}(x),I(x,0)=I_{0}(x),&x\in \Omega . \end{aligned}\right. \end{aligned}$$

(4.1)

Thanks to Theorem 3.1, we know that system (4.1) does no endemic equilibrium (E.E.)if ${\mathcal {R}}<1$. Therefore, we mainly consider the following case if ${\mathcal {R}}> 1$ in this section.

And then, clearly, system (4.1) exists the unique disease-free equilibrium (D.F.E.)$E_{0}:= \left( \frac{\Lambda }{m}, 0\right)$, the unique endemic equilibrium $E_{c}:= (S_{*}, I_{*} )$ if $\Lambda \beta >m{\overline{\gamma }}$, (i,e., ${\mathcal {R}}=\frac{\Lambda \beta }{m{\overline{\gamma }}}$), and its coordinates are given by $S_{*}=\frac{\Lambda }{m},I_{*}=\frac{1}{\alpha }\ln \left( \frac{\Lambda \beta }{m{\overline{\gamma }}}\right) .$ To investigate the global dynamics of the E.E. of (4.1), constructing a Lyapunov function, Theorem 4.1 is given as below.

Theorem 4.1

Assume that $\Lambda \beta >m{\overline{\gamma }}$, then the endemic equilibrium (E.E.) is globally attractive.

Proof

Motivated by [22], a function is considered as

$$\begin{aligned} E(t)=\mathop {\int }\limits _{\Omega }[L(S,I)]\textrm{d}x, \end{aligned}$$

where $L(S,I)=\mathop {\int }\limits _{\Omega }\left( \frac{S^{2}-S^{2}_{*}}{S^{2}}\right) \textrm{d}S+\mathop {\int }\limits _{\Omega }\left( \frac{(e^{\alpha I})^{2}-(e^{\alpha I_{*}})^{2}}{(e^{\alpha I})^{2}}\right) \textrm{d}I.$ Then, elementary computation yields

$$\begin{aligned} \frac{\textrm{d}E}{\textrm{d}t}&=\mathop {\int }\limits _{\Omega }[L(S,I)]'_{S}\frac{\textrm{d}S}{\textrm{d}t}+[L(S,I)]'_{I}\frac{\textrm{d}I}{\textrm{d}t}\textrm{d}x~~~~~~~~~~~\left( \textrm{where}~~L'_{S}=\frac{\textrm{d}L}{\textrm{d}S},L'_{I}=\frac{\textrm{d}L}{\textrm{d}I}\right) \\ {}&=\mathop {\int }\limits _{\Omega }\left( \frac{S^{2}-S^{2}_{*}}{S^{2}}\right) d_{1}\Delta S+\left( \frac{(e^{\alpha I})^{2}-(e^{\alpha I_{*}})^{2}}{(e^{\alpha I})^{2}}\right) d_{2}\Delta I\textrm{d}x\\&\quad +\mathop {\int }\limits _{\Omega }\left( \frac{S^{2}-S^{2}_{*}}{S^{2}}\right) (\Lambda -mS-\beta S Ie^{-\alpha I}+{\overline{\gamma }} I)+\left( \frac{(e^{\alpha I})^{2}-(e^{\alpha I_{*}})^{2}}{(e^{\alpha I})^{2}}\right) (\beta S Ie^{-\alpha I}-{\overline{\gamma }} I)\textrm{d}x\\ {}&=-\mathop {\int }\limits _{\Omega }\frac{2S^{2}_{*}}{S^{2}}d_{1}|\nabla S|^{2} +\frac{2\alpha (e^{\alpha I_{*}})^{2}}{(e^{\alpha I})^{2}}d_{2}|\nabla I|^{2}\textrm{d}x\\ {}&\quad +\mathop {\int }\limits _{\Omega }\left( \frac{S^{2}-S^{2}_{*}}{S^{2}}\right) (\Lambda -mS-\beta S Ie^{-\alpha I}+{\overline{\gamma }} I)+\left( \frac{(e^{\alpha I})^{2}-(e^{\alpha I_{*}})^{2}}{(e^{\alpha I})^{2}}\right) (\beta S Ie^{-\alpha I}-{\overline{\gamma }} I)\textrm{d}x\\ {}&=-\mathop {\int }\limits _{\Omega }\frac{2S^{2}_{*}}{S^{3}}d_{1}|\nabla S|^{2} +\frac{2\alpha (e^{\alpha I_{*}})^{2}}{(e^{\alpha I})^{2}}d_{2}|\nabla I |^{2}\textrm{d}x\\ {}&\quad +\mathop {\int }\limits _{\Omega }\left( \frac{S^{2}-S^{2}_{*}}{S^{2}}\right) ((mS_{*}-\beta S_{*} I_{*}e^{-\alpha I_{*}}+{\overline{\gamma }} I_{*})-m S-\beta S Ie^{-\alpha I}+{\overline{\gamma }} I)\\ {}&\quad +\left( \frac{(e^{\alpha I})^{2}-(e^{\alpha I_{*}})^{2}}{(e^{\alpha I})^{2}}\right) (\beta S Ie^{-\alpha I}-{\overline{\gamma }} I)\textrm{d}x\\ {}&\quad =-\mathop {\int }\limits _{\Omega }\frac{2S^{2}_{*}}{S^{3}}d_{1}|\nabla S|^{2} +\frac{2\alpha (e^{\alpha I_{*}})^{2}}{(e^{\alpha I})^{2}}d_{2}|\nabla I|^{2}\textrm{d}x\\ {}&\quad +\mathop {\int }\limits _{\Omega }\left( \frac{S^{2}-S^{2}_{*}}{S^{2}}\right) ((mS^{*})-mS-\beta S Ie^{-\alpha I}+{\overline{\gamma }} I)+\left( \frac{(e^{\alpha I})^{2}-(e^{\alpha I_{*}})^{2}}{(e^{\alpha I})^{2}}\right) (\beta S Ie^{-\alpha I}-{\overline{\gamma }} I)\textrm{d}x\\&\le -\mathop {\int }\limits _{\Omega }\frac{2S^{2}_{*}}{S^{3}}d_{1}|\nabla S|^{2} +\frac{2\alpha (e^{\alpha I_{*}})^{2}}{(e^{\alpha I})^{2}}d_{2}|\nabla I|^{2}\textrm{d}x\\ {}&\quad +\mathop {\int }\limits _{\Omega }\left( \frac{S^{2}-S^{2}_{*}}{S^{2}}\right) ((mS_{*})-mS)\textrm{d}x-\mathop {\int }\limits _{\Omega }\left( \frac{S^{2}-S^{2}_{*}}{S^{2}}\right) (\beta S Ie^{-\alpha I}-{\overline{\gamma }} I)\\ {}&\quad -\left( \frac{(e^{\alpha I})^{2}-(e^{\alpha I_{*}})^{2}}{(e^{\alpha I})^{2}}\right) (\beta S Ie^{-\alpha I}-{\overline{\gamma }} I)\textrm{d}x\\ {}&=-\mathop {\int }\limits _{\Omega }(\frac{2S^{2}_{*}}{S^{3}})d_{1}|\nabla S|^{2} +(\frac{2\alpha (e^{\alpha I_{*}})^{2}}{(e^{\alpha I})^{2}})d_{2}|\nabla I |^{2}\textrm{d}x\\ {}&\quad +\mathop {\int }\limits _{\Omega }\left( \frac{S^{2}-S^{2}_{*}}{S^{2}}\right) ((mS_{*})-mS)\textrm{d}x-\mathop {\int }\limits _{\Omega }\left[ (\frac{S^{2}-S^{2}_{*}}{S^{2}})-(\frac{(e^{\alpha I})^{2}-(e^{\alpha I_{*}})^{2}}{(e^{\alpha I})^{2}})\right] (\beta S Ie^{-\alpha I}-{\overline{\gamma }} I)\textrm{d}x\\ {}&=-\mathop {\int }\limits _{\Omega }\frac{2S^{2}_{*}}{S^{3}}d_{1}|\nabla S|^{2} +\frac{2\alpha (e^{\alpha I_{*}})^{2}}{(e^{\alpha I})^{2}}d_{2}|\nabla I|^{2}\textrm{d}x+\mathop {\int }\limits _{\Omega }\left( \frac{S^{2}-S^{2}_{*}}{S^{2}}\right) ((mS_{*})-mS)\textrm{d}x\\ {}&\quad -\beta I\frac{S}{e^{\alpha I_{*}}}\mathop {\int }\limits _{\Omega }\left[ (\frac{S^{2}-S^{2}_{*}}{S^{2}})-(\frac{(e^{\alpha I})^{2}-(e^{\alpha I_{*}})^{2}}{(e^{\alpha I})^{2}})\right] \left( \frac{e^{\alpha I_{*}}}{e^{\alpha I}}-\frac{S_{*}}{S} \right) \textrm{d}x\\ {}&=-\mathop {\int }\limits _{\Omega }\frac{2S^{2}_{*}}{S^{3}}d_{1}|\nabla S|^{2} +\frac{2\alpha (e^{\alpha I_{*}})^{2}}{(e^{\alpha I})^{2}}d_{2}|\nabla I|^{2}\textrm{d}x \\ {}&\quad -m\mathop {\int }\limits _{\Omega }\left( \frac{S+S_{*}}{S^{2}}\right) (S_{*}-S)^{2}\textrm{d}x-\beta I\frac{S}{e^{\alpha I_{*}}}\mathop {\int }\limits _{\Omega }\left( \frac{e^{\alpha I_{*}}}{e^{\alpha I}}+\frac{S_{*}}{S} \right) \left( \frac{e^{\alpha I_{*}}}{e^{\alpha I}}-\frac{S_{*}}{S}\right) ^{2}\textrm{d}x \leqslant 0, \end{aligned}$$

where we observe that ${\overline{\gamma }}=\beta S_{*}e^{-\alpha I_{*}}.$ Notice that, for any positive time t,  the continuously function E(t) is a Lyapunov function.

Furthermore, we know that for any $t>0,$ the continuously function $\frac{\textrm{d}E}{\textrm{d}t} <0$ along trajectories except at point $\left( \frac{\Lambda }{m},\frac{1}{\alpha }\ln \left( \frac{\Lambda \beta }{m{\overline{\gamma }}}\right) \right)$ where $\frac{\textrm{d}E}{\textrm{d}t} = 0$, then we have S(x, t) $\frac{\Lambda }{m},$ I(x, t) tends to$\frac{1}{\alpha }\ln \left( \frac{\Lambda \beta }{m{\overline{\gamma }}}\right) ,$ $x\in \partial \Omega .$

In addition, using proposition 2.1 in [29], for some ${\mathscr {M}}>0$, we here obtain

$$\begin{aligned} ||S(x,t)||_{L^{\infty }(\Omega )}+ ||I(x,t)||_{L^{\infty }(\Omega )}<{\mathscr {M}},\forall t\in (0,+\infty ). \end{aligned}$$

Utilizing Sobolev embedding theorem, we immediately obtain the following result

$$\begin{aligned} (S(x,t),I(x,t))\rightarrow \left( \frac{\Lambda }{m},\frac{1}{\alpha }\ln \left( \frac{\Lambda \beta }{m{\overline{\gamma }}}\right) \right) =(S_{*}, I_{*}),x\in \partial \Omega . \end{aligned}$$

Thus, it shows that point ($S_{*}, I_{*})$ attracts all solutions of system (2.1). Theorem 4.1 is proved. $\square$

5 Asymptotic profiles of the endemic equilibrium

We now investigate the asymptotic behavior of the E.E. of system (2.1), then the elliptic system is described as

$$\begin{aligned} \left\{ \begin{aligned}&d_{1}\Delta S +\Lambda (x)-m(x)S-\frac{\beta (x) S I}{e^{\alpha (x) I}}+{\overline{\gamma }}(x) I=0,&x\in \Omega , t\in (0,+\infty ),\\ {}&d_{2}\Delta I+ \frac{\beta (x) S I}{e^{\alpha (x) I}}-{\overline{\gamma }}(x) I=0,&x\in \Omega ,t\in (0,+\infty ),\\ {}&\frac{ \partial S}{ \partial n}=\frac{ \partial I}{ \partial n}=0,&x\in \partial \Omega ,\\ {}&S(x,0)=S_{0}(x),I(x,0)=I_{0}(x),&x\in \Omega . \end{aligned}\right. \end{aligned}$$

(5.1)

Observe that Theorem 3.1, when ${\mathcal {R}}>1$, then we know that system (5.1) exists at least one positive solution. Next, denote $(S, I )>0$ by the solutions of Eq. (5.1). Utilizing the $L^{1}$-bounds of the solution (S, I), and integrating both the S and I equations for (5.1) over region $\Omega$, then we give

$$\begin{aligned} \mathop {\int }\limits _{\Omega }\left[ m(x)S+\frac{\beta (x) S}{e^{\alpha (x) I}}I\right] \textrm{d}x=\mathop {\int }\limits _{\Omega }(\Lambda (x)+{\overline{\gamma }}(x) I)\textrm{d}x\end{aligned}$$

(5.2)

and

$$\begin{aligned} \mathop {\int }\limits _{\Omega }\left[ {\overline{\gamma }}(x) -\frac{\beta (x) S}{e^{\alpha (x) }}\right] I\textrm{d}x=0.\end{aligned}$$

(5.3)

Inserting (5.3) into (5.2), it then follows that

$$\begin{aligned} \mathop {\int }\limits _{\Omega }m(x)S\textrm{d}x=\mathop {\int }\limits _{\Omega }\Lambda (x)\textrm{d}x.\end{aligned}$$

(5.4)

From (5.4), it is clear that

$$\begin{aligned} \mathop {\int }\limits _{\Omega }S\textrm{d}x<\frac{\Lambda (x)|\Omega |}{m(x)}<\frac{\Lambda _{*}|\Omega |}{m^{*}}.\end{aligned}$$

(5.5)

Moreover, in view of Eqs. (5.3) and (5.5), by using $e^{\alpha (x) I}\ge \alpha (x) I+1$, we have

$$\begin{aligned}\mathop {\int }\limits _{\Omega }{\overline{\gamma }}(x)I\textrm{d}x=\mathop {\int }\limits _{\Omega }\beta (x) SIe^{-\alpha I}\textrm{d}x\le \mathop {\int }\limits _{\Omega }\frac{\beta (x) SI}{\alpha (x) I+1}\textrm{d}x<\frac{\beta (x) \Lambda (x)|\Omega |}{\alpha (x) m(x)}\triangleq \Xi ,\end{aligned}$$

which in turn yields

$$\begin{aligned} \mathop {\int }\limits _{\Omega }{\overline{\gamma }}(x)I\textrm{d}x=\mathop {\int }\limits _{\Omega }\beta (x) SIe^{-\alpha (x) I}\textrm{d}x\le \Xi <\frac{\beta _{*} \Lambda _{*}|\Omega |}{\alpha ^{*} m^{*}}. \end{aligned}$$

(5.6)

5.1 The case $d_{1}\rightarrow 0$

Theorem 5.1

If ${\mathcal {R}}>1$, fixing $d_{2}>0$, and let $d_{1}\rightarrow 0$, then every (S, I) of system (5.1) starting from positive initial value $(S_{0}, I_{0})$ satisfies $S\rightarrow {\hat{S}}_{**},~\textrm{and} ~I\rightarrow {\hat{I}}_{**}$ uniformly on region $\Omega$, where ${\hat{S}}_{**}={\mathcal {G}}(x, {\hat{I}}_{**})=\frac{[\Lambda (x)+{\overline{\gamma }}(x){\hat{I}}_{**}]e^{\alpha (x) {\hat{I}}_{**}}}{m(x)e^{\alpha (x) {\hat{I}}_{**}}+\beta (x){\hat{I}}_{**}}$, and ${\hat{I}}_{**}>0$ meets the following conditions

$$\begin{aligned} d_{2}\Delta {\hat{I}}_{**}+\beta (x){\mathcal {G}}(x, {\hat{I}}_{**}){\hat{I}}_{**}e^{-\alpha (x) {\hat{I}}_{**}}-{\overline{\gamma }}(x){\hat{I}}_{**}=0,~\textrm{variable}~ x\in \Omega , \frac{ \partial {\hat{I}}_{**}}{ \partial n}=0,~\textrm{variable}~x\in \partial \Omega . \end{aligned}$$

(5.7)

Proof

To establish this, we prove this result in three steps.

Step 1. We prove that the solutions S and I of (2.1) are $L^{2}$ estimates. Now, multiplying both of the first equation for system (5.1) by S, we have

$$\begin{aligned}0\leqslant d_{1}\mathop {\int }\limits _{\Omega }|\nabla S|^{2}\textrm{d}x=\mathop {\int }\limits _{\Omega }\left[ \frac{\Lambda (x)Se^{\alpha (x) I}-m(x)S^{2}e^{\alpha (x) I}-\beta (x) IS^{2}+{\overline{\gamma }}(x) ISe^{\alpha (x) I}}{e^{\alpha (x) I}}\right] \textrm{d}x.\end{aligned}$$

Further, we obtain

$$\begin{aligned}\mathop {\int }\limits _{\Omega }\left[ \frac{m(x)S^{2}e^{\alpha (x) I}+\beta (x) I S^{2}}{e^{\alpha (x) I}}\right] \textrm{d}x\le \mathop {\int }\limits _{\Omega }(\Lambda (x)S+{\overline{\gamma }}(x) IS)\textrm{d}x,\end{aligned}$$

which implies that

$$\begin{aligned} \mathop {\int }\limits _{\Omega }m(x)S^{2}\textrm{d}x\le \mathop {\int }\limits _{\Omega }[\Lambda (x)S+{\overline{\gamma }}(x) IS]\textrm{d}x.\end{aligned}$$

(5.8)

Notice that the solution I meets

$$\begin{aligned} \Delta I+\left( \frac{ \beta (x)S-{\overline{\gamma }}(x)e^{\alpha (x) I}}{ e^{\alpha (x) I}d_{2}}\right) I=0,\mathrm{~variable~} x\in \Omega ,\mathrm{~and~} \frac{ \partial I}{ \partial n}=0,\mathrm{~variable~} x\in \partial \Omega . \end{aligned}$$

(5.9)

Using Harnack-type inequality [42], then we can get

$$\begin{aligned} \max _{x\in \Omega } I<{\mathscr {M}}\min _{x\in \Omega } I,\end{aligned}$$

(5.10)

where ${\mathscr {M}}>0$ does not depend on $d_{1} > 0$.

From Eqs. (5.6) and (5.10), we have

$$\begin{aligned} I\le {\mathscr {M}}\min _{\Omega }I<\frac{{\mathscr {M}}}{|\Omega |}\mathop {\int }\limits _{\Omega }I\textrm{d}x<{\mathscr {M}}.\end{aligned}$$

(5.11)

From Eqs. (5.11) and (5.8), using Hölder inequality, it follows that

$$\begin{aligned}\mathop {\int }\limits _{\Omega }S^{2}\textrm{d}x<\frac{\Lambda _{*}+{\overline{\gamma }}_{*} {\mathscr {M}}}{m^{*}}\mathop {\int }\limits _{\Omega }S\textrm{d}x<{\mathscr {M}}\left( \mathop {\int }\limits _{\Omega }S^{2}\textrm{d}x\right) ^{\frac{1}{2}}.\end{aligned}$$

Thus, we have

$$\begin{aligned} \mathop {\int }\limits _{\Omega }S^{2}\textrm{d}x<{\mathscr {M}}.\end{aligned}$$

(5.12)

The $L^{\infty }$ bound of the solution I in system (5.11) implies that the $L^{2}$ bound of the solution I is also held.

Step 2. We prove that the solution I of (2.1) is convergence. First, we noted that I of (2.1) satisfies

$$\begin{aligned} d_{2}\Delta I+ \left[ \frac{\beta (x) S-{\overline{\gamma }}(x)e^{\alpha (x) I}}{e^{\alpha (x) I}}\right] I=0,\mathrm{~ variable~} x\in \Omega ,\mathrm{~ and~} \frac{ \partial I}{ \partial n}=0,\mathrm{~ variable~} x\in \partial \Omega . \end{aligned}$$

(5.13)

From Eq. (5.12), we immediately obtain

$$\begin{aligned}||\beta (x) SIe^{-\alpha (x) I}||_{L^{p}(\Omega )}<{\mathscr {M}},\forall p>1.\end{aligned}$$

Using $L^{p}$-estimate (see [3]), we have $|| I||_{W^{2,p}(\Omega )}<{\mathscr {M}},~\mathrm{for~any~given~integer}~p>1$. Taking a sufficiently large p and employing Embedding Theorem [3], one gives

$$\begin{aligned}|| I||_{C^{1+\theta }(\Omega )}<{\mathscr {M}},~~\mathrm{for~~ some}~~0<\theta <1.\end{aligned}$$

Thus, there exists a subsequence of diffusion rate $d_{1, n}\rightarrow 0$, as the integer $n\rightarrow +\infty$ that

$$\begin{aligned}d_{n}:= d_{1,n},~\textrm{satisfying} ~~d_{n}\rightarrow 0 ~,\end{aligned}$$

and (5.1) exists a corresponding solution $(S_{n}, I_{n}):= (S_{d_{1,n}}, I_{d_{1,n}} )>0$ with $d_{1} = d_{n}$, as the integer $n\rightarrow +\infty$ such that $I_{n}\rightarrow {\hat{I}}_{**} ~~\mathrm{uniformly~on~region }~\Omega ,$ where the solution ${\hat{I}}_{ **} \in C^{1}(\Omega )$ and the solution ${\hat{I}}_{ **} > 0$.

According to Eq. (5.10),

$$\begin{aligned} \mathrm{either~~~the~solution}~~{\hat{I}}_{ **}=0~~\mathrm{on~region}~\Omega , ~~\mathrm{or ~~the~solution} ~~{\hat{I}}_{ **} > 0 ~\mathrm{on~region}~~\Omega .\end{aligned}$$

(5.14)

Without loss of generality, if here the former of (5.14) holds, that is,

$$\begin{aligned} \mathrm{the~solution~}I_{n}\rightarrow 0 ~~\mathrm{uniformly~on~region }~\Omega ,~as ~n\rightarrow +\infty ,\end{aligned}$$

(5.15)

then, for a small number $\epsilon$ with the inequality $0<\epsilon < \min \limits _{x\in \Omega }\frac{\Lambda (x)}{m(x)}$, and for all large number n, we obtain $0<I_{n}(x,t)<\epsilon .$

In addition, from S-equation of (5.1), we know that for all large number n, the solution $(S_{n}, I_{n})$ gives

$$\begin{aligned}-d_{1}\Delta S_{n}\leqslant \Lambda (x)-m(x)S_{n}+{\overline{\gamma }}_{*} \epsilon ,~\textrm{variable} ~x\in \Omega ;~~\mathrm{and~}\frac{\partial S_{n}}{\partial n}=0, ~\textrm{variable} ~x\in \partial \Omega \end{aligned}$$

and

$$\begin{aligned}-d_{1}\Delta S_{n}\geqslant \Lambda (x)-m(x)S_{n}-\epsilon \beta _{*} S_{n},~\textrm{variable} ~ x\in \Omega ,~\mathrm{and~}\frac{\partial S_{n}}{\partial n}=0,~\textrm{variable} ~ x\in \partial \Omega .\end{aligned}$$

For any $n>0$, two auxiliary systems are considered as follows:

$$\begin{aligned} -d_{1}\Delta h= \Lambda (x)-m(x)h+{\overline{\gamma }}_{*} \epsilon ,~\textrm{variable} ~ x\in \Omega ;~\mathrm{and~}\frac{\partial h}{\partial n}=0,~\textrm{variable}~x\in \partial \Omega \end{aligned}$$

(5.16)

and

$$\begin{aligned} -d_{1}\Delta y= \Lambda (x)-m(x)y-\epsilon \beta _{*} y, ~\textrm{variable} ~x\in \Omega ;~\mathrm{and~}\frac{\partial y}{\partial n}=0,~\textrm{variable} ~x\in \partial \Omega .\end{aligned}$$

(5.17)

Suppose that Eqs. (5.16) and (5.17) exist the unique positive solutions $h_{n}$ and $y_{n}$, respectively. A simple discussion, for all large integer n, gives the following inequality

$$\begin{aligned} y_{n}\leqslant S_{n}\leqslant h_{n}~~\mathrm{on~region~ \Omega ~~}.\end{aligned}$$

(5.18)

By Lemma 2.4 in [3], it follows that

$$\begin{aligned}h_{n}\rightarrow \frac{\Lambda (x)+{\overline{\gamma }}_{*} \epsilon }{m(x)} ~~\mathrm{uniformly ~on~ region}~\Omega ,~\mathrm{as~the~ integer} ~n\rightarrow +\infty \end{aligned}$$

and

$$\begin{aligned}y_{n}\rightarrow \frac{\Lambda (x)}{m(x)+\epsilon \beta _{*}}~~\mathrm{uniformly ~on ~ region}~\Omega ,~\mathrm{as~the integer} ~n\rightarrow +\infty .\end{aligned}$$

Hence, setting $n\rightarrow \infty$ in (5.18), we obtain

$$\begin{aligned} \frac{\Lambda (x)}{m(x)+\epsilon \beta _{*}}\leqslant \liminf _{n\rightarrow \infty } S_{n}\leqslant \limsup _{n\rightarrow +\infty }S_{n} \leqslant \frac{\Lambda (x)+{\overline{\gamma }}_{*} \epsilon }{m(x)}.\end{aligned}$$

(5.19)

According to the arbitrary small $\epsilon$ in (5.19), namely

$$\begin{aligned} S_{n}\rightarrow \frac{\Lambda (x)}{m(x)}~~\mathrm{uniformly ~~on ~region ~~\Omega , as~the~ integer}~ n\rightarrow +\infty .\end{aligned}$$

(5.20)

Now, we know that the I-equation of (5.1), then

$$\begin{aligned}-d_{2}\Delta I_{n}= \beta (x) S_{n}e^{-\alpha (x) I_{n}} I_{n}-{\overline{\gamma }}(x) I_{n},~ \textrm{variable}~x\in \Omega ,~ \textrm{and}~\frac{ \partial I_{n}}{ \partial n}=0,~ \textrm{variable}~ x\in \partial \Omega .\end{aligned}$$

Define $I^{*}_{n}=\frac{I_{n}}{||I||_{L^{\infty }(\Omega )}},$ then, we know that norm $||I^{*}||_{L^{\infty }(\Omega )} = 1$ for the integer $n > 1$, and the solution ${^{\tilde{\,}}}$ $I^{*}_{n}$ satisfies

$$\begin{aligned} -d_{2}\Delta I^{*}_{n}= \left[ \frac{\beta (x)S_{n}-{\overline{\gamma }}(x)e^{\alpha (x) I_{n}}}{e^{\alpha (x) I_{n}}} \right] I^{*}_{n},~ \textrm{variable}~x\in \Omega ,~ \textrm{and}~\frac{ \partial I^{*}_{n}}{ \partial n}=0,~ \textrm{variable}~x\in \partial \Omega .\end{aligned}$$

(5.21)

Using a standard compactness argument for (5.21), and if necessary we may assume that a further subsequence is given as

$$\begin{aligned}~\mathrm{the~solution}~I^{*}_{n}\rightarrow I^{*} ~~\mathrm{uniformly ~on~~region }~\Omega ,~\mathrm{as~ the~integer} ~n\rightarrow \infty ,\end{aligned}$$

where the solution $I^{*} \in C^{1}(\Omega )$, the solution $I^{*}$ is positive on region $\Omega$, and the norm $||I^{*}||_{L^{\infty }(\Omega )}$ is equal to one.

According to Eqs. (5.15), (5.20) and (5.21), we know that the solution $I^{*}$ satisfies

$$\begin{aligned}-d_{2}\Delta I^{*}_{n}= \left[ \frac{\beta (x)\Lambda (x)-{\overline{\gamma }}(x)m(x)}{m(x)}\right] I^{*}_{n},~ \textrm{variable}~ x\in \Omega ,~ \textrm{and}~\frac{ \partial I^{*}_{n}}{ \partial n}=0,~ \textrm{variable}~ x\in \partial \Omega .\end{aligned}$$

Employing Harnack-type inequality [31], the solution ${^{\tilde{\,}}}$ $I^{*}$ is positive on region $\Omega$.

In addition, based on the uniqueness of the principal eigenvalue ${\hat{\lambda }}$ of (3.10), we know that ${\hat{\lambda }}$ satisfies ${\hat{\lambda }} = 0$, which is a contradiction with $\frac{\Lambda (x)\beta (x)}{m(x)}>{\overline{\gamma }}(x)$ (i,e, ${\mathcal {R}}>1$).

Therefore, (5.15) cannot hold, and so there exists the positive solution ${\hat{I}}_{**}$ of system on region $\Omega$, as $n \rightarrow \infty$ and,

$$\begin{aligned} ~~\mathrm{the~solution}~ I_{n}\rightarrow {\hat{I}}_{**}~~\mathrm{uniformly~~on~region}~~~\Omega .\end{aligned}$$

(5.22)

Step 3. We prove that the solution S is convergence. The S-equation of system (5.1) is satisfied by the solution $S_{n}$, then, we have

$$\begin{aligned} \left\{ \begin{aligned}&-d_{1}\Delta S_{n}=\Lambda (x)-m(x)S_{n}-\frac{\beta (x) S_{n} I_{n}}{e^{\alpha (x) I_{n}}}+{\overline{\gamma }}(x) I_{n},&x\in \Omega ,\\ {}&\frac{ \partial S_{n}}{ \partial n}=0,&x\in \partial \Omega . \end{aligned}\right. \end{aligned}$$

(5.23)

From (5.23), for a small number $\epsilon > 0$ and large n, we immediately have

$$\begin{aligned}\begin{aligned}\Lambda (x)-m(x)S_{n}-\beta (x) S_{n} I_{n}e^{-\alpha (x) I_{n}}+{\overline{\gamma }}(x) I_{n}&\leqslant \Lambda (x)-m(x)S_{n}-\frac{\beta (x) S_{n} ({\hat{I}}_{**}-\epsilon )}{e^{\alpha (x) ({\hat{I}}_{**}+\epsilon )}}+{\overline{\gamma }}(x) ({\hat{I}}_{**}+\epsilon )\\ {}&=\frac{({\mathfrak {g}}_{+}^{1,\epsilon }-S_{n}){\mathfrak {g}}_{-}^{1,\epsilon }}{e^{\alpha (x) ({\hat{I}}_{**}+\epsilon )}},\end{aligned}\end{aligned}$$

where

$$\begin{aligned}{\mathfrak {g}}_{-}^{1,\epsilon }=m(x)e^{\alpha (x) ({\hat{I}}_{**}+\epsilon )}+\beta (x) ({\hat{I}}_{**}-\epsilon ),~~{\mathfrak {g}}_{+}^{1,\epsilon }=\frac{[\Lambda (x)+{\overline{\gamma }}(x) ({\hat{I}}_{**}+\epsilon )]e^{\alpha (x) ({\hat{I}}_{**}+\epsilon )}}{m(x)e^{\alpha (x) ({\hat{I}}_{**}+\epsilon )}+\beta (x) ({\hat{I}}_{**}-\epsilon )}.\end{aligned}$$

For a fixing large positive number n, then, the following auxiliary problem is considered as

$$\begin{aligned} -d_{2}\Delta {\hat{I}}_{**}= \beta (x){\mathfrak {g}}_{+}^{1,\epsilon }{\hat{I}}_{**}e^{-\alpha {\hat{I}}_{**}}-{\overline{\gamma }}(x) {\hat{I}}_{**},\mathrm{~ variable}~ x\in \Omega , \frac{ \partial {\hat{I}}_{**}}{ \partial n}=0,\mathrm{~ variable}~ x\in \partial \Omega . \end{aligned}$$

(5.24)

It shows that the solution $S_{n}$ is a sub-solution of (5.24) and any sufficiently large number ${\mathscr {C}}>0$ satisfies $S_{n} <{\mathscr {C}}$, and then, Eq. (5.24) exists at least a solution (S, I) starting from this initial value $(S_{0},I_{0})$.

Now, denoted by $w_{n}$, and $S_{n} \leqslant w_{n}\leqslant {\mathscr {C}} \mathrm{~on~region}~~\Omega .$ Applying maximum principle [29], it shows that

$$\begin{aligned}\min _{x\in \Omega } {\mathfrak {g}}_{+}^{1,\epsilon }\leqslant \min _{x\in \Omega } w_{n}\leqslant w_{n}\leqslant \max _{x\in \Omega } w_{n}\le \max _{x\in \Omega } {\mathfrak {g}}_{+}^{1,\epsilon }.\end{aligned}$$

Using singular perturbation theory [29], we can conclude that solution $w_{n}>0$ of (5.24) satisfies

$$\begin{aligned}w_{n}\rightarrow {\mathfrak {g}}_{+}^{1,\epsilon }~~\mathrm{uniformly~~on ~region~~\Omega ,~as}~~ n \rightarrow +\infty .\end{aligned}$$

Based on $S_{n}\le w_{n} \le {\mathscr {C}}$ on region $\Omega$, we obtain

$$\begin{aligned} \limsup _{n\rightarrow \infty }S_{n}(x)\leqslant {\mathfrak {g}}_{+}^{1,\epsilon }.\end{aligned}$$

(5.25)

In addition, for large number $n>0$, we have

$$\begin{aligned} \begin{aligned}\frac{\Lambda (x)e^{\alpha (x) I_{n}}-e^{\alpha (x) I_{n}}m(x)S_{n}-\beta (x) S_{n} I_{n}+e^{\alpha (x) I_{n}}{\overline{\gamma }}(x) I_{n}}{e^{\alpha (x) I_{n}}}&\geqslant \Lambda (x)-m(x)S_{n}\\ {}&\quad -\frac{\beta (x) S_{n} ({\hat{I}}_{**}+\epsilon )}{e^{\alpha (x) ({\hat{I}}_{**}-\epsilon )}}+{\overline{\gamma }}(x) ({\hat{I}}_{**}-\epsilon )\\ {}&=\frac{({\mathfrak {g}}_{+}^{2,\epsilon }-S_{n}){\mathfrak {g}}_{-}^{2,\epsilon }}{e^{\alpha (x) ({\hat{I}}_{**}-\epsilon )}},\end{aligned}\end{aligned}$$

where ${\mathfrak {g}}_{-}^{2,\epsilon }=m(x)e^{\alpha (x) ({\hat{I}}_{**}-\epsilon )}+\beta (x) ({\hat{I}}_{**}+\epsilon ), {\mathfrak {g}}_{+}^{2,\epsilon }=\frac{[\Lambda (x)+{\overline{\gamma }}(x) ({\hat{I}}_{**}-\epsilon )]e^{\alpha (x) ({\hat{I}}_{**}-\epsilon )}}{m(x)e^{\alpha (x) ({\hat{I}}_{**}-\epsilon )}+\beta (x) ({\hat{I}}_{**}+\epsilon )}.$

Similarly, we have

$$\begin{aligned} \liminf _{n\rightarrow \infty }S_{n}(x)\geqslant {\mathfrak {g}}_{+}^{2,\epsilon }.\end{aligned}$$

(5.26)

Notice that ${\mathfrak {g}}_{+}^{1,\epsilon }= {\mathfrak {g}}_{+}^{2,\epsilon }= {\mathcal {G}}(x, {\hat{I}}_{**}).$ From Eqs.(5.25) and (5.26), we immediately obtain

$$\begin{aligned} S_{n}(x)~~\mathrm{tends~to}~ {\mathcal {G}}(x, {\hat{I}}_{**})={\hat{S}}_{**}~~\mathrm{uniformly ~~on~region}~~\Omega ,~~ \textrm{as}~~n \rightarrow +\infty .\end{aligned}$$

(5.27)

Clearly, it shows that the solution ${\hat{I}}_{**}$ satisfies (5.7), which completes the proof. $\square$

5.2 The case of $d_{2}\rightarrow 0$

We now consider the asymptotic dynamics of endemic equilibrium as $d_{2}\rightarrow 0$. Applying proposition 3.1 and Theorems 3.1 and 3.2, if the inequality $\frac{\Lambda (x)\beta (x)}{m(x)}>{\overline{\gamma }}(x)$ holds, i,e., ${\mathcal {R}}> 1$, and then we know that system (5.1) admits at least one E.E. for all small the diffusion rate $d_{2}> 0$. Thus, we have the result below.

Theorem 5.2

If the inequality $\frac{\Lambda (x)\beta (x)}{m(x)}>{\overline{\gamma }}(x)$ holds. Fix the diffusion rate $d_{1}> 0$, and let the diffusion rate $d_{2}\rightarrow 0$, then every (S, I) of system (5.1) starting from positive initial value satisfies $S\rightarrow {\hat{S}}^{**},~$ and $~ I\rightarrow {\hat{I}}^{**}$ uniformly   on region $\Omega$ where

$$\begin{aligned} {\hat{I}}^{**}=\left\{ \begin{aligned}&\left( \frac{\Lambda (x)\beta (x)}{m(x){\overline{\gamma }}(x)}-1\right) {\hat{S}}^{**},&\frac{\Lambda (x)\beta (x)}{m(x)}>{\overline{\gamma }}(x),\\ {}&0,&\frac{\Lambda (x)\beta (x)}{m(x)}<{\overline{\gamma }}(x) \end{aligned}\right. \end{aligned}$$

(5.28)

for x belong to region $\Omega$ and the solution ${\hat{S}}^{**}$ satisfies

$$\begin{aligned} \left\{ \begin{aligned}&-d_{1}\Delta {\hat{S}}^{**} = \Lambda (x)-\left[ m(x)-\beta (x) e^{-\alpha (x) {\hat{I}}^{**}}{\hat{I}}^{**}+\frac{{\overline{\gamma }}(x){\hat{I}}^{**}}{{\hat{S}}^{**}}\right] {\hat{S}}^{**},&x\in \Omega ,\\ {}&\frac{ \partial {\hat{S}}^{**}}{ \partial n}=0,&x\in \partial \Omega . \end{aligned}\right. \end{aligned}$$

(5.29)

Proof

To establish Theorem 5.2, for convenience, a positive constant ${\mathscr {C}}$ with respect to the positive diffusion rate $d_{2}$ is observed. In the following, we prove this result in four steps.

Step 1. We prove that the solution S has lower bound.

For any $x\in \Omega$, let $S(x_{0}) = \min \limits _{\Omega }\{S(x)\}$, using [21] and the first equation of system (5.1) that

$$\begin{aligned}\Lambda (x_{0})-m(x_{0})S(x_{0})-\beta (x_{0}) S(x_{0}) I(x_{0})e^{-\alpha (x_{0}) I(x_{0})}+{\overline{\gamma }}(x_{0}) I(x_{0})<0.\end{aligned}$$

From which we infer

$$\begin{aligned}\begin{aligned}\Lambda ^{*} \le \Lambda (x_{0}) + {\overline{\gamma }}(x_{0})I(x_{0})&<m(x_{0})S(x_{0})+\beta (x_{0})S(x_{0})I(x_{0})e^{-\alpha (x_{0}) I(x_{0})} \\ {}&\le m_{*}S(x_{0})+\beta _{*}\frac{1}{\alpha ^{*}e} S(x_{0}).\end{aligned}\end{aligned}$$

Then, we immediately have the following results

$$\begin{aligned} S(x) \geqslant \frac{\Lambda (x_{0})}{m(x_{0})+\frac{1}{\alpha (x_{0})e}\beta (x_{0})}\geqslant \frac{\Lambda ^{*}}{m_{*}+\frac{1}{\alpha ^{*}e}\beta _{*}}~~\mathrm{for~ all}~~ x \in \Omega .\end{aligned}$$

(5.30)

Thus, the solution S has lower bound.

Step 2. We prove that the solution S is $W^{1,q}$ bound for $q>0$.

From system (5.1), we have

$$\begin{aligned} \left\{ \begin{aligned}&-\Delta S+\frac{[\beta (x) Ie^{-\alpha (x) I}+m(x)]}{d_{1}}S=\frac{{\overline{\gamma }}(x) I+\Lambda (x)}{d_{1}},&x\in \Omega ,\\ {}&\frac{ \partial S}{ \partial n}=0,&x\in \partial \Omega . \end{aligned}\right. \end{aligned}$$

(5.31)

From Eq. (5.6), we can obtain

$$\begin{aligned} \mathop {\int }\limits _{\Omega } |\Lambda (x) + {\overline{\gamma }}(x)I (x)| \textrm{d}x \leqslant {\mathscr {C}}. \end{aligned}$$

(5.32)

Based on Eqs. (5.31) and (5.32), and employing the elliptic $L^{1}$-estimate [4], we have

$$\begin{aligned} ||S||_{W^{1,q} (\Omega )} \leqslant {\mathscr {C}}, \mathrm{~for~} q \in \left[ 1, 1+\frac{1}{n-1}\right) ~~\textrm{if}~~ n>1,or ||S||_{W^{1,q} (\Omega )} \leqslant {\mathscr {C}}, \forall 1 \leqslant q < \infty \text { if } n = 1.\end{aligned}$$

(5.33)

Thus, we know that the solution S is $W^{1,q}$ bound for small positive number q.

Step 3. We prove that solutions S and I are $L^{p}$-bound for any positive number p.

From Eq. (5.33), using the Sobolev embedding $W^{1,q}(\Omega )\hookrightarrow L^{p_{1}} (\Omega )$ and noticing $q \in [1,1+\frac{1}{n-1})$, then we have $||S||_{L^{p_{1}} (\Omega )} \leqslant {\mathscr {C}}, 1 < p_{1} \leqslant \frac{nq }{n-q}.$ When q tends to $\frac{n}{n-1}$, we immediately obtain

$$\begin{aligned} ||S||_{L^{p_{1}} (\Omega )} \leqslant {\mathscr {C}}, 1 < p_{1} \leqslant 1+\frac{2}{n- 2}.\end{aligned}$$

(5.34)

Assume $n \leqslant 2$, then (5.34) holds for $\forall< p_{1}<+\infty$.

Next, for any number $k > 0$, we multiply both of the second equation for (5.1) by solution $I^{k}$, and integrate two hands of (5.1) over region $\Omega$, then we obtain

$$\begin{aligned}d_{2} k \mathop {\int }\limits _{\Omega } I ^{k-1} |\nabla I |^{2} \textrm{d}x = \mathop {\int }\limits _{\Omega }\beta (x)SI ^{k+1}e^{-\alpha (x) I}\textrm{d}x -\mathop {\int }\limits _{\Omega }{\overline{\gamma }} (x)I ^{k+1}\textrm{d}x.\end{aligned}$$

Hence, one has

$$\begin{aligned} {\overline{\gamma }}^{*}\mathop {\int }\limits _{\Omega }I ^{k+1}\textrm{d}x \le \mathop {\int }\limits _{\Omega }{\overline{\gamma }}(x) I ^{k+1}\textrm{d}x <\mathop {\int }\limits _{\Omega }\beta (x)SI ^{k+1}e^{-\alpha (x) I}\textrm{d}x \le \frac{\beta _{*}}{\alpha ^{*}e}\mathop {\int }\limits _{\Omega }SI ^{k}\textrm{d}x.\end{aligned}$$

(5.35)

Choosing $k_{1} = \frac{1}{q_{1}}$ and $q_{1} = 1 + \frac{1}{(p_{1} - 1)} =\frac{ p_{1}}{(p_{1} - 1)},$ where $\frac{1}{p_{1}}+ \frac{1}{q_{1}}= 1$, from Eq. (5.35) and using Hölder inequality, it follows that

$$\begin{aligned} {\overline{\gamma }}^{*} \mathop {\int }\limits _{\Omega }I^{ k_{1}+1} \textrm{d}x<\frac{\beta _{*}}{\alpha ^{*}e} \mathop {\int }\limits _{\Omega }SI^{k_{1}}\textrm{d}x<\frac{ \beta _{*}}{\alpha ^{*}e}\left( \mathop {\int }\limits _{\Omega } S^{p_{1}} \textrm{d}x\right) ^{\frac{1}{p_{1}} }\left( \mathop {\int }\limits _{\Omega }I\textrm{d}x\right) ^{\frac{1}{q_{1}}} < {\mathscr {C}}.\end{aligned}$$

Observe that Eqs. (5.34) and (5.6), clearly, we immediately have, $||I||_{L^{k_{1}+1}(\Omega )} < {\mathscr {C}},$ further, taking $k_{2} = \frac{(k_{1} + 1)}{q_{1}} = \frac{1}{q_{1}}+ \frac{1}{q^{2}_{1}}$, (5.35) and using Hölder inequality again, yield

$$\begin{aligned} {\overline{\gamma }}^{*} \mathop {\int }\limits _{\Omega }I ^{k_{2}+1}\textrm{d}x<\frac{\beta _{*}}{\alpha ^{*}e}\mathop {\int }\limits _{\Omega }SI^{k_{2}}\textrm{d}x<\frac{\beta _{*}}{\alpha ^{*}e}\left( \mathop {\int }\limits _{\Omega } S^{p_{1}} \textrm{d}x\right) ^{\frac{1}{p_{1}}}\left( \mathop {\int }\limits _{\Omega }I^{k_{2}q_{1}}\textrm{d}x\right) ^{\frac{1}{q_{1}}} < {\mathscr {C}}.\end{aligned}$$

(5.36)

From Eqs. (5.34) and (5.36), thus, $||I||_{L^{k_{2}+1}(\Omega )}<{\mathscr {C}}.$ By repeating the iteration, we immediately obtain

$$\begin{aligned} ||I||_{L^{k_{\infty }+1}(\Omega )} < {\mathscr {C}},\end{aligned}$$

(5.37)

where $k_{\infty } = \frac{1}{q_{1}} + \frac{1}{q^{2}_{1}} + \frac{1}{q^{3}_{1}}+\cdot \cdots =\frac{1}{q_{1}- 1} = p_{1}-1.$ By Eq. (5.34), we know that (5.37) is true by using finitely many times of iterations). Thus, one has

$$\begin{aligned} ||I||_{L^{p_{1}}(\Omega )} < {\mathscr {C}}.\end{aligned}$$

(5.38)

Now, by Eqs. (5.31), (5.37) and using Elliptic $L^{p}$-theory, one has that $||I||_{W^{2,p_{1}}(\Omega )}<{\mathscr {C}}.$ Employing Sobolev embedding, that is, $W^{2,p_{1} }(\Omega ) \hookrightarrow L^{p_{2}} (\Omega ), 1< p_{2} < \frac{Np_{1}}{N- 2p_{1}}$ and the fact of $\frac{Np_{1}}{N-2p_{1}}$ tends to $\frac{N}{N-4}$ as $p_{1}$ tends to $\frac{N}{N-2}$ (refer to Eq. (5.34), then we obtain $||S||_{L^{p_{2}} (\Omega )}<{\mathscr {C}}, 1< p_{2} < \frac{N}{N - 4}~~ \textrm{if}~ N > 4,$ or $\forall 1< p_{2} <+\infty$ if $N \le 4$, then, one can get $||I||_{L^{p_{2}}(\Omega )} <{\mathscr {C}}.$ From Eq. (5.31) and applying elliptic $L^{p}$-theory again, we eventually obtain the following results

$$\begin{aligned} ||S||_{L^{p}(\Omega )}< {\mathscr {C}},~\mathrm{and~} ||I||_{L^{p}(\Omega ) }< {\mathscr {C}}, \forall 1< p <+\infty .\end{aligned}$$

(5.39)

Step 4. We prove that the solutions S and I are convergence.

By Eqs. (5.31) and (5.39), the following inequality is given as $||S||_{W^{2,p}(\Omega )}<{\mathscr {C}}$, and $\forall 1<p<\infty$, where the positive p is sufficiently large.

By using the standard embedding theory, ensure that $\{d_{2}\}$ of the diffusion rate $d_{2}\rightarrow 0$, that is,

$$\begin{aligned}d_{m}:= d_{2,m}~\mathrm{tends~ to~ zero~ with }~d_{m}\rightarrow 0~\textrm{as}~ m \rightarrow \infty ,\end{aligned}$$

and the sequence $(S_{m}, I_{m}):= (S_{d_{1,m}}, I_{d_{2,m}})>0$ of system (5.1) with $d_{2} = d_{2,m}$ satisfies

$$\begin{aligned}\mathrm{the ~solution}~S_{m} \rightarrow {\hat{S}}^{**}~~ \textrm{in}~~ C^{1}(\Omega ),~~ \textrm{as}~~ m\rightarrow \infty ,\end{aligned}$$

where the solution ${\hat{S}}^{**} \in C^{1}(\Omega )$ and ${\hat{S}}^{**}$ is positive on region $\Omega$ due to (5.30).

In addition, the solution $I_{m}$ of system (5.1) satisfies

$$\begin{aligned} \left\{ \begin{aligned}&-d_{1}\Delta I_{m}=\left[ \frac{\beta (x)S_{m}}{e^{\alpha (x)I_{m}}}-{\overline{\gamma }}(x)\right] I_{n},&x\in \Omega ,\\ {}&\frac{ \partial I_{m}}{ \partial n}=0,&x\in \partial \Omega . \end{aligned}\right. \end{aligned}$$

(5.40)

From (5.31) and (5.40), similarly to the step 3 of Theorem 5.2 (or see [11, 20]), one also has the solution  $I_{m}\rightarrow {\hat{I}}^{**}$ in $C^{1}(\Omega )$, as $m \rightarrow +\infty ,$ where the solution ${\hat{I}}^{**}$ is given by (5.28).

Obviously, the solution ${\hat{S}}^{**}$ satisfies (5.29); by the expression of solution ${\hat{I}}^{**}$, and then exists a unique positive solution of system (5.29) (refer to Ref. [29]). $\square$

5.3 The case of $d_{1}\rightarrow \infty$

In this part, the asymptotic dynamics of (5.1) is studied when the diffusion rate $d_{1}\rightarrow +\infty$, and then we give the following theorem.

Theorem 5.3

Assume that ${\mathcal {R}}>1$, fixing $d_{2} > 0$ and let $d_{1} \rightarrow +\infty$, then every (S, I) of system (5.1) starting from positive initial value satisfies $S\rightarrow {\hat{S}}^{\infty }, I\rightarrow {\hat{I}}^{\infty }$ uniformly on region $\Omega ,$ where ${\hat{S}}^{\infty }>0$ and the solution ${\hat{I}}^{\infty } > 0$ on region $\Omega$, and the point $({\hat{S}}^{\infty }, {\hat{I}}^{\infty })$ satisfies

$$\begin{aligned} \left\{ \begin{aligned}&\mathop {\int }\limits _{\Omega }\Lambda (x)-m(x){\hat{S}}^{\infty }-\frac{\beta (x) {\hat{S}}^{\infty } {\hat{I}}^{\infty }}{e^{\alpha (x) {\hat{I}}^{\infty }}}+{\overline{\gamma }}(x) {\hat{I}}^{\infty }\textrm{d}x=0, \\ {}&d_{2}\Delta {\hat{I}}^{\infty }+ \beta {\hat{S}}^{\infty } {\hat{I}}^{\infty }e^{-\alpha (x) {\hat{I}}^{\infty }}-{\overline{\gamma }}(x) {\hat{I}}^{\infty }=0,\\ {}&\frac{ \partial {\hat{I}}^{\infty }}{ \partial n}=0. \end{aligned}\right. \end{aligned}$$

(5.41)

Proof

To establish Theorem 5.3, we first know that (5.11) is held for ${\mathscr {C}}>0$ with respect to the positive diffusion rate $d_{1}$, and Eq. (5.30) is still held, and then, we have

$$\begin{aligned} \left\{ \begin{aligned}&-d_{1}\Delta S=\left[ \frac{\Lambda (x)}{S}-m(x)-\frac{\beta (x) I}{e^{\alpha (x) I}}+\frac{{\overline{\gamma }}(x) I}{S}\right] S,&x\in \Omega ,\\ {}&\frac{ \partial S}{ \partial n}=0,&x\in \partial \Omega . \end{aligned}\right. \end{aligned}$$

(5.42)

Employing elliptic Harnack inequality [42] and the inequality (5.5), for all positive number $d_{1}>1$, we have

$$\begin{aligned}S(x)< {\mathscr {C}} \min _{\Omega } S<\frac{{\mathscr {C}}}{|\Omega |} \mathop {\int }\limits _{\Omega }S\textrm{d}x < {\mathscr {C}}, \forall x \in \Omega .\end{aligned}$$

Now, by Eq. (5.41) and using a standard compactness argument, there exists a subsequence of $d_{1}$, labeled by the diffusion rate $d_{n}$ with $d_{n}$ tends to $\infty$ as $n\rightarrow \infty$ such that $(S_{n}, I_{n})$ of system (5.1) for $d_{1} = d_{n}$ satisfies the solution $S_{n}$ tends to ${\hat{S}}^{\infty }$ in $C^{1}(\Omega )$ as the integer $n\rightarrow \infty$, where ${\hat{S}}^{\infty }$ is positive number on region $\Omega$ due to (5.30). Further, the solution ${\hat{S}}^{\infty }$ satisfy the following equation $-\Delta {\hat{S}}^{\infty } = 0, x \in \Omega ;\frac{\partial {\hat{S}}^{\infty }}{\partial n}=0, x \in \partial \Omega .$ Obviously, we have the solution ${\hat{S}}^{\infty } > 0$ on region $\Omega$.

Similarly, from the second equation of system (5.1), by a similar discussion of a further subsequence, namely,

$$\begin{aligned} \mathrm{the~solution~~}I_{n} \rightarrow {\hat{I}}^{\infty }~~\textrm{in}~~ C^{1}(\Omega ),~~\mathrm{as~ the ~integer}~~ n \rightarrow +\infty ,\end{aligned}$$

(5.43)

where the solution ${\hat{I}}^{\infty } \in C^{1}(\Omega )$ is nonnegative. Furthermore, similar discussion proceeds to (5.43), we obtain that the positive solution ${\hat{I}}^{\infty }$ on region $\Omega$ is observed.

Hence, from Eq. (5.2) and system (5.1), it shows hat the point $({\hat{S}}^{\infty }, {\hat{I}}^{\infty })$ satisfies Eq. (5.41). Thus, this completes the proof. $\square$

5.4 The case of $d_{2} \rightarrow \infty$

In this part, we explore the limiting dynamical behaviors of positive solutions for system (5.1) when the diffusion rate $d_{2}\rightarrow \infty$. To ensure the existence of positive solutions of system (5.1) for all large number $d_{2}$, based on Proposition 3.1, then the following results are given as:

Theorem 5.4

If the inequality $\mathop {\int }\limits _{\Omega }\frac{\beta (x)\Lambda (x)}{m(x)}\textrm{d}x>\mathop {\int }\limits _{\Omega }{\overline{\gamma }}(x) \textrm{d}x$, fixing the diffusion rate $d_{1}>0$ and let the diffusion rate $d_{2}\rightarrow \infty$, then every (S, I) of system (5.1) starting from positive initial value satisfy $S\rightarrow {\hat{S}}_{\infty }, I\rightarrow {\hat{I}}_{\infty }$ uniformly  on  region $\Omega ,$ where the positive solution ${\hat{S}}_{\infty }$ and the positive solution ${\hat{I}}_{\infty }$ on region $\Omega$ satisfies the following equation

$$\begin{aligned} \left\{ \begin{aligned}&-d_{1}\Delta {\hat{S}}_{\infty }=\Lambda (x)-m(x){\hat{S}}_{\infty }-\frac{\beta (x) {\hat{S}}_{\infty }{\hat{I}}_{\infty }}{e^{\alpha (x) {\hat{I}}_{\infty }}}+{\overline{\gamma }}(x) {\hat{I}}_{\infty },&x\in \Omega ,\\ {}&\mathop {\int }\limits _{\Omega } \beta (x) S_{\infty } {\hat{I}}_{\infty }e^{-\alpha (x) {\hat{I}}_{\infty }}-{\overline{\gamma }}(x) {\hat{I}}_{\infty }\textrm{d}x=0,&\\ {}&\frac{ \partial {\hat{S}}_{\infty }}{\partial n}=0,&x\in \partial \Omega . \end{aligned}\right. \end{aligned}$$

(5.44)

Proof

To establish Theorem 5.4, we observe that (5.30) and (5.11) are true for some ${\mathscr {C}}>0$. Thus, similar to the proof of above Theorem 5.3, we know that there exists a subsequence of $\{d_{2}\}$ such that $(S_{d_{2}}, I_{d_{2}})$ of system (5.1) starting from positive initial value satisfies $(S_{d_{2}}, I_{d_{2}})$ tends  to  $({\hat{S}}_{\infty }, {\hat{I}}_{\infty })$ in $C^{1}(\Omega ),$ as $d_{2} \rightarrow \infty ,$ where the solutions ${\hat{I}}_{\infty }\ge 0$ and ${\hat{S}}_{\infty }>0$ on region $\Omega$.

Next, we prove that the solution ${\hat{I}}_{\infty }$ is a positive constant. To the contrary, if ${\hat{I}}_{\infty }=0$, we know that ${\hat{S}}_{\infty }=\frac{\Lambda (x)}{m(x)}$, let $I^{*}_{d_{2}}:=\frac{I_{d_{2}}}{||I_{d_{2}}||L^{\infty }(\Omega )}$, then norm $||I^{*}_{d_{2}}||_{L^{\infty }(\Omega )}=1$ for all positive number $d_{2}>1$, and the solution $I_{d_{2}}$ satisfies (5.21).

As above, similar to argument of a further subsequence of the diffusion rate $d_{2}$, we have

$$\begin{aligned} I^{*}_{d_{2}}\rightarrow 1 ~~\textrm{in}~~ C^{1}(\Omega ), ~~\textrm{as}~~ d_{2}\rightarrow \infty .\end{aligned}$$

(5.45)

In addition, by (5.21), we obtain $\mathop {\int }\limits _{\Omega }[\beta (x)S_{d_{2}} e^{-\alpha (x) I_{d_{2}}}-{\overline{\gamma }} (x)] I^{*}_{d_{2}}\textrm{d}x=0, \forall d_{2}>0.$ While $S_{d_{2}}\rightarrow {\hat{S}}_{\infty }=\frac{\Lambda (x)}{m(x)}>0$ on $\Omega$, by using $d_{2}\rightarrow +\infty$, (5.45) and $I_{d_{2}} \rightarrow 0$, $\mathop {\int }\limits _{\Omega }\frac{\beta (x)\Lambda (x)}{m(x)}\textrm{d}x>\mathop {\int }\limits _{\Omega }{\overline{\gamma }}(x) \textrm{d}x$, we have $\mathop {\int }\limits _{\Omega }[\beta (x){\hat{S}}_{\infty }-{\overline{\gamma }}(x)]\textrm{d}x=\mathop {\int }\limits _{\Omega }\left( \frac{\beta (x)\Lambda (x)}{m(x)}-{\overline{\gamma }} (x)\right) \textrm{d}x=0,$ which is a contradiction with ${\hat{I}}_{\infty }=0$. So we know that the solution ${\hat{I}}_{\infty }>0$. It shows that $({\hat{S}}_{\infty }, {\hat{I}}_{\infty })$ satisfies (5.44). The proof is complete.$\square$

Remark 1

It is worth pointing out that when the coefficients of system (2.1) are taken as $\Lambda (x)=0, m (x)=0,\alpha (x)=0$, then (2.1) degenerates to the system in [16]. Compared with [16, 23, 29], the difference of our paper uses the Lyapunov function to prove that when all coefficients of system (2.1) are constant, the disease equilibrium point of the system is globally attractive. Using the $L^{p}$ theorem and some inequality techniques, the well-posedness of the system with the item $SIe^{-\alpha I}$ is analyzed. In addition, compared with [23], our paper discusses an SIS model with linear terms $\Lambda (x)-m(x)S$ and the media effects $e^{-\alpha (x)I}$, but [23] has studied an SEIR model with fractional terms $\frac{\beta (x)SI}{S+I+E+R}$. Reference [23] only considered the coefficients $\beta$ and ${\overline{\gamma }}$ as a function of x, but we discuss all coefficients as a function of x in our paper. In addition, the local stability of the equilibrium is discussed in [23], but it gives the global stability of the system. Through the conclusions of this article, we know that $\mathop {\int }\limits _{\Omega }[\frac{\beta (x)\Lambda (x)}{m(x)}-{\overline{\gamma }}(x)]\textrm{d}x<0$ if the ratio $\frac{\Lambda (x)}{m(x)}$ is smaller. The main results show that the activities of infected individuals can only be at low risk, and then the virus eventually will be extinct, that is, to control the entry of viruses from abroad and increase the detection of domestic viruses.

Fig. 1

When ${\mathcal {R}}<1$ and $\alpha (x)=0.002$, $d_{1}=0.8, d_{2}=0.9,\Lambda (x)=0.3,m(x)=0.2,\beta (x)=0.1,{\overline{\gamma }}(x)=0.1$, the disease-free equilibrium of system (2.1) is globally asymptotically stable

Fig. 2

When ${\mathcal {R}}<1$ and $\alpha (x)=5$, $d_{1}=0.8, d_{2}=0.9,\Lambda (x)=0.3,m(x)=0.2,\beta (x)=0.1,{\overline{\gamma }}(x)=0.1$, the disease-free equilibrium of system (2.1) is globally asymptotically stable

6 Numerical simulations

In this section, we give some numerical simulations of two examples to validate the correctness of the theoretical results

Example 1

Consider a linear source epidemic system with diffusion and media impact

$$\begin{aligned} \left\{ \begin{aligned}&S_{t}=0.8\Delta S+1-S-0.1 S Ie^{-\alpha (x) I}+0.1 I,&(x,t)\in [0,1]\times (0,+\infty ),\\ {}&I_{t}=0.9\Delta I+ 0.1 S Ie^{-\alpha (x)I}-0.1I,&(x,t)\in [0,1]\times (0,+\infty ),\\ {}&\frac{\partial S}{ \partial n}=\frac{ \partial I}{\partial n}=0,&x\in 0 ~\textrm{or}~1,\\ {}&S(x,0)=S_{0}(x),I(x,0)=I_{0}(x),&x\in [0,1]. \end{aligned}\right. \end{aligned}$$

(6.1)

Choosing the following parameters $d_{1}=0.8, d_{2}=0.9,\Lambda (x)=1,m(x)=1,\beta (x)=0.1,{\overline{\gamma }}(x)=0.1$, $x\in [0,1]$, and the initial values are $S_{0}(x)=12,I_{0}(x)=8$. It shows that all the conditions in Theorems 3.1 are satisfied. Therefore, the disease-free equilibrium of the linear source epidemic system with diffusion and media impact in a spatially homogeneous environment is globally asymptotically stable. The numerical simulations are shown in Fig. 1 if $\alpha (x)=0.1$ and Fig. 2 if $\alpha (x)=5$.

Example 2

Consider a linear source epidemic system with diffusion and media impact

$$\begin{aligned} \left\{ \begin{aligned}&S_{t}=1.1\Delta S+50-S-0.18 S Ie^{-\alpha (x)I}+ I,&(x,t)\in [0,0.15]\times (0,+\infty ),\\ {}&I_{t}=0.8\Delta I+ 0.18S Ie^{-\alpha (x) I}-I,&(x,t)\in [0,0.15]\times (0,+\infty ),\\ {}&\frac{\partial S}{ \partial n}=\frac{ \partial I}{\partial n}=0,&x\in 0~\textrm{or}~0.15,\\ {}&S(x,0)=S_{0}(x),I(x,0)=I_{0}(x),&x\in [0,0.15]. \end{aligned}\right. \end{aligned}$$

(6.2)

Fig. 3

When $\Lambda \beta >m{\overline{\gamma }}$, $d_{1}=1.1,d_{2}=0.8,\Lambda (x)=50,m(x)=1,\beta (x)=0.18,\alpha (x)=0.001,{\overline{\gamma }}(x)=1$, the endemic equilibrium is globally attractive

Fig. 4

When $\Lambda \beta >m{\overline{\gamma }}$, $d_{1}=1.1,d_{2}=0.8,\Lambda (x)=50,m(x)=1,\beta (x)=0.18,\alpha (x)=0.2,{\overline{\gamma }}(x)=1$, the endemic equilibrium is globally attractive

Choosing the following parameters $d_{1}=1.1,d_{2}=0.8,\Lambda (x)=50,m(x)=1,\beta (x)=0.18,{\overline{\gamma }}(x)=1$, $x\in [0,0.15]$, and the initial values are $S_{0}(x)=20,I_{0}(x)=50$. $\Lambda \beta >m{\overline{\gamma }}$. This shows that all the conditions in Theorems 4.1 are satisfied. Therefore, the endemic equilibrium of the linear source epidemic system with diffusion and media impact in a spatially homogeneous environment is globally attractive. The numerical simulations are shown in Fig. 3 if $\alpha (x)=0.001$ and Fig. 4 if $\alpha (x)=0.2$.

Remark 2

Note that this article discusses the uniformity of spatial heterogeneity, where the coefficients of the model are constant. Although the susceptible individuals and the infected individuals in the model vary with space and time, by constructing appropriate Lyapunov functions, we obtain the globally stable equilibrium state of the model’s solution. The difference is that the two equilibrium states in our model are functions of position x. When considering the absence of diffusion effects in the model, the model in this paper will degenerate into an ordinary differential equation. Previous work has shown that the equilibrium state of the model is only a constant point and a fixed value. In addition, if we consider the case where the two diffusion rates are not equal to zero, there will be two scenarios for the solution of this manuscript: one scenario is the extinction of susceptible individuals, and the other scenario is the persistence of infected individuals and susceptible individuals. However, there is no effective proof of the global stability of a linear source epidemic systems with spatial heterogeneity in diffusion. Currently, only the proof of the Lyapunov function is given under the condition of constant coefficients. Therefore, there are no good results on the global stability of our model in the presence of diffusion. In the absence of diffusion effects, the degraded model in this paper can be found to be ultimately globally stable by constructing a Lyapunov function.

7 Conclusion and discussion

Recently, both theoretical and experimental evidences confirm that environmental heterogeneity and individuals mobility will seriously affect the dynamics of the diseases. For instance, in [6], one of the main problems is that the disease is the persistence or extinction.

In this paper, in order to better explain the meaning of our analysis results, for instance, in [2], the terms of low/hig/medium-risk dating place or habitat were considered. The authors have investigated the low/high/medium risk of habitat region $\Omega$ if the spatial average function $\mathop {\int }\limits _{\Omega }\frac{\beta (x)\Lambda (x)}{m(x)}\textrm{d}x$ is less than/greater than/equal to the spatial average function $\mathop {\int }\limits _{\Omega }{\overline{\gamma }}(x)\textrm{d}x$. In addition, they also have considered a low/high/medium risk of place x if the function $\frac{\beta (x)\Lambda (x)}{m(x)}$ of the infection disease is less than/ greater than/equal to its partial recovery rate function $\gamma (x)$.

In this article, we have found that in a spatially uniform environment, the system also has two equilibrium states of global attractivity, as shown in Theorems 3.1 and 4.1 in the paper. The significance of this theorem shows that the media coverage has a significant impact on the spread of infectious diseases. In cases where there are many infected cases, the media coverage will reduce the chances and probability of susceptible populations coming into contact with infections, thereby helping to control and prevent the further spread of diseases. In other words, a large media coverage coefficient will reduce the transmission of individual diseases. This article continues to discuss the spread of diseases under the influence of media and diffusion. We have found that under certain conditions, the infected individuals and the susceptible individuals will approach a disease-free equilibrium. In another form, the number of diseased individuals will persist. These dynamics provide that with some effective suggestions to prevent the spread of diseases. In addition, this paper focuses on the epidemic model with diffusion and media influence, where diffusion influence is more in line with real-life situations, as the transmission of susceptible individuals or infected individuals is not only temporal but also spatial. Therefore, this paper discusses the cases where the diffusion rate approaches 0 and infinity and provides the regional situation of disease transmission for individuals, which has practical guidance significance. In addition, considering the model with media coverage, and we have also conducted numerical simulations by providing different rates of media coverage. From Figs. 1 and 2 or Figs. 3 and 4, we know that the greater the media coverage rate $\alpha (x)$, the faster the rate of decline of susceptible individuals, which means the smaller the spread of diseases. Because the most public opinion will attract the attention of leaders during the spread process, many regions will implement measures such as isolating infected individuals in certain ways to control the spread of the disease. In short, we can effectively control and monitor the spread of diseases through the size of the diffusion rate and media influence rate. Therefore, the diffusion and media coverage has practical guiding significance.

In our article, we focus on an impact of media reaction–diffusion system (2.1) involving spatially heterogeneous environments. Based on ${\mathcal {R}}$, we study the threshold dynamics of epidemic model (2.1). In other words, if ${\mathcal {R}}<1$, the disease of system (2.1) will be eliminated, and if ${\mathcal {R}}>1$, the disease of system (2.1) will be persist. In some cases, as long as the space environment is homogeneous, we can obtain the global stability of the unique E.E. (see Theorem 4.1). Moreover, we further consider the asymptotic profiles of the epidemic equilibrium when the diffusion rate $d_{1}$ or $d_{2}$ is small or large. If the habitat of system (2.1) exists some high-risk place, it is shown that infection will lead to the disease to become extinct only in low/medium-risk place, and by controlling the movement speed of susceptible individuals. Thus, we know that the disease persists, that is, system (2.1) exists in high-risk place. According to the spatial average function, from the point of view $\mathop {\int }\limits _{\Omega }\frac{\beta (x) \Lambda (x)}{m(x)}\textrm{d}x$ when $\beta (x)$ is a positive constant if the ratio $\frac{\Lambda (x)}{m(x)}$ is smaller. The main results show that the activities of infected individuals can only be at low risk, and then the virus eventually will be extinct, that is, to control the entry of viruses from abroad and increase the detection of domestic viruses.

To sum up, based on the above discussion, it is shown that a impact of media model (2.1) with a constant total population was studied. In [17], the SIS model with linear external sources was investigated, and the authors in [12] studied SIS epidemic models with large-scale effects. But without delay and nonlinear external source, such as an impact of media SIS epidemic delay models with the general form is seldom considered. Then, those reactive diffusion models with spontaneous infections will be interesting, we plan to study them in the future.