Cut Singularity of Compressible Stokes Flow

Abstract

In this paper we study the cut singularity governed by a compressible Stokes system. The cut is a non-Lipshitz boundary. The divergence of the leading corner singularity vector, which has the singular exponent 1/2, has different trace values on either side of cut. In the consequence the pressure solution of the continuity equation must have a jump across the streamline emanating from the cut tip. We establish a piecewise regularity of the solution by the corner singularity and the contact singular function.

1 Introduction

In this paper we study the cut singularity governed by a compressible Stokes system. The cut is a non-Lipshitz boundary. The divergence of the leading corner singularity vector, which has the singular exponent 1/2, has different trace values on either side of cut. In the consequence the pressure solution of the continuity equation must have a jump across the streamline emanating from the cut tip. We establish a piecewise regularity of the solution by the corner singularity and the contact singular function.

We shall study the issues by a well-posed boundary value problem for the linearized compressible Stokes system

$$\begin{aligned} \begin{aligned} -\mu \Delta \textbf{u}-\nu \nabla \text{ div }\,\, \textbf{u}+\nabla p&=\textbf{f}\hspace{0.3cm} \text{ in } \Omega ,\\ \textbf{U}\cdot \nabla p+\text{ div }\,\,\textbf{u}&=g\hspace{0.3cm} \text{ in } \Omega ,\\ \textbf{u}&=0 \hspace{0.3cm} \text{ on } \Gamma ,\\ p&=0 \hspace{0.3cm} \text{ on } \Gamma _\textrm{in}, \end{aligned} \end{aligned}$$

(1.1)

where $\textbf{u}$ is the velocity vector, p is the pressure function; $\mu$ and $\nu$ are the viscous numbers with $\mu >0$; $\textbf{U}=(U,V)^t$ is a fixed vector field with $U>0$; $\textbf{f}$ and g are given functions; the set $\Gamma$ is the boundary of the domain $\Omega$, and the set $\Gamma _\textrm{in}=\{(x,y)\in \Gamma :\textbf{U}\cdot \textbf{n}<0\}$ is the inflow boundary where $\textbf{n}$ is the unit normal vector to the boundary $\Gamma$.

Throughout this paper, for simplicity, we set the vector $\textbf{U}=(1,0)^t$ and the Lamé operator ${\mathbb {L}}=\Delta +\nu _1\nabla \text{ div }\,$ where $\nu _1=\mu ^{-1}\nu$.

System (1.1) is a simplified and nonlinear version which is derived from the nonlinear compressible Navier–Stokes equations (see [10]). The first vector equation is the momentum one which is elliptic in the velocity variables and the second one is the continuity equation which is hyperbolic in the density variable. Mathematically it is of mixed type which is neither elliptic nor hyperbolic.

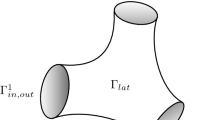
The cut flow is depicted in the following figure

Fig. 1

Flow through a cut

At the cut tip, say (0, 0), the leading singular exponent by the Lamé system is 1/2, which has two corresponding eigenvector functions $\varvec{\Theta }_i(\theta )$, $i=1,2$ (see (2.2) below). An interesting fact is that the function $\text{ div }\,(r^{1/2}\varvec{\Theta }_1(\theta ))$ has different traces on either side of the cut boundary, that is, for $x<0$,

$$\begin{aligned} \begin{aligned} \text{ div }\,(r^{1/2}\varvec{\Theta }_1(\theta ))\big |_{(x,0+)}&=-4|x|^{-1/2},\\ \text{ div }\,(r^{1/2}\varvec{\Theta }_1(\theta ))\big |_{(x,0-)}&=4|x|^{-1/2}, \end{aligned} \end{aligned}$$

(1.2)

while $\text{ div }\,(r^{1/2}\varvec{\Theta }_2(\theta ))$ has the same trace value 0 on the cut boundary. By transport property of the continuity equation, the pressure solution must have a nonzero jump value across the interface curve emanating from the cut tip, which results in that the pressure gradient given in the momentum equation is not well defined across the interface curve. The issue will be handled by constructing a mapping operator lifting the pressure jump value on the interface curve. Finally the smoother part of the velocity vector is shown to have the $\textbf{H}^{2,q}$ regularity.

So far, in the references [6]– [9] Kweon and Kellogg had studied corner singularity and regularity for the stationary compressible Stokes or Navier–Stokes equations on polygonal domains not having the cut boundary. In [13] the corner singularities derived by the Laplace problem with a slip-Navier boundary condition (see [12, 14]) along the cut boundary were implemented to the solutions of the compressible viscous Navier–Stokes equations. In [10] Kweon studied a jump discontinuity solution for the compressible viscous flows grazing a nonconvex corner.

Recently, in [11] Kweon and Lee studied a compressible viscosity fluid flow directed by a fixed vector field pointing a nonconvex corner of a bounded polygon. The fixed vector field was assumed to have a jump discontinuity after the nonconvex vertex so that the transport equation can be solvable along the streamline. Meanwhile, in the cut domain, the vector field (for instance, $\textbf{U}=(1,0)^t$) pointing toward the cut tip need not being jump discontinuous just after the cut tip. This advantage is used in the analysis of this paper.

In [3] Han, Kweon and Park show the interior jump discontinuity for a stationary compressible Stokes system with an inflow jump datum, and in [4], Han and Kweon study the nonlinear problem for general boundary data. Diverse applications on corner domains can be found in the references [15,16,17,18].

We consider the cut domain $\Omega$ defined by

$$\begin{aligned} \begin{aligned} \Omega&=(-1,1)\times (-1,1)\setminus \Gamma _c,\\ \Gamma _c&=\{(x,0):-1\le x\le 0\}. \end{aligned} \end{aligned}$$

(1.3)

With the vector field $\textbf{U}=(1,0)$ we define the inflow and outflow boundaries by

$$\begin{aligned} \begin{aligned} \Gamma _\textrm{in}&=\{(-1,y):-1<y<1\},\\ \Gamma _\textrm{out}&=\{(1,y):-1<y<1\}. \end{aligned} \end{aligned}$$

We define the set

$$\begin{aligned} \Upsilon =\{(x,0):0<x<1\}, \end{aligned}$$

which is the interface curve splitting the domain $\Omega$ into two subregions

$$\begin{aligned} \begin{aligned} \Omega _1&=\{(x,y)\in \Omega :y>0\},\\ \Omega _2&=\{(x,y)\in \Omega :y<0\}. \end{aligned} \end{aligned}$$

(1.4)

We set $\Omega _{\Upsilon }=\Omega \setminus \Upsilon =\Omega _1\cup \Omega _2$.

Fig. 2

The cut domain $\Omega$

We denote the symbol [f] by the jump of a function f across the curve $\Upsilon$, that is, for any $x\in (0,1)$,

$$\begin{aligned}{}[f(x,0)]=\lim _{y\downarrow 0}f(x,y)-\lim _{y\uparrow 0}f(x,y). \end{aligned}$$

(1.5)

We here state the main result of this paper.

Theorem 1.1

If $\textbf{f}\in \textbf{H}^{-1}$ and $g\in {\textrm{L}}^2$, then there exists a unique solution pair $\textbf{u}\in \textbf{H}^1_0$ and $p\in {\textrm{L}}^2$ of problem (1.1), with the estimation $\mu \Vert \textbf{u}\Vert _1+\Vert p\Vert _0+\Vert p\Vert _{0,\Gamma _\textrm{out}}\le C(\Vert \textbf{f}\Vert _{-1}+\Vert g\Vert _0)$ for a constant C.

On the other hand, assume that $\textbf{f}\in \textbf{L}^q$ and $g\in {\textrm{H}}^{1,q}$ for $q\in [2,4)$. Let ${\mathbf \Phi }$ be defined in (2.3) and $\varvec{\psi }$ the contact singularity defined in (2.5), respectively. Let $d(x)=-(\mu +\nu )^{-1}[p(x,0)]$ for $x\ge 0$ and ${{\mathcal {K}}}$ the lifting mapping defined in (2.4). Suppose the viscous number $\mu$ is sufficiently large. Then we have:

(i):

There exist a constant vector $\textbf{C}=({{\mathcal {C}}}_1,{{\mathcal {C}}}_2)^t\in \mathbb {R}^2$ and a velocity vector $\textbf{u}_R\in \textbf{H}^{2,q}(\Omega )$ such that the velocity solution $\textbf{u}$ can be written by

$$\begin{aligned} \textbf{u}=\textbf{K}+d(1)\varvec{\psi }+\textbf{C}{\mathbf \Phi }+\textbf{u}_R, \end{aligned}$$

(1.6)

where $\textbf{K}:=(0,K)^t$ is the vector function defined by

$$\begin{aligned} K={\left\{ \begin{array}{ll} {{\mathcal {K}}}d &{}\text{ in } \Omega _1,\\ 0 &{}\text{ in } \Omega _2. \end{array}\right. } \end{aligned}$$

(1.7)

(ii):

With the operator B defined by $\displaystyle (B h)(x,y)=\int \limits _{-1}^x h(s,y){\textrm{d}}s$, the pressure solution p can be written by

$$\begin{aligned} p=p_K+p_C+p_S+p_R, \end{aligned}$$

(1.8)

where

$$\begin{aligned} \begin{aligned} p_K&=-BK_y,\\ p_C&=-B\textrm{div}(d(1)\varvec{\psi }),\\ p_S&=-{{\mathcal {C}}}_1B\textrm{div}{\mathbf \Phi }_1-{{\mathcal {C}}}_2B\textrm{div}{\mathbf \Phi }_2,\\ p_R&=B(g-\textrm{div}\textbf{u}_R). \end{aligned} \end{aligned}$$

(iii):

Each component given in decompositions (1.6) and (1.8) is estimated as follows. There exists a constant $C=C(\Omega ,q)$ such that

$$\begin{aligned} \begin{aligned}&\Vert K\Vert _{2,q,\Omega _1}+|d(1)|+|\textbf{C}|+\Vert \textbf{u}_R\Vert _{2,q}\le C\mu ^{-1}(\Vert \textbf{f}\Vert _{0,q}+\Vert g\Vert _{1,q}),\\&\sum _{j=1}^2(\Vert p_K\Vert _{1,q,\Omega _j}+\Vert p_S\Vert _{1,q,\Omega _j}+\Vert p_R\Vert _{1,q,\Omega _j})\\&+\Vert p_C\Vert _{1,q}\le C(\mu ^{-1}\Vert \textbf{f}\Vert _{0,q}+\Vert g\Vert _{1,q}). \end{aligned} \end{aligned}$$

(1.9)

It is noted that the interval $2\le q<4$ is that the restriction $q<4$ is for bounding the pressure gradient of the corner singularity functions (see Lemma 3.2) and the one $q\ge 2$ is for employing the corner singularity expansion (see Theorem 4.1).

We next state the Rankine-Hugoniot jump conditions for the solutions $\textbf{u}$, p of problem (1.1) using the decompositions in (1.6) and (1.8).

Theorem 1.2

Suppose all conditions given in Theorem 1.1 hold. Then the solutions $\textbf{u}$, p have one-sided limits with respect to the curve $\Upsilon$ and satisfy the jump conditions on the interface curve $\Upsilon$

$$\begin{aligned}&\left[ \textbf{u}\right] =0, \end{aligned}$$

(1.10a)

$$\begin{aligned}&\left[ \textrm{div} \textbf{u}\right] =\mu _1^{-1}\left[ p\right] ,\,\,\left[ u_y-v_x\right] =0, \end{aligned}$$

(1.10b)

$$\begin{aligned}&\left[ p(x,0)\right] =[p(0,0)]e^{-x/\mu _1} \text{ for } x>0, \end{aligned}$$

(1.10c)

where $\mu _1=\mu +\nu$. Also, by (1.6) and (1.8), we have the jump properties

$$\begin{aligned} \begin{aligned}&\left[ K_y\right] =\left[ \textrm{div}\textbf{u}\right] ,\,\left[ K_x\right] =0=[K],\\&\left[ \textrm{div} (d\varvec{\psi })\right] =\left[ \textrm{div} (\textbf{C}\Phi )\right] =\left[ \textrm{div} \textbf{u}_R\right] =0, \\&\left[ p_K\right] \ne 0,\,\left[ p_S\right] \ne 0,\,\left[ p_R\right] \ne 0,\,\left[ p_C\right] =0. \end{aligned} \end{aligned}$$

(1.11)

Proof

The proof is similar to the ones given in the references [4, 10, 13] $\square$

In this paper we consider the following spaces and norms. We denote by ${\textrm{L}}^q(D)$, $q>1$, the space of all measurable functions defined on a bounded domain $D\subset \mathbb {R}^2$ for which $\Vert v\Vert _{0,q,D}:=\big (\int \limits _D|v(\textbf{x})|^q d\textbf{x}\big )^{1/q}<\infty$. For $s\ge 0$ we denote by the set ${\textrm{H}}^{s,q}(D)$ the usual fractional Sobolev space with norm $\Vert \,\cdot \,\Vert _{s,q,D}$ (see [1, 2]). For $s=0$ we write ${\textrm{L}}^q(D)={\textrm{H}}^{0,q}(D)$. We write ${\textrm{H}}^{1,q}_0(D)=\{u\in {\textrm{H}}^{1,q}(D):u|_{\partial D}=0\}$. We denote by ${\textrm{H}}^{-s,q}(D)$ the dual space of ${\textrm{H}}^{s,q'}_0(D)$ with norm

$$\begin{aligned} \Vert f\Vert _{-s,q,D}=\sup _{0\ne v\in {\textrm{H}}^{s,q'}_0(D)}\frac{\langle f,v\rangle }{\Vert v\Vert _{s,q',D}}, \end{aligned}$$

where $\langle ,\,\rangle$ denotes the duality pairing and $q'$ is the conjugate exponent of q. If $q=2$ we write ${\textrm{H}}^s(D)={\textrm{H}}^{s,q}(D)$ with norm $\Vert \,\cdot \,\Vert _{s,D}=\Vert \,\cdot \,\Vert _{s,q,D}$. When $D=\Omega$ we omit the domain in the space and its corresponding norm, for instance, ${\textrm{H}}^{s,q}={\textrm{H}}^{s,q}(\Omega )$ and $\Vert \,\cdot \,\Vert _{s,q}=\Vert \,\cdot \,\Vert _{s,q,\Omega }$, and so on. We will also use bold face, such as $\textbf{H}^{s,q}(D)={\textrm{H}}^{s,q}(D)\times {\textrm{H}}^{s,q}(D)$, to indicate vectorial function spaces.

Throughout this paper, C denotes a generic constant that may take different value in different place.

2 The preliminaries

The corner singularities at the cut tip. We use the corner singularity functions for the Lamé system with zero boundary condition. For the derivation we refer to [5, Chapter 3]. Let r and $\theta$ be the polar coordinates placed at the vertex (0, 0). The Lamé system ${\mathbb {L}}\textbf{u}=0$ in the infinite sector ${{\mathcal {S}}}=\{(r\cos \theta ,r\sin \theta ):r>0,\theta \in (-\pi ,\pi )\}$ with zero boundary condition has the solution of the form $r^\lambda \varvec{\Theta }(\theta )$ where $\lambda$ is the solution of the algebraic equation

$$\begin{aligned} \sin ^2(2\lambda \pi )=0. \end{aligned}$$

(2.1)

The singular exponents are $\lambda _i=i/2$ for $i=1,2,3,\cdots$, which are all multiple roots with multiplicity two (see [5, Chapter 3, Section 3.1.3]). Hence we have two orthogonal eigenvector functions corresponding to $\lambda _i$. In particular, for the leading value $\lambda _1=1/2$ we have the eigenvector functions $\varvec{\Theta }_1,\varvec{\Theta }_2$ given by

$$\begin{aligned} \begin{aligned} \varvec{\Theta }_1(\theta )&=\begin{pmatrix} \nu _1\sin (\theta /2)+\nu _1\sin (3\theta /2)\\ -(8+3\nu _1)\cos (\theta /2)-\nu _1\cos (3\theta /2) \end{pmatrix},\\ \varvec{\Theta }_2(\theta )&=\begin{pmatrix} -(8+5\nu _1)\cos (\theta /2)+\nu _1\cos (3\theta /2)\\ \nu _1\sin (\theta /2)+\nu _1\sin (3\theta /2) \end{pmatrix}. \end{aligned} \end{aligned}$$

(2.2)

In order to state the corner singularity function we consider a sufficiently smooth cutoff function $\chi$ defined by $\chi =1$ for $r\le r_0$ and $\chi =0$ for $r\ge 2r_0$ with a small $r_0\ll 1$. It is considered for localizing the corner singularity propagation near the vertex. We write the corner singularity functions by a simple vector form: For a vector $\textbf{C}=({{\mathcal {C}}}_1,{{\mathcal {C}}}_2)^t\in \mathbb {R}^2$,

$$\begin{aligned} \begin{aligned} {\mathbf \Phi }_j&=\chi (r) r^{1/2}\varvec{\Theta }_j(\theta ),\\ \textbf{C}{\mathbf \Phi }&={{\mathcal {C}}}_1{\mathbf \Phi }_1+{{\mathcal {C}}}_2{\mathbf \Phi }_2. \end{aligned} \end{aligned}$$

(2.3)

It is recalled that the value $\lambda _2=1$ is the second leading singular value which has two eigenfunctions $(\sin \theta ,0)^t$ and $(0,\sin \theta )^t$.

The lifting vector field. For a function f(x) defined on the interval (0, 1) we define the mapping ${{\mathcal {K}}}f$ by

$$\begin{aligned} ({{\mathcal {K}}}f)(x,y)=\int \limits _{b^-(x,y)}^{b^+(x,y)}\tilde{f}(s)ds, \end{aligned}$$

(2.4)

where $b^\pm (x,y)=x-\frac{y}{2}(x\pm 1)$ and $\tilde{f}$ is defined by $\tilde{f}(x)=f(-x)$ for $x\in (-1,0)$ and $\tilde{f}(x)=f(x)$ for $x\in [0,1)$.

Formula (2.4) was heuristically constructed so that conditions (4.6) (see Lemma 4.1 below) are satisfied. It is also employed in handling the pressure jump value on the interface curve $\Upsilon$.

Fig. 3

The lifting mapping K

The contact singularity. We consider the vector function $\varvec{\psi }$ as

$$\begin{aligned} \varvec{\psi }(x,y)=\chi ^*(r^*)\varvec{\zeta }(r^*,\theta ^*), \end{aligned}$$

(2.5)

where $(r^*,\theta ^*)$ is the polar coordinate at the point (1, 0) and $\chi ^*$ is a smooth cutoff function at the point (1, 0), which can be defined in a similar way as the cutoff $\chi$ of singularity function (2.3). The vector function $\varvec{\zeta }$ is defined as

$$\begin{aligned} \varvec{\zeta }(r^*,\theta ^*)=(c_2\pi )^{-1}(\nu _1\eta _3,\,c_1\eta _1+c_2\eta _2)^t, \end{aligned}$$

(2.6)

where $c_1=2\nu _1+2$, $c_2=\nu _1+2$, and

$$\begin{aligned} \begin{aligned} \eta _1&=r^*\sin (\theta ^*-3\pi /2)\log r^*,\\ \eta _2&=(\theta ^*-3\pi /2)\,r^*\cos (\theta ^*-3\pi /2),\\ \eta _3&=(\theta ^*-3\pi /2)\,r^*\sin (\theta ^*-3\pi /2). \end{aligned} \end{aligned}$$

(2.7)

In the half region ${{\mathcal {S}}}=\{(r^*\cos \theta ^*,r^*\sin \theta ^*)\in \mathbb {R}^2:r^*>0,\pi /2<\theta ^*<3\pi /2\}$ the vector $\varvec{\zeta }$ solves the equations

$$\begin{aligned} \begin{aligned} {\mathbb {L}}\varvec{\zeta }&=0{} & {} \text{ in } {{\mathcal {S}}},\\ \varvec{\zeta }&=(0,r^*)^t{} & {} \text{ on } \theta =\pi /2,\\ \varvec{\zeta }&=\textbf{0}{} & {} \text{ on } \theta =3\pi /2. \end{aligned} \end{aligned}$$

(2.8)

Fig. 4

The contact singularity

3 The transport problem on the cut domain

We consider the transport equation on the cut domain $\Omega$, with zero inflow boundary condition on $\Gamma _\textrm{in}$:

$$\begin{aligned} \begin{aligned} \textbf{U}\cdot \nabla p&=G{} & {} \text{ in } \Omega ,\\ p&=0{} & {} \text{ on } \Gamma _\textrm{in}. \end{aligned} \end{aligned}$$

(3.1)

We define the operator $B:{\textrm{L}}^q\mapsto {\textrm{L}}^q$ by $BG=p$ where p is the solution of (3.1). By integrating along the integral curves, the formula for the operator B is given by

$$\begin{aligned} (BG)(x,y)=\int \limits _{-1}^x G(s,y)ds. \end{aligned}$$

(3.2)

For $x>0$ the jump of BG is given by

$$\begin{aligned} \left[ BG(x,0)\right] =\int \limits _{-1}^0 G(s,0+)-G(s,0-)ds+\int \limits _0^x \left[ G(s,0)\right] ds. \end{aligned}$$

(3.3)

With formulas (3.2) and (3.3) one can easily derive the following properties:

Lemma 3.1

(i):

If $G\in {\textrm{L}}^q$, then $BG\in {\textrm{L}}^q$ and $\Vert BG\Vert _{0,q}\le C\Vert G\Vert _{0,q}$ for a constant $C=C(q)$.

(ii):

If $G\in {\textrm{H}}^{1,q}$ and $G(x,0+)\ne G(x,0-)$ for some $x<0$, then $BG\in {\textrm{H}}^{1,q}(\Omega _j)$ and $\Vert BG\Vert _{1,q,\Omega _j}\le C\Vert G\Vert _{1,q,\Omega _j}$ for $j=1,2$.

(iii):

If $G\in {\textrm{H}}^{1,q}$ and $G(x,0+)=G(x,0-)$ for $x<0$, then $BG\in {\textrm{H}}^{1,q}$ and $\Vert BG\Vert _{1,q}\le C\Vert G\Vert _{1,q}$.

Proof

The proof can be shown in a similar way as done in the references: [3, Lemma 3.1] and [10, Lemma 2.2]. $\square$

We recall that $\text{ div }\,{\mathbf \Phi }_1$ has different traces on either side of the cut boundary $\Gamma _c$ (see (1.2)). So the jump $\left[ B\text{ div }\,{\mathbf \Phi }_1\right] \ne 0$. On the other hand, since $\text{ div }\,{\mathbf \Phi }_2=0$ on either side of $\Gamma _c$, $\left[ B\text{ div }\,{\mathbf \Phi }_2\right] =0$.

We recall that the singularities ${\mathbf \Phi }_j$ defined in (2.3) are in the space $\textbf{H}^{s,q}$ for $s<1/2+2/q$. However, we have the following property:

Lemma 3.2

For $q<4$, $B\text{ div }\,{\mathbf \Phi }_1\in {\textrm{H}}^{1,q}(\Omega _j)$ for $j=1,2$ and $B\text{ div }\,{\mathbf \Phi }_2\in {\textrm{H}}^{1,q}$.

Proof

We first estimate $B\text{ div }\,(r^{1/2}\varvec{\Theta }_j(\theta ))$, $j=1,2$. By the direct calculation,

$$\begin{aligned} \begin{aligned} \text{ div }\,(r^{1/2}\varvec{\Theta }_1(\theta ))(x,y)&=2\sqrt{2}{\left\{ \begin{array}{ll} -r^{-1}\sqrt{r-x}, &{}y\ge 0,\\ r^{-1}\sqrt{r-x}, &{}y<0, \end{array}\right. }\\ \text{ div }\,(r^{1/2}\varvec{\Theta }_2(\theta ))(x,y)&=-2\sqrt{2}r^{-1}\sqrt{r+x}. \end{aligned} \end{aligned}$$

Then

$$\begin{aligned} \begin{aligned} B\text{ div }\,(r^{1/2}\varvec{\Theta }_1(\theta ))&={\left\{ \begin{array}{ll} 4\sqrt{2}(\phi _1(x,y)-\phi _1(-1,y)), &{}y\ge 0,\\ -4\sqrt{2}(\phi _1(x,y)-\phi _1(-1,y)), &{}y<0, \end{array}\right. }\\ B\text{ div }\,(r^{1/2}\varvec{\Theta }_2(\theta ))&=-4\sqrt{2}(\phi _2(x,y)-\phi _2(-1,y)), \end{aligned} \end{aligned}$$

(3.4)

where

$$\begin{aligned} \begin{aligned} \phi _1(x,y)&=(\sqrt{x^2+y^2}-x)^{1/2},\\ \phi _2(x,y)&=(\sqrt{x^2+y^2}+x)^{1/2}. \end{aligned} \end{aligned}$$

(3.5)

By (3.5), $\phi _1=\sqrt{2}r^{1/2}\sin (\theta /2)$ in $\Omega _1$. Clearly, $\phi _1\in {\textrm{L}}^q(\Omega _1)$. Also,

$$\begin{aligned} \nabla \phi _1(x,y)=\frac{1}{\sqrt{2}}r^{-1/2}(-\sin (\theta /2),\cos (\theta /2))^t. \end{aligned}$$

Hence $|\nabla \phi _1|\le Cr^{-1/2}$, so

$$\begin{aligned} \begin{aligned} \Vert \nabla \phi _1\Vert _{0,q,\Omega _1}^q&\le C\int \limits _{\Omega _1} r^{-q/2}{\textrm{d}}\textbf{x}\\&\le C\int \limits _{\Omega _1} r^{-q/2+1}drd\theta . \end{aligned} \end{aligned}$$

Since $q<4$, $-q/2+1>-1$, so

$$\begin{aligned} \int \limits _{\Omega _1} r^{-q/2+1}drd\theta <\infty . \end{aligned}$$

Hence $\nabla \phi _1\in \textbf{L}^q(\Omega _1)$ and $\phi _1\in {\textrm{H}}^{1,q}(\Omega _1)$. Likewise, $\phi _1\in {\textrm{H}}^{1,q}(\Omega _2)$. In a similar way, $\phi _2\in {\textrm{H}}^{1,q}(\Omega )$. Clearly $\phi _1(-1,y)\in {\textrm{H}}^{1,q}(\Omega _k)$ and $\phi _2(-1,y)\in {\textrm{H}}^{1,q}$, because

$$\begin{aligned} \lim _{y\rightarrow 0}\partial _y\phi _2(-1,y)=\lim _{y\rightarrow 0}\frac{y}{2((1+y^2)^{3/2}-(1+y^2))^{1/2}}=0. \end{aligned}$$

Since ${\mathbf \Phi }_j=\chi \, r^{1/2}\varvec{\Theta }_j$ we have $B\text{ div }\,{\mathbf \Phi }_j=B(r^{1/2}\varvec{\Theta }_j\cdot \nabla \chi )+B(\chi \text{ div }\,(r^{1/2}\varvec{\Theta }_j))$, which behaves like $B(\text{ div }\,(r^{1/2}\varvec{\Theta }_j))$ near the origin (0, 0). Thus the required results follow. $\square$

4 The Lamé system with an unbounded gradient across the curve $\Upsilon$

In this section we study the regularity for the Lamé system with an unbounded gradient

$$\begin{aligned} \begin{aligned} -{\mathbb {L}}\textbf{u}&=\nabla f{} & {} \text{ in } \Omega ,\\ \textbf{u}&=0{} & {} \text{ on } \Gamma , \end{aligned} \end{aligned}$$

(4.1)

where f is assumed to have a nonzero jump across $\Upsilon$.

We first state the corner singularity result of the Lamé system, which is derived in Sect. 6. A similar result can be found in the reference [8, Lemma 2.3].

Theorem 4.1

Let $q\ge 2$ be any number. Let $\textbf{u}$ be the solution of the boundary value problem

$$\begin{aligned} \begin{aligned} -{\mathbb {L}}\textbf{u}&={\textbf{h}}\hspace{0.3cm} \text{ in } \Omega ,\\ \textbf{u}&=\textbf{g}\hspace{0.3cm} \text{ on } \Gamma . \end{aligned} \end{aligned}$$

(4.2)

Let $s_j=j/2+2/q$, $j=1,2,\cdots$. Then the solution $\textbf{u}$ has the following properties. (i) For $s<s_1$, if ${\textbf{h}}\in \textbf{H}^{s-2,q}$ and $\textbf{g}\in \textbf{H}^{s-1/q,q}(\Gamma )$, then the solution $\textbf{u}\in \textbf{H}^{s,q}$ and satisfies

$$\begin{aligned} \Vert \textbf{u}\Vert _{s,q}\le C(\Vert {\textbf{h}}\Vert _{s-2,q}+\Vert \textbf{g}\Vert _{s-1/q,q,\Gamma }). \end{aligned}$$

(ii) For $s\in (s_1,s_3)$, there are bounded linear functional on $\textbf{H}^{s-2,q}\times \textbf{H}^{s-1/q,q}(\Gamma )$ such that if ${\textbf{h}}\in \textbf{H}^{s-2,q}$ and $\textbf{g}\in \textbf{H}^{s-1/q,q}(\Gamma )$, then solution $\textbf{u}$ of (4.2) has the decomposition

(4.3)

where $\textbf{u}_R\in \textbf{H}^{s,q}$ and satisfies the inequality

(4.4)

In particular, the linear functionals are defined as follows: For $q'=q/(q-1)$, there exist functions $\textbf{v}_j\in \textbf{H}^{2-s,q'}$, $j=1,2$, such that

(4.5)

where $a=32(\nu _1+2)(\nu _1+1)\pi$.

We now consider problem (4.1). Since $[f]\ne 0$ the gradient of f is not well-defined on $\Upsilon$. For dealing with this issue we use the lifting mapping ${{\mathcal {K}}}$ given in (2.4) and the contact singularity function $\varvec{\psi }$ constructed in (2.5).

We next derive the properties of the mapping ${{\mathcal {K}}}$ defined in (2.4) and its regularity.

Lemma 4.1

Suppose $q>2$. Let $f\in {\textrm{H}}^{1,q}(\Upsilon )$ be given. Let us write $f(x)=f(x,0)$, for simplicity. Let K be defined by $K={{\mathcal {K}}}f$ on $\Omega _1$ and $K=0$ on $\Omega _2$. Then K satisfies the interface conditions

$$\begin{aligned} K(x,0)=0,\,\,K_y(x,0)=-f(x),\,\,\forall x\in (0,1). \end{aligned}$$

(4.6)

Furthermore, $K\in {\textrm{H}}^{2,q}(\Omega _1)$ and there is a constant $C=C(q)$ satisfying the estimate

$$\begin{aligned} \Vert K\Vert _{2,q,\Omega _1}\le C\Vert f\Vert _{1,q,\Upsilon }. \end{aligned}$$

(4.7)

Proof

Obviously $K(x,0)=0$. Differentiating K with respect to the variables x and y,

$$\begin{aligned} \begin{aligned} K_x(x,y)&=(1-y/2)(\tilde{f}(b^+(x,y))-\tilde{f}(b^-(x,y))),\\ K_y(x,y)&=-(x/2+1/2)\tilde{f}(b^+(x,y))+(x/2-1/2)\tilde{f}(b^-(x,y)). \end{aligned} \end{aligned}$$

(4.8)

So $K_y(x,0)=-f(x)$ for $x\in (0,1)$. To show (4.7), recall that $-1<b^+(x,y)<b^-(x,y)<1$ for $(x,y)\in \Omega _1$. By the Hölder inequality,

$$\begin{aligned} \begin{aligned} \int \limits _{\Omega _1}|K|^q{\textrm{d}}\textbf{x}&=\int \limits _{-1}^1\int \limits _0^1\Big |\int \limits _{b^-}^{b^+}\tilde{f}(s)ds\Big |^qdydx\\&\le \int \limits _{-1}^1\int \limits _0^1 |y|^{q-1}\int \limits _{b^+}^{b^-}|\tilde{f}(s)|^qdsdydx\\&\le C\Vert \tilde{f}\Vert _{0,q,(-1,1)}^q. \end{aligned} \end{aligned}$$

(4.9)

By (4.8), one has

$$\begin{aligned} \int \limits _{\Omega _1}|\nabla K|^q{\textrm{d}}\textbf{x}\le C\int \limits _{\Omega _1}|\tilde{f}(b^+)|^q+|\tilde{f}(b^-)|^q{\textrm{d}}\textbf{x}. \end{aligned}$$

(4.10)

Letting $t=b^+(x,y)$,

$$\begin{aligned} \begin{aligned} \int \limits _{\Omega _1}|\tilde{f}(b^+)|^q{\textrm{d}}\textbf{x}&=\int \limits _0^1\int \limits _{-1}^1|\tilde{f}(b^+)|^q dxdy\\&\quad \le C\int \limits _0^1\int \limits _{-1}^{1-y}|\tilde{f}(t)|^q dtdy\\&\quad \le C\Vert \tilde{f}\Vert _{0,q,(-1,1)}^q. \end{aligned} \end{aligned}$$

Likewise, $\int \limits _{\Omega _1}|\tilde{f}(b^-)|^q{\textrm{d}}\textbf{x}\le C\Vert \tilde{f}\Vert _{0,q,(-1,1)}^q$. Hence, by (4.10),

$$\begin{aligned} \Vert \nabla K\Vert _{0,q,\Omega _1}\le C\Vert \tilde{f}\Vert _{0,q,(-1,1)}. \end{aligned}$$

(4.11)

The second-order partial derivatives of K with respect to x and y are

$$\begin{aligned} \begin{aligned} K_{xx}(x,y)&=(1-y/2)^2(\tilde{f}'(b^+)-\tilde{f}'(b^-)),\\ K_{xy}(x,y)&=(y/2-1)((x/2+1/2)\tilde{f}'(b^+)-(x/2-1/2)\tilde{f}'(b^-))\\&\quad -2^{-1}(\tilde{f}(b^+)-\tilde{f}(b^-)),\\ K_{yy}(x,y)&=(x/2+1/2)^2\tilde{f}'(b^+)-(x/2-1/2)^2\tilde{f}'(b^-). \end{aligned} \end{aligned}$$

As done in deriving inequality (4.11) one has

$$\begin{aligned} \begin{aligned} \Vert K_{xx}\Vert _{0,q,\Omega _1}+\Vert K_{yy}\Vert _{0,q,\Omega _1}&\le C\Vert \tilde{f}'\Vert _{0,q,(-1,1)},\\ \Vert K_{xy}\Vert _{0,q,\Omega _1}&\le C(\Vert \tilde{f}\Vert _{0,q,(-1,1)}+\Vert \tilde{f}'\Vert _{0,q,(-1,1)}). \end{aligned} \end{aligned}$$

(4.12)

Thus, by (4.9), (4.11) and (4.12),

$$\begin{aligned} \Vert K\Vert _{2,q,\Omega _1}\le C\Vert \tilde{f}\Vert _{1,q,(-1,1)}. \end{aligned}$$

(4.13)

One has $\Vert \tilde{f}\Vert _{1,q,(-1,1)}=2^{1/q}\Vert f\Vert _{1,q,\Upsilon }$. So (4.7) follows by (4.13). $\square$

By Lemma 4.1, $K\in {\textrm{H}}^{2-1/q,q}(\partial \Omega _j)$ for $f\in {\textrm{H}}^{1,q}(\Upsilon )$ but $K\notin {\textrm{H}}^{2-1/q,q}(\Gamma )$, because $K_y(1,y)=-f(1-y)$ for $y>0$ and $K_y(1,y)=0$ for $y<0$. To handle this, we use the function $\varvec{\psi }$ defined in (2.5). It has the regularity $\varvec{\psi }\in \textbf{H}^{s,q}(\Omega )$ for $s<1+2/q$. Indeed, $\eta _1=r^*\sin (\theta ^*-3\pi /2)\log r^*\in {\textrm{H}}^{s,q}$ by [4, Lemma 3.2]. It is clear for the functions $\eta _2$ and $\eta _3$.

Lemma 4.2

Let K be the function defined in Lemma 4.1. Let $\psi _2$ be the second component of $\varvec{\psi }=(\psi _1,\psi _2)$. If $f\in {\textrm{H}}^{1,q}(\Upsilon )$, then $K_1:=K+f(1)\psi _2\in {\textrm{H}}^{2-1/q,q}(\Gamma )$ and satisfies

$$\begin{aligned} \Vert K_1\Vert _{2-1/q,q,\Gamma }\le C\Vert f\Vert _{1,q,\Upsilon }. \end{aligned}$$

(4.14)

Proof

First we recall that $\psi _2(1,y)=\chi (y)y$ for $y\ge 0$ and 0 for $y<0$. Set $I=\{(1,y):-2r_0<y<2r_0\}$ for a number $r_0\ll 1$. Then $K_1=K$ on $\Gamma {\setminus } I$. Since $K\in {\textrm{H}}^{2-1/q,q}(\partial \Omega _j)$, $j=1,2$, and $K(x,0)=0$, we have $K_1\in {\textrm{H}}^{2-1/q,q}(\Gamma \setminus I)$. To show inequality (4.14), since $K_1(1,y)=0$ for $y<0$ and by (4.7),

$$\begin{aligned} \begin{aligned} \Vert K_1\Vert _{1,q,I}&\le \Vert K(1,\cdot )\Vert _{1,q,(0,2r_0)}+C|f(1)|\\&\le C\Vert K\Vert _{2,q,\Omega _1}+C|f(1)|\\&\le C\Vert f\Vert _{1,q,\Upsilon }. \end{aligned} \end{aligned}$$

To estimate $\Vert K_{1,y}\Vert _{1-1/q,q,I}$. For $y>0$, since $\psi _{2,y}(1,y)=1$ near $y=0$,

$$\begin{aligned} \begin{aligned} \lim _{y\downarrow 0}K_{1,y}(1,y)&=-f(1)+f(1)\lim _{y\downarrow 0}\psi _{2,y}(1,y)\\&=0. \end{aligned} \end{aligned}$$

Also, since $K_1(1,y)=0$ for $y<0$, we have

$$\begin{aligned} \lim _{y\uparrow 0}K_{1,y}(1,y)=0=\lim _{y\downarrow 0}K_{1,y}(1,y). \end{aligned}$$

So

$$\begin{aligned} \Vert K_{1,y}\Vert _{1-1/q,q,I}^q=(I)+(II), \end{aligned}$$

(4.15)

where

$$\begin{aligned} \begin{aligned} (I)&=\int \limits _0^{2r_0}\int \limits _0^{2r_0}\Big |\frac{K_{1,y}(1,y_1)-K_{1,y}(1,y_2)}{y_1-y_2}\Big |^qdy_1dy_2,\\ (II)&=2\int \limits _0^{2r_0}\int \limits _{-2r_0}^0\Big |\frac{K_{1,y}(1,y_2)}{y_1-y_2}\Big |^qdy_1dy_2. \end{aligned} \end{aligned}$$

Since $|\psi _{2,y}(1,y)|<\infty$, we have

$$\begin{aligned} \begin{aligned} (I)&\le C(\Vert K_y(1,y)\Vert _{1-1/q,q,(0,2r_0)}^q+|f(1)|^q)\\&\le C(\Vert K_y\Vert _{1,q,\Omega _1}^q+|f(1)|^q)\\&\le C\Vert f\Vert _{1,q,\Upsilon }^q. \end{aligned} \end{aligned}$$

To estimate (II). Since $|y_1-y_2|\ge |y_2|$ for $y_1<0$ and $y_2>0$,

$$\begin{aligned} (II)\le C\int \limits _0^{2r_0}\Big |\frac{K_{1,y}(1,y)}{y}\Big |^qdy. \end{aligned}$$

We recall that $K_{1,y}(1,0)=0$ and

$$\begin{aligned} K_{1,yy}(1,y)=f'(1-y)+f(1)\psi _{2,yy}(1,y), \end{aligned}$$

for $y>0$. Note that $|\psi _{2,yy}(1,y)|<\infty$. So, by the Hardy’s inequality,

$$\begin{aligned} \begin{aligned} (II)&\le C\int \limits _0^{2r_0}\Big |\frac{K_{1,y}(1,y)-K_{1,y}(1,0)}{y-0}\Big |^qdy\\&\le C\int \limits _0^{2r_0}|K_{1,yy}(1,y)|^qdy\\&\le C\left( \int \limits _0^{2r_0}|f'(1-y)|^qdy+|f(1)|^q\right) \\&\le C\Vert f\Vert _{1,q,\Upsilon }^q. \end{aligned} \end{aligned}$$

Hence, by (4.15), $\Vert K_{1,y}\Vert _{1-1/q,q,I}\le C\Vert f\Vert _{1,q,\Upsilon }$. Finally $K_1$ is smooth at the points $(1,\pm 2r_0)$. Thus (4.14) follows. $\square$

We next sort out the corner and contact singularities from the solution of problem (4.1) and show their regularities.

Theorem 4.2

If $f\in {\textrm{H}}^{-1}$, then there exists a unique solution $\textbf{u}\in {\textrm{H}}^1_0$ of (4.1) with $\Vert \textbf{u}\Vert _1\le C\Vert f\Vert _{-1}$ for a constant C. On the other hand, suppose that $f\in {\textrm{H}}^{1,q}(\Omega _j)$ and $[f]\in {\textrm{H}}^{1,q}(\Upsilon )$ for $q>2$. Let $\textbf{K}=(0,K)^t$ where $K=(1+\nu _1)^{-1}{{\mathcal {K}}}([f])$ in $\Omega _1$ and $K=0$ in $\Omega _2$. Then there exist a constant vector $\textbf{C}\in \mathbb {R}^2$ and $\textbf{u}_R\in \textbf{H}^{2,q}$ such that the solution $\textbf{u}$ of (4.1) can be decomposed into the following form:

$$\begin{aligned} \textbf{u}=\textbf{K}+d\varvec{\psi }+\textbf{C}{\mathbf \Phi }+\textbf{u}_R, \end{aligned}$$

(4.16)

where $d=(1+\nu _1)^{-1}\left[ f(1,0)\right]$ and $\textbf{C}{\mathbf \Phi }={{\mathcal {C}}}_1{\mathbf \Phi }_1+{{\mathcal {C}}}_2{\mathbf \Phi }_2$. Furthermore there is a constant C such that

$$\begin{aligned} \Vert \textbf{u}_R\Vert _{2,q}+\Vert \textbf{K}\Vert _{2,q,\Omega _2}+|\textbf{C}|+|d|\le C\Big (\sum _{j=1}^2\Vert \nabla f\Vert _{0,q,\Omega _j}+\Vert [f]\Vert _{1,q,\Upsilon }\Big ). \end{aligned}$$

(4.17)

Proof

We find the weak solution of (4.1) satisfying the equation

$$\begin{aligned} \int \limits _\Omega \nabla \textbf{u}\cdot \nabla \textbf{v}+\nu _1\text{ div }\,\textbf{u}\text{ div }\,\textbf{v}{\textrm{d}}\textbf{x}=-\int \limits _\Omega f\text{ div }\,\textbf{v}{\textrm{d}}\textbf{x},\quad \forall \textbf{v}\in \textbf{H}^1_0. \end{aligned}$$

(4.18)

By the integration by parts we have

$$\begin{aligned} \int \limits _\Omega f\text{ div }\,\textbf{v}{\textrm{d}}\textbf{x}=\int \limits _\Upsilon \left[ f\right] \textbf{n}\cdot \textbf{v}ds -\sum _{j=1}^{2}\int \limits _{\Omega _j}\nabla f\cdot \textbf{v}{\textrm{d}}\textbf{x}, \end{aligned}$$

(4.19)

where $\textbf{n}=(0,-1)^t$. It follows from Lemma 4.1 that the vector $\textbf{K}$ satisfies $\textbf{K}\in \textbf{H}^{1,q}\cap \textbf{H}^{2,q}(\Omega _1)$ and

$$\begin{aligned} \textbf{K}\Big |_\Upsilon =0,\,\,\frac{\partial \textbf{K}}{\partial \textbf{n}}=(1+\nu _1)^{-1}\left[ f\right] \textbf{n} \text{ on } \Upsilon . \end{aligned}$$

Also, by direct calculation,

$$\begin{aligned} \text{ div }\,\textbf{K}=(1+\nu _1)^{-1}\left[ f\right] \text{ on } \Upsilon . \end{aligned}$$

(4.20)

Therefore, for any $\textbf{v}\in \textbf{H}^1_0$,

$$\begin{aligned} \begin{aligned}&\int \limits _\Omega \nabla \textbf{K}\cdot \nabla \textbf{v}+\nu _1\text{ div }\,\textbf{K}\text{ div }\,\textbf{v}{\textrm{d}}\textbf{x}\\&=\int \limits _{\Omega _1}\nabla \textbf{K}\cdot \nabla \textbf{v}+\nu _1\text{ div }\,\textbf{K}\text{ div }\,\textbf{v}{\textrm{d}}\textbf{x}\\&=-\int \limits _{\Omega _1}{\mathbb {L}}\textbf{K}\cdot \textbf{v}{\textrm{d}}\textbf{x}+\int \limits _\Upsilon \Big (\frac{\partial \textbf{K}}{\partial \textbf{n}}+\nu _1\textbf{n}\text{ div }\,\textbf{K}\Big )\cdot \textbf{v}ds\\&=-\int \limits _{\Omega _1}{\mathbb {L}}\textbf{K}\cdot \textbf{v}{\textrm{d}}\textbf{x}+\int \limits _\Upsilon \left[ f\right] \textbf{n}\cdot \textbf{v}ds. \end{aligned} \end{aligned}$$

(4.21)

Combining (4.18)–(4.21), we have

$$\begin{aligned} \begin{aligned}&\int \limits _\Omega \nabla (\textbf{u}-\textbf{K})\cdot \nabla \textbf{v}+\nu _1\text{ div }\,(\textbf{u}-\textbf{K})\text{ div }\,\textbf{v}{\textrm{d}}\textbf{x}\\&=\sum _{j=1}^{2}\int \limits _{\Omega _j}(\nabla f+{\mathbb {L}}\textbf{K})\cdot \textbf{v}{\textrm{d}}\textbf{x},\,\,\,\forall \textbf{v}\in \textbf{H}^1_0, \end{aligned} \end{aligned}$$

Let $\textbf{F}_1=\nabla f+{\mathbb {L}}\textbf{K}$. Using the symbol $\nabla ^\perp =(-\partial _y,\partial _x)^t$ we write the term $\Delta f$ by $\Delta f=\nabla \text{ div }\,f+\nabla ^\perp \nabla ^\perp \cdot f$. So ${\mathbb {L}}\textbf{K}=(1+\nu _1)\nabla \text{ div }\,\textbf{K}+\nabla ^\perp \nabla ^\perp \cdot \textbf{K}$ and

$$\begin{aligned} \textbf{F}_1=\nabla (f+(1+\nu _1)\text{ div }\,\textbf{K})+\nabla ^\perp \nabla ^\perp \cdot \textbf{K}. \end{aligned}$$

Since $f+(1+\nu _1)\text{ div }\,\textbf{K}$ is continuous across $\Upsilon$ by (4.20) and $\nabla ^\perp \cdot \textbf{K}=K_x$ is continuous across $\Upsilon$, we have $\textbf{F}_1\in \textbf{L}^q$.

Now the vector $\textbf{w}_1:=\textbf{u}-\textbf{K}$ is the weak solution of the problem

$$\begin{aligned} \begin{aligned} -{\mathbb {L}}\textbf{w}_1&=\textbf{F}_1{} & {} \text{ in } \Omega ,\\ \textbf{w}_1&=-\textbf{K}{} & {} \text{ on } \Gamma . \end{aligned} \end{aligned}$$

(4.22)

We recall that $\textbf{K}\notin \textbf{H}^{2-1/q,q}(\Gamma )$ since $\textbf{K}_y(1,y)$ is not continuous across the contact point $(1,0)\in \Gamma$. For handling this we set $\textbf{w}_2=\textbf{w}_1-d\varvec{\psi }$ with $d=(1+\nu _1)^{-1}\left[ f(1,0)\right]$. We note that $\textbf{w}_2$ satisfies the following boundary value problem:

$$\begin{aligned} \begin{aligned} -{\mathbb {L}}\textbf{w}_2&=\textbf{F}_2{} & {} \text{ in } \Omega ,\\ \textbf{w}_2&=-\textbf{K}_1{} & {} \text{ on } \Gamma , \end{aligned} \end{aligned}$$

(4.23)

where $\textbf{F}_2:=\textbf{F}_1+d\,{\mathbb {L}}\varvec{\psi }$ and $\textbf{K}_1:=\textbf{K}+d\varvec{\psi }$. Since ${\mathbb {L}}\varvec{\psi }\in \textbf{L}^q$, $\textbf{F}_2\in \textbf{L}^q$. Also, by Lemma 4.2, $\textbf{K}_1\in \textbf{H}^{2-1/q,q}(\Gamma )$. Therefore, by Theorem 4.1, there exist a vector function $\textbf{u}_R\in \textbf{H}^{2,q}$ and a constant vector $\textbf{C}\in \mathbb {R}^2$ such that the solution $\textbf{w}_2$ of (4.23) becomes

$$\begin{aligned} \textbf{w}_2=\textbf{C}{\mathbf \Phi }+\textbf{u}_R. \end{aligned}$$

(4.24)

From (4.22)–(4.24) the solution $\textbf{u}$ of (4.1) is (4.16). By (4.4) and (4.7) we have

$$\begin{aligned} \begin{aligned} \Vert \textbf{K}\Vert _{2,q,\Omega _2}+|d|&\le C\Vert [f]\Vert _{1,q,\Upsilon },\\ \Vert \textbf{u}_R\Vert _{2,q}+|\textbf{C}|&\le C(\Vert \textbf{F}_2\Vert _{0,q}+\Vert \textbf{K}_1\Vert _{2-1/q,q,\Gamma }). \end{aligned} \end{aligned}$$

(4.25)

Since $\textbf{F}_2=\nabla f+{\mathbb {L}}(\textbf{K}+d\varvec{\psi })$, we have

$$\begin{aligned} \begin{aligned} \Vert \textbf{F}_2\Vert _{0,q}&\le C\Big (\sum _{j=1}^2\Vert \nabla f\Vert _{0,q,\Omega _j}+(\Vert \textbf{K}\Vert _{2,q,\Omega _2}+|d|)\Big )\\&\le C\Big (\sum _{j=1}^2\Vert \nabla f\Vert _{0,q,\Omega _j}+\Vert [f]\Vert _{1,q,\Upsilon }\Big ), \end{aligned} \end{aligned}$$

(4.26)

and, by (4.14),

$$\begin{aligned} \Vert \textbf{K}_1\Vert _{2-1/q,q,\Gamma }\le C\Vert [f]\Vert _{1,q,\Upsilon }. \end{aligned}$$

(4.27)

By (4.25)–(4.27), (4.17) follows. $\square$

5 Proof of Theorem 1.1

We consider the following spaces: For any $q\in [2,4)$,

$$\begin{aligned} \begin{aligned} \varvec{{{\mathcal {P}}}}&=\{\textbf{v}\in \textbf{H}^{1,q}_0:\textbf{v}\in \textbf{H}^{2,q}(\Omega _j),\,\,j=1,2\},\\ \varvec{{{\mathcal {X}}}}&=\varvec{{{\mathcal {P}}}}+{{\,\textrm{span}\,}}\{\varvec{\psi },{\mathbf \Phi }_1,{\mathbf \Phi }_2\}, \\ {{\mathcal {Q}}}&=\{\eta \in {\textrm{L}}^q:\eta \in {\textrm{H}}^{1,q}(\Omega _j),\,\,j=1,2\}, \end{aligned} \end{aligned}$$

(5.1)

with norms

$$\begin{aligned} \begin{aligned} \Vert \textbf{v}\Vert _{\varvec{{{\mathcal {P}}}}}&=\sum _{j=1}^2\Vert \textbf{v}\Vert _{2,q,\Omega _j},\\ \Vert \textbf{v}+d\varvec{\psi }+{{\mathcal {C}}}_1{\mathbf \Phi }_1+{{\mathcal {C}}}_2{\mathbf \Phi }_2\Vert _{\varvec{{{\mathcal {X}}}}}&=\Vert \textbf{v}\Vert _{\varvec{{{\mathcal {P}}}}}+|d|+\sum _{i=1}^2|{{\mathcal {C}}}_i|,\\ \Vert \eta \Vert _{{\mathcal {Q}}}&=\sum _{j=1}^2\Vert \eta \Vert _{1,q,\Omega _j}. \end{aligned} \end{aligned}$$

(5.2)

We define the solution operator ${{\mathcal {A}}}:\textbf{H}^{-1,q}\mapsto \textbf{H}^{1,q}$ defined by ${{\mathcal {A}}}\textbf{f}=\textbf{u}$, where $\textbf{u}$ solves the boundary value problem

$$\begin{aligned} \begin{aligned} -{\mathbb {L}}\textbf{u}&=\textbf{f}{} & {} \text{ in } \Omega ,\\ \textbf{u}&=0{} & {} \text{ on } \Gamma . \end{aligned} \end{aligned}$$

With the operators ${{\mathcal {A}}}$ and B we define the mapping ${{\mathcal {M}}}$ by

$$\begin{aligned} {{\mathcal {M}}}\textbf{v}&=\mu ^{-1}{{\mathcal {A}}}(\textbf{f}-\nabla p), \end{aligned}$$

(5.3a)

$$\begin{aligned} p&=B(g-\text{ div }\,\textbf{v}), \end{aligned}$$

(5.3b)

where $\textbf{f}$ and g are fixed.

Lemma 5.1

Set $\textbf{w}=\mu ^{-1}{{\mathcal {A}}}(\textbf{f}-\nabla p)$. If $\textbf{f}\in \textbf{L}^q$ and $p\in {{\mathcal {Q}}}$ with $[p]\in {\textrm{H}}^{1,q}(\Upsilon )$, then $\textbf{w}\in \varvec{{{\mathcal {X}}}}$ and satisfies the inequality

$$\begin{aligned} \Vert \textbf{w}\Vert _{\varvec{{{\mathcal {X}}}}}\le C\mu ^{-1}(\Vert \textbf{f}\Vert _{0,q}+\Vert p\Vert _{{\mathcal {Q}}}+\Vert [p]\Vert _{1,q,\Upsilon }). \end{aligned}$$

(5.4)

Proof

We write $\textbf{w}=\textbf{w}_1+\textbf{w}_2$ with

$$\begin{aligned} \begin{aligned} \textbf{w}_1&=\mu ^{-1}{{\mathcal {A}}}\textbf{f},\\ \textbf{w}_2&=-\mu ^{-1}{{\mathcal {A}}}\nabla p. \end{aligned} \end{aligned}$$

By Theorem 4.1 there exist a vector function $\textbf{w}_{1,R}\in \textbf{H}^{2,q}$ and $\textbf{C}_1:=\textbf{C}_1(\textbf{f})\in \mathbb {R}^2$ such that $\textbf{w}_1$ has the decomposition

$$\begin{aligned} \textbf{w}_1=\textbf{C}_1{\mathbf \Phi }+\textbf{w}_{1,R}, \end{aligned}$$

(5.5)

and satisfies the inequality $\Vert \textbf{w}_{1,R}\Vert _{2,q}+|\textbf{C}_1|\le C\mu ^{-1}\Vert \textbf{f}\Vert _{0,q}$. Also, by Theorem 4.2 there exist $\textbf{C}_2\in \mathbb {R}^2$ and $\textbf{w}_{2,R}\in \textbf{H}^{2,q}$ such that $\textbf{w}_2$ has the decomposition

$$\begin{aligned} \textbf{w}_2=\textbf{K}+d\varvec{\psi }+\textbf{C}_2{\mathbf \Phi }+\textbf{w}_{2,R}, \end{aligned}$$

(5.6)

where $\textbf{K}=(0,-\mu _1^{-1}{{\mathcal {K}}}[p])^t$, $d=-\mu _1^{-1}\left[ p(1,0)\right]$, and satisfies the inequality

$$\begin{aligned} \Vert \textbf{w}_{2,R}\Vert _{2,q}+|\textbf{C}_2|+\Vert \textbf{K}\Vert _{2,q,\Omega _1}+|d|\le C\mu ^{-1}\Big (\sum _{j=1}^2\Vert \nabla p\Vert _{0,q,\Omega _j}+\Vert [p]\Vert _{1,q,\Upsilon }\Big ). \end{aligned}$$

Hence, by (5.5)–(5.6),

$$\begin{aligned} \textbf{w}=\textbf{K}+d\varvec{\psi }+(\textbf{C}_1+\textbf{C}_2){\mathbf \Phi }+(\textbf{w}_{1,R}+\textbf{w}_{2,R}). \end{aligned}$$

Since $\textbf{K}+\textbf{w}_{1,R}+\textbf{w}_{2,R}\in \varvec{{{\mathcal {P}}}}$ we have $\textbf{w}\in \varvec{{{\mathcal {X}}}}$. So

$$\begin{aligned} \begin{aligned} \Vert \textbf{w}\Vert _{\varvec{{{\mathcal {X}}}}}&=\Vert \textbf{K}+\textbf{w}_{1,R}+\textbf{w}_{2,R}\Vert _{\varvec{{{\mathcal {P}}}}}+|d|+|\textbf{C}_1+\textbf{C}_2|\\&\le C\mu ^{-1}\Big (\Vert \textbf{f}\Vert _{0,q}+\sum _{j=1}^2\Vert \nabla p\Vert _{0,q,\Omega _j}+\Vert [p]\Vert _{1,q,\Upsilon }\Big ). \end{aligned} \end{aligned}$$

Hence the required result has been shown. $\square$

Lemma 5.2

Let $g\in {\textrm{H}}^{1,q}$ be fixed. If $\textbf{v}\in \varvec{{{\mathcal {X}}}}$, then the solution p by (5.3b) is in the space ${{\mathcal {Q}}}$ and satisfies the inequality

$$\begin{aligned} \Vert p\Vert _{{\mathcal {Q}}}\le C(\Vert g\Vert _{1,q}+\Vert \textbf{v}\Vert _{\varvec{{{\mathcal {X}}}}}). \end{aligned}$$

(5.7)

Proof

If $\textbf{v}\in \varvec{{{\mathcal {X}}}}$ then $\textbf{v}=\textbf{w}+d^*\varvec{\psi }+\textbf{C}^*{\mathbf \Phi }$ for a function $\textbf{w}\in \varvec{{{\mathcal {P}}}}$, a scalar $d^*$ and $\textbf{C}^*=({{\mathcal {C}}}^*_1,{{\mathcal {C}}}^*_2)^t\in \mathbb {R}^2$. We know that $g-\text{ div }\,\textbf{w}$ and $B\text{ div }\,\varvec{\psi }$ are in the space ${{\mathcal {Q}}}$. Also, by Lemma 3.2, $B\text{ div }\,{\mathbf \Phi }_j\in {{\mathcal {Q}}}$ for $j=1,2$. Hence $g-\text{ div }\,\textbf{v}\in {{\mathcal {Q}}}$ and by Lemma 3.1 we have $p\in {{\mathcal {Q}}}$. Inequality (5.7) follows by

$$\begin{aligned} \begin{aligned} \Vert p\Vert _{{\mathcal {Q}}}&\le C(\Vert g\Vert _{{\mathcal {Q}}}+\Vert \textbf{w}\Vert _{\varvec{{{\mathcal {P}}}}}+|d^*|+|\textbf{C}^*|)\\&=C(\Vert g\Vert _{1,q}+\Vert \textbf{v}\Vert _{\varvec{{{\mathcal {X}}}}}). \end{aligned} \end{aligned}$$

$\square$

We shall show the mapping ${{\mathcal {M}}}$ is Lipshitz continuous and contractive on the space $\varvec{{{\mathcal {X}}}}$. If so, there exists a solution $\textbf{u}\in \varvec{{{\mathcal {X}}}}$ of the fixed point problem $\textbf{u}={{\mathcal {M}}}\textbf{u}$. Also, $\textbf{u}$ and $p=B(g-\text{ div }\,\textbf{u})$ satisfy problem (1.1).

Lemma 5.3

Suppose $\textbf{f}\in \textbf{L}^q$ and $g\in {\textrm{H}}^{1,q}$ are given. Then the mapping ${{\mathcal {M}}}$ is well-defined on $\varvec{{{\mathcal {X}}}}$. Also there is a constant $C=C(\Vert \textbf{f}\Vert _{0,q},\Vert g\Vert _{1,q})$ such that

$$\begin{aligned} \Vert {{\mathcal {M}}}\textbf{v}\Vert _{\varvec{{{\mathcal {X}}}}}\le C\mu ^{-1}(\Vert \textbf{v}\Vert _{\varvec{{{\mathcal {X}}}}}+1),\,\,\forall \textbf{v}\in \varvec{{{\mathcal {X}}}}. \end{aligned}$$

(5.8)

Proof

Let $\textbf{u}={{\mathcal {M}}}\textbf{v}$ for $\textbf{v}\in \varvec{{{\mathcal {X}}}}$. Then by Lemma 5.2, $p\in {{\mathcal {Q}}}$ and satisfies

$$\begin{aligned} \Vert p\Vert _{{{\mathcal {Q}}}}\le C(\Vert g\Vert _{1,q}+\Vert \textbf{v}\Vert _{\varvec{{{\mathcal {X}}}}}). \end{aligned}$$

(5.9)

Since $\partial _x[p]=[g-\text{ div }\,\textbf{v}]=-[\text{ div }\,\textbf{v}]$ and $[\text{ div }\,\textbf{v}]\in {\textrm{L}}^q(\Upsilon )$ for $q<4$, we have $[p]\in {\textrm{H}}^{1,q}(\Upsilon )$, which satisfies

$$\begin{aligned} \begin{aligned} \Vert [p]\Vert _{1,q,\Upsilon }&\le C(\Vert g\Vert _{{{\mathcal {Q}}}}+\Vert \textbf{v}\Vert _{\varvec{{{\mathcal {X}}}}})\\&\le C(\Vert g\Vert _{1,q}+\Vert \textbf{v}\Vert _{\varvec{{{\mathcal {X}}}}}). \end{aligned} \end{aligned}$$

(5.10)

By Lemma 5.1, $\textbf{u}\in \varvec{{{\mathcal {X}}}}$ and satisfies

$$\begin{aligned} \Vert \textbf{u}\Vert _{\varvec{{{\mathcal {X}}}}}\le C\mu ^{-1}(\Vert \textbf{f}\Vert _{0,q}+\Vert p\Vert _{{\mathcal {Q}}}+\Vert [p]\Vert _{1,q,\Upsilon }). \end{aligned}$$

(5.11)

By (5.9)–(5.11),

$$\begin{aligned} \Vert \textbf{u}\Vert _{\varvec{{{\mathcal {X}}}}}\le C\mu ^{-1}(\Vert \textbf{v}\Vert _{\varvec{{{\mathcal {X}}}}}+\Vert \textbf{f}\Vert _{0,q}+\Vert g\Vert _{1,q}). \end{aligned}$$

Thus (5.8) is shown. $\square$

Lemma 5.4

Suppose $\textbf{f}\in \textbf{L}^q$ and $g\in {\textrm{H}}^{1,q}$ are given. Then the mapping ${{\mathcal {M}}}$ is Lipschitz continuous on the space $\varvec{{{\mathcal {X}}}}$. Also there is a constant $C'$ such that

$$\begin{aligned} \Vert {{\mathcal {M}}}\textbf{v}-{{\mathcal {M}}}\textbf{v}^*\Vert _{\varvec{{{\mathcal {X}}}}}\le C'\mu ^{-1}\Vert \textbf{v}-\textbf{v}^*\Vert _{\varvec{{{\mathcal {X}}}}},\,\,\,\forall \textbf{v},\forall \textbf{v}^*\in \varvec{{{\mathcal {X}}}}. \end{aligned}$$

(5.12)

Proof

Let $\textbf{v}$ and $\textbf{v}^*$ be fixed in $\varvec{{{\mathcal {X}}}}$. Let $p=B(g-\text{ div }\,\textbf{v})$ and $p^*=B(g-\text{ div }\,\textbf{v}^*)$. Then

$$\begin{aligned} {{\mathcal {M}}}\textbf{v}-{{\mathcal {M}}}\textbf{v}^*=\mu ^{-1}{{\mathcal {A}}}\nabla (p^*-p). \end{aligned}$$

(5.13)

By Theorem 4.2,

$$\begin{aligned} \Vert {{\mathcal {A}}}\nabla (p^*-p)\Vert _{\varvec{{{\mathcal {X}}}}}\le C(\Vert p^*-p\Vert _{{\mathcal {Q}}}+\Vert [p^*-p]\Vert _{1,q,\Upsilon }). \end{aligned}$$

(5.14)

Since $p^*-p=-B\text{ div }\,(\textbf{v}^*-\textbf{v})$ and by Lemma 5.2,

$$\begin{aligned} \Vert p^*-p\Vert _{{\mathcal {Q}}}+\Vert [p^*-p]\Vert _{1,q,\Upsilon }\le C\Vert \textbf{v}^*-\textbf{v}\Vert _{\varvec{{{\mathcal {X}}}}}. \end{aligned}$$

(5.15)

So, by (5.14)–(5.15),

$$\begin{aligned} \Vert {{\mathcal {A}}}\nabla (p^*-p)\Vert _{\varvec{{{\mathcal {X}}}}}\le C'(\Vert \textbf{v}^*-\textbf{v}\Vert _{\varvec{{{\mathcal {X}}}}}) \end{aligned}$$

and using (5.13), (5.12) follows. $\square$

Let $\alpha =C'\mu ^{-1}$ where $C'$ is the constant defined from Lemma 5.4. Assuming that $\mu$ is sufficiently large, we have $\alpha <1$. Consider the sequence $\{\textbf{u}^n\}$ on the space $\varvec{{{\mathcal {X}}}}$ by $\textbf{u}^n:={{\mathcal {M}}}\textbf{u}^{n-1}$ for $n=1,2,\cdots$, with the initial value $\textbf{u}^0=0$. By (5.12) and for integer $n\ge 1$,

$$\begin{aligned} \begin{aligned} \Vert \textbf{u}^{n+1}-\textbf{u}^n\Vert _{\varvec{{{\mathcal {X}}}}}&\le \alpha \Vert \textbf{u}^n-\textbf{u}^{n-1}\Vert _{\varvec{{{\mathcal {X}}}}}\\&\le \alpha ^n\Vert \textbf{u}^1\Vert _{\varvec{{{\mathcal {X}}}}}. \end{aligned} \end{aligned}$$

For any integer $m>n>0$,

$$\begin{aligned} \Vert \textbf{u}^m-\textbf{u}^n\Vert _{\varvec{{{\mathcal {X}}}}}\le \frac{\alpha ^n}{1-\alpha }\Vert \textbf{u}^1\Vert _{\varvec{{{\mathcal {X}}}}}. \end{aligned}$$

By (5.8), $\Vert \textbf{u}^1\Vert _{\varvec{{{\mathcal {X}}}}}\le C\mu ^{-1}=C(C')^{-1}\alpha$. So

$$\begin{aligned} \Vert \textbf{u}^m-\textbf{u}^n\Vert _{\varvec{{{\mathcal {X}}}}}\le C(C')^{-1}\frac{\alpha ^{n+1}}{1-\alpha }. \end{aligned}$$

Hence $\{\textbf{u}^n\}$ is a Cauchy sequence in the space $\varvec{{{\mathcal {X}}}}$, so there exists $\textbf{u}\in \varvec{{{\mathcal {X}}}}$ such that $\lim _{n\rightarrow \infty }\textbf{u}^n=\textbf{u}$. Also, $\textbf{u}={{\mathcal {M}}}\textbf{u}$.

Let $d(x)=-\mu _1^{-1}[p(x,0)]$ for $p=B(g-\text{ div }\,\textbf{u})$. Let $\textbf{K}=(0,K)^t$ be defined by $K={{\mathcal {K}}}d$ in $\Omega _1$ and $K=0$ in $\Omega _2$. Then, by Lemma 5.3, there exist a constant vector $\textbf{C}\in \mathbb {R}^2$ and $\textbf{u}_R\in \textbf{H}^{2,q}(\Omega )$ such that $\textbf{u}=\textbf{K}+d(1)\varvec{\psi }+\textbf{C}{\mathbf \Phi }+\textbf{u}_R$. Furthermore, by (4.7) and Theorems 4.1–4.2,

$$\begin{aligned} \begin{aligned} \Vert \textbf{K}\Vert _{2,q,\Omega _2}+|d(1)|&\le C\mu ^{-1}\Vert [p]\Vert _{1,q,\Upsilon },\\ \Vert \textbf{u}_R\Vert _{2,q}+|\textbf{C}|&\le C\mu ^{-1}(\Vert \textbf{f}\Vert _{0,q}+\Vert p\Vert _{{\mathcal {Q}}}+\Vert [p]\Vert _{1,q,\Upsilon }). \end{aligned} \end{aligned}$$

(5.16)

With (1.8) the pressure solution is $p=p_K+p_C+p_S+p_R$ and, using Lemmas 3.1–3.2,

$$\begin{aligned} \begin{aligned} \Vert p_K\Vert _{1,q,\Omega _1}&\le C\Vert \textbf{K}\Vert _{2,q,\Omega _1},\\ \Vert p_C\Vert _{1,q}&\le C|d(1)|,\\ \Vert p_S\Vert _{{\mathcal {Q}}}&\le C|\textbf{C}|,\\ \Vert p_R\Vert _{{\mathcal {Q}}}&\le C(\Vert g\Vert _{{\mathcal {Q}}}+\Vert \textbf{u}_R\Vert _{2,q}) \end{aligned} \end{aligned}$$

(5.17)

and

$$\begin{aligned} \begin{aligned} \Vert [p]\Vert _{1,q,\Upsilon }&\le \Vert [p_K]\Vert _{1,q,\Upsilon }+\Vert [p_S]\Vert _{1,q,\Upsilon }+\Vert [p_R]\Vert _{1,q,\Upsilon }\\&\le C(\Vert \textbf{K}\Vert _{2,q,\Omega _1}+|\textbf{C}|+\Vert \textbf{u}_R\Vert _{2,q}+\Vert g\Vert _{{\mathcal {Q}}}). \end{aligned} \end{aligned}$$

(5.18)

Combining (5.16)–(5.18) and assuming that the viscous number $\mu$ is sufficiently large, we have (1.9). Hence we have shown Theorem 1.1.

Appendix

Lemma 6.1

If $\textbf{f}\in \textbf{H}^{-1}$ and $g\in {\textrm{L}}^2$ then there are unique weak solutions $\textbf{u}\in \textbf{H}^1_0$ and $p\in {\textrm{L}}^2$ of (1.1), satisfying the inequality

$$\begin{aligned} \Vert \textbf{u}\Vert _1+\Vert p\Vert _0+\Vert p\Vert _{0,\Gamma _\textrm{out}}\le C(\Vert \textbf{f}\Vert _{-1}+\Vert g\Vert _0), \end{aligned}$$

(6.1)

where C is a generic constant depending on $\Omega$.

Proof

The proof easily follows by a weak formulation on the pair space $\textbf{H}^1_0\times {\textrm{L}}^2$. Letting $(,\,)$ denoting the ${\textrm{L}}^2$ inner product we consider the bilinear forms

$$\begin{aligned} \begin{aligned} a(\textbf{u},\textbf{v})&=\mu (\nabla \textbf{u},\nabla \textbf{v})+\nu (\text{ div }\,\textbf{u},\text{ div }\,\textbf{v}),\\ b(p,\textbf{v})&=-(p,\text{ div }\,\textbf{v}),\\ c(p,\eta )&=(\textbf{U}\cdot \nabla p,\eta ). \end{aligned} \end{aligned}$$

(6.2)

The weak form of problem (1.1) is to find the solutions $\textbf{u}\in \textbf{H}^1_0$ and $p\in {\textrm{L}}^2$ satisfying

$$\begin{aligned} \begin{aligned} a(\textbf{u},\textbf{v})+b(p,\textbf{v})&=(\textbf{f},\textbf{v}),\quad \forall \textbf{v}\in \textbf{H}^1_0,\\ c(p,\eta )-b(\eta ,\textbf{u})&=(g,\eta ),\quad \forall \eta \in {\textrm{L}}^2. \end{aligned} \end{aligned}$$

(6.3)

More detailed proof can be found in [9, Lemma 2.8]. $\square$

We next show Theorem 4.1 by constructing the dual functions used in the stress intensity coefficients.

Lemma 6.2

Let $q'=q/(q-1)$ for $q\ge 2$. For $s>s_1$ there are nontrivial vector functions $\textbf{v}_j\in \textbf{H}^{2-s,q'}$, $j=1,2$, such that $\textbf{v}_j$ satisfies the boundary value problem

$$\begin{aligned} \begin{aligned} {\mathbb {L}}\textbf{v}_j&=0{} & {} \text{ in } \Omega ,\\ \textbf{v}_j&=0{} & {} \text{ on } \Gamma , \end{aligned} \end{aligned}$$

and is orthogonal to the image of $\textbf{H}^{s,q}\cap \textbf{H}^{1,q}_0$ by the Lamé operator ${\mathbb {L}}$ in the ${\textrm{L}}^2$ inner product.

Proof

We define the function $\textbf{v}_j$, $j=1,2$, by $\textbf{v}_j={\mathbf \Phi }_j^*+\textbf{z}_j$, where ${\mathbf \Phi }_j^*=\chi r^{-1/2}\varvec{\Theta }_j^*(\theta )$ with

$$\begin{aligned} \begin{aligned} \varvec{\Theta }_1^*(\theta )&=\begin{pmatrix} \nu _1\sin {\theta /2}-\nu _1\sin {5\theta /2}\\ -(8+5\nu _1)\cos {\theta /2}+\nu _1\cos {5\theta /2} \end{pmatrix},\\ \varvec{\Theta }_2^*(\theta )&=\begin{pmatrix} -(8+3\nu _1)\cos {\theta /2}-\nu _1\cos {5\theta /2}\\ \nu _1\sin {\theta /2}-\nu _1\sin {5\theta /2} \end{pmatrix}, \end{aligned} \end{aligned}$$

and $\textbf{z}_j$ is the solution of the problem

$$\begin{aligned} \begin{aligned} -{\mathbb {L}}\textbf{z}_j&={\mathbb {L}}{\mathbf \Phi }_j^*{} & {} \text{ in } \Omega ,\\ \textbf{z}_j&=0{} & {} \text{ on } \Gamma . \end{aligned} \end{aligned}$$

(6.4)

Since ${\mathbb {L}}(r^{-1/2}\varvec{\Theta }_j^*(\theta ))=0$, ${\mathbb {L}}{\mathbf \Phi }_j^*\in \textbf{L}^q$ and the solution $\textbf{z}_j$ of (6.4) becomes $\textbf{z}_j=\textbf{C}{\mathbf \Phi }+\textbf{z}_{j,R}$ where $\textbf{C}$ is a constant vector and $\textbf{z}_{j,R}\in \textbf{H}^{2,q}$. Since ${\mathbf \Phi }_j\in \textbf{H}^{t,q}$ for $t<s_1$, $\textbf{z}_j\in \textbf{H}^{t,q}$. Also, since ${\mathbf \Phi }_j^*\in \textbf{H}^{2-s,q'}$ we have $\textbf{v}_j\in \textbf{H}^{2-s,q'}$. The vector function $\textbf{v}_j$ satisfies ${\mathbb {L}}\textbf{v}_j=0$ in $\Omega$ and $\textbf{v}_j|_\Gamma =0$. Therefore, for any $\textbf{w}\in \textbf{H}^{s,q}\cap \textbf{H}^{1,q}_0$ for $s>s_1$,

$$\begin{aligned} \begin{aligned} \int \limits _\Omega {\mathbb {L}}\textbf{w}\cdot \textbf{v}_j{\textrm{d}}\textbf{x}&=\int \limits _\Omega \textbf{w}\cdot {\mathbb {L}}\textbf{v}_j{\textrm{d}}\textbf{x}+\int \limits _\Gamma \frac{\partial \textbf{w}}{\partial \textbf{n}}\cdot \textbf{v}_j-\textbf{w}\cdot \frac{\partial \textbf{v}_j}{\partial \textbf{n}} ds\\&\hspace{0.5cm}+\nu _1\int \limits _\Gamma (\text{ div }\,\textbf{w})\textbf{n}\cdot \textbf{v}_j-(\text{ div }\,\textbf{v}_j)\textbf{n}\cdot \textbf{w}ds\\&=0. \end{aligned} \end{aligned}$$

Hence the required result follows. $\square$

To show (4.5), if we write the solution $\textbf{u}$ of (4.2) by $\textbf{u}=\textbf{C}{\mathbf \Phi }+\textbf{u}_R$ where $\textbf{C}=({{\mathcal {C}}}_1,{{\mathcal {C}}}_2)\in \mathbb {R}^2$ and $\textbf{u}_R\in \textbf{H}^{s,q}$, then $\textbf{u}_R=\textbf{g}$ on $\Gamma$ and

$$\begin{aligned} \begin{aligned} \int \limits _\Omega {\mathbb {L}}\textbf{u}_R\cdot \textbf{v}_j{\textrm{d}}\textbf{x}&=-\int \limits _\Gamma \textbf{g}\cdot \Big (\frac{\partial \textbf{v}_j}{\partial \textbf{n}}+\nu _1(\text{ div }\,\textbf{v}_j)\textbf{n}\Big )ds, \end{aligned} \end{aligned}$$

so

$$\begin{aligned} \begin{aligned} \int \limits _\Omega {\mathbb {L}}(\textbf{C}{\mathbf \Phi })\cdot \textbf{v}_j{\textrm{d}}\textbf{x}&=-\int \limits _\Omega ({\textbf{h}}+{\mathbb {L}}\textbf{u}_R)\cdot \textbf{v}_j{\textrm{d}}\textbf{x}\\&=-\int \limits _\Omega {\textbf{h}}\cdot \textbf{v}_j{\textrm{d}}\textbf{x}+\int \limits _\Gamma \textbf{g}\cdot \Big (\frac{\partial \textbf{v}_j}{\partial \textbf{n}}+\nu _1(\text{ div }\,\textbf{v}_j)\textbf{n}\Big )ds. \end{aligned} \end{aligned}$$

Then we have a linear system for ${{\mathcal {C}}}_1$ and ${{\mathcal {C}}}_2$:

$$\begin{aligned} \begin{aligned} a_{11}{{\mathcal {C}}}_1+a_{12}{{\mathcal {C}}}_2&=-\int \limits _\Omega {\textbf{h}}\cdot \textbf{v}_1{\textrm{d}}\textbf{x}+\int \limits _\Gamma \textbf{g}\cdot \Big (\frac{\partial \textbf{v}_1}{\partial \textbf{n}}+\nu _1(\text{ div }\,\textbf{v}_1)\textbf{n}\Big )ds,\\ a_{21}{{\mathcal {C}}}_1+a_{22}{{\mathcal {C}}}_2&=-\int \limits _\Omega {\textbf{h}}\cdot \textbf{v}_2{\textrm{d}}\textbf{x}+\int \limits _\Gamma \textbf{g}\cdot \Big (\frac{\partial \textbf{v}_2}{\partial \textbf{n}}+\nu _1(\text{ div }\,\textbf{v}_2)\textbf{n}\Big )ds, \end{aligned} \end{aligned}$$

(6.5)

where $a_{ij}=\int \limits _\Omega {\mathbb {L}}{\mathbf \Phi }_j\cdot \textbf{v}_i{\textrm{d}}\textbf{x}$. On the other hand, since $\textbf{v}_i={\mathbf \Phi }_i^*+\textbf{z}_i$,

$$\begin{aligned} \begin{aligned} a_{ij}&=\int \limits _\Omega {\mathbb {L}}{\mathbf \Phi }_j\cdot {\mathbf \Phi }_i^*+{\mathbf \Phi }_j\cdot {\mathbb {L}}\textbf{z}_i{\textrm{d}}\textbf{x}\\&=\int \limits _\Omega {\mathbb {L}}{\mathbf \Phi }_j\cdot {\mathbf \Phi }_i^*-{\mathbf \Phi }_j\cdot {\mathbb {L}}{\mathbf \Phi }_i^*{\textrm{d}}\textbf{x}. \end{aligned} \end{aligned}$$

Set $\Omega _\delta =\Omega \cap \{r>\delta \}$ for $\delta <r_0\ll 1$. By integration by parts,

$$\begin{aligned} \int \limits _{\Omega _\delta }{\mathbb {L}}{\mathbf \Phi }_j\cdot {\mathbf \Phi }_i^*-{\mathbf \Phi }_j\cdot {\mathbb {L}}{\mathbf \Phi }_i^*{\textrm{d}}\textbf{x}=\int \limits _{\partial \Omega _\delta }E_1(r,\theta )\text{ d }s+\nu _1\int \limits _{\partial \Omega _\delta }E_2(r,\theta )\text{ d }s, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} E_1(r,\theta )&=\frac{\partial {\mathbf \Phi }_j}{\partial \textbf{n}}\cdot {\mathbf \Phi }_i^*-{\mathbf \Phi }_j\cdot \frac{\partial {\mathbf \Phi }_i^*}{\partial \textbf{n}},\\ E_2(r,\theta )&=(\text{ div }\,{\mathbf \Phi }_j)\textbf{n}\cdot {\mathbf \Phi }_i^*-(\text{ div }\,{\mathbf \Phi }_i^*)\textbf{n}\cdot {\mathbf \Phi }_j, \end{aligned} \end{aligned}$$

and $\textbf{n}$ is the outward normal unit vector to the boundary $\partial \Omega _\delta$. Since $\chi =0$ for $r>2r_0$, we have

$$\begin{aligned} \begin{aligned} \int \limits _{\partial \Omega _\delta }E_1(r,\theta )\text{ d }s&=\int \limits _{2r_0}^\delta E_1(r,-\pi )dr+\int \limits _{-\pi }^\pi E_1(\delta ,\theta )\delta d\theta +\int \limits _\delta ^{2r_0} E_1(r,\pi )dr\\&=-\int \limits _{-\pi }^\pi \varvec{\Theta }_j\cdot \varvec{\Theta }_i^*d\theta . \end{aligned} \end{aligned}$$

Likewise,

$$\begin{aligned} \int \limits _{\partial \Omega _\delta }E_2(r,\theta )\text{ d }s=-\int \limits _{-\pi }^\pi E_{21}(\theta )+E_{22}(\theta )-E_{23}(\theta )d\theta , \end{aligned}$$

where for $\textbf{e}_1=(\cos \theta ,\sin \theta )^t$ and $\textbf{e}_2=(-\sin \theta ,\cos \theta )^t$,

$$\begin{aligned} \begin{aligned} E_{21}(\theta )&=(\textbf{e}_1\cdot \varvec{\Theta }_j)(\textbf{e}_1\cdot \varvec{\Theta }_i^*),\\ E_{22}(\theta )&=(\textbf{e}_2\cdot \varvec{\Theta }_j')(\textbf{e}_1\cdot \varvec{\Theta }_i^*),\\ E_{23}(\theta )&=(\textbf{e}_1\cdot \varvec{\Theta }_j)(\textbf{e}_2\cdot (\varvec{\Theta }_i^*)'). \end{aligned} \end{aligned}$$

Since $\Omega =\lim _{\delta \rightarrow 0}\Omega _\delta$,

$$\begin{aligned} \begin{aligned} a_{ij}&=\lim _{\delta \rightarrow 0}\int \limits _{\Omega _\delta }{\mathbb {L}}{\mathbf \Phi }_j\cdot {\mathbf \Phi }_i^*-{\mathbf \Phi }_j\cdot {\mathbb {L}}{\mathbf \Phi }_i^*{\textrm{d}}\textbf{x}\\&=-\int \limits _{-\pi }^\pi \varvec{\Theta }_j\cdot \varvec{\Theta }_i^*+\nu _1(E_{21}+E_{22}-E_{23})d\theta . \end{aligned} \end{aligned}$$

Therefore, $a_{11}=a_{22}=-32(\nu _1+2)(\nu _1+1)\pi$ and $a_{12}=a_{21}=0$. Hence, by (6.5), (4.5) follows. $\square$