1 Introduction

It is accepted that the equation of heat conduction in classical coupled thermoelasticity theory proposed by Biot [1] is based on Fourier’s law. Although Biot’s theory overcomes the shortcoming of the uncoupled thermoelastic theory, it still has a deficiency that thermal waves propagate instantaneously in this theory due to relying on the classical Fourier’s law. Since it violates the causality principle, it is not well accepted in view of physical phenomena. To overcome this drawback, hyperbolic type of energy equations were needed. The first such generalization is due to Lord and Shulman (LS) [2], who replaced classical Fourier’s law with a modified law of heat conduction involving the heat flux as well as its time derivative. The second modification to the classical coupled thermoelasticity theory using the concept of Green and Laws [3] was introduced by Green and Lindsay (GL) [4]. The GL theory incorporates temperature-rate terms among the constitutive relations; therefore, this theory is known as the temperature-rate-dependent thermoelasticity theory. Later on, by introducing thermal displacement as a new field variable, Green and Naghdi [5,6,7] proposed three alternative theories, GN-I, GN-II, and GN-III, respectively, the first of which is a linearized version of Biot’s theory.

Alternatively, Chen and Gurtin [8] and Chen et al. [9, 10] received considerable attention for their modification to heat conduction theory that involves two temperatures, the thermodynamic temperature \(\theta \) and the conductive temperature \(\phi \). They also demonstrated that the distinction between these two temperatures in a time independent situation is proportional to the heat supply and these two temperatures are identical when an external heat source is absent. They proposed a relation between these two temperatures and termed it as a two-temperature relation. Later on, taking into account this two-temperature relation, Youssef [11] developed the two-temperature generalized thermoelastic model in view of the LS model. Since the propagation speed of thermal waves is infinite in this theory, consequently Youssef and El-Bary [12] extended this theory and formulated the hyperbolic two-temperature thermoelasticity theory. In the context of two-temperature GL (TTGL) theory, Youssef [11] also stated the complete system of equations. This theory is also called the temperature-rate-dependent two-temperature theory. Further, using the fundamental laws of thermodynamics, Shivay and Mukhopadhyay [13] formulated this two-temperature GL theory. In this modified temperature-rate-dependent two-temperature (MTRDTT) thermoelastic model, the two-temperature relation is modified which contains temperature-rate terms associated with the thermodynamic and conductive temperatures.

Warren and chen [14] examined the propagation of waves for the thermoelasticity theory with two-temperature. Puri and Jordan [15] studied the propagation of harmonic plane waves under the two-temperature theory. In view of the two-temperature LS theory [11], Youssef and Al-Lehaibi [16] and further Kumar and Mukhopadhyay [17] discussed a one-dimensional thermoelastic problem and the propagation of plane harmonic waves, respectively. The growth and uniqueness of solutions under the two-temperature LS and GL models were investigated by Magana and Quintanilla [18]. Also, Kumar et al. [19, 20] discussed thermoelastic interactions and plane wave propagation under the TTGL model. Under two-temperature LS and GL theories, the spatial behavior of the solutions was investigated by Miranville and Quintanilla [21]. Variational and reciprocal principles under the MTRDTT model were obtained by Jangid and Mukhopadhyay [22]. Kumar et al. [23] analyzed thermoelastic interactions in the hyperbolic two-temperature thermoelasticity theory. Further, the uniqueness and exponential instability results in the MTRDTT theory were obtained by Fernández and Quintanilla [24]. Recently, thermomechanical interactions due to mode-I crack under this MTRDTT model were investigated by Shivay and Mukhopadhyay [25].

The goal of this current study is to use the MTRDTT thermoelasticity theory to investigate thermoelastic interactions inside an isotropic and homogeneous medium with a continuous line heat source. It is worth recalling that thermoelastic interactions caused by a continuous line heat source were investigated by Sherief and Anwar [26] in the LS model. Chandrasekharaiah and Murthy [27] examined thermoelastic interactions resulting from a line heat source in the GL model. Ezzat [28] also used thermoelasticity theory with two relaxation times to study thermoelastic interactions induced by a line heat source for cylindrical regions. It is also worth mentioning some contributions to the study of thermoelastic interactions resulting from a line heat source (see Refs. [29,30,31]) and one can find that there are significant dissimilarities in the predictions by different models regarding the effects of heat source.

In view of the above, the present work is motivated to discuss thermoelastic interactions under the MTRDTT theory inside an isotropic and homogeneous medium with a continuous line heat source. We study our problem with the unified form of two-temperature relation to compare the results for displacement, temperatures and stresses under the MTRDTT model with the corresponding results of the TTGL model. We apply the Laplace transform and Hankel transform techniques to solve the problem. Further, through the use of short-time approximation and inverse Laplace transform, the analytical solutions in the space-time domain are obtained. The obtained results are further illustrated numerically and distributions of field variables are depicted in various graphs. Some important observations are highlighted.

2 The mathematical model

We consider an isotropic and homogeneous thermoelastic body assuming that there are no body forces in the medium.

Thus, the governing equations in the context of MTRDTT thermoelasticity theory [13] can be written as follows:

The equation of motion:

$$\begin{aligned} \sigma _{ij,j}=\rho \ddot{u}_{i}. \end{aligned}$$
(1)

The stress–strain temperature relation:

$$\begin{aligned} \sigma _{ij}=\lambda e_{kk}\delta _{ij}+2\mu e_{ij}-\gamma \delta _{ij}\left( 1+\tau _{1}\frac{\partial }{\partial t}\right) \theta . \end{aligned}$$
(2)

The strain–displacement relation:

$$\begin{aligned} e_{ij}=\frac{1}{2}\left( u_{i,j}+u_{j,i}\right) . \end{aligned}$$
(3)

The heat conduction equation including a heat source is considered as:

$$\begin{aligned} K\phi _{,ii}=\rho C_{E}\left( \frac{\partial }{\partial t}+\tau _{2}\frac{\partial ^{2}}{\partial t^{2}}\right) \theta +\gamma \theta _{0}\frac{\partial e}{\partial t}-\rho R. \end{aligned}$$
(4)

Here, we will consider a line heat source which is as follows:

$$\begin{aligned} R=\frac{1}{2\pi r}R_{0}\delta (r)H(t), \end{aligned}$$
(5)

where \(R_{0}\) is a constant, H(t) is the Heaviside unit step function, and \(\delta (r)\) represents the Dirac delta function.

The two-temperature relation is expressed as follows:

$$\begin{aligned} \left( 1+\tau _{1}p\frac{\partial }{\partial t}\right) \phi -\left( 1+\tau _{1}p\frac{\partial }{\partial t}\right) \theta =a\phi _{,ii}, \end{aligned}$$
(6)

where a represents the two-temperature parameter and p is a dimensionless parameter that is adopted to express the unified two-temperature relation. These parameters satisfy following under GL model, TTGL model and MTRDTT model as follows:

  • GL model: \(p=a=0\)

  • TTGL model: \(p=0,\) \(a\ne 0\)

  • MTRDTT model: \(p\ne 0,\) \(a\ne 0.\)

In the above equations, \(\sigma _{ij}\) denotes the components of stress tensor, \(\lambda \) and \(\mu \) represent Lam\(\acute{\text {e}}\) constants, u is the displacement, \(\rho \) is the mass density, \(e_{ij}\) represents the components of strain tensor, \(\gamma =(3\lambda +2\mu )\alpha ,\) where \(\alpha \) denotes coefficient of linear thermal expansion. \(\tau _{1}\) and \(\tau _{2}\) are the thermal relaxation parameters, K is the thermal conductivity of the material, \(e=e_{ii}\) is the dilatation, \(C_{E}\) represents specific heat at constant strain. \(\theta _{0}\) is the reference temperature, \(\theta \) and \(\phi \) are the thermodynamic and conductive temperatures, respectively, measured from \(\theta _{0}\).

3 Formulation of the problem

In this work, an unbounded thermoelastic solid containing a line heat source is considered. We employ a cylindrical coordinate system \((r,\varphi ,z)\) throughout this paper. The heat source is assumed to be located along the z-axis. We consider that thermoelastic interactions are symmetrical about an axis therefore the displacement and temperature vectors will be dependent only on the space variables r and time t having only a radial component. There are two components of stress tensor, namely \(\sigma _{rr}\) and \(\sigma _{\varphi \varphi }\), where \(\sigma _{rr}\) is in radial direction and \(\sigma _{\varphi \varphi }\) denotes the circumferential stress in transverse direction. Therefore, the strain tensor has nonzero components as

$$\begin{aligned} e_{rr}=\frac{\partial u}{\partial r},e_{\varphi \varphi }=\frac{u}{r}, \end{aligned}$$
(7)

so that the dilatation is given by

$$\begin{aligned} e=e_{ii}=e_{rr}+e_{\varphi \varphi }=\frac{\partial u}{\partial r}+\frac{u}{r}. \end{aligned}$$
(8)

Now, the cylindrical form of equation of motion (1) is as follows:

$$\begin{aligned} \frac{\partial \sigma _{rr}}{\partial r}+\frac{\sigma _{rr}-\sigma _{\varphi \varphi }}{r}=\rho \frac{\partial ^{2}u}{\partial t^{2}}. \end{aligned}$$
(9)

Using Eq. (8), radial and circumferential stress components will take the forms

$$\begin{aligned} \sigma _{rr}&=\lambda \frac{u}{r}+(\lambda +2\mu )\frac{\partial u}{\partial r}-\gamma \left( 1+\tau _{1}\frac{\partial }{\partial t}\right) \theta , \end{aligned}$$
(10)
$$\begin{aligned} \sigma _{\varphi \varphi }&=\lambda \frac{\partial u}{\partial r}+(\lambda +2\mu )\frac{u}{r}-\gamma \left( 1+\tau _{1}\frac{\partial }{\partial t}\right) \theta . \end{aligned}$$
(11)

Substituting Eqs. (10) and (11) in (9), we obtain

$$\begin{aligned} \rho \frac{\partial ^{2}u}{\partial t^{2}}=(\lambda +2\mu )\left( \frac{\partial ^{2}}{\partial r^{2}}+\frac{1}{r}\frac{\partial }{\partial r}-\frac{1}{r^{2}}\right) u-\gamma \left( 1+\tau _{1}\frac{\partial }{\partial t}\right) \frac{\partial \theta }{\partial r}. \end{aligned}$$
(12)

Further, by combining Eqs. (4), (5) and (8), we get

$$\begin{aligned} K\nabla ^{2}\phi =\rho C_{E}\left( \frac{\partial }{\partial t}+\tau _{2}\frac{\partial ^{2}}{\partial t^{2}}\right) \theta +\gamma \theta _{0}\frac{\partial }{\partial t}\left( \frac{\partial u}{\partial r}+\frac{u}{r}\right) -\frac{\rho R_{0}}{2\pi r}\delta (r)H(t), \end{aligned}$$
(13)

where \(\nabla ^{2}=\frac{\partial ^{2}}{\partial r^{2}}+\frac{1}{r}\frac{\partial }{\partial r}.\)

Now, we will use the following dimensionless transformations for the sake of simplicity:

$$\begin{aligned} (t',\tau _{1}',\tau _{2}')&=c_{0}^{2}\eta (t,\tau _{1},\tau _{2}),(r',u')=c_{0}\eta (r,u),(\theta ',\phi ')=\frac{1}{\theta _{0}}(\theta ,\phi ),\\ (\sigma _{rr}',\sigma _{\varphi \varphi }'&)=\frac{1}{(\lambda +2\mu )}(\sigma _{rr},\sigma _{\varphi \varphi }),R'=\frac{\gamma R}{Kc_{0}^{4}\eta ^{2}}, \end{aligned}$$

where

$$\begin{aligned} c_{0}^{2}=\frac{\lambda +2\mu }{\rho }\quad {\text{ and }}\quad \eta =\frac{\rho C_{E}}{K}. \end{aligned}$$

Using the non-dimensional parameters and variables listed above, Eqs. (6) and (10)–(13) are reduced as follows (by omitting the primes for the sake of simplicity):

$$\begin{aligned} \frac{\partial ^{2}u}{\partial t^{2}}&=\left( \frac{\partial ^{2}}{\partial r^{2}}+\frac{1}{r}\frac{\partial }{\partial r}-\frac{1}{r^{2}}\right) u-a_{1}\left( 1+\tau _{1}\frac{\partial }{\partial t}\right) \frac{\partial \theta }{\partial r}, \end{aligned}$$
(14)
$$\begin{aligned} \nabla ^{2}\phi&=\left( \frac{\partial }{\partial t}+\tau _{2}\frac{\partial ^{2}}{\partial t^{2}}\right) \theta +a_{2}\frac{\partial }{\partial t}\left( \frac{\partial u}{\partial r}+\frac{u}{r}\right) -\frac{R_{0}}{2\pi ra_{1}}\delta (r)H(t), \end{aligned}$$
(15)
$$\begin{aligned} \sigma _{rr}&=\frac{\partial u}{\partial r}+\lambda _{1}\frac{u}{r}-a_{1}\left( 1+\tau _{1}\frac{\partial }{\partial t}\right) \theta , \end{aligned}$$
(16)
$$\begin{aligned} \sigma _{\varphi \varphi }&=\frac{u}{r}+\lambda _{1}\frac{\partial u}{\partial r}-a_{1}\left( 1+\tau _{1}\frac{\partial }{\partial t}\right) \theta , \end{aligned}$$
(17)
$$\begin{aligned}&\left( 1+\tau _{1}p\frac{\partial }{\partial t}\right) \phi -\left( 1+\tau _{1}p\frac{\partial }{\partial t}\right) \theta =a_{3}\nabla ^{2}\phi , \end{aligned}$$
(18)

where

$$\begin{aligned} a_{1}=\frac{\gamma \theta _{0}}{\lambda +2\mu },a_{2}=\frac{\gamma }{\rho C_{E}},a_{3}=ac_{0}^{2}\eta ^{2},\lambda _{1}=\frac{\lambda }{\lambda +2\mu }. \end{aligned}$$

4 The governing equations in the Laplace transform domain

In the present context, the homogeneous initial conditions are considered for all field variables assuming that the body is initially at rest in an unstressed and undeformed state at a constant temperature.

To get the solution, we use the Laplace transform defined by

$$\begin{aligned} \overline{f}(r,s)=\int \limits _{0}^{\infty }f(r,t)e^{-st}dt,{\text {Re}}(s)>0 \end{aligned}$$

to Eqs. (14)–(18). Therefore, we obtain

$$\begin{aligned} s^{2}\overline{u}&=\left( \frac{\partial ^{2}}{\partial r^{2}}+\frac{1}{r}\frac{\partial }{\partial r}-\frac{1}{r^{2}}\right) \overline{u}-a_{1}\left( 1+\tau _{1}s\right) \frac{\partial \overline{\theta }}{\partial r}, \end{aligned}$$
(19)
$$\begin{aligned} \nabla ^{2}\overline{\phi }&=\left( s+\tau _{2}s^{2}\right) \overline{\theta }+a_{2}s\left( \frac{\partial \overline{u}}{\partial r}+\frac{\overline{u}}{r}\right) -\frac{A_{1}\delta (r)}{rs}, \end{aligned}$$
(20)
$$\begin{aligned} \overline{\sigma }_{rr}&=\frac{\partial \overline{u}}{\partial r}+\lambda _{1}\frac{\overline{u}}{r}-a_{1}\left( 1+\tau _{1}s\right) \overline{\theta }, \end{aligned}$$
(21)
$$\begin{aligned} \overline{\sigma }_{\varphi \varphi }&=\frac{\overline{u}}{r}+\lambda _{1}\frac{\partial \overline{u}}{\partial r}-a_{1}\left( 1+\tau _{1}s\right) \overline{\theta }, \end{aligned}$$
(22)
$$\begin{aligned} \overline{\theta }&=\overline{\phi }-\left( \frac{a_{3}}{1+\tau _{1}ps}\right) \nabla ^{2}\overline{\phi }, \end{aligned}$$
(23)

where \(A_{1}=\frac{R_{0}}{2\pi a_{1}}.\)

Eliminating \(\overline{\theta }\) between Eqs. (19) and (23), we get

$$\begin{aligned} \left( \frac{\partial ^{2}}{\partial r^{2}}+\frac{1}{r}\frac{\partial }{\partial r}-\frac{1}{r^{2}}\right) \overline{u}-a_{1}\left( 1+\tau _{1}s\right) \frac{\partial }{\partial r}\left[ \overline{\phi }-\frac{a_{3}}{1+\tau _{1}ps}\left( \frac{\partial ^{2}}{\partial r^{2}}+\frac{1}{r}\frac{\partial }{\partial r}\right) \overline{\phi }\right] =s^{2}\overline{u}. \end{aligned}$$
(24)

Further, by combining Eq. (23) and Eq. (20), we obtain

$$\begin{aligned} \left[ 1+\frac{a_{3}}{1+\tau _{1}ps}\left( s+\tau _{2}s^{2}\right) \right] \left( \frac{\partial ^{2}}{\partial r^{2}}+\frac{1}{r}\frac{\partial }{\partial r}\right) \overline{\phi }=\left( s+\tau _{2}s^{2}\right) \overline{\phi }+a_{2}s\left( \frac{\partial \overline{u}}{\partial r}+\frac{\overline{u}}{r}\right) -\frac{A_{1}\delta (r)}{rs}. \end{aligned}$$
(25)

We consider that \(D\equiv \frac{\partial }{\partial r}\) and \(D^{*}\equiv \frac{\partial }{\partial r}+\frac{1}{r}\) are two operators.

Therefore, decoupling of Eqs. (24) and (25), we arrive at

$$\begin{aligned} \left( DD^{*}-m_{1}^{2}\right) \left( DD^{*}-m_{2}^{2}\right) \overline{u}&=\left[ A_{2}\left( DD^{*}\right) -A_{3}\right] \frac{\partial }{\partial r}\left( \frac{\delta (r)}{r}\right) , \end{aligned}$$
(26)
$$\begin{aligned} \left( D^{*}D-m_{1}^{2}\right) \left( D^{*}D-m_{2}^{2}\right) \overline{\phi }&=\left[ s-\frac{1}{s}\left( D^{*}D\right) \right] \frac{A_{1}\delta (r)}{r}. \end{aligned}$$
(27)

Here, \(A_{2}=\frac{a_{1}a_{3}(1+\tau _{1}s)A_{1}}{s(1+\tau _{1}ps)}\) and \(A_{3}=\frac{A_{1}a_{1}\left( 1+\tau _{1}s\right) }{s}\). Furthermore, \(m_{1}^{2}\) and \(m_{2}^{2}\) are the roots of the equation

$$\begin{aligned} \left( 1+b_{4}s+b_{5}s^{2}\right) m^{4}-\left( \epsilon s+b_{1}s^{2}+b_{2}s^{3}+b_{3}s^{4}\right) m^{2}+\left( s^{3}+b_{6}s^{4}+b_{7}s^{5}\right) =0, \end{aligned}$$
(28)

where we use the notations

$$\begin{aligned} b_{1}&=\beta +1+\tau _{1}p\epsilon ,\\ b_{2}&=a_{3}+\tau _{1}p(\beta +1),\\ b_{3}&=a_{3}\tau _{2},\\ b_{4}&=\tau _{1}p+a_{3}\epsilon ,\\ b_{5}&=a_{3}\beta ,\\ b_{6}&=\tau _{1}p+\tau _{2},\\ b_{7}&=\tau _{1}\tau _{2}p,\\ \beta&=\tau _{2}+a_{1}a_{2}\tau _{1},\\ \epsilon&=1+a_{1}a_{2}. \end{aligned}$$

The solutions to Eqs. (26) and (27) that are bounded at infinity can be taken as follows:

$$\begin{aligned} \overline{u}(r,s)&=\frac{1}{m_{1}^{2}-m_{2}^{2}}\sum _{i=1}^{i=2}(-1)^{i-1}m_{i} (A_{2}m_{i}^{2}-A_{3})K_{1}(m_{i}r), \end{aligned}$$
(29)
$$\begin{aligned} \overline{\phi }(r,s)&=\frac{A_{1}}{m_{1}^{2}-m_{2}^{2}}\sum _{i=1}^{i=2}(-1)^{i-1} \frac{(m_{i}^{2}-s^{2})}{s}K_{0}(m_{i}r), \end{aligned}$$
(30)

where, \(K_{0}(m_{i}r)\) and \(K_{1}(m_{i}r)\) denote the modified Bessel function of second kind having order zero and order one, respectively.

To find the solutions for other field variables, we will use the following identities:

$$\begin{aligned} \nabla ^{2}K_{0}(ar)=a^{2}K_{0}(ar),\frac{\partial }{\partial r}K_{1}(ar)=-aK_{0}(ar)-\frac{K_{1}(ar)}{r}. \end{aligned}$$
(31)

Therefore, combining Eqs. (30) and (23), we get

$$\begin{aligned} \overline{\theta }(r,s)=\frac{A_{1}}{m_{1}^{2}-m_{2}^{2}}\sum _{i=1}^{i=2}(-1)^{i-1}\frac{(m_{i}^{2} -s^{2})}{s}\left( 1-\frac{a_{3}m_{i}^{2}}{1+\tau _{1}ps}\right) K_{0}(m_{i}r). \end{aligned}$$
(32)

Further, making use of Eqs. (31) and (32), Eqs. (21) and (22) yield the following equations:

$$\begin{aligned}&\overline{\sigma }_{rr}= \; \frac{1}{m_{1}^{2}-m_{2}^{2}}\sum _{i=1}^{i=2}(-1)^{i-1}\nonumber \\&\qquad \left\{ m_{i}^{2}(A_{3}-A_{2}m_{i}^{2})+a_{1}\left( 1+\tau _{1}s\right) A_{1}\frac{(s^{2}-m_{i}^{2})}{s}\left( 1-\frac{a_{3}m_{i}^{2}}{1+\tau _{1}ps}\right) \right\} K_{0}(m_{i}r)\nonumber \\&\quad \qquad + \frac{1}{m_{1}^{2}-m_{2}^{2}}\sum _{i=1}^{i=2}(-1)^{i-1}\frac{(1-\lambda _{1})}{r}m_{i}(A_{3} -A_{2}m_{i}^{2})K_{1}(m_{i}r), \end{aligned}$$
(33)
$$\begin{aligned}&\overline{\sigma }_{\varphi \varphi }= \; \frac{1}{m_{1}^{2}-m_{2}^{2}}\sum _{i=1}^{i=2}(-1)^{i-1}\nonumber \\&\qquad \left\{ \lambda _{1}m_{i}^{2}(A_{3}-A_{2}m_{i}^{2})+a_{1}\left( 1+\tau _{1}s\right) A_{1}\frac{(s^{2} -m_{i}^{2})}{s}\left( 1-\frac{a_{3}m_{i}^{2}}{1+\tau _{1}ps}\right) \right\} K_{0}(m_{i}r)\nonumber \\&\quad \qquad + \frac{1}{m_{1}^{2}-m_{2}^{2}}\sum _{i=1}^{i=2}(-1)^{i-1}\frac{(\lambda _{1}-1)}{r}m_{i}(A_{3} -A_{2}m_{i}^{2})K_{1}(m_{i}r). \end{aligned}$$
(34)

The system of Eqs. (29)–(30) and (32)–(34) represents the solutions for displacement, temperatures and stresses, respectively, in the Laplace transform domain.

5 Short-time approximation

For the purpose of obtaining the solutions for the field variables in the space-time domain (r, t), we need to apply the inverse Laplace transform. Since the above equations involve the complicated terms on the Laplace transform parameter s, for this reason, it is a challenging task to invert Laplace transform analytically for arbitrary t and to find a closed form analytical solution. Furthermore, the present study is more applicable for the problems concerning short time duration. In view of this, we will take into account the case of short-time approximation and find the solution for large s (small value of t). Therefore we neglect higher power terms of 1/s.

Thus, the approximated roots \(m_{1}\) and \(m_{2}\) of Eq. (28) in the contexts of the MTRDTT and TTGL theories are obtained as

$$\begin{aligned} \left. \begin{array}{c} \begin{array}{cc} m_{1}\approx &{} a_{10}s+a_{11}+\frac{a_{12}}{s},\\ m_{2}\approx &{} a_{20}(s)^{1/2}+\frac{a_{21}}{(s)^{1/2}}+\frac{a_{22}}{(s)^{3/2}}, \end{array}\end{array}\right\} \quad {\hbox {for the MTRDTT model}} \end{aligned}$$
(35)
$$\begin{aligned} \left. \begin{array}{c} \begin{array}{cc} m_{1}\approx &{} b_{10}s+b_{11}+\frac{b_{12}}{s},\\ m_{2}\approx &{} b_{20}+\frac{b_{21}}{s^{2}}, \end{array}\end{array}\right\} \quad {\hbox {for the TTGL model}} \end{aligned}$$
(36)

where

$$\begin{aligned} a_{10}=&\; \sqrt{\frac{\tau _{2}}{\beta }},a_{11}=\sqrt{\frac{\tau _{2}}{\beta }} \left\{ \frac{\beta (a_{3}+\tau _{1})-\tau _{2}(\tau _{1}+a_{3}\epsilon )}{2\tau _{2}a_{3}\beta }\right\} ,\\ a_{12}=&\; \sqrt{\frac{\tau _{2}}{\beta }}\left[ \frac{\tau _{1}^{2}\left\{ \beta (-1+4\beta )-3\tau _{2}\right\} (\beta -\tau _{2})-a_{3}^{2}(\beta -\epsilon \tau _{2})(\beta +3\epsilon \tau _{2})}{8\beta ^{2}\tau _{2}^{2}a_{3}^{2}}\right. \\&\quad + \left. \frac{2a_{3}\left\{ 2\beta (\beta +\beta \epsilon \tau _{1}-\tau _{2})\tau _{2}+\tau _{1}(-\beta ^{2} -\beta (1+\epsilon +2\beta \epsilon )\tau _{2}+3\epsilon \tau _{2}^{2})\right\} }{8\beta ^{2}\tau _{2}^{2}a_{3}^{2}}\right] ,\\ a_{20}=&\; \sqrt{\frac{\tau _{1}}{a_{3}}},a_{21}=\sqrt{\frac{\tau _{1}}{a_{3}}}\left( \frac{a_{3}\tau _{2} -\tau _{1}^{2}}{2a_{3}\tau _{1}\tau _{2}}\right) ,\\ a_{22}=&\; -\sqrt{\frac{\tau _{1}}{a_{3}}}\left[ \frac{\tau _{1}^{4}(-3+4\beta -4\tau _{2}) +a_{3}^{2}\tau _{2}^{2}+2a_{3}\tau _{1}^{2}\left\{ (3+2\epsilon \tau _{1})\tau _{2}-2\tau _{1} (1+\epsilon \tau _{2})\right\} }{8a_{3}^{2}\tau _{1}^{2}\tau _{2}^{2}}\right] ,\\ b_{10}=&\; \sqrt{\frac{\tau _{2}}{\beta }},b_{11}=\sqrt{\frac{\tau _{2}}{\beta }} \left\{ \frac{\beta -\tau _{2}\epsilon }{2\tau _{2}\beta }\right\} ,\\ b_{12}=&\; -\sqrt{\frac{\tau _{2}}{\beta }}\left\{ \frac{a_{3}\epsilon \tau _{2}(2\beta -3\epsilon \tau _{2}) +4\beta \tau _{2}(\tau _{2}-\beta )-a_{3}\beta ^{2}}{8\beta ^{2}\tau _{2}^{2}a_{3}}\right\} ,\\ b_{20}=&\; \frac{1}{\sqrt{a_{3}}},b_{21}=\frac{-1}{\sqrt{a_{3}}}\left( \frac{1}{2a_{3}\tau _{2}}\right) . \end{aligned}$$

Now, substituting the values of \(m_{1}\) and \(m_{2}\) from Eqs. (35) and (36) into Eqs. (29), (30) and (32)–(34) and carrying out the detailed manipulations, we acquire the following short-time approximated expressions for displacement, temperatures and stresses in the domain of Laplace transform assuming s to be very large:

  1. 1.

    For the MTRDTT model:

    $$\begin{aligned} \overline{u}(r,s)=&\; \left( f_{41}+\frac{f_{42}}{s}+\frac{f_{43}}{s^{2}}\right) K_{1}\left( (a_{10}s+a_{11})r\right) +\left( \frac{f_{44}}{s^{5/2}}\right) K_{1}\left( a_{20}s^{1/2}r\right) , \end{aligned}$$
    (37)
    $$\begin{aligned} \overline{\phi }(r,s)=&\; \left( \frac{f_{45}}{s}+\frac{f_{46}}{s^{2}}\right) K_{0}\left( (a_{10}s+a_{11})r\right) +\left( \frac{f_{47}}{s}+\frac{f_{48}}{s^{2}}\right) K_{0}\left( a_{20}s^{1/2}r\right) , \end{aligned}$$
    (38)
    $$\begin{aligned} \overline{\theta }(r,s)=&\; \left( f_{49}+\frac{f_{50}}{s}+\frac{f_{51}}{s^{2}}\right) K_{0}\left( (a_{10}s +a_{11})r\right) +\left( \frac{f_{52}}{s^{2}}\right) K_{0}\left( a_{20}s^{1/2}r\right) , \end{aligned}$$
    (39)
    $$\begin{aligned} \overline{\sigma }_{rr}(r,s)=&\; \left( sf_{53}+\frac{f_{54}}{s}+\frac{f_{55}}{s^{2}}\right) K_{0} \left( (a_{10}s+a_{11})r\right) \nonumber \\&\quad + \left( \frac{f_{56}}{s}+\frac{f_{57}}{s^{2}}\right) K_{0}\left( a_{20}s^{1/2}r\right) \nonumber \\&\quad + \left( f_{58}+\frac{f_{59}}{s}+\frac{f_{60}}{s^{2}}\right) K_{1}\left( (a_{10}s+a_{11})r\right) +\left( \frac{f_{61}}{s^{5/2}}\right) K_{1}\left( a_{20}s^{1/2}r\right) , \end{aligned}$$
    (40)
    $$\begin{aligned} \overline{\sigma }_{\varphi \varphi }(r,s)=&\; \left( sf_{62}+f_{63}+\frac{f_{64}}{s}\right) K_{0} \left( (a_{10}s+a_{11})r\right) \nonumber \\&\quad + \left( \frac{f_{65}}{s}+\frac{f_{66}}{s^{2}}\right) K_{0}\left( a_{20}s^{1/2}r\right) \nonumber \\&\quad + \left( f_{67}+\frac{f_{68}}{s}+\frac{f_{69}}{s^{2}}\right) K_{1}\left( (a_{10}s+a_{11})r\right) +\left( \frac{f_{70}}{s^{5/2}}\right) K_{1}\left( a_{20}s^{1/2}r\right) . \end{aligned}$$
    (41)
  2. 2.

    For the TTGL model:

    $$\begin{aligned} \overline{u}(r,s)=&\; \left( sg_{41}+g_{42}+\frac{g_{43}}{s}\right) K_{1}\left( (b_{10}s+b_{11})r\right) +\left( \frac{g_{44}}{s^{2}}+\frac{g_{45}}{s^{3}}\right) K_{1}\left( b_{20}r\right) , \end{aligned}$$
    (42)
    $$\begin{aligned} \overline{\phi }(r,s)=&\; \left( \frac{g_{46}}{s}+\frac{g_{47}}{s^{2}}\right) K_{0}\left( (b_{10}s+b_{11})r\right) +\left( \frac{g_{48}}{s}+\frac{g_{49}}{s^{2}}\right) K_{0}\left( b_{20}r\right) , \end{aligned}$$
    (43)
    $$\begin{aligned} \overline{\theta }(r,s)=&\; \left( sg_{50}+g_{51}+\frac{g_{52}}{s}\right) K_{0}\left( (b_{10}s+b_{11})r\right) +\left( \frac{g_{53}}{s}+\frac{g_{54}}{s^{2}}\right) K_{0}\left( b_{20}r\right) , \end{aligned}$$
    (44)
    $$\begin{aligned} \overline{\sigma }_{rr}(r,s)=&\; \left( s^{2}g_{55}+sg_{56}+g_{57}+\frac{g_{58}}{s}\right) K_{0} \left( (b_{10}s+b_{11})r\right) \nonumber \\&\quad + \left( g_{59}+\frac{g_{60}}{s}+\frac{g_{61}}{s^{2}}\right) K_{0}\left( b_{20}r\right) \nonumber \\&\quad + \left( sg_{62}+g_{63}+\frac{g_{64}}{s}\right) K_{1}\left( (b_{10}s+b_{11})r\right) +\left( \frac{g_{65}}{s^{2}}+\frac{g_{66}}{s^{3}}\right) K_{1}\left( b_{20}r\right) , \end{aligned}$$
    (45)
    $$\begin{aligned} \overline{\sigma }_{\varphi \varphi }(r,s)=&\; \left( s^{2}g_{67}+sg_{68}+g_{69}+\frac{g_{70}}{s}\right) K_{0} \left( (b_{10}s+b_{11})r\right) \nonumber \\&\quad + \left( g_{71}+\frac{g_{72}}{s}+\frac{g_{73}}{s^{2}}\right) K_{0}\left( b_{20}r\right) \nonumber \\&\quad + \left( sg_{74}+g_{75}+\frac{g_{76}}{s}\right) K_{1}\left( (b_{10}s+b_{11})r\right) +\left( \frac{g_{77}}{s^{2}}+\frac{g_{78}}{s^{3}}\right) K_{1}\left( b_{20}r\right) . \end{aligned}$$
    (46)

Here, the above-mentioned notations are provided in “Appendix A.”

6 Analytical results

To find the solutions for short-time approximation in the physical domain (r, t),  we will use the following formulae of Laplace inversions (Oberhettinger and Badii [32]):

$$\begin{aligned} L^{-1}\left[ \frac{1}{s^{n}}\right]&=\frac{t^{n-1}}{(n-1)!},\\ L^{-1}\left[ K_{0}(asr)\right]&=\frac{H(t-ar)}{\sqrt{t^{2}-(ar)^{2}}},L^{-1}\left[ \frac{K_{0}(asr)}{s}\right] =H(t-ar) {\text {cosh}^{-1}}\left( \frac{t}{ar}\right) ,\\ L^{-1}\left[ \frac{K_{0}(asr)}{s^{2}}\right]&=H(t-ar) \left[ t{\text {cosh}^{-1}}\left( \frac{t}{ar}\right) -\sqrt{t^{2}-(ar)^{2}}\right] ,\\ L^{-1}\left[ K_{1}(asr)\right]&=\frac{H(t-ar)t}{ar\sqrt{t^{2}-(ar)^{2}}},L^{-1}\left[ \frac{K_{1}(asr)}{s}\right] =\frac{H(t-ar)}{ar}\sqrt{t^{2}-(ar)^{2}},\\ L^{-1}\left[ \frac{K_{1}(asr)}{s^{2}}\right]&=\frac{H(t-ar)}{ar}\left[ \frac{t}{2}\sqrt{t^{2}-(ar)^{2}} -\frac{(ar)^{2}}{2}{\text {cosh}^{-1}}\left( \frac{t}{ar}\right) \right] ,\\ L^{-1}\left[ K_{0}(ars^{1/2})\right]&=\frac{1}{2t}e^{\frac{-(ar)^{2}}{4t}},L^{-1} \left[ \frac{arK_{1}(ars^{1/2})}{s^{1/2}}\right] =e^{\frac{-(ar)^{2}}{4t}}. \end{aligned}$$

Finally, applying the inverse Laplace transform to Eqs. (37)–(46) and then using the above-mentioned formulae and the convolution theorem of Laplace transform, we arrive at the following solution in physical domain:

  1. 1.

    For the MTRDTT model:

    $$\begin{aligned} u(r,t)=&\; e^{-\alpha _{1}t}\left[ u_{11}\frac{H(t-a_{10}r)}{\sqrt{t^{2}-(a_{10}r)^{2}}}+u_{12}H(t-a_{10}r) \sqrt{t^{2}-(a_{10}r)^{2}}\right. \nonumber \\&\quad - \left. u_{13}H(t-a_{10}r) \,{\text {cosh}^{-1}}\left( \frac{t}{a_{10}r}\right) \right] +\frac{f_{44}}{a_{20}r}\int \limits _{0}^{t}(t-\tau )e^{-\frac{(a_{20}r)^{2}}{4\tau }}d\tau , \end{aligned}$$
    (47)
    $$\begin{aligned} \phi (r,t)=&\; e^{-\alpha _{1}t}\left[ \phi _{11}H(t-a_{10}r){\text {cosh}}^{-1}\left( \frac{t}{a_{10}r}\right) -\phi _{12}H(t-a_{10}r)\sqrt{t^{2}-(a_{10}r)^{2}}\right] \nonumber \\&\quad + \frac{f_{47}}{2}\int \limits _{0}^{t}\frac{1}{\tau }e^{-\frac{(a_{20}r)^{2}}{4\tau }}d\tau +\frac{f_{48}}{2} \int \limits _{0}^{t}\frac{t-\tau }{\tau }e^{-\frac{(a_{20}r)^{2}}{4\tau }}d\tau , \end{aligned}$$
    (48)
    $$\begin{aligned} \theta (r,t)=&\; e^{-\alpha _{1}t}\left[ f_{49}\frac{H(t-a_{10}r)}{\sqrt{t^{2}-(a_{10}r)^{2}}} +\theta _{11}H(t-a_{10}r){\text {cosh}^{-1}}\left( \frac{t}{a_{10}r}\right) \right] \nonumber \\&\quad - \left. \theta _{12}H(t-a_{10}r)\sqrt{t^{2}-(a_{10}r)^{2}}\right] +\frac{f_{52}}{2}\int \limits _{0}^{t} \frac{t-\tau }{\tau }e^{-\frac{(a_{20}r)^{2}}{4\tau }}d\tau , \end{aligned}$$
    (49)
    $$\begin{aligned} \sigma _{rr}(r,t)=&\; e^{-\alpha _{1}t}\left[ f_{53}\int \limits _{0}^{t}\delta '(t-\tau )\frac{H(\tau -a_{10}r)}{\sqrt{\tau ^{2}-(a_{10}r)^{2}}}d\tau +\sigma _{11}^{r}\frac{H(t-a_{10}r)}{\sqrt{t^{2}-(a_{10}r)^{2}}}\right. \nonumber \\&\quad + \left. \sigma _{12}^{r}H(t-a_{10}r){\text {cosh}^{-1}} \left( \frac{t}{a_{10}r}\right) -\sigma _{13}^{r}H(t-a_{10}r)\sqrt{t^{2}-(a_{10}r)^{2}}\right] \nonumber \\&\quad + \frac{f_{56}}{2}\int \limits _{0}^{t}\frac{1}{\tau }e^{-\frac{(a_{20}r)^{2}}{4\tau }}d\tau +\frac{f_{57}}{2}\int \limits _{0}^{t}\frac{t-\tau }{\tau }e^{-\frac{(a_{20}r)^{2}}{4\tau }}d\tau +\frac{f_{61}}{a_{20}r^{2}}\int \limits _{0}^{t}(t-\tau )e^{-\frac{(a_{20}r)^{2}}{4\tau }}d\tau , \end{aligned}$$
    (50)
    $$\begin{aligned} \sigma _{\varphi \varphi }(r,t)=&\; e^{-\alpha _{1}t}\left[ f_{62}\int \limits _{0}^{t}\delta '(t-\tau ) \frac{H(\tau -a_{10}r)}{\sqrt{\tau ^{2}-(a_{10}r)^{2}}}d\tau +\sigma _{11}^{\varphi }\frac{H(t-a_{10}r)}{\sqrt{t^{2}-(a_{10}r)^{2}}}\right. \nonumber \\&\quad + \left. \sigma _{12}^{\varphi }H(t-a_{10}r){\text {cosh}^{-1}} \left( \frac{t}{a_{10}r}\right) -\sigma _{13}^{\varphi }H(t-a_{10}r)\sqrt{t^{2}-(a_{10}r)^{2}}\right] \nonumber \\&\quad + \frac{f_{65}}{2}\int \limits _{0}^{t}\frac{1}{\tau }e^{-\frac{(a_{20}r)^{2}}{4\tau }}d\tau +\frac{f_{66}}{2} \int \limits _{0}^{t}\frac{t-\tau }{\tau }e^{-\frac{(a_{20}r)^{2}}{4\tau }}d\tau +\frac{f_{70}}{a_{20}r^{2}} \int \limits _{0}^{t}(t-\tau )e^{-\frac{(a_{20}r)^{2}}{4\tau }}d\tau , \end{aligned}$$
    (51)

    where \(\alpha _{1}=\frac{a_{11}}{a_{10}}.\)

  2. 2.

    For the TTGL model:

    $$\begin{aligned} u(r,t)=&\; e^{-\alpha _{2}t}\left[ u_{14}\int \limits _{0}^{t}\delta '(t-\tau )\frac{\tau H(\tau -b_{10}r)}{\sqrt{\tau ^{2}-(b_{10}r)^{2}}}d\tau +u_{15}\frac{H(t-b_{10}r)}{\sqrt{t^{2}-(b_{10}r)^{2}}}\right. \nonumber \\&\quad + \left. u_{16}H(t-b_{10}r)\sqrt{t^{2}-(b_{10}r)^{2}}\right] +u_{17}e^{-b_{20}r}, \end{aligned}$$
    (52)
    $$\begin{aligned} \phi (r,t)=&\; e^{-\alpha _{2}t}\left[ \phi _{13}H(t-b_{10}r){\text {cosh}}^{-1} \left( \frac{t}{b_{10}r}\right) -\phi _{14}H(t-b_{10}r)\sqrt{t^{2}-(b_{10}r)^{2}}\right] \nonumber \\&\quad + \phi _{15}e^{-b_{20}r}, \end{aligned}$$
    (53)
    $$\begin{aligned} \theta (r,t)=&\; e^{-\alpha _{2}t}\left[ g_{50}\int \limits _{0}^{t}\delta '(t-\tau )\frac{H(\tau -b_{10}r)}{\sqrt{\tau ^{2} -(b_{10}r)^{2}}}d\tau +\theta _{13}\frac{H(t-b_{10}r)}{\sqrt{t^{2}-(b_{10}r)^{2}}}\right] \nonumber \\&\quad + \left. \theta _{14}H(t-b_{10}r){\text {cosh}^{-1}}\left( \frac{t}{b_{10}r}\right) \right] +\theta _{15}e^{-b_{20}r}, \end{aligned}$$
    (54)
    $$\begin{aligned} \sigma _{rr}(r,t)=&\; e^{-\alpha _{2}t}\left[ g_{55}\int \limits _{0}^{t}\delta ''(t-\tau )\frac{H(\tau -b_{10}r)}{\sqrt{\tau ^{2}-(b_{10}r)^{2}}}d\tau +\sigma _{14}^{r}\int \limits _{0}^{t}\delta '(t-\tau )\frac{H(\tau -b_{10}r)}{\sqrt{\tau ^{2}-(b_{10}r)^{2}}}d\tau \right. \nonumber \\&\quad + \sigma _{15}^{r}\int \limits _{0}^{t}\delta '(t-\tau )\frac{\tau H(\tau -b_{10}r)}{\sqrt{\tau ^{2}-(b_{10}r)^{2}}}d\tau +\sigma _{16}^{r}\frac{H(t-b_{10}r)}{\sqrt{t^{2}-(b_{10}r)^{2}}}\nonumber \\&\quad + \left. g_{58}H(t-b_{10}r){\text {cosh}^{-1}}\left( \frac{t}{b_{10}r}\right) -\frac{g_{64}}{b_{10}r^{2}}H(t-b_{10}r)\sqrt{t^{2}-(b_{10}r)^{2}}\right] +\sigma _{17}^{r}e^{-b_{20}r}, \end{aligned}$$
    (55)
    $$\begin{aligned} \sigma _{\varphi \varphi }(r,t)=&\; e^{-\alpha _{2}t}\left[ g_{67}\int \limits _{0}^{t}\delta ''(t-\tau )\frac{H(\tau -b_{10}r)}{\sqrt{\tau ^{2}-(b_{10}r)^{2}}}d\tau +\sigma _{14}^{\varphi }\int \limits _{0}^{t}\delta '(t-\tau )\frac{H(\tau -b_{10}r)}{\sqrt{\tau ^{2}-(b_{10}r)^{2}}}d\tau \right. \nonumber \\&\quad + \sigma _{15}^{\varphi }\int \limits _{0}^{t}\delta '(t-\tau )\frac{\tau H(\tau -b_{10}r)}{\sqrt{\tau ^{2}-(b_{10}r)^{2}}}d\tau +\sigma _{16}^{\varphi }\frac{H(t-b_{10}r)}{\sqrt{t^{2}-(b_{10}r)^{2}}}\nonumber \\&\quad + \left. g_{70}H(t-b_{10}r){\text {cosh}^{-1}}\left( \frac{t}{b_{10}r}\right) -\frac{g_{76}}{b_{10}r^{2}}H(t-b_{10}r)\sqrt{t^{2}-(b_{10}r)^{2}}\right] +\sigma _{17}^{\varphi }e^{-b_{20}r}, \end{aligned}$$
    (56)

    where \(\alpha _{2}=\frac{b_{11}}{b_{10}}.\)

Here, the above-mentioned notations are presented in “Appendix B.” These expressions (47)–(56) denote the final short-time approximated solutions in the domain (r, t).

7 Analysis of the analytical results

In this section, we examine the solutions for short-time approximation as obtained above. From these solutions given by (47)–(56), one can clearly observe that each solution is made up of two distinct parts. The first part, which includes the term \(H(t-a_{10}r),\) expresses the role of an elastic wave that propagates with finite speed \(1/a_{10}\) near the wavefront \(r=\frac{t}{a_{10}}.\) Also, this wave decays exponentially and the decaying exponent is found to be strongly influenced by the dimensionless two-temperature parameter \(a_{3}.\) It is also concluded that the velocity of elastic waves depends on the thermal relaxation parameters as well as some other thermoelastic parameters. The rest part of the solution does not contribute to any wave, but this part was also found to be dependent on the dimensionless two-temperature parameter \(a_{3}.\)

Like the case of MTRDTT model, the first part of solutions in the TTGL model also contains the term \(H(t-b_{10}r)\) which expresses the role of an elastic wave nearby the wavefront \(r=\frac{t}{b_{10}}\) and propagates with finite speed \(1/b_{10}\). As opposed to the MTRDTT model, the decaying exponent in the first term does not depend on the dimensionless two-temperature parameter \(a_{3}.\) Similar to the MTRDTT model, another part of the solution makes no contribution to any wave, but it is dependent on the dimensionless two-temperature parameter \(a_{3}\). Therefore, the propagation speed is not finite for thermal waves in the two-temperature models.

Moreover, we conclude that the conductive temperature is continuous under the MTRDTT model and TTGL model, whereas other field variables including displacement, thermodynamic temperature and stresses are discontinuous in nature with an infinite discontinuity at the elastic wavefront.

Further comparing the results with the corresponding result obtained by Chandrasekharaiah and Murthy [27] and also by Ezzat [28] for the case of GL model, a significant difference is observed with the results predicted by MTRDTT and TTGL models. The solution of each field variable in the GL model, unlike the MTRDTT and TTGL models, consists of two waves decaying exponentially and each wave propagates with finite speed. Moreover, at both the elastic and thermal wavefronts, the temperature distribution shows discontinuity with finite jumps and the stresses \(\sigma _{rr}\) and \(\sigma _{\varphi \varphi }\) show infinite discontinuity in the case of GL model [27, 28]. Such significant dissimilarity in the prediction of two-temperature model as compared to the GL model is an important investigation of the present study.

Fig. 1
figure 1

a Variation of u along r at \(t=0.4\). b Variation of u along r at \(a_{3}=0.6\)

Full size image
Fig. 2
figure 2

a Variation of \(\phi \) along r at \(t=0.4\). b Variation of \(\phi \) along r at \(a_{3}=0.6\)

Full size image
Fig. 3
figure 3

a Variation of \(\theta \) along r at \(t=0.4\). b Variation of \(\theta \) along r at \(a_{3}=0.6\)

Full size image
Fig. 4
figure 4

a Variation of \(\sigma _{rr}\) along r at \(t=0.4\). b Variation of \(\sigma _{rr}\) along r at \(a_{3}=0.6\)

Full size image
Fig. 5
figure 5

a Variation of \(\sigma _{\varphi \varphi }\) along r at \(t=0.4\). b Variation of \(\sigma _{\varphi \varphi }\) along r at \(a_{3}=0.6\)

Full size image

8 Numerical results and discussion

To gain a more in-depth understanding of the behavior of short-time approximated solutions including heat sources, as well as to graphically represent the analytical findings, we carry out numerical work using computational tool Matlab. Throughout this computations, the copper material is considered. The values of physical parameters and material constants are taken as (Shivay and Mukhopadhyay [13])

$$\begin{aligned} \lambda&=7.76\times 10^{10}\,{\text {N}}\, {\text {m}}^{-2},\mu =3.86\times 10^{10}\,{\text {N}}\, {\text {m}}^{-2},C_{E}=383.1\,{\text {J}}\,{\text {kg}}^{-1}\,{\text {K}}^{-1},\\ \theta _{0}&=293\,{\text {K}},\rho =8954\,{\text {kg}}\, {\text {m}}^{-3},R_{0}=1\,{\text {W}}\, {\text {m}}^{-2},\alpha =1.78\times 10^{-5}\,{\text {K}}^{-1},\\ K&=386\,{\text {W}}\,{\text {m}}^{-1}\,{\text {K}}^{-1},\tau _{1}=0.15,\tau _{2}=0.10. \end{aligned}$$

The variations of these field quantities with respect to radial distance r are presented in different figures. The computation of these field variables is carried out under two different thermoelastic models, namely, the MTRDTT model and the TTGL model. The parts (a) and (b) of each figure are used to exhibit the figures independently. The part (a) of all the figures shows the effect of a non-dimensional parameter of two-temperature (\(a_{3})\) on the field quantities at a particular time \(t=0.4\), whereas part (b) displays the variation of field variables at various instants of time (\(t=0.25,\,0.45,\,0.65)\) at \(a_{3}=0.6.\) Our numerical results reveal that at the origin, all field variables have an infinite jump, where the heat source is located. According to our observations, the dimensionless speed of elastic waves is 1.0125 for both models. We further observe that all the field variables are identically zero beyond the elastic wavefront at any time. This completely agrees with the corresponding theoretical results provided in Eqs. (47)–(56). We also come across the following observations:

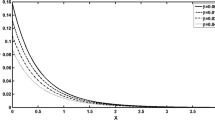
Figure 1a shows the nature of displacement for the three different values of \(a_{3}\) (\(a_{3}=0.1,\,0.5,\,1)\) with respect to radial distance r, whereas Fig. 1b displays the variation of displacement at different values of time (\(t=0.25,\,0.45,\,0.65)\) with respect to r. From Fig. 1a, b, we conclude that as r increases, displacement decreases from a very high value to zero for both models. However, just behind the elastic wavefront location, the displacement begins to rise abruptly and reaches a high positive value and jumps down to zero in the case of MTRDTT model. On the other hand, the displacement suddenly decreases to a high negative value just near the elastic wavefront location and then jumps up to zero value in the case of TTGL model. This is due to the impact of impulsive heat source. We further observe that as the value of \(a_{3}\) increases, the displacement increases and decreases in the cases of MTRDTT model and TTGL model, respectively. Hence, the two-temperature parameter has a prominent effect. This is clearly verified in Fig. 1a. Figure 1b verifies that behind the position of wavefront, the displacement component attains a higher value at the initial time of interaction (i.e., for smaller values of time). However, no disturbance has been observed for both models after the elastic wavefront location. Thus, a significant difference is observed in the results predicted by the MTRDTT and TTGL models for displacement near the location of the elastic wavefront.

The distribution of conductive temperature \((\phi )\) along the radial distance is depicted in Fig. 2a, b. Figure 2a b describes the variations of conductive temperature along with r for various values of \(a_{3}\) (\(a_{3}=0.1,\,0.5,\,1)\) and time (\(t=0.25,\,0.45,\,0.65)\), respectively in the contexts of MTRDTT and TTGL models. Figure 2a, b shows the similar nature of conductive temperature for the MTRDTT and TTGL models demonstrating that \(\phi \) for both the models begins with infinite value and then, decreases to zero as r increases. Therefore, this field has a decreasing nature. It can be seen that the value of temperature is higher for the MTRDTT model in comparison with the TTGL model. From Fig. 2a, we further observe that conductive temperature increases as the value of \(a_{3}\) increases for both the models. This indicates that parameter \(a_{3}\) has a prominent effect on both models. Moreover, Fig. 2b reports that the value of \(\phi \) also increases with the increasing value of t in the case of MTRDTT model. In contrast, the value of \(\phi \) remains the same for different values of time in the case of TTGL model. Furthermore, conductive temperature follows almost a similar trend under the MTRDTT and TTGL models at a given time.

Figure 3a, b represents the variation of thermodynamic temperature \((\theta )\) with respect to r for MTRDTT and TTGL models. From Fig. 3a, b, it is observed that under the MTRDTT model, the thermodynamic temperature increases from a negative infinity value, reaches a high value at the position of elastic wavefront and then jumps down to zero. At the same time, starting from a negative infinity value, \(\theta \) increases as r increases and just before the elastic wavefront, abruptly decreases to a high negative value and then approaches zero in view of the TTGL model. This field shows an infinite discontinuity at the wavefront under both models. This is clearly verified from Fig. 3a that before the position of elastic wavefront, \(\theta \) decreases as the value of \(a_{3}\) increases and it is identically zero after the elastic wavefront under both the models. Figure 3b discusses the variation of thermodynamic temperature at different instants of time and indicates that \(\theta \) behaves differently with time near the elastic wavefront. In the context of MTRDTT model, \(\theta \) increases before the elastic wavefront as time increases, whereas \(\theta \) has a decreasing trend for the case of TTGL model. Hence, we conclude that for this field variable, the MTRDTT model predicts prominently different behavior in comparison with the TTGL model.

The variation of radial stress \((\sigma _{rr})\) in the contexts of MTRDTT and TTGL models is illustrated by Fig. 4a, b. Figure 4a depicts the variation of radial stress for various values of \(a_{3}\), whereas the variation of radial stress for different values of t is presented in Fig. 4b. Figure 4a, b indicates that the radial stress under the MTRDTT and TTGL models behave similarly. From Fig. 4a, b, we notice that under the MTRDTT model, the radial stress increases from a negative infinity value, attains a very high positive value and then decreases to a zero value. This variation trend in \(\sigma _{rr}\) is very similar to the TTGL model. Therefore, it is concluded that \(\sigma _{rr}\) is an increasing function of r under both the models before the location of wavefront. We further notice that \(\sigma _{rr}\) increases with the increase of \(a_{3}\) at the wavefront location which is also clear in Fig. 4a. From Fig. 4b, it is observed that \(\sigma _{rr}\) attains a higher value at the wavefront position at the initial time. Under both these theories, the radial stress field shows an infinite discontinuity at the wavefront. Finally, we observe that the trend of radial stress under the MTRDTT model agrees with the TTGL model.

Figure 5a, b demonstrates the variations of circumferential stress \((\sigma _{\varphi \varphi })\) along with r for various values of \(a_{3}\) and time, respectively. From Fig. 5a, b, it can be seen that the circumferential stress for the MTRDTT model begins to decrease from a positive infinity value and just before the elastic wavefront, it suddenly increases to a high positive value and then jumps to zero. However, the behavior of \(\sigma _{\varphi \varphi }\) under the MTRDTT model is quite different as compared to the TTGL model indicating that \(\sigma _{\varphi \varphi }\) decreases with the increasing value of r and jumps up to zero value after attaining a high negative value at the elastic wavefront. This fact is also clearly verified in Fig. 5a, b. Also, from Fig. 5a, it is found that the \(\sigma _{\varphi \varphi }\) increases as \(a_{3}\) increases under the MTRDTT model; however, \(\sigma _{\varphi \varphi }\) decreases with the increasing value of \(a_{3}\) under the TTGL model. Furthermore, as shown in Fig. 5b, the trend of variation of \(\sigma _{\varphi \varphi }\) changes with time near the elastic wavefront for both the models. We finally conclude that the profile of circumferential stress for the MTRDTT model differs from the case of the TTGL model implying that the effects of temperature rate terms in two-temperature relation play a significant role in the thermoelastic interactions due to the presence of a heat source inside the medium.

9 Conclusion

In this work, the thermoelastic interactions inside an isotropic and homogeneous medium using the MTRDTT and TTGL thermoelastic models in the presence of a continuous line heat source are investigated. In order to investigate the effect of heat source on the field variables, the short-time approximated solutions are derived. To compare the outcomes predicted by the MTRDTT model and the TTGL model, the unified two-temperature relation is employed to study our problem. The theoretical results under both the models (MTRDTT and TTGL) are graphically displayed. Several important facts about the behavior of these field variables are highlighted. Some of these details can be categorized as follows:

  • Unlike the GL model that predicts finite speed for elastic as well as for thermal waves, the short-time approximated solutions obtained in the MTRDTT model and TTGL model clearly show that the solution for each field is divided into two distinct parts. The first part expresses the role of an elastic wave propagating with finite speed, whereas the rest part of the solution does not contribute to any wave under both the models. This signifies the fact that the temperature-rate-dependent two-temperature models do not admit finite wave speed of the thermal wave.

  • In the same way as in the GL model, the heat source’s effects for the MTRDTT and TTGL models are limited to a bounded but time-dependent region of space around it.

  • Except for the conductive temperature, which is continuous in both models, rest of the field variables show discontinuity at the elastic wavefront.

  • For displacement, temperature and circumferential stress fields, the difference between MTRDTT and TTGL models seems to be more apparent. However, in the case of radial stress, it is investigated that the variation of \(\sigma _{rr}\) is similar in nature under both the models.

  • As the value of \(a_{3}\) increases, the value of all the field variables increases at the position of wavefront under the MTRDTT model. As opposed to the MTRDTT model, the value of u,  \(\theta \) and \(\sigma _{\varphi \varphi }\) decreases with the increasing value of \(a_{3}\) at the position of wavefront in the context of TTGL model. However, as with the MTRDTT model, the value of \(\phi \) and \(\sigma _{rr}\) increases with the increasing value of \(a_{3}\) in the TTGL model.

  • Hence, the two-temperature parameter on all the field variables has a prominent effect on both the models. It is worth to be mentioned here that the effect of this modified two-temperature relation indicates a clear difference in the corresponding results predicated by the present models.