1 Introduction

Micromorphic continuum models provide an approach to describe micro-scale structural and mechanical effects in the continuum description of material behavior [1,2,3,4]. For micromorphic models to be representative, it is important to link the continuum fields with the micro-scale mechanisms. For instance, when we seek descriptions of the collective behavior of a large number of grains, as in the case in which a material’s granular microstructural effect need to be modeled, it is necessary to describe the effects of grain and grain–grain interface deformations (termed as micromechanics), which could be highly localized and directional, as in the case of Hertzian contacts [5, 6]. These grain deformations could be non-uniform due to the grain-shape and interfacial/surfacial characteristics or due to the grain-neighborhood structure (termed as microstructure). The grains can also experience rotations relative to their neighboring grains further contributing to the overall deformation of the collective system [7, 8]. These peculiarities of granular systems renders the modeling of the behavior that emerges at the macro-scale (containing large number of grains) particularly challenging. It is now widely accepted that the classical continuum approach (or the Cauchy format) fails woefully in representing the true nature of the microstructured material behavior and describe many observed phenomena at the macro-scale, even though it serves well for a number of engineering problems. There is growing realization that to describe the emerging macro-scale behavior of these materials faithfully and with increasing fidelity, it is necessary to consider continuum models in which the deformations at micro-scale are properly accounted. A key shortcoming of the classical continuum theory is its inability to describe the effects of complex kinematics and distribution of elastic energy in internal deformation modes within the continuum material point. In this regard, it is worthwhile to recall that in the early development of the continuum modeling of deformable media in the works of Navier, Cauchy, Poisson and Piola, the material was viewed as composed of molecules (particles) that attract and repel each other [9,10,11]. Many materials, particularly at the scale in which granular microstructures appear, can be treated in a similar sense in which the deformation of an interacting grain-pair can be effectively described in terms of the relative movements of the grain centroids/barycenters regardless of the location of the actual deformation within the grains. Indeed such a treatment can serve as a point of departure for both discrete and continuum models. Examples of discrete models range from atomistic and molecular (see among a very large literature base [12, 13]) to more recent large grain models (see among others [14, 15]). Continuum models of these materials that proceed from this approach are traced to early part of 20th century (see historical context in the review [16]) to more recent models such as those in [7, 17, 18] devised for the case of small deformations to account for internal deformation modes.

In discrete models, the key kinematic variable is the grain motion; thus, by their nature, these models describe the fate of every grain as a result of its interactions with the neighbors and by extension the whole collection. Discrete models, therefore, can result in grain trajectories (that can include grain translations and grain spins) and spatial distributions of deformation energies and their potential decomposition into various deformation modes. The extensive approach is also a principal drawback of discrete model as the detailed data is, in many cases, distinguished by the lack of accurate knowledge of grain locations, shapes and surface type/conditions and every possible grain-pair interaction relationships. Nevertheless, simulations using discrete models [19,20,21,22,23,24,25,26,27,28,29] have been suggestive and have led to the recognition of certain micro-scale phenomena, such as localization of energy into small zones of grain/atomic clusters [30, 31]or localization bands and vortices [32, 33], propensity of micro-rotation [34], identification of floppy modes [35], and so-called ’force-chains’ (see for example [14, 36,37,38]). Many of these micro-scale phenomena, particularly those related to certain clustering of grain displacements and coherent/incoherent grain rotations, are attested to by experimental measurements of grain motions such as [39, 40]. For describing the many relevant phenomena exhibited by grain collections detailed information regarding precise grain trajectory is unnecessary. However, the grain-scale kinematics have profound relevance in the macro-scale description of granular materials representing the emergent collective behavior of large number of grains. Indeed the practical pathway to the control of macro-scale behavior by accessing the micro-scale lies in their representative linkages based upon predictive theories [41]. The recent realization of metamaterials based on pantographic motif that link to second gradient continuum description [42,43,44,45,46,47,48,49,50] and chiral granular materials that link to Cosserat continuum are exemplar of such predictive micro–macro-theoretical identifications [51,52,53,54]. These works have shown that successful efforts to link micro- to macro-scale lead to generalized continuum theories, and these can, therefore, provide efficient ways for rational design of (meta)materials (as opposed to trial and error or other ad hoc approaches, see for example the review by [55, 56]). Remarkably these micro–macro-identifications indicate how the stored elastic energy can be distributed within internal deformation modes, including second [57,58,59,60,61,62,63,64,65,66,67,68,69] and higher [35] gradient modes, grain rotations/spins [7], and non-standard coupling of shear and rotations [70, 71].

In the spirit of developing such micro–macro-identifications in a generalized setting of finite deformations that account for geometric nonlinearity, we focus in this paper upon a micromorphic continuum description of materials in which granular microstructural effects need to be modeled. In these cases, Taylor expansion of only conventional macro-scale kinematic descriptor is not representative and additional kinematic descriptors may be introduced to accurately describe the response as in Cosserat or micromorphic media [17, 18, 51, 72,73,74,75,76,77,78,79,80,81,82,83]. To this end, we utilize neighboring grain-pair deformation as the fundamental building block and develop objective kinematic descriptors for relative displacements following Piola’s ansatz for micro–macro-identification. Micro-scale deformation energy is then introduced in terms of the developed objective relative displacement decomposed into a component along the vector that represents the directors of generic grain-pairs centroids in the system, termed as normal component, and a component in the orthogonal plane, termed as tangential component. For the present work, a quadratic form of the micro-scale deformation energy is utilized to obtain an identification for the case of geometrically nonlinear isotropic elasticity. As a result, expressions for elastic constants of a linear novel micromorphic continuum are obtained in terms of the micro-scale parameters. The plan of the paper is the following. Subsequent to this introduction, in Sect. 2, the discrete and continuous models describing a granular system are presented. Particularly, the discrete model, whose kinematics is ultimately specified in terms of a position and a micromorphic deformation gradient for each subsystem—a granular aggregate—termed here as sub-body is introduced first. The continuum model is then introduced and discrete-continuum kinematic bridging is performed through the Piola’s ansatz. Specialization of the proposed approach to Cosserat and strain-gradient continua through proper restrictions of the micromorphic deformation gradient is subsequently discussed. Section 3 builds on the previous sections, which are exclusively concerned with the kinematics of the studied systems, by introducing the elastic strain energy for the discrete model and the corresponding one for the continuum model as the result of a homogenization procedure based on the Piola’s ansatz. More specifically, relative deformation measures are introduced followed by the definition of the elastic strain energy function in the nonlinear case. Special emphasis is given to the nonlinear 3D isotropic case for no intergranular micromorphic deformation effects and to the linear 3D isotropic case for general intergranular micromorphic deformations. Finally, conclusions are briefly presented.

2 Discrete and continuous models for granular systems

2.1 Discrete model

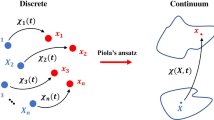
For a material with granular microstructure, the discrete granular model is illustrated, as a general example, in Fig. 1. In the reference configuration, we have N sub-bodies. Each sub-body is composed by many grains and is assumed to be a continuum, one point of which is labeled \(X_{n}\in B_{n}\) with \(n=1,\ldots N\). All other points of the sub-body are labeled \(X_{n}'\in B_{n}\). When this material undergoes deformation, the point \(X_{n}\) is placed, in the present configuration, at \(x_{n}\) via the placement function \(\chi _{n}\), i.e.,

$$\begin{aligned} x_{n}=\chi _{n}\left( t\right) ,\quad \forall t\in {\mathbb {R}},\quad \forall n=1,\ldots ,N, \end{aligned}$$
(1)

where t is the time variable. While all the other points \(X_{n}'\in B_{n}\) of the grain n are placed, in the present configuration, at \(x_{n}'\) via a different placement function \(\chi _{n}'\), i.e.,

$$\begin{aligned} x_{n}'=\chi _{n}'\left( X_{n}',t\right) ,\quad \forall t\in {\mathbb {R}},\quad \forall X_{n}'\in B_{n},\quad \forall n=1,\ldots ,N, \end{aligned}$$
(2)

in such a way that, evaluating this second placement function at \(X_{n}'=X_{n}\), we have

$$\begin{aligned} \chi _{n}'\left( X_{n},t\right) =\chi _{n}\left( t\right) ,\quad \forall t\in {\mathbb {R}},\quad \forall n=1,\ldots ,N. \end{aligned}$$

The sub-body \(B_{n}\) is assumed to be sufficiently small that a Taylor’s series expansion of \(\chi _{n}'\) centered at \(X_{n}'=X_{n}\) can be truncated at the first order, i.e.,

$$\begin{aligned} x_{n}'=\chi _{n}'\left( X_{n}',t\right) =\chi _{n}\left( t\right) +P_{n}\left( t\right) \left( X_{n}'-X_{n}\right) ,\quad \forall t\in {\mathbb {R}},\quad \forall n=1,\ldots ,N \end{aligned}$$
(3)

where deformation gradients are defined,

$$\begin{aligned} P_{n}\left( t\right) =\left. \frac{\partial \chi _{n}'}{\partial X_{n}'}\right| _{X_{n}'=X_{n}}, \end{aligned}$$

and the truncation is equivalent to assuming an affine deformation of each sub-body \(B_{n}\).

Thus, the kinematics of the discrete model is completely described, for each sub-body \(B_{n}\), by the following two functions

$$\begin{aligned} \chi _{n}\left( t\right) ,P_{n}\left( t\right) ,\quad \forall t\in {\mathbb {R}},\quad \forall n=1,\ldots ,N. \end{aligned}$$
Fig. 1
figure 1

Discrete model. Each sub-body \(B_{n}\) with \(n=1,\ldots N\) in the reference configuration is represented with black boundaries and is composed by many grains. Each grain is represented with blue boundaries. For each sub-body \(B_{n}\), two placements are defined. The placement of the point \(X_{n}\), belonging to one of the grain of the sub-body \(B_{n}\), is \(\chi _{n}\left( t\right) \), according to (1). The placement of the point \(X_{n}'\), belonging eventually to another grain of the sub-body \(B_{n}\), is \(\chi _{n}'\left( X_{n}',t\right) \), according to (2)

Full size image

2.2 Continuum model

The continuum model is described in Fig. 2. In the reference configuration, we have a continuum body \(C^{*}\). Each point of this continuum is called \(X\in C^{*}\). The same point X is the representative of a microstructure at a different, smaller scale, and may be another continuum. Any point within this microstructure is called \(X'\). The point X is placed, in the present configuration, at x via the placement function \(\chi \), i.e.,

$$\begin{aligned} x=\chi \left( X,t\right) ,\quad \forall t\in {\mathbb {R}},\quad \forall X\in C^{*}. \end{aligned}$$
(4)

Further, the points \(X'\) of the microstructure are placed, in the present configuration, at \(x'\) via a different placement function \(\chi \)’, i.e.,

$$\begin{aligned} x'=\chi '\left( X,X',t\right) ,\quad \forall t\in {\mathbb {R}},\quad \forall X\in C^{*}, \end{aligned}$$
(5)

in such a way that evaluating it at \(X'=X\), we have

$$\begin{aligned} \chi '\left( X,X,t\right) =\chi \left( X,t\right) ,\quad \forall t\in {\mathbb {R}},\quad \forall X\in C^{*}. \end{aligned}$$
(6)

The microstructure is assumed to be sufficiently small that a Taylor’s series expansion of the placement function \(\chi '\left( X,X',t\right) \) centered at \(X'=X\) can be truncated at the first order, i.e.,

$$\begin{aligned} x'=\chi '\left( X,X',t\right) =\chi \left( X,t\right) +P\left( X,t\right) \left( X'-X\right) ,\quad \forall t\in {\mathbb {R}},\quad \forall X\in C^{*} \end{aligned}$$
(7)

where the micromorphic deformation gradient \({\mathcal {P}}=P\left( X,t\right) \) of each microstructure is defined,

$$\begin{aligned} \mathfrak {{\mathcal {P}}}=P\left( X,t\right) =\left. \frac{\partial \chi '}{\partial X'}\right| _{X'=X},\quad \forall t\in {\mathbb {R}},\quad \forall X\in C^{*}. \end{aligned}$$
(8)

and where (6) has been considered. The truncation of (7) at first order is equivalent to assume an affine deformation of each microstructure. Thus, the kinematics of the continuum model is completely described by the following couple of functions

$$\begin{aligned} \chi \left( X,t\right) ,P\left( X,t\right) ,\quad \forall t\in {\mathbb {R}},\quad \forall X\in C^{*}. \end{aligned}$$

The deformation gradient, in this case, is defined by two gradients: the gradient \(\nabla \chi \) of the placement function, and the gradient \(\nabla P\) of the micromorphic deformation gradient

$$\begin{aligned} \mathfrak {{\mathcal {F}}}=F\left( X,t\right) =\nabla \chi =\frac{\partial \chi }{\partial X},\qquad \nabla P=\frac{\partial P}{\partial X}. \end{aligned}$$
(9)

Thus, the Green–Saint-Venant tensor G (or nonlinear macro-strain) and the micromorphic Green–Saint-Venant tensor M are defined as in (10)

$$\begin{aligned} G=\frac{1}{2}\left( \mathfrak {{\mathcal {F}}}^{\mathrm{T}}\mathfrak {{\mathcal {F}}}-I\right) ,\quad M=\frac{1}{2}\left( \mathfrak {{\mathcal {P}}}^{\mathrm{T}}\mathfrak {{\mathcal {P}}}-I\right) , \end{aligned}$$
(10)

In addition, a relative micro–macro-Green–Saint-Venant tensor (or nonlinear relative deformation) is defined as

$$\begin{aligned} \Upsilon =\left( I-{\mathcal {P}}^{\mathrm{T}}{\mathcal {F}}^{-T}\right) . \end{aligned}$$
(11)

Note that the tensor \(\Upsilon \) defined in (11) vanishes when \({\mathcal {P}}\equiv {\mathcal {F}}\), i.e. when the micromorphic deformation gradient \({\mathcal {P}}\) equals the deformation gradient \({\mathcal {F}}\). Such a tensor is nothing but a strain measure taking into account the differential deformations of the continuum element and the microstructure. Further, considering that a polar decomposition holds for both the micromorphic deformation gradient and the macro-deformation gradient, it can be concluded that the tensor \(\Upsilon \) takes into account also the differential rotation between the micro- and macro-scale. Remark that as it will be shown in the sequel, the definition of \(\Upsilon \) in (11) is only one of the possible nonlinear generalizations of the relative deformation \(\gamma \) defined in Mindlin’s work [1]. It is also worthwhile to define the following third-order tensors, the so-called first and second nonlinear micro-deformation gradients

$$\begin{aligned} \Lambda =\left( {\mathcal {F}}^{-1}\nabla P\right) ^{\mathrm{T}_{13}},\quad \Lambda ^{r}=\left( {\mathcal {P}}^{\mathrm{T}}\nabla P\right) ^{\mathrm{T}_{13}} \end{aligned}$$
(12)

where the transpose operator \(T_{13}\) refers to the first and to the third indices of the third-order tensors \(\Lambda \) and \(\Lambda ^{r}\) as better defined in index notation as follows:

$$\begin{aligned}&\Lambda _{ijh}=\left( \left[ {\mathcal {F}}^{-1}\nabla P\right] ^{\mathrm{T}_{13}}\right) _{ijh}=\left( {\mathcal {F}}^{-1}\nabla P\right) _{hji}=\left( {\mathcal {F}}^{-1}\right) _{ha}\left( \nabla P\right) _{aji}={\mathcal {F}}_{ha}^{-1}P_{aj,i}, \end{aligned}$$
(13)
$$\begin{aligned}&\Lambda _{ijh}^{r}=\left( \left[ {\mathcal {P}}^{\mathrm{T}}\nabla P\right] ^{\mathrm{T}_{13}}\right) _{ijh}=\left( {\mathcal {P}}^{\mathrm{T}}\nabla P\right) _{hji}=\left( {\mathcal {P}}^{\mathrm{T}}\right) _{_{ha}}\left( \nabla P\right) _{aji}={\mathcal {P}}_{ah}P_{aj,i}. \end{aligned}$$
(14)

We remark that the tensors defined in (10), (11) and (12) are objective as shown in the following. Let Q be a general orthogonal matrix giving a change of the frame of reference, let \(\left[ {\mathcal {F}}\right] \) be the matrix representation of the deformation gradient \({\mathcal {F}}\), \(\left[ {\mathcal {P}}\right] \) be that of the micromorphic deformation gradient \({\mathcal {P}}\) and \(\left[ \nabla P\right] \) be that of its gradient. This leads to

$$\begin{aligned} \left[ \overline{{\mathcal {F}}}\right] =Q\left[ {\mathcal {F}}\right] ,\quad \left[ \overline{{\mathcal {P}}}\right] =Q\left[ {\mathcal {P}}\right] ,\quad \left[ \overline{\mathcal {\nabla }P}\right] =Q\left[ \nabla P\right] , \end{aligned}$$

where \(\left[ \overline{{\mathcal {F}}}\right] \), \(\left[ \overline{{\mathcal {P}}}\right] \) and \(\left[ \overline{\mathcal {\nabla }P}\right] \) are the matrix representations of the same tensors \({\mathcal {F}}\), \({\mathcal {P}}\) and \(\nabla P\), respectively, in the rotated, via Q, frame of reference. It is straightforward to show that the matrix representation \(\left[ {\overline{G}}\right] \) of the Green–Saint-Venant tensor in this rotated frame of reference is the same as that in the initial frame of reference, denoted by \(\left[ G\right] \),

$$\begin{aligned} \left[ {\overline{G}}\right] =\frac{1}{2}\left( \left[ \overline{{\mathcal {F}}}\right] ^{\mathrm{T}}\left[ \overline{{\mathcal {F}}}\right] -\left[ I\right] \right) =\frac{1}{2}\left( \left[ {\mathcal {F}}\right] ^{\mathrm{T}}Q^{\mathrm{T}}Q\left[ {\mathcal {F}}\right] -\left[ I\right] \right) =\frac{1}{2}\left( \left[ {\mathcal {F}}\right] ^{\mathrm{T}}\left[ {\mathcal {F}}\right] -\left[ I\right] \right) =\left[ G\right] , \end{aligned}$$

where \(\left[ I\right] \) is the identity matrix. The same frame indifference can be demonstrated for the micromorphic Green–Saint-Venant tensor M, using the matrix representations \(\left[ {\overline{M}}\right] \) and \(\left[ M\right] \) as

$$\begin{aligned} \left[ {\overline{M}}\right] =\frac{1}{2}\left( \left[ \overline{{\mathcal {P}}}\right] ^{\mathrm{T}}\left[ \overline{{\mathcal {P}}}\right] -\left[ I\right] \right) =\frac{1}{2}\left( \left[ {\mathcal {P}}\right] ^{\mathrm{T}}Q^{\mathrm{T}}Q\left[ {\mathcal {P}}\right] -\left[ I\right] \right) =\frac{1}{2}\left( \left[ {\mathcal {P}}\right] ^{\mathrm{T}}\left[ {\mathcal {P}}\right] -\left[ I\right] \right) =\left[ M\right] , \end{aligned}$$

for the relative micro–macro-Green–Saint-Venant tensor \(\Upsilon \), using the matrix representations \(\left[ {\overline{\Upsilon }}\right] \) and \(\left[ \Upsilon \right] \) as

$$\begin{aligned} \left[ {\overline{\Upsilon }}\right] =\left[ I\right] -\left[ \overline{{\mathcal {P}}}\right] ^{\mathrm{T}}\left[ \overline{{\mathcal {F}}}\right] ^{-T}=\left[ {\mathcal {P}}\right] ^{\mathrm{T}}Q^{\mathrm{T}}Q\left[ {\mathcal {F}}\right] ^{-T}-I=\left[ {\mathcal {P}}\right] ^{\mathrm{T}}\left[ {\mathcal {F}}\right] ^{-T}-I=\left[ \Upsilon \right] , \end{aligned}$$

for the first relative micro-deformation gradient using with the matrix representations \(\left[ {\overline{\Lambda }}\right] \) and \(\left[ \Lambda \right] \) (or with that of its transpose 1–3 counterparts \(\left[ {\overline{\Lambda }}^{\mathrm{T}_{13}}\right] \) and \(\left[ \Lambda ^{\mathrm{T}_{13}}\right] \)) as

$$\begin{aligned} \left[ {\overline{\Lambda }}^{\mathrm{T}_{13}}\right] =\left[ \overline{{\mathcal {F}}}\right] ^{-1}\left[ \overline{\nabla P}\right] =\left[ {\mathcal {F}}\right] ^{-1}Q^{\mathrm{T}}Q\left[ \nabla P\right] =\left[ {\mathcal {F}}\right] ^{-1}\left[ \nabla P\right] =\left[ \Lambda ^{\mathrm{T}_{13}}\right] . \end{aligned}$$

and, for the second relative micro-deformation gradient, using the matrix representations \(\left[ {\overline{\Lambda }}_{r}\right] \) and \(\left[ \Lambda _{r}\right] \) (or with that of its transpose \(1-3\) counterparts \(\left[ {\overline{\Lambda }}_{r}^{\mathrm{T}_{13}}\right] \) and \(\left[ \Lambda _{r}^{\mathrm{T}_{13}}\right] \)) as,

$$\begin{aligned} \left[ {\overline{\Lambda }}_{r}^{\mathrm{T}_{13}}\right] =\left[ \overline{{\mathcal {P}}}\right] ^{\mathrm{T}}\left[ \overline{\nabla P}\right] =\left[ {\mathcal {P}}\right] ^{\mathrm{T}}Q^{\mathrm{T}}Q\left[ \nabla P\right] =\left[ {\mathcal {P}}\right] ^{\mathrm{T}}\left[ \nabla P\right] =\left[ \Lambda _{r}^{\mathrm{T}_{13}}\right] . \end{aligned}$$

.

Fig. 2
figure 2

Continuum model. The reference configuration of the continuum body is \(C^{*}\). Each point of it is called \(X\in C^{*}\), and its placement is \(\chi \left( X,t\right) \). Such a point X is the representative of a microstructure, e.g., the cube in the figure. Within the microstructure (thus, within the cube in the figure), two placements are defined. The first, according to (4), is the same placement \(\chi \left( X,t\right) \) of the point X. The second, according to (5), placement \(\chi '\left( X,X',t\right) \) define that of any other points \(X'\) of the microstructure

Full size image

2.3 Identification via Piola’s ansatz

In the continuum-discrete models identification, we follow Piola’s ansatz, such that

$$\begin{aligned}&\chi \left( X_{i},t\right) =\chi _{i}\left( t\right) ,\qquad P\left( X_{i},t\right) =P_{i}\left( t\right) ,\qquad \forall i=1,\ldots ,N,\quad \forall t\in {\mathbb {R}}. \end{aligned}$$
(15)

The (15) implies that the placements \(\chi _{i}\left( t\right) \) and the micro-deformation \(P_{i}\left( t\right) \), with \(i=1,\ldots ,N\), of the N sub-bodies \(B_{n}\) in the discrete model illustrated in Fig. 1 correspond to the placement \(\chi \left( X,t\right) \) and the micro-deformation \(P\left( X,t\right) \), evaluated, respectively, at the points \(X_{i}\) with \(i=1,\ldots ,N\), of the body \(C^{*}\) in the continuous model given in Fig. 2. With this in mind, we will utilize the discrete model only as a guiding justification for the constitutive assumptions postulated in Sect. 3. Needless to say, the content of this paper refers to the continuous model of Fig. 2. The connection with the discrete model is only suggestive of possible micro-scale mechanism that could be revealed through the Piola’s ansatz (15) and is useful for the introduction of the indicated constitutive assumptions. We note that no attempt is made here to give an evolution equation of each grain as one would for a completely discrete description.

2.4 Cosserat and strain-gradient continua obtained by proper restrictions of the micro-deformation \({\mathcal {P}}\)

We note that restrictions on the micro-deformation \({\mathcal {P}}=P\left( X,t\right) \) define different type of microstructural continua. First of all, no restriction on \({\mathcal {P}}\) defines a micromorphic continua, but (i) an orthogonal micro-deformation \({\mathcal {P}}\) define from (10) Cosserat continua,

$$\begin{aligned} {\mathcal {P}}\in \mathrm{Orth},\qquad \Longrightarrow \qquad M=0, \end{aligned}$$

and (ii) second gradient continua are obtained when the micro-deformation \({\mathcal {P}}\) is identified with the deformation gradient \({\mathcal {F}}\),

$$\begin{aligned} {\mathcal {P}}={\mathcal {F}}=\left( \nabla \chi \right) , \end{aligned}$$

that implies (iia) zero nonlinear relative deformation \(\Upsilon \) from (11), (iib) identification of the Green–Saint-Venant tensor G and of the micromorphic Green–Saint-Venant tensor M from (10),

$$\begin{aligned} \Upsilon =0,\qquad G=M, \end{aligned}$$

(iic) identification of the 13-transpose second relative micro-deformation gradient \(\Lambda ^{r}\) and nonlinear macro-strain-gradient tensor \(\nabla G\),

$$\begin{aligned} \left( \Lambda ^{r}\right) ^{\mathrm{T}_{13}}={\mathcal {P}}^{\mathrm{T}}\nabla P={\mathcal {F}}^{\mathrm{T}}\nabla F=\nabla G, \end{aligned}$$

and (iid) the following relation between the first relative micro-deformation gradient \(\Lambda \) and the nonlinear macro-strain-gradient \(\nabla G\),

$$\begin{aligned} \left( \Lambda \right) ^{\mathrm{T}_{13}}={\mathcal {P}}^{\mathrm{T}}\nabla P={\mathcal {F}}^{-1}\nabla F={\mathcal {F}}^{-1}{\mathcal {F}}^{-\mathrm{T}}{\mathcal {F}}^{\mathrm{T}}\nabla F=C^{-1}\nabla G, \end{aligned}$$

where the left Cauchy–Green deformation tensor C is defined,

$$\begin{aligned} C={\mathcal {F}}^{\mathrm{T}}{\mathcal {F}}. \end{aligned}$$

3 Elastic strain energy

3.1 Relative deformation measures

Let us now assume that two sub-bodies, n and p, respectively, placed in the reference configuration at \(X_{n}\) and \(X_{p}\), are neighboring ones that their distance is L in the reference configuration and that the unit vector \({\hat{c}}\) is defined as follows:

$$\begin{aligned} X_{n}-X_{p}={\hat{c}}L. \end{aligned}$$
(16)

In the reference configuration, therefore, the vector attached to the position \(X_{n}\) and pointing to the position \(X_{p}\) is \({\hat{c}}L\) and given in (16). Further, let us restrict the present model to the case in which the sub-bodies, n and p, place and deform similarly in the present configuration, and therefore the following Taylor’s series expansions are possible and yield

$$\begin{aligned}&\chi \left( X_{n},t\right) \cong \chi \left( X_{p},t\right) +\left( \nabla \chi \right) _{X_{p}}\left( X_{n}-X_{p}\right) =\chi \left( X_{p},t\right) +{\mathcal {F}}\left( X_{n}-X_{p}\right) . \end{aligned}$$
(17)
$$\begin{aligned}&P\left( X_{n},t\right) \cong P\left( X_{p},t\right) +\left( \nabla P\right) _{X_{p}}\left( X_{n}-X_{p}\right) . \end{aligned}$$
(18)
$$\begin{aligned}&F\left( X_{n},t\right) \cong F\left( X_{p},t\right) . \end{aligned}$$
(19)

We can now define the following 3 objective tensors that may be utilized to represent the material deformation that are traceable to the micro-scale grain-pair relative displacements

$$\begin{aligned} g^{np}\left( t\right)&=\frac{1}{2}\left[ F^{\mathrm{T}}\left( X_{p},t\right) F\left( X_{n},t\right) -I\right] , \end{aligned}$$
(20)
$$\begin{aligned} m^{np}\left( t\right)&=\frac{1}{2}\left[ P^{\mathrm{T}}\left( X_{p},t\right) P\left( X_{n},t\right) -I\right] , \end{aligned}$$
(21)
$$\begin{aligned} \gamma ^{np}\left( t\right)&=I-P^{\mathrm{T}}\left( X_{n},t\right) F^{-\mathrm{T}}\left( X_{p},t\right) , \end{aligned}$$
(22)

where the superscripts n and p refers to the microstructures placed at \(X_{n}\) and at \(X_{p}\). We call the tensor \(g^{np}\) in (20) the macro-deformation, the tensor \(m^{np}\) in (21) the micro-deformation and the tensor \(\gamma ^{np}\) in (22) the micro–macro-deformation. The proof of their objectivity is analogous with that derived at the end of Sect. 2.2.

By insertion of the Taylor’s series expansions (18–19) into the 3 definitions (20–22), yield, respectively,

$$\begin{aligned} g^{np}\left( t\right)&=\frac{1}{2}\left[ F^{\mathrm{T}}\left( X_{p},t\right) F\left( X_{n},t\right) -I\right] =\frac{1}{2}\left[ F^{\mathrm{T}}\left( X_{p},t\right) F\left( X_{p},t\right) -I\right] , \end{aligned}$$
(23)
$$\begin{aligned} m^{np}\left( t\right)&=\frac{1}{2}\left[ P^{\mathrm{T}}\left( X_{p},t\right) P\left( X_{n},t\right) -I\right] \nonumber \\&=\frac{1}{2}\left[ P^{\mathrm{T}}\left( X_{p},t\right) P\left( X_{p},t\right) -I\right] +\frac{1}{2}P^{\mathrm{T}}\left( X_{p},t\right) \left( \nabla P\right) _{X_{p}}\left( X_{n}-X_{p}\right) , \end{aligned}$$
(24)
$$\begin{aligned} \gamma ^{np}\left( t\right)&=I-P^{\mathrm{T}}\left( X_{n},t\right) F^{-\mathrm{T}}\left( X_{p},t\right) =\nonumber \\&=I-P^{\mathrm{T}}\left( X_{p},t\right) F^{-\mathrm{T}}\left( X_{p},t\right) -\left[ \left( \nabla P^{\mathrm{T}}\right) _{X_{p}}\left( X_{n}-X_{p}\right) \right] F^{-\mathrm{T}}\left( X_{p},t\right) . \end{aligned}$$
(25)

The use of objective Green–Saint-Venant tensors in (10), (11) and (12) into (23), (24) and (25), yield,

$$\begin{aligned} g^{np}&=G \end{aligned}$$
(26)
$$\begin{aligned} m^{np}&=M+\frac{L}{2}P^{\mathrm{T}}\nabla P{\hat{c}}=M+\frac{L}{2}\left( {\hat{c}}\Lambda ^{r}\right) ^{\mathrm{T}}\end{aligned}$$
(27)
$$\begin{aligned} \gamma ^{np}&=\Upsilon -L\left[ \left( \nabla P^{\mathrm{T}}\right) {\hat{c}}\right] F^{-\mathrm{T}}=\Upsilon -L{\hat{c}}\Lambda \end{aligned}$$
(28)

The last two equations are derived easily in index notation as follows:

$$\begin{aligned}&m_{ij}^{np}=M_{ij}+\frac{L}{2}\left( P^{\mathrm{T}}\right) _{ia}\left( \nabla P\right) _{ajk}{\hat{c}}_{k}=M_{ij}+\frac{L}{2}P_{ai}P_{aj,k}{\hat{c}}_{k}=M_{ij}+\frac{L}{2}\Lambda _{kji}^{r}{\hat{c}}_{k},\\&\gamma _{ij}^{np}=\Upsilon _{ij}-L\left( \nabla P^{\mathrm{T}}\right) _{iab}{\hat{c}}_{b}\left( F^{-\mathrm{T}}\right) _{aj}=\Upsilon _{ij}-LP_{ai,b}{\hat{c}}_{b}F_{ja}^{-1}=\Upsilon _{ij}-LF_{ja}^{-1}P_{ai,b}{\hat{c}}_{b}=\Upsilon _{ij}-L{\hat{c}}_{b}\Lambda _{bij}, \end{aligned}$$

where the definitions (13) and (14) have been considered.

Thus, we define the objective relative displacement, i.e., the macro-relative displacement, with (26),

$$\begin{aligned} u^{np}=2Lg^{np}{\hat{c}}=2LG{\hat{c}}, \end{aligned}$$
(29)

the micro–macro-relative displacement, with (28),

$$\begin{aligned} d^{np}=L\gamma ^{np}{\hat{c}}=L\left( \Upsilon -L{\hat{c}}\Lambda \right) {\hat{c}} \end{aligned}$$
(30)

and the micro-relative-displacement, with (27),

$$\begin{aligned} r^{np}=2Lm^{np}{\hat{c}}=2LM{\hat{c}}+L^{2}{\hat{c}}\left( {\hat{c}}\Lambda ^{r}\right) \end{aligned}$$
(31)

that, in index notation, are

$$\begin{aligned} u_{i}^{np}=2LG_{ij}{\hat{c}}_{j},\qquad d_{i}^{np}=L\Upsilon _{ij}{\hat{c}}_{j}-L^{2}\Lambda _{bij}{\hat{c}}_{b}{\hat{c}}_{j},\qquad r_{i}^{np}=2LM_{ij}{\hat{c}}_{j}+L^{2}\Lambda _{abi}^{r}{\hat{c}}_{a}{\hat{c}}_{b} \end{aligned}$$

The half projection of the objective relative displacements on the unit vector \({\hat{c}}\), defined in (16), is the so called normal displacements \(u_{\eta }\). In the same way, \(d_{\eta }\) is defined as the normal micro–macro-relative displacement and \(r_{\eta }\) is defined as the normal micro-relative displacement,

$$\begin{aligned}&u_{\eta }=\frac{1}{2}u^{np}\cdot {\hat{c}}=LG_{ij}{\hat{c}}_{i}{\hat{c}}_{j},\quad d_{\eta }=d^{np}\cdot {\hat{c}}=L\Upsilon _{ij}{\hat{c}}_{j}{\hat{c}}_{i}-L^{2}\Lambda _{abc}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}, \end{aligned}$$
(32)
$$\begin{aligned}&r_{\eta }=r^{np}\cdot {\hat{c}}=2LM_{ij}{\hat{c}}_{j}{\hat{c}}_{i}+L^{2}\Lambda _{abc}^{r}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}. \end{aligned}$$
(33)

Their squares are

$$\begin{aligned}&u_{\eta }^{2}=\left( LG_{ij}{\hat{c}}_{i}{\hat{c}}_{j}\right) \left( LG_{ab}{\hat{c}}_{a}{\hat{c}}_{b}\right) ,\\&d_{\eta }^{2}=\left( L\Upsilon _{ij}{\hat{c}}_{j}{\hat{c}}_{i}-L^{2}\Lambda _{ijh}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{h}\right) \left( L\Upsilon _{ab}{\hat{c}}_{a}{\hat{c}}_{b}-L^{2}\Lambda _{abc}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}\right) ,\\&r_{\eta }^{2}=\left( 2LM_{ij}{\hat{c}}_{j}{\hat{c}}_{i}+L^{2}\Lambda _{ijh}^{r}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{h}\right) \left( 2LM_{ab}{\hat{c}}_{a}{\hat{c}}_{b}+L^{2}\Lambda _{abc}^{r}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}\right) , \end{aligned}$$

and therefore

$$\begin{aligned} u_{\eta }^{2}&=L^{2}G_{ij}G_{ab}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}, \end{aligned}$$
(34)
$$\begin{aligned} d_{\eta }^{2}&=L^{2}\Upsilon _{ij}\Upsilon _{ab}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}-2L^{3}\Upsilon _{ij}\Lambda _{abc}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}+L^{4}\Lambda _{ijh}\Lambda _{abc}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c},\end{aligned}$$
(35)
$$\begin{aligned} r_{\eta }^{2}&=4L^{2}M_{ij}M_{ab}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}+4L^{3}M_{ij}\Lambda _{abc}^{r}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}+L^{4}\Lambda _{ijh}^{r}\Lambda _{abc}^{r}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c},\end{aligned}$$
(36)
$$\begin{aligned} u_{\eta }d_{\eta }&=L^{2}G_{ij}\Upsilon _{ab}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}-L^{3}G_{ij}\Lambda _{abc}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c},\end{aligned}$$
(37)
$$\begin{aligned} u_{\eta }r_{\eta }&=2L^{2}G_{ij}M_{ab}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}+L^{3}G_{ij}\Lambda _{abc}^{r}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c},\end{aligned}$$
(38)
$$\begin{aligned} r_{\eta }d_{\eta }&=2L^{2}M_{ij}\Upsilon _{ab}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}+L^{3}\Upsilon _{ij}\Lambda _{abc}^{r}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c} \nonumber \\&\quad -L^{3}M_{ij}\Lambda _{abc}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}-L^{4}\Lambda _{ijh}^{r}\Lambda _{abc}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}. \end{aligned}$$
(39)

The tangent displacement \(u_{\tau }\) is defined

$$\begin{aligned} u_{\tau }=u^{np}-\left( u^{np}\cdot {\hat{c}}\right) {\hat{c}}. \end{aligned}$$
(40)

as well as its square

$$\begin{aligned}&u_{\tau }^{2}=u^{np}\cdot u^{np}-u_{\eta }^{2}=4L^{2}G_{ij}G_{ab}\left( \delta _{ia}{\hat{c}}_{j}{\hat{c}}_{b}-{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}\right) \end{aligned}$$
(41)

The tangent micro–macro-relative displacement \(d_{\tau }\) and the tangent micro-relative displacement \(r_{\tau }\) are defined

$$\begin{aligned}&d_{\tau }=d^{np}-\left( d^{np}\cdot {\hat{c}}\right) {\hat{c}}. \end{aligned}$$
(42)
$$\begin{aligned}&r_{\tau }=r^{np}-\left( r^{np}\cdot {\hat{c}}\right) {\hat{c}}. \end{aligned}$$
(43)

Thus, their squares are calculated as follows:

$$\begin{aligned} d_{\tau }^{2}&=L^{2}\Upsilon _{ij}\Upsilon _{ab}\left[ {\hat{c}}_{j}{\hat{c}}_{b}\delta _{ia}-{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}\right] \nonumber \\&\quad -2L^{3}\Upsilon _{ij}\Lambda _{abc}\left[ {\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{c}\delta _{ib}-{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}\right] +L^{4}\Lambda _{ijh}\Lambda _{abc}\left[ {\hat{c}}_{i}\delta _{jb}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{c}-{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}\right] ,\end{aligned}$$
(44)
$$\begin{aligned} r_{\tau }^{2}&=4L^{2}M_{ij}M_{ab}\left[ {\hat{c}}_{j}{\hat{c}}_{b}\delta _{ia}-{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}\right] \nonumber \\&\quad +4L^{3}M_{ij}\Lambda _{abc}^{r}\left[ {\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{c}\delta _{ib}-{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}\right] +L^{4}\Lambda _{ijh}^{r}\Lambda _{abc}^{r}\left[ {\hat{c}}_{i}\delta _{jb}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{c}-{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}\right] . \end{aligned}$$
(45)

3.2 Definition of the elastic strain energy function in the nonlinear case

The elastic energy function for a given couple of sub-bodies, say the couple n–p considered in Sect. 3.1, is assumed to be a quadratic form of normal and tangent components of the macro-relative displacement (29), of the micro–macro-relative displacement (30) and of the micro-relative displacement (31),

$$\begin{aligned} U^{np}=\frac{1}{2}k_{\eta }u_{\eta }^{2}+\frac{1}{2}k_{\tau }u_{\tau }^{2}+\frac{1}{2}k_{d\eta }d_{\eta }^{2}+\frac{1}{2}k_{d\tau }d_{\tau }^{2}+\frac{1}{2}k_{r\eta }r_{\eta }^{2}+\frac{1}{2}k_{r\tau }r_{\tau }^{2}+k_{ud}u_{\eta }d_{\eta }+k_{ur}u_{\eta }r_{\eta }+k_{rd}r_{\eta }d_{\eta }, \end{aligned}$$
(46)

where \(k_{\eta }\), \(k_{\tau }\), \(k_{d\eta }\), \(k_{d\tau }\), \(k_{r\eta }\), \(k_{r\tau }\), \(k_{ud}\), \(k_{ur}\) and \(k_{rd}\) are 9 elastic constitutive coefficients of the present formulation. In principle, in the anisotropic case, they all are a function of the unit vector \({\hat{c}}\), i.e., they are nine orientation distribution function of the stiffness of the continuum. In particular, \(k_{\eta }\) and \(k_{\tau }\) are the normal and tangent stiffness defined and used in [84]. Here, the kinematic characterization of the material is more complicated, and we have also the normal \(k_{d\eta }\) and tangent \(k_{d\tau }\) micro–macro-relative stiffness and the normal \(k_{r\eta }\) and tangent \(k_{r\tau }\) micro-relative stiffness. Besides, the presence of three scalar invariants \(u_{\eta }\), \(d_{\eta }\) and \(r_{\eta }\) makes possible three kinds of elastic interactions, i.e., the displacement-micro–macro-relative interaction with the homonymous stiffness \(k_{ud}\), the displacement-micro-relative interaction with the homonymous stiffness \(k_{ur}\) and the micro–macro–micro-relative interaction with the homonymous stiffness \(k_{rd}\). We also note that the quadratic assumption in (46) is a first step. Other potential functions can be introduced that can lead to material nonlinearity, and for the case of asymmetric tension-compression response evolving anisotropy (see for example [85]) and chirality [84] can emerge at the macro-scale when subjected to loading. Insertion of (34–41–35–44–36–45–37–38–39) into (46) and integrating over all the orientations of the unit circle \({\mathcal {S}}^{1}\) in the 2D case or over the unit sphere \({\mathcal {S}}^{2}\) in the 3D case yields

$$\begin{aligned} U&=\int \limits _{{\mathcal {S}}^{1,2}}U^{np}=\int _{{\mathcal {S}}^{1}}\frac{1}{2}k_{\eta }\left( L^{2}G_{ij}G_{ab}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}\right) +\frac{1}{2}k_{\tau }\left( 4L^{2}G_{ij}G_{ab}\left( \delta _{ia}{\hat{c}}_{j}{\hat{c}}_{b}-{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}\right) \right) \\&\quad +\int \limits _{{\mathcal {S}}^{1,2}}\frac{1}{2}k_{d\eta }L^{2}\Upsilon _{ij}\Upsilon _{ab}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}+\frac{1}{2}k_{d\tau }L^{2}\Upsilon _{ij}\Upsilon _{ab}\left[ {\hat{c}}_{j}{\hat{c}}_{b}\delta _{ia}-{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}\right] \\&\quad -\int \limits _{{\mathcal {S}}^{1,2}}\frac{1}{2}k_{d\eta }2L^{3}\Upsilon _{ij}\Lambda _{abc}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}+\frac{1}{2}k_{d\tau }2L^{3}\Upsilon _{ij}\Lambda _{abc}\left[ {\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{c}\delta _{ib}-{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}\right] \\&\quad +\int \limits _{{\mathcal {S}}^{1,2}}\frac{1}{2}k_{d\eta }L^{4}\Lambda _{ijh}\Lambda _{abc}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}+\frac{1}{2}k_{d\tau }L^{4}\Lambda _{ijh}\Lambda _{abc}\left[ {\hat{c}}_{i}\delta _{jb}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{c}-{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}\right] \\&\quad +\int \limits _{{\mathcal {S}}^{1,2}}k_{ud}L^{2}G_{ij}\Upsilon _{ab}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}-k_{ud}L^{3}G_{ij}\Lambda _{abc}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}\\&\quad +\int \limits _{{\mathcal {S}}^{1,2}}\frac{1}{2}k_{r\eta }4L^{2}M_{ij}M_{ab}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}+\frac{1}{2}k_{r\tau }4L^{2}M_{ij}M_{ab}\left[ {\hat{c}}_{j}{\hat{c}}_{b}\delta _{ia}-{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}\right] \\&\quad +\int \limits _{{\mathcal {S}}^{1,2}}\frac{1}{2}k_{r\eta }4L^{3}M_{ij}\Lambda _{abc}^{r}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}+\frac{1}{2}k_{r\tau }4L^{3}M_{ij}\Lambda _{abc}^{r}\left[ {\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{c}\delta _{ib}-{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}\right] \\&\quad +\int \limits _{{\mathcal {S}}^{1,2}}\frac{1}{2}k_{r\eta }L^{4}\Lambda _{ijh}^{r}\Lambda _{abc}^{r}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}+\frac{1}{2}k_{r\tau }L^{4}\Lambda _{ijh}^{r}\Lambda _{abc}^{r}\left[ {\hat{c}}_{i}\delta _{jb}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{c}-{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}\right] \\&\quad -\int \limits _{{\mathcal {S}}^{1,2}}k_{rd}L^{4}\Lambda _{ijh}^{r}\Lambda _{abc}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}\\&\quad +\int \limits _{{\mathcal {S}}^{1,2}}k_{ur}2L^{2}G_{ij}M_{ab}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}+k_{ur}L^{3}G_{ij}\Lambda _{abc}^{r}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}\\&\quad +\int \limits _{{\mathcal {S}}^{1,2}}k_{rd}2L^{2}M_{ij}\Upsilon _{ab}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}+k_{rd}L^{3}\Upsilon _{ij}\Lambda _{abc}^{r}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}-k_{rd}L^{3}M_{ij}\Lambda _{abc}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c} \end{aligned}$$

or, in a compact form we have

$$\begin{aligned} U&=\frac{1}{2}{\mathbb {C}}_{ijkl}G_{ij}G_{kl}+\frac{1}{2}{\mathbb {B}}_{ijab}\Upsilon _{ij}\Upsilon _{ab}+\frac{1}{2}{\mathbb {A}}_{ijhabc}\Lambda _{ijh}\Lambda _{abc}\nonumber \\&\quad +{\mathbb {D}}_{ijklm}\Upsilon _{ij}\Lambda _{klm}+{\mathbb {F}}_{ijklm}\Lambda _{ijk}G_{lm}+{\mathbb {G}}_{ijkl}\Upsilon _{ij}G_{kl},\nonumber \\&\quad +\frac{1}{2}{\mathbb {C}}_{ijkl}^{r}M_{ij}M_{kl}+{\mathbb {D}}_{ijklm}^{r}M_{ij}\Lambda _{klm}^{r}+{\mathbb {D}}_{ijklm}^{rr}\left( \Upsilon _{ij}\Lambda _{klm}^{r}-M_{ij}\Lambda _{klm}\right) \nonumber \\&\quad +\frac{1}{2}{\mathbb {A}}_{ijhabc}^{r}\Lambda _{ijh}^{r}\Lambda _{abc}^{r}+{\mathbb {G}}_{ijkl}^{r}M_{ij}G_{kl}+{\mathbb {F}}_{ijklm}^{r}\Lambda _{ijk}^{r}G_{lm}+{\mathbb {B}}_{ijab}^{r}M_{ij}\Upsilon _{ab} \end{aligned}$$
(47)

where the elastic stiffness \({\mathbb {C}}\), \({\mathbb {B}}\), \({\mathbb {A}}\), \({\mathbb {D}}\), \({\mathbb {D}}^{r}\), \({\mathbb {D}}^{rr}\), \({\mathbb {F}}\), \({\mathbb {F}}^{r}\), \({\mathbb {G}}\), \({\mathbb {C}}^{r}\), \({\mathbb {A}}^{r}\) and \({\mathbb {B}}^{r}\) are identified in (47) as follows, with the symmetrization induced by the symmetry of the strain tensors G and M

$$\begin{aligned} {\mathbb {C}}_{ijkl}&=L^{2}\int \limits _{{\mathcal {S}}^{1,2}}\left( k_{\eta }-4k_{\tau }\right) {\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{k}{\hat{c}}_{l} \end{aligned}$$
(48)
$$\begin{aligned}&\quad +L^{2}\int \limits _{{\mathcal {S}}^{1,2}}k_{\tau }\left( \delta _{ik}{\hat{c}}_{j}{\hat{c}}_{l}+\delta _{il}{\hat{c}}_{j}{\hat{c}}_{k}+\delta _{jk}{\hat{c}}_{i}{\hat{c}}_{l}+\delta _{jl}{\hat{c}}_{i}{\hat{c}}_{k}\right) ,\nonumber \\ {\mathbb {B}}_{ijab}&=L^{2}\int \limits _{{\mathcal {S}}^{1,2}}\left[ \left( k_{d\eta }-k_{d\tau }\right) {\hat{c}}_{i}{\hat{c}}_{a}+k_{d\tau }\delta _{ia}\right] {\hat{c}}_{j}{\hat{c}}_{b},\end{aligned}$$
(49)
$$\begin{aligned} {\mathbb {A}}_{ijhabc}&=L^{4}\int \limits _{{\mathcal {S}}^{1,2}}\left[ \left( k_{d\eta }-k_{d\tau }\right) {\hat{c}}_{j}{\hat{c}}_{b}+k_{d\tau }\delta _{jb}\right] {\hat{c}}_{i}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{c},\end{aligned}$$
(50)
$$\begin{aligned} {\mathbb {D}}_{ijabc}&=-L^{3}\int \limits _{{\mathcal {S}}^{1,2}}\left[ \left( k_{d\eta }-k_{d\tau }\right) {\hat{c}}_{i}{\hat{c}}_{b}+k_{d\tau }\delta _{ib}\right] {\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{c},\end{aligned}$$
(51)
$$\begin{aligned} {\mathbb {D}}_{ijabc}^{r}&=2L^{3}\int \limits _{{\mathcal {S}}^{1,2}}\left( k_{r\eta }-k_{r\tau }\right) {\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{b}+\frac{1}{2}k_{r\tau }\left[ \left( {\hat{c}}_{j}\delta _{ib}+{\hat{c}}_{i}\delta _{jb}\right) \right] {\hat{c}}_{a}{\hat{c}}_{c},\end{aligned}$$
(52)
$$\begin{aligned} {\mathbb {D}}_{ijabc}^{rr}&=L^{3}\int \limits _{{\mathcal {S}}^{1,2}}k_{rd}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c},\end{aligned}$$
(53)
$$\begin{aligned} {\mathbb {F}}_{ijklm}&=-L^{3}\int \limits _{{\mathcal {S}}^{1,2}}k_{ud}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{k}{\hat{c}}_{l}{\hat{c}}_{m},\quad {\mathbb {F}}_{ijklm}^{r}=L^{3}\int \limits _{{\mathcal {S}}^{1,2}}k_{ur}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{k}{\hat{c}}_{l}{\hat{c}}_{m},\end{aligned}$$
(54)
$$\begin{aligned} {\mathbb {G}}_{ijkl}&=L^{2}\int \limits _{{\mathcal {S}}^{1,2}}k_{ud}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{k}{\hat{c}}_{l},\quad {\mathbb {G}}_{ijkl}^{r}=L^{2}\int \limits _{{\mathcal {S}}^{1,2}}k_{ur}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{k}{\hat{c}}_{l},\end{aligned}$$
(55)
$$\begin{aligned} {\mathbb {C}}_{ijkl}^{r}&=4L^{2}\int \limits _{{\mathcal {S}}^{1,2}}\left( k_{r\eta }-k_{r\tau }\right) {\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{k}{\hat{c}}_{l}\end{aligned}$$
(56)
$$\begin{aligned}&\quad L^{2}\int \limits _{{\mathcal {S}}^{1,2}}k_{r\tau }\left( \delta _{ik}{\hat{c}}_{j}{\hat{c}}_{l}+\delta _{il}{\hat{c}}_{j}{\hat{c}}_{k}+\delta _{jk}{\hat{c}}_{i}{\hat{c}}_{l}+\delta _{jl}{\hat{c}}_{i}{\hat{c}}_{k}\right) ,\nonumber \\ {\mathbb {A}}_{ijhabc}^{r}&=\frac{1}{2}L^{4}\int \limits _{{\mathcal {S}}^{1,2}}\left( k_{r\eta }-k_{r\tau }-2k_{rd}\right) {\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{b}{\hat{c}}_{c}+k_{r\tau }{\hat{c}}_{i}\delta _{jb}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{c},\end{aligned}$$
(57)
$$\begin{aligned} {\mathbb {B}}_{ijab}^{r}&=2L^{2}\int \limits _{{\mathcal {S}}^{1,2}}k_{rd}{\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{k}{\hat{c}}_{l}. \end{aligned}$$
(58)

3.3 Nonlinear 3D isotropic case in the absence of micro-deformation \(m^{np}\)

Let us assume that the micro-deformation \(m^{np}\) do not have a role in contributing to the elastic deformation energy (47). In this case, we can see from (31) that the micro-relative displacement \(r^{np}\) does not contribute to the elastic deformation energy (47). The consequence is that micro-relative displacement \(r_{\eta }\) and \(r_{\tau }\) play no role in the elastic energy expression (47), as seen from (33) and (43). Therefore, we assume that the corresponding stiffness constants with subscript r, are null, that is

$$\begin{aligned} k_{r\eta }=k_{r\tau }=k_{ur}=k_{rd}=0, \end{aligned}$$

Thus from (52), (53), (54)\(_{2}\), (55)\(_{2}\), (56), (57) and (58), we have that the corresponding stiffness tensors with superscripts r,

$$\begin{aligned} {\mathbb {D}}^{r}=0,\quad {\mathbb {D}}^{rr}=0,\quad {\mathbb {F}}^{r}=0,\quad {\mathbb {G}}^{r}=0,\quad {\mathbb {C}}^{r}=0,\quad {\mathbb {A}}^{r}=0,\quad {\mathbb {B}}^{r}=0, \end{aligned}$$

are null and therefore the elastic energy (47) is reduced to be in a form that is the analogous of that in eq. (5.1) in Mindlin [1],

$$\begin{aligned} U&=\frac{1}{2}{\mathbb {C}}_{ijkl}G_{ij}G_{kl}+\frac{1}{2}{\mathbb {B}}_{ijab}\Upsilon _{ij}\Upsilon _{ab}+\frac{1}{2}{\mathbb {A}}_{ijhabc}\Lambda _{ijh}\Lambda _{abc}\nonumber \\&\quad +{\mathbb {D}}_{ijklm}\Upsilon _{ij}\Lambda _{klm}+{\mathbb {F}}_{ijklm}\Lambda _{ijk}G_{lm}+{\mathbb {G}}_{ijkl}\Upsilon _{ij}G_{kl}. \end{aligned}$$
(59)

We will prove in Sect. 3.4 that (59) is nothing else than a possible nonlinear geometric generalization of eq. (5.1) in Mindlin [1]. Besides, in the isotropic case Mindlin [1] in eq. (5.4) has given, among the isotropic identification \({\mathbb {D}}=0\) and \({\mathbb {F}}=0\) (at the end of page 15 in Mindlin [1]), the following representations

$$\begin{aligned} {\mathbb {C}}_{ijkl}&=\lambda \delta _{ij}\delta _{kl}+\mu _{1}\delta _{ik}\delta _{jl}+\mu _{2}\delta _{il}\delta _{jk}, \end{aligned}$$
(60)
$$\begin{aligned} {\mathbb {B}}_{ijkl}&=b_{1}\delta _{ij}\delta _{kl}+b_{2}\delta _{ik}\delta _{jl}+b_{3}\delta _{il}\delta _{jk}, \end{aligned}$$
(61)
$$\begin{aligned} {\mathbb {G}}_{ijkl}&=g_{1}\delta _{ij}\delta _{kl}+g_{2}\delta _{ik}\delta _{jl}+g_{3}\delta _{il}\delta _{jk}, \end{aligned}$$
(62)
$$\begin{aligned} {\mathbb {A}}_{ijklmn}&=a_{1}\delta _{ij}\delta _{kl}\delta _{mn}+a_{2}\delta _{ij}\delta _{km}\delta _{nl}+a_{3}\delta _{ij}\delta _{kn}\delta _{lm} \nonumber \\&\quad +\,a_{4}\delta _{jk}\delta _{il}\delta _{mn}+a_{5}\delta _{jk}\delta _{im}\delta _{nl}+a_{6}\delta _{jk}\delta _{in}\delta _{lm}\nonumber \\&\quad +\,a_{7}\delta _{ki}\delta _{jl}\delta _{mn}+a_{8}\delta _{ki}\delta _{jm}\delta _{nl}+a_{9}\delta _{ki}\delta _{jn}\delta _{lm}\nonumber \\&\quad +\,a_{10}\delta _{il}\delta _{jm}\delta _{kn}+a_{11}\delta _{jl}\delta _{km}\delta _{in}+a_{12}\delta _{kl}\delta _{im}\delta _{jn}\nonumber \\&\quad +\,a_{13}\delta _{il}\delta _{jn}\delta _{km}+a_{14}\delta _{jl}\delta _{kn}\delta _{im}+a_{15}\delta _{kl}\delta _{in}\delta _{jm}, \end{aligned}$$
(63)

with those conditions that are made explicit at the end of page 16 in Mindlin [1], i.e.,

$$\begin{aligned}&\mu _{1}=\mu _{2}=\mu ,\quad g_{2}=g_{3},\quad a_{1}=a_{6},\quad a_{2}=a_{9},\quad a_{5}=a_{7},\quad a_{11}=a_{12}. \end{aligned}$$
(64)

Insertion of (64) into (60), (61), (62) and (63) into the compact form of the strain energy (59), we have

$$\begin{aligned} U&=\frac{1}{2}\lambda \delta _{ij}\delta _{kl}G_{ij}G_{kl}+\frac{1}{2}\mu \delta _{ik}\delta _{jl}G_{ij}G_{kl}+\frac{1}{2}\mu \delta _{il}\delta _{jk}G_{ij}G_{kl}\\&\quad +\frac{1}{2}b_{1}\delta _{ij}\delta _{kl}\Upsilon _{ij}\Upsilon _{kl}+\frac{1}{2}b_{2}\delta _{ik}\delta _{jl}\Upsilon _{ij}\Upsilon _{kl}+\frac{1}{2}b_{3}\delta _{il}\delta _{jk}\Upsilon _{ij}\Upsilon _{kl}\\&\quad +\frac{1}{2}a_{1}\delta _{ij}\delta _{kl}\delta _{mn}\Lambda _{ijk}\Lambda _{lmn}+\frac{1}{2}a_{2}\delta _{ij}\delta _{km}\delta _{nl}\Lambda _{ijk}\Lambda _{lmn}+\frac{1}{2}a_{3}\delta _{ij}\delta _{kn}\delta _{lm}\Lambda _{ijk}\Lambda _{lmn}\\&\quad +\frac{1}{2}a_{4}\delta _{jk}\delta _{il}\delta _{mn}\Lambda _{ijk}\Lambda _{lmn}+\frac{1}{2}a_{5}\delta _{jk}\delta _{im}\delta _{nl}\Lambda _{ijk}\Lambda _{lmn}+\frac{1}{2}a_{1}\delta _{jk}\delta _{in}\delta _{lm}\Lambda _{ijk}\Lambda _{lmn}\\&\quad +\frac{1}{2}a_{5}\delta _{ki}\delta _{jl}\delta _{mn}\Lambda _{ijk}\Lambda _{lmn}+\frac{1}{2}a_{8}\delta _{ki}\delta _{jm}\delta _{nl}\Lambda _{ijk}\Lambda _{lmn}+\frac{1}{2}a_{2}\delta _{ki}\delta _{jn}\delta _{lm}\Lambda _{ijk}\Lambda _{lmn}\\&\quad +\frac{1}{2}a_{10}\delta _{il}\delta _{jm}\delta _{kn}\Lambda _{ijk}\Lambda _{lmn}+\frac{1}{2}a_{11}\delta _{jl}\delta _{km}\delta _{in}\Lambda _{ijk}\Lambda _{lmn}+\frac{1}{2}a_{11}\delta _{kl}\delta _{im}\delta _{jn}\Lambda _{ijk}\Lambda _{lmn}\\&\quad +\frac{1}{2}a_{13}\delta _{il}\delta _{jn}\delta _{km}\Lambda _{ijk}\Lambda _{lmn}+\frac{1}{2}a_{14}\delta _{jl}\delta _{kn}\delta _{im}\Lambda _{ijk}\Lambda _{lmn}+\frac{1}{2}a_{15}\delta _{kl}\delta _{in}\delta _{jm}\Lambda _{ijk}\Lambda _{lmn}\\&\quad +g_{1}\delta _{ij}\delta _{kl}\Upsilon _{ij}G_{kl}+g_{2}\delta _{ik}\delta _{jl}\Upsilon _{ij}G_{kl}+g_{2}\delta _{il}\delta _{jk}\Upsilon _{ij}G_{kl} \end{aligned}$$

or, expanding the Kronecker symbols, it yields a geometrical nonlinear generalization of eq. (5.5) in Mindlin [1],

$$\begin{aligned} U&=\frac{1}{2}\lambda G_{ii}G_{jj}+\mu G_{ij}G_{ij}+\frac{1}{2}b_{1}\Upsilon _{ii}\Upsilon _{jj}+\frac{1}{2}b_{2}\Upsilon _{ij}\Upsilon _{ij}\nonumber \\&\quad +\frac{1}{2}b_{3}\Upsilon _{ij}\Upsilon _{ji}+g_{1}\Upsilon _{ii}G_{jj}+g_{2}\left( \Upsilon _{ij}+\Upsilon _{ji}\right) G_{ij}\nonumber \\&\quad +a_{1}\Lambda _{iik}\Lambda _{kmm}+a_{2}\Lambda _{iik}\Lambda _{jkj}+\frac{1}{2}a_{3}\Lambda _{iik}\Lambda _{jjk}+\frac{1}{2}a_{4}\Lambda _{ijj}\Lambda _{ikk}\nonumber \\&\quad +a_{5}\Lambda _{ijj}\Lambda _{kik}+\frac{1}{2}a_{8}\Lambda _{iji}\Lambda _{kjk}+\frac{1}{2}a_{10}\Lambda _{ijk}\Lambda _{ijk}+a_{11}\Lambda _{ijk}\Lambda _{jki}\nonumber \\&\quad +\frac{1}{2}a_{13}\Lambda _{ijk}\Lambda _{ikj}+\frac{1}{2}a_{14}\Lambda _{ijk}\Lambda _{jik}+\frac{1}{2}a_{15}\Lambda _{ijk}\Lambda _{kji}. \end{aligned}$$
(65)

The aim of this subsection is to identify the corresponding 18 isotropic micromorphic constitutive coefficients, i.e., \(\lambda \), \(\mu \), \(b_{1}\), \(b_{2}\), \(b_{3}\), \(g_{1}\), \(g_{2}\), \(a_{1}\), \(a_{2}\), \(a_{3}\), \(a_{4}\), \(a_{5}\), \(a_{8}\), \(a_{10}\), \(a_{11}\), \(a_{13}\), \(a_{14}\) and \(a_{15}\). To do this, we impose the isotropic condition by assuming no dependence of the five elastic stiffness \(k_{\eta }\), \(k_{\tau }\), \(k_{d\eta }\), \(k_{d\tau }\) and \(k_{ud}\) with respect to the orientation \({\hat{c}}\) (or, in the present 3D case, to the co-latitude \(\theta \) and to the longitude \(\varphi \)), i.e.,

$$\begin{aligned} k_{\eta }\left( \theta ,\varphi \right)&=\frac{{\bar{k}}_{\eta }}{4\pi },\quad k_{\tau }\left( \theta ,\varphi \right) =\frac{{\bar{k}}_{\tau }}{4\pi },\quad k_{d\eta }\left( \theta ,\varphi \right) =\frac{{\bar{k}}_{d\eta }}{4\pi },\quad k_{d\tau }\left( \theta ,\varphi \right) =\frac{{\bar{k}}_{d\tau }}{4\pi }, \end{aligned}$$
(66)
$$\begin{aligned} k_{ud}\left( \theta ,\varphi \right)&=\frac{{\bar{k}}_{ud}}{4\pi },\quad {\hat{c}}_{1}=\cos \theta \cos \varphi \quad {\hat{c}}_{2}=\cos \theta \sin \varphi \quad {\hat{c}}_{3}=\sin \theta , \end{aligned}$$
(67)

where \({\bar{k}}_{\eta }\), \({\bar{k}}_{\tau }\), \({\bar{k}}_{d\eta }\), \({\bar{k}}_{d\tau }\) and \({\bar{k}}_{ud}\) are the averaged stiffness over the unit sphere \(S^{2}\) that are defined in the general anisotropic case as follows:

$$\begin{aligned} {\bar{k}}_{\eta }&=\int \limits _{0}^{2\pi }\left[ \int \limits _{0}^{\pi }k_{\eta }\left( \theta ,\varphi \right) \sin \theta \mathrm{d}\theta \right] \mathrm{d}\varphi ,\qquad {\bar{k}}_{\tau }=\int \limits _{0}^{2\pi }\left[ \int \limits _{0}^{\pi }k_{\tau }\left( \theta ,\varphi \right) \sin \theta \mathrm{d}\theta \right] \mathrm{d}\varphi ,\\ {\bar{k}}_{d\eta }&=\int \limits _{0}^{2\pi }\left[ \int \limits _{0}^{\pi }k_{\mathrm{d}\eta }\left( \theta ,\varphi \right) \sin \theta \mathrm{d}\theta \right] d\varphi ,\qquad {\bar{k}}_{d\tau }=\int \limits _{0}^{2\pi }\left[ \int \limits _{0}^{\pi }k_{\mathrm{d}\tau }\left( \theta ,\varphi \right) \sin \theta \mathrm{d}\theta \right] \mathrm{d}\varphi ,\\ {\bar{k}}_{ud}&=\int \limits _{0}^{2\pi }\left[ \int \limits _{0}^{\pi }k_{ud}\left( \theta ,\varphi \right) \sin \theta \mathrm{d}\theta \right] \mathrm{d}\varphi . \end{aligned}$$

Insertion of (66–67) into (48), (61), (62) and (63) yields the following and desired identification:

$$\begin{aligned}&\lambda ={\mathbb {C}}_{1122}=\frac{L^{2}}{15}\left( {\bar{k}}_{\eta }-4{\bar{k}}_{\tau }\right) ,\quad \mu ={\mathbb {C}}_{1212}=\frac{L^{2}}{15}\left( {\bar{k}}_{\eta }+6{\bar{k}}_{\tau }\right) \end{aligned}$$
(68)
$$\begin{aligned}&b_{1}={\mathbb {B}}_{1122}={\mathbb {B}}_{1221}=b_{3}=\frac{L^{2}}{15}\left( {\bar{k}}_{d\eta }-{\bar{k}}_{d\tau }\right) ,\quad {\mathbb {B}}_{1212}=b_{2}=\frac{L^{2}}{15}\left( {\bar{k}}_{d\eta }+4{\bar{k}}_{d\tau }\right) ,\end{aligned}$$
(69)
$$\begin{aligned}&{\mathbb {G}}_{1122}=g_{1}={\mathbb {G}}_{1212}=g_{2}=\frac{L^{2}}{15}{\bar{k}}_{ud},\end{aligned}$$
(70)
$$\begin{aligned}&{\mathbb {A}}_{112233}=a_{1}={\mathbb {A}}_{112323}=a_{2}={\mathbb {A}}_{112332}=a_{3}=\frac{L^{4}}{105}\left( {\bar{k}}_{d\eta }-{\bar{k}}_{d\tau }\right) ,\end{aligned}$$
(71)
$$\begin{aligned}&{\mathbb {A}}_{122133}=a_{4}={\mathbb {A}}_{122313}=a_{5}={\mathbb {A}}_{121323}=a_{8}=\frac{L^{4}}{105}\left( {\bar{k}}_{d\eta }-{\bar{k}}_{d\tau }\right) ,\end{aligned}$$
(72)
$$\begin{aligned}&{\mathbb {A}}_{123231}=a_{11}={\mathbb {A}}_{123132}=a_{13}={\mathbb {A}}_{123213}=a_{14}=\frac{L^{4}}{105}\left( {\bar{k}}_{d\eta }-{\bar{k}}_{d\tau }\right) \end{aligned}$$
(73)
$$\begin{aligned}&{\mathbb {A}}_{123123}=a_{10}={\mathbb {A}}_{123321}=a_{15}=\frac{L^{4}}{105}\left( {\bar{k}}_{d\eta }+6{\bar{k}}_{d\tau }\right) . \end{aligned}$$
(74)

3.4 Linear 3D isotropic case for general micro-deformation \(m^{np}\)

From the definition of the deformation gradient \(F=\nabla \chi \) in (9)\(_{1}\) and of the micromorphic deformation gradient P in (8), we define the displacement gradient H and the transpose micromorphic displacement gradient \(\Psi \),

$$\begin{aligned} {\mathcal {F}}=I+H,\quad {\mathcal {P}}=I+\Psi ^{\mathrm{T}}. \end{aligned}$$
(75)

Thus, the first nonlinear micro-deformation gradient, for small displacement approximations, is simplified from (13),

$$\begin{aligned} \Lambda _{ijh}={\mathcal {F}}_{ha}^{-1}P_{aj,i}\cong \left( \delta _{ha}-H_{ha}\right) P_{aj,i}\cong \delta _{ha}P_{aj,i}=P_{hj,i}=\Psi _{jh,i}=\kappa _{ijh}, \end{aligned}$$
(76)

and the second nonlinear micro-deformation gradient, for small displacement approximations, is simplified from (14),

$$\begin{aligned} \Lambda _{ijh}^{r}={\mathcal {P}}_{ah}P_{aj,i}=\left( \delta _{ah}+\Psi _{ha}\right) P_{aj,i}\cong \delta _{ah}P_{aj,i}=P_{hj,i}=\Psi _{jh,i}=\kappa _{ijh}, \end{aligned}$$
(77)

that means that in the linear approximation, the first \(\Lambda \) and the second \(\Lambda ^{r}\) nonlinear micro-deformation gradients are the same third-order tensor \(\kappa \), that is called the micro-deformation gradient. Besides, the Green–Saint-Venant tensor G (or nonlinear macro-strain), the micromorphic Green–Saint-Venant tensor M and the micro–macro-Green–Saint-Venant tensors \(\Upsilon \) (or nonlinear relative deformation), for small displacement approximations, are simplified from (10) and (11)

$$\begin{aligned}&G=\frac{1}{2}\left( H+H^{\mathrm{T}}+H^{\mathrm{T}}H\right) \cong \frac{1}{2}\left( H+H^{\mathrm{T}}\right) =\epsilon ,\end{aligned}$$
(78)
$$\begin{aligned}&\Upsilon \cong I-\left( I+\Psi \right) \left( I-H^{\mathrm{T}}\right) \cong H^{\mathrm{T}}-\Psi =\gamma ,\end{aligned}$$
(79)
$$\begin{aligned}&M=\frac{1}{2}\left( \Psi +\Psi ^{\mathrm{T}}+\Psi \Psi ^{\mathrm{T}}\right) \cong \frac{1}{2}\left( \Psi +\Psi ^{\mathrm{T}}\right) =\frac{1}{2}\left( H^{\mathrm{T}}-\gamma +H-\gamma ^{\mathrm{T}}\right) =\epsilon -\frac{1}{2}\left( \gamma +\gamma ^{\mathrm{T}}\right) , \end{aligned}$$
(80)

that means from (80) that in the linear approximation, the micromorphic Green–Saint-Venant tensor M depends upon the Green–Saint-Venant tensor G and upon the micro–macro-Green–Saint-Venant tensor \(\Upsilon \) and it is not anymore an independent strain measure. Besides, the nonlinear macro-strain G is simplified from (78) in the macro-strain \(\epsilon \) and the nonlinear relative deformation \(\Upsilon \) is simplified from (79) in the relative deformation \(\gamma \). Thus, the three strain measure from (78), (79) and (76) are the same defined in Mindlin [1], respectively, in eqns. (1.10), (1.11) and (1.12), viz.,

$$\begin{aligned} \epsilon _{ij}=\frac{1}{2}\left( u_{i,j}+u_{j,i}\right) ,\quad \gamma _{ij}=u_{j,i}-\Psi _{ij},\quad \kappa _{ijk}=\Psi _{jk,i} \end{aligned}$$
(81)

Insertion of the linear approximations (76–80) into the general form of the elastic energy (47) yields

$$\begin{aligned} U&=\frac{1}{2}{\mathbb {C}}_{ijkl}^{n}\epsilon _{ij}\epsilon _{kl}+\frac{1}{2}{\mathbb {B}}_{ijkl}^{n}\gamma _{ij}\gamma _{kl}+\frac{1}{2}{\mathbb {A}}_{ijhabc}^{n}\kappa _{ijh}\kappa _{abc} \end{aligned}$$
(82)
$$\begin{aligned}&\quad +{\mathbb {D}}_{ijklm}^{n}\gamma _{ij}\kappa _{klm}+{\mathbb {F}}_{ijklm}^{n}\kappa _{ijk}\epsilon _{lm}+{\mathbb {G}}_{ijkl}^{n}\gamma _{ij}\epsilon _{kl} \end{aligned}$$
(83)

where new constitutive tensors (with the super-script n) are defined in terms of that defined in (48–58),

$$\begin{aligned}&{\mathbb {C}}_{ijkl}^{n}={\mathbb {C}}_{ijkl}+{\mathbb {C}}_{ijkl}^{r}+2{\mathbb {G}}_{ijkl}^{r}, \end{aligned}$$
(84)
$$\begin{aligned}&{\mathbb {B}}_{ijkl}^{n}={\mathbb {B}}_{ijkl}+{\mathbb {C}}_{\left( ij\right) \left( kl\right) }^{r}+2{\mathbb {B}}_{\left( ij\right) kl}^{r},\end{aligned}$$
(85)
$$\begin{aligned}&{\mathbb {A}}_{ijhabc}^{n}={\mathbb {A}}_{ijhabc}+{\mathbb {A}}_{ijhabc}^{r},\end{aligned}$$
(86)
$$\begin{aligned}&{\mathbb {D}}_{ijklm}^{n}={\mathbb {D}}_{ijklm}+{\mathbb {D}}_{\left( ij\right) klm}^{r}+{\mathbb {D}}_{\left[ ij\right] klm}^{rr},\end{aligned}$$
(87)
$$\begin{aligned}&{\mathbb {F}}_{ijklm}^{n}={\mathbb {F}}_{ijklm}+{\mathbb {D}}_{lmijk}^{r}-{\mathbb {D}}_{lmijk}^{rr}+{\mathbb {F}}_{ijklm}^{r},\end{aligned}$$
(88)
$$\begin{aligned}&{\mathbb {G}}_{ijkl}^{n}={\mathbb {G}}_{ijkl}+{\mathbb {C}}_{ij\left( kl\right) }^{r}+{\mathbb {G}}_{\left( ij\right) kl}^{r}+{\mathbb {B}}_{ijkl}^{r}, \end{aligned}$$
(89)

where the symmetrization and skew-symmetrization rules

$$\begin{aligned} A_{\left( ij\right) }=\frac{1}{2}\left( A_{ij}+A_{ji}\right) ,\qquad A_{\left[ ij\right] }=\frac{1}{2}\left( A_{ij}-A_{ji}\right) , \end{aligned}$$

have been used in (84–89). Insertion of (48–58) into (84–89) yields the explicit identification of the new constitutive tensors,

$$\begin{aligned} {\mathbb {C}}_{ijkl}^{n}&=L^{2}\int \limits _{{\mathcal {S}}^{2}}\left( k_{\eta }-4k_{\tau }+4k_{r\eta }-4k_{r\tau }+2k_{ur}\right) {\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{k}{\hat{c}}_{l} \end{aligned}$$
(90)
$$\begin{aligned}&\quad +\,L^{2}\int \limits _{{\mathcal {S}}^{2}}\left( k_{\tau }+k_{r\tau }\right) \left( \delta _{ik}{\hat{c}}_{j}{\hat{c}}_{l}+\delta _{il}{\hat{c}}_{j}{\hat{c}}_{k}+\delta _{jk}{\hat{c}}_{i}{\hat{c}}_{l}+\delta _{jl}{\hat{c}}_{i}{\hat{c}}_{k}\right) ,\nonumber \\ {\mathbb {B}}_{ijkl}^{n}&=L^{2}\int \limits _{{\mathcal {S}}^{2}}\left[ \left( k_{d\eta }-k_{d\tau }+4k_{r\eta }-4k_{r\tau }+4k_{rd}\right) {\hat{c}}_{i}{\hat{c}}_{k}{\hat{c}}_{j}{\hat{c}}_{l}\right] \end{aligned}$$
(91)
$$\begin{aligned}&\quad +\,L^{2}\int \limits _{{\mathcal {S}}^{2}}\left( k_{r\tau }+k_{d\tau }\right) \left( \delta _{ik}{\hat{c}}_{j}{\hat{c}}_{l}\right) +k_{r\tau }\left( \delta _{il}{\hat{c}}_{j}{\hat{c}}_{k}+\delta _{jk}{\hat{c}}_{i}{\hat{c}}_{l}+\delta _{jl}{\hat{c}}_{i}{\hat{c}}_{k}\right) ,\nonumber \\ {\mathbb {A}}_{ijhabc}^{n}&=L^{4}\int \limits _{{\mathcal {S}}^{2}}\left[ \left( k_{d\eta }-k_{d\tau }+\frac{1}{2}k_{r\eta }-\frac{1}{2}k_{r\tau }-k_{rd}\right) {\hat{c}}_{j}{\hat{c}}_{b}+\left( k_{d\tau }+\frac{1}{2}k_{r\tau }\right) \delta _{jb}\right] {\hat{c}}_{i}{\hat{c}}_{h}{\hat{c}}_{a}{\hat{c}}_{c},\end{aligned}$$
(92)
$$\begin{aligned} {\mathbb {D}}_{ijabc}^{n}&=L^{3}\int \limits _{{\mathcal {S}}^{2}}\left[ \left( -k_{d\eta }+k_{d\tau }+2k_{r\eta }-2k_{r\tau }\right) {\hat{c}}_{i}{\hat{c}}_{b}{\hat{c}}_{j}+\left( k_{r\tau }-k_{d\tau }\right) \delta _{ib}{\hat{c}}_{j}+k_{r\tau }{\hat{c}}_{i}\delta _{jb}\right] {\hat{c}}_{a}{\hat{c}}_{c},\end{aligned}$$
(93)
$$\begin{aligned} {\mathbb {F}}_{ijklm}^{n}&=L^{3}\int \limits _{{\mathcal {S}}^{2}}\left( k_{ur}-k_{ud}+2k_{r\eta }-2k_{r\tau }-k_{rd}\right) {\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{k}{\hat{c}}_{l}{\hat{c}}_{m}+k_{r\tau }\left[ \left( {\hat{c}}_{j}\delta _{ib}+{\hat{c}}_{i}\delta _{jb}\right) \right] {\hat{c}}_{a}{\hat{c}}_{c},\end{aligned}$$
(94)
$$\begin{aligned} {\mathbb {G}}_{ijkl}^{n}&=L^{2}\int \limits _{{\mathcal {S}}^{2}}\left( k_{ud}+k_{ur}+4k_{r\eta }-4k_{r\tau }+2k_{rd}\right) {\hat{c}}_{i}{\hat{c}}_{j}{\hat{c}}_{k}{\hat{c}}_{l}, \end{aligned}$$
(95)

In the isotropic case, among (66) and (67), we assume also the independence of the remaining stiffness with respect to the unit vector \({\hat{c}}\), i.e.,

$$\begin{aligned} k_{r\eta }\left( \theta ,\varphi \right) =\frac{{\bar{k}}_{r\eta }}{4\pi },\qquad k_{r\tau }\left( \theta ,\varphi \right) =\frac{{\bar{k}}_{r\tau }}{4\pi },\qquad k_{ur}\left( \theta ,\varphi \right) =\frac{{\bar{k}}_{ur}}{4\pi },\qquad k_{rd}\left( \theta ,\varphi \right) =\frac{{\bar{k}}_{rd}}{4\pi }. \end{aligned}$$
(96)

In this case the Lame’s constant in (68) are differently identified from insertion of (66–67–96) into (90)

$$\begin{aligned}&\lambda ={\mathbb {C}}_{1122}^{n}=\frac{1}{15}L^{2}\left( {\bar{k}}_{\eta }-4{\bar{k}}_{\tau }+4{\bar{k}}_{r\eta }-4{\bar{k}}_{r\tau }+2{\bar{k}}_{ur}\right) \end{aligned}$$
(97)
$$\begin{aligned}&\mu ={\mathbb {C}}_{1212}^{n}=\frac{1}{15}L^{2}\left( {\bar{k}}_{\eta }+6{\bar{k}}_{\tau }+4{\bar{k}}_{r\eta }+6{\bar{k}}_{r\tau }+2{\bar{k}}_{ur}\right) \end{aligned}$$
(98)

so that the Young’s modulus and the Poisson’s ratio,

$$\begin{aligned} Y=\mu \frac{3\lambda +2\mu }{\lambda +\mu },\quad \nu =\frac{\lambda }{2\left( \lambda +\mu \right) }, \end{aligned}$$
(99)

are identified as

$$\begin{aligned}&Y=\frac{1}{15}L^{2}\left( {\bar{k}}_{\eta }+6{\bar{k}}_{\tau }+4{\bar{k}}_{r\eta }+6{\bar{k}}_{r\tau }+2{\bar{k}}_{ur}\right) \frac{\left( 5{\bar{k}}_{\eta }+20{\bar{k}}_{r\eta }+10{\bar{k}}_{ur}\right) }{2\left( {\bar{k}}_{\eta }+{\bar{k}}_{\tau }+4{\bar{k}}_{r\eta }+{\bar{k}}_{r\tau }+2{\bar{k}}_{ur}\right) },\end{aligned}$$
(100)
$$\begin{aligned}&\nu =\frac{\left( {\bar{k}}_{\eta }-4{\bar{k}}_{\tau }+4{\bar{k}}_{r\eta }-4{\bar{k}}_{r\tau }+2{\bar{k}}_{ur}\right) }{4\left( {\bar{k}}_{\eta }+{\bar{k}}_{\tau }+4{\bar{k}}_{r\eta }+{\bar{k}}_{r\tau }+2{\bar{k}}_{ur}\right) } \end{aligned}$$
(101)

These expressions for the stiffness parameters in 90–95 provide an essential seed for an initial estimation of all the elastic parameters that characterize a micromorphic continuum. It is remarkable that these first estimates indicate that such materials are described by several characteristic lengths, which can be multiples of relevant grain-size, and represent the influence of grain-scale micromechanisms on the emergent behavior at the macro-scale. These micromechanisms may include those that resemble the floppy behavior of pantograph, best described by second-gradient macro-scale continua analyzed in [35, 86], or other mechanisms that require additional kinematical descriptors to capture the deformation energy of grain-pair [7, 17, 51, 71]. It is also noteworthy that it is possible to estimate the elastic parameters a micromorphic continuum in terms of a few parameters that link to the micromechanisms without recourse to ad hoc prescriptions or a priori (over) simplifications. For certain, relatively simple micromechanisms and structures, such linkages can indeed be identified, synthesized and experimentally characterized as discussed in [51, 52]and [42,43,44,45,46,47,48,49,50, 87,88,89,90].

4 Conclusion

For accurate and tractable description of the mechanical behavior of a large class of materials which at some spatial scale possess granular microstructure, refined models, such as the micromorphic models, are needed. Such models are particularly significant for bridging, in a heuristic way, across spatial scales ranging from that at grain interactions to collective behavior of large numbers of grains. At meso-scales of few grains to tens of thousands of grains, discrete simulations can be conceived that provide the trajectories and distribution of grain-scale deformation energies. It is worthwhile to note here that although discrete models have proliferated over the past several decades, their systematic validation through experimentally measured particle trajectories and grain-scale energy distributions have been characteristically sparse (absent to the knowledge of these authors). At the macro-scales consisting of large number of grains of various sizes, interfaces/surfaces, composition and arrangement (collectively micromechano-morphology), discrete models could be intractable. In these cases, micromorphic continuum models can serve as effective reduced-order models that can capture many essential aspects of the grain-scale mechanisms. This paper describes an approach to construct such micromorphic models in the framework of finite (geometrically nonlinear) deformations using the concepts of granular micromechanics. The key aspect of the described approach is the identification of the appropriate kinematic measures that describe the macro-deformation and link it to the micro-deformation, formulation of the deformation energies in terms of these measures and the application of energy methods to identify the constitutive relations. Such an approach permits potential identification of inner deformation modes that store elastic energy contributing to the emergent behavior at the macro-scale, and indicates the pathway to access these modes with the view of rational design of (meta) materials.

Furthermore, we would like to identify a number of potential outlook of the presented approach. First, the isotropic identification we have shown can be extended to an anisotropic one by the use of proper non constant orientation distribution function instead of (66–67–96). Second, the truncation of the Taylor’s series expansions (18–19) up to the first order in terms of the kinematic descriptors results in a first-grade continuum theory. Such a limitation can be removed to obtain higher order gradient continuum theories without unduly augmenting the number of the constitutive coefficients that need to be experimentally identified. Third, the quadratic assumption (46) can be generalized, such as with Leonard–Jones-type potential to take into account elastic-hardening effects and tension-compression asymmetry that can lead to emergence of anisotropy. Fourth, dissipative phenomena such as damage [84] and plasticity [91] can be included by using for example an hemivariational approach or by assuming dissipation energy in terms of additional entropic irreversible kinematical descriptors. It is further remarkable that plastic deformation in the present micromorphic form can give rise to inelastic microstructural rotation.