Families of nested graphs with compatible symmetric-group actions

Abstract

For fixed positive integers n and k, the Kneser graph $KG_{n,k}$ has vertices labeled by k-element subsets of $\{1,2,\dots ,n\}$ and edges between disjoint sets. Keeping k fixed and allowing n to grow, one obtains a family of nested graphs, each of which is acted on by a symmetric group in a way which is compatible with these inclusions and the inclusions of each symmetric group into the next. In this paper, we provide a framework for studying families of this kind using the ${{\,\mathrm{FI}\,}}$-module theory of Church et al. (Duke Math J 164(9):1833–1910, 2015), and show that this theory has a variety of asymptotic consequences for such families of graphs. These consequences span a range of topics including enumeration, concerning counting occurrences of subgraphs, topology, concerning Hom-complexes and configuration spaces of the graphs, and algebra, concerning the changing behaviors in the graph spectra.

1 Introduction

1.1 Motivation

Let ${{\,\mathrm{FI}\,}}$ denote the category whose objects are the finite sets $[n] := \{1,\ldots ,n\}$, and whose morphisms are injections. In their seminal work, Church et al. [10] introduced the notion of an ${{\,\mathrm{FI}\,}}$-module to formalize the connection between a large number of seemingly unrelated phenomena in topology and representation theory. Formally, an ${{\,\mathrm{FI}\,}}$-module is a functor from ${{\,\mathrm{FI}\,}}$ to the category of real vector spaces. Noting that the endomorphisms in ${{\,\mathrm{FI}\,}}$ are permutations, one may imagine an ${{\,\mathrm{FI}\,}}$-module as a series of representations of the symmetric groups ${\mathfrak {S}}_n$, with n increasing, which are compatible in some sense.

Recently there has been a push in the literature to use the same philosophy underlying ${{\,\mathrm{FI}\,}}$-modules to study combinatorial objects. For instance, in his recent work [21] Gadish studies what he calls ${{\,\mathrm{FI}\,}}$-posets and ${{\,\mathrm{FI}\,}}$-arrangements. In this work, we will be mostly focused on ${{\,\mathrm{FI}\,}}$-graphs, functors from ${{\,\mathrm{FI}\,}}$ to the category of graphs. For us, a graph is a finite 1-dimensional simplicial complex. Given a graph G, we write V(G) for the set of vertices of G and E(G) for the set of edges. Note that V(G) and E(G) are, by how we have defined graph, both necessary finite. Just as with the work of Gadish, we will discover that a relatively simple combinatorial condition on ${{\,\mathrm{FI}\,}}$-graphs will allow us to conclude a plethora of interesting structural properties of the graphs which comprise it.

Throughout this paper we will often denote ${{\,\mathrm{FI}\,}}$-graphs by $G_\bullet$, and use $G_n$ as a short-hand for its evaluation on [n]. The transition maps of $G_\bullet$ are the graph morphisms induced by the morphisms of ${{\,\mathrm{FI}\,}}$ which are not permutations. We say that an ${{\,\mathrm{FI}\,}}$-graph $G_\bullet$ is vertex-stable of stable degree $\le d$ if for all $n \ge d$, every vertex of $G_n$ appears in the image of some transition map. Some common examples of vertex-stable ${{\,\mathrm{FI}\,}}$-graphs include:

• The complete graphs $K_n$;

• The Kneser graphs $KG_{n,r}$, for each fixed r. These are the graphs whose vertices are r-element subsets of [n], and whose edges indicate disjointness;

• The Johnson graphs $J_{n,r}$, for each fixed r. These are the graphs whose vertices are r-element subsets of [n], and whose edges indicate that the intersection of the two subsets has size $r-1$.

Other examples of vertex-stable ${{\,\mathrm{FI}\,}}$-graphs are given at the end of Sect. 3.1. While it is straightforward to verify that the above examples are vertex-stable, one might also observe that they have a variety of other symmetries. The main structure theorem of vertex-stable ${{\,\mathrm{FI}\,}}$-graphs is that the condition of vertex-stability automatically yields several other symmetries.

Theorem A

Let $G_\bullet$ be a vertex-stable ${{\,\mathrm{FI}\,}}$-graph. Then for all $n \gg 0$:

• 1. The transition maps originating from $G_n$ are injective;

• 2. The transition maps originating from $G_n$ have induced images (see Definition 2.1);

• 3. Every edge of $G_{n+1}$ is the image of some edge of $G_n$ under some transition map;

• 4. For any fixed $r \ge 1$ and any collection of vertices $\{v_1,\ldots ,v_r\}$ of $G_{n+1}$, there exists a collection of r vertices of $G_n$, $\{w_1,\ldots ,w_r\}$ which map to $\{v_1,\ldots ,v_r\}$ under some transition map.

One should note two recurring themes in the above theorem. Firstly, many of the results in this work (indeed, many of the results in the theory of ${{\,\mathrm{FI}\,}}$-modules) are only true asymptotically. Secondly, while one can prove the existence of certain behaviors in general, it is usually quite difficult to make such existential statements effective (see Theorem 3.31 for an instance where this is not the case). This is a consequence of the methods used to prove such statements. In this work, the main proof techniques which will be employed fall under what one might call a Noetherian method. Namely, we rephrase what needs to be proven in terms of finite generation of some associated module. We then prove that this module is a submodule of something which is easily seen to be finitely generated, and apply standard Noetherianity arguments to conclude that the original module was finitely generated. It is an interesting question to ask which, if any, of our results can be made effective through more combinatorial means.

Following the proof of Theorem A, we spend the majority of the body of the paper illustrating various applications. These applications come in three flavors: enumerative, topological, and algebraic.

1.2 Enumerative applications

We begin by asking the following question: Given a vertex-stable ${{\,\mathrm{FI}\,}}$-graph $G_\bullet$, is it possible to count the occurrences of some fixed substructure in $G_n$, as a function of n?

If G is a graph, then an induced subgraph of G is a graph obtained from G by deleting some subset of the vertices and any edges involving those vertices, and a subgraph of G is a graph obtained from G by deleting some subset of the vertices, any edges involving those vertices, and some subset of the remaining edges. For a graph H, there could be multiple ways to realise it as a subgraph of G, by deleting different vertices and/or edges. This gives an instance of the above question. Can we count the number of times a given graph H occurs in $G_n$ as a function of n? We answer this question in the affirmative.

Theorem B

Let $G_\bullet$ be a vertex-stable ${{\,\mathrm{FI}\,}}$-graph of stable degree $\le d$, and let H be a graph. Then there exists a polynomial $p_H(x) \in {\mathbb {Q}}[x]$ of degree $\le |V(H)|\cdot d$ such that for all $n \gg 0$ the function

$$\begin{aligned} n \mapsto \text { the number of subgraphs of }G_n\text { isomorphic to }H \end{aligned}$$

agrees with $p_H(n)$.

Remark 1.1

For a fixed pair of graphs G and H, the number of subgraphs of G isomorphic to H is not the number of graph injections from H to G. Indeed, usually one is concerned with counting the number of such injections up to composition with automorphisms of H. Because H is independent of n, the above theorem remains true regardless of how the counting problem is interpreted.

To convince themselves of this theorem, one should consider the case of the complete graphs $K_n$. In this case, one can count the number of occurrences of H by first choosing |V(H)| vertices, and then counting the number of copies of H in the induced $K_{|V(H)|}$ subgraph. We will see in Sect. 3.1 that ${{\,\mathrm{FI}\,}}$-graphs are fairly diverse, and therefore one should not expect the general case to be quite this straightforward. However, the idea that one should begin by choosing |V(H)| vertices of $G_n$ remains relevant. From this point one proceeds by applying the fourth part of Theorem A.

Another interesting enumerative consequence of vertex-stability involves counting degrees of vertices. Recall that in a given graph G, the degree of a vertex v is the number of edges adjacent to v. We usually write $\Delta (G)$ for the maximum degree of a vertex in G, and $\delta (G)$ for the minimum degree.

Theorem C

Let $G_\bullet$ be a vertex-stable ${{\,\mathrm{FI}\,}}$-graph of stable degree $\le d$. Then the functions

$$\begin{aligned} n \mapsto \Delta (G_n) \text {and} \quad n \mapsto \delta (G_n) \end{aligned}$$

each agree with a polynomial of degree at most d for all $n \gg 0$.

While Theorem C appears very similar to Theorem B, there is one subtle difference. In the case of Theorem B, one reduces to the case of ${{\,\mathrm{FI}\,}}$-modules by considering the family of symmetric group representations induced by the symmetric group action on copies of H inside $G_n$. It is unclear, however, whether such an approach can work to prove Theorem C, as the maximum and minimum degrees of $G_n$ cannot in any obvious way be realized as the dimension of some symmetric group representation. The proof of Theorem C is therefore a bit more subtle, and can be considered more traditionally combinatorial than that of Theorem B.

To conclude our enumerative applications, we consider the question of counting walks in $G_n$. Recall that for a fixed integer $r \ge 0$ and a graph G, a walk of length r in G is an $(r+1)$-tuple of vertices of G, $(v_0,\ldots ,v_r)$, such that for all $0 \le i \le r-1$, $\{v_i,v_{i+1}\} \in E(G)$. We say that a walk $(v_0,\ldots ,v_r)$ is closed if $v_r = v_0$.

Theorem D

Let $G_\bullet$ be a vertex-stable ${{\,\mathrm{FI}\,}}$-graph of stable degree $\le d$. Then the functions

$$\begin{aligned} n \mapsto |\{\text {walks in }G_n\text { of length }r\}| \quad \text {and} \quad n \mapsto |\{\text {closed walks in }G_n\text { of length }r\}| \end{aligned}$$

each agree with a polynomial of degree at most $(r+1)d$ whenever $n \gg 0$.

1.3 Topological applications

In this paper we will be primarily concerned with two topological applications of the theory of vertex-stable ${{\,\mathrm{FI}\,}}$-graphs. Our major results will prove that certain natural topological spaces associated to vertex-stable ${{\,\mathrm{FI}\,}}$-graphs will be representation stable in the sense of Church and Farb [12] (see Definition 2.19).

Remark 1.2

In the language of [12], representation stability is a property of sequences of symmetric group representations. In this paper, we expand this definition to sequences of topological spaces with symmetric group actions, by asserting that the homology groups of spaces are representation stable in the original sense. This use of the terminology is not standard in the literature.

The first of our applications is related to the so-called ${{\,\mathrm{Hom}\,}}$-complexes. Let H and G be two graphs. A multi-homomorphism from H to G is a map of sets,

$$\begin{aligned} \alpha :V(H) \rightarrow {\mathcal {P}}(V(G))-\emptyset \end{aligned}$$

such that for all edges $\{x,y\} \in E(H)$, and all choices of $v \in \alpha (x)$ and $w \in \alpha (y)$, one has $\{v,w\} \in E(G)$. The ${{\,\mathrm{Hom}\,}}$-complex of H and G, denoted ${\mathscr {H}}om(H,G)$, the polyhedral complex whose cells are indexed by multi-homomorphisms between H and G, such that the closure of any cell given by subset inclusion (See Definition 2.4 for details). These complexes first rose to popularity through the work of Babson and Koslov [4, 5], which expanded upon famous work of Lovász [28]. For instance, it is shown in those works that the topological connectivity of the space ${\mathscr {H}}om(K_2,G)$ can be used to bound the chromatic number of G.

Theorem E

Let $G_\bullet$ be a vertex-stable ${{\,\mathrm{FI}\,}}$-graph. Then for any graph H, the functor

$$\begin{aligned} n \mapsto {\mathscr {H}}om(H,G_n) \end{aligned}$$

is representation stable (see Definition 2.19). In particular, if $i \ge 0$ is fixed, then the function

$$\begin{aligned} n \mapsto \dim _{\mathbb {R}}(H_i(|{\mathscr {H}}om(H,G_n)|;{\mathbb {R}})) \end{aligned}$$

eventually agrees with a polynomial of degree at most $|V(H)|\cdot d(i+1)$.

While this result might seem somewhat technical, it has one particularly notable consequence about counting graph homomorphisms into ${{\,\mathrm{FI}\,}}$-graphs.

Corollary F

Let $G_\bullet$ denote a vertex-stable ${{\,\mathrm{FI}\,}}$-graph of stable degree at most d. Then for any graph H the function

$$\begin{aligned} n \mapsto |{{\,\mathrm{Hom}\,}}(H,G_n)| \end{aligned}$$

agrees with a polynomial of degree at most $|V(H)|\cdot d$ for all $n \gg 0$.

Remark 1.3

The algebraic theory of graph homomorphisms implies that there are very concrete connections between counting homomorphisms into a graph, counting injective homomorphisms into a graph, and counting induced homomorphisms into a graph (see, for instance, [29, Chapter 5]). In particular, Corollary F, Theorem D, and Theorem B are not independent of each other, and can be in certain cases deduced from one another. Our presentation of the material was chosen to stress the interpretation that the polynomial behavior of homomorphisms can be thought of as a consequence of the fact that a certain family of topological spaces exhibits representation stability.

It is a well known fact that n-colorings of vertices of a graph H are in bijection with ${{\,\mathrm{Hom}\,}}(H,K_n)$, where $K_n$ is the complete graph on n vertices. The above theorem can therefore be thought of as an extension of the theorem which posits the existence of the chromatic polynomial.

Remark 1.4

The idea of treating the chromatic polynomial as an “${{\,\mathrm{FI}\,}}$ phenomenon” was conveyed to the first author by John Wiltshire-Gordon and Jordan Ellenberg. This observation was a large part of the motivation for the present work.

Following our treatment of the ${{\,\mathrm{Hom}\,}}$-complex, we next turn our attention to configuration spaces of graphs. Given a topological space X, the n-stranded configuration space of X is the topological space of n distinct points on X,

$$\begin{aligned} {{\,\mathrm{Conf}\,}}_n(X) := \{(x_1,\ldots ,x_n) \in X^n \mid x_i \ne x_j, i \ne j\}. \end{aligned}$$

Configuration spaces are in many ways the prototypical topological application of ${{\,\mathrm{FI}\,}}$-module theory. In fact, one of the results which eventually inspired the study of ${{\,\mathrm{FI}\,}}$-modules was Church’s proof that configuration spaces of manifolds are often representation stable [7]. It is unfortunately true, however, that if G is any graph then the family of topological spaces $\{{{\,\mathrm{Conf}\,}}_n(G)\}_n$ cannot be representation stable. In fact, they are extremely unstable in this sense, exhibiting factorial growth in their Betti numbers (see the discussion following Theorem 2.10). In this paper we therefore adapt a different approach, recently used by Lütgehetmann [27]. We consider the spaces ${{\,\mathrm{Conf}\,}}_m(G_\bullet )$, where m is fixed and $G_\bullet$ is a vertex-stable ${{\,\mathrm{FI}\,}}$-graph.

Theorem G

Let $G_\bullet$ be a vertex-stable ${{\,\mathrm{FI}\,}}$-graph with stable degree at most d whose transition maps are all injective and whose constituent graphs $G_n$ are all connected. Then for any $m \ge 1$ the functor

$$\begin{aligned} n \mapsto {{\,\mathrm{Conf}\,}}_m(G_n) \end{aligned}$$

is representation stable (see Definition 2.19). In particular, if $i \ge 0$ is fixed, then the function

$$\begin{aligned} n \mapsto \dim _{\mathbb {R}}(H_i({{\,\mathrm{Conf}\,}}_m(G_n);{\mathbb {R}})) \end{aligned}$$

eventually agrees with a polynomial of degree at most 2dm.

Remark 1.5

Theorem A implies that the transition maps of any vertex-stable ${{\,\mathrm{FI}\,}}$-graph are eventually injective. Because the content of the previous theorem is asymptotic, we may always replace our ${{\,\mathrm{FI}\,}}$-graph with a new ${{\,\mathrm{FI}\,}}$-graph whose transition maps are injective and agrees with our original graph for all $n \gg 0$. In particular, the assumption that the transition maps of our ${{\,\mathrm{FI}\,}}$-graph must be injective is not particularly restrictive.

The condition that $G_n$ be connected is also not necessary, although the eventual conclusion is a bit less clean if it is not assumed. The most general version of Theorem G is proven as Theorem 4.12 below.

This theorem was proven for a particular ${{\,\mathrm{FI}\,}}$-graph (see Example 3.9) by Lütgehetmann [27], although he did not use this language. His approach in that work is very topological, and sharpens certain bounds that we discover in this work, although it is limited to that example. Our approach is much more combinatorial in nature, and has the benefit of proving the above theorem for all vertex-stable ${{\,\mathrm{FI}\,}}$-graphs.

1.4 Algebraic applications

Our final kind of application involves studying the spectrum of vertex-stable ${{\,\mathrm{FI}\,}}$-graphs. For any graph G, let ${\mathbb {R}}V(G)$ denote the real vector space with basis indexed by the vertices of G. Then there are many natural endomorphisms of ${\mathbb {R}}V(G)$ which are of interest in algebraic graph theory. Perhaps the most significant is the adjacency matrix of G. This is the matrix $A_G$ defined on vertices $v \in V(G)$ by

$$\begin{aligned} A_Gv = \sum _{\{w,v\} \in E(G)} w \end{aligned}$$

The adjacency matrix of any graph is a real symmetric matrix, and therefore its eigenvalues must be real. This justifies the hypotheses of the following theorem.

Theorem H

Let $G_\bullet$ be a vertex-stable ${{\,\mathrm{FI}\,}}$-graph, and let $A_n$ denote the adjacency matrix of $G_n$. We may write the distinct eigenvalues of $A_n$ as,

$$\begin{aligned} \lambda _1(n)> \lambda _2(n)> \cdots > \lambda _{r(n)}(n), \end{aligned}$$

for some function r(n). Then for all $n \gg 0$

• 1. The function r(n) is constant. In particular, the number of distinct eigenvalues of $A_n$ is eventually constant;

• 2. For any i the function

  $$\begin{aligned} n \mapsto \lambda _i(n) \end{aligned}$$

  agrees with an function which is algebraic over the field ${\mathbb {Q}}(n)$;

• 3. For any i the function

  $$\begin{aligned} n \mapsto \text { the multiplicity of }\lambda _i(n) \end{aligned}$$

  agrees with a polynomial.

Remark 1.6

The proof of the above theorem will appear in upcoming work of the authors and David Speyer [36]. It is included in this paper for completeness’s sake. Hints toward the proof are given in Sect. 4.3.

Further note that the most general version of Theorem H allows one to work with matrices other than the adjacency matrix. For instance, one reaches the same conclusion working with the Laplacian matrix (see Definition 2.6).

Perhaps the simplest example one can call upon to illustrate this theorem is the complete graph. In this instance the eigenvalues of the adjacency matrix $A_n$ are $-1$ and $n-1$, with multiplicities $n-1$ and 1 respectively. Hence the number of distinct eigenvalues of $A_n$ becomes constantly 2 beginning at $n = 2$, and the multiplicities of these eigenvalues are given by polynomials.

Table 1 summarizes these results.

Table 1 A summary of the quantities shown in this paper to be eventually polynomial, and bounds on the degree of that polynomial in terms of the stable degree d of the ${{\,\mathrm{FI}\,}}$-graph

1.5 Outline

The overall structure of the present work is as follows. We begin by recalling necessary background. This ranges from graph theory (Sect. 2.1) to the configuration spaces of graphs (Sect. 2.2) to the theory of ${{\,\mathrm{FI}\,}}$-modules and representation stability (Sect. 2.3). Our hope is that this background will be sufficient so that readers from a large variety of fields can better follow the work in the body of the paper.

Following this, we turn our attention to the basic definitions and examples from the theory of ${{\,\mathrm{FI}\,}}$-graphs (Sect. 3.1). We then describe the phenomenon of vertex-stability and its major structural consequences (Sect. 3.2). This third section is then capped off by a more technical chapter which solves the question of when the transition maps of a vertex-stable ${{\,\mathrm{FI}\,}}$-graph must begin to have induced image (Sect. 3.3). The fourth section is dedicated to proving the applications detailed above, as well as various smaller consequences that one might find interesting.

To conclude the work, we consider generalization of the theory of ${{\,\mathrm{FI}\,}}$-graphs in two distinct directions. Firstly, we consider what would happen if instead of ${{\,\mathrm{FI}\,}}$, one considered functors from certain other categories into the category of graphs (Sect. 5.1). In particular, we argue that virtually everything described in the paper will have some analog for ${{\,\mathrm{FI}\,}}^m$-graphs and ${{\,\mathrm{VI}\,}}(q)$-graphs (see Definition 5.1). Secondly, we consider higher dimensional analogs of ${{\,\mathrm{FI}\,}}$-graphs. Namely, we consider general ${{\,\mathrm{FI}\,}}$-simplicial-complexes and show that certain structural facts will continue to work in this context (Sect. 5.2).

1.6 Future directions

In an upcoming paper of the authors and David Speyer [36], we classify finitely generated ${{\,\mathrm{FI}\,}}$-sets and investigate the behavior of relations between ${{\,\mathrm{FI}\,}}$-sets, proving for instance the present Theorem H.

Other forthcoming work concerns the behavior of random walks on ${{\,\mathrm{FI}\,}}$-graphs. We show that expected hitting times of simple random walks on ${{\,\mathrm{FI}\,}}$-graphs eventually agree with algebraic functions, and give bounds for the mixing times of these walks in terms of the relative sizes of vertex and edge orbits.

It would be interesting to investigate which graph theoretic properties stabilize as one moves along an ${{\,\mathrm{FI}\,}}$-graph, particularly global properties which do not follow from our observations on local structure. Example 3.16 provides an example of an ${{\,\mathrm{FI}\,}}$-graph for which the existence of a Hamiltonian cycle need not stabilize. Another particularly interesting question concerns the chromatic number. The examples considered in this paper whose chromatic number have been computed each have chromatic number eventually agreeing with a polynomial, though it is unknown whether this is something one should expect for all ${{\,\mathrm{FI}\,}}$-graphs. A result in this direction would be particularly relevant to the Johnson graphs, whose chromatic number is still not known.

Recent work of Bahran has applied the theory of ${{\,\mathrm{FI}\,}}$-graphs to questions in finite group theory [2].

2 Background

2.1 Graph theory

For the purposes of this paper, we will only consider finite graphs with no multi-edges or self-loops. Graphs will be permitted to be disconnected.

Definition 2.1

A graph is a finite 1-dimensional simplicial complex. Given a graph G, we will write V(G) to denote its vertex set, and E(G) to denote its edge set. Both V(G) and E(G) are necessarily finite. If $v \in V(G)$, then $\mu (v)$ will be used to denote its degree, which is the number of edges having v as one of their endpoints. The minimum degree of a vertex of G will be denoted $\delta (G)$, while the maximum degree will be written $\Delta (G)$.

A homomorphism of graphs $\phi :G \rightarrow G'$ is a map of sets $\phi :V(G) \rightarrow V(G')$ such that if $\{x,y\} \in E(G)$, then $\{\phi (x),\phi (y)\} \in E(G')$. The category of graphs and graph homomorphisms will be denoted $\mathbf {Graph}$.

A subgraph of a graph G is a graph $G'$ with inclusions $V(G') \subseteq V(G)$ and $E(G') \subseteq E(G)$. We say that a subgraph $G'$ is induced if for all $x,y \in V(G')$, $\{x,y\} \in E(G')$ whenever $\{x,y\} \in E(G)$.

In this work, we will be applying the theory of ${{\,\mathrm{FI}\,}}$-modules to the study of certain natural families of graphs. Our applications will be grouped into three categories: enumerative, topological, and algebraic.

To begin, we review some elementary facts and notations from enumerative graph theory. Much of what follows can be found in any standard text in graph theory (see, for instance, [3]).

Definition 2.2

Let G and H be graphs. We write $\eta _H(G)$ to denote the total number of distinct subgraphs of G which are isomorphic to H. We will also write $\eta ^{ind}_H(G)$ to denote the total number of distinct induced subgraphs of G which are isomorphic to H

Remark 2.3

When one speaks of computing the number of copies of H inside G, one is usually talking about counting the number of graph injections from H to G up to composition of automorphisms of H. This is the perspective we take in this work.

The question of determining whether $\eta _H(G) > 0$ is known as the subgraph isomorphism problem. It is known, for general choices of H and G, that the subgraph isomorphism problem is NP-complete [8, 26]. The analogous induced subgraph isomorphism problem is also known to be NP-complete, although it is also known to be solvable in polynomial time in many instances [38]. In this paper, we will be concerned with computing these two counting invariants across the members of certain families of graphs (see Theorem 4.1).

After enumerative considerations, we next turn our attention to topological applications of the ${{\,\mathrm{FI}\,}}$-graph structure. Our first application is related to so called Hom-complex construction. Interest in these complexes originates from work of Lovász [28], wherein similar spaces were used to resolve the Kneser conjecture. Babson and Koslov later showed that the the spaces used in Lovász’s work were specific examples of ${{\,\mathrm{Hom}\,}}$-complexes [4, 5]. Following this, there has been some amount of interest in various topological aspects of these spaces (see [16, 17] for some examples). For instance, it is known that every simplicial complex can be realized as a subdivision of the Hom-complex of some pair of graphs [17]. In this paper, we will approach the Hom-complex from the perspective of representation stability.

Definition 2.4

Let H, G be graphs. A multi-homomorphism from H to G is a map of sets

$$\begin{aligned} \alpha :V(H) \rightarrow {\mathcal {P}}(V(G))-\emptyset \end{aligned}$$

between the vertices of H and the power set of the vertices of G, such that if $\{x,y\} \in E(H)$ then for all $x' \in \alpha (x)$ and all $y' \in \alpha (y)$, $\{x',y'\} \in E(G)$. The Hom-complex of H and G , ${\mathscr {H}}om(H,G)$, is the polyhedral complex whose cells are in bijection with multi-homomorphisms from H to G. Given two multi-homomorphisms $\alpha$ and $\tau$, we have that the cell corresponding to $\alpha$ is contained in the closure of the cell corresponding to $\tau$ if and only if $\alpha (x) \subseteq \tau (x)$ for all $x \in H$.

Remark 2.5

In the literature, the ${{\,\mathrm{Hom}\,}}$-complex is sometimes defined to be the order complex of the poset of multi-homomorphisms and inclusions [16, 17]. This simplicial definition of the ${{\,\mathrm{Hom}\,}}$-complex can be realized as a subdivision of our chosen polyhedral complex construction (See the discussion following [4, Definition 1.2]). We use the definition of the Hom-complex as a polyhedral complex provided by [4], as it makes the arguments which follow a bit easier.

We will later construct large families of graphs $G_n$, indexed by the natural numbers, such that for any graph H, the complexes ${\mathscr {H}}om(H,G_n)$ are representation stable in the sense of Church and Farb (see Theorem 4.9 and Definition 2.19).

Following this, we will spend some time proving facts about configuration spaces of graphs. The background for this material is detailed in the next section.

The final type of application we will concern ourselves with relates to spectral properties of graphs. More specifically, we will concern ourselves with eigenspaces and eigenvalues of adjacency and Laplacian matrices.

Definition 2.6

Let G be a graph. The adjacency matrix of G , $A_G$, is the matrix whose columns and rows are labeled by vertices of G and whose entries are defined by

$$\begin{aligned} (A_G)_{(v,w)} := {\left\{ \begin{array}{ll} 1 &{}\text { if }\{v,w\} \in E(G)\\ 0 &{}\text { otherwise.}\end{array}\right. } \end{aligned}$$

The Laplacian matrix of G , $L_G$, is the difference $D_G - A_G$, where $D_G$ is the diagonal matrix whose entries display the degrees of the vertices of G.

The collection of eigenvalues of $A_G$ will be referred to as the spectrum of G.

There are many things that one may immediately observe from the fact that $A_G$ and $L_G$ are real and symmetric. For instance:

• 1. The matrices $A_G$ and $L_G$ are diagonalizable.

• 2. The eigenvalues of $A_G$ and $L_G$ are real. Therefore, they can be ordered as $\lambda _1 \ge \lambda _2 \ge \cdots \ge \lambda _{|V(G)|}$.

In our work we will be largely concerned with the following two questions: Given certain natural families of graphs $G_n$, indexed by the natural numbers, how many distinct eigenvalues can $A_{G_n}$and $L_{G_n}$ have (as a function of n), and how do the multiplicities of these eigenvalues change with n? For instance, the adjacency matrix of the complete graph $K_n$, with $n \ge 2$, has distinct eigenvalues $n-1$ and $-1$ with multiplicities 1 and $n-1$, respectively. In other words, so long as n is sufficiently large, the complete graph $K_n$ has a fixed number of distinct eigenvalues, and the corresponding eigenspaces have dimensions which are polynomial in n. One of the main motivations for this paper is proving a framework which explains such behavior.

For references on graph spectra, see [3, 9, 14, 15].

2.2 Configuration spaces of graphs

Definition 2.7

Let G be a graph. Then the $\varvec{m}$-stranded configuration space of G is the topological space

$$\begin{aligned} {{\,\mathrm{Conf}\,}}_m(G) := \{(x_1,\ldots ,x_m) \in G^m \mid x_j \ne x_i, i \ne j.\} \end{aligned}$$

Configuration spaces of various topological spaces have a long history including work of McDuff [33], and Church et al. [10], among many others. Much of the literature is focused on the configuration spaces of manifolds. Recently, some attention has been given to the configuration spaces of graphs, due to their connections with robotics [23]. Much of the newly emerging literature seems to indicate that these configuration spaces are heavily influenced by the combinatorics of the graph (see [1, 13, 19, 22, 23, 27, 35], for a small sampling). For instance, the following theorem of Abrams puts a very natural cellular structure on ${{\,\mathrm{Conf}\,}}_m(G)$, which depends highly on the vertices of G of degree at least 3. Cellular models have also been proposed by Światkowski [37], Ghrist [23], Lütgehetmann [27], and Wiltshire-Gordon [42].

Definition 2.8

Let G be a graph. The $\varvec{m}$th subdivision of G is the graph $G^{(m)}$ obtained from G by adding $m-1$ vertices of degree 2 to every edge of G.

Theorem 2.9

[1] Let G be a graph, and let ${{\,\mathrm{DConf}\,}}_m(G)$ denote the sub-complex of the cubical complex $G^m$ comprised of cells of the form

$$\begin{aligned} \sigma _1 \times \cdots \times \sigma _m \end{aligned}$$

where $\sigma _i$ is either an edge or vertex of G, and for each $i \ne j$,

$$\begin{aligned} \partial (\sigma _i) \cap \partial (\sigma _j) = \emptyset . \end{aligned}$$

Then ${{\,\mathrm{DConf}\,}}_m(G^{(m)})$ is homotopy equivalent to ${{\,\mathrm{Conf}\,}}_m(G^{(m)})$.

The original work of Abrams is more precise than the above, but this is sufficient for what follows. We note that for any graph G, ${{\,\mathrm{Conf}\,}}_m(G^{(m)})$ is identical to ${{\,\mathrm{Conf}\,}}_m(G)$. We observe that ${{\,\mathrm{DConf}\,}}_m(G)$ is the largest subcomplex of $G^m$ which avoids the diagonals $x_i = x_j$. Abrams’ theorem therefore states that this complex will contain the same topological information as ${{\,\mathrm{Conf}\,}}_m(G)$ so long as there are enough vertices in G such that every coordinate in a given configuration can fit on a single edge using only vertices.

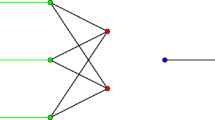
It is often convenient to visualize the cells of ${{\,\mathrm{DConf}\,}}_m(G^{(m)})$ as living on the graph $G^{(m)}$. In such a visualization, we bolden the vertices and edges appearing in the cell on the graph $G^{(m)}$, and label the position in which they appear in the cell. For instance, Fig. 1 shows a cell of ${{\,\mathrm{DConf}\,}}_2(G^{(2)})$ for a particular choice of G.

Fig. 1

The cell $(v_0,e_{4,7})$

Among the many incredible theoretical properties of configuration spaces of graphs is the precise computation of their Euler characteristic. The following result is due to Gal, and provides a large part of the motivation for this work.

Theorem 2.10

[22] Let G be a graph, and let ${\mathfrak {e}}(t)$ denote the exponential generating function

$$\begin{aligned} {\mathfrak {e}}(t) = \sum _{m \ge 0} \frac{\chi ({{\,\mathrm{Conf}\,}}_m(G))}{m!}t^m. \end{aligned}$$

Then

$$\begin{aligned} {\mathfrak {e}}(t) = \frac{\prod _{v \in V(G)}(1-(1-\mu (v))t)}{(1-t)^{|E(G)|}}. \end{aligned}$$

A theorem of Ghrist [23] and Światkowski [37] implies that $H_i({{\,\mathrm{Conf}\,}}_m(G)) = 0$ for all graphs G and all i larger than the number of vertices of G of degree at least 3. In particular, this is independent of m. It follows from this fact, as well as the theorem of Gal, that the Betti numbers of ${{\,\mathrm{Conf}\,}}_m(G)$ should be expected to grow in m like m!. Such growth precludes ${{\,\mathrm{Conf}\,}}_m(G)$ from being representation stable (see Definition 2.19 for the definition of representation stable, and Theorem 2.18 to see why the above precludes ${{\,\mathrm{Conf}\,}}_m(G)$ from having this property). Looking again at the theorem of Gal, we see that the Euler characteristic of ${{\,\mathrm{Conf}\,}}_m(G)$, as a function of m, looks like m! multiplied by a polynomial in invariants of G. In other words, the extreme growth in the Euler characteristic seems to be primarily influenced by the number of points being configured, rather than the the graph G itself.

One guiding philosophy of the present work is that if we fix the number of points begin configured, and instead allow the graph itself to vary, then the collection of spaces ${{\,\mathrm{Conf}\,}}_m(G_n)$ will be representation stable in the sense of Definition 2.19.

This philosophy has also appeared in recent work of Lütgehetmann [27]. Theorem G extends the main theorem of that work.

2.3 ${{\,\mathrm{FI}\,}}$-modules and representation stability

The main tool we introduce in this paper are objects we refer to as ${{\,\mathrm{FI}\,}}$-graphs. Before working through the technical details of that construction, we must first discuss a key auxiliary concept: ${{\,\mathrm{FI}\,}}$-modules.

Definition 2.11

Let ${{\,\mathrm{FI}\,}}$ denote the category whose objects are the finite sets $[n] := \{1,\ldots ,n\}$ and whose maps are injections. An ${{\,\mathrm{FI}\,}}$-module is a (covariant) functor from ${{\,\mathrm{FI}\,}}$ to the category of ${\mathbb {R}}$-vector spaces.

Remark 2.12

${{\,\mathrm{FI}\,}}$-modules can be put into more concrete terms. Observe that for any set [n], the endomorphisms in ${{\,\mathrm{FI}\,}}$ are precisely the permutations on n letters, ${\mathfrak {S}}_n$. Therefore, if V is an ${{\,\mathrm{FI}\,}}$-module, each of the vector spaces V([n]) is actually a representation of the symmetric group ${\mathfrak {S}}_n$. An ${{\,\mathrm{FI}\,}}$-module may be thought of as a sequence of vector spaces

$$\begin{aligned} V_0 \rightarrow V_1 \rightarrow \cdots \end{aligned}$$

such that each $V_n$ is a representation of ${\mathfrak {S}}_n$, and each of the forward maps $V_n \rightarrow V_{n+1}$ is a linear map which is equivariant with respect to the action of ${\mathfrak {S}}_n$, where ${\mathfrak {S}}_n \le {\mathfrak {S}}_{n+1}$ as the subgroup of permutations which fix the element $n+1$.

More precisely, Remark 3.3.1 of [10] says that such a sequence of spaces and maps forms an ${{\,\mathrm{FI}\,}}$-module if and only if for any n and k, any element of ${\mathfrak {S}}_{n+k}$ which fixes all of [n] acts trivially on the image of $V_n$ in $V_{n+k}$.

Remark 2.13

Note that most works in the literature allow ${{\,\mathrm{FI}\,}}$-modules to be valued in any module category over a commutative ring. For our purposes, we will mostly consider ${{\,\mathrm{FI}\,}}$-modules which are valued in vector spaces over ${\mathbb {R}}$. In certain areas of the paper, such as Lemma 4.6, we consider ${{\,\mathrm{FI}\,}}$-modules over ${\mathbb {Z}}$, i.e. functors from ${{\,\mathrm{FI}\,}}$ to the category of abelian groups. Most of the definitions and theorems in this section work equally well in this case.

For an ${{\,\mathrm{FI}\,}}$-module V, we will often write $V_n := V([n])$ and $f_\text {*}:= V(f)$. One should note that for any n, the endomorphisms of [n] in ${{\,\mathrm{FI}\,}}$ are precisely the permutations on n letters, ${\mathfrak {S}}_n$. Functoriality therefore implies that, for each n, $V_n$ is a representation of ${\mathfrak {S}}_n$.

Just as with the study of vector spaces, it is often reasonable to restrict one’s attention to those objects which are finitely generated in the appropriate sense. Before describing how such a condition can be applied to ${{\,\mathrm{FI}\,}}$-modules, we note that the category of ${{\,\mathrm{FI}\,}}$-modules and natural transformations is abelian. Indeed, one may define the usual abelian operations point-wise. In fact, one may very naturally define constructions such as direct sums and products, tensor products, symmetric products, etc. for ${{\,\mathrm{FI}\,}}$-modules.

Definition 2.14

An ${{\,\mathrm{FI}\,}}$-module V is said to be finitely generated in degree $\le d$ if there is a finite set

$$\begin{aligned} \{v_i\} \subseteq \sqcup _{n = 0}^d V_n \end{aligned}$$

which no proper submodule of V contains. Equivalently, the set $\{v_i\}$ generates V if, for all n, the vector space $V_n$ is spanned by the images of the $v_i$ under the various maps $f_\text {*}$ induced by V from injections of sets.

Perhaps the most remarkable thing about finitely generated ${{\,\mathrm{FI}\,}}$-modules is that they exhibit a Noetherian property. The following was first proven by Snowden [39], and later repoven by Church et al. [10].

Theorem 2.15

[10, 39] Let V be a finitely generated ${{\,\mathrm{FI}\,}}$-module. Then every submodule of V is also finitely generated.

We will use the above Noetherian property to deduce various somewhat surprising combinatorial facts about ${{\,\mathrm{FI}\,}}$-graphs.

As one might expect, if V is an ${{\,\mathrm{FI}\,}}$-module generated in degree $\le d$, then it is not necessarily the case that submodules of V are also generated in degree $\le d$. Despite this, one may still conclude certain things about submodules of V based on properties of V. For this reason, we introduce the following.

Definition 2.16

We say that a finitely generated ${{\,\mathrm{FI}\,}}$-module V is $\varvec{d}$-small if V is a subquotient of an ${{\,\mathrm{FI}\,}}$-module which is finitely generated in degree $\le d$.

Proposition 2.17

[10] If V is finitely generated in degree $\le d$ and W is finitely generated in degree $\le e$, then

• 1. The ${{\,\mathrm{FI}\,}}$-module $V \oplus W$ is generated in degree $\le \max \{d,e\}$, where $(V \oplus W)_n = V_n \oplus W_n$;

• 2. The ${{\,\mathrm{FI}\,}}$-module $V \otimes W$ is generated in degree $\le d+e$, where $(V \otimes W)_n = V_n \otimes W_n$.

The following list of properties are proven throughout [10].

Theorem 2.18

[10] Let V be an ${{\,\mathrm{FI}\,}}$-module. If V is finitely generated then for all $n \gg 0$ and all injections $f:[n] \rightarrow [n+1]$,

• 1. The function $f_\text {*}$ is injective;

• 2. The vector space $V_{n+1}$ is spanned as an ${\mathfrak {S}}_{n+1}$-representation by $f_\text {*}(V_n)$;

• 3. The ${\mathfrak {S}}_n$-representation $V_n$ admits a decomposition of the form

  $$\begin{aligned} V_n = \bigoplus _{\lambda , |\lambda | \le d} m_\lambda V(\lambda )_n \end{aligned}$$

  where the coefficient $m_\lambda$ is independent of n and d is some constant independent of n (see [10] for details on the representations $V(\lambda )$). In particular, the multiplicity of the trivial representation in $V_n$ is eventually independent of n.

• 4. If V is d-small, then there exists a polynomial $p_V(X)\in {\mathbb {Q}}[X]$ of degree $\le d$ such that for all $n \gg 0$, $p_V(n) = \dim _{\mathbb {Q}}V_n$.

The above will be used extensively in what follows.

The notion of representation stability was first introduced by Church and Farb in their seminal work [12]. From these beginnings the field has seen a boom in the literature and has been proven to be applicable to a large collection of subjects. For the purposes of this paper, we state the following definition, which is a modernized version of the original definition of Church and Farb.

Definition 2.19

Let $X_\bullet$ denote a functor from ${{\,\mathrm{FI}\,}}$ to the category of topological spaces. Then we say that $X_\bullet$ is representation stable if for all $i \ge 0$ the ${{\,\mathrm{FI}\,}}$-module over ${\mathbb {Z}}$

$$\begin{aligned} H_i(X_\bullet ;{\mathbb {Z}}) \end{aligned}$$

is finitely generated.

Note that this definition describes what is meant by an ${{\,\mathrm{FI}\,}}$-space being representation stable, not an ${{\,\mathrm{FI}\,}}$-module.

Remark 2.20

Again we note that this definition is not standard in the literature. Observe that being representation stable in the above sense implies that the ${{\,\mathrm{FI}\,}}$-module $H_i(X_\bullet ;{\mathbb {R}})$ is finitely generated in at most the same degree. This is much more similar, in spirit, to the original work of Church and Farb [12].

It was famously proven by Church [7], and later reexamined by Church et al. [10], that if M is a compact orientable manifold with boundary of dimension at least two then

$$\begin{aligned} n \mapsto {{\,\mathrm{Conf}\,}}_n(M) \end{aligned}$$

is representation stable. We have already seen, however, that an analogous statement cannot be true if we replace M with a graph (see the discussion following Theorem 2.10). We therefore change our approach and instead consider the functors

$$\begin{aligned} n \mapsto {{\,\mathrm{Conf}\,}}_m(G_n) \end{aligned}$$

(2.1)

where m is fixed, and $G_\bullet$ is a particularly nice ${{\,\mathrm{FI}\,}}$-graph (see the statement of Theorem G). The main theorem of this paper can be restated to say that in this case the functor (2.1) is representation stable. Our approach will be largely combinatorial, and we will use structural facts about ${{\,\mathrm{FI}\,}}$-graphs as well as the cellular model of Theorem 2.9. This is in contrast to the work of Lütgehetmann, which proves that $n \mapsto {{\,\mathrm{Conf}\,}}_m(G_n)$ is representation stable for a particular choice of $G_\bullet$ (see Example 3.9) using very topological methods. We will find that our method provides a stronger bound on the degree of the polynomial encoding the Betti numbers in this case, while Lütgehetmann’s method provides bounds on the degree of generation of the ${{\,\mathrm{FI}\,}}$-modules $H_i({{\,\mathrm{Conf}\,}}_m(G_\bullet ))$.

Remark 2.21

For future use, we now explicitly point out the properties of ${{\,\mathrm{FI}\,}}$-modules over ${\mathbb {Z}}$ which will be used in the sequel. These are:

• 1. ${{\,\mathrm{FI}\,}}$-modules over ${\mathbb {Z}}$ satisfy the Noetherian property. That is, submodules of finitely generated modules are once again finitely generated [11, Theorem A];

• 2. If V is a finitely generated ${{\,\mathrm{FI}\,}}$-module over ${\mathbb {Z}}$, then the function $n \mapsto {{\,\mathrm{rank}\,}}(V_n)$ agree with a polynomial for $n \gg 0$ [11, Theorem B];

• 3. If V is a finitely generated ${{\,\mathrm{FI}\,}}$-module over ${\mathbb {Z}}$, then transition maps of V are eventually injective [11, Lemma 2.15].

• 4. If V and W are finitely generated ${{\,\mathrm{FI}\,}}$-modules over ${\mathbb {Z}}$, then both $V \otimes W$ and $V \oplus W$ are also finitely generated [10, Proposition 2.61].

Note that the primary differences between ${{\,\mathrm{FI}\,}}$-modules and ${{\,\mathrm{FI}\,}}$-modules over ${\mathbb {Z}}$ involve the behaviors of the ${\mathfrak {S}}_n$-representations $V_n$. This can be thought of as a consequence of the fact that representation theory, and the representation theory of the symmetric groups specifically, is generally much less well behaved over ${\mathbb {Z}}$.

3 FI-graphs

3.1 Definitions and examples

The primary objective of this section is to provide a framework through which one can study families of graphs in the spirit of Kneser graphs and their generalizations. Recall that, for any fixed integers $n \ge k$, one defines the Kneser graph $KG_{n,k}$ as the graph whose vertices are labeled by k-element subsets of [n], and whose edges connect disjoint sets.

It is clear that for each n, elements of ${\mathfrak {S}}_n$ act on $KG_{n,k}$ by graph automorphisms. What is perhaps more subtle, is that if $f:[n] \hookrightarrow [m]$ is any injection, then there is an induced map of graphs

$$\begin{aligned} KG(f):KG_{n,k} \rightarrow KG_{m,k} \end{aligned}$$

Looking back at the definition of ${{\,\mathrm{FI}\,}}$-modules, one is therefore motivated to make the following definition.

Definition 3.1

An ${{\,\mathrm{FI}\,}}$-graph is a functor from the category ${{\,\mathrm{FI}\,}}$ to the category $\mathbf {Graph}$ of (simple) graphs. We will usually denote an ${{\,\mathrm{FI}\,}}$-graph by $G_\bullet :{{\,\mathrm{FI}\,}}\rightarrow \mathbf {Graph}$. We will use G(f) to denote the induced maps of $G_\bullet$.

Remark 3.2

We may consider ${{\,\mathrm{FI}\,}}$-graphs in a more concrete fashion, similar to how ${{\,\mathrm{FI}\,}}$-modules were treated in Remark 2.12. An ${{\,\mathrm{FI}\,}}$-graph may be thought of as a sequence of graphs

$$\begin{aligned} G_0 \rightarrow G_1 \rightarrow \cdots \end{aligned}$$

such that each $G_n$ carries a vertex action by ${\mathfrak {S}}_n$, and each of the forward maps $G_n \rightarrow G_{n+1}$ is a graph theoretic homomorphism which is equivariant with respect to the action of ${\mathfrak {S}}_n$, where ${\mathfrak {S}}_n \le {\mathfrak {S}}_{n+1}$ as the subgroup of permutations which fix $n+1$.

As in Remark 2.12, such a sequence of graphs and maps may not be an ${{\,\mathrm{FI}\,}}$-graph, but following Remark 3.3.1 of [10], the sequence of graphs and maps forms an ${{\,\mathrm{FI}\,}}$-graph if and only if for any n and k, any element of ${\mathfrak {S}}_{n+k}$ which fixes all of [n] acts trivially on the image of $G_n$ in $G_{n+k}$. Example 3.15 shows the behavior that may occur without this assumption.

While the above definition captures the core of the above discussion, it is still a bit too general for our purposes. For instance, if

$$\begin{aligned} G_0 \subseteq G_1 \subseteq G_2 \subseteq \cdots \end{aligned}$$

is any chain of graphs, then we may define an ${{\,\mathrm{FI}\,}}$-graph by setting the ${\mathfrak {S}}_n$-action to be trivial for each n, and having the transition maps be the given inclusions. An arbitrary chain of graphs like the above can become rather complicated, and there won’t necessarily be any way to gather meaningful information above the invariants of any $G_n$ from those that came before it. What is needed is some notion of finite generation for ${{\,\mathrm{FI}\,}}$-graphs. For this purpose, we define the following.

Definition 3.3

Let $G_\bullet$ be an ${{\,\mathrm{FI}\,}}$-graph. We say that $G_\bullet$ is vertex-stable with stable degree $\le d$ if for all $n \ge d$, and every vertex $v \in V(G_{n+1})$ there exists some vertex $w \in V(G_n)$ and some injection $f:[n] \hookrightarrow [n+1]$ such that $G(f)(w) = v$.

That is, an ${{\,\mathrm{FI}\,}}$-graph is vertex-stable with stable degree $\le d$ if for each $n > d$, every vertex in $G_{n}$ is in the image of one of the transition maps. Informally, no ‘new’ vertices appear after the graph $G_d$, up to symmetric group actions.

We will find that this fairly simple combinatorial condition is sufficient to prove a plethora of facts about the graphs $G_n$. Before we delve into these details, we first introduce the various examples which motivated this paper. In most of these examples, vertices are labeled by elements of $[n] = \{1,2,\dots ,n\}$ or by sets or tuples (unordered or ordered, respectively) of such elements. The symmetric group ${\mathfrak {S}}_n$ acts on such vertices by acting on each element individually. It is a result of the upcoming work [36] that all vertex-stable ${{\,\mathrm{FI}\,}}$-graphs arise from such constructions, slightly generalized.

Example 3.4

For any fixed $k \ge 0$, the Kneser graphs $KG_{\bullet ,k}$ form a vertex-stable ${{\,\mathrm{FI}\,}}$-graph with stable degree k (or stable degree 1 if $k = 0$). The same can therefore be said about the complete graphs $K_\bullet = KG_{\bullet ,1}$.

More generally, if n, k,  and r are fixed integers, then we define the generalized Kneser graph $KG_{n,k,\le r}$ to have vertices labeled by subsets of [n] of size k and edges connecting subsets whose intersection has size at most r. In particular, $KG_{n,k} = KG_{n,k,0}$. The generalized Kneser graphs $KG_{\bullet ,k,\le r}$ form a vertex-stable ${{\,\mathrm{FI}\,}}$-graph for each fixed k and r, again with stable degree k.

Rather than putting edges between subsets whose intersection is of at most a certain size, we could instead require that the intersection have exactly that size—for instance, let $KG_{n,k,r}$ be the graph whose vertices are subsets of size k and with an edge between two vertices if their subsets have an intersection of exactly size r. The graphs $KG_{\bullet ,k,r}$ also form a vertex-stable ${{\,\mathrm{FI}\,}}$-graph with stable degree k.

We could generalize this example further, allowing edges to correspond to intersections of various specified sizes.

Example 3.5

For any fixed $k \ge 0$, we can define a variant of the Kneser graph, which we denote $KG_{n,\le k}$. The vertices of $KG_{n,\le k}$ will be labeled by subsets of [n] of size at most k, and the edges will connect disjoint subgraphs, just as was the case with the Kneser graph. Because self-loops are forbidden, we do not connect the empty set to itself.

Note that for each n, the symmetric group action on $KG_{n,\le k}$ is not transitive. Despite this, the collection $KG_{\bullet ,\le k}$ still forms a vertex-stable ${{\,\mathrm{FI}\,}}$-graph with stable degree k. It will be useful to consider the orbits of vertices under the symmetric group actions. Our examples tend to have few orbits for the sake of being simple examples, but this is not a restriction on general ${{\,\mathrm{FI}\,}}$-graphs.

Example 3.6

For any fixed $k \ge 0$, the complete bipartite graphs $K_{\bullet ,k}$ form a vertex-stable ${{\,\mathrm{FI}\,}}$-graph with stable degree 1. Here, our transition maps and permutations fix the vertices in the part of size k. It follows that the series of star graphs, Star$_\bullet = K_{\bullet ,1}$ form a vertex-stable ${{\,\mathrm{FI}\,}}$-graph.

Example 3.7

For any fixed $n,k \ge 0$, define the Johnson graph $J_{n,k}$ as that whose vertices are labeled by subsets of [n] with size k, and whose edges connect subsets with intersection size $k-1$. Then $J_{\bullet ,k}$ naturally forms a vertex-stable ${{\,\mathrm{FI}\,}}$-graph with stable degree k.

In the notation of Example 3.4, the Johnson graph $J_{n,k}$ is the generalized Kneser graph $KG_{n,k,k-1}$.

Example 3.8

Recall that the n-cube graph $Q_n$ is defined to be the 1-skeleton of the n-dimensional hypercube. This collection cannot be endowed with the structure of a vertex-stable ${{\,\mathrm{FI}\,}}$-graph, as its number of vertices grows too fast (see Theorem 4.3). There is, however, a variation of the n-cube graph which can be endowed with the structure of a finitely generated ${{\,\mathrm{FI}\,}}$-graph.

For fixed $n,k \ge 0$, let $Q_{n,k}$ denote the graph whose vertices are ordered k-tuples of elements of [n], where two vertices are connected if they differ in only one coordinate. This graph is sometimes called the k-lattice graph of characteristic n. The cubic lattice graph of characteristic n is notable in that it can be entirely characterized by certain simple combinatorial properties (see [30]). For our purposes, we simply note that for any fixed k the family $Q_{\bullet ,k}$ can be endowed with the structure of a vertex-stable ${{\,\mathrm{FI}\,}}$-graph. Indeed, let $n > k$, and let $(i_1,\ldots ,i_k)$ be a vertex of $Q_{n+1,k}$. Because $k < n$, we know that there is some integer $l \in [n]$ such that $l \ne i_j$ for any j. Then $(i_1,\ldots ,i_k)$ is in the image of the transition map induced by the injection $f:[n] \hookrightarrow [n+1]$ given by,

$$\begin{aligned} f(x) = {\left\{ \begin{array}{ll} n+1 &{}\text { if }x = l,\\ x &{}\text { otherwise.}\end{array}\right. } \end{aligned}$$

This ${{\,\mathrm{FI}\,}}$-graph has stable degree k.

Example 3.9

Our next example appears in earlier work of Lütgehetmann [27]. Let G, H be any pair of pointed graphs. Then we can construct a new graph by wedging G with H n times, producing the graph

$$\begin{aligned} G_n := G \bigvee H^{\vee n} \end{aligned}$$

Then we may endow $G_n$ with the structure of an ${{\,\mathrm{FI}\,}}$-graph by having the symmetric group act by permuting the factors of H. This ${{\,\mathrm{FI}\,}}$-graph has stable degree 1.

The examples thus far have been quite regular, in the sense that for each n, the construction of the vertices and edges of the graph $G_n$ has been the same. It is worth examining how this can be varied, particularly because results later in this section will limit how wild such variation can be.

Example 3.10

Let $G_\bullet$ be an ${{\,\mathrm{FI}\,}}$-graph, and modify it by removing all edges from each $G_i$, for $i = 1$ to $k-1$.

Example 3.11

Let $G_\bullet$ be an ${{\,\mathrm{FI}\,}}$-graph, and modify it by replacing each $G_i$ by the empty graph, for $i = 1$ to $k-1$.

While Examples 3.10 and 3.11 remove vertices and edges from graphs in the first few degrees, this cannot necessarily be done in later degrees. The transition maps are permitted to map pairs of vertices not connected by an edge to pairs of vertices connected by an edge, but not the reverse. Two vertices joined by an edge may not map to the same vertex, because there cannot be an edge from this vertex to itself. For instance, if $G_n$ contains a complete graph on k vertices then $G_{n+1}$ also contains a complete graph on k vertices.

Disjoint unions of ${{\,\mathrm{FI}\,}}$-graphs are ${{\,\mathrm{FI}\,}}$-graphs, and it is possible to increase the number of copies from a certain point onwards.

Example 3.12

Fix a positive integer k, and let $G_\bullet$ be any ${{\,\mathrm{FI}\,}}$-graph with stable degree at most k. We create a new ${{\,\mathrm{FI}\,}}$-graph $H_\bullet$ as follows. For $i < k$, the graph $H_i$ is equal to $G_i$. For $i \ge k$, the graph $H_i$ is a disjoint union of two copies of $G_i$. For concreteness, color vertices and edges in one of these subgraphs red and in the other, blue. The action of ${\mathfrak {S}}_n$ preserves the color of vertices. Transition maps preserve the color of vertices and take uncolored vertices to red vertices. This ${{\,\mathrm{FI}\,}}$-graph has stable degree k.

Example 3.12 did not need the two graphs to be the same—the new graphs introduced from degree k could have been the respective components of any ${{\,\mathrm{FI}\,}}$-graph.

It is also possible to decrease the number of components. This does require the use of transition maps which are not injective.

Example 3.13

Let $G_\bullet$ be any ${{\,\mathrm{FI}\,}}$-graph. Fix a positive integer k, and create a new ${{\,\mathrm{FI}\,}}$-graph $H_\bullet$ as follows. For $i < k$, the graph $H_i$ is a disjoint union of two copies of $G_i$. Color vertices and edges in one of these subgraphs red and in the other, blue. For $i \ge k$, the graph $H_i$ is equal to $G_i$. The action of ${\mathfrak {S}}_n$ preserves the color of vertices. Transition maps preserve the color of vertices if their image is in $G_i$ with $i < k$, and forget colors otherwise.

An ${{\,\mathrm{FI}\,}}$-graph may be modified by changing the times at which the various ‘types’ of edges begin to appear, as in the following variant of the Kneser graph.

Example 3.14

Let the vertex set of $G_n$ be indexed by subsets of [n] of size r, and let $a_0$ to $a_r$ be $r+1$ fixed positive integers. In $G_n$, there is an edge between two vertices if and only if $n \ge a_k$, where k is the number of elements the two vertices have in common.

That is, Example 3.14 is describing a sequence of graphs where edges between disjoint sets are present from the $a_0$th graph onwards, edges between sets with a single element in common are present from the $a_1$th graph onwards, and so on.

Example 3.14 could be generalized further by taking the vertices to be ordered r-tuples, in which case there would be more edge orbits—two tuples may be compared not just by how many elements they have in common, but also by which positions these overlaps occupy. For instance, if the vertices are ordered pairs, then there are five orbits of edges rather than three in the unordered case—between pairs of vertices ((a, b), (a, c)),((a, b), (c, b)),((a, b), (b, c)),((a, b), (c, a)), and ((a, b), (c, d)).

There are also examples whose vertices are in between sets (unordered) and tuples (ordered)—we could start with vertices indexed by r-tuples, choose a subgroup H of the symmetric group ${\mathfrak {S}}_r$, and identify two tuples if the action of H takes one to the other. For instance, we might care about the order of an r–tuple up to cyclic permutation. It turns out that all finitely-generated ${{\,\mathrm{FI}\,}}$-graphs may be constructed in essentially this way—see Theorem A of [36].

The next example fails to be an ${{\,\mathrm{FI}\,}}$-graph in a subtle way. If it was an ${{\,\mathrm{FI}\,}}$-graph, it would violate Theorem 3.31.

Example 3.15

For each $i \ne 2$, let $G_i$ be the complete graph on the vertex set [i], with the natural symmetric group action where the group ${\mathfrak {S}}_i$ permutes the set [i]. Let $G_2$ have vertex set $\{1,2,3\}$, with edges 13 and 23 and the nonidentity element of ${\mathfrak {S}}_2$ interchanging the vertices 1 and 2 and fixing 3. Transition maps from $G_n$ to $G_{n+1}$ are obtained by including $G_n$ into $G_{n+1}$, using the same symbols for the vertex labels of each graph, and then acting by any element of ${\mathfrak {S}}_{n+1}$. We shall not attempt to define further transition maps, because this cannot be done in a consistent manner, as we shall now see.

From Remark 3.2, we know that for $G_\bullet$ to be an ${{\,\mathrm{FI}\,}}$-graph, the transposition $(3 \; 4)$ would need to fix the image of $G_2$ in $G_4$, because it fixes 1 and 2. But this isn’t the case, so $G_\bullet$ can’t be an ${{\,\mathrm{FI}\,}}$-graph. This is perhaps a surprising failure, because transition maps from each $G_i$ to the next graph $G_{i+1}$ can be defined naturally, and it is only longer-range maps which fail. Attempts to define such transition maps in a consistent way will run into difficulties deciding where to send the vertex 3 from $G_2$. This example illustrates the consistency condition required by Remark 3.2.

Fig. 2

The ${{\,\mathrm{FI}\,}}$-graph of Example 3.16. The key feature is that there are n ‘bridges’ from the right side of the graph to the left, and any Hamiltonian path must cross each of them

If rather than ${{\,\mathrm{FI}\,}}$ we were working over a category where maps from [2] to [n] were instead sequences of maps from [2] to [3] to [4] and so on, then this construction would not fail in this way, and so over such a category, the analogue of Theorem 3.31 is false.

Example 3.16

Consider the ${{\,\mathrm{FI}\,}}$-graph defined as follows. Let $G_n$ have five orbits of n vertices, indexed by the colors red, orange, yellow, green, and blue. At the moment, these orbits are isomorphic, though they will differ once we introduce the edges. The symmetric group action and the transition maps both preserve the colors. The graph $G_n$ has edges between

• Each red vertex and each red or orange vertex

• Each yellow vertex and the orange and green vertices of equal label, and

• Each green or blue vertex and each blue vertex.

See Fig. 2 for a schematic of this graph.

This particular ${{\,\mathrm{FI}\,}}$-graph is of theoretical interest, as it provides an example of a global property which does not stabilize in n. In particular, we claim that $G_n$ admits a Hamiltonian cycle if and only if n is even.

When n is even, consider the path which starts at the top left of Fig. 2 and ‘snakes’ downward by moving all the way to the right, takes one step down, moves all the way to the left, takes a step down, and repeats. The initial and final vertices of this path are adjacent, so this is a Hamiltonian cycle.

When n is odd, each time a non-backtracking path passes through a yellow vertex, it switches between the left and right pieces of the graph, comprised of red and orange or green and blue vertices, respectively. There is no other way to move between the two sides, and there are an odd number of yellow vertices, so any path passing through each vertex once must end on the opposite side to which it started.

3.2 Vertex-stability and its consequences

While it is clearly the case that the examples of Sect. 3.1 are vertex-stable, one might also note that these cases seem to have much more structure than this. For instance, it is natural to go a step further and make the following definitions:

Definition 3.17

• 1. An ${{\,\mathrm{FI}\,}}$-graph is eventually injective if for $n \gg 0$, the transition maps of $G_\bullet$ are injective;

• 2. An ${{\,\mathrm{FI}\,}}$-graph is eventually induced if for $n \gg 0$, the image of any transition map is an induced subgraph;

• 3. An ${{\,\mathrm{FI}\,}}$-graph is edge-stable with edge-stable degree $\le k$ if for $n \ge k$ and any $\{x,y\} \in E(G_{n})$ there is an edge $\{v,w\} \in V(G_k)$ and an injection $f:[k] \hookrightarrow [n]$ such that $G(f)(v) = x$ and $G(f)(w) = y$;

• 4. An ${{\,\mathrm{FI}\,}}$-graph is $\varvec{r}$-vertex-stable if for all $n \gg 0$, and any collection of r vertices of $V(G_{n+1})$, $\{x_1,\ldots ,x_r\}$, there is a collection of vertices of $G_n$, $\{v_1,\ldots ,v_r\}$, and an injection $f:[n] \hookrightarrow [n+1]$, such that $G(f)(v_i) = x_i$ for each i.

These stability properties may occur at quite different times, and at different times to vertex-stability. Example 3.13 is injective only from degree k onwards, Example 3.12 is vertex-stable and edge-stable from degree k onwards, and Example 3.14 is vertex-stable in degree r, but edge-stable only once the degree is greater than all of $a_0$ through $a_r$.

The Kneser graphs $KG_{\bullet ,k}$ (Example 3.4) are vertex-stable in degree k, edge-stable in degree 2k, and r-vertex-stable in degree rk. In contrast, the lattice graphs $Q_{\bullet ,k}$ (Example 3.8) are vertex-stable in degree k, edge-stable in degree $k+1$, and r-vertex-stable in degree rk.

It is left to the reader to verify that all of the examples of the previous section satisfy each of the above conditions. Somewhat miraculously, it turns out that this is not a coincidence.

Theorem 3.18

Let $G_\bullet$ be a vertex-stable ${{\,\mathrm{FI}\,}}$-graph. Then:

• 1. $G_\bullet$ is r-vertex-stable for all $r \ge 1$;

• 2. $G_\bullet$ is edge-stable;

• 3. $G_\bullet$ is eventually injective and induced.

It is worth noting that vertex-stability is strictly stronger than edge-stability, as shown by the following example.

Example 3.19

For each n, let $G_n$ be the union of the complete graph $K_n$ and n isolated vertices. The symmetric group ${\mathfrak {S}}_n$ acts naturally on the complete graph and fixes each of the other vertices. This ${{\,\mathrm{FI}\,}}$-graph is edge-stable in degree 2, but is not vertex-stable.

Edge stability may happen either before or after 2-vertex-stability, because edge-stability includes only pairs of vertices which are connected by edges, but it is possible for edges to not appear until long after any pair of vertices are contained in the image of some transition map. Example 3.14 is 2-vertex-stable in degree 2r, but is not edge-stable until the degree equal to the maximum of the $a_i$.

Before we prove Theorem 3.18, it will be useful to us to rephrase the above properties in terms of finite generation of certain ${{\,\mathrm{FI}\,}}$-modules.

Definition 3.20

Let $G_\bullet$ denote an ${{\,\mathrm{FI}\,}}$-graph, and let $r \ge 1$ be fixed. We write

$$\begin{aligned} {\mathbb {R}}\left( {\begin{array}{c}V(G_\bullet )\\ r\end{array}}\right) \end{aligned}$$

to denote the ${{\,\mathrm{FI}\,}}$-module whose evaluation at [n] is the ${\mathbb {R}}$ vector space with basis indexed by collections of r vertices of $G_n$. We will often write ${\mathbb {R}}V(G_\bullet ) := {\mathbb {R}}\left( {\begin{array}{c}V(G_\bullet )\\ 1\end{array}}\right)$. Note that the image of a collection of r vertices under a transition map may not be a collection of r vertices if this transition map is not injective on vertices. In this case we simply declare the map to be zero on this collection. Similarly, we define ${\mathbb {R}}E(G_\bullet )$ to be the ${{\,\mathrm{FI}\,}}$-module whose evaluation at [n] is the ${\mathbb {R}}$ vector space with basis indexed by the edges of $E(G_n)$.

Remark 3.21

The modules ${\mathbb {R}}\left( {\begin{array}{c}V(G_\bullet )\\ r\end{array}}\right)$ can also be constructed in the following fashion. Observe that if $G_\bullet$ is an ${{\,\mathrm{FI}\,}}$-graph, then $\left( {\begin{array}{c}V(G_\bullet )\\ r\end{array}}\right)$ is an ${{\,\mathrm{FI}\,}}$-set, i.e. a functor from ${{\,\mathrm{FI}\,}}$ to the category of finite sets. There is a functor from the category of finite sets to the category of ${\mathbb {R}}$ vector spaces given by linearization. Specifically, this is the functor which sends a set to the ${\mathbb {R}}$ vector space with a basis indexed by the elements of the set. The module ${\mathbb {R}}\left( {\begin{array}{c}V(G_\bullet )\\ r\end{array}}\right)$ can therefore be realized as a composition of the functor $\left( {\begin{array}{c}V(G_\bullet )\\ r\end{array}}\right)$ with linearization. This perspective is pervasive through the sequel work [36], where ${{\,\mathrm{FI}\,}}$-sets are a more primary focus. In this work we will not dive too deeply into this idea.

Lemma 3.22

Let $G_\bullet$ be an ${{\,\mathrm{FI}\,}}$-graph.

• 1. $G_\bullet$ is vertex-stable with stable degree $\le d$ if and only if ${\mathbb {R}}V(G_\bullet )$ is finitely generated in degree $\le d$.

• 2. $G_\bullet$ is eventually injective if and only if the transition maps of ${\mathbb {R}}V(G_\bullet )$ are eventually injective.

• 3. $G_\bullet$ is edge-stable with edge-stable degree $\le d$ if and only if ${\mathbb {R}}E(G_\bullet )$ is finitely generated in degree $\le d$.

• 4. $G_{\bullet }$ is r-vertex-stable if and only if ${\mathbb {R}}\left( {\begin{array}{c}V(G_\bullet )\\ r\end{array}}\right)$ is finitely generated.

Proof

All of these assertions follow from the relevant definitions. $\square$

Remark 3.23

Note that this lemma is critically dependent on the assumption that $G_n$ has finitely many vertices and edges for each n. For instance, consider the collection of infinite graphs

$$\begin{aligned} V(G_n) := {\mathbb {N}},\quad E(G_n) := \{\{1,2\},\{2,3\},\ldots , \{n-1,n\}\} \end{aligned}$$

We can introduce an ${{\,\mathrm{FI}\,}}$-structure on $G_\bullet$ by having the symmetric group act trivially. Then it is clear that ${\mathbb {R}}V(G_n)$ is not finitely generated, despite $G_\bullet$ being “vertex-stable” in some sense. Also note that the collection $G_\bullet$ is not edge-stable in this case, seemingly violating Theorem 3.18.

This lemma is the key piece in the proof of Theorem 3.18.

Proof of Theorem 3.18

To begin, Lemma 3.22 implies that we must show that ${\mathbb {R}}\left( {\begin{array}{c}V(G_\bullet )\\ r\end{array}}\right)$ is finitely generated. We note that there is a surjection of ${{\,\mathrm{FI}\,}}$-modules

$$\begin{aligned} {\mathbb {R}}V(G_\bullet )^{\otimes r} \rightarrow {\mathbb {R}}\left( {\begin{array}{c}V(G_\bullet )\\ r\end{array}}\right) \end{aligned}$$

Indeed, this is induced by the assignments

$$\begin{aligned} x_1 \otimes \cdots \otimes x_r \mapsto {\left\{ \begin{array}{ll} \{x_1,\ldots ,x_r\} &{} \text { if }x_i \ne x_j\text { for }i \ne j\\ 0 &{} \text { otherwise.}\end{array}\right. } \end{aligned}$$

By assumption ${\mathbb {R}}V(G_\bullet )$ is finitely generated, whence the same is true of $({\mathbb {R}}V(G_\bullet ))^{\otimes r}$ by Proposition 2.17. This concludes the proof of the first statement.

The second statement follows from the Noetherian property as well as the inclusion

$$\begin{aligned} {\mathbb {R}}E(G_\bullet ) \hookrightarrow {\mathbb {R}}\left( {\begin{array}{c}V(G_\bullet )\\ 2\end{array}}\right) . \end{aligned}$$

Eventual injectivity follows from Theorem 2.18.

By definition, $G_\bullet$ is eventually induced if and only if for n large enough and for $\{x,y\} \notin E(G_n)$ any pair of nonadjacent vertices of $G_n$, then the images of x and y under any injection $f:[n] \hookrightarrow [n+1]$, $f_\text {*}(x)$ and $f_\text {*}(y)$, are not connected by an edge in $G_{n+1}$. For each n, let ${\mathcal {O}}_n$ denote the set of ${\mathfrak {S}}_n$-orbits of pairs of vertices in $G_n$. Note that ${\mathcal {O}}_n$ may be partitioned into two subsets, depending on whether or not pairs in the orbit correspond to edges or not. Further note that the transition maps of $G_\bullet$ will send an “edge” orbit to an edge orbit. On the other hand, the third part of Theorem 2.18 implies that $|{\mathcal {O}}_n|$ is eventually independent of n, as it is equal to the multiplicity of the trivial representation in ${\mathbb {R}}\left( {\begin{array}{c}V(G_n)\\ 2\end{array}}\right)$.

For similar reasons the orbits of pairs corresponding to edges must stabilize as well. Note that even once the number of orbits of pairs of orbits has stabilized (that is, that $|{\mathcal {O}}_k|$ is constant for all $k \ge n$), it may not be the case that the edge orbits have already stabilized at the same graph n. Rather, this value of $|{\mathcal {O}}_k|$ gives a finite upper bound on the number of times that the number of edge orbits may increase, which shows that this number eventually stabilizes. However, there is no bound on how long this may take, as can be seen by considering Example 3.14 and taking any of the $a_k$ to be arbitrarily large.

Once the edge orbits have stabilized, non-edged orbits will eventually map exclusively into non-edged orbits, as desired. $\square$

Remark 3.24

Proposition 2.17 and the above proof together imply that ${\mathbb {R}}\left( {\begin{array}{c}V(G_\bullet )\\ r\end{array}}\right)$ is generated in degree $\le r d$, where d is the generating degree of ${\mathbb {R}}V(G_\bullet )$. In particular, ${\mathbb {R}}E(G_\bullet )$ is 2d-small.

Remark 3.25

It is possible to prove one part of Theorem 3.18 directly. Consider any set of k vertices $v_1$ through $v_k$ in $G_n$, for $n \ge kr$. Each $v_i$ is in the image of a transition map from $G_k$ to $G_n$, and each of these transition maps is induced by an injection from [k] to [n]. Let $f_1$ through $f_k$ be these injections. Take f to be an injection from [kr] to n whose image includes the image of each $f_i$. Then each $f_i$ factors through f, so each $v_i$ is in the image of the transition map induced by f. This completes the proof.

The proof of r-vertex-stability in Theorem 3.18 relies on the tensor product of finitely generated ${{\,\mathrm{FI}\,}}$-modules being finitely generated. The proof of this fact may be made explicit, and this is what lies behind the proof given above.

An application of Theorem 3.18 is the following construction of new vertex-stable ${{\,\mathrm{FI}\,}}$-graphs from existing vertex-stable ${{\,\mathrm{FI}\,}}$-graphs.

Definition 3.26

Let G be a graph. The line graph of G, L(G), is the graph whose vertices are labeled by the edges of G such that two vertices are connected if and only if the corresponding edges of G share an end point.

Line graphs have been studied extensively. One avenue of research is the question of how much of the graph G can be determined by studying its line graph. A celebrated theorem of Whitney [41] implies that the line graph almost always uniquely determines the original graph. Indeed, the only exception to this is the fact that $L(K_3) = L(K_{3,1})$. Algebraically, one is also interested in the question of deciding when a line graph is determined by its spectrum (See, for instance, [25] or Chapter 1.3 of [14]).

Corollary 3.27

Let $G_\bullet$ denote a vertex-stable ${{\,\mathrm{FI}\,}}$-graph. Then the collection of line graphs $L(G_\bullet )$ can be endowed with the structure of a vertex-stable ${{\,\mathrm{FI}\,}}$-graph.

Proof

This result follows immediately from Theorem 3.18 and the definition of the line graph. $\square$

Remark 3.28

We note that the line graph $L(K_n)$ is isomorphic to the Johnson graph $J_{n,2}$. The line graphs of the complete bipartite graphs $K_{n,m}$ have been studied (see, for instance, [32] or the references in [14]), and are sometimes referred to as the rook graphs, as they can be thought of as encoding legal rook moves on an $m \times n$ chess board.

3.3 Determining when the induced property begins

Theorem 3.18 implies that all ${{\,\mathrm{FI}\,}}$-graphs are eventually induced. In this section we consider the question of bounding when this behavior begins. To begin we impose the following technical condition on the ${{\,\mathrm{FI}\,}}$-graph $G_\bullet$. We will see this condition return again when we consider configuration spaces of graphs.

Definition 3.29

We say an ${{\,\mathrm{FI}\,}}$-graph $G_\bullet$ is torsion-free if for all injections $f:[n] \hookrightarrow [m]$ the transition map G(f) is injective.

Most of the examples in Sect. 3.1 are torsion-free. Example 3.13 is not torsion-free.

Remark 3.30

We say an ${{\,\mathrm{FI}\,}}$-module is torsion-free if all of its transition maps are injective. The above definition is intended to emulate this.

Theorem 3.18 insists that vertex-stability implies edge-stability. In particular, at some point the transition maps of a vertex-stable ${{\,\mathrm{FI}\,}}$-graph will contain every edge in the union of their respective images. It is therefore natural for one to guess that it will be at this point that the image of these transition maps must be induced. We do indeed find this to be the case for torsion-free ${{\,\mathrm{FI}\,}}$-modules.

Theorem 3.31

Let $G_\bullet$ be a torsion-free vertex-stable ${{\,\mathrm{FI}\,}}$-graph with edge-stable degree $\le d_E$. Then for any $n \ge d_E$ and any injection $f:[n] \hookrightarrow [n+1]$ the image of $G_n$ under the transition map G(f) is an induced subgraph of $G_{n+1}$.

While it might seem natural for there to be some kind of pigeon-hole or counting argument for the above theorem, such an argument has thus far eluded the authors. Just like much of the rest of this work, we instead prove Theorem 3.31 through the algebra of ${{\,\mathrm{FI}\,}}$-modules. To begin, we must rephrase the eventually induced property in the language of ${{\,\mathrm{FI}\,}}$-modules.

Definition 3.32

The coinvariants functor $\Phi$ from ${{\,\mathrm{FI}\,}}$-modules to graded ${\mathbb {R}}[x]$-modules is defined by

$$\begin{aligned} \Phi (V)_n := V_n \otimes _{{\mathfrak {S}}_n} {\mathbb {R}}\end{aligned}$$

Multiplication by x is induced by the action of the transition maps.

In the setting of ${{\,\mathrm{FI}\,}}$-graphs and their associated ${{\,\mathrm{FI}\,}}$-modules, the coinvariants functor takes a particularly nice form.

Recall that we define ${\mathbb {R}}\left( {\begin{array}{c}V(G_\bullet )\\ 2\end{array}}\right)$ to be the ${{\,\mathrm{FI}\,}}$-module encoding pairs of vertices of $G_\bullet$. The coinvariants of ${\mathbb {R}}\left( {\begin{array}{c}V(G_\bullet )\\ 2\end{array}}\right)$ can be constructed in the following way. We define $\Phi$ to be the graded ${\mathbb {R}}[x]$-module for which $\Phi _n$ is the free ${\mathbb {R}}$ vector space with basis indexed by the orbits of the symmetric group action on pairs of vertices of $G_n$. For each n we may define $\iota _n:[n] \hookrightarrow [n+1]$ to be the standard inclusion. Then $G(\iota _n)$ induces a map between the orbits of pairs of vertices of $G_n$ and those of $G_{n+1}$. Multiplication by x in the module $\Phi$ will be defined by this map.

Lemma 3.33

Let V be a finitely generated ${{\,\mathrm{FI}\,}}$-module. If V is torsion-free as an ${{\,\mathrm{FI}\,}}$-module, then $\Phi (V)$ is torsion-free as a ${\mathbb {R}}[x]$-module.

Proof

This follows from the fact that coinvariants are exact over fields of characteristic 0. $\square$

This lemma is the key piece needed to prove Theorem 3.31.

Proof of Theorem 3.31

Let $G_\bullet$ be a torsion-free vertex-stable ${{\,\mathrm{FI}\,}}$-graph, and assume that $G_\bullet$ has edge-stable degree $\le d_E$. Assume by way of contradiction that there is some $n \ge d_E$ such that the image of $G_n$ under any transition map $G(f):G_n \rightarrow G_{n+1}$ is not an induced subgraph. This implies that there is some pair of vertices $\{v_1,v_2\}$ in $G_n$, which are not connected by an edge, while $G(f)(\{v_1,v_2\})$ is an edge of $G_{n+1}$. On the other hand, because $n \ge d_E$, there must be some transition map G(h), as well as some edge $e \in E(G_n)$ such that $G(h)(e) = G(f)(\{v_1,v_2\})$. We may apply some element of ${\mathfrak {S}}_{n+1}$ to conclude the following: The transition map G(f) must map some non-edge of $G_n$, as well as some edge of $G_n$, to the same ${\mathfrak {S}}_{n+1}$ orbit on the pairs of vertices of $G_{n+1}$. In particular, this would imply that the coinvariants of ${\mathbb {R}}\left( {\begin{array}{c}V(G_\bullet )\\ 2\end{array}}\right)$ has torsion. This contradicts Lemma 3.33. $\square$

4 Applications

In the following sections we prove the variety of applications of the primary structure theorem that were claimed in the introduction. Many of these proofs ultimately take the same form: one encodes the invariant or homology groups as the graded pieces of a finitely generated ${{\,\mathrm{FI}\,}}$-module (over ${\mathbb {Z}}$). Finite generation in these cases is usually proven by embedding the ${{\,\mathrm{FI}\,}}$-module into a larger ${{\,\mathrm{FI}\,}}$-module which is known to be finitely generated, and then applying the Noetherian property. These “bigger” ${{\,\mathrm{FI}\,}}$-modules which we embed into are almost always ${\mathbb {R}}\left( {\begin{array}{c}V(G_\bullet )\\ j\end{array}}\right)$ (Remark 3.24), as well as tensor products of the modules ${\mathbb {R}}\left( {\begin{array}{c}V(G_\bullet )\\ j\end{array}}\right)$ (Proposition 2.17).

4.1 Enumerative consequences of vertex-stability

We begin this section by revisiting the invariants $\eta _H$ and $\eta _H^{ind}$ for some fixed graph H. In particular, if $G_\bullet$ is a vertex-stable ${{\,\mathrm{FI}\,}}$-graph, we consider the functions

$$\begin{aligned} n \mapsto \eta _H(G_n) \text { and } n \mapsto \eta _H^{ind}(G_n). \end{aligned}$$

Our primary result in this direction is the following.

Theorem 4.1

Let $G_\bullet$ be a vertex-stable graph with stable degree $\le d$. Then for any graph H there exists polynomials $p_H(X), p_H^{ind}(X) \in {\mathbb {Q}}[X]$ of degree $\le d\cdot |V(H)|$ such that for all $n \gg 0$,

$$\begin{aligned} p_H(n) = \eta _H(G_n) \text { and } p_H^{ind}(n) = \eta _H^{ind}(G_n) \end{aligned}$$

Proof

We will count the number of graph injections from H to $G_\bullet$. This quantity is a constant multiple of $\eta _H(G_\bullet )$, and it is therefore sufficient to count. Let $V^H_\bullet$ denote the ${{\,\mathrm{FI}\,}}$-module whose evaluation at [n] is the ${\mathbb {R}}$ vector space with basis indexed by the distinct graph theoretic injections of H into $G_n$. To make sure the transition maps are well defined, we will set $V^H_{n} = 0$ before the point where the transition maps of $G_\bullet$ are both induced and injective. We therefore see that $V^H_\bullet$ can be realized as a submodule

$$\begin{aligned} V^H_\bullet \hookrightarrow ({\mathbb {R}}V(G_\bullet ))^{\otimes |V(H)|} \end{aligned}$$

via the point-wise assignment,

$$\begin{aligned} \phi \mapsto \bigotimes _{x \in V(H)}(\phi (x)). \end{aligned}$$

Proposition 2.17 implies that $V^H_\bullet$ is $(d\cdot |V(H)|)$-small, and Theorem 2.18 implies the existence of our desired polynomial. The proof for the induced case is the same. $\square$

Example 4.2

Looking the ${{\,\mathrm{FI}\,}}$-graph $K_\bullet$ of complete graphs, the above result is clear. H cannot appear in $K_n$ when $n < |V(H)|$. If we call $\gamma _H$ the number of copies of H in $K_{|V(H)|}$, then

$$\begin{aligned} p_H(n) = \left( {\begin{array}{c}n\\ |V(H)|\end{array}}\right) \gamma _H \end{aligned}$$

The content of Theorem 4.1 is that this behavior is common to all vertex-stable ${{\,\mathrm{FI}\,}}$-graphs. The examples of the previous section illustrate that vertex-stable ${{\,\mathrm{FI}\,}}$-graphs can be fairly diverse, and so this might come as a bit of a surprise.

Fix $k \ge 2$ and let $KG_{\bullet ,k}$ be the ${{\,\mathrm{FI}\,}}$-graph which encodes the Kneser graphs. In this case we may easily count the number of triangles which appear in $KG_{n,k}$. Indeed, to form a triangle, one needs to provide three mutually disjoint subsets of [n] of size k. It follows that

$$\begin{aligned} p_{K_3}(n) = \frac{\left( {\begin{array}{c}n\\ 3k\end{array}}\right) \left( {\begin{array}{c}3k\\ k,k,k\end{array}}\right) }{6}. \end{aligned}$$

Note that if we take the usual convention that $\left( {\begin{array}{c}n\\ k\end{array}}\right) = 0$ whenever $n < k$, then the above polynomial agrees with $\eta _{K_3}(KG_{n,k})$ for all $n \ge 0$. If we instead try to count the number of occurrences of the six-vertex graph which looks like the letter H, things get considerably more complicated. Despite the seeming drastic increase in difficulty, Theorem 4.1 assures us that the value of $\eta _H(KG_{n,k})$ must (eventually) agree with a polynomial, and that this polynomial will have degree at most 6k.

As an immediate corollary to the above, we find that vertex-stable ${{\,\mathrm{FI}\,}}$-graphs have very controlled growth in their vertices and edges, as well as in the degrees of their vertices.

Corollary 4.3

Let $G_\bullet$ be a vertex-stable ${{\,\mathrm{FI}\,}}$-graph. Then the following functions are each equal to a polynomial for $n \gg 0$:

• 1. $n \mapsto |V(G_n)|$;

• 2. $n \mapsto |E(G_n)|$;

• 3. $n \mapsto \delta (G_n)$;

• 4. $n \mapsto \Delta (G_n)$.

If the stable degree of $G_\bullet$ is at most d, then these polynomials have degree at most d in the first, third, and fourth cases, and degree at most 2d in the second case ($n \mapsto |E(G_n)|)$.

Proof

The first two statements follow from a direct application of Theorem 4.1 with H being an isolated vertex and a single edge, respectively.

For the final two statements, we prove a more general statement. Fix $m \gg 0$, and let $v \in V(G_m)$. Then every vertex in the ${\mathfrak {S}}_m$-orbit of v, which we denote ${\mathcal {O}}_v(m)$, has the same degree. Let ${\mathbb {R}}{\mathcal {O}}_v(\bullet )$ denote the submodule of ${\mathbb {R}}V(G_\bullet )$ generated by v, and for $n \ge m$ let $\mu ({\mathcal {O}}_v(n))$ denote the degree of any (and therefore all) vertices in ${\mathcal {O}}_v(n)$. We will prove that the map

$$\begin{aligned} n \mapsto \mu ({\mathcal {O}}_v(n)) \end{aligned}$$

is equal to a polynomial. To see that this implies the final two statements of our corollary, note that the final part of Theorem 2.18 implies that the total number of distinct orbits of $V(G_n)$ is eventually independent of n. Because non-equal polynomials are only permitted to be equal at finitely many points, the above implies that there is a well-defined polynomial which outputs the smallest (or largest) degree of any vertex of $G_n$ when n is large enough.

To prove our more general claim, we need a bit of notation. We will write ${\mathbb {R}}E({\mathcal {O}}_v(\bullet ))$ for the submodule of ${\mathbb {R}}E(G_\bullet )$ whose n-th piece is spanned by edges whose both end points are in ${\mathcal {O}}_v(n)$. We will also write $N({\mathcal {O}}_v(n))$ to denote the subgraph of $G_n$ comprised of all vertices and edges that one may encounter by beginning at a vertex in ${\mathcal {O}}_v(n)$ and moving along any single edge adjacent to it. Put another way, $N({\mathcal {O}}_v(n))$ is the neighborhood graph on the vertex set ${\mathcal {O}}_v(n)$. By setting $N({\mathcal {O}}_v(n)) = \emptyset$ whenever $n < m$, we see that $N({\mathcal {O}}_v(\bullet ))$ is actually a vertex-stable ${{\,\mathrm{FI}\,}}$-graph. Therefore, by the second part of this corollary,

$$\begin{aligned} n \mapsto |E(N({\mathcal {O}}_v(n)))| \end{aligned}$$

is eventually equal to a polynomial. On the other hand, we may count the set $|E(N({\mathcal {O}}_v(n)))|$ in the following alternative way,

$$\begin{aligned} |E(N({\mathcal {O}}_v(n)))| = \mu ({\mathcal {O}}_v(n)) \cdot |{\mathcal {O}}_v(n)| - |E({\mathcal {O}}_v(n))|. \end{aligned}$$

In other words, if we sum the degrees of all vertices in ${\mathcal {O}}_v(n)$, then we would have counted each edge in $E({\mathcal {O}}_v(n))$ exactly twice. Because ${\mathbb {R}}{\mathcal {O}}_v(\bullet )$ is a submodule of ${\mathbb {R}}V(G_\bullet )$, we know that its dimension is eventually equal to a polynomial. A similar statement can also be made about $|E({\mathcal {O}}_v(n))|$. Solving for $\mu ({\mathcal {O}}_v(n))$, we find that it is equal to a rational function for n sufficiently large. However, the only rational functions which can take integral values at all sufficiently large integers are polynomials. This concludes the proof. $\square$

Another consequence of vertex-stability concerns finite walks in the graph $G_n$. Recall that a walk of length r in a graph G is a tuple of vertices of G, $(v_0,\ldots ,v_r)$, such that for each i, $\{v_i,v_{i+1})$ is an edge of G. We say that a walk is closed if $v_r = v_0$.

Theorem 4.4

Let $G_\bullet$ be a vertex-stable ${{\,\mathrm{FI}\,}}$-graph with stable degree $\le d$. Then the following functions are each equal to a polynomial, of degree $\le (r+1)d$ in the first case and of degree $\le rd$ in the second, for $n \gg 0$ and any fixed $r \ge 0$:

• 1. $n \mapsto |\{\text {walks in }G_n\text { of length }r\}|$;

• 2. $n \mapsto |\{\text {closed walks in }G_n\text { of length }r\}|$.

Proof

Our strategy here is similar to the strategy of much of the rest of the paper. Encode the objects we hope to count as the dimension of some vector space, and use the Noetherian property to prove that the collection of all these vector spaces form a finitely generated ${{\,\mathrm{FI}\,}}$-module. Let $W_r(G_\bullet )$ denote the ${{\,\mathrm{FI}\,}}$-module for which $W_r(G_n)$ is the formal vector space spanned by walks of length r in $G_n$. Similarly define $W_r^c(G_\bullet )$ for closed walks. Note that these ${{\,\mathrm{FI}\,}}$-modules may not be well defined if the transition maps of $G_\bullet$ are not injective. While injectivity may not be the case for small n, Theorem 3.18 implies that it certainly will be the case for $n \gg 0$. Therefore, we simply define $W_r(G_n)$, and $W_r^c(G_n)$ to be zero before injectivity takes effect. To prove that $W_r(G_\bullet )$ is finitely generated, we simply note that there is an embedding,

$$\begin{aligned} W_r(G_\bullet ) \hookrightarrow {\mathbb {R}}V(G_\bullet )^{\otimes (r+1)} \end{aligned}$$

defined on points by

$$\begin{aligned} (v_0,\ldots ,v_r) \mapsto v_0 \otimes v_1 \otimes \cdots \otimes v_r \end{aligned}$$

The module ${\mathbb {R}}V(G_\bullet )^{\otimes (r+1)}$ is finitely generated in degree $\le (r+1) \cdot d$ by Proposition 2.17. The Noetherian property concludes the proof. Note that in the case of closed walks, the fact that $v_0 = v_r$ removes a degree of freedom in our choices of vertices. In particular, we may embed $W_r^c(G_\bullet )$ into ${\mathbb {R}}V(G_\bullet )^{\otimes r}$. By consequence, the dimension of $W_r^c(G_\bullet )$ is bounded by a polynomial of degree $\le rd$, as required. $\square$

The above work illustrates how certain invariants of $G_n$ can grow with n. We also find, however, there are some invariants which must eventually stabilize.

Proposition 4.5

Let $G_\bullet$ denote a vertex-stable ${{\,\mathrm{FI}\,}}$-graph. Then the following invariants are independent of n for $n \gg 0$:

• 1. The diameter of $G_n$;

• 2. The girth (i.e. the size of the smallest cycle) of $G_n$;

Proof

For both statements, it suffices to show that the relevant invariant is eventually weakly decreasing in n. If $n \gg 0$, and $u,v \in V(G_n)$, then by Theorem 3.18 there exists $x,y \in V(G_{n-1})$ and an injection $f:[n-1] \hookrightarrow [n]$ such that $u = G(f)(x), v = G(f)(y)$. In particular, if P is any path in $G_{n-1}$ connecting x and y, then G(f)(P) is a path in $G_n$ connecting u to v. This shows that the shortest path between u and v cannot be longer than the shortest path between x and y. By definition, the diameter of $G_n$ cannot be bigger than the diameter of $G_{n-1}$. A similar argument works for girth. $\square$

4.2 Topological consequences of vertex-stability

In this section we consider a collection of topological applications of vertex-stability. Our first applications are simple consequences of the work in the previous section, as well as facts from our background sections.

Lemma 4.6

Let H be a graph, $G_\bullet$ a vertex-stable ${{\,\mathrm{FI}\,}}$-graph of stable degree $\le d$, and ${{\mathcal {C}}}^H_{n,i}$ denote the free ${\mathbb {Z}}$-module with basis indexed by the i-cells of ${\mathscr {H}}om(H,G_n)$. Then ${{\mathcal {C}}}^H_{\bullet ,i}$ can be endowed with the structure of a finitely generated ${{\,\mathrm{FI}\,}}$-module over ${\mathbb {Z}}$ which is $(d(|V(H)| + i))$-small.

Proof

We first recall the definition of the Hom-complex ${\mathscr {H}}om(H,G_n)$. The cells of ${\mathscr {H}}om(H,G_n)$ are multi-homomorphisms, where $\alpha$ is contained in the closure of $\tau$ if and only if $\alpha (x) \subseteq \tau (x)$ for all x. It is clear that the transition maps of $G_\bullet$ induce the transition maps of ${{\mathcal {C}}}^H_{\bullet ,i}$, turning this collection of abelian groups into an ${{\,\mathrm{FI}\,}}$-module over ${\mathbb {Z}}$.

We have that i-cells of the complex correspond to multi-homomorphisms $\alpha$ satisfying

$$\begin{aligned} \sum _{x \in V(H)}|\alpha (x)| =|V(H)| + i \end{aligned}$$

The data of an i-cell can therefore be encoded as an |V(H)|-tuple

$$\begin{aligned} (\alpha _x)_{x \in V(H)} \end{aligned}$$

such that:

• Each $\alpha _x$ is a non-empty subset of $V(G_n)$;

• $\sum _{x \in V(H)} |\alpha _x| = |V(H)|+i$;

• If $\{x,y\} \in E(H)$ then for all $v \in \alpha _x$ and $w \in \alpha _y$, $\{v,w\} \in E(G_n)$.

Just as we have done previously, such as in the proof of Theorem 3.18, we may realize ${{\mathcal {C}}}^H_{\bullet ,i}$ as a submodule of

$$\begin{aligned} \bigoplus _{r_1 + \cdots + r_{|V(H)|} = |V(H)| + i} \left( \bigotimes _{k} {\mathbb {R}}\left( {\begin{array}{c}V(G_\bullet )\\ r_k\end{array}}\right) \right) \end{aligned}$$

The Noetherian property, as well as previous discovered facts about the modules ${\mathbb {R}}\left( {\begin{array}{c}V(G_\bullet )\\ j\end{array}}\right)$ (see the proof of Theorem 3.18) imply our lemma. $\square$

Lemma 4.6 is the main tool we will need in proving that Hom-complexes of vertex-stable ${{\,\mathrm{FI}\,}}$-graphs are representation stable in the sense of Church and Farb. Before we get to this theorem, we observe the following consequence of the above in terms of counting homomorphisms into $G_\bullet$.

Corollary 4.7

Let H be any graph, and let $G_\bullet$ be a vertex-stable ${{\,\mathrm{FI}\,}}$-graph of stable degree $\le d$. Then for $n \gg 0$, then the function

$$\begin{aligned} n \mapsto |{{\,\mathrm{Hom}\,}}(H,G_\bullet )| \end{aligned}$$

agrees with a polynomial of degree $\le d\cdot |V(H)|$.

Proof

This follows from Theorem 2.18, Lemma 4.6, and the fact that the module ${{\mathcal {C}}}^H_{n,0}$ from Lemma 4.6 has basis indexed by ${{\,\mathrm{Hom}\,}}(H,G_n)$. $\square$

Remark 4.8

It is easily seen that homomorphisms ${{\,\mathrm{Hom}\,}}(H,K_n)$ are in bijection with vertex colorings of H for which no adjacent vertices are of the same color. The above corollary therefore recovers the existence of the so-called chromatic polynomial. Note that the chromatic polynomial exists for all $n \ge 0$, while the above only guarantees it for $n \gg 0$. One can recover the fact that the chromatic polynomial exists for $n \ge 0$ by showing that the collection of vector spaces ${\mathbb {R}}{{\,\mathrm{Hom}\,}}(H,K_\bullet )$ can be endowed with the structure of an ${{\,\mathrm{FI}\,}}_\sharp$-module (see [10]).

Note that a similar idea, i.e. using ${{\,\mathrm{FI}\,}}$-module techniques to recover the chromatic polynomial, was conveyed to the authors by John Wiltshire-Gordon and Jordan Ellenberg. This alternative technique was very similar in spirit, but used FA-modules instead of ${{\,\mathrm{FI}\,}}$-modules. Here, FA is the category of finite sets and all maps (see, for instance, [42]).

Theorem 4.9

Let H be a graph, $G_\bullet$ a vertex-stable ${{\,\mathrm{FI}\,}}$-graph of stable degree $\le d$, and let $i \ge 0$ be a fixed integer. Then the ${{\,\mathrm{FI}\,}}$-module over ${\mathbb {Z}}$

$$\begin{aligned} H_i({\mathscr {H}}om(H,G_\bullet )) \end{aligned}$$

is $(d(|V(H)| + i))$-small.

Proof

Recall the groups ${{\mathcal {C}}}^H_{n,i}$ from the Lemma 4.6. Standard polyhedral homology informs us that there is a complex,

$$\begin{aligned} {{\mathcal {C}}}^H_{n,\star }: \cdots \rightarrow {{\mathcal {C}}}^H_{n,i} {\mathop {\rightarrow }\limits ^{\partial }} {{\mathcal {C}}}^H_{n,i-1} \rightarrow \cdots \rightarrow {{\mathcal {C}}}^H_{n,0} \rightarrow 0 \end{aligned}$$

with homology isomorphic to $H_\star ({\mathscr {H}}om(H,G_n))$. Lemma 4.6 tells us that for each fixed i the groups ${{\mathcal {C}}}^H_{\bullet ,i}$ form a finitely generated ${{\,\mathrm{FI}\,}}$-module over ${\mathbb {Z}}$. It isn’t hard to show that the action of the transition maps of ${{\mathcal {C}}}^H_{\bullet ,i}$ commute with the differentials $\partial$. It follows that there is a complex of ${{\,\mathrm{FI}\,}}$-modules over ${\mathbb {Z}}$

$$\begin{aligned} {{\mathcal {C}}}^H_{\bullet ,\star }: \cdots \rightarrow {{\mathcal {C}}}^H_{\bullet ,i} {\mathop {\rightarrow }\limits ^{\partial }} {{\mathcal {C}}}^H_{\bullet ,i-1} \rightarrow \cdots \rightarrow {{\mathcal {C}}}^H_{\bullet ,0} \rightarrow 0 \end{aligned}$$

whose homology agrees with the ${{\,\mathrm{FI}\,}}$-modules $H_i({\mathscr {H}}om(H,G_\bullet ))$. The Noetherian property and Lemma 4.6 imply our result. $\square$

To conclude this section, we review some fundamental concepts and definitions which will be used in the proof of Theorem G.

For the remainder of this section, we fix a vertex-stable, torsion-free ${{\,\mathrm{FI}\,}}$-graph $G_\bullet$ as well as a positive integer m. We will assume that $G_\bullet$ has stable degree $\le d$ and edge-stable degree $\le d_E$.

To begin, we note that the necessary edge subdivisions of Theorem 2.9 can be accomplished in a way consistent with the ${{\,\mathrm{FI}\,}}$-module structure of $G_\bullet$.

Proposition 4.10

There exists an ${{\,\mathrm{FI}\,}}$-graph, $G^{(m)}_\bullet$, for which $G^{(m)}_n$ is the m-th subdivision of $G_n$ and for any injection of sets $f:[n] \hookrightarrow [r]$ one has

$$\begin{aligned} G^{(m)}(f)(x) = G(f)(x) \end{aligned}$$

for all $x \in V(G_n)$. If $G_\bullet$ has stable degree $\le d$ and edge-stable degree $\le d_E$, then $G^{(m)}_\bullet$ has stable degree $\le \max \{d,d_E\}$ and edge-stable degree $\le d_E$.

Proof

The existence of $G^{(m)}_\bullet$ follows from the definition of the m-th subdivision. If $x,y \in V(G_n)$ are connected via an edge, then the same must be true of G(f)(x) and G(f)(y), for any f. Therefore, if we enumerate the subdivision vertices of $\{x,y\}$ (resp. $\{G(f)(x),G(f)(y)\}$) as $v_1, \ldots , v_{m-1}$ (resp. $w_1,\ldots ,w_{m-1}$), where $v_1$ is adjacent to x (resp. $w_1$ to G(f)(x)), then we set $G(f)(v_i) = w_i$. The statement on stable degrees follows from the fact that subdivision creates new vertices and edges within existing edges. $\square$

This proposition will prove to be critical for us, as it essentially asserts, with Theorem 2.9, that there exists a combinatorial model of ${{\,\mathrm{Conf}\,}}_m(G_\bullet )$ which interacts nicely with the ${{\,\mathrm{FI}\,}}$-graph structure of $G_\bullet$.

We are now ready to provide the main novel computational construction of this section. Recall that we have fixed a vertex-stable torsion-free ${{\,\mathrm{FI}\,}}$-graph $G_\bullet$.

Definition 4.11

Fix integers $m,n,i \ge 0$. We write ${\mathcal {K}}_{n,m,i}$ to denote the free ${\mathbb {Z}}$-module with basis vectors indexed by the i-dimensional cells of the cubical complex ${{\,\mathrm{DConf}\,}}_m(G^{(m)}_n)$. Given any injection of sets $f:[n] \hookrightarrow [r]$, Proposition 4.10 implies that the transition map G(f) induces a transition map $G^{(m)}_n \rightarrow G^{(m)}_r$, which, in turn, induces a map

$$\begin{aligned} f_\text {*}: {\mathcal {K}}_{n,m,i} \rightarrow {\mathcal {K}}_{r,m,i}. \end{aligned}$$

This procedure equips the family $\{{\mathcal {K}}_{n,m,i}\}_n$ with the structure of an ${{\,\mathrm{FI}\,}}$-module over ${\mathbb {Z}}$.

Having observed the ${{\,\mathrm{FI}\,}}$-module structure on the families ${\mathcal {K}}_{\bullet ,m,i}$, the strategy of our proof of Theorem G becomes clear. We begin by proving that, for all choices of m and i, the ${{\,\mathrm{FI}\,}}$-module ${\mathcal {K}}_{\bullet ,m,i}$ is finitely generated. In fact, we will prove that ${\mathcal {K}}_{\bullet ,m,i}$ is $(\max \{d,d_E\}(m-i) + d_Ei)$-small, where d is the stable degree of $G_\bullet$. Following this one notes that the action of ${{\,\mathrm{FI}\,}}$ on the collection $\{K_{n,m,i}\}_n$ commutes with the usual differentials

$$\begin{aligned} \partial _{n,i,m}: {\mathcal {K}}_{n,m,i} \rightarrow {\mathcal {K}}_{n,m,i-1}. \end{aligned}$$

This implies that the collection of complexes

$$\begin{aligned} \cdots \rightarrow {\mathcal {K}}_{n,m,i} \rightarrow {\mathcal {K}}_{n,m,i-1} \rightarrow \cdots \rightarrow {\mathcal {K}}_{n,m,0} \rightarrow 0 \end{aligned}$$

can be pieced together to form a complex of ${{\,\mathrm{FI}\,}}$-modules. The Noetherian property is then sufficient for us to prove the main theorem.

We observe that this approach has the downside that it cannot be used to estimate the generating degree of the ${{\,\mathrm{FI}\,}}$-module over ${\mathbb {Z}}$, $H_i({{\,\mathrm{Conf}\,}}_m(G_\bullet ))$. It is the belief of the authors that proving a result of this kind will require a deeper topological understanding of the spaces ${{\,\mathrm{Conf}\,}}_m(G_n)$ as n-varies. This seems like a rich avenue for future research, as surprisingly little is thus far understood about these spaces.

Theorem 4.12

Assume that $G_\bullet$ has stable degree $\le d$ and edge-stable degree $\le d_E$. Then for all choices of $m,i \ge 0$, the ${{\,\mathrm{FI}\,}}$-module over ${\mathbb {Z}}$, ${\mathcal {K}}_{\bullet ,m,i}$, is $(\max \{d,d_E\}(m-i) + d_Ei)$-small. In the case wherein $G_n$ is connected for $n \gg 0$, the module ${\mathcal {K}}_{\bullet ,m,i}$ is $d_Em$-small.

Proof

Note that it follows from definition that ${\mathbb {R}}V(G_\bullet )$ is generated in degrees $\le d$, while ${\mathbb {R}}E(G_\bullet )$ is generated in degrees $\le d_E$. Propositions 2.17 and 4.10 imply that the ${{\,\mathrm{FI}\,}}$-module

$$\begin{aligned} Q_i := \bigoplus _{f:[n] \rightarrow \{V,E\}, |f^{-1}(E)| = i}\bigotimes _{j=1}^n Q_{f,j} \end{aligned}$$

is generated in degrees $\le \max \{d,d_E\}(m-i) + d_Ei$, where,

$$\begin{aligned} Q_{f,j} = {\left\{ \begin{array}{ll} {\mathbb {R}}E(G^{(m)}_\bullet ) &{}\text { if }f(j) = E\\ {\mathbb {R}}V(G^{(m)}_\bullet ) &{}\text { otherwise.}\end{array}\right. } \end{aligned}$$

We have that ${\mathcal {K}}_{\bullet ,m,i}$ is a submodule of $Q_i$, whence it is $(\max \{d,d_E\}(m-i) + d_Ei)$-small.

In the case where $G_n$ is connected for $n \gg 0$, it is a fact that $d_E = \max \{d,d_E\}$. This concludes the proof. $\square$

Example 4.13

Let $G_\bullet$ be the ${{\,\mathrm{FI}\,}}$-graph of Example 3.9. Then the above implies that the Betti numbers of $H_i({{\,\mathrm{Conf}\,}}_m(G_n))$ eventually agree with a polynomial of degree $\le m$. This bound is sharp for $m \ge 2$, and $i = 1$ in the case wherein G is a single point, and H is an edge. Namely, the case where $G_\bullet =$Star$_\bullet$ (see [23] for this computation).

4.3 Algebraic consequences of vertex-stability

In this section, we consider adjacency and Laplacian matrices associated to an ${{\,\mathrm{FI}\,}}$-graph. We focus on properties of the eigenspaces associated to these matrices.

To begin, note that we may view the adjacency and Laplacian matrices of a graph G as linear endomorphisms of ${\mathbb {R}}V(G)$. Given an ${{\,\mathrm{FI}\,}}$-graph $G_\bullet$, it is unfortunately not the case that the collections $A_{G_\bullet }$ and $L_{G_\bullet }$ can be considered as endomorphisms of the ${{\,\mathrm{FI}\,}}$-module ${\mathbb {R}}V(G_\bullet )$. Despite this, we will find that these matrices have some surprising interactions with the ${{\,\mathrm{FI}\,}}$-module structures. To begin, we have the following key observation.

Lemma 4.14

Let $G_\bullet$ be an ${{\,\mathrm{FI}\,}}$-graph. Then for each n the matrices $A_{G_n}$ and $L_{G_n}$ commute with the action of ${\mathfrak {S}}_n$. In particular, the eigenspaces of these matrices are sub-representations of ${\mathbb {R}}V(G_n)$.

Proof

For a fixed vertex $v \in V(G_n)$, we write N(v) to denote the collection of vertices adjacent to v. Then,

$$\begin{aligned} A_{G_n}v = \sum _{w \in N(v)} w. \end{aligned}$$

Therefore if $\sigma \in {\mathfrak {S}}_n$,

$$\begin{aligned} A_{G_n}\sigma (v) = \sum _{w \in N(\sigma (v))} w = \sum _{w' \in N(v)} \sigma (w') = \sigma (A_{G_n}v). \end{aligned}$$

The same proof works for the Laplacian matrix.

The second half of the lemma follows from linear algebra. If two matrices commute, then they preserve each others’ eigenspaces. $\square$

As an immediate consequence of Lemma 4.14, we obtain the following:

Proposition 4.15

Let $G_\bullet$ be a vertex-stable ${{\,\mathrm{FI}\,}}$-graph. Then there is a constant c, independent of n, such that the number of distinct eigenvalues of the adjacency matrix (resp. the Laplacian) of $G_n$ is bounded by c for all n.

Proof

This follows from Lemma 4.14 as well as the third part of Theorem 2.18. In particular, we see that the number of distinct eigenvalues are both bounded from above by the (eventually constant) number of irreducible factors of the ${\mathfrak {S}}_n$-representation ${\mathbb {R}}V(G_n)$. $\square$

Remark 4.16

Proposition 4.15 can be used in certain cases to prove that certain families of graphs cannot be endowed with the structure of a vertex-stable ${{\,\mathrm{FI}\,}}$-graph. For example, the cycle graphs $C_n$ and the wheel graphs $W_n$ have n distinct eigenvalues.

In fact Proposition 4.15 is the first piece of evidence describing a much more robust structure. The following theorem follows as a consequence of upcoming work of David Speyer and the authors [36].

Theorem 4.17

[36] Let $G_\bullet$ denote a vertex-stable ${{\,\mathrm{FI}\,}}$-graph. Then there exist constants $c_A,c_L$ such that for all $n \gg 0$, $A_{G_n}$ (resp. $L_{G_n}$) has $c_A$ (resp. $c_L$) distinct eigenvalues. For $i= 1,\ldots c_A$ (resp. $i = 1,\ldots , c_L$) and $n \gg 0$, let $\lambda ^A_i(n)$ (resp. $\lambda ^L_i(n)$) denote the i-th largest eigenvalue of $A_{G_n}$ (resp. $L_{G_n}$). Then the for all i and all $n \gg 0$ the functions

$$\begin{aligned} n \mapsto \text { the multiplicity of }\lambda _i^A(n), \quad n \mapsto \text { the multiplicity of }\lambda _i^L(n) \end{aligned}$$

each agree with a polynomial.

Example 4.18

We illustrate the above theorem with some examples. Let $G_\bullet = K_\bullet$ denote the ${{\,\mathrm{FI}\,}}$-graph of complete graphs. Then for $n \ge 1$, the ${\mathfrak {S}}_n$-representation ${\mathbb {R}}V(G_n)$ is isomorphic to the usual permutation representation on ${\mathbb {R}}^n$. This decomposes into a pair of irreducible representations

$$\begin{aligned} {\mathbb {R}}^n \cong {\mathbb {R}}\oplus S_n, \end{aligned}$$

where ${\mathbb {R}}$ is the trivial representation, and $S_n$ is the standard irreducible $(n-1)$-dimensional representation of ${\mathfrak {S}}_n$. We note that the decomposition ${\mathbb {R}}^n \cong {\mathbb {R}}\oplus S_n$ agrees with the eigenspace decomposition of ${\mathbb {R}}V(G_n)$ with respect to both the adjacency matrix and the Laplacian matrix. The trivial representation is the eigenspace for $n-1$ (resp. 0), while $S_n$ is the eigenspace for $-1$ (resp. $-n$). It is easy to see that the collection $S_\bullet$ actually forms a submodule of the ${{\,\mathrm{FI}\,}}$-module ${\mathbb {R}}V(G_n)$, and is therefore finitely generated. This implies that $\dim _{\mathbb {R}}S_n$ agrees with a polynomial for $n \gg 0$, which implies the same about the eigenvalue multiplicities in question.

Next let $G_\bullet =$ Star$_\bullet = K_{\bullet ,1}$. For simplicity we only work with the eigenspaces for the adjacency matrix, although the Laplacian is not much different. For $n \ge 1$, the distinct eigenvalues of $G_n$ are $\pm \sqrt{n}$ and 0. We may decompose the representation ${\mathbb {R}}V(G_n)$ as

$$\begin{aligned} {\mathbb {R}}V(G_n) = {\mathbb {R}}\oplus {\mathbb {R}}\oplus S_n \end{aligned}$$

where $S_n$ is as in the previous example, and ${\mathbb {R}}$ is once again the trivial representation. As before, this decomposition of ${\mathbb {R}}V(G_n)$ as a representation corresponds exactly to its decomposition in terms of eigenspaces.

Of course, one should not expect these eigenspaces to be irreducible as ${\mathfrak {S}}_n$-representations in general. For example if we instead consider $G_\bullet = K_{\bullet ,m}$, where $m > 1$, then the eigenspaces of the adjacency matrix are not all irreducible as ${\mathfrak {S}}_n$-representations. Generally, one will find it much easier to use the fact that the adjacency and Laplacian matrices preserve isotypic components of ${\mathbb {R}}V(G_n)$ to work with these submodules instead of the eigenspaces themselves. Indeed, the proof of the previous theorem involves working with a filtration of the ${{\,\mathrm{FI}\,}}$-module ${\mathbb {R}}V(G_\bullet )$ by its isotypic pieces.

5 Generalizations and alterations

In this final section, we briefly discuss how the work of the previous sections can be generalized and altered to prove facts about different families of graphs and other simplicial complexes. We begin by considering graphs over categories other than ${{\,\mathrm{FI}\,}}$, and then move on to higher dimensional analogues to the previous work. Note that these sections are intended to be more motivation for further study, and should by no means be considered exhaustive.

5.1 Other categories

The representation theory of categories has seen a recent explosion in the literature, largely motivated by its connections with representation stability. In this section we consider representations of the categories ${{\,\mathrm{VI}\,}}(q)$, where q is a power of a prime, and ${{\,\mathrm{FI}\,}}^m$, where m is a positive integer. These categories can be seen discussed in [20, 24, 31, 34, 40].

Definition 5.1

Let m be a fixed positive integer, and let q be a power of a fixed prime p. The category ${{\,\mathrm{VI}\,}}(q)$ is that whose objects are free vector spaces over the finite field ${\mathbb {F}}_q$, and whose morphisms are injective linear maps. The category ${{\,\mathrm{FI}\,}}^m$ is defined to be the categorical product of ${{\,\mathrm{FI}\,}}$ with itself m times. That is, it is the category whose objects are m-tuples of non-negative integers $(n_1,\ldots ,n_m)$, and whose morphisms are m-tuples of injective maps $(f_1,\ldots ,f_m):[n_1] \times \cdots \times [n_m] \hookrightarrow [n'_1] \times \cdots \times [n'_m]$, where $f_i: [n_i] \rightarrow [n'_i]$.

One may think of ${{\,\mathrm{VI}\,}}(q)$ as an analog of ${{\,\mathrm{FI}\,}}$, where the relevant acting groups are the finite general linear groups GL(n, q). Similarly, ${{\,\mathrm{FI}\,}}^m$ is the analog of ${{\,\mathrm{FI}\,}}$ where the relevant acting groups are ${\mathfrak {S}}_{n_1} \times \cdots \times {\mathfrak {S}}_{n_m}$. Just as with ${{\,\mathrm{FI}\,}}$, a module over either of these categories will be defined to be a functor from the category to ${\mathbb {R}}$ vector spaces. Definitions such as finite generation carry over in the obvious way

The following facts can be found in [20, 24, 31, 34, 40].

Theorem 5.2

Let ${{\mathcal {C}}}$ denote either the category ${{\,\mathrm{FI}\,}}^m$ or ${{\,\mathrm{VI}\,}}(q)$. Then:

• 1. [20, 31] If ${{\mathcal {C}}}= {{\,\mathrm{FI}\,}}^m$, and V is a finitely generated ${{\mathcal {C}}}$-module, then there exists a polynomial $p_V(x_1,\ldots ,x_m) \in {\mathbb {Q}}[x_1,\ldots ,x_m]$ such that for all $(n_1,\ldots ,n_m)$ with $\sum _i n_i \gg 0$,

  $$\begin{aligned} \dim _{\mathbb {R}}(V_{n_1,\ldots ,n_m}) = p_V(n_1,\ldots ,n_m) \end{aligned}$$

• 2. [20, 40] If V, W are finitely generated ${{\mathcal {C}}}$-modules, then the same is true of $V \otimes W$.

• 3. [24] If V is a finitely generated ${{\,\mathrm{VI}\,}}(q)$-module, then there exists a polynomial $p_V(x) \in {\mathbb {Q}}[x]$ such that for all $n \gg 0$

  $$\begin{aligned} p_V(q^n) = \dim _{\mathbb {R}}V({\mathbb {F}}_q^n). \end{aligned}$$

• 4. If V is a finitely generated ${{\mathcal {C}}}$-module, then the transition maps of V are all eventually injective.

• 5. [34, 40] If V is a finitely generated ${{\mathcal {C}}}$-module, then all submodules of V are also finitely generated.

As one can see, these two categories have very similar properties to ${{\,\mathrm{FI}\,}}$-modules. Indeed, it is sufficient for us to recover virtually everything that was proven in previous sections.

Definition 5.3

Let ${{\mathcal {C}}}$ denote either the category ${{\,\mathrm{FI}\,}}^m$ or ${{\,\mathrm{VI}\,}}(q)$. Then a ${{\mathcal {C}}}$-graph is a functor $G_\bullet :{{\mathcal {C}}}\rightarrow \mathbf {Graph}$. We say that $G_\bullet$ is vertex-stable if the associated ${{\mathcal {C}}}$-module ${\mathbb {R}}V(G_\bullet )$ is finitely generated.

Borrowing notation and proofs from the previous sections, we conclude the following.

Theorem 5.4

Let ${{\mathcal {C}}}$ denote either ${{\,\mathrm{VI}\,}}(q)$ or ${{\,\mathrm{FI}\,}}^m$, and let $G_\bullet$ be a vertex-stable ${{\mathcal {C}}}$-graph. Then:

• 1. The ${{\mathcal {C}}}$-module ${\mathbb {R}}E(G_\bullet )$ is finitely generated;

• 2. For any $r \ge 1$, the ${{\mathcal {C}}}$-module ${\mathbb {R}}\left( {\begin{array}{c}V(G_\bullet )\\ r\end{array}}\right)$ is finitely generated;

• 3. If ${{\mathcal {C}}}= {{\,\mathrm{FI}\,}}^m$, and H is any fixed graph, then there exist polynomials $p_H(x_1,\ldots ,x_m), p_H^{ind}(x_1,\ldots ,x_m) \in {\mathbb {R}}[x]$ such that for all ${\mathbf {n}} := (n_1,\ldots ,n_m)$ with $\sum _i n_i \gg 0$

  $$\begin{aligned} p_H({\mathbf {n}}) = \eta _H(G_{{\mathbf {n}}}), \text { and } p_H^{ind}({\mathbf {n}}) = \eta _H^{ind}(G_{{\mathbf {n}}}) \end{aligned}$$

• 4. If ${{\mathcal {C}}}= {{\,\mathrm{VI}\,}}(q)$, and H is any fixed graph, then there exist polynomials $p_H(x),p_H^{ind}(x) \in {\mathbb {Q}}[x]$ such that for all $n \gg 0$

  $$\begin{aligned} p_H(q^n) = \eta _H(G_{{\mathbb {F}}_q^n}), \text { and } p_H^{ind}(q^n) = \eta _H^{ind}(G_{{\mathbb {F}}_q^n}) \end{aligned}$$

• 5. If ${{\mathcal {C}}}= {{\,\mathrm{FI}\,}}^m$, and $r \ge 1$ is fixed, then there exist polynomials $p_r(x),p_r^{c}(x) \in {\mathbb {Q}}[x_1,\ldots ,x_m]$ such that for all ${\mathbf {n}} := (n_1,\ldots ,n_m)$ with $\sum _i n_i \gg 0$

  $$\begin{aligned} p_r({\mathbf {n}})= & {} |\{\text {number of walks in }G_{{\mathbf {n}}}\text { of length }r\}|, \text { and } p_r^{c}({\mathbf {n}}) \\= & {} |\{\text {number of closed walks in }G_{{\mathbf {n}}}\text { of length }r\}|. \end{aligned}$$

• 6. If ${{\mathcal {C}}}= {{\,\mathrm{VI}\,}}(q)$, and $r\ge 1$ is fixed, then there exist polynomials $p_r(x),p_r^c(x) \in {\mathbb {Q}}[x]$ such that for all $n \gg 0$

  $$\begin{aligned} p_r(q^n)= & {} |\{\text {number of walks in }G_n\text { of length }r\}|, \text { and } p_r^{c}(q^n) \\= & {} |\{\text {number of closed walks in }G_n\text { of length }r\}| \end{aligned}$$

• 7. For any fixed i, and any fixed graph H the ${{\mathcal {C}}}$-module over ${\mathbb {Z}}$, $H_i({{\,\mathrm{Hom}\,}}(H,G_\bullet ))$, is finitely generated;

• 8. If $G_\bullet$ is torsion-free then for any fixed m, i the ${{\mathcal {C}}}$-module over ${\mathbb {Z}}$, $H_i({{\,\mathrm{Conf}\,}}_m(G_n))$, is finitely generated.

To conclude this section, we consider various natural examples of ${{\,\mathrm{FI}\,}}^m$ and ${{\,\mathrm{VI}\,}}(q)$ graphs. The reader should keep in mind Theorem 5.4 while reading what follows.

Example 5.5

Recall that for fixed m, we considered the vertex-stable ${{\,\mathrm{FI}\,}}$-graph $K_{\bullet ,m}$. While this yielded various results, it is perhaps more correct to allow m to vary, and consider the vertex-stable ${{\,\mathrm{FI}\,}}^2$-graph $K_{\bullet _1,\bullet _2}$. More generally, we can consider the complete r-partite graph $K_{\bullet _1,\ldots ,\bullet _r}$ as a vertex-stable ${{\,\mathrm{FI}\,}}^r$-graph.

If G, H are any graphs, then there are multiple ways one can define the product of G and H. One such method is with the tensor (or categorical) product $G \times H$. The graph $G \times H$ is that whose vertex set is given by $V(G \times H) = V(G) \times V(H)$ and for which $\{(x_1,y_1),(x_2,y_2)\} \in E(G \times H)$ if and only if $\{x_1,x_2\},\{y_1,y_2\} \in E(G) \cup E(H)$. If $G_\bullet$ and $H_\bullet$ are two vertex-stable ${{\,\mathrm{FI}\,}}$-graphs, then we may define the ${{\,\mathrm{FI}\,}}^2$-graph $G_\bullet \times H_\bullet$ by the assignments

$$\begin{aligned} (G_\bullet \times H_\bullet )_{n_1,n_2} = G_{n_1} \times H_{n_2}. \end{aligned}$$

It is clear that this family is vertex-stable as an ${{\,\mathrm{FI}\,}}^2$-graph. Note that a similar statement will hold for many of the other common graph products such as strong products and Cartesian products (see any standard reference on algebraic graph theory for definitions of these products such as [3]).

Turning our attention to ${{\,\mathrm{VI}\,}}(q)$, one is immediately reminded of the Grassmann graphs $J_q(n,k)$. The vertices of $J_q(n,k)$ are k-dimensional subspaces of ${\mathbb {F}}_q^n$, and two vertices form an edge if and only if the intersection of the corresponding subspaces is non-trivial. Note that one may think of $J_q(n,k)$ is a “q-version” of the Johnson graph J(n, k). In fact, many of the ${{\,\mathrm{FI}\,}}$-graphs we previously studied will have associated ${{\,\mathrm{VI}\,}}(q)$-graphs. For instance, we may define $KG_q(n,k)$ to be the graph whose vertices are subspaces of ${\mathbb {F}}_q^n$ of dimension k, and for which two vertices are connected if and only if their corresponding subspaces have trivial intersection.

5.2 ${{\,\mathrm{FI}\,}}$-simplicial-complexes

In this section, we generalize the work of the previous sections to higher dimensional simplicial complexes.

Definition 5.6

Let X be a (compact) simplicial complex. We will write $V_i(X)$ for the set of i-simplices of X. A simplicial map between simplicial complexes X, Y is a continuous morphism $f:X\rightarrow Y$ such that $f(V_i(X)) \subseteq V_i(Y)$.

An ${{\,\mathrm{FI}\,}}$-simplicial-complex is a (covariant) functor from ${{\,\mathrm{FI}\,}}$ to the category of simplicial complexes and simplicial maps. Given an ${{\,\mathrm{FI}\,}}$-simplicial complex $X_\bullet$, we write ${\mathbb {R}}V_0(X_\bullet )$ for the ${{\,\mathrm{FI}\,}}$-module whose evaluation at [n] is the vector space with basis indexed by ${\mathbb {R}}V_0(X_n)$. We similarly define the ${{\,\mathrm{FI}\,}}$-modules ${\mathbb {R}}V_i(X_\bullet )$, and $\left( {\begin{array}{c}V_i(X_\bullet )\\ r\end{array}}\right)$ for all $i,r \ge 0$.

We say that an ${{\,\mathrm{FI}\,}}$-simplicial complex $X_\bullet$ is vertex-stable with stable degree $\le d$ if the ${{\,\mathrm{FI}\,}}$-module ${\mathbb {R}}V_0(X_\bullet )$ is finitely generated in degree $\le d$.

The following theorem is proven in the exact same way as Theorem 3.18.

Theorem 5.7

Let $X_\bullet$ be a vertex-stable ${{\,\mathrm{FI}\,}}$-simplicial-complex with stable degree $\le d$. Then:

• 1. For all i the ${{\,\mathrm{FI}\,}}$-modules ${\mathbb {R}}V_i(X_\bullet )$ are $(d(i+1))$-small;

• 2. For all i, r the ${{\,\mathrm{FI}\,}}$-modules $\left( {\begin{array}{c}V_i(X_\bullet )\\ r\end{array}}\right)$ are $(rd(i+1))$-small;

From the perspective of representation stability, the above reveals something a bit striking about ${{\,\mathrm{FI}\,}}$-simplicial-complexes. Note that the following was also true about graphs, though in that case it is less interesting.

Corollary 5.8

Let $X_\bullet$ be a vertex-stable ${{\,\mathrm{FI}\,}}$-simplicial-complex with stable degree $\le d$. Then for all $i \ge 0$ the ${{\,\mathrm{FI}\,}}$-module over ${\mathbb {Z}}$

$$\begin{aligned} H_i(X_\bullet ) \end{aligned}$$

is $d(i+1)$-small.

Proof

This follows from the first part of Theorem 5.7, as well as the usual complex for computing simplicial homology and the Noetherian property of ${{\,\mathrm{FI}\,}}$-modules. $\square$

Another interesting corollary of Theorem 5.7 relates to counting colorings of a simplicial complex T. Just as in the graph case, the colorings we will consider are intimately linked with simplicial maps into a certain ${{\,\mathrm{FI}\,}}$-simplicial-complex. To begin, we therefore note the following.

Theorem 5.9

Let $X_\bullet$ denote a vertex-stable ${{\,\mathrm{FI}\,}}$-simplicial-complex. Then for any simplicial complex T, the ${{\,\mathrm{FI}\,}}$-module,

$$\begin{aligned} {\mathbb {R}}{{\,\mathrm{Hom}\,}}(T,X_\bullet ), \end{aligned}$$

whose evaluation on [n] is the real vector space with basis indexed by ${{\,\mathrm{Hom}\,}}(T,X_n)$, is finitely generated. In particular, for $n \gg 0$, the function

$$\begin{aligned} n \mapsto |{{\,\mathrm{Hom}\,}}(T,X_n)| \end{aligned}$$

agrees with a polynomial of degree $\le |V_0(T)|\cdot d$, where d is the vertex degree of $X_\bullet$.

Proof

The ${{\,\mathrm{FI}\,}}$-module ${\mathbb {R}}{{\,\mathrm{Hom}\,}}(T,X_\bullet )$ can be realized as a submodule of $({\mathbb {R}}V_0(X_\bullet ))^{\otimes |V_0(T)|}$. This module is finitely generated by Proposition 2.17, so the Noetherian property implies our result. The bound on the degree of the polynomial follows immediately from the fact that we have embedded our ${{\,\mathrm{FI}\,}}$-module into the vector space $({\mathbb {R}}V_0(X_n))^{\otimes |V_0(T)|}$, whose dimension agrees with a polynomial of the required degree. $\square$

Definition 5.10

Let (r, s) be a pair of positive integers. An (r, s)-coloring of a simplicial complex T is a map of sets $f:V_0(T) \rightarrow [r]$ such that if $\{v_0,\ldots ,v_i\} \in V_i(T)$, then at most s of the vertices $v_0,\ldots ,v_i$ share the same color.

Colorings of simplicial complexes have recently seen interest in the literature, and seem to have deep connections with Stanley–Reisner theory [6, 18].

Corollary 5.11

Let T be a simplicial complex, and let $s \ge 1$ be an integer. If we write $V^{T,s}_\bullet$ to denote the ${{\,\mathrm{FI}\,}}$-module whose evaluation on [r] is the real vector space with basis indexed by (r, s)-colorings of T, then $V^{T,s}_\bullet$ is finitely generated and $|V_0(T)|$-small. In particular, for $r \gg 0$, the function

$$\begin{aligned} r \mapsto |\{(r,s)\text {-colorings of T}\}| \end{aligned}$$

agrees with a polynomial of degree $\le |V_0(T)|$.

Proof

Let $X_\bullet$ denote the ${{\,\mathrm{FI}\,}}$-simplicial-complex for which $V_0(X_r) = [r] \times V_0(T)$, and for which the i-cells are given by all possible collections of pairs of size i. It is clear that $X_\bullet$ is vertex-stable with vertex degree 1, whence ${\mathbb {R}}{{\,\mathrm{Hom}\,}}(T,X_\bullet )$ is finitely generated. Given an element of $V_r^{T,s}$, we may associate a morphism $f \in {{\,\mathrm{Hom}\,}}(T,X_r)$ by assigning

$$\begin{aligned} f(v) = (i_v,v) \end{aligned}$$

where $i_v$ is the color of the vertex $v \in V_0(T)$. This defines an injective map of ${{\,\mathrm{FI}\,}}$-modules

$$\begin{aligned} V^{T,s}_\bullet \hookrightarrow {\mathbb {R}}{{\,\mathrm{Hom}\,}}(T,X_\bullet ) \end{aligned}$$

as desired. From the proof of Theorem 5.9, we see that ${\mathbb {R}}{{\,\mathrm{Hom}\,}}(T,X_\bullet )$ is $|V_0(T)|$-small, and so we conclude the same about $V^{T,s}_\bullet$. $\square$