Fan Valuations and Spherical Intrinsic Volumes

Abstract

We generalize valuations on polyhedral cones to valuations on (plane) fans. For fans induced by hyperplane arrangements, we show a correspondence between rotation-invariant valuations and deletion– restriction invariants. In particular, we define a characteristic polynomial for fans in terms of spherical intrinsic volumes and show that it coincides with the usual characteristic polynomial in the case of hyperplane arrangements. This gives a simple deletion–restriction proof of a result of Klivans–Swartz. The metric projection of a cone is a piecewise-linear map, whose underlying fan prompts a generalization of spherical intrinsic volumes to indicator functions. We show that these intrinsic indicators yield valuations that separate polyhedral cones. Applied to hyperplane arrangements, this generalizes a result of Kabluchko on projection volumes.

1 Introduction

Let $\mathcal {S}$ be a collection of sets closed under taking intersections. A map $\varphi$ from $\mathcal {S}$ into some abelian group G is a valuation if

$$\begin{aligned} \varphi (S \cup T) \ = \ \varphi (S) + \varphi (T) - \varphi (S \cap T) \,, \end{aligned}$$

for any $S,T \in \mathcal {S}$, such that $S \cup T \in \mathcal {S}$. For geometric objects such as convex polytopes, polyhedra, or subspaces, valuations are a gateway between geometry and combinatorics, amply demonstrated in [5, 17]. In particular, Ehrenborg and Readdy [10] showed how generalizations of Zaslavsky’s famous formula for the number of regions of a hyperplane arrangement can be easily inferred using valuations. The purpose of this note is to further the ties between geometry and combinatorics by studying valuations on more general arrangements of geometric objects.

A fan in $\mathbb {R}^d$ is a finite collection $\mathcal {N}$ of equi-dimensional polyhedral cones that pairwise meet in faces. A fan $\mathcal {N}$ is plane if all cones have the same linear span. Thus, for plane fans, we can speak of fans relative to subspaces of $\mathbb {R}^d$. Throughout, we will assume that all fans are plane and will drop the adjective plane. To define valuations on fans, we adapt Sallee’s notion of weak valuations [24] on polytopes: A map $\varphi : \textbf{Fans}_d \rightarrow G$ is a fan valuation if for every fan $\mathcal {N}\in \textbf{Fans}_d$ and linear hyperplane H

$$\begin{aligned} \varphi (\mathcal {N}) \ = \ \varphi (\mathcal {N}\cap H^{\le }) + \varphi (\mathcal {N}\cap H^{\ge }) - \varphi (\mathcal {N}\cap H) \,, \end{aligned}$$

where $H^\le ,H^\ge$ denote the two halfspaces induced by H. We defer precise definitions to Sect. 2. Any arrangement $\mathcal {A}$ of linear hyperplanes in some subspace $U \subseteq \mathbb {R}^d$ induces a fan $\mathcal {N}(\mathcal {A})$ whose maximal cones are the closures of the regions in the complement of $\mathcal {A}$. For a hyperplane $H \in \mathcal {A}$, we write $\mathcal {A}/H$ for the hyperplane arrangement induced in H by the hyperplanes $\mathcal {A}\backslash H$, called the restriction of $\mathcal {A}$ to H. In Proposition 2.3, we show that fan valuations on arrangements satisfy

$$\begin{aligned} \varphi (\mathcal {N}(\mathcal {A})) \ = \ \varphi (\mathcal {N}(\mathcal {A}\backslash H)) + \varphi (\mathcal {N}(\mathcal {A}/H)) \,. \end{aligned}$$

Such deletion–restriction-type invariants are well studied in the combinatorial theory of hyperplane arrangements ([27, Sect. 3.11], [11]) and, more generally, (simple) matroids [8]. The main difference is that we do not impose special treatment when H is a coloop of $\mathcal {A}$. The benefit is that these weak deletion–restriction invariants have the structure of an abelian group. More precisely, let $\mathcal {L}(\mathcal {A})$ be the lattice of flats of $\mathcal {A}$ and write $w_0(\mathcal {A}),\dots ,w_d(\mathcal {A})$ for the Whitney numbers of the first kind, i.e., the coefficients of the unsigned characteristic polynomial of $\mathcal {A}$. Then, the group of weak deletion–restriction invariants is spanned by the Whitney numbers.

We show that fan valuations invariant under rotation yield precisely the weak deletion–restriction invariants.

Theorem 1.1

Let $\varphi : \textbf{Fans}_d \rightarrow G$ be a rotation-invariant fan valuation. Then, there are $g_0,\dots ,g_d \in G$, such that for any hyperplane arrangement $\mathcal {A}$

$$\begin{aligned} \varphi (\mathcal {N}(\mathcal {A})) \ = \ g_0 w_0(\mathcal {A}) + \cdots + g_d w_d(\mathcal {A}) \,. \end{aligned}$$

Conversely, for any deletion–restriction invariant $\psi$ on hyperplane arrangements, there is a fan valuation $\varphi$ with $\psi (\mathcal {A}) =\varphi (\mathcal {N}(\mathcal {A}))$.

For the latter part, we consider fan valuations induced by spherical intrinsic volumes, also known as projection volumes. Let $B_d(v,r)$ be the closed ball in $\mathbb {R}^d$ centered at $v \in \mathbb {R}^d$ of radius r, and let $B_d = B_d(0,1)$, where 0 indicates the origin. The kth spherical intrinsic volume $v_k(C)$ of a cone $C \subset \mathbb {R}^d$ is the probability, with respect to the uniform distribution on $B_d$, that the point of C closest to a randomly chosen $x \in B_{d}$ is contained in the relative interior of a face $F_x \subseteq C$ of dimension k. We refer to [2, 3] for much more on intrinsic volumes. The definition is extended to fans by setting $v_k(\mathcal {N}) ~{:}{=}\sum _{C \in \mathcal {N}} v_k(C)$. With that, we define the (unsigned) characteristic polynomial of a fan $\mathcal {N}$ by

$$\begin{aligned} \overline{\chi }_{\mathcal {N}}(t) \ ~{:}{=}\ v_0(\mathcal {N}) + v_1(\mathcal {N}) t + \cdots +v_d(\mathcal {N}) t^d \,. \end{aligned}$$

We argue that $\overline{\chi }_{\mathcal {N}}(t)$ is a suitable generalization of the characteristic polynomial of a hyperplane arrangement. We show that it satisfies Zaslavsky’s fundamental results

$$\begin{aligned} \overline{\chi }_{\mathcal {N}}(1) \ = \ \# \text { regions of}\, \mathcal {N}\text {and, if}\, \mathcal {N}\,\text {is not a single subspace, } \ \overline{\chi }_{\mathcal {N}}(-1) \ = \ 0 \,. \end{aligned}$$

While the first statement is evident, the second can be found in [2, Corollary 4.4]. We derive the latter from an identity of Hug–Kabluchko [15], for which we provide a self-contained proof (Theorem 3.13).

Most importantly, we show $\overline{\chi }_{\mathcal {N}(\mathcal {A})}(t) = (-1)^{\dim \mathcal {A}}\chi _{\mathcal {A}}(-t)$, where $\chi _{\mathcal {A}}(t)$ is the usual characteristic polynomial of an arrangement. This gives a simple deletion–restriction proof of the main result of Klivans–Swartz [18] which identifies projection volumes with the Whitney numbers of $\mathcal {L}(\mathcal {A})$.

Whereas Hadwiger’s famous classification theorem [14] states that the linear space of continuous and rigid-motion invariant valuations on convex bodies is spanned by the usual intrinsic volumes, there is no such result for spherical convex sets. McMullen [13, Problem 49] conjectured that the linear space of continuous and rotation-invariant valuations on spherical convex bodies is spanned by the spherical intrinsic volumes. From this perspective, Theorem 1.1 together with the result of Klivans–Swartz can be seen as an indication for this conjecture.

In the second part of the paper, we take a more refined look at spherical intrinsic volumes. The collection of points $x \in \mathbb {R}^d$ such that the nearest point in C is contained in a fixed face $F \subseteq C$ is a polyhedral cone $\Pi _F(C)$ and $\mathcal {M}(C) ~{:}{=}\{ \Pi _F(C): F \subseteq C \text { face}\}$ is a complete fan, which we call the Moreau fan of C. The face lattice of $\mathcal {M}(C)$ is isomorphic to the interval poset of the face lattice of C. Such fan structures were considered by Björner under the name of anti-prisms in connection with a question of Lindström and our findings reconfirm results announced in [7].

It is known that $C \mapsto v_k(C)$ is a cone valuation [22]. We prove a generalization that this holds on the level of simple indicator functions: Consider the set $\Pi _k(C) = \bigcup _F \Pi _F(C)$, where the union is over all k-dimensional faces of C. Its simple indicator is the function $V_k(C): \mathbb {R}^d \rightarrow \mathbb {Z}$ that agrees with the indicator of $\Pi _k(C)$ on a dense open set; see Sect. 3.2 for details. We show that $C \mapsto V_k(C)$ is a valuation (Theorem 3.2) and that C can be recovered from $V_k(C)$ for all $\dim {{\,\textrm{lineal}\,}}(C) \le k \le \dim C$ with $2k \ne d$ (Theorem 3.5).

For the function $V_k(\mathcal {N}(\mathcal {A})) = \sum _{C \in \mathcal {N}(\mathcal {A})}V_k(C)$ of a hyperplane arrangement $\mathcal {A}$, it follows that $V_k(\mathcal {N}(\mathcal {A}))(x) = w_k(\mathcal {A})$ for all generic $x \in \mathbb {R}^d$. Kabluchko[16] showed that the exceptional set $\{x: V_k(\mathcal {N}(\mathcal {A}))(x) \ne w_k(\mathcal {A}) \}$ coincides with the support of a hyperplane arrangement. We generalize Kabluchko’s result in Theorem 3.9 with a short proof that also allows us to give a simple interpretation for the associated arrangement.

2 Fan Valuations and Deletion–Restriction Invariants

For a set $S \subset \mathbb {R}^d$, ${{\,\textrm{aff}\,}}(S) \subset \mathbb {R}^d$ is the affine hull of S, which is the inclusion-minimal affine space containing S. The linear hull ${{\,\textrm{lin}\,}}(S)$ is the inclusion-minimal linear subspace containing S and the lineality space ${{\,\textrm{lineal}\,}}(S)$ is the inclusion-maximal linear subspace contained in S. We note that if S contains the origin, then ${{\,\textrm{lin}\,}}(S) = {{\,\textrm{aff}\,}}(S)$. The relative interior ${{\,\textrm{relint}\,}}(S) \subseteq S$ is the usual interior of S relative to ${{\,\textrm{aff}\,}}(S)$.

A nonempty set $C \subset \mathbb {R}^d$ is a convex cone if $\alpha x + \beta y \in C$ for all $x,y \in C$ and $\alpha ,\beta \ge 0$. The cone hull ${{\,\textrm{cone}\,}}(S)$ of S is the intersection of all convex cones C that contain S. A convex cone C is a polyhedral cone if $C = {{\,\textrm{cone}\,}}(S)$ for some finite S. All cones considered here are polyhedral and we will simply refer to them as cones. A relatively open cone is the relative interior of a cone.

A face of a polyhedral cone C is a cone $F \subseteq C$, such that for any $x,y \in C$, if $x + y \in F$, then $x,y \in F$. A plane fan in $\mathbb {R}^d$ is a finite collection $\mathcal {N}$ of polyhedral cones, such that for all $C, C' \in \mathcal {N}$

• (i) $C \cap C'$ is a face of C and $C'$, and

• (ii) ${{\,\textrm{lin}\,}}(C) = {{\,\textrm{lin}\,}}(C')$.

It follows that all cones in $\mathcal {N}$ are of the same dimension. We set $\dim \mathcal {N}~{:}{=}\dim C$ and ${{\,\textrm{lin}\,}}(\mathcal {N}) ~{:}{=}{{\,\textrm{lin}\,}}(C)$ as well as ${{\,\textrm{lineal}\,}}(\mathcal {N}) ~{:}{=}{{\,\textrm{lineal}\,}}(C)$ for any $C \in \mathcal {N}$. The rank of $\mathcal {N}$ is $r(\mathcal {N}) = \dim (\mathcal {N}) - \dim {{\,\textrm{lineal}\,}}(\mathcal {N})$. Note that our definition differs from the usual definition of fans (see, for example, [28, Section 7.1]) in that we only retain the inclusion-maximal cones. Adding to $\mathcal {N}$ the faces of all $C \in \mathcal {N}$, we recover pure fans supported on a subspace. As we are exclusively dealing with plane fans throughout, we will drop the adjective ‘plane’ henceforth.

Denote by $\textbf{Fans}_d$ the collection of fans in $\mathbb {R}^d$. We define for any set $S \subseteq \mathbb {R}^d$

$$\begin{aligned} \mathcal {N}\cap S ~{:}{=}\ \{ C \cap S: C \in \mathcal {N},\; {{\,\textrm{relint}\,}}(C) \cap S \ne \varnothing \} \,. \end{aligned}$$

For a linear hyperplane $H \subset \mathbb {R}^d$, that is, a linear subspace of dimension $d-1$, we denote the two induced closed halfspaces by $H^\le$ and $H^\ge$.

Proposition 2.1

Let $\mathcal {N}$ be a fan in $\mathbb {R}^d$ and H a hyperplane. Then, $\mathcal {N}\cap H$, $\mathcal {N}\cap H^\le$, and $\mathcal {N}\cap H^\ge$ are fans.

Proof

If $C' \in \mathcal {N}\cap H$, then there is some $C \in \mathcal {N}$ such $C' = C \cap H$. Since H meets $C'$ in its relative interior, C is unique and $\dim C' = \dim C - 1$. This shows that $\mathcal {N}\cap H$ is a collection of cones with the same linear hull. If $C'_1,C'_2 \in \mathcal {N}\cap H$ with $C'_i = C_i \cap H$ for $i=1,2$, then $C'_1 \cap C'_2 = (C_1 \cap C_2) \cap H$ and hence $C'_1 \cap C'_2$ is a face of $C'_1$ and $C'_2$. The proof for the two halfspaces is analogous. $\square$

A map $\varphi$ from $\textbf{Fans}_d$ into some abelian group G is a fan valuation if $\varphi (\varnothing ) = 0$ and for any $\mathcal {N}\in \textbf{Fans}_d$ and hyperplane H

$$\begin{aligned} \varphi (\mathcal {N}) \ = \ \varphi (\mathcal {N}\cap H^{\le }) + \varphi (\mathcal {N}\cap H^{\ge }) - \varphi (\mathcal {N}\cap H) \,. \end{aligned}$$

Let $\textbf{Cones}_d$ be the intersectional family of polyhedral cones in $\mathbb {R}^d$. A cone valuation is a map $\varphi ': \textbf{Cones}_d \rightarrow G$, such that for any two cones $C,D \in \textbf{Cones}_d$ with $C \cup D \in \textbf{Cones}_d$

$$\begin{aligned} \varphi '( C \cup D ) \ = \ \varphi '(C) + \varphi '(D) - \varphi '(C \cap D) \,. \end{aligned}$$

Sallee [24] called a map $\varphi ': \textbf{Cones}_d \rightarrow G$ a weak valuation if for every cone C and hyperplane H

$$\begin{aligned} \varphi '(C) \ = \ \varphi '(C \cap H^\le ) + \varphi '(C \cap H^\ge ) - \varphi '(C \cap H) \,. \end{aligned}$$

Clearly, every cone valuation is a weak valuation and it was shown in [24] that the converse holds: every weak valuation on cones is a cone valuation.

If $\varphi '$ is a cone valuation, then

$$\begin{aligned} \varphi (\mathcal {N}) \ ~{:}{=}\ \sum _{C \in \mathcal {N}} \varphi '(C) \end{aligned}$$

(1)

is a fan valuation. Indeed, for any hyperplane H, the cones $C \in \mathcal {N}$ for which, say, $C \subseteq H^\le$ only yields a cone in $\mathcal {N}\cap H^\le$. Consequently, $\varphi '(C)$ only contributes to $\varphi (\mathcal {N}\cap H^\le )$. The cones $C \in \mathcal {N}$ with ${{\,\textrm{relint}\,}}(C) \cap H \ne \varnothing$ give rise to cones in $\mathcal {N}\cap H^\le$, $\mathcal {N}\cap H^\ge$, as well as $\mathcal {N}\cap H$ and the weak valuation property ensures that the total contribution is $\varphi '(C)$.

The next result shows that every fan valuation is of that form. For that, we note that if C is a cone, then $\{C\}$ is a fan.

Proposition 2.2

Let $\varphi$ be a fan valuation. Then

$$\begin{aligned} \varphi (\mathcal {N}) \ = \ \sum _{C \in \mathcal {N}} \varphi (\{C\}) \,. \end{aligned}$$

Thus, we will write $\varphi (C)$ instead of $\varphi (\{C\})$ from now on.

Proof

The claim follows trivially if $\mathcal {N}$ is empty or if it consists of a single cone. If $\dim \mathcal {N}= 1$, then the only nontrivial case is $\mathcal {N}= \{\mathbb {R}_{\ge 0}c, -\mathbb {R}_{\ge 0}c\}$ for some $c \in \mathbb {R}^d \setminus \{0\}$. Now, $H = \{0\}$ is the unique linear hyperplane in ${{\,\textrm{lin}\,}}(\mathcal {N})$ and $\mathcal {N}\cap H = \varnothing$. The assertion follows from the definition of fan valuations.

Assume now that the statement holds for all fans consisting of less than k cones and whose dimension is smaller than e for some $k \ge 2$ and $e \ge 2$. Let $\mathcal {N}$ be a fan with k cones and $\dim \mathcal {N}= e$. For $C,C' \in \mathcal {N}$, let H be a separating hyperplane, that is, $C \cup C' \not \subseteq H$ and $C',C''$ are contained in distinct halfspaces. Then, $\mathcal {N}\cap H^\ge$ and $\mathcal {N}\cap H^\le$ have less than k cones and $\dim (\mathcal {N}\cap H) < e$. Let $X = \{C \in \mathcal {N}: {{\,\textrm{relint}\,}}C \cap H \ne \varnothing \}$. Then

$$\begin{aligned} \varphi (\mathcal {N})&= \varphi (\mathcal {N}\cap H^\le ) + \varphi (\mathcal {N}\cap H^\ge ) - \varphi (\mathcal {N}\cap H)\\&= \sum _{C \in \mathcal {N}\setminus X} \varphi (\{C\}) + \sum _{C \in X} \big (\varphi (\{C \cap H^\le \}) + \varphi (\{C \cap H^\ge \}) - \varphi (\{C \cap H\})\big )\\&= \sum _{C \in \mathcal {N}\setminus X} \varphi (\{C\}) + \sum _{C \in X} \varphi (\{C\}) \ = \ \sum _{C \in \mathcal {N}} \varphi (\{C\}) \, , \end{aligned}$$

where the second equality uses induction and the fact that every $C \in \mathcal {N}{\setminus } X$ is either contained in $\mathcal {N}\cap H^\le$ or $\mathcal {N}\cap H^\ge$ but not in both. For $C \in X$, we use the weak valuation property together with the fact $C \mapsto \varphi (\{C\})$ is a weak valuation. This yields the third equality. $\square$

2.1 Hyperplane Arrangements

Let $\mathcal {A}$ be a finite collection of linear hyperplanes in a subspace L of $\mathbb {R}^d$. The complement $L \setminus \bigcup \mathcal {A}$ is a collection of open sets in L whose closures are polyhedral cones. These cones define a fan that we denote by $\mathcal {N}(\mathcal {A})$. For a hyperplane H contained in L, such that $H \not \in \mathcal {A}$ observe that $\mathcal {N}(\mathcal {A}) \cap H = \mathcal {N}(\mathcal {A}/H)$, where $\mathcal {A}/H ~{:}{=}\{ H' \cap H: H' \in \mathcal {A}, H' \ne H \}$ is the restriction of $\mathcal {A}$ to H. If $H \in \mathcal {A}$, we write $\mathcal {A}\backslash H = \{H' \in \mathcal {A}: H' \ne H\}$ for the deletion of H. A k -singleton, or simply, a singleton, is a hyperplane arrangement consisting of a single hyperplane in some k-dimensional subspace of $\mathbb {R}^d$, where $1 \le k \le d$.

Proposition 2.3

Let $\varphi$ be a fan valuation and $\mathcal {A}$ a hyperplane arrangement which is not a singleton. For any $H \in \mathcal {A}$

$$\begin{aligned} \varphi (\mathcal {N}(\mathcal {A})) \ = \ \varphi (\mathcal {N}(\mathcal {A}\backslash H)) + \varphi (\mathcal {N}(\mathcal {A}/H)) \,. \end{aligned}$$

Proof

Let $H \in \mathcal {A}$ and set $\mathcal {A}' = \mathcal {A}\backslash H$. The valuation property yields

$$\begin{aligned} \varphi (\mathcal {N}(\mathcal {A}')) \ = \ \varphi (\mathcal {N}(\mathcal {A}') \cap H^\le ) + \varphi (\mathcal {N}(\mathcal {A}') \cap H^\ge ) - \varphi (\mathcal {N}(\mathcal {A}') \cap H). \end{aligned}$$

We infer from Proposition 2.2 that $\varphi (\mathcal {N}(\mathcal {A})) = \varphi (\mathcal {N}(\mathcal {A}') \cap H^\le ) + \varphi (\mathcal {N}(\mathcal {A}') \cap H^\ge )$. By definition, $\varphi (\mathcal {N}(\mathcal {A}' \cap H)) = \varphi (\mathcal {N}(\mathcal {A}/H))$, which now yields the claim.

$\square$

The group $\textrm{SO}(\mathbb {R}^d)$ of rotations acts on $\textbf{Fans}_d$ by $g \,\,\cdot \mathcal {N}~{:}{=}\{g\,\,C: C \in \mathcal {N}\}$. We call a fan valuation $\varphi$ invariant if $\varphi (g \cdot \mathcal {N}) = \varphi (\mathcal {N})$ for all $g \in \textrm{SO}(\mathbb {R}^d)$ and $\mathcal {N}\in \textbf{Fans}_d$. Clearly, if $\varphi$ is invariant, it assigns the same value to all k-singletons.

We define the unsigned characteristic polynomial $\overline{\chi }_\mathcal {A}(t)$ of an arrangement $\mathcal {A}$ recursively as follows. If $\mathcal {A}$ is a k-singleton, then $\overline{\chi }_{\mathcal {A}}(t) ~{:}{=}t^k + t^{k-1}$. If $\mathcal {A}$ consists of more than one hyperplane, then for $H \in \mathcal {A}$

$$\begin{aligned} \overline{\chi }_{\mathcal {A}}(t) \ ~{:}{=}\ \overline{\chi }_{\mathcal {A}\backslash H}(t) + \overline{\chi }_{\mathcal {A}/H}(t) \, . \end{aligned}$$

(2)

The unsigned characteristic polynomial is related to the usual characteristic polynomial (cf. [27, Sect. 3.11]) by $\overline{\chi }_\mathcal {A}(t) = (-1)^{\dim L} \chi _\mathcal {A}(-t)$. It is well known that the characteristic polynomial of a hyperplane arrangement is independent of the order in which the hyperplanes are deleted and contracted, and thus, the unsigned characteristic polynomial is also independent of this choice. The coefficients of $\overline{\chi }_\mathcal {A}(t)$ are the (unsigned) Whitney numbers of the first kind denoted by $w_i(\mathcal {A})$.

Theorem 2.4

Let $\varphi$ be an invariant fan valuation taking values in an abelian group G. Then, there are $a_0,\dots ,a_d \in G$, such that for every arrangement $\mathcal {A}$

$$\begin{aligned} \varphi (\mathcal {N}(\mathcal {A})) \ = \ a_0 w_0(\mathcal {A}) + \cdots + a_{d-1} w_{d-1}(\mathcal {A}) \, . \end{aligned}$$

(3)

Moreover, the $a_i$’s are determined by the values $\varphi (\mathcal {A}^k)$, where $\mathcal {A}^k$ is a k-singleton, $1 \le k \le d$.

Proof

Let $b_k ~{:}{=}\varphi (\mathcal {N}(\mathcal {A}^k))$ for any k-singleton $\mathcal {A}^k$ and set $a_{k-1} ~{:}{=}\sum _{i = k}^d (-1)^{k-i} b_i$ for ${1 \le k \le d}$. We proceed by induction on the number of hyperplanes in $\mathcal {A}$. Since $a_{k-1} + a_k = b_k$, clearly (3) holds for k-singletons. Otherwise, let $H \in \mathcal {A}$. Then

$$\begin{aligned} \varphi (\mathcal {N}(\mathcal {A}))&= \varphi (\mathcal {N}(\mathcal {A}\backslash H)) + \varphi (\mathcal {N}(\mathcal {A}/H))\\&= \sum _{i = 0}^{d-1} a_i w_i(\mathcal {A}\backslash H) + \sum _{i = 0}^{d-1} a_i w_i(\mathcal {A}/H) \ = \ \sum _{i = 0}^{d-1} a_i w_i(\mathcal {A}) \, , \end{aligned}$$

where the second equality above follows by induction. $\square$

2.2 Spherical Intrinsic Volumes

In this section, we introduce characteristic polynomials of fans via spherical intrinsic volumes. This underlines the connection between invariant fan valuations and certain deletion–restriction-type invariants on arrangements as indicated by Theorem 2.4

Given a polyhedral cone $C \subseteq \mathbb {R}^d$ and a point $x \in \mathbb {R}^d$, there is a unique point $\pi _C(x) \in C$ minimizing the Euclidean distance $\Vert x - \pi _C(x)\Vert _2$. The map $\pi _C: \mathbb {R}^d \rightarrow C$ is called the metric projection or nearest-point map of C; cf. [25, Sect. 1.2]. Let us denote by $F_x$ the unique face of C that contains $\pi _C(x)$ in its relative interior and $\Pi _k(C) ~{:}{=}\{ x \in \mathbb {R}^d: \dim F_x = k \}$. The k -th spherical intrinsic volume is given by

$$\begin{aligned} v_k(C) \ ~{:}{=}\ \frac{{{\,\textrm{vol}\,}}(\Pi _k(C) \cap B_d)}{{{\,\textrm{vol}\,}}(B_d)} \,, \end{aligned}$$

where $B_d$ is the unit ball. In the next section, we will consider the sets $\Pi _k(C)$ more closely and, in particular, deduce the known fact that $C \mapsto v_k(C)$ is a cone valuation (Corollary 3.3). It is apparent that $v_k$ is $\textrm{SO}(\mathbb {R}^d)$-invariant. We define the induced kth spherical intrinsic volume of a fan $\mathcal {N}$ as

$$\begin{aligned} v_k(\mathcal {N}) \ ~{:}{=}\ \sum _{C \in \mathcal {N}} v_k(C), \end{aligned}$$

and we define the characteristic polynomial of $\mathcal {N}$ as

$$\begin{aligned} \overline{\chi }_{\mathcal {N}}(t) \ ~{:}{=}\ v_0(\mathcal {N}) + v_1(\mathcal {N}) t + \cdots + v_d(\mathcal {N}) t^d \,. \end{aligned}$$

The characteristic polynomial shares a number of similarities with that of a hyperplane arrangement. Since the $\Pi _k(C)$ cover $\mathbb {R}^d$ and $\Pi _k(C) \cap \Pi _l(C)$ has measure zero, it follows that:

$$\begin{aligned} \overline{\chi }_{\mathcal {N}}(1) \ = \ |\mathcal {N}|, \, \end{aligned}$$

and it follows from Theorem 3.13 in the next section that if $\mathcal {N}\ne \{ L \}$ for some linear subspace L, then

$$\begin{aligned} \overline{\chi }_{\mathcal {N}}(-1) \ = \ 0 \,. \end{aligned}$$

These two statements are counterparts to Zaslavsky’s famous results concerning characteristic polynomials of hyperplane arrangements.

For the case $\mathcal {N}= \mathcal {N}(\mathcal {A})$, the spherical intrinsic volumes $v_k(\mathcal {N}) = \sum _{C \in \mathcal {N}} v_k(C)$ were studied by Klivans and Swartz and the following is the main result of [18].

Corollary 2.5

Let $\mathcal {A}$ be a linear hyperplane arrangement. Then

$$\begin{aligned} \overline{\chi }_{\mathcal {N}(\mathcal {A})}(t) \ = \ \overline{\chi }_{\mathcal {A}}(t) \,. \end{aligned}$$

Proof

In light of Proposition 2.3 and (2), it suffices to compute $\overline{\chi }_{\mathcal {N}(\mathcal {A}^k)}(t)$, where $\mathcal {A}^k$ is a k-singleton in some linear subspace L. More specifically, if $H^\le \subset L$ is a halfspace, then $v_{k}(H^\le ) = v_{k-1}(H^\le ) = \frac{1}{2}$ and $v_{j}(H^\le ) = 0$ for all other j. This shows $\overline{\chi }_{\mathcal {N}(\mathcal {A}^k)}(t) = t^k + t^{k-1}$. Hence, $\overline{\chi }_{\mathcal {N}(\mathcal {A})}(t)$ and $\overline{\chi }_{\mathcal {A}}(t)$ satisfy the same deletion–restriction recurrence with identical starting conditions. $\square$

3 Anti-prism Fans and Intrinsic Volumes

In this section, we take a closer look at the geometric combinatorics of spherical intrinsic volumes by way of associated indicator functions.

3.1 Moreau Fans and Anti-prisms

Let $C \subseteq \mathbb {R}^d$ be a polyhedral cone. It is straightforward to verify that if $x,y \in \mathbb {R}^d$, such that $\pi _C(x),\pi _C(y) \in F$ for some face $F \subseteq C$, then $\pi _C(x+y) \in F$. Hence, $\Pi _F(C) ~{:}{=}\pi ^{-1}_C(F)$ is a closed, full-dimensional polyhedral cone. Moreau [23] considered the decomposition of space into the collection of cones

$$\begin{aligned} \mathcal {M}(C) \ ~{:}{=}\ \{ \Pi _F(C): F \,\text {is a nonempty face of}~C \}, \end{aligned}$$

and we call $\mathcal {M}(C)$ the Moreau fan of C.

The combinatorics of Moreau fans can be nicely described in terms of Lindström’s interval posets [20]. Let $(\mathcal {L},\preceq )$ be a partially ordered set. The interval poset $I(\mathcal {L})$ is the collection of nonempty intervals $[a,c] = \{ b: a \preceq b \preceq c \}$ ordered by reverse inclusion. The maximal elements are precisely [a, a], and if $\mathcal {L}$ has a top and bottom element $\hat{1}$ and $\hat{0}$, respectively, then $[\hat{0},\hat{1}]$ is the unique minimum of $I(\mathcal {L})$. Lindström [20] asked if $I(\mathcal {F}(P))$ is the face lattice of a polytope whenever $\mathcal {F}(P)$ is the face lattice of a polytope P. Björner affirmatively answered Lindström’s question for 3-dimensional polytopes. The complete question was resolved in the negative by Dobbins [9].

Björner [7] also announced that $I(\mathcal {F}(P))$ is the face poset of a complete fan (or star-convex sphere), the anti-prism fan of P. We briefly reconfirm this result by showing that the Moreau fan of $C = {{\,\textrm{cone}\,}}( P \times \{1\} )$ realizes $I(\mathcal {F}(P))$. Let $\mathcal {L}^\textrm{op}$ be the dual (or opposite) poset of $\mathcal {L}$. Then

$$\begin{aligned} I(\mathcal {L}) \ \cong \ \{ (a,b): a \preceq b \} \ \subseteq \ \mathcal {L}\times \mathcal {L}^\textrm{op}\,. \end{aligned}$$

The face lattice $\mathcal {F}(C)$ of C is the collection of nonempty faces of C partially ordered by inclusion. This is a graded poset ranked by dimension and we denote by $\mathcal {F}_k(C)$ the set of k-dimensional faces of C. For $F \in \mathcal {F}(C)$, let

$$\begin{aligned} N_FC \ ~{:}{=}\ \{ c \in \mathbb {R}^d: \langle {c,x} \rangle \le \langle {c,y} \rangle \text { for all } x \in C, y \in F \} \end{aligned}$$

be the normal cone of C at F. The polar to C is $C^\vee = N_{{{\,\textrm{lineal}\,}}(C)} C$. Moreover, $F \mapsto N_FC$ gives an isomorphism from $\mathcal {F}(C)$ to $\mathcal {F}(C^\vee ) = \mathcal {F}(C)^\textrm{op}$; cf. [28, Section 2.3].

Let $x \in \mathbb {R}^d$. It follows from $\Vert x - \pi _C(x)\Vert \le \Vert x - z\Vert$ for all $z \in C$ that $x-\pi _C(x) \in N_{F_x}C$. Hence, $\Pi _F(C) = F + N_FC$ for all nonempty faces $F \subseteq C$. Moreover

$$\begin{aligned} (F + N_FC) \cap (G + N_GC) \ = \ (F \cap G) + (N_GC \cap N_FC) \, , \end{aligned}$$

(4)

which shows the following.

Proposition 3.1

Let $C \subseteq \mathbb {R}^d$ be a polyhedral cone. The face lattice of the Moreau fan $\mathcal {M}(C)$ is isomorphic to the interval poset $I(\mathcal {F}(C))$.

3.2 Conical Functions

For a subset $S \subseteq \mathbb {R}^d$, we denote its indicator function by $[S]: \mathbb {R}^d \rightarrow \{0, 1\}$, which is defined by $[S](x) = 1$ if and only if $x \in S$. Let $\mathfrak {C}_d \subseteq \textrm{Fun}(\mathbb {R}^d,\mathbb {Z})$ be the abelian subgroup spanned by [C] for $C \in \textbf{Cones}_d$. Since $[C] = [C \cap H^\le ] + [C \cap H^\ge ] - [C \cap H]$, the map $C \mapsto [C] \in \mathfrak {C}_d$ is a cone valuation. Moreover, any homomorphism $\widetilde{\varphi }: \mathfrak {C}_d \rightarrow G$ gives a valuation on cones by $\varphi (C) ~{:}{=}\widetilde{\varphi }([C]) \,$ and Groemer [12] showed every cone valuation arises that way.

For a cone $C \subseteq \mathbb {R}^d$, define

$$\begin{aligned} V_k(C) \ ~{:}{=}\ \sum _{F \in \mathcal {F}_k(C)} [\Pi _F(C)] \ \in \ \mathfrak {C}_d \,. \end{aligned}$$

This is an indicator generalization of the spherical intrinsic volumes and we recover the spherical intrinsic volumes as $v_k(C) = \frac{1}{{{\,\textrm{vol}\,}}(B_d)}\int _{B_d}V_k d\mu$. Note that $V_k: \textbf{Cones}_d \rightarrow \mathfrak {C}_d$ is not a valuation: For the augmentation $\epsilon : \mathfrak {C}_d \rightarrow \mathbb {Z}$ with $\epsilon ([C]) = 1$ for all nonempty cones C, we see that $\epsilon (V_k(C))$ is the number of k-dimensional faces of C, which is not a valuation. Nonetheless, we can view $V_k$ as a valuation taking values in the group of simple indicator functions

$$\begin{aligned} \mathfrak {S}_d \ ~{:}{=}\ \mathfrak {C}_d / U \,, \end{aligned}$$

where U is the subgroup generated by all [C] with $C \in \textbf{Cones}_d$ and $\dim C < d$.

Theorem 3.2

Let $C \subset \mathbb {R}^d$ be a cone and H a hyperplane. Then

$$\begin{aligned} V_k(C) \ = \ V_k(C \cap H^\le ) + V_k(C \cap H^\ge ) - V_k(C \cap H) \end{aligned}$$

as simple indicator functions.

Proof

Observe that $f = g$ for $f,g \in \mathfrak {S}_d$ if $f(x) = g(x)$ for almost all $x \in \mathbb {R}^d$. Thus, let $x \in \mathbb {R}^d$ a generic point. Let $C^\le , C^\ge ,$ and $C^=$ denote $C \cap H^\le , C \cap H^\ge ,$ and $C \cap H$, respectively. Let $\pi _C(x) = y$ and $F \subseteq C$ the unique face with $y \in {{\,\textrm{relint}\,}}(F)$. We may assume that $y \in H^\le$, that is, $y = \pi _{C^\le }(x)$ and $F^\le = F \cap H^\le$. Define $y^=, y^\ge$ with corresponding faces $F^=,F^\ge$.

If $y = y^\ge$, then $y \in H$ and $F \cap H \ne \varnothing$. If $F \subseteq H$, then $F = F^\le = F^= = F^\ge$ and we are done. The case $F \not \subseteq H$ is not relevant, as x is generic: perturbing x parallel to ${{\,\textrm{lin}\,}}(F)$ moves y away from H.

If $y^\ge \ne y$, then $y^\ge = y^=$. Indeed, any point on the segment $z \in [y,y^\ge )$ satisfies $\Vert x-z\Vert < \Vert x-y^\ge \Vert$ and $[y,y^\ge ]$ meets H. It follows that $F^\ge = F^=$ and $\dim F = \dim F^\le$. This proves the claim. $\square$

The spherical intrinsic volume $\sigma _{d-1}(C) ~{:}{=}\frac{{{\,\textrm{vol}\,}}_d(C \cap B_d)}{{{\,\textrm{vol}\,}}_d(B_d)}$ is a simple valuation and hence extends to a linear function $\sigma _{d-1}: \mathfrak {S}_d \rightarrow \mathbb {R}$.

Corollary 3.3

The spherical intrinsic volumes $v_k(C) = \sigma _{d-1}(V_k(C))$ are cone valuations.

Similar to the situation for polytopes, the valuations $V_k$ separate $\mathfrak {C}_d$. The proof of the next result needs the following observation.

Lemma 3.4

Let $C \subseteq \mathbb {R}^d$ be a cone and $0 \le k \le d$. Then $V_k(C) = V_{d-k}(C^\vee )$.

Proof

Let $F \subseteq C$ be a face of dimension k. The normal cone $N_FC := F^\diamond$ is a face of the polar $C^\vee = N_{{{\,\textrm{lineal}\,}}(C)} C$ of dimension $d - \dim F$. Using standard facts from cone polarity (cf. [4]), a direct calculation shows that the normal cone of $C^\vee$ at $F^\diamond$ is precisely F. Recall that $\Pi _F(C) = F + N_FC$ and thus $\Pi _F(C) = \Pi _{F^\diamond }(C^\vee )$. $\square$

Theorem 3.5

Let $C \subseteq \mathbb {R}^d$ be a cone and $\dim {{\,\textrm{lineal}\,}}(C) \le k \le \dim C$. If $2k \ne d$, then C can be recovered from $V_k(C)$.

By the previous lemma, we can directly see that for $2k = d$ we have $V_k(C) = V_k(C^\vee )$, making this assumption necessary.

Proof

First, note that $V_k(C) = 0$ whenever $k > \dim C$ or, by Lemma 3.4, $k < \dim {{\,\textrm{lineal}\,}}(C)$.

Now, let $S \subset \mathbb {R}^d$ be the collection of points for which $V_k(C)$ does not vanish on a small neighborhood. This is the union of the interiors of $\Pi _F(C) = F + N_F C$, where F ranges over the k-dimensional faces of C. It follows from (4) that $\dim \Pi _F(C) \cap \Pi _G(C) < d$ for any two distinct $F, G \in \mathcal {F}_k(C)$, and hence, we can recover the cones $\Pi _F(C)$ from S.

We may use Lemma 3.4 to assume that $k < \frac{d}{2}$. Every k-face E of $\Pi _F(C) = F + N_FC$ is of the form $E = E' + N_{E''}C$, where $E' \subseteq F \subseteq E''$ are faces with $d - k = \dim E'' - \dim E'$. We say that E is free, if there exists no k-face G of C, such that $E = \Pi _F(C) \cap \Pi _G(C)$. Equivalently, E is not free, if and only if there exist another k-faces $G \ne F$, such that $E' \subseteq G \subseteq E''$. Thus, E is free, if and only if $F = E'$ or $F = E''$, and since $\dim E'' - \dim E' = d - k > k$, the case $F = E''$ is impossible. Note that if $F = E'$, then $E'' = C$, so $E = F + N_CC = F$. Therefore, the set of all free faces is precisely the set k-faces of C, from which we can recover C. $\square$

3.3 Characteristic Indicators

Corollary 2.5 can be generalized to the setting of indicator functions. Let $\rho : \mathfrak {C}_d \rightarrow \mathfrak {S}_d$ be the canonical projection. Then, we define $\overline{\mathcal {X}}: \textbf{Fans}_d \rightarrow \mathfrak {S}_d[t]$ as

$$\begin{aligned} \overline{\mathcal {X}}_\mathcal {N}(t) \ ~{:}{=}\ \sum _{k = 0}^d \rho (V_k(\mathcal {N})) t^k \ \in \ \mathfrak {S}_d[t]. \end{aligned}$$

This is a natural generalization of $\overline{\chi }_\mathcal {N}(t)$.

Corollary 3.6

Let $\mathcal {A}$ be an arrangement and $0 \le k \le d$. Then, as elements of $\mathfrak {S}_d[t]$

$$\begin{aligned} \overline{\mathcal {X}}_{\mathcal {N}(\mathcal {A})}(t) \ = \ \overline{\chi }_\mathcal {A}(t) \cdot \rho ([\mathbb {R}^d]) \, . \end{aligned}$$

(5)

Proof

The proof of Corollary 2.5 applies verbatim on noting that

$$\begin{aligned} \overline{\mathcal {X}}_{\mathcal {N}(\mathcal {A}^k)}(t) \ = \ (t^k + t^{k-1}) \cdot \rho ([\mathbb {R}^d]) \ = \ \overline{\chi }_{\mathcal {A}^k}(t) \cdot \rho ([\mathbb {R}^d]) \end{aligned}$$

for all k-singletons $\mathcal {A}^k$, $1 \le k \le d$. $\square$

Already in dimension 2, one can see that (5) holds only for generic points. It was shown in [16] that the exceptional set of points $x \in \mathbb {R}^d$ where $V_k(\mathcal {A})(x) \ne w_k(\mathcal {A})$ is a hyperplane arrangement. We will slightly generalize the results of [16] with a simpler proof that prompts a simple interpretation for the exceptional set.

For the proof, as well as the precise statement of our results, we recall two well-known ring structures on $\mathfrak {C}_d$; see, for example, [19] for an excellent exposition. First, note that $(\mathfrak {C}_d, +, \cdot )$ is a commutative ring with unit $1 = [\mathbb {R}^d]$ with respect to pointwise multiplication of functions. For $C, C' \in \textbf{Cones}_d$, we have

$$\begin{aligned} ([C] \cdot [C'])(x) \ ~{:}{=}\ [C](x) \cdot [C'](x) \ = \ [C \cap C'](x). \end{aligned}$$

A second ring structure $(\mathfrak {C}_d, +, *)$ is obtained with respect to taking conical hulls $C \vee C' ~{:}{=}{{\,\textrm{cone}\,}}(C \cup C')$

$$\begin{aligned} ([C] *[C'])(x) \ ~{:}{=}\ [C \vee C'](x). \end{aligned}$$

These two ring structures are related via polarity: The map $\mathcal {D}: \mathfrak {S}_d \rightarrow \mathfrak {S}_d$ $[C] \mapsto \mathcal {D}([C]) = [C^\vee ]$ is additive [4, Theorem 1.5], and since $(C \cap D)^\vee = C^\vee + D^\vee$ for all $C, D \in \textbf{Cones}_d$ for which $C \cup D$ is convex [26, Theorem 1.6.9], we see that polarity gives an isomorphism of rings $(\mathfrak {C}, +, \cdot ) \cong (\mathfrak {C}, +, *)$.

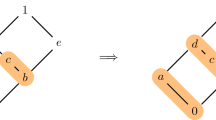
Let $\mathcal {A}$ be a hyperplane arrangement in a subspace U of $\mathbb {R}^d$. The lattice of flats $\mathcal {L}(\mathcal {A})$ is the collection of subspaces formed by intersections of hyperplanes in $\mathcal {A}$ ordered by reverse inclusion. The minimal element is $\hat{0}= U$ and $\hat{1}= {{\,\textrm{lineal}\,}}(\mathcal {A})$ is the maximal element. The Möbius function $\mu _\mathcal {L}$ of a finite partially ordered set $(\mathcal {L}, \preceq )$ is recursively defined for $x \preceq y \in \mathcal {L}$ as follows: If $x = y$, then $\mu _\mathcal {L}(x, y) = 1$ otherwise

We will suppress the subscript of $\mu$ if $\mathcal {L}$ is clear from the context. It is well known that $\mu = \mu _{\mathcal {L}(\mathcal {A})}$ alternates in sign, or, more precisely, $|\mu (L, M)| = (-1)^{\dim L - \dim M} \mu (L, M)$; see [27, Section 3.10]. Let $\delta (L, K) = 1$ if $L = K$ and $= 0$ otherwise. Denote by $\mathcal {F}(\mathcal {N})$ the set of all nonempty faces of all cones of $\mathcal {N}$. We will first show the following lemma, which will be essential to our generalization of Corollary 3.6:

Lemma 3.7

Let $\mathcal {A}$ be a hyperplane arrangement with lattice of flats $\mathcal {L}(\mathcal {A})$. Then

$$\begin{aligned} \sum _{C \in \mathcal {N}(\mathcal {A})} [C] \ = \ \sum _{L \in \mathcal {L}(\mathcal {A})} |\mu (\hat{0}, L)| \cdot [L] \end{aligned}$$

as elements in $\mathfrak {C}_d$.

Using the defining property of weak valuations, it is straightforward to verify that the map $C \mapsto (-1)^{\dim C}[{{\,\textrm{relint}\,}}(C)] \in \mathfrak {C}_d$ is a valuation. The Euler map is the induced homomorphism $\mathcal {E}: \mathfrak {C}_d \rightarrow \mathfrak {C}_d$.

Lemma 3.8

The Euler map is an involution, that is, $\mathcal {E}\circ \mathcal {E}= \textrm{id}$.

Proof

Using Möbius inversion on the face lattice of a cone C (cf. [6, Section 3.5]), one infers that

$$\begin{aligned} \mathcal {E}([C]) \ = \ (-1)^{\dim C }[{{\,\textrm{relint}\,}}(C)] \ = \ \sum _{F} (-1)^{\dim F} [F] \,, \end{aligned}$$

where F runs over all faces of C. Applying the Euler map to the right-hand side, we get

$$\begin{aligned} \sum _{F} [{{\,\textrm{relint}\,}}(F)] \ = \ [C] \,. \end{aligned}$$

$\square$

Proof of Lemma 3.7

Let $\mathcal {A}$ be an arrangement in $\mathbb {R}^d$ and let $L \in \mathcal {L}(\mathcal {A})$. Since

$$\begin{aligned}{}[L] \ = \ \sum _{F \in \mathcal {F}(\mathcal {A}), F \subseteq L } [{{\,\textrm{relint}\,}}(F)], \end{aligned}$$

it follows that:

$$\begin{aligned}{}[L] \ = \ (-1)^{\dim L } \mathcal {E}([L]) \ = \ \sum _{F \in \mathcal {F}(\mathcal {A}), F \subseteq L} (-1)^{\dim L - \dim F} [F] \,. \end{aligned}$$

We calculate

$$\begin{aligned} \sum _{L \in \mathcal {L}(\mathcal {A})} |\mu (\hat{0}, L)| \cdot [L] \ =&\ \sum _{L \in \mathcal {L}(\mathcal {A})} (-1)^{d - \dim L}\mu (\hat{0}, L) \sum _{F \in \mathcal {F}(\mathcal {A}) \atop F \subseteq L} (-1)^{\dim L - \dim F} [F]\\ \ =&\ \sum _{F \in \mathcal {F}(\mathcal {A})} (-1)^{d - \dim F} \sum _{L \in \mathcal {L}(\mathcal {A}) \atop F \subseteq L} \mu (\hat{0}, L) [F]\\ \ =&\ \sum _{F \in \mathcal {F}(\mathcal {A})} (-1)^{d - \dim F} \delta (\hat{0}, {{\,\textrm{lin}\,}}(F)) [F] \ = \ \sum _{C \in \mathcal {N}(\mathcal {A})} [C] \, . \end{aligned}$$

$\square$

Theorem 3.9

For all $0 \le k \le d$, as elements in $\mathfrak {C}_d$

$$\begin{aligned} V_k(\mathcal {N}(\mathcal {A})) \ = \ \sum _{L \in \mathcal {L}_k(\mathcal {A})} \left( \sum _{K \in \mathcal {L}(\mathcal {A}) \atop K \subseteq L} |\mu (L, K)| \cdot [K]\right) *\left( \sum _{M \in \mathcal {L}(\mathcal {A}) \atop L \subseteq M} |\mu (\hat{0}, M)| \cdot [M^\perp ]\right) \, . \end{aligned}$$

(6)

The proof is inspired by the arguments leading to [18, Theorem 5]. The additional bookkeeping is delegated to the ring structure on $\mathfrak {C}_d$.

Proof

We can rewrite the left-hand side

$$\begin{aligned} V_k(\mathcal {N}(\mathcal {A}) )&= \sum _{P \in \mathcal {N}(\mathcal {A})} \sum _{F \in \mathcal {F}_k(P)} [F] *[N_FP] \ = \ \sum _{F \in \mathcal {F}_k(\mathcal {A})} [F] *\left( \sum _{P \in \mathcal {N}(\mathcal {A}) \atop F \le P} [N_FP] \right) \, . \end{aligned}$$

Let $L = {{\,\textrm{lin}\,}}(F)$ and denote by $\mathcal {A}_L ~{:}{=}\{H \in \mathcal {A}: L \subseteq H\}$ the localization of $\mathcal {A}$ at L. Note that there is a one-to-one correspondence between the regions C of $\mathcal {A}_L$ and $P \in \mathcal {N}(\mathcal {A})$ with $F \subseteq P$ and that under this correspondence $C^\vee = N_FP$. Thus

$$\begin{aligned} \sum _{F \in \mathcal {F}_k(\mathcal {A})} [F] *\left( \sum _{P \in \mathcal {N}(\mathcal {A}) \atop F \le P} [N_FP] \right) \ = \ \sum _{L \in \mathcal {L}_k(\mathcal {A})} \left( \sum _{F \in \mathcal {N}(\mathcal {A}^L)} [F]\right) *\left( \sum _{C \in \mathcal {N}(\mathcal {A}_L)} [C^\vee ]\right) . \end{aligned}$$

Using Lemma 3.7 on the inner sums gives the result

$$\begin{aligned} \sum _{F \in \mathcal {N}(\mathcal {A}^L)} [F] \ = \ \sum _{K \in \mathcal {A}^L} |\mu _{\mathcal {A}^L}(L, K)| \cdot [K] \ = \ \sum _{K \in \mathcal {L}(\mathcal {A}) \atop K \subseteq L} |\mu _{\mathcal {A}}(L, K)| \cdot [K]\,, \end{aligned}$$

and

$$\begin{aligned} \sum _{C \in \mathcal {N}(\mathcal {A}_L)} [C^\vee ]&= \left( \sum _{C \in \mathcal {N}(\mathcal {A}_L)} [C]\right) ^\vee \ = \ \left( \sum _{M \in \mathcal {A}_L} |\mu _{\mathcal {A}_L}(\hat{0}, M)| \cdot [M]\right) ^\vee \nonumber \\&= \sum _{M \in \mathcal {L}(\mathcal {A}) \atop L \subseteq M} |\mu _{\mathcal {A}}(\hat{0}, M)| \cdot [M^\perp ]\,. \end{aligned}$$

(7)

$\square$

For direct comparison with Theorem 1.4 of [16], note that for $K \subseteq L \subseteq M \in \mathcal {L}(\mathcal {A})$, we have $\dim (K + M^\perp ) = d$ if and only if $K = L = M$. Thus, for a generic point $x \in \mathbb {R}^d$, the evaluation $([K] *[M^\perp ])(x) = 0$ if $K \ne L$ or $L \ne M$. This proves Corollary 3.6 coefficientwise

$$\begin{aligned} V_k(\mathcal {A})(x) \ = \ \sum _{L \in \mathcal {L}_k(\mathcal {A})} |\mu (L, L)| \cdot |\mu (\mathbb {R}^d, L)| \cdot ([L] *[L^\perp ])(x) \ = \ w_k(\mathcal {A})\,, \end{aligned}$$

where we used that the terms $|\mu (\mathbb {R}^d, L)|$ sum up to $w_k(\mathcal {A})$ (cf. [27, Section 3.10]). Since all summands in (6) are positive, this also shows that ${V_k(\mathcal {A})(x) {\ge } w_k}$ for (non-generic) points $x \in \mathbb {R}^d$. We have $V_k(\mathcal {A})(x) > w_k$ precisely when $x \in K + M^\perp$ for $K \subseteq L \subseteq M$, such that $\dim L = k$ and $\dim (K + M^\perp ) = d - 1$. The collection of these hyperplanes $K + M^\perp$ defines a hyperplane arrangement, which can be given a concrete interpretation. If $\mathcal {A}'$ is any hyperplane arrangement in some linear subspace $U \subset \mathbb {R}^d$, then $\mathcal {A}' + U^\perp ~{:}{=}\{ H + U^\perp : H\in \mathcal {A}' \}$ is an arrangement of hyperplanes in $\mathbb {R}^d$ with lineality space $U^\perp$.

Corollary 3.10

Let $\mathcal {A}$ be an arrangement of hyperplanes in $\mathbb {R}^d$. Then, $V_k(\mathcal {A})(x) > w_k$ for some $0 \le k \le d$ if and only if x is contained in the arrangement

$$\begin{aligned} \Pi (\mathcal {A}) \ ~{:}{=}\ \bigcup _{L \in \mathcal {L}(\mathcal {A})} (\mathcal {A}/L) + L^\perp \,. \end{aligned}$$

A point $x \in \mathbb {R}^d$ is contained in $(\mathcal {A}/L) + L^\perp$ if and only if the orthogonal projection of x onto L is contained in $\mathcal {A}/L$. The exceptional set of Theorem 3.9 was also considered by Lofano–Paolini [21]. For a subspace $U \subset \mathbb {R}^d$ and $x \in \mathbb {R}^d$, let $d_U(x) ~{:}{=}\Vert x - \pi _U(x)\Vert$ be the distance of x to U. Lofano–Paolini call a point $x \in \mathbb {R}^d$ generic with respect to an arrangement $\mathcal {A}$ if $d_L(x) \ne d_{L'}(x)$ for all distinct $L,L' \in \mathcal {L}(\mathcal {A})$. The set of non-generic points lies on a collection of quadrics and is in general not a hyperplane arrangement. A characterization of the points away from $\Pi (\mathcal {A})$ is as follows; cf. Lemma 5.2 of [21].

Lemma 3.11

Let $\mathcal {A}$ be a hyperplane arrangement in $\mathbb {R}^d$ and $x \in \mathbb {R}^d$. Then, $x \not \in \bigcup \Pi (\mathcal {A})$ if and only if $d_{L'}(x) > d_L(x)$ for all flats $L,L' \in \mathcal {L}(\mathcal {A})$ with $L' \subsetneq L$. Equivalently, this is the case if and only if $d_H(x) > d_L(x)$ for all flats L and $H \in \mathcal {A}/L$.

Remark 3.12

The proof of Theorem 3.9 and Lemma 3.7 applies ad verbatim to affine hyperplane arrangements. For those, one has to work in the ring $(\mathfrak {X}_d, +, *)$ of indicator functions of polyhedra instead of polyhedral cones, where $*$ is defined via the Minkowski-sum, $[Q] *[Q'] = [Q + Q']$. The only problem is our use of polarity in (7). Here, we use that (7) holds in $(\mathfrak {C}_d, +, *)$, which canonically embeds into $(\mathfrak {X}_d, +, *)$, since $C \vee C' = C + C'$ for $C, C' \in \textbf{Cones}_d$.

Finally, we also want to give a proof that $\overline{\chi }_\mathcal {N}(-1) = 0$, which we also do on the level of indicator functions. For this, we give a simple (algebraic) proof of a result of Schneider [26] and its generalization to polyhedra by Hug–Kabluchko [15]. Recall that $\mathcal {F}(Q)$ denotes the set of nonempty faces of a polyhedron Q. The Euler-Characteristic of Q, is defined as

$$\begin{aligned} \varepsilon (Q) ~{:}{=}\sum _{F \in \mathcal {F}(Q)} (-1)^{\dim F}. \end{aligned}$$

Recall from [6, Theorem 3.4.11] that for a polyhedron Q with $L = {{\,\textrm{lineal}\,}}(Q)$, we have $\varepsilon (Q) = 0$ if $L = 0$ and Q is unbounded and $\varepsilon (Q) = (-1)^{\dim L}\varepsilon (\pi _{L^\perp }(Q))$ otherwise.

Theorem 3.13

Let $Q \subseteq \mathbb {R}^d$ be a polyhedron. Then, as elements in $\mathfrak {X}_d$:

$$\begin{aligned} \varepsilon (Q) \cdot [\mathbb {R}^d] \ = \ \sum _{F \in \mathcal {F}(Q)} (-1)^{\dim F} [F - N_FQ]. \end{aligned}$$

Proof

Note that $(-1)^{\dim Q - \dim F} = \mu (F, Q)$, where $\mu = \mu _{\mathcal {F}(Q)}$. Denote by $T_FC ~{:}{=}(N_FC)^\vee$ the tangent cone of C at Q. By the Sommerville relation (cf. [1, Lem. 4.1]), we have for any cone $D \in \textbf{Cones}_d$

$$\begin{aligned} \sum _{G \in \mathcal {F}(D)} (-1)^{\dim G} \cdot [T_GD] \ = \ (-1)^{\dim D} [-{{\,\textrm{relint}\,}}D]. \end{aligned}$$

Applying the Euler map $\mathcal {E}$ on both sides, using $\dim T_GD = \dim D$, and the fact that $\mathcal {E}$ is an involution (Lemma 3.8), we get

$$\begin{aligned} \sum _{G \in \mathcal {F}(D)} (-1)^{\dim G} \cdot [{{\,\textrm{relint}\,}}T_GD] \ = \ (-1)^{\dim D} [-D]. \end{aligned}$$

If we set $D ~{:}{=}N_FQ$, we have $T_{G'}(N_FQ) = N_FG$ for $G' ~{:}{=}N_GQ$, so this reads:

$$\begin{aligned} (-1)^{\dim Q - \dim F} [-N_FQ]&= \sum _{G' \in \mathcal {F}(N_FQ)} (-1)^{\dim G'} \cdot [{{\,\textrm{relint}\,}}T_{G'}(N_FQ)]\\&= \sum _{F \subseteq G \in \mathcal {F}(Q)} (-1)^{\dim Q - \dim G} \cdot [{{\,\textrm{relint}\,}}N_FG]\,. \end{aligned}$$

Now, we can simply compute

$$\begin{aligned} \sum _{F \in \mathcal {F}(Q)} (-1)^{\dim F} \cdot [F] *[-N_FQ]&= \sum _{F \in \mathcal {F}(Q)} [F] *\sum _{F \subseteq G \in \mathcal {F}(Q)} (-1)^{\dim G} \cdot [{{\,\textrm{relint}\,}}N_FG]\\&= \sum _{G \in \mathcal {F}(Q)} (-1)^{\dim G} \sum _{F \in \mathcal {F}(G)} [F] *[{{\,\textrm{relint}\,}}N_FG]\\&= \sum _{G \in \mathcal {F}(Q)} (-1)^{\dim G} \cdot [\mathbb {R}^d] \ = \ \varepsilon (Q) \cdot [\mathbb {R}^d]\,. \end{aligned}$$

$\square$

That $\overline{\chi }_\mathcal {N}(-1) = 0$ follows now immediately by noting that:

$$\begin{aligned} \sigma _{d-1}(F + N_FC) \ = \ \sigma _{d-1}(F - N_FC) \end{aligned}$$

for all cones $C \in \mathcal {N}$ and faces F of C.