Proof of the Plethystic Murnaghan–Nakayama Rule Using Loehr’s Labelled Abacus

Abstract

The plethystic Murnaghan–Nakayama rule describes how to decompose the product of a Schur function and a plethysm of the form $p_r\circ h_m$ as a sum of Schur functions. We provide a short, entirely combinatorial proof of this rule using the labelled abaci introduced in Loehr (SIAM J Discrete Math 24(4):1356–1370, 2010).

1 Introduction

In 2010, Loehr [7] introduced a labelled abacus as a combinatorial model for antisymmetric polynomials $a_{\beta }$. By considering appropriate moves of labelled beads and their collisions, he proved standard formulas for decompositions of products of Schur polynomials with other symmetric polynomials, namely Pieri’s rule, Young’s rule, the Murnaghan–Nakayama rule and the Littlewood–Richardson rule, as well as the equivalence of the combinatorial and the algebraic definitions of Schur polynomials and a formula for inverse Kostka numbers. We follow the slogan ‘when beads bump, objects cancel’ from [7] and enrich this collection of results by proving the plethystic Murnaghan–Nakayama rule.

Theorem 1.1

(Plethystic Murnaghan–Nakayama rule) Let $\mu$ be a partition and r and m be positive integers. Then

$$\begin{aligned} s_{\mu }(p_r\circ h_m)=\sum _{\mu \subseteq \lambda \in {{\,\textrm{Par}\,}}(|\mu |+rm)}{{\,\textrm{sgn}\,}}_r(\lambda /\mu )s_{\lambda }. \end{aligned}$$

See Sect. 2.1 for definitions of ${{\,\textrm{sgn}\,}}_r$ and r-decomposable skew partitions, which are the skew partitions for which ${{\,\textrm{sgn}\,}}_r$ is non-vanishing.

More precisely, we prove the formula in Theorem 1.1 for symmetric polynomials in N variables where $N\ge |\mu |+rm$. This is equivalent to Theorem 1.1 as both sides of the formula have degree $|\mu |+rm$. One can easily extend the result to a decomposition of $s_{\mu }\left( p_{\rho }\circ h_{\nu } \right)$ as a sum of Schur functions for any non-empty partitions $\rho$ and $\nu$ by iterating Theorem 1.1 and using the formula $p_{\rho }\circ h_{\nu }=\prod _{i,j} p_{\rho _i}\circ h_{\nu _j}$.

The plethystic Murnaghan–Nakayama rule is a generalisation of the usual Murnaghan–Nakayama rule, which can be obtained from Theorem 1.1 by letting $m=1$, that is by replacing the plethysm $p_r\circ h_m$ with $p_r$. By letting $r=1$ instead, one obtains Young’s rule which describes the decomposition of $s_{\mu }h_m$ as a sum of Schur functions.

Whilst a description of the plethysm $p_r\circ h_m = p_r\circ s_{(m)}$ is known and follows from Theorem 1.1 after letting $\mu =\o$, in general, it is a difficult problem to decompose a plethysm as a sum of Schur functions; see [11, Problem 9], which asks for a decomposition of plethysms of the form $s_{(a)}\circ s_{(b)}$. Plethysms play an important role not only in the study of symmetric functions but also in the representation theory of symmetric groups and general linear groups; see [10, Chapter 7: Appendix 2]. The connexion of plethysms and representation theory was used, for instance, in [1] to find the maximal constituents of plethysms of Schur functions using the highest weight vectors.

The plethystic Murnaghan–Nakayama rule appeared first in [3, p.29], where it was proved using Muir’s rule. Since then, it has been proved using several different methods: in [4, Proposition 4.3] characters of symmetric groups are used, [12] uses James’ (unlabelled) abacus and induction on m and [2, Corollary 3.8] uses vertex operators. In comparison to these proofs, our elementary proof using the labelled abaci arises naturally by ‘merging’ the proofs from [7] of the Murnaghan–Nakayama rule and Young’s rule.

Since the publication of the original paper introducing the labelled abaci, Loehr has used it to prove the Cauchy product identities in [6], and together with Wills they introduced abacus-tournaments to study Hall–Littlewood polynomials in [8].

2 Definitions

2.1 Partitions

A partition $\lambda =(\lambda _1,\lambda _2,\dots ,\lambda _l)$ is a non-increasing sequence of positive integers. The size of a partition $\lambda$, denoted by $|\lambda |$, equals $\sum _{i=1}^l \lambda _i$. We call the number of elements of $\lambda$ the length of $\lambda$ and denote it by $\ell (\lambda )$. We use the convention that for $i>\ell (\lambda )$ we have $\lambda _i=0$, and we allow ourselves to attach extra zeros to a partition without changing it. We write ${{\,\textrm{Par}\,}}_{\le N}$ for the set of partitions of length at most N, ${{\,\textrm{Par}\,}}(n)$ for the set of partitions of size n and ${{\,\textrm{Par}\,}}_{\le N}(n)$ for the intersection of these two sets.

The Young diagram of a partition $\lambda$ is $Y_{\lambda }=\left\{ (i,j)\in \mathbb {N}^2: i\le \ell (\lambda ), j\le \lambda _i \right\}$ and we refer to its elements as boxes. We write $\mu \subseteq \lambda$ whenever $Y_{\mu }\subseteq Y_{\lambda }$. A skew partition $\lambda /\mu$ is a pair of partitions $\mu \subseteq \lambda$ and its Young diagram is $Y_{\lambda /\mu }=Y_{\lambda }\setminus Y_{\mu }$. We define the top of a skew partition $\lambda /\mu$, denoted as $t(\lambda /\mu )$, to be 0 if $\lambda =\mu$, and the least i such that $\lambda _i\ne \mu _i$ otherwise. We similarly define the bottom $b(\lambda /\mu )$ of a skew partition by replacing the word ‘least’ with ‘greatest’.

Let r be a positive integer. An r-border strip is a skew partition $\lambda /\mu$ consisting of r edge-adjacent boxes such that for all $(i,j)\in Y_{\lambda /\mu }$, we have $(i+1,j+1)\notin Y_{\lambda /\mu }$. It follows from the definition that for any partition $\lambda$ and a non-negative integer t, there is at most one r-border strip $\lambda /\mu$ with $t(\lambda /\mu )=t$. A skew partition $\lambda /\mu$ is r-decomposable if there are partitions

$$\begin{aligned} \mu =\gamma ^{(0)}\subseteq \gamma ^{(1)}\subseteq \dots \subseteq \gamma ^{(d)}=\lambda \end{aligned}$$

(1)

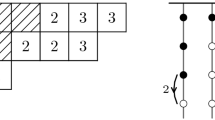
such that the skew partition $\gamma ^{(i+1)}/\gamma ^{(i)}$ is an r-border strip for all $0\le i\le d-1$ and $t(\gamma ^{(1)}/\gamma ^{(0)})\ge t(\gamma ^{(2)}/\gamma ^{(1)})\ge \dots \ge t(\gamma ^{(d)}/\gamma ^{(d-1)})$. If such a decomposition exists, it is unique as there is a unique choice for $\gamma ^{(d-1)}$ as $\lambda /\gamma ^{(d-1)}$ is an r-border strip with $t(\lambda /\gamma ^{(d-1)})=t(\lambda /\mu )$ and an inductive argument then applies. Examples of Young diagrams of r-border strips and an r-decomposable partition are in Fig. 1.

Fig. 1

Let $\gamma ^{(0)}=\mu =(5,3,3,2,2,1), \gamma ^{(1)}=(5,4,4,4,3,1), \gamma ^{(2)}=(5,5,5,5,5,1)$ and $\gamma ^{(3)}=\lambda =(8,6,6,5,5,1)$. The above dashed lines, labelled by $i=1,2,3$, pass through the Young diagrams of 5-border strips $\gamma ^{(i)}/\gamma ^{(i-1)}$. The bottoms of these 5-border strips are 5, 5 and 3, respectively, whilst their tops are 2, 2 and 1, respectively. As the tops are in non-increasing order, the skew partition $\lambda /\mu$ is 5-decomposable

For an r-border strip $\lambda /\mu$, we define its $\textit{sign}$ denoted by ${{\,\textrm{sgn}\,}}(\lambda /\mu )$ as $(-1)^{b(\lambda /\mu )-t(\lambda /\mu )}$. For any skew partition $\lambda /\mu$, we then let ${{\,\textrm{sgn}\,}}_r(\lambda /\mu )={{\,\textrm{sgn}\,}}(\gamma ^{(1)}/\gamma ^{(0)}){{\,\textrm{sgn}\,}}(\gamma ^{(2)}/\gamma ^{(1)})\dots {{\,\textrm{sgn}\,}}(\gamma ^{(d)}/\gamma ^{(d-1)})$ where $\gamma ^{(i)}$ are as in (1) if $\lambda /\mu$ is r-decomposable, and ${{\,\textrm{sgn}\,}}_r(\lambda /\mu )=0$ otherwise. Looking at Fig. 1, the signs of the 5-border strips there are $-1,-1$ and 1, respectively, and hence ${{\,\textrm{sgn}\,}}_5(\lambda /\mu )=1$.

2.2 Symmetric Polynomials

A composition of a non-negative integer m is a sequence $\beta =(\beta _1,\beta _2,\dots ,\beta _N)$ of non-negative integers such that $\sum _{i=1}^N \beta _i=m$. The length of a composition is the number of its elements and we write ${{\,\textrm{Com}\,}}_N(m)$ for the set of compositions of m of length N.

We now introduce the required elements of the ring of symmetric polynomials in N variables, called $\Lambda _N$, as defined, for instance, in [9, §I.2]. For a positive integer m, the complete homogeneous symmetric polynomial $h_{m}(x_1,x_2,\dots ,x_{N})$ is defined as $\sum _{\beta \in {{\,\textrm{Com}\,}}_N(m)}x^{\beta }$, where $x^{\beta }$ is the monomial $x_1^{\beta _1}x_2^{\beta _2}\dots x_N^{\beta _N}\in \mathbb {Z}\left[ x_1,x_2,\dots ,x_N \right]$. If r is a positive integer, the power sum symmetric polynomial $p_r(x_1,x_2,\dots ,x_{N})$ is defined as $\sum _{i=1}^N x_i^r$.

If g is an element of $\Lambda _N$, we define the plethysm $p_r\circ g (x_1,x_2,\dots ,x_{N})$ as $g(x^r_1,x^r_2,\dots ,x^r_{N})$. In particular, if $g=h_m$, we get $p_r\circ h_m(x_1,x_2,\dots ,x_{N})=\sum _{\beta \in {{\,\textrm{Com}\,}}_N(m)}x^{r\beta }$, where $r\beta =(r\beta _1,r\beta _2,\dots ,r\beta _{N})$. One can define a plethysm $f\circ g$ for any elements f and g of $\Lambda _N$ by extending the map $\cdot \circ g$ to an endomorphism of the $\mathbb {Q}$-algebra $\mathbb {Q}\otimes _{\mathbb {Z}}\Lambda _N$. It can be checked that for any $g\in \Lambda _N$, we have $p_r\circ g = g \circ p_r$; thus, in particular, $p_r\circ h_m = h_m \circ p_r$.

To define the final ingredient, Schur polynomials, we introduce the antisymmetric polynomials $a_{\beta }$: for a positive integer N and a composition $\beta$ of length N, we let $a_{\beta }=\det (x_i^{\beta _j})_{i,j\le N}$. Given a partition $\lambda$ of length at most N, we now define the Schur polynomial

$$\begin{aligned} s_{\lambda }(x_1,x_2,\dots ,x_{N})=\frac{a_{\lambda +\delta (N)}}{a_{\delta (N)}}, \end{aligned}$$

(2)

where $\delta (N)=(N-1,N-2,\dots ,0)$ and $\lambda +\delta (N)=(\lambda _1+N-1,\lambda _2+N-2,\dots , \lambda _N)$. Whilst compared to other definitions such as [10, Definition 7.10.1], it is not immediately obvious that Schur polynomials are polynomials, we use this definition as one requires antisymmetric polynomials to use the labelled abaci.

Example 2.1

Let $N=3$. Then

$$\begin{aligned} h_{2}(x_1,x_2,x_3)&=x_1^2+x_2^2+x_3^2+x_1x_2+x_2x_3+x_1x_3,\\ p_4(x_1,x_2,x_3)&=x_1^4 + x_2^4 +x_3^4,\\ p_4\circ h_2(x_1,x_2,x_3)&=x_1^8+x_2^8+x_3^8+x_1^4x_2^4+x_2^4x_3^4+x_1^4x_3^4,\\ s_{(2,1)}(x_1,x_2,x_3)&=\frac{a_{(4,2,0)}}{a_{(2,1,0)}}=\frac{(x_1^2-x_2^2)(x_2^2-x_3^3)(x_1^2-x_3^2)}{(x_1-x_2)(x_2-x_3)(x_1-x_3)}\\&=(x_1+x_2)(x_2+x_3)(x_1+x_3)\\&=x_1^2x_2 + x_1^2x_3+x_1x_2^2+x_1x_3^2+x_2^2x_3+x_2x_3^2+2x_1x_2x_3.\\ \end{aligned}$$

2.3 Labelled Abacus

Most of our terminology and notation for labelled abaci comes from [7]. A labelled abacus with Nbeads is a sequence $w=(w_0,w_1,w_2,\dots )$ indexed from 0 with precisely N non-zero entries, which are $1,2,\dots ,N$. For $1\le B\le N$, we let $w^{-1}(B)$ to be the index i such that $w_i=B$. We write $\iota _1(w)>\iota _2(w)>\dots >\iota _N(w)$ for the indices i such that $w_i$ is non-zero and define the support ${{\,\textrm{supp}\,}}(w)$ to be $\left\{ \iota _i(w): 1\le i\le N \right\}$. Finally, the sign ${{\,\textrm{sgn}\,}}(w)$ is the sign of the permutation $\sigma _w\in S_N$ given by $\sigma _w(B)=w_{\iota _{B}(w)}$.

Example 2.2

If $w=(5,0,6,4,1,0,0,3,0,2,0,0,\dots )$, a labelled abacus with 6 beads, then $\sigma _w=(1\; 2\; 3)(5\;6)$. Hence, ${{\,\textrm{sgn}\,}}(w)=-1$.

One should imagine that a labelled abacus w consists of a single runner with positions $0,1,2,\dots$, where the position i is empty if $w_i=0$, and is occupied by a bead labelled by $w_i$ otherwise. The value $w^{-1}(B)$ is the position of bead B, the support is the set of the non-empty positions and $\iota _t(w)$ is the t-th largest occupied position. The permutation of beads in w, starting from beads ordered in decreasing order, is then $\sigma _w$. With this in mind, we introduce the following intuitive terminology.

Fix positive integer r and $B\ne C\le N$ and write $y=w^{-1}(B)$ and $z=w^{-1}(C)$ for the positions of beads B and C, respectively. A labelled abacus $w'$ is obtained from w by swapping beads $\textit{B}$ and $\textit{C}$ if $w'_{y}=C$, $w'_{z}=B$ and $w'_i=w_i$ otherwise. Bead B is r-mobile if $w_{y+r}=0$. If that is the case, a labelled abacus $w'$ is obtained from w by r-moving bead $\textit{B}$ if $w'_y=0$, $w'_{y+r}=B$ and $w'_i=w_i$ otherwise. If bead B in not r-mobile, we say that it r-collides with bead $w_{y+r}$. Similarly, bead B is left-$\textit{r}$-mobile if $y\ge r$ and $w_{y-r}=0$. If that is the case, a labelled abacus $w'$ is obtained from w by r-moving bead $\textit{B}$ leftwards if w is obtained from $w'$ by r-moving bead B. Finally, for $t\le N$, the t-th rightmost bead of w is $\sigma _w(t)$.

It is easy to see how the sign changes when performing the above operations. To state the formula, we define the number of beads between positions $i_1<i_2$ as $|{{\,\textrm{supp}\,}}(w)\cap \left\{ i_1+1,i_2+2,\dots ,i_2-1\right\} |$.

Lemma 2.3

Let w be a labelled abacus with N beads. Fix $B\le N$ and write $y=w^{-1}(B)$ for the position of bead B.

• (i) If $C\le N$ and $C\ne B$ and $w'$ is obtained from w by swapping beads B and C, then ${{\,\textrm{sgn}\,}}(w')=-{{\,\textrm{sgn}\,}}(w)$.

• (ii) If bead B is r-mobile for some chosen positive integer r and $w'$ is obtained from w by r-moving bead B, then ${{\,\textrm{sgn}\,}}(w')=(-1)^u{{\,\textrm{sgn}\,}}(w)$, where u is the number of beads between y and $y+r$.

Proof

In (i), $\sigma _{w'}\sigma _w^{-1}$ is the transposition $(B\; C)$. In (ii), $\sigma _{w'}\sigma _w^{-1}$ is a $\left( u+1\right)$-cycle. $\square$

For a labelled abacus w with N beads, we define its weight ${{\,\textrm{wt}\,}}(w)$ as the monomial $\prod _{i\in {{\,\textrm{supp}\,}}(w)}x_{w_i}^i$. We also define the shape ${{\,\textrm{sh}\,}}(w)$ to be the partition $(\iota _1(w)-N+1, \iota _2(w)-N+2,\dots , \iota _N(w))$, and given $\lambda \in {{\,\textrm{Par}\,}}_{\le N}$ we write ${{\,\textrm{Abc}\,}}_N(\lambda )$ for the set of labelled abaci with N beads and shape $\lambda$. Thus, ${{\,\textrm{Abc}\,}}_N(\lambda )$ contains N! elements. An example of labelled abaci is in Fig. 2.

Fig. 2

The upper labelled abacus with 6 beads w has support $\left\{ 10,7,6,4,3,1 \right\}$. The permutation $\sigma _w$ equals $(1\; 3)(2\; 6\; 4\; 5)$ and thus ${{\,\textrm{sgn}\,}}(w)=1$. We have, for instance, $w^{-1}(5)=4$ and $w^{-1}(1)=6$. The weight of w is $x_1^6x_2^3x_3^{10}x_4x_5^{4}x_6^7$ and the shape of w is (5, 3, 3, 2, 2, 1). Bead 4 is not 5-mobile, but the other beads are. By 5-moving bead 2, we obtain the lower labelled abacus $w'$. One computes that $\sigma _{w'}\sigma _w^{-1}=(2\; 5\; 1 \; 6)$, which is in accordance with the proof of Lemma 2.3(ii)

The importance of labelled abaci comes from the simple identity

$$\begin{aligned} a_{\lambda +\delta (N)}=\sum _{w\in {{\,\textrm{Abc}\,}}_N(\lambda )}{{\,\textrm{sgn}\,}}(w){{\,\textrm{wt}\,}}(w), \end{aligned}$$

(3)

which holds for any $\lambda \in {{\,\textrm{Par}\,}}_{\le N}$; see [7, p.1359]. Note that the identity is just the expansion of $a_{\lambda +\delta (N)}=\det (x_i^{\lambda _j+N-j})_{i,j\le N}$.

3 Proof of the Plethystic Murnaghan–Nakayama Rule

The following is an immediate consequence of a well-known result connecting moves on an (unlabelled) abacus and removals of border strips.

Lemma 3.1

Let r, t and N be positive integers such that $t\le N$. For $\lambda \in {{\,\textrm{Par}\,}}_{\le N}$ and $w\in {{\,\textrm{Abc}\,}}_N(\lambda )$ the following holds:

• (i) There is a bijection $\theta$ between left-r-mobile beads of w and r-border strips of the form $\lambda /\mu$ given by mapping bead B to an r-border strip $\lambda /\mu$, where $\mu$ is the shape of the labelled abacus obtained from w by r-moving bead B leftwards.

• (ii) If $\lambda /\mu$ is an r-border strip with top t, then $\theta ^{-1}(\lambda /\mu )$ is the t-th rightmost bead of w.

• (iii) With $\mu$ as in (ii), the number of beads between positions $\iota _t(w)$ and $\iota _t(w)-r$ equals $b(\lambda /\mu )-t(\lambda /\mu )$.

• (iv) Continuing with the same $\mu$, there is a bijection $\phi :{{\,\textrm{Abc}\,}}_N(\lambda )\rightarrow {{\,\textrm{Abc}\,}}_N(\mu )$ given by r-moving the t-th rightmost bead leftwards.

Proof

Part (i) (without labels) is [5, Lemma 2.7.13]. Now suppose that $w'$ is obtained from w by r-moving bead B leftwards. If j is the least index in which ${{\,\textrm{sh}\,}}(w)$ and ${{\,\textrm{sh}\,}}(w')$ differ, then bead B is the j-th rightmost bead of w. Similarly, if j is the largest such index, then bead B is the j-th rightmost bead of $w'$. Thus we deduce (ii) and (iii). Finally, (iv) follows from (i) and (ii). $\square$

Example 3.2

Let w be the lower labelled abacus from Fig. 2 and $\lambda ={{\,\textrm{sh}\,}}(w)=(5,4,4,4,3,1)$. Since the second rightmost bead of w is left-5-mobile, there is a corresponding 5-border strip $\lambda /\mu$ with top 2. Indeed, this is the 5-border strip labelled by 1 from Fig. 1. The bijection from Lemma 3.1(iv) then pairs the labelled abaci in Fig. 2.

The next step is to iterate the previous lemma. To do this, for positive integers r, m, N and $\lambda ,\mu \in {{\,\textrm{Par}\,}}_{\le N}$, we define a set $K_N^{r,m}(\mu ,\lambda )$ as the set of sequences $(w^{(0)},w^{(1)},\dots ,w^{(m)})$ of labelled abaci with N beads such that ${{\,\textrm{sh}\,}}(w^{(0)})=\mu$, ${{\,\textrm{sh}\,}}(w^{(m)})=\lambda$, for all $1\le j\le m$ the labelled abacus $w^{(j)}$ is obtained from $w^{(j-1)}$ by r-moving a bead, say bead $w^{(j-1)}_{i_j}$, and the inequalities $i_1<i_2<\dots <i_m$ hold. We refer the reader to Fig. 3 for a diagrammatic example of two such sequences.

Lemma 3.3

Let r, m and N be positive integers and $\lambda ,\mu \in {{\,\textrm{Par}\,}}_{\le N}$.

• (i) The set $K_N^{r,m}(\mu ,\lambda )$ is empty unless $\lambda /\mu$ is an r-decomposable skew partition of size $|\mu |+rm$.

• (ii) If $\lambda /\mu$ is an r-decomposable skew partition of size $|\mu |+rm$, then the map $(w^{(0)},w^{(1)},\dots ,w^{(m)})\mapsto w^{(m)}$ is a bijection from $K_N^{r,m}(\mu ,\lambda )$ to ${{\,\textrm{Abc}\,}}_N(\lambda )$.

• (iii) For $(w^{(0)},w^{(1)},\dots ,w^{(m)})\in K_N^{r,m}(\mu ,\lambda )$ we have that ${{\,\textrm{sgn}\,}}(w^{(m)}) = {{\,\textrm{sgn}\,}}_r(\lambda /\mu ){{\,\textrm{sgn}\,}}(w^{(0)})$.

Proof

For any sequence of labelled abaci $(w^{(0)},w^{(1)},\dots ,w^{(m)})$, let $\gamma ^{(j)}={{\,\textrm{sh}\,}}(w^{(j)})$. From Lemma 3.1(i), the condition that $w^{(j)}$ is obtained from $w^{(j-1)}$ by r-moving a bead, say bead $w^{(j-1)}_{i_j}$, implies that $\gamma ^{(j)}/\gamma ^{(j-1)}$ is an r-border strip. Suppose that this is the case for all $1\le j\le m$. Let bead $w^{(j-1)}_{i_j}$ be the $t_j$-th rightmost bead of $w^{(j)}$. The key observation is that $i_1<i_2<\dots <i_m$ if and only if $t_1\ge t_2\ge \dots \ge t_m$, which, by Lemma 3.1(ii), is equivalent to $t(\gamma ^{(1)}/\gamma ^{(0)})\ge t(\gamma ^{(2)}/\gamma ^{(1)})\ge \dots \ge t(\gamma ^{(m)}/\gamma ^{(m-1)})$.

Hence, if $(w^{(0)},w^{(1)},\dots ,w^{(m)})$ lies in $K_N^{r,m}(\mu ,\lambda )$, then $\mu =\gamma ^{(0)}\subseteq \gamma ^{(1)}\subseteq \dots \subseteq \gamma ^{(m)}=\lambda$ is a chain witnessing that $\lambda /\mu$ is r-decomposable, as in (1); thus (i) is proven. Moreover, since the chain (1) is unique, there is a unique choice of shapes of the labelled abaci in any sequence $(w^{(0)},w^{(1)},\dots ,w^{(m)})\in K_N^{r,m}(\mu ,\lambda )$. We can now apply Lemma 3.1(iv) m-times to obtain (ii). Finally, Lemma 2.3(ii) and Lemma 3.1(iii) show that if $(w^{(0)},w^{(1)},\dots ,w^{(m)})\in K_N^{r,m}(\mu ,\lambda )$, then ${{\,\textrm{sgn}\,}}(w^{(j)})= {{\,\textrm{sgn}\,}}(\gamma ^{(j)}/\gamma ^{(j-1)}) {{\,\textrm{sgn}\,}}(w^{(j-1)})$ for all $1\le j\le m$. Multiplying these equalities, we obtain (iii). $\square$

We can rephrase this result to obtain a characterisation of r-decomposable partitions. In the statement, one should bear in mind that in (ii) and (iii) the r-moves are made consecutively, and thus a bead may r-move multiple times.

Corollary 3.4

Let r and N be positive integers and let $\lambda ,\mu \in {{\,\textrm{Par}\,}}_{\le N}$. The following are equivalent:

• (i) $\lambda /\mu$ is an r-decomposable skew partition.

• (ii) There are labelled abaci $w\in {{\,\textrm{Abc}\,}}_N(\mu )$ and $w'\in {{\,\textrm{Abc}\,}}_N(\lambda )$ such that $w'$ is obtained from w by a series of r-moves of beads from positions $i_1,i_2,\dots ,i_{m}$, where $i_1<i_2<\dots <i_m$.

• (iii) For each $w'\in {{\,\textrm{Abc}\,}}_N(\lambda )$ there exists $w\in {{\,\textrm{Abc}\,}}_N(\mu )$ such that $w'$ is obtained from w by a series of r-moves of beads from positions $i_1,i_2,\dots ,i_{m}$, where $i_1<i_2<\dots <i_m$.

Moreover, if (i)–(iii) holds true, then the choice of w and the series of r-moves in (iii) is unique, $|\lambda |=|\mu |+mr$ where m is the number of r moves in (ii) and (iii) and ${{\,\textrm{sgn}\,}}(w')={{\,\textrm{sgn}\,}}_r(\lambda /\mu ){{\,\textrm{sgn}\,}}(w)$.

We are now ready to prove the main theorem.

Proof of Theorem 1.1

Fix a partition $\mu$ and positive integers r, m and N such that $N\ge |\mu |+rm$. Using the definition of Schur polynomials by antisymmetric polynomials in (2), our desired equality (in N variables) becomes

$$\begin{aligned} a_{\mu +\delta (N)}\left( p_r\circ h_m(x_1,x_2,\dots ,x_{N})\right) =\sum _{\mu \subseteq \lambda \in {{\,\textrm{Par}\,}}(|\mu |+rm)}{{\,\textrm{sgn}\,}}_r(\lambda /\mu ) a_{\lambda +\delta (N)}. \end{aligned}$$

(4)

Using (3) and the definition of the plethysm $p_r\circ h_m$, we can expand the left-hand side as

$$\begin{aligned} \sum _{\begin{array}{c} w\in {{\,\textrm{Abc}\,}}_N(\mu ) \\ \beta \in {{\,\textrm{Com}\,}}_{N}(m) \end{array}}{{\,\textrm{sgn}\,}}(w){{\,\textrm{wt}\,}}(w)x^{r \beta }=\sum _{\begin{array}{c} w\in {{\,\textrm{Abc}\,}}_N(\mu ) \\ \beta \in {{\,\textrm{Com}\,}}_{N}(m) \end{array}}{{\,\textrm{sgn}\,}}(w,\beta ){{\,\textrm{wt}\,}}_r(w,\beta ), \end{aligned}$$

(5)

where the weight ${{\,\textrm{wt}\,}}_r(w,\beta )$ equals ${{\,\textrm{wt}\,}}(w)x^{r \beta }$ and the sign ${{\,\textrm{sgn}\,}}(w,\beta )$ is just ${{\,\textrm{sgn}\,}}(w)$.

Given a labelled abacus $w\in {{\,\textrm{Abc}\,}}_N(\mu )$ and a composition $\beta \in {{\,\textrm{Com}\,}}_{N}(m)$, we consider a process on w in which we read w from left, and every time we see bead B with $\beta _B\ge 1$, we attempt to r-move it, provided that we have not already r-moved it $\beta _B$-times.

In more detail, we use v and $\alpha$ to denote the current labelled abacus and composition, respectively, during the process. At the start, we set $v=w$ and $\alpha =\beta$. For $i=0,1,\dots$ we look at $B=v_i$. If it is zero, we move to the next i. Otherwise, we look at $\alpha _B$. If it is zero, we move to the next i. Otherwise, we check whether bead B is r-mobile. If it is not, we terminate the process and say that the pair $(w,\beta )$ is unsuccessful. If it is r-mobile, we update $\alpha$ by decreasing $\alpha _{B}$ by 1 and also update v by r-moving bead B. After the updates, if $\alpha$ is the zero sequence, we terminate the process and say that the pair $(w,\beta )$ is successful. Otherwise, we move to the next i, working, of course, with the updated v and $\alpha$ (thus, the next bead we attempt to r-move may be the same bead though it does not have to). See Fig. 3 for an example.

Fig. 3

For $N=6$, $r=5$, $m=3$ and $\mu =(5,3,3,2,2,1)$, the diagrams above the dashed line show all the values of $\alpha$ and v in the process with the initial labelled abacus $w=(0,4,0,2,5,0,1,6,0,0,3,0,0,\dots )$ and the initial composition $\beta =(0,2,0,0,1,0)$. The shapes of these labelled abaci are the partitions $\gamma ^{(i)}$ from Fig. 1. If we use the initial composition $\beta =(0,2,1,0,0,0)$ instead, we obtain the diagrams below the dashed line. Compared to the previous diagrams, the first two 5-moves are both with bead 2. If we change the initial composition once more, this time to $\beta =(0,2,0,1,0,0)$, the process terminates when we reach $i=1$ as bead 4 is not 5-mobile

The process always terminates as when we look at position i, the beads which are yet to be r-moved (that is beads C such that $\alpha _C\ge 1$) lie on positions greater or equal to i. We write I and J for the set of pairs $(w,\beta )$ which are unsuccessful and successful, respectively. For $(w,\beta )\in I$, write B for the label of the non-r-mobile bead which terminated the process and C for the label of the bead that bead B r-collided with. We define a labelled abacus $w'$ to be obtained from w by swapping beads B and C. We also define a sequence $\beta '$ of length N by

$$\begin{aligned} \beta '_j={\left\{ \begin{array}{ll} \beta _B-\frac{w^{-1}(C) - w^{-1}(B)}{r} &{} \textrm{if}\quad j=B,\\ \beta _C+\frac{w^{-1}(C) - w^{-1}(B)}{r} &{} \textrm{if}\quad j=C,\\ \beta _j &{} otherwise. \end{array}\right. } \end{aligned}$$

(6)

We then define $\epsilon (w,\beta )$ as $(w',\beta ')$. For $(w,\beta )\in J$, we define a labelled abacus $\psi (w,\beta )$, which is the labelled abacus v at the end of the process. See Fig. 4 for an example.

Fig. 4

Let w be the labelled abacus from Fig. 3. As observed, we have $(w,(0,2,0,0,1,0)), (w,(0,2,1,0,0,0))\in J$ and $(w,(0,2,0,1,0,0))\in I$. The diagrams above display the images of maps $\epsilon$ and $\psi$ applied to these three pairs

We claim that (4) follows once we establish the following two statements:

• (i) The map $\epsilon$ is a weight-preserving involution on I, which reverses the sign.

• (ii) The map $\psi$ is a weight-preserving bijection from J to $\bigcup _{\lambda }{{\,\textrm{Abc}\,}}_N(\lambda )$, where the union is taken over partitions $\lambda \in {{\,\textrm{Par}\,}}(|\mu |+rm)$ such that $\lambda /\mu$ is an r-decomposable skew partition. Moreover, for any $(w,\beta )\in J$ we have ${{\,\textrm{sgn}\,}}(\psi (w,\beta )) = {{\,\textrm{sgn}\,}}_r(\lambda /\mu ){{\,\textrm{sgn}\,}}(w,\beta )$, where $\lambda$ is the shape of $\psi (w,\beta )$.

We now prove this claim. We can split the final sum of (5), which equals the left-hand side of (4), as

$$\begin{aligned} \sum _{(w,\beta )\in I}{{\,\textrm{sgn}\,}}(w,\beta ){{\,\textrm{wt}\,}}_r(w,\beta ) + \sum _{(w,\beta )\in J}{{\,\textrm{sgn}\,}}(w,\beta ){{\,\textrm{wt}\,}}_r(w,\beta ). \end{aligned}$$

The first sum is zero from (i), whilst the second sum can be rewritten, using (ii), as

$$\begin{aligned}&\sum _{\begin{array}{c} \mu \subseteq \lambda \in {{\,\textrm{Par}\,}}(|\mu |+rm) \\ \lambda /\mu \text { is { r}-decomposable} \end{array}}{{\,\textrm{sgn}\,}}_r(\lambda /\mu )\sum _{w\in {{\,\textrm{Abc}\,}}_N(\lambda )}{{\,\textrm{sgn}\,}}(w){{\,\textrm{wt}\,}}(w)=\\ {}&\sum _{\mu \subseteq \lambda \in {{\,\textrm{Par}\,}}(|\mu |+rm)}{{\,\textrm{sgn}\,}}_r(\lambda /\mu )\sum _{w\in {{\,\textrm{Abc}\,}}_N(\lambda )}{{\,\textrm{sgn}\,}}(w){{\,\textrm{wt}\,}}(w), \end{aligned}$$

which is the right-hand side of (4) by (3), as required.

Thus, it remains to show (i) and (ii). For (i), let $(w,\beta )\in I$ and write $(w',\beta ')$ for $\epsilon (w,\beta )$. We keep the notations B and C for the labels of the beads such that the process terminated with non-r-mobile bead B which r-collided with bead C. Clearly, $w'$ lies in ${{\,\textrm{Abc}\,}}_N(\mu )$. We now check that $\beta$ lies in ${{\,\textrm{Com}\,}}_N(m)$. Since the beads only r-move, we have $r\mid w^{-1}(C)-w^{-1}(B)$; thus, $\beta '$ is an integral sequence. We also see that bead C has not r-moved during the process; hence, $w^{-1}(C) > w^{-1}(B)$ and we must have checked whether bead B is r-mobile at least $\left( \left( w^{-1}(C)-w^{-1}(B)\right) /r\right)$-times. The latter statement implies that $\beta _B\ge \left( w^{-1}(C)-w^{-1}(B)\right) /r$, and in turn the entries of $\beta '$ are non-negative. From (6), clearly, $\beta '$ and $\beta$ have the same sum of entries, and hence $\beta '\in {{\,\textrm{Com}\,}}_N(m)$.

By Lemma 2.3(i), we have ${{\,\textrm{sgn}\,}}(w')=-{{\,\textrm{sgn}\,}}(w)$. The equality of weights ${{\,\textrm{wt}\,}}_r(w,\beta )={{\,\textrm{wt}\,}}_r(w',\beta ')$ holds true as $w^{-1}(B)+r\beta _B=w^{-1}(C) + r(\beta _B -(w^{-1}(C)-w^{-1}(B))/r)$ and $w^{-1}(C)+r\beta _C=w^{-1}(B) + r(\beta _C +(w^{-1}(C)-w^{-1}(B))/r)$. Hence, it remains to verify that $(w',\beta ')$ lies in I and $\epsilon (w',\beta ')=(w,\beta )$.

The process with $(w',\beta ')$ coincides with the process with $(w,\beta )$ where r-moves of bead B are replaced with r-moves of bead C as long as $\beta '_C\ge (w'^{-1}(B)-w'^{-1}(C))/r$. This inequality holds true as the right-hand side is $(w^{-1}(C)-w^{-1}(B))/r$ which is at most $\beta '_C$ by (6). Hence, $(w',\beta ')\in I$ and the process ends with bead C r-colliding with bead B. Writing $(w'',\beta '')=\epsilon (w',\beta ')$, we see that $w''=w$ and since ${{\,\textrm{wt}\,}}_r(w,\beta )={{\,\textrm{wt}\,}}_r(w',\beta ')={{\,\textrm{wt}\,}}_r(w'',\beta )$, we immediately conclude that also $\beta ''=\beta$.

We now move to (ii). Clearly, during the process, the weight of $(v,\alpha )$ does not change. Hence, ${{\,\textrm{wt}\,}}_r(w,\beta )= {{\,\textrm{wt}\,}}_r(\psi (w,\beta ),(0,0,\dots ,0))={{\,\textrm{wt}\,}}(\psi (w,\beta ))$, that is $\psi$ preserves weights. The rest of the claim follows from Corollary 3.4. In more detail, the statement about sizes in the ‘moreover’ part of Corollary 3.4 together with implications (ii)$\implies$(i) and (i)$\implies$(iii) shows that the map $\psi$ takes values in the desired set and is surjective, respectively. The uniqueness statement in the ‘moreover’ part shows that $\psi$ is injective and the statement about signs in the ‘moreover’ part shows that ${{\,\textrm{sgn}\,}}(\psi (w,\beta )) = {{\,\textrm{sgn}\,}}_r(\lambda /\mu ){{\,\textrm{sgn}\,}}(w,\beta )$, where $\lambda ={{\,\textrm{sh}\,}}(\psi (w,\beta ))$. $\square$

Remark 3.5

If we let $r=1$, respectively, $m=1$ in the proof, we obtain the proof of Young’s rule, respectively, the Murnaghan–Nakayama rule from [7].