Some Infinite-Dimensional Representations of Certain Coxeter Groups

Abstract

A Coxeter group admits infinite-dimensional irreducible complex representations if and only if it is not finite or affine. In this paper, we provide a construction of some of those representations for certain Coxeter groups using some topological information of the corresponding Coxeter graphs.

1 Introduction

Let (W, S) be an irreducible Coxeter group of finite rank, i.e., its Coxeter graph is connected and $|S |< \infty$. If W is finite, then irreducible representations (over $\mathbb {C}$) of W are certainly finite dimensional. If W is an affine Weyl group, then it is also well known that its irreducible representations are of finite dimension (one may refer to [3, 4, proof of Prop. 5.13], [7, Prop. 1.2] for more details). In general, we have the following fact.

Theorem 1.1

All irreducible complex representations of W are of finite dimension if and only if W is a finite group or an affine Weyl group.

The author owes a proof of this theorem to an anonymous referee of a previous version of this paper (see the “Appendix”). Nevertheless, the proof only tells us the existence of infinite-dimensional irreducible representations of infinite non-affine Coxeter groups, but it fails to construct such representations.

The main aim of this paper is to construct some irreducible representations of infinite dimension of a Coxeter group (W, S) satisfying either of the following:

• (1) there are at least two circuits in the Coxeter graph;

• (2) there is at least one circuit in the Coxeter graph, and $m_{st} \ge 4$ for some $s,t \in S$ (for $s,t \in S$, we denote by $m_{st}$ the order of st).

The main idea is to glue together many copies of representations of different dihedral subgroups of W, so that they form a “big” representation of W. The way of gluing is encoded in some topological information of the Coxeter graph. This method is inspired by the author’s previous work [1].

The paper is organized as follows. Section 2 records some basic facts about representations of dihedral groups, as well as coverings and fundamental groups of graphs. Section 3 deals with case (1), in which the fundamental group of the Coxeter graph is a non-abelian free group. We utilize an infinite-dimensional irreducible representation of this free group to do the “gluing”. In Sect. 4, we use the universal covering of the Coxeter graph to achieve our goal for case (2). In Sect. 5, we give another example of infinite-dimensional irreducible representation of a specific Coxeter group whose Coxeter graph has no circuits. Finally, in the appendix, we present the proof of Theorem 1.1 which is given by an anonymous referee.

2 Preliminaries

In this section, we recollect some notations and terminology used in this paper. We use e to denote the identity in a group. Coxeter groups considered throughout this paper are all irreducible and of finite rank.

2.1 Representations of Dihedral Groups

For a finite dihedral group $D_m := \langle r,t \mid r^2 = t^2 = (rt)^m = e \rangle$, we denote by $\mathbb {1}$ and $\varepsilon ,$ respectively, the trivial and the sign representation, i.e., $\mathbb {1} : r,t \mapsto 1$, $\varepsilon : r,t \mapsto -1$. If m is even, there are two more representations of dimension 1, i.e.,

$$\begin{aligned} \varepsilon _r: r \mapsto -1, t \mapsto 1; \quad \quad \varepsilon _t: r \mapsto 1, t \mapsto -1. \end{aligned}$$

Let $\mathbb {C} \beta _r \oplus \mathbb {C} \beta _t$ be a vector space with formal basis $\{\beta _r, \beta _t\}$. For any integer k satisfying $1 \le k < m/2$, let $\rho _k$ denote the irreducible representation of $D_m$ on $\mathbb {C} \beta _r \oplus \mathbb {C} \beta _t$ defined by

$$\begin{aligned} r \cdot \beta _r&= - \beta _r,&r \cdot \beta _t&= \beta _t + 2\cos \frac{k\uppi }{m} \beta _r,\\ t\cdot \beta _t&= - \beta _t,&t \cdot \beta _r&= \beta _r + 2\cos \frac{k\uppi }{m} \beta _t. \end{aligned}$$

Intuitively, r and t act on the (real) plane by two reflections with respect to two lines with an angle of $\frac{k \uppi }{m}$; see Fig. 1.

Fig. 1

The representation $\rho _k: D_m \rightarrow {\text {GL}}(\mathbb {C} \beta _r \oplus \mathbb {C} \beta _t)$

Remark 2.1

If m is even and $k = m/2$, we may define $\rho _{m/2}$ as well by the same formulas, but then $\rho _{m/2} \simeq \varepsilon _r \oplus \varepsilon _t$ is reducible.

Remark 2.2

We have described the full set of irreducible representations of $D_m$, namely,

$$\begin{aligned} \{\mathbb {1}, \varepsilon \} \cup \{\rho _1, \dots , \rho _{\frac{m-1}{2}}\}, \quad \text {if } m \text { is odd}; \\ \{\mathbb {1}, \varepsilon , \varepsilon _r, \varepsilon _t\} \cup \{\rho _1, \dots , \rho _{\frac{m}{2}-1}\}, \quad \text {if } m \text { is even}. \end{aligned}$$

The following lemma will be frequently used in Sects. 3 and 4 to prove our “gluing” is feasible.

Lemma 2.3

The $+1$-eigenspaces of r and t in $\rho _k$ are both one dimensional. However, there is no nonzero vector that can be fixed by r and t simultaneously.

2.2 Graphs and the Universal Covering

The way we glue these representations will be encoded in some topological information of the Coxeter graph.

By definition, an (undirected) graph $G = (S,E)$ consists of a set S of vertices and a set E of edges, and elements in E are of the form $\{s,t\} \subseteq S$ (unordered). For our purpose, we only consider graphs without loops and multiple edges, i.e., there is no edge of the form $\{s,s\}$, and each edge $\{s,t\}$ occurs at most once in E. In a Coxeter graph, $m_{st}$ is regarded as a label on the edge rather than a multiplicity. We say G is a finite graph if S is a finite set.

A sequence $(s_1, s_2, \dots , s_n)$ of vertices is called a path in G if $\{s_i, s_{i+1}\} \in E, \forall i$. If $s_1 = s_n$, then we say such a path is a closed path. If further $s_1, \dots , s_{n-1}$ are distinct in this closed path, then the path is called a circuit.

If every two vertices can be connected by a path, then we say G is a connected graph. A connected graph without circuits is called a tree. For a connected graph $G = (S,E)$, if $T = (S, E_0)$ is a tree with the same vertices set S and $E_0 \subseteq E$, then T is called a spanning tree of G. This condition is equivalent to say $|E_0 |= |S |- 1$ when G is a connected finite graph. Any connected graph has a spanning tree, but not unique in general.

Let $G = (S, E)$ and $G^\prime = (S^\prime , E^\prime )$ be two graphs. If $p : S \rightarrow S'$ is a map of sets such that for any edge $\{s,t\}$ in G,  we have $p(s) \ne p(t)$ and $\{p(s), p(t)\}$ is also an edge in $G'$, then we say that p is a morphism of graphs. We simply denote a morphism by $p : G \rightarrow G'$.

For any $s \in S$, we denote

$$\begin{aligned} E_s := \{t \in S \mid \{s,t\} \in E\}. \end{aligned}$$

Suppose $G'$ is connected and finite, and suppose $p : G \rightarrow G'$ is a morphism. If $p(S) = S'$, and if for any $s \in S$ the restriction of p to $E_s$ gives rise to a bijection $E_s \xrightarrow {\sim } E'_{p(s)}$, then p is called a covering. It is natural to regard $G^\prime$ and G as locally finite simplicial complexes. Then p is also a covering of topological spaces.

Conversely, we view G as a topological space and suppose $p: X \rightarrow G$ is a covering of the topological space G. Then X has a graph structure such that p is a morphism of graphs (see [6, Theorem 83.4]). In particular, if p is the universal covering, then X is a tree. Thus for any connected finite graph, we can talk about its universal covering graph.

2.3 The Fundamental Group of a Graph

Let $G = (S, E)$ be a connected graph, and $T = (S, E_0)$ be a spanning tree. For any edge $\mathfrak {e} \in E \setminus E_0$, if we choose a vertex $s_\mathfrak {e}$ of $\mathfrak {e}$ to be its head and the other $t_\mathfrak {e}$ to be its tail, then $\mathfrak {e} = \{s_\mathfrak {e}, t_\mathfrak {e}\}$ and there is a unique circuit $c^\prime _\mathfrak {e}$ in $(S, E_0 \cup \{\mathfrak {e}\})$ of the form $c^\prime _\mathfrak {e} = (s_\mathfrak {e}, t_\mathfrak {e}, \dots , s_\mathfrak {e})$.

Fix a vertex $s_0 \in S$. For any $c^\prime _\mathfrak {e}$, there is a unique path in T without repetitive vertices from $s_0$ to $s_\mathfrak {e}$. We denote the path by $p_\mathfrak {e}$. Define $c_\mathfrak {e}$ to be the concatenation of $p_\mathfrak {e}, c^\prime _\mathfrak {e}, p_\mathfrak {e}^{-1}$, where $p_\mathfrak {e}^{-1}$ is the inverse path in the obvious sense. Then each $c_\mathfrak {e}$ is a closed path from $s_0$ to itself. If we view G as a topological space, then we have the following result on its fundamental group $\pi _1(G)$.

Lemma 2.4

[6, Theorem 84.7] $\pi _1(G)$ is a free group with a set of free generators $\{c_\mathfrak {e} \mid \mathfrak {e} \in E \setminus E_0\}$. In particular, if there is more than one circuit in G, then $\pi _1(G)$ is non-abelian.

Remark 2.5

Note that $p_\mathfrak {e}$ is a path in T. Thus, all edges in $c_\mathfrak {e}$ except $\mathfrak {e}$ lie in $E_0$, and $\mathfrak {e}$ appears in $c_\mathfrak {e}$ only once. If $\mathfrak {e}^\prime \in E\setminus E_0$ is another edge, then $\mathfrak {e}^\prime$ does not appear in $c_\mathfrak {e}$.

3 Representations via Fundamental Groups of Coxeter Graphs

From now on, suppose (W, S) is an irreducible Coxeter group of finite rank with Coxeter graph $G = (S,E)$. Then, G is a connected finite graph.

In this section, we assume that

$$\begin{aligned} \text {there are at least two circuits in}\; G. \end{aligned}$$

Thus, by Lemma 2.4, $\pi _1(G)$ is a non-abelian free group. In this section, we use an infinite-dimensional irreducible representation of $\pi _1(G)$ to construct another such representation for W.

For convenience, we may further assume

$$\begin{aligned} m_{st} < \infty , \quad \forall s,t \in S. \end{aligned}$$

This is not essential. If some $m_{st}$’s are infinity, then we replace them by any integer larger than 2 (e.g., 3), so that we obtain another Coxeter group $(W_1,S)$ and a surjective homomorphism $W \twoheadrightarrow W_1$, $s \mapsto s$. Ignoring labels on edges, the two Coxeter groups have the same Coxeter graph in a topological sense. An irreducible representation of $W_1$ becomes an irreducible representation of W via pulling back by the homomorphism.

3.1 The Construction

We fix $s_0 \in S$. Let $T = (S, E_0)$ be a spanning tree of $G = (S,E)$. Then we obtain a set of free generators of $\pi _1(G)$ by the method in Sect. 2.3, say $c_1, \dots , c_l$ ($l < \infty$ since G is a finite graph), with $s_0$ on each of them.

We have $|E \setminus E_0 |\ge 2$ since we assume that there is more than one circuit in G. We then fix two distinct edges:

$$\begin{aligned} \{s_1, t_1\}, \{s_2, t_2\} \in E \setminus E_0. \end{aligned}$$

We may assume that $\{s_1, t_1\}, \{s_2, t_2\}$ lie in $c_1, c_2,$ respectively, and $c_1$ goes through $t_1$ first and then $s_1$, and $c_2$ goes through $t_2$ first and then $s_2$. In our choice of $c_i$, the edge $\{s_1, t_1\}$ appears in $c_1$ only once, while it does not appear in other $c_i$’s (see Remark 2.5). Similar for $\{s_2, t_2\}$. The two edges might share a common vertex, like $s_1 = s_2$, but it does not matter.

We define a vector space V with formal basis $\{\alpha _{s,n} \mid n \in \mathbb {Z}, s \in S \}$,

$$\begin{aligned} V := \bigoplus _{n \in \mathbb {Z}, s \in S} \mathbb {C} \alpha _{s,n}. \end{aligned}$$

For any $s,t \in S$ and $n \in \mathbb {Z}$, we define $s \cdot \alpha _{t,n}$ as follows:

• (1) if $s = t$, then $s \cdot \alpha _{s,n} : = - \alpha _{s,n}$;

• (2) $s_1 \cdot \alpha _{t_1, n} := \alpha _{t_1, n} + 2 \cos \frac{\uppi }{m_{s_1t_1}} \alpha _{s_1, n+1}$, $t_1 \cdot \alpha _{s_1, n+1} := \alpha _{s_1, n+1} + 2 \cos \frac{\uppi }{m_{s_1t_1}} \alpha _{t_1,n}$; $s_2 \cdot \alpha _{t_2, n} := \alpha _{t_2, n} + 2^{n+1} \cos \frac{\uppi }{m_{s_2t_2}} \alpha _{s_2, n+1}$, $t_2 \cdot \alpha _{s_2, n+1} := \alpha _{s_2, n+1} + 2^{-n+1} \cos \frac{\uppi }{m_{s_2t_2}} \alpha _{t_2,n}$;

• (3) if the unordered pair $\{s,t\} \ne \{s_1, t_1\}$ or $\{s_2, t_2\}$, and if $s \ne t$, then $s \cdot \alpha _{t,n} := \alpha _{t,n} + 2 \cos \frac{\uppi }{m_{st}} \alpha _{s,n}$.

Looking at case (2), one can see that the vectors $\alpha _{t_2,n}$ and $2^n \alpha _{s_2, n+1}$ span an irreducible representation isomorphic to $\rho _1$ (see Sect. 2.1) of the dihedral subgroup $\langle s_2, t_2 \rangle$. The vectors $\alpha _{t_2,n}$ and $2^n \alpha _{s_2, n+1}$ play the same roles as the $\beta$’s in Sect. 2.1. Similarly, $\{\alpha _{t_1,n}, \alpha _{s_1,n+1}\}$ span an irreducible representation isomorphic to $\rho _1$ of $\langle s_1, t_1 \rangle$.

In case (3), if $m_{st} = 2$, then $s \cdot \alpha _{t,n} = \alpha _{t,n}$; if $m_{st} \ge 3$, then $\{\alpha _{t,n}, \alpha _{s,n}\}$ span an irreducible representation isomorphic to $\rho _1$ of $\langle s,t \rangle$.

Lemma 3.1

V is a representation of W with the action defined above.

Proof

Obviously, $s^2$ acts as the identity for any $s \in S$.

For $s,t \in S$ and $m_{st} = 2$, we need to show $st \cdot \alpha _{r,n} = ts \cdot \alpha _{r,n}$, $\forall r \in S$. Note that we have

$$\begin{aligned}s \cdot \alpha _{t, n} = \alpha _{t,n} \text { and } t \cdot \alpha _{s,n} = \alpha _{s,n} \text { for any } n \in \mathbb {Z},\end{aligned}$$

since $m_{st} = 2$. If $r = s$ or $r = t$, then clearly it holds $st \cdot \alpha _{r,n} = ts \cdot \alpha _{r,n}$. If $r \ne s$ and $r \ne t$, then

$$\begin{aligned}s \cdot \alpha _{r,n} = \alpha _{r,n} + c_1 \alpha _{s, n_1} \text { and } t \cdot \alpha _{r,n} = \alpha _{r,n} + c_2 \alpha _{t, n_2}\end{aligned}$$

for some $c_1, c_2 \in \mathbb {C}$ and $n_1, n_2 \in \{n, n \pm 1\}$, and then

$$\begin{aligned} st \cdot \alpha _{r,n}&= s \cdot (\alpha _{r,n} + c_2 \alpha _{t ,n_2}) = \alpha _{r,n} + c_1 \alpha _{s, n_1} + c_2 \alpha _{t ,n_2}, \\ ts \cdot \alpha _{r,n}&= t \cdot (\alpha _{r,n} + c_1 \alpha _{s, n_1}) = \alpha _{r,n} + c_2 \alpha _{t, n_2} + c_1 \alpha _{s, n_1}. \end{aligned}$$

Therefore, we have $st \cdot \alpha _{r,n} = ts \cdot \alpha _{r,n}$ as desired.

Now, assume $m_{st} \ge 3$. We need to verify that $(st)^{m_{st}} \cdot \alpha _{r,n} = \alpha _{r,n}$. This is also obvious if $r = s$ or $r = t,$ since we are in the dihedral world. If s, t, r are distinct, then we have the following cases.

• (1) If any two of s, t, r are not $\{s_1, t_1\}$ or $\{s_2, t_2\}$, then the three-dimensional subspace spanned by $\alpha _{r,n}$, $\alpha _{s,n}$, $\alpha _{t,n}$, denoted by U, stays invariant under the actions of s and t. We write $U_s := \{v \in U \mid s \cdot v = v\}$, $U_t := \{v \in U \mid t \cdot v = v\}$. Then $\dim U_s = \dim U_t = 2$, and thus there exists $0 \ne v_0 \in U$ such that $s \cdot v_0 = t \cdot v_0 = v_0$. Note that $3 \le m_{st} < \infty$ and $\mathbb {C} \alpha _{s,n} \oplus \mathbb {C} \alpha _{t,n}$ forms a representation isomorphic to $\rho _1$ of $\langle s,t \rangle$. Hence, $v_0 \notin \mathbb {C} \alpha _{s,n} \oplus \mathbb {C} \alpha _{t,n}$ by Lemma 2.3, and then $\{ v_0, \alpha _{s,n}, \alpha _{t,n}\}$ is a basis of U. Now, we can see that $(st)^{m_{st}} \cdot \alpha _{r,n} = \alpha _{r,n}$.

• (2) If $m_{rt} = 2$, then there exists $k \in \{n-1, n, n+1\}$ and $q \in \{k-1, k, k+1\}$ such that $\alpha _{r,n}, \alpha _{s,k}, \alpha _{t,q}$ span an s, t-invariant subspace. By the same arguments in case (1), we have $(st)^{m_{st}} \cdot \alpha _{r,n} = \alpha _{r,n}$. The case $m_{rs} = 2$ is similar. In the following cases, we assume s, t, r do not commute with each other.

• (3) If $s = s_1$, $t = t_1$, while $s_2, t_2$ do not occur simultaneously in s, r, t, then $\alpha _{s_1, n+1}$, $\alpha _{t_1,n}$, $\alpha _{r,n}$, $\alpha _{s_1, n}$, $\alpha _{t_1, n-1}$ span a five-dimensional s, t-invariant subspace U. Define $U_s$, $U_t$ as in case (1), then $\dim U_s = \dim U_t = 3$. The same argument shows that $(s_1t_1)^{m_{s_1t_1}} \cdot \alpha _{r,n} = \alpha _{r,n}$.

• (4) If $s = s_1$, $r = t_1$, while $s_2, t_2$ do not occur simultaneously in s, r, t, then $\alpha _{s_1,n}$, $\alpha _{t,n}$, $\alpha _{r,n}$, $\alpha _{s_1, n+1}$, $\alpha _{t, n+1}$ span an s, t-invariant subspace. The same argument works.

• (5) If $s = s_1$, $t = t_1 = t_2$, $r = s_2$, then $\alpha _{r,n}, \alpha _{s,n}, \alpha _{t, n-1}$ span an s, t-invariant subspace. The same argument works.

• (6) If $s = s_1$, $t = t_1 = s_2$, $r = t_2$, then $\alpha _{t_1, n-1}$, $\alpha _{s_1,n}$, $\alpha _{r,n}$, $\alpha _{s_2, n+1}$, $\alpha _{s_1, n+2}$ span an s, t-invariant subspace. The same argument works.

• (7) If $s = s_1$, $t = s_2$, $r = t_1 = t_2$, then $\alpha _{s_1, n+1}$, $\alpha _{r,n}$, $\alpha _{s_2, n+1}$ span an s, t-invariant subspace. The same argument works.

• (8) If $s = s_1$, $t = t_2$, $r = t_1 = s_2$, then $\alpha _{t_2,n+1}$, $\alpha _{s_1, n+1}$, $\alpha _{r,n}$, $\alpha _{t_2, n-1}$, $\alpha _{s_1, n-1}$ span an s, t-invariant subspace. The same argument works. In the above cases, if we exchange the letters s, t or the indices 1, 2, then the arguments are totally the same. Thus, we always have $(st)^{m_{st}} \cdot \alpha _{r,n} = \alpha _{r,n}$.

$\square$

3.2 The Infinite-Dimensional Irreducible Quotient

Theorem 3.2

Recall that (W, S) is irreducible, and that there are at least two circuits in its Coxeter graph G. Let V be defined as in Sect. 3.1, and

$$\begin{aligned} V_0 := \{v \in V \mid s \cdot v = v, \forall s \in S\}. \end{aligned}$$

Then the representation $V / V_0$ of W is irreducible of infinite dimension.

Proof

We denote $V_-^s := \{v \in V \mid s \cdot v = -v\}$. Then $V_-^s = \bigoplus _n \mathbb {C} \alpha _{s,n}$. For any edge $\{s,t\}$ in G, $V_-^s \oplus V_-^t$ is a subrepresentation of $\langle s,t \rangle$ in V, isomorphic to an infinite direct sum of $\rho _1$. For any $v \in V_-^s$, let $f_{st}(v) := (t \cdot v - v) / 2 \cos \frac{\uppi }{m_{st}}$. Then $f_{st}(v) \in V_-^t$, and the linear map $f_{st}: V_-^s \rightarrow V_-^t$ is a linear isomorphism of vector spaces. For example, when $\{s,t\} \ne \{s_1,t_1\}$ or $\{s_2,t_2\}$, we have $f_{st}(\alpha _{s,n}) = \alpha _{t,n}$. Moreover, $f_{st}(v)$ lies in the subrepresentation generated by v.

Let $0 \ne v \in V$, and let U be the subrepresentation generated by v. If $v \notin V_0$, say, $t \cdot v \ne v$, then $t \cdot v - v \in V_-^t \cap U$. Suppose $(r_0 = t, r_1, \dots , r_k = s_0)$ is a path connecting t and $s_0$. Here, $s_0$ is the vertex fixed in Sect. 3.1. Then,

$$\begin{aligned} v_0 : = f_{r_{k-1}r_k} \cdots f_{r_1r_2} f_{r_0 r_1} (t \cdot v - v) \in V_-^{s_0} \cap U \text { and } v_0 \ne 0. \end{aligned}$$

Apply the maps $f_{**}$ along the closed paths $c_1, \dots , c_l$ chosen in Sect. 3.1. Then we obtain l linear isomorphisms of $V_-^{s_0}$, denoted by $X_1, \dots , X_l,$ respectively. This makes $V_-^{s_0}$ form a representation of the free group $\pi _1(G)$. Except $X_1$ and $X_2$, other $X_i$s are identity maps of $V_-^{s_0}$, and we have

$$\begin{aligned} X_1 (\alpha _{s_0, n}) = \alpha _{s_0, n+1}, \quad X_2 (\alpha _{s_0, n}) = 2^n \alpha _{s_0, n+1}. \end{aligned}$$

It is easy to verify that $V_-^{s_0}$ is an irreducible representation of $\pi _1(G)$. Notice that $0 \ne v_0 \in V_-^{s_0} \cap U$, $X_i^{\pm 1} (v_0) \in U$. Thus, $V_-^{s_0} \subseteq U$. Since G is connected, $V_-^{s_0}$ generates the whole representation V. Hence, $V = U$. We have proved that $V / V_0$ is an irreducible representation of W.

Note that $s_0$ acts on $V_-^{s_0}$ by $-1$. So $V_-^{s_0} \cap V_0 = 0$, and thus $\dim V/V_0 = \infty$. $\square$

4 Representations via Universal Coverings of Coxeter Graphs

In this section we assume that

$$\begin{aligned} \text {the Coxeter graph}\,\,G = (S,E)\,\,\text {is not a tree,} \\ \text {and there exist}\,\,s_1, s_2 \in S\,\,\text {such that }m_{s_1s_2} \ge 4. \end{aligned}$$

In this section, we use the universal covering of G to construct an infinite-dimensional representation of W, then find an irreducible (sub)quotient in it.

For the same reason stated before Sect. 3.1, we may further assume

$$\begin{aligned} m_{st} < \infty , \quad \forall s,t \in S. \end{aligned}$$

4.1 The Construction

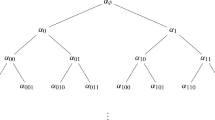
We fix $s_1, s_2 \in S$ such that $m_{s_1s_2} \ge 4$. Let $p: G^\prime \rightarrow G$ be the universal covering of G, where $G^\prime = (S^\prime , E^\prime )$. Fix an edge $\{s_1^\prime , s_2^\prime \}$ in $G^\prime$ such that $p(s_1^\prime ) = s_1$, $p(s_2^\prime ) = s_2$, as shown in Fig. 2.

Fig. 2

The edge $\{s_1^\prime , s_2^\prime \}$

We define a vector space V with formal basis $\{\alpha _a \mid a\in S^\prime \}$,

$$\begin{aligned} V := \bigoplus _{a \in S^\prime } \mathbb {C} \alpha _a. \end{aligned}$$

For any $s \in S$ and $a \in S'$, we define $s \cdot \alpha _a$ as follows:

• (1) if $s = p(a)$, then $s \cdot \alpha _a : = - \alpha _a$;

• (2) if $s = s_1$, $a = s_2^\prime$, then $s_1 \cdot \alpha _{s_2^\prime } : = \alpha _{s_2^\prime } + 2 \cos \frac{2 \uppi }{m_{s_1s_2}} \alpha _{s_1^\prime }$;

• (3) if $s = s_2$, $a = s_1^\prime$, then $s_2 \cdot \alpha _{s_1^\prime } : = \alpha _{s_1^\prime } + 2 \cos \frac{2 \uppi }{m_{s_1s_2}} \alpha _{s_2^\prime }$;

• (4) if it is not in the cases above, and if s is not adjacent to p(a) in G, then $s \cdot \alpha _a := \alpha _a$;

• (5) if it is not in the cases above, and if s is adjacent to p(a) in G, then we denote by b the vertex adjacent to a in $p^{-1} (s)$ (see Fig. 3), and $s \cdot \alpha _a := \alpha _a + 2 \cos \frac{\uppi }{m} \alpha _b$, where $m := m_{s,p(a)} \ge 3$.

Fig. 3

The vertex b in $p^{-1}(s)$ adjacent to a

In particular, $\mathbb {C} \alpha _{s_1^\prime } \oplus \mathbb {C} \alpha _{s_2^\prime }$ forms a representation of the dihedral subgroup $\langle s_1,s_2 \rangle$, isomorphic to $\rho _2$ (note that if $m_{s_1s_2} = 4$, then this representation splits, see Remark 2.1). While for other pairs of adjacent vertices $\{a,b\}$ in $G^\prime$, $\mathbb {C} \alpha _a \oplus \mathbb {C} \alpha _b$ forms an irreducible representation of $\langle p(a), p(b) \rangle$ isomorphic to $\rho _1$.

Lemma 4.1

V is a representation of W with the action defined above.

Proof

From the construction, it is clear that $s^2$ acts by identity for any $s \in S$. Suppose $s,t \in S$ and $s\ne t$. We need to verify that $(st)^{m_{st}} \cdot \alpha _a = \alpha _a$ for any $a \in S^\prime$. If $p(a) = s$ or t, then $\alpha _a$ lies in a subrepresentation of $\langle s,t \rangle$. Thus, we have $(st)^{m_{st}} \cdot \alpha _a = \alpha _a$. If $p(a) \ne s$ and $p(a) \ne t$, then the relationship of the three vertices p(a), s, t in G is in one of the following cases (ignoring labels like $m_{st}$ on edges),

(In cases (iii) and (v), exchanging letters s and t does not cause an essential difference. So we omit them.) In cases (i) (iii) (iv), we may verify directly by definition that $st \cdot \alpha _a = ts \cdot \alpha _a$. In case (ii), it is also clear that $(st)^{m_{st}} \cdot \alpha _a = \alpha _a$.

Suppose we are in case (v). We denote by $s^\prime$ the vertex adjacent to a in $p^{-1}(s)$, and by $t^\prime$ the vertex adjacent to $s^\prime$ in $p^{-1}(t)$. Then a is not adjacent to $t^\prime$, as shown in Fig. 4. The three-dimensional subspace spanned by $\alpha _a, \alpha _{s^\prime }, \alpha _{t^\prime }$ stays invariant under the action of s and t. By the same arguments as in the proof of Lemma 3.1, it holds that $(st)^{m_{st}} \cdot \alpha _a = \alpha _a$.

Fig. 4

The vertices $s^\prime$ and $t^\prime$

Fig. 5

The vertices $s^\prime , t^\prime , s^{\prime \prime }$ and $t^{\prime \prime }$

Suppose we are in case (vi). We denote by $s^\prime$ the vertex adjacent to a in $p^{-1}(s)$, by $t^\prime$ the vertex adjacent to $s^\prime$ in $p^{-1}(t)$, by $t^{\prime \prime }$ the vertex adjacent to a in $p^{-1}(t)$, and by $s^{\prime \prime }$ the vertex adjacent to $t^{\prime \prime }$ in $p^{-1}(s)$ (see Fig. 5). Then $a, t^\prime , s^{\prime \prime }$ are not adjacent to each other. Then $\alpha _a, \alpha _{s^\prime }, \alpha _{s^{\prime \prime }}, \alpha _{t^\prime }, \alpha _{t^{\prime \prime }}$ span an s, t-invariant subspace of dimension 5. The same arguments as in the proof of Lemma 3.1 yield $(st)^{m_{st}} \cdot \alpha _a = \alpha _a$. $\square$

4.2 The Infinite-Dimensional Irreducible (Sub)quotient

Let a and b be two arbitrary vertices in $G^\prime$. Since $G^\prime$ is a tree, there is a unique path $(a = t_0, t_1, \dots , t_n = b)$ connecting a, b such that all $t_i$s are distinct. We define ${\text {d}}(a,b) := n$ to be the distance between a and b. We define also

$$\begin{aligned} S_1^\prime := \{a \in S^\prime \mid {\text {d}}(a, s_1^\prime )< {\text {d}}(a, s_2^\prime )\}, \quad S_2^\prime := \{a \in S^\prime \mid {\text {d}}(a, s_2^\prime ) < {\text {d}}(a, s_1^\prime )\}. \end{aligned}$$

Then one of them is an infinite set. Without loss of generality, we assume $|S_1^\prime |= \infty$. Let

$$\begin{aligned} V_1 := \bigoplus _{a\in S_1^\prime } \mathbb {C} \alpha _a, \quad V_0 := \{v \in V \mid s \cdot v = v, \forall s \in S\}. \end{aligned}$$

Then $\dim V_1 = \infty$. If $m_{s_1s_2} = 4$, then $V_1$ is a subrepresentation of W in V.

Lemma 4.2

• (1) If $m_{s_1s_2} > 4$ and $v \in V \setminus V_0$, then V is generated by v as a representation of W.

• (2) If $m_{s_1s_2} = 4$ and $v_1 \in V_1 \setminus V_0$, then $V_1$ is generated by $v_1$ as a representation of W.

Proof

(1). Suppose $s \cdot v \ne v$, $s \in S$. Then by definition we know that $v - s\cdot v$ is a finite sum of the form $\sum _{a \in p^{-1}(s)} x_a \alpha _a$, where each $x_a$ is a complex number. Let $u_0 := v - s \cdot v$, and U be the subrepresentation generated by v. Then $u_0 \in U$. We take $a_0 \in p^{-1} (s)$ such that $x_{a_0} \ne 0$. Suppose the shortest path in $G^\prime$ connecting $a_0$ and $s_1^\prime$ is

$$\begin{aligned} (a_0, a_1, \dots , a_n = s_1^\prime ). \end{aligned}$$

Let $t_i := p(a_i) \in S$, $u_i := u_{i-1} - t_{i} \cdot u_{i-1}$. Inductively, we can see that $u_i$ is of the form $\sum _{b \in p^{-1}(t_i)} x_{i,b} \alpha _b$, where $x_{i,b} \in \mathbb {C}$. Since p is a covering map, there is only one vertex (namely, $a_{i-1}$) in $p^{-1}(t_{i-1})$ adjacent to $a_i$. Thus in the expression of $u_i,$ the coefficient $x_{i,a_i}$ of $\alpha _{a_i}$ is nonzero. In particular, taking $i = n$, we know that $u_n \in U$ and the coefficient of $\alpha _{s_1^\prime }$ is nonzero.

We view V as a representation of the finite dihedral group $D := \langle s_1, s_2 \rangle$. Since the group algebra $\mathbb {C}[D]$ is semisimple, V decomposes into a direct sum of some copies of irreducible representations of D. From the construction of V, the only irreducible representations of D which are possible to occur in V are $\mathbb {1}, \rho _1, \rho _2$. Moreover, $\rho _2$ appears only once, namely, $\mathbb {C} \alpha _{s_1^\prime } \oplus \mathbb {C} \alpha _{s_2^\prime }$. Therefore, there is an element $d \in \mathbb {C}[D]$ such that $d \cdot u_n = \alpha _{s_1^\prime }$, and hence $\alpha _{s_1^\prime } \in U$. Note that $G^\prime$ is a connected graph. From the definition of V, we know that $\alpha _{s_1^\prime }$ generates the whole V. Thus, $U = V$.

(2). The proof is similar. As above, we take a vertex $a_0 \in p^{-1}(s) \cap S_1^\prime$ such that $\alpha _{a_0}$ has nonzero coefficient in the linear expression of $v_1 - s \cdot v_1$ ($\ne 0$), and do the same discussion along the shortest path connecting $a_0$ and $s_1^\prime$ (note that all of the vertices in this path belong to $S_1^\prime$). Then we know that in the subrepresentation generated by $v_1,$ there is a vector $u_n$ with nonzero coefficient of $\alpha _{s_1^\prime }$.

Decompose $V_1$ into a direct sum of irreducible representations of $D = \langle s_1, s_2 \rangle$. Then only $\mathbb {1}, \rho _1, \varepsilon _{s_1}$ occur. Moreover, the subrepresentation $\varepsilon _{s_1}$, spanned by $\alpha _{s_1^\prime }$, is of multiplicity one. Thus, $\alpha _{s_1^\prime }$ lies in the subrepresentation generated by $v_1$, while $\alpha _{s_1^\prime }$ generates the whole representation $V_1$. $\square$

Let

$$\begin{aligned} \overline{V} := V / V_0, \quad \overline{V_1} := V_1 / (V_1 \cap V_0). \end{aligned}$$

(V is defined in Sect. 4.1, while $V_1$ and $V_0$ are defined in Sect. 4.2.)

Theorem 4.3

Recall that $m_{s_1s_2} \ge 4$ and there is a circuit in the Coxeter graph. If $m_{s_1s_2} > 4$, then $\overline{V}$ is an irreducible representation of W. If $m_{s_1s_2} = 4$, then $\overline{V_1}$ is an irreducible representation of W. Moreover, $\overline{V}$ and $\overline{V_1}$ are both infinite dimensional.

Proof

From Lemma 4.2, we already know that the representations mentioned in this theorem are irreducible. Thus, it suffices to show they are both infinite dimensional. Obviously, $\dim \overline{V} \ge \dim \overline{V_1}$. Thus, we only need to show $\dim \overline{V_1} = \infty$. Let $s \in S$ be arbitrary. Then, $p^{-1} (s) \cap S_1^\prime$ is an infinite set. Let

$$\begin{aligned} U := \bigoplus _{a \in p^{-1} (s) \cap S_1^\prime } \mathbb {C} \alpha _a. \end{aligned}$$

Then $U \subseteq V_1$, and $\dim U = \infty$. For any $0 \ne v \in U$, we have $s \cdot v = -v$. Thus, $U \cap V_0 = 0$, and $\overline{V_1} = V_1 / (V_1 \cap V_0)$ is infinite dimensional. $\square$

Remark 4.4

In the theorem, it is necessary to take the quotient by $V_0$ ($V_0$ might be nonzero). For example, consider the universal covering in Fig. 6, where $p(s_i^\prime ) = p(s_i^{\prime \prime }) = s_i$, $p(t_i^\prime ) = t_i$, $p(r_i^\prime ) = r_i$, $\forall i$, and all edges in the Coxeter graph are labelled by 3 (hence omitted) except the triangle $s_0s_1s_2$. In this situation, the vector

$$\alpha _{t_1^\prime } + \alpha _{t_2^\prime } + \alpha _{t_3^\prime } + \alpha _{t_4^\prime } + 2 \alpha _{t_0^\prime } - 2 \alpha _{r_0^\prime } - \alpha _{r_1^\prime } - \alpha _{r_2^\prime } - \alpha _{r_3^\prime } - \alpha _{r_4^\prime } $$

is fixed by every $s_i$, $r_i$ and $t_i$. Besides, under the setting of Sect. 3 it is also necessary to take the quotient by $V_0$ in Theorem 3.2 (an example can be given in a similar way).

Fig. 6

A universal covering

5 Another Example

In this section, we construct an infinite-dimensional irreducible representation of a specific Coxeter group whose Coxeter graph is a tree. Suppose the Coxeter graph G of (W, S) is

This Coxeter group is isomorphic to ${\text {PGL}}(2,\mathbb {Z})$ (see [2, §5.1]).

Recall that the dihedral subgroup $\langle s_1, s_2 \rangle$ has an irreducible representation $\rho _1$ on $\mathbb {C} \beta _{s_1} \oplus \mathbb {C} \beta _{s_2}$ (see Sect. 2.1). There is a basis $\{u,v\}$ of this space such that u, v are eigenvectors of $s_1$ with eigenvalues $+1, -1,$ respectively. The vectors u, v can be chosen so that $s_2 \cdot u = (3v-u)/2$, $s_2 \cdot v = (u+v)/2$, as illustrated in Fig. 7.

Fig. 7

The basis vectors u, v of the representation $\rho _1$

Let

$$\begin{aligned} V := \mathbb {C} u_0 \oplus \bigoplus _{i \in \mathbb {N}_{>0}} (\mathbb {C} u_i \oplus \mathbb {C} v_i) \end{aligned}$$

be the vector space with basis $\{u_i, v_j \mid i \in \mathbb {N}, j \in \mathbb {N}_{>0}\}$, and let $s_1, s_2$ act on V by

$$\begin{aligned}&\quad s_1 \cdot u_0 = s_2 \cdot u_0 = u_0, \\ s_1 \cdot u_i =&u_i, \quad s_1 \cdot v_i = -v_i, \quad \forall i\in \mathbb {N}_{>0}, \\ s_2 \cdot u_i =&\frac{3v_i-u_i}{2}, \quad s_2 \cdot v_i = \frac{u_i+v_i}{2}, \quad \forall i \in \mathbb {N}_{>0}. \end{aligned}$$

Then as a representation of $\langle s_1, s_2 \rangle$, V is a direct sum of a trivial representation $\mathbb {1}$ and infinite many copies of $\rho _1$.

To make V be a representation of W, we only need to find an involution on V commuting with $s_1$, and let $s_3$ act by this involution. Let

$$\begin{aligned} s_3 \cdot u_{2k}&= u_{2k+1}, \quad s_3 \cdot u_{2k+1} = u_{2k}, \quad \forall k \in \mathbb {N}, \\ s_3 \cdot v_{2k}&= v_{2k-1}, \quad s_3 \cdot v_{2k-1} = v_{2k}, \quad \forall k \in \mathbb {N}_{>0}. \end{aligned}$$

Intuitively, $s_3$ permutes these basis vectors:

Obviously, the action of $s_3$ is an involution and commutes with the action of $s_1$. Thus, V forms a representation of W.

Similar to the proof of Lemma 4.2, $u_0$ lies in any nonzero subrepresentation of V. Note that $u_0$ generates the whole V. So V is an irreducible representation of W.

Remark 5.1

Similar constructions also give irreducible representations of infinite dimension when $m_{s_1s_2} = 3$ is replaced by larger integers.

Appendix: A Sketched Proof of Theorem 1.1

This proof is given by an anonymous referee of a previous version of this paper. The proof uses the following fact.

Lemma 6.1

[5, Corollary 2] Suppose (W, S) is an infinite non-affine irreducible Coxeter group of finite rank. Then there exists a subgroup $Y^\prime \subseteq W$ of finite index and a surjective homomorphism $\varphi ^\prime : Y^\prime \twoheadrightarrow F^\prime$, where $F^\prime$ is a non-abelian free group.

Now we can prove Theorem 1.1, and we only need to prove the “only if” part.

Suppose (W, S) is infinite and non-affine. Let $Y^\prime$, $\varphi ^\prime$, $F^\prime$ be as in Lemma 6.1. Let Y be the intersection of all conjugates of $Y^\prime$ in W. Then Y is a normal subgroup of W of finite index. Since Y is of finite index in $Y^\prime$, the image $\varphi ^\prime (Y)$ is a subgroup of $F^\prime$ of finite index. Therefore, $\varphi ^\prime (Y)$ is also a non-abelian free group (see, for example, [6, Theorem 85.1]). Let $X_1, X_2$ be two free generators of $\varphi ^\prime (Y)$, and let $F = \langle X_1, X_2 \rangle$. Then F is a free group of rank two, and we have a surjection $\varphi ^\prime (Y) \twoheadrightarrow F$. By composing this surjection with the map $\varphi ^\prime |_Y$, we obtain a surjective homomorphism $\varphi : Y \twoheadrightarrow F$.

Let V be an infinite-dimensional irreducible representation of F (for example, $V := \bigoplus _{n \in \mathbb {Z}} \mathbb {C} \alpha _{n}$, and let $X_1 \cdot \alpha _n = \alpha _{n+1}$, $X_2 \cdot \alpha _n = 2^n \alpha _{n+1}$, as in the proof of Theorem 3.2). By pulling back this F-representation along $\varphi$, V becomes an irreducible representation of Y.

We consider the induced representation $V_Y^W: = \mathbb {C}[W] \otimes _{\mathbb {C}[Y]} V$ of W, and we choose $w_1, \dots , w_n$ as coset representatives for Y in W. Then $V_Y^W = \bigoplus _{1 \le i \le n} w_i \otimes V$ as a vector space. Since Y is a normal subgroup of W, each summand $w_i \otimes V$ is an irreducible representation of Y. Thus, $V_Y^W$ is a semisimple Noetherian and Artinian $\mathbb {C}[Y]$-module, and hence a Noetherian and Artinian $\mathbb {C}[W]$-module. Consequently, there exists an irreducible W-representation $M \subseteq V_Y^W$ as a subrepresentation.

If we view M as a $\mathbb {C}[Y]$-module, then, by semi-simplicity of the $\mathbb {C}[Y]$-module $V_Y^W$ and Schur’s lemma, M is isomorphic to a direct sum of some $\mathbb {C}[Y]$-modules $w_i \otimes V$. In particular, M is infinite dimensional. Theorem 1.1 is proved.