Edge Metric Dimension of Some Generalized Petersen Graphs

Abstract

The edge metric dimension problem was recently introduced, which initiated the study of its mathematical properties. The theoretical properties of the edge metric representations and the edge metric dimension of generalized Petersen graphs GP(n, k) are studied in this paper. We prove the exact formulae for GP(n, 1) and GP(n, 2), while for other values of k a lower bound is stated.

1 Introduction

The concept of the metric dimension of graph G was introduced independently by Slater [1] and Harary and Melter [2]. This concept is based on the notion of a resolving set R of vertices, which has the property that each vertex is uniquely identified by its metric representation with respect to R. The minimal cardinality of resolving sets is called the metric dimension of the graph G.

1.1 Literature Review

Kelenc et al. [3] recently introduced a similar concept of edge metric dimension and initiated the study of its mathematical properties. They made a comparison between the edge metric dimension and the standard metric dimension of graphs while presenting realization results concerning the edge metric dimension and the standard metric dimension of graphs. They also proved that the edge metric dimension problem is NP-hard and provided approximation results. Additionally, for several classes of graphs, exact values for the edge metric dimension were presented, while several others were given upper and lower bounds. In [4] and [5], the authors presented results of the mixed metric dimension alongside the edge metric dimension for some classes of graphs. Additionally, Peterin and Yero [6], provided exact formulas for join, lexicographic and corona products of graphs.

Zubrilina [7], firstly proposed the classification of graphs of n vertices for which the edge metric dimension is equal to its upper bound $n-1$. The second result states that the ratio between the edge metric dimension and the metric dimension of an arbitrary graph is not bounded from above. The third result characterizes the change of the edge dimension of an arbitrary graph upon taking a Cartesian product with a path, and changes of the edge dimension upon adding a vertex adjacent to all the original vertices. The edge metric dimension of the Erdös-Rényi random graph G(n, p) is given by Zubrilina [8] and it is equal to $(1 + o(1)) \cdot \frac{4 log(n)}{log (1/q)}$, where $q=1-2p(1-p)^2(2-p)$.

Independently, Epstein et al. [9], introduced another edge metric dimension definition related to the line graphs, where a line graph of a graph G(V, E) is defined as: $L(G)=(E,F)$ where $F=\{e_{i}e_{j} | e_i, e_j \in E, e_i \; \text {is incident with} \; e_j \}$. Their edge metric dimension of a graph G is defined as the metric dimension of L(G), which is called edge variant of metric dimension by some authors, e.g. Liu et al. [10].

1.2 Generalized Petersen Graphs

Generalized Petersen graphs were first studied by Coxeter [11]. Each such graph, denoted as GP(n, k), is defined for $n \ge 3$ and $1 \le k < n/2$. It has 2n vertices and 3n edges, with vertex set V(GP(n, k)) = {$u_i, v_i \;|\; 0 \le i \le n-1\}$ and edge set E(GP(n, k)) = {$u_iu_{i+1},\;u_iv_i, \;v_iv_{i+k}\;|\;0 \le i \le n-1$}. It should be noted that vertex indices are taken modulo n.

Example

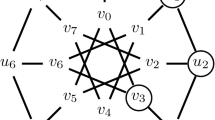
Consider the Petersen graph, numbered GP(5, 2), shown in Fig. 1. It is easily calculated by using the total enumeration technique, that its edge metric dimension is equal to 4 (it is also presented in Table 6). Figure 2 shows GP(6, 1) where the edge metric dimension equals 3. This can also be concluded by Theorem 2.4.

Fig. 1

Petersen graph GP(5,2)—edge metric base is colored red (color figure online)

Fig. 2

Graph GP(6,1)—edge metric base is colored red (color figure online)

The metric dimension of generalized Petersen graphs GP(n, k) is studied for different values of k:

• Case $k=1$ is concluded in [12];

• Case $k=2$ is proven in [13];

• Case $k=3$ in [14].

Various other properties of generalized Petersen graphs have recently been theoretically investigated in the following areas: Hamiltonian property [15], the cop number [16], the total coloring [17], etc.

1.3 Definitions and Previous Work

Given a simple connected undirected graph $G = (V,E)$, by d(u, v) we denote the distance between two vertices $u,v \in V$, i.e. the length of a shortest $u-v$ path. A vertex x of the graph G is said to resolve two vertices u and v of G if $d(x,u) \ne d(x,v)$. An ordered vertex set R = {$x_1, x_2, ..., x_k$} of G is a resolving set of G if every two distinct vertices of G are resolved by some vertex of R. A metric basis of G is a resolving set of minimum cardinality. The metric dimension of G, denoted by $\beta (G)$, is the cardinality of its metric basis.

Similarly, for a given connected graph G, a vertex $w \in V$, and an edge $uv \in E$, the distance between the vertex w and the edge uv is defined as $d(w,uv) = \min \{d(w, u), d(w, v)\}$. A vertex $w \in V$ resolves two edges $e_1$ and $e_2$ ($e_1,e_2 \in E$), if $d(w, e1) \ne d(w, e2)$. A set S of vertices in a connected graph G is an edge metric generator for G if every two edges of G are resolved by some vertex of S. The smallest cardinality of an edge metric generator of G is called the edge metric dimension and is denoted by $\beta _E(G)$. An edge metric basis for G is the edge metric generator of G with cardinality $\beta _E(G)$. Given an edge $e \in E$ and an ordered vertex set S = {$x_1, x_2, ..., x_k$}, the k-touple r(e, S) = ($d(e,x_1), d(e,x_2), ..., d(e,x_k)$) is called the edge metric representation of e with respect to S.

Example

Consider the generalized Petersen graph GP(6, 1) given in Fig. 2. The set $S_1=\{u_0, u_1, u_3\}$ is an edge metric generator for G since the vectors of metric coordinates for edges of G with respect to $S_1$ are mutually different. This can be seen in Table 1.

From Corollary 2.3, it holds that for GP(6, 1), as for any other generalized Petersen graph, the cardinality of an edge metric generator must be at least 3, so $S_1$ is an edge metric basis for GP(6, 1). This implies that its edge metric dimension is equal to 3, i.e. $\beta _E(GP(6,1)) = 3$.

Table 1 Edge metric representations for GP(6, 1) with respect to $S_1$

Two edges are incident, if both contain one common endpoint. For a given vertex $v \in V$, its degree $deg_v$ is equal to the number of its neighbors, i.e. the number of edges in which it is the endpoint. The maximum and minimum degrees over all vertices of graph G are denoted as $\Delta (G)$ and $\delta (G)$, respectively. Formally, $\Delta (G) = \max \nolimits _{v \in V} \,{\deg _v}$ and $\delta (G) = \min \nolimits _{v \in V} \,{\deg _v}$.

In the following text, we briefly show three propositions from [3] that are relevant for our work. The first proposition is related to paths and cycles and classification of graphs having the edge metric dimension equal to 1. The last two give bounds of the edge metric dimension based on the degree of vertices.

Proposition 1.1

[3]. For $n \ge 2$ it holds $\beta _E(P_n) = \beta (P_n) = 1$, $\beta _E(C_n) = \beta (C_n) = 2$, $\beta _E(K_n) = \beta (K_n) = n-1$. Moreover, $\beta _E(G)=1$ if and only if G is a path $P_n$.

Proposition 1.2

[3]. Let G be a connected graph and let $\Delta (G)$ be the maximum degree of G. Then $\beta _E(G) \ge log_2 \Delta (G)$

Proposition 1.3

[3]. Let G be a connected graph and let S be an edge metric basis with $|S| = k$. Then S does not contain a vertex with the degree greater than $2^{k-1}$.

From each of these propositions, given in [3], the next two corollaries follow:

Corollary 1.4

The edge metric dimension of any 3-regular graph is at least 2.

Corollary 1.5

$\beta _E(GP(n,k)) \ge 2$.

As previously mentioned, Epstein et al. [9] introduced another edge metric dimension definition based on line graphs. In order to avoid any misunderstanding, $\beta _E'(G)$ will denote this second definition of the edge metric dimension of graph G, also called the edge version of metric dimension [10], i.e. $\beta _E'(G)=\beta (L(G))$. Based on this definition, in [18], the authors obtained the results for n-sunlet graphs and prism graphs.

Difference between these definitions can be demonstrated with the following example. Let $G_1=(V_1,E_1)$ be the graph with $V_1=\{v_0, v_1, v_2, v_3\}$ and $E_1=\{e_0, e_1, e_2, e_3, e_4\}$ such that $e_0=v_0v_1, \; e_1=v_1v_2, \; e_2=v_0v_2, \; e_3=v_1v_3, \; e_4=v_2v_3$. Line graph of $G_1$ is $L(G_1)=(E_1, F_1)$ where $F_1=\{e_0e_1, e_0e_2, e_0e_3, e_1e_2, e_1e_3, e_1e_4, e_2e_4, e_3e_4\}$. Graphs $G_1$ and $L(G_1)$ are presented in Fig. 3.

Fig. 3

Graph from Example 1 and its corresponding line graph (edge metric base is colored red) (color figure online)

By using the total enumeration technique, it can be shown that $\beta _E(G_1)=3$ with a edge metric base $\{v_0, v_1, v_2\}$. On the other hand, $\beta _E'(G_1)=\beta (L(G_1))=2$ with a metric base $\{e_0, e_2\}=\{v_0v_1, v_0v_2\}$.

2 Main Results

2.1 Lower Bound

Having in mind the fact that vertices from an edge metric base are also endpoints for some (incident) edges, the bound presented in Proposition 1.2, could be improved in some cases.

Theorem 2.1

Let G be a connected graph and let $\delta (G)$ be the minimum degree of G. Then, $\beta _E(G) \ge 1 + \lceil log_2 \delta (G) \rceil$.

Proof

Let $S=\{w_1,w_2,...,w_p\}$ be an edge metric generator of graph G with a minimal cardinality, i.e. $p=\beta _E(G)$. Vertex $w_1$ is incident to at least $\delta (G)$ edges. Name them $e_1$, ..., $e_{\delta (G)}$. Since $w_1$ is incident with $e_1$, ..., $e_{\delta (G)}$, it is obvious that $d(e_1,w_1)=...=d(e_{\delta (G)},w_1)=0$. By the definition of the distance between vertex and edge, it is clear that for an arbitrary vertex $v \in V (G)$ there can be only two different distances to a set of incident edges. Then, for each i, $i=2,...,p$, distances $d(e_1,w_i)$, ..., $d(e_{\delta (G)},w_i)$ have only two different values, so since $d(e_1,w_1)=...=d(e_{\delta (G)},w_1)=0$, there exist at most $2^{p-1}$ different edge metric representations of edges $e_1$, ..., $e_{\delta (G)}$ with respect to S, so $\delta (G) \le 2^{p-1}$. Next, because p is integer, it follows that $\lceil log_2 \delta (G) \rceil \le p-1$ $\Rightarrow$ $\beta _E(G) = p \ge 1+\lceil log_2 \delta (G) \rceil$. $\square$

In the case of regular graphs, the bound presented in Proposition 1.2 is improved by 1.

Corollary 2.2

Let G be an r-regular graph. Then, $\beta _E(G) \ge 1 + \lceil log_2 r \rceil$.

Since GP(n, k) are 3-regular graphs, and $\lceil log_2 3 \rceil =2$ then the next corollary holds.

Corollary 2.3

$\beta _E(GP(n,k)) \ge 3$.

2.2 Exact Value for GP(n, 1)

In this section, we are giving the exact value of the edge metric dimension of the generalized Petersen graphs GP(n, 1).

Theorem 2.4

$\beta _E(GP(n,1))=3$.

Proof

Let $S=\{u_0, u_1, v_0\}$.

Case 1. $n = 2t$

Edge metric representations with respect to S are:

$$\begin{aligned} r(u_i u_{i+1},S)= & {} {\left\{ \begin{array}{ll} (0,0,1), \; i=0 \\ (i,i-1,i+1),\; 1 \le i \le t-1 \\ (t-1,t-1,t), \; i=t \\ (2t-1-i,2t-i,2t-i),\; t+1 \le i \le 2t-1 \\ \end{array}\right. }.\\ r(u_i v_i,S)= & {} {\left\{ \begin{array}{ll} (0,1,0), \; i=0 \\ (i,i-1,i),\; 1 \le i \le t \\ (2t-i,2t+1-i,2t-i),\; t+1 \le i \le 2t-1 \\ \end{array}\right. }.\\ r(v_i v_{i+1},S)= & {} {\left\{ \begin{array}{ll} (1,1,0), \; i=0 \\ (i+1,i,i),\; 1 \le i \le t-1 \\ (t,t,t-1), \; i=t \\ (2t-i,2t+1-i,2t-1-i),\; t+1 \le i \le 2t-2 \\ (1,2,0), \; i=2t-1 \\ \end{array}\right. }. \end{aligned}$$

Since all edge metric representations with respect to S are pairwise different, we deduce that S is an edge metric generator. Since $|S|=3$, from Corollary 2.3, it follows $\beta _E(GP(2t,1)) = 3$.

Case 2. $n = 2t+1$

Edge metric representations with respect to S are:

$$\begin{aligned} r(u_i u_{i+1},S)= & {} {\left\{ \begin{array}{ll} (0,0,1), \; i=0 \\ (i,i-1,i+1),\; 1 \le i \le t \\ (2t-i,2t+1-i,2t+1-i),\; t+1 \le i \le 2t \\ \end{array}\right. }.\\ r(u_i v_i,S)= & {} {\left\{ \begin{array}{ll} (0,1,0), \; i=0 \\ (i,i-1,i),\; 1 \le i \le t \\ (t,t,t), \; i=t+1 \\ (2t+1-i,2t+2-i,2t+1-i),\; t+2 \le i \le 2t \\ \end{array}\right. }.\\ r(v_i v_{i+1},S)= & {} {\left\{ \begin{array}{ll} (1,1,0), \; i=0 \\ (i+1,i,i),\; 1 \le i \le t \\ (2t+1-i,2t+2-i,2t-i),\; t+1 \le i \le 2t \\ \end{array}\right. }. \end{aligned}$$

Similarly to Case 1, all edge metric representations with respect to S are pairwise different, so S is an edge metric generator. Having in mind that $|S|=3$, from Corollary 2.3 it follows $\beta _E(GP(2t+1,1)) = 3$. $\square$

Table 2 Edge metric representations for GP(4t, 2)

Table 3 Edge metric representations for $GP(4t+1,2)$

Table 4 Edge metric representations for $GP(4t+2,2)$

Table 5 Edge metric representations for $GP(4t+3,2)$

Table 6 Edge resolving bases of GP(n, 2)

In [3], the authors consider the relation between the metric dimension and the edge metric dimension of some graphs (called realization question). They concluded that it is possible to find all three cases, i.e. graphs G such that $\beta _E(G) = \beta (G)$, $\beta _E(G) > \beta (G)$ or $\beta _E(G) < \beta (G)$. For GP(n, 1) there are only two cases, since, from [12], it follows $\beta (GP(n,1))= {\left\{ \begin{array}{ll} 2, \,\,n \;is \; odd \\ 3, \,\,n \;is \; even \\ \end{array}\right. }$. When $n=2t$, it holds $\beta _E(GP(n,1)) = \beta (GP(n,1))=3$, while for $n=2t+1$, it holds $3=\beta _E(GP(n,1)) > \beta (GP(n,1))=2$.

Another interesting discussion is comparison between $\beta _E(GP(n,1))$ and $\beta _E'(GP(n,1))$. From [18], it follows that $\beta _E'(GP(n,1))=3$, which matches $\beta _E(GP(n,1))=3$ from Theorem 2.4.

2.3 Exact Value for GP(n, 2)

In this section, we are giving the exact value of the edge metric dimension of the generalized Petersen graphs GP(n, 2).

Theorem 2.5

$\beta _E(GP(n,2))={\left\{ \begin{array}{ll} 3, \; \quad n=8 \vee n \ge 10 \\ 4, \; \quad n \in \{5,6,7,9\} \end{array}\right. }$

Proof

In the case of $n=4t$, $t \ge 4$, let $S=\{u_0, v_3, v_{2t+3}\}$. All edge metric representations with respect to S are given in Table 2. The first column is related to edge $e \in E(GP(4t,2))$, the second column presents its edge metric representation r(e), while the last column gives the condition in which the statement in the second column is true. As can be observed from Table 2, all edge metric representations with respect to S are pairwise different, so S is an edge metric generator for GP(4t, 2). Having in mind that $|S|=3$, from Corollary 2.3 it follows that, for $t \ge 4$, $\beta _E(GP(4t,2)) = 3$ holds.

If $n=4t+1$, $t \ge 4$, then let $S=\{u_0, v_{2t-5}, v_{2t-4}\}$. All edge metric representations with respect to S are given in Table 3. As can be seen in Table 3 all edge metric representations with respect to S are pairwise different, so S is an edge metric generator for $GP(4t+1,2)$. Again, having in mind that $|S|=3$, from Corollary 2.3 it follows that, for $t \ge 4$, $\beta _E(GP(4t+1,2)) = 3$ holds.

For $t \ge 4$, in cases when $n=4t+2$ or $n=4t+3$, let us define $S=\{u_0, v_{2t-2}, v_{2t-1}\}$. All edge metric representations of $GP(4t+2,2)$ and $GP(4t+3,2)$, with respect to S, are given in Tables  4 and 5, respectively. It can be seen in Table 4 that all edge metric representations of $GP(4t+2,2)$, with respect to S, are pairwise different, so S is an edge metric generator for $GP(4t+2,2)$. Again, having in mind that $|S|=3$, from Corollary 2.3 it follows that, for $t \ge 4$, $\beta _E(GP(4t+2,2)) = 3$ holds. The same conclusion can be drawn for $GP(4t+3,2)$, since all its edge metric representations presented in Table 5 are also pairwise different, so for $t \ge 4$, $\beta _E(GP(4t+3,2)) = 3$ holds.

For the remaining cases when $n \le 15$, the edge metric dimension of GP(n, 2) is found by the total enumeration technique, and it is presented in Table 6, along with the corresponding edge metric bases. It should be stated that the edge metric dimension is equal to 3, except in cases for $n \in \{5,6,7,9\}$, when it is equal to 4. $\square$

For GP(n, 2) there are only two cases for the realization question given in [4]. From [13] it follows that $\beta (GP(n,2))=3$, so for $n \notin \{5,6,7,9\}$ the edge metric dimension of GP(n, 2) is equal to its metric dimension. Only in cases when $n \in \{5,6,7,9\}$, it holds $4=\beta _E(GP(n,2)) > \beta (GP(n,2))=3$.

Another interesting discussion is the comparison between $\beta _E(GP(n,2))$ and $\beta _E'(GP(n,2))$. In contrast to GP(n, 1), the values of $\beta _E(GP(n,2))$ and $\beta _E'(GP(n,2))$ sometimes differ. For example, $\beta _E(GP(9,2))=4$, while $\beta _E'(GP(n,2))=3$.

3 Conclusions

In this article, the recently introduced edge metric dimension problem is considered. The exact formulae for generalized Petersen graphs GP(n, 1) and GP(n, 2) are stated and proved. Moreover, a lower bound for 3-regular graphs, which holds for all generalized Petersen graphs, is given.

Possible future research could be the finding of the edge metric dimension of other challenging classes of graphs or the construction of the metaheuristic approach for solving the edge metric dimension problem.