Asymptotic Behavior and Global Structure of Oscillatory Bifurcation Diagrams

Abstract

This paper is concerned with the nonlinear eigenvalue problem

$$\begin{aligned} -u''(t) = \lambda f(u(t)), u(t) > 0, t \in I := (-1,1), u(\pm 1) = 0. \end{aligned}$$

Here, $f(u) = u^{2n+1} + \frac{\sin (u^2)}{u}$ ($n = 0,1,2, \ldots$) and $\lambda > 0$ is a bifurcation parameter. Since $f(u) > 0$ for $u > 0$, $\lambda$ is a continuous function of the maximum norm $\alpha = \Vert u_\lambda \Vert _\infty$ of the solution $u_\lambda$ associated with $\lambda$, and is expressed as $\lambda = \lambda (\alpha )$. In this paper, by the argument of the stationary phase method, we establish the precise asymptotic formulas for $\lambda (\alpha )$ as $\alpha \rightarrow \infty$, which seem to be new, and $\alpha \rightarrow 0$ for the better understanding the global structure of $\lambda (\alpha )$.

1 Introduction

This paper is concerned with the following nonlinear eigenvalue problems

$$\begin{aligned} -u''(t)= & {} \lambda f(u(t)), \quad t \in I := (-1,1), \end{aligned}$$

(1.1)

$$\begin{aligned} u(t)> & {} 0, \quad t \in I, \end{aligned}$$

(1.2)

$$\begin{aligned} u(-1)= & {} u(1) = 0, \end{aligned}$$

(1.3)

where $f(u) = u^{2n+1} + (\sin (u^2))/u$ ($u > 0$), $f(0):= 0$ ($n = 0,1,2, \ldots$) and $\lambda > 0$ is a bifurcation parameter. Since $f(u) > 0$ for $u > 0$, we know from [10] that for any given $\alpha > 0$, there exists a unique classical solution pair $(\lambda , u_\alpha )$ of (1.1–1.3) satisfying $\alpha = \Vert u_\alpha \Vert _\infty$. Furthermore, $\lambda$ is parameterized by $\alpha$ as $\lambda = \lambda (\alpha )$ and is a continuous function for $\alpha > 0$.

A large number of researches about global and local structure of bifurcation diagrams has been carried out, since many topics have been proposed from mathematical physics, biology, engineering, and they have been investigated by many authors intensively. We refer to [2, 3, 5] and the references therein. It should be mentioned that oscillatory phenomena of bifurcation curves are one of the important topics to think about. Besides, the study of oscillatory bifurcation curves is expected to develop a new aspect in the field of bifurcation theory. We refer to [6,7,8,9, 12,13,14,15] and the references therein.

The Eqs. (1.1)–(1.3) with $f(u) = u + \sin \sqrt{u}$ has been studied in Cheng [4], which was motivated by [1]. It was proposed as a model equation which produces an oscillatory bifurcation curve. It was proved in [4] that there exists arbitrary many solutions near $\lambda = \pi ^2/4$.

Theorem 1.1

[4, Theorem 6]. Let $f(u) = u + \sin \sqrt{u}$ $(u \ge 0)$. Then for any integer $r \ge 1$, there is $\delta > 0$ such that if $\lambda \in (\pi ^2/4-\delta , \pi ^2/4 + \delta )$, then (1.1)–(1.3) has at least r distinct solutions.

It seems reasonable to expect that, in the situation of Theorem 1.1, $\lambda (\alpha )$ oscillates and intersects the line $\lambda = \pi ^2/4$ infinitely many times for $\alpha \gg 1$. To obtain a positive answer to this question, the following asymptotic formula for $\lambda (\alpha )$ has been established in [14].

Theorem 1.2

[14, Theorem 1.1].

• (i) Let $f(u) = u + \sin \sqrt{u}$ ($u \ge 0$). Then as $\alpha \rightarrow \infty$,

  $$\begin{aligned} \lambda (\alpha ) = \frac{\pi ^2}{4} - \pi ^{3/2} \alpha ^{-5/4} \sin \left( \sqrt{\alpha }-\frac{\pi }{4}\right) + o(\alpha ^{-5/4}). \end{aligned}$$

  (1.4)

• (ii) Let $f(u) = u+\sin (u^2)$. Then as $\alpha \rightarrow \infty$,

  $$\begin{aligned} \lambda (\alpha )= & {} \frac{\pi ^2}{4} - \frac{\pi ^{3/2}}{2}\alpha ^{-2} \sin \left( \alpha ^2-\frac{1}{4}\pi \right) + o(\alpha ^{-2}). \end{aligned}$$

  (1.5)

Theorem 1.2 was proved by the time-map method and the asymptotic formulas for some special functions. Especially, Fresnel’s integral played an important role in the proof of Theorem 1.2 (ii).

Besides, by using the time-map formula and stationary phase method, the precise asymptotic formula for $\lambda (\alpha )$ of (1.1)–(1.3) with more general nonlinear term $f(u) = u + u^p\sin (u^q)$ ($0 \le p < 1$, $0 < q \le 1$) as $\alpha \rightarrow \infty$ was established in [15].

Theorem 1.3

[15]. Let $f(u) = u + u^p\sin (u^q)$ ($u \ge 0$), where $0 \le p < 1$ and $0 < q \le 1$ are fixed constants. Then as $\alpha \rightarrow \infty$,

$$\begin{aligned} \lambda (\alpha ) = \frac{\pi ^2}{4} - \frac{\pi ^{3/2}}{\sqrt{2q}} \alpha ^{p-1-(q/2)} \sin \left( \alpha ^q - \frac{\pi }{4}\right) + o(\alpha ^{p-1-(q/2)}). \end{aligned}$$

(1.6)

The following is the rough graph of the bifurcation curve in (1.6) with $p + q > 1$. Theorem 1.3 gives us the clear picture about the total shape of bifurcation curve of (1.1) with $f(u) = u + u^p\sin (u^q)$.

Fig. 1

$\lambda (\alpha )$ for (1.6) ($p + q > 1$)

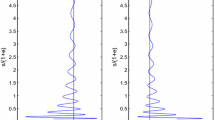
Unfortunately, however, the case where $p < 0$ has not been treated in [15]. The reason why is as follows. In the proof of Theorem 1.3, the standard argument of stationary phase method in [9, Lemmas 2.24 and 2.25] can be applicable, because the phase function appeared there has only one stationary point. However, to treat the case where $f(u) = u^{2n+1} + (\sin (u^2))/u$ ($u > 0$) by the stationary phase method, two stationary points appear in the phase function, and it makes the argument difficult (Fig. 1).

The purpose of this paper is to overcome this difficulty and treat the case where $p = -1$, $q=2$ (as Theorem 1.2 (ii)) and $n = 0, 1, 2, \ldots$ in order to obtain a new asymptotic behavior of oscillatory bifurcation curves. It seems that the bifurcation problems with such kind of nonlinear terms have not been considered yet.

Now we state our main results.

Theorem 1.4

(Main Theorem) Let $\displaystyle {f(u) = u^{2n+1} + \frac{\sin (u^2)}{u}}$ ($u > 0$) and $f(0) := 0$ ($n = 0,1,2,\ldots$). Then as $\alpha \rightarrow \infty$,

$$\begin{aligned} \lambda (\alpha )&= (n+1)\alpha ^{-2n}\nonumber \\&\quad \times \left\{ C_n^2 - \sqrt{\pi } \alpha ^{-(2n+3)}\left( \frac{1}{\sqrt{n+1}}\sin \left( \alpha ^2-\frac{\pi }{4}\right) + \frac{n+1}{\sqrt{2}}\right) \right. \nonumber \\&\left. \qquad \qquad + O(\alpha ^{-(2n+4)})\right\} , \end{aligned}$$

(1.7)

where

$$\begin{aligned} C_n:= \int _0^1 \frac{1}{\sqrt{1-s^{2n+2}}}ds . \end{aligned}$$

(1.8)

We remark that the second term of (1.7) includes both oscillatory term and a constant. This phenomenon characterizes the difference between the asymptotic behavior of bifurcation curves in Theorems 1.3 and 1.4. As far as the author knows, it does not seem that such formula was obtained before.

We next establish the asymptotic formulas for $\lambda (\alpha )$ as $\alpha \rightarrow 0$ to obtain the whole structure of $\lambda (\alpha )$.

Theorem 1.5

(Main Theorem). Let $\displaystyle {f(u) = u^{2n+1} + \frac{\sin (u^2)}{u}}$ ($u > 0$), $f(0) := 0$ ($n = 0, 1,2,\ldots$). Then as $\alpha \rightarrow 0$, the following asymptotic formulas for $\lambda (\alpha )$ hold.

• (i) Let $n = 0$. Then

  $$\begin{aligned} \lambda (\alpha ) = \frac{\pi ^2}{8} + \frac{5}{768}\pi ^2\alpha ^4 + o(\alpha ^4). \end{aligned}$$

  (1.9)

• (ii) Let $n = 1$, Then

  $$\begin{aligned} \lambda (\alpha ) = \frac{\pi ^2}{4} - \frac{3}{16}\pi ^2\alpha ^2 + o(\alpha ^2). \end{aligned}$$

  (1.10)

• (iii) Let $n = 2$. Then

  $$\begin{aligned} \lambda (\alpha ) = \frac{\pi ^2}{4} - \frac{25}{192}\pi ^2\alpha ^4 + o(\alpha ^4). \end{aligned}$$

  (1.11)

• (iv) Let $n \ge 3$. Then

  $$\begin{aligned} \lambda (\alpha ) = \frac{\pi ^2}{4} + \frac{5}{192}\pi ^2\alpha ^4 + o(\alpha ^4). \end{aligned}$$

  (1.12)

The proof of Theorem 1.5 is carried out easily by time-map method and Taylor expansion theorem. By Theorems 1.4 and 1.5, we find that the rough shape of $\lambda (\alpha )$ is like the graph below (Figs. 2, 3).

Fig. 2

$\lambda (\alpha )$ for $n = 0$

Fig. 3

$\lambda (\alpha )$ for $n \ge 1$

2 Proof of Theorem 1.4

In what follows, we denote by C the various positive constants independent of $\alpha$. In this section, let $\alpha \gg 1$, and for $u \ge 0$, let $f(u) = u^{2n+1} + g(u)$, where $g(u) = \displaystyle {\frac{\sin (u^2)}{u}}$ and

$$\begin{aligned} G(u) := \int _0^u g(s)ds. \end{aligned}$$

(2.1)

It is known that if $(u_\alpha , \lambda (\alpha )) \in C^2(\bar{I}) \times \mathbb {R}_+$ satisfies (1.1)–(1.3), then

$$\begin{aligned}&u_\alpha (t) = u_\alpha (-t), \quad 0 \le t \le 1, \end{aligned}$$

(2.2)

$$\begin{aligned}&u_\alpha (0) = \max _{-1\le t \le 1}u_\alpha (t) = \alpha , \end{aligned}$$

(2.3)

$$\begin{aligned}&u_\alpha '(t) > 0, \quad -1< t < 0. \end{aligned}$$

(2.4)

By (1.1), we have

$$\begin{aligned} \left( u_\alpha ''(t) + \lambda \left( u_\alpha (t)^{2n+1} + g(u_\alpha (t))\right) \right) u_\alpha '(t) = 0. \end{aligned}$$

By this, (2.3) and putting $t = 0$, we obtain

$$\begin{aligned}&\frac{1}{2} u_\alpha '(t)^2 + \lambda \left( \frac{1}{2n+2}u_\alpha (t)^{2n+2} + G(u_\alpha (t))\right) = \text{ constant }\\&\quad = \lambda \left( \frac{1}{2n+2}\alpha ^{2n+2} + G(\alpha )\right) . \end{aligned}$$

This along with (2.4) implies that for $-1 \le t \le 0$,

$$\begin{aligned} u_\alpha '(t) = \sqrt{2\lambda }\sqrt{(\alpha ^{2n+2} - u_\alpha (t)^{2n+2})/(2n+2) + (G(\alpha ) - G(u_\alpha (t)))}. \end{aligned}$$

(2.5)

Let $n = 0$. We fix an arbitrary constant $0 < \epsilon \ll 1$. Let $0 \le s \le \epsilon /\alpha$. Then

$$\begin{aligned} \vert G(\alpha ) - G(\alpha s)\vert\le & {} \left| \int _{\alpha s}^\epsilon \frac{\sin (x^2)}{x}dx\right| + \left| \int _{\epsilon }^\alpha \frac{\sin (x^2)}{x}dx\right| \nonumber \\\le & {} \int _{\alpha s}^\epsilon x dx + \int _{\epsilon }^{\alpha } \frac{1}{x}dx \nonumber \\\le & {} \epsilon (\epsilon - \alpha s) + \frac{1}{\epsilon }(\alpha - \epsilon ) \le \frac{1}{\epsilon }(\alpha - \alpha s). \end{aligned}$$

(2.6)

Let $\epsilon /\alpha \le s \le 1$. Then

$$\begin{aligned} \vert G(\alpha ) - G(\alpha s)\vert \le \int _{\alpha s}^\alpha \frac{1}{x}dx \le \int _{\alpha s}^\alpha \frac{1}{\epsilon }dx \le \frac{1}{\epsilon } \alpha (1-s). \end{aligned}$$

(2.7)

By (2.6) and (2.7), for $0 \le s \le 1$, we obtain

$$\begin{aligned} \left| \frac{G(\alpha ) - G(\alpha s)}{\alpha ^{2}(1-s^{2})}\right| \le C\frac{\alpha (1-s^{2})}{\alpha ^{2}(1-s^{2})} \le C\alpha ^{-1} \ll 1. \end{aligned}$$

(2.8)

Let $n \ge 1$. For $0 \le s \le 1$, we have

$$\begin{aligned} \vert G(\alpha ) - G(\alpha s)\vert \le \left| \int _{\alpha s}^\alpha \frac{\sin (x^2)}{x}dx \right| \le \left| \int _{\alpha s}^\alpha x dx \right| = \frac{1}{2}\alpha ^2(1-s^2). \end{aligned}$$

(2.9)

By this, for $0 \le s \le 1$, we obtain

$$\begin{aligned} \left| \frac{G(\alpha ) - G(\alpha s)}{\alpha ^{2n+2}(1-s^{2n+2})}\right| \le C\frac{\alpha ^{2}(1-s^{2})}{\alpha ^{2n+2}(1-s^{2n+2})} \le C\alpha ^{-2n} \ll 1. \end{aligned}$$

(2.10)

By (2.5), (2.8) and (2.10), putting $\theta = u_\alpha (t) = \alpha s$ and Taylor expansion, we obtain

$$\begin{aligned}&\sqrt{\frac{\lambda }{n+1}}\nonumber \\&\quad = \int _{-1}^0 \frac{u_\alpha '(t)}{\sqrt{(\alpha ^{2n+2}-u_\alpha (t)^{2n+2}) + 2(n+1)(G(\alpha ) -G(u_\alpha (t)))}}dt \nonumber \\&\quad = \int _0^\alpha \frac{1}{\sqrt{(\alpha ^{2n+2}-\theta ^{2n+2}) + 2(n+1)(G(\alpha )-G(\theta ))}}d\theta \nonumber \\&\quad = \alpha ^{-n}\int _0^1 \frac{1}{\sqrt{1-s^{2n+2}}} \nonumber \\&\qquad \times \frac{1}{\sqrt{1 + 2(n+1)(G(\alpha )-G(\alpha s))/(\alpha ^{2n+2}(1-s^{2n+2}))}} ds \nonumber \\&\quad = \alpha ^{-n}\int _0^1 \frac{1}{\sqrt{1-s^{2n+2}}} \nonumber \\&\qquad \times \left\{ 1 - \frac{(n+1)(G(\alpha )-G(\alpha s))}{\alpha ^{2n+2}(1-s^{2n+2})} (1 + O(\alpha ^{-1}))\right\} ds \nonumber \\&\quad = \alpha ^{-n}\left( C_n - (n+1)\alpha ^{-(2n+2)}(1 + O(\alpha ^{-1})) \int _0^1\frac{G(\alpha )-G(\alpha s)}{(1-s^{2n+2})^{3/2}}ds \right) .\nonumber \\ \end{aligned}$$

(2.11)

We put

$$\begin{aligned} K(\alpha ) := \int _0^1\frac{G(\alpha )-G(\alpha s)}{(1-s^{2n+2})^{3/2}}ds. \end{aligned}$$

(2.12)

To calculate $K(\alpha )$, we introduce the following Lemma 2.1, which is the special case of stationary phase methods. Namely, the phase function w(x) has two stationary points.

Lemma 2.1

Assume that $h \in C^2[0,1]$. Consider

$$\begin{aligned} I(\mu ) := \int _0^1 h(x)e^{i\mu w(x)}dx, \end{aligned}$$

(2.13)

where $w(x) = \cos ^2(\pi x/2)$. Then as $\mu \rightarrow \infty$,

$$\begin{aligned} I(\mu ) = \sqrt{\frac{1}{\mu \pi }}h(0)e^{i(\mu -\pi /4)} + \sqrt{\frac{1}{\mu \pi }}h(1)e^{i\pi /4} + O(\mu ^{-1}). \end{aligned}$$

(2.14)

In particular,

$$\begin{aligned} I_s(\mu ):= & {} \text{ Im } I(\mu ) = \int _0^1 h(x)\sin \left( \mu w(x)\right) \nonumber \\= & {} \sqrt{\frac{1}{\mu \pi }}\left( h(0) \sin \left( \mu -\frac{\pi }{4}\right) + \frac{1}{\sqrt{2}}h(1) \right) + O(\mu ^{-1}). \end{aligned}$$

(2.15)

Proof

The proof is a variant of [9, Lemmas 2.24 and 2.25]. For completeness, we give the proof. We note that both $x = 0$ and $x = 1$ are stationary points of w(x). Therefore, [9, Lemma 2.25] cannot be applied directly. So, let $I(\mu ):= I_1(\mu ) + I_2(\mu )$, where

$$\begin{aligned} I_1(\mu ):= \int _0^{1/2} h(x)e^{i\mu w(x)}dx, \quad I_2(\mu ):= \int _{1/2}^1 h(x)e^{i\mu w(x)}dx. \end{aligned}$$

(2.16)

We put $x = t/2$ and $\tilde{w}(t) = w(x)$. Since $\tilde{w}''(0) = -\pi ^2/8$, by [7, Lemma 2], we obtain

$$\begin{aligned} I_1(\mu )= & {} \frac{1}{2}\int _0^1 h\left( \frac{1}{2}t\right) e^{i\mu \tilde{w}(t)}dt \nonumber \\= & {} \frac{1}{4}h(0)e^{i(\mu \tilde{w}(0) - \pi /4)} \sqrt{\frac{2\pi }{\mu \vert \tilde{w}''(0)\vert }} \nonumber \\= & {} \sqrt{\frac{1}{\mu \pi }}h(0)e^{i(\mu - \pi /4)} + O(\mu ^{-1}). \end{aligned}$$

(2.17)

We know from [9, Lemma 2.24] that for a given constant $a>0$ and $h_1(t) \in C^2[0,a]$, as $\mu \rightarrow \infty$,

$$\begin{aligned} \int _0^a h_1(t)e^{i\mu t^2}dt = \frac{1}{2}\sqrt{\frac{\pi }{\mu }}e^{i\pi /4}h_1(0) + O(\mu ^{-1}). \end{aligned}$$

(2.18)

Let $x = 1-y$, $t = \sin (\pi y/2)$ and $h_1(y) := h(1-y)$. By (2.16) and (2.18), we obtain

$$\begin{aligned} I_2(\mu )= & {} \int _0^{1/2} h(1-y)e^{i\mu \sin ^2(\pi y/2)}dy\nonumber \\= & {} \int _0^{1/2} h_1(y)e^{i\mu \sin ^2(\pi y/2)}dy \nonumber \\= & {} \frac{2}{\pi }\int _0^{1/\sqrt{2}} h_1\left( \frac{2}{\pi }\sin ^{-1}t\right) \frac{1}{\sqrt{1-t^2}}e^{i\mu t^2}dt \nonumber \\= & {} \frac{1}{\sqrt{\mu \pi }}h(1)e^{i\pi /4} + O(\mu ^{-1}). \end{aligned}$$

(2.19)

By (2.16), (2.17) and (2.19), we obtain (2.14). Thus the proof is complete. $\square$

We emphasize that Lemma 2.1 is able to be applied to the case where the phase function w(x) has two stationary points $x = 0$ and $x = 1$, namely, $w'(0) = w'(1) = 0$. In a standard stationary phase method, only $x = 0$ is allowed to be the stationary point (cf. [9, Lemmas 2.25]). We also refer to [11, Theorem 2.3], in which the cases where w(x) with many stationary points have been considered. However, since the proof of [11, Theorem 2.3] is rather complicated, it seems that the proof of Lemma 2.1 above is more straghtforward and easy to understand.

Lemma 2.2

As $\alpha \rightarrow \infty$,

$$\begin{aligned} K(\alpha ) = \frac{\sqrt{\pi }}{2} \alpha ^{-1} \left( \frac{1}{(n+1)^{3/2}}\sin \left( \alpha ^2-\frac{\pi }{4}\right) + \frac{1}{\sqrt{2}} \right) + O(\alpha ^{-2}). \end{aligned}$$

(2.20)

Proof

We put $s = \sin \theta$ in (2.12). Then by integration by parts, we obtain,

$$\begin{aligned} K(\alpha )= & {} \int _0^{\pi /2} \frac{G(\alpha )-G(\alpha \sin \theta )}{(1-\sin ^2\theta )^{3/2} (1 + \sin ^2\theta + \cdots + \sin ^{2n}\theta )^{3/2}} \cos \theta d\theta \nonumber \\= & {} \int _0^{\pi /2} \frac{1}{\cos ^2\theta }\frac{G(\alpha )-G(\alpha \sin \theta )}{ (1 + \sin ^2\theta + \cdots + \sin ^{2n}\theta )^{3/2}} d\theta \end{aligned}$$

(2.21)

$$\begin{aligned}= & {} \left[ \tan \theta \frac{G(\alpha )-G(\alpha \sin \theta )}{(1 + \sin ^2\theta + \cdots + \sin ^{2n}\theta )^{3/2}}\right] _0^{\pi /2} \nonumber \\&+ \int _0^{\pi /2} \frac{\alpha \sin \theta g(\alpha \sin \theta )}{(1+\sin ^2\theta + \cdots + \sin ^{2n}\theta )^{3/2}}d\theta \nonumber \\&+ 3\int _0^{\pi /2} (G(\alpha )-G(\alpha \sin \theta )) \nonumber \\&\times \frac{\sin ^2\theta (1 + 2\sin ^2\theta + \cdots + n\sin ^{2(n-1)}\theta )}{(1 + \sin ^2\theta + \cdots + \sin ^{2n}\theta )^{5/2}}d\theta \nonumber \\:= & {} K_0(\alpha ) + K_1(\alpha ) + 3K_2(\alpha ). \end{aligned}$$

(2.22)

By l’Hôpital’s rule, we obtain

$$\begin{aligned}&\lim _{\theta \rightarrow \pi /2} \frac{G(\alpha ) - G(\alpha \sin \theta )}{\cos \theta } = \lim _{\theta \rightarrow \pi /2}\frac{\alpha \cos \theta g(\alpha \sin \theta )}{\sin \theta } = 0. \end{aligned}$$

(2.23)

Therefore, we see that $K_0(\alpha ) = 0$. Next, by putting $\theta = \pi /2-y$ and $y = \pi x/2$, we obtain

$$\begin{aligned} K_1(\alpha )= & {} \int _0^{\pi /2} \frac{\alpha \sin \theta g(\alpha \sin \theta )}{(1+\sin ^2\theta + \cdots + \sin ^{2n}\theta )^{3/2}}d\theta \nonumber \\= & {} \int _0^{\pi /2}\frac{1}{(1+\sin ^2\theta + \cdots + \sin ^{2n}\theta )^{3/2}} \sin (\alpha ^2\sin ^2\theta )d\theta \nonumber \\= & {} \int _0^{\pi /2}\frac{1}{(1+\cos ^2y + \cdots + \cos ^{2n}\theta )^{3/2}} \sin (\alpha ^2\cos ^2y)dy \nonumber \\ \nonumber= & {} \frac{\pi }{2}\int _0^1 \frac{1}{\left( 1 + \cos ^2\left( \frac{\pi }{2}x\right) + \cdots + \cos ^{2n}\left( \frac{\pi }{2}x\right) \right) ^{3/2}} \nonumber \\&\times \sin \left( \alpha ^2\cos ^2\left( \frac{\pi }{2}x\right) \right) dx. \end{aligned}$$

(2.24)

We put $\mu = \alpha ^2$ and $h(x) = \left( 1 + \cos ^2\left( \frac{\pi }{2}x\right) + \cos ^{2n}\left( \frac{\pi }{2}x\right) \right) ^{-3/2}$. By direct calculation, we obtain $h(0) = (n+1)^{-3/2}$ and $h(1)=1$. Then by Lemma 2.1, we obtain

$$\begin{aligned} K_1(\alpha ) = \frac{\sqrt{\pi }}{2} \alpha ^{-1} \left( (n+1)^{-3/2}\sin \left( \alpha ^2-\frac{\pi }{4}\right) + \frac{1}{\sqrt{2}} \right) + O(\alpha ^{-2}). \end{aligned}$$

(2.25)

Finally, we calculate $K_2(\alpha )$. We put

$$\begin{aligned} M(\theta ) := \int _0^{\theta }\frac{\sin ^2x (1 + \sin ^2x + \cdots + n\sin ^{2(n-1)}x)}{(1+\sin ^2x + \sin ^{2n}x)^{5/2}}dx. \end{aligned}$$

(2.26)

By this and integration by parts, we obtain

$$\begin{aligned} K_2(\alpha )= & {} \int _0^{\pi /2} M'(\theta )(G(\alpha )-G(\alpha \sin \theta ))d\theta \nonumber \\= & {} \left[ M(\theta )(G(\alpha )-G(\alpha \sin \theta ))\right] _0^{\pi /2} + \alpha \int _0^{\pi /2} M(\theta )\cos \theta g(\alpha \sin \theta )d\theta \nonumber \\= & {} \alpha \int _0^{\pi /2} M(\theta )\cos \theta g(\alpha \sin \theta )d\theta . \end{aligned}$$

(2.27)

By this, putting $\theta = \pi /2 - y, y = \pi t/2$, we obtain

$$\begin{aligned} K_2(\alpha )= & {} \int _0^{\pi /2} M(\theta )\frac{\cos \theta }{\sin \theta } \sin (\alpha ^2\sin ^2\theta )d\theta \nonumber \\= & {} \int _0^{\pi /2} M\left( \frac{\pi }{2}-y\right) \frac{\sin y}{\cos y} \sin (\alpha ^2\cos ^2 y)dy \nonumber \\= & {} \frac{\pi }{2}\int _0^1 k(t)\sin \left( \alpha ^2 \cos ^2\left( \frac{\pi }{2}t\right) \right) dt, \end{aligned}$$

(2.28)

where

$$\begin{aligned} k(t):= M\left( \frac{\pi }{2}(1-t)\right) \tan \left( \frac{\pi }{2}t\right) . \end{aligned}$$

(2.29)

It is clear that k(t) is $C^2[0,1)$. The regularity of k(t) near $t = 1$ is obtained as follows. We put $x:= 1-t$ and $v(x) := k(t)$. Then by Taylor expansion, for $0 < x \ll 1$, we have

$$\begin{aligned} M\left( \frac{\pi }{2}x\right) = \frac{\pi ^3}{24}x^3 + O(x^5). \end{aligned}$$

(2.30)

By this, for $0 < x \ll 1$, we obtain

$$\begin{aligned} v(x)= & {} \frac{M\left( \frac{\pi }{2}x\right) }{\sin \left( \frac{\pi }{2}x\right) } \cos \left( \frac{\pi }{2}x\right) = \frac{\frac{\pi ^2}{12}x^2 + O(x^4)}{1-\frac{\pi ^2}{24}x^2 + O(x^4)} \cos \left( \frac{\pi }{2}x\right) . \end{aligned}$$

(2.31)

This assures $C^2$-regularity of v(x) near $x = 0$, namely, k(t) is $C^2$ near $t = 1$. Since $k(0) = k(1) = 0$ by direct calculation, by Lemma 2.1, we obtain $K_2(\alpha ) = O(\alpha ^{-2})$. By this and (2.25), we obtain (2.20). Thus the proof is complete. $\square$

Now Theorem 1.4 is a direct consequence of (2.11) and Lemma 2.2. Thus the proof is complete. $\square$

3 Proof of Theorem 1.5

In this section, let $0 < \alpha \ll 1$.

Proof of Theorem 1.5 (i)

Let $n = 0$. Then it follows from (1.1) and Taylor expansion that

$$\begin{aligned} -u_\alpha ''(t) = \lambda (2u_\alpha (t) -\frac{1}{6} u_\alpha (t)^5(1 + o(1))). \end{aligned}$$

(3.1)

By this and the same argument as that to obtain (2.5), for $-1 \le t \le 0$, we have

$$\begin{aligned} u_\alpha '(t) = \sqrt{2\lambda } \sqrt{\alpha ^2-u^2-\frac{1}{36}(\alpha ^6-u^6)(1 + o(1))}. \end{aligned}$$

(3.2)

By this, putting $u_\alpha (t) = \alpha s$, Taylor expansion and direct calculation, we obtain

$$\begin{aligned} \sqrt{\lambda }= & {} \frac{1}{\sqrt{2}} \int _{-1}^0 \frac{u_\alpha '(t)}{\sqrt{\alpha ^2-u^2-\frac{1}{36}(\alpha ^6-u^6)(1 + o(1))}}dt\nonumber \\= & {} \frac{1}{\sqrt{2}}\int _0^1 \frac{1}{\sqrt{1-s^2 - \frac{1}{36}\alpha ^4(1-s^6)(1 +o(1))}}ds \nonumber \\= & {} \frac{1}{\sqrt{2}}\int _0^1 \frac{1}{\sqrt{1-s^2}\sqrt{1-\frac{1}{36} \alpha ^4(1+s^2+s^4)(1 + o(1))}}ds \nonumber \\= & {} \frac{1}{\sqrt{2}}\int _0^1 \frac{1}{\sqrt{1-s^2}} \left\{ 1 + \frac{1}{72}\alpha ^4(1 + s^2 + s^4)(1+o(1))\right\} ds \nonumber \\= & {} \frac{1}{\sqrt{2}}\left( \frac{\pi }{2} + \frac{5}{384}\pi \alpha ^4 + o(\alpha ^4)\right) . \end{aligned}$$

(3.3)

This implies (1.9). Thus the proof is complete. $\square$

Proof of Theorem 1.5 (ii)

Let $n = 1$. Then it follows from (1.1) and Taylor expansion that

$$\begin{aligned} -u_\alpha ''(t) = \lambda (u_\alpha (t) + u_\alpha (t)^3(1 + o(1))). \end{aligned}$$

(3.4)

By this and the same argument as that to obtain (2.5), for $-1 \le t \le 0$, we have

$$\begin{aligned} u_\alpha '(t) = \sqrt{\lambda } \sqrt{\alpha ^2-u^2+\frac{1}{2}(\alpha ^4-u^4)(1 + o(1))}. \end{aligned}$$

(3.5)

By this, putting $u_\alpha (t) = \alpha s$ and the same calculation as that to obtain (3.3), we obtain

$$\begin{aligned} \sqrt{\lambda }= & {} \int _{-1}^0 \frac{u_\alpha '(t)}{\sqrt{\alpha ^2-u^2 + \frac{1}{2}(\alpha ^4-u^4)(1 + o(1))}}dt\nonumber \\= & {} \int _0^\alpha \frac{1}{\sqrt{\alpha ^2-\theta ^2 + \frac{1}{2}(\alpha ^4-\theta ^4)(1 + o(1))}}d\theta \nonumber \\= & {} \int _0^1 \frac{1}{\sqrt{1-s^2}} \frac{1}{\sqrt{1 + \frac{1}{2}\alpha ^2(1 + s^2)(1 + o(1))}}ds \nonumber \\= & {} \int _0^1 \frac{1}{\sqrt{1-s^2}} \left\{ 1 - \frac{1}{4}\alpha ^2(1 + s^2)(1 + o(1))\right\} ds \nonumber \\= & {} \int _0^1 \frac{1}{\sqrt{1-s^2}}ds - \frac{1}{4}\alpha ^2\int _0^1 \frac{1+s^2}{\sqrt{1-s^2}}ds + o(\alpha ^2) \nonumber \\= & {} \frac{\pi }{2} - \frac{3}{16}\pi \alpha ^2 + o(\alpha ^2). \end{aligned}$$

(3.6)

By this, we obtain (1.10). Thus the proof is complete. $\square$

Proof of Theorem 1.5 (iii) and (iv)

It follows from (1.1) and Taylor expansion that

$$\begin{aligned} -u_\alpha ''(t)= & {} \lambda \left( u_\alpha (t) + \frac{5}{6}u_\alpha (t)^5(1 + o(1))\right) \quad (n = 2), \end{aligned}$$

(3.7)

$$\begin{aligned} -u_\alpha ''(t)= & {} \lambda \left( u_\alpha (t) - \frac{1}{6}u_\alpha (t)^5(1 + o(1))\right) \quad (n \ge 3). \end{aligned}$$

(3.8)

By this, and the same argument as (3.2) and (3.3), we obtain (1.11) and (1.12). Thus the proof is complete. $\square$