1 Introduction

Geophysical models can benefit greatly from the combined inversion of multiple data sets. Different methods are sensitive to different petrophysical parameters and different parts of the subsurface, and they usually have uncorrelated noise components. Even the use of multiple data sets from the same method can be beneficial, as the noise components of data sets collected at different times are also likely to be uncorrelated. Thus, additional information available for inversion will improve the quality of the resulting model by reducing solution non-uniqueness (Muñoz and Rath 2006). Standard joint inversion approaches are generally used for data that are sensitive to the same petrophysical parameter, such as electrical and electromagnetic resistivity (Yang and Tong 1988; Abubakar et al. 2011) and seismic velocities (Julià et al. 2000), or methods that are sensitive to different physical parameters, but have a structural connection (Gallardo and Meju 2003, 2007; Commer and Newman 2009; Jegen et al. 2009; Moorkamp et al. 2011).

The classical approach to the joint inversion problem is based on a scalar objective function that combines misfit measures for all data sets and also includes a joint term that connects the different data sets (Haber and Oldenburg 1997; De Stefano et al. 2011). Weighting has to be employed to aggregate all misfits into one objective function. Data sets may be weighted equally (Dobróka et al. 1991; de Nardis et al. 2005), have individual weightings (Julià et al. 2000; Mota and Santos 2006), or use sophisticated techniques such as fuzzy c-means coupling for the joint inversion (Carter-McAuslan et al. 2014). The choice of weights can vary between problems (Treitel and Lines 1999), and the choice of inappropriate weights can lead to bias in the results (De Stefano et al. 2011). A set of guidelines for setting weights is given by Marler and Arora (2010).

The use of a combined objective function also makes it difficult to judge the compatibility of data sets: it is important to determine whether data sets are sensitive to similar features and if the assumed relationship between the data sets is valid. Forcing incompatible data sets into a joint model may yield a model that is worse than the corresponding single data set models, because an inversion algorithm will produce unnecessary artefacts trying to compensate for an underlying incompatibility.

One alternative to the conventional approaches is the group of multi-objective evolutionary algorithms, which mimic natural evolution processes (Holland 1975). Such algorithms treat each data set as a separate objective rather than aggregating them into a single objective function, which circumvents forced weighting. Calculating individual objective values allows for detailed statistical analysis. For example, it leads to the creation of trade-off surfaces, which allow inference of data set compatibility. These methods are direct search methods (Lewis et al. 2000), which do not require linearisation approximations or any gradient information. They create an ensemble of solutions rather than a single best fit result, which has the added advantage that the solution ensemble can be evaluated to infer qualitative estimates of model uncertainty.

Multi-objective evolutionary algorithms have demonstrated potential to solve problems in engineering, computer sciences, and finance (Coello et al. 2007; Zhou et al. 2011), but they have been sparsely used in the geophysics community. Kozlovskaya et al. (2007) compared conventional and multi-objective methods for seismic anisotropy investigations, but used a neighbourhood algorithm (Sambridge 1999a, b) instead of an evolutionary algorithm. The earliest applications of multi-objective evolutionary algorithms in geophysics included (Moorkamp et al. 2007, 2010), to jointly invert teleseismic receiver functions and magnetotelluric data, as well as receiver functions, surface wave dispersion curves, and magnetotelluric data. Other work has been done on seismic data (Giancarlo 2010), magnetic resonance and vertical electric soundings (Akca et al. 2014), cross-borehole tomography (Paasche and Tronicke 2014), and reservoir modelling (Emami Niri and Lumley 2015).

We present here a multi-objective joint optimisation algorithm, which is based on the Borg multi-objective evolutionary algorithm by Hadka and Reed (2013). In this work, we focus on the application of the algorithm to quantify data set compatibility and also produce a solution ensemble. We will first explain the algorithm in detail and show how the solution ensemble can be used to generate reliable models. We will then demonstrate the functionality of our data set compatibility measure in synthetic model tests and evaluate influences of noise and data error estimates. In our study, we focus on two sets of magnetotelluric data; however, the concept may be extended to any pair of geophysical data.

2 Theory

2.1 Definition of Multi-dimensional Pareto-Optimality

When dealing with multiple conflicting objectives, it is impossible to define a single best solution without introducing weighting of the objectives. In combination with solution non-uniqueness, this is the reason that conventional approaches, which search for a single best fit solution to a joint-inversion problem, produce biased results.

To mitigate this problem, an alternative way to define optimality has to be employed. In the field of multi-objective optimisation, the most widely used concept to rate solution quality is that of pareto-optimality, which was first introduced by Edgeworth (1881) and Pareto (1896). A solution is considered pareto-optimal if there is no other feasible solution that can improve an objective without deteriorating any other objective, and the entirety of solutions fulfilling this criterion is called the pareto-optimal set. When the pareto-optimal set is projected onto a surface, it is referred to as the pareto-front, which comprises a trade-off surface between the different objectives.

The objective value vectors of the pareto-optimal solutions are pareto-non-dominated. For a minimisation problem with N objectives, the objective vector \(\mathbf x ^* = (x^*_1, x^*_2, \ldots , x^*_N)\), containing the N objective function values for a given solution, is defined to pareto-dominate another vector \(\mathbf x = (x_1, x_2, \ldots , x_N)\) if and only if:

$$\begin{aligned} x^*_i \le x_i \quad \forall i \in \{1, 2,\ldots , N\}~~\wedge ~~\exists j \in \{1, 2, \ldots , N\}: x^*_j < x_j, \end{aligned}$$
(1)

which is denoted by \(\mathbf x ^*\prec _p\mathbf x\) (see, e.g., Coello et al. 2007, p. 10–11).

In a pareto sense, all non-dominated solutions are rated as optimal and no non-dominated solution is considered better than any of the others. In our case, pareto-optimality is a minimal optimality condition that will not always produce physically meaningful results, but rating of the solutions using pareto-efficiency allows for solving the optimation free of weighting biases.

2.2 Multi-objective Evolutionary Algorithm (MOEA)

The multi-objective joint optimisation algorithm is a stochastic approach to yield an ensemble of model solutions to an inversion problem. It is based on the auto-adaptive Borg Multiobjective Evolutionary Algorithm (Hadka and Reed 2013).

The Borg algorithm was chosen as it is a state-of-the-art multi-objective evolutionary algorithm capable of adapting to various problems. Multi-objective evolutionary algorithms generally deteriorate in performance for more than three objectives (Ishibuchi et al. 2008; Zhou et al. 2011); however, the Borg algorithm performs well on problems with many objectives (Hadka and Reed 2013). Other advantages of the algorithm include good convergence and high solution diversity of the solution ensemble, which is necessary to infer model ranges and generate reliable information on the compatibility of different objectives.

Evolutionary algorithms are direct search methods that do not require computation of Frechet derivatives. Such methods require significantly more function evaluations than conventional inversion algorithms, but parallelisation of codes is often possible and enhanced computing power is readily available. The stochastic component inherent in evolutionary algorithms makes them very robust against local minima.

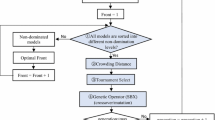
The workflow is illustrated in Fig. 1. A starting population is initiated with random parameters inside predetermined parameter thresholds. All member solutions of the population are then evaluated against the measured data sets and objective values calculated for every objective. This is followed by an evaluation of the domination status of each solution. The objective values are usually expressed as root mean square (RMS) deviations \(\delta\), the misfit of the forward calculated response of a set of model parameters \(\mathbf m\) to a set of n observed data points \(\mathbf d\), normalised by the errors of the observed data points \(\mathbf {\sigma }_d\):

$$\begin{aligned} \delta = \sqrt{\frac{1}{n} \sum _{i = 0}^n \left( \frac{d_{\text {i}} - F({\textbf{m}} )_{i}}{\sigma _{d_i}}\right) ^2}. \end{aligned}$$
(2)

The algorithm also allows the user to set misfit constraints, which effectively limits the feasible region of objective space. Solutions outside the feasible region are treated as invalid.

In addition to the misfit functions, a regularisation measure has to be defined to stabilise the inversion. This measure is treated as separate objective, resulting in pareto-fronts between the model misfits and model complexity. This provides stability by making solutions with lower model complexity outrank solutions with higher complexity for an equal model misfit. The calculation of the regularisation measure is customisable and depends on the model parameters and geometries. In a conventional inversion scheme, the regularisation functional is part of the objective function and its influence in comparison with the misfit measure(s) is determined by a weighting factor, which has to be determined appropriately. Treating the regularisation functional separately from the objective-functions eliminates the need to find this weight factor.

Fig. 1
figure 1

Flowchart of the algorithm’s functionality. A starting population is initiated with random parameters and objective values are calculated. After the domination status for each solution is determined, new population members are created via recombination based on the current population. The new population is then evaluated and the loop is repeated until a termination criterion is reached. After search termination, the results are analysed statistically

Full size image

New population members are created via recombination operators after the solutions are evaluated and their domination status is determined. The solutions to be used for recombination are chosen via tournament selection (Miller and Goldberg 1995). There are a variety of different recombination operators available, but usually, only one is implemented in a given algorithm. Different kinds of operators have different degrees of effectiveness, depending on the type and nature of each individual search problem. This led to the proposal of adaptive operators (Vrugt and Robinson 2007; Vrugt et al. 2009). Hadka and Reed (2013) implemented the Borg algorithm with the capability to auto-adaptively select from six different recombination operators: simulated binary crossover (Deb and Agarwal 1994), differential evolution (Storn and Price 1997), parent-centric recombination (Deb et al. 2002), unimodal normal distribution crossover (Kita et al. 1999; Deb et al. 2002), simplex crossover (Tsutsui et al. 1999; Higuchi et al. 2000), and uniform mutation (Syswerda 1989). The algorithm adapts the probability of a given operator to be used according to its success rate in producing solutions in non-dominated solutions. For a given problem, generally, one of the operators will be dominant (Hadka and Reed 2013). New solutions produced by all recombination operators, except for the uniform mutation operator, are subjected to polynomial mutation (Deb and Goyal 1996). Mutation operators randomly mutate a given parameter of a solution and add a stochastic component to the search, ensuring better search space exploration and robustness of the search against local minima.

The new population produced by the recombination and mutation process is then evaluated and the loop is repeated until a termination criterion—usually a maximum number of solution evaluations—is reached.

It is important to retain optimal solutions during the search to ensure optimisation success and convergence of the search (Zitzler 1999; Zitzler et al. 2000). Borg exercises this so-called elitism by keeping an archive of the non-dominated solutions. When using pareto-efficiency as the optimality criterion for a multi-objective optimisation approach, one has to ensure that the calculated pareto-front is as complete and as close to the real pareto-front as possible. As population and archive cannot be of infinite size, a multi-objective evolutionary algorithm will eventually eliminate solutions, even though they might be non-dominated, known as deterioration of the pareto-front (Hanne 1999). Preventing the pareto-front from deteriorating requires active diversity management (Purshouse and Fleming 2007). Borg employs a modified version of \(\varepsilon\)-dominance (Hanne 1999; Laumanns et al. 2002) to ensure solution diversity.

The N-dimensional objective space is discretised by dividing it into hyper-rectangles (Coxeter 1973) with side lengths \(\varepsilon > 0\) (Fig. 2). Using the notation \(\left\lfloor \frac{\mathbf {x}}{\varepsilon } \right\rfloor = \left( \left\lfloor \frac{x_1}{\varepsilon } \right\rfloor , \left\lfloor \frac{x_2}{\varepsilon } \right\rfloor , \dots , \left\lfloor \frac{x_N}{\varepsilon } \right\rfloor \right)\) (\(\left\lfloor \cdot \right\rfloor\) denotes the floor function) for a \(\varepsilon\)-box index vector for an N-objective problem, dominance [Eq. (1)] is redefined as discrete \(\varepsilon\)-box dominance. An objective vector \(\mathbf x ^* = (x^*_1, x^*_2, \ldots , x^*_N)\) is defined to \(\varepsilon\)-box dominate a vector \(\mathbf x = (x_1, x_2, \ldots , x_N)\) if and only if one of the following equivalent conditions holds:

$$\begin{aligned} \left\lfloor \frac{{\mathbf {x}}^*}{\varepsilon } \right\rfloor&\prec _p \left\lfloor \frac{\mathbf {x}}{\varepsilon } \right\rfloor ,\quad \text {or}\end{aligned}$$
(3a)
$$\begin{aligned} \left\lfloor \frac{{\mathbf {x}}^*}{\varepsilon } \right\rfloor&=\left\lfloor \frac{\mathbf {x}}{\varepsilon } \right\rfloor ~\wedge ~\left| \left| {\mathbf {x}}^* - \varepsilon \left\lfloor \frac{{\mathbf {x}}^*}{\varepsilon } \right\rfloor \right| \right| < \left| \left| {\mathbf {x}} - \varepsilon \left\lfloor \frac{\mathbf {x}}{\varepsilon } \right\rfloor \right| \right| , \end{aligned}$$
(3b)

which is denoted by \(\mathbf x ^*\prec _{\varepsilon }{} \mathbf x\) (after Hadka and Reed 2013). The algorithm also allows for individual \(\varepsilon _i > 0 \quad \forall ~i~,~i = \{1, \ldots , N\}\) to be assigned for each objective.

Fig. 2
figure 2

Illustration of \(\varepsilon\) dominance and \(\varepsilon\) progress for a hypothetical two objective case. Filled circles mark existing archive members, open circles mark solutions that are newly added to the archive, and grey \(\varepsilon\) boxes mark the area dominated by the existing archive members. Solutions (a) and (c) will replace existing archive members, solutions (b) and (c) also satisfy the conditions for \(\varepsilon\) progress, and the \(\varepsilon\) boxes marked with a chequerboard pattern are newly dominated. Modified from Hadka and Reed (2013)

Full size image

Only one solution per \(\varepsilon\) box is added to the archive. If a new solution is found that \(\varepsilon\) box dominates another solution in the same \(\varepsilon\) box, the former solution will be replaced with the new one.

The \(\varepsilon\)-box criterion is also used to monitor search progress. The so-called \(\varepsilon\) progress is achieved if a new-found solution not only \(\varepsilon\) dominates at least on existing archive entry, but is also located in a previously unoccupied \(\varepsilon\) box. \(\varepsilon\) progress is checked sporadically and search restarts will be triggered if search stagnation is detected. If a restart is triggered, the size of the main population is adjusted in relation with the current archive size, according to a predetermined population-to-archive ratio and the population is purged and refilled with new solutions. These new solutions are generally made up of (mutated) archive entries, or new randomly initialised solutions. Maintaining a constant population-to-archive ratio can assist in the avoidance of local minima (Tang et al. 2006). This constant ratio also means that the \(\varepsilon\) values limit the archive and population sizes and the \(\varepsilon\) values can be chosen to control these.

We have adapted the Borg algorithm to jointly invert multiple geophysical data sets, such as electromagnetic resistivity well-logs, and seismic. Each data set is treated as a separate objective represented by its own objective function (see Eq. 2). We have added modules for the statistical evaluation of the resulting solution ensembles of the final archive and intermediate archives, to calculate model statistics and uncertainties, and to determine data set compatibilities.

2.3 Solution Ensemble Appraisal

The \(n_{\text {arch.}}\) solutions contained in the final archive represent the full range of pareto-optimal solutions found by the algorithm before the termination criterion was reached. A pareto-set exists whether or not the data are compatible, but the shape of the distribution of pareto-set members in conjunction with the evolution of this distribution during the optimisation process is dependent on the degree of compatibility. This final solution ensemble can be used to analyse the variability of the model parameters across all solutions to estimate parameter uncertainties. An ideal point in objective space is determined and the solutions close to the ideal point are evaluated to determine the variability of these solutions in parameter space, which indicates parameter uncertainties (Kozlovskaya et al. 2007). The solution with the smallest Euclidean distance to the ideal point is taken as the optimal solution found by the algorithm. This point is chosen as the ideal point under the assumption that with correctly estimated data errors, the normalised misfit will reach a value of \(\delta ^j_{i} = 1\) for the optimal solution.

In our tests, we will consider the hypothetical solution with a misfit of \(\varvec{\delta }= \mathbf {1}\) in all objectives as the ideal solution or ideal point for our tests, with

$$\begin{aligned} \varvec{\delta }&= (\delta _{1}, \delta _{2}, \ldots , \delta _{N})^{\text {T}}\\ \mathbf {1}&= (1, 1, \ldots , 1)^{\text {T}}. \end{aligned}$$

Achieving a misfit of unity is reliant on correct error estimation, and the ideal point will need to be changed if there is reason to believe that error estimates are systematically higher or lower than the given values. Individual misfits are normalised relative to their ideal point, such that

$$\begin{aligned} \delta ^j_{i; \text {norm.}} = \frac{\delta ^j_i}{\left( {\varvec{\delta }^j}\right) }. \end{aligned}$$
(4)

Weighted means \(\overline{x}\) and the corresponding variances \(\sigma _{x}^2\) are calculated for all parameters \(\{x_k\}_{k = 1\ldots n_{\text {arch.}}}\):

$$\begin{aligned} \overline{x}&= \frac{\sum _{k=1}^{n_{\text {arch.}}} w_k \cdot x_{k}}{\sum _{k=1}^{n_{\text {arch.}}} w_k}, \end{aligned}$$
(5a)
$$\begin{aligned} \sigma _{x}^2&= \frac{\left( \sum _{k=1}^{n_{\text {arch.}}} w_k \cdot (x_k - \overline{x})^2\right) \cdot \sum _{k=1}^{n_{\text {arch.}}} w_k}{\left( \sum _{k=1}^{n_{\text {arch.}}} w_k\right) ^2 - \sum _{k=1}^{n_{\text {arch.}}} w_k^2}. \end{aligned}$$
(5b)

The weights \(\{w_k\}\) are chosen as the distance of a given solution k to the ideal solution in objective space:

$$\begin{aligned} w_k&= ||(\varvec{\delta }_k - \mathbf {1})||_2, \end{aligned}$$
(6)

to ensure that solutions closest to the ideal point have the largest influence on the result. The regularisation objective is not included in the computation of the weights, as it is not calculated as a misfit-function. The solution’s distance from the ideal point is also used to assess the convergence of the population during an inversion by calculating the median of the distances of all analysed solutions.

2.4 Data Set Compatibility

The concept of data-set compatibility is closely related to the concept of conflicting objectives and tries to quantify the degree of conflict. Pareto-front objective trade-off surfaces can be used to analyse compatibility of the different conflicting objectives.

Identical data sets are considered maximally compatible. Hence, for any solution, the misfits \(\{{\varvec{\delta }}_k\}_{k = 1\ldots n_{\text {arch.}}}\) for perfectly compatible data sets would be identical across all N objectives and would be distributed in objective misfit space along \(\delta _{k,1} = \delta _{k,2} = \cdots = \delta _{k,N}\forall ~k\). Therefore, in two-objective misfit space, the ideal fit is equivalent to a line with slope \(m_{\text {ideal}} = 1\).

To assess the pairwise compatibility of any two objectives, we calculate a linear fit for the solutions in the 2-D plane of objective misfit space of the objectives in question. The deviation of this fit from the ideal line with slope 1 gives information about the degree of compatibility between the two data sets. This scheme is illustrated in Fig. 3.

Fig. 3
figure 3

Conceptual misfit visualisation of two objectives for a hypothetical archive of two compatible data sets. The archive members of the pareto-optimal set are scattered around the ideal line with slope 1. The optimal solution is defined as the archive member with the smallest norm deviation from the point \(\mathbf {1}\) in the space of normalised misfits

Full size image

The standard linear least squares regression (Lawson and Hanson 1974) is a non-robust measure (McKean 2004). We choose the robust Theil–Sen estimator (Theil 1950; Sen 1968) as a regression method to avoid bias from outliers without needing to analyse the data set for outliers and remove them. This estimator for a set of Q 2-D points \(\{(x_i,y_i)~|~i=1\ldots Q\}\) is calculated as the median \(\tilde{m}\) of the slopes \(\{m_{i,j}~|~ i,j = 1\ldots Q\}\) calculated between every possible two point combination:

$$\begin{aligned} m_{i,j} = \frac{y_j - y_i}{x_j - x_i} \quad \forall \quad i\ne j, \quad i>j;\quad \tilde{m} = {\text {median}} \{m_{i,j}\}. \end{aligned}$$
(7)

The opening angle \(\gamma\) between the ideal line and the fitted line is assessed to make the analysis independent of objective misfit scale choice, and we assess

$$\begin{aligned} \tan {\gamma } = \left| \frac{\tilde{m} - m_{\text {ideal}}}{1+\tilde{m} \cdot m_{\text {ideal}}}\right| = \left| \frac{\tilde{m} - 1}{1+\tilde{m}}\right| . \end{aligned}$$
(8)

Representing the ideal line and fitted line graphically, and using identically scaled axes, perfect compatibility results in a deviation angle from the ideal line of \(\gamma = 0^\circ\), and maximum incompatibility results in a deviation angle of \(\gamma = 90^\circ\). Deviation angles of \(\gamma < 45^\circ\) indicate data compatibility, whereas deviation angles of \(\gamma > 45^\circ\) indicate incompatibility. Figure 4 demonstrates the conceptual differences between the misfits of solutions for compatible and incompatible data sets, respectively.

Fig. 4
figure 4

Conceptual misfit visualisations for two hypothetical pairs of data sets: one pair of compatible data sets (blue) and one pair of incompatible data sets (orange). The slopes of the Theil–Sen regressions through both archives are indicated by the labelled ‘compatible’ and ‘incompatible’ regions

Full size image

For real-world data sets, perfect compatibility can never be achieved due to a variety of reasons, which will have different manifestations in the way the pareto-fronts deviate from the ideal line: different methods can have different sensitivities and resolution, different depth of investigation, or data sets might have different levels of data error. Different sensitivities or different depth of investigation can cause data sets to neither be fully compatible nor incompatible, but rather partially compatible or disconnected. The pareto-front surfaces for disconnected or partially compatible data sets will have different characteristics than fronts of truly incompatible data sets.

3 Synthetic Tests

We demonstrate the functionality of our approach using sets of synthetic data. We use simulated 1-D magnetotellurics (MT) data sets and resistivity well-logs, which will be inverted for isotropic resistivity and layer thickness.

Using 1-D MT data, we ensure complete controllability of the compatibility of the data sets, while still being able to simulate a variety of different compatibility situations, such as partially compatible data sets with different depths of sensitivity (penetration depth is proportional to the root of signal period). The choice of 1-D data sets also enables easy implementation and greatly reduces the runtime of the algorithm, allowing for intensive testing.

The misfit for the \(\nu\)th frequency is calculated as

$$\begin{aligned} \delta ^\text {F}_{\nu } = \sqrt{\left( \frac{d_{\nu } - F({\mathbf{m}})_{\nu }}{\sigma _{d_{\nu }}}\right) ^2}. \end{aligned}$$
(9)

To assess partial compatibility, we analyse the misfits for each individual recording frequency, in addition to the standard misfits, calculated from the sum of all individual misfits.

There are a variety of different regularisation functionals with different characteristics (Pek and Santos 2006, p. 144) of which we use the discretised version (discretisation h) of the total variation functional (Rudin et al. 1992)

$$\begin{aligned} \sum _{i=1}^{n_{\text{layers}}}\sqrt{(\textbf{m}_i-{\textbf{m}}_{i-1})^2 + \beta ^2} {\xrightarrow {^{ h {\rightarrow} 0 }}} {\int _0^{\infty } |\nabla }{\textbf{m}}({z})|\,{\text {d}}{z} , \end{aligned}$$
(10)

with a small regularisation constant \(\beta >0\) for numerical stabilisation. We chose the total variation as it can conserve sharp contrast in the model. This is advantageous, as sharp contrasts are often required in layered models.

We created two different synthetic resistivity models (Fig. 5). Model I is the reference model with a low resistivity anomaly between 500 and 600 m and Model II has been designed to generate data incompatible to the first set. Model II has higher resisitivities than Model I in the top 1290 m of the model and lower resisitivities below that depth.

Fig. 5
figure 5

Synthetic 9-layer model Model I (blue) and the synthetic 7-layer model Model II (red)

Full size image

3.1 Data Set Properties

For each of the models, two MT data sets with different frequency ranges are created using Wait’s recursion formula (Wait 1954). This allows us to assess how the compatibility measures behave for data with different depths of sensitivity. The MT data sets have 17 frequencies each, with a frequency range of 6–1448 Hz [broadband (BB) data set], and 128–32768 Hz, respectively [audio-magnetotelluric (AMT) data set]. Eight data points of each of the two different types of MT data lie within the overlapping frequency range of 128–1448 Hz. Everything deeper than the penetration depth corresponding to a 128 Hz signal can, therefore, only be detected by the simulated BB MT measurements. In addition, a resistivity well-log was built for each model, ranging from a depth of 150–1000 m, with a 0.25 m sample interval.

Gaussian noise with a standard deviation equivalent to 3% of the impedance tensor amplitude is added to both the MT data types. Accordingly, error estimates equal to 3% of the impedance tensor amplitudes are assigned. Gaussian noise of 5% is added to the well-log data and error estimates equal to 5% of the parameter values are assigned.

All tests were run for 250,000 solution evaluations each. For the data set compatibility analysis, intermediate solution archives are extracted after 1000, 10,000, and 100,000 solution evaluations in addition to the final archive. As all non-dominated solutions are retained during the processing, the same solutions can be contained in multiple iterations of the archive. Hence, whenever solutions from multiple archives are analysed together, only unique solutions are considered to avoid skewing the statistical analysis.

3.2 Resulting Model Distribution

During the model building, the layer thicknesses are variable, but the number of layers nlayers is held constant across all models. The resulting ensemble of models is evaluated with regard to the geometry and the resistivity of the layers. To account for the inherently different data sensitivities and resolutions of different geophysical data, as well as to increase comparability between the different archive solutions, the depth interval between the surface and the deepest overall estimate for the bottom of the last layer is evenly divided into small discrete model segments of constant thickness. A layer-interface can occur at the top of each individual segment. For each solution, the parameter values at a certain depth are mapped to the corresponding segments for each solution, transferring all solutions into a unified segment space. For example, for MT data, the sensitivity decreases with depth dependent on the frequency range. By keeping the segment thickness constant, it is guaranteed that no information is lost when jointly working with data sets from different methods, which have varying sensitivities and resolution.

The segment resistivities are analysed by calculating weighted averages across all extracted solutions.

The layer geometry is evaluated by computing the probability for an interface to be located in a specific segment. This is calculated by using the number of archive solutions that have an interface in a given segment \(c_i\) and the total number of final archive solutions \(n_{\text {arch.}}\):

$$\begin{aligned} p^{\text {interface}}_i&= \frac{c_i}{n_{\text {arch.}}}, i \in \{1, 2,\ldots ,n_{\text {seg.}}\} \end{aligned}$$
(11a)
$$\begin{aligned} \Rightarrow \sum _i^{n_{\text {seg.}}} p^{\text {interface}}_i&= n_{\text {layers}}. \end{aligned}$$
(11b)

If all solutions have an interface in the same segment, the interface probability at that segment will be 1. Including the top interface of the first layer, which is assigned a probability of 1, the sum of all interface probabilities over all segments equals the number of model layers.

In addition to the standard misfit for all data points as defined in Eq. 2, for the MT data sets, we calculate the cumulative misfit over the eight overlapping frequencies 128–1448 Hz (Eq. 9), to allow for a detailed comparison of the regions of equal sensitivity for the different MT data types:

$$\begin{aligned} \delta ^{\text {CMOF}}= \sqrt{\frac{1}{8}\sum _{\nu =0}^{8} {\delta ^\text {F}_{\nu }}^{2}}. \end{aligned}$$
(12)

4 Modelling

To demonstrate the feasibility of the approach, we analyse the example data sets successively and in detail to illustrate the influences of the various parameters. First, we demonstrate the overall functionality and present the algorithm’s outputs using compatible data sets. Then, we characterise incompatible data sets, and extend the concepts from two to multiple objectives. Finally, we discuss the negative influence of ill posed problems and the lack of adequate regularisation.

4.1 Two Objectives—Compatible Data Sets

We will first evaluate a simple case with two compatible objectives to introduce the concepts of the method. The objectives are built from AMT and BB MT data sets, combined with regularisation. This compatible data example uses the MT data sets that both have been calculated from Model I.

Figure 6 shows the best solution and the average result for the compatible case calculated from the final solution archive. The optimal solution achieved misfits of \(\delta _{\text {AMT}_\text {I}} = 1.3\) and \(\delta _{\text {BB}_\text {I}} = 1.5\) and was at a distance of 0.5 from the ideal point. The average model exhibits an average standard deviation of 21% relative to the segment values. There is an overestimation of the resistivity in the low resistivity zone, which reaches values of \(30~\Omega\)m for the best solution and \(43~\Omega\)m for the average model, as opposed to the \(10~\Omega\)m of the true model. There is also an underestimation of the resistivities at greater depths, with the best solution showing a closer fit than the average solution. The locations of layer interfaces are well determined at low depths, but are subject to higher uncertainty at larger depths. The depth interval of 700–800 m is jointly constrained by the two data sets, resulting in well constrained layer boundaries. Below this depth, the model is only constrained layer boundaries. Below this depth, the model is only sensitive to the broadband data, which relies on lower frequencies and, therefore, has a lower resolution, making it incapable of determining well constrained interfaces.

Fig. 6
figure 6

Model results from the two-objective case with 3% noise. The red line shows the true synthetic model and the green line represents the weighted average model based on the 1142 solutions of the final archive, including the model uncertainties in grey. This are calculated using Eqs. (5a) and (5b). The optimal solution is presented in blue. It achieved misfits of \(\delta _{\text {AMT}_\text {I}} = 1.3\) and \(\delta _{\text {BB}_\text {I}} = 1.5\) and was at a distance of 0.5 from the ideal point. The average model exhibits an average standard deviation of 21% relative to the segment values. The interface probabilities are presented in black calculated from the final archive solutions

Full size image

The CMOF are shown in Fig. 7a. The solutions are distributed along the ideal line. The linear fit deviates from the ideal line by 3\(^{\circ }\).

Fig. 7
figure 7

Archive solutions for AMT objective and the BB-objective in the compatible two-objective case with 3% noise. The 2440 unique solutions combined from the archives after 1000, 10,000, 100,000, and 250,000 solutions evaluations are displayed, as well as the corresponding Theil–Sen regression, the ideal line, and the ideal point. a Cumulative objective mists over the overlapping frequencies. b Objective mists over all frequencies

Full size image

Figure 7b displays the locations in objective space of all the solutions extracted from the archives. The different depths of investigation of the two data set cause the solutions to be distributed in a cone shape, shifted towards higher BB misfits. The main cluster extends over a misfit of about 1.3–2.4 in the direction of the AMT misfit and from about 1.5–6.8 in direction of the BB misfit, with the optimal solution found with misfits of \(\delta _{\text {AMT}_\text {I}} = 1.3\) and \(\delta _{\text {BB}_\text {I}} = 1.5\), at a distance of 1.9 from the ideal point. The deviation from the ideal line of the linear fit is 23\(^{\circ }\) (Table 1).

It should be noted that in Fig. 7b, a combination of archive members after 1000, 10,000, 100,000, and 250,000 evaluations is plotted. Although each individual archive does not contain dominated solutions, earlier archive solutions are likely dominated by members of later archives. The dominated solutions of earlier archives are included to capture the evolution of the solution distribution, which is a major indicator of the objective compatibility. Therefore, all results are included during the compatibility analysis; however, in the final consideration of a representative model, dominated solutions should be discarded.

Table 1 Analysis of the deviation from the ideal line and median distance from the ideal point (1,1) for the compatible two-objective case (with 3% noise). The analysis is performed for archives at different stages of the inversion run, as well as for all extracted archive members combined and the CMOF of the combined archive members
Full size table

4.2 Two Objectives—Incompatible Data Sets

We have established how resulting model distributions behave for compatible data. Now, we explore the results of the algorithm for incompatible data. The AMT data set is built from Model I and the BB data set is calculated using Model II to simulate data incompatibility.

The resulting pareto-fronts are shown in Fig. 8a. The CMOF are distributed along a line with a deviation of 65\(^{\circ }\) from the ideal line and a median distance from the ideal point of 20.64 (Table 2), which contrasts the analysis of compatible data. The main cluster of solutions covers AMT misfits of 4–350 and BB misfits of 5–170. These differences in misfit ranges are caused by the fact that the models for Model I and Model II exhibit greater similarity at depth than close to the surface. Hence, the misfits of the lower frequency BB data set are smaller.

Table 2 Analysis of the deviation from the ideal line and median distance from the ideal point (1,1) for the incompatible data two-objective case with 3% Gaussian noise on the data. The analysis is performed for archives at different stages of the inversion run, as well as for all extracted archive members combined and the CMOF of the combined archive members
Full size table

The same pattern can be observed for the full frequency range misfits (Fig. 8b). Compared to the CMOF the line shows a higher degree of scatter, a slight curvature, and exhibits a deviation from the ideal line of 71\(^\circ\). This curvature is caused by the different frequency ranges of the two data sets.

Fig. 8
figure 8

Archive members for AMT objective and the BB objective in the incompatible two-objective case with 3% noise. As there is no compatibility between the objectives, there is no pareto front in this case. The 22,148 unique solutions combined from the archives after 1000, 10,000, 100,000, and 250,000 solution evaluations are displayed, as well as the corresponding Theil–Sen regression, the ideal line, and the ideal point. a Cumulative objective misfits over the over lapping frequencies. b Objective mists over all frequencies

Full size image

The distances from the ideal solution and the large deviation from the ideal line illustrate that the algorithm is able to find solutions with low misfits for each of the objectives individually, but it is impossible to find a solution that reaches acceptable misfits for both objectives at the same time.

4.3 Multiple Objectives

We perform two test runs with three objectives to investigate the behaviour of the compatibility measures for compatible and incompatible cases with more objectives. Both tests use the AMT and the BB data set based on Model I. The test simulating compatible data sets uses the synthetic resistivity well-log based on Model I and the test for incompatible data uses the Model II resistivity well-log. Both well-logs cover depths of 150–1000 m.

Figure 9 shows the best and average results for the compatible three-objective case. The added information from the well-log helps to better define the position and resistivity of the low resistivity anomaly compared to the two-objective case (Fig. 6). The anomaly is identified at the true location and has a resistivity of \(11.8\,\Omega\)m for the best found solution and \(24.5\,\Omega\)m for the average solution. The benefit of the constraints added by the well-log is also reflected in the smaller error bars of the average solution, as compared to the two-objective case, with the average model exhibiting an average standard deviation of 18% relative to the segment values.

Fig. 9
figure 9

Model results from the multi-objective case. The red line shows the true synthetic model and the green line represents the weighted average model based on the 6771 solutions of the final archive, including the model uncertainties in grey. The optimal solution is presented in blue. It achieved misfits of \(\delta _{\text {AMT}_\text {I}} = 1.3\), \(\delta _{\text {BB}_\text {I}} = 1.7\), and \(\delta _{\text {WELL}_\text {I}} = 1.4\) and was at a distance of 0.8 from the ideal point. The average model exhibits an average standard deviation of 18% relative to the segment values. The interface probabilities are presented in black calculated from the final archive solutions

Full size image
Fig. 10
figure 10

Pareto-fronts for pairwise AMT-BB objectives (blue triangles), AMT-WELL objectives (red squares), and BB-WELL objectives (green diamonds) with the corresponding Theil–Sen regressions in the same colour for the multi-objective case for both the a compatible and b incompatible cases. The ideal point is represented by a magenta star and the broken black line represents the ideal line. For both cases, the objective misfits are shown over all frequencies. The calculated pareto-front is actually 3D, but here, we visualise the 2D components. Inset in both cases are zoomed out versions of the graph showing the overall structure of the regressions

Full size image
Table 3 Analysis of the deviation from the ideal line and median distance from the ideal point (1,1,1) for the multi-objective case inversion runs. The analysis is performed for archives at different stages of the inversion run, as well as for all extracted archive members combined and the CMOF of the combined archive members. The three datasets are audiomagnetotelluric (A), broadband magnetotelluric (BB), and well-log (W)
Full size table

As there are three objectives competing in this test, the compatibility analysis is performed pairwise for each of the three possible two-objective combinations. In the case of compatible data sets, the linear fits for extracted solutions exhibit deviations from the ideal line of \(\gamma _{\text {~comp;AMT-BB}} = 5^\circ\), \(\gamma _{\text {~comp;AMT-WELL}} = 6^\circ\) and \(\gamma _{\text {~comp;BB-WELL}} = 15^\circ\), indicating good compatibility between all objectives (Table 3). The optimal found solution has objective values of \(\delta _{\text {AMT}_\text {I}} = 1.3\), \(\delta _{\text {BB}_\text {I}} = 1.7\) and \(\delta _{\text {WELL}_\text {I}} = 1.4\), and is at a distance of 0.8 from the ideal point. The median distance from the ideal point achieved by the solutions from the final archive is 4.85.

Good objective compatibility is also indicated for the two MT objectives in the case of incompatible data, with the linear fit for all solutions deviating by \(\gamma _{\text {~incomp;AMT-BB}} = 3^\circ\). The two objective combinations featuring the well-log data on the other hand show clear signs of incompatibility. The linear fit of the solutions projected onto the objective space plane of the AMT misfit and the well-log misfit exhibits a deviation of \(\gamma _{\text {~incomp;AMT-WELL}} = 83^\circ\) from the ideal line, and for the combination of BB MT data set and well-log the deviation is \(\gamma _{\text {~incomp;BB-WELL}} = 57^\circ\) (Table 3). This smaller deviation for the BB-WELL projection compared to the AMT-WELL combination is caused by the larger penetration depth of the BB data that exceeds the depth range constrained by the well-log, whereas most of the depth range that the AMT data are sensitive to is constrained by the well-log. The median distance from the ideal point is 9.1, and as such significantly larger than for the compatible data.

The clear separation into compatible and incompatible data apparent from the analysis of the deviations of the linear fits from the ideal line is less obvious from a visual inspection of the solution distributions (Fig. 10). The objective combinations including the well-log show similar distributions for the compatible and the incompatible case. In each case, the main solution clusters have a width of about 10 in direction of the well-log objectives and a width of 40–90 in direction of the MT objectives. This asymmetry is caused by the fact that the well-log only constrains part of the model, so that models fitting the well-log can still vary significantly in the misfit of the MT data sets.

5 Discussion

The evaluation of jointly inverted or jointly interpreted geophysical data is complicated, and it is vital to assess if information from different data sets can be jointly analysed in the first place. We have demonstrated that the output of the algorithm can be interpreted as a measure for the mutual compatibility of multiple data sets.

Using a linear regression allows us to make direct meaningful analysis of the geometry of the solution space. The chosen tool, Theil–Sen regression, is also very robust with respect to outliers. The slope of the Theil–Sen regression to the projection of the solution distribution into 2-D objective space is a good indicator for objective compatibility. Incompatible objectives generally show deviations of \(\gamma > 45^\circ\) and compatible objectives exhibit deviations of \(\gamma < 45^\circ\).

The results for the deviation angles are consistent across individual archives, but cases can occur were the deviation angle results based on different intermediate archives vary significantly. Analysing only individual archives could, therefore, lead to false conclusions about the level of objective compatibility. Archives from the early stage of an inversion in particular often contain only a small number of solutions, yielding misleading results. Hence, a maximal number of solutions should be extracted during inversion runs to be analysed together.

The necessity for a statistical analysis of the solution distributions is illustrated by the multi-objective tests. This case demonstrates that visual inspection can be deceiving and Theil–Sen analysis is required. Inspecting the solution distributions of the MT–well-log projections, the distributions look very similar for the compatible and the incompatible case, but the Theil–Sen analysis detects major differences in the distributions and correctly indicates the compatibility in both cases. The close clustering of a large number of solutions can especially lead to false interpretations, as distribution patterns may be obscured.

The deviation angles show values just above the compatibility threshold, whereas the distances from the ideal point are very low and indicate that acceptable misfits are reached for both objectives. Only the analysis of the misfits for the coinciding frequencies yields a deviation angle below the threshold, with \(\gamma = 25^\circ\). These are the kind of solution distributions that also have been found to represent compatible objectives by Moorkamp et al. (2007). In cases like this a thorough visual and numerical analysis of the solution distributions has to be performed. This has to be done carefully, as close clustering of many solutions can give false impressions. In the test situation, the linear fit is dominated by solutions that extend along the \(\delta _{\text {BB}_\text {I}}\)-direction. This is caused by the BB MT data sets fully constraining the AMT data set, as the BB data have a higher penetration depth, which is expressed in the solution distribution being shifted towards higher BB data misfits. These types of shifted distribution can also be observed in Moorkamp et al. (2010), especially for the combination of Rayleigh wave dispersion data and MT data.

For the assessment of the balance of mutual data constraint, it is important that the misfits of the objectives are of comparable magnitude. The normalisation of the data misfits by the data error (Eq. (2)) ensures that the misfits become comparable to some extend and also guarantees that fits below the error level are expressed in misfits of \(\delta < 1\) regardless of the type of data. Nevertheless, different data types and/or varying error levels can influence the deviation measure and may bias the assessment of the mutual constraint balance.

In addition to assessing the compatibility of inverted data sets, the generated solution ensembles can be used to estimate average models and model errors. However, in our case, these are of qualitative rather than objective nature, as it is not statistically possible to extract robust estimates of model covariance from a single solution ensemble generated by a genetic algorithm. The trade-off for fast convergence of genetic algorithms compared to Monte Carlo methods is that the final ensemble is not generated completely independently, but often depends on good models from the early iterations. Robust statistical model averages and model errors can be determined by performing several inversion runs (Stoffa and Sen 1991) or resampling the final solution ensemble (Sambridge 1999b).

The inversion runs for this study had run times of 1–20 min for 100,000–250,000 solution evaluations. General run-time analysis for multi-objective evolutionary algorithms has been performed (Laumanns et al. 2004), but precise run-time predictions are difficult as they are highly problem dependent. The run times are dependent on the number of objectives and the degree of compatibility between the objectives, as compatible objectives make it easier to find well fitting solutions and, therefore, show accelerated convergence. The adaptive nature of the Borg algorithm makes run-time predictions especially difficult, as the variable population and archive sizes and the search restarts performed to mitigate search stagnation can not be projected.

6 Conclusions

Multiple approaches to joint inversion modelling of geophysical data exist, but the application of evolutionary algorithms is not common in this field. The ability to jointly invert a number of data sets without the need for data weighting, while providing model uncertainty and data set compatibility information makes multi-objective approaches advantageous over conventional linearised schemes.

We have developed and implemented a pareto-optimal multi-objective inversion algorithm for the analysis of geophysical data, the advantages of which are as follows. The use of an evolutionary algorithm allows the evaluation of a distribution of solution models. This distribution can be analysed with regard to the physical implications of the model parameters and with respect to the quality of the data. Potential contained ambiguities and resolution restrictions of the data can be expressed in terms of data set compatibility. We have presented a scheme to effectively assess this compatibility. This analysis can be applied independent of the actual modelling part, and it can be combined with other (multi-objective) inversion and modelling software to independently assess data set quality. This can improve the overall data and model interpretation, and it, therefore, is a valuable addition to the general toolbox for geophysical data inversion modelling.

We have demonstrated the capabilities of this algorithm by applying it to synthetic data. By defining different objective functions, the application of the algorithm to other data sets, both synthetic and real, is a straight forward process and does not require major alterations of the code.