Observation-Driven Method Based on IIR Wiener Filter for Microseismic Data Denoising

Abstract

Reliable analysis of low-energy earthquakes (microseismic) depends on how accurately one can detect and pick the arrival times, which are strongly influenced by the noise content. The study of microseismic events becomes even more challenging when the sensors are located on the surface because of the poor signal-to-noise ratio (SNR). Consequently, efficient and robust techniques for denoising microseismic data are necessary. In this study, we propose a method based on an infinite impulse response (IIR) Wiener filter. The proposed method uses statistics based on signal observations (noisy data) and the underlying noise, both recorded by various sensors. The method presented here precludes the need for statistics or prior knowledge of the signal of interest. The second-order statistics of the noise and the noisy data are extracted from the recorded data only. As an advantage, in deriving the filter’s impulse response, no underlying structure of noise is assumed. Therefore, our method works for various types of noise, e.g., uncorrelated, spatially correlated, temporally correlated, Gaussian and non-Gaussian noise. Hence, the proposed method can be suitable as well for microseismic data recorded in diverse seismic noise environments. The criteria used to optimize the filter impulse response is the minimization of the mean square error. The proposed method is tested on synthetic and field data sets and found to be effective in denoising microseismic data with very low SNR ($-~12$ dB).

1 Introduction

A microseismic event is considered to be a small magnitude earthquake, having a magnitude as low as $-~3$ (Maxwell et al. 2008). It can occur as a natural phenomenon or as a result of human activities within the earth. Analysis of artificially induced microseismic events is essential for oil and gas reservoir geophysics (e.g., Kendall et al. 2011) and in geologic carbon dioxide storage (e.g., Verdon 2011). Both these examples of applications of microseismic monitoring are related to conventional reservoirs. However, microseismic analysis is used extensively in unconventional reservoirs as well for imaging the fracture networks. Moreover, microseismic monitoring has been common in the mining industry for over 100 years where it is primarily used for safety from rockbursts and assessing the state of stress within a mine (Mendecki 1993; Castellanos and van der Baan 2013) in the study of water reservoir-induced seismicity for at least 5 decades (Simpson et al. 1988) and in the geothermal industry (Pearson 1981), but its application in the oil and gas industry is relatively new. High-pressure fluid is typically injected to fracture the rock and increase permeability, thus enhancing production. During such a process, microfractures can be induced in the vicinity of the injection well. Monitoring and analyzing these microfractures help understand the rock-breaking mechanisms during the injection process and reservoir exploitation (e.g., Maxwell 2011). To locate the microseismic hypocenters, the accurate identification of microseismic events is crucial.

To monitor these microseismic events, typically 8–12 three-component sensors are placed in nearby wells or on the earth’s surface (Eaton et al. 2014; Caffagni et al. 2016). Since it is more cost effective to place geophones on the surface than burying them deeply in a borehole, several hundred sensors can be used in surface arrays (Duncan 2012). Moreover, surface arrays offer other advantages as well. For example, it is known that the accuracy and precision of the hypocenter locations in microseismic monitoring depend on both the signal-to-noise ratio (SNR) of the recorded data and the spatial distribution of the receivers. Usually, downhole monitoring provides better detection because of a higher SNR; however, the precise location of events might be difficult, especially in the case of a single monitoring well (Eisner et al. 2010). Unlike the accurate depth estimation, epicentral errors for microseismic event locations using downhole arrays increase as a function of distance from the monitoring well. On the other hand, although surface monitoring often suffers from low SNR, the ability to place receivers in multiple azimuths and offsets allows for precise epicenter (horizontal) event location (Mousavi et al. 2016a). The surface microseismic data are characterized by a low SNR (Shemeta and Anderson 2010); consequently, the main challenge in the study of microseismic events is to enhance the SNR by suppressing/removing the noise.

Generally, several denoising or SNR enhancement methods exist in the literature. Seismic interferometry is a well-known technique to enhance the SNR of the seismic data record, which includes cross-correlation, stacking and convolution (Al-shuhail et al. 2012; Mallinson et al. 2011; Bharadwaj et al. 2013). A different approach that allows the reconstruction of signals from noisy observations is based on time-frequency analysis (Mousavi and Langston 2016a; Vera Rodriguez et al. 2012; Mousavi et al. 2016b). This filtering method encodes the noisy signal as the instantaneous frequency of a frequency modulated analytic signal. The signal is recovered by estimating the peak of the time-frequency distribution of the analytic signal. This approach is sensitive to the noise interferences that detract the energy concentration in time-frequency distribution. Furthermore, the wavelet transform is used to decompose the noisy signal into time-frequency components using the appropriate mother wavelet. Here, a threshold is necessary to obtain the enhanced signal. Proper selection of the mother wavelet and the number of decomposition levels are crucial for these methods. A reassignment strategy, together with pre- and post-processing steps, is added in the time-frequency based method for improving the denoising results (Mousavi and Langston 2017). A data-driven approach that derives the basis function from the noisy signal is known as empirical mode decomposition (Han and van der Baan 2015). However, for this decomposition, the basis function might not be accurate because of the strong noise that affects the denoising results in a low SNR environment. There are other denoising methods that are based on thresholding in time-frequency transforms, e.g., the Radon transform (Sabbione et al. 2013, 2015), reduced-rank filtering (Sabbione and Velis 2013; Iqbal et al. 2016) and damped multichannel singular spectrum analysis (Huang et al. 2016).

Denoising using a Wiener filter approach is also a commonly used method in active seismic surveying and has been used for more than 4 decades (e.g., Peacock and Treitel 1969; Haldorsen et al. 1994). However, the Wiener filter method requires the knowledge of the statistics of the signal, which is not normally available in practice. A solution to this difficulty is to use the wavelet transform to partially differentiate the signal from the noise in an initial stage, and then the Wiener filter is applied after calculating the signal statistics (Aghayan et al. 2016; Kimiaefar et al. 2016). In these methods, wavelets are used to extract the high and low frequency components. The high frequency components are assumed to be noise. Of course a threshold and a basis function (mother wavelet) are needed for this purpose. Proper selection of the mother wavelet is crucial in wavelet transform, and denoising results are greatly affected by the type of wavelet. Improving the SNR of speech signals using the Wiener filter without knowing the signal statistics was proposed by Chen et al. (2006), who calculated the noise statistics using the silence intervals in speech that represent pure noise (including electronically produced noise). Similar approaches are also used in seismology by intuitively finding the noise-only part in data prior to an earthquake or controlled source occurrence (Wang et al.2008, 2009; Coughlin et al. 2014; Mousavi and Langston 2016c; Khadhraoui and Özbek 2013; Baziw and Weir-Jones 2002). Intuitively finding the noise-only part in surface microseismic data is very difficult because of the low SNR. Hence, the main challenge in microseismic surface monitoring is the realistic estimation of the seismic noise. In this study, the noise is estimated blindly, i.e., without the wavelet transform (thus avoiding having to select a proper mother wavelet) or using the assumption that the noise-only portion of the data is available and known. Mousavi and Langston (2016b) proposed minimally controlled recursive averaging in the short-time Fourier transform domain for estimating the noise. Their method was based on the work of Martin (2001) and Cohen (2003). However, their approach requires a large adaptation time (which, unfortunately, gives incorrect locations of events), and the threshold is also fixed for all the frequencies (see Rangachari and Loizou 2006). Eventually, an IIR Wiener filter is used for the first time in a non-similar approach to that used in the FIR Wiener filter together with a noise estimation method similar to the one proposed by Rangachari and Loizou (2006).

In this study, a method is proposed based on two features of the microseismic data. First, the occurrence of microseismic events is sporadic over time. Therefore, a suitable monitoring period is necessary; hence, portions of the recorded traces are occupied by pure noise. Second, the statistical knowledge (for designing the Wiener filter) of the microseismic event is unknown in advance. Considering these two features, in this study an observation-driven denoising method based on the IIR Wiener filter is proposed. The method works by estimating the statistics of the noise and the observation (signal plus noise) from the received data without any prior knowledge of the signal or the noise statistics. The filter gives promising results when applied to synthetic, semi-synthetic and field data sets at very low SNR of $-~12$ dB, without assuming any specific type of noise. Thus, this makes it suitable for denoising surface microseismic data with any type of noise, e.g., Gaussian, non-Gaussian, correlated, uncorrelated and coherent noise. Note that this article presents a contribution to the SNR enhancement using a data-driven IIR Wiener filter, which, to the best of our knowledge, has never been proposed before in microseismic investigation.

In the following section, a derivation of the IIR Wiener filter is presented. Next, the estimation of the autocorrelation of the noise and the noisy observations from the recorded traces, which is needed for the filter, is discussed. Finally, the proposed method is validated using synthetic and field data sets.

2 IIR Wiener Filter Design for Microseismic Denoising

The Wiener filter is used to statistically estimate the desired signal from the noisy seismic trace, usually in the case of additive noise. Typically, filters are designed for a specific frequency response. However, the Wiener filter adopts a different approach. It is required to have prior statistical knowledge of the desired signal and the noise (or the observation) and the filter is designed so that its output signal matches with the original desired signal as much as possible. With the proper design, a Wiener filter can be used to filter out the noise to get the underlying signal of interest. In this work, we will design the Wiener filter without prior statistical knowledge. To clarify this technique, let A, B and C be the desired signal, the noisy signal and the output of the Wiener filter, respectively. Mathematically, we can write the error $e_r$ as

$$\begin{aligned} e_r=C-A. \end{aligned}$$

The Wiener filter is designed by minimizing the mean-square error, i.e.,

$$\begin{aligned} {\mathrm{{min}}} \ E\{e_r^2\}, \end{aligned}$$

where E is the mathematical expectation (Proakis 1985).

In signal processing and mathematics, a discrete-time signal, which is a sequence of complex or real numbers, can be converted to a complex frequency domain representation using the z-transform. This is equivalent to the Laplace transform in continuous time. For more details about the Wiener filter and z-transform, see Proakis and Manolakis (2006), Sayed (2008) and Haykin (2002). In this section, we present the IIR Wiener filter, which is designed to estimate the microseismic signal from the noisy records. The analysis is carried out using the z-transform. In the ensuing, the derivation of the filter is reported.

2.1 Filter Derivation

Consider M sensors placed over a monitoring area for recording microseismic data. Each of these sensors records a time series of sampled measurements, i.e., a microseismic trace, say $y^i_k$, as

$$\begin{aligned} y^i_{k}= \, & {} s^i_{k} + w^i_{k}, i=1,2,\ldots ,M, \end{aligned}$$

(1)

where $s^i_k$ and $w^i_k$ represent the signal and noise sample, respectively, at time instant $t = kT$ of the ith trace (T is the sampling interval). For the derivation, the time series $y^i_k$, $s^i_k$ and $w^i_k$ are concatenated into vectors as follows:

$$\begin{aligned} {\mathbf{y}}^i_{k}= \, & {} \left[ y^i_{k}, y^i_{k-1}, y^i_{k-2},\ldots \right] ^T,\end{aligned}$$

(2)

$$\begin{aligned} {\mathbf{s}}^i_{k}= \, & {} \left[ s^i_{k}, s^i_{k-1},s^i_{k-2},\ldots \right] ^T, \end{aligned}$$

(3)

$$\begin{aligned} {\mathbf{w}}^i_{k}= \, & {} \left[ w^i_{k}, w^i_{k-1}, w^i_{k-2},\ldots \right] ^T. \end{aligned}$$

(4)

For our derivations, real numbers are assumed. The target is to design an IIR filter ${\mathbf{g}}^i$ for each trace to estimate the signal $s_k^i$ as a linear transformation of the measurement $y_k^i$. The output of the filter is given as

$$\begin{aligned} \hat{{s}}^i_{k}= \, & {} {\mathbf{g}}^i{\mathbf{y}}^i_{k}, \end{aligned}$$

(5)

where ${\mathbf{g}}^i=\left[ g^i_0,g^i_1,g^i_2,\ldots \right]$. The filter is of an infinite length duration and so is the data sequence. To estimate the filter coefficients, the mean squared error (MSE) cost function is minimized according to

$$\begin{aligned} J^i_k= \, & {} E\left\{ \tilde{\mathbf{s}}^i_{k}\tilde{\mathbf{s}}^{iT}_k \right\} , \end{aligned}$$

(6)

where the estimation error is $\tilde{\mathbf{s}}^i_{k}={\mathbf{s}}^i_{k}-\hat{\mathbf{s}}^i_{k}$, and $E\{.\}$ and $(.)^T$ represent the mathematical expectation (which gives the most expected value, i.e., the predictor) and the transposition operation, respectively. Here, we use the fact that minimizing the MSE is equivalent to finding the solution by considering the error to be orthogonal to each of the data points in the estimation process. Equation (6) can be solved directly using the correlation of $\tilde{{s}}^i_{k}$ and ${\mathbf{y}}^i_{k}$ (Sayed 2008, p. 36), which is

$$\begin{aligned} E\left\{ \tilde{{s}}^i_{k}{\mathbf{y}}^{iT}_{k} \right\}= \, & {} E\left\{ \left[ {s}^i_{k}- \hat{{s}}^i_{k}\right] {\mathbf{y}}^{iT}_{k} \right\} \nonumber \\= \, & {} E\left\{ {s}^{i}_{k}{\mathbf{y}}^{iT}_{k} - {\mathbf{g}}^{i}{\mathbf{y}}^{i}_{k}{\mathbf{y}}^{iT}_{k} \right\} \nonumber \\= \, & {} E\left\{ {y}^{i}_{k}{\mathbf{y}}^{iT}_{k} -{w}^{i}_{k}{\mathbf{y}}^{iT}_{k}- \mathbf {g}^{i}{\mathbf{y}}^{i}_{k}{\mathbf{y}}^{iT}_{k} \right\} \nonumber \\= \, & {} E\left\{ {y}^{i}_{k}{\mathbf{y}}^{iT}_{k}-{w}^{i}_{k}{\mathbf{s}}^{iT}_{k}-{w}^{i}_{k}{\mathbf{w}}^{iT}_{k}- \mathbf {g}^{i}{\mathbf{y}}^{i}_{k}{\mathbf{y}}^{iT}_{k} \right\} \nonumber \\= \, & {} {\mathbf{p}}_{yy,k}^{i}- \, {\mathbf{p}}_{ws,k}^{i}-{\mathbf{p}}_{ww,k}^i-\mathbf {g}^{i}{\mathbf{P}}_{yy,k}^i, \end{aligned}$$

(7)

where ${\mathbf{p}}^i_{ab,k}$ denotes the correlation between signals a and b of the ith trace. Assuming that the noise and the signal are uncorrelated, i.e., ${\mathbf{p}}_{ws,k}^{i}=0$ and therefore, (7) looks like:

$$\begin{aligned} E\left\{ \tilde{{s}}^i_{k}{\mathbf{y}}^{iT}_{k} \right\} = \,& {} {\mathbf{p}}_{yy,k}^i-{\mathbf{p}}_{ww,k}^i-\mathbf {g}^i{\mathbf{P}}_{yy,k}^{i}. \end{aligned}$$

(8)

According to the principle of orthogonality (Haykin 2002), i.e., the estimate $\hat{{s}}_k^i$, that minimizes the MSE cost function as in Eq. (6), is the orthogonal projection of $\tilde{{s}}_k^i$ into the space spanned by the observations. This is equivalent to requiring $E\left\{ \tilde{{s}}^i_{k}{\mathbf{y}}^{iT}_{k} \right\} =0$, which yields

$$\begin{aligned} \mathbf {g}^i{\mathbf{P}}_{yy,k}^i= \, & {} {\mathbf{p}}_{yy,k}^{i}-{\mathbf{p}}_{ww,k}^i. \end{aligned}$$

(9)

Since Eq. (9) holds for an infinite length of filter, it can not be solved directly using a set of linear equations nor can it be solved using the z-transform because the Wiener filter is causal, i.e., $g_k^i=0$ for $k<0$ (Proakis and Manolakis 2006, Chapter 12). To address this issue, the noisy observation ${\mathbf{y}}^i_{k}$ will be represented by another equivalent process, $\mathbf {\bar{y}}^i_{k}$, and this is done by passing it through a noise-whitening filter. Mathematically, this reads as

$$\begin{aligned} {\bar{y}}^i_{k} = \mathbf {v}^i {\mathbf{y}}^i_{k}= \underbrace{\mathbf {v}^i{\mathbf{s}}^i_{k}}_{{\bar{s}}^i_{k}} + \underbrace{ \mathbf {v}^i{\mathbf{w}}^i_{k}}_{{\bar{w}}^i_{k}}. \end{aligned}$$

(10)

where $\mathbf {v}^i=\left[ v^i_0,v^i_1,v^i_2,\ldots \right]$ is the impulse response of the whitening filter. Now $\hat{{s}}^i_{k}$ can be written as

$$\begin{aligned} \hat{{s}}^i_{k}= \, & {} \mathbf {q}^i\mathbf {\bar{y}}^i_{k}, \end{aligned}$$

(11)

where $\mathbf {q}^i= \, \left[ q^i_0,q^i_1,q^i_2,\ldots \right]$. The IIR Wiener filter can be seen as a cascade of the whitening filter $V^{i}(z)$ and another filter $\mathbf {Q}^{i}(z)$ in the z-domain, where $V^{i}(z)${$\mathbf {Q}^{i}(z)$} is the z-transform of $\mathbf {v}^i${$\mathbf {q}^i$}(Proakis and Manolakis 2006, pp. 818–822). Application of the principle of orthogonality, $E\left\{ \tilde{{s}}_k^i\mathbf {\bar{y}}_k^{iT} \right\} =0$, leads to

$$\begin{aligned} \mathbf {q}^i{\mathbf{P}}_{\bar{y} \bar{y},k}^i =\, & {} {\mathbf{p}}_{y \bar{y},k}^{i}-{\mathbf{p}}_{w \bar{w},k}^i. \end{aligned}$$

(12)

Since $\mathbf {\bar{y}}^i_{k}$ is white, therefore, ${\mathbf{P}}_{\bar{y} \bar{y},k}^i$ is a diagonal matrix with $\sigma ^2_{\bar{y}}$ as diagonal entries and Eq. (12) becomes

$$\begin{aligned} \mathbf {q}^i = \, & {} {1 \over \sigma ^2_{\bar{y}}} \left( {\mathbf{p}}_{y \bar{y},k}^{i}-{\mathbf{p}}_{w \bar{w},k}^i \right) . \end{aligned}$$

(13)

Now define the z-domain as $\mathbf {z}^+=[1,z^1,z^2,\ldots ]$ and $\mathbf {z}^-=[1,z^{-1},z^{-2},\ldots ]$. Hence, Eq. (13) in the z-domain is

$$\begin{aligned} \mathbf {Q}^i(z) = \, & {} {1 \over \sigma ^2_{\bar{y}}} \underbrace{\mathbf {z}^-\left( {\mathbf{p}}_{y \bar{y},k}^{i}-{\mathbf{p}}_{w \bar{w},k}^i \right) ^T}_{C_{\bar{y} \bar{w},k}^{i+}(z)}. \end{aligned}$$

(14)

$C_{\bar{y} \bar{w},k}^{i+}(z)$ represents the z-transform of the one-sided autocorrelation sequence ${\mathbf{p}}_{y \bar{y},k}^{i}-{\mathbf{p}}_{w \bar{w},k}^i$ (Proakis and Manolakis 2006, pp. 818–822) and

$$\begin{aligned} {\mathbf{p}}_{y \bar{y},k}^{i}-{\mathbf{p}}_{w \bar{w},k}^i = \, & {} E \left\{ {y}^{i}_{k}\mathbf {\bar{y}}^{iT}_{k} -{w}^{i}_{k}\mathbf {\bar{w}}^{iT}_{k}\right\} \nonumber \\ = \, & {} \left[ \mathbf {v}^iE\left\{ \left( {y}^{i}_{k}\mathbf { y}^{iT}_{k} -{w}^{i}_{k}\mathbf { w}^{iT}_{k}\right) ^{T}\right\} ,\mathbf {v}^iE\left\{ \left( {y}^{i}_{k}\mathbf { y}^{iT}_{k-1} -{w}^{i}_{k}\mathbf { w}^{iT}_{k-1}\right) ^{T}\right\} ,\ldots \right] ^{T}\nonumber \\= \, & {} \left[ \mathbf {v}^i\left( {\mathbf{p}}^{i}_{yy,k} -{\mathbf{p}}^{i}_{ww,k}\right) ^{T},\mathbf {v}^i\left( \mathbf { p}^{i}_{yy,k+1} -{\mathbf{p}}^{i}_{ww,k+1}\right) ^{T},\ldots \right] ^{T}. \end{aligned}$$

(15)

Taking the z-transform of Eq. (15), we get

$$\begin{aligned} C_{\bar{y} \bar{w},k}^{i}(z)= \, & {} \mathbf {z}\left[ \ldots ,\mathbf {v}^i\left( {\mathbf{p}}^{i}_{yy,k-1} -{\mathbf{p}}^{i}_{ww,k-1}\right) ^{T},\mathbf {v}^i\left( {\mathbf{p}}^{i}_{yy,k} -{\mathbf{p}}^{i}_{ww,k}\right) ^{T}, \mathbf {v}^i\left( \mathbf { p}^{i}_{yy,k+1} -{\mathbf{p}}^{i}_{ww,k+1}\right) ^{T},\ldots \right] ^{T}\nonumber \\= \, & {} \mathbf {v}^i\left[ \ldots ,\mathbf {z}\left( {\mathbf{p}}^{i}_{yy,k-1} -{\mathbf{p}}^{i}_{ww,k-1}\right) ^{T},\mathbf {z}\left( {\mathbf{p}}^{i}_{yy,k} -{\mathbf{p}}^{i}_{ww,k}\right) ^{T}, \mathbf {z}\left( \mathbf { p}^{i}_{yy,k+1} -{\mathbf{p}}^{i}_{ww,k+1}\right) ^{T},\ldots \right] ^{T}\nonumber \\= \, & {} \mathbf {z}^+\mathbf {v}^{iT}\mathbf {z}\left( {\mathbf{p}}^{i}_{yy,k} -{\mathbf{p}}^{i}_{ww,k}\right) ^{T}\nonumber \\= \, & {} V^{i}(z^{-1})\left( C_{ y y,k}^{i}(z) - C_{ ww,k}^{i}(z) \right) . \end{aligned}$$

(16)

Using spectral decomposition, we can write $C_{ y y,k}^{i}(z)$ as

$$\begin{aligned} C_{ y y,k}^{i}(z)=\sigma ^2_{\bar{y}}W(z)W(z^{-1}). \end{aligned}$$

(17)

W(z) is the minimum-phase part, which is analytic in the region $|z|>r$ and $r<1$. With spectral factorization the whitening filter becomes $V^{i}(z)={1 / W(z)}$. Therefore,

$$\begin{aligned} C_{\bar{y} \bar{w}}^{i+}(z)= \, & {} \left[ {C_{ y y,k}^{i}(z) - C_{ ww,k}^{i}(z) \over W(z^{-1})}\right] ^+ = \left[ \sigma ^2_{\bar{y}} W(z)- {C_{ ww,k}^{i}(z) \over W(z^{-1})}\right] ^+. \end{aligned}$$

(18)

Now,

$$\begin{aligned} \mathbf {Q}^i(z)= \, & {} \left[ W(z)- {C_{ ww,k}^{i}(z) \over \sigma ^2_{\bar{y}}W(z^{-1})}\right] ^+. \end{aligned}$$

(19)

and finally

$$\begin{aligned} \mathbf {G}^i(z)= \, & {} {\mathbf {Q}^i(z)\over W(z)} ={\left[ W(z)- {C_{ ww,k}^{i}(z) \over \sigma ^2_{\bar{y}}W(z^{-1})}\right] ^+ \over W(z)}. \end{aligned}$$

(20)

For more details on Eqs. (15)–(20), it is recommended to see the book (Proakis and Manolakis 2006, pp. 818–822). In short, to design an IIR Wiener filter we are required to do spectral factorization of $C_{ y y,k}^{i}(z)$, obtain the minimum-phase part W(z) and finally solve for the causal part of [$W(z)- {C_{ ww,k}^{i}(z) / \sigma ^2_{\bar{y}}W(z^{-1})}$].

2.2 Signal-to-Noise Ratio

The SNR is commonly defined as

$$\begin{aligned} \mathrm{{SNR}}= \, & {} \frac{\sigma _s^2}{\sigma _w^2}, \end{aligned}$$

(21)

where $\sigma _s^2$ and $\sigma _w^2$ are the signal and noise powers, respectively. Using this definition, the following interpretation of the IIR Wiener filter in terms of the SNR can be deduced by considering the two limiting cases of a noise-free signal and an extreme noisy signal, which respectively are given by

$$\begin{aligned} \lim _{\mathrm{{SNR}}\rightarrow \infty } \mathbf {G}^i(z)= \, & {} 1, \end{aligned}$$

(22)

$$\begin{aligned} \lim _{\mathrm{{SNR}}\rightarrow 0} \mathbf {G}^i(z)= \, & {} 0. \end{aligned}$$

(23)

The justification of Eqs. (22) and (23) is as follows. When $\mathrm{{SNR}}\rightarrow \infty$, this corresponds to zero noise content and therefore $\sigma _w^2=0$ and similarly $C_{ ww,k}^{i}(z)=0$ and consequently $\mathbf {G}^i(z)= 1$. However, when $\mathrm{{SNR}} \rightarrow 0$, this corresponds to a zero signal content, i.e., $\sigma _s^2=0,$ which results in $\sigma _{\bar{y}}^2=\sigma _{\bar{w}}^2$ and $C_{ ww,k}^{i}(z)=\sigma ^2_{\bar{y}}W(z)W(z^{-1})$ and consequently $\mathbf {G}^i(z)= 0$. This means that at a very high $\mathrm{{SNR}}$, the filter applies very little or no attenuation to the noise-free signal, whereas when there is only noise, the filter enters the stop band region, i.e., does not allow the input signal (which is only noise) to pass through, since the filter response is $\mathbf {G}^i(z)= 0$. In the time domain, $\mathbf {G}^i(z)= 1$ corresponds to $g^i_1=1$ and $\mathbf {G}^i(z)= 0$ corresponds to $g^i_n=0, \forall \ n$ (see the properties of z-transform, Proakis and Manolakis 2006, p. 165). The plot for the two cases highlighted above (Eqs. 22, 23) is shown in Fig. 1. To see the response of the filter, for $\mathrm{{SNR}}\rightarrow \infty$, we have used only a Ricker wavelet of center frequency 30 Hz without noise and for $\mathrm{{SNR}}\rightarrow 0$, we have used only noise.

Fig. 1

The response of the IIR filter is plotted for $\mathrm{{SNR}}\rightarrow \infty$ and $\mathrm{{SNR}}\rightarrow 0$. A Ricker wavelet of 30 Hz without noise is used for $\mathrm{{SNR}} \rightarrow \infty$, which gives the filter response a $g^i_1=1$, i.e., the filter offers no attenuation to the noise-free signal. Only noise is used for $\mathrm{{SNR}}\rightarrow 0$, which gives the filter response, b $g^i_1=0$, i.e., the filter does not allow the noise to pass

3 Estimation of the z-Transform of the Observation (Noisy Trace)

In this section, the estimations of the autocorrelation sequence of the observation and its corresponding z-transform in practical scenarios are detailed. To estimate the autocorrelation of the noisy observation (and ultimately the z-transform), first the noisy observation is modeled as an auto-regressive (AR) process. For this purpose, the following model is used for the observed data $\mathbf y$ at instant k

$$\begin{aligned} y_{k} = -\mathbf {a}_{l_y} {\mathbf{y}}_{k-1}+\gamma _k, \end{aligned}$$

(24)

where $\mathbf {a}_{l_y}=[a_1,a_2,\ldots ,a_l]$ are AR coefficients (l is the number of coefficients), ${\mathbf{y}}_{k-1}=[y_{k-1},y_{k-2},\ldots ,y_{k-l}]^T$ and $\gamma _k$ is the white noise with zero mean and variance $\sigma ^2_{\gamma _y}$. To find $\mathbf {a}_{l_y}$, the Yule-Walker method (Haykin 2002, Chapter 1) is used. Here, post multiplying Eq. (24) with ${\mathbf{y}}^T_{k-1}$ and taking the mathematical expectation, we obtain

$$\begin{aligned} E\left\{ y_{k}{\mathbf{y}}^T_{k-1}\right\} = -E\left\{ \mathbf {a}_{l_y}{\mathbf{y}}_{k-1} {\mathbf{y}}_{k-1}^T\right\} +E\left\{ {\mathbf{y}}_{k-1}^{T}\gamma _k\right\} . \end{aligned}$$

(25)

Assuming that data and noise are uncorrelated and the noise has zero mean, Eq. (25) becomes

$$\begin{aligned} -\,{\mathbf{p}}_{yy}={\mathbf{P}}_{yy}\mathbf {a}_{l_y}^T, \end{aligned}$$

(26)

and $\mathbf {a}_{l_y}^T$ is calculated as

$$\begin{aligned} \mathbf {a}_{l_y}^T= \, - \, {\mathbf{P}}_{yy}^{-1}{\mathbf{p}}_{yy}, \end{aligned}$$

(27)

where ${\mathbf{p}}_{yy}=[p_{y,1},p_{y,2},\ldots ,p_{y,l}]^T$, ${\mathbf{P}}_{yy}={\text {Toeplitz}}([p_{y,0},p_{y,1},\ldots ,p_{y,l-1}],[p_{y,0},p_{y,-1},\ldots ,p_{y,-l+1}])$, and $p_{y,m}=p_{y,-m}$ (Proakis and Manolakis 2006, p. 798). The first column and first row of the Toeplitz matrix ${\mathbf{p}}_{yy}$ are $[p_{y,0},p_{y,1},\ldots ,p_{y,l-1}]$ and $[p_{y,0},p_{y,-1},\ldots ,p_{y,-l+1}]$, respectively (here we have used Matlab-like syntax to represent a Toeplitz matrix). To ensure that the autocorrelation matrix in Eq. (27) is positive definite, a biased form of the estimator is used for $p_{y,m}$, i.e., $p_{y,m}={1 \over N}\sum _{k=0}^{N-m-1}y_k y_{k+m},m=0,1,\ldots ,l-1$, where N is the number of samples in the trace. This estimator results in a stable AR model. To avoid inversion in Eq. (27), the Levinson-Durbin algorithm (Haykin 2002) can be used, which is a recursive and computationally efficient method that utilizes the Toeplitz structure of the correlation matrix. After finding $\mathbf {a}_{l_y}$, then the z-transform of the autocorrelation sequence can be found as follows. Equation (24) can be rewritten as

$$\begin{aligned} \mathbf {a}'_{l_y} {\mathbf{y}}_{k}=\gamma _k, \end{aligned}$$

(28)

where $\mathbf {a}'_{l_y}=[1,a_1,a_2,\ldots ,a_l]$ and ${\mathbf{y}}_{k}=[y_{k},y_{k-1},\ldots ,y_{k-l}]^T$. Now, taking the z-transform of Eq. (28), we get

$$\begin{aligned} Y(z)\left( \mathbf {a}'_{l_y}\mathbf {z}^-\right) =\gamma (z). \end{aligned}$$

(29)

Multiplying each side of this equation by its respective time-reversed version (Proakis and Manolakis 2006) gives

$$\begin{aligned} C_{ yy,k}(z)\left( \mathbf {a}'_l\mathbf {z}^-\right) \left( \mathbf {a}'_l\mathbf {z}^+\right) =\sigma ^2_{\gamma _y}. \end{aligned}$$

(30)

In this way, the noisy observation is modeled by an AR process, and the respective z-transform of the autocorrelation sequence can be obtained as

$$\begin{aligned} C_{ yy,k}(z)={\sigma ^2_{\gamma _y} \over \left( \mathbf {a}'_{l_y}\mathbf {z}^-\right) \left( \mathbf {a}'_{l_y}\mathbf {z}^+\right) }. \end{aligned}$$

(31)

Now, $\sigma ^2_{\gamma _{y}}$ can be found by multiplying Eq. (28) by its complex conjugate (*) and taking the mathematical expectation, and since $\gamma _k$ is a real-valued number, therefore, $E\{|\gamma _k|^2\}=\sigma ^2_{\gamma _y}$. Now from Eq. (28)

$$\begin{aligned} E\{\gamma _k\gamma _k^*\}= \, & {} E\{\mathbf {a}'_{l_y} {\mathbf{y}}_{k} {\mathbf{y}}_{k}^T\mathbf {a}'^T_{l_y}\},\end{aligned}$$

(32)

$$\begin{aligned} \sigma ^2_{\gamma _y}= \, & {} \mathbf {a}'_{l_y}E\{ {\mathbf{y}}_{k} {\mathbf{y}}_{k}^T\}\mathbf {a}'^T_{l_y},\end{aligned}$$

(33)

$$\begin{aligned} \sigma ^2_{\gamma _y}= \, & {} \mathbf {a}'_{l_y} {\mathbf{p}}_{yy}\mathbf {a}'^T_{l_y}. \end{aligned}$$

(34)

Details of the above derivation can be found in Sayed (2008). From Eq. (31), it is clear that $C_{ yy,k}(z)$ can be found using the knowledge of $\mathbf {a}_{l_y}$ and $\sigma _{\gamma _y}^2$. This yields the estimation of the z-transform of the observation autocorrelation sequence.

4 Estimation of z-Transform of Noise

To estimate the noise autocorrelation matrix, we use the approach of Rangachari and Loizou (2006). It consists of five steps, namely, the initial power spectrum estimation, the minimum tracking, the event detection, the smoothing factor calculation and the noise spectrum update. The steps are detailed next.

4.1 Initial Power Spectrum Estimation of Noisy Data

The smoothed power spectrum of the noisy data is estimated using the first-order recursive relation (Rangachari and Loizou 2006; Doblinger 1995) as follows,

$$\begin{aligned} \mathcal {P}_i(\lambda )=\eta \mathcal {P}_i(\lambda -1)+(1-\eta )|\mathcal {Y}_i(\lambda )|^{2}, \end{aligned}$$

(35)

where $\mathcal {Y}_i(\lambda )$ is the short-time Fourier transform of the noisy data, $\eta$ is the forgetting factor (which gives less weight to older samples), and $\lambda$ is the frame index (Doblinger 1995). The power spectrum $|\mathcal {Y}_i(\lambda )|^{2}$ is obtained by taking the absolute value of each element and squaring it. The size of $\mathcal {Y}_i(\lambda )$ is $\bar{N}$, and the step size (or hop size) to calculate the short-time Fourier transform is h.

4.2 Tracking the Minimum of the Noisy Data

The minimum of the noisy data is tracked by a non-linear approach that averages the the past values continuously as follows (Doblinger 1995):

$$\begin{aligned} \nonumber \mathcal {P}_{i,min}(\lambda )= \, & {} [\mathcal {P}_{i,min}(\lambda -1)<\mathcal {P}_{i}(\lambda )]\odot [\gamma \mathcal {P}_{i,min}(\lambda -1)+{1-\gamma \over 1-\beta }(\mathcal {P}_{i}(\lambda )-\beta \mathcal {P}_{i}(\lambda -1))]\nonumber \\&+[\mathcal {P}_{i,min}(\lambda -1)>\mathcal {P}_{i}(\lambda )]\odot \mathcal {P}_{i}(\lambda ), \end{aligned}$$

(36)

where $[\mathcal {P}_{i,min}(\lambda -1)<\mathcal {P}_{i}(\lambda )]$ represents element-by-element comparison, and its resultant vector contains 1s (if condition is true) and 0s (otherwise), “$\odot$” denotes the Hadamard product (element-by-element multiplication), and $\mathcal {P}_{i,min}(\lambda -1)$ is the local minimum of the noisy data power spectrum. $\gamma$ and $\beta$ are the adaptation constants that are determined experimentally (Rangachari and Loizou 2006; Doblinger 1995).

4.3 Microseismic Event Detection Probability

To detect the presence of microseismic events, the ratio of the noisy data spectrum to its local minimum, $\mathcal {S}_i(\lambda )$, is defined as (Cohen and Berdugo 2002),

$$\begin{aligned} \mathcal {S}_i(\lambda )=\mathcal {P}_{i}(\lambda )\oslash \mathcal {P}_{i,min}(\lambda ), \end{aligned}$$

(37)

where “$\oslash$” represents the element-by-element division. The ratio is based on the fact that the power spectrum of the noisy trace will be nearly equal to its local minimum when a microseismic event is absent. The smaller the ratio in Eq. (37) is, the higher the probability that the event is absent. The ratio is compared with a frequency-dependent threshold $\delta$, and consequently the event presence probability $\mathcal {I}_i(\lambda )$ is updated, using first-order recursion, as (Rangachari and Loizou 2006),

$$\begin{aligned} \mathcal {I}_i(\lambda )=\alpha _p\mathcal {I}_i(\lambda -1)+(1-\alpha _p)[\mathcal {S}_{i}(\lambda )>\delta )], \end{aligned}$$

(38)

where $[\mathcal {S}_{i}(\lambda )>\delta )]$ represents a comparison of each element in $\mathcal {S}_{i}(\lambda )$ with the frequency-dependent threshold $\delta$ (to be discussed later in the results section) and its result is a vector with 1s (if the condition is true) and 0s (otherwise). The quantity $\alpha _p$ is a smoothing constant (Rangachari and Loizou 2006). The recursion in Eq. (38) implicity exploits the correlation among the frames for detecting the event.

4.4 Calculation of the Smoothing Factor

The time-frequency dependent smoothing factor is computed as (Cohen and Berdugo 2002),

$$\begin{aligned} \alpha _s=\alpha _d + (1-\alpha _d)\mathcal {I}_i(\lambda ). \end{aligned}$$

(39)

where $\alpha _d$ is a constant and $\alpha _s$ is a time-varying smoothing parameter. Note that $\alpha _s$ has values in the range of $\alpha _d\le \alpha _s\le 1$ (Rangachari and Loizou 2006).

4.5 Updating the Estimation of the Noise Spectrum

Finally, the noise power spectrum estimate $\mathcal {N}_i(\lambda )$ is updated according to

$$\begin{aligned} \mathcal {N}_i(\lambda )=\alpha _s\mathcal {N}_i(\lambda -1)+(1-\alpha _s)|\mathcal {Y}_i(\lambda )|^2. \end{aligned}$$

(40)

The above procedure is done for all frequency bins altogether, as obvious by using the vector notation in equations. Note that constants (mixing parameters) $\eta ,\gamma ,\beta ,\alpha _p$ and $\alpha _d$ can easily be determined experimentally, and their values lie between 0 and 1 (Rangachari and Loizou 2006). The overall algorithm can be summarized as follows. After classifying the frequency bins as event absent/present, the event presence probability is updated using Eq. (38). Using this probability, the time-frequency-dependent smoothing factor is updated as in Eq. (39). Finally, the noise power spectrum is estimated using update Eq. (40). After obtaining the noise power spectrum estimate, it is averaged over all $\lambda$’s ${\mathcal {N}}_{a}=\sum\nolimits_{\lambda} {N_{i} (\lambda)}$ and converted back to the time domain, which gives the noise autocorrelation estimate $p_{w,0},p_{w,1},\ldots ,p_{w,l-1}$. Then, from these estimates, ${\mathbf{p}}_{ww}$ and ${\mathbf{P}}_{ww}$ are found (as done for ${\mathbf{p}}_{yy}$ and ${\mathbf{P}}_{yy}$). To find the z-transform of the noise autocorrelation sequence, the procedure outlined in Sect. 3 has been used.

5 Summary of the Denoising Method

In this section, we summarize our proposed method and suggest some enhancements for estimating the correlation matrices.

5.1 Proposed Denoising Method

The outline of our proposed denoising method can be summarized as follows:

• 1. Find the autocorrelation of noisy data and noise using $p_{y,m}={1 \over N}\sum _{k=0}^{N-m-1}y_ky_{k+m}$ and $p_{w,m}={1 \over N}\sum _{k=0}^{N-m-1}w_kw_{k+m},m\ge 0$, respectively, and then form ${\mathbf{p}}_{yy}, {\mathbf{P}}_{yy}$, ${\mathbf{p}}_{ww}$ and ${\mathbf{P}}_{ww}$ for each trace.

• 2. Find the AR parameters for the noisy observation and the noise using $\mathbf {a}_{l_y}^T= - \, {\mathbf{P}}_{yy}^{-1}{\mathbf{p}}_{yy}$ and $\mathbf {a}_{l_w}^T= - \, {\mathbf{P}}_{ww}^{-1}{\mathbf{p}}_{ww}$, respectively.

• 3. Find the z-transform of the autocorrelation sequence for the observed data and the noise as $C_{yy,k}(z)={\sigma ^2_{\gamma _{y}} \over \left( \mathbf {a}'_{l_y}\mathbf {z}^-\right) \left( \mathbf {a}'_{l,y}\mathbf {z}^+\right) }$ and $C_{ww,k}(z)={\sigma ^2_{\gamma _{w}} \over \left( \mathbf {a}'_{l_w}\mathbf {z}^-\right) \left( \mathbf {a}'_{l,w}\mathbf {z}^+\right) }$, respectively, where $\sigma ^2_{\gamma _y} = \mathbf {a}'_{l_y}{\mathbf{p}}_{yy}^T\mathbf {a}'^T_{l_y}$ and $\sigma ^2_{\gamma _w} = \mathbf {a}'_{l_w} {\mathbf{p}}_{ww}^T\mathbf {a}'^T_{l_w}$ .

• 4. Find W(z) by calculating the roots of $C_{yy,k}(z)$ that fall inside the unit circle in the z-plane and $\sigma ^2_{\bar{y}}=\sigma ^2_{\gamma _{y}}$.

• 5. Find the causal part of $\left[ W(z)- {C_{ ww,k}^{i+}(z) \over \sigma ^2_{\bar{y}}W(z^{-1})}\right]$.

• 6. Finally, find the transfer function of the IIR filter using $\mathbf {G}^i(z) =\frac{\left[ W(z)- {C_{ ww,k}^{i+}(z) \over \sigma ^2_{\bar{y}}W(z^{-1})}\right] ^+}{W(z)}$ and filter the noisy observation to get the clean signal.

• 7. The procedure is repeated in an iterative fashion to get a clearer signal.

The work flow for the proposed denoising method is presented in Fig. 2. For simplicity of the notation, the superscript i (that corresponds to the ith trace) is omitted, and the work flow is the same for all traces.

5.2 Proposed Enhancement Method

Assuming that the noise has the similar autocorrelation (or power spectral density in frequency-domain) for various traces (Caffagni et al. 2016; Cieplicki et al. 2014), the estimation of the autocorrelation sequences for data and noise can be improved by stacking over the adjacent traces and/or components in case of 3C sensors. This is done as follows.

First, the autocorrelation of noisy data and noise is found using $p^{ij}_{y,m}={1 \over N}\sum _{k=0}^{N-m-1}y^{ij}_ky^{ij}_{k+m}$ and $p^{ij}_{w,m}={1 \over N}\sum _{k=0}^{N-m-1}w^{ij}_kw^{ij}_{k+m},m\ge 0$, respectively, for the ith trace and jth component of a 3C sensor. Second, after finding these autocorrelations for all the traces, the autocorrelations are stacked to improve the estimation, i.e.,

$$\begin{aligned} p_{w,m}={1 \over 3M}\sum _{j=1}^{3}\sum _{i=1}^{M}p^{ij}_{w,m}, \end{aligned}$$

(41)

A similar procedure is used for estimating the autocorrelation of observation, i.e.,

$$\begin{aligned} p_{y,m}={1 \over 3M}\sum _{j=1}^{3}\sum _{i=1}^{M}p^{ij}_{y,m}, \end{aligned}$$

(42)

After finding the autocorrelation of the noisy data $p_{y,m}$, and noise $p_{w,m}$, the autocorrelation matrices ${\mathbf{p}}_{yy}, {\mathbf{P}}_{yy}$, ${\mathbf{p}}_{ww}$ and ${\mathbf{P}}_{ww}$ are formed, and the rest of the procedure is the same as for the proposed method.

Importantly, in the proposed enhancement method, we are not stacking the traces prior to the autocorrelation but we are stacking the autocorrelations of the traces, i.e., first the autocorrelations are found for each trace followed by the stacking of the autocorrelations. The autocorrelations do not need to be aligned as they are already aligned. The estimation improves if traces have similar power spectral densities, i.e., traces have white noise or Brownian noise, etc. Now the question arises, if traces have the similar power spectral densities but different noise levels (variances), are the results affected? More importantly, our method compensates automatically for the difference in the variances. The IIR Wiener filter is the ratio of two autocorrelations. Hence, if the noise level changes, the level of the noisy observation also changes and so does the magnitude of the autocorrelations of the noisy observation and noise (remember that the autocorrelations are derived from the traces). Since the filter is a ratio of autocorrelations (Eq. 13) or power spectral densities (Eq. 20), it will compensate for the effect. Even if a bias is present because of a broken channel, this will not affect the results.

In summary, the proposed denoising method estimates the autocorrelation in a trace-by-trace manner, whereas the proposed enhancement method improves the estimation of the autocorrelation by averaging over the adjacent traces.

Other steps of the denoising method remain the same. With the improvement of the autocorrelation sequence estimation, the proposed method will hereafter be called the proposed enhanced method.

6 Results

In this section, the IIR Wiener filter is tested on synthetic, semi-synthetic and field data. To test the robustness of the proposed method, two cases for noise (correlated and uncorrelated noise) are used.

6.1 Synthetic Data Set

For the synthetic data set, a Ricker wavelet with a center frequency of 5 Hz is used as the microseismic source signature to generate the data set. Fifty receivers are placed inline, and the middle receiver is assumed to be the closest to the source. Moreover, a constant medium velocity is assumed, and the sampling frequency is set to 1 kHz. The resulting data are depicted in Fig. 3. For the proposed method, the number of AR coefficients is set to $l=10$ for all the data sets used. Testing revealed that increasing the number of parameters does not improve the SNR. However, large values of l increase the complexity because of the inversion of the large matrix in Eq. (27). Finally, N needs to be known for the estimation of the autocorrelation of the observation, $p_{y,m}$. The observation or the observed data in our case are traces; therefore, N is equal to the number of samples in each trace. For long recordings, the data can be divided into windows instead of processing the whole data altogether, and then the proposed method can be applied to these windows. The test revealed that the optimum values of the constants used for noise estimation are $\eta =0.85,\gamma =0.998,\beta =0.85,\alpha _p=0.2,\alpha _d=0.95, \bar{N} = N/10,$ and $h=N/20$.

Fig. 2

Work flow of the proposed denoising method. For simplicity of the notation, the superscript i (that corresponds to the ith trace) is omitted. The work flow is the same for all traces

The two kinds of noise (correlated and uncorrelated noise) are added to the raw traces (Fig. 3) to test the proposed method. The SNR [defined as $10\log _{10}\{\sigma _s^2/\sigma _w^2\}$ in decibel (dB)] of the noisy observation in both cases is equal to $-~12$ dB. It is apparent that the traces are noisy and the microseismic event is difficult to identify, as can be seen in Fig. 4a, b. For generating the correlated noise, white Gaussian noise is filtered using a geophone’s impulse response given by Hons and Stewart (2006). After filtering, the spectrum and autocorrelation of noise are shown in Fig. 5a, b, respectively. The spectrum is not flat, and the autocorrelation is not an impulse, unlike white noise (uncorrelated), which has a flat spectrum, and its autocorrelation is that of an impulse-type function at zero time lag (zero correlation index). The spectrum in Fig. 5a is flat except for frequencies greater than 150 Hz.

Here, the noise is estimated first using the procedure discussed in Sect. 4. For trace 1, the power spectrum of the noiseless data and event-presence probability $\mathcal {I}_i$ (with white Gaussian noise), calculated using Eq. (38), is shown in Fig. 6a, b. Note that by defining a suitable value of the threshold, the event can be detected with higher confidence. As seen in Fig. 6b, some noise-only regions are detected as the events. This overestimation of events is not likely to affect the enhanced event (after denoising), since the detection probability improves with the iteration, hence eliminating the false event detected regions (Fig. 6b–e). The threshold value used is

$$\begin{aligned} \delta = \left\{ \begin{array}{l l} 2, &{} 1\le \lambda \le F\\ 5, &{} F\le \lambda \le f_s/2,\\ \end{array} \right. \end{aligned}$$

(43)

where F is the frequency bin corresponding to 100 Hz frequency. Above 100 Hz, a higher value of the threshold is used because the event will be in the low frequency range (within 100 Hz).

In the first experiment with white Gaussian noise (uncorrelated case), when the filter is applied to the data, the noise is increasingly suppressed with each iteration (Fig. 7), and the microseismic event is dominating. This proves the effectiveness of our proposed method. Figure 8a, b shows the denoising results (after iteration 4) under the white Gaussian noise case using the proposed method and the proposed enhanced method, respectively. In the second experiment with correlated noise, again the filter attenuates the noise, and the event becomes clearer (Fig. 8c, d after iteration 4). Next, to show the improvement in the SNR in each iteration, the noise level is plotted against the number of iterations, as depicted in Fig. 9. It is apparent from the figure that the SNR is improving with every iteration. With more iterations, we lose the basic assumption that noise and signal are uncorrelated; hence, the SNR starts to decrease after the fourth iteration. Consequently, we used only four iterations throughout our simulation results. To ensure that we get the best results in terms of denoising, after the fourth iteration of applying the filter, the wavelet-based denoising can also be applied before the final output (results shown in Figs. 7 and 8 are without the wavelet-based denoising method). This is necessary to remove any in-band noise present after the filter application. The details of the wavelet denoising method are presented later.

The blind estimation of the noise is clearly an advantage of the proposed method. However, the nature of the noise is really important. With white noise, the spectrum is flat, and when we move to the time-frequency domain for the noise estimation, the noise contents are more or less equally distributed along the frequency. On the other hand, with colored noise, the spectrum is concentrated in some frequency bands (which include the band of the events). Since we have used the same variance (level) of the noise in both cases (white and color), the in-band noise (noise in the band of event) is less in the white noise case (contents are equally distributed along the spectrum) than in the colored noise case (contents are concentrated in some bands). Therefore, the performance of estimation in the colored noise case is somewhat lower than in the white noise case.

6.2 Comparison of Denoising Methods

The quantitative assessment of the proposed method can be verified by comparing the mean square error (MSE), mean absolute error (MAE), SNR, peak-signal-to-noise ratio (PSNR) and maximum correlation coefficient (CC), which are listed in Table 1. In this table, the performance of the proposed method in the case of a synthetic data set with white Gaussian noise is compared with bandpass filtering, wavelet decomposition, empirical mode decomposition and FIR Wiener filtering. For denoising using wavelet decomposition, the ‘wden’ function in the wavelet toolbox of MATLAB is used (Misiti et al. 1996). Various wavelet basis functions with their variants, i.e., Daubechies (db2, db3, db4), Coiflets (co2, co4, co5) and Symlets (sy2, sy3, sy4) (Daubechies 1992; Mallat 1989), are tested on the pseudo-real data set, and then the coif5 wavelet is selected for comparison based on its best performance over the other wavelets. Furthermore, we used soft thresholding with the principle of Stein’s unbiased risk (Stein 1981).¹ Another method used for comparison is the empirical mode decomposition (Rilling et al. 2007) that derives the basis function from the observed data. This is also a well-known method used for denoising in geophysics. There are several different methods for denoising seismic data based on empirical mode decomposition. Here, we have used the ensemble empirical mode decomposition with the adaptive thresholding method (Han and van der Baan 2015). One more widely used method used for enhancing the SNR of noisy seismic data is interferometry (Al-Shuhail et al. 2013). Comparison of the above-mentioned methods reveals that our proposed method is superior to the other methods (see Table 1). Moreover, comparing the performance of the proposed method with the wavelet-based method, we can see that the IIR-based filter has improved the performance by $15\%$ at the cost of doubling the computational complexity. For the proposed enhanced method, stacking is done (see Eq. 42) over the adjacent three traces. In comparing the FIR Wiener filter with the IIR Wiener filter, the length of the FIR Wiener filter is taken to be equal to N / 10 (for performance and complexity compromise). Due to the inversion of a large matrix, the FIR Wiener filter took 9 s as compared to 4 s by the IIR Wiener filter as shown in Table 1.

6.3 Semi-synthetic Data Set

Next, an earthquake data set is used to validate the proposed method. The data set is obtained from Incorporated Research Institutions for Seismology (IRIS). The event occurred on 9 October 2017 in Central Alaska, USA, and had a magnitude of $Ml = 5.2$. The data were recorded on four tri-component (3C) sensors at a sampling frequency of 250 Hz.

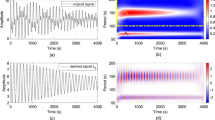
The noiseless and noisy data (corrupted with correlated noise, hereafter denominated “semi-real” or “semi-synthetic” data set) are shown in Fig. 10a, b, respectively (for compactness three components are plotted on the same figure). An improvement in SNR of about 13 dB is achieved with the proposed method (Fig. 10c) and 14-dB improvement with the proposed enhanced method (Fig. 10d).

Table 1 Mean square error (MSE), mean absolute error (MAE), signal-to-noise ratio (SNR), peak-signal-to-noise ratio (PSNR) and maximum correlation coefficient (CC) from the synthetic data experiment (white Gaussian noise case) using bandpass filtering, interferometry, wavelet decomposition, empirical mode decomposition, FIR Wiener filtering and the proposed method

6.4 Field Data Set

Finally, the proposed method is applied to a real data set. Figure 11a shows the amplitude normalized and mean subtracted version of the data set. This data set is obtained from the IRIS website, and the sampling rate is 4 ms. Similar to Mousavi and Langston (2016c), this microearthquake data set has a magnitude $Ml = 0.4$ and a depth of 4.8 km with the seismometer located on the surface. The earthquake occurred in the California-Nevada Border Region. This scenario is taken to prove the effectiveness of the proposed method in the case of microearthquakes. The parameters used here are the same as those used for the synthetic data set.

The result of the filtering process is shown in Fig. 11b. The results are shown after the fourth iteration and application of the wavelet-based denoising approach. As demonstrated in this figure, our proposed method is indeed able to detect the earthquake signal effectively and attenuated the noise.

The aforementioned test was on a natural microearthquake. The algorithm was originally tested on a real induced microseismic data set from the local oil industry in the Middle East. However, due to legal issues we are unable to report the results here. To demonstrate the effectiveness of the proposed denoising method, we apply it on another field data set that is used by Liu et al. (2017) (Fig. 12a). These data come from the High Resolution Seismic Network (HRSN) operated by Berkeley Seismological Laboratory, University of California, Berkeley. The sampling frequency is 250 Hz. The effectiveness of the proposed method can be appreciated from Fig. 12b, which shows the P- and S-arrivals clearly.

Fig. 3

Synthetic data without noise. A Ricker wavelet with a center frequency of 5 Hz is used. Fifty receivers are placed inline, and the middle receiver is assumed to be the closest to the source. A constant medium velocity is assumed, and the sampling frequency is set to 1 kHz

Fig. 4

a Synthetic data with white Gaussian noise. b Synthetic data with correlated noise. The SNR of the noisy observation in both cases is set to $-~12$ dB. It is apparent that the traces are noisy, and the microseismic event is difficult to identify. For generating the correlated noise, white Gaussian noise is filtered using a geophone’s impulse response given by Hons and Stewart (2006)

Fig. 5

Correlated noise specifications: a spectrum of correlated noise. b Its corresponding autocorrelation. For generating the correlated noise, white Gaussian noise is filtered using a geophone’s impulse response given by Hons and Stewart (2006). The spectrum is not flat and the autocorrelation is not an impulse, unlike white noise (uncorrelated), which has a flat spectrum and its autocorrelation is that of an impulse-type function at zero time lag (zero correlation index)

Fig. 6

a Power spectrum of the noiseless synthetic data using short-time Fourier transform. Event presence probability $\mathcal {I}_1$ of noisy version of trace 1,  iteration 1, c iteration 2, d iteration 3, e iteration 4. The detection probability improves with the iteration, hence eliminating the false event detected region

Fig. 7

Denoised synthetic data using proposed method: a iteration 1, b iteration 2, c iteration 3, d iteration 4. The noise is increasingly suppressed with each iteration, and the microseismic event is dominating

Fig. 8

Denoised synthetic data: a proposed method (white noise case), b proposed enhanced method with stacking of adjacent traces (white noise case), c proposed method (correlated noise case), d proposed enhanced method with stacking of adjacent traces (correlated noise case). In the second experiment with correlated noise, again the filter attenuated the noise, and the event became clearer with the iteration

7 Discussion

Typical microseismic data are characterized by low SNR and highly non-stationary noise. Suppressing noise will drastically improve signal detection, seismogram composition studies, source discrimination for small local/regional seismic sources as well as fracture characterization and monitoring in oil and gas reservoir. The SNR-enhancing methods usually rely on cross-correlation from the seismic traces recorded by geophone arrays. In this work, we propose a data-driven method to denoise seismic data. To isolate the noise from the signal, we need to acquire knowledge of the second-order statistics of the noise and the noisy signal. Since the occurrence of microseismic events is sporadic, the statistics are estimated directly from the received data. In this study, noise is first estimated and then removed from the receiver record. This makes a practical sense for microseismic denoising, since it is usually possible to estimate the statistics of the noise but not for the signal. The autocorrelations needed for the filter are either estimated from each trace separately or from multiple traces. In the former case, the advantage is that we can use the filter in the case of a single sensor, e.g., microseismic recorded by a single station or use parallel processing as in the case of a sensor array. However, in the latter case, the correlation estimation is improved by stacking the correlation estimates obtained from multiple seismic traces recorded by a geophone array. The stacking does not involve alignment of traces, since the proposed method relies on the autocorrelation. Hence, ambiguities resulting from misalignment are also eliminated here. Another advantage of the proposed method is that it does not impose any assumption on the noise statistics, which makes it suitable for applications with different noise types. Similar denoised results are obtained for the correlated and uncorrelated noise. It is also worth mentioning that our focus in this study is on low SNR seismic signals to prove the effectiveness of the proposed method. However, it is expected to perform well in case of earthquakes with magnitude greater than 2 and active (controlled source) seismic data. The reason is that no underlying assumption about the type of data is used, while designing the filter. Application of the proposed method on synthetic and field microseismic traces with both uncorrelated and correlated noise shows promising results. Our filtering procedure has been applied in an iterative fashion and improvements in SNR shown (see Fig. 9).

8 Conclusion

Fig. 9

Noise level versus number of iterations. Curves for SNR before and after denoising (for white noise and correlated noise case) using the proposed method. The SNR is improving with every iteration. With more iterations, we lose the basic assumption that noise and signal are uncorrelated; hence, the SNR starts to decrease after the fourth iteration. Consequently, we used only four iterations throughout our simulation results

Fig. 10

The field data set was obtained from the Incorporated Research Institutions for Seismology (IRIS). The event occurred on 9 October 2017 in Central Alaska, USA, and has magnitude $Ml = 5.2$. The data were recorded on a 3C sensor with sampling frequency of 250 Hz (resampled). a Field data set without noise. b Field data set with added white Gaussian noise (SNR = $-~7$ dB). c Denoised data using the proposed method (SNR= 5.9 dB). d Denoised data using the proposed enhanced method (SNR = 7.2 dB). Wavelet-based denoising method is used after forth iteration for these results

Fig. 11

a Noisy field data; b denoised field data. The parameters used here are the same as those used for the synthetic data set. Results are shown after the fourth iteration and application of the wavelet denoising method

Fig. 12

a Field data set (Liu et al. 2017) from the High Resolution Seismic Network (HRSN) operated by Berkeley Seismological Laboratory, University of California, Berkeley. The sampling frequency is 250 Hz. b Denoised traces using the proposed denoising method

In this study, we proposed an IIR Wiener filter-based denoising method. The proposed method is directly based on the second-order statistics of the noise and the observations, which can be obtained easily from the recorded time-series data. The proposed method gives a promising performance in a low SNR situation. The filter does not assume any specific noise statistics; this is desirable for applicability of the denoising method to field data recorded in diverse seismic noise environments. More importantly, its computational complexity is much lower in comparison to an equivalent FIR filter approach.