The Linearized Bregman Method for Frugal Full-waveform Inversion with Compressive Sensing and Sparsity-promoting

Abstract

Full-waveform inversion (FWI) reconstructs the subsurface properties from acquired seismic data via minimization of the misfit between observed and simulated data. However, FWI suffers from considerable computational costs resulting from the numerical solution of the wave equation for each source at each iteration. To reduce the computational burden, constructing supershots by combining several sources (aka source encoding) allows mitigation of the number of simulations at each iteration, but it gives rise to crosstalk artifacts because of interference between the individual sources of the supershot. A modified Gauss–Newton FWI (MGNFWI) approach showed that as long as the difference between the initial and true models permits a sparse representation, the $\ell _1$-norm constrained model updates suppress subsampling-related artifacts. However, the spectral-projected gradient $\ell _1$ (SPG$\ell _1$) algorithm employed by MGNFWI is rather complicated that makes its implementation difficult. To facilitate realistic applications, we adapt a linearized Bregman (LB) method to sparsity-promoting FWI (SPFWI) because of the efficiency and simplicity of LB in the framework of $\ell _1$-norm constrained optimization problem and compressive sensing. Numerical experiments performed with the BP Salt model, the Marmousi model and the BG Compass model verify the following points. The FWI result with LB solving $\ell _1$-norm sparsity-promoting problem for the model update outperforms that generated by solving $\ell _2$-norm problem in terms of crosstalk elimination and high-fidelity results. The simpler LB method performs comparably and even superiorly to the complicated SPG$\ell _1$ method in terms of computational efficiency and model quality, making the LB method a viable alternative for realistic implementations of SPFWI.

1 Introduction

Full-waveform inversion (FWI) is a powerful tool used for obtaining the properties (e.g., velocity, density, quality factor Q) of the subsurface media from collected seismic data. Due to progresses in computer science and technology, FWI has been ameliorated by many researchers over the past decades. FWI can be implemented either in the time domain (e.g., Tarantola 1986; Mora 1987; Bunks et al. 1995; Ren et al. 2014) or in the frequency domain (e.g., Pratt et al. 1998; Pratt 1999; Sirgue and Pratt 2004; Anagaw and Sacchi 2014). The reader is recommended to Virieux and Operto (2009) for an excellent overview of FWI. There are some methods for solsving the nonlinear least-squares (LS) FWI problem, e.g., the steepest-descent method, the conjugate gradient method, the Gauss–Newton (GN) method (Li et al. 2012, 2016), the truncated Newton method (Métivier et al. 2013; Castellanos et al. 2015), and the full-Newton method (Pan et al. 2016). Designing a suitable optimization scheme for FWI is still an area of active research. In this study, we will assume that an accurate starting model is available and the source wavelet is known. The central objective of this paper was to develop a new optimization method for FWI that conciliates computational efficiency and high-fidelity results.

In FWI, the forward modeling is carried out for each single source. As a result, the computational burden of FWI is roughly proportional to the number of shots involved (Li et al. 2012). This is correct for time domain FWI, but it is not fully correct for frequency domain FWI. In the frequency domain, once the LU decomposition of the forward matrix is done, the solution by backward substitution for any given source is fast; however, the computational cost is still roughly in proportion to the number of shots. The computational cost of FWI is expensive, because dense sources and receivers are utilized in modern seismic acquisition (Herrmann et al. 2013). In the case of massive 3D data composed of thousands of shots, it results in an even greater computational burden, even on today’s computing resources (Métivier et al. 2014). Many geophysicists have proposed reducing the computational burden by randomly subsampling or source encoding (e.g., Romero et al. 2000; Krebs et al. 2009; Tang 2009; Choi and Alkhalifah 2011; Ben-Hadj-Ali et al. 2011; Moghaddam et al. 2013; Son et al. 2014; Castellanos et al. 2015). However, as discussed in Schuster et al. (2011), Herrmann and Li (2012) and Li et al. (2016), an excessive data/source subsampling may weaken subsurface illumination or generate subsampling-related artifacts.

The compressed sensing (CS) theory (Donoho 2006; Tsaig and Donoho 2006) has shown that if the signals’ energy is concentrated in a few significant coefficients, these signals can be recovered from small subsets of data by solving sparsity-promoting problems (Candès et al. 2006). CS has been prospered for years ever since the works of Candès et al. (2006) and Donoho (2006), who laid solid mathematical foundations for sparsity-promoting reconstruction. The assumption is that the signals could be sparsely represented in some domains. Herrmann et al. (2008) observed that curvelets lead to sparsity of seismic images. With this observation and that random subsampling-related artifacts are not sparse in the curvelet domain, Li et al. (2012) modify the Gauss–Newton subproblem of FWI by incorporating a curvelet operator on the model update and obtain the model update by solving $\ell _1$-norm constrained sparsity-promoting optimization problems (named as the MGNFWI method). Li et al. (2016) explained that in certain cases it could be beneficial to promote sparsity on the Gauss–Newton updates instead of directly promoting sparsity on the model itself. Although constraining the $\ell _1$-norm of the descent directions of FWI does not alter the underlying FWI objective, the constrained model updates remain descent directions and eliminate subsampling-related artifacts. Li et al. (2016) investigated and analyzed this behavior, in which nonlinear inversions benefit from sparsity-promoting constraints on the model updates.

In the MGNFWI scheme, Li et al. (2012, 2016) solve the $\ell _1$-norm constrained sparsity-promotion subproblem relying on a spectral-gradient method (i.e., SPG$\ell _1$), which is an open-source MATLAB solver for $\ell _1$-norm regularized least-squares problem (van den Berg and Friedlander 2008). Nevertheless, SPG$\ell _1$ is rather complicated so that it is difficult to implement MGNFWI with SPG$\ell _1$ on realistic problems (Herrmann et al. 2015). The complexity of SPG$\ell _1$ is represented, in part, by a multitude of parameters involved (see Table 1), many subfunctions inset, and hundreds of lines of the codes (which are not preferred for the expensive FWI). To make this paper self-contained, Appendix 1 provides a brief introduction of SPG$\ell _1$ based on the work of van den Berg and Friedlander (2008).

Table 1 Comparison of the main options between SPG$\ell _1$ and linearized Bregman (LB)

To facilitate realistic applications, we adapt a relatively simple and effective linearized Bregman (LB) method (Cai et al. 2009c, b; Yin 2010; Lorenz et al. 2014a, b) to solve the large-scale sparsity-promoting GNFWI subproblem. The LB method recently has attracted a lot of attention because of its efficiency and simplicity in solving $\ell _1$-constrained problems in CS (e.g., Herrmann et al. 2015; Chai et al. 2017b). Lorenz et al. (2014b) stated that the LB method is useful for inverse problems in which the linear measurements are expensive and slow to obtain. Using the LB method, Herrmann et al. (2015) presented a fast online least-squares migration (LSM) and concluded that the LB method converges to a mixed one-two-norm penalized solution while working on small subsets of data, making it particularly suitable for large-scale and parallel industrial implementations.

The rest of the paper is organized as follows: First, the fundamental theory for the forward and inverse problems of FWI is described in brief. We then detail the theory and methodology of the linearized Bregman method and its adaptation to a frugal FWI with compressive sensing and sparsity-promoting. Numerical experiments demonstrate the performance of the proposed method. After discussing the technical aspects, limitations and extensions of this approach, we summarize our conclusions.

2 Theory and Methodology

2.1 FWI Forward Problem

The FWI theory is well-documented by many researchers; however, for better elaboration of the method proposed here, we transcribe some key formulaes of FWI below, considering the technical nature of this paper. We refer the reader to Virieux and Operto (2009) for an excellent overview of FWI in exploration geophysics. The forward modeling problem takes up a vital role in FWI, and the majority of the running time is spent on modeling of wave propagation. Success of FWI strongly relies on the accuracy, efficiency, and the level of physics included in the modelling stencil. The reader is referred to Carcione et al. (2002), Robertsson et al. (2007), Ren and Liu (2015) for a series of publications on seismic modeling methods. We use the matrix notations to denote the partial-differential operators of the wave equation. In the time domain, the wave equation can be written compactly as (Marfurt 1984)

$$\begin{aligned} {\mathbf {K}} {\mathbf {u}}(t) - {\mathbf {M}} \frac{\partial ^2 {\mathbf {u}}(t)}{\partial t^2} = - {\mathbf {s}}(t), \end{aligned}$$

(1)

where ${\mathbf {K}}$ is the stiffness matrix, the spatial coordinates (x, y, z) are omitted for avoiding notational clutter, ${\mathbf {u}}$ is the discretized wavefield arranged as a column vector, t denotes the time, ${\mathbf {M}}$ is the mass matrix, and ${\mathbf {s}}$ is the source term, also arranged as a column vector. The stiffness and mass matrices are computed by forming a discrete representation of the underlying spatial partial-differential-equations (PDEs) and the parameters.

Taking the temporal Fourier transform of Eq. 1 yields the frequency domain equation (aka the Helmholtz equation)

$$\begin{aligned} {\mathbf {H}}(\omega ) {\mathbf {u}}(\omega ) = {\mathbf {s}}(\omega ), \end{aligned}$$

(2)

where ${\mathbf {H}}$ is the sparse complex-valued impedance matrix, which is not perfectly symmetric because of absorbing boundary conditions (Hustedt et al. 2004). The most popular method for discretizing the wave equations is the finite-difference method (Plessix and Mulder 2004; Operto et al. 2007; Pan et al. 2012; Ren and Liu 2015; Chen et al. 2017), although more sophisticated approaches (e.g., finite-element method) can be considered (Marfurt 1984).

The subsurface properties that we aim to obtain are embedded in the coefficients of matrices ${\mathbf {K}}$, $\mathbf {M}$, ${\mathbf {H}}$ of Eqs. 1–2. The relationship between the wavefield and the subsurface parameters is nonlinear and can be written compactly through an operator ${\mathbf {G}}$, i.e., ${\mathbf {u}} = \mathbf {G}({\mathbf {m}})$. The model ${\mathbf {m}}$ represents some physical parameters of the subsurface discretized over the computational domain. The data modeled ${\mathbf {d}}_{\mathrm {mod}}$ can be related to the wavefield ${\mathbf {u}}$ by a detection operator $\varvec{\mathcal {D}}$, which extracts the values of the wavefields computed in the full computational domain at the receiver positions for each source, i.e., ${\mathbf {d}}_{\mathrm {mod}} = \varvec{\mathcal {D}} {\mathbf {u}} = \varvec{\mathcal {D}} {\mathbf {G}}(\mathbf {m}) = \varvec{\mathcal {F}}({\mathbf {m}})$, where $\varvec{\mathcal {F}}$ is the wrapped wave-equation-based nonlinear forward modeling operator.

2.2 FWI Inverse Problem

FWI is based on minimization of the data residual between the observed data ${\mathbf {d}}_{\mathrm {obs}}$ and the modeled data ${\mathbf {d}}_{\mathrm {mod}}$. Because of the size of problems we are dealing with and the computational cost involved, it is mostly infeasible to consider a global optimization approach. Therefore, the local optimization methods are commonly adopted to solve the nonlinear FWI problem. Defining the misfit vector $\delta {\mathbf {d}}$ as the differences at the receiver positions between ${\mathbf {d}}_{\mathrm {obs}}$ and ${\mathbf {d}}_{\mathrm {mod}}$ for each source-receiver pair gives $\delta d_j = d_{\mathrm {obs}_j} - d_{\mathrm {mod}_j},~j=(1,2,\ldots ,N)$, where the subscripted quantities $\delta d_j$, $d_{\mathrm {obs}_j}$, and $d_{\mathrm {mod}_j}$ are the individual elements of $\delta {\mathbf {d}}$, $\mathbf {d}_{\mathrm {obs}}$ and ${\mathbf {d}}_{\mathrm {mod}}$. A norm $\phi ({\mathbf {m}})$ of this misfit vector $\delta {\mathbf {d}}$ is referred to as the objective function. As is common in many inverse problems, we concentrate below on the $\ell _2$-norm, i.e.,

$$\begin{aligned} \phi ({\mathbf {m}}) = \frac{1}{2} \left\| \delta {\mathbf {d}} \right\| _2^2 = \frac{1}{2} \delta {\mathbf {d}}^* \delta {\mathbf {d}}, \end{aligned}$$

(3)

where the asterisk denotes the adjoint (transpose conjugate), ensuring the objective function $\phi ({\mathbf {m}})$ is real-valued for complex-valued data.

Letting the model ${\mathbf {m}}$ be represented as the summation of an initial model ${\mathbf {m}}_0$ and a perturbation model $\delta {\mathbf {m}}$, the minimum of $\phi ({\mathbf {m}})$ is sought in the vicinity of ${\mathbf {m}}_0$. The model variation vector $\delta {\mathbf {m}}$ is given by

$$\begin{aligned} \delta {\mathbf {m}} = -\left[ \frac{\partial ^2 \phi ({\mathbf {m}}_0)}{\partial {\mathbf {m}}^2} \right] ^{-1} \frac{\partial \phi ({\mathbf {m}}_0)}{\partial {\mathbf {m}}}. \end{aligned}$$

(4)

The perturbation model is searched in the opposite direction of the steepest ascent (i.e., the gradient) of the misfit function at ${\mathbf {m}}_0$. The second-order derivative of the misfit function is the Hessian ${\mathbf {H}}$, where ${\mathbf {H}}_{l,j} = \frac{\partial ^2 \phi ({\mathbf {m}}_0) }{\partial m_l \partial m_j}$. Detailed derivations of the first- and second-order derivatives of the LS misfit function with respect to the model parameter (i.e., $\frac{\partial \phi ({\mathbf {m}})}{\partial {\mathbf {m}}}$ and $\frac{\partial ^2 \phi ({\mathbf {m}})}{\partial {\mathbf {m}}^2}$) can be found in Virieux and Operto (2009).

The gradient in FWI, i.e., $\frac{\partial \phi ({\mathbf {m}}_0)}{\partial {\mathbf {m}}} = - \mathbf {J}^*({\mathbf {m}}_0) \delta {\mathbf {d}}$, is equivalent to a reverse time migration (RTM) image constructed using a cross-correlation imaging condition (Li et al. 2012). ${\mathbf {J}}$ is the Fréchet derivative matrix (aka the Jacobian matrix), which is the matrix of all first-order partial derivatives of a vector-valued function. The elements of ${\mathbf {J}}$ are given by ${\mathbf {J}}_{ij} = \frac{ \partial d_{\mathrm {mod}_i}}{\partial m_j},~(i = 1,2,\ldots ,N),~(j = 1,2,\ldots ,M)$. And

$$\begin{aligned} {\mathbf {H}} = \frac{\partial ^2 \phi ({\mathbf {m}}_0)}{\partial {\mathbf {m}}^2} = \mathbf {J}^*({\mathbf {m}}_0) \mathbf {J}({\mathbf {m}}_0) - \left[ \frac{\partial {\mathbf {J}}^*(\mathbf {m}_0)}{\partial m_1} \delta {\mathbf {d}}~ \frac{\partial {\mathbf {J}}^*(\mathbf {m}_0)}{\partial m_2} \delta {\mathbf {d}}~ \cdots ~ \frac{\partial {\mathbf {J}}^*(\mathbf {m}_0)}{\partial m_M} \delta {\mathbf {d}} \right] . \end{aligned}$$

(5)

Equation 5 can be rewritten as a sum of a first-order term ${\mathbf {H}}_{\mathrm {a}}$ and a second-order term ${\mathbf {R}}$, i.e., ${\mathbf {H}} = \mathbf {H}_{\mathrm {a}} + {\mathbf {R}}$, where ${\mathbf {H}}_{\mathrm {a}} = {\mathbf {J}}^*(\mathbf {m}_0) {\mathbf {J}}(\mathbf {m}_0)$ and ${\mathbf {R}} = - \left[ \frac{\partial {\mathbf {J}}^*(\mathbf {m}_0)}{\partial m_1} \delta {\mathbf {d}}~ \frac{\partial {\mathbf {J}}^*(\mathbf {m}_0)}{\partial m_2} \delta {\mathbf {d}}~ \cdots ~ \frac{\partial {\mathbf {J}}^*(\mathbf {m}_0)}{\partial m_M} \delta {\mathbf {d}} \right]$. ${\mathbf {H}}_{\mathrm {a}}$ is referred to as the approximate Hessian (Pratt et al. 1998). The elements in ${\mathbf {R}}$ are computed by cross-correlating second-order partial derivatives with the data residuals (Pan et al. 2016). The role of the term ${\mathbf {R}}$ in the framework of FWI is correcting the gradient for double-scattering effects. Inserting the gradient and the Hessian into Eq. 4 yields

$$\begin{aligned} \delta {\mathbf {m}} = \left[ {\mathbf {J}}^*(\mathbf {m}_0) {\mathbf {J}}(\mathbf {m}_0) + {\mathbf {R}} \right] ^{-1}{\mathbf {J}}^*(\mathbf {m}_0) \delta {\mathbf {d}}. \end{aligned}$$

(6)

The method solving Eq. 6 is referred to as the Newton method, whereas the method solving Eq. 6 when only ${\mathbf {H}}_{\mathrm {a}}$ is computed, i.e.,

$$\begin{aligned} \delta {\mathbf {m}} = \left[ {\mathbf {J}}^*({\mathbf {m}}_0) \mathbf {J}({\mathbf {m}}_0)\right] ^{-1} {\mathbf {J}}^*(\mathbf {m}_0) \delta {\mathbf {d}}, \end{aligned}$$

(7)

is referred to as the Gauss–Newton method (Pratt et al. 1998). The first-order term ${\mathbf {H}}_{\mathrm {a}}$ is relatively convenient to calculate, whereas the second-order term ${\mathbf {R}}$ is difficult to deal with. Thus, it is mostly ignored (Pan et al. 2015). Although advances in computer science and technology are impressive, due to the huge amounts of memory and computation required, the explicit calculations of ${\mathbf {H}}$ and $\mathbf {H}^{-1}$ are still beyond current computational capability (Métivier et al. 2013). To avoid expensive cost of computing and inverting large Hessian matrices, we concentrate on the Gauss–Newton method.

2.3 Gauss–Newton FWI with Compressive Sensing and Sparsity-promoting

The GN method utilizes the pseudo-inverse of the reduced Hessian, given by the combined action of the Jacobian operator ${\mathbf {J}}(\mathbf {m}_0)$ and its adjoint ${\mathbf {J}}^*(\mathbf {m}_0)$. From Eq. 7, we obtain

$$\begin{aligned} {\mathbf {J}}^*(\mathbf {m}_0) {\mathbf {J}}(\mathbf {m}_0) \delta {\mathbf {m}} = \mathbf {J}^*({\mathbf {m}}_0) \delta {\mathbf {d}}, \end{aligned}$$

(8)

which is equivalent to the least square solution of the following equation

$$\begin{aligned} {\mathbf {J}}(\mathbf {m}_0) \delta {\mathbf {m}} = \delta {\mathbf {d}}. \end{aligned}$$

(9)

We refer to the problem of solving Eq. 9 as the GNFWI subproblem. Specifically, we focus on the frequency-domain FWI in this paper. In the frequency domain, each iteration for the GNFWI subproblem requires 4K PDEs to be solved: two to compute the action of ${\mathbf {J}}(\mathbf {m}_0)$ and two for the action of its adjoint ${\mathbf {J}}^*(\mathbf {m}_0)$, where $K = n_f n_s$, with $n_f$ and $n_s$ being the number of frequencies and sources (Herrmann and Li 2012). To reduce the number of PDEs to be solved, researchers proposed to assemble the sources and the observed data into a smaller volume via source-encoding and frequency subsampling. In source-encoded FWI (e.g., Moghaddam et al. 2013), FWI is performed on a linear combination of all shots, called a supershot, rather than on each single shot separately. Each individual shot contributes to the supershot with a random weight that changes for each iteration during the optimization. Then we solve

$$\begin{aligned} \underline{{\mathbf {J}}({\mathbf {m}}_0)} \delta {\mathbf {m}} = \underline{\delta {\mathbf {d}}}. \end{aligned}$$

(10)

We denote these randomly subsampled (or source-encoded) quantities with the underbar. However, as discussed in Schuster et al. (2011) and Herrmann and Li (2012), an excessive subsampling will introduce source crosstalks into the result.

The CS theory shows that compressible signals can be restored from severely sub-Nyquist sampling rates of incomplete and inaccurate measurements via solving a sparsity-promoting problem (Aldawood et al. 2014). To maximally exploit the sparsity, one can employ some transforms (e.g., curvelet) that afford a sparse representation of the target solution. With the CS theory, we solve the following basis pursuit denoising (BPDN) problem:

$$\begin{aligned} \min _{\widetilde{\delta {\mathbf {m}}}} \Vert \widetilde{\delta {\mathbf {m}}}\Vert _1 \quad \mathrm {subject\,to}~ \frac{1}{2} \Vert \underline{{\mathbf {J}}(\mathbf {m}_0)} \mathcal {S}^* \widetilde{\delta {\mathbf {m}}} - \underline{\delta {\mathbf {d}}} \Vert _2^2 \le \sigma ^2, \end{aligned}$$

(11)

where $\mathcal {S}^*$ denotes the adjoint of the sparsifying transform operator $\mathcal {S}$, determining $\delta {\mathbf {m}} = \mathcal {S}^* \widetilde{\delta {\mathbf {m}}}$, with $\widetilde{\delta {\mathbf {m}}}$ a vector of transform coefficients of $\delta {\mathbf {m}}$. We refer to problem 11 as the sparsity-promoting GNFWI subproblem. To facilitate further formulation, we cast problem 11 in a canonical form of

$$\begin{aligned} \min _{\mathbf {x}} \Vert {\mathbf {x}}\Vert _1 \quad \mathrm {subject\,to}~ \frac{1}{2} \Vert {\mathbf {A}}{\mathbf {x}} - {\mathbf {b}}\Vert _2^2 \le \sigma ^2, \end{aligned}$$

(12)

where ${\mathbf {A}} = \underline{{\mathbf {J}}({\mathbf {m}}_0)} \mathcal {S}$, ${\mathbf {x}} = \widetilde{\delta {\mathbf {m}}}$, $\mathbf {b} = \underline{\delta {\mathbf {d}}}$. The more sparse of ${\mathbf {x}}$, the better of the solution.

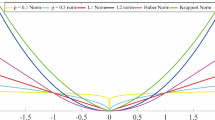
Herrmann et al. (2008) showed that curvelets give rise to sparsity of seismic images. Figure 1 depicts a comparison between the decay of coefficients in the physical domain and the curvelet domain. We can speculate that the BP Salt model is a good example to promote sparsity in the curvelet domain because it is made of nearly homogeneous layers delineated by sharp contrasts (see Figs. 1a and 3). A significantly faster decay of the curvelet coefficients is evident, which indicates that the curvelet domain offers a better sparse representation of the model update $\delta {\mathbf {m}}$ than the physical domain. Computing curvelet transforms on the search directions does not introduce serious computational overhead with respect to the cost of the PDEs to be solved. The MGNFWI method developed by Li et al. (2012, 2016) solves problem 12 with SPG$\ell _1$, which is rather complicated so that it is difficult to apply it on realstic problems. We, therefore, adapt a linearized Bregman (LB) method (Cai et al. 2009b; Lorenz et al. 2014a, b) for solving the large-scale sparsity-promoting Gauss–Newton FWI subproblem.

Fig. 1

Transform coefficients of the model update $\delta {\mathbf {m}}$, sorted from large to small, normalized and plotted in percent of the number of the transform coefficients. Gray line — physical domain (i.e., no transform is applied). Black line — Curvelet domain. a For $\delta {\mathbf {m}}$ of the BP Salt model. b For $\delta {\mathbf {m}}$ of the Marmousi2 model (Martin et al. 2006). c For $\delta {\mathbf {m}}$ of the BG Compass model

2.4 The linearized Bregman Method for FWI with CS and Sparsity-promoting

The LB method was introduced by Yin et al. (2008) and analyzed by Yin (2010), Cai et al. (2009b), and Osher et al. (2010) to approximately solve the basis pursuit (BP) problem in CS. It is proved by Cai et al. (2009a) that the LB method converges to a solution of

$$\begin{aligned} \min _{\mathbf {x}} {\mu \Vert {\mathbf {x}}\Vert _1 + \frac{1}{2} \Vert {\mathbf {x}}\Vert ^2_2 } \quad \mathrm {subject\,to}~ \frac{1}{2}\left\| {\mathbf {Ax}}-\mathbf {b}\right\| _2^2\le \sigma ^2, \end{aligned}$$

(13)

where $\mu > 0$. Algorithm 1 gives the pseudo-code of the LB method for solving the linear equation system ${\mathbf {Ax}} = \mathbf {b}$. The simplicity and efficiency serve as the main flavor of the LB method, making it attractive relative to other Gauss–Newton optimizations. For completeness, Appendix 1 provides a brief introduction of the theory of the Bregman method based on the works of Yin (2010) and Lorenz et al. (2014a).

The dynamic step-size $t_l$ is defined as (Lorenz et al. 2014a)

$$\begin{aligned} t_l = \left\| {\mathbf {A}}{\mathbf {x}}_{l} - {\mathbf {b}} \right\| _2^2 / \left\| {\mathbf {A}}^* \Pi _{\sigma } ({\mathbf {A}}{\mathbf {x}}_{l} - {\mathbf {b}}) \right\| _2^2. \end{aligned}$$

(14)

The projection function $\Pi _{\sigma }({\mathbf {Ax}} - {\mathbf {b}})$ is designed to handle the presence of noise, which involves orthogonal projection onto the $\ell _2$-norm ball and is given by (Lorenz et al. 2014a)

$$\begin{aligned} \Pi _{\sigma }({\mathbf {Ax}} - {\mathbf {b}}) = \max \left( 0, 1 - \sigma / \left\| {\mathbf {Ax}} - {\mathbf {b}}\right\| _2 \right) ({\mathbf {Ax}} - \mathbf {b}). \end{aligned}$$

(15)

The component-wise soft shrinkage function $\mathrm {shrink}(x, \mu )$ is given by

$$\begin{aligned} \mathrm {shrink}(x, \mu ) = \max (\left| x\right| - \mu , 0)\mathrm {sign}(x), \end{aligned}$$

(16)

where $\max (\cdot )$ obtains the maximum value, $|\cdot |$ gets the absolute value, $\mu$ is the threshold, and $\mathrm {sign}(\cdot )$ extracts the sign of a real number x. The shrinkage operator makes a vector sparse (and denoises). From algorithm 1 we can see that the inversion of matrices is not required.

Algorithm 2 provides the pseudo-code of adapting the LB method to FWI. Lines 9–10 denote the LB iterations. The frequency-domain FWI is disintegrated into successive inversions of frequency batches with a limited overlap. Each group consists of a limited number of discrete frequencies that significantly reduces the intrinsic redundancy of the data inverted (Anagaw and Sacchi 2014). The high-frequency component increases from one frequency batch to the next, in consequence defining a multi-scale FWI approach, which is helpful to mitigate the non-linearity of FWI (Bunks et al. 1995; Sirgue and Pratt 2004).

The outer (multiscale) loop in line 3 moves from one frequency group to the next. The data vector ${\mathbf {d}}_{\mathrm {obs}}$ changes accordingly. The current stopping criterion of the iterations of the nonlinear iteration loop (line 5) and the linear iteration loop (line 7) is a crude one. However, one can use a criterion based on model quality or data fit. This would have provided a more comprehensive assessment of the convergence rate and computational efficiency (see, Castellanos et al. 2015). We regenerate the random codes/weights on top of the linear loop (line 8), but not on top of the nonlinear one (line 6). In algorithm 2 line 8, we then subsample over source experiments (i.e., implement source encoding) by randomized source superimpositions via the action of a source-encoding matrix ${\mathbf {E}}\in {\mathbb {R}}^{n_s \times n_s^{\mathrm {sub}}}$, which has randomized Gaussian-distributed entries. $n_s^{\mathrm {sub}}$ is the number of the supershots, where $n_s^{\mathrm {sub}} \ll n_s$. The source encoding strategy implemented here is consistent with that introduced by Li et al. (2012, 2016).

For the stopping criteria in algorithm 2 line 3, it will stop when it has visited all the frequency batches. For the threshold $\mu$, we generally sort the transform coefficients in the descending order and set $\mu$ to be the value corresponding to a user-specified percentage of the total number of the transform coefficients. We can also set $\mu$ as a fraction of the maximum value of the solution calculated at the first iteration.

3 Numerical Experiments on Sparse Recovery Problems

One goal here is to provide a justification of the superiority of the $\ell _1$-norm regularized sparsity-promotion for sparse recovery compared with the $\ell _2$-norm. Another goal is to show that the much simpler LB method outperforms the rather complicated SPG$\ell _1$ advocated by MGNFWI (Li et al. 2016). We conducted a series of experiments on an underdetermined sparse recovery problem. Figure 2a shows the true model with 50 nonzero entries. There are 500 unknowns and 350 measurements in this experiment (see Fig. 2a, b). For simulating noisy data, noises were randomly generated as a percent (e.g., 100% in this experiment) of the $\ell _2$-norm of the noise-free data and then added to the noise-free data. To obtain a $\ell _2$-norm solution, we use the LSQR algorithm implemented in MATLAB to optimize

$$\begin{aligned} \min _{\mathbf {x}}\frac{1}{2}\left\| {\mathbf {x}}\right\| _2^2\quad \text {subject to }\frac{1}{2}\left\| {\mathbf {Ax}}-{\mathbf {b}}\right\| _2^2\le \sigma ^2. \end{aligned}$$

(17)

With the true model ${\mathbf {m}}_{\mathrm {true}}$ and the inverted model ${\mathbf {m}}_{\mathrm {inv}}$, we use two strategies, the relative least-squares error (RLSE) and the signal-to-noise ratio (SNR), to evaluate the quality of the model inverted. The RLSE is defined as (Moghaddam et al. 2013)

$$\begin{aligned} \mathrm {RLSE} = \left\| {\mathbf {m}}_{\mathrm {inv}} - {\mathbf {m}}_{\mathrm {true}} \right\| _2^2 / \left\| {\mathbf {m}}_{\mathrm {true}} \right\| _2^2. \end{aligned}$$

(18)

The smaller the RLSE, the better the inversion results. SNR is computed by

$$\begin{aligned} \mathrm {SNR(dB)} = -20\log _{10} \frac{\left\| {\mathbf {m}}_{\mathrm {true}} - {\mathbf {m}}_{\mathrm {inv}} \right\| _2 }{ \left\| {\mathbf {m}}_{\mathrm {true}} \right\| _2 }. \end{aligned}$$

(19)

Figure 2 shows the performances of LSQR, SPG$\ell _1$, and LB. The same number of iterations (10) is used. The parameter $\tau$ of SPG$\ell _1$ is set to be zero as suggested by its authors (van den Berg and Friedlander 2008). The noise-factor $\sigma$ is set as zero for both noise-free and noisy data, since we do not have an optimal $\sigma$ value for field seismic data. There are many artifacts in the results produced by LSQR, i.e., $\ell _2$-norm constrained optimization for sparse recovery (see Fig. 2c, d). Both SPG$\ell _1$ and LB produce high-accuracy results with correct amplitude for noise-free data. Comparison of Fig. 2c, e, and g verifies the superiority of sparsity-promoting via $\ell _1$-norm. For the noisy case, in comparison to the relatively low SNR (almost zero, see Fig. 2b) of the observed data (100% random noise added), the sparse recovery results produced by LB (Fig. 2h) are acceptable relative to that generated by SPG$\ell _1$ (Fig. 2f). Comparison of Fig. 2e–h shows that the simpler LB method does a better job (e.g., higher SNR and lower RLSE) than SPG$\ell _1$. In addition, the elapsed time of LB is shorter than that of SPG$\ell _1$. We further investigate this simple, efficient, and effective method, which has potential applications in academic and industrial fields.

Fig. 2

a Randomly generated sparse signal. The gray and black lines in panel b show the noise-free and noisy measurements, respectively. The solutions for noise-free and noisy measurements produced by LSQR (c, d), SPG$\ell _1$ (e, f), LB (g, h) are separately displayed. The SNR, RLSE, and elapsed time for the algorithms are correspondingly shown on the top of the panels

4 Numerical Experiments on FWI

We then conducted experiments on LB adapted to FWI. The tests were performed in the 2D frequency domain using the acoustic modeling of the wave propagation. The density was assumed to be constant. The perfectly matched layer (PML) absorbing boundary conditions (Berenger 1994) were implemented along all of the edges of the model (including the surface) to avoid edge reflections; therefore the surface-related multiples were not taken into account in this study. We use an optimal nine-point finite-difference scheme for the Helmholtz equation with PML (Chen et al. 2013). We used a well-documented strategy in FWI that is inverting the data starting from low frequencies and gradually moving toward higher frequencies, which is beneficial to mitigate some of the issues with local minima. When using source encoding and frequency subsampling, the same number of supershots, frequencies, and iterations were used for all optimization methods involved. The source was a band-passed wavelet and no energy existed below 3 Hz.

4.1 Portion of the BP Salt model

This model contains low- and high-velocity anomalies, and the size of the model (Fig. 3a) is $151 \times 601$ with a grid spacing of $d_x$ = $d_z$ = 20 m. We used a Ricker wavelet with a 12-Hz peak frequency and a 0-s phase shift. A total number of 41 frequencies in the frequency range [3 23] Hz were modeled. All simulations were carried out with 301 shot and 601 receiver positions sampled at 40 m and 20 m intervals, respectively. We began with a smooth model (Fig. 3b) and worked with small batches of frequency data at a time, each using 8 frequencies and 30 randomly formulated simultaneous shots in Algorithm 2 line 8, moving from low to high frequencies in overlapping batches of 4. We used 10 GN outer iterations for each frequency group and took the end result as initial guess for the next frequency band. For each GN subproblem, we carried out 20 inner iterations with the LB method. Figure 3c shows the inverted velocity model, which illustrates that the main characteristics of the true model are precisely recovered, validating the feasibility of the proposed approach.

Fig. 3

a Portion of the BP velocity model used for the numerical test of the method proposed. b Initial model for the inversion. c Model inverted

4.2 Marmousi2 Model

The grid size of the model shown in Fig. 4 is $281 \times 601$ with a grid spacing of $d_x$ = $d_z$ = 12.5 m. We used a Ricker wavelet with a peak frequency of 10 Hz and a phase shift of 0.1 s. A total number of 21 frequencies in the frequency range [3 13] Hz were generated. All simulations were carried out with 301 shot and 601 receiver positions correspondingly sampled at 25 m and 12.5 m intervals. We started with a smooth model shown in Fig. 4b using 6 frequencies and 10 randomly formulated simultaneous shots and moving from low toward high frequencies in overlapping batches of 3. We used 10 GN outer iterations for each frequency group and 20 inner iterations of LSQR and LB for each GN subproblem.

The final velocity model for noise-free data produced by LB (Fig. 4d) is close to the true model. Except at the edges of the model where the illumination is incomplete, the full complexity of the 2D feature is reconstructed with high-fidelity. The velocity model for noise-free data generated by LSQR (Fig. 4c) is evidently worse than that obtained by LB. The deep parts seem to be badly dealt with by LSQR.

In the presence of noise, the ill-posedness of FWI increases. In order to invert the noise-contaminated data, we added 20% random noise to the noise-free data. The FWI result generated by LB (Fig. 4f) shows that the noise slightly corrupts the model, but the result still yields an accurate identification of the model. The agreement with the true velocity profile is satisfactory, considering the crudeness of the noise-corrupted data. The results produced by LSQR become more noisy than by LB. This test for data with the presence of noise indicates the stability of the proposed approach for imperfect data. Figure 4 demonstrates that the FWI result with the LB method solving the $\ell _1$-norm sparsity-promoting problem is better than the FWI result with LSQR solving the $\ell _2$-norm LS problem. This is due to the benefits of sparsity-promotion and the fact that utilizing the $\ell _1$-norm as a measurement of sparsity is better than using the $\ell _2$-norm (Herrmann and Li 2012; Chai et al. 2014, 2016, 2017a).

Fig. 4

FWI results for a down-sampled Marmousi2 model dataset. a True velocity model. b Starting velocity model. c, d show the FWI results inverted with LSQR and LB for the noise-free data, respectively. e, f correspondingly display the results generated by LSQR and LB for the noisy data. The SNR and RLSE of the corresponding FWI results are listed out in Table 2

Table 2 SNR and RLSE of the FWI results generated by the LSQR and LB methods for the noise-free and noisy Marmousi data

4.3 BG Compass Model

The experiment on a sedimentary part of the BG Compass model aims to convince the readers that the simple LB method can compete with and even outperforms the complicated SPG$\ell _1$, and thus can be an alternative option for MGNFWI (Li et al. 2016). We used the same data set and inversion parameters as Li et al. (2012). Specifically, the synthetic BG North Sea Compass model (Fig. 5a) with a large degree of variability constrained by well log data was used to generate the observed data with a 12-Hz Ricker wavelet. A smooth starting model without any lateral information (Fig. 5b) was used for FWI. This velocity model was designed to evaluate the potential ability of FWI to resolve fine reservoir-scale variations in the velocities, which makes it ideal for SPFWI because this model can be well approximated by only 5% of the largest curvelet coefficients (see Fig. 1c) (Li et al. 2016). The model size is $205 \times 701$ with a grid spacing of $d_x$ = $d_z$ = 10 m. A total number of 58 frequencies in the frequency range [3 22.5] Hz were generated. All simulations were carried out with 351 shot and 701 receiver positions sampled at 20-m and 10-m intervals, respectively, yielding a maximum offset of 7 km. The inversions were carried out sequentially in 10 overlapping frequency batches, each using 7 different randomly selected simultaneous shots and 10 selected frequencies. Therefore, a single evaluation of the misfit was 50 times cheaper than an evaluation of the full misfit. We used 10 GN iterations for each frequency group. For each GN subproblem, we used 20 inner iterations of SPG$\ell _1$ and LB. No changes were made to the codes and results of Li et al. (2012).

The FWI results (shown in Fig. 5c, d) were calculated using the same computing resources (1 node, 11 workers). The running time of FWI with LB was substantially less than that with SPG$\ell _1$, where the reduction was approximately $\frac{1}{3}$ of the original time. Comparison of Fig. 5c, d reveals that both are comparable to the true model. Furthermore, the structures and amplitudes produced by LB are more clear and closer to the true model than those generated by SPG$\ell _1$. Therefore, the much simpler LB method does an excellent job compared to SPG$\ell _1$ in this case. Figure 6 shows two representative velocity profiles within the model, from which it may be concluded that not only were the features accurately inverted, but also that the magnitudes of the velocity perturbations were precisely imaged.

Fig. 5

BG Compass model. a True velocity model. b Starting velocity model. c Inverted velocity model with the method developed in Li et al. (2012), for which SPG$\ell _1$ is used to solve the $\ell _1$ sparsity-promoting problems to get the model updates, and SNR = 26.2944 (dB), RLSE = 0.0023. d Inverted velocity model with the linearized Bregman method, where SNR = 26.9938 (dB), RLSE = 0.0020

Fig. 6

Well data comparison at 2 km for methods SPG$\ell _1$ (a) and LB (b), respectively

5 Discussion

The computational cost is an important factor for realstic applications of FWI. The computational time for producing a gradient accounts for the majority of the cost, which is also in proportion to the total iteration number. The computational time for the curvelet transform and for the solution of $\delta {\mathbf {m}} = \mathcal {S}^*{\mathbf {x}}$ is almost negligible with respect to the cost of the PDEs to be solved. For the test examples of FWI, the number of outer (nonlinear) and inner (linear) iterations is empirically set to be 10 and 20, respectively. The number of inner (linear) iterations should be designed according to the LB algorithm (generally less than 30, especially for the expensive and local optimization FWI problems). How to optimally design these two iteration levels is still an open issue. For all the FWI test examples, we sort the transform coefficients of $\delta {\mathbf {m}}$ in the descending order and set $\mu$ to be the value corresponding to 5% of the total number of the transform coefficients, as suggested by Fig. 1.

This study is based on CS theory, and the hidden assumption is that the model variation at each iteration $\delta {\mathbf {m}}$ could be sparsely represented with the curvelet-transform. When the initial model is close to the true model, the model difference $\delta {\mathbf {m}}$ contains mostly small scale structures. Probably, the curvelet-transformed $\delta {\mathbf {m}}$ could easily cluster into a few coefficients. If the initial model is not sufficiently close to the true model, the performance of the assessed method will be reduced. The FWI scheme proposed here or MGNFWI is essentially a migration-based FWI method, which employs a LSM step to obtain the model perturbation. Overall, this paper considers two methodological ingredients: source encoding and $\ell _1$-norm regularization with linearized Bregman optimization. The first-order motivation of the paper is to promote the use of the linearized Bregman optimization in a general FWI context, rather than to optimize the performance of source encoding. The $\ell _1$-norm regularization with Bregman optimization is also beneficial without source encoding. We recommend the reader to Chai et al. (2017b) for examples on the imaging results obtained with and without source encoding when the $\ell _1$-norm regularization with LB optimization is used.

Like most FWI schemes, we assume having an appropriate starting model that is close to the global solution allowing successive relinearizations. Such models can be obtained by reflection tomography, velocity analysis, and first-arrival traveltime analysis (Woodward et al. 2008; Taillandier et al. 2009), etc. The objective function in Eq. 3 ignores incorporation of a priori information on the data or on the model. More realistic prior information can be exploited for numerical stability. The implementation in this paper is 2-D isotropic acoustic frequency domain FWI. However, the LB method can be straightforwardly applied to 2D/3D time/frequency domain FWI/migration.

6 Conclusions

This study presents an implementation of a relatively simple linearized Bregman method to solve the large-scale sparsity-promoting Gauss–Newton FWI subproblem. The assessed optimization algorithm relies on compressive sensing implemented with a $\ell _1$-norm regularization in the curvelet domain applied to the model update rather than the model itself and a linearized Bregman optimization scheme. From the inverted velocity model (and the representative velocity profiles within the model), not only are the main structures correctly inverted, but also that most of the magnitudes of the velocity are accurately recovered. The FWI result with the linearized Bregman method solving the $\ell _1$-norm sparsity-promoting problems is better than the FWI result with LSQR solving the $\ell _2$-norm LS problems, in terms of crosstalk elimination and model resolution. This is due to the benefits of sparsity-promotion. The much simpler LB method does a comparable and even superior job compared to the complicated SPG$\ell _1$ in terms of computational efficiency and model quality, making the LB method a viable alternative for realstic applications of FWI with compressive sensing and sparsity-promoting.

Appendices

Appendix A

1.1 Deriving a Sparse Solution with SPG$\ell _1$

To solve the BPDN problem 12, SPG$\ell _1$ solves a series of the $\ell _1$-constrained LS problems, aka the LASSO problems, abbreviated for “Least Absolute Shrinkage and Selection Operator”:

$$\begin{aligned} \min _{\mathbf {x}} \Vert {\mathbf {A}}{\mathbf {x}}-{\mathbf {b}}\Vert _2\quad \mathrm {subject\,to}~ \Vert {\mathbf {x}}\Vert _1\le \tau , \end{aligned}$$

(20)

where $\tau$ is a sparsity constraint on the solution ${\mathbf {x}}$. For proper parameter selections of $\sigma$ and $\tau$, the solutions of BPDN and LASSO are consistent, and problems 12 and 20 are to some degree equivalent, which are closely related by the Pareto curve defining the trade-off between the $\ell _2$-norm of the data residual (i.e., the LASSO objective function) and the $\ell _1$-norm of the unknown vector ${\mathbf {x}}$ (i.e., the BPDN objective function) (van den Berg and Friedlander 2008).

SPG$\ell _1$ uses a Newton-based root-finding algorithm on the Pareto curve to obtain the value of $\tau$ given an estimate of the noise-level $\sigma$ and solves a sequence of LASSO problems for gradually increasing $\tau$. The solution for the current LASSO problem serves as an initial candidate for the next LASSO problem. Solving each LASSO problem itself utilizing the SPG method involves some gradient updates. The SPG procedure relies on the capability to project iterates onto the feasible set $\left\{ {\mathbf {x}}~|~\Vert \mathbf {x}\Vert _1\le \tau \right\}$. This is achieved by an operator $P_{\tau }({\mathbf {c}}):= \left\{ \mathop {\arg \min }_{\mathbf {x}} \Vert {\mathbf {c}}-{\mathbf {x}}\Vert _2 \quad {\mathrm {subject\,to}}~ \Vert {\mathbf {x}}\Vert _1\le \tau \right\}$ giving the projection of a vector ${\mathbf {c}}$ onto the $\ell _1$-norm ball with radius $\tau$. Each iteration of the SPG algorithm searches the projected gradient path $P_{\tau }({\mathbf {x}}_l - \alpha {\mathbf {g}}_l)$, where $\alpha$ is the step length and ${\mathbf {g}}_l$ is the current gradient for the function $\Vert {\mathbf {A}}{\mathbf {x}}-{\mathbf {b}}\Vert ^2_2$ (van den Berg and Friedlander 2008).

Let ${\mathbf {x}}_{\tau }$ denotes a LASSO solution, and the single-parameter function $\phi (\tau )= \Vert {\mathbf {A}}{\mathbf {x}}_{\tau }-{\mathbf {b}}\Vert _2$ gives the $\ell _2$-norm of the data residual for each $\tau \ge 0$. Each iteration of the root-finding algorithm requires the evaluation of $\phi$ and its derivative $\phi '$ at some $\tau$, and thus the minimization of the LASSO problem. This is an expensive subproblem potentially, and the validity of SPG$\ell _1$ rests with the ability to solve this subproblem. The implementation of SPG$\ell _1$ is structured around major and inner iterations. Each major iteration is responsible for determining the next element of the sequence $\left\{ \tau _k \right\}$ and for activating the SPG method to determine approximate values of $\phi \left( \tau _k \right)$ and $\phi ' \left( \tau _k \right)$ (van den Berg and Friedlander 2008).

Appendix B

1.1 The Bregman Distance and the Bregman Method

The Bregman and LB methods are based on Bregman distance (Bregman 1967). Let $J(\cdot )$ denotes a convex function. Bregman distance with respect to J between points ${\mathbf {x}}$ and ${\mathbf {y}}$ is defined as (Yin 2010)

$$\begin{aligned} D^{\mathbf {p}}_J({\mathbf {x}},{\mathbf {y}}) := J({\mathbf {y}}) - J({\mathbf {x}}) - \left\langle {\mathbf {p}}, {\mathbf {y}}-{\mathbf {x}} \right\rangle , \end{aligned}$$

(21)

where ${\mathbf {p}} \in \partial J({\mathbf {x}})$ is some subgradient in the subdifferential of J at ${\mathbf {x}}$, and $\left\langle {\mathbf {a}}, {\mathbf {b}} \right\rangle$ gives an inner product of vectors ${\mathbf {a}}$ and ${\mathbf {b}}$. If $J({\mathbf {x}}) = \frac{1}{2} \Vert {\mathbf {x}}\Vert ^2_2$, $D^{\mathbf {p}}_J({\mathbf {x}},{\mathbf {y}}) = \frac{1}{2} \Vert {\mathbf {x}} - {\mathbf {y}}\Vert ^2_2$ (Lorenz et al. 2014a). Note that $D^{\mathbf {p}}_J({\mathbf {x}},{\mathbf {y}})$ is not a distance in the usual (metric) sense, because it is in general neither necessarily symmetric, i.e., $D^{\mathbf {p}}_J({\mathbf {x}},{\mathbf {y}}) \ne D^{\mathbf {p}}_J({\mathbf {y}},{\mathbf {x}})$, nor positive definite and does not have to obey a (quasi-) triangle inequality (Lorenz et al. 2014a). Nevertheless, it does measure the closeness between ${\mathbf {x}}$ and ${\mathbf {y}}$ in the sense that $D^{\mathbf {p}}_J({\mathbf {x}},{\mathbf {y}}) \geqslant 0$ and $D^{\mathbf {p}}_J({\mathbf {x}},{\mathbf {y}}) \geqslant D^{\mathbf {p}}_J({\mathbf {z}},{\mathbf {y}})$ for all points ${\mathbf {z}}$ on the line segment connecting ${\mathbf {x}}$ and ${\mathbf {y}}$ (Yin 2010; Osher et al. 2010).

The original Bregman approach solves a series of convex problems in an iterative scheme

$$\begin{aligned} {\mathbf {x}}^{k+1} \leftarrow \min _{\mathbf {x}}D^{{\mathbf {p}}^k}_J({\mathbf {x}},{\mathbf {x}}^k) + \frac{1}{2} \left\| {\mathbf {A}}{\mathbf {x}} - {\mathbf {b}} \right\| ^2_2, \end{aligned}$$

(22)

for $k = 0, 1, \cdots$, starting from ${\mathbf {x}}^0 = {\mathbf {0}}$ and ${\mathbf {p}}^0 = {\mathbf {0}}$. In expression 22, each ${\mathbf {p}}^{k+1}$ is obtained based on the optimality condition (Yin 2010)

$$\begin{aligned} {\mathbf {0}} \in \partial J({\mathbf {x}}^{k+1}) - {\mathbf {p}}^{k} + {\mathbf {A}}^* ({\mathbf {A}}{\mathbf {x}}^{k+1} - {\mathbf {b}}), \end{aligned}$$

(23)

yielding ${\mathbf {p}}^{k+1} := {\mathbf {p}}^{k} - {\mathbf {A}}^* \left( {\mathbf {A}}{\mathbf {x}}^{k+1} - {\mathbf {b}}\right)$. To improve the performance of Bregman iteration, the LB iteration was invented, the idea of which is to approximate the last term in expression 22 by its Taylor expansion around ${\mathbf {x}}^{k}$ (Yin 2010). Specifically, LB is obtained by linearizing the last term in 22 into $\left\langle {\mathbf {A}}^* \left( {\mathbf {A}}{\mathbf {x}}^{k} - {\mathbf {b}}\right) , {\mathbf {x}} \right\rangle$ and adding the $\ell _2$-proximity term $\left\| {\mathbf {x}} - {\mathbf {x}}^k \right\| ^2_2$.