Three Least-Squares Minimization Approaches to Interpret Gravity Data Due to Dipping Faults

Abstract

We have developed three different least-squares minimization approaches to determine, successively, the depth, dip angle, and amplitude coefficient related to the thickness and density contrast of a buried dipping fault from first moving average residual gravity anomalies. By defining the zero-anomaly distance and the anomaly value at the origin of the moving average residual profile, the problem of depth determination is transformed into a constrained nonlinear gravity inversion. After estimating the depth of the fault, the dip angle is estimated by solving a nonlinear inverse problem. Finally, after estimating the depth and dip angle, the amplitude coefficient is determined using a linear equation. This method can be applied to residuals as well as to measured gravity data because it uses the moving average residual gravity anomalies to estimate the model parameters of the faulted structure. The proposed method was tested on noise-corrupted synthetic and real gravity data. In the case of the synthetic data, good results are obtained when errors are given in the zero-anomaly distance and the anomaly value at the origin, and even when the origin is determined approximately. In the case of practical data (Bouguer anomaly over Gazal fault, south Aswan, Egypt), the fault parameters obtained are in good agreement with the actual ones and with those given in the published literature.

1 Introduction

Estimation of the depth and the dip angle of a plane of a faulted structure from gravity anomalies has drawn considerable attention. Most numerical methods have focused on determining the depth only of the faulted structure from gravity data. The methods include, for example, least-squares minimization approaches (Gupta 1983; Lines and Treitel 1984; Abdelrahman et al. 2003; Abdelrahman and Essa 2013), Euler Deconvolution method (Reid et al. 1990), special functions method (Phillips et al. 2007), and quasi-singular points methods (Eliseyeva 1998; Utyupin and Mishenin 2012).

Few methods are used for interpreting gravity anomalies caused by a dipping faulted thin slab model to find the dip angle of faulted structure. A curve-matching technique was discussed by Geldart et al. (1966). Paul et al. (1966) showed the use of upward continuation of the observed anomaly in estimating the dip angle. Based on the Hilbert transform relationship between two derivatives, Green (1976) pointed out how the vertical derivative can be used in interpreting the dip angle. Abdelrahman et al. (1989) and Gupta and Pokhriyal (1990) developed methods to estimate the dip angle based on determining the maximum and minimum gravity. However, most of these methods use a few characteristic points and distances, nomograms, and standardized curves to determine the model parameters. As a result, the drawback to these approaches is that they are highly subjective and, therefore, can lead to large errors in estimating the depth and the dip angle of a buried fault from the gravity anomaly profile. Also, the accuracy of the depth and dip estimates obtained by most of these methods depends upon the accuracy to which the residual anomaly can be separated from observed gravity data.

Very recently, Essa (2013) described a variance analysis method to interpret gravity data due to a dipping fault from numerical horizontal gravity gradients. However, his method can not be applied to a composite gravity anomaly of a buried dipping faulted thin slab and first-order regional polynomial. Also, Abdelrahman et al. (2013) developed a least-squares window curves method to determine simultaneously the depth and the dip angle of a buried dipping fault from moving residual gravity anomalies. However, the window curves method is a graphical method, and hence it is highly subjective in determining the model parameters of the buried fault structure from gravity data.

We present a new numerical method that uses three different least-squares approaches to determine the depth, dip angle, and the amplitude coefficient of a buried dipping fault from first moving average residual gravity anomalies. A scheme for analyzing the gravity data has been formulated for determining the model parameters of the fault. The validity of the method is tested on a synthetic example and on a field example from Egypt.

2 Method

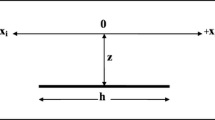
The formula for the gravity anomaly generated along the profile normal to the strike of a dipping faulted thin slab having infinite strike length (Fig. 1) is given by the following equation (Telford et al. 1976)

Fig. 1

The two-dimensional gravity dipping fault model

$$ g(x_{i} ,z,h,\alpha )\, = \,K\left[ {\pi + \tan^{ - 1} \left( {\frac{{x_{i} }}{z} + \cot \alpha } \right) - \tan^{ - 1} \left( {\frac{{x_{i} }}{h} + \cot \alpha } \right)} \right], $$

(1)

where z and h are the depths of the centers of the upper and lower portions of the layer, respectively, α is the angle of dip, K is the amplitude coefficient related to the thickness t, and density contrast of the faulted slab, and x _i is the horizontal coordinate position.

In cases where the throw of the fault is extremely large, i.e., h approaches infinity, then Eq. (1) can be reduced to (Essa 2013; Abdelrahman et al. 2013)

$$ g(x_{i} ,z,\alpha )\, = \,K\,\left[ {\pi + \tan^{ - 1} \left( {\frac{{x_{i} }}{z} + \cot \alpha } \right)} \right]\,. $$

(2)

Equation (2) does not distinguish either from a normal or reverse fault but it can be used to estimate the model parameters of the fault which might be used to gain geological insight concerning the subsurface.

The first moving average (grid method) is an important and simple technique for the separation of gravity anomalies into residual and regional components. The basic theory of the first moving average method is described by Griffin (1949) and application of least-squares to the first moving average is described by Agocs (1951). The first moving average residuals (grid residuals) are proportional to the second derivative values (Rao and Radhakrishnamurthy 1965) and hence have high resolving power, particularly when the graticule spacing is very large.

Let us consider three observation points (x _i  − s, x _i , and x _i  + s) along the anomaly profile, where s = 1, 2,., M spacing units and is called the window length. The first moving average residual gravity anomaly R(x _i , z, α, s) at point x _i is defined as (Abdelrahman and El-Araby 1993):

$$ R\,(x_{i} ,z\,,\alpha ,s)\, = \,\frac{K}{2}\left[ {2\,\tan^{ - 1} \left( {\frac{{x_{i} }}{z} + \cot \alpha } \right) - \tan^{ - 1} \left( {\frac{{x_{i} + s}}{z} + \cot \alpha } \right) - \tan^{ - 1} \left( {\frac{{x_{i} - s}}{z} + \cot \alpha } \right)} \right]. $$

(3)

For all depths and angles, Eq. (3) gives the following value at x _i  = 0

$$ R(0) = \frac{K}{2}\left[ {2\tan^{ - 1} \,\left( {\cot \alpha } \right)\, - \,\tan^{ - 1} \,\left( {\frac{s}{z} + \cot \alpha } \right) - \tan^{ - 1} \,\left( {\frac{ - s}{z} + \cot \alpha } \right)} \right], $$

(4)

where R(0) is the first moving average residual gravity anomaly value at the origin.

Using Eq. (4), (3) can be written as:

$$ R\,(x_{i} ,z,\alpha ,\,s)\, = \,R(0)\frac{{\left[ {2\,\tan^{ - 1} \left( {\frac{{x_{i} }}{z} + \cot \alpha } \right) - \tan^{ - 1} \left( {\frac{{x_{i} + s}}{z} + \cot \alpha } \right) - \tan^{ - 1} \left( {\frac{{x_{i} - s}}{z} + \cot \alpha } \right)} \right]}}{{\left[ {2\tan^{ - 1} \,\left( {\cot \alpha } \right)\, - \,\tan^{ - 1} \,\left( {\frac{s}{z} + \cot \alpha } \right) - \tan^{ - 1} \,\left( {\frac{ - \,s}{z} + \cot \alpha } \right)} \right]}}, $$

(5)

The moving average residual gravity anomaly profile attains its zero value at x_o which is the nearest zero-anomaly distance from the origin of the moving average residual gravity anomaly profile. Thus, setting Eq. (5) to zero, we obtain:

$$ \left[ {2\,\tan^{ - 1} \left( {\frac{{x_{o} }}{z} + \cot \alpha } \right) - \tan^{ - 1} \left( {\frac{{x_{o} + s}}{z} + \cot \alpha } \right) - \tan^{ - 1} \left( {\frac{{x_{o} - s}}{z} + \cot \alpha } \right)} \right] = 0, $$

(6)

from which we get

$$ \cot \alpha = \frac{{ - x_{o} }}{z}, $$

(7)

because the numerical sum of the two terms [$\tan^{ - 1} (\frac{{x_{o} + s}}{z} + \cot \alpha ) + \tan^{ - 1} (\frac{{x_{o} - s}}{z} + \cot \alpha )$] in Eq. (6) is equal to zero. The nearest x _o value from the origin is read either directly from the anomaly profile or by interpolation between observations.

Substituting Eq. (7) into Eq. (5), we obtain the following non-linear equation in z

$$ R(x_{i} ,z,s)\, = R(0)W(x_{i} ,z,s), $$

(8)

where

$$ W(x_{i} ,z,s)\, = \frac{{\left[ {2\,\tan^{ - 1} \left( {\frac{{x_{i} - x_{o} }}{z}} \right) - \tan^{ - 1} \left( {\frac{{x_{i} + s - x_{o} }}{z}} \right) - \tan^{ - 1} \left( {\frac{{x_{i} - s - x_{o} }}{z}} \right)} \right]}}{{\left[ {2\tan^{ - 1} \,\left( {\frac{{ - x_{o} }}{z}} \right)\, - \,\tan^{ - 1} \,\left( {\frac{{s - x_{o} }}{z}} \right) + \tan^{ - 1} \,\left( {\frac{{\,s + x_{o} }}{z}} \right)} \right]}}\,.\,\,\, $$

The unknown depth z in Eq. (8) can be obtained by minimizing

$$ \varphi (z)\, = \,\sum\limits_{i = 1}^{N} {\left[ {L(x_{i} ) - \,R(0)\,W(x_{i} ,z,s)} \right]^{2} } , $$

(9)

where L(x _i ) is the first moving average residual gravity anomaly at x _i calculated from the observed gravity data g(x _i ) using the following equation

$$ L(x_{i} )\, = \,\frac{{2g(x_{i} )\, - \,g(x_{i} - s)\, - \,g(x_{i} + s)}}{2}, $$

(10)

and where R(0) is the value of the moving average residual gravity anomaly at the origin and remains fixed in the process.

Setting the derivative of φ(z) with respect to z to zero leads to the following nonlinear equation in z;

$$ f\,(z)\, = 2\,\sum\limits_{i = 1}^{N} {\left[ {L(x_{i} ) - \,R(0)\,W(x_{i} ,z,s)} \right]\,W^{*} (x_{i} ,z,s)\, = \,0} , $$

(11)

where

$$ W^{*} (x_{i} ,z,s)\, = \,\frac{{d\,W(x_{i} ,z,s)}}{dz}. $$

Equation (11) can be solved for z using standard methods for nonlinear equation. Here, it is solved by Newton–Raphson method (Press et al. 1986). The source depth is estimated by solving one non-linear equation in z.

Substituting the estimated depth (z _c) as a fixed parameter in Eq. (5), we obtain:

$$ R\,(x_{i} ,\alpha ,\,s)\, = \,R(0)V(x_{i} ,\alpha ,s), $$

(12)

where

$$ V(x_{i} ,\alpha ,s) = \frac{{\left[ {2\,\tan^{ - 1} \left( {\frac{{x_{i} }}{{z_{c} }} + \cot \alpha } \right) - \tan^{ - 1} \left( {\frac{{x_{i} + s}}{{z_{c} }} + \cot \alpha } \right) - \tan^{ - 1} \left( {\frac{{x_{i} - s}}{{z_{c} }} + \cot \alpha } \right)} \right]}}{{\left[ {2\tan^{ - 1} \,\left( {\cot \alpha } \right)\, - \,\tan^{ - 1} \,\left( {\frac{s}{{z_{c} }} + \cot \alpha } \right) - \tan^{ - 1} \,\left( {\frac{ - \,s}{{z_{c} }} + \cot \alpha } \right)} \right]}}. $$

The unknown dip angle (α) in Eq. (12) can be obtained by minimizing

$$ \psi (\alpha )\, = \,\sum\limits_{i = 1}^{N} {\left[ {L(x_{i} ) - \,R(0)\,V(x_{i} ,\alpha ,s)} \right]^{2} } . $$

(13)

Setting the derivative of ψ(α) with respect to α to zero leads to the following nonlinear equation in α;

$$ q\,(\alpha )\, = \,2\sum\limits_{i = 1}^{N} {\left[ {L(x_{i} ) - \,R(0)\,V(x_{i} ,\alpha ,s)} \right]\,V^{*} (x_{i} ,\alpha ,s)\, = \,0} , $$

(14)

where

$$ V^{*} (x_{i} ,\alpha ,s)\, = \,\frac{{{\text{d}}\,V(x_{i} ,\alpha ,s)}}{{{\text{d}}\alpha }}. $$

Equation (14) can be solved for α using standard methods for nonlinear equation. Here, it is solved also by the Newton–Raphson method (Press et al. 1986). The source dip angle is estimated by solving one nonlinear equation in α.

Setting the estimated dip angle (α _c) and the estimated depth (z _c) in Eq. (3) as fixed parameters, we obtain:

$$ R\,(x_{i} ,s)\, = \,\frac{K}{2}\left[ {2\,\tan^{ - 1} \left( {\frac{{x_{i} }}{{z_{c} }} + \cot \alpha_{c} } \right) - \tan^{ - 1} \left( {\frac{{x_{i} + s}}{{z_{c} }} + \cot \alpha_{c} } \right) - \tan^{ - 1} \left( {\frac{{x_{i} - s}}{{z_{c} }} + \cot \alpha_{c} } \right)} \right]\,. $$

(15)

Finally, applying the least-squares method to Eq. (15), the unknown amplitude coefficient K can be determined from

$$ K_{c} = \frac{{2\sum\nolimits_{i = 1}^{N} {L(x_{i} )} \left[ {2\,\tan^{ - 1} \left( {\frac{{x_{i} }}{{z_{c} }} + \cot \alpha_{c} } \right) - \tan^{ - 1} \left( {\frac{{x_{i} + s}}{{z_{c} }} + \cot \alpha_{c} } \right) - \tan^{ - 1} \left( {\frac{{x_{i} - s}}{{z_{c} }} + \cot \alpha_{c} } \right)} \right]}}{{\sum\nolimits_{i = 1}^{N} {\left[ {2\,\tan^{ - 1} \left( {\frac{{x_{i} }}{{z_{c} }} + \cot \alpha_{c} } \right) - \tan^{ - 1} \left( {\frac{{x_{i} + s}}{{z_{c} }} + \cot \alpha_{c} } \right) - \tan^{ - 1} \left( {\frac{{x_{i} - s}}{{z_{c} }} + \cot \alpha_{c} } \right)} \right]^{2} } }}\,\,. $$

(16)

Theoretically, one value of s is enough to estimate the model parameters (z, α, K). In practice, more than one value of s is desirable because of the presence of noise in data.

An interpretation scheme based on the above equations for analyzing field data is as follows:

• 1. Determine the origin of the anomaly profile using geological or other geophysical data.

• 2. Digitize the anomaly profile at several points including the central point x _i  = 0.

• 3. Apply several moving average filters of successive window lengths to the digitized data. In this way several moving average residual anomaly profiles are obtained.

• 4. For each moving average residual gravity anomaly profile, estimate the depth (z), dip angle (α), and amplitude coefficient (K) from Eqs. (11), (14), and (16), respectively.

• 5. Determine the average value of the estimated parameters obtained in the step 4 from all moving average residual gravity anomaly profiles.

3 Effect of Using Different Initial Guesses

To demonstrate the dependence or independence of initial guesses of z and α in estimating the depth, the dip angle, and the amplitude coefficient of a synthetic 2 % noise-corrupted gravity anomaly due to a dipping fault (K = 200 mGal, z = 6 m, α = 45°, profile length = 80 m, and sampling interval = 1 m) from its moving average residual gravity anomalies of window length of 5 m using Eqs. (11), (14), and (16), respectively, the following experiment is presented.

The usefulness of the present method can be demonstrated by some extreme examples, namely, estimating the parameters of the indicated fault using different initial guess values of the depth (1, 2, 3,…, and 10 m) in case an initial guess of dip angle equals 10 degrees. We then use different initial guess values of the dip angle (10°, 20°, 30°,…, and 80°) in case an initial guess of depth equals 2 m. The results of this experiment are shown in Tables 1 and 2, respectively.

Table 1 Numerical results of the present method applied to the dipping fault synthetic example (K = 200 mGal, z = 6 m, α = 45°, profile length = 80 m, and sampling interval = 1 m) noise-corrupted data (with 2 % of random noise) using a fixed initial guess of α = 10°

Table 2 Numerical results of the present method applied to the dipping fault synthetic example (K = 200 mGal, z = 6 m, α = 45°, profile length = 80 m, and sampling interval = 1 m) noise-corrupted data (with 2 % of random noise) using a fixed initial guess of z = 2 m

We verified numerically that our method does not depend on initial guesses of depth (z) and dip angle (α). The maximum error in the model parameters is 5 %. This demonstrates that our method works well in cases where any initial guesses of the depth and dip angle are used, even when the data is noise-corrupted.

4 Error Response of the Method

4.1 Effect of Errors in x _o and R(0)

In studying the error response of the three least-squares method, synthetic examples of a composite gravity anomaly consisting of the sum of the gravity effects of a dipping faulted thin slab (K = 100 mGal, z = 10 m, α = 50°, profile length = 80 m, and sampling interval = 1 m) and a linear regional polynomial (Fig. 2) were considered. The model equation is

Fig. 2

Composite gravity anomaly (∆g) of a buried dipping faulted thin slab and first-order regional as obtained from Eq. (17)

$$ \Delta g(x_{i} )\, = \,100\,\left( {\pi + \tan^{ - 1} \left( {\frac{{x_{i} }}{10} + \cot {\text{50}}^\circ} \right)\,} \right)\,\,\,\, + \,5x_{i} + 5. $$

(17)

The composite gravity anomaly is subjected to a regional–residual separation technique using the moving average method with a window length of 3 m (Fig. 3).

Fig. 3

Moving average residual gravity anomalies with and without random errors due to a buried dipping faulted thin slab for s = 3 m obtained from the composite gravity anomaly

Errors of ±1, ±2, ±3, ….,±5 % of the magnitude value of R(0) and x _o were added to both in the correct values of R(0) and x _o. Following the interpretation method, values of three model parameters (z, α, K) were computed and the percentage of errors in the model parameters were mapped (Figs. 4a, 5a, 6a). When the zero-anomaly distance (x _o) and the residual anomaly value at the origin R(0) have errors of equal magnitude and of opposite signs simultaneously, the interpreted depth, dip angle, and amplitude coefficient values will not differ much from the true values. When both R(0) and x _o possess errors of equal magnitude and of the same signs simultaneously, the interpreted z and α values will vary by up to 2 %, but K will vary up to 3.5 %. When x _o has no error, the percentage of error in model parameters is 1.5 %. Finally, when R(0) has no error, the maximum percentage of error in the model parameters is 2 %. In all cases, the error in the parameters is smaller than the imposed error. This demonstrates that the present approach is less sensitive to the exact values of both R(0) and x _o than traditional approaches.

Fig. 4

A map showing error response in depth estimates. a Using synthetic data and b using data with random errors. Abscissa percent error imposed in R(0). Ordinate percent error imposed in x _o. Contour interval = 0.5 %

Fig. 5

A map showing error response in dip angle estimates. a Using synthetic data and b using data with random errors. Abscissa percent error imposed in R(0). Ordinate percent error imposed in x _o. Contour interval = 0.5 %

Fig. 6

A map showing error response in amplitude coefficient estimates. a Using synthetic data and b using data with random errors. Abscissa percent error imposed in R(0). Ordinate percent error imposed in x _o. Contour interval = 0.5 %

The composite gravity anomaly is then contaminated with random errors of 2 % of the anomaly value at each x _i and is subjected to the moving average method with a window length of 3 m (Fig. 3). Following the same interpretation method, the percentage of error in the model parameters is obtained (Figs. 4b, 5b, 6b). In the case examined, an initial guess of 5 m for the depth is used in solving Eq. (11) and an initial guess of 30° for the dip angle is used in solving Eq. (14).

We verified numerically that the maximum errors of the estimated depth, dip angle, and amplitude coefficient are within 8, 6.5, and 12 %, respectively. These results show that our technique is robust in the presence of noise.

4.2 Effect of Wrong Origin

Uncertain knowledge of the origin may lead to error in the model parameters (z, α, K) when interpreting real data. In this subsection we investigate this effect.

In Eq. (17), the origin of the dipping faulted thin slab was assumed to be chosen incorrectly by introducing errors (offset) of ±2, ±1.75, ±1.5,…, ±0.25 m in the horizontal coordinate x _i using synthetic data with and without random errors. Following the same interpretation method, the results are shown in Fig. 7. In all cases examined, an initial guess of 5 m for the depth is used in solving Eq. (11) and an initial guess of 30° for the dip angle is used in solving Eq. (14).

Fig. 7

Error response in model parameter estimates when using synthetic data with and without random errors

In cases using noise-free synthetic data, the estimated depth and amplitude coefficient are in excellent agreement with the actual ones. However, the percentage of error in the dip angle increases with increasing offset. The maximum error in α is about 15 % when the offset is extremely large (2 m).

On the other hand, in cases using data with random error, we verified numerically that the maximum error in depth is 6 %. The dip angle obtained is within 13 %, whereas the amplitude coefficient is within 11 %. This indicates that good results would be obtained by using the present algorithm when the origin of the structure is only approximately determined. It may be noted that the maximum error in alpha is about 15 % in the case of noise-free data. On the other hand, the maximum error is about 13 % in the case of noise-corrupted data. This may be because when using noise-free synthetic data, the depth and the amplitude coefficient determined by the present method do not affected by the value of the offset in the origin, whereas the error in the estimated dip angle increases with increase in the offset (Fig. 7). On the other hand, when using noise-corrupted data, the estimated depth is affected by the presence of the random errors in the data which in turns affects the error in the dip angle. Accordingly, the error in the dip angle when using noise-corrupted data is less or greater than the error in case of using noise-free data.

4.3 Effect of Window Length

The same noise-corrupted gravity anomaly was subjected to seven moving average windows (s = 2, 3,…,8 m). Following the same interpretation method, the estimated model parameters, the average value of each parameter, and the standard deviation are given in Table 3. In all cases examined, an initial guess of 5 m for the depth is used in solving Eq. (11), and an initial guess of 30° for the dip angle is used in solving Eq. (14).

Table 3 Numerical results of the present method applied to the dipping fault synthetic example (K = 100 mGal, z = 10 m, α = 50°, profile length = 80 m, and sampling interval = 1 m) noise-corrupted data (with 2 % of random noise) using seven successive window lengths (s = 2, 3,…, 8 m)

We verified numerically that the method does not depend on the window length when using synthetic data without random errors. On the other hand, the method depends on window length when the data are contaminated with random noise. In this case, for each s value, different measurements with different sets of random errors are used in computing the moving average residual gravity anomalies. However, the average values of the model parameters obtained using several window lengths are in very good agreement with the actual model parameters because of their small standard deviation. The small standard deviation values indicate that the average gets closer to the true parameter values. As a result, it is recommended to apply more than one value of s to field data to obtain reliable model parameters.

5 Application to Field Data

To illustrate the practical application of the theory developed in the previous section, a Bouguer gravity anomaly profile over the Gazal fault, south Aswan, Egypt (Fig. 8) is interpreted to determine the depth, dip angle, and amplitude coefficient. The fault affected both the basement and the sedimentary rocks, and crops out on the surface (Abdelrahman et al. 1999). The depth to the top of the crystalline basement is found to be about 200 m as obtained from drilling information (Evans et al. 1991). In this example, the fault trace point is determined on the gravity profile, as usual, by projecting the point of intersection between the fault and the ground surface vertically. The gravity profile has been digitized at an interval of 31.25 m. The obtained Bouguer gravity anomalies have been subjected to a separation technique using the moving average method. Filters were applied in seven successive windows (s = 156.25, 187.5, 218.75, 250, 281.25, 312.5, and 343.75 m). In this way, seven moving average residual anomaly profiles were obtained (Fig. 9). It may be noted that none of the several moving average residual gravity anomalies of Fig. 9 look like the residual computed for synthetic data, shown in Fig. 3. This is may be due to the presence of gravity interference from neighboring structures and/or noise. The same procedure described for the synthetic examples was used to estimate the depth, dip angle, and amplitude coefficient of the fault. The value of x _o was computed from each moving average residual gravity anomaly profile using a linear interpolation technique (Davis 1973). The nearest zero-anomaly distance to the origin on each residual anomaly profile was always chosen. The result is shown in Table 4. The average model parameters determined are: z = 202 ± 17 m, α = 57.7 ± 4^o and K = 2.4 ± 0.3 mGal. This suggests that Gazal fault resembles a dipping fault and not a vertical fault as approximated by Abdelrahman et al. (2003) who applied least-squares derivative analysis method to the same field data. The depth obtained by the present method (202 m) agrees very well with that obtained from drilling information (~200 m) (Evans et al. 1991; their Figs. 1b and 3). Also, this interpretation agrees very well with the results obtained by Essa (2013) and Abdelrahman et al. (2013).

Fig. 8

Gazal fault gravity anomaly, south Aswan, Egypt

Fig. 9

Moving average residual gravity anomalies due to Gazal fault for s = 156.25, 187.5, 218.75, 250, 281.25, 312.5, and 343.75 m

Table 4 Interpreted depth, angle of dip, and amplitude coefficient from moving average residuals of Gazal gravity anomaly, south Aswan, Egypt using the present method

Using the estimated parameters z, α and K, we generated the predicted gravity anomaly and subtracted it from the observed anomaly, to see which part of the observed Bouguer gravity anomaly was explained. The observed gravity anomaly, the residual gravity anomaly and the regional gravity anomaly are shown in Fig. 10. Figure 10 indicates that the regional gravity anomaly can be represented by a first-order polynomial. The residual gravity anomaly is related to the near surface fault structure and regional gravity is related to the deep-seated structure. Figure 10 shows also that the shape of the predicted gravity anomaly (residual anomaly) explains mainly the shape of the observed gravity anomaly.

Fig. 10

Observed gravity anomaly and its two components. Gazal fault, south Aswan, Egypt. The residual gravity anomaly is related to the near surface faulted structure and the regional gravity anomaly is related to the deep-seated structure

Finally, the depth obtained by our method is not deep enough to be considered “infinite” as defined in Eq. (2). However, approximation and assumption in gravity interpretation is usually accepted (Hammer 1974; Nettleton 1976). It is evident from this field example that our method gives good insight from gravity data concerning the nature of the fault structure.

6 Conclusions

The problem of determining the depth, dip angle, and amplitude coefficient of a buried dipping faulted thin slab from observed gravity data has transformed into the problem of solving two nonlinear equations and one linear equation, respectively. The method involves using the dipping faulted thin slab model convolved with the same moving average filter as applied to the observed data. As a result, our method also can be applied not only to residuals, but also to measured gravity data. A scheme for interpreting the gravity data to obtain the model parameters based on the three least-squares method provides two advantages over the pervious least-squares window curves techniques: (1) each model parameter is computed from all observed data, (2) the method does not require constraining the model parameters of the buried dipping fault to obtain the actual parameters, any initial estimate for depth and dip angle works well, and (3) the method gives good results when the gravity anomaly is contaminated with random noise. The depth, dip angle, and the amplitude coefficient obtained by the present method might be used to gain geologic insight concerning the subsurface.