Anisotropic Ising Model in $d+s$ Dimensions

Abstract

In this note, we consider the asymmetric nearest neighbor ferromagnetic Ising model on the $(d+s)$-dimensional unit cubic lattice ${\mathbb {Z}}^{d+s}$, at inverse temperature $\beta =1$ and with coupling constants $J_s>0$ and $J_d>0$ for edges of ${\mathbb {Z}}^s$ and ${\mathbb {Z}}^d$, respectively. We obtain a lower bound for the critical curve in the phase diagram of $(J_s,J_d)$. In particular, as $J_d$ approaches its critical value from below, our result is directly related to the so-called dimensional crossover phenomenon.

1 Introduction

In this paper, we consider an asymmetric nearest neighbor ferromagnetic Ising model on the $(d+s)$-dimensional unit cubic lattice $\mathbb {Z}^{d+s}$, with coupling constants $J_d>0$ and $J_s>0$ in the hyperplanes $\mathbb {Z}^{d}$ and $\mathbb {Z}^{s}$, respectively.

Anisotropic lattice spin systems have been the subject of great interest within the physics community since the sixties. The study of such models has been tackled both numerically, mainly via Monte Carlo simulations (see, e.g., [1,2,3,4] and references therein), and theoretically, via mean-field, Bethe approximation, truncated high-temperature expansion of the susceptibility, etc. (see, e.g., [4,5,6,7,8,9,10,11]). A strong motivation to study anisotropic systems is to investigate finite-size effects in realistic materials modeled by quasi-two-dimensional (thin films) and quasi-one-dimensional spin systems. Furthermore, exploring these systems could provide valuable insights into isotropic models, notably the three-dimensional Ising model (see, e.g., [12] and references therein).

Rigorous results on the asymmetric Ising model on $\mathbb {Z}^{d+s}$ have been obtained mainly in the case $\mathbb {Z}^{1+s}$ with strong coupling in one dimension and small coupling in the remaining directions. In particular, in a well-known article (see [13]), Fisher derived an asymptotic bound on the critical temperature of the $\mathbb {Z}^{1+s}$ anisotropic Ising model in the limit $\frac{J_s}{J_1}\rightarrow 0$. It has also been shown rigorously (see [14]) that the free energy of the Ising model on $\mathbb {Z}^{1+s}$ is analytic for any inverse temperature $\beta$ if $J_s$ is small enough (depending on $J_1$ and the inverse temperature). These rigorous results rely heavily on the fact that when $d=1$ the one-dimensional system is in the gas phase at all temperatures so that the standard high-temperature expansion can be used with effectiveness. On the other hand, to obtain the same kind of results of references [13, 14] in the case $\mathbb {Z}^{d+s}$, $d\ge 2$ is expected to be trickier since the $d-$dimensional system exhibits a phase transition and the usual high-temperature expansion turns to be much more difficult to control.

In this paper, we somehow extend the results obtained in [13] and [14] for the case $\mathbb {Z}^{1+s}$ to the case $\mathbb {Z}^{d+s}$ with $d\ge 1$. Namely, we show that for all $J_d$ above the critical reduced temperature $J_d^c$, the susceptibility of the $(d+s)$-dimensional system is finite when the coupling $J_s$ is sufficiently small (inversely proportional to the susceptibility $\chi (J_d)$ of the d-dimensional system). A similar result was obtained by two of us in [15] for the Bernoulli anisotropic bond percolation model on $\mathbb {Z}^{d+s}$, in which edges in the $\mathbb {Z}^{d}$ hyperplane are open with probability $p<p_c(d)$ and edges parallel in the $\mathbb {Z}^{s}$ hyperplane are open with probability q. In [15], probabilistic arguments were applied and in particular, a crucial use of the van den Berg–Kesten (BK) inequality has been made. In the present paper, to get the analogous result for the anisotropic Ising model in $\mathbb {Z}^{d+s}$ (for which BK inequalities are not available), we use an alternative (w.r.t. the high temperature) expansion of the Ising partition function, namely the so-called random current representation. This powerful technique, introduced in the eighties by Aizenman [16], was widely used by several authors in the following decades, and recently, it has employed as a crucial tool in several remarkable papers, e.g., [17]–[19]]. We remind that the high-temperature phase of any d dimensional Ising model satisfies strong spatial mixing, which is equivalent to the Dobrushin–Shlosman “Complete Analyticity-CA” condition. Therefore also in $d+s$ dimensions under a sufficiently weak s-dimensional perturbation, the CA-condition holds implying analyticity of the free energy (see [20] for a recent proof of CA).

As mentioned earlier, our results may be of interest in the study of realistic quasi-two-dimensional magnets which can be modeled by a two-dimensional sub-critical Ising bilayer. When the interaction between the two two-dimensional layers is weak and the transverse interaction is sub-critical, the bilayer system is expected to still exhibit sub-critical behavior. However, as the coupling between the layers strengthens, the overall system may exhibit spontaneous magnetization. Our result implies rigorously that as long as the inter-layer interaction between layers is below the inverse two-dimensional susceptibility (with a constant factor 1/(2 s)), the global system remains sub-critical. The understanding of how several layers of 2D slightly sub-critical systems with small interactions between them can start to behave as a $(2+s)$-dimensional system, is the so-called dimensional crossover phenomenon (see, e.g., Sec. VI in [6]). This phenomenon is characterized by a critical exponent, which is believed to depend on the original dimension of the layers, but not on the target dimension. Moreover, numerical simulations and formal calculations (see, e.g., [6, 7]), suggest that this critical exponent equals the exponent of the susceptibility of the original dimension. Our results imply rigorously an inequality between the two exponents.

2 The Model and Results

Let ${\mathbb {Z}}^{d+s}={\mathbb {Z}}^d\times {\mathbb {Z}}^s$ be the $(d+s)$-dimensional unit cubic lattice. We will denote by $\mathbb {E}^{d+s}$ the set of nearest neighbor pairs of $\mathbb {Z}^{d+s}$ so that $\mathbb {G}^{d+s}$ is the graph with vertex set $\mathbb {Z}^{d+s}$ and edge set $\mathbb {E}^{d+s}$. Given two vertices $x,y\in \mathbb {Z}^{d+s}$, we denote by $|x-y|$ the usual graph distance between x and y (i.e., the edge length of the shortest path between x and y). We will suppose that $\mathbb {Z}^{d+s}$ is equipped with the usual operation of sum. We represent hereafter a site $x\in \mathbb {Z}^{d+s}$ as $x=(u,t)$, where $u\in \mathbb {Z}^{d}$ and $t\in \mathbb {Z}^{s}$.

Given an integer N, we denote by $\Lambda _N\subset \mathbb {Z}^{d+s}$ the hypercube with side length $2N+1$, centered at the origin, so that $\Lambda _N\rightarrow \infty$ means that $N\rightarrow \infty$. We denote by $E_N$ the set of edges of $\mathbb {E}^{d+s}$ with both endpoints in $\Lambda _N$, so that $\mathbb {G}^{d+s}|_{\Lambda _N}=(\Lambda _N, E_N$) is the restriction of $\mathbb {G}^{d+s}$ to $\Lambda _N$. Note that $\Lambda _N=\bar{\Lambda }_N\times \hat{\Lambda }_N$ where $\bar{\Lambda }_N$ denotes the d-dimensional hypercube in ${\mathbb {Z}}^d$ of size $2N+1$ centered at the origin and $\hat{\Lambda }_N$ denotes the s-dimensional hypercube in ${\mathbb {Z}}^s$ of size $2N+1$ centered at the origin. Given $w\in \hat{\Lambda }_N$, we set $\Lambda ^w_{N}=\{(u,t)\in {\mathbb {Z}}^{d+s}: t=w\}$. Namely $\Lambda ^w_{N}$ is the subset of $\Lambda _N$ formed by sites of $\Lambda _N$ with w as the second set of coordinates. Similarly, $E^w_N$ will denote the set of edges with both endpoints in $\Lambda _N^w$. Observe that $\Lambda _N^w$ is a d-dimensional box of side length $2N+1$ centered at (0, w).

To each vertex $x\in \Lambda _N$, we associate a random variable $\sigma _x$ taking values in the set $\{+1, -1\}$. A spin configuration in $\Lambda _N$ is a function $\varvec{\sigma }: \Lambda _N\rightarrow \{+1, -1\}:x\mapsto \sigma _x$. The energy of a configuration $\varvec{\sigma }$ is given by the (free boundary condition) Hamiltonian

$$\begin{aligned} H_{\Lambda _N}(\varvec{\sigma })= -\sum _{\{x,y\}\in E_N}J_{\{x,y\}}\sigma _x\sigma _y, \end{aligned}$$

where

$$\begin{aligned} J_{\{x,y\}}={\left\{ \begin{array}{ll} J_s & \textrm{if}\;\;x=(u,t)\;\;\textrm{and}\;\; y=(u, t')\;\; \textrm{with}\;\;|t-t'|=1,\\ J_d & \textrm{if}\;\;x=(u,t)\;\;\textrm{and}\;\; y=(u', t)\;\; \textrm{with}\;\;|u-u'|=1, \end{array}\right. } \end{aligned}$$

with $J_s>0$ and $J_d>0$. In what follows, an edge $\{x,y\}\in E_N$ is called vertical if $x=(u,t)$, $y=(u, t')$ with $|t-t'|=1$, and called planar if $x=(u,t)$, $y=(u', t)$ with $|u-u'|=1$. So $J_{\{x,y\}}=J_s$ if $\{x,y\}$ is vertical and $J_{\{x,y\}}=J_d$ if $\{x,y\}$ is planar.

The partition function of the system is given by

$$\begin{aligned} Z_{\Lambda _N}(J_d,J_s)= \int d\mu _{\Lambda _N}(\varvec{\sigma }) e^{-H_{\Lambda _N}(\varvec{\sigma })}=\int d\mu _{\Lambda _N}(\varvec{\sigma })\prod _{\{x,y\}\in E_N}e^{J_b\sigma _x\sigma _y}, \end{aligned}$$

where $\int d\mu _{\Lambda _N}(\varvec{\sigma })$ is a short notation for $\prod _{x\in \Lambda _N}\frac{1}{2}\sum _{\sigma _x=\pm 1}$ (a product probability measure). Moreover, without loss of generality, we have set the inverse temperature $\beta =1$.

The two-point correlation function of the $(d+s)$-system is then defined as

$$\begin{aligned} \langle \sigma _x \sigma _y \rangle _{\Lambda _N}= \frac{\int d\mu _{\Lambda _N}(\varvec{\sigma })\sigma _x\sigma _y e^{- H_{\Lambda _N}(\sigma _\Lambda )}}{Z_{\Lambda _N}(J_d,J_s)} =\frac{\int d\mu _{\Lambda _N}(\varvec{\sigma })\sigma _x\sigma _y\prod _{\{x,y\}\in E_N}e^{J_b\sigma _x\sigma _y}}{Z_{\Lambda _N}(J_d,J_s)}.\nonumber \\ \end{aligned}$$

(1)

In general, for any set $U\subset \Lambda _N$, letting $E_U=\{\{x,y\}\in E_N: \{x,y\}\subset U\}$, we set

$$\begin{aligned} H_{U}(\varvec{s})= -\sum _{\{x,y\}\in E_U}J_{\{x,y\}}\sigma _x\sigma _y, \\ Z_{U}(J_d,J_s)= \int d\mu _{\Lambda _N}(\varvec{\sigma }) e^{-H_{U}(\varvec{\sigma })}, \end{aligned}$$

and, for any $x,y\in U$,

$$\begin{aligned} \langle \sigma _x \sigma _y \rangle _{U}= \frac{\int d\mu _{\Lambda _N}(\varvec{\sigma })\sigma _x\sigma _y e^{- H_{U}(\sigma _\Lambda )}}{Z_{U}(J_d,J_s)}. \end{aligned}$$

According to the above notations, for any $t\in \hat{\Lambda }_N$, we have that

$$\begin{aligned} \langle \sigma _x \sigma _y \rangle _{\Lambda ^t_N}= \frac{\int d\mu _{\Lambda _N}(\varvec{\sigma })\sigma _x\sigma _ye^{- H_{\Lambda ^t_N}(\sigma _\Lambda )}}{Z_{\Lambda _N^t}(J_d,J_s)}, \end{aligned}$$

The finite volume susceptibility function of the system is defined as

$$\begin{aligned} \chi _{\Lambda _N}(J_d,J_s):=\sup _{x\in \Lambda _N}\Bigg \{\sum _{y\in \Lambda _N}\langle \sigma _x\sigma _y\rangle _{\Lambda _N}\Bigg \}, \end{aligned}$$

so that

$$\begin{aligned} \chi _{d+s}(J_d,J_s)= \lim _{N\rightarrow \infty }\chi _{\Lambda _N}(J_d,J_s) \end{aligned}$$

(2)

is the susceptibility of the anisotropic $(d+s)$-dimensional Ising model.

For any $t\in \hat{\Lambda }_N$, let

$$\begin{aligned} \chi _{\Lambda _N^t}(J_d)=\sup _{x\in \Lambda _N^t} \Bigg \{\sum _{y\in \Lambda _N^t}\langle \sigma _x\sigma _y\rangle _{\Lambda _N^t}\Bigg \}, \end{aligned}$$

(3)

so that

$$\begin{aligned} \chi _d(J_d)=\lim _{N\rightarrow \infty }\chi _{\Lambda _N^t}(J_d) \end{aligned}$$

(4)

is the susceptibility of the d-dimensional Ising model with ferromagnetic interaction $J_d$.

We are now in a position to state our main result.

Theorem 1

Take any $J_d$ such that

$$\begin{aligned} \chi _d(J_d)<+\infty , \end{aligned}$$

and let $J_s$ such that

$$\begin{aligned} \tan \,\textit{h}(J_s)< \frac{1}{2s\chi _{d}(J_d)}. \end{aligned}$$

Then,

$$\begin{aligned} \chi _{d+s}(J_d, J_s)<+\infty . \end{aligned}$$

Remark 1

As mentioned in the introduction, Theorem 1 is related to the so-called dimensional crossover phenomenon. One can define, for any $J_d>0$, the function $J_s^c(J_d):[0,\infty )\rightarrow [0,\infty )$, where

$$\begin{aligned} J_s^c(J_d)=\sup \{J_s: \chi _{d+s}(J_d,J_s)<+\infty \}. \end{aligned}$$

(5)

Denoting by $J_d^c$ the critical inverse reduced temperature of the d-dimensional system, we have that by definition, $J_s^c(J_d)=0$ if $J_d\ge J^c_d$. Theorem 1 determines a region in the $(J_d,J_s)$ plane where no phase transition occurs in the $(d+s)$-system and it also gives an upper bound for the function $J_s^c(J_d)$ as $J_d$ varies in the interval $[0, J_d^c)$. There is a strong interest in understanding the behavior of the function $J_s^c(J_d)$ when $J_d<J_d^c$, and in particular, it is widely believed that there exists a constant $\phi _d>0$ such that

$$\begin{aligned} J_s^c(J_d)\approx |J_d-J_d^c|^{\phi _d}, ~~\textrm{as} ~~ J_d\uparrow J_d^c, \end{aligned}$$

where the symbol $\approx$ stands for log equivalence, that is, $f(x)\approx g(x)$ if $\displaystyle \lim _{\beta \uparrow \beta _c}\frac{\log f(x)}{\log g(x)}=1$. The constant $\phi _d$ is the so-called crossover critical exponent. On the other hand, the d-dimensional Ising susceptibility $\chi _d(J_d)$ is known to behave like

$$\begin{aligned} \chi _d(J_d)\approx |J_d-J_d^c|^{-\gamma _d}, \text{ as } J_d\uparrow J_d^c, \end{aligned}$$

where $\gamma _d>0$ is the susceptibility d-dimensional critical exponent.

As an immediate corollary, Theorem 1 implies that $\phi _d\le \gamma _d$ for all $d\ge 2$, and a lower bound for $J_s^c(J_d)$ still inversely proportional to $\chi _d(J_d)$ would imply that $\phi _d=\gamma _d$. The conjectured equality of the crossover critical exponent $\phi _d$ and susceptibility critical exponent $\gamma _d$ has been discussed in the physics literature by several authors, see, for instance, [3, 5, 6, 9, 21]. See also [22] for a recent example of dynamical approach to dimensional crossover.

3 The Random Current Representation

As mentioned in the introduction, in order to prove Theorem 1 we will use the so-called random current representation for the Ising model introduced by Aizenman in [16]. We will describe this technique here below following mainly reference [23].

Let $\mathfrak {F}(E_N)$ be the set of all functions $\eta : E_N\rightarrow \mathbb {N}:b\mapsto \eta _b$. Then, we can expand the exponential inside the product and rewrite the partition function $Z_{\Lambda _N}(J_d,J_s)$ as

$$\begin{aligned} Z_{\Lambda _N}(J_d,J_s)= \sum _{\eta \in \mathfrak {F}(E_N)}W(\eta )\int d\mu _{\Lambda _N}(\varvec{\sigma })\prod _{x\in \Lambda _N} (\sigma _x)^{\sum _{b\ni x}\eta _b}, \end{aligned}$$

where we have denoted shortly

$$\begin{aligned} \sum _{b\ni x}\eta _b=\sum _{b\in E_N\atop x\in b}\eta _b \end{aligned}$$

and we have set

$$\begin{aligned} W(\eta )=\prod _{b\in E_N} \frac{(J_b)^{\eta _b}}{\eta _b!}. \end{aligned}$$

Observe that the integral $I(\eta )=\int d\mu _{\Lambda _N}(\varvec{\sigma })\prod _{x\in \Lambda _N} (\sigma _x)^{\sum _{b\ni x}\eta _b}$ is zero, unless $\sum _{b\ni x}\eta _b$ is even for all $x\in \Lambda$, in which case $I(\eta )=1$. Hence,

$$\begin{aligned} Z_{\Lambda _N}(J_d,J_s)= \sum _{\begin{array}{c} \eta \in \mathfrak {F}(E_N)\\ \partial \eta =\emptyset \end{array}}W(\eta ), \end{aligned}$$

where we have set

$$\begin{aligned} \partial \eta =\bigg \{x\in \Lambda : \;\sum _{\begin{array}{c} b\ni x \end{array}}\eta _b \;\text{ is } \text{ odd }\bigg \}. \end{aligned}$$

In general, given any $\eta \in \mathfrak {F}(E_N)$, the vertices in $\partial \eta$ are called sources of $\eta$, and if $\partial \eta =\emptyset$, then $\eta$ is called sourceless. Proceeding similarly, we have that the random current expansion for the two-point function is

$$\begin{aligned} \langle \sigma _x \sigma _y \rangle _{\Lambda _N}=\sum _{\begin{array}{c} \eta \in \mathfrak {F}(E_N)\\ \partial \eta =\{x,y\} \end{array}}\frac{W(\eta )}{Z_{\Lambda _N}(J_d,J_s)}. \end{aligned}$$

We now rewrite the function $\langle \sigma _x \sigma _y \rangle _{\Lambda _N}$ as a sum of edge-self-avoiding walks from x to y. Given an edge $\{x,y\}\in E_N$, the ordered pair (x, y) will be called a step from x to y. For any $x\in \Lambda _N$, we establish an arbitrary order (denoted by $\preceq$) for the set of steps emerging from x (i.e., for those (x, y) such that $|x-y|=1$). For each site x, and each step (x, z), we consider the set $\Gamma _{(x,z)}$ formed by the edges $b=\{x,y\}$ such that $(x,y)\preceq (x,z)$. This set will be referred to as the set of edges canceled by (x, z). In particular, since $(x,y)\preceq (x,y)$, a step $\{x,y\}$ cancels itself.

We recall that a path in $\Lambda _N$ is a sequence $p=\{x_0,x_1,...,x_n\}$ of vertices of $\Lambda _N$ such that $\{x_{i-1},x_i\}\in E_N$ for all $i= 1,\cdots ,n$. We say that a path $p=\{x_0,x_1,...,x_n\}$ is consistent if, for each $k=1,...,n$, we have that $\{x_{k-1},x_k\}\notin \cup _{i=1}^{k-1}\Gamma _{(x_{i-1},x_i)}$. That is, each step used in this path is not associated with an edge that was canceled by the previous steps. If $p=\{x_0,x_1,...,x_n\}$ is a consistent path, we denote by ${p}^*$ the set of all edges canceled by p, that is, $p^*=\cup _{i=1}^{n}\Gamma _{(x_{i-1},x_i)}$. Clearly, by construction, a consistent path is always edge-self-avoiding. We denote by $C_{xy}(\Lambda _N)$ the set of all consistent paths in $\Lambda _N$ from x to y.

We now define a function $\Omega$, which associates with each current configuration $\eta$ with $\partial \eta =\{x,y\}$, a consistent path $\omega =\Omega (\eta )$ from x to y, which belongs to $C_{xy}(\Lambda _N)$. As in [23], such a consistent path will be called the backbone of $\eta$.

Given $\eta$ with $\partial \eta =\{x,y\}$, let $\Gamma _\eta$ be the set of edges $b\in E$ such $\eta _b$ is odd. Then, $\Gamma _\eta$ forms a subgraph of $(\Lambda _N,E_N)$ (in general not connected) such that every vertex has degree either even or zero, except on x and y, whose degrees are odd. The graph $\Gamma _\eta$ necessarily contain a connected component, say $\gamma _\eta ^{x,y}$, which contains x and y. Therefore, we can look at this connected component $\gamma _\eta ^{x,y}$ (seen as a set of edges in $E_N$), uniquely determined by $\eta$, and associate with it a consistent path $\omega =\Omega (\eta )$. This is the path $\omega =\{z_0=x,z_1\},\{z_1,z_2\}, \dots , \{z_{k-1},z_k=y\}$ for some $k\ge |x-y|$ such that for any $i=1,2,\dots , k$, $(z_{i-1},z_i)$ is the minimal step according to the order established among the steps emerging from $z_{i-1}$ associated with edges of $\gamma _\eta ^{x,y}-\{z_0,z_1\}\cup \{z_1,z_2\}\cup \dots \cup \{z_{1-2},z_{i-1}\}$.

Once the function $\Omega$ is defined, we now can rewrite $\langle \sigma _x \sigma _y \rangle _{\Lambda _N}$ as

$$\begin{aligned} \langle \sigma _x \sigma _y \rangle _{\Lambda _N}= \sum _{\omega \in C_{xy}(\Lambda _N)}\sum _{\begin{array}{c} \eta \in \mathfrak {F}(E_N)\\ \partial \eta =\{x,y\}, \Omega (\eta )=\omega \end{array}}\frac{W(\eta )}{Z_{\Lambda _N}(J_d,J_s)}. \end{aligned}$$

Note that if $\Omega (\eta )=\omega$, then $\eta$ is odd on the edges of the set $\omega$ and is even on the edges of $\omega ^*\setminus \omega$. Also, $\eta$ restricted to $E_N\setminus \omega$, as well as to $E_N\setminus \omega ^*$, is such that $\partial \eta =\emptyset$. Therefore, setting shortly $Z_N=Z_{\Lambda _N}(J_d,J_s)$, we have that

$$\begin{aligned} \begin{aligned} \sum _{\begin{array}{c} \eta \in \mathfrak {F}(E_N)\\ \partial \eta =\{x,y\}, \Omega (\eta )=\omega \end{array}}\frac{W(\eta )}{Z_N}&=\prod _{b\in \omega }\sinh ( J_b) \prod _{b\in \omega ^*\setminus \omega }\cosh ( J_b)\sum _{\begin{array}{c} \eta \in \mathfrak {F}(E_N\setminus \omega ^*)\\ \partial \eta =\emptyset \end{array}}\frac{W(\eta )}{Z_N}\\&= \prod _{b\in \omega }\tan \,\textit{h}(J_b) \prod _{b\in \omega ^*}\cosh ( J_b)\sum _{\begin{array}{c} \eta \in \mathfrak {F}(E_N\setminus \omega ^*)\\ \partial \eta =\emptyset \end{array}}\frac{W(\eta )}{Z_N}\\&= \prod _{b\in \omega }\tan \,\textit{h}(J_b) \sum _{\begin{array}{c} \eta \in \mathfrak {F}(E_N):\;\partial \eta =\emptyset \\ \eta \;\mathrm{even\; on}\;\omega ^* \end{array}} \frac{W(\eta )}{Z_N}, \end{aligned} \end{aligned}$$

where the last summation is over all sourceless current configurations $\eta$ on $E_N$ with the additional restriction that $\eta _b$ is even on all edges b canceled by $\omega$. Hence, we can rewrite $\langle \sigma _x\sigma _y\rangle _{\Lambda _N}$ as

$$\begin{aligned} \langle \sigma _x\sigma _y\rangle _{\Lambda _N} =\sum _{\omega \in C_{xy}(\Lambda _N)}\rho _{E_N}(\omega ), \end{aligned}$$

(6)

where

$$\begin{aligned} \rho _{E_N}(\omega )=\prod _{b\in \omega }\tan \,\textit{h}(J_b) \sum \limits _{\begin{array}{c} \eta \in \mathfrak {F}(E_N):\;\partial \eta =\emptyset \\ \eta \;\mathrm{even\; on}\;\omega ^* \end{array}}\frac{W(\eta )}{Z_N}. \end{aligned}$$

(7)

Observing that

$$\begin{aligned} \sum \limits _{\begin{array}{c} \eta \in \mathfrak {F}(E_N):\;\partial \eta =\emptyset \\ \eta \;\mathrm{even\; on}\;\omega ^* \end{array}}\frac{W(\eta )}{Z_N} \le \frac{\sum _{\eta \in \mathfrak {F}(E_N):\, \partial \eta =\emptyset }W(\eta )}{Z_N}=1, \end{aligned}$$

we obtain straightforwardly the following upper bound

$$\begin{aligned} \rho _E(\omega )\le \prod _{b\in \omega }\tanh (J_b). \end{aligned}$$

(8)

4 Proof of Theorem 1

To prove Theorem 1, we shall use two properties of the weights $\rho _{E_N}(\omega )$ defined in (7). The interested reader can check their proofs in Section 4.2 of [23].

a):

Let $U\subset E_N$ be a set of edges of $\Lambda _N$, and let and $\omega \subset U$ be a consistent path. Then,

$$\begin{aligned} \rho _{E_N}(\omega )\le \rho _{U}(\omega ). \end{aligned}$$

(9)

b):

If $\omega _1\circ \omega _2$ is a consistent path, where $\circ$ denotes the usual concatenation of paths, then

$$\begin{aligned} \rho _{E_N}(\omega _1\circ \omega _2)=\rho _{E_N}(\omega _1)\rho _{E_N\setminus {\omega ^*_1}}(\omega _2). \end{aligned}$$

As shown in Sect. 3, the backbone expansion (6) for the two-point function on $\Lambda _N$ is given by

$$\begin{aligned} \langle \sigma _x\sigma _y\rangle _{\Lambda _N} = \sum _{\omega \in C_{xy}(\Lambda _N)}\rho _{E_N}(\omega ), \end{aligned}$$

where $x=(u_0,t_0)$, $y=(u, t)$ and $C_{xy}(\Lambda _N)$ is the set of all consistent paths $\omega$ with extremes $\partial \omega =\{x,y\}$ using edges of $E_N$.

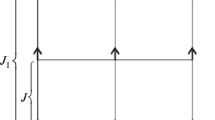
Let $\omega$ be a consistent path connecting x to y. It is possible to break this path into $n+1$ “planar” pieces $\omega _i$, and n “vertical” steps $s_i$ (i.e., such that $|s_i|=1$) connecting two d-dimensional hyperplanes. (Note that there are 2s possibilities for the choice of $s_i$.) Namely, we can write

$$\begin{aligned} \omega =\omega _1\circ s_1\circ \omega _2 \circ s_2\circ ...\circ s_n\circ \omega _{n+1}. \end{aligned}$$

(10)

We are denoting by $\omega _1$ the initial piece of the path $\omega$ all contained in $\Lambda _N^{t_0}$. This initial piece $\omega _1$ of the path $\omega$ is a “planar” path connecting the site $(u_0,t_0)$ to the site $(u_1,t_0)$, which is the last site of $\Lambda _N^{t_0}$ visited by $\omega$ before leaving $\Lambda _N^{t_0}$; this path only uses edges of $E_N^{t_0}$. Then, $s_1$ is the first vertical step, that is, the edge connecting $(u_1,t_0)$ to $(u_1,t_1)$ (where $t_1=t_0+s_1$), which is the first site visited by the path $\omega$ after reaching a new hyperplane. Similarly, for each $k=1,...,n$, we denote by $\omega _k$ the consistent piece of $\omega$ that connects $(u_{k-1},t_{k-1})$ to $(u_k,t_{k-1})$, using only edges of $E(\Lambda _N^{t_{k-1}})$. Here, $(u_{k-1},t_{k-1})$ is the first site of $\Lambda _N^{t_{k-1}}$ visited after the last vertical step $s_{k-1}$ and $(u_{k},t_{k-1})$ is the last site of this hyperplane visited by $\omega$ before it makes another jump, that is, before it reaches another hyperplane. Also, we denote by $s_k$ the vertical jump, that is, the single bond connecting $(u_k,t_{k-1})$ to $(u_k,t_k)$, the first site visited by the path $\omega$ in a hyperplane different from $\Lambda _N^{t_{k-1}}$. Finally, the last piece $\omega _{n+1}$ of the path $\omega$ connects $(u_{n},t_{n})$ to $(u_{n+1},t_{n})=(u,t)=y$, using only edges of $E_N^{t_n}$. Note that $t_k=t_0+\sum _{j=1}^{k}s_j$, for any $k=1, \dots , n$. See Fig. 1 for a sketch of this construction.

Fig. 1

A sketch of a possible consistent path $\omega$

We stress that since $\omega$ is consistent, each one of its pieces $\omega _i$ is also consistent. Let us set $F_1=\emptyset$ and, for $k=2,\dots , n+1$, we set $F_k=\omega _1\circ s_1\circ \dots \circ \omega _{k-1}\circ s_{k-1}$ so that $F^*_k$ is the set of edges of $\Lambda _N$ canceled by the steps preceding $\omega _k$ and $s_k$.

By definition, the piece $\omega _k$ of the path $\omega$ is in the d-dimensional hypercube $\Lambda _N^{t_{k-1}}$. This hypercube may have already been visited by some piece $\omega _i$ of the path $\omega$ with $i<k-1$ (e.g., in Fig. 1, $\omega _4$ is in the same hyperplane as $\omega _2$). Since the path $\omega$ is consistent, $\omega _k$ must avoid edges of the set $F_k$. Therefore, $\omega _k$ is a consistent path which is a subset of $E_{N}^{{t_{{k - 1}} }} \backslash F_{k}$, and we denote by $C_k$ the set of all such paths with these properties (Fig. 2).

Fig. 2

A sketch of a transition between hyperplanes

Now, for $n=0,1,2,\dots$, set $\mathcal {U}_n=(u_1,...,u_{n+1})$ and $\mathcal {S}_n=(s_1,...,s_n)$, with the convention that $\mathcal {S}_0=\emptyset$. Then, we can write

$$\begin{aligned} \langle \sigma _x\sigma _y\rangle _{\Lambda _N}=\sum _{n\ge 0}\sum _{\begin{array}{c} \mathcal {U}_n,\mathcal {S}_n \\ u_{n+1}=u \\ t_n=t \end{array}}\sum _{\omega _1\in C_1}...\sum _{\omega _{n+1}\in C_{n+1}}\rho _{E_N}(\omega ), \end{aligned}$$

with $\omega$ given by (10). Summing over $y\in \Lambda _N$, we get

$$\begin{aligned} \sum _{y\in \Lambda _N}\langle \sigma _x\sigma _y\rangle _{\Lambda _N} = \sum _{n\ge 0}\sum _{\mathcal {U}_n,\mathcal {S}_n}\sum _{\omega _1\in C_1}...\sum _{\omega _{n+1}\in C_{n+1}}\rho _{E_N}(\omega ). \end{aligned}$$

(11)

By Property b) given at the beginning of this section, we get

$$\begin{aligned} \rho _{E_N}(\omega )=\rho _{E_N-F_{n+1}}(\omega _{n+1})\prod _{k=1}^{n}\rho _{E_N-F_k}(\omega _k)\rho _{E_N-F^*_k}(s_k), \end{aligned}$$

where we recall $F_1:=\varnothing$.

Now, using the bound (8), and recalling that $s_k$ is a single vertical edge (and thus with $J_{s_k}=J_s$), it holds that

$$\begin{aligned} \rho _{E_N-F^*_k}(s_k)\le \tan \,\textit{h}( J_s), \end{aligned}$$

for any $k=1,\cdots ,n$. Therefore,

$$\begin{aligned} \rho _{E_N}(\omega )\le [\tan \,\textit{h}( J_s)]^n\prod _{k=1}^{n+1}\left[ \rho _{E_N- F_k}(\omega _k)\right] . \end{aligned}$$

Observe that $E_N^{t_{k-1}}-F_k\subset E_N- F_k$. Moreover, since $\omega$ is consistent, $\omega _k$ only uses edges of $E_N^{t_{k-1}}-F_k$. Hence, we can apply Property a) and inequality (9) to obtain

$$\begin{aligned} \rho _{E_N- F_k}(\omega _k)\le \rho _{E_N^{t_{k-1}}- F_k}(\omega _k), \end{aligned}$$

for any $k=1\cdots ,n+1$, yielding

$$\begin{aligned} \rho _{E_N}(\omega )\le [\tan \,\textit{h}(J_s)]^n\prod _{k=1}^{n+1} \rho _{E_N^{t_{k-1}}- F_k}(\omega _k). \end{aligned}$$

(12)

Plugging (12) in (11), we write

$$\begin{aligned} \sum _{y\in \Lambda _N}\langle \sigma _x\sigma _y\rangle _{\Lambda _N} \le \sum _{n\ge 0} [\tan \,\textit{h}( J_s)]^n\sum _{\mathcal {U}_n,\mathcal {S}_n}S_1\cdot ...\cdot S_{n+1}, \end{aligned}$$

where, for $k=1,...,n+1$, we have set

$$\begin{aligned} S_k=S_k(u_{k-1},u_k, t_{k-1}) = \sum _{\omega _k\in C_{k}}\rho _{\Lambda _N^{t_{k-1}}- F_k}(\omega _k). \end{aligned}$$

Then, we can write

$$\begin{aligned} \sum _{\mathcal {U}_n,\mathcal {S}_n}S_1\cdot ...\cdot S_{n+1}=\sum _{u_1} S_1\sum _{s_1}\sum _{u_2}S_2\dots \sum _{u_{n-1}}S_{n-1}\sum _{s_{n-1}}\sum _{u_n}S_n\sum _{s_n}\sum _{u_{n+1}}S_{n+1}. \end{aligned}$$

Observe now that, for any $k=1,\cdots ,n$,

$$\begin{aligned} \begin{aligned} S_k&= \sum _{\omega _k\in C_{k}}\rho _{\Lambda _N^{t_{k-1}}-F_k}(\omega _k)\\ &=\langle \sigma _{(u_{k-1},t_{k-1})}\sigma _{(u_{k},t_{k-1})}\rangle _{\Lambda _N^{t_{k-1}}-F_{k}}\\&\le \langle \sigma _{(u_{k-1},t_{k-1})}\sigma _{(u_{k},t_{k-1})}\rangle _{\Lambda _N^{t_{k-1}}}. \end{aligned} \end{aligned}$$

where the last line follows by the GKS inequalities. Therefore, for any fixed $u_1,\dots ,u_n$, and any fixed $s_1,\dots ,s_{n-1}$, we get

$$\begin{aligned} \begin{aligned} \sum _{s_n}\sum _{u_{n+1}}S_{n+1}&\le \sum _{s_n} \sum _{u_{n+1}}\langle \sigma _{(u_n,t_n)} \sigma _{(u_{n+1},t_n)}\rangle _{\Lambda _N^{t_{n}}}\\&\le \sum _{s_n}\sup _{u\in \Lambda _N^{t_n}}\sum _{u_{n+1}}\langle \sigma _{(u,t_n)}\sigma _{(u_{n+1},t_n)}\rangle _{\Lambda _N^{t_{n}}} \\&= \sum _{s_n} \chi _{\Lambda _N^{t_n}}(J_d)\\&= 2s \chi _{\Lambda _N^{t_n}}(J_d)\\&= 2s \chi _{\Lambda _N^{0}}(J_d).\\ \end{aligned} \end{aligned}$$

where in the penultimate line we remind that that there are 2s possibilities for the choice of the vertical steps $s_i$. Proceeding iteratively for the sums $\sum _{s_{k-1}}\sum _{u_{k}}S_{k}$ (with $k=n, n-1, \dots , 1$), and with the convention that $\sum _{s_0}=1$, we obtain

$$\begin{aligned} \sum _{\mathcal {U}_n,\mathcal {S}_n}S_1\cdot ...\cdot S_{n+1}\le (2s)^n[\chi _{\Lambda _N^{0}}(J_d)]^{n+1}, \end{aligned}$$

whence, for any $x\in \Lambda _N$,

$$\begin{aligned} \sum _{y\in \Lambda _N}\langle \sigma _x\sigma _y\rangle _{\Lambda _N}\le \sum _{n\ge 0}(2s\tan \,\textit{h}( J_s))^{n}[\chi _{\Lambda _N^{0}}(J_d)]^{n+1}. \end{aligned}$$

Finally, taking the limit $N\rightarrow \infty$ and recalling the definitions of $\chi _{d+s}(J_d,J_s)$ and $\chi _{d}(J_d)$ given in (2) and (4), respectively, we get

$$\begin{aligned} \chi _{d+s}(J_d,J_s)\le \sum _{n\ge 0}(2s\tan \,\textit{h}( J_s))^{n}[\chi _{d}(J_d)]^{n+1}. \end{aligned}$$

The r.h.s. of the inequality above is finite provided that

$$\begin{aligned} \tan \,\textit{h}(J_s)< \frac{1}{2s\chi _{d}(J_d)}, \end{aligned}$$

and thus, the proof of Theorem 1 is concluded.