Abstract
We give several quantum dynamical analogs of the classical Kronecker–Weyl theorem, which says that the trajectory of free motion on the torus along almost every direction tends to equidistribute. As a quantum analog, we study the quantum walk \(\exp (-\textrm{i}t \Delta ) \psi \) starting from a localized initial state \(\psi \). Then, the flow will be ergodic if this evolved state becomes equidistributed as time goes on. We prove that this is indeed the case for evolutions on the flat torus, provided we start from a point mass, and we prove discrete analogs of this result for crystal lattices. On some periodic graphs, the mass spreads out non-uniformly, on others it stays localized. Finally, we give examples of quantum evolutions on the sphere which do not equidistribute.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Classical ergodic theorems say that if T is an ergodic transformation on some measure space \((\Omega ,\mu )\), then averaging an observable f over the trajectory under T of a.e. point x is the same as averaging the observable over the whole space:
Let us consider the case where the classical transformation is the geodesic flow. For the flat torus, the Kronecker–Weyl theorem says that for any \(a\in C^0(\mathbb {T}^d)\) and \(x_0\in \mathbb {T}^d\), if \(y_0\in \mathbb {R}^d\) has rationally independent entries, then
This means that the trajectory \(\{x_0+ty_0\}_{t\ge 0}\) becomes uniformly distributed after large enough time, so that averaging a function over it is the same as the uniform average.
In contrast, consider the standard Euclidean sphere \(\mathbb {S}^2\subset \mathbb {R}^3\). This is a classical example in which the geodesic flow is not ergodic. A free particle moving with its kinetic energy simply travels along a great circle, its trajectory is very far from being dense in \(\mathbb {S}^2\).
In this paper, we are interested in giving quantum dynamical analogs of such results. Instead of starting from a point \(x_0\) on the torus or sphere and integrating a test function over its trajectory \(\phi _t(x_0)\), we will start from an initial state \(\delta _{x_0}\) which is essentially a Dirac distribution at the point \(x_0\), apply the evolution semigroup \(\textrm{e}^{\textrm{i}t\Delta }\delta _{x_0}\) and check whether this state, which was highly localized at time zero, becomes equidistributed as time goes on. Our criterion for such an equidistribution is to compare \(\int a(x) |(\textrm{e}^{\textrm{i}t\Delta }\delta _{x_0})(x)|^2\,\textrm{d}x\) with the uniform average \(\int a(x)\,\textrm{d}x\) and show that they are close, for any test function a(x). We will see that this is indeed the case for the flat torus, for the analogous discrete problem in \(\mathbb {Z}^d\) and more generally for a large family of \(\mathbb {Z}^d\)-periodic lattices (which yield a more interesting mass profile), but untrue for the sphere.
The evolution semigroup \(\textrm{e}^{-\textrm{i}tH}\) for a Hamiltonian H is known as a continuous-time quantum walk in the literature. The framework is usually to work on graphs such as \(\mathbb {Z}^d\) in this context, but one can expect similarities in the continuum, which motivates the study of both cases in this paper. The terminology “quantum walk” is due to a quantum analogy with a random walk, which is more apparent in the case of discrete-time quantum walks, the simplest example being a particle on \(\mathbb {Z}\) walking (jumping a finite distance) under the action of a unitary operator U at each time step \(t=1,2,\dots \), and being in general in a superposition of states. We refer to [1] for the basics and [30] for a systematic study. In contrast, in the continuous-time case, for \(\textrm{e}^{-\textrm{i}t\mathcal {A}_\mathbb {Z}}\delta _0\) we have a nonzero probability of being arbitrarily far from 0 as soon as \(t>0\), i.e., we can have \(|(\textrm{e}^{-\textrm{i}t\mathcal {A}_{\mathbb {Z}}}\delta _0)(n)|^2\ne 0\) with \(n\gg 1\).
This paper is not the first work to give quantum analogs of ergodicity. This topic has first been explored by Shnirel’man, Colin de Verdière and Zelditch [11, 34, 38] and has since inspired research in many directions. The point of view of these quantum ergodicity theorems is to show that in cases where the geodesic flow is ergodic, any orthonormal basis of eigenfunctions \((\psi _j)\) of the Laplace operator has a density one subsequence which becomes equidistributed in the high energy limit. More precisely, \(|\psi _j(x)|^2\,\textrm{d}x\) approaches the uniform measure \(\textrm{d}x\). Discrete analogs of this appeared for graphs. In this case, one considers instead a sequence of finite graphs \(G_N\) converging in an appropriate sense (Benjamini–Schramm) to an infinite graph having a delocalized spectrum and shows an equidistribution property for the eigenfunctions of \(G_N\), see, e.g., [2, 3, 6, 28] and [25, 29]. In the present work, our quantum interpretation is to follow instead how initially localized states (point masses) spread out under the action of the dynamics. This seems like a more direct translation of the classical picture. Our work in the continuum has relations with [4, 5, 22,23,24] which we explain in Sect. 1.4. A common difficulty in all the models we consider here is how to work with the high multiplicity of eigenvalues.
Notation. As many articles in the quantum walks literature use the Dirac bra-ket notation, let us briefly explain the standard Hilbert space notation that we use in the paper. If G is a graph, then \((\delta _v)_{v\in G}\) stands for the standard basis of \(\ell ^2(G)\) given by \(\delta _v(u)=1\) if \(u=v\) and zero otherwise. The scalar product is given by \(\langle \phi ,\psi \rangle = \sum _{v\in G} \overline{\phi (v)}\psi (v)\). Given a linear operator \(A:\ell ^2(G)\rightarrow \ell ^2(G)\) we have in particular \(\langle \phi , A\psi \rangle = \sum _{v\in G} \overline{\phi (v)}(A\psi )(v)\). If a is a function a(v), then \(\langle \phi , a\phi \rangle = \sum _{v\in G} a(v) |\phi (v)|^2\).
In the bra-ket notation, \(\{\delta _v\}_{v\in G}\) is replaced by \(\{ |v\rangle : v\in G\}\). An operator A acts on a vector \(|\phi \rangle \) by \(A|\phi \rangle \). The time evolution \(\psi (t)=\textrm{e}^{-\textrm{i}tH} \psi \) is denoted by \(|\psi (t)\rangle = U(t)|\psi \rangle \). Our \(\langle \phi ,\psi \rangle \) equals \(\langle \phi |\psi \rangle \) and our \(\langle \phi , A\psi \rangle \) equals \(\langle \phi | A | \psi \rangle \). If H is a Hamiltonian, expanding \(\textrm{e}^{-\textrm{i}tH}\psi _0\) over an orthonormal eigenbasis \((\phi _j)\) of H reads \(\psi (t)=\textrm{e}^{-\textrm{i}tH} \psi _0 = \sum _j \langle \phi _j,\psi _0\rangle \textrm{e}^{-\textrm{i}t\lambda _j} \phi _j\) in our notation, \(|\psi (t)\rangle = \sum _j |\phi _j\rangle \textrm{e}^{-\textrm{i}t\lambda _j} \langle \phi _j|\psi _0\rangle \) in the bra-ket notation.
We now discuss our results, first for the adjacency matrix on \(\mathbb {Z}^d\), then more generally for periodic graphs in Sect. 1.1. We next move to the flat torus in Sect. 1.2, and then, we conclude with the case of the sphere in Sect. 1.3.
1.1 Case of Graphs
For transparency, we begin with \(\mathbb {Z}^d\). Consider a sequence of cubes \(\Lambda _N = [\![0,N-1]\!]^d\), and let \(A_N\) be the adjacency matrix on \(\Lambda _N\) with periodic conditions. We denote the torus by \(\mathbb {T}_*^d=[0,1)^d\).
Theorem 1.1
For any \(v\in \Lambda _N\), we have
where \(\langle a\rangle = \frac{1}{N^d}\sum _{u\in \Lambda _N} a(u)\), for the following class of observables \(a_N\):
-
\(a_N(n) = f(n/N)\) for some \(f\in H_s(\mathbb {T}_*^d)\) with \(s>d/2\),
-
\(a_N\) the restriction to \(\Lambda _N\) of some \(a\in \ell ^1(\mathbb {Z}^d)\).
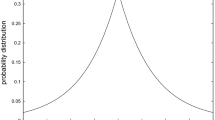
Note that \(\langle \textrm{e}^{-\textrm{i}tA_N} \delta _v, a\textrm{e}^{-\textrm{i}tA_N} \delta _v\rangle = \sum _{u\in \Lambda _N} a(u)|(\textrm{e}^{-\textrm{i}tA_N}\delta _v)(u)|^2\). So (1.2) shows that the probability density \(\mu _{v,T}^N(u):=\frac{1}{T}\int _0^T |(\textrm{e}^{-\textrm{i}tA_N}\delta _v)(u)|^2\,\textrm{d}t\) on \(\Lambda _N\) approaches the uniform density \(\frac{1}{N^d}\), provided T and N are large enough, that is, the time average \(\sum _{u\in \Lambda _N} a(u)\mu _{v,T}^N(u)\) approaches the space average \(\frac{1}{N^d}\sum _{u\in \Lambda _N} a(u)\) in analogy to (1.1). See Fig. 1.
A positive aspect of this result is that it holds for any v, whereas in the eigenfunction interpretation, equidistribution only holds for a density one subsequence in general. The evolution moreover “forgets the initial state v”, a known signature of ergodicity.
The first class of observables allows taking bump functions f supported on balls \(B_R(x_0)\subset \mathbb {T}_*^d\). Then, the result implies that \(\sum _{u\in \Lambda _N} f(u/N)\mu _{v,T}^N(u) \approx \frac{1}{N^d} \sum _{u\in \Lambda _N} f(n/N) \approx \int _{\mathbb {T}_*^d} f(x)\,\textrm{d}x\), which is independent of \(x_0\). This implies that for any macroscopic ball \(B\subset \Lambda _N\) of size \(|B|=\alpha N^d\), we have \(\mu _{v,T}^{(N)}(B) \approx \alpha \) for \(N,T\gg 0\) (e.g., take \(\alpha =\frac{1}{2}\) or \(\alpha =\frac{1}{4}\) and vary B).
Note that the two cases (\(a_N=f(\cdot /N)\) and \(a\in \ell ^1(\mathbb {Z}^d)\)) are distinct, in the sense that \(\lim _{N\rightarrow \infty } \sum _{n\in \Lambda _N} |f(n/N)| = \infty \) in general.
We may extend Theorem 1.1 as follows:
Theorem 1.2
Under the same assumptions on \(a_N\), we also have for \(v\ne w\),
More generally, for any \(\phi ,\psi \) of compact support, we have
There are many natural questions that arise when looking at these results.
First, why not work on \(\mathbb {Z}^d\) directly? One issue is that the dynamics are dispersive [35] on \(\mathbb {Z}^d\), more precisely \(|\textrm{e}^{-\textrm{i}t \mathcal {A}_{\mathbb {Z}^d}}\delta _v(w)|^2 = \prod _{j=1}^d |J_{v_j-w_j}(2t)|^2\), where \(J_k\) is the Bessel function of order k, and \(|J_k(t)|\lesssim t^{-1/3}\) uniformly in k, see [21]. So as time grows large, the probability measure \(|\textrm{e}^{-\textrm{i}t \mathcal {A}_{\mathbb {Z}^d}}\delta _v(w)|^2\) on \(\mathbb {Z}^d\) simply converges to zero. One could instead consider the limit of the process rescaled per unit time. We did this previously in [8] and computed the limiting measure explicitly.
Still, this does not tell whether we can possibly invert the order of limits in the theorem. The answer is in fact negative.Footnote 1
Proposition 1.3
There exists a sequence of observables \(a_N\) on \(\Lambda _N\) of the form f(n/N) such that
for all time. The same statement holds for the averaged dynamics \(\frac{1}{T}\int _0^T\).
This indicates that the limit over time should be considered first. But can one get rid of the time average and consider the limit directly in t? The answer is negative.
Proposition 1.4
There exists a sequence of observables \(a_N\) on \(\Lambda _N\) of the form f(n/N) such that \(\langle \textrm{e}^{-\textrm{i}tA_N} \delta _v, a_N \textrm{e}^{-\textrm{i}tA_N}\delta _v\rangle \) has no limit as \(t\rightarrow \infty \).
The limit of the corresponding average \(\int _{T-1}^T\langle \textrm{e}^{-\textrm{i}tA_N} \delta _v, a_N \textrm{e}^{-\textrm{i}tA_N}\delta _v\rangle \,\textrm{d}t\) also doesn’t exist.
The last point illustrates that a “full” average \(\frac{1}{T}\int _0^T\) is needed.
Proposition 1.3 shows that we should consider the large time limit first. But is it actually necessary to take N to infinity? The answer is yes.
Proposition 1.5
For each N there exists \(a_N\) such that
with \(b_N(v)\ne 0\). Here, \(b_N(v)\rightarrow 0\) as \(N\rightarrow \infty \) at the rate \(N^{-1}\).
Proposition 1.5 shows that we cannot expect a faster rate of convergence in Theorem 1.1 than \(N^{-1}\). We indeed achieve this upper bound in the proof in Sect. 2.
Theorem 1.1 can be generalized to \(\mathbb {Z}^d\)-periodic graphs (crystals). This requires some vocabulary which we prefer to postpone to Sect. 3, so we will explain the theorem in words here instead and refer to Theorem 3.1 for a more precise statement.
Theorem 1.6
Theorem 1.1 holds true more generally for periodic Schrödinger operators on \(\mathbb {Z}^d\)-periodic graphs, provided they satisfy a certain Floquet condition. This condition is satisfied in particular for the adjacency matrix on infinite strips, on the honeycomb lattice, and for Schrödinger operators with periodic potentials on the triangular lattice and on \(\mathbb {Z}^d\), for any d. The average \(\langle a_N\rangle \) may not be the uniform average of \(a_N\) in general, but a certain weighted average.
See Figs. 2 and 3 for examples of this.
A point mass on the ladder eventually equidistributes (left). On the strip of width 3, if the initial point mass lies in the top layer, it eventually (center) puts \(\frac{3}{8}\) of its mass over the top and bottom layers and \(\frac{1}{4}\) on the middle. If the point mass was in the middle layer, it eventually (right) puts \(\frac{1}{4}\) on the top and bottom layers and \(\frac{1}{2}\) in the middle layer
In this result, we focus on the two most natural choices of initial states: point masses (Theorem 3.1) and initial states uniformly spread over a single fundamental cell (Remark 3.3). Still, we give an expression (3.12) for more general states.
As we explain in the end of Sect. 3, some Floquet condition must be assumed at least to rule out flat bands. Figure 4 shows how an initial state may stay localized otherwise.
1.2 Torus Dynamics
We now turn our attention to the continuum and consider the torus \(\mathbb {T}_*^d\). This model is rather unusual compared to the quantum walk literature, which typically studies evolutions on graphs, but has the advantage of being directly comparable to the Kronecker–Weyl theorem (1.1). The technical issue however is that we can no longer consider Dirac distributions \(\delta _x\) directly as in the case of graphs. We will thus regularize (approximate) them in two ways: in momentum space, then in position space.
For the momentum-space approximation, we consider \(\delta _y^E:=\frac{1}{\sqrt{N_E}} \textbf{1}_{(-\infty ,E]}(-\Delta )\delta _y\), where \(N_E\) is the number of Laplacian eigenvalues in \((-\infty ,E]\). This truncated Dirac function has previously been considered in [5]. In our case, \(\delta _y^E\) is a trigonometric polynomial, see Sect 4.1.
Theorem 1.7
We have for any \(T>0\),
-
(1)
For any \(y\in \mathbb {T}_*^d\), any \(a\in H^s(\mathbb {T}_*^d)\), \(s>d/2\),
$$\begin{aligned} \lim _{E\rightarrow \infty } \frac{1}{T}\int _0^T \langle \textrm{e}^{\textrm{i}t\Delta } \delta _y^E, a \textrm{e}^{\textrm{i}t\Delta } \delta _y^E\rangle \,\textrm{d}t = \int _{\mathbb {T}_*^d} a(x)\,\textrm{d}x. \end{aligned}$$ -
(2)
If \(x\ne y\), then for \(a\in H^s(\mathbb {T}_*^d)\), \(s>d/2\),
$$\begin{aligned} \lim _{E\rightarrow \infty } \frac{1}{T}\int _0^T \langle \textrm{e}^{\textrm{i}t\Delta } \delta _x^E, a \textrm{e}^{\textrm{i}t\Delta } \delta _y^E\rangle \,\textrm{d}t = 0. \end{aligned}$$ -
(3)
Result (1) remains true if \(a=a^E\) depends on the semiclassical parameter E, as long as all partial derivatives of order \(\le s\) are uniformly bounded by \(c E^{r}\) for some \(r<\frac{1}{4}\). More precisely, \(\lim \nolimits _{E\rightarrow \infty } |\frac{1}{T}\int _0^T \langle \textrm{e}^{\textrm{i}t\Delta }\delta _y^E, a^E\textrm{e}^{\textrm{i}t\Delta }\delta _y^E\rangle \,\textrm{d}t - \int _{\mathbb {T}_*^d} a^E(x)\,\textrm{d}x| =0\).
-
(4)
The probability measure \(\textrm{d}\mu _{y,T}^E(x)=(\frac{1}{T}\int _0^T |\textrm{e}^{\textrm{i}t\Delta } \delta _y^E(x)|^2\,\textrm{d}t)\textrm{d}x\) on \(\mathbb {T}_*^d\) converges weakly to the uniform measure \(\textrm{d}x\) as \(E\rightarrow \infty \).
Hence, averaging a over \(\textrm{d}\mu _{y,T}^E(x)=(\frac{1}{T}\int _0^T|\textrm{e}^{\textrm{i}t\Delta } \delta _y^E(x)|^2\textrm{d}t)\,\textrm{d}x\) is the same as averaging a over the uniform measure \(\textrm{d}x\), after the initial state becomes sufficiently localized.
Remarkably, equidistribution occurs immediately if we are initially sufficiently close to a Dirac distribution. We do not need to wait for large time T. Compare with (1.1).Footnote 2
The third point allows taking observables of shrinking support. This problem was recently studied by [14, 15]. More precisely, we can allow observables concentrated near any \(x_0\in \mathbb {T}_*^d\), with support shrinking like \(E^{-\beta }\) for \(\beta = \frac{1}{2(d+1)}\). In fact, starting from any fixed smooth a supported in a ball \(B_R\) around the origin, define \(a^{E,x_0}(x) = a(E^\beta (x-x_0))\). This is supported in the ball \(B_{R E^{-\beta }}(x_0)\). It satisfies \(\partial _{x_i}^k a^{E,x_0} = E^{\beta k} \partial _{x_i}^k a(E^{\beta }(x-x_0))\), hence \(\Vert \partial _{x_i}^k a^{E,x_0}\Vert _\infty \le E^{\beta k} \Vert \partial _{x_i}^ka\Vert _\infty \). We thus need \(\beta s<\frac{1}{4}\) for point (3). We also need \(s>d/2\) to respect the assumptions. Choosing \(s=\frac{d}{2}+\frac{1}{4}\), we see that \(\beta = \frac{1}{2(d+1)}\) suffices.
This gives a sharper verification that the mass of \(|\textrm{e}^{\textrm{i}t\Delta } \delta _y^E(x)|^2\,\textrm{d}x\) equidistributes on average. Namely, equidistribution remains true if we zoom in near any point \(x_0\in \mathbb {T}_*^d\).
Interestingly, \((\textrm{e}^{\textrm{i}t \Delta } \delta _y^E)(x) = \frac{1}{\sqrt{N_E}}\sum _{\lambda _\ell \le E} \overline{e_\ell (y)} \textrm{e}^{-\textrm{i}t\lambda _\ell } e_\ell (x)\) with \(\lambda _\ell =4 \pi ^2 \ell ^2\) is a normalized truncated theta function if \(d=1\), which is important in number theory [16, 20].
Theorem 1.7 extends immediately to more general energy cutoffs of \(\delta _y\), i.e., there is some flexibility in the choice of \(\delta _y^E\). We can also consider more general tori \(\mathbb {T}=\times _{i=1}^d[0,b_i)\). See Sect. 4.2 for details. As before,
Lemma 1.8
Time averaging is necessary, even when \(\lim _{E\rightarrow \infty } \langle \textrm{e}^{\textrm{i}t\Delta }\delta _y^E,a\textrm{e}^{\textrm{i}t\Delta }\delta _y^E\rangle \) exists, it generally depends on the value of t and it may not be equal to \(\int a(x)\,\textrm{d}x\).
We next give a result by approximating in position space.
Theorem 1.9
Fix any \(y\in \mathbb {T}_*^d\) and consider \(\phi _y^\varepsilon = \frac{1}{\sqrt{\varepsilon _1\varepsilon _2\cdots \varepsilon _d}} \textbf{1}_{\times _{i=1}^d [y_i,y_i+\varepsilon _i]}\). Then, for any \(a\in H^s(\mathbb {T}_*^d)\), \(s>d/2\), \(T>0\),
where \(\varepsilon \downarrow 0\) means more precisely that \(|\varepsilon |=\sqrt{\varepsilon _1^2+\dots +\varepsilon _d^2}\rightarrow 0\). If \(x\ne y\), then
Furthermore, the probability measure \(\textrm{d}\mu _{y,T}^\varepsilon (x)=(\frac{1}{T}\int _0^T |\textrm{e}^{\textrm{i}t\Delta } \phi _y^\varepsilon (x)|^2\,\textrm{d}t)\textrm{d}x\) on \(\mathbb {T}_*^d\) converges weakly to the uniform measure \(\textrm{d}x\) as \(\varepsilon \downarrow 0\).
This theorem says that once our initial state is close enough (in position space) to a Dirac mass, its averaged dynamics will become equidistributed.
Theorem 1.9 is actually valid for a more general class of initial states \((\phi _\varepsilon )\), see Sect. 4.3.
Theorems 1.7 and 1.9 remain true if we first take the limit over T and then over E/\(\varepsilon \), i.e.,
holds in addition to Theorem 1.7(1), and a corresponding statement holds in addition to Theorem 1.9. This is in fact easier to prove, see Remark 4.2. What is remarkable is that we don’t need to consider a large time in Theorems 1.7 and 1.9 for equidistribution to occur. Also notice that the limits over E and T can be interchanged, in view of the theorems and (1.5).
1.3 Sphere Dynamics
As we mentioned in the introduction, classical evolution on the sphere is far from being ergodic. We have a confirmation of this as follows.
Theorem 1.10
Fix \(\xi \in \mathbb {S}^{d-1}\). There exists a normalized approximate Dirac distribution \(S_\xi ^{(n)}\) such that \(\lim _{T\rightarrow \infty } \frac{1}{T}\int _0^T |\textrm{e}^{\textrm{i}t\Delta } S_\xi ^{(n)}(\eta )|^2\,\textrm{d}t\) is not equidistributed on the sphere as \(n\rightarrow \infty \) and actually diverges for \(\eta =\xi \).
If \(d=3\), there exists an observable a such that the analog of (1.5) is violated.
This result may seem intuitively clear, however remember that the sphere is a rather counter-intuitive example in which almost all eigenbases are quantum uniquely ergodic [37] in spite of our classical intuition. The proof of Theorem 1.10 can get quite technical depending on how we choose the initial (approximate) point mass, and the theorem does not exclude the possibility that some point masses do equidistribute with time.
1.4 Earlier Results and Perspectives
The time evolution of quantum walks is a central topic. Let us mention [9, 17] in relation to mixing time. We are not aware of earlier works showing equidistribution, and it would be very interesting to see which discrete-time quantum walks satisfy this phenomenon. We mention [26] in which the evolution of a Grover walk in large boxes in \(\mathbb {Z}^2\) was shown to localize, and [12] where (non)-thermalization of fullerene graphs was investigated. See also [33] for thermalization in a free fermion chain.
A study of the quantum dynamics on the torus appeared previously in the more general setting of Schrödinger operators in [4, 23]. It is shown in [4] that if \((u_n)\) is a sequence in \(L^2(\mathbb {T}_*^d)\) such that \(\Vert u_n\Vert = 1\), if \(H = -\Delta + V\) is a Schrödinger operator on \(\mathbb {T}_*^d\) and if \(\textrm{d}\mu _n(x) = (\int _0^1 |(\textrm{e}^{-\textrm{i}tH} u_n)(x)|^2\,\textrm{d}t)\,\textrm{d}x\), then any weak limit of \(\mu _n\) is absolutely continuous.
This is much broader than our framework. As a special case, this result implies that any weak limit of the measures \(\mu _{y,T}^E\) and \(\mu _{y,T}^\varepsilon \) in Theorems 1.7 and 1.9 is absolutely continuous. More general statements regarding Wigner distributions can also be found in [4].
At this level of generality, this result cannot be improved to ensuring convergence to the uniform measure. For example, if we take \(d=1\), \(V=0\) and \(u_n(x) = \sqrt{2}\cos (2\pi x)\) for all n, then \(\textrm{d}\mu _n(x) = (\int _0^1 2|\textrm{e}^{-\textrm{i}t (4\pi ^2)} \cos (2\pi x)|^2\,\textrm{d}t)\,\textrm{d}x = 2\cos ^2(2\pi x)\,\textrm{d}x\), which is not the uniform measure. Similarly, if we take \(u_n(x) = \sqrt{2}\cos (2\pi x)\) for even n and \(u_n(x) = \sqrt{2}\sin (2\pi x)\) for odd n, we see that \(\mu _n\) does not converge, having two limit points.
As this preprint was being circulated, Maxime Ingremeau and Fabricio Macià explained to us that it is possible to prove the first point in each of Theorem 1.7 and 1.9 by first computing the semiclassical measures of \((\delta _y^E)\) and \((\phi _y^\varepsilon )\), which lives in phase space \(T^*\mathbb {T}_*^d\). There should be a unique limit for each sequence, of the form \(\mu _0(\textrm{d}x,\textrm{d}\xi )=\delta _y f(\xi )\,\textrm{d}\xi \), which does not charge the resonant frequencies, so one could apply [23, (8) and Prp. 1], which rely on the microlocal analysis developed in [22]. It seems this can work even in the presence of a potential if one uses [4, Th. 3]. Our proof, on the other hand, is very simple, using explicit computations, we make no use of microlocal analysis as our framework is more special, because we had different aims in mind. Concerning the sphere, one could consider sequences of the form \(\rho _y^h(x)=h^{-d/2}\rho (\frac{x-y}{h})\) in local coordinates, where \(\rho \) is in \(L^2\). The semiclassical measure should have a similar form. Using [22, Thm. 4], one should be able to deduce that \(\textrm{d}\mu _{y,T}^h(x) = (\frac{1}{T}\int _0^T |\textrm{e}^{\textrm{i}t\Delta }\rho _y^h(x)|^2\,\textrm{d}t)\textrm{d}S^{d-1}(x)\) will be absolutely continuous as \(h\rightarrow 0\) (more precisely, a weighted superposition of uniform orbit measures modulated by \(|\widehat{\rho }(\xi )|^2\)). In the same spirit, after some work, one can use [24, Prp. 2.2.(i) and Th.4.3] to deduce that \(\textrm{d}\mu _{\xi ,T}^n(\eta ) = (\frac{1}{T}\int _0^T |\textrm{e}^{\textrm{i}t\Delta }S_\xi ^{(n)}(\eta )|^2\,\textrm{d}t)\textrm{d}S^{d-1}(\eta )\) is absolutely continuous as \(n\rightarrow \infty \). This is not our aim in Theorem 1.10, but is an interesting complementary information. We finally mention that the preceding applications of [4, 22,23,24] are quoted from private communication; it would be interesting to work out the details.
As for negative curvature, the authors in [5] consider the case of a compact Anosov manifold M and show that if \(\delta _y^h\) is an h-truncated Dirac distribution, then as \(h\rightarrow 0\), \(\frac{1}{T}\int _0^T \langle \textrm{e}^{\textrm{i}t\Delta /2} \delta _y^h, \textrm{Op}_h(a) \textrm{e}^{\textrm{i}t\Delta /2}\delta _y^h\rangle \,\textrm{d}t \approx \int _{S^*M} a\,\textrm{d}L\) for most y. This is another instance where equidistribution occurs immediately once \(\delta _y^h\) becomes close enough to \(\delta _y\): there is no need to take \(T\rightarrow \infty \). The fact that it holds for most y means more precisely that the volume of \(y\in M\) where this doesn’t hold vanishes as \(h\rightarrow 0\). In this respect, the fact that our equidistribution results for the torus (and graphs) hold for each y is worth emphasizing.
We finally mention the paper [32] in the context of the evolution of Lagrangian states. These are localized in speed rather than in position.
As we mentioned earlier, there is a large literature on eigenfunction quantum ergodicity, in particular [27, 39]. It is natural to ask if this property is related to the present quantum dynamical picture. We discuss this in Appendix A. In particular, while there are several proofs of eigenfunction ergodicity for regular graphs with few cycles [3], it is not very clear how to prove the dynamical criterion in that context; this seems like an interesting direction for future considerations.
2 Case of the Integer Lattice
Here, we prove Theorems 1.1 and 1.2 and Propositions 1.3–1.5. Throughout, \(a:=a_N\).
Proof of Theorem 1.1
Consider the orthonormal basis \(e_m^{(N)}(n) {=} \frac{1}{N^{d/2}}\textrm{e}^{2\pi \textrm{i}m\cdot n/N}\). Given \(\psi {=} \sum _{\ell \in \Lambda _N} \psi _\ell ^{(N)} e_\ell ^{(N)}\), where \(\psi _\ell ^{(N)}{=}\langle e_\ell ^{(N)},\psi \rangle \), since \(A_N e_k^{(N)}{ =} \lambda _k^{(N)} e_k^{(N)}\), for \(\lambda _k^{(N)} = \sum _{i=1}^d 2\cos (\frac{2\pi k_i}{N})\), we have \(\textrm{e}^{-\textrm{i}tA_N}\psi = \sum _{\ell \in \Lambda _N} \psi _\ell ^{(N)} \textrm{e}^{-\textrm{i}t\lambda _\ell ^{(N)}} e_\ell ^{(N)}\).
Expand \(a = \sum _{m \in \Lambda _N} a_m^{(N)} e_m^{(N)}\). Then using that \(e_m^{(N)}e_\ell ^{(N)} = \frac{1}{N^{d/2}} e_{\ell +m}^{(N)}\), we obtain
In particular, as \(\psi _\ell ^{(N)} = \overline{e_\ell ^{(N)}(v)}\) for \(\psi = \delta _v\), we get
where we used that \(a_0^{(N)}e_0^{(N)}(v) = \frac{1}{N^d}\sum _{w\in \Lambda _N} a(w)\) for any v.
If \(\lambda _{\ell +m}^{(N)}\ne \lambda _\ell ^{(N)}\) then \(\frac{1}{T}\int _0^T \textrm{e}^{\textrm{i}t(\lambda _{\ell +m}^{(N)}-\lambda _\ell ^{(N)})}\,\textrm{d}t = \frac{\textrm{e}^{\textrm{i}T(\lambda _{\ell +m}^{(N)}-\lambda _{\ell }^{(N)})}-1}{T(\lambda _{\ell +m}^{(N)}-\lambda _\ell ^{(N)})}\rightarrow 0\) as \(T\rightarrow \infty \). Thus,
Let \(A_m = \{ \ell \in \Lambda _N:\lambda _{\ell +m}^{(N)}=\lambda _\ell ^{(N)}\}\). We show that
We have \(A_m = \{\ell \in [\![0,N-1 ]\!]^d: \sum _{j=1}^d \cos (\frac{2\pi (\ell _j+m_j)}{N})-\cos (\frac{2\pi \ell _j}{N}) = 0\}\). Consider the projection of this surface onto a plane. More precisely, suppose \(m_j\ne 0\) and consider \(P_{e_j^\bot } \ell = (\ell _1,\dots ,\ell _{j-1},0,\ell _{j+1},\dots ,\ell _d)\). Suppose \(n,k \in A_m\) and \(P_{e_j^\bot } n = P_{e_j^\bot } k\). Then \(n_i = k_i\) for all \(i\ne j\). So \(\cos (\frac{2\pi (n_j+m_j)}{N})-\cos (\frac{2\pi n_j}{N}) = - \sum _{i\ne j} \cos (\frac{2\pi (n_i+m_i)}{N})-\cos (\frac{2\pi n_i}{N}) = - \sum _{i\ne j} \cos (\frac{2\pi (k_i+m_i)}{N})-\cos (\frac{2\pi k_i}{N}) = \cos (\frac{2\pi (k_j+m_j)}{N})-\cos (\frac{2\pi k_j}{N})\). Since \(\cos \theta -\cos \varphi = -2\sin (\frac{\theta +\varphi }{2})\sin (\frac{\theta -\varphi }{2})\), this implies that \(\sin \pi (\frac{2n_j+m_j}{N})\sin \frac{\pi m_j}{N} = \sin \pi (\frac{2k_j+m_j}{N})\sin \frac{\pi m_j}{N}\). Since \(m_j\in [\![1,N-1 ]\!]\), this implies \(\sin \pi (\frac{2n_j+m_j}{N}) = \sin \pi (\frac{2k_j+m_j}{N})\). But \(\frac{2n_j+m_j}{N}\le 3\) and \(\frac{2k_j+m_j}{N}\le 3\). So we must have \(\pi \frac{2n_j+m_j}{N} = \pi \frac{2k_j+m_j}{N}\) or \(\pi - \pi \frac{2k_j+m_j}{N}\) or \(2\pi + \pi \frac{2k_j+m_j}{N}\). This leads to \(n_j = k_j\) or \(n_j = \frac{N}{2}-k_j-m_j\) or \(n_j = N+k_j\). The last case is excluded as \(n_j<N\).
We thus showed that any \((n_1,\dots ,n_{j-1},0,n_{j+1},\dots ,n_d)\) has at most two preimages within \(A_m\) under the mapping \(P_{e_j^\bot }\). This implies that \(\# A_m \le 2N^{d-1}\) for any \(m\ne 0\).
In the special case \(a(w) = \textrm{e}^{2\pi \textrm{i}k\cdot w/N} = N^{d/2} e_k^{(N)}(w)\), we have \(a_m^{(N)} = 0\) for \(m\ne k\) and \(a_k^{(N)} = N^{d/2}\). So the RHS in (2.2) reduces to
More generally, suppose \(a_N(n) = f(n/N)\) for some \(f\in H_s(\mathbb {T}_*^d)\), with \(s>d/2\). Here \(H_s(\mathbb {T}_*^d)\) is the Sobolev space of order s, with norm \(\Vert f\Vert _{H^s}^2 = \sum _{k\in \mathbb {Z}^d} |\hat{f}_k|^2\langle k\rangle ^{2\,s}\), where \(\hat{f}_k = \int _{\mathbb {T}_*^d} \textrm{e}^{-2\pi \textrm{i}k\cdot x}f(x)\,\textrm{d}x\) and \(\langle k\rangle = \sqrt{1+|k|^2}\). Then \(\Vert \hat{f}\Vert _1:=\sum _k |\hat{f}_k| \le C_s \Vert f\Vert _{H^s}\), where \(C_s^2=\sum _k\langle k\rangle ^{-2\,s}<\infty \) since \(2\,s>d\). On the other hand, \(f = \sum _k \hat{f}_k e_k\) with \(e_k(x) = \textrm{e}^{2\pi \textrm{i}k\cdot x}\), so \(a_m^{(N)} = \langle e_m^{(N)}, f(\cdot /N)\rangle _{\ell ^2(\Lambda _N)} = \sum _{k\in \mathbb {Z}^d} \hat{f}_k \langle e_m^{(N)},e_k(\cdot /N)\rangle _{\ell ^2(\Lambda _N)} = \hat{f}_m N^{d/2}\), since \(e_k(n/N) = N^{d/2} e_k^{(N)}(n)\).
We showed that \(a_m^{(N)} e_m^{(N)}(v) = \hat{f}_m \textrm{e}^{2\pi \textrm{i}m\cdot v/N}\). Thus,
The estimate is also true if \(a_N\) is the restriction to \(\Lambda _N\) of some \(a\in \ell ^1(\mathbb {Z}^d)\). In that case, we have \(a = \sum _{n\in \mathbb {Z}^d} c_n \delta _n\) with \(\Vert a\Vert _1=\sum _{n\in \mathbb {Z}^d} |c_n|<\infty \). On the other hand, \(a_m^{(N)} = \sum _{n\in \mathbb {Z}^d} c_n \langle e_m^{(N)},\delta _n\rangle = \sum _{n\in \mathbb {Z}^d} c_n \overline{e_m^{(N)}(n)}\). So \(|a_m^{(N)} e_m^{(N)}(v)| \le \frac{1}{N^d} \Vert a\Vert _1\); hence, \(\sum _{m\in \Lambda _N} |a_m^{(N)} e_m^{(N)}(v)| \le \Vert a\Vert _1\) and we may conclude as before. \(\square \)
Proof of Theorem 1.2
Arguing as before, we find that
Here, the term \(m=0\) is \(\frac{1}{N^d}\sum _{\ell \in \Lambda _N} \textrm{e}^{\frac{2\pi \textrm{i}\ell \cdot (v-w)}{N}} a_0 e_0(v) = 0\) since \(v\ne w\). The remaining terms \(\sum _{m\ne 0,\ell \in \Lambda _N}\) tend to zero as T followed by N tend to infinity by the same argument as before (the phase \(\textrm{e}^{\frac{2\pi \textrm{i}\ell \cdot (v-w)}{N}}\) makes no difference). This proves the first part.
For the second part, assume \(\phi ,\psi \) are supported in a compact \(K\subset \Lambda _N\), N large enough. Then, \(\phi = \sum _{v\in K} \phi (v)\delta _v\) and \(\psi = \sum _{v\in K} \psi (v)\delta _v\). Thus,
Hence,
We see that (1.4) follows from (1.2) and (1.3). \(\square \)
Proof of Proposition 1.3
Take \(a_N(n) = f(n/N)\) for \(f(x)=\prod _{i=1}^d(1-x_i)\) on \(\mathbb {T}_*^d\). Then \(f\ge 0\). Now
where we extend f to \(\mathbb {R}^d\) arbitrarily in a continuous fashion and we define \(\textrm{e}^{-\textrm{i}tA_N}\delta _v(n):=0\) for \(n\notin \Lambda _N\).
Now \(\textrm{e}^{-\textrm{i}tA_N}\delta _v(w) \rightarrow \textrm{e}^{-\textrm{i}t\mathcal {A}_{\mathbb {Z}^d}}\delta _v(w)\) for any w. This can be seen, for example, from the explicit expression of the kernels through the Fourier transform, which shows that if \(\phi (x)=\sum _{i=1}^d 2\cos 2\pi x_i\) for \(x\in \mathbb {T}_*^d\), then \(\textrm{e}^{-\textrm{i}tA_N}(w,v)= \frac{1}{N^d}\sum _{n\in \Lambda _N} \textrm{e}^{2\pi \textrm{i}(w-v)\cdot n/N}\textrm{e}^{-\textrm{i}t \phi (n/N)}\) for \(v,w\in \Lambda _N\) and \(\textrm{e}^{-\textrm{i}t\mathcal {A}_{\mathbb {Z}^d}}(w,v) = \int _{\mathbb {T}_*^d} \textrm{e}^{2\pi \textrm{i}(w-v)\cdot x}\textrm{e}^{-\textrm{i}t\phi (x)}\,\textrm{d}x\).
We thus have \(\lim _{N\rightarrow \infty } f(n/N) \chi _{\Lambda _N}(n) |\textrm{e}^{-\textrm{i}tA_N} \delta _v(n)|^2 = f(0) |\textrm{e}^{-\textrm{i}t\mathcal {A}_{\mathbb {Z}^d}}\delta _v(n)|^2\) for any n. So by Fatou’s lemma,
where we used \(f(0)=1\) and \(\sum _n |\textrm{e}^{-\textrm{i}t\mathcal {A}_{\mathbb {Z}^d}}\delta _v(n)|^2 = \Vert \textrm{e}^{\textrm{i}t\mathcal {A}_{\mathbb {Z}^d}} \delta _v\Vert ^2 = \Vert \delta _v\Vert ^2=1\).
On the other hand, by Riemann integration, \( \langle a_N\rangle = \frac{1}{N^d}\sum _{n\in \Lambda _N} f(n/N) \rightarrow \int _{\mathbb {T}_*^d} f(x)\,\textrm{d}x = \frac{1}{2^d}\). This proves the result.
The statement holds for the average dynamics since \(\textrm{e}^{-\textrm{i}tA_N}\delta _v(w) \rightarrow \textrm{e}^{-\textrm{i}t\mathcal {A}_{\mathbb {Z}^d}}\delta _v(w)\) implies \(\frac{1}{T}\int _0^T |\textrm{e}^{-\textrm{i}tA_N}\delta _v(w)|^2\,\textrm{d}t \rightarrow \frac{1}{T}\int _0^T |\textrm{e}^{-\textrm{i}t\mathcal {A}_{\mathbb {Z}^d}}\delta _v(w)|^2\,\textrm{d}t\), as \(|\textrm{e}^{-\textrm{i}tA_N}\delta _v(w)|^2 \le \Vert \textrm{e}^{-\textrm{i}tA_N}\Vert ^2=1\). The (averaged) lower bound (2.4) still holds by Tonelli’s theorem. \(\square \)
Proof of Proposition 1.4
Take \(d=1\) and \(a_N(x) = \textrm{e}^{2\pi \textrm{i}x/N}\), so that \(a_m = \sqrt{N}\delta _{m,1}\). Since \(\lambda _\ell = 2\cos \frac{2\pi \ell }{N}\), (2.1) reduces to \(\frac{\textrm{e}^{\frac{2\pi \textrm{i}v}{N}}}{N}\sum _{\ell =0}^{N-1} \textrm{e}^{-4\textrm{i}t \sin \frac{\pi }{N}(2\ell +1)\sin \frac{\pi }{N}}\). Specializing to \(t=n\in \mathbb {N}\), it is shownFootnote 3 in [13, Lemma C.2] that this sum has no limit as \(n\rightarrow \infty \). In particular, \(\langle \textrm{e}^{-\textrm{i}tA_N} \delta _v, a_N\textrm{e}^{-\textrm{i}tA_N}\delta _v\rangle \) has no limit as \(t\rightarrow \infty \).
The same lemma shows that \(\int _{T-1}^T \langle \textrm{e}^{-\textrm{i}tA_N} \delta _v, a_N\textrm{e}^{-\textrm{i}tA_N}\delta _v\rangle \,\textrm{d}t\) has no limit as \(T\rightarrow \infty \). Here, the expression becomes \(\frac{\textrm{e}^{\frac{2\pi \textrm{i}v}{N}}}{N}\sum _{\ell =0}^{N-1} \textrm{e}^{\textrm{i}T b_\ell }\frac{(1-\textrm{e}^{-\textrm{i}b_\ell })}{\textrm{i}b_\ell }\) for \(b_\ell = -4\sin \frac{\pi }{N}(2\ell +1)\sin \frac{\pi }{N}\). \(\square \)
Proof of Proposition 1.5
If N is odd, consider \(a_N(n) = 2\cos (\frac{2\pi n_1}{N})\). Then, \(a_m^{(N)} = N^{d/2}\) if \(m = \pm \mathfrak {e}_1\), where \(\mathfrak {e}_1=(1,0,\dots ,0)\), and \(a_m^{(N)}=0\) otherwise. So the RHS (2.2) reduces to
Since \(\lambda _k^{(N)} = \sum _{i=1}^d 2\cos \frac{2\pi k_i}{N}\), we have \(\lambda _{\ell +\mathfrak {e}_1}^{(N)} = \lambda _\ell ^{(N)}\) iff \(\cos (\frac{2\pi (\ell _1+1)}{N}) = \cos (\frac{2\pi \ell _1}{N})\), i.e., \(\sin \pi (\frac{2\ell _1+1}{N})\sin \frac{\pi }{N}=0\). This occurs iff \(\frac{2\ell _1+1}{N} = 0,1,2\), i.e., \(\ell _1 = \frac{-1}{2}\), \(\frac{N-1}{2}\) or \(\frac{2N-1}{2}\), respectively. The only choice in \(\{0,\dots ,1\}\) is \(\ell _1 = \frac{N-1}{2}\). Since \(\ell _j\) can be arbitrary for \(j\ge 2\), we see that \(\frac{\#\{\ell \in \Lambda _N: \lambda _{\ell +\mathfrak {e}_1}^{(N)}=\lambda _\ell ^{(N)}\}}{N^d} = \frac{1}{N}\). Similarly, \(\lambda _{\ell -\mathfrak {e}_1}^{(N)} = \lambda _\ell ^{(N)}\) iff \(\frac{2\ell _1-1}{N} = 0,1,2\), and the only valid choice is \(\ell _1 = \frac{N+1}{2}\). We thus showed that the RHS of (2.2) is \(b_N(v) = \frac{2\cos (\frac{2\pi v_1}{N})}{N}\).
If N is even, we take \(a_N(n) = 2\cos (\frac{4\pi n_1}{N})\). Then, \(a_m^{(N)}=N^{d/2}\) if \(m=\pm 2\mathfrak {e}_1\) and zero otherwise. Here, \(\lambda _{\ell \pm 2\mathfrak {e}_1}^{(N)}=\lambda _\ell ^{(N)}\) iff \(\frac{2\ell _1\pm 2}{N}=0,1,2\), and we conclude as before that \(b_N(v) = \frac{4\cos (\frac{4\pi v_1}{N})}{N}\). \(\square \)
Remark 2.1
We can take T to depend on N, provided it grows fast enough. To see this, back to (2.1), we notice that in the expansion of \(\frac{1}{T}\int _0^T\langle \textrm{e}^{\textrm{i}tA_N}\delta _v,a\textrm{e}^{-\textrm{i}tA_N}\delta _v\rangle \,\textrm{d}t\), we should now account for the additional term
This can be bounded crudely by \(\sum _{m\ne 0} |a_m^{(N)}e_m^{(N)}(v)|\cdot \frac{2}{T}\cdot \sup _{\lambda _j^{(N)}\ne \lambda _k^{(N)}} |\lambda _j^{(N)}-\lambda _k^{(N)}|^{-1}\). We showed in the proof that \(\sum _{m} |a_m^{(N)} e_m^{(N)}(v)|\) stays bounded for all N for our choice of observables a. Thus, if \(T = T(N)\) grows faster than the smallest spectral gap between distinct eigenvalues of \(A_N\), the term (2.5) will vanish as required as \(N\rightarrow \infty \). For \(d=1\), it suffices that T grows faster than \(N^2\).
3 Periodic Graphs
We here extend ergodicity to \(\mathbb {Z}^d\)-periodic graphs \(\Gamma \). We assume there exist linearly independent vectors \(\mathfrak {a}_1,\dots ,\mathfrak {a}_d\) in a Euclidean space \(\mathbb {R}^D\) such that, if \(n_\mathfrak {a}= \sum _{i=1}^d n_i \mathfrak {a}_i\) and \(\mathbb {Z}_\mathfrak {a}^d = \{n_\mathfrak {a}:n\in \mathbb {Z}^d\}\), then
where \(V_f\) is the fundamental cell containing a finite number \(\nu \) of vertices, which is then repeated periodically under translations by \(n_\mathfrak {a}\in \mathbb {Z}_\mathfrak {a}^d\).
For example, \(\Gamma =\mathbb {Z}^d\) has \(V_f=\{0\}\) and \(\mathfrak {a}_j=\mathfrak {e}_j\) the standard basis. An infinite strip of width k has \(V_f = P_k\), the k-path, \(d=1\) and \(\mathfrak {a}_1=\mathfrak {e}_1\). See [28, 31] for more examples.
We endow \(V_f\) with a potential \((Q_1,\dots ,Q_\nu )\) and copy these values across the blocks \(V_f+n_\mathfrak {a}\). This turns Q into a periodic potential on \(\Gamma \). We consider the Schrödinger operator \(\mathcal {H}= \mathcal {A}_\Gamma +Q\).
From (3.1), any \(u\in \Gamma \) takes the form \(u=u_\mathfrak {a}+\{u\}_\mathfrak {a}\) for some \(u_\mathfrak {a}\in \mathbb {Z}_\mathfrak {a}^d\) and \(\{u\}_\mathfrak {a}\in V_f\).
Fix a large N and let \(\Gamma _N = \cup _{n\in \mathbb {L}_N^d} (V_f+n_\mathfrak {a})\), where \(\mathbb {L}_N^d = \{0,\dots ,N-1\}^d\). We consider the restriction \(H_N\) on \(\Gamma _N\) with periodic boundary conditions. Then, it holds that [28], if \(U:\ell ^2(\Gamma _N)\rightarrow \mathop \oplus _{j\in \mathbb {L}_N^d} \ell ^2(V_f)\) is the Floquet transform defined by
then U is unitary and
where \(b_1,\dots ,b_\nu \) is the dual basis of \((\mathfrak {a}_i)\) satisfying \(\mathfrak {a}_i\cdot \mathfrak {b}_j = 2\pi \delta _{i,j}\), \(n_\mathfrak {b}= \sum _{i=1}^d n_i \mathfrak {b}_i\) and
Much like \(\mathcal {A}_{\mathbb {Z}^d}\) is unitarily equivalent to multiplication by a function that is a sum of cosines via the Fourier transform, (3.2) is a finite version of the fact that \(\mathcal {H}\) is unitarily equivalent to multiplication by a \(\nu \times \nu \) matrix function \(H(\theta _\mathfrak {b})\) via the Floquet transform.
Denote by \(E_s(\theta _\mathfrak {b})\), \(s=1,\dots ,\nu \) the eigenvalues of \(H(\theta _\mathfrak {b})\), and by \(P_{E_s}(\theta _\mathfrak {b})\) the orthogonal projection onto the eigenspace corresponding to \(E_s(\theta _\mathfrak {b})\).
As initial state, we consider \(\psi = \delta _{v_p}\otimes \delta _{n_\mathfrak {a}}\), more precisely \(\psi (v_i+k_\mathfrak {a}):= \delta _{v_p}(v_i)\delta _{n}(k)\) for \(v_i\in V_f\) and \(k\in \mathbb {Z}^d\). In other words, we start from a point mass.
Theorem 3.1
Assume that
as \(N\rightarrow \infty \). Suppose the observable \(a_N\) satisfies one of the following conditions:
-
(i)
\(a_N(k_\mathfrak {a}+v_q) = f^{(q)}(k/N)\) for some \(\nu \) functions \(f^{(q)}\in H^s(\mathbb {T}_*^d)\), with \(s>d/2\),
-
(ii)
or, \(a_N\) is the restriction to \(\Gamma _N\) of an integrable function \(a\in \ell ^1(\Gamma )\).
Then
where, denoting \(\langle a(\cdot +v_q)\rangle := \frac{1}{N^d} \sum _{n\in \mathbb {L}_N^d} a(n_\mathfrak {a}+v_q)\),
The Floquet condition (3.4) was used as a requirement for quantum ergodicity in [28]. It is a bit stronger than asking that H has purely absolutely continuous spectrum. We refer to [28] for numerous examples which satisfy (3.4).
In the special case, \(\langle a(\cdot +v_q)\rangle = \langle a(\cdot +v_1)\rangle \) \(\forall q=1,\dots ,\nu \), (3.5) reduces to \(\langle a(\cdot +v_1)\rangle \). In fact, we get
This scenario occurs in particular if a is locally constant, i.e., takes a fixed value on each periodic block \(V_f+n_\mathfrak {a}\), which depends on n but not on \(v_q\in V_f\).
In general, (3.5) gives not the uniform average of a, but a weighted average, with weights depending on the initial point \(v_p\) and the spectral decomposition of the Floquet matrix. Note however that \(\frac{1}{\nu }\sum _{p=1}^\nu \langle a\rangle _p = \frac{1}{\nu }\sum _{q=1}^\nu \langle a(\cdot +v_q)\rangle \) is the uniform average. So the mean density \(\mu _{n,T}^{(N)}(u)=\frac{1}{T}\int _0^T \frac{1}{\nu }\sum _{p=1}^\nu |(\textrm{e}^{-\textrm{i}tH_N} \delta _{v_p}\otimes \delta _{n_\mathfrak {a}})(u)|^2\,\textrm{d}t\) on \(\Gamma _N\) approaches the uniform measure \(\frac{1}{\nu N^d}\) for \(T,N\gg 0\).
Example 3.2
Let \(Q\equiv 0\), so \(H(\theta _\mathfrak {b})=A(\theta _\mathfrak {b})\). The average \(\langle a\rangle _p\) is the uniform average if:
-
(i)
\(\nu =1\), for example \(\Gamma =\mathbb {Z}^d\) or the triangular lattice. See [28, Sect. 4.1] for more examples. Indeed, in this case (3.5) reduces to \(\langle a(\cdot +v_1)\rangle = \frac{1}{N^d}\sum _{n\in \Gamma _N} a(u)\).
-
(ii)
\(\Gamma \) is the hexagonal lattice or \(\Gamma \) is an infinite ladder (strip of width 2). The argument is given in [28, Sect. 4.2,4.3]. Both of these graphs have \(\nu =2\).
Let us now discuss two examples in which \(\langle a\rangle _p\) is not the uniform average. Both of them are Cartesian products \(\mathbb {Z}\mathop \square G_F\), where \(G_F\) is a finite graph (in the following \(G_F\) will be a 3-path and a 4-cycle, respectively). The Floquet matrix takes a very simple form in this case [28, Lemma 3.1]. We will here compute the matrix by hand from definition (3.3) to help the reader understand it better.
If \(\Gamma \) is the infinite strip of width 3 as in Fig. 2, we clearly can choose as fundamental domain \(V_f\) a vertical segment \(V_f=\{v_1,v_2,v_3\}\), where \(v_1\) is the top vertex, \(v_2\) is the middle one and \(v_3\) is the bottom one. Here \(d=1\) and \(\mathfrak {a}_1=\mathfrak {e}_1\). The vertex \(v_1\) has three neighbors: \(v_1\pm \mathfrak {e}_1\) and \(v_2\). We have \(\lfloor v_i\pm \mathfrak {e}_1\rfloor _\mathfrak {a}= \pm \mathfrak {e}_1\) and \(\{ v_i\pm \mathfrak {e}_1\}_\mathfrak {a}=v_i\), while \(\lfloor v_j\rfloor _\mathfrak {a}=0\) and \(\{v_j\}_\mathfrak {a}=v_j\). Finally, \(\theta _\mathfrak {b}=2\pi \theta \mathfrak {e}_1\). Thus, (3.3) tells us that
Arguing similarly for \(v_2\) and \(v_3\), we see that \(A(\theta _\mathfrak {b}) = \begin{pmatrix} c_\theta &{} 1&{}0\\ 1&{}c_\theta &{}1\\ 0&{}1&{}c_\theta \end{pmatrix}\) for \(c_\theta = 2\cos 2\pi \theta \). The eigenvectors are independent of \(\theta \) and given by \(w_1 = \frac{1}{2}(1,\sqrt{2},1)\), \(w_2=\frac{1}{\sqrt{2}}(-1,0,1)\) and \(w_3 = \frac{1}{2}(1,-\sqrt{2},1)\) for \(E_1=c_\theta +\sqrt{2}\), \(E_2 = c_\theta \), \(E_3 = c_\theta -\sqrt{2}\). It follows that \((P_i\delta _{v_q})(v_p) = w_i(v_p)w_i(v_q)\).
Suppose we take \(v_p=v_1\). Then,
For \(q=1,2,3\), this gives \(\frac{3}{8}\), \(\frac{1}{4}\) and \(\frac{3}{8}\), respectively. So \(\langle a\rangle _1 = \frac{3\langle a(\cdot +v_1)\rangle + 2\langle a(\cdot +v_2)\rangle + 3\langle a(\cdot + v_3)\rangle }{8}\), which is not the uniform average: there is more weight to both sides of the strip.
For comparison, suppose we take \(v_p=v_2\), the central vertex. Then,
For \(q=1,2,3\), this gives \(\frac{1}{4}\), \(\frac{1}{2}\) and \(\frac{1}{4}\), respectively. So \(\langle a\rangle _2 = \frac{\langle a(\cdot +v_1)\rangle + 2\langle a(\cdot +v_2)\rangle + \langle a(\cdot + v_3)\rangle }{4}\), which is not the uniform average either. There is more weight to the center of the strip.
More surprisingly perhaps, the spreading is not uniform in cylinders either, which are regular, very homogeneous graphs.
A point mass (left) spreads \(\frac{3}{8}\) of its mass over both its line and the line diagonally opposite to it, and only \(\frac{1}{8}\) of its mass on each of the other two lines (right). If the cylinder has size 4N, then each dark blue vertex carries a mass \(\frac{3}{8N}\) and each light blue vertex carries a mass \(\frac{1}{8N}\)
For example, for the 4-cylinder in Fig. 3, computing as in (3.6), we find that \(A(\theta _\mathfrak {b}) = c_\theta \textrm{Id}_4 + \mathcal {A}_{C_4}\), where \(C_4\) is the 4-cycle, so \(A(\theta _\mathfrak {b})\) shares the eigenvectors of \(\mathcal {A}_{C_4}\) given by
respectively. If \(w_i\) are the eigenvectors in this order, then the three eigenprojections are again independent of \(\theta \) (this holds in general for Cartesian products such as \(\mathbb {Z}^d\mathop \square G_F\), with \(G_F\) finite) and given by \((P_{E_1}\delta _{v_q})(v_p) = w_1(v_p)w_1(v_q)\), \((P_{E_3} \delta _{v_q})(v_p) = w_4(v_p)w_4(v_q)\) and \((P_{E_2}\delta _{v_q})(v_p) = w_2(v_p)w_2(v_q)+w_3(v_p)w_3(v_q)\). Hence, \(|(P_{E_1}\delta _{v_q})(v_p)|^2 = |(P_{E_3}\delta _{v_q})(v_p)|^2 = \frac{1}{16}\). We may assume \(v_p=v_1\) by homogeneity. Then \(\sum _{i=1}^3 |(P_{E_i}\delta _{v_q})(v_1)|^2 = \frac{1}{8} + \frac{|w_3(v_q)|^2}{2}\). For \(q=1,2,3,4\), this gives \(\frac{3}{8}\), \(\frac{1}{8}\), \(\frac{3}{8}\) and \(\frac{1}{8}\), respectively. This is illustrated in Fig. 3.
It was observed in [28] that some eigenbases of the cylinder are uniformly distributed while others are not. We see that having one equidistributed eigenbasis is not enough to obtain the dynamic equidistribution that we discuss in this paper. This is in contrast to the folklore physics heuristics of Sect. A.1.
Proof of Theorem 3.1
It is shown in [28, Lemma 2.2] that
where
and \(a_m^{(N)}(v_q) = \langle e_m^{(N)},a(\cdot _\mathfrak {a}+v_q)\rangle = \sum _{n\in \mathbb {L}_N^d} \overline{e_m^{(N)}(n)}a(n_\mathfrak {a}+v_q)\).
If \(\psi = \delta _{v_p}\otimes \delta _{n_\mathfrak {a}}\), then \((U\psi )_r(v_\ell ) = \frac{1}{N^{d/2}} \delta _{v_p}(v_\ell ) \textrm{e}^{\frac{-2\pi \textrm{i}r\cdot n}{N}}\). Hence,
Since \(\langle A\delta _{v_p}\otimes \delta _{n_\mathfrak {a}},B \delta _{v_p}\otimes \delta _{n_\mathfrak {a}}\rangle = (A^*B\delta _{v_p}\otimes \delta _{n_\mathfrak {a}})(v_p+n_\mathfrak {a})\), we consider
Taking the limit \(T\rightarrow \infty \), this reduces to [28],
where, denoting \(S_r = \{(m,s,w):E_s(\frac{r_\mathfrak {b}+m_\mathfrak {b}}{N})-E_w(\frac{r_\mathfrak {b}}{N})=0\}\), we have
If in (3.9) we consider only the term \(m=0\) from (3.10), with \(v_i=v_\ell =v_p\), we get
where \(\nu '\) is the number of distinct eigenvalues. To prove the theorem, we should show that
Let \(A_m = \{(r,s,w):E_s(\frac{r_{\mathfrak {b}}+m_{\mathfrak {b}}}{N})-E_w(\frac{r_{\mathfrak {b}}}{N})=0\}\). Then \((m,s,w)\in S_r\iff (r,s,w)\in A_m\) so the above is
Assume \(\sum _m\sum _{q=1}^\nu |a_m^{(N)}(v_q)e_m^{(N)}(n)|\le C_a\) (observable condition). By (3.4), \(\sup _{m\ne 0} \frac{|A_m|}{N^d}\rightarrow 0\). Hence, the above tends to 0 as required, since \(|P_s(\theta _\mathfrak {b})(v,w)|\le 1\).
The observable condition is satisfied for the two classes we have. If \(a_N(k_\mathfrak {a}+v_q) = f^{(q)}(k/N)\) with \(f^{(q)}\in H^s(\mathbb {T}_*^d)\), \(s>d/2\), then \(a_m^{(N)}(v_q) = \langle e_m^{(N)},f^{(q)}(\cdot /N)\rangle _{\ell ^2(\mathbb {L}_N^d)} = \hat{f}_m^{(q)}N^{d/2}\). As before, this implies that \(\sum _{m}\sum _q |a_m^{(N)}(v_q)e_m^{(N)}(n)|\le \sum _{q} \Vert \hat{f}^{(q)}\Vert _1\), which is finite.
The second scenario is that \(a_N\) is the restriction to \(\Gamma _N\) of some \(a\in \ell ^1(\Gamma )\). Here, \(a = \sum _{n\in \mathbb {Z}^d}\sum _{q=1}^\nu c_{n,q}\delta _{n_\mathfrak {a}+v_q}\) with \(\sum _{n,q}|c_{n,q}|<\infty \). Then \(a_m^{(N)}(v_q) = \sum _{n\in \mathbb {Z}^d} c_{n,q} \overline{e_m^{(N)}(n)}\). This implies \(|a_m^{(N)}(v_q)e_m^{(N)}(n)|\le \frac{1}{N^d}\Vert a\Vert _1\) for all q implying the hypothesis. \(\square \)
Remark 3.3
(Another natural initial state). We may ask what happens if instead of starting from a point mass \(\delta _{v_p}\otimes \delta _{n_\mathfrak {a}}\), our initial state is equally distributed on the fundamental set, that is \(\psi _0 = \frac{1}{\sqrt{\nu }} \textbf{1}_{V_f}\otimes \delta _{n_\mathfrak {a}}\) for some fixed \(n\in \mathbb {L}_N^d\). In case of the ladder for instance, this corresponds to a vector localized on the two vertices of \(V_f\), each carrying mass \(\frac{1}{\sqrt{2}}\). We will see that the limiting distribution is still not the uniform average in general.
Revisiting the proof, we now have \((U\psi _0)_r(v_\ell ) = \frac{1}{\sqrt{\nu }N^{d/2}} \textrm{e}^{\frac{-2\pi \textrm{i}r\cdot n}{N}}\), so the RHS of (3.8) becomes \(\frac{1}{\sqrt{\nu }N^{d/2}}\sum _r \textrm{e}^{\frac{-2\pi \textrm{i}r\cdot n}{N}}\sum _{\ell =1}^\nu F_T(k,r,v_i,v_\ell ) e_r^{(N)}(k)\). Here, we have\(\langle \frac{1}{\sqrt{\nu }} \textbf{1}_{V_f}\otimes \delta _{n_\mathfrak {a}},\phi \rangle = \frac{1}{\sqrt{\nu }}\sum _{i=1}^\nu \phi (n+v_i)\), so (3.9) is replaced by \(\frac{1}{\nu N^d} \sum _r\sum _{\ell ,i=1}^\nu b(n,r,v_i,v_\ell )\). Consequently, instead of (3.11) we get \(\frac{1}{\nu N^d}\sum _r \sum _{\ell ,i=1}^\nu \sum _{q=1}^\nu \langle a(\cdot +v_q)\rangle \sum _{s=1}^{\nu '} P_{E_s}\big (\frac{r_{\mathfrak {b}}}{N}\big )(v_i,v_q)P_{E_s}\big (\frac{r_{\mathfrak {b}}}{N}\big )(v_q,v_\ell )\). This simplifies to
The rest of the proof is the same, so our theorem now says that averaging a over the evolution of \(\psi _0\) is close to \(\textbf{E}(a)\). Comparing with Example 3.2, in case of the ladder and the honeycomb lattice, this is again the uniform average. In case of the strip of width 3, we here have \((P_i\textbf{1}_{V_f})(v_q) = \langle w_i,\textbf{1}_{V_f}\rangle w_i(v_q)\), so
For \(q=1,2,3\), this gives \(\frac{(2+\sqrt{2})^2+(2-\sqrt{2})^2}{16}=\frac{3}{4}\), \(\frac{(2+\sqrt{2})^2+(2-\sqrt{2})^2}{8}=\frac{3}{2}\) and \(\frac{3}{4}\), respectively. Thus, \(\textbf{E}(a)=\frac{1}{3}\cdot \frac{3\langle a(\cdot +v_1)\rangle + 6\langle a(\cdot +v_2)\rangle +3\langle a(\cdot +v_3)\rangle }{4} = \frac{\langle a(\cdot +v_1)\rangle + 2\langle a(\cdot +v_2)\rangle +\langle a(\cdot +v_3)\rangle }{4}\). So we still don’t get the uniform average; there is more weight given to the middle line. Curiously, this is the same as starting from a point mass in the middle.
In case of the cylinder, \(P_{E_1} \textbf{1}_{V_f} = \langle w_1,\textbf{1}_{V_f}\rangle w_1 = 2 w_1\), while \(P_{E_2}\textbf{1}_{V_f} = P_{E_3} \textbf{1}_{V_f}=0\), since \(w_2,w_3,w_4\) are all orthogonal to \(\textbf{1}_{V_f}\). It follows that \(\sum _{i=1}^4 |P_{E_s} \textbf{1}_{V_f}(v_q)|^2 = 4 |w_1(v_q)|^2 = 1\). Thus, \(\textbf{E}(a) = \frac{1}{4}\sum _{q=1}^4 \langle a(\cdot +v_q)\rangle \) is now the uniform average, in contrast to the case of an initial state consisting of a point mass which was discussed in Example 3.2.
In general, if the initial state \(\psi _0\) has a compact support, the limiting average becomes
Regarding the Floquet assumption (3.4), it is likely to be necessary in view of [28, Prp. 1.6]. It is clear that it cannot be completely dropped, as this would allow the presence of “flat bands”, that is infinitely degenerate eigenvalues for \(\mathcal {H}\) with eigenvectors of compact support. If we take such an eigenvector as an initial state, it will not spread, since we simply get \(\textrm{e}^{-\textrm{i}tH_N} \psi _0 = \textrm{e}^{-\textrm{i}t \lambda } \psi _0\), so \(|\textrm{e}^{-\textrm{i}tH_N} \psi _0| = |\psi _0|\) for all times. An example is given in Fig. 4. See [28, 31] for more background on this phenomenon. Hence, at least pure AC spectrum for \(\mathcal {H}\) should be assumed, but (3.4) is stronger than this.
4 Continuous Case
4.1 Regularizing in Momentum Space
The Dirac distribution \(\delta _y\) on \(\mathbb {R}^d\) satisfies \(\langle \delta _y,f\rangle = f(y)\). As in [5], we consider here a normalized truncated Dirac distribution defined by \(\delta _y^I:=\frac{1}{\sqrt{N_I}} \textbf{1}_I(-\Delta )\delta _y\), where I is an interval and \(N_I\) is the number of eigenvalues of \(-\Delta \) in I. Let us fix \(I=(-\infty ,E]\) and denote \(N_E= N_I\), \(\delta _y^E = \delta _y^I\) and \(\textbf{1}_{\le E} = \textbf{1}_I\).
In our framework, \(\delta _y^E\) is a trigonometric polynomial, as we can see by defining \(\delta _y^E\) through its Fourier expansion, \(\delta _y^E:= \sum _j \langle e_j, \delta _y^E\rangle e_j = \frac{1}{\sqrt{N_E}}\sum _{\lambda _j\le E} \overline{e_j(y)} e_j\), for \(e_j(x)=\textrm{e}^{2\pi \textrm{i}j\cdot x}\). This function satisfies \(\delta _y^E(y) = \sqrt{N_E} \rightarrow \infty \) as \(E\rightarrow \infty \) and \(\delta _y^E(x) \rightarrow 0\) as \(E\rightarrow \infty \) for \(x\ne y\in \mathbb {T}_*^d\) (see the proof of (2) below). Also, \(\Vert \delta _y^E\Vert ^2 = \frac{1}{N_E} \sum _{\lambda _j,\lambda _k\le E} e_{k-j}(y)\langle e_j,e_k\rangle = 1\) and \(\langle \delta _y^E,f\rangle = \frac{1}{\sqrt{N_E}} \sum _{\lambda _j\le E} e_j(y) \langle e_j,f\rangle = \frac{1}{\sqrt{N_E}} [\textbf{1}_{\le E}(-\Delta ) f](y)\).
Proof of Theorem 1.7
We first note that if \(a= \sum _m a_m e_m\), then
since we assumed that \(\Vert a\Vert _{H_s}^2 = \sum _m |a_m|^2 \langle m\rangle ^{2\,s} <\infty \) for \(\langle m\rangle = \sqrt{1+m^2}\) and \(s>d/2\).
We have \(\textrm{e}^{\textrm{i}t \Delta } \delta _y^E = \frac{1}{\sqrt{N_E}}\sum _{\lambda _\ell \le E} \overline{e_\ell (y)} \textrm{e}^{-\textrm{i}t\lambda _\ell } e_\ell \) and \(a = \sum _m a_m e_m\). As \(e_me_\ell = e_{m+\ell }\), we get \(\textrm{e}^{-\textrm{i}t \Delta } a\textrm{e}^{\textrm{i}t\Delta } \delta _y^E = \frac{1}{\sqrt{N_E}} \sum _m a_m \sum _{\lambda _\ell \le E} \overline{e_\ell (y)} \textrm{e}^{\textrm{i}t(\lambda _{\ell +m}-\lambda _\ell )} e_{m+\ell }\).
Thus, \(\langle \delta _y^E, \textrm{e}^{-\textrm{i}t\Delta } a \textrm{e}^{\textrm{i}t\Delta } \delta _y^E\rangle = \frac{1}{N_E} \sum \nolimits _{\begin{array}{c} m,\ell \in \mathbb {Z}^d,\\ \lambda _\ell ,\lambda _{m+\ell }\le E \end{array}} a_m \textrm{e}^{\textrm{i}t(\lambda _{\ell +m}-\lambda _\ell )}e_m(y)\). The term \(m=0\) corresponds to \(\frac{1}{N_E} \sum _{\lambda _\ell \le E} a_0 e_0(y) = \int _{\mathbb {T}_*^d} a(x)\,\textrm{d}x\). Since \(\frac{1}{T}\int _0^T \textrm{e}^{\textrm{i}t(\lambda _{\ell +m}-\lambda _\ell )}\textrm{d}t = \frac{1}{T}\cdot \frac{\textrm{e}^{\textrm{i}T(\lambda _{\ell +m}-\lambda _\ell )}-1}{\textrm{i}(\lambda _{\ell +m}-\lambda _\ell )}\) for \(\lambda _{\ell +m}\ne \lambda _\ell \), we get
The second term. Now \(\lambda _k = 4\pi ^2 k^2\), for \(k^2:= k_1^2+\dots +k_d^2\). We have \(N_E = \#\{\ell : \ell ^2 \le \frac{E}{4\pi ^2}\} \sim c_d E^{d/2}\) by known Weyl asymptotics, which say that \(N_E\) is asymptotic to the volume of the d-dimensional ball of radius \(\frac{\sqrt{E}}{2\pi }\). On the other hand, the constraint \(\lambda _{\ell +m} = \lambda _\ell \) means that \(\ell \cdot m = -m^2/2\). This defines an affine hyperplane in \(\mathbb {R}^d\). Hence, for any \(m\ne 0\), \(\{\ell :\lambda _\ell \le E, \lambda _{\ell +m}=\lambda _\ell \}\) is itself the number of points on a \((d-1)\)-dimensional ball of radius \(\le \frac{\sqrt{E}}{2\pi }\), and as such, is bounded by \(c_{d-1}E^{(d-1)/2}\), uniformly in \(m\ne 0\) (by varying m we may get fewer, but not more than \(c_{d-1}E^{(d-1)/2}\) points). We thus see that
as \(E\rightarrow \infty \). By (4.1), it follows that the second error term in (4.2) decays like \(E^{-1/2}\).
The third term. Let us show that \(\lim _{E\rightarrow \infty }\frac{1}{N_E}\sum \nolimits _{\begin{array}{c} \ell \,:\,\lambda _\ell \le E\\ \lambda _{\ell +m}\ne \lambda _\ell \end{array}} \frac{1}{|\lambda _{\ell +m}-\lambda _\ell |} = 0\) uniformly in m. Roughly speaking, this is a Cesàro argument (if \(c_n\rightarrow 0\) then \(\frac{1}{n}\sum _{k=1}^n c_k \rightarrow 0\)).
Let \(\varepsilon >0\) and fix \(m\ne 0\), say \(m_i\ne 0\) and write \(\ell = (\hat{\ell }_i,\ell _i)\) with \(\hat{\ell }_i\in \mathbb {Z}^{d-1}\). We have \(\lambda _{\ell +m}-\lambda _\ell = 2\ell \cdot m+m^2\). So \(\frac{1}{N_E}\sum _{\begin{array}{c} \ell : \lambda _\ell \le E\\ |2\ell \cdot m+m^2|\ge \frac{2}{\varepsilon } \end{array}} \frac{1}{|\lambda _{\ell +m}-\lambda _\ell |}\le \frac{\varepsilon }{2}\).
On the other hand, if \(B_E = \{\lambda _\ell \le E\}\), then
so \(|\{\ell \in B_E: \ell \cdot m = 0\}| \lesssim E^{(d-1)/2}\), with the implicit constant depending on the dimension, but not m. Similarly, note that \(|2\ell \cdot m+m^2|<\frac{2}{\varepsilon }\) implies
There are at most \(\frac{2}{|m_i|\varepsilon }+1\) values of \(\ell _i\) in this interval. We see by applying the previous argument to each such value that \(|\{\ell \in B_E: |2\ell \cdot m+m^2|<\frac{2}{\varepsilon }\}| \lesssim \varepsilon ^{-1} E^{(d-1)/2}\), since \(|m_i|\ge 1\). Summarizing, we have
by choosing \(\varepsilon \asymp E^{-1/4}\). Using (4.1), this implies the third term vanishes like \(E^{-1/4}\).
This completes the proof of (1), and (3), as \(\Vert a^E\Vert _1\le C_s\Vert a^E\Vert _{H^s}\le C_sE^r\) and \(E^{r-\frac{1}{4}}\rightarrow 0\).
Proof of (2). \(\langle \delta _x^E, \textrm{e}^{-\textrm{i}t\Delta } a \textrm{e}^{\textrm{i}t\Delta } \delta _y^E\rangle = \frac{1}{N_E} \sum \nolimits _{\begin{array}{c} m,\ell \in \mathbb {Z}^d,\\ \lambda _\ell ,\lambda _{m+\ell }\le E \end{array}} \textrm{e}^{2\pi \textrm{i}\ell \cdot (x-y)}a_m \textrm{e}^{\textrm{i}t(\lambda _{\ell +m}-\lambda _\ell )}e_m(y)\) by the same calculations. Let \(x\ne y\). Note that \(x_j-y_j\in (-1,1)\) for all j since \(x,y\in \mathbb {T}_*^d\), and \(x_i-y_i\ne 0\) for at least one i. The term \(m=0\) corresponds to \(\frac{\langle a\rangle }{N_E}\sum _{\lambda _\ell \le E} \textrm{e}^{2\pi \textrm{i}\ell \cdot (x-y)}\), where \(\langle a\rangle = \int _{\mathbb {T}_*^d} a(w)\textrm{d}w\). Here \(\lambda _\ell \le E \iff \ell ^2 \le \frac{E}{4\pi ^2}\). Consider first the simplest case \(d=1\), so the sum runs over \([-\frac{\sqrt{E}}{2\pi },\frac{\sqrt{E}}{2\pi }]\) and equals \(\frac{\textrm{e}^{2\pi \textrm{i}\alpha (\beta +1)}-\textrm{e}^{-2\pi \textrm{i}\alpha \beta }}{\textrm{e}^{2\pi \textrm{i}\alpha }-1}\) for \(\alpha =x-y\) and \(\beta = \frac{\sqrt{E}}{2\pi }\). Since \(\alpha \ne 0\), this may be bounded by some \(c_\alpha \) independent of E, so \(\frac{\langle a\rangle }{N_E}\sum _{\lambda _\ell \le E} \textrm{e}^{2\pi \textrm{i}\ell \cdot (x-y)} \rightarrow 0\).
When \(d>1\), if \(\alpha =x-y\), \(\alpha _i\ne 0\) and we denote \(\ell = (\ell _i,\hat{\ell }_i)\) with \(\hat{\ell }_i\in \mathbb {R}^{d-1}\), then the finite sum over the ball \(B_E = \{\ell ^2\le \frac{E}{4\pi ^2}\}\) can be rearranged into sections \(\ell _i\in B_E(\hat{\ell }_i)\), for each \(\hat{\ell }_i\) such that \((\ell _i,\hat{\ell }_i)\in B_E\). And each \(\sum _{\ell _i\in B_E(\hat{\ell }_i)} \textrm{e}^{2\pi \textrm{i}\ell _i \alpha _i}\) can again be bounded by some \(C_{\alpha _i}\) independently of E. By the Weyl asymptotics, we see that \(|\sum _{\ell \in B_E} \textrm{e}^{2\pi \textrm{i}\ell \cdot \alpha }|\le C_{\alpha _i,d} E^{(d-1)/2}\). Since \(N_E\sim E^{d/2}\), this implies \(\frac{\langle a\rangle }{N_E}\sum _{\lambda _\ell \le E} \textrm{e}^{2\pi \textrm{i}\ell \cdot (x-y)} \rightarrow 0\).
We have shown that the term \(m=0\) vanishes as \(E\rightarrow \infty \). On the other hand, the sum over nonzero m is controlled as in (1); the presence of the phase \(\textrm{e}^{2\pi \textrm{i}\ell \cdot (x-y)}\) makes no difference. We conclude that if \(x\ne y\), then \(\frac{1}{T}\int _0^T \langle \textrm{e}^{\textrm{i}t\Delta }\delta _x^E,a\textrm{e}^{\textrm{i}t\Delta }\delta _y^E\rangle \,\textrm{d}t\rightarrow 0\) as \(E\rightarrow \infty \).
Weak convergence. \(\frac{1}{T}\int _0^T\langle \textrm{e}^{\textrm{i}t\Delta } \delta _y^E, a\textrm{e}^{\textrm{i}t\Delta }\delta _y^E\rangle \,\textrm{d}t = \frac{1}{T}\int _0^T \int _{\mathbb {T}_*^d}a(x)|(\textrm{e}^{\textrm{i}t\Delta }\delta _y^E)(x)|^2\,\textrm{d}x\textrm{d}t\). The continuous function a is bounded on the compact \(\mathbb {T}_*^d\), so \(\int _0^T\int _{\mathbb {T}_*^d}|a(x)||(\textrm{e}^{\textrm{i}t\Delta }\delta _y^E)(x)|^2\,\textrm{d}x\textrm{d}t \le T\Vert a\Vert _\infty \Vert \textrm{e}^{\textrm{i}t\Delta }\delta _y^E\Vert ^2 = T\Vert a\Vert _\infty \) is finite. By the Fubini theorem, we get \(\frac{1}{T}\int _0^T\langle \textrm{e}^{\textrm{i}t\Delta } \delta _y^E, a\textrm{e}^{\textrm{i}t\Delta }\delta _y^E\rangle = \int _{\mathbb {T}_*^d} a(x)(\frac{1}{T}\int _0^T |(\textrm{e}^{\textrm{i}t\Delta }\delta _y^E)(x)|^2\textrm{d}t)\,\textrm{d}x = \int _{\mathbb {T}_*^d} a(x)\,\textrm{d}\mu _{y,T}^E(x)\).
It follows from (1) that \(\int _{\mathbb {T}_*^d} a(x)\,\textrm{d}\mu _{y,T}^E(x) \rightarrow \int _{\mathbb {T}_*^d} a(x)\,\textrm{d}x\) for any Sobolev function a, in particular for any smooth function on \(\mathbb {T}_*^d\). Combining [18, Cor 15.3, Thm 13.34], we deduce that \(\textrm{d}\mu _{y,T}^E(x) \xrightarrow {w} \textrm{d}x\) as \(E\rightarrow \infty \). \(\square \)
Proof of Lemma 1.8
Consider \(d=1\) and \(a(x) = e_1(x) = \textrm{e}^{2\pi \textrm{i}x}\). The calculation in the previous proof shows that
where we used \(a_m = \delta _{m,1}\) and \(\lambda _k=4\pi ^2 k^2\).
If \(t=\frac{n}{4\pi }\), this gives \(\frac{\textrm{e}^{\textrm{i}\pi n}e_1(y)}{N_E} \sum _{\lambda _\ell ,\lambda _{\ell +1}\le E} \textrm{e}^{2\ell n \pi \textrm{i}} = c_E (-1)^n e_1(y)\) for \(c_E = \frac{\sqrt{E}-\pi }{\sqrt{E}}\).
On the other hand, if \(t = \frac{2n+1}{8\pi }\), then (4.3) becomes \(\frac{e_1(y)\textrm{e}^{\textrm{i}\frac{(2n+1)\pi }{2}}}{N_E}\sum _{\lambda _{\ell },\lambda _{\ell +1}\le E} \textrm{e}^{\textrm{i}(2n+1)\pi \ell } = \frac{e_1(y)\textrm{e}^{\textrm{i}\frac{(2n+1)\pi }{2}}}{N_E}\sum _{\lambda _{\ell },\lambda _{\ell +1}\le E} (-1)^\ell \in \{0, \pm \frac{e_1(y)\textrm{e}^{\textrm{i}\frac{(2n+1)\pi }{2}}}{N_E}\}\).
The limits over E are different: in the first case it gives \((-1)^n e_1(y)\), in the second case it gives 0. The latter case corresponds to \(\langle a\rangle =\langle e_1\rangle =0\), but not the former. \(\square \)
4.2 Generalizations
It is not very clear what would be the analog of (1.4). The limit \(\lim _{T\rightarrow \infty } \frac{1}{T}\int _0^T \langle \textrm{e}^{\textrm{i}t\Delta }\phi , a\textrm{e}^{\textrm{i}t\Delta }\psi \rangle \,\textrm{d}t\) is not necessarily equal to \(\langle \phi ,\psi \rangle \langle a\rangle \) even if \(\phi ,\psi \) are smooth. For example, take \(\phi =e_j\) and \(\psi =e_k\). Then \(\langle \textrm{e}^{\textrm{i}t\Delta }e_j, a\textrm{e}^{\textrm{i}t\Delta } e_k\rangle = \textrm{e}^{\textrm{i}t(\lambda _k-\lambda _j)}\langle e_j,ae_k\rangle \). We see that if \(k\ne j\) but \(\lambda _k=\lambda _j\) (e.g., \(k=(0,1)\), \(j=(1,0)\)), then \(\frac{1}{T}\int _0^T\langle \textrm{e}^{\textrm{i}t\Delta } e_j, a\textrm{e}^{\textrm{i}t\Delta } e_k\rangle = \langle e_j,ae_k\rangle \). Taking \(a = e_{j-k}\), this has value 1. In contrast, \(\langle e_j,e_k\rangle \langle a\rangle = 0\).
Instead of \(\delta _y^E\), we can consider variants such as \(\chi _y^E:= \frac{1}{\sqrt{\sum _j \chi _E(\lambda _j)^2}} \chi _E(-\Delta )\delta _y\). In other words, \(\chi _y^E = \frac{1}{\sqrt{\sum _j \chi _E(\lambda _j)^2}} \sum _{j} \chi _E(\lambda _j) \overline{e_j(y)}e_j\). Here, instead of \(\chi _E = \textbf{1}_{\le E}\), we only ask \(\chi _E(\lambda ) = 0\) if \(\lambda >E\) and \(0<c_0\le \chi _E(\lambda )\le c_1\) on \([0,E-1]\). This allows, for example, to consider smooth cutoffs. Then, the proof carries over. In fact, (4.2) becomes
For the second term, we bound the fraction by \(\frac{c_1^2}{c_0^2}\cdot \frac{\#\{\ell :\lambda _\ell \le E,\,\lambda _{\ell +m}\le E,\,\lambda _{\ell +m}=\lambda _\ell \}}{N_{E-1}}\), which converges to zero uniformly in m by the same argument. Similarly, the third term is controlled as before since \(|\chi _E(\lambda _\ell )\chi _E(\lambda _{\ell +m})|\le c_1^2\) and \(\sum _{\lambda _\ell \le E} \chi _E(\lambda _\ell )^2\ge c_0N_{E-1}\).
Finally, the proof can be generalized to tori of the form \(\mathbb {T}= \times _{i=1}^d [0,b_i)\). Here we use the basis \(e_\ell (x) = \frac{\textrm{e}^{\frac{2\pi x_1\ell _1}{b_1}}\cdots \textrm{e}^{\frac{2\pi x_d\ell _d}{b_d}} }{\sqrt{b_1\cdots b_d}}\), with eigenvalues \(\lambda _\ell = 4\pi ^2 \sum _{i=1}^d \frac{\ell _i^2}{b_i^2}\). The set \(B_E = \{\lambda _\ell \le E\}\) now consists of points in an ellipsoid of axes \(\frac{b_i\sqrt{E}}{2\pi }\). We still have \(N_E\sim C_{b,d} E^{d/2}\) and the proof carries over mutatis mutandis. If we assume some irrationality condition, the second term decays faster with E as the multiplicity reduces; however, it seems that the third error term does not improve.
4.3 Regularizing in Position Space
Our aim here is to prove Theorem 1.9. We fix an arbitrary sequence \((\phi _\varepsilon )\) for \(\varepsilon =(\varepsilon _1,\dots ,\varepsilon _d)\) which satisfies the following:
-
\(\phi _\varepsilon = \mathop \otimes _{i=1}^d \phi _{\varepsilon _i}\), that is, \(\phi _\varepsilon (x) = \phi _{\varepsilon _1}(x_1)\cdots \phi _{\varepsilon _d}(x_d)\) for some functions \(\phi _{\varepsilon _i}\) on \(\mathbb {R}\).
-
\(\Vert \phi _{\varepsilon _i}\Vert =1\) for each i.
-
\(\sup _{r\in \mathbb {Z}}|\langle \phi _{\varepsilon _i},e_r\rangle | \rightarrow 0\) as \(\varepsilon _i\rightarrow 0\), where \(e_r(s) = \textrm{e}^{2\pi \textrm{i}rs}\) for \(s\in \mathbb {T}_*\).
The most important example is \(\phi _\varepsilon = \frac{1}{\sqrt{\varepsilon _1\varepsilon _2\cdots \varepsilon _d}} \textbf{1}_{\times _{i=1}^d [y_i,y_i+\varepsilon _i]}\). Here, \(\langle \phi _{\varepsilon _i},e_r\rangle = \sqrt{\varepsilon _i}\) if \(r=0\) and \(\langle \phi _{\varepsilon _i},e_r\rangle = \frac{1}{\sqrt{\varepsilon _i}} \cdot \frac{\textrm{e}^{2\pi \textrm{i}r(y_i+\varepsilon _i)}-\textrm{e}^{2\pi \textrm{i}r y_i}}{2\pi r}\) if \(r\ne 0\). Since \(|\textrm{e}^{\textrm{i}x}-1|\le |x|\), we see that \(|\langle \phi _{\varepsilon _i},e_r\rangle |\le \sqrt{\varepsilon _i}\). This can be regarded as a normalized point mass in the sense that if \(\widetilde{\phi }_\varepsilon = \frac{1}{\varepsilon _1\cdots \varepsilon _d} \textbf{1}_{\times _{i=1}^d [y_i,y_i+\varepsilon _i]}\), then for any integrable g, we have \(\langle \widetilde{\phi }_\varepsilon , g\rangle \rightarrow g(y)\) for a.e. y by the Lebesgue differentiation theorem. Also, \(\widetilde{\phi }_\varepsilon (y) = \frac{1}{\varepsilon _1\cdots \varepsilon _d}\rightarrow \infty \) and \(\widetilde{\phi }_\varepsilon (x)\rightarrow 0\) for \(x\ne y\).
Theorem 4.1
For any \((\phi _\varepsilon )\) and \((\psi _\varepsilon )\) as above, any \(a\in H^s(\mathbb {T}_*^d)\), \(s>d/2\), any \(T>0\),
where \(\varepsilon \downarrow 0\) means more precisely that \(|\varepsilon |=\sqrt{\varepsilon _1^2+\dots +\varepsilon _d^2}\rightarrow 0\).
If \(\phi _\varepsilon =\psi _\varepsilon \), the scalar product on the right is \(\Vert \phi _\varepsilon \Vert ^2=1\). This implies Theorem 1.9. In fact, if we take \(\psi _\varepsilon =\frac{1}{\sqrt{\varepsilon _1\varepsilon _2\cdots \varepsilon _d}} \textbf{1}_{\times _{i=1}^d [y_i,y_i+\varepsilon _i]}\) and \(\phi _\varepsilon = \frac{1}{\sqrt{\varepsilon _1\varepsilon _2\cdots \varepsilon _d}} \textbf{1}_{\times _{i=1}^d [x_i,x_i+\varepsilon _i]}\) for \(x\ne y\), then \(\lim _{\varepsilon \downarrow 0}\langle \phi _\varepsilon ,\psi _\varepsilon \rangle =0\).
Proof
We have \(\textrm{e}^{\textrm{i}t\Delta } \psi = \sum _{\ell } \textrm{e}^{-\textrm{i}t\lambda _\ell }\psi _\ell e_\ell \) and \(a=\sum _m a_m e_m\), so using \(e_m e_{\ell } = e_{m+\ell }\), we get \(\textrm{e}^{-\textrm{i}t\Delta } a\textrm{e}^{\textrm{i}t\Delta }\psi = \sum _{m,\ell } a_m \psi _\ell \textrm{e}^{\textrm{i}t(\lambda _{\ell +m}-\lambda _\ell )} e_{m+\ell }\). This implies that
Thus,
For \(\phi =\phi _\varepsilon \) and \(\psi =\psi _\varepsilon \), the first term has the form
Second term: We prove that \(\lim _{\varepsilon \rightarrow 0} \sum _{m\ne 0} a_m \sum _{\ell \,:\, 2\ell \cdot m = -m^2} \langle e_\ell , \psi _\varepsilon \rangle \langle \phi _\varepsilon ,e_{\ell +m}\rangle = 0\).
First assume \(d=1\). Then, \(m\ne 0\) and \(2\ell m=-m^2\) implies \(\ell = -m/2\). So we get \(\sum _{m\ne 0} a_m \langle e_{-m/2},\psi _\varepsilon \rangle \langle \phi _\varepsilon ,e_{m/2}\rangle \). By hypothesis, the general term vanishes as \(\varepsilon \rightarrow 0\). Moreover, it is bounded by \(|a_m|\cdot \Vert \psi _\varepsilon \Vert \Vert \phi _\varepsilon \Vert \Vert e_{-m/2}\Vert \Vert e_{m/2}\Vert = |a_m|\), which is summable. By dominated convergence, the result follows.
Now let \(d>1\). Using \(|\sum _{m\ne 0} F(m)|\le \sum _{i=1}^d \sum _{m_i\ne 0} |F(m)|\), it suffices to show that \(\lim _{\varepsilon \downarrow 0} \sum _{i=1}^d\sum _{m_i\ne 0} |a_m| |\sum _{\ell :2\ell \cdot m=-m^2} \langle e_\ell , \psi _\varepsilon \rangle \langle \phi _\varepsilon ,e_{\ell +m}\rangle | = 0\).
By hypothesis, \(\phi _\varepsilon = \mathop \otimes _{i=1}^d \phi _{\varepsilon _i}\). It follows that \(\langle e_k, \phi _\varepsilon \rangle = \prod _{j=1}^d \langle e_{k_j},\phi _{\varepsilon _j}\rangle \). Suppose that \(m_i\ne 0\). Then, \(\ell _i = \frac{-m^2-2\hat{\ell }_i\cdot \hat{m}_i}{2 m_i}\), where for \(x\in \mathbb {R}^d\), we denoted \(x = (\hat{x}_i,x_i)\) with \(\hat{x}_i\in \mathbb {R}^{d-1}\). We thus consider
We first show the general term \(F_\varepsilon (m)\rightarrow 0\) as \(\varepsilon \rightarrow 0\). For this, we bound
by hypothesis. On the other hand, the general term can be bounded by
which is summable. By dominated convergence, the result follows.
Third term. We need to show the following term vanishes as \(\varepsilon \downarrow 0\):
Let \(m\ne 0\), say \(m_i\ne 0\). We have
Now \(\ell \cdot m = r \iff \ell _i = \frac{r-\hat{\ell }_i\cdot \hat{m}_i}{m_i}\). Recalling \(\phi _\varepsilon =\otimes \phi _{\varepsilon _i}\), this can be written as
where we used that \(\frac{r-\hat{\ell }_i\cdot \hat{m}_i}{m_i}\) and \(\frac{m_i^2+r-\hat{\ell }_i\cdot \hat{m}_i}{m_i}\) are both integers and the Cauchy-Schwarz inequality.
If \(m^2\in 2\mathbb {Z}\), then \( \frac{1}{4}\sum _{r\ne \frac{-m^2}{2}}\frac{1}{(r+\frac{m^2}{2})^2} = \frac{1}{4}\sum _{k\ne 0} \frac{1}{k^2} = \frac{\pi ^2}{12}\).
If \(m^2\notin 2\mathbb {Z}\), then \(k_0:=\lfloor \frac{-m^2}{2}\rfloor = \frac{-m^2}{2}-\frac{1}{2}\). So \(\frac{1}{4}\sum _{r}\frac{1}{(r+\frac{m^2}{2})^2} = \frac{1}{4}(\frac{1}{(1/2)^2} + \frac{1}{(1/2)^2} + \sum _{r\notin \{k_0,k_0+1\}} \frac{1}{(r-k_0-\frac{1}{2})^2})\le \frac{1}{4}(8+\sum _{k\ne 0}\frac{1}{k^2}) = 2+\frac{\pi ^2}{12}\).
Either way, the sum is bounded by 3. We thus showed that
which tends to zero uniformly in m by our hypotheses.
Finally turning back to (4.4), we have proved that as a sum over m, the general term vanishes as \(\varepsilon \downarrow 0\). Moreover, the general term is bounded by \(|a_m| \frac{1}{T} \sum _{\ell } |\langle e_\ell ,\psi _{\varepsilon }\rangle \langle \phi _\varepsilon ,e_{\ell +m}\rangle | \le \frac{|a_m|}{T}\) by Cauchy-Schwarz and \(\Vert \psi _\varepsilon \Vert =\Vert \phi _\varepsilon \Vert =1\). Since \(\sum _m |a_m|<\infty \), we conclude by dominated convergence that (4.4) vanishes as \(\varepsilon \downarrow 0\). \(\square \)
Remark 4.2
It is clear that the proofs of Theorems 1.7 and 1.9 continue to hold if we take the limit \(T\rightarrow \infty \) before considering \(E\rightarrow \infty \). The proofs become in fact simpler as such a limit over T kills the third term in (4.2) and (4.4), thereby avoiding the finer analysis we performed. See also [19] for this regime. If we do take the limit over \(T\rightarrow \infty \) first, then we can also replace \(\int _0^T\) by \(\sum _{t=0}^{T-1}\). For example, (4.4) becomes \(\sum _{m\ne 0} a_m \sum _{\ell :\lambda _{\ell +m}\ne \lambda _\ell } \frac{\textrm{e}^{\textrm{i}T(\lambda _{\ell +m}-\lambda _\ell )}-1}{\textrm{i}T(\textrm{e}^{\textrm{i}(\lambda _{\ell +m}-\lambda _\ell )}-1)} \langle e_\ell ,\psi _\varepsilon \rangle \langle \phi _\varepsilon , e_{\ell +m}\rangle \), which vanishes as \(T\rightarrow \infty \) (here \(0\ne \lambda _{\ell +m}-\lambda _\ell = 4\pi ^2(2\ell \cdot m+m^2)\notin 2\pi \mathbb {Z}\)). We cannot however consider \(\sum _{t=0}^{T-1}\) in Theorems 1.7 and 1.9, as the finer analysis of the third term that we performed used the fact that \(\frac{1}{|\lambda _{\ell +m}-\lambda _\ell |}\rightarrow 0\) as \(\ell \rightarrow \infty \), which is not true of \(\frac{1}{|\textrm{e}^{\textrm{i}(\lambda _{\ell +m}-\lambda _\ell )}-1|}\).
5 Case of the Sphere
Consider the sphere \(\mathbb {S}^{d-1}\subset \mathbb {R}^d\), \(d\ge 3\). We have \(L^2(\mathbb {S}^{d-1}) = \mathop \oplus _{k=0}^\infty \mathbb {Y}_k^d\), where \(\mathbb {Y}_k^d\) is the spherical harmonic space of order k in dimension d. Any nonzero function in \(\mathbb {Y}_k^d\) is an eigenfunction of the Laplacian on the sphere \(-\Delta _{\mathbb {S}^{d-1}}\) with eigenvalue \(k(k+d-2)\) and multiplicity \(N_{k,d} = \dim \mathbb {Y}_k^d = \frac{(2k+d-2)(k+d-3)!}{k!(d-2)!}\). See [7, Th. 2.38, Prp. 3.5]. If we define the zonal harmonic of degree k, \(Z_\xi ^{(k)}(\eta ):= \frac{N_{k,d}}{|\mathbb {S}^{d-1}|} P_{k,d}(\xi \cdot \eta )\), where \(|\mathbb {S}^{d-1}| = \frac{2\pi ^{d/2}}{\Gamma (d/2)}\) is the volume of the sphere and \(P_{k,d}(t)\) satisfies the Poisson identity \(\sum _{k=0}^\infty r^k N_{k,d}P_{k,d}(t) = \frac{1-r^2}{(1+r^2-2rt)^{d/2}}\) for \(|r|<1\) and \(t\in [-1,1]\), then \(Z_\xi ^{(k)}\) satisfies the reproducing property [7, (2.33)],
We have \(Z_\xi ^{(k)} = \sum _{j=1}^{N_{k,d}} Y_{k,j}(\xi ) \overline{Y_{k,j}}\) for any orthonormal basis of \(\mathbb {Y}_k^d\), see [7, Th. 2.9]. In particular \(Z_\xi ^{(k)}\in \mathbb {Y}_k^d\) and as such \(Z_\xi ^{(k)}\) is an eigenfunction of \(-\Delta _{\mathbb {S}^{d-1}}\) for the eigenvalue \(k(k+d-2)\). Moreover, \(\Vert Z_\xi ^{(k)}\Vert _{L^2(\mathbb {S}^{d-1})}^2 = \frac{N_{k,d}}{|\mathbb {S}^{d-1}|}\) by [7, (2.40)] and \(Z_\xi ^{(k)}(\xi ) = \frac{N_{k,d}}{|\mathbb {S}^{d-1}|}\) by [7, (2.35)], which is the maximum of \(Z_\xi ^{(k)}\). Finally, if \(C_{n,\nu }\) is the Gegenbauer ultraspherical polynomial, then \(C_{n,\frac{d-2}{2}}(t) = \left( {\begin{array}{c}n+d-3\\ n\end{array}}\right) P_{n,d}(t)\) for \(d\ge 3\), [7, (2.145)].
In view of the Dirac-like Eq. (5.1), one can consider the evolution of
where \(\widetilde{Z}_\xi ^{(k)} = \sqrt{\frac{|\mathbb {S}^{d-1}|}{N_{k,d}}} Z_\xi ^{(k)}\) has norm one.
However, since \(Z_\xi ^{(k)}\) is an eigenfunction of \(-\Delta _{\mathbb {S}^{d-1}}\), this reduces to \(\langle \widetilde{Z}_\xi ^{(k)},a \widetilde{Z}_\xi ^{(k)}\rangle \).
Lemma 5.1
The density \(|\widetilde{Z}_\xi ^{(k)}(\eta )|^2\) is not uniformly distributed as \(k\rightarrow \infty \). It has peaks at \(\pm \xi \) and stays bounded for \(\eta \ne \pm \xi \).
More precisely, \(|\widetilde{Z}_\xi ^{(k)}(\pm \xi )|^2\rightarrow \infty \) as \(k\rightarrow \infty \).
Proof
In fact, \(|\widetilde{Z}_\xi ^{(k)}(\pm \xi )|^2 = \frac{|\mathbb {S}^{d-1}|}{N_{k,d}}\cdot \frac{N_{k,d}^2}{|\mathbb {S}^{d-1}|^2} \rightarrow \infty \) as \(k\rightarrow \infty \). On the other hand, if \(\eta \ne \pm \xi \), then \(t:= \xi \cdot \eta \) satisfies \(|t|<1\). By [7, (2.117)], \(|P_{n,d}(t)| < \frac{\Gamma (\frac{d-1}{2})}{\sqrt{\pi }}[\frac{4}{n(1-t^2)}]^{\frac{d-2}{2}}\), hence \(|\widetilde{Z}_\xi ^{(k)}(\eta )|^2<\frac{N_{k,d}}{|\mathbb {S}^{d-1}|}\cdot \frac{c_{d,\eta }}{k^{d-2}}\). Since \(\Gamma (x+\alpha )\sim \Gamma (x)x^\alpha \), then \(N_{k,d} =\frac{(2k+d-2)}{(d-2)!}\frac{\Gamma (k+d-2)}{\Gamma (k+1)} \sim \frac{2}{(d-2)!}k^{d-2}\), hence \(|\widetilde{Z}_\xi ^{(k)}(\eta )|^2\) stays bounded as \(k\rightarrow \infty \). The upper bound we used is sharp in n, i.e., \(P_{n,d}(t)\asymp \frac{1}{n^{\frac{d-2}{2}}}\), by [36, Th. 8.21.8]. \(\square \)
A closer analogue to \(\delta _y^E = \frac{1}{\sqrt{N_E}}\sum _{\lambda _j\le E} \overline{e_j(y)}e_j\), our Dirac truncation for the torus, would be \(S_\xi ^{(n)} = \frac{1}{\sqrt{M_{n,d}}}\sum _{k=0}^n \mu _{n,k,d} Z_\xi ^{(k)}\), where \(M_{n,d}=\sum _{k=0}^n \mu _{n,k,d}^2 \frac{N_{k,d}}{|\mathbb {S}^{d-1}|} \) and \(\mu _{n,k,d} = \frac{n!(n+d-2)!}{(n-k)!(n+k+d-2)!}\). In fact, if \(R_\xi ^{(n)} = \sum _{k=0}^n \mu _{n,k,d} Z_{\xi }^{(k)}\), then (see [7, §2.8.1]):
-
\(\langle R_\xi ^{(n)},f\rangle _{L^2(\mathbb {S}^{d-1})} \rightarrow f(\xi )\) uniformly in \(\xi \), for any continuous f,
-
\(R_\xi ^{(n)}(\xi ) = \sum _{k=0}^n \mu _{n,k,d}\frac{N_{k,d}}{|\mathbb {S}^{d-1}|} = E_{n,d} =\frac{(n+d-2)!}{(4\pi )^{\frac{d-1}{2}}\Gamma (n+\frac{d-1}{2})} \rightarrow \infty \),
-
\(\Vert R_\xi ^{(n)}\Vert _{L^2(\mathbb {S}^{d-1})}^2 = \Vert \sum _{k=0}^n \mu _{n,k,d}Z_\xi ^{(k)}\Vert _2^2 = \sum _{k=0}^n \mu _{n,k,d}^2 \Vert Z_\xi ^{(k)}\Vert ^2 = M_{n,d}\). Here we used that \(Z_\xi ^{(k)}\perp Z_\xi ^{(r)}\) for \(k\ne r\), as they belong to \(\mathbb {Y}_k^d\) and \(\mathbb {Y}_r^d\), respectively, which are in direct sum (they are in distinct eigenspaces).
This says that \(R_\xi ^{(n)}\) is a \(\delta _\xi \)-sequence and that \(S_\xi ^{(n)}\) is its normalization.
Lemma 5.2
The density \(p_\xi ^{(n)}(\eta ) = \lim _{T\rightarrow \infty } \frac{1}{T}\int _0^T |\textrm{e}^{\textrm{i}t\Delta }S_\xi ^{(n)}(\eta )|^2\,\textrm{d}t\) is not uniformly distributed as \(n\rightarrow \infty \). It has peaks at \(\pm \xi \) and stays bounded for \(\eta \ne \pm \xi \).
Again, this means more precisely that \(p_\xi ^{(n)}(\pm \xi )\rightarrow \infty \) as \(n\rightarrow \infty \).
Proof
As \(\textrm{e}^{\textrm{i}t\Delta } S_\xi ^{(n)} = \frac{1}{\sqrt{M_{n,d}}} \sum _{k=0}^n \textrm{e}^{-\textrm{i}t \lambda _k}\mu _{n,k,d} Z_\xi ^{(k)}\), \(\lambda _k = k(k+d-2)\), then \(|\textrm{e}^{\textrm{i}t\Delta } S_\xi ^{(n)}(\eta )|^2 = \frac{1}{M_{n,d}}\sum _{k=0}^n \mu _{n,k,d}^2|Z_\xi ^{(k)}(\eta )|^2 + \frac{1}{M_{n,d}} \sum _{k\ne k'} \textrm{e}^{\textrm{i}t(\lambda _{k'}-\lambda _k)}\mu _{n,k,d}\mu _{n,k',d} Z_\xi ^{(k)}(\eta )\overline{Z_\xi ^{(k')}(\eta )}\). But \(\lambda _k\ne \lambda _{k'}\) for \(k\ne k'\), because the eigenspaces \(\mathbb {Y}_k^d\) are in direct sum (alternatively, \(\lambda _k=\lambda _{j}\) for \(k\ne j\) would imply \((k^2-j^2)+(d-2)(k-j)=0\), so \(k+j+d-2=0\), a contradiction since \(d\ge 3\) and \(k,j\ge 0\)). It follows that \(\frac{1}{T}\int _0^T |\textrm{e}^{\textrm{i}t\Delta } S_\xi ^{(n)}(\eta )|^2\,\textrm{d}t \rightarrow \frac{1}{M_{n,d}} \sum _{k=0}^n \mu _{n,k,d}^2|Z_\xi ^{(k)}(\eta )|^2=:p_\xi ^{(n)}(\eta )\).
Now \(p_\xi ^{(n)}(\pm \xi ) = \frac{1}{M_{n,d}}\sum _{k=0}^n \mu _{n,k,d}^2\frac{N_{k,d}^2}{|\mathbb {S}^{d-1}|^2}\) diverges as \(n\rightarrow \infty \). In fact, \((\sum _{k=0}^n a_k)^2 \le (n+1)\sum _{k=0}^n a_k^2\). Applying this to \(a_k = \mu _{n,k,d}\frac{N_{k,d}}{|\mathbb {S}^{d-1}|}\), we get \(E_{n,d}^2\le (n+1) \sum _{k=0}^n a_k^2\), so \(\frac{1}{M_{n,d}}\sum _{k=0}^n a_k^2\ge \frac{E_{n,d}^2}{(n+1)M_{n,d}} \rightarrow \infty \) for \(d>3\), because \(\frac{E_{n,d}^2}{(n+1)M_{n,d}} \ge \frac{E_{n,d}}{n+1} \asymp \frac{n^{\frac{d-1}{2}}}{n} \rightarrow \infty \). Here, we used that \(\mu _{n,k,d}\le 1\). For \(d=3\), this lower bound is not useful. So we argue as follows.
We have \(\sum _{k=0}^n \mu _{n,k,d}\frac{N_{k,d}}{|\mathbb {S}^{d-1}|} = E_{n,d}\). By Cauchy-Schwarz, we have on the one hand \((\sum _{k=0}^n \mu _{n,k,d}\frac{N_{k,d}}{|\mathbb {S}^{d-1}|})^2 \le (n+1) \sum _{k=0}^n \mu _{n,k,d}^2 \frac{N_{k,d}^2}{|\mathbb {S}^{d-1}|^2}\), so that \(\sum _{k=0}^n \mu _{n,k,d}^2 \frac{N_{k,d}^2}{|\mathbb {S}^{d-1}|^2} \ge \frac{E_{n,d}^2}{n+1}\). On the other hand, \(M_{n,d}^2=(\sum _{k=0}^n \mu _{n,k,d}^2 \frac{N_{k,d}}{|\mathbb {S}^{d-1}|})^2\le (\sum _{k=0}^n \mu _{n,k,d}^2)(\sum _{k=0}^n \mu _{n,k,d}^2\frac{N_{k,d}^2}{|\mathbb {S}^{d-1}|^2})\) and so \(\frac{\sum _{k=0}^n \mu _{n,k,d}^2 \frac{N_{k,d}^2}{|\mathbb {S}^{d-1}|^2}}{M_{n,d}} =(\sum _{k=0}^n \mu _{n,k,d}^2\frac{N_{k,d}^2}{|\mathbb {S}^{d-1}|^2})^{1/2}\cdot \frac{(\sum _{k=0}^n \mu _{n,k,d}^2 \frac{N_{k,d}^2}{|\mathbb {S}^{d-1}|^2})^{1/2}}{M_{n,d}} \ge \frac{(\sum _{k=0}^n \mu _{n,k,d}^2 \frac{N_{k,d}^2}{|\mathbb {S}^{d-1}|^2})^{1/2}}{(\sum _{k=0}^n \mu _{n,k,d}^2)^{1/2}}\). The two inequalities imply that \(\frac{\sum _{k=0}^n \mu _{n,k,d}^2 \frac{N_{k,d}^2}{|\mathbb {S}^{d-1}|^2}}{M_{n,d}} \ge \frac{E_{n,d}}{\sqrt{n+1}(\sum _{k=0}^n \mu _{n,k,d}^2)^{1/2}}\).
Specializing to \(d=3\), we have \(E_{n,3} = \frac{n+1}{4\pi }\). Also, \(\sum _{k=0}^n \mu _{n,k,3}^2 = \sum _{k=0}^n (\frac{n!(n+1)!}{(n-k)!(n+k+1)!})^2 = \sum _{k=0}^\infty \frac{(1)_k(-n)_k(-n)_k}{(n+2)_k(n+2)_kk!} = {}_3 F_2(1,-n,-n;n+2,n+2;1)\). Here \((r)_k = r(r+1)\cdots (r+k-1)\). If \(r\in \mathbb {N}^*\), then \((r)_k = \frac{(r+k-1)!}{(r-1)!}\) for any k, while \((-r)_k = -r(-r+1)\cdots (-r+k-1) = (-1)^k r(r-1)\cdots (r-k+1) = (-1)^k \frac{r!}{(r-k)!}\) holds for \(k\le r\) and \((-r)_k=0\) for \(k>r\).
By Dixon’s identity, \({}_3 F_2(1,-n,-n;n+2,n+2;1) = \frac{\Gamma (\frac{3}{2})\Gamma (\frac{3}{2}+2n)\Gamma (2+n)^2}{\Gamma (2)\Gamma (2+2n)\Gamma (\frac{3}{2}+n)^2}\). Using the asymptotic \(\Gamma (x+\alpha )\sim \Gamma (x)x^\alpha \), this shows that \(\sum _{k=0}^n \mu _{n,k,3}^2 \sim \frac{\sqrt{\pi }}{2}\cdot \frac{(n^{1/2})^2}{(2n)^{1/2}} = \frac{1}{2}\sqrt{\frac{\pi n}{2}}\).
We thus get that \(\frac{\sum _{k=0}^n \mu _{n,k,3}^2 \frac{N_{k,3}^2}{|\mathbb {S}^{2}|^2}}{M_{n,3}} \gtrsim \frac{n+1}{4\pi \sqrt{n+1}(\frac{1}{2}\sqrt{\frac{\pi n}{2}})^{1/2}} \asymp n^{1/4}\rightarrow \infty \).
We showed that \(p_\xi ^{(n)}(\pm \xi )\rightarrow \infty \). If \(\eta \ne \pm \xi \), then as in Lemma 5.1, we have \(p_\xi ^{(n)}(\eta )< \frac{1}{M_{n,d}} \sum _{k=0}^n \mu _{n,k,d}^2 \frac{N_{k,d}^2}{|\mathbb {S}^{d-1}|^2} \frac{c_{d,\eta }}{k^{d-2}}\) with \(N_{k,d} \sim \frac{2}{(d-2)!}k^{d-2}\), so that \(M_{n,d} = \sum _{k=0}^n \mu _{n,k,d}^2 \frac{N_{k,d}}{|\mathbb {S}^{d-1}|}\) and \(\sum _{k=0}^n \mu _{n,k,d}^2 \frac{N_{k,d}^2}{|\mathbb {S}^{d-1}|^2} \frac{c_{d,\eta }}{k^{d-2}}\) grow at the same speed with n, and \(p_\xi ^{(n)}(\eta )\) stays bounded. \(\square \)
To see more explicitly that ergodicity is violated, we can compare averages of specific observables. For simplicity, let us choose a such that for the \(\xi \) we fixed, \(a(\eta ) = a(\xi \cdot \eta )\). This allows to use the Funk–Hecke formula [7, Th. 2.22]: for any \(Y_n\in \mathbb {Y}_n^d\),
For \(Y_n = Z_\xi ^{(n)}\) and \(f(\xi \cdot \eta ) = a(\xi \cdot \eta ) P_{n,d}(\xi \cdot \eta )\frac{N_{n,d}}{|\mathbb {S}^{d-1}|}=a(\xi \cdot \eta )Z_{\xi }^{(n)}(\eta )\) we get
On the other hand (case \(n=0\) of Funk–Hecke, cf. [7, (2.87)]),
Let us check the asymptotics of (5.2). We take \(d=3\). Then, \(|\mathbb {S}^{d-1}|=4\pi \), \(|\mathbb {S}^{d-2}|=2\pi \), \(N_{k,d} = 2k+1\) and \(P_{n,d}(t) = P_n(t)\) is the Legendre polynomial, which satisfies [7, (2.79)]
Since \((n+1)P_{n+1}(t)+nP_{n-1}(t)=(2n+1)tP_n(t)\), see [7, p. 52], we deduce that
Lemma 5.3
Let \(d=3\). There exists an observable a such that for any \(T>0\),
Proof
Given \(\xi \), we have for \(a(\eta ):= a(\xi \cdot \eta )\), with \(a(t)=t^2\), that
This tends to \(\frac{1}{2}\) as \(k\rightarrow \infty \). On the other hand, by (5.3),
This completes the proof. \(\square \)
A similar phenomenon holds for \(S_\xi ^{(n)}\).
Lemma 5.4
Let \(d=3\). There exists an observable a such that
Proof
Our arguments in Lemma 5.2 show that
Choosing again \(d=3\) and \(a(\eta ) = a(\xi \cdot \eta )\) for \(a(t) = t^2\), this becomes
But the expression in parentheses is
and \(\frac{2k^2+2k-1}{4k^2+4k-3} \ge \frac{1}{2}\) for \(k\ge 1\). Thus, as \(\mu _{n,0,3}=1\), the limit is
since \(M_{n,3} = \sum _{k=0}^n \mu _{n,k,3}^2\frac{N_{k,3}}{|\mathbb {S}^2|}\ge \frac{1}{4\pi }\sum _{k=0}^n \mu _{n,k,3}^2 \asymp \sqrt{n}\rightarrow \infty \) as we saw in Lemma 5.2. Summarizing, we have shown that
In view of (5.4), this completes the proof. \(\square \)
The results of this section suggest that unitary evolution of the Laplacian on the sphere does not make point masses equidistributed as time goes on, hence a lack of ergodicity. This is in accord with the classical picture.
Still, our analysis is based on the evolution of some specific normalized \(\delta \)-sequence \(S_\xi ^{(n)}\). It would be interesting to see if equidistribution continues to be violated for other choices.
Notes
Still, we can take the two limits simultaneously to infinity in a certain regime. See Remark 2.1.
One interpretation is that in semiclassical analysis, one considers evolutions of \(-h^2\Delta \) instead, with \(h\rightarrow 0\), so in this sense, we do study long times.
In [13, Lemma C.2] it is assumed the sum takes the form \(\Gamma (n) = \sum _{j=1}^t c_j \textrm{e}^{2\pi \textrm{i}n \theta _j}\) for some distinct \(\theta _j\in [0,1)\). In our case, for \(N>4\), \(|4\sin \frac{\pi }{N}|<\pi \), so \(\vartheta _j:= \frac{-4\sin \frac{\pi }{N}(2j+1)\sin \frac{\pi }{N}}{2\pi }\in (-\frac{1}{2},\frac{1}{2})\). If \(N_1>1\) is the number of distinct \(\vartheta _j\), then we may rearrange our sum as \(\frac{\textrm{e}^{\frac{2\pi \textrm{i}v}{N}}}{N}\sum _{\ell =1}^{N_1} c_\ell \textrm{e}^{2\pi \textrm{i}n\vartheta _\ell }\) and the proof is the same.
References
Ambainis, A., Bach, E., Nayak, A., Vishwanath, A., Watrous, J.: One-dimensional quantum walks, In: Proceedings of the Thirty-Third Annual ACM Symposium on Theory of Computing (2001), 37–49
Anantharaman, N., Le Masson, E.: Quantum ergodicity on large regular graphs. Duke Math. J. 164, 723–765 (2015)
Anantharaman, N.: Quantum ergodicity on regular graphs. Comm. Math. Phys. 353, 633–690 (2017)
Anantharaman, N., Macià, F.: Semiclassical measures for the Schrödinger equation on the torus. J. Eur. Math. Soc. 16(6), 1253–1288 (2014)
Anantharaman, N., Rivière, G.: Dispersion and controllability for the Schrödinger equation on negatively curved manifolds. Anal. PDE 5, 313–338 (2012)
Anantharaman, N., Sabri, M.: Quantum ergodicity on graphs: from spectral to spatial delocalization. Ann. Math. 189, 753–835 (2019)
Atkinson, K., Han, W.: Spherical harmonics and approximations on the unit sphere: an introduction, LNM vol. 2044, Springer (2012)
Boutet de Monvel, A., Sabri, M.: Ballistic transport in periodic and random media. In: “From Complex Analysis to Operator Theory: A Panorama, In Memory of Sergey Naboko”. Oper. Theory Adv. Appl. 291, 163–216 (2023)
Chakraborty, S., Luh, K., Roland, J.: How fast do quantum walks mix? Phys. Rev. Lett. 124, 050501 (2020)
Cipolloni, G., Erdös, L., Schröder, D.: Rank-uniform local law for Wigner matrices. Forum Math. Sigma 10(e96), 43 (2022)
Colin de Verdière, Y.: Ergodicité et fonctions propres du laplacien. Comm. Math. Phys. 102, 497–502 (1985)
Dhamapurkar, S., Dahlsten, O.: Quantum walks as thermalizations, with application to fullerene graphs, arXiv:2304.01572
Klein, A.: Spreading of wave packets in the anderson model on the bethe lattice. Commun. Math. Phys. 177, 755–773 (1996)
Han, X.: Small scale quantum ergodicity on negatively curved manifolds. Nonlinearity 28, 3263–3288 (2015)
Hezari, H., Rivière, G.: \(L^p\) norms, nodal sets, and quantum ergodicity. Adv. Math. 290, 938–966 (2016)
Hiary, G.A.: A nearly-optimal method to compute the truncated theta function, its derivatives, and integrals. Ann. of Math. 174, 859–889 (2011)
Kargin, V.: Bounds for mixing time of quantum walks on finite graphs. J. Phys. A: Math. Theor. 43, 335302 (2010)
Klenke A.: Probability Theory. A Comprehensive Course, Third Edition, Springer (2020)
Klimek, S., Kondracki, W.: Ergodic properties of the quantum geodesic flow on tori. Math. Phys. Anal. Geom. 8, 173–186 (2005)
Kuznetsov, A.: Computing the truncated theta function via Mordell integral. Math. Comput. 84, 2911–2926 (2015)
Landau, L.J.: Bessel functions: monotonicity and bounds. J. London Math. Soc. 61, 197–215 (2000)
Macià, F.: Semiclassical measures and the Schrödinger flow on Riemannian manifolds. Nonlinearity 22, 1003–1020 (2009)
Macià, F.: High-frequency propagation for the Schrödinger equation on the torus. J. Funct. Anal. 258, 933–955 (2010)
Macià, F., Rivière, G.: Concentration and non-concentration for the Schrödinger evolution on Zoll manifolds. Comm. Math. Phys. 345, 1019–1054 (2016)
Magee, M., Thomas, J., Zhao, Y.: Quantum unique ergodicity for Cayley graphs of quasirandom groups. Comm. Math. Phys. 402, 3021–3044 (2023)
Mandal, A., Sarkar, R.S., Adhikari, B.: Localization of two dimensional quantum walks defined by generalized Grover coins. J. Phys. A: Math. Theor. 56, 025303 (2023)
Marklof, J., Rudnik, Z.: Almost all eigenfunctions of a rational polygon are uniformly distributed. J. Spectr. Theory 2, 107–113 (2012)
McKenzie, T., Sabri, M.: Quantum ergodicity for periodic graphs. Comm. Math. Phys. 403, 1477–1509 (2023)
Naor, A., Sah, A., Sawhney, M., Zhao, Y.: Cayley graphs that have a quantum ergodic eigenbasis. Israel J. Math. 256, 599–617 (2023)
Portugal, R.: Quantum Walks and Search Algorithms, Second Edition, Springer (2018)
Sabri, M., Youssef, P.: Flat bands of periodic graphs. J. Math. Phys. 64, 092101 (2023)
Schubert, R.: Semiclassical behaviour of expectation values in time evolved lagrangian states for large times. Commun. Math. Phys. 256, 239–254 (2005)
Shiraishi, N., Tasaki H.: Nature abhors a vacuum. A simple rigorous example of thermalization in an isolated macroscopic quantum system, arXiv:2310.18880
Šnirel’man, A.I.: Ergodic properties of eigenfunctions. Uspehi Mat. Nauk 29, 181–182 (1974)
Stefanov, A., Kevrekidis, P.G.: Asymptotic behaviour of small solutions for the discrete nonlinear Schrödinger and Klein-Gordon equations. Nonlinearity 18, 1841–1857 (2005)
Szegö, G.: Orthogonal Polynomials, AMS Colloquium Publications vol. XXIII, (1939)
VanderKam, J.M.: \(L^\infty \) norms and quantum ergodicity on the sphere. Internat. Math. Res. Notices 7, 329–347 (1997)
Zelditch, S.: Uniform distribution of eigenfunctions on compact hyperbolic surfaces. Duke Math. J. 55, 919–941 (1987)
Zelditch, S.: Quantum ergodicity on the sphere. Comm. Math. Phys. 146, 61–71 (1992)
Acknowledgements
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Alain Joye.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Discussion
Discussion
1.1 Eigenfunction Thermalization
One could heuristically deduce the present dynamical criterion of ergodicity using quantum ergodicity of eigenvectors as follows. Suppose that \(H_N\) is a self-adjoint operator on a finite graph \(G_N\) of order N having a quantum ergodic basis \((\psi _j^{(N)})\). Fix a normalized initial state \(\phi \), assume for simplicity that it is well-defined as N varies (e.g., \(G_N\subset G_{N+1}\) or \(G_{N+1}\) is a cover of \(G_N\)). Expanding \(\phi = \sum _{k=1}^N \langle \psi _k^{(N)},\phi \rangle \psi _k^{(N)}\), so that \(\textrm{e}^{-\textrm{i}t H_N} \phi = \sum _{k=1}^N \langle \psi _k^{(N)},\phi \rangle \textrm{e}^{-\textrm{i}t\lambda _k^{(N)}}\psi _k^{(N)}\), we obtain
From here one could argue that \(\langle \psi _m^{(N)}, a\psi _n^{(N)}\rangle \approx \delta _{m,n}\langle a\rangle \) if the eigenfunctions satisfy a strong form of quantum ergodicity. If not, one could take a time average \(\frac{1}{T}\int _0^T\) and assume the spectrum is simple, so that the double sum of oscillatory terms vanishes as \(T\rightarrow \infty \). Since \(\sum _{n=1}^N |\langle \psi _n^{(N)},\phi \rangle |^2 \langle \psi _n^{(N)}, a_N\psi _n^{(N)}\rangle \approx \sum _{n=1}^N |\langle \psi _n^{(N)},\phi \rangle |^2\langle a_N\rangle = \langle a_N\rangle \Vert \phi \Vert ^2=\langle a_N\rangle \) by the assumed eigenfunction ergodicity, we get that \(\langle \textrm{e}^{-\textrm{i}t H_N}\phi , a_N \textrm{e}^{-\textrm{i}tH_N}\phi \rangle \approx \langle a_N\rangle \) or \(\lim _{T\rightarrow \infty }\frac{1}{T}\int _0^T \langle \textrm{e}^{-\textrm{i}t H_N}\phi , a_N \textrm{e}^{-\textrm{i}tH_N}\phi \rangle \,\textrm{d}t \approx \langle a_N\rangle \), respectively. The same heuristic can be used in the continuum, for example, on the torus.
This heuristic is folklore in the physics community and is commonly known as eigenfunction thermalization. It can be made rigorous for some models of random matrices, see, for example, the discussion in [10]. Note that it only requires one special basis of eigenfunctions \((\psi _j^{(N)})\) to be ergodic in a strong sense, e.g., quantum uniquely ergodic. For specific (deterministic) graphs it seems to us that making this argument rigorous can be more difficult than proving the theorem from scratch. In particular, for the case of \(\mathbb {Z}^d\), the eigenvalues have a high multiplicity, which complicates this scheme even though we have a very nice ergodic basis \(\psi _j^{(N)}(n) = \frac{1}{N^{d/2}} \textrm{e}^{2\pi \textrm{i}j\cdot n/N}\) at disposal. Also note that on the torus, this conclusion is simply wrong if we choose \(\phi (x)=\sqrt{2}\cos (2\pi x)\) since \(\textrm{e}^{\textrm{i}t\Delta }\phi = \textrm{e}^{-4\pi ^2 \textrm{i}t}\phi \), so at least in this model where the spectrum is highly degenerate, there must be some assumption on \(\phi \).
1.2 Other Interpretations
It may be interesting to explore other quantum dynamical interpretations of ergodicity.
Since in the classical picture on the torus, we calculate the mean value \(\frac{1}{T}\int _0^T a(x_0+ty_0)\,\textrm{d}t\) of an observable a over an orbit of \(x_0\), one could naively replace a(y) by \(\langle \delta _y, a\rangle \) and thus consider the limit of \(\frac{1}{T}\int _0^T \langle \textrm{e}^{\textrm{i}t\Delta }\delta _y,a\rangle \,\textrm{d}t\) and see if it approaches \(\int a(x)\,\textrm{d}x\). Let us check what this gives.
Let H be a self-adjoint operator on a Hilbert space \(\mathscr {H}\) and let \(\phi ,\psi \in \mathscr {H}\). Then, by the functional calculus we have
This interpretation would rely entirely on the spectral projection at 0. It does not seem entirely convincing. For example, both the torus and sphere Laplacian satisfy that \(\chi _{\{0\}}(-\Delta )\) is the orthogonal projection onto the flat function, that is, \((\chi _{\{0\}}(-\Delta _{\mathbb {T}_*^d})a)(y) = \int _{\mathbb {T}_*^d} a(x)\,\textrm{d}x\) and \((\chi _{\{0\}}(-\Delta _{\mathbb {S}^{d-1}})a)(y) = \frac{1}{|\mathbb {S}^{d-1}|}\int _{\mathbb {S}^{d-1}} a(x)\,\textrm{d}S^{d-1}(x)\), so that the RHS of (A.1) in both cases is \(\langle \phi \rangle \langle \psi \rangle \), although the dynamics are very different in each case.
1.3 Further Comments
In general, ergodic theorems apply to integrable functions f and assert that \(\lim _{n\rightarrow \infty }\frac{1}{n}\sum _{k=1}^n f(T^k x) = g(x)\), where g is such that \(\int g = \int f\). If T is ergodic, then g must be constant, and this constant is \(\frac{1}{\mu (\Omega )} \int _{\Omega } f(y)\,\textrm{d}\mu (y)\).
On the quantum side, the long-time convergence of \(\frac{1}{T}\int _{0}^T |(\textrm{e}^{\textrm{i}tH}\psi )(x)|^2\) is quite trivial if \(\mathscr {H}\) is finite dimensional (e.g., working on a finite graph). In fact, if \(P_k\) are the spectral projections for the distinct eigenvalues of H, then
Since \(\frac{1}{T}\int _0^T \textrm{e}^{\textrm{i}t(E_k-E_\ell )}\,\textrm{d}t = \frac{1}{\textrm{i}T}\cdot \frac{\textrm{e}^{\textrm{i}T(E_k-E_\ell )}-1}{E_k-E_\ell } \rightarrow 0\), we get that
The function on the RHS clearly satisfies that its integral (or its sum over the graph) is equal to \(\psi \). So the hard part here is to prove ergodicity rather than convergence, i.e., proving that for certain models the RHS is constant. This is what we did for the case of cubes, asymptotically in N. We do not use (A.2) for this purpose, as the high multiplicity of eigenvalues complicates the calculation of \(P_k\psi \). We emphasize that for the torus, we do not need to consider long time T, so (A.2) is useless.
In the context of quantum walks, the papers [9, 17] investigate the mixing time, namely, how fast does \(\frac{1}{T}\int _0^{T} |(\textrm{e}^{\textrm{i}tH}\psi )(x)|^2\,\textrm{d}t\) becomes \(\epsilon \)-close to its limit \(\sum _{k=1}^m |(P_k\psi )(x)|^2\).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Boutet de Monvel, A., Sabri, M. Ergodic Theorems for Continuous-Time Quantum Walks on Crystal Lattices and the Torus. Ann. Henri Poincaré (2024). https://doi.org/10.1007/s00023-024-01470-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00023-024-01470-x