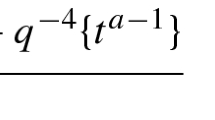1 Introduction

This paper is to be situated in the framework of classical harmonic analysis, a function theory focusing on the Laplace operator \(\Delta _x = \sum _j \partial _{x_j}^2\) acting on scalar-valued functions \(f(\underline{x})\) on \(\mathbb {R}^m\). Null solutions for \(\Delta _x\) in the polynomial ring \(\mathcal {P}(\mathbb {R}^m,\mathbb {R}):= \mathbb {R}[x_1,\ldots ,x_m]\) are referred to as harmonic polynomials, their restrictions to the sphere \(S^{m-1} \subset \mathbb {R}^m\) are spherical harmonics: these are often indexed by a positive integer \(\ell \in \mathbb {Z}^+\) which then refers to the degree of homogeneity of the harmonic polynomial it uniquely extends to. From a purely algebraic point of view, the operator \(\Delta _x\) arises naturally if one wants to understand the behaviour of the space \(\mathcal {P}(\mathbb {R}^m,\mathbb {R})\) as a representation for the (special) orthogonal group SO(m), under the regular action. It is well-known that under this action, one has that

$$\begin{aligned} \mathcal {P}(\mathbb {R}^m,\mathbb {R}) = \bigoplus _{k = 0}^\infty \mathcal {P}_k(\mathbb {R}^m,\mathbb {R}) = \bigoplus _{k = 0}^\infty \bigoplus _{j = 0}^{\lfloor \frac{k}{2} \rfloor }r^{2j}\mathcal {H}_{k - 2j}(\mathbb {R}^m,\mathbb {R})\, \end{aligned}$$
(1.1)

where \(\mathcal {H} = \mathcal {P} \cap \ker \Delta _x\) and \(r^2 = x_1^2 + \ldots + x_m^2\) denotes the squared norm of the vector \(\underline{x}\in \mathbb {R}^m\). Here, the spaces \(\mathcal {H}_k\) of k-homogeneous harmonic polynomials define an irreducible module for SO(m) with highest weight \((k,0,\ldots ,0)\).

A crucial observation which can be made here is that the Lie algebra spanned by \(\Delta _x\) and \(r^2\), seen as a subalgebra of the Weyl algebra \(\mathcal {W}(\mathbb {R}^m)\) acting on the space \(\mathcal {P}(\mathbb {R}^m,\mathbb {R})\), is given by

$$\begin{aligned} \mathfrak {sl}(2)&= Alg (X,Y,H) \cong Alg \left( \frac{1}{2}r^2,-\frac{1}{2}\Delta _x,\mathbb {E}_x + \frac{m}{2}\right) \, \end{aligned}$$
(1.2)

with \(\mathbb {E}_x = \sum _j x_j\partial _{x_j}\) the so-called Euler operator (which acts as a constant k on homogeneous polynomials of degree k). This had led to the celebrated Howe duality theorem, which in this particular case allows to turn formula (1.1) into a decomposition which is multiplicity-free (see for instance [6, 8]). There are several ways in which the theory of spherical harmonics can be generalised, but the topic of this paper is based on the observation that the function space \(\mathcal {P}(\mathbb {R}^m,\mathbb {R})\) can be seen as the homogeneous coordinate ring for the projective space \(\mathbb {P}^{m-1}\) of lines through the origin in \(\mathbb {R}^m\). Since this is merely the simplest example of a flag manifold, the extension to other Grassmann varieties is an obvious generalisation. In the present paper, we will therefore consider the (oriented) Grassmannian of 2-planes in \(\mathbb {R}^m\): this (projective) variety also has a homogeneous coordinate ring, which defines a module for a suitable action of GL(m) that can thus be decomposed into irreducible representations for the (special) orthogonal group SO(m). Howe and Lee observed that the summands in this decomposition can be defined in terms of a differential operator which generalises the role of the operator \(\Delta _x\) in the classical case. This operator is sometimes referred to as the Cayley-Laplace operator, and also appears for instance in the work of Khelako [10] and Rubin [13].

In [9] the authors studied the (polynomial) solution spaces for this Cayley–Laplace operator on spaces of k-planes in \(\mathbb {R}^m\), using the general language of representation theory, and in [2] we focused on the special case \(k = 2\) to obtain a generalisation of the Howe duality mentioned above. It was observed that the Higgs algebra \(H_3\) (a polynomial deformation of the Lie algebra \(\mathfrak {su}(2)\), see [7, 15]) arises as a dual partner defined in terms of the Cayley-Laplace operator. As an application, a Pizzetti formula for the integral of a function over the Grassmannian \(\text {Gr}_+(m,2)\) was obtained.

In the present paper we will shift our attention to the reproducing kernels for these spaces of wedge polynomials (the homogeneous subspaces of the homogeneous coordinate ring mentioned above), and show how these kernels will give rise to a special function which somehow generalises the role played by the exponential function in classical harmonic analysis. This then leads to so-called wedge binomial polynomials, which are related to a generalisation of Pascal’s triangle known as the Narayana triangle, and a generating function for the zonal solutions for the Cayley-Laplace operator.

2 The Cayley–Laplace Operator

The Cayley–Laplace operator (abbreviated as CL-operator from now on) is defined on functions which satisfy a special symmetry requirement. In order to explain what we mean by this, we first recall the fact that the homogeneous coordinate ring of the oriented real Grassmannian \(Gr _+(m,2)\) can be identified with a polynomial algebra (see for instance [4, 14]):

$$\begin{aligned} \mathcal {R}(Gr _+(m,2)) = \mathcal {P}(\mathbb {R}^{m \times 2},\mathbb {R})^{SL (2)}\, \end{aligned}$$
(2.1)

whereby the action of \(h \in SL (2)\) is defined as the (right) regular H-action on polynomials in a matrix variable \(X:= (\underline{x},\underline{u}) \in \mathbb {R}^{m \times 2}\), given by

$$\begin{aligned} H (h)[P(\underline{x},\underline{u})] := P((\underline{x},\underline{u})h)\ . \end{aligned}$$

The invariance under SL(2), which is what the upper index notation refers to in (2.1), can more conveniently be expressed in terms of the corresponding derived action \(dH \). This action gives then rise to a realisation of the Lie algebra \(\mathfrak {sl}(2)\) in terms of the so-called ‘skew Euler operators’

$$\begin{aligned} \langle \underline{x},\underline{\partial }_{u} \rangle := \sum _{j = 1}^m x_{j}\partial _{u_j} \quad \text{ and } \quad \langle \underline{u},\underline{\partial }_x \rangle := \sum _{j = 1}^m u_{j}\partial _{x_j} \end{aligned}$$
(2.2)

defined as a contraction between a vector variable and a Dirac operator (or a gradient operator). To be precise, one then has that

$$\begin{aligned} \mathcal {R}(Gr _+(m,2)) = \big \{P(X) \in \mathcal {P}(\mathbb {R}^{m \times 2},\mathbb {R}): \langle \underline{x},\underline{\partial }_u \rangle P = 0 = \langle \underline{u},\underline{\partial }_x \rangle P\big \}\, \end{aligned}$$
(2.3)

whereby the notation \(X = (\underline{x},\underline{u})\) will sometimes be used in this paper to denote the matrix variable in \(\mathbb {R}^{m \times 2}\). This means that that we are dealing with polynomials depending on the components of the wedge variable \(\underline{x}\wedge \underline{u}\), just like a function \(f(\underline{x})\) depends on the scalar components \(x_j\). For a wedge variable, these are the scalar variables \(X_{ab}:= x_au_b - x_bu_a\) with \(1 \le a < b \le m\). Note that these variables are not independent (which makes them different from the classical case \(k = 1\)), since there are Plücker relations to be satisfied. In other words, one can also say that

$$\begin{aligned} \mathcal {R}(Gr _+(m,2)) = \mathbb {R}[X_{12},X_{13},\cdots ,X_{m-1,m}]/\mathfrak {I} \end{aligned}$$

with \(\mathfrak {I}\) the 2-sided ideal generated by \(X_{ab}X_{cd} - X_{ac}X_{bd} + X_{ad}X_{bc}\). Finally, the CL-operator can then be defined as the orthogonally invariant operator of order 4 acting on \(P(X) \in \mathcal {R}(Gr _+(m,2))\), and is explicitly given by

$$\begin{aligned} \Delta _{xu} := \sum _{a< b}\partial _{ab}^2 = \sum _{a < b}\big (\partial _{x_a}\partial _{u_b} - \partial _{x_b}\partial _{u_a}\big )^2 = \Delta _x\Delta _u - \langle \underline{\partial }_x,\underline{\partial }_u \rangle ^2\ . \end{aligned}$$

Put differently, this is a determinant operator in terms of all the possible ‘mixed Laplace operators’ obtained by contracting two Dirac operators (this gives a standard Laplace operator when an operator is contracted with itself). This operator \(\Delta _{xu}\) was observed to realise a copy of the Higgs algebra in [2]. Note that we can refer to this operator as the invariant operator, since it is unique in the following sense:

Lemma 2.1

The space \(span (\Delta _x, \Delta _u, \langle \underline{\partial }_{x},\underline{\partial }_{u} \rangle )\) of mixed Laplace operators on \(\mathbb {R}^{m \times 2}\) realises the irreducible representation space \(Sym ^2(\mathbb {R}^2)\) for \(\mathfrak {sl}(2)\) in terms of the skew Euler operators. Moreover, the CL-operator \(\Delta _{xu}\) then realises the unique trivial summand \(\mathbb {R}\) inside the 2-fold tensor product of this irreducible representation space with itself.

Proof

This statement follows from the Clebsch–Gordon rule for the tensor decomposition of irreducible representations (irreps) for \(\mathfrak {sl}(2)\), hereby taking into account that the space spanned by the mixed Laplace operators realises the irrep \(\mathbb {V}_2\) with highest weight 2 (a space of dimension 3). A straightforward calculation indeed shows that the unique summand \(\mathbb {V}_0 \subset \mathbb {V}_2 \otimes \mathbb {V}_2\) is given by the operator \(\Delta _{xu}\), up to a multiplicative constant. \(\square \)

In a way, the symbols \(X_{ab}\) and \(\partial _{ab}\) generalise the role played by \(x_i\) and \(\partial _{x_j}\) in the classical case (for \(k = 1\), i.e. classical harmonic analysis). However, whereas the algebra generated by \(x_i\) and \(\partial _{x_j}\) is the Heisenberg algebra (with the Weyl algebra as its universal enveloping algebra), we get a completely different algebraic structure for wedge variables. In the following lemma we specify this algebra:

Lemma 2.2

The Lie algebra generated by the skew variables \(X_{ab}\) and their corresponding derivatives \(\partial _{ab}\) (with \(1 \le a < b \le m\)) is a graded Lie algebra \(\mathfrak {g} = \mathfrak {g}_{-2} \oplus \mathfrak {g}_0 \oplus \mathfrak {g}_{+2}\) with

$$\begin{aligned} \mathfrak {g}_{+2}&= span \big (X_{ab} : 1 \le a< b \le m\big ) \cong \Lambda ^2 \mathbb {R}^m \\ \mathfrak {g}_{-2}&= span \big (\partial _{ab} : 1 \le a < b \le m\big ) \cong \Lambda ^2\mathbb {R}^m \end{aligned}$$

two abelian subalgebras, for which \([\mathfrak {g}_{-2},\mathfrak {g}_{+2}] \subset \mathfrak {g}_0\). Here, the zero-graded part is given by \(\mathfrak {g}_0 \cong \mathfrak {gl}(m)\), which means that \([\mathfrak {g}_0,\mathfrak {g}_{\pm 2}] \subset \mathfrak {g}_{\pm 2}\). Moreover, the subalgebra \(\mathfrak {g}_0\) contains a copy of \(\mathbb {R}\) which then serves as the centre of \(\mathfrak {gl}(m)\), realised in terms of the grading element \(Z = \mathbb {E}_{x} + \mathbb {E}_{u} + m\). Finally, defining for all \(1 \le a < b \le m\) the operator \(\mathbb {E}_{ab}:= x_{a}\partial _{x_{a}} + x_{b}\partial _{x_{b}} + u_{a}\partial _{u_{a}} + u_{b}\partial _{u_{b}}\), we also note that

$$\begin{aligned} Alg \big (X_{ab},-\partial _{ab},\mathbb {E}_{ab} + 2\big ) \cong \mathfrak {sl}(2). \end{aligned}$$

Proof

To prove this, one can start from an arbitrary \(X_{ab}\) and \(\partial _{pq}\), for which the commutator reduces to 1 of 3 possibilities depending on the size of the set \(\{a,b\} \cap \{p,q\}\). When \(\{a,b\} = \{p,q\}\), an easy calculation confirms that we will indeed get a realisation for the Lie algebra \(\mathfrak {sl}(2)\). When \(\{a,b\}\) and \(\{p,q\}\) have just one index in common (w.l.o.g. we can then put \(b = p\)), a quick calculation reveals that \([X_{ap},\partial _{pq}] = x_{a}\partial _{x_{q}} + u_{a}\partial _{u_{q}}\), with \(a \ne q\). The only thing left to verify is that the resulting operators give rise to a copy of the Lie algebra \(\mathfrak {gl}(m)\), which is a matter of straight-forward calculations (the operator \(x_{a}\partial _{x_{q}} + u_{a}\partial _{u_{q}}\) hereby corresponds to the matrix with a single entry on row a and column q in the classical matrix realisation). The central grading element is (up to a scalar factor) equal to the sum of all the ‘diagonal’ elements \(\mathbb {E}_{ab}\). \(\square \)

The last statement in the previous lemma will come in handy later, since it allows us to reduce calculations in the coordinate ring as algebraic identities in the universal enveloping algebra \(\mathcal {U}(\mathfrak {sl}(2))\).

3 Reproducing Series Operators

In order to understand how one can generalise the role played by the standard exponential function in classical harmonic analysis when switching to wedge variables, we will start from the following well-known fact:

Definition 3.1

For all positive integers \(\ell \), the reproducing kernel for the vector space \(\mathcal {P}_\ell (\mathbb {R}^m,\mathbb {R})\) of \(\ell \)-homogeneous polynomials in a vector variable \(\underline{x}\in \mathbb {R}^m\) is given by \(Z_\ell (\underline{x},\underline{y}) = \frac{1}{\ell !}\langle \underline{x},\underline{y}\rangle ^\ell \). This kernel acts as follows:

$$\begin{aligned} \big \langle Z_\ell (\underline{x},\underline{y}) , P_\ell (\underline{x}) \big \rangle _F = \frac{1}{\ell !}\langle \underline{y},\underline{\partial }_x \rangle ^\ell P_\ell (\underline{x})\bigg \vert _{x = 0} = P_\ell (\underline{y})\ . \end{aligned}$$

The notation \(\langle \cdot ,\cdot \rangle _F\) hereby refers to the Fischer inner product (replacing each variable \(x_j\) by its corresponding partial derivative \(\partial _{x_j}\), and evaluating the action of the resulting operator on \(P_\ell (\underline{x})\) in \(\underline{x}= \underline{0}\)).

If we were to add all these kernels (leading to a formal series), and get rid of the ‘evaluation in zero’ which characterises the final step in the definition of the Fischer inner product, we arrive at the following exponential function:

$$\begin{aligned} \sum _{\ell = 0}^\infty Z_\ell (\underline{x},\underline{y}) = \sum _{\ell = 0}^\infty \frac{1}{\ell !}\langle \underline{x},\underline{y}\rangle ^\ell = \exp \big (\langle \underline{x},\underline{y}\rangle \big )\ . \end{aligned}$$

This operator has a few interesting properties, which will be listed here.

Theorem 3.2

The action of the operator \(\exp (\langle \underline{y},\underline{\partial }_x \rangle )\) on functions \(f(\underline{x})\) on \(\mathbb {R}^m\) intertwines the action of the Laplace operator:

$$\begin{aligned} \Delta _y \exp \big (\langle \underline{y},\underline{\partial }_x \rangle \big )f(\underline{x}) = \exp \big (\langle \underline{y},\underline{\partial }_x \rangle \big ) \Delta _x f(\underline{x})\ . \end{aligned}$$

Proof

This can be shown by first expanding the exponential operator into a formal series, and then letting the operator \(\Delta _y\) act on the variable \(\underline{y}\in \mathbb {R}^m\), hereby using the fact that

$$\begin{aligned} \Delta _y \langle \underline{y},\underline{\partial }_x \rangle ^\ell = \ell (\ell -1)\langle \underline{y},\underline{\partial }_x \rangle ^{\ell -2}\Delta _x\ . \end{aligned}$$

Relabeling the terms in the series then does the rest. \(\square \)

What this theorem says, is that one can use the exponential operator to obtain functions depending on two vector variables, in such a way that harmonics will be sent to harmonics. Moreover, the result is symmetric in the following sense:

Theorem 3.3

The action of \(\exp \big (\langle \underline{y},\underline{\partial }_x \rangle \big )\) on a polynomial \(P_\ell (\underline{x}) \in \mathcal {P}_\ell (\mathbb {R}^m,\mathbb {R})\) is symmetric in \(\underline{x}\leftrightarrow \underline{y}\), in the sense that

$$\begin{aligned} \exp \big (\langle \underline{y},\underline{\partial }_x \rangle \big )P_\ell (\underline{x}) = Q_\ell (\underline{x},\underline{y}) = Q_\ell (\underline{y},\underline{x}) = \exp \big (\langle \underline{x},\underline{\partial }_y \rangle \big )P_\ell (\underline{y})\ . \end{aligned}$$

Note that \(Q_\ell (\underline{x},\underline{y})\) is a polynomial in two vector variables which has a total degree of homogeneity equal to \(\ell \).

Proof

This result follows immediately from the fact that the exponential operator \(\exp (\langle \underline{y},\underline{\partial }_x \rangle )\) generates translations. \(\square \)

The main idea behind the paper is the following: one can look at the spaces of \(\ell \)-homogeneous polynomials in a wedge variable \(X_{ab}\) and construct the corresponding reproducing kernel for the Fischer inner product. First of all, we note the following:

Definition 3.4

For all positive integers \(\ell \), we define the space \(\mathcal {P}^S_\ell (\mathbb {R}^{m \times 2},\mathbb {R})\) as the space of \(\ell \)-homogeneous polynomials in the wedge variables \(X_{ab}\). Note that \(\ell \) refers to the degree in both \(\underline{x}\) and \(\underline{u}\in \mathbb {R}^m\) (or, put differently, the total degree of this polynomial is equal to \(2\ell \) when looking at the degree in \(x_j\) and \(u_j\) separately), and that the superscript ‘S’ refers to the invariance for SL(2).

In view of the fact that \(\mathcal {P}_\ell ^S(\mathbb {R}^{m \times 2},\mathbb {R}) \subset \mathcal {P}_\ell (\mathbb {R}^{m},\mathbb {R}) \otimes \mathcal {P}_\ell (\mathbb {R}^{m},\mathbb {R})\), we can start from two reproducing kernels \(Z_\ell (\underline{x},\underline{y})\) and \(Z_\ell (\underline{u},\underline{v})\) to construct a reproducing kernel (for the Fischer inner product) for the space defined above.

Lemma 3.5

The reproducing kernel for \(\mathcal {P}^S_\ell (\mathbb {R}^{m \times 2},\mathbb {R})\) is given by

$$\begin{aligned} \mathcal {Z}_\ell (\underline{x}\wedge \underline{u},\underline{y}\wedge \underline{v}) := \frac{\langle \underline{x}\wedge \underline{u},\underline{y}\wedge \underline{v}\rangle ^\ell }{\ell !(\ell +1)!}\ , \end{aligned}$$

whereby the inner product between wedge products is defined as

$$\begin{aligned} \langle \underline{x}\wedge \underline{u},\underline{y}\wedge \underline{v}\rangle&= \left| \begin{array}{cc} \langle \underline{x},\underline{y}\rangle & \langle \underline{x},\underline{v}\rangle \\ \langle \underline{u},\underline{y}\rangle & \langle \underline{u},\underline{v}\rangle \end{array}\right| \ . \end{aligned}$$

Proof

First note that there are two natural realisations of the 2-dimensional representation \(\mathbb {V}_1\) for \(\mathfrak {sl}(2)\) at play here: the space spanned by \(\langle \underline{x},\underline{y}\rangle \) and \(\langle \underline{u},\underline{y}\rangle \) on the one hand, and the space spanned by \(\langle \underline{x},\underline{v}\rangle \) and \(\langle \underline{u},\underline{v}\rangle \) on the other hand. To see why this is true, it suffices to recall the fact that \(\langle \underline{x},\underline{\partial }_u \rangle \) and \(\langle \underline{u},\underline{\partial }_x \rangle \) generate a copy of \(\mathfrak {sl}(2)\). This means that \(Z_\ell (\underline{x},\underline{y})\) and \(Z_\ell (\underline{u},\underline{v})\) belong to the space \(\mathbb {V}_\ell \) (the irrep of dimension \(\ell +1\)). Because we are letting the product of these kernels act on polynomials of wedge variables, which are invariant with respect to \(\mathfrak {sl}(2)\), it thus suffices to project \(Z_\ell (\underline{x},\underline{y})Z_\ell (\underline{u},\underline{v})\), considered as an element of the representation space \(\mathbb {V}_\ell \otimes \mathbb {V}_\ell \), on the unique summand \(\mathbb {V}_0\) sitting inside this tensor product. This can be done using the Clebsch–Gordon rules, or see Lemma 5 in [2] for a similar calculation. \(\square \)

Once this kernel has been found, we can again consider the (formal) series obtained by summing these kernels over all indices \(\ell \in \mathbb {Z}^+\). This gives rise to the generalised exponential operator in the setting of two-wedge variables. Note that we can make use of the following:

Definition 3.6

The Bessel–Clifford function \(\mathcal {C}_k(z)\) in a complex variable \(z \in \mathbb {C}\) is defined through its power series as

$$\begin{aligned} \mathcal {C}_k(z)&= \sum _{j = 0}^\infty \frac{1}{\Gamma (1 + k + j)}\frac{z^j}{j!}. \end{aligned}$$
(3.1)

Indeed, it is readily seen that in terms of this definition we have that

$$\begin{aligned} \sum _{\ell = 0}^\infty \mathcal {Z}_\ell (\underline{x}\wedge \underline{u},\underline{y}\wedge \underline{v})&= \sum _{\ell = 0}^\infty \frac{\langle \underline{x}\wedge \underline{u},\underline{y}\wedge \underline{v}\rangle ^\ell }{\ell !(\ell +1)!} = \mathcal {C}_1\big (\langle \underline{x}\wedge \underline{u},\underline{y}\wedge \underline{v}\rangle \big ). \end{aligned}$$
(3.2)

Remark 3.7

It is tempting to think that the classical exponential function corresponds to the function \(\mathcal {C}_0(z)\), which would indicate a clear pattern here, but this is not true. There is a more subtle pattern in play here, which becomes important when considering wedge variables for the Grassmannian \(\text {Gr}_+(m,k)\), but this will be treated in an upcoming paper.

Note that our function becomes a generalised translation operator under the following action (on functions which behave well, for instance \(\mathbb {R}\)-analytic in the scalar variables \(X_{ab}\)):

$$\begin{aligned} f(\underline{x}\wedge \underline{u}) \mapsto g(\underline{x}\wedge \underline{u};\underline{y}\wedge \underline{v}) := \mathcal {C}_1\big (\langle \underline{y}\wedge \underline{v},\underline{\partial }_x\wedge \underline{\partial }_u \rangle \big )f(\underline{x}\wedge \underline{u}) \ . \end{aligned}$$

It is however crucial to point out that this does not behave like a ‘standard translation’, in the sense that for instance

$$\begin{aligned} X_{ab}^2 \mapsto \left( 1 + \frac{1}{2}Y_{ab}\partial _{ab} + \frac{1}{12}Y_{ab}^2\partial _{ab}^2\right) X_{ab}^2 = X_{ab}^2 + 3X_{ab}Y_{ab} + Y_{ab}^2\ , \end{aligned}$$

where the factor 3 may be surprising. Indeed, note we do not get \((X_{ab} + Y_{ab})^2\) under the action of our Bessel-Clifford function, which may raise the question why the term ‘generalised translation operator’ is appropriate here. This is the reason why Theorems 3.2 and 3.3 were mentioned, since we can prove a similar result with respect to the CL-operator \(\Delta _{xy}\).

Theorem 3.8

The action of the generalised exponential function on functions \(f(\underline{x}\wedge \underline{u})\) on \(\mathbb {R}^{m \times 2}\) intertwines the action of the Cayley–Laplace operator:

$$\begin{aligned} \Delta _{yv} \mathcal {C}_1\big (\langle \underline{y}\wedge \underline{v},\underline{\partial }_x\wedge \underline{\partial }_u \rangle \big ) f(\underline{x}\wedge \underline{u}) = \mathcal {C}_1\big (\langle \underline{y}\wedge \underline{v},\underline{\partial }_x\wedge \underline{\partial }_u \rangle \big ) \Delta _{xu} f(\underline{x}\wedge \underline{u})\ . \end{aligned}$$

Proof

To see why this is true, we will invoke the invariance of inner products under rotations. Writing these as conjugations (i.e. using an element s of the spin group rather than a matrix M in the orthogonal group), we know that

$$\begin{aligned} \langle \underline{y}\wedge \underline{v},\underline{x}\wedge \underline{u}\rangle = \langle s(\underline{y}\wedge \underline{v})\overline{s},s(\underline{x}\wedge \underline{u})\overline{s} \rangle = \langle s\underline{y}\overline{s} \wedge s\underline{v}\overline{s},s\underline{x}\overline{s} \wedge s\underline{u}\overline{s} \rangle \ . \end{aligned}$$

Note that we have switched to variables \(X_{ab}\) instead of derivatives \(\partial _{ab}\) here, but this will not affect the argument (one merely has to switch to the Fourier image so to speak). Because rotations act transitively on two-frames, we can always find an element s such that \(s(\underline{x}\wedge \underline{u})\overline{s} = \lambda e_{12}\). The invariance of the inner product then tells us that \(\langle \underline{x}\wedge \underline{u},\underline{x}\wedge \underline{u}\rangle = |\underline{x}\wedge \underline{u}|^2 = \lambda ^2\), with \(\lambda \in \mathbb {R}\). If we now denote \(s\underline{y}\overline{s} \wedge s\underline{v}\overline{s}\) by means of \(\underline{y}^* \wedge \underline{v}^*\), we get:

$$\begin{aligned} \Delta _{yv}\langle \underline{y}\wedge \underline{v},\underline{x}\wedge \underline{u}\rangle ^k= & \lambda ^k\Delta ^*_{yv}(y_1^*v_2^* - y_2^*v_1^*)^k\nonumber \\= & [k(k+1)][(k-1)k]\lambda ^k(y_1^*v_2^* - y_2^*v_1^*)^{k-2}\, \end{aligned}$$
(3.3)

where we made use of the rotational invariance of the CL-operator (which allows us to say that \(\Delta _{yv} = \Delta _{yv}^*\)) and the fact that

$$\begin{aligned} \partial _{ab}X_{ab}^j = j(j+1)X_{ab}^{j-1}\ . \end{aligned}$$

This last relation either follows from direct calculations or from the fact that \(\partial _{ab}\) and \(X_{ab}\) realise a copy of the Lie algebra \(\mathfrak {sl}(2)\) which means that one can make use of commutator identities in the universal enveloping algebra for \(\mathfrak {sl}(2)\). It then suffices to ‘rotate back’, which means that

$$\begin{aligned} \lambda ^k(y_1^*v_2^* - y_2^*v_1^*)^{k-2}&= \lambda ^2\langle s\underline{y}\overline{s} \wedge s\underline{v}\overline{s},\lambda e_{12} \rangle ^{k-1} \\ &= |\underline{x}\wedge \underline{u}|^2 \langle \underline{y}\wedge \underline{v},\underline{x}\wedge \underline{u}\rangle ^{k-2}\ . \end{aligned}$$

Finally, the constant appearing in formula (3.3) allows us to reorder the summation index in the series representation for the Bessel–Clifford function, which concludes the proof. \(\square \)

This thus means that the generalised translation operator maps solutions for \(\Delta _{xy}\) to functions in the kernel of both \(\Delta _{yv}\) and \(\Delta _{xu}\). This already hints towards the fact that the function becomes symmetric under the operation \((\underline{x},\underline{u}) \leftrightarrow (\underline{y},\underline{v})\), and one can show that this is indeed the case.

Theorem 3.9

The action of the operator \(\mathcal {C}_1\big (\langle \underline{y}\wedge \underline{v},\underline{\partial }_x\wedge \underline{\partial }_u \rangle \big )\) on a polynomial \(P_\ell (\underline{x}\wedge \underline{u}) \in \mathcal {P}^S_\ell (\mathbb {R}^{m \times 2},\mathbb {R})\) is symmetric in \((\underline{x},\underline{u}) \leftrightarrow (\underline{y},\underline{v})\), in the sense that

$$\begin{aligned} \mathcal {C}_1\big (\langle \underline{y}\wedge \underline{v},\underline{\partial }_x\wedge \underline{\partial }_u \rangle \big )P_\ell (\underline{x}\wedge \underline{u}) = Q_\ell (\underline{x}\wedge \underline{u},\underline{y}\wedge \underline{v}) = Q_\ell (\underline{y}\wedge \underline{v},\underline{x}\wedge \underline{u})\ . \end{aligned}$$

Note that \(Q_\ell (\underline{x}\wedge \underline{u},\underline{y}\wedge \underline{v})\) is a polynomial in two wedge variables (i.e. four standard vector variables in \(\mathbb {R}^{m \times 4}\)) which has a total degree of homogeneity equal to \(\ell \) in the wedge variables.

Proof

To see why this is true, we will show that

$$\begin{aligned} \sum _{j = 0}^k \frac{\langle \underline{x}\wedge \underline{u},\underline{\partial }_y\wedge \underline{\partial }_v \rangle ^j}{j!(j+1)!}P_k(\underline{y}\wedge \underline{v}) = \sum _{j = 0}^k \frac{\langle \underline{y}\wedge \underline{v},\underline{\partial }_x\wedge \underline{\partial }_u \rangle ^j}{j!(j+1)!}P_k(\underline{x}\wedge \underline{u}). \end{aligned}$$
(3.4)

Now, in view of the fact that

$$\begin{aligned} P_k(\underline{x}\wedge \underline{u}) = \frac{\langle \underline{x}\wedge \underline{u},\underline{\partial }_y\wedge \underline{\partial }_v \rangle ^k}{k!(k+1)!}P_k(\underline{y}\wedge \underline{v}) \end{aligned}$$

we can rewrite Eq. (3.4) as a difference of two operators which should act trivially on an arbitrary \(P_k(\underline{y}\wedge \underline{v})\). Temporarily denoting \(\langle \underline{x}\wedge \underline{u},\underline{\partial }_y\wedge \underline{\partial }_v \rangle \) as \(D_{yv}\) (similarly for \(D_{xu}\)), we must thus have that

$$\begin{aligned} \left( \frac{D_{yv}^j}{j!(j+1)!} - \frac{D_{xu}^{k-j}}{(k-j)!(1+k-j)!}\frac{D_{yv}^k}{k!(k+1)!}\right) P_k(\underline{y}\wedge \underline{v}) = 0 \end{aligned}$$

for all \(0 \le j \le k\). For this to be true, it is sufficient to show that

$$\begin{aligned} D_{xu}D_{yv}^{k - a}P_k(\underline{y}\wedge \underline{v}) = (1 + a)(2+a)(k-a)(1 + k - a)D_{yv}^{k - a - 1}P_k(\underline{y}\wedge \underline{v})\ , \end{aligned}$$

for all \(0 \le a \le k\), as this will lead to the desired result. To do so, we will use the fact that

$$\begin{aligned} D_{xu} = \langle \underline{y}\wedge \underline{v},\underline{\partial }_x\wedge \underline{\partial }_u \rangle = \langle \underline{y},\underline{\partial }_x \rangle \langle \underline{v},\underline{\partial }_u \rangle - \langle \underline{v},\underline{\partial }_x \rangle \langle \underline{y},\underline{\partial }_u \rangle \ , \end{aligned}$$

and carefully calculate the action of both terms on \(D_{yv}^{k - a}P_k(\underline{y}\wedge \underline{v})\). Note that it is crucial to take into account that everything is acting on an element of \(\mathcal {P}_k^S(\mathbb {R}^{m \times 2},\mathbb {R})\), since Euler operators will appear which then act as a constant depending on the parameters k and a. First of all, we get that

$$\begin{aligned} \langle \underline{y},\underline{\partial }_x \rangle D_{yv}^{k - a}P_k&= (k - a)\big (\mathbb {E}_y\langle \underline{u},\underline{\partial }_v \rangle - \langle \underline{y},\underline{\partial }_v \rangle \langle \underline{u},\underline{\partial }_y \rangle \big )D_{yv}^{k - a - 1}P_k\\&= (k - a)\langle \underline{u},\underline{\partial }_v \rangle (1 + \mathbb {E}_y)D_{yv}^{k - a - 1}P_k\\&= (k - a)(a+2)\langle \underline{u},\underline{\partial }_v \rangle D_{yv}^{k - a - 1}P_k\ , \end{aligned}$$

where we made use of the fact that \(\langle \underline{y},\underline{\partial }_v \rangle P_k(\underline{y}\wedge \underline{v}) = 0\). Acting with the operator \(\langle \underline{v},\underline{\partial }_u \rangle \) on this result then leads to

$$\begin{aligned}&(k - a)(a + 2)\big (\mathbb {E}_v - \mathbb {E}_u + \langle \underline{u},\underline{\partial }_v \rangle \langle \underline{v},\underline{\partial }_u \rangle \big )D_{yv}^{k - a - 1}P_k\\ =&-(k - a)(a+2)(k - 2a - 2)D_{yv}^{k - a - 1}P_k\\&+ (a+2)(a+3)(k - a)(k - a - 1)D_{yv}^{k - a- 2}\langle \underline{u},\underline{\partial }_v \rangle \langle \underline{x},\underline{\partial }_y \rangle P_k\ . \end{aligned}$$

Acting with the second term, i.e. the operator \(\langle \underline{v},\underline{\partial }_x \rangle \langle \underline{y},\underline{\partial }_u \rangle \), and subtracting the result (obtained using completely similar calculations) from the previous leads to \(D_{yv}^{k - a- 1}P_k\) times the constant

$$\begin{aligned}&-2(k-a)(k-2-2a)(a+2) + (a+2)(a+3)(k - a)(k - a- 1)\\ =&(a + 1)(a + 2)(k - a)(k - a + 1)\ , \end{aligned}$$

as was to be shown. \(\square \)

Our generalised translation operator clearly bears some similarities with the classical exponential translation operator, hence the name, which means that one can use this resemblance to look for similar properties. One of the most important properties that the exponential function satisfies is the fact that it gives rise to a group morphism between \((\mathbb {R},+)\) and \((\mathbb {R}^+_0,\cdot )\), with \(e^se^t = e^{s + t}\). Before we can investigate what a decent analogue would be in the framework of wedge variables, we first mention the following property, which generalises the fact that \(\exp (\langle \underline{y},\underline{\partial }_x \rangle )\exp (\langle \underline{x},\underline{z}\rangle ) = \exp (\langle \underline{y},\underline{z}\rangle )\exp (\langle \underline{x},\underline{z}\rangle )\):

Theorem 3.10

The Bessel–Clifford operator satisfies the following relation:

$$\begin{aligned} \mathcal {C}_1\big (\langle \underline{y}\wedge \underline{v}, \underline{\partial }_x \wedge \underline{\partial }_u \rangle \big )\mathcal {C}_1\big (\langle \underline{x}\wedge \underline{u}, \underline{z} \wedge \underline{w} \rangle \big ) = \mathcal {C}_1\big (\langle \underline{y}\wedge \underline{v}, \underline{z} \wedge \underline{w} \rangle \big )\mathcal {C}_1\big (\langle \underline{x}\wedge \underline{u}, \underline{z} \wedge \underline{w} \rangle \big ). \end{aligned}$$

Proof

First of all, because the identity above deals with operators expressed in terms of inner products, we can pick up an element s in the spin group such that \(s(\underline{z} \wedge \underline{w})\overline{s} = \lambda e_{12}\) and all other vector variables are mapped to ‘starred variables’ such as \(\underline{y}^* = s\underline{y}\overline{s}\), which means that we are left with calculating

$$\begin{aligned} \sum _{j = 0}^\infty \frac{(y_1^*v_2^* - y_2^*v_1^*)^j \partial _{12}^j}{j!(j+1)!}\sum _{\ell = 0}^\infty \frac{\lambda ^\ell X_{12}^\ell }{\ell !(\ell +1)!}\ . \end{aligned}$$

Given a fixed index \(j \in \mathbb {Z}^+\), we have that

$$\begin{aligned} \frac{(y_1^*v_2^* - y_2^*v_1^*)^j \partial _{12}^j}{j!(j+1)!}\sum _{\ell = j}^\infty \frac{\lambda ^\ell X_{12}^\ell }{\ell !(\ell +1)!}&= \frac{(y_1^*v_2^* - y_2^*v_1^*)^j}{j!(j+1)!}\sum _{\ell = j}^\infty \frac{\lambda ^\ell X_{12}^{\ell - j}}{(\ell - j)!(1 + \ell - j)!}\\&= \frac{(y_1^*v_2^* - y_2^*v_1^*)^j \lambda ^j}{j!(j+1)!}\mathcal {C}(\lambda X_{12})\ . \end{aligned}$$

It then suffices to sum all these terms over the index \(j \in \mathbb {Z}^+\), and to use the inverse rotation to prove the statement. \(\square \)

Before we can formulate the algebraic structure underlying the symmetry transformations expressed in terms of the Bessel-Clifford function, we first need to introduce the equivalent of the binomial polynomials and coefficients.

4 Bessel–Clifford Binomial Polynomials

In the classical case, there exists an intimate connection between the binomial coefficients and the exponential function (via the translation operator):

$$\begin{aligned} \exp \left( y\frac{d}{dx}\right) x^k = (x+y)^k = \sum _{j = 0}^k {k \atopwithdelims ()j}x^{k-j} y^{j}\ . \end{aligned}$$

In view of the fact that we now have a generalised translation operator in the setting of wedge variables at our disposal, we can also expect a similar property here.

Definition 4.1

For a fixed wedge product \(Z = \underline{z} \wedge \underline{w}\), we define the polynomial

$$\begin{aligned} B_k(X,Y;Z) := \mathcal {C}_1\big (\langle \underline{y}\wedge \underline{v},\underline{\partial }_x \wedge \underline{\partial }_u \rangle \big )\langle \underline{x}\wedge \underline{u}, \underline{z} \wedge \underline{w} \rangle ^k\ , \end{aligned}$$

where \(k \in \mathbb {Z}^+\) is an arbitrary positive integer. The capital letters X, Y and Z hereby refer to the wedge variables \(\underline{x}\wedge \underline{u}\) and so on.

Note that the role of \(Z = \underline{z} \wedge \underline{w}\) is not important here, it merely generalises the fact that the classical situation can be seen as the action of a translation operator on powers of the variable \(x = \langle \underline{x},\underline{e}_1 \rangle \). As a matter of fact, a quite natural choice would be to take \(Z = e_{ab}\) a constant (considered as a wedge product of two basis vectors in an orthonormal frame for \(\mathbb {R}^m\)). A calculation based on the rule \(\partial _{ab}X_{ab}^j = j(j+1)X_{ab}^{j-1}\) then leads to the following:

Definition 4.2

The generalised two-wedge binomial polynomials (or Bessel–Clifford binomial polynomials) are defined as

$$\begin{aligned} B_k(X,Y;e_{ab}) = \sum _{j = 0}^k c_j(k) X_{ab}^{k-j} Y_{ab}^{j} = \sum _{j = 0}^k {k \atopwithdelims ()j}{k+1 \atopwithdelims ()j+1} \frac{X_{ab}^{k-j} Y_{ab}^{j}}{1+k-j}\ . \end{aligned}$$

Note that \(c_j(k) = c_{k - j}(k)\) for all \(0 \le j \le k\), as was to be expected.

These polynomials can then be used to formulate the following property:

Theorem 4.3

For all \(\lambda \in \mathbb {C}\) one has that

$$\begin{aligned} \mathcal {C}_1\big (\langle \underline{y}\wedge \underline{v}, \underline{\partial }_x \wedge \underline{\partial }_u \rangle \big )\mathcal {C}_1\big (\lambda \langle \underline{x}\wedge \underline{u}, \underline{z} \wedge \underline{w} \rangle \big ) = \sum _{k = 0}^\infty \frac{B_k(X,Y;Z)}{k!(k+1)!}\lambda ^k\ . \end{aligned}$$

Proof

To see why this is true we can actually take \(\underline{z} \wedge \underline{w}\), which leads to

$$\begin{aligned} \mathcal {C}_1( Y_{ab}\partial _{ab})\mathcal {C}_1(\lambda X_{ab})&= \sum _{k = 0}^\infty \frac{\lambda ^k}{k!(k+1)!}\mathcal {C}_1( Y_{ab}\partial _{ab})X_{ab}^k\\&= \sum _{k = 0}^\infty \frac{\lambda ^k}{k!(k+1)!}B_k(X,Y;e_{ab}) \end{aligned}$$

where we have made use of Definition 4.2. \(\square \)

Since we have introduced wedge binomial polynomials \(B_k(X,Y;e_{ab})\), we can expect a generalised Pascal-like triangle to show up. The first few numbers in this triangle look as follows:

$$\begin{aligned} \begin{array}{c|ccccccc} 0 & 1 & & & & & & \\ 1 & 1 & 1 & & & & & \\ 2 & 1 & 3 & 1 & & & & \\ 3 & 1 & 6 & 6 & 1 & & & \\ 4 & 1 & 10 & 20 & 10 & 1\\ 5 & 1 & 15 & 50 & 50 & 15 & 1\\ 6 & 1 & 21 & 105 & 175 & 105 & 21 & 1 \end{array} \end{aligned}$$

The sum of all the numbers in a fixed row of our generalised Pascal triangle may be recognised as the first few Catalan numbers: 1, 2, 5, 14, 42 and so on. This is not a coincidence, because it turns out that the triangle above is known as the so-called Narayana triangle (see e.g. [1, 11, 12]) which appears naturally in the setting of Catalan numbers. Note that we have enumerated the rows in our triangle above in a slightly different manner though, as k refers to the degree of the polynomial \(B_k(X,Y;Z)\) in our case. As a matter of fact, the numbers \(c_j(k)\) appearing in the wedge binomial polynomials are known in the literature as follows:

Definition 4.4

The Nayarana numbers are defined for all integers \(k \ge 0\) and \(0 \le j \le k\) by means of

$$\begin{aligned} \left[ \begin{array}{c} k\\ j \end{array}\right] = \frac{1}{1 + k - j}{k \atopwithdelims ()j}{k+1 \atopwithdelims ()j+1} = \frac{1}{k+1}{k+1 \atopwithdelims ()j}{k + 1 \atopwithdelims ()j+1}\ . \end{aligned}$$

Remark 4.5

Note that some authors refer to these Nayarana numbers as the ‘tribinomial coefficients’, since they can also be defined as the analogue of binomial coefficients whereby the standard natural numbers are replaced by triangular numbers:

$$\begin{aligned} \left[ \begin{array}{c} k\\ j \end{array}\right] = \frac{t_k t_{k-2} t_{k - 2} \cdots t_2 t_1}{(t_j t_{j-1} \cdots t_2 t_1)(t_{n - j} t_{n - j - 1} \cdots t_2 t_1)}\ , \end{aligned}$$

with \(t_j = \frac{1}{2}j(j+1)\). In other words, each factorial in the classical binomial constant is thus replaced by a product of consecutive triangular numbers. This connection becomes even more apparent if one rescales the operator \(\partial _{ab}\) by a factor \(\frac{1}{2}\). One the one hand, the relation \(\frac{1}{2}\partial _{ab}X_{ab}\) mimics the classical relation \(\partial _{x_j}x_j = 1\) (which then comes closer to the philosophy of considering \(X_{ab}\) as a ‘variable’ in the homogeneous coordinate ring of the Grassmann manifold), on the other hand we get that \(\frac{1}{2}\partial _{ab}X_{ab}^k = t_kX_{ab}^{k-1}\). This relation becomes intuitively clear if one looks at this relation from a combinatorial point of view: whereas there are k ways to eat away a single exponent in the classical case, there are indeed \(t_k\) ways to eat away a single exponent in the two-wedge case. One can eat away both indices a and b from a single variable (k choices), or combine two different variabels to eat away these indices (with \(t_{k-1}\) ways to do so). Together we arrive at the number \(t_k = k + t_{k-1}\).

One of the main properties of these numbers is the following:

Theorem 4.6

The sum of all the numbers on the kth row of the generalised Pascal triangle is given by:

$$\begin{aligned} \sum _{j = 0}^k c_j(k) = \sum _{j = 0}^k\frac{1}{1 + k - j}{k \atopwithdelims ()j}{k+1 \atopwithdelims ()j+1} = C_{k+1}\ , \end{aligned}$$

whereby \(C_p = \frac{1}{p+1}{2p \atopwithdelims ()p}\) denotes the pth Catalan number.

Proof

This follows from direct calculations. \(\square \)

An obvious question is whether there exists a formula relating the numbers in this triangle (an analogue of Pascal’s identity). For that purpose it is useful to note that one can use the exponential translation operator to prove Pascal’s identity, noting that

$$\begin{aligned} \exp \left( y\frac{d}{dx}\right) x^{n + 1}&= \left( x\exp \left( y\frac{d}{dx}\right) + \left[ \exp \left( y\frac{d}{dx}\right) ,x\right] \right) x^n\\&= (x + y)\exp \left( y\frac{d}{dx}\right) x^n\ . \end{aligned}$$

The main thing to observe here is that the commutator does the main piece of work here, because this allows us to prove the classical statement (note that this proof is different from the standard induction argument). In the wedge variable case we still have a commutator identity, but as we can see in the lemma below it is more complicated:

Lemma 4.7

The generalised translation operator \(\mathcal {C}_1(Y_{ab}\partial _{ab})\), with a and b fixed but arbitrary indices, satisfies the following property:

$$\begin{aligned} \mathcal {C}_1(Y_{ab}\partial _{ab})X_{ab} = \big ( X_{ab} + Y_{ab} \big )\mathcal {C}_1(Y_{ab}\partial _{ab}) + Y_{ab}\mathbb {E}_{ab}\sum _{j = 0}^\infty \frac{Y_{ab}^j\partial _{ab}^j}{j!(j+2)!}\ . \end{aligned}$$

Note that \(X_{ab}\) has to be seen as a multiplication operator here (i.e. the formula above is an operator identity acting on functions of wedge variables).

Proof

Using the series expansion of the generalised translation operator, we get the following:

$$\begin{aligned} [\mathcal {C}_1(Y_{ab}\partial _{ab}),X_{ab}]&= \sum _{j = 1}^\infty \frac{Y_{ab}^j}{j!(j+1)!}[\partial _{ab}^j,X_{ab}]\\&= \sum _{j = 1}^\infty \frac{Y_{ab}^j}{j!(j+1)!}j(\mathbb {E}_{ab} + j + 1)\partial _{ab}^{j - 1}\ , \end{aligned}$$

where we have made use of the fact that \(X_{ab}\) and \(\partial _{ab}\) generate the Lie algebra \(\mathfrak {sl}(2)\), see also Lemma 2.2, to calculate the commutator. A rearrangement of the terms then proves the statement. \(\square \)

What this lemma essentially says is that the coefficients of our wedge binomial polynomials can be expressed in terms of a ‘classical relation’ (a proper Pascal identity) plus an additional term which comes from the second function at the right-hand side in the lemma above.

Theorem 4.8

The wedge binomial coefficients \(c_j(k)\) with \(1 \le j \le k+1\) satisfy the following relation:

$$\begin{aligned} c_{j}(k+1)&= c_j(k) + c_{j-1}(k) + \frac{2(1 + k - j)}{j(j+1)}{k \atopwithdelims ()j-1}{k+1 \atopwithdelims ()j-1}\ , \end{aligned}$$

whereby the third term at the right-hand side is the deformation term which makes this situation different from the Pascal identity.

Proof

Using the previous lemma (and temporarily suppressing the indices a and b), we have that

$$\begin{aligned} \mathcal {C}_1(Y\partial _X)X^{k + 1}&= (X+Y)\mathcal {C}_1(Y\partial _X)X^k + Y\mathbb {E}\sum _{j = 0}^{k-1}\frac{Y^j\partial _X^j}{j!(j+2)!}X^k\ . \end{aligned}$$

Note that the summation runs from \(j = 0\) to \(k-1\) (and not to k, which is what one would naively expect), because \(\mathbb {E}\partial ^k X^k = 0\). In order to arrive at our identity for \(c_{j+1}(k+1)\), it then suffices to pick up the numerical coefficient of the term \(X^{k-j}Y^{1+j}\). \(\square \)

As a result, we have the following relation between Narayana numbers (which, to the best of our knowledge, seems to be a new result):

Theorem 4.9

For all positive integers k and \(0 < j \le k\) we have that

$$\begin{aligned} \left[ \begin{array}{c} k + 1\\ j \end{array}\right]&= \frac{k + j + 2}{k - j + 2}\left[ \begin{array}{c} k\\ j \end{array}\right] + \left[ \begin{array}{c} k\\ j-1 \end{array}\right] \ . \end{aligned}$$

Proof

It suffices to note that the ‘deformation term’ in the previous theorem (coming from the commutator) can be rewritten as follows:

$$\begin{aligned} \frac{2(1+k - j)}{j(j+1)}{k \atopwithdelims ()j-1}{k+1 \atopwithdelims ()j-1}&= \frac{2j}{(k+1)(k+2-j)}{k+1 \atopwithdelims ()j}{k+1 \atopwithdelims ()j+1}\\&= \frac{2j}{k+2-j} \left[ \begin{array}{c} k\\ j \end{array}\right] \ . \end{aligned}$$

It then suffices to add this term to the term \(c_j(k)\) to arrive at the result. \(\square \)

Remark 4.10

Note that the factor \(\frac{k+j+2}{k-j+2}\) is not always an integer, but the product with the Nayarana number \(c_j(k)\) will be (for all indices k and j).

If we interpret \(\mathcal {C}_1\big (\langle \underline{y}\wedge \underline{v}, \underline{\partial }_x \wedge \underline{\partial }_u \rangle \big )\) as a symmetry for the CL-operator, it makes sense to investigate whether we can undo this operation (the generalised translation). In sharp contrast to the classical exponential function, where the aforementioned connection with one-parameter subgroups allows us to invert a translation using the exponential of the opposite of the original argument (i.e. \(-\tau \) instead of \(\tau \)), we will need a different approach here. Let us try to fix the coefficients \(\gamma _j\) in such a way that

$$\begin{aligned} \sum _{j = 0}^\infty \gamma _j Y^j\partial ^j \mathcal {C}_1(Y\partial _X) = \sum _{j = 0}^\infty \gamma _j Y^j \partial ^j \sum _{k = 0}^\infty \frac{Y^k \partial ^k}{k!(k+1)!} = 1\ , \end{aligned}$$

which means that the first series expansion (involving the unknow coefficients \(\gamma _j\)) can be interpreted as the inverse symmetry (note that we have switched to the notation Y and \(\partial _X\) here, for the sake of notational ease). Since Y and \(\partial _X\) commute, this can be written as a recursive system of equations. Indeed, using the shorthand notation \(c_k\) for the coefficients appearing in the Bessel-Clifford function, we get:

$$\begin{aligned} 1 =&\ c_0\big (\gamma _0 + \gamma _1 Y\partial _X + \gamma _2 Y^2 \partial _X^2 + \gamma _3 Y^3\partial _X^3 + \cdots \big ) + \\&\ c_1\big (\gamma _0 Y\partial _X + \gamma _1 Y^2\partial _X^2 + \gamma _2 Y^3\partial _X^3 + \cdots \big ) + \\&\ c_2\big (\gamma _0 Y^2\partial _X^2 + \gamma _1 Y^3\partial _X^3 + \cdots ) + \cdots \end{aligned}$$

In other words, the coefficients \(\gamma _j\) are fixed via the recursive relation

$$\begin{aligned} \gamma _j = -\sum _{k = 1}^j c_k\gamma _{j - k} \qquad (j > 0)\, \end{aligned}$$
(4.1)

where it is easily seen that \(\gamma _0 = 1\). It is interesting to point out that one can do this for the exponential function too (which amounts to saying that \(c_j\) becomes a coefficient in the series expansion for \(e^x\)), and this will then (obviously) give \(\gamma _j = (-1)^j c_j\). In the present framework, the situation is more complicated though:

Theorem 4.11

The solution for the recursive relation (4.1) is given by

$$\begin{aligned} \gamma _j = \frac{\nu _j}{j!(j+1)!}\ , \end{aligned}$$

whereby the numbers \(\nu _j\) (with \(j \ge 1\)) appear as matrix entries of the inverse of the Narayana triangle.

Proof

To see why this is true, we will rewrite the recursion relation (4.1) in terms of the rescaled parameters \(\nu _j\). For example, the constant \(\nu _3\) is fixed by the following relation:

$$\begin{aligned} \frac{\nu _3}{3!4!} + \frac{\nu _2}{2!3!}\frac{1}{1!2!} + \frac{\nu _1}{1!2!}\frac{1}{2!3!} + \frac{\nu _0}{3!4!} = 0\ . \end{aligned}$$

If we now rewrite the second and third term we arrive at the relation

$$\begin{aligned} \frac{1}{3!4!}\big ( \nu _3 + 6\nu _2 + 6\nu _1 + \nu _0 \big ) = 0\ , \end{aligned}$$

where one can indeed see the entries 1, 6, 6, 1 from the Nayarana triangle. This idea generalises to arbitrary indices \(k > 0\) and therefore hinges on a numerical relation between the products \(k!(k+1)!\) and the Nayarana numbers. The general recursion relation can be written as

$$\begin{aligned} \frac{\nu _k}{k!(k+1)!} + \frac{\nu _{k-1}}{(k-1)!k!}\frac{1}{1!2!} + \cdots + \frac{\nu _1}{1!2!}\frac{1}{k!(k+1)!} + \nu _0\frac{1}{k!(k+1)!} = 0\, \end{aligned}$$
(4.2)

which means that we are left with proving that

$$\begin{aligned} \frac{1}{j!(j+1)!}\frac{1}{(k-j)!(k-j+1)!} = \frac{1}{k!(k+1)!}\left[ \begin{array}{c} k\\ j \end{array}\right] \ . \end{aligned}$$

This is easily done, since

$$\begin{aligned} \frac{k!(k+1)!}{j!(j+1)!(k-j)!(k-j+1)!} = \frac{1}{1+k-j}{k \atopwithdelims ()j}{k+1 \atopwithdelims ()j+1}\ , \end{aligned}$$

which is the definition for the Nayarana number. Together with the fact that \(\nu _0 = 1\), we can thus read the relation (4.2) as the product of a row (in the Nayarana triangle) with a column (in the inverse of this matrix), which defines \(\nu )j\) for all \(j > 0\). \(\square \)

Remark 4.12

Note that the numbers \(\nu _j\) appear in the OEIS as A103365, and they are given by (starting with \(\nu _1\)) \(-1, 2, -7, 39, -321, 3681, -56197, \cdots \) and so on. There one can also find general facts about the generating function, which seem to imply the result proven in the theorem above, but we decided to include an independent proof for the sake of completeness.

Let us define \(\mathbb {R}^\infty [\alpha ,\beta ,\ldots ]\) as the (real) polynomial ring in uncountably many variables (Greek letters for now, but we will soon replace these by our wedge variables \(X_{ab}\)). Note that having access to an infinite amount of variables is not required here (so everything always stays well-defined), but this allows us to not specify the number of variables at the start. We will then work with functions

$$\begin{aligned} \Phi : \mathbb {N} \rightarrow \mathbb {R}^\infty [\alpha ,\beta ,\ldots ]: n \mapsto \Phi [n] \in \mathbb {R}^\infty _n[\alpha ,\beta ,\ldots ]\, \end{aligned}$$

which means that the input n fixes the total degree of homogeneity of the polynomial (we essentially get a sequence of polynomials indexed by degree). The maps \(\Phi \) will now be built in terms of two basic ingredients: ‘pure variable maps’ \(\Phi _\alpha \) mapping \(n \in \mathbb {N} \mapsto \Phi _\alpha [n]:= \alpha ^n\) and (binary) combinations of such maps involving the ‘combinator map’ given by

$$\begin{aligned} B(\Phi _1,\Phi _2)&:&\mathbb {N} \rightarrow \mathbb {R}^\infty [\alpha ,\beta ,\ldots ] \nonumber \\ & : n \mapsto B(\Phi _1,\Phi _2)[n]:= \sum _{j = 0}^n \left[ \begin{array}{c} k\\ j \end{array}\right] \Phi _1[j]\Phi _2[k-j]. \end{aligned}$$
(4.3)

From this definition, it should be (inductively) clear that if \(\Phi _j\) acting on \(n_j \in \mathbb {N}\) gives a polynomial in \(k_j\) variables, then the map \(B(\Phi _1,\Phi _2)\) will send positive integers to polynomials in (at most) \(k_1 + k_2\) variables (note that variables could be repeated). Note that this map is commutative, since we will always end up with a polynomial in commuting variables \(\alpha , \beta \) and so on. To see this this map is also associative, we must show that

$$\begin{aligned} B\big (B(\Phi _1,\Phi _2),\Phi _3\big )[n] = B\big (\Phi _1,B(\Phi _2,\Phi _3)\big )[n] \end{aligned}$$

holds for all \(n \in \mathbb {N}\). This is equivalent to saying that

$$\begin{aligned} \sum _{j = 0}^n \sum _{i = 0}^j \left[ \begin{array}{c} n\\ j \end{array}\right] \left[ \begin{array}{c} j\\ i \end{array}\right] \Phi _1^{i}\Phi _2^{j - i}\Phi _3^{n-j} = \sum _{j = 0}^n \sum _{i = 0}^j \left[ \begin{array}{c} n\\ j \end{array}\right] \left[ \begin{array}{c} n-j\\ i \end{array}\right] \Phi _1^{j}\Phi _2^{i}\Phi _3^{n-j-i}\ . \end{aligned}$$

To see that this is indeed equal, we first note that

$$\begin{aligned} \left[ \begin{array}{c} n\\ k+i \end{array}\right] \left[ \begin{array}{c} k+i\\ i \end{array}\right] = \left[ \begin{array}{c} n\\ n-i \end{array}\right] \left[ \begin{array}{c} n-i\\ k \end{array}\right] \, \end{aligned}$$

where \(0 \le i \le n\) and \(0 \le k \le n-i\), a useful relation which follows from simple calculations involving the definition of the Nayarana numbers. It then suffices to note that we can reorder the summation over j and i as

$$\begin{aligned} \sum _{j = 0}^n \sum _{i = 0}^j = \sum _{i = 0}^n\sum _{j = i}^n = \sum _{i = 0}^n \sum _{k = 0}^{n - i}\, \end{aligned}$$

where we have defined \(k = n-j\). We thus get that

$$\begin{aligned} \sum _{j = 0}^n \sum _{i = 0}^j \left[ \begin{array}{c} n\\ j \end{array}\right] \left[ \begin{array}{c} j\\ i \end{array}\right] \Phi _1^{i}\Phi _2^{j - i}\Phi _3^{n-j}&= \sum _{i = 0}^n \sum _{k = 0}^{n-i} \left[ \begin{array}{c} n\\ k+i \end{array}\right] \left[ \begin{array}{c} k+i\\ i \end{array}\right] \Phi _1^{i}\Phi _2^{k}\Phi _3^{n - i - k}\\&= \sum _{i = 0}^n \sum _{k = 0}^{n-i} \left[ \begin{array}{c} n\\ n-i \end{array}\right] \left[ \begin{array}{c} n-i\\ k \end{array}\right] \Phi _1^{i}\Phi _2^{k}\Phi _3^{n - i - k}\\&= \sum _{i = 0}^n \sum _{k = 0}^{n-i} \left[ \begin{array}{c} n\\ i \end{array}\right] \left[ \begin{array}{c} n-i\\ k \end{array}\right] \Phi _1^{i}\Phi _2^{k}\Phi _3^{n - i - k} \end{aligned}$$

where we have made use of the symmetry \(i \leftrightarrow n-i\) in the last line. Together with the base case \(B(\Phi _\alpha ,0)[n] = \alpha ^n\) we now have everything at our disposal to reformulate theorem 4.3 in the following way:

Theorem 4.13

For two variables \(\alpha \) and \(\beta \), the Bessel-Clifford function \(\mathcal {C}_1(\cdot )\) satisfies the relation \(\mathcal {C}_1(\Phi _\alpha )\mathcal {C}_1(\Phi _\beta ) = \mathcal {C}_1(B(\Phi _\alpha ,\Phi _\beta ))\). Nested expressions like

$$\begin{aligned} \mathcal {C}_1(\Phi _1)\mathcal {C}_1(\Phi _2)\mathcal {C}_1(\Phi _3) = \mathcal {C}_1\bigg (B\big (\Phi _1,B(\Phi _2,\Phi _3)\big )\bigg ) \end{aligned}$$

and so on are also well-defined, since the combinator map is associative.

Proof

This can be shown by expanding both Taylor series, using properties of the Nayarana numbers and the previous lemma. \(\square \)

Remark 4.14

We can now contrast this situation with the classical case, for the exponential function. There, one would have a different ‘combinator map’ S sending ‘pure variable maps’ to \(S(\Phi _\alpha ,\Phi _\beta ):= \Phi _{\alpha + \beta }\). This means that

$$\begin{aligned} S(\Phi _\alpha ,\Phi _\beta )[n] = \sum _{j = 0}^n {n \atopwithdelims ()j}\Phi _\alpha [n - j]\Phi _\beta [j] = \sum _{j = 0}^n {n \atopwithdelims ()j}\alpha ^{n-j}\beta ^j = (\alpha + \beta )^n. \end{aligned}$$
(4.4)

Note that we could again have defined the action of \(S(\cdot ,\cdot )\) via the (classical) binomial polynomials, but this is not really necessary in view of the binomial theorem. From this point of view, one can see the combinator map \(B(\cdot ,\cdot )\) for the Bessel–Clifford function as the generalisation of the sum operation from the classical case. There is a subtle difference though: in the classical case, the product \(e^\alpha e^\beta \) becomes \(e^{\alpha +\beta }\), which means that we can evaluate our exponential function in a ‘single new argument’ (the sum of two variables). In the present case, we cannot do such a thing: when evaluating \(\mathcal {C}_1(B(\alpha ,\beta ))\), one cannot see this as the value of our function \(\mathcal {C}_1\) in a ‘single new argument’. In a sense, this is due to the fact that (special) functions are defined in terms of power series, which happen to satisfy the relation (4.4) from above.

Finally, this means that we can slightly reformulate Theorem 4.3 in the present language:

$$\begin{aligned} \mathcal {C}_1\big (\langle \underline{y}\wedge \underline{v}, \underline{\partial }_x \wedge \underline{\partial }_u \rangle \big )\mathcal {C}_1\big (\lambda \langle \underline{x}\wedge \underline{u}, \underline{z} \wedge \underline{w} \rangle \big ) = \mathcal {C}_1\big (\lambda B(X,Y;Z)\big )\ , \end{aligned}$$

where B is now to be seen as the combinator map from above (i.e. the degree of our generalised binomial polynomial is selected by the action of B on the running index k in the summation of the power series expansion for the Bessel-Clifford function).

5 Series Expansions via Kelvin Inversions

In classical harmonic analysis (for \(m \ge 3\)), there is a fundamental solution (Green’s function in some circles) which satisfies the following identity in distributional sense: \(\Delta _x |\underline{x}|^{2 - m} = \delta (\underline{x})\). Together with Theorem 3.2 this tells us that as long as we stay away from the singularities we can conclude that

$$\begin{aligned} \Delta _x |\underline{x}|^{2 - m} = 0\ \Rightarrow \ \Delta _y \big ( e^{\langle \underline{y},\underline{\partial }_x \rangle }|\underline{x}|^{2 - m} \big ) = \Delta _y |\underline{x}+ \underline{y}|^{2 - m} = 0\ . \end{aligned}$$

This relation is the starting point for the so-called series expansion of the Newtonian potential.

Remark 5.1

Note that this is often expressed in terms of the difference \(|\underline{x}- \underline{y}|\), but this is not essential here: it suffices to replace \(\underline{y}\) by its opposed vector in the formulas.

To see how the series expansion for the potential arises here it is useful to relate the fundamental solution (in its ‘unperturbed version’, i.e. with a singularity at the origin) to the Kelvin inversion:

Definition 5.2

The action of the Kelvin inversion \(\mathcal {I}_x\) on a function of \(\underline{x}\in \mathbb {R}^m\) with \(m \ge 3\) is defined as

$$\begin{aligned} \mathcal {I}_x[f(\underline{x})] = |\underline{x}|^{2 - m}f\left( \frac{\underline{x}}{|\underline{x}|^2}\right) \ . \end{aligned}$$

This is a generalised symmetry for the Laplace operator, i.e. it maps harmonic functions to harmonic functions.

Recognising the fundamental solution for \(\Delta _x\) as the inversion of the constant function 1 on \(\mathbb {R}^m\) and invoking the fact that the Kelvin inversion acts as an involution, we can say that

$$\begin{aligned} e^{\langle \underline{y},\underline{\partial }_x \rangle }\mathcal {I}_x[1] = \mathcal {I}_x^2 e^{\langle \underline{y},\underline{\partial }_x \rangle } \mathcal {I}_x[1] = \mathcal {I}_x \sum _{k = 0}^\infty \left( \mathcal {I}_x \frac{\langle \underline{y},\underline{\partial }_x \rangle ^k}{k!} \mathcal {I}_x[1]\right) \, \end{aligned}$$
(5.1)

where we have thus expanded the exponential translation operator in a formal series. The important thing to note here is that the terms between the big brackets at the right-hand side are k-homogeneous polynomial solutions for the operators \(\Delta _x\) and \(\Delta _y\). The former follows from the fact that the Kelvin inversion defines a generalised symmetry for \(\Delta _x\), the latter follows from the intertwining relation. Said polynomials are the ‘Gegenbauer harmonics’, also known as ‘zonal solutions’ for the subgroup SO\((m-1)\) in SO(m) which fixes the vector \(\underline{y}\). The more classical formulation of identity (5.1) is the following:

$$\begin{aligned} \frac{1}{|\underline{x}- \underline{y}|^{m - 2}} = \sum _{k = 0}^\infty \frac{|\underline{y}|^k}{|\underline{x}|^{k + m - 2}} C_k^{\frac{m}{2}-1}\left( \frac{\langle \underline{x},\underline{y}\rangle }{|\underline{x}|\;|\underline{y}|}\right) . \end{aligned}$$
(5.2)

Note that we have switched to \(-\underline{y}\) here, and that this is only valid for \(|\underline{x}| > |\underline{y}|\). In view of the fact that we have constructed an analogue of the exponential translation operator in this paper, we can also formulate an analogue for this expansion. This hinges upon the following crucial fact:

Definition 5.3

The action of the Kelvin inversion \(\mathcal {I}_{xu}\) on a function of \(\underline{x}\wedge \underline{u}\) in \(\mathbb {R}^{m \times 2}\) is defined as

$$\begin{aligned} \mathcal {I}_{xu}[f(\underline{x}\wedge \underline{u})] = |\underline{x}\wedge \underline{u}|^{3 - m}f\left( \frac{\underline{x}\wedge \underline{u}}{|\underline{x}\wedge \underline{u}|^2}\right) \ . \end{aligned}$$

This is a (generalised) symmetry for the CL-operator \(\Delta _{xu}\), i.e. it also maps solutions (for \(\Delta _{xu}\)) to solutions.

This definition is based on a result which can be found in e.g. [5], or one can varify that this ‘inversion’ satisfies the requirements using straight-forward (albeit elaborate) calculations. In particular, we can again consider the action on the constant function 1 as this leads to the fundamental solution for the CL-operator \(\Delta _{xu}\) (when \(m \ge 4\)). Together with Theorem 3.8 we thus get the following (away from the singularities, i.e. for \(\underline{x}\wedge \underline{u}\) non-zero):

$$\begin{aligned} \Delta _{xu}|\underline{x}\wedge \underline{u}|^{3 - m} = 0\ \Rightarrow \ \Delta _{yv}\bigg (\mathcal {C}_1\big (\langle \underline{y}\wedge \underline{v},\underline{\partial }_x\wedge \underline{\partial }_u \rangle \big )|\underline{x}\wedge \underline{u}|^{3-m}\bigg ) = 0\ . \end{aligned}$$

Because \(\mathcal {I}_{xu}\) acts as an involution, we can arrive at a series expansion using a similar argument as before:

$$\begin{aligned} \mathcal {C}_1\big ( \langle \underline{y}\wedge \underline{v},\underline{\partial }_x\wedge \underline{\partial }_u \rangle \big )\mathcal {I}_{xu}[1] = \mathcal {I}_{xu} \sum _{k = 0}^\infty \left( \mathcal {I}_{xu} \frac{\langle \underline{y}\wedge \underline{v},\underline{\partial }_x\wedge \underline{\partial }_u \rangle ^k}{k!(k+1)!} \mathcal {I}_{xu}[1]\right) . \end{aligned}$$
(5.3)

The terms between brackets at the right-hand side are again special, in that these are k-homogeneous solutions for the CL-operators \(\Delta _{xu}\) and \(\Delta _{yv}\) which are symmetric in \((\underline{x},\underline{u}) \leftrightarrow (\underline{y},\underline{v})\). They are also ‘zonal’, as they can be defined (up to a multiplicative factor) as the unique solutions for both CL-operators which are invariant under the subgroup SO\((m-2)\) in SO(m) which fixes the two-frame \(\underline{y}\wedge \underline{v}\). These polynomials first appeared in [3], the formula above can thus be seen as the series expansion for these polynomials obtained from a suitable symmetry acting on the fundamental solution.

Remark 5.4

Up to this point, it is not clear to the author whether one can rewrite the left-hand side of identity (5.3) in terms of a simple manipulation of the argument, so that it looks like \(|\phi (\underline{x}\wedge \underline{u},\underline{y}\wedge \underline{v})|^{3 - m}\) with \(\phi \) the unknown function (in the classical case, the function \(\phi (\underline{x},\underline{y})\) would just be \(\underline{x}+ \underline{y}\)).

6 Conclusion

In this paper we have shown how the exponential function and its role as a translation operator in classical harmonic analysis generalises to the Bessel-Clifford function in the setting of wedge variables (for the specific case of two-wedges \(\underline{x}\wedge \underline{u}\)). This then allows the construction of ‘new’ binomial polynomials, expressed in terms of Nayarana numbers, which also appear in the algebraic interpretation of the symmetry algebra. In what follows we will look at further generalisations of this procedure, hereby focusing our attention on general Grassmann manifolds.