A new nonparametric approach for multiplicity control:Optimal Subset procedures

Summary

A new approach for multiplicity control (Optimal Subset) is presented. This is based on the selection of the best subset of partial (univariate) hypotheses producing the minimal p-value. In this work, we show how to perform this new procedure in the permutation framework, choosing suitable combining functions and permutation strategies. The optimal subset approach can be very useful in exploratory studies because it performs a weak control for multiplicity which can be a valid alternative to the False Discovery Rate (FDR). A comparative simulation study and an application to neuroimaging real data shows that it is particularly useful in presence of a high number of hypotheses. We also show how stepwise regression may be a special case of Optimal Subset procedures and how to adjust the p-value of the selected model taking into account for the multiplicity arising from the possible different models selected by a stepwise regression.

1 Introduction

The problem of multiplicity control arises in all cases where the number of hypotheses to be tested is greater than one. This is certainly the most widespread scenario in many application fields. The most common aim is to select potentially active hypotheses (i.e. under the alternative). A property that is generally required is the strong control of the Familywise Error Rate (FWE), i.e. the probability of making one or more errors on the whole of the considered hypotheses (Marcus et al., 1976). On the other hand, a weak control of the FWE means simply controlling the α-level for the global test (i.e. the test where all hypotheses are null). Although the latter is a more lenient control, it does not allow the selection of active variables because it simply produces a global p-value that does not allow interesting hypotheses to be selected, so the former is usually preferred because it allows us to make inference on each (univariate) hypothesis. An alternative approach to multiplicity control is given by the False Discovery Rate (FDR). This is the maximum proportion of type I errors in the set of elementary hypotheses. The FWE guarantees a more severe control than the FDR, which in fact only controls the FWE in the case of global null hypotheses, i.e. when all involved variables are under H₀ (Benjamini and Hochberg, 1995).

The advisability of adopting one of the two methods depends on the experimental hypotheses. In confirmatory studies, for example, it is usually better to strongly control the FWE. This guarantees a suitable inference when we wish to avoid making even one type I error. There are several cases (generally all exploratory studies) in which the aim is to highlight a pattern of potentially involved variables. Testing for the FWE in these cases seems to be excessively strict, particularly when the experiment is characterised by a large number of hypotheses (sometimes thousands). In these cases the FDR would appear to be a more reasonable approach. In this way it is accepted that part (no greater than the α proportion) of the rejected hypotheses are in fact under the null. Although FDR is more powerful than FWE, it can still be lacking in power when there are many hypotheses (e.g. in neuroimaging data, studies on microarrays or association tests in the genetic field). A new approach to this problem is presented below, based on both the selection of the best sub-hypothesis (i.e. associated with the minimum p-value) and multiplicity adjustment.

2 The Optimal Subset procedures

Let us suppose we are making inference on a set of m hypotheses. Interpreting the p-value as a measure of the distance of a possible evidence in the data from the null hypothesis (Fisher 1955) gives rise to the idea of looking for the subset of variables which give the stronger (p-value based) evidence on the alternative. The correction for multiplicity of the p-value associated with the selected subset becomes unavoidable since each p-value has been selected among a multiplicity of possible subsets.

Let us consider a set $\mathcal{H}=\left\{H_{1}, \ldots, H_{m}\right\}$ composed of m (null) elementary hypotheses, where m₀ are true and m₁ are false. Let $\mathcal{H}_{\Omega}$ be the set of cardinality M of (not necessarily all) possible intersections of m hypotheses in $\mathcal{H}$. $\mathcal{H}_{\Omega}$ is therefore a set of multivariate hypotheses: a generic element $\mathcal{C}=\{H_{1}, \cap \ldots \cap H_{C}\}(\mathcal{C} \in \mathcal{H}_{\Omega})$ identifies a subset which is under the null hypothesis if each of its elementary hypotheses H₁, …, H_C is, in turn, under the null hypothesis. Ω indicates the criterion according to which $\mathcal{H}_{\Omega}$ is constructed. Three elements are therefore necessary to characterise an Optimal Subset procedure:

• a) the Ω criterion which generates $\mathcal{H}_{\Omega}$, the set of possible subsets of $\mathcal{H}$;

• b) the tests Φ(H_c; H_c ∈ C, c = 1,…, C) $\mathcal{C} \in \mathcal{H}_{\Omega}$ for the multivariate hypothesis in $\mathcal{H}_{\Omega}$;

• c) the test $\Psi\left(\mathcal{C} ; \mathcal{C} \in \mathcal{H}_{\Omega}\right)$ which identifies the Optimal Subset and adjusts the selected p-value for the hypotheses in $\mathcal{H}_{\Omega}$.

The Ω criterion defines the set of multivariate hypotheses. The terms “elementary hypotheses” are used to define the elements of $\mathcal{H}_{\Omega}$, i.e. the multivariate hypothesis from the intersection (allowed by Ω) of univariate hypotheses. Each Φ test is an unbiased test for the (elementary) hypotheses in $\mathcal{H}_{\Omega}$. It can be based on a combination of partial statistics or p-values. Once we obtain a test for each hypothesis in $\mathcal{H}_{\Omega}$, we select the elementary hypothesis (C_min) associated to the minimum p-value. In order to obtain an unbiased global test, we need to adjust for multiplicity the selected minimum p-value taking into account the fact that it has been chosen from a set of p-values. This is the task accomplished by the Ψ test. If it leads to the rejection of H₀, we reject all the univariate hypotheses composing the selected elementary hypothesis $\mathcal{C}_{\min } \in \mathcal{H}_{\Omega}$. Therefore Ψ is an unbiased test for $\mathcal{C}_{\min }$; it rejects $\mathcal{C}_{\min }$ with probability less or equal to α when all its univariate hypotheses are under the null. On the contrary, $\mathcal{C}_{\min }$ is under the alternative if at least one elementary hypothesis is under the alternative. This makes it clear why an Optimal Subset procedure does not strongly control the FWE: it does not test each single hypothesis, but only the multivariate hypothesis generated by an “optimal” intersection of elementary hypotheses — where “optimal” is defined as the multivariate hypothesis associated with the minimal p-value. In this way Optimal Subset procedures perform a weak control of the FWE over $\mathcal{H}_{\Omega}$, i.e. not over the set of univariate hypotheses, but over the set of elementary hypotheses allowed by Ω.

For the multivariate tests $\Phi\left(H_{i} ; H_{i} \in \mathcal{C}\right)$; $\mathcal{C} \in \mathcal{H}_{\Omega}$ we shall refer widely to the NonParametric Combination (NPC) methodology (Pesarin, 2001), which easily takes into account the dependences among variables. However any suitable test for the multivariate hypothesis $C \in \mathcal{H}_{\Omega}$ can be used.

For the Ψ test, the NPC methodology is even more useful. Indeed, apart for particular cases, the elements of $\mathcal{H}_{\Omega}$ are dependent given that the same univariate hypotheses are considered in several elements of $\mathcal{H}_{\Omega}$. In this work we shall mainly adopt a Tippett combining function within the NPC methodology which is a Bonferroni-like test where the dependences are taken in account within conditional permutation methods.

3 Optimal Subset procedures and permutation tests

Let us suppose that an appropriate permutation strategy and appropriate test statistics, suitable for testing for m hypotheses, in $\mathcal{H}$ exist. For example, in the case of m comparisons for two independent samples, the strategy is to randomly permute the vector indicating the cases/controls. If the samples are paired, a valid permutation strategy consists of independently switching the observations of the same subject between the two samples. In the case of quantitative variables, a possible test statistic is based on the usual t-statistic.

Any permutation strategy will produce a multivariate permutation space of T statistics. This can be represented as a B × m matrix where each of the B rows is associated with a different permutation of the data (and therefore an element of the space) and the i-th column is the marginal distribution of the statistic suitable for testing the i-th hypothesis in $\mathcal{H}$. The generic element of T is called t_bi (b = 1, …, B;i = 1, …, m). The procedure proposed here is based on this permutation space and is therefore applicable to any experimental design (C sample, quantitative/ordinal traits and others).

From T it is possible to calculate the permutation space of the corresponding p-values; the generic element p_bi (b = 1, …, B; i = 1, …, m) of matrix P is calculated from the proportion of elements which, in the correspondig column of matrix T, is greater than or equal to the statistic in that column. The row of P corresponding to the p-values referring to the observed statistics (i.e. the test statistics calculated on observed data) is therefore the vector of p-values for the m hypotheses in$\mathcal{H}$.

Let us suppose we wish to test a generic multivariate hypothesis $\mathcal{C}=H_{1} \cap \ldots \cap$ $H_{C}\left(H_{c} \in \mathcal{H}, \forall c=1, \ldots, C\right)$. An unbiased and consistent test $\Phi(\mathcal{C})$ is based on T_c, the subspace of T (or P), induced by the hypothesis $\mathcal{C}$(i.e. the sub-matrix defined by the columns referring to the hypotheses H_c; c = 1, …, C).

In order to obtain a combined (i.e. multivariate) test, it is necessary to define an appropriate combining function. In this work we mainly take into consideration the combining functions presented in Pesarin (2001) and discussed below. By applying the same combining function on each row of the sub-matrix of T or P we obtain the (univariate) permutation distribution of the multivariate statistic. The associated p-value is calculated on the proportion of elements greater than or equal to the observed statistic. Given positive weights $w_{c},\ \ c=1, \dots, C$ fixed a priori, the following combining functions may be considered:

• Direct combining function: $T_{D}^{\prime \prime}=\sum_{1 \leq c \leq C} w_{c} t_{c}$. This combining function is based on the direct sum of the test statistics. It is applicable when all partial tests have the same asymptotic distribution and the same asymptotic support, which is at least unbounded on the right.

• Fisher’s omnibus function: $T_{F}^{\prime \prime}=-2 \cdot \sum\nolimits_{1 \leq c \leq C} w_{c} \log (p_{c})$

• Tippett’s combining function: $T_{T}^{\prime \prime}=\max\nolimits_{1 \leq c \leq C}(w_{c}(1-p_{c}))$. In the case of independent variables, this combining function is asymptotically equivalent to the Bonferroni test.

• Liptak’s combining function: $T_{L}^{\prime \prime}=\sum\nolimits_{1 \leq c \leq C} w_{c} \Phi^{-1}(1-\lambda_{c})$ (where Φ, in this case, indicates a standard normal c.d.f.).

The set of T″ vectors calculated on each element of the $\mathcal{H}_{\Omega}$ set defines the multivariate permutation space T_Ω. Working on T_Ω, by using the same procedure adopted to determine P from T, it is possible to obtain P_ω from T_Ω. All the above combining functions, except for Tippett’s, are based on sums of elements, hence each element plays a role in the value of the statistic. Because of this “synergic” property, we recommend using one of them for the Φ test.

The Ψ test is a global test for the hypotheses in $\mathcal{H}_{\Omega}$, so an unbiased test can be obtained using any combining function on the space of its T_Ω statistics or P_Ω p-values. Although every combining function produces unbiased and consistent tests, we suggest using Tippett’s because it focuses on the minimum p-value.

From now on, we shall suppose appropriate Φ and Ψ tests exist and we shall pay more attention to the characterization of the Ω criterion defining $\mathcal{H}_{\Omega}$.

3.1 Closure set of $\mathcal{H}$

The most intuitive characterisation of Ω is given by all possible non empty intersections of the m univariate hypotheses in $\mathcal{H}$. $\mathcal{H}_{\Omega}$ is therefore defined by the closure set of $\mathcal{H}$ (excluding the empty set). It has a cardinality of M = 2^m − 1.

As previously pointed out, the definition of the Ω criterion plays a crucial role in the definition of an Optimal Subset procedure. The definition of $\mathcal{H}_{\Omega}$ ensures that we find out the minimum p-value among all the possible intersections of elementary hypotheses. On the contrary, reducing the number of elements of $\mathcal{H}_{\Omega}$ means limiting the search to a lower number of subsets and therefore limiting the chance of finding a “good model” (i.e. a p_min low enough). As a trade-off, limiting the number of elements of $\mathcal{H}_{\Omega}$ means “making more lenient corrections”, i.e. obtaining a more powerful procedure. Suppose we use Bonferroni’s correction as the Ψ test; in this case the minimum p-value is multiplied by the number of sets in $\mathcal{H}_{\Omega}$. Now consider a set $\mathcal{H}_{\Omega_{1}}$ defined by a different criterion with a cardinality of less than M = 2^m−1. If it includes the hypothesis H_min associated with the minimum multivariate p-value, $\mathcal{H}_{\Omega}$ is strictly less powerful than the Optimal Subset defined by $\mathcal{H}_{\Omega_{1}}$.

In most real cases the size of $\mathcal{H}_{\Omega}(M=2^{m}-1)$ is a huge number, leading to an extremely conservative correction of the global p-value and making the testing problem computationally unfeasible. Therefore a “good” Ω criterion lies within the delicate balance of these two requirements: a low p-value for the multivariate hypotheses versus a low p-value for the multiplicity correction Ψ. Our attention should therefore turn out to the definition of an “efficient” $\mathcal{H}_{\Omega}$.

3.2 Step-up procedures

The rationale behind such procedures is that lower univariate p-values tend to produce lower combined p-values. The idea is therefore to consider the hypothesis with the lowest p-value, the multivariate hypothesis given by the two elementary hypotheses with lowest p-values, then look for the multivariate hypothesis formed by the three elementary hypotheses with the three lowest p-values and so on until the set of all m hypotheses is defined. All these multivariate hypotheses are tested using a Φ test and finally the minimum of these multivariate p-values is adjusted by an adequate Ψ test (see below for its definition).

Thus, let us consider the vector of p-values arranged in increasing order $p_{(1)} \leq p_{(2)} \leq \ldots \leq p_{(m)}\ (p_{i} ; H_{i} \in \mathcal{H})$; $\mathcal{H}_{\Omega}$ is defined by: $\mathcal{H}_{\Omega}=\{H_{1}=H_{(1)}, H_{12}=(H_{(1)} \cap H_{(2)}), \ldots, H_{1, \ldots m}=(H_{(1)} \cap H_{(2)} \cap \ldots \cap H_{(m)}) \}$

$\mathcal{H}_{\Omega}$ has a cardinality equals to m, which is much lower than the cardinality of 2^m − 1 found in the “closure set of $\mathcal{H}$” and in case of independent variables $\mathcal{H}_{\Omega}$ is an asymptotically optimal set.

It is worth noting that the multivariate test in $\mathcal{H}_{\Omega}$ is biased, since the univariate hypotheses are not chosen a priori independently from the observed p-values. Instead, a “Step-up” procedure selects only the p-values producing the largest multivariate statistic. In this way the multivariate p-values associated with $\mathcal{H}_{\Omega}$ do not have a uniform distribution under the null hypothesis. In order to obtain an unbiased test for each element of $\mathcal{H}_{\Omega}$ we could multiply the p-value of the generic multivariate hypothesis H_{1,…, i}, by $k=\left(\begin{array}{c}{m} \\ {i}\end{array}\right)$; where k the number of possible sets of exactly i elements chosen among m. This correction would severely penalize the procedure producing extremely conservative tests. By adopting the NPC methodology we do not need to consider Φ unbiased tests. All that is needed is to repeat the same criterion for each random permutation, thus a) sorting the p-values, b) combining them in the same step-up fashion used for calculating the observed p-values and c) searching for the minimum multivariate p-value. In this way the vector of minimum p-values obtained from the B random permutations corresponds to the min-p statistic (i.e. Tippett’s combining function) and the proportion of p-values greater than or equal to the observed minimum p-value is the global p-value corrected for multiplicity.

3.3 Trimmed and step-up procedures

The permutation approach is very flexible w.r.t. different criteria. In general it is sufficient to define a rule and repeat it for the observed data and for each permutation of them. An interesting criterion is based on trimmed combining functions that allow us to search for the hypotheses which do not exceed a certain threshold of significance λ.

Consider the vector of sorted p-values, defined as in 3.2, $\mathcal{H}_{\Omega}=\{H_{1}=H_{(1)}, H_{12}=(H_{(1)} \cap H_{(2)}), \ldots, H_{1, \ldots, t}=(H_{(1)} \cap H_{(2)} \cap \ldots \cap H_{(t)}) \}$, where t = max(i : p_(i) ≤ λ). The combined test is simply a special case of the NPC methodology; in fact it corresponds to a combining function with weights equal to: w_i = 1 if i ≤ t and 0 otherwise (i=l, …, m). The adoption of such a trimmed function provides at least two practical advantages: it further restricts the size of $\mathcal{H}_{\Omega}$, and if λ = α, the search for “good models” is restricted to only singularly significant tests. This constraint also seems to have an appealing justification. Other threshold criteria can be taken into consideration as, for example, by considering the r hypotheses with lower p-values. Valid criteria which exploit information a priori can also be defined; if, for example, there is an expectation for a certain number of significant hypotheses, this can be used as a threshold value.

4 Stepwise regressions as a special case of Optimal Subset procedures

In this section we emphasize the link between Optimal Subset procedures and stepwise regressions. In a multivariate regression, the F-test based on the ratio between the variance explained by the model and the variance of the error terms (or the likelihood test if we consider logistic regression), is a multivariate testing of the hypothesis that none of the independent variables are under the alternative. Hence, this is a proper Φ test being under the null hypothesis if all the elementary hypotheses are under the null; instead, it is under the alternative if at least one independent variable is associated with the response (the dependent variable). The forward and the backward stepwise procedures are the two most popular (Brook and Arnold, 1985). Forward stepwise regression starts with no model terms except for the intercept. At each step it adds the most statistically significant term until there are none left. Backward stepwise regression starts with all possible terms in the model and removes the least significant terms until all the remaining terms are statistically significant. These two procedures properly define Ω criteria.

Although stepwise regression is very similar to the Optimal Subset procedure, the former differs from the latter failing in the multiplicity correction. In fact no global Ψ test is taken into account. The usual properties of Least Square estimates are invalid when a subset is selected on the basis of the data. Thus the coefficients for a selected subset will be biased, and as a result the usual measures of fit will be too optimistic, sometimes markedly so (Copas, 1983, Freedman et al. 1992). Hence the greater the number of variables considered, the greater the possibility of getting a significant F-test for the selected model even when none of the independent variables is associated to response Y. Following the discussion in 3.2, the issue is easily resolved; all that is needed is to perform a stepwise regression on B random permutations of the Y vector calculating the F-test for the selected model. The adjusted p-value is given by the proportion of p-values (related to the selected model) less than or equal to the p-value calculated from the observed data. This leads to an exact permutation test controlling the multiplicity for all possible models explored by the stepwise regression.

5 Comparative simulation study

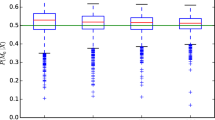
This paragraph shows the results of a comparative simulation study aimed at evaluating the behaviour of the Optimal Subset procedures under different proportions of active variables. The simulation study considers a comparison between two independent samples on 100 independent standard normal variables. The fixed effects of the second sample for the variables under H₁ are generated by a normal N(0, .7) distribution; the alternative hypotheses are bi-directional and α is equal to .10. The number of random permutations (Conditional Monte Carlo [CMC] iterations) for each test and the number of random generations of data are set equal to 1000.

The procedures considered are the so-called “Raw-p” procedure, the Bonferroni-Holm procedure (Holm, 1979) and the FDR-procedure (Benjamini and Hochberg, 1997). The first of these procedures rejects each hypothesis with a p-value of less than α; multiplicity is not considered at all. The second (step-down) procedure considers Bonferroni’s inequality and strongly controls the FWE; the third, as said before, controls the FDR. For the Optimal Subset procedures the Direct and Fisher’s combining functions are considered. Three criteria were considered for both combining functions: Step-up Procedure; Trimmed and Step-up Procedure with a threshold equals to α = 10% (shown by Trimmed 10%); and Trimmed and Step-up Procedure with a threshold equals to the proportion of active variables (shown by Trimmed H₁%). In this way the first solution considers all hypotheses involved, the second only the significant p-values and the third adds up the most significant k p-values, where k is equal to the number of variables under the alternative.

As pointed out before, Optimal Subset procedures do not strongly control the FWE nor the FDR. The control of the FWE is weak, i.e. it is verified only in the case of a global null configuration (all hypotheses are null). The results of the simulation study under H₀ are shown in the second column of table 1 (percentage of variables under H₁ equals to 0%). Columns two to five in table 1 shows the power for these procedures. It is important to emphasise that the comparison among powers of the considered procedures is not a proper comparison due to the fact that multiplicity control is carried out differently for the Bonferroni, FDR and Optimal Subset procedures. However, the results highlights that Optimal Subset procedures are generally more able to identify the hypotheses under the alternative w.r.t. other considered procedures.

Table 1 Simulation results: percentage of rejected alternative hypotheses (power).

6 An application to neuroimaging data

In an exploratory study on correlates of Obsessive Compulsive Disorder (OCD) symptoms (Sherlin and Congedo, 2003), eight clinical individuals were compared to eight age-matched controls using frequency domain LORETA (Low-Resolution Electromagnetic Tomography: Pascual-Marqui, 1999). The intra-cranial grey matter volume was divided into 2394 voxels of dimensions 7 × 7 × 7 mm. (Pascual-Marqui, 1999) and current density therein for one high-frequency bandpass (Betal: 12–16 Hz) region was estimated. Details of the method used in LORETA clinical studies can be found in Lubar et al. (2003). The statistical problem here is to simultaneously test 2394 elementary hypotheses (one per voxel). Previous experimental knowledge suggests the use of directional alternatives. A suitable test-statistic for each hypothesis is the Student’s t-test for paired samples. The data appear to be “far from normality” and spatial neighbourhood induces strong dependences that are difficult to characterize in a parametric form. In this case, the use of permutation tests guarantees unbiased univariate tests and allows for an easy combination of them. Moreover the low sample size (n = 8) induces a “tight” permutation space (of cardinality B=2⁸=256).

The number of elementary hypotheses associated to a (raw) p-value of less then α = .01 were 1214 out of 2394. According to the FWE-controlling Bonferroni-Holm procedure none of them was significant after correction for multiplicity. The Tippett’s step-down permutation (Bonferroni-like) procedures take the dependences between p-values into account. However, again no significant results were found using the Tippett step-down procedure. Other closed testing (FWE-controlling) procedures are not applicable in this case because of the high number of hypotheses being tested (2²³⁹⁴ − 1). Even the FDR-procedure fails in this case (no hypotheses were rejected). By performing a step-up Optimal Subset procedure using a t-sum combining function, 81 voxels are selected. Hence, the Optimal Subset procedure produces a significant global test and indicates a “potential” evidence against the (global) null hypotheses.

7 Conclusions

The Optimal Subset procedures perform a less stringent multiplicity control than FWE and FDR. Instead of controlling the multiplicity of the univariate tests, these procedures select the multivariate hypotheses which produce the most significant combined tests. The p-value of this multivariate hypothesis is then corrected for the multiplicity of multivariate hypotheses considered in $\mathcal{H}_{\Omega}$. In this way, therefore, the Optimal Subset procedures supply a “global” response and not a specific response on the single partial test. By way of compensation, however, they show sensitivity in identifying the hypotheses under the alternative. These two characteristics (weaker multiplicity control and greater power) suggest their use in exploratory studies and, more generally, in all studies which consider a multiplicity of variables and which are more interested in a global overview of the phenomenon rather than strongly inferring on single univariate hypotheses as FWE and FDR controlling procedures do. We have also shown how normal stepwise regressions can become a special case of Optimal Subset procedures, explaining the appeal of this new procedure.

The software has been developed in Matlab 6.5 (Mathwork inc. ©) and is available upon request from the authors.