Introduction

A wealth of research conducted over the past several decades has demonstrated the presence and importance of a core set of processes, known as the approximate number system (ANS), that are devoted to the non-symbolic understanding of number (Dehaene, Dehaene-Lambertz, & Cohen, 1998; Feigenson, Dehaene, & Spelke, 2004; Livingstone et al., 2014; Manuela Piazza, 2010; Sulkowski, 2001). This system underlies the ability to estimate quantities rapidly without counting or using symbols. The general capacity is present very early in human development (Feigenson et al., 2004; Izard, Sann, Spelke, & Streri, 2009; Lipton & Spelke, 2004), and has also been identified both in non-human primates (Nieder, 2016; Nieder & Dehaene, 2009) and in other non-human animals (Dehaene et al., 1998).

The ANS has been of particular interest to educational researchers due to findings indicating a positive correlation between ANS ability and mathematics performance. Such a relation has been found in many different age-groups – including in preschoolers (Libertus, Feigenson, & Halberda, 2011), kindergarteners (Gilmore, McCarthy, & Spelke, 2010), and 8-year-olds (Inglis, Attridge, Batchelor, & Gilmore, 2011). This includes work involving both typically-developing individuals and studies of individuals with dyscalculia (severe difficulties with mathematics). For example, Pinheiro-Chagas et al. (2014) found that children with math difficulties had impairments in performing multiple ANS-related tasks, in particular in non-symbolic numerical comparison and non-symbolic addition (but see Castronovo & Göbel, 2012; Fuhs & McNeil, 2013; Göbel, Watson, Lervåg, & Hulme, 2014, for studies that failed to find a relation between the ANS and mathematics abilities).

In addition to these correlational studies, longitudinal studies examining scores across two or more time points have found the same basic positive relation. For instance, Starr, Libertus, and Brannon (2013) found that 6-month-old infants’ numerical preference scores correlated with their standardized math test scores and non-symbolic number comparison scores at 3.5 years of age. Similarly, Halberda et al. (2008) found that ANS acuity of 14-year-olds correlated with their past standardized math scores going as far back as kindergarten. Libertus, Odic, and Halberda (2012) similarly found a positive relationship between ANS scores measured in college students and their past Quantitative SAT (SAT-Q) scores, even when controlling for SAT-Verbal scores.

The observed correlation between the ANS and mathematics performance has led to interest in whether the ANS can be altered (e.g., Wilson, Revkin, Cohen, Cohen, & Dehaene, 2006). Such interest has been further spurred by cross-sectional studies showing that ANS ability continues to increase from age 3 into adolescence, suggesting that the system is plastic (at least for some time during development – see Halberda, Ly, Wilmer, Naiman, & Germine, 2012, and Piazza & Izard, 2009 for a meta-analysis of this literature). And indeed, the few intervention studies that exist in this domain have provided some evidence that ANS training can produce enhancements in mathematics performance (e.g., DeWind & Brannon, 2012; Park & Brannon, 2014a; Pinheiro-Chagas et al., 2014; Price, Palmer, Battista, & Ansari, 2012).

However, these previous studies have typically been quite short (e.g., between one and six sessions). The longest reported study involved training young children for approximately 25 10-min sessions on numerical tasks, which was associated with improvements on a standard ANS test when compared to children in a control group (Van Herwegen, Costa, & Passolunghi, 2017). However, this study did not systematically test the degree of generalization, nor did it involve precise control and analysis of training sessions. Interestingly, in studies that do report performance across several days of training (e.g., DeWind & Brannon, 2012; Park & Brannon, 2014 – six training sessions), very little improvement in ANS ability was found after the first session (for a discussion of this pattern of results, see Lindskog & Winman, 2016). This lack of improvement after the first several hundred trials stands in stark contrast to most studies in the domain of perceptual learning, where improvements often continue for thousands or tens of thousands of trials (Fahle & Edelman, 1993; Larcombe, Kennard, & Bridge, 2017; Yang & Maunsell, 2004).

Despite the published empirical results showing some degree of generalization to mathematics, even from somewhat short ANS training, several critical reviews have emerged pointing out numerous design limitations that the authors claim undermine strong causal claims that ANS training transfers to higher-order mathematical skills (Lindskog & Winman, 2016; Merkley, Matejko, & Ansari, 2017; Szűcs & Myers, 2017). For example, Szűcs and Myers (2017) have suggested that many studies that have claimed to train the ANS (e.g., studies using the Number Race; Wilson et al., 2006) actually train a variety of cognitive skills ranging from basic ANS functions to more advanced symbolic number skills or even the retrieval of explicit facts. As for studies that have trained the ANS in the strict sense (i.e., trained on an explicit ANS task rather than having trained on a non-ANS task that is nonetheless meant to enhance ANS ability; DeWind & Brannon, 2012; Park & Brannon, 2013; 2014), Szűcs and Myers (2017) argue that active mental operations on the quantities, rather than mere experience with quantity comparison, is critical for any observed transfer. These same authors also discuss two additional ANS training studies that they categorize as “brief exposure,” and therefore argue that they do not qualify as training studies per se (Hyde, Khanum, & Spelke, 2014; Wang, Odic, Halberda, & Feigenson, 2016a). These criticisms have maintained that different timescales of improvements (e.g., minutes vs. days vs. weeks) are likely to involve distinct mechanisms of change, ranging from rapid task response mapping to lasting perceptual augmentation. Long-term change specifically, which has not yet been conclusively demonstrated in the ANS training literature, is likely to result in the most practically relevant outcomes (e.g., lasting educational benefits). It is therefore important to experimentally test the time course of change in ANS training.

Here we sought to resolve the issue of whether ANS performance is susceptible to enhancement via long-term training. Specifically, we used a common definition of the ANS derived from previous studies paired with a much longer training regimen. We then quantitatively modeled the time course of change over this long duration. This is important because the time course of improvements may implicate different mechanisms of change as well as different routes for applied training programs (e.g., Ahissar & Hochstein, 1993; Ahissar & Hochstein, 2004; Ball & Sekuler, 1987; Crist, Kapadia, Westheimer, & Gilbert, 1997; Fiorentini & Berardi, 1980; Shiu & Pashler, 1992). If learning is only observed in a fast, early phase, with performance then hitting a hard asymptote, this would likely be consistent with what is sometimes referred to as “learning about the task,” but with no true improvements in the underlying process(es) of interest (i.e., would encompass things like learning to use buttons to respond, learning the procedure, etc.). Conversely, if learning follows a protracted time-course, particularly one captured by the same function (e.g., exponential) throughout, this would be consistent with continued improvements in the ability to complete the task due to changes in the underlying ability. Indeed, the extent to which learning follows an exponential form has been of interest in a number of domains, because this is consistent with improvements in a single underlying process (as improvements in multiple processes with different time courses, either simultaneous or cascading, will produce a power function rather than an exponential function; Dosher & Lu, 2007; Heathcote, Brown, & Mewhort, 2000).

While the previous research on ANS training has been interpreted as evidence for a “fast phase” of learning that takes place over the first few sessions after which learning asymptotes, because the longest of these studies stopped after around 1,000 trials, it is unclear whether learning continues to progress beyond this early part of learning (DeWind & Brannon, 2012). Indeed, the current data leave two distinct possibilities: (1) that there is truly a disjunctive fast-phase followed by a hard asymptote; or (2) that what was previously identified as a “fast phase” is simply part of a continuous exponential learning process. Here we made use of classic perceptual learning approaches in the service of training performance on the approximate number comparison task and thus provide the first evidence to truly address this issue.

In doing so, we made use of many of the commonly accepted best practices in the domain of perceptual learning. For instance, because one of the single best predictors of improvements on a perceptual learning task is simply time on task (as is true of most, if not all learning tasks – Badiru, 1992; Fahle & Edelman, 1993; Heathcote, Brown, & Mewhort, 2000), we made use of an extremely large number of training trials (8,000+). Indeed, given the shape of most perceptual learning curves, without employing a substantial number of training trials, it can often be quite difficult to determine whether learning has truly reached a hard asymptote at some final level of performance or instead is continuing to improve in the slow phase of an exponential function (Fahle & Edelman, 1993). Furthermore, again consistent with best practices in training, practice was distributed through time (Larcombe et al., 2017), immediate informative feedback was provided (Fahle & Edelman, 1993; Herzog & Fahle, 1997; Shiu & Pashler, 1992), and task difficulty was modified throughout training to keep the task difficult, but doable (C. S. Green & Bavelier, 2008). Finally, we took an additional method from classic studies in perceptual learning by making use of experienced psychophysical observers (although see Discussion for the limitations of this approach, including the ability to generalize to the broader population). Our final sample included two of the authors (A.C. & L.C.) as well as eight other individuals from the laboratory of the senior author (C.S.G). The approach of using trained observers has historically been used when the question at hand focuses on whether a given task is learnable, from the perspective that if motivated and experienced individuals are unable to show improvements through intensive training, it is unlikely that naïve participants would be so capable. This is particularly true when the task necessitates performing a task in peripheral vision (or parafoveal vision as is the case here) where the ability to consistently fixate on a non-target stimulus (in our case, a central fixation cross) is key.

While the primary question at hand was whether individuals would continue improving their ANS ability through extended training on an ANS task, because previous examinations of ANS learning/generalization have not included adequate measures of low-level transfer, we selected generalization measures both from the domains of perceptual learning as well as from the domain of mathematical cognition. In particular, perceptual learning is commonly retinotopically specific (Hung & Seitz, 2014; Intriligator & Cavanagh, 2001; Schoups, Vogels, & Orban, 1995; Tootell et al., 1998). This means that no benefits of training are observed if the trained task/stimuli are presented in a spatial location other than the trained location. We thus chose to examine whether learning would generalize to new spatial locations, which is the first, to our knowledge, assessment of generalization of ANS training across retinotopic locations. This is particularly relevant given the evidence for topographic cortical representations of ANS (Harvey, Klein, Petridou, & Dumoulin, 2013).

In addition to these more perceptual-based transfer assessments, we also made use of additional generalization tasks that one might think of as being perceptually “above” and “below” the trained task in a hierarchical sense. The training task, a typical non-symbolic numerical comparison task, involved viewing a large number of black and white dots and then indicating which color had more dots. An operation “below” this numerical comparison then would be estimation of numerosity itself. However, this also involves a process that is not necessary in numerical comparison tasks, namely conversion of approximate number into a symbolic number. The conversion is a crucial link between the low-level approximate number system and its educational applications, but its absence in our numerical comparison task does obscure the degree to which enumeration is strictly “lower-level” than our training. To test the degree to which training would generalize to magnitude estimation combined with symbolic-number labeling, we employed a simple dot enumeration paradigm.

An operation “above” numerical comparison would be a comparison of comparisons (i.e., seeing two different clouds of black and white dots and indicating in which cloud the ratio of black-to-white was larger). We thus employed a previously studied ratio comparison task (Matthews et al., 2016). Like other studies, we also examined potential generalization to mathematical competence (as measured by a standardized mathematics test: The Woodcock-Johnson Test of Achievement math fluency subtest). Generalization of numerical comparison training to math ability would be somewhat surprising from both the perceptual learning perspective and the previous ANS training literature (Park & Brannon, 2014), but testing this generalization can still provide evidence (or a lack thereof) for certain mechanisms of training-related improvements (e.g., low-level vs. high-level changes). Finally, we employed a peripheral multiple-object tracking (MOT) task (Pylyshyn & Storm, 1988). The purpose of this task was to rule out the possibility that, if we saw improvements on the numerical comparison training task, this was due to simple changes in peripheral vision or peripheral visual attention (as opposed to estimations of number). We did not predict generalization to performance on MOT or math tasks, but instead expected them to demonstrate the limits of learning generalization.

Our expectation was that clear evidence of long-term learning (i.e., improvements that continue beyond just the first session or first few sessions) would be observed. Indeed, there are few (if any) examples in the domain of perceptual learning wherein properly designed dedicated training on a perceptual task has failed to produce enhancements in that task. The predictions for the generalization tasks were less clear. In terms of generalization to new spatial locations, we know that perceptual learning is commonly retinotopically specific. This, combined with recent evidence suggesting that brain areas involved in ANS computations may also have retinotopic representations (Harvey, Fracasso, Petridou, & Dumoulin, 2015; Harvey et al., 2013), suggested that we may fail to see any generalization of learning to new locations. However, if learning is truly at the level of numerical estimation, one might expect to see significant generalization across spatial locations. And in terms of generalization to the other tasks, no research to our knowledge has assessed whether dedicated numerical comparison training positively impacts simple estimates of numerosity. Furthermore, although number comparison and ratio comparison both involve comparisons and could be thought of as being related hierarchically (i.e., with the comparison of ratios being “above” single ratio tasks), recent evidence has suggested that these tasks might in fact depend on separable abilities (Matthews et al., 2016). We therefore predicted limited transfer from the ANS task to the ratio comparison task.

Methods

Participants

Eleven individuals participated in the study (five male, Mage = 22.1, SDage = 3.5). All 11 participants were, at the time of their participation, members of the Learning and Transfer lab at the University of Wisconsin-Madison (the lab of senior author C.S.G). The participants included two of the authors (L.C. & A.C.). Both of these participants were aware of the experimental hypotheses and were also experienced psychophysical observers, including some limited experience with both the to-be-trained task and the generalization tasks (e.g., through piloting/preparing the tasks). Of the remaining nine participants, none were aware of the experimental hypotheses. All nine were, to varying degrees, experienced psychophysical observers, though none had experience with either the to-be-trained task or any of the generalization tasks. The use of this sample was motivated by the need for compliance and motivation over the course of several weeks of training. Previous experience with psychophysical tasks was particularly important for participants’ ability to maintain a central fixation throughout training. All participants had normal or corrected-to-normal vision. All participants were compensated with lab-credit for their participation.

Given effect sizes reported in previous ANS training studies (e.g., a training-induced difference in means of over 50 standard errors; Park & Brannon, 2014), training-task improvements should be detectable using a t-test with 80% power with only two participants. While our sample size was small, it should be more than enough to detect changes in ANS ability with training.

Experimental setup

All computerized tasks were programmed in MATLAB using the Psychophysics Toolbox (Brainard, 1997; Kleiner, Brainard, & Pelli, 2007). These tasks were presented on a 22-in. Dell widescreen monitor by a Dell Optiplex computer running Windows 7. Participants sat approximately 59 cm from the screen.

Experiment overview

The experiment was a standard pre-test ➔ training ➔ post-test design (see below for additional details about each individual task). The pre-test battery consisted of eight different tasks. All tasks had short (approximately five-trial) practice components consisting of very easy trials. Furthermore, before each task, participants were given written instructions, which among other things, emphasized the importance of keeping their eyes on the fixation cross (for tasks where stimuli were presented peripherally) and trying not to shift their eyes to the stimuli once the stimuli appeared. The pre-test began with four versions of the non-symbolic numerical comparison task. These versions were identical except for the spatial position of the task. The first block of testing was always at the to-be-trained spatial location for the given participant, which was pseudo-randomly assigned.

This was followed by a block where the task appeared in the location across the vertical meridian from the to-be-trained location, a block where the task appeared in the location across the horizontal meridian from the to-be-trained location, and then, finally, a block where the task appeared in the direct center of the screen (e.g., if the top-left quadrant was going to be trained, the participant would complete the task in the top-left quadrant, then the top-right quadrant, then the bottom-left quadrant, then the screen center).

The participants then completed an enumeration task, followed by a ratio comparison task, a timed arithmetic task, and a multiple-object tracking task (MOT). The pre-test was completed in a single session with breaks available in between each task. At least 24 h after the pre-test was completed, participants began their training. The training consisted of repeated practice on the non-symbolic numerical comparison task in a single quadrant (same quadrant throughout training, chosen pseudorandomly for each participant). All participants completed a minimum of 13 sessions of the training task over a minimum span of 30 days (range of sessions completed: 13–41; range of days to complete: 30–103; see Supplementary Information for additional detail on individual training completion).

One of the participants completed fewer than 20 sessions of training and we thus report results from the remaining ten participants (range of sessions complete: 22–41). Each training session consisted of 384 trials. Participants were allowed to complete no more than one session per day. At least 24 h after the conclusion of training, participants completed a post-test, which consisted of the same tasks as in the pre-test.

Stimuli and tasks

Non-symbolic numerical comparison task

Basic stimuli

The stimuli consisted of intermixed black and white dots presented on a gray background. The color of dots with the smaller number (set to be between 5 and 23) on a given trial had a randomly selected mean diameter of .35°, .4°, .45°, or .5° of visual angle (DVA), with each dot’s size randomly varying by 25% above or below the mean size. The mean dot size of the larger number (determined by multiplying the smaller number by a number ratio) on a given trial was randomly selected from .7, .9, 1.1, or 1.3 times the size of the smaller-number dots, also with a 25% random variation, then this larger-number dot size was ad hoc adjusted to minimize the within-session correlation between total dot area ratio and numerosity ratio (r = .02; while still maintaining a small correlation between mean dot size ratio and numerosity ratio, r= -.35). These procedures are similar to those used throughout the ANS literature (e.g., Gebuis & Reynvoet, 2012; Halberda et al., 2012; Halberda et al., 2008; Piazza, Izard, Pinel, Le Bihan, & Dehaene, 2004), and meet, or exceed, the typical control over the relation between numerosity, spatial extent, and density. Critically, our use of intermixed dots also minimizes concerns about convex hull (e.g., Gebuis & Reynvoet, 2012), as the numerosities share a single outer contour. The dots were constrained to fall within an invisible circular aperture (radius = 5°). Dot locations were chosen from amongst the relevant crossing points (i.e., nodes) of a square grid, circumscribed within a circle, then randomly jittered by up to .25°. The grid size (i.e., the number of nodes) for each trial was determined by adding five free nodes to the number of nodes necessary to hold the black and white dots. The grid was then rotated at a random angle. Black and white dots were then assigned, one by one, to random nodes in the grid based upon the number ratio for the given trial (see below). The center of the circular aperture in which the dots could appear was offset from the screen center and corresponding fixation cross by 5° in both the x- and y-direction (with the direction of offsets depending on the quadrant being assessed/trained) in all versions except the central version (where the circular aperture was centered on the screen center). Additionally, as part of a concurrent task to ensure fixation for all peripheral task versions, a red dot appeared randomly at the end of either the top or the bottom arm of the fixation cross (for similar methods see Green, Kattner, Siegel, Kersten, & Schrater, 2015; Lu, Chu, Dosher, & Lee, 2005). This secondary task was trivially easy when fixating properly. While adding task demands may have increased overall difficulty and therefore improved generalization (Schmidt & Bjork, 1992; Xiao et al., 2008; cf. Jaeggi et al., 2010), central tasks such as this are designed to require minimal effort from experienced participants such as ours.

Trial by trial procedure

Figure 1 outlines the stimulus events for this task. An 800-Hz beep signaled the start of a new trial. Simultaneously, the first stimulus screen appeared with a red dot presented either on the top or the bottom arm of a fixation cross, for a random duration between 250 ms and 500 ms. Next, the number ratio stimuli, consisting of the black and white dots presented in the assigned quadrant, appeared for 500 ms. After these two stimulus screens, participants were first asked to indicate, via a key press, whether they believed there were more white dots or black dots presented. They were then asked to indicate whether the red dot appeared on the top or bottom arm of the fixation cross. Feedback was given (incorrect = low tone (600 Hz); correct = no tone) after each response (fixation response and main response) during training. No feedback was given during pre-test or post-test.

Fig. 1
figure 1

Illustration of non-symbolic numerical comparison task. A fixation cross, paired with an auditory preparatory beep, was first presented. This was followed by the cloud of black and white dots. Participants then were asked to make two responses. In the first response, they were asked to indicate whether they perceived there to be more black dots or more white dots. They then had to indicate the position of the red dot on the fixation cross. Note that auditory feedback was given during training, but not during the pre-test or post-test

Full size image

Number ratios used for pre-test/post-test and total trials

Actual number ratios tested could deviate from the preset ratios, which ranged from 1.1 to 1.8 in .10 increments, due to the need to increment dots by whole numbers (for examples of different ratio displays, see Supplemental Information). For all analyses, actual number ratios were calculated and recorded for each combination of smaller number and preset number ratios. The total set of trials were determined by performing a complete crossed design on the smaller number (i.e., 5, 11, 17, and 23), number ratio, and size ratio parameters. All pre-test/post-test task versions consisted of 32 repetitions per number ratio, or 256 actual trials. Each task took approximately 15 min to complete. Before each task, ten practice trials were given using easier number ratios (outside the range used for both training and generalization tasks).

Number ratios used for training and total trials

The same basic parameters were used for training sessions, with the exception of the number of repetitions per number ratio. In training, each number ratio was repeated 48 times, resulting in 384 trials per session (no practice trials were given prior to any training session). Each training session lasted approximately 25 min. The number ratios used in each training session were set adaptively based upon prior participant performance, with the goal of keeping the task continuously challenging, but do-able. After each training session, a 79% threshold was calculated and recorded in a training log file. At the beginning of each successive training session, the program read in the previous session’s 79% threshold and set the easiest number ratio to be .05 greater than the 79% threshold. For the first six training sessions, the range of number ratios was set to eight number ratios decreasing in .10 increments from the easiest number ratio (set to 1.8 for first session). Afterwards, the range of number ratios was set to eight number ratios decreasing in .05 increments from the easiest number ratio. If the easiest number ratio exceeded 1.6 for any of the training sessions, the easiest number ratio was set to 1.6 (upper bound for easiest ratio). Likewise, if the easiest ratio fell below 1.1 for any of the training sessions, the easiest ratio was set back to 1.1 (lower bound for easiest ratio). When any of the eight number ratios fell below 1.01, the number ratio for that trial was set to 1.01 (lower bound for hardest ratio), effectively meaning that the high-number color had one more dot than the low-number color.

Enumeration task

Figure 2b outlines the stimulus events for this task. The stimuli for this task appeared in the same quadrant used for training. The stimuli consisted of either all black or all white dots (random across trials) on a gray background. The dot positions were generated in a similar manner as described above in the numerical comparison task. On each trial, an 800-Hz beep signaled the start of a new trial. A fixation cross with a red dot either on the top or the bottom arm was presented for a random duration between 250 ms and 500 ms, followed by an array of black or white dots presented for 500 ms in the participant’s assigned quadrant. Then, a white number line with tick marks from 0 to 100 in five number increments was shown either at the top or the bottom of the screen depending on the stimuli presentation quadrant. Any response between 0 and 100 was allowed. The number line was at the top if the quadrant was a top-quadrant and bottom if the quadrant was a bottom-quadrant, in order to decrease the distance between the number line and the presented stimuli and, thus, reduce the distance the participants’ eyes need to shift in between stimulus events. The participant clicked on the number line to indicate the number of dots he/she believed was presented and then indicated whether the red dot was on the top- or bottom-arm of the fixation cross via a keypress. The number of dots presented ranged from 11 to 74. This range reflected the range of total number of dots participants saw during training. Three repetitions per numerosity were used, resulting in 192 trials. The dot sizes used were .3, .4, .55, and .6 in degrees of visual angle. Prior to the start of the task, four practice trials were given to give participants a sense of the range of numerosities in the task. One trial presented a numerosity between 11 and 20, one trial between 25 and 35, one between 45 and 55, and one between 65 and 74. The task took approximately 15 min to complete.

Fig. 2
figure 2

Schematic depiction of transfer tasks. Stimulus events are displayed vertically for tasks (b), (c), (d), and the training quadrant of (e). Task (a) depicts the four quadrants used to test for retinotopic specificity of approximate number system (ANS) learning (four total non-symbolic numerical comparison tasks). Task (b) represents the enumeration task. This task began with a fixation point after which a cloud of dots (of a single color) was presented. Participants then used a number line to indicate how many dots they believed were presented. The location of the number line (top or bottom) matched the location of presented cloud of dots (top or bottom). Task (c) represents the ratio comparison task. It was conceptually similar to the task in (a) except, rather than a single mixed cloud of black and white dots, two such clouds were presented. Participants then needed to indicate which cloud had the bigger ratio. Task (d) represents the standard Woodcock Johnson math fluency sub-test. Task (e) represents the multiple object-tracking task (presented in both the trained quadrant and the fully opposite diagonal quadrant)

Full size image

Ratio comparison task

Figure 2c outlines the stimulus events for this task. An 800-Hz beep signaled the start of a new trial. On each trial, a fixation cross with a red dot either on the top or bottom arm was presented for a random time between 250 ms and 500 ms. Next, two clouds (one cloud presented to the left of fixation and one cloud to the right of fixation separated by 4°) of intermixed black and white dots (dot locations generated in a manner consistent with that described in the numerical comparison task above) for 1,000 ms. Participants were asked to indicate via a keypress which cloud, the left or the right, had a larger ratio, and then indicate whether the red dot appeared on the top or at the bottom of the fixation cross.

Table 1 outlines the parameters used for our transfer tasks. Comparison ratios refer to the ratio of one cloud’s ratio of dots to another cloud’s ratio of dots. As with all number comparison tasks, cloud ratios tested could deviate slightly from the preset ratios, which in this case were 1.2, 1.3, 1.8, 2.1, and 3. In all cases, actual cloud ratios were calculated and used in setting the comparison ratios. The comparison ratios were then set to 1.33, 1.5, 1.8, 2.4, and 4 (or the closest possible value; as always, actual ratios were used in all analyses). Trials were determined by performing a complete crossed design on the smaller number, cloud ratio, and comparison ratio parameters. In all, there were 50 repetitions per comparison ratio, or 250 actual trials that took approximately 15 min to complete. Ten practice trials were given that used easier comparison ratios (that did not overlap with the ones used in the generalization task).

Table 1 Parameter ranges used for transfer tasks
Full size table

Arithmetic test

We used the Woodcock-Johnson III Test of Achievement, a common standardized test that has often been used as a math outcome measure in studies of ANS acuity (Halberda et al., 2008; Inglis et al., 2011; Lourenco, Bonny, Fernandez, & Rao, 2012), as a measure of (relatively) far transfer to assess whether prolonged non-symbolic numerical comparison training increases arithmetic fluency and accuracy. In this study, we used the math fluency subtest as it is easy to administer, consisting of a 3-min timed test, and covers a range of arithmetic operations, including addition, subtraction, and multiplication. While fluency is only one dimension of arithmetic ability, this simple test does allow for a basic test of generalization from low-level training to higher-level skills. We used Forms A and B (one at pre-test and one at post-test) counterbalanced across participants. Birthdates, test dates, raw score, and time left were recorded for each participant and entered in CompuScore® to calculate scaled scores and grade equivalents.

Multiple object-tracking (MOT) task

Figure 2e outlines the stimulus events. A white fixation cross was present at the center of the screen throughout the task. A white circle with a radius of 6° was centered in one of the quadrants (in one block of trials, the trained quadrant, in the other block, the diagonally opposite quadrant). At the beginning of each trial, a number of moving blue (N=2) and yellow (N=6) dots, 0.4° (diameter), appeared in the white circle. After 2 s, the two blue circles changed to yellow. The (now all yellow) circles continued to move for two additional seconds. The dots did not bounce off one another, but instead passed through one another. Finally, one of the eight circles changed to white and the participant had to indicate whether or not this white probe circle was one of the original blue target circles.

Note that the parameters of the task were chosen based upon pilot data. In particular, because the task was performed in the participant’s periphery, most of the parameters (e.g., number of targets, number of distractors, movement speed, tracking time, etc.) were easier than the corresponding values when the task is performed at fixation. The task consisted of 20 trials per location and took approximately 5 min to complete.

Data analyses

Non-symbolic numerical comparison task – generalization tasks

All relevant tasks were programmed simply in terms of the ratio of the larger number of dots (or the larger ratio) to the smaller number of dots (or the smaller ratio), with the color identity randomly assigned. For analysis, this ratio was converted into a symmetric distribution around zero by first subtracting from 1 all ratios wherein there were more black dots (e.g., a ratio of 1.2 black dots to every 1 white dot would be converted into a ratio of .8), then subtracting 1 from all ratios. This scaled the ratio space such that larger negative values indicated more black dots relative to white dots, while larger positive values indicated more white dots for each black dot. The absolute value of the exact decimal value indicates the percent more of one color than the other color that was present. These values were then fit to a standard logistic psychophysical function and a 79% threshold (a psychophysical convention indicating the number ratio at which performance would be expected to be approximately 79% correct; Leek, 2001) was calculated, thus providing an estimate of the percent more of a given color that has to be present for a person to reliably identify it as the larger-number color (i.e., a threshold of .2 would mean that a person could reliably identify the larger-number color at a ratio of 1.2:1). In this, and all pre- and post-test tasks described below, only trials with correct fixation tasks were used in data analysis. In all cases, performance on the fixation task was near ceiling (e.g., trained quadrant pre-test mean = 91% correct, trained quadrant post-test mean = 95% correct), indicating good compliance with fixation instructions.

Additional statistical tests, including those that are robust to violations of some assumptions of the logistic fits and t-tests discussed below, are reported in the Supplemental Information. For all t-tests, corresponding Bayes factors are reported on a log10 scale to assist with interpretability (e.g., a BF of about .3 indicates twice as much evidence for the alternative than the null, a BF of -.6 indicates four times as much evidence for the null than the alternative, a BF of 1 indicates 10 times as much evidence for the alternative than the null).

Non-symbolic numerical comparison task – training

To examine performance on the trained task, we fit a hierarchical parametric continuous logistic function to the responses. We have previously shown that an exponentially changing logistic function provides a better fit to perceptual learning data than the more typical block-by-block fitting approach (see Kattner, Cochrane, & Green, 2017, for details). As an extension of previous by-participant fitting methods, here we fit all subjects simultaneously in a hierarchical model using R package lme4 (Bates, Mächler, Bolker, & Walker, 2015). In brief, this approach models performance as a continuous change in threshold across all trials of training. To accomplish this, threshold (θ) for each participant is each fit as a three-parameter exponentially decaying function of time (i.e., on a trial-by-trial basis), while bias (β) is fit as a by-participant constant (for full equations, see Supplemental Information). The approach thus provides an estimate of the 79% threshold on each trial of training. All participants are fit simultaneously, drawing participant-level performance parameters from group-level parameters. We note that none of the conclusions of the paper depend on this choice of data analysis and more traditional block-by-block data fitting (with learning being assessed by a comparison of the first block threshold and last block threshold) reveals the same learning patterns (see Results and Supplementary Information).

Results

Question 1: Is performance on the non-symbolic numerical comparison task improved via training, and, if so, does the improvement follow a protracted time course?

Consistent with our hypotheses, every participant's performance improved over the course of training (see Fig. 3). The estimated last-trial thresholds (M = 0.15, SD = 0.03) were reliably lower than the estimated first-trial thresholds (M = 0.27, SD = 0.10, paired-samples t-test t(9) = -4.22, p = .002, BF=1.32). This result is mirrored when examining the change in performance from pre-test to post-test (see Fig. 5). Performance on the trained quadrant improved significantly from pre-test to post-test (t(8) = -3.77, p = .005, BF=1.08). Because the trained quadrant was always tested first, the analysis above may overestimate the size of the change (participants may have still been learning how to perform the task during the pre-test). However, the outcome is unchanged (i.e., significant learning is still found) if the post-test threshold in the trained-quadrant is compared to either the average of all pre-test thresholds (t(9) = -4.64, p = .001, BF=1.54) or to the last quadrant tested during pre-testing (t(9) = -3.46, p = .007, BF=0.909). Thus, performance on this task shows unambiguous improvement via dedicated training. Consistent with earlier approaches to the interactions between stimulus dimensions (e.g., DeWind & Brannon, 2012), we analyzed pre-test and post-test differences in performance depending on the overall ratio of black and white area (i.e., pixels) on the screen. These analyses revealed no systematic pre-test or post-test differences due to stimulus area (see Supplemental Information).

Fig. 3
figure 3

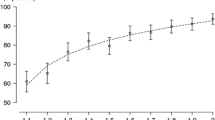
Participant-level approximate number system (ANS) threshold fits. Each line is the best-fit threshold for a participant, evaluated as random effects using the hierarchical time-evolving logistic regression. As is clear, not only do all participants show clear evidence of learning, they show evidence of protracted learning (i.e., still showing significant improvements even after 1,000 s of training trials)

Full size image

Critically, the training data also demonstrate that improvement followed a protracted time course. The hierarchical learning model fit converged with group-level starting threshold of 0.263 ±.0080, asymptote of 0.145 ±.0019, and learning rate of 3.394 ±.0439. This estimate corresponds to a typical learner starting by responding 79% correctly on number ratios of approximately 20:25 and, by trial 8,000, responding 79% correct on number ratios of approximately 20:23, while taking about 1,717 trials to complete half of this improvement. While there is quite a large range in learning rate across participants (see Fig. 3), the results are clearly indicative of a reasonably slow learning process (perhaps too slow to be detected in the previous literature – see Discussion). Further evidence for this can be seen in Fig. 4, which shows that performance on days 1 through 5 are each significantly different than participants’ thresholds on training session 22 (i.e., the last day of training that all participants completed).

Fig. 4
figure 4

Approximate number system (ANS) threshold T plot. Paired t-tests were calculated to compare each participants’ 22nd day (i.e., the last day that all participants completed) with their previous days’ thresholds. Holm-Bonferroni adjusted significance is denoted with a black outline. When testing the difference between participants’ thresholds on their 22nd training day to their previous training days, their first 5 days (including over 1,900 trials) have significantly higher thresholds than their 22nd day. Clearly improvement is a very gradual process

Full size image

Question 2: Did the training gains generalize to untrained spatial positions?

If the improvements in ANS were specific to the trained location in the visual field, we would expect no change in threshold in the untrained quadrants. If, on the other hand, the learning generalized completely across spatial locations, we would expect a significant reduction in the thresholds seen in the untrained locations. The latter pattern of results, consistent with significant learning generalization, was observed (see Fig. 5). All of the quadrants' post-test thresholds (both trained and untrained) were reliably lower than their pre-test thresholds (trained quadrant: t(8) = -3.77., p = .005, BF = 1.08, horizontally switched quadrant: t(8) = -4.85, p < .001, BF = 1.65, vertically switched quadrant: t(9) = -3.55, p = .006, BF = 0.96). Robust comparisons provide evidence for the same conclusions (see Supplementary Information). Furthermore, the post-test quadrants' (i.e., both the trained and untrained quadrants) thresholds were not different from one another (F(2,18)= 0.72, p> .4). In all, this is consistent with learning that has fully generalized across spatial location.

Fig. 5
figure 5

Approximate number system (ANS) thresholds fit to pre- and post-blocks, separated by quadrant. Each pair of bars presents the pre- (left bar/red) and post-test (right bar/teal) performance at a given location. The first pair is at the trained location. The next pair is data in the quadrant across the horizontal meridian from the trained location. The third pair is data in the quadrant across the vertical meridian from the trained location. The key finding is that all post-test blocks are very similar and are vastly superior to pre-test performance. This indicates not only learning, but fully generalized learning. Note that pre-test blocks likely differ primarily because the trained quadrant was always completed first. Error bars represent 95% confidence intervals

Full size image

Question 3: Were any changes noted in the additional generalization tasks?

Enumeration

In general, enumeration performance was consistent with previous studies of enumeration (e.g., Izard & Dehaene, 2008; Krueger, 1984). Participants’ estimates increased with numerosity, but tended to underestimate the actual numerosity, with the degree of underestimation increasing with increasing numerosity. In terms of improvement, there are two metrics that are typically used to assess number estimation performance: (1) power exponents, which reflects how well the participants’ response set matches the objective number of dots (Krueger, 1984) and (2) coefficient of variance (CV), which indexes the amount of noise in participants’ estimates (ideally corresponding to the perceptual discrimination thresholds; see Cordes, Gelman, Gallistel, & Whalen, 2001, for a discussion). Alternative analyses, which indicate a mix of significant and non-significant effects, are reported in the Supplemental Information.

We fit each participant’s data to a three-parameter power curve using the likelihood function defined in Odic, Im, Eisinger, Ly, and Halberda (2016; see Table S2 in Supplementary Information for individual participant’s fit values). We found no improvement in power exponents from pre-test (M = .63, SD = .19) to post-test (M = .64, SD = .08), t(9) = -.192, p =.852, BF = -0.50. The coefficients of variance decreased from pre-test (M = .23, SD = .06) to post-test (M = .16, SD = .14), but this difference was not significant, t(9) = 1.725, p = .119, BF = -.03. See Supplementary Information for enumeration plots.

Ratio comparison

In a paired-samples t-test, the difference between ratio comparison threshold at post-test (M = 1.71, SD = 1.37) and ratio comparison threshold at pre-test (M = 4.1, SD = 7.61) was not significant, t(9) = -1.23, p > .2, BF = -0.25. One participant had particularly poor performance at pre-test. Analyses that account for this outlier can be found in the Supplementary Information.

Arithmetic task

In a paired-samples t-test, the difference between scaled score at pre-test (M = 112.3, SD = 12.1) and post-test (M = 114.1 SD = 9.5) was not significant, t(9) = 0.726, p = .49, BF = -0.41. Examination of the raw scores showed a significant increase from pre-test (M = 142.7, SD = 20.9) to post-test (M = 150.6, SD = 18.6), t(9) = 3.43, p < .001, BF=0.90, but this was partially offset by a nonsignificant increase in time taken from pre-test (M = 2:53, SD = 11 s) to post-test (M = 2:56, SD = 6.2 s). Because of (1) the possibility for speed-accuracy trade-offs and (2) the bounded nature of the task (max time allotted was 3 min), Woodcock-Johnson manuals and materials indicate that scaled scores should be used for comparative analyses. When the amount of time taken is considered, via the scaled score, we find no evidence for transfer from our ANS training task to formal math fluency, despite longer and more intensive training than used in other studies.

Multiple-object tracking

The difference between MOT untrained-quadrant percent correct at pre-test (M = 0.78, SD = 0.16) and at post-test (M = 0.86, SD = 0.12) was not significant, t(8) = 1.322, p > .2, BF = -0.20. Although several participants have missing data due to a misunderstanding regarding the task instructions, trained-quadrant MOT shows a similar pattern (pre-test M = 0.8, SD = 0.15; post-test M = 0.81, SD = 0.1; t(5) = 0.208, p > .8, BF = -0.42).

Discussion

Here we applied perceptual learning methods to examine the extent to which the approximate number system (ANS) can be improved via long-term training. As has been found in many other domains in visual processing, we found that performance on a non-symbolic number comparison task can be enhanced by extensive experience. In contrast to previous ANS training studies (e.g., Park & Brannon, 2014), we found that improvements in ANS task performance continue over the course of thousands of training trials. Remarkably, some participants did not appear to reach a performance asymptote even after training for over 20 days including over 8,000 trials. This protracted time course of learning implicates slowly progressing neuroplastic change. In addition to having more training sessions, our study also had more days of spacing in between training days (M = 3.32 days, SD = 2.20 days; see Supplementary Information – Table S3 for details on spacing for each individual) than previous ANS studies; for example, Park and Brannon (2014) had six sessions across an average of 9 days, or an average of .6 intervening.

We also tested the specificity of the ANS improvements through a battery of tests with varying degrees of transfer distance. Perceptual learning paradigms often produce very specific improvements in processing, with an extreme example being a lack of transfer even to untrained retinotopic locations. Given the commonness of specificity of perceptual learning, and the exploratory nature of this study (we know of no other ANS training study of this duration), we included several near-transfer tasks to test for retinotopic specificity (vertically switched quadrant differences) and hemifield specificity (horizontally switched quadrant differences above and beyond the top-vertically switched differences) as well as far-transfer tests to higher-level and lower-level tasks. We found no evidence for retinotopic specificity, with all locations improving considerably with final post-test values that were statistically indistinguishable. It is important to note that although the fixation task (i.e., determine whether a red dot appeared at the top or bottom of the fixation cross) was implemented to ensure that the stimuli were presented in participants’ periphery and performance on this task (90%+) showed compliance with fixation instructions, we do not have direct data evidence that participants’ eyes did not, in fact, move from fixation cross to stimuli during the 250-ms to 500-ms interval between their presentations. Eye movement was possible, though we believe unlikely due to the highly-trained participants’ ability and motivation to comply with instructions (for similar approaches see, e.g., Green et al., 2015; Samaha & Postle, 2017).

Importantly, we found no evidence for generalization to a more-complex ratio comparison task and the arithmetic task, while the evidence for generalization to a numeric estimation task was also not reliable. These patterns of results indicate that our trained participants had induced improvements in a general-purpose approximate number processing that was not specific to the trained location in their visual field, but may not have been sufficient to affect beneficial changes in related tasks.

The transfer of improvements across the vertical meridian of visual processing, however, suggests cortical changes at a fairly high level (at some point along the visual processing hierarchy where the full visual field is represented rather than a single hemifield). This is interesting, as some other perceptual effects on numerosity have been shown to be restricted to one hemifield. For example, in the numerosity adaptation effect (Burr & Ross, 2008; Ross & Burr, 2010), participants first adapted to two dot arrays composed of different numbers of dots, one in each hemifield. After adaptation, a negative after-effect of numerosity was observed: the hemifield that previously contained the larger numerosity was perceived as containing the smaller numerosity. As this illusion depends on separate estimates of numerosity in each hemifield, it was inferred that it arose from adaptation of neurons that represent (at most) an entire hemifield, and which do not integrate across the hemifields to yield a single estimate of numerosity. Given that our training effects transferred across all visual locations equally, we infer that they must occur after the stage at which numerosity adaptation takes place.

In contrast to our clear evidence for perceptual learning, and contrary to previous studies, we did not find compelling evidence for transfer to non-ANS tasks. This is especially striking given that our training duration was at least eight times longer than the training durations in those studies. One interpretation of these results is that mere non-symbolic numerical comparison is insufficient to elicit transfer to other non-ANS tasks (Szűcs & Myers, 2017), as other studies that have found some evidence for training (e.g., Park & Brannon, 2014) used training paradigms that included not only estimation, but also mental arithmetic on non-symbolic quantities. Indeed, a direct comparison of ANS training with mental arithmetic and two conditions without mental arithmetic (non-symbolic numerical comparison, as we have done here, and matching) suggested that only non-symbolic arithmetic training yielded improvements in exact symbolic arithmetic (Park & Brannon, 2014).

Another possibility for the lack of generalization to non-ANS tasks may be the particular tasks used. For instance, the Woodcock-Johnson Test of Achievement math fluency subtest may have been an inappropriate measure for assessing arithmetic improvements from ANS training as the test largely relies on the retrieval of a known number facts (i.e., simple and automatic arithmetic knowledge). This stands in contrast to arithmetic that requires individuals to work through problems, which may rely more upon an understanding of relative magnitude to solve arithmetic problems. This is especially important to consider in a developmental context; while the math fluency test is an assessment of highly automatized processes in adults, it is more likely to test effortful processes in children, and in even in adults may reflect lifetime learning history. Finally, the literature on whether performance on the Woodcock-Johnson math fluency test, in particular, correlates with ANS acuity is inconclusive (see De Smedt et al., 2013; Schneider et al., 2017). We speculate that effortful versus automatic task demands in this test may mediate magnitude-dependent versus magnitude-independent processing, which in turn could determine the influence of ANS training on math test performance. However, this speculation is far outside the scope of the current work, and we hope that future research may test this hypothesis.

For the enumeration task, we used a number line from 0 to 100 with tick marks in increments of 5, which may have biased participants to give estimates to decades and mid-points between decades and encouraged them to use the full range (0–100) for estimates. This in turn may have influenced the change in estimation from pre-test to post-test as there was more room on the number line for huge shifts in estimates than in the range presented (11–74). While most participants gave estimates within the range of numerosities presented, Subject 7 and Subject 8 gave many estimates in the range 75–100 at post-test (see Supplemental Information, Fig. S2).

Finally, the different tasks may have unexpected working memory demands related to the fixation task. Holding the answer to the fixation task in working memory may have been more difficult for some tasks, such as the enumeration task where the response is a numerical guess that needs to be located on the number line as opposed to a left-right key response. In addition, participants had practice accounting for this working memory demand for the non-symbolic numerical comparison task during training, but not for the non-ANS tasks.

Despite the lack of compelling transfer to non-ANS tasks, caution is warranted in interpreting this as evidence against the possibility of utilizing ANS training for applied contexts (e.g., education). Our small proof-of-concept test involved relatively high-performing adults, and thus the applicability to other populations is unclear. Rather, our clear improvements in ANS performance over many days of performance (with less than 30 min a day of training), combined with the lack of retinotopic specificity characteristic of some perceptual learning as well as the possible improvements seen in the enumeration task, should encourage further investigations into whether ANS training can be applied to other non-ANS tasks. Our long-term training with experienced psychophysical observers indicates the existence of protracted ANS plasticity that may be used to inform the construction and test of future applications. Indeed, the base learning results are consistent with a number of recent models in the domain of perceptual learning including those that involve changes in certain forms of noise (Lu & Dosher, 2009), those that involve the development of better templates for the key information in the task and through this more efficient accumulation of statistical evidence (Bejjanki et al., 2014; Green, Pouget, & Bavelier, 2010), and those that view perceptual learning as involving a mixture of low-level (e.g., sensory) and high-level (e.g., task-related) learning (Shibata, Sagi, & Watanabe, 2014; Wang et al., 2016). These hypotheses can be disambiguated via more definitive patterns of generalization and this would be a key future direction.

Indeed, the approach utilized here was specifically meant to show that ANS performance can be improved through training (cf. Lindskog & Winman, 2016), that improvements continue for many sessions (cf. Park & Brannon, 2014), and that these improvements do not have the location-specificity characteristic of low-level perceptual learning. We did not intend this study to definitively answer questions about the possibility for generalization to non-ANS tasks. Future studies in this vein would require a shift in a number of the methods (e.g., as the use of an appropriately chosen control group Green, Strobach, & Schubert, 2014). However, to this point, we also note that participants in general did not show changes in the abilities of the sort that would be controlled for via such studies (e.g., changes in performance from pre-test to post-test were not uniform across tasks).

Studies designed with the goal of engendering learning generalization would also likely need to be adapted to incorporate principles known to increase the likelihood/magnitude of learning generalization (Deveau, Lovcik, & Seitz, 2013; Vinogradov, Fisher, & de Villers-Sidani, 2012). For instance, in the current study, we utilized the exact same task throughout training with no variety/variability in any aspect (other than the particular number ratios in the blocks). While this will tend to be effective in producing learning on the task, it is not the best procedure for inducing learning generalization – which would necessitate additional variety of experience (Braun, Aertsen, Wolpert, & Mehring, 2009; Schmidt & Bjork, 1992; Xiao et al., 2008).

It may also be the case that our pattern of results would be different in a less expert group. For instance, it is currently unclear whether expertise should amplify or suppress learning generalization (Behrmann & Ewell, 2003; Rosalie & Müller, 2014). These, plus the fact that the use of a highly-selected population leads to concerns regarding the ability to generalize results to a broader population, mean that further studies with novice psychophysics participants are necessary. In addition, we hope that the neuroplasticity in high-functioning young adults we demonstrated will be tested in higher-powered studies including children and individuals with dyscalculia in order to inform the development of the applications of this extended training paradigm.

We have demonstrated plasticity in ANS using extensive training, and these improvements are not specific to the exact task trained. Our data complement the plasticity observed in previous short-term training studies while also providing the motivation for future long-term training in novices.