1 INTRODUCTION

Based on the methods of reference integral curves (RICs) [2] and the generalized optimal invariant-unbiased estimation [3], a method is developed in [1] that allows constructing the approximate general solution to the equation describing a dynamical object (DO) in the given domain of admissibility (considered in the current work) and computing the values of different continuous linear functionals (CLFs) (in the following, called numerical characteristics) of integral curves of DO based on incorrect data (this question will be considered in the subsequent works). These data are represented by the additive observations of readings of integral curve, fluctuation error, and singular interference. The traditional Gaussian noise model was used to describe the error, and the corresponding finite linear combinations with the given basis functions and unknown spectral coefficients were applied to form the models of the curve and interference.

A family of RICs and the principle of smooth dependence of the sought solution on the time, on the initial condition, and on the uncertainty parameters in the right-hand side of the differential equation were used to construct the approximate solution in [1] for a wide class of DOs. The CLF values were determined based on the idea of autocompensating optimal estimation invariant to the singular interference, not requiring the traditional extension of the state space, and admitting separate estimation of any linear numerical characteristic of the integral curve of this equation. Experience shows [4–7] that it is exactly this approach that is particularly fruitful in creating prospective information-measurement complexes intended to processing data in real time.

The following facts belong to the disadvantages of the method considered in [1]: only the scalar DO is considered and directly the integral curve of the DO plays a role of the measured parameter, which, as a rule, not fully corresponds to the practice needs. In addition, only the estimation of the CLF of this curve is concerned, although for most applied problems it is more topical to estimate numerical characteristics (for instance, the derivatives of different orders) of the measured output of the DO [5–7].

The method of [1] must be significantly updated in order to orient its main concepts and results to the real information-measurement complexes in the construction of which the basic criterion is the accuracy/speed criterion with account for strict constraints on the computational resources. In the current work we propose the modified numerical-analytic method for describing and estimating the input and output parameters of the multidimensional DO intended to analyzing the general solution to the differential equation and the measured output of this DO approximately for a given domain of admissibility.

2 PROBLEM FORMULATION

Suppose that the multidimensional DO is described by the ordinary differential equation (in the Cauchy form)

$$\frac{dx}{dt}=f(t,x),\quad t\in G_{t}=[t_{0},t_{0}+T],\quad x\in G_{x},$$
(1)

where \(t\) is the time, \(x=x(t,x_{0})=[x_{i}(t,x_{0})\), \(i=\overline{1,I}]^{\top}\) is the vector solution to the equation with the initial condition \(x_{0}=x(t_{0},x_{0})=[x_{i0}\), \(i=\overline{1,I}]^{\top}\in G_{x0}\subseteq G_{x}\), \(G_{x}\) is the closed convex domain corresponding to all possible states of DO starting with any initial condition belonging to the hyperparallelepiped \(G_{x0}=\{x_{0}\in G_{x0}\): \(c_{i}\leq x_{i0}\leq d_{i}\), \(i=\overline{1,I}\}\), \(G_{t}=[t_{0},t_{0}+T]\) is the time interval at which the DO state is considered, \(f(t,x)\) is the function satisfying the known conditions of existence and uniqueness of the solution to Eq. (1) with the Lipshitz constant \(L_{0}\) on the set \(G_{xt}=\{G_{x},G_{t}\}\) and, in addition, ensuring the necessary smoothness of this solution on \(G_{xt}\) typical for the considered class of DOs.

Equation (1) may be put into correspondence with the approximate analytic solution \(\tilde{x}=\tilde{x}(t,x_{0})\), where \(\tilde{x}_{0}=\tilde{x}(t_{0},x_{0})\); here, in the general case

$$||\tilde{x}_{0}-x_{0}||=\max\limits_{i}|\tilde{x}_{i0}-x_{i0}|\neq 0,\quad i=\overline{1,I}.$$

We think that \(\tilde{x}=\tilde{x}(t,x_{0})=[\tilde{x}_{i}(t,x_{0})\), \(i=\overline{1,I}]^{\top}\) is the solution \(\varepsilon_{0}\)-approximate by the residual [8], that is,

$$||\tilde{x}_{0}-x_{0}||\leq\varepsilon_{0},\quad\frac{d\tilde{x}_{i}}{dt}=f_{i}(t,\tilde{x})+\chi_{i}(t),$$

where the residuals \(\chi_{i}(t)\) satisfy the inequality

$$||\chi(t)||=\max\limits_{i,t}|\chi_{i}(t)|\leq\varepsilon_{0},\quad t\in G_{t}.$$

Here, the constant \(\varepsilon_{0}>0\) determines the accuracy of the generated approximate analytic solution in the domain \(G_{xt}=\{G_{x},G_{t}\}\) with account for the fact that \(x_{0}\), \(\tilde{x}_{0}\in G_{x0}\).

We characterize proximity of the exact \(x_{i}=x_{i}(t,x_{0})\) and approximate \(\tilde{x}_{i}=\tilde{x}_{i}(t,x_{0})\) phase coordinates of DO in \(G_{xt}\) by the residual

$$\varepsilon_{xi}(x_{0})=||\tilde{x}_{i}-x_{i}||=\max\limits_{t}|\tilde{x}_{i}(t,x_{0})-x_{i}(t,x_{0})|,\quad t\in G_{t},$$

respectively, for estimating proximity of their \(r\)th-order derivatives, we introduce the residual

$$\varepsilon_{xi}^{(r)}(x_{0})=\max\limits_{t}||\tilde{x}_{i}^{(r)}-x_{i}^{(r)}||.$$

To estimate proximity of solutions \(x=x(t,x_{0})\), \(\tilde{x}=\tilde{x}(t,x_{0})\) and their derivatives, we use the residuals \(\varepsilon_{x}(x_{0})=\max\limits_{i}\varepsilon_{xi}(x_{0})\) and \(\varepsilon_{x}^{(r)}(x_{0})=\max\limits_{i}\varepsilon_{xi}^{(r)}(x_{0})\), respectively.

We also prescribe the vector equation of the measured output of DO [9, 10]:

$$y=\varphi(t,x),\quad y\in G_{yt},$$
(2)

where \(y=[y_{j}(t,x_{0})\), \(j=\overline{1,J}]^{\top}\) is the vector of variable parameters (in the general case it is a nonlinear function of the output), and \(\varphi(t,x)\) is a smooth function of its arguments.

As applied to the domains \(G_{x0}\) and \(G_{t}\), we need to generate the algorithm for constructing the numerical-analytic general solution \(\tilde{x}(t,x_{0})\) for a multidimensional DO (1), discuss the issues of accuracy and optimization of the choice of parameters of this algorithm, and develop the algorithm for constructing the numerical-analytic expression for the vector measured output of the DO (2).

3 NUMERICAL-ANALYTIC SOLUTION TO DIFFERENTIAL EQUATION FOR A MULTIDIMENSIONAL DYNAMICAL OBJECT

In the domain \(G_{x0}\) we consider the grid consisting of nodes \(x_{0(r)}\in G_{x0}\), \(r\in\overline{1,M}\). We put these nodes into correspondence with the family of RICs

$$x_{i(r)}=x_{i}(t,x_{0(r)}),\quad i=\overline{1,I},\quad r=\overline{1,M_{x}},$$
(3)

where \(t\) is the time and \(x_{0(r)}\) is the initial condition \(x_{0}\) corresponding to the \(r\)th node.

In the following, we will ignore the errors of RIC construction (similar to works [1, 2]). In practice these RICs are specified in the tabular form.

Next, in the domain \(G_{t}\) we generate the small-sized grid \(\{t_{(k)}\}_{k=1}^{M_{t}}\) in time \(t\) (sufficient for representation of phase coordinates \(x_{i}(t,x_{0(r)})\) in the domain \(G_{xt}=\{G_{x},G_{t}\}\) with the required accuracy) and generate the sample of numbers on this grid

$$x_{i(rk)}=x_{i}(t_{(k)},x_{0(r)}),\quad i=\overline{1,I},\quad r=\overline{1,M_{x}},\quad k=\overline{1,M_{t}}.$$
(4)

By interpolating this sample corresponding to the fixed \(i\) and \(r\), we associate the RIC \(x_{i}(t,x_{0(r)})\) with the function of the known class

$$\tilde{x}_{i(r)}(t)=J_{i}(t,a_{ir}),$$
(5)

where \(a_{ir}=[a_{irk}\), \(k=\overline{1,M_{t}}]^{\top}\) is the vector of coefficients which is selected so that the values \(\tilde{x}_{i(r)}(t)\) coincide with the values \(x_{i}(t,x_{0(r)})\) in the \(M_{t}\) in the interpolation nodes,

$$\tilde{x}_{i(r)}(t_{(k)})=J_{i}(t_{(k)},a_{ir})=\tilde{x}_{i(rk)}=x_{i(rk)},\quad k=\overline{1,M_{t}}.$$
(6)

The coefficients \(\{a_{irk}\}_{k=1}^{M_{t}}\) are found with account for satisfaction of these equalities and can be tabulated or stored in the computer memory.

Now, we proceed to the grid in the initial condition \(x_{0}\) with the nodes \(x_{0(r)}\in G_{x0}\). For fixed \(i\in\overline{1,I}\) and \(k\in\overline{1,M_{t}}\) we put the nodes \(x_{0(1)},\dots,x_{0(M_{x})}\) into correspondence with the set of values \(a_{i1k},\dots,a_{iM_{x}k}\) and perform their interpolation by associating them with the function of the known class

$$a_{ik}(x_{0})=w_{i}(x_{0},b_{ik}),$$
(7)

where \(b_{ik}=[b_{irk}\), \(r=\overline{1,M_{x}}]^{\top}\) is the vector of coefficients chosen by the condition

$$a_{ik}(x_{0(r)})=w_{i}(x_{0(r)},b_{ik})=a_{irk},\quad r=\overline{1,M_{x}}.$$
(8)

The coefficients \(\{b_{irk}\}_{r=1}^{M_{x}}\) may also be tabulated or stored in the computer memory. Similarly to the above discussed technique, we carry out interpolation for all \(i=\overline{1,I}\), \(r\in\overline{1,M_{x}}\), and \(k\in\overline{1,M_{t}}\).

We may present the numerical-analytic solution to Eq. (1) in the following vector form

$$\tilde{x}=\tilde{x}(t,x_{0})=J(t,A(x_{0})),$$
(9)

where \(J(t,A(x_{0}))=[J_{i}(t,A_{i}(x_{0}))\), \(i=\overline{1,I}]^{\top}\) and \(A_{i}(x_{0})=[a_{ik}(x_{0})\), \(k=\overline{1,M_{t}}]^{\top}\).

If we use the procedures of linear interpolation or approximation (similarly to works [1, 2]) for describing the DO in the domain \(G_{xt}=\{G_{x},G_{t}\}\), then we write the approximate solution as

$$\tilde{x}_{i}=A_{i}^{\top}(x_{0})\Psi_{x}(t),\quad i=\overline{1,I},\quad x_{0}\in G_{x0},\quad t\in G_{t},$$
(10)

where \(A_{i}(x_{0})=[a_{ik}(x_{0})\), \(k=\overline{1,M_{t}}]^{\top}\) is the functional vector of unknown coefficients \(a_{ik}(x_{0})\) that possess the necessary smoothness with respect to the argument \(x_{0}\) and \(\Psi_{x}(t)=[\psi_{xk}(t)\), \(k=\overline{1,M_{t}}]^{\top}\) is the vector of prescribed smooth basis functions of the argument \(t\), which is in general dependent on the index \(i\in\overline{1,I}\).

To characterize the elements of the vector \(A_{i}(x_{0})\), we use the notation

$$a_{ik}(x_{0})=B_{ik}^{\top}\Lambda_{xi}(x_{0}),$$
(11)

where \(B_{ik}=[b_{irk}\), \(r=\overline{1,M_{x}}]^{\top}\) is the vector of unknown coefficients, \(\Lambda_{xi}(x_{0})=[\lambda_{xir}(x_{0})\), \(r=\overline{1,M_{x}}]^{\top}\) is the vector of prescribed smooth basis functions of the argument \(x_{0}\).

As a result, we obtain the solution

$$\tilde{x}_{i}(t,x_{0})=\sum\limits_{k=1}^{M_{t}}a_{ik}(x_{0})\psi_{xk}(t)=\sum\limits_{k=1}^{M_{t}}\sum\limits_{r=1}^{M_{x}}b_{irk}\lambda_{xir}(x_{0})\psi_{xk}(t)=\Psi_{x}^{\top}(t)B_{i}\Lambda_{xi}(x_{0}),\quad i=\overline{1,I},$$
(12)

where \(B_{i}=[b_{irk}\), \(k=\overline{1,M_{t}}\), \(r=\overline{1,M_{x}}]\) is the matrix of unknown coefficients corresponding to the \(i\)th phase coordinate of the DO state vector.

In order to determine the coefficients \(b_{irk}\), we use the family of RICs. We perform interpolation or approximation of the given array (for a fixed \(i\in\overline{1,I}\) ) with account for (12) and find the estimate \(B_{i}^{*}\) of the matrix \(B_{i}\). Here, the conditions are fulfilled for the interpolation

$$\tilde{x}_{i}(t_{(k)},x_{0(r)})=\Psi_{x}^{\top}(t_{(k)})B_{i}\Lambda_{xi}(x_{0(r)})=x_{i(rk)},\quad r=\overline{1,M_{x}},\quad k=\overline{1,M_{t}}.$$
(13)

They form the system of linear equations. After its solution we obtain the sought estimate \(B_{i}^{*}\) of the matrix \(B_{i}\). In the case of approximation the solution \(B_{i}^{*}\) (for a fixed \(i\)) is determined in the form

$$B_{i}^{*}=\arg\max\limits_{B_{i}}\sum\limits_{k=1}^{M_{t}}\sum\limits_{r=1}^{M_{x}}[\Psi_{x}^{\top}(t_{(k)})B_{i}\Lambda_{xi}(x_{0(r)})-x_{i(rk)}]^{2}.$$
(14)

After determining the matrices \(B_{i}^{*}\) for all \(i\), we construct the sought numerical-analytic solution \(\tilde{x}(t,x_{0})=[\tilde{x}_{i}(t,x_{0})\), \(i=\overline{1,I}]^{\top}\) to differential Eq. (1),

$$\tilde{x}_{i}(t,x_{0})=\sum\limits_{k=1}^{M_{t}}\sum\limits_{r=1}^{M_{x}}b_{irk}^{*}\lambda_{xir}(x_{0})\psi_{xk}(t)=\Psi_{x}^{\top}(t)B_{i}^{*}\Lambda_{xi}(x_{0}),\quad i=\overline{1,I}.$$
(15)

We must keep in mind that, in the construction of the family of RICs, we apply the temporal computational grid of a large size which is many times the size \(M_{t}\) of the interpolation (approximation) grid \(\{t_{(k)}\}_{k=1}^{M_{t}}\) in \(t\). In addition, for many DOs the dependence of the solution \(x(t,x_{0})\) on \(x_{0}\) is weakly pronounced, which considerably reduces the size \(M_{x}\) of the computational grid in the initial condition \(x_{0}\) and simplifies the interpolation (approximation) procedure for constructing the numerical-analytic solution \(\tilde{x}(t,x_{0})\) to Eq. (1) describing the DO.

Using the rational choice of the main parameters in expressions (3)–(15) of the developed method, we may construct the solution \(\tilde{x}(t,x_{0})\) to Eq. (1) that provides the accuracy of DO analysis in the domain of admissibility \(G_{xt}\) required in practice. We may designate the sizes of the used grids (\(M_{t}\) and \(M_{x}\)) as the parameters which allow achieving such accuracy.

Let us specify the procedure for constructing \(\tilde{x}(t,x_{0})\) in the case when the fundamental interpolation polynomials (as a tensor product of one-dimensional fundamental polynomials [11]) are used in expression (12). For this purpose, in the domain \(G_{x0}\) of possible initial conditions we prescribe the small-sized multidimensional calculation grid \(\{x_{0(m)}\}=\{x_{0(m_{1},\dots,m_{I})}\}\) (where \(m=(m_{1},\dots,m_{I})\) is the multidimensional node, \(m_{i}=\overline{1,M_{xi}}\), \(i=\overline{1,I}\), and \(\prod\limits_{i=1}^{I}M_{xi}=M_{x}\) is the grid size). For all its nodes we construct the family of RICs using any of the known high-precision numerical methods [11–13] on some large-sized temporal grid covering the domain \(G_{t}\) (for convenience’s sake we use continuous time):

$$x_{i(m)}=x_{i(m_{1},\dots,m_{I})}=x_{i}(t,x_{0(m)})=x_{i}(t,x_{0(m_{1},\dots,m_{I})}),\quad i=\overline{1,I}.$$
(16)

In the segment \(c_{i}\leq x_{i0}\leq d_{i}\), we specify the nodes \(x_{i0(1)},\dots,x_{i0(M_{xi})}\) and set

$$\psi_{xk}(t)=L_{(k)}(t)=\prod\limits_{j=1,\ j\neq k}^{M_{t}}\frac{t-t_{(j)}}{t_{(k)}-t_{(j)}}.$$

In this case solution (12) may be represented as

$$\tilde{x}_{i}(t,x_{0})=\sum\limits_{k=1}^{M_{t}}\sum\limits_{m}x_{i(mk)}L_{(k)}(t)L_{(m)}(x_{0}),\quad i=\overline{1,I},$$
(17)

where \(\sum\limits_{m}\) is the multidimensional sum,

$$L_{(m)}(x_{0})=L_{(m_{1},\dots,m_{I})}(x_{01},\dots,x_{0I})=\prod\limits_{i=1}^{I}L_{(m_{i})}(x_{i0}),$$
$$L_{(m_{i})}(x_{i0})=\sum\limits_{q=1,\ q\neq m_{i}}^{M_{xi}}\frac{x_{i0}-x_{i0(q)}}{x_{i0(m_{i})}-x_{i0(q)}}.$$

In addition to that, it is sometimes purposeful to use irregular spased grids, for instance, such that has the interpolation nodes \(x_{i0(m_{i})}\) and \(t_{(k)}\) coinciding with the roots of Chebyshev polynomials [1]. In this case the following estimate is valid for the residual \(\varepsilon_{xi}\) between the phase coordinates \(x_{i}(t,x_{0})\) and \(\tilde{x}_{i}(t,x_{0})\) (similarly to [8])

$$\varepsilon_{xi}(x_{0})=||\tilde{x}_{i}(t,x_{0})-x_{i}(t,x_{0})||\leq\varepsilon_{0}[(L_{0}^{-1}+1)\exp(L_{0}|t-t_{0}|)-L_{0}^{-1}].$$
(18)

Analogously, we have the estimate for assessing proximity of the solutions \(x(t,x_{0})\) and \(\tilde{x}(t,x_{0})\),

$$\varepsilon_{x}(x_{0})=\max\limits_{i}\varepsilon_{xi}(x_{0})\leq\varepsilon_{0}\{\sqrt{I}\exp(L_{0}I^{2}T)+(L_{0}I)^{-1}[\exp(L_{0}I^{2}T)-1]\}.$$
(19)

At \(I=1\) estimate (18) follows from (19).

The obtained relations allow optimizing the choice of parameters of the developed method for constructing the approximate analytic solution characterizing the DO state. We rely on works [11–13] and may also evaluate the contribution of the inherited and roundoff errors to the total error of the approximate solution to Eq. (1) for the domain \(G_{xt}=\{G_{x},G_{t}\}\).

Relations (3)–(19) reflect the essence of the numerical-analytic method for describing the state vector of multidimensional DO for a given set of addmissibility of the temporal coordinate and initial condition.

4 NUMERICAL-ANALYTIC DESCRIPTION OF MEASURED OUTPUT FOR A MULTIDIMENSIONAL DYNAMICAL OBJECT

The exact measured vector output of the multidimensional DO may be represented as

$$y=\varphi(t,x(t,x_{0}))=\gamma(t,x_{0}),$$
(20)

where \(x_{0}\in G_{x0}\), \(t\in G_{t}\), \(y\in G_{yt}\), and \(\varphi\): \(G_{xt}\to G_{yt}\).

Therefore, for the approximate DO output we have

$$\tilde{y}=\varphi(t,\tilde{x}(t,x_{0}))=\tilde{\gamma}(t,x_{0}),\quad x_{0}\in G_{x0},\quad t\in G_{t},\quad y\in G_{yt}.$$
(21)

For the numerical-analytic description of the measured output of DO, we may also use the family of RICs and apply the principle of smooth dependence \(y=\gamma(t,x_{0})\) on the initial condition \(x_{0}\in G_{x0}\). To this end, we put the family of RICs \(x_{(r)}=x(t,x_{0(r)})\), \(r=\overline{1,M_{x}}\) into correspondence with the family of output trajectories

$$y_{j(r)}=\varphi_{j}(t,x(t,x_{0(r)}))=\gamma_{j}(t,x_{0(r)}),\quad j\in\overline{1,J},$$
(22)

which may be presented as an array of numbers

$$y_{j(rk)}=\varphi_{j}(t_{(k)},x(t_{(k)},x_{0(r)}))=\gamma_{j}(t_{(k)},x_{0(r)}),\quad r=\overline{1,M_{x}},\quad k=\overline{1,K}.$$
(23)

Then, we use the approximation

$$\tilde{y}_{j}=V_{j}^{\top}(x_{0})\Psi_{yj}(t),\quad x_{0}\in G_{x0},\quad t\in G_{t},$$
(24)

where \(V_{j}(x_{0})=[v_{jk}(x_{0})\), \(k=\overline{1,M_{t}}]^{\top}\) is the functional vector of unknown coefficients \(v_{jk}(x_{0})\) which have the necessary smoothness with respect to the argument \(x_{0}\); \(\Psi_{yj}(t)=[\psi_{yjk}(t)\), \(k=\overline{1,M_{t}}]^{\top}\) is the vector of prescribed smooth basis functions of the argument \(t\) (in the choice of vector \(\Psi_{yj}(t)\) we account for possibility of accurate and sufficient description of the output trajectory \(y_{j}=\gamma_{j}(t,x_{0})\) in the domain \(G_{yt}\) and some computational aspects).

We determine the elements of vector \(V_{j}(x_{0})\) by

$$v_{jk}(x_{0})=W_{jk}^{\top}\Lambda_{yj}(x_{0}),$$
(25)

where \(W_{jk}=[w_{jrk}\), \(r=\overline{1,M_{x}}]^{\top}\) is the vector of unknown coefficients, \(\Lambda_{yj}(x_{0})=[\lambda_{yjr}(x_{0})\), \(r=\overline{1,M_{x}}]^{\top}\) is the vector of smooth basis functions of \(x_{0}\), which is in general dependent on the index \(j\in\overline{1,J}\).

Thus, the \(j\)th scalar measured output of DO may be characterized in the numerical-analytic form

$$\tilde{y}_{j}=\tilde{\gamma}_{j}(t,x_{0})=\sum\limits_{k=1}^{M_{t}}v_{jk}(x_{0})\psi_{yjk}(t)=\sum\limits_{k=1}^{M_{t}}\sum\limits_{r=1}^{M_{x}}w_{jrk}\lambda_{yjr}(x_{0})\psi_{yjk}(t)=\Psi_{yj}^{\top}(t)W_{j}\Lambda_{yj}(x_{0}),$$
(26)

where \(W_{j}=[w_{jrk}\), \(k=\overline{1,M_{t}}\), \(r=\overline{1,M_{x}}]\) is the matrix of unknown coefficients.

To determine the estimate \(W_{j}^{*}\) of the matrix \(W_{j}\), we may also use the interpolation or the approximation approach. In the first case we account for the corresponding characteristic interpolation conditions (for a fixed \(j\)):

$$\tilde{\gamma}_{j}(t_{(k)},x_{0(r)})=\Psi_{yj}^{\top}(t_{(k)})W_{j}\Lambda_{yj}(x_{0(r)})=y_{j(rk)},\quad k=\overline{1,M_{t}},\quad r=\overline{1,M_{x}}.$$
(27)

They specify the system of linear equations. We solve this system and find the desired estimate \(W_{j}^{*}\) of the matrix \(W_{j}\). In the second case the solution \(W_{j}^{*}\) (for a fixed \(j\)) is represented as

$$W_{j}^{*}=\arg\max\limits_{W_{j}}\sum\limits_{k=1}^{M_{t}}\sum\limits_{r=1}^{M_{x}}[\Psi_{yj}^{\top}(t_{(k)})W_{j}\Lambda_{yj}(x_{0(r)})-y_{j(rk)}]^{2}.$$
(28)

After determining the matrices \(W_{j}^{*}\) for all \(j\), we construct the sought numerical-analytic representation \(\tilde{y}(t)=[\tilde{\gamma}_{j}(t,x_{0})\), \(j=\overline{1,J}]^{\top}\) for the measured output of DO,

$$\tilde{y}_{j}=\tilde{\gamma}_{j}(t,x_{0})=\sum\limits_{k=1}^{M_{t}}\sum\limits_{r=1}^{M_{x}}w^{*}_{jrk}\lambda_{yjr}(x_{0})\psi_{yjk}(t)=\Psi_{yj}^{\top}(t)W_{j}^{*}\Lambda_{yj}(x_{0}),\quad j=\overline{1,J}.$$
(29)

In the special case, by analogy with (17) we may represent the measured output of the DO in the form

$$\tilde{y}_{j}=\tilde{\gamma}_{j}(t,x_{0})=\sum\limits_{k=1}^{M_{t}}\sum\limits_{m}y_{j(mk)}L_{j(k)}(t)L_{j(m)}(x_{0}),\quad j=\overline{1,J}.$$
(30)

Expression (30) is most convenient in numerical-analytic calculations.

Thus, on the basis of (20)–(30), by choosing the main parameters of the developed method rationally, we may construct the approximate analytic expression for the vector of measured parameters \(y=\varphi(t,x(t,x_{0}))=\gamma(t,x_{0})\) which provides the practically required accuracy of analysis of the DO output vector in the domain of admissibility \(G_{yt}\). Among these parameters are constants \(M_{t}\) and \(M_{x}\) and functions \(\Lambda_{yj}(x_{0})\) and \(\Psi_{yj}(t)\).

5 SOME GENERALIZATIONS, COMPUTATIONAL ASPECTS, AND RECOMMENDATIONS

It is not hard to generalized the above proposed approach for constructing the approximate analytic solution to Eq. (1) for the multidimensional DO to the DOs of the form

$$\frac{dz}{dt}=\bar{f}(t,z,\eta),\quad z\in G_{z},\quad\eta\in G_{\eta},$$

where \(z=[z_{i}\), \(i=\overline{1,I_{1}}]^{\top}\) is the DO state vector, \(\eta=[\eta_{i}\), \(i=\overline{1,I_{2}}]^{\top}\) is the vector of constant parameters for which we can only point some domain of admissibility \(G_{\eta}\).

We suppose

$$t\in G_{t}=[t_{0},t_{0}+T];\quad z_{0}=z(t_{0})\in G_{z0}=\{[c_{1},d_{1}],[c_{2},d_{2}],\dots,[c_{I_{1}},d_{I_{1}}]\};\quad G_{z0}\subseteq G_{z};$$
$$\eta\in G_{\eta}=\{[r_{1},p_{1}],[r_{2},p_{2}],\dots,[r_{I_{2}},p_{I_{2}}]\}.$$

We introduce the extended vector \(x=[z^{\top},\eta^{\top}]^{\top}\) of dimension \(I=I_{1}+I_{2}\) and take into account that \(d\eta/dt\equiv 0\), thus arriving at Eq. (1), in which

$$f(t,x)=[f_{i}(t,x),\ i=\overline{1,I}]^{\top}=[\bar{f}_{i}(t,z,\eta),\ i=\overline{1,I_{1}},\quad\bar{f}_{i}(t,z,\eta),\ i=\overline{I_{1}+1,I}]^{\top},$$

where \(\bar{f}_{i}(t,z,\eta)\equiv 0\), \(i=\overline{I_{1}+1,I}\), and \(G_{xt}=\{G_{z},G_{\eta},G_{t}\}\).

Thus, the class of more general DOs which are widely used in practice (for instance, in ballistics [14] and several problems of identification and optimal control [15]) also fits the sphere of application of the developed method.

6 ILLUSTRATIVE EXAMPLE

To estimate the efficiency of the proposed method, we restrict ourselves with the DO corresponding to a rocket moving in the homogeneous gravity field with the linear law of mass flow rate without resistance of surrounding medium. It was shown in [16] that the considered case is a well illustrative example for testing various numerical-analytic methods. The curvilinear motion of a rocket is described by the system of differential equations (here, time is measured in seconds)

$$\frac{dz_{1}}{dt}=-g_{0}z_{2}^{-1},\quad\frac{dz_{2}}{dt}=c_{v}\eta(1-\eta t)^{-1}-g_{0}\text{th}\,(z_{1}),$$

where \(z_{1}=x_{1}\) is the phase (dimensionless) coordinate corresponding to the angle \(\beta\) (rad) of inclination of the velocity vector to the horizon

$$z_{1}=\ln[\textrm{tan}\ (\pi/4+\beta/2)],$$

\(z_{2}=x_{2}\) is the rocket velocity (m/s), \(g_{0}\) is the gravity acceleration (m/s\({}^{2}\)), \(\eta=x_{3}\) is the rocket specific mass flow rate (s\({}^{-1}\)), which is regarded as an uncertainty parameter, and \(c_{v}\) is the relative velocity of expelled particles (m/s).

Next, we suppose that \(g_{0}=9.80665\), \(c_{v}=2290\), \(t_{0}=0\), \(T=70\), \(x_{i0}=x_{i}(0)\in G_{xi}=[c_{i},d_{i}]\), \(i=\overline{1,3}\), \(c_{1}=1.0107\), \(d_{1}=2.4362\), \(c_{2}=100\), \(d_{2}=200\), \(c_{3}=r=0.0060\), and \(d_{3}=p=0.0100\).

As a measured parameter \(y\) we use the angle \(\beta\), that is, \(J=1\), \(y=\beta\) (in the formulas below we omit the index \(j\)), \(I_{1}=2\), \(I_{2}=1\), and

$$f_{1}(t,x)=-g_{0}x_{2}^{-1},\quad f_{2}(t,x)=c_{v}x_{3}(1-x_{3}t)^{-1}-g_{0}\text{th}\,(x_{1}),\quad f_{3}(t,x)\equiv 0,$$
$$m=(m_{1},m_{2},m_{3}),\quad M_{x1}=4,\quad M_{x2}=6,\quad M_{x3}=5,\quad M_{x}=M_{x1}M_{x2}M_{x3}=120,$$
$$M_{t}=11,\quad\psi_{xk}(t)=L_{(k)}(t),\quad t_{(k)}=7(k-1);\quad k=\overline{1,11},$$
$$L_{(m)}(x_{0})=L_{(m_{1},m_{2},m_{3})}(x_{01},x_{02},x_{03})=L_{(m_{1})}(x_{10})L_{(m_{2})}(x_{20})L_{(m_{3})}(x_{30}).$$

In the computations the accuracy of floating-point data was \(2{,}2\cdot 10^{-16}\). The results of computations are rounded up to the fourth decimal places.

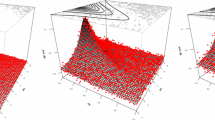
To construct the family of RICs, we used the fourth-order Runge–Kutta method. For the illustrative purposes we applied the special residual \(\bar{\varepsilon}_{xi}=|x_{i}(t,x_{0})-\tilde{x}_{i}(t,x_{0})|\), \(i\in\{1,2\}\) as a function of time \(t\) and initial condition \(x_{0}\) to estimate the accuracy. Thus, Fig. 1 presents the dependence of the special residual \(\bar{\varepsilon}_{x1}\) on \(t\) and \(x_{10}\) for fixed values \(x_{20}=104\) and \(x_{30}=0.0063\). Here, in the original domain \(\{G_{x0},G_{t}\}\) we have the general residual \(\varepsilon_{x1}=\max\limits_{x_{0}}\varepsilon_{x1}(x_{0})=0.0020\), where

$$\varepsilon_{x1}(x_{0})=\max\limits_{t}|\tilde{x}_{1}(t,x_{0})-x_{1}(t,x_{0})|,$$

which counts to 0.3237\(\%\). This maximum corresponds to the node with the coordinates \(t=27\), \(x_{10}=2.1466\), \(x_{20}=104\), and \(x_{30}=0.0063\). In the truncated domain \(\{\bar{G}_{x0},\bar{G}_{t}\}\) (where \(\bar{G}_{x0}=\{[1.3170,1.7454],[120,180],[0.0070,0.0090]\}\) and \(\bar{G_{t}}=[7,63]\)) we obtained the total residual \(\varepsilon_{x1}=0.0004\), which counts to 0.1853\(\%\). The maximum corresponds to the node (\(t=36\), \(x_{10}=1.5065\), \(x_{20}=128\), \(x_{30}=0.0070\)).

Fig. 1
figure 1

Special residual \(\bar{\varepsilon}_{x1}\) over \(t\) and \(x_{10}\) for fixed values \(x_{20}\) and \(x_{30}\).

Full size image

Figure 2 shows the dependence of the special residual \(\bar{\varepsilon}_{x2}\) on \(t\) and \(x_{30}\) for fixed values \(x_{10}=2.1466\) and \(x_{20}=124\). Here, in the original domain \(\{G_{x0},G_{t}\}\) we have the total residual \(\varepsilon_{x2}=\max\limits_{x_{0}}\varepsilon_{x2}(x_{0})=4.0542\), where

$$\varepsilon_{x2}(x_{0})=\max\limits_{t}|\tilde{x}_{2}(t,x_{0})-x_{2}(t,x_{0})|,$$

which counts to 0.17441\(\%\). This maximum corresponds to the node (\(t=70\), \(x_{10}=2.14658\), \(x_{20}=124\), \(x_{30}=0.01\)). In the truncated domain \(\{\bar{G}_{x0},\bar{G}_{t}\}\) we obtain the total residual \(\varepsilon_{x2}=0.6355\), which counts to 0.036708\(\%\). The maximum corresponds to the node (\(t=63\), \(x_{10}=1.506454\), \(x_{20}=180\), \(x_{30}=0.009\)).

Fig. 2
figure 2

Special residual \(\bar{\varepsilon}_{x2}\) over \(t\) and \(x_{30}\) for fixed values \(x_{10}\) and \(x_{20}\).

Full size image

These results vividly demonstrate the capability of significant improvement in the accuracy of the numerical-analytic solution to the differential equation when the original domain \(\{G_{x0},G_{t}\}\) is truncated.

We take into account that the measured parameter may be represented as

$$y=\beta=2\{\textrm{arctan}\ [\exp(z_{1})]-\pi/4\}$$

and provide in Fig. 3 the three-dimensional graph of special residual

$$\bar{\varepsilon}_{\beta}=|\gamma(t,x_{0})-\tilde{\gamma}^{*}(t,x_{0})|$$

as a function of \(t\) and \(x_{10}\) for fixed values \(x_{20}=108\) and \(x_{30}=0.00625\).

Fig. 3
figure 3

Special residual \(\bar{\varepsilon}_{\beta}\) over \(t\) and \(x_{10}\) for fixed values \(x_{20}\) and \(x_{30}\).

Full size image

Analogously, in Fig. 4 we consider the case of dependence of \(\bar{\varepsilon}_{\beta}\) on \(t\) and \(x_{30}\) for fixed values \(x_{10}=2.1466\) and \(x_{20}=108\). Here, in the original domain \(\{G_{x0},G_{t}\}\) we have the general residual \(\varepsilon_{\beta}=\max\limits_{x_{0}}\varepsilon_{\beta}(x_{0})=0.098842\), where

$$\varepsilon_{\beta}(x_{0})=\max\limits_{t}|\tilde{\beta}(t,x_{0})-\beta(t,x_{0})|,$$

which counts to 0.3303\(\%\). The maximum is found in the node (\(t=31\), \(x_{10}=2.14658\), \(x_{20}=108\), \(x_{30}=0.00625\)). In the truncated domain \(\{\bar{G}_{x0},\bar{G}_{t}\}\) we obtain the total residual \(\varepsilon_{\beta}=0.01993\), which means 0.2197\(\%\). The maximum is in the node (\(t=38\), \(x_{10}=1.506454\), \(x_{20}=128\), \(x_{30}=0.007\)).

Fig. 4
figure 4

Special residual \(\bar{\varepsilon}_{\beta}\) over \(t\) and \(x_{30}\) for fixed values \(x_{10}\) and \(x_{20}\).

Full size image

Similarly, in the original domain \(\{G_{x0},G_{t}\}\) we have the total residual \(\varepsilon_{\beta}^{(1)}=\max\limits_{x_{0}}\varepsilon_{\beta}^{(1)}(x_{0})=5.4919\) for the derivative \(y^{(1)}=\beta^{(1)}\), where

$$\varepsilon_{\beta}^{(1)}(x_{0})=\max\limits_{t}|\tilde{\beta}^{(1)}(t,x_{0})-\beta^{(1)}(t,x_{0})|,$$

which counts to 6.952\(\%\). The maximum corresponds to the node (\(t=1\), \(x_{10}=2.436246\), \(x_{20}=100\), \(x_{30}=0.006\)). In the truncated domain \(\{\bar{G}_{x0},\bar{G}_{t}\}\) we obtain the total residual \(\varepsilon_{\beta}^{(1)}=3.1612\), which is 5.586\(\%\). The maximum is found in the node (\(t=8\), \(x_{10}=1.735415\), \(x_{20}=120\), \(x_{30}=0.007\)).

The results of the numerical experiment readily illustrate the capability of qualitative description of both input and output parameters of DOs even on the small-sized computational grids using the developed numerical-analytic method. To reduce the negative boundary effects, we must narrow the domains of definition of the parameters \(t\) and \(x_{0}\).

7 CONCLUSIONS

The developed numerical-analytic method for studying multidimensional DOs is oriented mostly to the cases related with solution of applied problems [4–7, 9, 10, 14, 15] that require computations in real time. This method suggests taking out the core amount of computations to the preliminary stage directly not associated with the observation of DO. At the end of this stage, based on the family of RICs, we must formulate the analytic solution to the differential equation and the analytic expression for the measured output of DO which are valid for the given domain of variation in the temporal coordinate, initial condition, and uncertainty parameters.

Using the method of [1], the obtained results may be easily extended to the problem of active identification of the measured output of multidimensional DO. When the vector of measured parameters has the corresponding dimension (when the necessary condition of observability is satisfied), these results may be extended to the problem of active identification of the mathematical model of the DO itself. Such identification is related with execution of the previously planned experiment [10].