Parameter estimation and inference in dynamic systems described by linear partial differential equations

Abstract

Differential equations (DEs) are commonly used to describe dynamic systems evolving in one (ordinary differential equations or ODEs) or in more than one dimensions (partial differential equations or PDEs). In real data applications, the parameters involved in the DE models are usually unknown and need to be estimated from the available measurements together with the state function. In this paper, we present frequentist and Bayesian approaches for the joint estimation of the parameters and of the state functions involved in linear PDEs. We also propose two strategies to include state (initial and/or boundary) conditions in the estimation procedure. We evaluate the performances of the proposed strategy through simulated examples and a real data analysis involving (known and necessary) state conditions.

1 Introduction

Dynamic systems are commonly described by differential equations (DEs). In real data applications, the parameters involved in the DE models are usually unknown and need to be estimated from the available measurements together with the state functions. For one- dimensional applications, this estimation task has been extensively discussed in the statistical literature. The most popular procedures rely on nonlinear least squares (Biegler et al. 1986). These approaches are computationally intensive and often poorly suited for statistical inference. An attractive alternative is represented by the penalized smoothing framework introduced by Ramsay et al. (2007). This approach can be viewed as a generalization of the L-spline theory (see, for example, Schultz and Varga (1967) among others) where the flexibility acquired by a high-dimensional B-spline basis expansion of the state function is counterbalanced by a penalty term expressed using the (set of) ODE(s) that needs to be solved. The fidelity of the final fit to the hypothesized differential model is then tuned using an ODE-compliance parameter. Jaeger and Lambert (2013) adapt the latter approach to a full Bayesian framework. This Bayesian alternative offers two major advantages with respect to the frequentist one: the selection of the ODE-compliance parameter becomes automatic and uncertainty measures about the parameters can readily be obtained using MCMC.

When dealing with dynamics evolving in more than one dimension, partial differential equations (or PDEs) are usually invoked. Inference in models specified by PDEs has not received a large attention in the literature. Here, we discuss statistical approaches to deal with dynamics described by linear PDEs. Such equations are used to model large classes of phenomena (e.g., diffusion, heat transfer, price of financial instruments, etc.). The general form of a deterministic PDE system can be written as:

$$\begin{aligned} \mathcal {F}\left( x_{1}, \ldots , x_{p}, u, \frac{\partial u}{\partial x_{1}}, \ldots , \frac{\partial u}{\partial x_{p}}, \frac{\partial ^{2} u}{\partial x_{1} ^ {2}}, \ldots , \frac{\partial ^{2} u}{\partial x_{1} \partial x_{p}}, \dots ,\varvec{\theta }\right) = 0, \end{aligned}$$

(1)

where $u\left( \varvec{x}\right)$ is the state function evaluated in $\varvec{x} = \left( x_{1},\ldots , x_{p}\right) ^{\top }\in \mathbb {R}^{p}$ and $\varvec{\theta }$ is the vector of PDE parameters. In this paper, we further assume that $\mathcal {F}$ is a linear function in u and its derivatives. Examples of this kind of PDE can be found in Eqs. (14), (15). In particular, we are interested in estimating the vector of unknown $\varvec{\theta }$ using a set of measurements $\varvec{\zeta } = \zeta \left( \varvec{x}\right) = u\left( \varvec{x}\right) + \varvec{\epsilon }$ where $\varvec{\epsilon }$ can be considered as a vector of independent normally distributed measurement errors.

Xun et al. (2013) have proposed frequentist and Bayesian approaches for the estimation of parameters in model driven by PDEs. The frequentist approach could be viewed as a multidimensional generalization of the framework introduced by Ramsay et al. (2007). The state function solving the differential problem is approximated using tensor product of B-splines. The flexibility of the approximation is then counterbalanced by a penalty related to the PDE. In the frequentist proposal, the PDE penalty is represented by the integral of the PDE operator evaluated at the B-spline approximation to the solution. In their Bayesian approach, they combine a PDE-based penalty with one defined using finite differences [i.e., through a roughness penalty in the spirit of Eilers and Marx (1996)]. In this paper, we present both frequentist and Bayesian frameworks for the joint estimation of the parameters and the state function involved in PDEs. Our methods generalize those proposed in one-dimensional applications by exploiting a PDE-based penalized tensor product B-spline smoothing approach.

B-splines belong to the class of sieve estimators (Grenander 1981; Shen 1997), i.e., they approximate an infinite dimensional parameter space with a finite surrogate. Many sieves are available for function approximation. Our choice in favor of tensor product B-spline bases can be justified by different arguments. First, they are a fundamental tool in the P-spline framework (Eilers and Marx 1996, 2003, 2010) to which we refer in this paper. Indeed, analogously to P-spline smoothing approaches, we approximate (e.g., smooth) the observed multidimensional dynamics using a rich set of bases functions and shrink the estimated coefficients through a suitable penalty term. The PDE-based shrinkage term we adopt in what follows frames into a B-spline collocation scheme for the (numerical) solution of partial differential equations (see e.g., Golub and Ortega 1992). Within the available bases functions for the approximation of DE solutions, B-splines are particularly convenient. Indeed, their compact supports lead to sparse collocation matrices that can be treated by fast matrix algorithms and allow for efficient storage strategies (see e.g., Botella 2002). Furthermore, their piecewise polynomial nature avoids numerical interpolation distortion effects (such as Runge’s phenomena, see, for example, Epperson (1987) for a detailed discussion on this aspect).

The choice of the optimal number of spline knots and their location has been extensively discussed in the literature and both frequentist and Bayesian selection approaches have been proposed. Examples include the stepwise selection method of Friedman and Silverman (1989) or the Bayesian procedures introduced by Denison et al. (1998) and Biller (2000). The knot selection process is usually computationally demanding and some alternatives are available. For example, within the ODE-based penalized smoothing framework (Ramsay et al. 2007), it is common to locate a knot at each data point. However, for multidimensional analyses, this strategy becomes easily impractical given the tensor product nature of the bases functions involved in the estimation process and the amount of available measurements. For this reason, following the suggestion by Eilers and Marx (2010) within the general P-spline framework and by Xun et al. (2013) for PDE-based smoothing, we prefer to define the spline basis over a generous number of knots at fixed locations. This a priori spline knot selection can eventually be guided by prior knowledge about the nature of the phenomenon under study (such an example is discussed in Sect. 5).

Finally, when the dimensionality of the estimation problem increases (e.g., by dealing with PDEs defined over more than two dimensions), tensor product B-splines can be computationally suboptimal if compared with other alternatives such as radial basis functions. Radial bases are defined by kernels evaluated exclusively over the observed domain. This allows for efficient surface smoothing algorithms (see e.g., Holmes and Mallick 1998; Smith et al. 2002). On the other hand, few classes of compact kernel functions are available (see e.g., Wu 1995) and they require the definition of a “compactness” parameter to be selected by some optimality criterion (e.g., AIC, BIC or cross-validation). This selection step can be computationally expensive. For this reason, we recommend to use tensor product B-splines when dealing with differential problems involving up to three dimensions.

This paper is organized as follows. In Sect. 2, we introduce our estimation procedures. Both frequentist and Bayesian approaches can be adapted to include the state (initial, boundary or mixed) conditions in the estimation process (see Sect. 3). In Sect. 4, we evaluate the performance of our approach and compare it with competitors using simulations. In Sect. 5, we illustrate our proposals dealing with a real data analysis based on the Black and Scholes (1973) model. Our application represents one of those situations in which the state condition of the differential model (namely the no-arbitrage conditions) is known and need to be satisfied to obtain reasonable results. We conclude the paper with a discussion in Sect. 6.

2 Estimation of the unknown differential parameters for unknown state conditions

In this section, we introduce the PDE-based penalized tensor product B-spline smoothing approach both in frequentist and Bayesian frameworks without taking the state conditions (initial and/or boundary) into account.

2.1 Frequentist approach

Assume that one observes $\left\{ \left( \varvec{\zeta }; \varvec{x}\right) = \left( \zeta _{n}; x_{1, n}, \ldots , x_{p,n}\right) ; n=1,\ldots ,N\right\}$ describing the evolution of the state function u whose dynamics is driven by (1). Our task is to jointly estimate the state function u and the vector of parameters $\varvec{\theta }$. Following Ramsay et al. (2007), we suggest to exploit a DE-based-penalized smoothing approach. More precisely, we denote by $\widetilde{u}\left( \varvec{x}\right)$ the B-spline tensor product approximation of $u(\varvec{x})$:

$$\begin{aligned} \widetilde{u}(\varvec{x})= & {} \left( \varvec{B_{x_{p}}} \otimes \cdots \otimes \varvec{B_{x_{1}}}\right) \varvec{c} \nonumber \\= & {} \varvec{\mathcal {B}} \varvec{c}, \end{aligned}$$

(2)

where $\varvec{B_{x_{p}}}$ is the $(N \times M)$ B-spline matrix defined on the p-th direction where a generous numbers of internal knots were placed and $\varvec{c}$ is the $M^{p}$-vector of spline coefficients. The placement of the knots on the $x_{p}$-direction can be either regular or not. To simplify the notation, we suppose that the number of B-splines in each direction is the same and equal to M. The spline coefficients are shrunk by adding (to the log-likelihood) a multiple of a penalty defined using the PDE model (1):

$$\begin{aligned} PEN\left( \varvec{c} | \varvec{\theta }\right) = \int {\mathcal {F}\left( \varvec{x}, \widetilde{u}, \varvec{\theta }\right) ^{2}d\varvec{x}}. \end{aligned}$$

(3)

This penalty term will be close to zero, for given PDE parameters $\varvec{\theta }$, if the approximation $\widetilde{u}(\varvec{x})$ to the solution of (1) is consistent with the PDE model. As we are considering linear PDEs, this penalty is just a polynomial of degree 2 in the spline coefficients:

$$\begin{aligned} PEN\left( \varvec{c} | \varvec{\theta }\right) = \varvec{c}^{\top } \varvec{R}\left( \varvec{\theta }\right) \varvec{c} + 2 \varvec{c}^{\top } \varvec{r}\left( \varvec{\theta }\right) + l\left( \varvec{\theta }\right) , \end{aligned}$$

where $\varvec{R}\left( \varvec{\theta }\right)$ is the penalty matrix, $\varvec{r}\left( \varvec{\theta }\right)$ is the penalty vector and $l\left( \varvec{\theta }\right)$ is a constant not depending on the spline coefficients. A fast procedure to compute these penalty components is given in Appendix 3.

The compromise between data fitting and fidelity to the differential model can be assessed using the penalized least square criterion:

$$\begin{aligned} J\left( \varvec{c} | \varvec{\theta }, \gamma , \varvec{\zeta }\right) = \frac{N}{2}\log \left( \tau \right) - \frac{\tau }{2}\left\| \varvec{\zeta } - \widetilde{u}\left( \varvec{x}\right) \right\| ^{2} - \frac{\gamma }{2}{PEN}\left( \varvec{c} | \varvec{\theta }\right) , \end{aligned}$$

(4)

where $\tau$ is the inverse of the error variance (i.e., the precision of measurement). Similar to Ramsay et al. (2007), the estimation process for $\varvec{\theta }$ and $\varvec{c}$ implies the iteration of two profiling steps. First, for a given value of $\varvec{\theta }$, $\tau$ and $\gamma$, the spline coefficients $\varvec{c}$ are estimated as the maximizer of J:

$$\begin{aligned} \hat{\varvec{c}} = \mathop {\text{ argmax }}_{\varvec{c}} J\left( \varvec{c} | \varvec{\theta }, \tau , \gamma , \varvec{\zeta }\right) = \left( \tau \varvec{\mathcal {B}}^{\top }\varvec{\mathcal {B}} + \gamma \varvec{R}\left( \varvec{\theta }\right) \right) ^{-1}\left( \tau \varvec{\mathcal {B}}^{\top }\varvec{\zeta } - \gamma \varvec{r}\left( \varvec{\theta }\right) \right) . \end{aligned}$$

(5)

Then, given the last available spline coefficients $\hat{\varvec{c}}$, the PDE parameters $\varvec{\theta }$ and the precision of measurements $\tau$ are estimated by maximizing:

$$\begin{aligned} H\left( \varvec{\theta }, \tau | \hat{\varvec{c}}, \varvec{\zeta }\right) = \frac{N}{2}\log \left( \tau \right) - \frac{\tau }{2}\left\| \varvec{\zeta } - \varvec{\mathcal {B}} \hat{\varvec{c}}\right\| ^{2}. \end{aligned}$$

(6)

The $\gamma$ parameter weighs and controls the relative emphasis on goodness-of-fit and on solving the partial differential equation. This parameter measures the confidence that one has in the PDE to describe the dynamics in the system. Therefore, we suggest to name it “PDE-compliance parameter”. As usual in penalized smoothing approach, the parameter $\gamma$ has to be selected in a higher optimization level (e.g., using cross-validation, AIC, etc.). Following the mixed model interpretation of penalized smoothing splines (Ruppert et al. 2003), the PDE-compliance parameter can be seen as the ratio of the variances of the residuals and of the penalty. For this reason, we recommend to adopt the following EM-type procedure for the estimation (Schall 1991): update till convergence $\gamma = \widehat{\sigma }^{2}_{\epsilon }/\widehat{\sigma }^{2}_{PEN}$ with $\widehat{\sigma }^{2}_{PEN} = \Vert PEN (\varvec{c} | \varvec{\theta })\Vert ^{2} / \text{ ED }$ where $\text{ ED } = \text{ tr }(\varvec{\mathcal {B}}(\tau \ \varvec{ \mathcal {B}}^{\top }\varvec{\mathcal {B}} + \gamma PEN (\varvec{c} | \varvec{\theta }))^{-1}\tau \varvec{\mathcal {B}}^{\top })$ is the effective dimension of the smoother (Hastie and Tibshirani 1990). Note that for high PDE compliance the effective dimension is usually much lower than the number of spline coefficients (an example is presented in Fig. 2).

By estimating $\sigma ^{2}_{\epsilon }$ as $\Vert \varvec{\zeta } - \widetilde{u}(\varvec{x})\Vert ^{2}/(N - \text{ ED })$, it is possible to profile $H\left( \varvec{\theta }, \tau |, \hat{\varvec{c}}, \varvec{\zeta }\right)$ w.r.t. the precision of measurements. Then, the function to be minimized to estimate the unknown PDE parameters becomes:

$$\begin{aligned} H\left( \varvec{\theta }| \hat{\tau }, \hat{\varvec{c}}, \varvec{\zeta }\right) = - \frac{\hat{\tau }}{2}\left\| \varvec{\zeta } - \varvec{\mathcal {B}} \hat{\varvec{c}}\right\| ^{2}. \end{aligned}$$

(7)

Confidence intervals for the PDE parameters cannot easily be obtained. Xun et al. (2013) studied the asymptotic properties of the described PDE parameters and spline coefficients estimators. When the hypotheses listed in their appendix A.2 hold, the results presented by the authors can be extended to our procedure and their variance formulas can be used to quantify uncertainty for the estimated unknowns. On the other hand, following the suggestions by Rodriguez-Fernandez et al. (2006) and Xue et al. (2010), we found that a reasonable approximation to the variance–covariance of the $\varvec{\theta }$ parameters can be obtained using the observed pseudo-information matrix given by the inverse of the Hessian of H in (7). Furthermore, approximated piecewise confidence bounds for the spline coefficients can easily be obtained in case of linear PDE penalties. By defining the hat matrix as $A = \varvec{\mathcal {B}}(\tau \varvec{\mathcal {B}}^{\top }\varvec{\mathcal {B}} + \gamma PEN (\varvec{c} | \varvec{\theta }))^{-1}\tau \varvec{\mathcal {B}}^{\top }$ and noting that $\text{ var }(\widetilde{u}(\varvec{x}))\approx \hat{\tau }^{-1} \left( A^{\top } A\right)$, the approximate pointwise confidence bands for the estimated state function are computed as $\widetilde{u}(\varvec{x}) \pm 2\sqrt{\text{ diag }[\text{ var }(\widetilde{u}(\varvec{x}))]}$.

Alternatively, as suggested by Xue et al. (2010), inference on the model parameters can be done using the weighted bootstrap (Ma and Kosorok 2005). Differently from empirical bootstrap, this approach suggests to solve repeatedly the minimization problem in Eq. (6) by weighting the residual sum of squares by a set of i.i.d. random weights with unitary mean and variance.

2.2 Bayesian approach

We propose to adapt the frequentist proposal into a Bayesian framework. Contrary to Xun et al. (2013), we will use the same PDE penalty than in the frequentist approach. The penalty term in Eq. (4) appears as a quantity subtracted from the log-likelihood. The log of the joint posterior yields the same fitting criterion using the following model specification:

$$\begin{aligned} \left\{ \begin{array}{rcl} \varvec{\zeta }|\varvec{c},\tau &{} \sim &{} \mathcal {N}_{N}\left( \varvec{\mathcal {B}} \varvec{c};\tau ^{-1}\varvec{I_{N}}\right) ,\\ p(\varvec{c}|\varvec{\theta }, \gamma ) &{} \propto &{} \exp \left( - \displaystyle \frac{\gamma }{2}{PEN}\right) . \end{array} \right. \end{aligned}$$

The corresponding prior distribution for the spline coefficients is a multivariate normal distribution with mean $\varvec{V_{1}}^{-1}\varvec{v_{1}}$ and variance–covariance $\varvec{V_{1}}^{-1}$ where $\varvec{v_{1}} = - \gamma \varvec{r}\left( \varvec{\theta }\right)$ and $\varvec{V_{1}} = \gamma \varvec{R}\left( \varvec{\theta }\right)$.

Further prior distributions must be specified. For the precision of measurement $\tau$, it is convenient to take a gamma distribution $\mathcal {G}\left( a_{\tau }, b_{\tau }\right)$ with mean $a_{\tau }/b_{\tau }$. If no prior information is available on this precision parameter, we recommend either to set $a_{\tau } = b_{\tau }$ equal to a small value (e.g., $10^{-6}$) or to set $a_{\tau }$ equal to 1.0 and $b_{\tau }$ to a small value (e.g., $10^{-6}$).

The PDE-compliance parameter appears as a precision parameter in the specification of the prior distribution for the spline coefficients. It is therefore convenient to take a gamma distribution $\mathcal {G}\left( a_{\gamma }, b_{\gamma }\right)$ as prior. To express prior confidence in the PDE model, we recommend to set $a_{\gamma }$ to one and $b_{\gamma }$ to a small value (e.g., $10^{-8}$). Indeed, such a prior for $\gamma$ is rather flat although it puts slightly more weight on value of $\log _{10}\left( \gamma \right)$ around $-\log _{10}\left( b_{\gamma }\right)$ (Jaeger and Lambert 2013, 2014).

For the PDE parameter $\varvec{\theta }$, the prior distribution depends on contextual information and is denoted by $p\left( \varvec{\theta }\right)$.

The log joint posterior distribution for $\left( \varvec{c}, \varvec{\theta }, \gamma , \tau | \varvec{\zeta }\right)$ can be shown to be:

$$\begin{aligned} \log \left( p\left( \varvec{c}, \varvec{\theta }, \gamma , \tau | \varvec{\zeta }\right) \right)= & {} \displaystyle \frac{N}{2} \log \left( \tau \right) - \displaystyle \frac{\tau }{2} \left\| \varvec{\zeta } - \varvec{\mathcal {B}c} \right\| ^ {2} \nonumber \\&+ \displaystyle \frac{1}{2} \log \left( \text{ det }\left( \varvec{V}_{1}\right) \right) - \displaystyle \frac{1}{2}\left\{ \varvec{c}^{\top }\varvec{V_{1}c} - 2 \varvec{c}^{\top }\varvec{v_{1}} + \varvec{v_{1}}^{\top }\varvec{V_{1}}^{-1}\varvec{v_{1}}\right\} \nonumber \\&+ \left( a_{\tau } - 1\right) \log \left( \tau \right) - b_{\tau }\tau \nonumber \\&+ \left( a_{\gamma } - 1\right) \log \left( \gamma \right) - b_{\gamma } \gamma \nonumber \\&+ \log \left( p\left( \varvec{\theta }\right) \right) . \end{aligned}$$

(8)

It can easily be shown that the conditional posterior distribution for the spline coefficients is a multivariate normal with mean $\varvec{V_{2}}^{-1}\varvec{v_{2}}$ and variance–covariance $\varvec{V_{2}}^{-1}$ where $\varvec{V_{2}} = \tau \varvec{\mathcal {B}}^{\top }\varvec{\mathcal {B}} + \varvec{V_{1}}$ and $\varvec{v_{2}} = \tau \varvec{\mathcal {B}}^{\top } \varvec{\zeta } + \varvec{v_{1}}$:

$$\begin{aligned} \varvec{c} | \varvec{\theta }, \tau , \gamma , \varvec{\zeta } \sim \mathcal {N}_{M^{p}}\left( \varvec{V_{2}}^{-1}\varvec{v_{2}}; \varvec{V_{2}}^{-1}\right) . \end{aligned}$$

The conditional posterior distribution for the precision of measurements and for the PDE-compliance parameter is gamma distributed:

$$\begin{aligned} \tau | \varvec{c}, \varvec{\zeta }\sim & {} \mathcal {G}\left( \frac{N}{2} + a_{\tau }; \frac{\left\| \varvec{\zeta } - \varvec{\mathcal {B}c} \right\| ^ {2}}{2} + b_{\tau }\right) , \\ \gamma | \varvec{\theta }, \varvec{c}\sim & {} \mathcal {G}\left( \frac{M^{p}}{2} + a_{\gamma }; \frac{\varvec{c}^{\top }\varvec{R} \left( \varvec{\theta }\right) \varvec{c} + 2 \varvec{c}^{\top }\varvec{r}\left( \varvec{\theta }\right) + \varvec{r}\left( \varvec{\theta }\right) ^{\top } \varvec{R}\left( \varvec{\theta }\right) ^{-1} \varvec{r}\left( \varvec{\theta }\right) }{2}+ b_{\gamma }\right) . \end{aligned}$$

The conditional posterior distribution for the PDE parameters $\varvec{\theta }$ is not necessarily of a familiar type. In addition, high posterior correlation could occur between the spline coefficients $\varvec{c}$ and the elements of $\varvec{\theta }$.

From Eq. (8), it appears that the constant of normalization of the prior distribution of the spline coefficients is given by the determinant of the PDE-penalty matrix and hence depends on the unknown $\varvec{\theta }$ parameters. Disregarding this normalizing constant when computing the joint posterior is incorrect and leads to biased parameter estimates.

Finally, following Jaeger and Lambert (2013, 2014), we recommend to marginalize the joint posterior distribution with respect to the spline coefficients, as given in Appendix 1. This marginalization enables us to sample only the PDE parameters with a mixing of the MCMC chains not hindered by the posterior correlation with spline coefficients. The latter quantities can be sampled in a second step if found necessary.

3 Estimation of the unknown differential parameters including state conditions

In many applications, state (initial and/or boundary) conditions naturally arise or are implicitly defined by the observed dynamics (a clear real example is the analysis discussed in Sect. 5). Such information can be included in the statistical framework of Sect. 2.

Consider the general partial problem given by:

$$\begin{aligned} \left\{ \begin{array}{rcl} \mathcal {F}\left( \varvec{x}, u, \varvec{\theta }\right) &{} = &{} 0, \\ \displaystyle \frac{\partial ^ {\left( i\right) }}{\partial x_{0}^{\left( i\right) }}u(\varvec{x_{0}}) &{} = &{} v\left( \varvec{x_{0}}\right) , \end{array} \right. \end{aligned}$$

(9)

where $\varvec{x_{0}}$ is a part of the domain where the state function u and/or its ith order derivatives are forced to be equal to the function v. Using the B-spline approximation, these conditions can be translated into:

$$\begin{aligned} \varvec{Hc} = v\left( \varvec{x_{0}}\right) , \end{aligned}$$

(10)

where $\varvec{H}$ is a tensor product B-spline matrix evaluated on the desired support points. In the frequentist framework, we propose two methods to introduce the state conditions in the penalized smoothing approach: one is based on least squares and the other on Lagrange multipliers. In the Bayesian setting, we only include the conditions using a least square type strategy.

3.1 Frequentist approach

One way to take into account the conditions related to a generic PDE is to consider them as an extra penalty. In the frequentist approach, the fitting criterion J is modified as follows:

$$\begin{aligned} J\left( \varvec{c} | \varvec{\theta }, \gamma , \kappa , \varvec{\zeta }\right)= & {} \frac{N}{2}\log \left( \tau \right) - \frac{\tau }{2}\left\| \varvec{\zeta } - \widetilde{u}\left( \varvec{x}\right) \right\| ^{2} - \frac{\gamma }{2}{PEN}\left( \varvec{\theta } | \varvec{c}\right) \nonumber \\&- \frac{\kappa }{2}\left( \varvec{Hc} - v\left( \varvec{x_{0}}\right) \right) ^{\top }\left( \varvec{Hc} - v\left( \varvec{x_{0}}\right) \right) . \end{aligned}$$

(11)

Note that with such a least square penalty, the approximated state function is not forced to be exactly equal to the conditions. With this fitting criterion, the optimal spline coefficients are computed as:

$$\begin{aligned} \hat{\varvec{c}}= & {} \mathop {\text{ argmax }}_{\varvec{c}} J\left( \varvec{c} | \varvec{\theta }, \tau , \gamma , \kappa , \varvec{\zeta }\right) \nonumber \\= & {} \left( \tau \varvec{\mathcal {B}}^{\top }\varvec{\mathcal {B}} + \gamma \varvec{R}\left( \varvec{\theta }\right) + \kappa \varvec{H}^{\top }\varvec{H}\right) ^{-1}\left( \tau \varvec{\mathcal {B}}^{\top }\varvec{\zeta } - \gamma \varvec{r}\left( \varvec{\theta }\right) + \kappa \varvec{H}^{\top }v\left( \varvec{x_{0}}\right) \right) . \end{aligned}$$

(12)

If $\kappa$ tends to infinity, we simply force the state function to be equal to the state conditions at the prescribed points. On the other hand, if $\kappa$ is equal to zero, then we just go back to the case of Sect. 2.

Using Lagrange multipliers in a frequentist framework, we can force the smoothing function to be exactly consistent with the conditions. The Lagrange function for our constrained maximization problem is:

$$\begin{aligned} \mathcal {L}\left( \varvec{c}, \varvec{\omega } | \varvec{\theta }, \tau , \gamma , \varvec{\zeta }\right)= & {} \frac{N}{2}\log \left( \tau \right) - \frac{\tau }{2}\left\| \varvec{\zeta } - \widetilde{u}\left( \varvec{x}\right) \right\| ^{2} - \frac{\gamma }{2}{PEN}\left( \varvec{\theta } | \varvec{c}\right) \nonumber \\&-\frac{1}{2}\varvec{\omega }^{\top }\left( \varvec{Hc} - v\left( \varvec{x_{0}}\right) \right) , \end{aligned}$$

(13)

where $\varvec{\omega }$ is the vector of Lagrange multipliers. As in Currie (2013), the maximization with respect to $\left( \varvec{c}, \varvec{\omega }\right)$ follows from the solution of:

$$\begin{aligned} \left( \begin{array}{c c} \tau \varvec{\mathcal {B}}^{\top } \varvec{\mathcal {B}} + \gamma \varvec{R} \left( \varvec{\theta }\right) &{} \varvec{H}^{\top } \\ \varvec{H} &{} \varvec{0} \end{array} \right) \left( \begin{array}{c} \varvec{c} \\ \varvec{\omega } \end{array} \right) = \left( \begin{array}{c} \tau \varvec{\mathcal {B}}^{\top } \varvec{\zeta } - \gamma \varvec{r} \left( \varvec{\theta }\right) \\ v\left( \varvec{x_{0}}\right) \end{array} \right) . \end{aligned}$$

The precision of measurement $\tau$ and the PDE parameters $\varvec{\theta }$ are then estimated in the same way as in Eq. (6).

3.2 Bayesian approach

In a Bayesian setting, the frequentist least squares strategy can be translated into the following prior for the spline coefficients:

$$\begin{aligned} p\left( \varvec{c} | \varvec{\theta }, \gamma , \kappa \right) \propto \exp \left( \frac{\gamma }{2}{PEN} - \frac{\kappa }{2}\left( \varvec{Hc} - v\left( \varvec{x_{0}}\right) \right) ^{\top }\left( \varvec{Hc} - v\left( \varvec{x_{0}}\right) \right) \right) . \end{aligned}$$

This prior distribution corresponds to a multivariate normal distribution with mean $\varvec{V_{1}}^{-1}\varvec{v_{1}}$ and variance–covariance $\varvec{V_{1}}^{-1}$ where $\varvec{v_{1}} = - \gamma \varvec{r}\left( \varvec{\theta }\right) + \kappa \varvec{H}^{\top }v\left( \varvec{x_{0}}\right)$ and $\varvec{V_{1}} = \gamma \varvec{R}\left( \varvec{\theta }\right) + \kappa \varvec{H}^{\top }\varvec{H}$.

One can either fix $\kappa$ to a large value or consider it as random with a gamma prior distribution $\mathcal {G}\left( a_{\kappa }, b_{\kappa }\right)$ where $a_{\kappa }$ is equal to one and $b_{\kappa }$ is equal to a small value (e.g., $10^{-6}$). This choice for the prior distribution for $\kappa$ translates prior confidence in the state conditions. The log joint posterior distribution, the log marginalized posterior distribution and all the conditional posterior distributions can be found in Appendix 2. For the Lagrange multipliers strategy, the possible Bayesian translation would require to project the spline coefficients on a parameter sub-space where the constraints are met: we have no practical implementation of such a strategy for the moment.

4 Simulation

An intensive simulation study was set up to study the properties of the proposed estimation strategies. We consider the following advection-decay partial differential equation:

$$\begin{aligned} \mathcal {F}\left( x_{1}, x_{2}, u, \frac{\partial u}{\partial x_{1}}, \frac{\partial u}{\partial x_{2}}, \theta _{1}, \theta _{2}\right) = u_{x_1} + \theta _{1} u_{x_2} + \theta _{2} u = 0,\quad \text{ with }\ x_{1} \in \mathbb {R},\ x_{2} \in \mathbb {R}^{+},\nonumber \\ \end{aligned}$$

(14)

where $u_{x_{i}}$ denotes the first derivative of the state function with respect to $x_{i}$. The general solution of (14) is:

$$\begin{aligned} u(x_{1}, x_{2}) = g(\theta _{1} x_{2} - x_{1}) \exp (- 2 \theta _{2} x_{1}), \end{aligned}$$

where $g(\cdot )$ is an unknown function to be determined from the state conditions. For simulation purposes, we take $\theta _{1} = 0.5$ and $\theta _{2} = 1.5$ and consider the condition $u(x_{1}, 0) = \displaystyle \frac{1}{1 + x_{1}^{2}}$ (note that it is, in a certain sense, analogous to the terminal condition of the equation discussed in Sect. 5). Applying this state condition, the differential problem has the following closed-form solution:

$$\begin{aligned} u(x_{1}, x_{2}) = \frac{\exp (- 3 x_{2})}{1 + 4 x_{2}^{2} - 4 x_{1} x_{2} + x_{1}^{2}}. \end{aligned}$$

This expression contaminated with Gaussian noise is used to generate the data. This PDE appears particularly attractive as it has a closed-form solution, enabling an objective comparison of the merits of the proposed constrained approaches with the nonlinear least squares one (see Sect. 4.1.2). Furthermore, the estimation abilities of our proposals will be compared with the methods presented by Xun et al. (2013) (see Sect. 4.2).

4.1 Simulation using the PDE-P-splines approaches

The data used for the simulations of this section have been obtained by adding a Gaussian noise component to the analytic solution computed on the grid of equidistant points $x_{1, i}\ \text{ in }\ [-3, 3],\ x_{2, j}\ \text{ in }\ [0, 1]$ with $i = 1,\ldots ,50$ and $j = 1,\ldots ,50$. Different levels for the precision of measurements $\tau = \{10000, 400, 100\}$ have been used to simulate the data in such a way to obtain a low, medium and large level of noise in the measurements. Figure 1 shows three possible simulated data clouds (the gray and black level lines on the top of each perspective plot indicate cross-sections, i.e., the contour plots, of the simulated data and of the PDE solution, respectively).

Fig. 1

Three simulated data sets (dots) obtained considering an advection-decay dynamics and different levels for the precision of measurements. The surfaces represent the signal used in the simulation. The contour lines on the top of the perspective plots give a 1D representation of the simulated data (solid gray lines) and of the signal (solid black lines)

We are interested in evaluating the efficiency of the proposed estimation procedures. For this reason, we consider 500 simulated datasets per noise level and compute, for the frequentist approaches, the relative bias (in percent), the relative root mean squared error and the standard deviation of the estimated differential equation parameters together with the precision of measurements and the optimal compliance parameter. On the other hand, with the Bayesian approaches, we compute the relative bias (based on the posterior mean), the relative root mean squared error (based on the posterior mean), the mean posterior standard deviation and the 80 and 95 % coverage probabilities (based on the HPD intervals).

Table 1 Frequentist and Bayesian simulation for advection-decay PDE smoothing example with unknown state conditions

In this simulation study, we stress our proposal with and without taking into account the state conditions. For the frequentist procedures, we include the state conditions using either the least squares or the Lagrange multiplier strategy. For the Bayesian approach, we only investigate the least squares strategy as it enables to marginalize the joint posterior distribution with respect to the spline coefficients. Finally, the performances of our PDE-P-spline approaches are compared with those achieved using a (frequentist) nonlinear least square estimation procedure (that requires an explicit solution of the PDE and the knowledge of the state conditions).

In this simulation study, we consider non-equally spaced knots. We use a set of 28 spline basis in the $x_{1}$ direction and 13 spline basis in the $x_{2}$ direction. In both direction, more knots have been located in the part of the domain where variation of the signal appears more evident. The selection of knot location is not mandatory as a fine grid of equidistant knots produces similar estimates (but requires higher computational efforts). For the degree of the B-splines, we found that a useful rule of thumb is to set it equal to the degree of the differential equation plus two. This heuristic rule can be justified by examining the properties of B-spline functions and their derivatives. The dth order derivative of a B-spline basis of degree q is obtained by finite differentiation of spline functions of degree $q-d$. On the other hand, a qth degree B-spline is $q-1$ times continuously differentiable over the domain span (see e.g., Golub and Ortega 1992; Dierckx 1995). By defining bases of degree equal to the order of the PDE plus two, we ensure that the splines used to approximate the highest order derivative appearing in the differential model are at least one time continuously differentiable over the entire domain mesh.

4.1.1 Simulation results when ignoring the state conditions

’The results of the simulation study described above are provided in Table 1. In this case, the state conditions have not been taken into account in the estimation process. The cited table shows some interesting features. The relative bias (in percent) for the estimated parameters is small both for the frequentist and Bayesian approaches. On the other hand, looking at the estimated PDE parameters, the relative bias obtained within the Bayesian framework is positive and larger (but still very small) than for the frequentist estimates, while the estimates for the precision parameter look similar for the two approaches. This could be explained by the choice of the posterior mean for the point estimate. The RMSEs seem to be larger for the PDE parameters in the Bayesian approach and larger for the precision of measurement in the frequentist approach. This can be explained looking at the bias. On the other hand, based on the STDs, the estimation procedure seems quite robust against the noise level. For the Bayesian estimates, the mean posterior standard deviations tend to increase with the level of noise for the PDE parameters and to decrease for the $\tau$ parameter. Only some estimated coverage probabilities (at 80 and 95 % level) are in agreement with the nominal values. On the other hand, for a high level of noise, there is evidence of an under coverage effect that could be explained by the fact that the true state conditions are ignored in the estimation process. Finally, the (average) optimal compliance parameters $\gamma$ shown at the bottom of each sub-table are fairly large, indicating a strong (posterior) confidence in the appropriateness of the differential model used in the penalty to describe the observed dynamics. Figure 2 shows three possible smoothing surfaces coming from this simulation study. As expected, if we do not include the state conditions in the estimation procedure, the fitted surface tends to be sensitive to the level of noise, showing wiggly parts for large values of $x_{1}$ and moderate value of $x_{2}$ (see first column of Fig. 2).

Fig. 2

Typical profiles for the frequentist approaches. The first column shows the smoothing surfaces estimated for unknown conditions. The middle column shows the smoothing surfaces estimated using the state conditions imposed by least squares, while the third column shows the smoothing surface using the Lagrange multipliers approach. The gray level lines represent the cross-sections of the simulated cloud of points (contour lines). In the upper right legend of each panel, the optimal PDE-compliance parameters and the effective smoother dimensions are reported

Table 2 Frequentist and Bayesian simulation for advection-decay PDE smoothing example considering the state conditions

Table 3 Frequentist nonlinear least squares simulation for advection-decay PDE smoothing example

4.1.2 Simulation results considering the state conditions

The results of the simulation study taking into account the state conditions through a least square penalty (frequentist and Bayesian approaches with fixed $\kappa = 10^{6}$) or Lagrange multipliers (only frequentist approach) are shown in Table 2. The simulation performances obtained using a nonlinear least square solution of the state function are also shown in Table 3 (as made possible by the availability of a unique and explicit solution when state conditions are known). It appears that the relative bias for the estimated parameters is small both for the frequentist and Bayesian approaches. One can notice that the bias decreases in absolute value when the state conditions are introduced in the estimation procedure in the case of moderate and high noise variability. For frequentist estimates, the RMSEs seem to increase together with the level of measurement noise. On the other hand, based on the STDs, the estimation procedure seems quite robust to the noise level. The estimated standard deviations for the PDE parameters seem to be smaller when the state conditions are ignored. Looking at the frequentist estimates, the results obtained by imposing conditions using least squares or Lagrange multipliers look really similar. For the Bayesian estimates, the mean posterior standard deviations for the PDE parameters increase with the level of noise and decrease for parameter $\tau$. As expected, the mean standard deviation for the PDE parameters tends to decrease when forcing the state conditions. The estimate coverage probabilities are in agreement with the nominal values in almost all the simulation settings. This is probably due to the fact that the conditions are explicitly specified and not estimated. The average optimal compliance parameters $\gamma$ given in each sub-table indicate a stronger (posterior) confidence in the PDE model as descriptor of the dynamics of the observed state. The middle and the third column of Fig. 2 show three smoothing surfaces extracted from the simulation runs. Compared to the first column, the inclusion of the state conditions forces the smoothing surface to be adherent to the closed-form solution over the entire domain even for lower precision of the measurements. Finally, the performance of the proposed frequentist and Bayesian estimation procedures are compatible with those obtained through nonlinear least squares estimation of the parameters involved in the analytic solution (see Table 3) in the exceptional case where it has a closed-form expression.

4.2 Comparison of the PDE-P-splines approaches with the one by Xun et al. (2013)

In their Bayesian framework, Xun et al. (2013) propose to use a penalty combining PDE compliance (in a $L^{2}$ sense) and smoothness of the estimated surface (achieved by an extra finite difference penalty). Our interest is to compare this proposal with our Bayesian approaches (that are, as shown above, usable with known and unknown state conditions). Furthermore, we also consider a modified version of the penalty proposed by Xun et al. (2013) by discarding the extra finite difference penalties to evaluate their impact on the quality of the estimates. The two main differences between our proposals and the one by Xun et al. (2013) lay in the construction of the penalty term and in the inclusion of the normalizing constant of the prior distribution of the spline coefficients when computing the conditional posterior for PDE parameters $\varvec{\theta }$ (see Jaeger and Lambert (2013, 2014) for a discussion on this crucial point). Our regularization term is defined as an integrated penalty ensuring the compliance of the B-spline approximation to the proposed PDE. Note that our Bayesian approach is a faithful “Bayesianization” of the frequentist one. As appears in Eq. (8), we compute the normalizing constant of the prior distribution for the spline coefficients as the determinant of the PDE-penalty matrix whereas Xun et al. (2013) approximate it by a power of the smoothing parameters.

The data (100 samples) used for the comparison have been obtained by adding a Gaussian noise component ($\sigma _{\epsilon }^{2} = 0.05^{2}$) to the analytic solution of the PDE given in Eq. (14) computed on the grid of equidistant points $x_{1, i}\ \text{ in }\ [-4, 4],\ x_{2, j}\ \text{ in }\ [0, 1]$ with $i = 1,\ldots ,n$, where $n \times m = 40 \times 20, 60 \times 40, 100 \times 50, 200 \times 100$. The performances of the competing methods are shown in Table 4. It appears that our PDE-P-spline approach (ignoring the state conditions) guarantees better performances than the competing approach in terms of estimation bias. This is particularly evident when looking at the results obtained for smaller sample sizes. For moderate sample sizes, also the RMSEs obtained with the proposed procedure are smaller than those achieved by the competitors. By comparing the estimation performances of the approach by Xun et al. (2013) with those obtained using an analogous model specification without extra finite difference penalties, it appears that the extra smoothing term has the effect to reduce the estimation bias. Finally, similar to the preceding discussion, the inclusion of the state conditions increases the quality of the estimates.

In Figs. 3 and 4, we present the estimates obtained from a single set of data simulated by adding a Student t noise (with 5 degrees of freedom) to the solution of Eq. (14). Figure 3 shows the estimated surfaces obtained using the four approaches. For the large sample sizes, all the estimated smoothing surfaces correctly estimate the underlying state function. When the sample size decreases, our approaches seem to perform better than the competitors in recovering the underlying signal. In the case where the sample is limited, the approach of Xun et al. (2013) tends to oversmooth the data and seems to put (relatively) lesser weight on the PDE-model penalty. On the other hand, for the same simulation settings, the modified version of the model by Xun et al. (2013) without the extra finite difference penalty seems to catch the signal slightly better than its original formulation for intermediate sample sizes. The posterior densities for the PDE parameters in the modified Xun et al. approach appear clearly left shifted (see Fig. 4). The extra finite difference penalty mitigates the introduced bias. The inclusion of the exact normalizing constant in the prior distribution for the spline coefficient centers the marginal posterior distributions around the true PDE parameters. Finally, whatever the sample size, the variability of the posteriors decreases when the state conditions are introduced in the model.

Table 4 Bayesian simulation for advection-decay PDE smoothing example using PDE-P-splines (with and without state conditions) and the Xun et al. (2013) approach (with and without the extra finite difference penalties)

Fig. 3

Posterior pointwise smoothing surfaces estimated either using the Xun et al. (2013) approach with and without the extra finite difference penalty (fourth and third rows) and the PDE-P-splines approaches, without and with the boundary conditions imposed by least squares (first and second rows). In each column, the surfaces estimated for different sample sizes are depicted ($n = 40 \times 20$ in the left column, $n = 60 \times 40$ and $n = 100 \times 50$ in the middle columns and $n = 200 \times 100$ in the right column). The gray level lines indicate cross-sections of the simulated cloud of points (contour lines). The data have been simulated by adding a noise drawn from a Student t distribution with 5 degrees of freedom to the analytic solution of the PDE in (14). The optimal PDE-compliance parameters and the RMSE between the simulated and approximated signals are reported in the legend of each panel

Fig. 4

Posterior densities for $\theta _{1} = 0.5$ and $\theta _{2} = 1.5$, respectively. Densities in gray are those obtained using the approaches proposed by Xun et al. (2013) (gray curves: solid with the extra finite difference penalty and dashed without it). Densities in black are those obtained using the PDE-P-splines approaches (solid curve for unknown state conditions and dashed for known conditions). In each column, the posterior densities for different sample sizes are depicted ($n = 40 \times 20$ in the left column, $n = 60 \times 40$ and $n = 100 \times 50$ in the middle columns and $n = 200 \times 100$ in the right column). The data have been simulated by adding a 5 degrees of freedom Student t distributed noise to the analytic solution of the PDE in (14)

5 Application

In this section, we evaluate the performance of the proposed approaches in a real data application. We analyze a set of prices of “option contracts” traded for different “strike prices” and “maturities”. Cox et al. (1979), an option is a contract that gives the right, but not the obligation, to buy or sell a risky asset at a predetermined fixed price within (American style) or at (European style) a given date (maturity of the contract). This kind of financial instrument allows to bet on the future evolution of the price of the underlying asset that can be another contract (a stock for example), a market index or a commodity. Options and other related instruments are often called “derivatives” given that their price is derived from the market value (S) of the underlying risky asset.

Two different kinds of option contracts are distinguished according to the right that they give to the holder. “Call” options give the right to buy the underlying asset, while “put” give the right to sell it. These characteristics determine the payoff functions at maturity (T):

$$\begin{aligned} C(S, T)= & {} \left\{ \begin{array}{l@{\quad }l} 0\ &{} \text{ if }\ S_{T} \le E \\ S_{T} - E\ &{} \text{ if }\ S_{T} > E, \end{array} \right. \\ P(S, T)= & {} \left\{ \begin{array}{l@{\quad }l} 0\ &{}\text{ if }\ S_{T} \ge E \\ E-S_{T}\ &{} \text{ if }\ S_{T} < E, \end{array} \right. \end{aligned}$$

where C and P indicate call and put prices, respectively, E is the strike price and $S_{T}$ represents the market price of the underlying asset at maturity. The current price of the contract is then computed as the present value of the payoff at maturity. For this reason, it is necessary to describe the dynamics of the underlying asset to price the derivative contract “written” on it.

Fig. 5

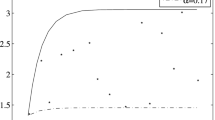
Left upper panel: observations (red dots) and smoothing surface obtained applying a frequentist constrained PDE-P-spline estimation procedure to the SP-500 European call option prices analyzed by Carmona (2004). The prices in the plot are scaled by the observed strikes and the moneyness is defined as the log of the ratio between the observed spot and strike prices. The estimated implied volatility was $\hat{\sigma } = 1.003\text{ E }-01$ with an optimal compliance parameter equal to $\hat{\gamma } = 47385275$. Left lower panel posterior density of the implied volatility parameter (Bayesian estimates). Right panels histogram and qq-plot of the residuals (call price scale)

The Black and Scholes (1973) framework is the most famous pricing model for financial derivatives. This model assumes that the price of the underlying risky asset follows a geometric Brownian motion in the instantaneous time with a constant standard deviation (volatility). This assumption leads to the well-known second-order partial differential equation describing the value (C) of a call option:

$$\begin{aligned} \mathcal {F}\left( S, t, C, \frac{\partial C}{\partial S}, \frac{\partial C}{\partial t}, \frac{\partial ^{2} C}{\partial S^{2}}, \sigma \right) = \frac{\partial C}{\partial t} + r S \frac{\partial C}{\partial S} + \frac{1}{2} \sigma ^{2} S^{2} \frac{\partial ^{2} C}{\partial S^{2}} - r C = 0, \end{aligned}$$

(15)

where the parameter $\sigma$ identifies the “implied volatility” and r is the observed risk-free interest rate (e.g., the Libor rate). For European options (exercise allowed only at a given date), a closed-form solution can be found by introducing the following no-arbitrage terminal (related to the expiration of the contract) and boundary conditions:

$$\begin{aligned}&C(0, t) = 0,\nonumber \\&C(S, t) \approx S \quad \text{ for }\ S \rightarrow \infty ,\nonumber \\&C(S, T) = \max (S-E, 0) = (S-E)^{+}. \end{aligned}$$

(16)

This framework provides a concise and easy-to-interpret description of the price dynamics. Here, we aim to approximate the solution of the Black and Scholes PDE and estimate its implied volatility by including (15) and no-arbitrage conditions (16) in a PDE-P-spline approach. Note that we share with the theoretical model the strong assumption of constant (implied) volatility over strikes and maturities. On the other hand, besides the limitations of the differential model, we believe that the proposed estimation procedure is flexible enough to ensure appropriate estimates. As data example, we consider the option prices already analyzed by Carmona (2004). The dataset counts 2800 prices of European call options written on the SP-500 index and traded in 1993 with expiration between 1993 and 1994. The six variables included in the dataset indicate the value of the index, the strike prices of the option, the time to expiration (in fraction of year), the spot interest rate, the observed implied volatilities and the prices of the options. This application is, in our opinion, particularly interesting since it represents one of those cases in which the state conditions are known a priori (given by theoretical arguments) and need to be taken into account to obtain valid estimates.

The raw data and the estimated smoothing surface (obtained through a soft constrained frequentist approach) are shown in Fig. 5. According to the option-pricing theory, the payoff surface was expected to be rather flat over large portions of the domain mesh. For this reason, we decided to build our smoother using tensor product of B-splines of degree four defined on 25 equidistant internal knots for both the maturity and moneyness directions. The moneyness parametrization of the PDE (see Piché and Kanniainen (2007)) allows for a simple formulation of the penalty and of the necessary state conditions.

The estimated implied volatilities are equal to 1.003E-01 and 1.014E-01 for the frequentist and Bayesian procedures, respectively, and are in agreement with the median of the ones observed in the dataset. The frequentist 95 % approximate confidence interval (obtained using the observed pseudo-information matrix) is [9.967E-02; 1.015E-01], while the corresponding credibility interval has been found to be equal to [1.007E-01; 1.020E-01]. The lower left panel of Fig. 5 shows the posterior distribution of the estimated parameter.

The estimates obtained using our approach show some desirable properties. First of all, we are able to extrapolate the prices associated with strikes and maturities not traded, and these estimates are consistent with the no-arbitrage constraints (due to the compliance to the Black and Scholes model). Furthermore, it is particularly appreciable in real data analysis to have confidence/credible bounds for prices associated to unobserved strikes and/or maturities. On the other hand, the PDE-P-spline approach enables here to obtain point and interval estimates of the implied volatility consistent with the Black and Scholes equation while ensuring a good performance in terms of data fitting.

6 Discussion

In this paper, we propose a PDE-based penalized tensor product B-spline smoothing approach to solve and estimate unknown parameters in partial differential equations. Our aim was to introduce frequentist and Bayesian procedures to analyze data which dynamics is defined over more than one dimension. Both approaches exploit a tensor product B-spline approximation to the state function, while the consistency of the final estimates to the PDE is ensured by PDE-based soft constraints. The compromise between data fitting and consistency with the PDE is tuned by a compliance parameter. As in Xun et al. (2013), we estimate the spline coefficients, the PDE parameters and the precision of measurement using the available observations. If state conditions are not included in the model, our frequentist approach and the one by Xun et al. (2013) are comparable except that we provide an automatic EM-like procedure to select the PDE-compliance parameter (Schall 1991). In our Bayesian approach, differently from Xun et al. (2013), we use the same PDE-based penalty as with the frequentist approach. In particular, our Bayesian formulation takes into account the functional dependence of the normalizing constant of the spline coefficient prior on PDE parameters. Note that prior confidence in the PDE model is introduced by a specific choice for the prior distribution of the compliance parameter.

Even if their knowledge is not strictly required for the application of the proposed methods, we are able to improve the quality of the estimates by introducing state conditions as extra constraints using either a $L^{2}$ penalty or Lagrange multipliers. On the other hand, the introduction of these conditions sometimes arises naturally from theoretical arguments and cannot be omitted during the estimation process. This is the case for the real data analysis in Sect. 5.

We demonstrate through simulations that our PDE-P-spline approaches show desirable properties and that the inclusion of the state conditions has an influence on the estimation performances by reducing the variability of the PDE parameters and by improving the coverages of credible regions. For known state conditions, the appropriateness of our proposal has been tested by comparing its performances with those achieved via nonlinear least squares inversion of the analytic state function.

We have also compared our Bayesian proposals with the one suggested by Xun et al. (2013). By simulating 100 synthetic data sets with Gaussian noise, we found that, the introduction of an additional finite difference penalty, within their Bayesian approach, helps to reduce the bias of the PDE parameter estimates and mitigates the effect of the miss-specified constant of normalization in the prior of the spline coefficients. The effectiveness of this correction seems to decrease with the size of the data sample. This appears also from the results presented in Figs. 3 and 4 showing the approximated state functions and the PDE parameters posterior densities obtained for a simulated set of data with Student t distributed noise. For small sample sizes, the extra penalty term tends to produce smoothing surface not compliant with the state function. These undesirable features are not shared by our Bayesian proposal. Indeed, even for small sample sizes and/or large level of noise, the use of the proper prior for the spline coefficients ensures good fitting and estimation performances.

As real data application, we have analyzed the SP-500 call option prices discussed in Carmona (2004). The proposed example represents one of those cases where the state conditions (as defined in Sect. 3) are known (due to theoretical arguments) and cannot be ignored to estimate a smoothing surface consistent with the necessary no-arbitrage constraints. We used the well-known Black and Scholes model to define a suitable PDE-based penalty. Despite its simplicity, the presented analysis based on the Black and Scholes differential equation ensured satisfactory results in terms of signal extraction and PDE parameter estimation.

Extensions of our approaches are possible. First of all, the analysis of the call option prices in Sect. 5 could be improved. In the Black and Scholes model, the volatility parameter is supposed to be constant over time. This assumption is obviously unrealistic. One way to allow for time-varying volatility could be to adopt a more realistic differential pricing model (e.g., the stochastic volatility model of Heston (1993)). The same result could be achieved, in our opinion, by allowing the implied volatility parameter in the Black and Scholes equation to vary (e.g., using P-splines) with the time to maturity.

In this paper, we have considered only linear partial differential equations. Moving to nonlinear partial differential equation would lead to additional challenges. First of all, the PDE-penalty term would no longer be a second-order homogeneous polynomial in the spline coefficients. In the frequentist approach, this would require the use of the implicit function theorem to estimate the PDE parameters (Ramsay et al. 2007). On the other hand, in a Bayesian setting, the constant of normalization for the prior distribution for the spline coefficients would not have an explicit form anymore.

Appendices

Appendix 1: Logarithm of the marginalized posterior distribution

The joint posterior distribution given in Eq. (8) is marginalized with respect to the spline coefficients. The log of the marginalized posterior distribution can be shown to be:

$$\begin{aligned} \log \left( p\left( \varvec{\theta }, \gamma , \tau | \varvec{\zeta }\right) \right)= & {} \displaystyle \frac{N}{2} \log \left( \tau \right) - \displaystyle \frac{\tau }{2} \varvec{\zeta }^{\top }\varvec{\zeta }\\&+ \displaystyle \frac{1}{2} \log \left( \text{ det }\left( V_{1}\right) \right) - \displaystyle \frac{1}{2}\varvec{v_{1}}^{\top } \varvec{V_{1}}^{-1}\varvec{v_{1}}\\&- \displaystyle \frac{1}{2} \log \left( \text{ det }\left( V_{2}\right) \right) + \displaystyle \frac{1}{2}\varvec{v_{2}}^{\top } \varvec{V_{2}}^{-1}\varvec{v_{2}}\\&+ \left( a_{\tau } - 1\right) \log \left( \tau \right) - b_{\tau }\tau \\&+ \left( a_{\gamma } - 1\right) \log \left( \gamma \right) - b_{\gamma } \gamma \\&+ \log \left( p\left( \varvec{\theta }\right) \right) . \end{aligned}$$

Appendix 2: Posterior distributions including the DE conditions by least squares

The log joint posterior distribution can be shown to be:

$$\begin{aligned} \log \left( p\left( \varvec{c}, \varvec{\theta }, \gamma , \kappa , \tau | \varvec{\zeta }\right) \right)= & {} \displaystyle \frac{N}{2} \log \left( \tau \right) - \displaystyle \frac{\tau }{2} \left\| \varvec{\zeta } - \varvec{\mathcal {B}c} \right\| ^ {2} \\&+ \displaystyle \frac{1}{2} \log \left( \text{ det }\left( V_{1}\right) \right) - \displaystyle \frac{1}{2}\left\{ \varvec{c}^{\top }\varvec{V_{1}c} - 2 \varvec{c}^{\top }\varvec{v_{1}} + \varvec{v_{1}}^{\top }\varvec{V_{1}}^{-1} \varvec{v_{1}}\right\} \\&+ \left( a_{\tau } - 1\right) \log \left( \tau \right) - b_{\tau }\tau \\&+ \left( a_{\gamma } - 1\right) \log \left( \gamma \right) -b_{\gamma } \gamma \\&+ \left( a_{\kappa } - 1\right) \log \left( \kappa \right) -b_{\kappa } \kappa \\&+ \log \left( p\left( \varvec{\theta }\right) \right) . \end{aligned}$$

From this joint posterior distribution, only two conditional posterior distribution can be identified. The conditional posterior distribution for the spline coefficients is a multivariate normal distribution:

$$\begin{aligned} \varvec{c} | \varvec{\theta }, \tau , \gamma , \varvec{\zeta } \sim \mathcal {N}_{M^{p}}\left( \varvec{V_{2}}^{-1}\varvec{v_{2}}; \varvec{V_{2}}^{-1}\right) . \end{aligned}$$

where $\varvec{V_{2}} = \tau \varvec{\mathcal {B}}^{\top }\varvec{\mathcal {B}} + \varvec{V_{1}}$ and $\varvec{v_{2}} = \tau \varvec{\mathcal {B}}^{\top } \varvec{\zeta } + \varvec{v_{1}}$. For the precision of measurement, the conditional posterior distribution is a gamma distribution:

$$\begin{aligned} \tau | \varvec{c}, \varvec{\zeta } \sim \mathcal {G}\left( \frac{N}{2} + a_{\tau }; \frac{\left\| \varvec{\zeta } - \varvec{\mathcal {B}c} \right\| ^ {2} }{2} + b_{\tau }\right) . \end{aligned}$$

The joint posterior distribution can be marginalized with respect to the spline coefficients. The log of the marginalized posterior distribution can be shown to be:

$$\begin{aligned} \log \left( p\left( \varvec{\theta }, \gamma , \tau | \varvec{\zeta }\right) \right)= & {} \displaystyle \frac{N}{2} \log \left( \tau \right) - \displaystyle \frac{\tau }{2} \varvec{\zeta }^{\top }\varvec{\zeta }\\&+ \displaystyle \frac{1}{2} \log \left( \text{ det }\left( V_{1}\right) \right) - \displaystyle \frac{1}{2}\varvec{v_{1}}^{\top } \varvec{V_{1}}^{-1}\varvec{v_{1}}\\&- \displaystyle \frac{1}{2} \log \left( \text{ det }\left( V_{2}\right) \right) + \displaystyle \frac{1}{2}\varvec{v_{2}}^{\top } \varvec{V_{2}}^{-1}\varvec{v_{2}}\\&+ \left( a_{\tau } - 1\right) \log \left( \tau \right) - b_{\tau }\tau \\&+ \left( a_{\gamma } - 1\right) \log \left( \gamma \right) - b_{\gamma } \gamma \\&+ \left( a_{\kappa } - 1\right) \log \left( \kappa \right) - b_{\kappa } \kappa \\&+ \log \left( p\left( \varvec{\theta }\right) \right) . \end{aligned}$$

Appendix 3: Elementary penalty elements

The penalty term, dealing with linear PDEs, can be seen as a homogeneous polynomial of second degree in the spline coefficients. The computations needed to construct the penalty term are:

$$\begin{aligned} PEN(\mathbf {c}|\varvec{\theta })= & {} \varvec{c}^{\top } \varvec{R}\left( \varvec{\theta }\right) \varvec{c} + 2 \varvec{c}^{\top } \varvec{r}\left( \varvec{\theta }\right) + l\left( \varvec{\theta }\right) . \end{aligned}$$

The $\varvec{R}$ matrix is given by the sum of a series of elementary penalty matrices:

$$\begin{aligned} \mathbf {P}_{i_{p},\ldots ,i_{1}}^{j_{p},\ldots ,j_{1}}= & {} \int \left( \mathbf {B}_{p}^{(i_{p})} (x_{p}) \otimes \cdots \otimes \mathbf {B}_{1}^{(i_{1})}(x_{1})\right) \left( \mathbf {B}_{p}^{(j_{p})} (x_{p}) \otimes \cdots \otimes \mathbf {B}_{1}^{(j_{1})}(x_{1})\right) ^{\top }dx_{p} \ldots dx_{1},\\= & {} \int \mathbf {B}_{p}^{(i_{p})} (x_{p}) \left( \mathbf {B}_{p}^{(j_{p})} (x_{p}) \right) ^{\top }dx_{p} \otimes \cdots \otimes \int \mathbf {B}_{1}^{(i_{1})} (x_{1}) (\mathbf {B}_{1}^{(j_{1})} (x_{1}) )^{\top } dx_{1},\\= & {} \mathcal {S}_{p}^{(i_p, j_p)} \otimes \cdots \otimes \mathcal {S}_{1}^{(i_1, j_1)}, \end{aligned}$$

where the matrix $\mathcal {S}_{h}^{(i_h, j_h)}$ can be approximated using a trapezoidal rule. The $\varvec{r}$ vector can be constructed as the sum of elementary penalty vectors:

$$\begin{aligned} \mathbf {p}_{i_{p},\ldots ,i_{1}}= & {} \int \mathbf {B}_{p}^{(i_{p})} (x_{p}) \otimes \cdots \otimes \mathbf {B}_{1}^{(i_{1})}(x_{1}) dx_{p} \ldots dx_{1},\\= & {} \int \mathbf {B}_{p}^{(i_{p})} (x_{p}) dx_{p} \otimes \cdots \otimes \int \mathbf {B}_{1}^{(i_{1})} (x_{1}) dx_{1},\\= & {} \mathbf {s}_{p}^{(i_p)} \otimes \cdots \otimes \mathbf {s}_{1}^{(i_1)}, \end{aligned}$$

as before, a trapezoidal rule can be applied to approximate the vector $\mathbf {s}_{h}^{(i_h)}$.