A need to reinforce the traction power supply system in alternating current sections appears when there are restrictions on the power of traction substations, the voltage level on the current collector of electric rolling stock, and the heating of contact suspension wires. The restrictions are due to a continuous increase in freight traffic, an increase in the unit weight of trains, and the introduction of multiple traction. The growth of traction loads is limited by the load capacity of the main elements of the traction network.

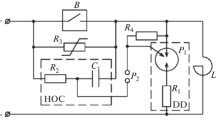
In ac sections, various methods are used for purposes of reinforcement: replacing traction transformers with more powerful ones; construction of additional traction substations, sectioning posts, and parallel connection points; hanging reinforcing and shielding wires; the use of volt-boost transformers, installation of longitudinal and lateral compensation; and transition to a traction power supply system of 2–25 kV with autotransformers [1–3]. Strengthening the traction power supply system of alternating current in cargo-intensive and high-speed sections can be done, according to [4], by using a power supply system (PSS) with a high-voltage power wire (HVPW) (PSS HVPW). A schematic diagram of a traction power supply system with a high-voltage power wire is shown in Fig. 1 [4, 5].

Fig. 1.
figure 1

Principal electrical equivalent circuit of the HVPW PSS.

Full size image

The power supply system with the HVPW operates as follows. Separation–balancing three-phase–two-phase transformers 1 are connected to phases A, B, and C of power line 2 with linear voltage UOPL equal to 110 kV. In this case, transformers 1 separate power line 2 from the traction network and prevent the flow of zero-sequence currents in line 2. The voltage transformation in the first part of the primary winding with a transformation coefficient equal to nT1 = 1 and in the second part with a transformation coefficient equal to nT2 = \(\frac{{\sqrt 3 }}{2}\) provides voltages equal to the linear voltage of the transmission line of 110 kV on the terminals of the secondary windings of both parts. The secondary windings of the first part are connected between contact suspensions 3 and 4 and power (high voltage) wires 5 and 6. The output terminals of the second part of the secondary winding are connected to contact suspension 7 and power wire 8. Since three- and two-phase transformers 1 are connected according to a Scott scheme, the voltages of the first and second parts of the primary windings are mutually perpendicular in phase and will be also mutually perpendicular to the voltage of the secondary windings. This significantly reduces the asymmetry of the currents in overhead power line (OPL) 2, while complete symmetrical loading of OPL 2 is ensured at the same load on the substation shoulders. When connecting autotransformers 14 with the primary windings between longitudinal supply wire 8 and rails 13 to a voltage of 85 kV and with secondary windings between contact suspension 7 and rails 13, the permissible voltage in the traction network is provided at the power points of contact suspension 7. Located on the stage, electric locomotives 15 are powered by two neighboring autotransformers 14, while electric locomotives 15 located between the substation and the closest autotransformer 14 are powered by this autotransformer 14 and by part of the secondary winding of three-phase–two-phase transformer 1, the special output of which is connected to rails 13 using a section line 10. Since a voltage of 110 kV is provided between contact suspension 7 and supply wire 8, the current load of suspension wires 7 and wire 8 is reduced, as are the voltage and power loss in the traction network. In this case, a voltage of 25 kV is created between the contact suspension and the rails, while a voltage of 85 kV is generated between the power wire and the rails.

To power electric locomotives located between the traction substation and the first point with an autotransformer, the secondary windings of the transformers of the traction substations have special leads connected to the rails. The power wire can be suspended on special consoles on the supports of the contact network from the field side. In some cases, specially arranged supports may be provided for positioning the power supply wires.

Note that single-phase transformers with the primary winding connected between the contact network and the HVPW and the secondary winding connected between the contact network and rails 13 can be used instead of autotransformers 14.

A number of problems that need to be addressed arise when introducing an HVPW PSS. These primarily include grounding of contact network supports, protection of electrical installations and nontraction power supply networks (for example, self-locking devices and SCB devices) from pulse overvoltages (lightning and internal switching) arising in an HVPW PSS, and reduction to permissible values ​​of the electrical effect of the HVPW SE on nontraction power supply OPLs.

The most promising way to solving the problem of protection from pulse overvoltages (lightning and switching) arising in an HVPW PSS in electrical installations and nontraction power supply systems, in particular, self-blocking and SCB devices, is to do without a rail track to the ground contact network supports on which the HVPW is suspended [3, 5].

Grounding of the contact network supports and protection of floor SCB devices from switching overvoltages in an HVPW PSS can be provided by connecting the contact network supports to an extended ground conductor (GC) (electrode) located on the ground and not connected to the rail track. For purposes of safer maintenance of the poles of a contact network and the operation of rail circuits, the length of one section of an artificial ground conductor must be at least 400 m, with the ground conductor being located under the ground at a depth of no less than 0.5 m. The experience of using GCs for lightning protection of high-voltage OPLs in in regions with rocky and permafrost soils is known [6].

The use of the GC along with the restriction of pulse overvoltages on the insulation of the contact network supports provides reliable protection of traction networks from short circuit currents [5]. Indeed, the input resistance of the GC is significantly less than the analogous parameter when grounding supports with a group grounding cable in the absence of its connection to the rail.

In the general case, the electrical circuit for replacing a GC is represented by a circuit with distributed parameters, the primary characteristics of which depend on the frequency due to the surface effect in the ground and the metal strip. High frequencies prevail in the spectral composition of the lightning current. When lightning currents flow through a metal grounding conductor, its active resistance and the internal and external inductances of the “grounding conductor–ground” circuit vary widely due to the surface effect. To a greater extent, the surface effect at frequencies ω = 104–105 s–1 or higher affects the active resistance and internal inductance of the GC.

A method for calculating the parameters of the equivalent circuit of a steel conductor (rails) was proposed in [7]. We will use these results to construct the equivalent circuit of the strip ground conductor.

The problem of the surface effect in steel conductors is solved of the basis on a joint solution of the Maxwell equations written in a cylindrical coordinate system:

$$\frac{{\partial H}}{{\partial r}} + \frac{H}{r} = \gamma E,$$
$$\frac{{\partial E}}{{\partial r}} + \frac{{\partial B}}{{\partial t}},$$
(1)

where B and H are the instantaneous values ​​of induction and strength of a magnetic field, E is the instantaneous value of the electric field strength in a metal conductor with a specific electrical conductivity of the material (γ), and t is time.

Let us present the dependence of magnetic induction in steel on the magnetic field in the form of the equation [8]

$$B = kH + \alpha \arctan \beta H\,\,{\text{at}}\,\, - \infty < H < + \infty ,$$

where coefficients k, α, and β are determined by the method of the selected points.

Solving Eqs. (1) together, we obtain

$$\frac{{{{\partial }^{2}}H}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial H}}{{\partial r}} - \frac{1}{{{{r}^{2}}}}H = \gamma \frac{{\partial B}}{{\partial H}}\frac{{\partial H}}{{\partial t}}.$$
(2)

Derivative \(\frac{{\partial B}}{{\partial H}} = {{\mu }_{g}}\), the differential magnetic permeability of the steel of which the metal strip (with a size of (4 × 5) × 10–4 m2) is made, is calculated by the following formula:

$${{\mu }_{g}} = k + \frac{{\alpha \beta }}{{1 + {{\beta }^{2}}{{H}^{2}}}}.$$

It is established that, in relation to the steel from which the metal strip is made, k = n1μ0 ≈ 25μ0, where n1 = 25, and α = n2μ0 = 360 μ0 at n2 = 360 A/m and β = 0.75 m/A, where μ0 = 12.56 × 10–7 G/m is the absolute magnetic permeability of the vacuum.

We rewrite equation Eqs. (1) and (2) in relative units:

$$\begin{gathered} \frac{{{{\partial }^{2}}{{\bar{\text{H}}}}}}{{{{\partial }^{2}}{{\bar{\text{r}}}}}} + \frac{{\partial {{\bar{\text{H}}}}}}{{\partial {{\bar{\text{r}}}}}}\frac{1}{{{{\bar{\text{r}}}}}} - \frac{{{{\bar{\text{H}}}}}}{{{{{{{\bar{\text{r}}}}}}^{2}}}} = \left( {{{n}_{1}} + \frac{{{{n}_{2}}\beta }}{{1 + {{{(0.5\beta {{E}_{e}}{{r}_{e}}\gamma {{\bar{\text{H}}})}}}^{2}}}}} \right)\frac{{\partial {{\bar{\text{H}}}}}}{{\partial {{\bar{\text{t}}}}}}, \\ \frac{{\partial {{\bar{\text{H}}}}}}{{\partial {{\bar{\text{r}}}}}} + \frac{{{{\bar{\text{H}}}}}}{{{{\bar{\text{r}}}}}} = {{\bar{\text{E}}},} \\ \end{gathered} $$

at

$$\begin{gathered} {{\bar{\text{H}}}}\,{\text{ = }}\frac{H}{{{{H}_{e}}}};\,\,\,{{\bar{\text{r}}}}\,{\text{ = }}\frac{r}{{{{r}_{e}}}};\,\,\,{{\bar{\text{t}}}} = \frac{t}{{{{t}_{e}}}};\,\,\,{{\bar{\text{E}}}} = \frac{E}{{{{E}_{e}}}},\,\,\,{{E}_{e}} = \frac{{2{{H}_{e}}}}{{\gamma {{r}_{e}}}}, \hfill \\ {{H}_{e}} = \frac{{{{I}_{g}}}}{{2\pi {{r}_{e}}}} = \frac{{\gamma {{E}_{e}}\pi r_{e}^{2}}}{{2\pi {{r}_{e}}}} = \frac{1}{2}\gamma {{E}_{e}}{{r}_{e}},\,\,\,{{t}_{e}} = \gamma {{\mu }_{0}}r_{e}^{2}, \hfill \\ \end{gathered} $$

where He and Ee are the magnetic and electric field strengths on the surface of the cylinder with radius re corresponding to the steady-state value of the current when it is turned on at a constant voltage.

To determine the boundary conditions, we take into account that the electric field strength is instantly established on the cylinder surface. Then, the first boundary condition in the relative form at \({{\bar{\text{r}}}}\) = 1 is

$$\frac{{\partial {{\bar{\text{H}}}}}}{{\partial {{\bar{\text{r}}}}}} + {{\bar{\text{H}}}} = 2.$$

The second boundary condition is

$${{\bar{\text{H}}}} = {\text{ }}0\,\,{\text{at}}\,\,{{\bar{\text{r}}}}~ = 0.$$

We numerically find the solution of differential equations (2) using the finite difference method. Substituting in formulas (2) the difference expressions of derivatives of the first and second orders, we obtain

$$\begin{gathered} {{{{{\bar{\text{H}}}}}}_{{i,j + 1}}} = {{\bar{\text{S}}}}\left( {\frac{{{{{{{\bar{\text{H}}}}}}_{{i + 1,j}}} - 2{{{{{\bar{\text{H}}}}}}_{{i - 1,j}}}}}{{{{{{{\bar{\text{I}}}}}}^{2}}}} + \frac{{{{{{{\bar{\text{H}}}}}}_{{i + 1,j}}} - {{{{{\bar{\text{H}}}}}}_{{i - 1,j}}}}}{{2{{\bar{\text{I}}}}{{{{{\bar{\text{r}}}}}}_{i}}}} - \frac{{{{{{{\bar{\text{H}}}}}}_{{i,j}}}}}{{{{\bar{\text{r}}}}_{i}^{2}}}} \right) \\ \times \,\,\frac{1}{{\left( {{{n}_{1}} + \frac{{{{n}_{2}}\beta }}{{1 + {{{(0.5\beta {{E}_{e}}{{r}_{e}}\gamma {{{{{\bar{\text{H}}}}}}_{{i,j}}})}}^{2}}}}} \right)}} + {{{{{\bar{\text{H}}}}}}_{{i,j}}} \\ \end{gathered} $$

at

$${{\bar{\text{S}}}} = \frac{S}{{{{t}_{e}}}}\,\,{\text{and}}\,\,{{\bar{\text{I}}}} = \frac{1}{{{{r}_{e}}}},$$

where \({{\bar{\text{S}}}}\) and \({{\bar{\text{I}}}}\) are the integrating steps over the variables \({{\bar{\text{t}}}}\) and \({{\bar{\text{r}}}}\) expressed in relative units.

In determining the first boundary condition, we take into account that

$${{\left( {\frac{{\partial {{\bar{\text{H}}}}}}{{\partial {{\bar{\text{r}}}}}}} \right)}_{{i,j}}} = \frac{{{{{{{\bar{\text{H}}}}}}_{{i,j}}} - {{{{{\bar{\text{H}}}}}}_{{i - 1,j}}}}}{{{{\bar{\text{I}}}}}}.$$

Then, the first boundary condition is written in the following form:

$$\frac{{{{{{{\bar{\text{H}}}}}}_{{i,j}}} - {{{{{\bar{\text{H}}}}}}_{{i - 1,j}}}}}{{{{\bar{\text{I}}}}}} + \frac{{{{{{{\bar{\text{H}}}}}}_{{i - 1,j}}}}}{{{{{{{\bar{\text{r}}}}}}_{e}}}} = 2$$

at \({{{{\bar{\text{r}}}}}_{e}}\) = 1.

To switch from a steel cylinder to a metal strip with cross-section perimeter P, instead of 0.5 re, it is necessary to introduce parameter Ss/P, where Ss is the cross-sectional area of ​​the strip. In this case,

$${{\bar{\text{t}}}} = \frac{t}{{{{t}_{e}}}} = \frac{{{{P}^{2}}}}{{4\gamma {{\mu }_{0}}S_{{\text{s}}}^{2}}}t.$$

Let us represent the instantaneous current value in a metallic strip that is calculated by a numerical method when it is turned on at a constant voltage by an expression of the following form:

$$i = {{I}_{g}}(1 - {{\alpha }_{1}}{{e}^{{{{\beta }_{1}}t}}} - {{\alpha }_{2}}{{e}^{{{{\beta }_{2}}t}}}),$$
(3)

where αi and βi are the coefficients obtained by approximating the current in a metal strip when it is turned on at a constant voltage that is calculated by the numerical method.

Using expression (3) and performing the circuit synthesis, we obtain the equivalent circuit of the metal strip in the form of a passive two-terminal network consisting of series-connected active resistance R1 and inductance L1, which are, in turn, connected to parallel-connected resistance R2 and inductance L2. Let R1 be the resistance of the metal strip to direct current. The three other equivalent circuit parameters are calculated from the following ratios:

$$\begin{gathered} L_{1}^{'} = \frac{{{{R}_{1}}}}{{{{\alpha }_{1}}{{\beta }_{1}} + {{\alpha }_{2}}{{\beta }_{2}}}};\,\,\,{{R}_{2}} = {{R}_{1}}\frac{{{{\alpha }_{1}}{{\alpha }_{2}}{{{({{\beta }_{2}} - {{\beta }_{1}})}}^{2}}}}{{{{{({{\alpha }_{1}}{{\beta }_{1}} - {{\alpha }_{2}}{{\beta }_{2}})}}^{2}}}}; \\ {{L}_{2}} = {{R}_{1}}\frac{{{{\alpha }_{1}}{{\alpha }_{2}}{{{({{\beta }_{2}} - {{\beta }_{1}})}}^{2}}}}{{{{\beta }_{1}}{{\beta }_{2}}{{{({{\alpha }_{1}}{{\beta }_{1}} - {{\alpha }_{2}}{{\beta }_{2}})}}^{2}}}}. \\ \end{gathered} $$

The following parameters of the equivalent circuit were obtained for a metal strip with sizes of (4 × 5) × 10–4 m2:

$${{R}_{1}} = 0.1\,\,\,{\Omega \mathord{\left/ {\vphantom {\Omega {{\text{km}},}}} \right. \kern-0em} {{\text{km}},}}\,\,\,L_{1}^{'} = 0.25 \times {{10}^{{ - 3}}}\,\,{{\text{H}} \mathord{\left/ {\vphantom {{\text{H}} {{\text{km}}}}} \right. \kern-0em} {{\text{km}}}};$$
$${{L}_{2}} = 4.2 \times {{10}^{{ - 3}}}\,\,{{\text{H}} \mathord{\left/ {\vphantom {{\text{H}} {{\text{km}}}}} \right. \kern-0em} {{\text{km}}}};\,\,\,{{R}_{2}} = 1.25\,\,{\Omega \mathord{\left/ {\vphantom {\Omega {{\text{km}}}}} \right. \kern-0em} {{\text{km}}}}.$$

Finally, the electrical equivalent circuit of the steel strip is obtained by adding in series with \(L_{2}^{'}\) the external inductance of the “strip–ground” circuit calculated according to the Pollyachek formula [9] for an equivalent frequency determined from the relation

$$\omega = \frac{\pi }{\tau } = \frac{{3.14}}{{50 \times {{{10}}^{{ - 6}}}}} = 6 \times {{10}^{4}}\,\,{{{\text{s}}}^{{ - 1}}},$$

where τ is the duration of the lightning current.

Given the possibility of representing the elementary section of the strip ground conductor as a passive two-terminal network, the calculated equivalent circuit of the ground conductor located in the ground has the form of a line with distributed parameters (Fig. 2).

Fig. 2.
figure 2

Calculated electrical equivalent circuit of a strip GC.

Full size image

In Fig. 2, g is the transverse conductivity of a strip grounding conductor–earth circuit determined according to [5], u(t) is the pulse voltage at the input of the ground conductor, and x is the current coordinate.

When constructing the electrical equivalent circuit of the strip ground conductor, it was taken into account that the strip GC capacity relative to the plane of the zero potential can be neglected [6].

The operator expressions of the wave resistance and propagation coefficient of a strip GC system are

$${{Z}_{{\text{w}}}}({\text{p}}) = \sqrt {\frac{{{{{\text{p}}}^{2}}{{L}_{1}}{{L}_{2}} + {\text{p}}({{L}_{1}}{{R}_{2}} + {{L}_{2}}{{R}_{1}} + {{L}_{2}}{{R}_{2}}) + {{R}_{1}}{{R}_{2}}}}{{({\text{p}}{{L}_{2}} + {{R}_{2}})g}}} ;$$
$$\gamma ({\text{p}}) = \sqrt {\frac{{{{{\text{p}}}^{2}}{{L}_{1}}{{L}_{2}} + {\text{p}}({{L}_{1}}{{R}_{2}} + {{L}_{2}}{{R}_{1}} + {{L}_{2}}{{R}_{2}}) + {{R}_{1}}{{R}_{2}}}}{{({\text{p}}{{L}_{2}} + {{R}_{2}})}}g} .$$

Given that the line in question operates in the idle mode, the operator expression of the transient conductivity is

$${{Y}_{{{\text{tr}}}}}({\text{p}}) = \frac{1}{{p{{Z}_{{\text{w}}}}({\text{p}})}}\tanh \gamma ({\text{p}})l.$$

Taking into account that, with an insignificant error for the spectral composition of the lightning current, we can write, according to [5, 10],

$$\frac{{\tanh \gamma ({\text{p}})l}}{{r({\text{p}})l}} = \frac{\theta }{{\theta + {{\gamma }^{2}}({\text{p}}){{l}^{2}}}},\,\,\,\theta \approx 4.1.$$

We denote that

$${{F}_{1}}({\text{p}}) = ({\text{p}}{{L}_{2}} + {{R}_{2}})\theta gl;$$
$$\begin{gathered} {{F}_{3}}({\text{p}}) = {{{\text{p}}}^{2}}{{L}_{1}}{{L}_{2}}g{{l}^{2}} \\ + \,\,{\text{p}}(({{L}_{1}}{{R}_{2}} + {{L}_{2}}{{R}_{1}} + {{L}_{2}}{{R}_{2}})g{{l}^{2}} + \theta {{L}_{2}}) + {{R}_{1}}{{R}_{2}}g{{l}^{2}} + \theta {{R}_{2}}. \\ \end{gathered} $$

The original of the transient conductivity is calculated according to the Heaviside theorem:

$${{Y}_{{{\text{tr}}}}}({\text{p)}}\,\,{\text{ + }}\,\,{{{\text{Y}}}_{{{\text{tr}}}}}(t) = \frac{{{{F}_{1}}(0)}}{{{{F}_{3}}(0)}} + \sum\limits_{k = 1}^2 {\frac{{{{F}_{1}}({{{\text{p}}}_{k}})}}{{{{{\text{p}}}_{k}}F_{3}^{'}({{{\text{p}}}_{k}})}}} {{e}^{{{{{\text{p}}}_{k}}t}}},$$

where the poles of function Ytr(p) are determined by the formula

$$\begin{gathered} {{{\text{p}}}_{1}}_{{,2}} = - \frac{{({{L}_{1}}{{R}_{2}} + {{L}_{2}}{{R}_{1}} + {{L}_{2}}{{R}_{2}})g{{l}^{2}} + \theta {{L}_{2}}}}{{{{r}_{{\text{p}}}}{{L}_{1}}{{L}_{2}}g{{l}^{2}}}} \\ \pm \,\,\sqrt {{{{\left[ {\frac{{({{L}_{1}}{{R}_{2}} + {{L}_{2}}{{R}_{1}} + {{L}_{2}}{{R}_{2}})g{{l}^{2}} + \theta {{L}_{2}}}}{{2{{L}_{1}}{{L}_{2}}g{{l}^{2}}}}} \right]}}^{2}} - \frac{{{{R}_{1}}{{R}_{2}}g{{l}^{2}} + \theta {{R}_{2}}}}{{{{L}_{1}}{{L}_{2}}g{{l}^{2}}}}} . \\ \end{gathered} $$

The final expression to determine transient conductivity is

$${{y}_{{{\text{tr}}}}}(t) = \frac{{\tanh \sqrt {{{R}_{1}}g{{l}^{2}}} }}{{\sqrt {\frac{{{{R}_{1}}}}{g}} }}\left( {1 - \frac{{\sqrt {\frac{{{{R}_{1}}}}{g}} }}{{\tanh \sqrt {{{R}_{1}}g{{l}^{2}}} }}\sum\limits_{k = 1}^2 {{{\varepsilon }_{k}}{{e}^{{{{{\text{p}}}_{k}}t}}}} } \right)$$

at

$${{\varepsilon }_{k}} = \frac{{{{F}_{1}}({{{\text{p}}}_{k}})}}{{{{{\text{p}}}_{k}}F_{3}^{'}({{{\text{p}}}_{k}})}}.$$

In further calculations, we will represent the pulse voltage in the form of oblique angular pulses (Fig. 3, dashed lines).

Fig. 3.
figure 3

Results of calculating the transient conductivity and current at the input of an extended GC.

Full size image

At 0 ≤ t ≤ tf, u = k1t; at tf ≤ t, u = k1t – (k1 + k2)(t – τf). In the above expressions,

$${{k}_{1}} = \frac{{{{U}_{{\text{p}}}}}}{{{{t}_{{\text{f}}}}}};\,\,\,{{k}_{2}} = \frac{{0.5{{U}_{{\text{p}}}}}}{{{{\tau }_{{\text{p}}}} - {{t}_{{\text{f}}}}}},$$

where τf and tp are the duration of the front and pulse of the voltage.

To determine current i(t, x = 0), we use the Duhamel integral. For a known transient conductivity and a specified instantaneous voltage value at the input of a strip GC in the form of u = k1t in the time interval of 0 ≤ t ≤ tf,

$$i(t,x = 0) = {{k}_{1}}\frac{{\tanh \sqrt {{{R}_{1}}gl} }}{{\sqrt {\frac{{{{R}_{1}}}}{g}} }}t - \sum\limits_{k = 1}^2 {\frac{{{{k}_{1}}{{\varepsilon }_{k}}}}{{{{{\text{p}}}_{k}}}}} ({{e}^{{{{{\text{p}}}_{k}}t}}} - 1).$$

The instantaneous value of the current flowing into an extended GC is determined at tf ≤ t by the superposition method:

$$i(t) = i(t,x = 0) - (1 + {{{{k}_{2}}} \mathord{\left/ {\vphantom {{{{k}_{2}}} {{{k}_{1}}}}} \right. \kern-0em} {{{k}_{1}}}})i(t - {{t}_{{\text{f}}}},\,\,x = 0).$$

As an example of calculating the lightning current flowing into an extended GC with a finite length, we consider the case of voltage Un = 104 V occurring at its input, tf = 2 × 10–6 s, and τp = 50 × 10–6 s. We assume that g = 0.5 1/(Ω km) and the GC length is 400 m. We obtain

$${{y}_{{{\text{tr}}}}}(t) = 0.198 - 0.0024{{e}^{{ - 294t}}} - 0.1956{{e}^{{ - 2.077 \times {{{10}}^{5}}t}}}.$$

The results of calculating the lightning current flowing into an extended GC during a lightning discharge in the HVPW and supports grounding of the contact network with the GC are shown in Fig. 3.

Since the circuit is of active-inductive nature, at a length of an artificial GC of 400 m or more, the levels of switching overvoltages are commensurate with the overvoltages that occur when using a rail track as a natural ground conductor. In addition, the pulse resistance of the artificial GC (approximately 6 Ω) is significantly less than the resistance to support ground spreading (7.5 Ω) when using a group–ground cable and in the absence of its connection with the rail track.

This, in turn, indicates the appropriateness of using a partitioned strip artificial GC for lightning protection and grounding of the contact network supports when a high-voltage power wire is located at the supports.

For power supply to nontraction consumers located in close proximity to newly constructed or reconstructed electrified lines of high-speed railways, it is appropriate to use OPLs with a voltage of 20 or 35 kV.

These OPLs can be located both on the supports of the contact network and on supports located at some distance from the HVPW PSS. The layout of the OPL wires to determine electrical effect of the contact network and the HVPW is shown in Fig. 4.

Fig. 4.
figure 4

Location of the HVPW PSS and OPL wires on the contact network support: CW is the contact wire, NT is the carrying cable, HVPW is the high-voltage power wire, and A, B, and C are the linear OPL wires.

Full size image

The three-phase OPL is powered by an almost symmetrical system of voltages (both linear and phase) from the power source. The linear voltages of OLPs are equal in magnitude, and the voltage of the OLP–ground wire differ significantly in amplitude and phase. In this case, when they are decomposed into symmetrical components, the phase voltages of the three-phase system relative to the ground will include zero-sequence voltage U0 that is caused mainly by the electrical effect of the voltages of the contact network and the HVPW [3].

The complex values ​​of the phase voltages of OLPs relative to the ground are

$${{\dot {U}}_{A}} = {{\dot {\varphi }}_{A}} - {{\dot {\varphi }}_{0}} = {{\dot {U}}_{{a0}}} + {{\dot {U}}_{0}},$$
$${{\dot {U}}_{B}} = {{\dot {\varphi }}_{B}} - {{\dot {\varphi }}_{0}} = {{\dot {U}}_{{b0}}} + {{\dot {U}}_{0}} = {{\dot {U}}_{{a0}}}{{e}^{{ - j120^\circ }}} + {{\dot {U}}_{0}},$$
$${{\dot {U}}_{C}} = {{\dot {\varphi }}_{C}} - {{\dot {\varphi }}_{0}} = {{\dot {U}}_{{c0}}} + {{\dot {U}}_{0}} = {{\dot {U}}_{{a0}}}{{e}^{{ - j120^\circ }}} + {{\dot {U}}_{0}},$$

where \({{\dot {U}}_{0}}\) is the zero-sequence voltage vector:

$${{\dot {U}}_{0}} = \frac{1}{3}({{\dot {U}}_{A}} + {{\dot {U}}_{B}} + {{\dot {U}}_{C}}).$$

Let α11, α22, and α33 be the intrinsic potential coefficients of the OPL, HVPW, and contact network wires and α12, α13, α14, and α15 be mutual potential coefficients between the OPL and HVPW wires, OPL wire and contact network, between OPL wires, and between the contact network and HVPW. The expressions for finding the intrinsic ​​and mutual potential coefficients are given in [11].

To find the electrical effect of the HVPW PSS on the 10-kV OPL, we apply a system of Maxwell equations written as follows [11]:

$${{\dot {U}}_{A}} = {{\dot {q}}_{a}}{{\alpha }_{{11}}} + {{\dot {q}}_{b}}{{\alpha }_{{14}}} + {{\dot {q}}_{c}}{{\alpha }_{{14}}} + {{\dot {q}}_{{\text{C}}}}{{\alpha }_{{13}}} + {{\dot {q}}_{{\text{P}}}}{{\alpha }_{{12}}};$$
$${{\dot {U}}_{B}} = {{\dot {q}}_{a}}{{\alpha }_{{14}}} + {{\dot {q}}_{b}}{{\alpha }_{{11}}} + {{\dot {q}}_{c}}{{\alpha }_{{14}}} + {{\dot {q}}_{{\text{C}}}}{{\alpha }_{{13}}} + {{\dot {q}}_{{\text{P}}}}{{\alpha }_{{12}}};$$
$${{\dot {U}}_{C}} = {{\dot {q}}_{a}}{{\alpha }_{{14}}} + {{\dot {q}}_{b}}{{\alpha }_{{14}}} + {{\dot {q}}_{c}}{{\alpha }_{{11}}} + {{\dot {q}}_{{\text{C}}}}{{\alpha }_{{13}}} + {{\dot {q}}_{{\text{P}}}}{{\alpha }_{{12}}};$$
$${{\dot {U}}_{{\text{C}}}} = ({{\dot {q}}_{a}} + {{\dot {q}}_{b}} + {{\dot {q}}_{c}}){{\alpha }_{{13}}} + {{\dot {q}}_{{\text{C}}}}{{\alpha }_{{33}}} + {{\dot {q}}_{{\text{P}}}}{{\alpha }_{{15}}};$$
$${{\dot {U}}_{{\text{P}}}} = ({{\dot {q}}_{a}} + {{\dot {q}}_{b}} + {{\dot {q}}_{c}}){{\alpha }_{{12}}} + {{\dot {q}}_{{\text{C}}}}{{\alpha }_{{15}}} + {{\dot {q}}_{{\text{P}}}}{{\alpha }_{{22}}},$$

where \({{\dot {U}}_{{\text{C}}}}\) and \({{\dot {U}}_{{\text{P}}}}\) are the voltage of the contact network and power wire relative to the ground and \({{\dot {q}}_{i}}\) are the charges of i-th wires.

When composing Eqs. (4), we assume that the intrinsic potential coefficients of the OPL wires are equal to each other and the mutual potential coefficients of the OPL and HVPW wires are also equal [11]. After simple simplifications, the zero-sequence voltages of phase voltages of the OPLs are determined from the following relation:

$$\begin{gathered} {{{\dot {U}}}_{0}} = \left[ {\left( {{{{\dot {U}}}_{{\text{C}}}}\frac{{{{\alpha }_{{13}}}}}{{{{\alpha }_{{11}}}{{\alpha }_{{33}}} - \alpha _{{13}}^{2}}} + {{{\dot {U}}}_{{\text{P}}}}\frac{{{{\alpha }_{{12}}}}}{{{{\alpha }_{{11}}}{{\alpha }_{{22}}} - \alpha _{{12}}^{2}}}} \right)} \right] \\ \times \,\,\frac{{({{\alpha }_{{11}}}{{\alpha }_{{33}}} - \alpha _{{13}}^{2})({{\alpha }_{{11}}}{{\alpha }_{{22}}} - \alpha _{{12}}^{2})}}{{{{\alpha }_{{13}}}({{\alpha }_{{11}}}{{\alpha }_{{22}}} - \alpha _{{12}}^{2}) + {{\alpha }_{{12}}}({{\alpha }_{{11}}}{{\alpha }_{{33}}} - \alpha _{{13}}^{2})}}. \\ \end{gathered} $$

It is established that, with an insignificant error, the voltage induced in the OPL can be determined from the expression

$${{\dot {U}}_{0}} = \frac{{{{{\dot {U}}}_{{\text{P}}}}{{C}_{1}} + {{{\dot {U}}}_{{\text{C}}}}{{C}_{2}}}}{{{{C}_{1}} + {{C}_{2}} + {{C}_{\Phi }}}},$$

where the capacitance between the OPL wire and the high-voltage wire due to its proximity to the OPL is

$${{C}_{1}} = \frac{{{{\alpha }_{{12}}}}}{{{{\alpha }_{{11}}}{{\alpha }_{{22}}} - \alpha _{{12}}^{2}}},$$

while the capacitance between the OPL wire and the contact network is

$${{C}_{2}} = \frac{{{{\alpha }_{{13}}}}}{{{{\alpha }_{{11}}}{{\alpha }_{{22}}} - \alpha _{{13}}^{2}}}.$$

When arranging the wires according to the diagram in Fig. 4, the capacity of the OPL wires relative to the ground [11] is

$${{C}_{\Phi }} = \frac{{2\pi {{\varepsilon }_{0}}}}{{\ln \frac{{2{{h}_{D}}}}{{{{R}^{3}}\sqrt {(4{{h}^{2}} + {{D}^{2}})\sqrt {{{h}^{2}} + {{D}^{2}}} } }}}},$$

where ε0 is the dielectric constant of air, h is the height of the OPL suspension above the upper track structure, D is the distance between the nearest OPL wires, and R is the radius of the OPL wire.

In power supply systems with an HVPW, when a 20-kV OPL is on the contact network supports, the zero-sequence voltage significantly exceeds the permissible value of 1735 V [12] and reaches several kV. To limit the zero-sequence voltage to the permissible values, zero-sequence voltage filters introduced on the network of electrified railways may be used [10].

However, given the special requirements for ensuring train traffic safety at heavy and high-speed sections, it is advisable to place OPL wires on separate supports outside the reserved strip. The necessity of making such a decision is also determined by preventing the HVPW voltage from getting on the OPL wire in the case of its possible breakage.