System of Traction AC Power Supply with Catenary Supports Not Connected with a Railway Track

Abstract

A system of traction ac power supply is suggested. It is revealed that grounding the supports of group grounding cables is the most promising way of providing reliable operation of existing types of distance protective systems. The probabilistic characteristics of the voltages at the catenary supports are determined taking into account the random character of parameters determining the voltage levels at the supports upon short circuits in the traction network. The mathematical expectation of the number of dangerous situations over a 100-km piece of line is calculated when using a railway track to ground supports and when using the proposed system of grounding catenary supports. It is revealed that the number of dangerous situations when grounding of the catenary supports is not done does not exceed the corresponding value over electrified piece of lines where a railway track is used to ground the supports. It was established that, when the value of resistance of the group-grounding-cable–support system is less than 7.5 Ω, the operation of traction power supply during thunderstorms is no worse than with a traction network when a railway track is used to support grounding.

An appreciable increase in the reliability of automatic locking devices, including railway track circuits and signaling, centralization, and blocking devices, during a thunderstorm is possible due to a decrease in the number of lightning strokes of a railway track. This can be achieved by abstaining from grounding ac catenary supports. However, the operation of current and distance protective systems of traction power supply systems is made more complicated in this case.

Grounding catenary supports of a group grounding cable is a quite promising means of providing the reliable operation of existing types of distance protective systems, for what the cable with the length no more than 600 m by grounding wires is connected in two places with artificial grounding conductors. The spreading resistance of each grounding conductor does not exceed 15 Ω.

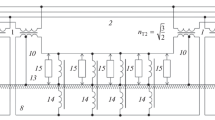
The design diagram to define the complex values of impedances of zones that are protected by distance protective systems in the piece of lines with supports disconnected from the railway track is shown in Fig. 1.

Fig. 1.

(1) Estimated circuit of the traction network at part of a line with catenary supports disconnected from railway track: traction substations A and B, (2) contact network of even and odd railway tracks, (3) switches of section switch box, (4) switches of traction substations, (5) insulators of catenary supports, (6) catenary supports, (7) group grounding cable, (8) spreading resistance of artificial grounding conductor, and (9) railway track; sc1 and sc2 are the locations of short circuits of the contact network to the GGC; Z_ciA and Z_ciB are the complex impedances of external power supply system and traction substations A and B reduced to a voltage of 25 kV [1]; ${{\dot {E}}_{{\text{A}}}}$, ${{\dot {E}}_{{\text{B}}}}$ are the idling voltages on the buses of traction substations A and B in the absence of loads at the zone under consideration and neighboring zones; and ${{\dot {I}}_{{\text{A}}}}$ and ${{\dot {I}}_{{\text{B}}}}$ are the currents in the supply lines of traction substations A and B.

In accordance with the mesh-current method, we have

$${{\dot {I}}_{{\text{A}}}} = \frac{{{{{\dot {U}}}_{{\text{I}}}}{{Z}_{{{\text{t}}{\text{.nII}}}}} - {{U}_{{{\text{II}}}}}{{Z}_{{{\text{III}}}}}}}{{{{Z}_{{{\text{t}}{\text{.n}}}}}{{Z}_{{{\text{t}}{\text{.nII}}}}} - Z_{{{\text{III}}}}^{2}}},\,\,\,{{\dot {I}}_{{\text{B}}}} = \frac{{{{{\dot {U}}}_{{{\text{II}}}}}{{Z}_{{{\text{t}}{\text{.nI}}}}} - {{U}_{{\text{I}}}}{{Z}_{{{\text{III}}}}}}}{{{{Z}_{{{\text{t}}{\text{.nI}}}}}{{Z}_{{{\text{t}}{\text{.nII}}}}} - Z_{{{\text{III}}}}^{2}}},$$

At ${{\dot {U}}_{{\text{I}}}}$ = ${{\dot {E}}_{{\text{A}}}}$ – ${{\dot {I}}_{{{\text{IA}}}}}{{Z}_{{{\text{CA}}}}}$, ${{\dot {U}}_{{{\text{II}}}}}$™ = ${{\dot {E}}_{{\text{B}}}}$ – ${{\dot {I}}_{{{\text{IB}}}}}{{Z}_{{{\text{CB}}}}}$,

$$\begin{gathered} {{Z}_{{{\text{t}}{\text{.nI}}}}} = {{Z}_{{{\text{e}}{\text{.iI}}}}} - \frac{{Z_{{12}}^{2}}}{{{{Z}_{2}}}}{{l}_{1}} + \frac{{{{Z}_{{12}}}({{Z}_{{12}}} - {{Z}_{2}})}}{{{{Z}_{2}}\gamma }}(1 - {{e}^{{ - \gamma {{l}_{1}}}}}) \\ + \,\,\frac{1}{2}{{Z}_{{\text{B}}}} + {{R}_{{\text{B}}}} + {{Z}_{{{\text{e}}{\text{.iIII}}}}}, \\ \end{gathered} $$

$$\begin{gathered} {{Z}_{{{\text{t}}{\text{.nII}}}}} = {{Z}_{{{\text{e}}{\text{.iII}}}}} - \frac{{Z_{{12}}^{2}}}{{{{Z}_{2}}}}{{l}_{2}} + \frac{{{{Z}_{{12}}}({{Z}_{{12}}} - {{Z}_{2}})}}{{{{Z}_{2}}\gamma }}(1 - {{e}^{{ - \gamma {{l}_{2}}}}}) \\ + \,\,\frac{1}{2}{{Z}_{{\text{B}}}} + {{R}_{{\text{B}}}} + {{Z}_{{{\text{e}}{\text{.iIII}}}}}, \\ \end{gathered} $$

$$\begin{gathered} {{Z}_{{{\text{t}}{\text{.nIII}}}}} = \frac{{{{Z}_{{12}}}({{Z}_{{12}}} - {{Z}_{2}})}}{{{{Z}_{2}}\gamma }}(1 - {{e}^{{ - \gamma {{l}_{1}}}}})(1 - {{e}^{{ - \gamma {{l}_{2}}}}}) \\ + \,\,\frac{{{{Z}_{{12}}}}}{{2\gamma }}(1 - {{e}^{{ - \gamma ({{l}_{1}} + {{l}_{2}})}}}) + \frac{1}{2}{{Z}_{{\text{B}}}}{{e}^{{ - \gamma ({{l}_{1}} + {{l}_{2}})}}} + {{R}_{{\text{B}}}} + {{Z}_{{{\text{e}}{\text{.iIII}}}}}. \\ \end{gathered} $$

The equivalent electrical parameters of the contact network, for example, in the node power-supply circuit, are

$${{Z}_{{{\text{e}}{\text{.iI}}}}} = 0.5({{Z}_{1}} + {{Z}_{{\text{a}}}}){{l}_{1}} + {{Z}_{{{\text{t}}{\text{.sA}}}}},$$

$${{Z}_{{{\text{e}}{\text{.iII}}}}} = 0.5({{Z}_{1}} + {{Z}_{{\text{a}}}}){{l}_{2}} + {{Z}_{{{\text{t}}{\text{.sB}}}}},$$

$${{Z}_{{{\text{e}}{\text{.iIII}}}}} = ({{Z}_{1}} + {{Z}_{{\text{a}}}})\frac{{{{l}_{{{\text{t}}{\text{.s}}}}} + {{l}_{1}}}}{{2{{l}_{{{\text{t}}{\text{.s}}}}}}}{{l}_{1}},$$

where Z₁ is the impedance of 1 km of the contact network–ground circuit, Z_a is the mutual inductive reactance of 1 km between the contact network–ground circuit of the first railway track and the contact network–ground circuit of the second railway track, Z₁₂ is the mutual inductive reactance of 1 km between the contact network–ground circuit and the rails–ground circuit, Z₂ is the complex impedance of 1 km of the railway tracks—ground circuit; γ and Z_w are the propagation coefficient and the wave impedance of the railway track, R_g is the spreading resistance of two in-parallel groundings, and l_1,2 is the distance from traction substations A and B to the point of insulation failure.

When currents ${{\dot {I}}_{{\text{A}}}}$ and ${{\dot {I}}_{{\text{B}}}}$ are known, the current distribution in the contact networks of the first and of the second railway tracks is determined, for example, when a node connects a circuit by the formulas (the short circuit is at point K2, Fig. 1)

$$\begin{gathered} {{{\dot {I}}}_{{\text{a}}}} = {{{\dot {I}}}_{{\text{A}}}}\dot {E} - {{{\dot {I}}}_{{\text{B}}}}(0.5 - E), \\ {{{\dot {I}}}_{{\text{b}}}} = {{{\dot {I}}}_{{\text{A}}}}(1 - E) + {{{\dot {I}}}_{{\text{B}}}}(0.5 - E), \\ {{{\dot {I}}}_{{\text{c}}}} = {{{\dot {I}}}_{{\text{A}}}}\dot {E} - {{{\dot {I}}}_{{\text{B}}}}(0.5 + E), \\ {{{\dot {I}}}_{{\text{d}}}} = {{{\dot {I}}}_{{\text{D}}}} = 0.5{{{\dot {I}}}_{{\text{B}}}}, \\ \end{gathered} $$

at Е = 0.5 l₁/l_t.s.,where l_t.s is the distance from traction substation A to the section switch box.

The design formulas for equivalent electrical parameters and when other connecting circuits of contact network are presented in [2].

It was established in [3] that, when voltage supply to the support is disconnected from the railway track, distance protective systems are reliably triggered, sending a signal to disconnect the faulted piece of line.

The data obtained above on the possibility of using the existing distance protective systems at the piece of lines with the supports disconnected from the railway track were confirmed with experiments carried out by the personnel of the Railroad Electrotechnical Laboratory of the North Caucasus Railway. It was noted that the spreading resistance of the support foundation has a nonlinear behavior and when supplying the voltage of 25 kV the spreading resistance of the support foundation decreases on average by 20% as compared with the data obtained by measurements with a high-resistance ohmmeter. This is explained by increasing the designed length of the support foundation due to sparking in the ground.

CALCULATION OF VOLTAGES ON A SUPPORT DISCONNECTED FROM A RAILWAY TRACK UPON INSULATION FAILURE OF A CONTACT NETWORK

Catenary supports need to be disconnected from railway tracks is necessary to carry out, assuming that electrical safety conditions are met when working near the supports, which are largely determined by the possibility of reinforcing a concrete support and the structure of the metal support relative to the remote ground.

The support potential relative to the remote ground in conditions of insulation failure is

$${{\dot {\varphi }}_{{\text{o}}}} = \dot {I}{{R}_{{\sup }}},$$

((1))

where $\dot {I}$ is the complex value of short-circuit current flowing through supports, the spreading resistance of foundation of which is R_sup.

When several supports are connected with a group grounding cable (GGC), which is connected with two artificial grounding conductors, by R_sup should be understood equivalent resistance R_e.i, which is defined by the relation

$$\frac{1}{{{{R}_{{{\text{e}}{\text{.i}}}}}}} = \sum\limits_{i = 1}^n {\frac{1}{{{{R}_{{\sup }}}}} + \frac{1}{{{{R}_{{{\text{g}}1}}}}} + \frac{1}{{{{R}_{{{\text{g}}2}}}}}} ,$$

where n is the number of supports connected with the GGC into one piece of line; there are n ≈ 8–9 supports; and R_g1 and R_g2 are the spreading resistances of artificial grounding conductors, which is 15 Ω.

The computation scheme of spreading resistance of the catenary support foundation is presented in detail in [2].

The results of analytical calculations suggest that it is advisable to connect a support reinforcement to a GGC. This will permit in some cases to do without building artificial grounding conductors that are connected to a GGC.

The voltages on the railway track and the GGC depend on a number of random parameters: the rails-to-earth transition resistance, the spreading resistance of the support foundation, the distance from the traction substation to the short circuit, and the resistance of supply power system [1].

Based on the calculations by formula (1) and their statistical analysis, the characteristics of a log-normal law of voltage distribution at the supports connected with a GGC were determined: the mathematical expectation was m𝓁qU₀, and the standard deviation was σ𝓁qU₀. The characteristics are presented in Table 1.

Table 1.   Voltages on the support when grounding to the railway track is nor used (the numerator corresponds to impedance of the external power supply system Z_S = j3.5 Ω, and the denominator corresponds to impedance of the external power supply system Z_S = j5.0 Ω)

In addition, it was established that the potential relative to ground of the supports connected with the group grounding cable when it grounding in two places to artificial grounding conductors, at insulation failure of the contact network is practically independent of the rails-ground transition resistance and at confidence probability β = 0.95 has confidence interval U₀β = 0.95 = 10.5–18 kV.

PROBABILISTIC AND STATISTICAL ESTIMATION OF ELECTRICAL SAFETY CONDITIONS OF PERSONNEL PLACING NEARBY THE DISCONNECTED FROM RAILWAY TRACK CATENARY SUPPORTS

It was proposed in [2, 4] to determine the conditions of electrical safety to use the mathematical expectation of the number of dangerous situations caused by insulation failure at catenary supports:

$${\text{M}}({\text{P}}) = P1{{N}_{{{\text{n}}{\text{.p}}}}},$$

where P1 is the probability of one person experiencing an electrical shock and N_n.p is the number of people near the catenary supports.

Then, one can write

$$P1 \cdot {\text{s}}{\text{.c}} = {\text{1}} - {\text{(1}} - P{\text{1)}}{{N}_{{{\text{s}}{\text{.c}}}}},$$

where N_s.c is the number of short circuits in the traction network on the piece of line (L_d) for 1 year.

The probability of a person suffering an electric shock (P1 ⋅ s.c) when coming into contact with the support is equal to the product of the probabilities of a number of independent events: appearance of the short circuit mode in the contact network for the time of touching the person to the support; exceeding the voltages generating when short circuit by permissible values (P_u); coincidence of the times of electric current pulse effect and the most vulnerable phase of the cardiac cycle (P_t). Thus, we have [4]

$${\text{M}}({\text{P}}) = \frac{{\eta A{{N}_{{{\text{s}}{\text{.c}}}}}}}{{{{T}_{0}}}}{{P}_{u}}{{P}_{l}},$$

where A is the total time the person is near the catenary support, η is a coefficient taking into account the time during which the person on the ground is in direct contact with the support, and T₀ = 8760 is the number of hours in a year.

The obtained expression makes it possible to take into account the dependence of the probability of a person experiencing an electric shock on the distance from one section of supports connected with the group grounding cable to the short circuit.

The probability of a dangerous situation appearing for a person working near the support when there is a short circuit on the railway track at any point on a 100-km railroad is

$${{P}_{{ur}}} = \frac{1}{{N_{{\text{P}}}^{2}}}\frac{1}{L}\int\limits_0^L {d1} \frac{1}{{{{N}_{{\sup }}}}}\sum\limits_{j = 1}^{{{N}_{{\sup }}}} P \{ {{\bar {U}}_{0}}({{1}_{j}},{{x}_{j}}) > \bar {U}(t)\} ,$$

((2))

at N_st = 100/L, where N_st is the average number of the stages between traction substations; L is the distance between adjacent traction substations, km; and N_sup is the average number of supports on the piece of line with length L.

Let us consider the case of a short circuit arising as a result of insulation failure on a catenary support. As the short circuit can arise with equal probability at any support and the person also can be placed with equal probability at any support, then from the formula of total probability we will obtain:

$$\begin{gathered} {{P}_{{{\text{i}}0}}} = \frac{1}{{N_{{{\text{st}}}}^{2}N_{{\sup }}^{2}}}\sum\limits_{j = 1}^{{{N}_{{j{\text{st}}}}}} {\sum\limits_{j - 1}^{{{N}_{{j{\text{st}}}}}} {[P\{ {{{\bar {U}}}_{0}}({{l}_{i}},{{x}_{j}}) > \bar {U}(t)\} } } \\ + \,\,P\{ {{{\bar {U}}}_{{\sup }}}({{l}_{i}},{{x}_{j}}) > \bar {U}(t)\} \\ + \,\,2P\{ {{{\bar {U}}}_{{{\text{gr}}}}}({{l}_{i}},{{x}_{j}}) > \bar {U}(t)\} ], \\ \end{gathered} $$

where U₀(l_i; x_j), U_sup(l_i; x_j), and U_gr(l_i; x_j) are the voltages that are generated at the support and at the artificial grounding conductor at distance x_j from the traction substation when the short circuit is at distance l_i from the traction substation.

The obtained expression differs from the analogous expression presented in [4] in the amount of the third term in square brackets.

Let us denote as U₀(l; x) the voltage at the supports of a section located at distance X from traction substation, which is generated as a result of a short circuit to the railway track in the point at distance 𝓁 from the substation.

The probability of exceeding the permissible value of actuating voltage is

$$P\{ {{U}_{0}}(l,x) > {{U}_{g}}(t)\} ,$$

where U_g(t) is the permissible voltage at the support depending on the time of activation of protection [2].

Let us determine this probability assuming that U_g(t) is a random variable distributed by log-normal law. It follows from the monotony of the logarithm that

$$P\{ {{U}_{0}}(l,x) > {{U}_{g}}(t)\} = F(\log {{U}_{0}}(l,x)\} .$$

((3))

All short circuits in the catenary can separated by two groups: short circuits of the catenary directly at the supports combined in a line part, and short circuits of a catenary to the railway track outside the part.

Let us denote as P₀ the probability that the short circuit occurred due to insulation failure of the contact network located at the supports combined into sections. The value of P_ins is then found by the formula of total probability [5]:

$${{P}_{{{\text{ins}}}}} = {{P}_{0}}{{P}_{{{\text{ins}}0}}} + (1 + {{P}_{0}}){{P}_{{{\text{i}}{\text{.r}}}}},$$

where P_i0 and P_i.r are the probabilities of a person experiencing an electric shock upon insulation failure on the support of the section and the appearance of a short circuit on the railway track.

We will assume that the locations of the part of the line of supports connected with the GGC and of the short circuit have equal probabilities of being anywhere between the traction substations. Then x and ℓ are independent random variables distributed by a uniform law on the segment [0; L], where L is the distance between traction substations. Therefore, the probability of a person experiencing an electrical shock upon a short circuit at the railway track at any point of the railway track piece of a line with length L_c is

$${{P}_{{{\text{i}}{\text{.r}}}}} = \frac{1}{{{{N}_{{{\text{s}}{\text{.c}}}}}}}\sum\limits_{i = 1}^{{{N}_{{{\text{s}}{\text{.p}}}}}} {\frac{1}{{{{N}_{{{\text{s}}{\text{.p}}}}}}}} \int\limits_0^1 {\frac{{dl}}{L}} P\{ {{U}_{0}}(l,x) > {{U}_{g}}\} ,$$

((4))

where N_s.c = L_c/L is the average number of substation zones on calculated piece of line L_c (for example, when L_c = 100 km, N_i.s = L/Δ is the average number of sections at the piece of line with length L) and Δ is the distance between pieces of line, i.e., the length of one piece of line equal to 600 m.

We will write formula (4) taking into account formula (3) in the form

$${{P}_{{{\text{i}}{\text{.r}}}}} = \frac{\Delta }{{{{L}_{{\text{c}}}}L}}\sum\limits_{i = 1}^{{L \mathord{\left/ {\vphantom {L \Delta }} \right. \kern-0em} \Delta }} {\frac{1}{{{{N}_{{{\text{s}}{\text{.p}}}}}}}\int\limits_0^L {F[\log {{U}_{0}}(l,x)]dl} } .$$

Let us consider the short circuit arising from insulation failure of the contact network directly in the section.

Since the short circuit can arise with the same probability in any section, then, by the formula of total probability, finally the expression for finding the probability of exceeding the permissible values of real voltages will be of the form

$$\begin{gathered} {{P}_{{\text{i}}}} = {{P}_{0}}\frac{{{{\Delta }^{2}}}}{{{{L}_{{\text{c}}}}L}}\sum\limits_{i = 1}^{{{N}_{{{\text{i}}{\text{.s}}}}}} {\sum\limits_{j = 1}^{{{N}_{{{\text{i}}{\text{.s}}}}}} {F[\log {{U}_{0}}({{l}_{i}},{{x}_{j}})]} } \\ + \,\,\frac{{(1 - {{P}_{0}})\Delta }}{{{{L}_{{\text{c}}}}L}}\sum\limits_{i = 1}^{{{N}_{{{\text{i}}{\text{.s}}}}}} {\int\limits_0^L F [\log {{U}_{0}}({{l}_{j}},{{x}_{i}})]dl,} \\ \end{gathered} $$

((5))

where l_i = iΔ; x_j = jΔ are the distances from the ith and jth sections up to the traction substation and U₀(l_i; x_j) is the voltage generated at the jth section upon insulation failure of the contact network of the ith section.

The formulas corresponding to the various grounding methods of catenary supports can be derived from the general expression for probability P_i of the actuating voltages exceeding permissible values.

Let M(P1) and M(P2) be the mathematical expectations of the number of dangerous situations for personnel when using the railway track for grounding supports and using as a grounding conductor only reinforcements of supports connected into sections with a length of 600 m.

Assuming reliable operation of the protective systems of traction systems at parts of lines with catenary supports disconnected from a railway track, we have

$$\begin{gathered} \frac{{{\text{M}}({{{\text{P}}}_{1}})}}{{{\text{M}}({{{\text{P}}}_{2}})}} = \left[ {\frac{{\sum\limits_{i = 1}^{{{N}_{{{\text{i}}{\text{.s}}}}}} {\sum\limits_{j = 1}^{{{N}_{{{\text{i}}{\text{.s}}}}}} {F[\log {{\varphi }_{1}}({{l}_{j}},{{x}_{j}})} ]} }}{{\sum\limits_{i = 1}^{{{N}_{{{\text{i}}{\text{.s}}}}}} {F[\log {{\varphi }_{3}}({{l}_{j}})} }}} \right. \\ + \,\,\left. {\frac{{(1 - {{P}_{0}})\sum\limits_{i = 1}^{{{N}_{{{\text{i}}{\text{.s}}}}}} {\int\limits_0^L F [\log {{\varphi }_{1}}(l,{{x}_{j}})]dl} }}{{{{P}_{0}}\Delta \sum\limits_{i = 1}^{{{N}_{{{\text{i}}{\text{.s}}}}}} {F[\log {{\varphi }_{3}}({{l}_{j}})]} }}} \right]\frac{{{{N}_{{{\text{s}}{\text{.c}}}}}}}{{{{N}_{{{\text{cis}}}}}}}, \\ \end{gathered} $$

where N_con is the number of insulation failures of contact network for a year in the sections of the supports located at the calculated part of the line.

Let us note that permissible voltages U_g(t) are random variables distributed by a logarithmic-normal law.

According to the described methodology, the mathematical expectations of the number of dangerous situations at a part of a line with a length of 100 km when railway track supports are used for grounding M(P1) and with the proposed grounding system of the catenary supports M(P2) were calculated (Table 2).

Table 2.   Estimated values of parameter M(P1)/M(P2)

It follows from Table 2 that the number of dangerous situations when grounding catenary supports are not used does not exceed the analogous values at electrified parts of lines at which a railway track is used to support grounding.

Therefore, when disconnection of emergency state the system of traction electric supply with disconnected from the railway track supports, based on the requirements of electrical safety, is more safety than the system, in which the railway track is used for grounding.

ESTIMATION OF THE LEVELS OF LIGHTNING OVERVOLTAGES IN A CONTACT NETWORK AT PARTS OF A LINE WITH SUPPORTS DISCONNECTED FROM A RAILWAY TRACK

As noted above, not using a railway track as a natural grounder is the most promising way to increase the operating reliability of electrified parts of rail lines.

When lightning current flows from a railway track, an overvoltage arises on low-voltage power lines of signaling, centralization, blocking, and communication devices, which significantly exceeds the permissible values for insulation of electrical installations.

Possible causes of damage to the insulation of a contact network are low reliability of lightning arresters, including surge arresters, as well as specific features of the lightning protection of traction networks, in which the propagation velocities of electromagnetic waves in the contact network and railway track differ significantly.

The circuit of lightning current distribution in the contact network at the piece of lines with supports disconnected from a railway track is shown in Fig. 2.

Fig. 2.

Estimated circuit of distribution of lightning current in the contact network at parts of lines with supports disconnected from railway tracks: (1) contact network, (2) insulator of support, (3) parameters R₀ and L₀ of catenary support, (4) lightning protection device, and (5) grounding conductor of lightning protection device.

Let us approximate the instantaneous value of lightning current flowing in the contact network right at the place of discharge [2]:

$$i = {{I}_{{m1}}}{{e}^{{ - at}}}\sin \omega t.$$

((7))

The parameters in expression (7) were defined in [2].

With a wave approaching a surge wave coming to the catenary support, the voltage at insulation changes by the law

$${{u}_{{\sup }}} = i{{Z}_{{{\text{c}}{\text{.w}}{\text{.i}}}}} = {{I}_{{m1}}}{{Z}_{{{\text{c}}{\text{.w}}{\text{.i}}}}}{{e}^{{ - a\left( {t - \frac{{{{l}_{1}}}}{v}} \right)}}}\sin \left[ {\omega \left( {t - \frac{{{{l}_{1}}}}{v}} \right)} \right],$$

and the voltage at lightning arresters changes by the law

$${{U}_{{{\text{lt}}}}} = {{I}_{{m1}}}{{Z}_{{{\text{c}}{\text{.w}}{\text{.i}}}}}{{e}^{{ - a\left( {t - \frac{{{{l}_{1}}}}{v}} \right)}}}\sin \omega \left( {t - \frac{{{{l}_{1}}}}{v}} \right),$$

where v is the propagation velocity of a electromagnetic wave in the contact network; Z_cw is the wave impedance of the contact network, which can be taken equal to 200 Ω [6]; Z_w is the wave impedance of the lightning current channel, which is equal to 300 Ω [7]; and 𝓁₁ and 𝓁₂ are the distances from the lightning discharge into contact network to the support and lightning protection device.

The presented relations make it possible to calculate the voltage in the contact network until the point of time of insulation breakdown of the catenary support.

When the pulse voltage at the support reaches 50% of the permissible value (U_per), insulation breakdown occurs. The time at which an insulation breakdown occurs is calculated from the relation

$${{U}_{{{\text{per}}}}} = {{I}_{{m1}}}{{Z}_{{{\text{c}}{\text{.w}}{\text{.i}}}}}{{e}^{{ - a\left( {t - \frac{{{{l}_{1}}}}{v}} \right)}}}\sin \omega \left( {{{t}_{{{\text{br}}}}} - \frac{{{{l}_{1}}}}{v}} \right).$$

With an inappreciable error, one can write

$${{t}_{{{\text{br}}}}} = \frac{{{{e}_{1}}}}{v} - \frac{1}{\alpha }1n\frac{{{{U}_{{{\text{per}}}}}}}{{{{I}_{{m1}}}{{Z}_{{{\text{c}}{\text{.w}}{\text{.i}}}}}}}.$$

Upon breakdown of the insulation of the contact network at point of time t = t_br, reflected and refracted waves are generated. To evaluate the operation of the lightning protection apparatus, the refracted waves in the contact network at the parts of a line with supports disconnected from the railway track are important.

We will calculate the refracted waves in the contact network and in the support using the Peterson circuit (Fig. 3).

Fig. 3.

Peterson circuit for calculation of refracted (reflected) waves of voltage and current at the disconnected from railway track supports.

The expression for incident voltage in operator form in accordance with the Peterson circuit (Fig. 3) has the form

$${{U}_{{{\text{inc}}}}}(P) = \frac{{{{I}_{{m1}}}{{Z}_{{{\text{c}}{\text{.w}}{\text{.i}}}}}\omega }}{{{{{(\rho + \alpha )}}^{2}} + {{\omega }^{2}}}}{{e}^{{ - {{t}_{{{\text{inc}}}}}\rho }}}.$$

((8))

The refracted wave of voltage in the contact network is then defined from the relation: at t_br ≤ t,

$$\begin{gathered} {{u}_{{{\text{ref}}}}}(t) = {{I}_{{m1}}}\omega \frac{{{{Z}_{{{\text{c}}{\text{.w}}{\text{.i}}}}}{{R}_{0}}}}{{{{Z}_{{{\text{c}}{\text{.w}}{\text{.i}}}}} + {{R}_{0}}}}x\left\{ {\frac{{ - \beta }}{{{{{(\alpha - \beta )}}^{2}} + {{\omega }^{2}}}}{{e}^{{ - \beta (t - {{t}_{{{\text{br}}}}})}}}} \right. \\ + \,\left. {\,\frac{1}{\omega }\sqrt {\frac{{{{\alpha }^{2}} + {{\beta }^{2}}}}{{{{{(\alpha - \beta )}}^{2}} + {{\omega }^{2}}}}} {{e}^{{ - \alpha (t - {{t}_{{{\text{br}}}}})}}}\sin [\omega (t - {{t}_{{{\text{br}}}}} - \lambda )]} \right\}, \\ \end{gathered} $$

where

$$\beta = \frac{{2{{R}_{0}} + {{Z}_{{{\text{c}}{\text{.w}}{\text{.i}}}}}}}{{2{{Z}_{{\text{c}}}}}},\,\,\,\lambda = \arctan \left( { - \frac{\omega }{\alpha }} \right) - \arctan \frac{\omega }{{\beta - \alpha }}.$$

The obtained expression makes it possible to determine the voltage propagating along the contact network from the point of time immediately after breakdown of the support insulation until the point of time at which the lightning protection device is activated.

Consequently, the voltage at the lightning protection device changes according to the expressions

$$\frac{{{{l}_{2}}}}{v} \leqslant t \leqslant \frac{{{{l}_{2}}}}{v} + {{t}_{{{\text{br}}}}}$$

at

$${{U}_{\Gamma }} = {{I}_{{m1}}}{{Z}_{{{\text{c}}{\text{.w}}{\text{.i}}}}}{{e}^{{ - a\left( {t - \frac{{{{l}_{2}}}}{v}} \right)}}}\sin \omega \left( {t - \frac{{{{l}_{2}}}}{v}} \right),$$

but, when $\frac{{{{l}_{2}}}}{v} + {{t}_{{{\text{br}}}}} < t$, the sum of $\frac{{{{l}_{2}}}}{v} + {{t}_{{{\text{br}}}}}$ is substituted for t_br.

The duration of this voltage is determined by the time the possible response of the lightning arrester. It is determined by approximate methods assuming that the instantaneous voltage at the arrester/overvoltage limiter taking into account its volt–second characteristic is known.

To simplify the calculations, we will assume that support inductance L_sup = 0. The voltage of the refracted wave is then

$${{U}_{{{\text{ref}}}}} = {{I}_{{m1}}}{{Z}_{{{\text{c}}{\text{.w}}{\text{.i}}}}}{{e}^{{ - a\left( {t - \frac{{{{l}_{2}}}}{v}} \right)}}}\sin \omega \left( {{{t}_{{{\text{br}}}}} - \frac{{{{l}_{1}}}}{v}} \right)\frac{{2{{R}_{0}}}}{{2{{R}_{0}} + {{Z}_{{{\text{c}}{\text{.w}}{\text{.i}}}}}}}.$$

When insulation breakdown occurs, reflected and refracted waves are generated at the catenary support. The input impedance of the support foundation is significantly less than the wave impedance of the contact network. The maximum voltage value of the refracted wave is

$${{U}_{{\max {\text{ref}}}}} = {{I}_{{m1}}}{{Z}_{{{\text{c}}{\text{.w}}{\text{.i}}}}}\frac{{2{{R}_{{\text{e}}}}}}{{{{R}_{{\text{e}}}} + {{Z}_{{{\text{c}}{\text{.w}}{\text{.i}}}}}}},$$

or the expression will take the approximate form

$${{U}_{{\max {\text{ref}}}}} = 2{{I}_{{m1}}}{{R}_{{\text{e}}}}.$$

Thus, at I_m = 10 kA, the resistance of the foundation part of supports is R_sup = 10 Ω and Z_ref.w = 200 Ω. The maximum value of the voltage of the refractive wave in the contact network is U_max.ref = 0.25 × 10 × 2 × 10 = 50 kV.

Diagrams of the probability of the amplitudes of lightning currents according to the data of different authors are presented in [7]. In particular instances, the maximum value of lightning currents reaches about 100 kA. In this case, the maximum value of the voltage of a refracted wave will significantly exceed the permissible voltage of the insulators of the contact network [6]. To keep them from breaking down, it is needed to mount the overvoltage limiter on the support; however, it is economically unfeasible to do this on all supports. Using a lightning protection conductor to avoid lightning current coming into the contact network is not possible for both technical and economic considerations.