INTRODUCTION

The friction surfaces of the working elements of the disc brake are not perfectly smooth. Due to waviness and roughness, their contact interaction is discrete and occurs in three areas: nominal, due to the size of the rubbing surface of the lining; contour, formed at the points of contact of waves and macrodeviations; actual, consisting of a set of contacts of microroughnesses within the contour area of contact [1]. According to the hypothesis of summation of temperatures of A.V. Chichinadze, the maximum temperature of the friction surface is equal to the sum of the average temperature of the nominal contact area and the temperature of the actual contact area (temperature flash) [2]. The calculation of the average temperature of the friction surface is usually performed with a constant value of the area of the nominal contact area [3–6]. When a temperature flash is found, the areas of the contour and actual contact areas changing during deceleration are used [7, 8].

Objective—development of an analytical model for calculating the average temperature of the friction surface of a disc brake, taking into account the relationship between the contour and nominal areas. Study on this basis of the evolution of speed, specific friction power, and temperature of a multi-disc brake with rubbing elements made of a carbon friction composite material (CFCM).

CALCULATION MODEL

For a given initial value of kinetic energy \({{W}_{0}}\), a decrease in velocity \(V\) with time \(t\) from initial value \({{V}_{0}}\) at \(t = 0\) to zero at the moment of stop \(t = {{t}_{s}}\) describes the relationship [3]:

$$V(t) = {{V}_{0}}\left[ {1 - \frac{{{{V}_{0}}}}{{{{W}_{0}}}}\int\limits_0^t {F(s)ds} } \right],\,\,\,\,0 \leqslant t \leqslant {{t}_{s}},$$
(1)

where friction force \(F\) acting in the contour area with area \({{A}_{c}}\) has form

$$F(t) = fp(t){{A}_{c}}(t),\,\,\,\,0 \leqslant t \leqslant {{t}_{s}}.$$
(2)

Taking into account the monotonic increase in pressure \(p\) from zero to nominal value \({{p}_{0}}\):

$$p(t) = {{p}_{0}}p{\kern 1pt}^{*}{\kern 1pt} (t),\,\,\,\,p{\kern 1pt}^{*}{\kern 1pt} (t) = 1 - {{e}^{{{t \mathord{\left/ {\vphantom {t {{{t}_{i}}}}} \right. \kern-0em} {{{t}_{i}}}}}}},\,\,\,\,0 \leqslant t \leqslant {{t}_{s}},$$
(3)

and relations [9, 10]:

$${{A}_{c}}(t) = {{A}_{a}}A{\kern 1pt}^{*}{\kern 1pt} (t),\,\,\,\,A{\kern 1pt}^{*}{\kern 1pt} (t) = 0.4 + \frac{{0.5t}}{{{{t}_{s}}}},\,\,\,\,0 \leqslant t \leqslant {{t}_{s}},$$
(4)

after integration from formulas (1), (2) we obtain:

$$\begin{gathered} V(t) = {{V}_{0}}V{\kern 1pt}^{*}{\kern 1pt} (t), \\ V{\kern 1pt}^{*}{\kern 1pt} (t) = 1 - \frac{{tA{\kern 1pt}^{*}{\kern 1pt} (t) - {{t}_{i}}p{\kern 1pt}^{*}{\kern 1pt} (t)A{\kern 1pt}^{*}{\kern 1pt} (t) - \frac{{0.25t}}{{{{t}_{s}}}}(t - 2{{t}_{i}}{{e}^{{{{ - t} \mathord{\left/ {\vphantom {{ - t} {{{t}_{i}}}}} \right. \kern-0em} {{{t}_{i}}}}}}})}}{{t_{s}^{0}}}, \\ 0 \leqslant t \leqslant {{t}_{s}}, \\ \end{gathered} $$
(5)
$$t_{s}^{0} = \frac{{{{W}_{0}}}}{{{{q}_{0}}{{A}_{a}}}},\,\,\,\,{{q}_{0}} = f{{p}_{0}}{{V}_{0}}.$$
(6)

The duration of braking was determined numerically from condition of stop \(V{\kern 1pt}^{*}{\kern 1pt} ({{t}_{s}}) = 0\).

We present the change in the specific power of friction in form:

$$q(t) = {{q}_{0}}q{\kern 1pt}^{*}{\kern 1pt} (t),\,\,\,\,q{\kern 1pt}^{*}{\kern 1pt} (t) = p{\kern 1pt}^{*}{\kern 1pt} (t)V{\kern 1pt}^{*}{\kern 1pt} (t),\,\,\,\,0 \leqslant t \leqslant {{t}_{s}},$$
(7)

where the time profiles of pressure \(p{\kern 1pt}^{*}{\kern 1pt} (t)\) and velocity \(V{\kern 1pt}^{*}{\kern 1pt} (t)\) were determined by formulas (3)–(6), respectively. We look for the specific friction work in form:

$$\begin{gathered} w(t) = {{w}_{0}}w{\kern 1pt}^{*}{\kern 1pt} (t),\,\,\,\,{{w}_{0}} = {{q}_{0}}{{t}_{s}},\,\,\,\,w{\kern 1pt}^{*}{\kern 1pt} (t) = t_{s}^{{ - 1}}\int\limits_0^t {q{\kern 1pt}^{*}{\kern 1pt} (t)dt} , \\ 0 \leqslant t \leqslant {{t}_{s}}. \\ \end{gathered} $$
(8)

Substituting function \(q{\kern 1pt}^{*}{\kern 1pt} (t)\) (7) under the integral sign in formula (8), we find

$$\begin{gathered} w{\kern 1pt} ^{*}{\kern 1pt} (t) = \frac{1}{{t_{s}^{0}{{t}_{s}}}} \\ \times \,\,\left\{ \begin{gathered} t_{s}^{0}t - \frac{1}{5}{{t}^{2}} + \frac{1}{4}\left( {t_{i}^{2} - {{t}_{i}}t - \frac{1}{3}{{t}^{2}}} \right)\frac{t}{{{{t}_{s}}}} \\ + \,\,\left[ \begin{gathered} \frac{1}{4}{{t}^{2}} - {{t}_{i}}^{2} - t_{s}^{0}{{t}_{s}} \\ + \,\,\frac{2}{5}{{t}_{s}}(t - {{t}_{i}}) \\ \end{gathered} \right]\frac{{{{t}_{i}}}}{{{{t}_{s}}}}p{\kern 1pt} ^{*}{\kern 1pt} (t) \\ + \,\,\frac{1}{4}\left( {\frac{4}{5}{{t}_{s}} + \frac{3}{2}{{t}_{i}} + t} \right)\frac{{t_{i}^{2}}}{{{{t}_{s}}}}p{\kern 1pt}^{*}{\kern 1pt} (2t) \\ \end{gathered} \right\},\,\,\,\,0 \leqslant t \leqslant {{t}_{s}}. \\ \end{gathered} $$
(9)

To determine the temperature of the contour region, we will use the design scheme of the thermal contact of two semi-bounded bodies, taking into account frictional heat generation. The evolution of the average temperature of the contact surface of such a tribosystem is determined by formulas [11, 12]:

$$T(t) = {{T}_{a}} + \gamma {{T}_{0}}T{\kern 1pt}^{*}{\kern 1pt} (\tau ),\,\,\,\,0 \leqslant t \leqslant {{t}_{s}},$$
(10)
$$\begin{gathered} T{\kern 1pt}^{*}{\kern 1pt} (\tau ) = \frac{{\text{1}}}{{\sqrt \pi }}\int\limits_0^\tau {\frac{{q{\kern 1pt}^{*}{\kern 1pt} (s)}}{{\sqrt {\tau - s} }}} {\kern 1pt} ds,\,\,\,\,0 \leqslant \tau \leqslant {{\tau }_{s}}, \\ \gamma = \frac{{\sqrt {k{\kern 1pt}^{*}} }}{{\sqrt {k{\kern 1pt}^{*}} + \sqrt {K{\kern 1pt}^{*}} }},\,\,\,\,{{T}_{0}} = \frac{{{{q}_{0}}a}}{{{{K}_{1}}}},\,\,\,\,\tau = \frac{{{{k}_{1}}t}}{{{{a}^{2}}}},\,\,\,\,{{\tau }_{s}} = \frac{{{{k}_{1}}{{t}_{s}}}}{{{{a}^{2}}}}, \\ \end{gathered} $$
(11)
$$\tau _{s}^{0} = \frac{{{{k}_{1}}{{t}_{s}}}}{{{{a}^{2}}}},\,\,\,\,{{\tau }_{i}} = \frac{{{{k}_{1}}{{t}_{i}}}}{{{{a}^{2}}}},\,\,\,\,K{\kern 1pt}^{*} = \frac{{{{K}_{2}}}}{{{{K}_{1}}}},\,\,\,\,k{\kern 1pt}^{*} = \frac{{{{k}_{2}}}}{{{{k}_{1}}}},$$
(12)

\(a = \max ({{a}_{l}})\), \({{a}_{l}} = \sqrt {3{{k}_{l}}t_{s}^{0}} \) are the effective depths of heat penetration. Hereinafter, all values related to the disc and the pad are provided with subscripts \(l = 1\) and \(l = 2\), respectively.

Substituting under the integral sign in formula (11) function \(q{\kern 1pt}^{*}{\kern 1pt} (\tau )\) (7), taking into account relations (3) and (5), we obtain:

$$\begin{gathered} T{\kern 1pt}^{*}{\kern 1pt} (\tau ) = \frac{{\text{1}}}{{\sqrt \pi }}\int\limits_0^\tau {\left\{ {1 - \frac{1}{{\tau _{s}^{0}}}\left[ \begin{gathered} \frac{2}{5}s + \frac{{{{s}^{2}}}}{{4{{\tau }_{s}}}} - (1 - {{e}^{{{{ - s} \mathord{\left/ {\vphantom {{ - s} {{{\tau }_{i}}}}} \right. \kern-0em} {{{\tau }_{i}}}}}}}) \\ \times \,\,\left( {\frac{2}{5} + \frac{{{{\tau }_{i}}}}{{2{{\tau }_{s}}}}} \right){{\tau }_{i}} + \frac{{{{\tau }_{i}}s}}{{2{{\tau }_{s}}}}{{e}^{{{{ - s} \mathord{\left/ {\vphantom {{ - s} {{{\tau }_{i}}}}} \right. \kern-0em} {{{\tau }_{i}}}}}}} \\ \end{gathered} \right]} \right\}} \\ \times \,\,\frac{{(1 - {{e}^{{{{ - s} \mathord{\left/ {\vphantom {{ - s} {{{\tau }_{i}}}}} \right. \kern-0em} {{{\tau }_{i}}}}}}})}}{{\sqrt {\tau - s} }}ds,\,\,\,\,0 \leqslant \tau \leqslant {{\tau }_{s}}. \\ \end{gathered} $$
(13)

Designating:

$${{I}_{{m,n}}}(\tau ) = \frac{1}{{\sqrt \pi }}\int\limits_0^\tau {\frac{{{{s}^{m}}{{e}^{{{{ - ns} \mathord{\left/ {\vphantom {{ - ns} {{{\tau }_{i}}}}} \right. \kern-0em} {{{\tau }_{i}}}}}}}}}{{\sqrt {\tau - s} }}} {\kern 1pt} ds,\,\,\,\,m,n = 0,1,2.$$
(14)

integral (13) can be written in form

$$\begin{gathered} T{\kern 1pt}^{*}{\kern 1pt} (\tau ) = \left( {1 + \frac{{2{{\tau }_{i}}}}{{5\tau _{s}^{0}}} + \frac{{\tau _{i}^{2}}}{{2\tau _{s}^{0}{{\tau }_{s}}}}} \right){{I}_{{0,0}}}(\tau ) \\ - \,\,\left( {1 + \frac{{4{{\tau }_{i}}}}{{5\tau _{s}^{0}}} + \frac{{\tau _{i}^{2}}}{{\tau _{s}^{0}{{\tau }_{s}}}}} \right){{I}_{{0,1}}}(\tau ) + \frac{{{{\tau }_{i}}}}{{\tau _{s}^{0}}}\left( {\frac{2}{5} + \frac{{{{\tau }_{i}}}}{{2{{\tau }_{s}}}}} \right){{I}_{{0,2}}}(\tau ) \\ - \,\,\frac{2}{{5\tau _{s}^{0}}}{{I}_{{1,0}}}(\tau ) - \frac{1}{{\tau _{s}^{0}}}\left( {\frac{2}{5} + \frac{{{{\tau }_{i}}}}{{2{{\tau }_{s}}}}} \right){{I}_{{1,1}}}(\tau ) \\ + \,\,\frac{{{{\tau }_{i}}}}{{2\tau _{s}^{0}{{\tau }_{s}}}}{{I}_{{1,2}}}(\tau ) - \frac{1}{{4\tau _{s}^{0}{{\tau }_{s}}}}[{{I}_{{2,0}}}(\tau ) - {{I}_{{2,1}}}(\tau )]. \\ \end{gathered} $$
(15)

Using substitution \(x = \sqrt {\tau - s} \), integrals (14) are presented as follows:

$${{I}_{{m,n}}}(\tau ) = \frac{1}{{\sqrt \pi }}\int\limits_0^{\sqrt \tau } {(\tau - {{x}^{2}}} {{)}^{m}}{{e}^{{{{ - n(\tau {\kern 1pt} - {\kern 1pt} {{x}^{2}})} \mathord{\left/ {\vphantom {{ - n(\tau {\kern 1pt} - {\kern 1pt} {{x}^{2}})} {{{\tau }_{i}}}}} \right. \kern-0em} {{{\tau }_{i}}}}}}}dx,\,\,\,m,n = 0,1,2.$$
(16)

First, let us consider the particular case when \(n = 0\). Using result [13]

$$\int\limits_0^{\sqrt \tau } {{{{(\tau - {{x}^{2}})}}^{m}}} dx = {{\tau }^{m}}\sqrt \tau B(m + 1;0.5),\,\,\,\,m = 0,1,2,$$

taking into account the values of beta function \(B(1;\,\,0.5) = 2\), \(B(2;\,\,0.5) = {4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}\), and \(B(3;\,\,0.5) = {{16} \mathord{\left/ {\vphantom {{16} {15}}} \right. \kern-0em} {15}}\) [14], from formula (16) we obtain

$$\begin{gathered} {{I}_{{0,0}}}(\tau ) = 2\sqrt {\frac{\tau }{\pi }} ,\,\,\,\,{{I}_{{1,0}}}(\tau ) = \frac{4}{3}\tau \sqrt {\frac{\tau }{\pi }} , \\ {{I}_{{2,0}}}(\tau ) = \frac{{16}}{{15}}{{\tau }^{2}}\sqrt {\frac{\tau }{\pi }} {\kern 1pt} . \\ \end{gathered} $$
(17)

For \(n = 1,\,2\) the integrals in formula (16) can be represented in form:

$$\begin{gathered} I_{{0,n}}^{{}}(\tau ) = {{J}_{{0,n}}}(\tau ),\,\,\,\,I_{{1,n}}^{{}}(\tau ) = \tau {{J}_{{0,n}}}(\tau ) - {{J}_{{2,n}}}(\tau ), \\ I_{{2,n}}^{{}}(\tau ) = {{\tau }^{2}}{{J}_{{0,n}}}(\tau ) - 2\tau {{J}_{{2,n}}}(\tau ) + {{J}_{{4,n}}}(\tau ), \\ \end{gathered} $$
(18)
$${{J}_{{l,n}}}(\tau ) = \frac{2}{{\sqrt \pi }}{{e}^{{{{ - n\tau } \mathord{\left/ {\vphantom {{ - n\tau } {{{\tau }_{i}}}}} \right. \kern-0em} {{{\tau }_{i}}}}}}}\int\limits_0^{\sqrt \tau } {{{x}^{l}}{{e}^{{{{n{{x}^{2}}} \mathord{\left/ {\vphantom {{n{{x}^{2}}} {{{\tau }_{i}}}}} \right. \kern-0em} {{{\tau }_{i}}}}}}}} dx,\,\,\,\,l = 0,2,4.$$
(19)

After substitution \(y = {{n{{x}^{2}}} \mathord{\left/ {\vphantom {{n{{x}^{2}}} {{{\tau }_{i}}}}} \right. \kern-0em} {{{\tau }_{i}}}}\), integrals (19) can be written as follows:

$$\begin{gathered} {{J}_{{l,n}}}(\tau ) = \frac{1}{{\sqrt \pi }}{{\left( {\frac{{{{\tau }_{i}}}}{n}} \right)}^{{{{(l{\kern 1pt} + {\kern 1pt} 1)} \mathord{\left/ {\vphantom {{(l{\kern 1pt} + {\kern 1pt} 1)} 2}} \right. \kern-0em} 2}}}}{{e}^{{{{ - n\tau } \mathord{\left/ {\vphantom {{ - n\tau } {{{\tau }_{i}}}}} \right. \kern-0em} {{{\tau }_{i}}}}}}}\int\limits_0^{{{n\tau } \mathord{\left/ {\vphantom {{n\tau } {{{\tau }_{i}}}}} \right. \kern-0em} {{{\tau }_{i}}}}} {{{y}^{{{{(l{\kern 1pt} - {\kern 1pt} 1)} \mathord{\left/ {\vphantom {{(l{\kern 1pt} - {\kern 1pt} 1)} 2}} \right. \kern-0em} 2}}}}{{e}^{y}}} dy, \\ l = 0,2,4,\,\,\,\,n = 1,2. \\ \end{gathered} $$
(20)

By integrating by parts, taking into account substitution \(s = \sqrt y \), from formulas (20) we obtain:

$$\begin{gathered} {{J}_{{0,n}}}(\tau ) = \sqrt \tau D\left( {\sqrt {n\frac{\tau }{{{{\tau }_{i}}}}} } \right), \\ {{J}_{{2,n}}}(\tau ) = \frac{{{{\tau }_{i}}}}{n}\left[ {\sqrt {\frac{\tau }{\pi }} - \frac{1}{2}{{J}_{{0,n}}}(\tau )} \right], \\ {{J}_{{4,n}}}(\tau ) = \frac{{{{\tau }_{i}}}}{n}\left[ {\tau \sqrt {\frac{\tau }{\pi }} - \frac{3}{2}{{J}_{{2,n}}}(\tau )} \right], \\ \end{gathered} $$
(21)
$$D(x) = \frac{2}{{\sqrt \pi }}\frac{{{{e}^{{ - {{x}^{2}}}}}}}{x}\int\limits_0^x {{{e}^{{{{s}^{2}}}}}} ds.$$
(22)

Taking into account relations (21), (22), it follows from formulas (18):

$$\begin{gathered} {{I}_{{0,n}}}(\tau ) = \sqrt \tau D\left( {\sqrt {\frac{{n\tau }}{{{{\tau }_{i}}}}} } \right), \\ {{I}_{{1,n}}}(\tau ) = \left( {\frac{{{{\tau }_{i}}}}{{2n}} + \tau } \right){{I}_{{0,n}}}(\tau ) - \frac{{{{\tau }_{i}}}}{n}\sqrt {\frac{\tau }{\pi }} , \\ \end{gathered} $$
(23)
$$\begin{gathered} {{I}_{{2,n}}}(\tau ) = \left[ {\frac{{{{\tau }_{i}}}}{n}\left( {\frac{{3{{\tau }_{i}}}}{{4n}} + \tau } \right) + {{\tau }^{2}}} \right]{{I}_{{0,n}}}(\tau ) \\ - \,\,\frac{{{{\tau }_{i}}}}{n}\left( {\frac{{3{{\tau }_{i}}}}{{2n}} + \tau } \right)\sqrt {\frac{\tau }{\pi }} ,\,\,\,\,n = 1,2. \\ \end{gathered} $$
(24)

Substituting functions Im,n(τ) (17), (23), (24) to the right side of solution (15), we get:

$$\begin{gathered} T{\kern 1pt}^{*}{\kern 1pt} (\tau ) = \left[ \begin{gathered} 2 + \frac{1}{{5\tau _{s}^{0}}}\left( {2{{\tau }_{i}} - \frac{8}{3}\tau } \right) + \frac{1}{{\tau _{s}^{0}{{\tau }_{s}}}} \\ \times \,\,\left( {\frac{7}{8}\tau _{i}^{2} - \frac{1}{4}\tau {{\tau }_{i}} - \frac{4}{{15}}{{\tau }^{2}}} \right) \\ \end{gathered} \right]\sqrt {\frac{\tau }{\pi }} \\ + \,\,\frac{{{{\tau }_{i}}}}{{\tau _{s}^{0}}}\left[ {\frac{2}{5} - \frac{1}{{2{{\tau }_{s}}}}\left( {\frac{3}{4}{{\tau }_{i}} - \tau } \right)} \right]\sqrt \tau D\left( {\sqrt {2\frac{\tau }{{{{\tau }_{i}}}}} } \right) \\ - \,\,\frac{1}{{\tau _{s}^{0}}}\left[ \begin{gathered} \frac{1}{5}(3{{\tau }_{i}} - 2{{\tau }_{i}}) + \frac{1}{{4{{\tau }_{s}}}} \\ \times \,\,\left( {\frac{1}{4}\tau _{i}^{2} + {{\tau }_{i}}\tau - {{\tau }^{2}}} \right) + \tau _{s}^{0} \\ \end{gathered} \right]\sqrt \tau D\left( {\sqrt {\frac{\tau }{{{{\tau }_{i}}}}} } \right), \\ 0 \leqslant \tau \leqslant {{\tau }_{s}}. \\ \end{gathered} $$
(25)

When calculating function \(D(x)\) (22) in solution (25) we used expansions [15]:

$$\begin{gathered} D(x) = \frac{2}{{\sqrt \pi }}\sum\limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty {{{{( - 1)}}^{n}}\frac{{{{{(2{{x}^{2}})}}^{n}}}}{{(2n + 1){\kern 1pt} !!}}} ,\,\,\,\,0 \leqslant x \leqslant 3, \\ D(x) = \frac{2}{{\sqrt \pi }}\sum\limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty {\frac{{(2n - 1){\kern 1pt} !!}}{{{{{(2{{x}^{2}})}}^{{n + 1}}}}}} ,\,\,\,\,x > 3. \\ \end{gathered} $$

Knowing the time profile of dimensionless temperature (25), using formulas (10), (12), we find the temperature change during deceleration.

The volumetric temperature, averaged over the braking time, of the brake elements is determined by formulas [3]:

$$\begin{gathered} {{\theta }_{l}} = {{T}_{a}} + {{\gamma }_{l}}\,{{\theta }_{{l,0\,}}}\theta {\kern 1pt}^{*},\,\,\,\,{{\theta }_{{l,0}}} = \frac{{{{\psi }_{l}}{{W}_{0}}}}{{{{c}_{l}}{{G}_{l}}}}, \\ {{G}_{l}} = {{A}_{a}}{{a}_{l}}{{\rho }_{l}},\,\,\,\,l = 1,2, \\ \end{gathered} $$
(26)
$$\theta {\kern 1pt}^{*} = \frac{2}{{{{t}_{s}}}}\int\limits_0^{{{t}_{s}}} {w{\kern 1pt}^{*}{\kern 1pt} (t)dt} ,$$
(27)

where \({{\gamma }_{1}} = 1 - \gamma \), \({{\gamma }_{2}} = \gamma \) are coefficients of distribution of heat flows, \({{\psi }_{l}}\) are correction factors taking into account the temperature decrease due to heat propagation to the sides of the friction track. Taking into account relation (9) from formula (27) we obtain:

$$\begin{gathered} \theta {\kern 1pt}^{*} = 1 + \frac{{{{t}_{i}}}}{{{{t}_{s}}t_{s}^{0}}} \\ \times \,\,\left\{ \begin{gathered} \left[ {\frac{2}{5}({{t}_{s}} + {{t}_{i}} - 5t_{s}^{0}) - \frac{{t_{i}^{2}}}{{{{t}_{s}}}}\left( {2\frac{{{{t}_{i}}}}{{{{t}_{s}}}} + \frac{{31}}{{20}}} \right) - \frac{7}{{40}}\frac{{t_{s}^{2}}}{{{{t}_{i}}}}} \right] \\ + \,\,\frac{{t_{i}^{2}}}{{{{t}_{s}}}}\left[ \begin{gathered} \left( {\frac{{11}}{{20}} - \frac{3}{{10}}\frac{{{{t}_{s}}}}{{{{t}_{i}}}} + 2\frac{{t_{s}^{0}}}{{{{t}_{i}}}} + 3\frac{{{{t}_{i}}}}{{{{t}_{s}}}}} \right)p{\kern 1pt}^{*}{\kern 1pt} ({{t}_{s}}) \\ - \,\,\frac{1}{2}\left( {\frac{9}{{10}} + \frac{{{{t}_{i}}}}{{{{t}_{s}}}}} \right)p{\kern 1pt}^{*}{\kern 1pt} (2{{t}_{s}}) \\ \end{gathered} \right] \\ \end{gathered} \right\}. \\ \end{gathered} $$
(28)

Let us consider two particular cases of the model under consideration that are frequently encountered in applications. The first of these is constant contact pressure at the contour site. Passing in formulas (3), (5), (7), (9), (25), and (28) to limit \({{t}_{i}} \to 0\), we obtain

$$\begin{gathered} p{\kern 1pt}^{*}{\kern 1pt} (t) = 1,\,\,\,\,V{\kern 1pt}^{*}{\kern 1pt} (t) = 1 - \left( {0.4 + \frac{{0.25t}}{{{{t}_{s}}}}} \right)\frac{t}{{t_{s}^{0}}}, \\ q{\kern 1pt}^{*}{\kern 1pt} (t) = 1 - \frac{{0.4t + \frac{{0.25{{t}^{2}}}}{{{{t}_{s}}}}}}{{t_{s}^{0}}}, \\ w{\kern 1pt}^{*}{\kern 1pt} (t) = \left[ {1 - \left( {0.2 + \frac{t}{{12{{t}_{s}}}}} \right)\frac{t}{{t_{s}^{0}}}} \right]\frac{t}{{{{t}_{s}}}},\,\,\,\,0 \leqslant t \leqslant {{t}_{s}}, \\ T{\kern 1pt}^{*}{\kern 1pt} (\tau ) = 2\sqrt {\frac{\tau }{\pi }} \left[ {1 - \left( {1 - \frac{{2\tau }}{{{{\tau }_{s}}}}} \right)\frac{{4\tau }}{{15\tau _{s}^{0}}}} \right],\,\,\,\,0 \leqslant \tau \leqslant {{\tau }_{s}}, \\ \theta {\kern 1pt}^{*} = 1 - \frac{{7{{t}_{s}}}}{{40t_{s}^{0}}}, \\ \end{gathered} $$

and from the stop condition we find braking time \({{t}_{s}} = {{20} \mathord{\left/ {\vphantom {{20} {(13t_{s}^{0})}}} \right. \kern-0em} {(13t_{s}^{0})}} \cong 1.54t_{s}^{0}\).

The second case concerns the determination of the characteristics of the braking process at a constant value of contour area (\(A{\kern 1pt}^{*}{\kern 1pt} (t) = 1\)). With monotonically increasing pressure \(p{\kern 1pt}^{*}{\kern 1pt} (t)\) (3) time profiles of speed, specific power and work of friction, as well as temperature and volumetric temperature have form [16]:

$$\begin{gathered} V{\kern 1pt}^{*}{\kern 1pt} (t) = 1 - \frac{{t - {{t}_{i}}p{\kern 1pt}^{*}{\kern 1pt} (t)}}{{t_{s}^{0}}}, \\ q{\kern 1pt} ^{*}{\kern 1pt} (t) = \left( {1 - \frac{{t - {{t}_{i}}p{\kern 1pt}^{*}{\kern 1pt} (t)}}{{t_{s}^{0}}}} \right)p{\kern 1pt}^{*}{\kern 1pt} (t), \\ \end{gathered} $$
(29)
$$\begin{gathered} w{\kern 1pt}^{*}{\kern 1pt} (t) = \left( {1 - \frac{{0.5t}}{{t_{s}^{0}}}} \right)\frac{t}{{t_{s}^{0}}} \\ - \,\,p{\kern 1pt}^{*}{\kern 1pt} (t)\left( {1 - \frac{t}{{t_{s}^{0}}}} \right)\frac{{{{t}_{i}}}}{{t_{s}^{0}}} - 0.5{{\left( {\frac{{p{\kern 1pt}^{*}{\kern 1pt} (t){{t}_{i}}}}{{t_{s}^{0}}}} \right)}^{2}},\,\,\,\,0 \leqslant t \leqslant {{t}_{s}}, \\ \end{gathered} $$
(30)
$$\begin{gathered} T{\kern 1pt}^{*}{\kern 1pt} (\tau ) = \sqrt \tau \left[ \begin{gathered} 2\frac{{1 + \frac{{0.5{{\tau }_{i}}}}{{\tau _{s}^{0}}}}}{{\sqrt \pi }} - \left( {1 - \frac{\tau }{{\tau _{s}^{0}}} + \frac{{1.5{{\tau }_{i}}}}{{\tau _{s}^{0}}}} \right) \\ \times \,\,D\sqrt {\frac{\tau }{{{{\tau }_{i}}}}} + \frac{{{{\tau }_{i}}}}{{\tau _{s}^{0}}}D\sqrt {\frac{{2\tau }}{{{{\tau }_{i}}}}} \\ \end{gathered} \right], \\ 0 \leqslant \tau \leqslant {{\tau }_{s}}, \\ \end{gathered} $$
(31)
$$\theta {\kern 1pt}^{*} = \frac{{\left\{ \begin{gathered} {{t}_{s}} - 2{{t}_{i}} + \frac{{t_{i}^{2} + {{t}_{i}}{{t}_{s}} - \frac{{t_{s}^{2}}}{3}}}{{t_{s}^{0}}} \\ + \,\,2\left( {\frac{1}{{{{t}_{s}}}} - \frac{1}{{t_{s}^{0}}}} \right)t_{i}^{2}p{\kern 1pt}^{*}{\kern 1pt} ({{t}_{s}}) - [0.5 + p{\kern 1pt}^{*}{\kern 1pt} (2{{t}_{s}})]\frac{{t_{i}^{3}}}{{3{{t}_{s}}t_{s}^{0}}} \\ \end{gathered} \right\}}}{{t_{s}^{0}}},$$
(32)

for \({{t}_{s}} \cong t_{s}^{0} + 0.99{{t}_{i}}\).

NUMERICAL ANALYSIS

Investigated the characteristics of the braking system, consisting of three identical discs made of CFCM Termar-ADF. Due to the geometric and force symmetry, the temperature regime of such a system can be determined using the analytical two-element model proposed above. The values of the input parameters are as follows [16]: \({{p}_{0}} = 0.602\) MPa, \({{V}_{0}} = 23.8\) m/s, \({{W}_{0}} = 103.54\) kJ, \({{A}_{a}} = 22.1\) cm2, \(f = 0.27\), \({{t}_{i}} = 0.5\) s with, \({{\rho }_{l}} = 7100\) kg/m3, and \({{\psi }_{l}} = 0.92\), \(l = 1,2\). Then, from formulas (6) and (8) we find \({{q}_{0}} = 3.87\) MW/m2, \({{w}_{0}} = 46.87\) MJ/m2. Calculations are made taking into account the change in contour area \({{A}_{c}}\) (4) (variant 1) and at a constant, averaged over deceleration time \({{\bar {A}}_{c}} = 0.65{{A}_{a}}\) (variant 2). The thermal sensitivity of the disc material was taken into account by using in the calculations instead of the values of the thermophysical properties \({{K}_{l}} = 21\) W/(m K), \({{c}_{l}} = 728.5\) J/(kg K) at initial temperature \({{T}_{a}} = 20^\circ {\text{C}}\), their values at bulk temperature \({{\theta }_{l}}\), \(l = 1,2\) (26), (28), and (32) equal to \(585^\circ {\text{C}}\) (variant 1) and \(566^\circ {\text{C}}\) (variant 2). Using experimental data in the form of curves of the dependence of thermal conductivity coefficients and the specific heat capacity of Termar-ADF on temperature [9], it was found that \({{K}_{l}} = 16.5\) W/(m K), \({{c}_{l}} = 1737\) J/(kg K), and \(l = 1,2\).

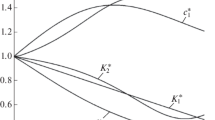
Velocity change over time \(V\), specific power of friction \(q\), and specific friction work \(w\) as well as temperature \(T\) for variants 1 (solid curves) and 2 (dashed curves) are shown in Fig. 1. When calculating according to variant 2, we used formulas (29)–(32). With the constant value of the contour area equal to 0.65Aa, braking occurs with constant deceleration and lasts 19.13 s (Fig. 1a). Linear increase of \({{A}_{c}}\) in the process of braking leads to the appearance of nonlinearity in the time profile of the velocity and insignificant reduction of the stop time up to the 18.95 s. The time profile of the specific power of friction with a maximum after the start of the process (Fig. 1b) is characteristic of rational braking modes [2]. The specific work of friction monotonically increases with the deceleration time, reaching maximum values \(40.11\) MJ/m2 (variant 1) and \(36.04\) MJ/m2 (variant 2) at the moment of stop (Fig. 1c). The evolution of the temperature of the contour area depends on the time profile of the specific power of friction. Its characteristic feature in a rational braking mode is the presence of a temperature maximum, which is reached, depending on the pressure rise time, approximately in the middle of the braking time (Fig. 1d). In the case under consideration, maximum temperature values \(714^\circ {\text{C}}\) (variant 1) and \(645^\circ {\text{C}}\) (variant 2) were achieved respectively after \(10.7\,\,{\text{s}}\) and \(9.8\,\,{\text{s}}\) from the start of braking. At the moment of stop, the temperature was \(525^\circ {\text{C}}\) (variant 1) and \(462^\circ {\text{C}}\) (variant 2).

Fig. 1.
figure 1

Changes during braking of the: (a) sliding velocity \(V\); (b) specific power of friction \(q\); (c) specific work of friction \(w\); and (d) temperature \(T\) calculated with (solid lines) and without (dashed lines) consideration of the contour contact area variations.

Full size image

The results presented in Fig. 1 were obtained at a fixed value of the nominal contact area with a variable (variant 1) or constant (variant 2) contour area. Taking previously used value \({{A}_{a}} = 2212\) mm2 for the base, Fig. 2 shows the change in maximum temperature \({{T}_{{\max }}}\), the time to reach it \({{t}_{{\max }}}\), and the duration of braking \({{t}_{s}}\) for values \(\lambda {{A}_{a}}\), \(0.5 \leqslant \lambda \leqslant 2\). When the nominal contact area is halved compared to the baseline, the maximum temperature rises to \(1007\) and \(733^\circ {\text{C}}\), the time to reach it increases to \(21\) and \(19\) s, and the braking process continues for \(37.6\) and \(37.8\) s when calculating according to variants 1 and 2, respectively. With an increase in the nominal contact area, all of the above characteristics monotonically decrease and for value \(2{{A}_{a}}\) equal: \({{T}_{{\max }}} = 507\) and \(376^\circ {\text{C}}\), \({{t}_{{\max }}} = 5.6\) and \(5.19\) s, \({{t}_{s}} = 9.6\) and \(9.8\) s.

Fig. 2.
figure 2

Dependences on the nominal area of friction contact \({{A}_{a}}\) of the: (a) maximum temperature \({{T}_{{\max }}}\); (b) the time of its reaching \({{t}_{{\max }}}\) and stopping time \({{t}_{s}}\) calculated with (solid lines) and without (dashed lines) consideration of the contour contact area variations.

Full size image

CONCLUSIONS

An exact solution to the thermal problem of friction for a disc brake is obtained, taking into account the linear increase with time of the contour contact area and the thermal sensitivity of materials. The calculations were performed for a friction pair consisting of two identical discs made of Termar-ADF CFCM. The change in the process of deceleration of the sliding speed, power and work of friction, as well as temperature at a changing (variant 1) and constant, averaged over time (variant 2), the contour contact area is investigated. It is shown that the temperature obtained in the calculations according to variant 1 is always slightly higher than that found according to variant 2. In this case, the relative difference between the corresponding maximum temperatures does not exceed 10%. An increase in the contour contact area leads to an insignificant, not more than 1%, reduction in the duration of braking. Consequently, the calculation of the temperature regime of the tribosystem under consideration can be performed with sufficient accuracy at a constant value of the contour area.

Additionally, the influence of the dimensions of the nominal friction surface on some characteristics of the braking process has been studied. In both design variants, it was found that an increase in the nominal contact area leads to a reduction in the braking time, a decrease in the maximum temperature, and a decrease in the time to reach it.

NOTATION

\({{A}_{a}}\) nominal contact area

\({{A}_{c}}\) contour contact area

\({{\bar {A}}_{c}}\) averaged contour area

\(c\) specific heat

\(F\) friction force

\(f\) coefficient of friction

\(K\) thermal conductivity

\(p\) contact pressure

\({{p}_{0}}\) nominal contact pressure

\(q\) specific power of friction

\({{q}_{0}}\) nominal value of specific friction power

\(T\) temperature

\({{T}_{a}}\) ambient temperature

\({{T}_{{\max }}}\) maximum temperature

\(t\) time

\({{t}_{i}}\) time of pressure increase

\({{t}_{s}}\) time of braking

\(V\) velocity

\({{V}_{0}}\) initial velocity

\({{W}_{0}}\) initial kinetic energy

\(w\) specific work of friction

\({{w}_{0}}\) nominal value of specific friction work

\(\theta \) volumetric temperature

\(\rho \) density

Subscripts:

\(l = 1\) disc

\(l = 2\) pad