Kinetic Alfvén Waves’ Generation in Front of the Earth’s Main Shock Wave

Abstract

We investigated the possibility of generating kinetic Alfvén waves by beams of high-speed protons in front of the Earth’s main shock wave. An analytical solution is obtained for the hose-type instability of kinetic Alfvén waves caused by the beam’s dynamic pressure. The effect of the temperature of high-speed beams and the temperature of solar wind protons on the characteristics of the generated disturbances is studied. The temperature has a significant effect on the transverse scales of disturbances: the higher the temperature of the beam protons and the lower the temperature of the surrounding plasma, the more stringent the restrictions imposed on the transverse wavelength scales. The development of instability during the propagation of beams of reflected, intermediate, and diffused protons in the region ahead of the Earth’s main shock wave is considered. The dynamics of the movement of disturbances in this region are analyzed.

INTRODUCTION

Alfvén waves are inextricably linked with the global magnetic structures of various astrophysical objects and, therefore, are essential in most dynamic processes occurring in space plasma. The study of the behavior of Alfvén waves suggests that, with sufficiently small transverse wavelength scales, they have unique properties, and their behavior essentially depends on the parameters of the medium in which they propagate. Indeed, in a very low-pressure plasma, Alfvén waves can propagate at velocities less than the Alfvén velocity but cannot overpass it. In low-, intermediate-, and high-pressure plasmas, on the contrary, Alfvén waves can propagate at velocities exceeding the Alfvén speed but cannot propagate at velocities lower than the Alfvén speed [26, 58, 62, 63]. The interaction of waves with plasma particles also significantly depends on the transverse scales of wavelengths and parameters of the medium. Such an interaction can be so strong that waves with sufficiently small transverse scales decay almost aperiodically [37]. Given the special behavior of Alfvén waves with small transverse scales, they are often referred to as dispersive Alfvén waves (DAW). In very low- and low-pressure plasmas, DAW are often referred to as inertial terms (IAW) for very low-pressure plasma and kinetic Alfvén waves (KAW) for low-pressure plasma) [26, 37, 58].

Most of the works devoted to the study of the behavior of Alfvén waves in astrophysical plasma are devoted to conventional Alfvén waves and their effect on the processes occurring in various astronomical objects [10, 36, 55, 56, 60, 61]. However, DAW can cause certain phenomena occurring in the space environment in many cases, since, unlike the conventional Alfvén waves, they interact well with plasma particles and can be one of the main sources of particle heating and acceleration. Dispersive Alfvén waves are essential in the processes occurring in the Earth’s magnetosphere [3, 5, 24, 34, 48], planetary magnetospheres [27, 31], the solar wind [13, 29, 45, 46, 5], atmospheres of comets [16], solar atmosphere [25, 29, 54, 59], coronal loops [19], solar flares [7, 9, 41, 64], interstellar medium [47, 50], galactic jets [30], and supernova remnants [44].

Given the role played by DAW in the dynamics of astrophysical plasma, it is urgently needed to discover how, where, and under what conditions such waves can be generated, and how the transverse wavelength scales affect their generation. Various mechanisms of generation of low-frequency waves are known [6, 38], for example, resonant [2, 23], current [19, 21], compensated current [8, 15, 22, 40, 65], anisotropic [17, 18, 27, 33, 35, 49, 52], or gradient [57]. In this paper, we focus on the variety of conventional hose instability, that is, the hose instability caused by the beam’s dynamic pressure. We have demonstrated earlier [38, 39] that such instability can lead to the generation of both Alfvén and magnetosonic waves in a low-pressure plasma. It is interesting to reveal whether beams of high-speed protons propagating in the space medium can lead to the generation of not only Alfvén and magnetosonic waves but also kinetic Alfvén waves. Below, we investigate how the beam temperature and background plasma temperature affect the generation and characteristics of such waves. We also assess the possibility of the development of instability in the presence of propagating beams of reflected, intermediate, and diffused protons in the preshock region of the main shock wave on Earth.

FORMULATION OF THE PROBLEM

Let us consider a three-component (background protons, background electrons, proton beam) quasi-neutral homogeneous magnetized plasma with a Maxwellian particle velocity distribution shifted along the magnetic field (z axis)

$${{f}_{{0\alpha }}} = \frac{{{{n}_{{o\alpha }}}}}{{{{{(2\pi {{T}_{\alpha }}{\text{/}}{{m}_{\alpha }})}}^{{3/2}}}}}\exp \left( {\frac{{{{m}_{\alpha }}{v}_{ \bot }^{2}}}{{2{{T}_{\alpha }}}} - \frac{{{{m}_{\alpha }}{{{({{{v}}_{{||}}} - {{{v}}_{{0\alpha }}})}}^{2}}}}{{2{{T}_{\alpha }}}}} \right),$$

(1)

where n_0α, and m_α are the undisturbed density and mass of particles of type α (α = e, i, bi are the background electrons, background protons, and proton beam, respectively), v_z and ${{{v}}_{ \bot }}$ are the longitudinal (relative to the undisturbed uniform magnetic field B₀) and transverse particle velocities, T_α is the temperature of type α particles, and v_0α is the propagation velocity of type α particles along the magnetic field.

We use the coordinate system associated with immobile background protons. In this coordinate system, the speed of background protons is zero; v_0i = 0.

We assume the proton beam current is compensated by the background plasma electron current,

$$q{{n}_{{0e}}}{{{v}}_{{0e}}} = q{{n}_{{0bi}}}{{{v}}_{{0bi}}},$$

(2)

where q is the proton charge.

Let us study the case of propagation of a high-speed low-density beam in a plasma. It follows from Eq. (2) that the velocity of background plasma electrons is much smaller than the beam velocity: v_0e ⪡ v_0bi.

We consider low-pressure plasma

$${{m}_{e}}/{{m}_{i}} \ll {{b}_{i}} \ll 1,\,\,\,\,{{{v}}_{{Ti}}} \ll {{{v}}_{A}} \ll {{{v}}_{{Te}}},$$

(3)

where β_i = 8$\pi {{n}_{{0i}}}{{T}_{i}}/B_{0}^{2} = 2{v}_{{Ti}}^{2}/{v}_{A}^{2}$ is the ratio of the gas-kinetic pressure of the background protons to the pressure of the magnetic field; B₀ is the undisturbed magnetic field; ${v}_{{Ti}}^{2} = {{T}_{i}}/{{m}_{i}}\,{\text{and}}\,{v}_{{Te}}^{2} = {{T}_{e}}/{{m}_{e}}$ are the squares of the thermal velocities of the background protons and electrons, respectively; and v_A = B₀/(4πn_0im_i)^1/2 is the Alfvén velocity.

DISPERSION OF KINETIC ALVEN WAVES IN A LOW-PRESSURE PLASMA WITH A HIGH-SPEED BEAM

To obtain the expression for the frequency of kinetic Alfvén waves, we use the general dispersion equation [1]

$$\left| {{{k}^{2}}{{\delta }_{{ij}}} - {{k}_{i}}{{k}_{j}} - \frac{{{{\omega }^{2}}}}{{{{c}^{2}}}}{{\varepsilon }_{{ij}}}} \right| = 0,$$

(4)

where k, k_z, and k_x are the modulus and projection of the wave vector onto the directions along (z axis) and across (x axis) of the magnetic field (the wave vector lies in the xz plane); ω is the wave frequency; ε_ij is the permittivity tensor; c is the speed of light; and δ_ij is the Kronecker symbol.

Now, we use the kinetic approach. To calculate the permittivity tensor, we apply the Vlasov kinetic equation without collisions [1],

$$\frac{{\partial {{f}_{\alpha }}}}{{\partial t}} + {\mathbf{v}}\frac{{\partial {{f}_{\alpha }}}}{{\partial {\mathbf{r}}}} + \left( {{{q}_{\alpha }}\text{E} + \frac{{{{q}_{\alpha }}}}{c}[{\mathbf{vB}}]} \right)\frac{{\partial {{f}_{\alpha }}}}{{\partial {\mathbf{p}}}} = 0,$$

(5)

where f_α is the particle distribution function, v is the particle velocity, E is the electric field strength vector, B is the magnetic field induction vector, and q_α is the charge of type α particles.

Solving the linearized Vlasov kinetic equation (5) and taking into account that the undisturbed distribution function is a shifted Maxwellian distribution (1), one can obtain an expression for the disturbed distribution function and calculate the current, which enables the calculation of the tensor [1].

We are interested in kinetic Alfvén waves, which are low-frequency waves (ω/ω_Bi ⪡ 1), which significantly simplify the permittivity tensor. Omitting intermediate calculations, we obtain for the dielectric permittivity tensor of low-frequency waves ${{\left( {\omega _{\alpha }^{'}/{{\omega }_{{Bi}}}} \right)}^{2}} \ll 1,\,\,{{\left( {{{k}_{z}}{{{v}}_{{T\alpha }}}/{{\omega }_{{B\alpha }}}} \right)}^{2}} \ll 1$:

$$\begin{gathered} {{\varepsilon }_{{xx}}} \approx 1 + \sum\limits_\alpha {{{{\left( {\frac{{{{\omega }_{{P\alpha }}}}}{{{{\omega }_{{B\alpha }}}}}} \right)}}^{2}}{{{\left( {\frac{{\omega _{\alpha }^{'}}}{\omega }} \right)}}^{2}}\frac{{1 - {{A}_{0}}\left( {{{z}_{\alpha }}} \right)}}{{{{z}_{\alpha }}}},} \\ {{\varepsilon }_{{xy}}} = - {{\varepsilon }_{{yx}}} \approx - i\sum\limits_\alpha {\left( {\frac{{\omega _{{P\alpha }}^{2}}}{{{{\omega }_{{B\alpha }}}}}} \right)} \left( {\frac{{\omega _{\alpha }^{'}}}{{{{\omega }^{2}}}}} \right)A_{0}^{'}({{z}_{\alpha }}), \\ {{\varepsilon }_{{xz}}} = {{\varepsilon }_{{zx}}} \approx \sum\limits_\alpha {{{{\left( {\frac{{{{\omega }_{{P\alpha }}}}}{{{{\omega }_{{B\alpha }}}}}} \right)}}^{2}}\frac{{\omega _{\alpha }^{'}{{k}_{x}}{{u}_{{z\alpha }}}}}{{{{\omega }^{2}}}}} \frac{{(1 - {{A}_{0}}({{z}_{\alpha }}))}}{{{{z}_{\alpha }}}}, \\ {{\varepsilon }_{{yy}}} \approx {{\varepsilon }_{{xx}}} + 2\sum\limits_\alpha {{{{\left( {\frac{{{{\omega }_{{P\alpha }}}}}{\omega }} \right)}}^{2}}} {{z}_{\alpha }}A_{0}^{'}({{z}_{\alpha }}){{J}_{ + }}({{\xi }_{\alpha }}), \\ {{\varepsilon }_{{yz}}} = - {{\varepsilon }_{{zy}}} \approx i\sum\limits_\alpha {\frac{{\omega _{{P\alpha }}^{2}{{k}_{x}}{{u}_{{z\alpha }}}}}{{{{\omega }_{{B\alpha }}}{{\omega }^{2}}}}A_{0}^{'}({{z}_{\alpha }})} - i\frac{{{{k}_{x}}}}{{{{k}_{z}}}}\sum\limits_\alpha {\frac{{\omega _{{P\alpha }}^{2}}}{{{{\omega }_{{B\alpha }}}\omega }}A_{0}^{'}({{z}_{\alpha }})[1 - {{J}_{ + }}({{\xi }_{\alpha }})]} , \\ {{\varepsilon }_{{zz}}} \approx 1 + \sum\limits_\alpha {{{{\left( {\frac{{{{\omega }_{{P\alpha }}}}}{{{{k}_{z}}{{{v}}_{{T\alpha }}}}}} \right)}}^{2}}} {{A}_{0}}({{z}_{\alpha }})\left[ {1 - {{J}_{ + }}({{\xi }_{\alpha }})} \right] + {{\sum\limits_\alpha {\left( {\frac{{{{\omega }_{{P\alpha }}}}}{{{{\omega }_{{B\alpha }}}}}} \right)} }^{2}}{{\left( {\frac{{{{k}_{x}}{{u}_{{z\alpha }}}}}{\omega }} \right)}^{2}}\frac{{\left( {1 - {{A}_{0}}({{z}_{\alpha }})} \right)}}{{{{z}_{\alpha }}}}, \\ \end{gathered} $$

(6)

where

$\begin{gathered} \omega _{\alpha }^{'} = \omega - {{k}_{z}}{{u}_{{z\alpha }}},{\text{ }}{{A}_{0}}({{z}_{\alpha }}) = {{I}_{0}}({{z}_{\alpha }})\exp ( - {{z}_{\alpha }}),{\text{ }}{{z}_{\alpha }} = {{({{k}_{x}}{{{v}}_{{T\alpha }}}/{{\omega }_{{B\alpha }}})}^{2}} \\ {{\alpha }_{\alpha }} = \omega _{\alpha }^{'}{\text{/(}}{{k}_{z}}{{{v}}_{{T\alpha }}}{\text{)}}{\text{, }}\,{{J}_{{\text{ + }}}}{\text{(}}{{\xi }_{\alpha }}{\text{)}} = - i{{{\text{(}}\pi {\text{/2)}}}^{{{\text{1/2}}}}}{{\xi }_{\alpha }}W{\text{(}}{{\xi }_{\alpha }}{\text{/}}{{{\text{2}}}^{{{\text{1/2}}}}}{\text{) [6]}}{\text{,}} \\ W\left( x \right) = \exp \left( { - {{x}^{2}}} \right)\left[ {1 + \frac{{2i}}{{\sqrt \pi }}\int\limits_0^x {{{e}^{{{{t}^{2}}}}}dt} } \right], \\ \end{gathered}$

I₀(z_α) is the modified zero-order Bessel function, $A_{0}^{'}$(z_α) is the derivative of the function A₀(z_α), ω_Pα and ω_Bα are the plasma and cyclotron frequencies, and v_Tα is the thermal velocity of type α particles. Upon deriving Eqs. (6), an infinite series of Bessel functions were added.

Next, we obtain the dispersion of kinetic Alfvén waves in a low-pressure plasma in the presence of a high-speed v_0bi/v_A ⪢ 1 proton beam. To do this, we substitute the permittivity tensor (6) into the dispersion equation (4). With low-pressure plasma β_i ⪡ 1, when the thermal pressure of the background plasma is much smaller than the pressure of the magnetic field, for small nonisothermality T_i/T_e > 1, and considering the low beam density, we obtain the following expression from the dispersion equation (4) for kinetic Alfvén waves:

$${{\omega }^{2}} = \left[ {1 - \frac{{{{n}_{{0bi}}}}}{{{{n}_{{0i}}}}}{{{\left( {\frac{{{{{v}}_{{0bi}}}}}{{{{{v}}_{A}}}}} \right)}}^{2}}\frac{{\left( {1 - {{A}_{0}}({{z}_{{bi}}})} \right)}}{{{{z}_{{bi}}}}}} \right]{{({{k}_{z}}{{{v}}_{A}})}^{2}}{{z}_{i}}\left[ {\frac{1}{{(1 - {{A}_{{0i}}}({{z}_{i}}))}} + \frac{{{{T}_{e}}}}{{{{T}_{i}}}}} \right].$$

(7)

Equation (7) suggests that, in the absence of a proton beam, we obtain a standard solution corresponding to kinetic Alfvén waves [26, 37, 58],

$${{\omega }^{2}} = {{({{k}_{z}}{{{v}}_{A}})}^{2}}{{z}_{i}}\left[ {\frac{1}{{(1 - {{A}_{{0i}}}({{z}_{i}}))}} + \frac{{{{T}_{e}}}}{{{{T}_{i}}}}} \right].$$

(8)

Note that kinetic Alfvén waves are a continuation of the Alfvén branch into the region of small transverse wavelengths commensurate with the Larmor radius of protons [37]. This makes it easy to obtain the dispersion of Alfvén waves from Eq. (8). Indeed, for long wavelengths, much larger than the Larmor radius, which corresponds to small transverse wave vectors z_i ⪡ 1, the dispersion of kinetic Alfvén waves transforms into the dispersion of Alfvén waves [1, 4],

$${{\omega }^{2}} = {{({{k}_{z}}{{{v}}_{A}})}^{2}}.$$

(9)

Solution (7) describes the hose-type instability of kinetic Alfvén waves caused by the beam’s dynamic pressure. For large wavelengths, much larger than the Larmor radius (z_i ⪡ 1), solution (7) smoothly transforms into the solution for conventional Alfvén waves [38], which describes the hose-type instability of Alfvén waves,

$${{\omega }^{2}} = {{({{k}_{z}}{{{v}}_{A}})}^{2}}\left[ {1 - \frac{{{{n}_{{0bi}}}}}{{{{n}_{{0i}}}}}{{{\left( {\frac{{{{{v}}_{{0bi}}}}}{{{{{v}}_{A}}}}} \right)}}^{2}}\frac{{\left( {1 - {{A}_{0}}({{z}_{{bi}}})} \right)}}{{{{z}_{{bi}}}}}} \right].$$

(10)

Solutions (7) and (9) suggest that, for sufficiently high concentrations and beam velocities, the Alfvén kinetic waves (Alfvén waves) become unstable.

Let us obtain the main characteristics of kinetic Alfvén waves, which can be generated by the propagation of a high-speed proton beam in magnetically active space plasma.

Criterion for the development of instability. It can be seen from solution (7) that kinetic Alfvén waves become unstable when the term in the first square bracket becomes smaller than zero. The function (1 ‒ A₀(z_bi))/z_bi decreases monotonically from 1 to 0 as z_bi grows, so the negative term takes its maximum value at z_bi > 0, that is, when Alfvén waves propagate strictly along the magnetic field. For the longitudinal propagation of Alfvén waves k_x = 0, we have the following for the dispersion:

$${{\omega }^{2}} = {{({{k}_{z}}{{{v}}_{A}})}^{2}}\left[ {1 - \frac{{{{n}_{{0bi}}}}}{{{{n}_{{0i}}}}}{{{\left( {\frac{{{{{v}}_{{0bi}}}}}{{{{{v}}_{A}}}}} \right)}}^{2}}} \right].$$

(11)

Using Eq. (11), we can easily find the criterion for the development of the hose instability of kinetic Alfvén waves,

$${{a}_{A}} = \frac{{{{n}_{{0bi}}}}}{{{{n}_{{0i}}}}}{{\left( {\frac{{{{{v}}_{{0bi}}}}}{{{{{v}}_{A}}}}} \right)}^{2}} > 1,$$

(12)

which, as expected, completely coincides with the criterion for the development of the hose instability of Alfvén and magnetosonic waves [38, 39].

Region of wave instability. Let us determine the value of the transverse wave vector k_x1, above which the stabilization of the instability occurs. Considering the definition of z_α = ${{\left( {{{k}_{x}}{{{v}}_{{T\alpha }}}/{{\omega }_{{B\alpha }}}} \right)}^{2}}$, it can be considered as the square of the normalized transverse wave vector z_α = ${{\left( {{{k}_{x}}/{{k}_{{T\alpha }}}} \right)}^{2}}$, where ${{k}_{{T\alpha }}} = {{{v}}_{{T\alpha }}}/{{\omega }_{{B\alpha }}}$. For convenience, we consider the restrictions directly on the square of the normalized wave vector z_0bi1 rather than on the transverse wave vector. From Eq. (7) for the boundary values of the transverse wave vector, we obtain

$$\frac{{{{z}_{{bi1}}}}}{{\left( {1 - {{A}_{0}}({{z}_{{bi1}}})} \right)}} = \frac{{{{n}_{{0bi}}}}}{{{{n}_{{0i}}}}}{{\left( {\frac{{{{{v}}_{{0bi}}}}}{{{{{v}}_{A}}}}} \right)}^{2}}.$$

(13)

Let us determine the region of variation of the transverse wave vectors for which the system is unstable. It follows from Eq. (7) that perturbations whose transverse wave vectors satisfy the following inequality are unstable:

$$0 \leqslant {{z}_{{bi}}} < {{z}_{{bi}}}_{1}.$$

(14)

In the general case, Eq. (13) should be solved numerically. However, using the approximation, one can get a good approximate solution. Considering that the function (1 – A₀(x))/x can be represented with high accuracy as

$$\frac{{\left( {1 - {{A}_{0}}(x)} \right)}}{x} = \frac{1}{{1 + x}},$$

(15)

we obtain the solution from Eq. (13) for the boundary values of the square of the normalized transverse wave vector,

$${{z}_{{bi1}}} = \frac{{{{n}_{{0bi}}}}}{{{{n}_{{0i}}}}}{{\left( {\frac{{{{{v}}_{{0bi}}}}}{{{{{v}}_{A}}}}} \right)}^{2}} - 1.$$

(16)

Expression (16) is valid for all ranges of parameter changes; in particular, it helps determine the limiting values of the transverse wave vector for systems that are at the threshold of instability. If the plasma is resistant to hose instability, the right side of Eq. (16) becomes negative, and, accordingly, there are no boundary values of the transverse wave vector, since the first term of Eq. (16) is the square of the normalized transverse wave vector, which must always be positive.

Let us write Eq. (16) in terms of the Alfvén wave kineticity parameter z_i. Alfvén waves can be called kinetic Alfvén waves when the transverse wavelength is comparable to (z_i ~ 1) or smaller than (z_i > 1) of the Larmor radius. Since the value of z_bi is related to the kinetic parameter z_i as

$${{z}_{{bi}}} = \frac{{{{T}_{{bi}}}}}{{{{T}_{i}}}}{{z}_{i}},$$

(17)

for the boundary values of the square of the normalized transverse wave vector (16), we obtain

$${{z}_{{i1}}} = \frac{{{{T}_{i}}}}{{{{T}_{{bi}}}}}\left[ {\frac{{{{n}_{{0bi}}}}}{{{{n}_{{0i}}}}}{{{\left( {\frac{{{{{v}}_{{0bi}}}}}{{{{{v}}_{A}}}}} \right)}}^{2}} - 1} \right].$$

(18)

The value of z_i, unlike z_bi, is related not to the parameters of the solar vector but to the parameters of the proton beam. This is more convenient for comparing events with different values of the temperature, density, velocity of proton beams, and the same values of temperature and density of background solar wind protons.

The value of the transverse wave vector of unstable perturbations depends significantly on the ratio of the background plasma temperature to the beam temperature. Indeed, if the beam temperature is very high compared to the temperature of the background protons, then, as seen from Eq. (18), the value of z_i1 can be small, much less than unity, and kinetic Alfvén waves in such a system cannot develop. Although the value of z_i for background protons can be tiny, the value of z_bi for beam protons can be large, so the modified Bessel function in Eqs. (7) and (10) must be considered, despite the small parameter z_i. Indeed, z_bi = (T_bi/T_i)z_i; therefore, for T_bi/T_i ~ 10³ for beam protons, we obtain z_bi ~ 10³z_i

Maximum increment. Let us estimate the maximum growth rate of the hose instability of kinetic Alfvén waves. Solution (7) was obtained with the approximation of low-frequency waves (ω/ω_Bi)² ⪡ 1. With an increase in the longitudinal wave vector, the wave frequency increases and can exceed the cyclotron frequency and go beyond the application limits of calculations. In rough estimates, by selecting slightly larger frequency values than at the threshold for applying the approximations (ω/ω_Bi)² ⪡ 1, that is, ω/ω_Bi ~ 0.5, we get roughly estimated values of the increment maximum

$${{\gamma }_{{max}}}\sim 0.5{{\omega }_{{Bi}}}.$$

(19)

Let us proceed directly to the consideration of the propagation of high-speed proton beams in the front region of the Earth’s main shock wave.

GENERATION OF KINETIC ALFVÉN WAVES IN FRONT OF THE EARTH’S MAIN SHOCK WAVE

Consider the instability of waves in the solar wind in front of the Earth’s main shock wave, where high-velocity proton beams propagate reflected from the leading edge of the main shock wave [11, 12, 14, 42, 43, 51]. Beams of charged particles can be divided into four main types: electron beams, reflected proton beams, intermediate proton beams, and diffused proton beams. These types of beams differ significantly from each other in their characteristics: velocity, concentration, temperature, and temperature anisotropy and have their spatial localization and generation region. Electrons have a small mass compared to protons, so electron beams with the same speed exert a much lower dynamic pressure on the medium than proton beams. Estimates indicate that electron beams propagating in front of the Earth’s main shock wave do not have a sufficiently high velocity to cause the development of a hose-type instability, so we consider only proton beams.

First, we study the possibility of the development of hose instability by beams of reflected protons [14, 43, 51], which have the highest velocity among all beams formed near the Earth’s main shock wave and a sufficiently high density to cause instability.

Beams of reflected protons. For the reflected beams in the region of the Earth’s main shock wave, we have v_0bi = (2–4)v_sw = 800–1600 km/s, T_bi ~ 7 × 10⁶ K, (v_Tbi ≈ 415 km/s), n_0bi = 0.02–0.8 cm^–3 (average value n_0bi ~ 0.1 cm^–3) at an average value of background plasma density (solar wind proton density) n_0i ~ 5 cm^–3, average temperature of background protons T_i ~ 10⁵ K, (v_Ti ≈ 50 km/s), the average value of the Alfvén velocity v_A ≈ 80 km/s, the average solar wind velocity v_sw ~ 400 km/s, the cyclotron frequency of protons ω_Bi ~ 0.5 s^–1, and the Larmor radius of background protons ρ_Ti ~ 100 km [14, 43, 51].

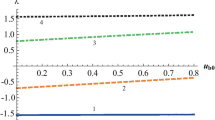
Let us estimate the possibility of the development of instability. At the maximum values of the velocity and concentration of the beams, we obtain the value of a_A ~ 100 for the critical parameter of the development of the hose instability of kinetic Alfvén waves, a_A ≈ 8 for the average values of the velocity and concentration, and a_A ≈ 0.9 for the minimum values of the velocity and concentration. The critical parameter, in most cases, is much greater than unity; therefore, it can be concluded that the hose instability of Alfvén waves should develop in the region of propagation of reflected beams in the solar wind in front of the Earth’s main shock wave. We can determine whether the generated waves can be kinetic Alfvén waves and not just conventional Alfvén waves [37]. To do this, it is necessary to estimate how large the transverse wave vectors can be. Alfvén waves can be called kinetic if the transverse wavelength is of the order of the proton Larmor radius or smaller. Here, the value of the kinetic parameter of Alfvén waves is z_i $\gtrsim$ 1. Let us estimate the kinetic parameter of Alfvén waves using Eq. (18) for the normalized transverse wave vector. For the highest values of the velocity and density of the beams, we obtain z_i ≈ 1.4. This means that not only classical Alfvén waves but also kinetic Alfvén waves can be generated in front of the Earth’s main shock wave with maximum values of the beam parameters. For the average values of the parameters of reflected beams, we obtain z_i ~ 0.1 for the kineticity parameter. This means that, in this case, conventional Alfvén waves are generated rather than kinetic Alfvén waves. Thus, we conclude that kinetic Alfvén waves can be generated in front of the Earth’s main shock wave in the region of propagation of reflected beams but only if the velocity and concentration of the beam are sufficiently high and exceed the average values for the beams. Otherwise, only conventional Alfvén waves are generated.

Beams of intermediate protons. Let us consider the possibility of the development of hose instability by beams of intermediate protons. These beams have intermediate parameter values between reflected and diffused beams. For intermediate beams near the region of the Earth’s main shock wave, we have v_0bi = (1.2–2)v_sw = 480–800 km/s; T_bi ≈ 2 × 10⁷ K (v_Tbi ≈ 702 km/s); n_0bi = 0.03–0.5 cm^–3 (mean value n_0bi ≈ 0.1 cm^–3) [14, 43, 51].

To assess the ability to generate kinetic Alfvén waves, we use the criterion for the development of instability (Eq. (12)). At maximum velocities of intermediate proton beams, we obtain the value a_A ≈ 22 for the critical parameter for the development of hose instability. At average values of speed and concentration, we have а_А ≈ 3.4; at minimum values of speed and concentration, we get а_А ≈ 0.726. In most cases, the value of the critical parameter is greater than unity; therefore, in the region of propagation of intermediate protons, the hose instability of Alfvén waves most often develops. Let us determine the possibility of generating kinetic Alfvén waves in the region of propagation of intermediate proton beams. We obtain z_i ~ 0.1 for the maximum values of the beam parameters and the kineticity parameter of Alfvén waves from Eq. (18). The kineticity parameter is too small, so such Alfvén waves cannot be kinetic Alfvén waves. For minimal values of the beam parameters, no waves are generated; therefore, the generation of kinetic Alfvén waves is impossible. The average values of the parameters of the intermediate beam give z_i ≈ 0.012 for the kinetic parameter of Alfvén waves with Eq. (18). The parameter values are again small; therefore, during the propagation of intermediate protons, which have average values of the speed and density of the beam, kinetic Alfvén waves are also not generated, but conventional Alfvén waves are generated. Thus, we conclude that kinetic Alfvén waves are not generated in the region of propagation of intermediate protons.

Beams of diffused protons. Let us now consider the possibility of generating kinetic Alfvén waves in front of the Earth’s main shock wave in the propagation region of diffused protons. Such beams have the lowest propagation velocity and the highest temperature compared to other beams propagating in the Earth’s preshock region. For diffused proton beams, in the region of the Earth main shock wave, we have v_0bi = (0.8–1.2)v_sw = 320–480 km/s; T_bi = 4 × 10⁷–2 × 10⁸ K, v_Tbi = 993–2220 km/s; n_0bi = 0.04–0.2 cm^–3, with an average value of n_0bi ≈ 0.1 cm^–3 [14, 32, 43, 51].

Let us estimate the possibility of the development of hose instability for diffused beams. For the maximum values of the beam parameters for the critical instability parameter, we obtain a_A ≈ 4.84. For average values of the diffusion beam parameters, we obtain a_A ∼ 2 for the critical parameter. The critical parameter is greater than unity, so the instability develops. For the minimum values of the beam parameters, we have a_A ≈ 0.65. The critical parameter is less than unity; therefore, at the minimum values of the diffused beam parameters, the hose instability of Alfvén waves does not develop. Let us determine whether the generation of kinetic Alfvén waves is possible in the region of propagation of diffused beams. For the minimum values of the beam, Alfvén waves are not generated; therefore, we estimate only for beams of diffused protons, which have the maximum and average values of the parameters. Equation (18) yields z_i ≈ 0.0019 for the kineticity parameter of Alfvén waves at the maximum values of the parameters and z_i ≈ 0.0013 at the average values. The values of the kineticity parameter of Alfvén waves generated by diffused beams are small; therefore, only conventional Alfvén waves can be generated in the propagation region of diffused proton beams.

CONCLUSIONS

An analysis of beam propagation in the region in front of the Earth’s shock wave suggests that when beams propagate in the preshock region, a hose-type instability of Alfvén waves can develop, caused by the beam dynamic pressure. The possibility of the development of instability depends on the beam parameters—velocity, concentration, and temperature. The most favorable conditions for wave generation are created in the region of propagation of reflected beams, where the conditions for the onset and development of instability are always satisfied. In the region of propagation of intermediate protons, located closer to the Earth on the Sun–Earth line, the conditions for the onset of instability are less favorable, but Alfvén waves are also mainly generated. The least favorable conditions for the development of instability are created in the region where diffused protons propagate. This region is located much closer to the Earth than the region of distribution of intermediate protons. Here, instability develops only during the propagation of sufficiently dense and fast beams, the density and speed of which are higher than the average values. Although the conditions for the development of instability in the preshock region of the Earth shock wave are quite favorable, the generation of kinetic Alfvén waves is much more complicated. This is because the temperature of the beams is significantly high compared to the temperature of the background plasma (solar wind plasma). This circumstance has a substantial effect on the possibility of generating kinetic Alfvén waves. It follows from Eq. (18) that the maximum value of the kineticity parameter z_i of Alfvén waves depends significantly on the temperature of the solar wind protons and the proton beam temperature, z_i ≈ T_i /T_bi. The ratio of the temperature of solar wind protons, for example, to the temperature of diffused protons, is small (0.0025–0.0005). Naturally, at such temperature ratios, kinetic Alfvén waves do not form. Therefore, kinetic Alfvén waves cannot be generated in the propagation region of diffused protons. In the region of propagation of intermediate protons, the beam temperatures are also quite high, while the velocities and concentrations, on the contrary, are not high enough for kinetic Alfvén waves to be generated. Here, only conventional Alfvén waves are generated, as in the propagation region of diffused protons. The most favorable conditions for the generation of kinetic Alfvén waves are created in the region of propagation of beams of reflected protons. However, due to high beam temperatures, kinetic Alfvén waves are generated only for beams whose velocities and concentrations exceed the average values. Considering the localization and region of beam propagation, we conclude that the generation of low-frequency disturbances begins in the region of propagation of beams of reflected protons and continues as the disturbances are transferred closer to the Earth into the region of propagation of intermediate protons. Kinetic Alfvén waves are generated only in the region of propagation of reflected beams and are carried away towards the Earth by the solar wind. The maximum wave amplitude is reached in the region of propagation of diffused protons.

Beams of charged particles are a common phenomenon in space plasma. They are formed in various astrophysical objects and structures, for example, stars, shock waves, and planetary magnetospheres, and propagate in the interplanetary and interstellar medium over considerable distances. Such beams can be an effective mechanism for generating low-frequency Alfvén and magnetosonic waves as well as kinetic Alfvén waves.