Ion Acceleration at the Earth’s Bow Shock

Abstract

The Earth’s bow shock is the most studied example of a collisionless shock in the solar system. It is also widely used to model or predict the behaviour at other astrophysical shock systems. Spacecraft observations, theoretical modelling and numerical simulations have led to a detailed understanding of the bow shock structure, the spatial organization of the components making up the shock interaction system, as well as fundamental shock processes such as particle heating and acceleration. In this paper we review the observations of accelerated ions at and upstream of the terrestrial bow shock and discuss the models and theories used to explain them. We describe the global morphology of the quasi-perpendicular and quasi-parallel shock regions and the foreshock. The acceleration processes for field-aligned beams and diffuse ion distribution types are discussed with connection to foreshock morphology and shock structure. The different possible mechanisms for extracting solar wind ions into the acceleration processes are also described. Despite several decades of study, there still remain some unsolved problems concerning ion acceleration at the bow shock, and we summarize these challenges.

1 Introduction

As part of the interaction between the solar wind and the Earth’s magnetosphere a fast-mode bow shock forms upstream of the magnetopause obstacle, where the solar wind flow decelerates from supersonic to subsonic and the density and magnetic field increase. The Earth’s bow shock, and the precursor region known as the foreshock, have been studied by a multitude of missions from pioneering single spacecraft to multi-point and constellation missions. This has given us a uniquely detailed and comprehensive view of the bow shock, which forms the basis for understanding similar systems, such as other planetary bow shocks, the shocks upstream of coronal mass ejections and the heliospheric termination shock. The shape of the Earth’s bow shock, approximately a paraboloid of rotation on the dayside, combined with the orientation of the interplanetary magnetic field (IMF) results in a changing magnetic geometry over the shock surface. According to the angle θ _Bn between the shock normal and the upstream magnetic field direction, shocks are classified as quasi-perpendicular (θ _Bn >45^∘) or quasi-parallel (θ _Bn <45^∘). Consequently, the shock type varies around the surface of the bow shock from perpendicular (where the field line is tangent to the surface), through quasi-perpendicular to quasi-parallel. This sequence in space also corresponds in time to the geometry of the contact point on the shock of a field line convecting with the solar wind (for the nominal Parker spiral angle of the IMF, i.e., 45^∘ to the solar wind direction). This is illustrated in Fig. 1 showing the plane containing the solar wind magnetic field and velocity. In broad terms, the overall structure of the shock magnetic transition is controlled by θ _Bn , with a thin, quasi-laminar transition at the quasi-perpendicular shock, and a broad, turbulent transition at the quasi-parallel shock, as shown in Fig. 1 with typical shock crossings.

Fig. 1

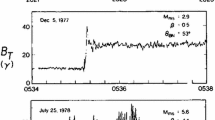
Schematic representation of the Earth’s bow shock for a nominal interplanetary magnetic field direction. The inserts show typical shock transition profiles from the Cluster magnetometer and upstream ion distributions from the ISEE plasma instrument for the quasi-perpendicular (lower left) and quasi-parallel (upper left) shock. In the inserts the scales are 10 nT per major tick mark for B, and in time cover an interval of 30 (20) minutes for the quasi-perpendicular and quasi-parallel examples, respectively

From the mid-1960’s observations of energetic particles (electrons and ions) in the region upstream of the bow shock have been reported. These observations have led to a sophisticated model of the foreshock with different regions corresponding to different energetic particle and wave types. The foreshock is the region upstream of the bow shock populated by energetic particles that can stream upstream from the shock. Due to the IMF angle, the E×B drift (in the bow shock frame) plays an important role in the motion of backstreaming particles, producing velocity dispersion across the foreshock. This is seen clearly in observations of electrons accelerated at the quasi-perpendicular shock in the so-called electron foreshock (Anderson et al. 1979). The high speed of accelerated electrons ensures that the electron foreshock is seen nearest the tangent field line (Fig. 1). Deeper into the foreshock first ion beams (with energies up to 10–20 keV) and then more isotropic (“diffuse”) energetic ion distributions (energies up to several 100’s keV) are seen. An “intermediate” class of ion beams has also been identified observationally with a broadened pitch angle distribution compared to field aligned beams seen at the upstream edge of the energetic ion foreshock. This variation of energetic ion distributions across the foreshock corresponds to magnetic connection changing from quasi-perpendicular to quasi-parallel, as illustrated in Fig. 1. The energetic ion distributions are sources of free energy which can drive waves via various instabilities. Thus the foreshock is also characterized by different types of upstream waves, with the waves at any point a combination of in-situ generation and convection from other locations. The most prominent are the large amplitude ULF waves seen in the foreshock connected to the quasi-parallel shock, which play a fundamental role in both the structure at the quasi-parallel shock and the acceleration of the diffuse ions.

In this paper we review the observations, models and theories of ion acceleration at the Earth’s bow shock. In particular we emphasize how the study of the bow shock has enabled us to understand the mechanisms for taking some particles from the incident solar wind into the acceleration process. This is sometimes referred to as the “injection problem,” although the bow shock seems to show us that in many cases there is no problem at all. Although the bow shock is much studied and widely used as a model for other collisionless shock systems, it should be remembered that it is, relatively speaking, a rather small shock system, and its shape and size have to be considered if results are generalized to other different shock systems. For example, interplanetary shocks at corotating interaction regions are of much larger scale and are more close to planar than the Earth’s bow shock. It also has to be remembered that the Earth’s magnetosphere is itself a source of energetic ions, independent of any acceleration processes at the bow shock (see later for a discussion of this point). This paper only discusses shock structure where it is relevant to ion acceleration. Recent reviews exist for the quasi-perpendicular shock (Bale et al. 2005), the quasi-parallel shock (Burgess et al. 2005) and the foreshock (Eastwood et al. 2005; Burgess 1997). Desai and Burgess (2008) have presented a comparative review of CME shock and bow shock acceleration.

2 Ion Acceleration at the Quasi-perpendicular Shock

2.1 Ion Specular Reflection

A common feature of high Mach number collisionless shocks, such as the Earth’s bow shock, is the presence of specular (or near-specular) reflected ions. In the context of the Earth’s bow shock, high Mach number is used to refer to super-critical shocks, in which resistivity alone is insufficient to provide the required dissipation (Kennel et al. 1985). Specular reflection means that some ions from the incident solar wind distribution approximately reverse their component of velocity normal to the shock within a very short distance, typically of the scale of the shock ramp (or a similar large magnetic field increase), i.e., of the order of a proton inertial length, or less. The observational signature of such ions is a cold beam with velocity spread roughly the same as that of the solar wind. Specular reflected ions are important both to the shock structure (which in turn plays a role in ion acceleration) and to ion acceleration directly, since reflection corresponds to a step up in energy and the first stage towards gaining increasingly high energies.

Specular reflected ions play a major role in the physics of quasi-perpendicular shocks. At low Mach number shocks there is only a small increase in the magnetic field, and reflected ions are not produced in sufficient number to affect the shock structure. At high Mach number, above a certain critical Mach number, reflected ions are necessary to produce the shock heating required by the shock conservation equations; such shocks are termed super-critical. The critical Alfvénic Mach number depends on the plasma parameters, but is typically in the range 2–3 (Kennel et al. 1985). Reflected ions to a large extent control the magnetic shock structure at such shocks. At the Earth’s bow shock observations show that up to 20 % of the upstream incident protons are reflected (Sckopke et al. 1983). The upstream orientation of the magnetic field causes the specular reflected ions to gyrate around the field upstream of the main magnetic ramp where the ions are reflected. These reflected-gyrating ions form a magnetic “foot” ahead of the shock ramp, whose scale length is related to their gyroradius, which in turn depends on the Mach number. The overall characteristic magnetic profile at a super-critical quasi-perpendicular shock of foot-ramp-overshoot is almost entirely governed by the dynamics of specular reflected protons. The reflected-gyrating ions re-encounter the shock and now pass downstream where they form a suprathermal population with a large perpendicular temperature anisotropy. The proton downstream distribution isotropises rapidly as found in observations and hybrid simulations (Sckopke et al. 1990; McKean et al. 1995). Thus the process of specular reflection leads to downstream heated ion distributions with a velocity spread roughly proportional to Mach number. This allows ion heating to provide the requisite dissipation, and to do so even for high Mach number shocks. It is an important feature of the Earth’s bow shock that the downstream heating is dominated by the ions, while electron heating is only relatively modest.

Specularly reflected ions at the quasi-perpendicular shock are not only responsible for the downstream heating process, and thus for shock dissipation, but lead to a temporal variability of the shock on the time scale of an ion gyroperiod. This has become the subject of increased interest in recent years. From the four-spacecraft Cluster mission there is evidence for nonstationarity of the quasi-perpendicular bow shock. Magnetic field observations at the four spacecraft when they were several hundred kilometers apart revealed structures in the foot region (Horbury et al. 2001). The highly localized magnetic field activity in the foot was not phase-standing but was convected into the shock. During other quasi-perpendicular bow shock crossings Horbury et al. (2001) found very markedly different magnetic field profiles at the four spacecraft so that they actually had to discard these examples for a determination of the bow shock orientation and motion. Mazelle et al. (2010) presented evidence for reformation of the quasi-perpendicular bow shock by a statistical analysis of Cluster bow shock crossings. Lobzin et al. (2007) investigated in detail a Cluster crossing of a quasi-perpendicular bow shock with θ _Bn ≈81^∘ and an Alfvén Mach number of M _A ≈10. The magnetic field profiles at the four spacecraft differed considerably from each other. The distances between spacecraft during the event analyzed by Lobzin et al. (2007) lie within the range 380–980 km. Oscillations in the frequency range from 3 to 8 Hz were superimposed on the large scale structure and are interpreted as a whistler wave train nested in the shock. After removing fluctuations with frequencies higher than 2 Hz by Fourier-filtering one or two large amplitude structures with a characteristic time of about 2 sec survived, and it was concluded from cross-correlation studies that the structures were temporal and not spatial.

There are essentially four different models for shock nonstationarity, which are all based on kinetic particle-in-cell simulations of collisionless shocks. At shocks below the whistler critical Mach number

$$ M_w={(1/2)}({m_i/m_e})^{1/2} \cos \theta _{Bn} $$

(1)

a linear whistler train can phase stand in the upstream flow in front of the shock (Kennel et al. 1985). Here m _i and m _e are the ion and electron mass, respectively. In oblique shocks above the whistler critical Mach number a nonlinear instability between incoming (solar wind) and reflected ion beams can occur if there is also present a spatially periodic electric field due to the almost phase-standing whistler train (Biskamp and Welter 1972). The free energy for this instability is the velocity difference between incoming and reflected ions. Scholer and Burgess (2007) have recently performed full particle simulations of oblique shocks with the physical ion to electron mass ratio and have confirmed the Biskamp and Welter (1972) whistler induced reformation (WIR) scenario for the lower θ _Bn regime (θ _Bn below ≈80^∘): above the whistler critical Mach number the whistler amplitude in the foot grows, leading to vortices of the incoming ions and of the reflected ions in velocity phase space and eventually to phase mixing and reformation.

A second model for shock reformation relies on accumulation of reflected ions at the upstream edge of the foot. When the density of the reflected ions is large the compression of the magnetic field at the upstream edge of the foot where the reflected ions are turned around can ignite the emergence of a new shock ramp (Lembege and Dawson 1987). Hada et al. (2003) have developed a semi-analytical model for this shock reformation process, which is based on the coupling between incoming and reflected ions. They determined a critical fraction of reflected to incoming ions beyond which no stationary solution for the coupling process exists. In other words, for a high reflection rate the coupling becomes so strong that the shock is nonstationary and reforms. As pointed out by Hada et al. (2003) this proposed model applies for the case where the reflected ions can be described by a mono-energetic ion population, which is approximately true for low ion beta. The reformation process disappears in PIC simulations of higher beta shocks (β _i of the order of 1) (Hada et al. 2003; Scholer et al. 2003). Scholer et al. (2003) pointed out that the important quantity which determines whether reformation occurs or not is actually not the ion beta, but the difference between the upstream plasma velocity and the ion thermal velocity: when this difference is large the incoming and reflected ion beam interact at the upstream edge of the foot, and this interaction starts a reformation process. When this difference is small, as in β _i >0.4 simulations of medium Mach number shocks, the incoming and reflected ion beams overlap in velocity space in the region close to the shock ramp. The interaction then occurs smoothly over the whole foot and a stationary profile results.

The Lembege and Dawson/Hada et al. model applies to exactly perpendicular shocks. From an evaluation of the linear theory for parameters appropriate to the foot of quasi-perpendicular shocks Matsukiyo and Scholer (2003) have shown that the modified two-stream instability (MTSI) can be excited in the foot region. Specularly reflected ions propagate upstream away from the shock and are responsible for the foot. Here the incoming electrons are decelerated in order to achieve zero electrical current in the shock normal direction. In the case that the upstream magnetic field is not exactly perpendicular to the shock normal, i.e., when wave vectors with a component parallel to the magnetic field are allowed, the resulting velocity difference between incoming ions and incoming electrons leads to the excitation of the MTSI. Investigation of this process requires simulations with realistic ion to electron mass ratio, since the growth rate of the MTSI in units of the inverse ion gyrofrequency depends strongly on m _i /m _e . For a mass ratio below ∼400 the growth rate is smaller than the ion gyroperiod and the instability cannot be excited within one gyromotion of the reflected ions. The wavelength of maximum growth is of the order of 2πλ _e (λ _e =electron inertial length) and is thus much smaller than the size of the foot, which is of the order of the convected ion gyroradius. The instability results in growing small scale vortices of the incoming solar wind ions in v _x −x phase space in the foot and subsequent phase mixing between incoming and specularly reflected ions. After thermalization a new shock front appears at the upstream edge of the foot (Scholer and Matsukiyo 2004).

A fourth process for shock reformation has been proposed by Krasnoselskikh et al. (2002). Above a nonlinear whistler critical Mach number given by

$$ M_{nw}=\bigl({1}/{\sqrt{2}}\bigr)({m_i}/{m_e})^{1/2}\cos \theta _{Bn} $$

(2)

the nonlinear upstream whistler train becomes unstable to a gradient catastrophe. This is supposedly due to the fact that the nonlinear steepening of the wave train cannot be balanced anymore by the effects of dispersion and dissipation. The wave train then becomes unstable with respect to overturning and reformation results. The whistler induced reformation (WIR) described by Biskamp and Welter (1972) is different from the Krasnoselskikh et al. (2002) catastrophe model: in the WIR mechanism the free energy source for the instability is the velocity difference between reflected and incoming ions.

The simulations discussed above have been performed in one spatial dimension only. In a realistic situation more degrees of freedom are available and this can lead to modifications. Hellinger et al. (2007) claimed on the basis of 2-D hybrid and full particle simulations of exactly perpendicular shocks that shock reformation is suppressed by an oblique whistler in the foot which is not seen in 1-D simulations. Lembège et al. (2009) also reported full particle simulations of an exactly perpendicular shock with a mass ratio of 400 and showed that whistler waves are excited in the foot which inhibit shock reformation. Umeda et al. (2010) have shown that the shock magnetic field averaged over the tangential direction does indeed not exhibit reformation cycles. However, the time evolution of the local shock magnetic field, in 2-D simulations, also exhibits periodic oscillations. Similar behaviour can be found in 2D hybrid simulations (Burgess and Scholer 2007). Nonstationarity may thus occur in patches on the shock surface, or simply be occurring at different phases across the shock surface.

As the preceding discussion shows, much of the work into mechanisms for non-stationarity has been based on simulations or theoretical models. It is relevant to ask about the implications for the Earth’s bow shock. If there is non-stationary behaviour then this will play a role in particle acceleration, since extraction of ions from the thermal population by specular reflection significantly depends on the shock structure. But it seems that non-stationarity is most likely to occur at low ion beta, high Mach number shocks, and this is not a common situation at the Earth’s bow shock. Observational evidence for nonstationarity is gradually accumulating, but the links between observations and the (simulation-based) models are not yet fully established. In particular it might be the case that other sources of fluctuations at the shock (i.e., “turbulence” and/or other instability driven fluctuations) may be as important for particle acceleration.

2.2 Properties of Field-Aligned Beams

Field-aligned ion beams (FAB) are found upstream of the bow shock, close to the foreshock boundary, where the observer is magnetically connected to the quasi-perpendicular shock at rather large θ _Bn angles, which is therefore identified as the source region of these beams. However, most of the beams have been observed at θ _Bn <70^∘, with their characteristics largely independent of θ _Bn (Bonifazi and Moreno 1981a, 1981b; Paschmann et al. 1981), except that the observed fluxes fall off substantially with large θ _Bn and the beam energy increases with increasing θ _Bn . The beams appear scatter-free, narrowly peaked in energy and angle, with a velocity spread perpendicular to the magnetic field typically much larger than parallel to B, i.e., exhibiting beam temperature anisotropies T _⊥/T _∥≈4–9 (Paschmann et al. 1981). Figure 2 shows intensity contours of the ion velocity distribution function f(v _x ,v _y ,v _z =0) of a FAB. The analysis plane is again parallel to the ecliptic plane and v _x points toward the sun, zero velocity is indicated by the cross in the centre and the large arrow is the direction of the magnetic field projected through the solar wind (heavy dot) on to the v _x −v _y plane. The bulk velocity of the FAB is directed along the magnetic field and its speed exceeds the solar wind speed. As can be seen from the elliptical shape of the iso-intensity contours the beam temperature perpendicular to the magnetic field T _⊥ exceeds the parallel temperature T _∥. There are large variations in beam velocity and beam density, the latter may vary between 0.3 % and 15 % of the solar wind density. These quantities are related to the local θ _Bn at the point of intersection of a field line from the observation point with the bow shock: as θ _Bn increases the velocity increases and the density decreases.

Fig. 2

Iso-intensity contours of ion distributions found upstream of the quasi-perpendicular Earth’s bow shock in the v _x −v _y plane. The array of solid circles shows the instrument sampling pattern in the region of interest. From Paschmann et al. (1981)

A model for the energy dependence as a function of θ _Bn was first proposed by Sonnerup (1969), in which a fraction of the solar wind is reflected under conservation of the magnetic moment μ in a frame moving along the bow shock with the de Hoffmann-Teller velocity, i.e., where no motional electric field is present, as discussed in more detail below. Paschmann et al. (1980) later expanded this model to allow for arbitrary orientation of the magnetic field, shock normal, and solar wind vector in three dimensions. Figure 3 shows a comparison of observed peak energies of field-aligned beams with the predicted energy according to the direct reflection model. While the rather narrow beams close to the upstream ion foreshock boundary do not show any association with waves over and above the general solar wind background wave activity, beams with wider angular distributions, which are seen further into the foreshock region, can be associated with high-frequency (∼1 Hz) waves (Hoppe et al. 1981; Hoppe and Russell 1983). Contrary to the situation for diffuse ion populations upstream of the quasi-parallel shock, which show a strong correlation in their He2+/H+ ratio with that in concurrent solar wind (Ipavich et al. 1984), field-aligned beams are substantially depleted in He2+ relative to H+ by up to two orders of magnitude (Ipavich et al. 1988; Fuselier and Schmidt 1994; Fuselier and Thomsen 1992). Fuselier and Thomsen (1992) concluded on these grounds alone that field-aligned beams cannot be the seed population for diffuse ions upstream of the quasi-parallel bow shock, as had been speculated before.

Fig. 3

Comparison of observed field-aligned beam energies with model predictions based on direct reflection under conservation of the magnetic moment. From Paschmann et al. (1980)

2.3 Models for Field-Aligned Beams

Early observations of energetic ions upstream of the Earth’s bow shock prompted Sonnerup (1969) to point out that the appropriate frame for considering the interaction of solar wind particles with the shock was the de Hoffmann-Teller frame (HTF). In this frame the shock is stationary but the incoming upstream flow is parallel to the magnetic field, so that the electric field is zero (assuming uniform and steady conditions) and consequently particle energy is conserved. The HTF is related to the normal incidence frame (NIF) by a transformation velocity parallel to the shock surface, whose value increases with the shock normal angle θ _Bn . Sonnerup showed that reversing a solar wind particle’s v _∥ in the HT frame results in an energy increase of a factor 2–10, similar to that observed. Sonnerup did not specify the mechanics of the reflection, but the model included the possibility of adiabatic reflection (μ conserving reflection). In this case the mechanism is basically fast Fermi acceleration, as later proposed for electron acceleration (Wu 1984). The original Sonnerup analysis had a number of free parameters, but it is most often used to refer to the case of μ conserving reflection, where, in the HTF the beam particle velocity is the reversed upstream flow velocity, as given by Schwartz et al. (1983):

$$ v_\|' = v_{\|i} = V_i \frac{\cos \theta_{Vn}}{\cos \theta_{Bn}} $$

(3)

where $v_{\|}'$ is the HTF beam speed, v _∥i the HTF incident flow speed, V _i the upstream flow speed in the observation frame, and the angles θ _Bn and θ _Vn define the direction of the flow in the observation frame. θ _Vn is the angle between the upstream flow and the shock normal direction. Sonnerup also made the important point that in any frame other than the HTF, such as the NIF, the energization process would be seen as the result of a drift along the motional electric field, and the finite size of the bow shock would thus limit the energy that could be gained in this way. The μ conserving reflection model is attractive to explain the observed energies, but difficult to justify on theoretical grounds, given that the scale of the shock is comparable to, or less than the gyroradius of a reflected particle.

Leakage from the downstream heated ion distribution was suggested by Edmiston et al. (1982) as a source of the upstream ion beams. This model relied on the strong ion heating at the quasi-perpendicular shock and the low density of FAB, so that leakage of only a small fraction of the most energetic downstream particles might be responsible for FAB production. The leakage model was refined by Tanaka et al. (1983) who considered that the downstream thermalization was due to the Alfvén ion cyclotron instability driven by the anisotropy of reflected-gyrating ions, and that leakage of a portion of this population was responsible for FAB production.

The leakage model of Edmiston et al. (1982) did not include the effects of any shock structure, in particular the shock magnetic overshoot which could act as a barrier for downstream to upstream transmission. Schwartz et al. (1983) and Schwartz and Burgess (1984) assessed the different models of the time on the basis of beam speed as a function of shock θ _Bn for a limited number of observed events. On that basis, although most events (particularly at higher energies) were consistent with μ conserving reflection, it was suggested that leakage might be a viable explanation for some, but not all, events.

The Tanaka et al. (1983) model is intrinsically nonlocal in the sense that the downstream ion distribution is assumed to be isotropized at a certain distance downstream of the shock. This would allow particles to enter the bow shock at one value of θ _Bn , travel downstream, be scattered in the isotropization process and stream back to the shock where the shock normal angle took another value. Burgess and Luhmann (1986) using more realistic magnetosheath fields showed that such a nonlocal leakage scenario was unlikely. Furthermore, the Tanaka et al. model is not supported by observations (Sckopke et al. 1990) and simulations (McKean et al. 1995) that show that ion isotropization occurs closely downstream of the high Mach number quasi-perpendicular shock.

To examine the extraction of solar wind ions to FAB particles it is necessary to account for the shock structure of the cross-shock potential and magnetic foot and overshoot. Hybrid simulations of the self-consistent generation of FAB (Burgess 1987b) showed that oblique shocks with θ _Bn >45^∘ could produce FAB in good agreement with observed properties. For example, the beam velocity increases and density decreases as θ _Bn increases. The trajectories include multiple encounters with the shock as the particles stay within one gyro-diameter from the shock. During this interaction the ions drift along the motional electric field and gain energy (as seen in the NIF). When the particle has sufficient energy, and is in the appropriate region of velocity space, it may escape the shock in the upstream direction. Many of the properties of the beams, such as the observed anisotropy (in the beam frame) and velocity dependence with θ _Bn , are dependent on this free escape criterion. The acceleration mechanism is the same as that suggested to operate at quasi-perpendicular interplanetary shocks, namely shock drift acceleration SDA (Burgess 1987a). When an ensemble of FAB particle trajectories is considered it is found from the hybrid simulations that μ is conserved on average. This explains the approximate agreement of the μ conserving reflection model within the Sonnerup (1969) framework. It was also shown that the FAB particles in the simulation originated from the wings of the incident solar wind ion population, explaining the slight differences to the comparisons with observations based on reflection of cold solar wind ions (Schwartz et al. 1983). Strong support for the multiple encounter trajectory model (i.e., shock drift acceleration) as an explanation for FAB production is the observed low relative abundance for alpha particles (Ipavich et al. 1988), which was also confirmed in hybrid simulations (Burgess 1989a). More recently, Oka et al. (2005) used a test particle simulation of an observed FAB event to show that the multiple encounter trajectory behaviour of an SDA-like mechanism was a satisfactory explanation. This study also found a density variation with θ _Bn consistent with the results of the earlier hybrid simulations.

2.4 Possible Relation Between Reflected Gyrating Ions and Field-Aligned Beams

While for a long time reflected gyrating ions and field-aligned beams were seen as two distinct particle distributions at the quasi-perpendicular bow shock, multi-spacecraft observations with Cluster have changed this view. Consecutive and simultaneous observation of reflected gyrating ion distributions and beams at various distances from the shock suggest the emergence of ion beams out of the reflected gyrating ion distribution likely through scattering. Figure 4 shows the spatial evolution of reflected gyrating ions and field aligned beams with distance from the shock. The colour-coded angular distributions on the left show clearly that the gyrating ion distributions in the shock ramp, as shown in panels c and d, extend all the way into the phase space of the field-aligned beams that persist to much larger distances from the shock, shown in panels a and b. The temporal plots on the right show the integrated fluxes for the phase space occupied by the beam (top, for S/C 1, 3, and 4) and for the phase space occupied by the gyrating ions (centre, for S/C 4), along with the magnetic field strength to provide the context of where the observations are obtained relative to the shock front. It should be noted that the CODIF sensor on S/C 1 and 3 was run with its full geometric factor, while on S/C 4 it was run with its reduced geometric factor (a factor of ≈50 lower than its full geometric factor). The reduced setting on S/C 4 allows observation of the gyrating ions without saturation, and the full geometric factor on S/C 1 and 3 provides sufficient counting statistics for the field aligned beams with full time resolution. As can be seen in the top panel, the flux level of the field-aligned beam remains the same whether the beam population is still part of the extended gyrating ion population or constitutes a separate beam population farther away from the shock. Based on this finding, Möbius et al. (2001) concluded that the field-aligned beams they observed most likely originated from the gyrating ion population produced in the shock ramp by specular reflection. However, this scenario requires effective pitch-angle scattering of the gyrating ion population by strong fluctuations in the shock front. An alternative interpretation would be that the FAB ions gain energy by multiple traversals of the shock, or that the multiple traversals appear as pitch angle scattering.

Fig. 4

Angular distributions of the Cluster 1 CODIF H+ observations in a colour coded map at the peak beam energy (left) for four locations relative to the shock, as indicated in the time series of integrated fluxes over the field-aligned beam portion (S/C 1, 3, 4) and the gyrating ion portion (S/C 4) as well as the magnetic field strength (from top to bottom on the right). From Möbius et al. (2001)

The reflected gyrating ion population contributes substantially to the dissipation of directed energy into thermal energy at supercritical shocks, where, downstream, it rapidly merges and isotropizes with the directly transmitted part of the distribution (Sckopke et al. 1990). If the resulting heating of the shocked ion population is effective enough, a fraction of the ions may be able to outrun the shock along the magnetic field lines, and this could be a viable mechanism to produce field-aligned ion beams. This has led to a series of models discussed earlier to explain these beams through leakage from the magnetosheath (e.g., Edmiston et al. 1982; Tanaka et al. 1983). Such a model would require that ions with energies actually observed in ion beams upstream of the shock are also observed in the magnetosheath. In a study of field-aligned beams from low Mach number quasi-perpendicular shocks Kucharek et al. (2004) demonstrated that the phase space region of the beam was actually empty immediately downstream of the shock, while the angular distribution of the gyrating ions in the shock ramp provided the flux necessary to feed the ion beam further upstream of the shock. Figure 5 shows 2-dimensional cuts through the ion distribution at three consecutive locations, immediately downstream of the shock, in the shock ramp, and about 7 minutes after the shock crossing. These observations provide a strong indication that at least in these cases the magnetosheath cannot be the source, and the ion beams must stem from the gyrating ion population in the shock ramp. These observations appear to favour a model with ion reflection in the ramp and subsequent scattering by low frequency waves: ions whose velocity, after scattering, fulfill the escape condition can escape upstream and will constitute in the upstream region field-aligned beams. However, in order to explain the increase of energy with increasing θ _Bn the scattering has to be such that the energy is conserved in the de Hoffmann-Teller frame (Bale et al. 2005). Wave excitation, and in turn scattering may depend on M _A and the plasma beta.

Fig. 5

2-Dimensional cut through distribution function of ions in the B−V _SW plane, taken immediately downstream of the shock (left), in the ramp (centre), and upstream of the shock (right), along with the magnetic field as a function of time over the shock crossing. From Kucharek et al. (2004)

Using observations from Geotail, Oka et al. (2005) came to similar conclusions. They also found that the gyrating ions are connected with field-aligned beams. Figure 6 demonstrates how the peak energy of the field-aligned beam overlaps with the ion distribution in the shock ramp, but exceeds in energy the distribution found immediately downstream of the shock. Oka et al. (2005) also compared their observations with test particle simulations of ions for the average shock conditions observed during the occurrence of the field-aligned beam. They found that a combination of ions that have undergone a single reflection and some with multiple reflections is consistent with their observations.

Fig. 6

Phase space density as a function of speed for several consecutive cuts through the distribution of field-aligned beams, gyrating reflected, and gyrating transmitted ions at the bow shock. From Oka et al. (2005)

More recently, Meziane et al. (2011) have shown Cluster observations of field-aligned beams that include a component with about twice the energy of the primary beam, which follows the energy condition described by Sonnerup (1969) and Paschmann et al. (1980). So far such an additional component at higher energies has not been explained with the available models, including test particle simulations of the reflection and energization.

2.5 Beam Production and Remote Diagnostics of Shock Topology

The peak energy of field-aligned beams as a function of solar wind speed and θ _Bn was derived by Sonnerup (1969) and Paschmann et al. (1981), as given in (3). Observations of FABs generally follow this relation closely when in the vicinity of a shock transition, but the actual beam energy measured at some point upstream exhibits temporal variations. Kucharek et al. (2004) described a beam observation for which the ions could not have escaped the shock into the upstream region, given the observed θ _Bn at the time of the shock crossing. Such changes are likely caused by variations in the orientation of the shock normal at the source location of the field-aligned beam, although it is not possible to directly observe these changes at the shock. Periodic variations of the shock normal have been observed in multi-spacecraft studies of the shock topology and are due to surface waves and/or ripples on the shock front (Moullard et al. 2006; Lobzin et al. 2007).

In turn, the variation of the beam energy with time presents an opportunity to probe the shock orientation remotely. Making use of consecutive outbound and inbound shock crossings as anchor points where the true shock orientation was able to be found, Miao et al. (2009) determined the spatio-temporal history of the shock orientation between these two points from the variation of the field-aligned beam energy. In their derivation, they assumed that (3) was strictly fulfilled for the beams. Figure 7 shows a schematic representation how the field-aligned beams are traced back to their origin from the inferred spacecraft distance relative to the shock, assuming homogeneous interplanetary magnetic field over the distance from the spacecraft to the bow shock. To obtain the actual distance of the spacecraft from the bow shock at any time between the shock crossings, the shock speed is determined at both crossings using the timing method with the four Cluster spacecraft (Schwartz 1998). The distance from the shock is then described by a third power polynomial, matching location and speed at the outbound and inbound crossing. With the same multi-spacecraft method, the average normal direction of the bow shock is determined at the two crossings (indicated in Fig. 7 by the black horizontal line). Together with the observed field orientation, this implies an average value of θ _Bn for the beam event. The temporal variation of θ _Bn at the beam source location (as required to explain the ion beam velocity) is then used to infer the spatial variation of the bow shock orientation. The surface variations as inferred from this remote sensing method is in good agreement with wavelengths and amplitudes obtained by multi-spacecraft studies (Moullard et al. 2006; Lobzin et al. 2007).

Fig. 7

Schematic view of the method used by Miao et al. (2009) to trace the field-aligned beams back to their origin along the red arrow and the determination of the predicted θ _Bn for the bow shock orientation (solid black line) as obtained during the outbound crossing. Also shown are potential shock ripples (dashed black line)

3 Diffusive Ion Acceleration

3.1 Properties of Diffuse Ions

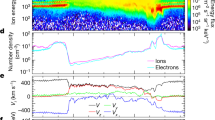
The clearest evidence for particle acceleration at collisionless shocks comes from in situ observations at Earth’s bow shock. Spacecraft have traversed the bow shock many times and the relatively low velocity between the spacecraft and the shock allows a detailed view of the shock structure and of the accelerated particles. Figure 8 shows the most commonly observed ion distributions observed upstream of the quasi-parallel bow shock. Shown are iso-intensity contours of the ion velocity distribution function f(v _x ,v _y ,v _z =0). The analysis plane is parallel to the ecliptic plane; v _x points toward the Sun, v _y points downward (see B, upper right) and is positive toward the dusk meridian, and zero velocity in the spacecraft frame (approximately the shock frame) is indicated by a cross in the centre. Part A of Fig. 8 shows the so-called diffuse ion distribution (Paschmann et al. 1981). Indicated in Part A is the location of the solar wind peak by a solid circle. The projection of the magnetic field onto the v _x −v _y plane is drawn through the solar wind position. The broken circle is drawn in such a way that it is close to one of the contours. The centre of the broken circle is indicated by an asterisk on the magnetic field projection. This centre indicates the direction of the bulk velocity of the diffuse ions: the bulk velocity, as seen in the solar wind frame, is directed upstream with a velocity smaller than the solar wind. Thus in the shock frame the velocity is directed toward the bow shock. To the upper right hand side (B) of Fig. 8 is shown a so-called gyrating ion distribution (Fuselier et al. 1986). The distribution consists only of ions which gyrate within a certain pitch angle range and have a limited velocity. Such a distribution will cut the v _x −v _y plane at two different positions displaced equally about the magnetic field. Also indicated in plot B is the solar wind distribution. These gyrating ions are moving in the shock frame with a small velocity upstream. On the bottom of Fig. 8 we show two distributions (C, D) which have been shown to be nearly specular reflection at the quasi-parallel shock (Gosling et al. 1989). These nearly specularly reflected ions can be seen as a cold beams in addition to the solar wind distribution and diffuse ions or gyrating ions, respectively.

Fig. 8

Iso-intensity contours of ion distributions found upstream of the quasi-parallel Earth’s bow shock in the v _x −v _y plane. For details see text. After Paschmann et al. (1981) (A), Fuselier et al. (1986) (B), and Gosling et al. (1989) (C and D)

The total density of diffuse ions is about 2 % of the solar wind. Panel A of Fig. 8 shows only the very low energy range of diffuse ions: note that the outermost contour is at a velocity of about 2000 km/sec. However, diffuse ions at the bow shock extend to energies of about 200 keV. In the energy range above about 15 keV the spectra of these ions can be fitted by exponentials in energy (Ipavich et al. 1979). When representing the spectra of ions with different charge states (protons, He⁺⁺ and ions of the C, N, O group with charge states of about 8) in terms of energy per charge the spectra are similar, i.e., the e-folding energy per charge is about the same for ions with different charge states but differs from event to event ranging from 15 keV/charge to 25 keV per charge. Figure 9 show energy spectra of protons, alpha particles and ions of the C, N, O group plotted linearly against energy per charge over a limited energy range during an extended diffuse ion event upstream of the bow shock. During this bow shock event, the spectra are exponentials in energy per charge with an e-folding energy per charge of about 17 keV/Q.

Fig. 9

Differential energy spectra of protons, Helium, and CNO plotted linearly against energy per charge. From Ipavich et al. (1979)

Diffuse energetic ion events observed upstream of the bow shock exhibit typical inverse velocity dispersion, i.e., the lower energy ions appear before the higher energy ions. Figure 10 shows an event which lasts for about two hours when the spacecraft (ISEE 1) was near apogee at some 6 R_E upstream of the nominal bow shock. While the lower energy (30–36 keV) protons reach their maximum flux within about 20 min after connection between spacecraft and the quasi-parallel bow shock first occurs, the higher energy protons (112–157 keV) are considerably delayed (Scholer et al. 1979; Ipavich et al. 1981). This can be explained in terms of time-dependent acceleration with a diffusion coefficient increasing with energy after the magnetic field at the spacecraft position is suddenly connected to the quasi-parallel bow shock. In the lower energy range the events exhibit typical top-hat profiles, while they are more spiky in the higher energy range. The ordering of different species in terms of energy per charge shows also in the intensity-time profiles: intensity-time profiles of protons and alpha particles at the same energy per charge are almost identical (Ipavich et al. 1981). Figure 11 shows an upstream diffuse particle event lasting for over four hours. ISEE 1 was during this time period about 1 R_E upstream of the nominal bow shock position. Shown are count rates of protons (solid line) and He⁺⁺ (dashed line) at 30–36 keV/charge where the count rate of protons has been multiplied with the constant factor 0.08. In particular during the rise phase but also during intensity changes during the plateau phase the profiles of the two species are nearly indistinguishable. A comparison between He⁺⁺ and protons in upstream particle events and in the solar wind has shown that the ratio of the intensity in upstream events between 30 and 130 keV/charge is directly proportional to the density ratio in the solar wind (Ipavich et al. 1984). The intensity ratio in upstream events is, on average, enhanced by a factor of about 1.6 relative to the solar wind density ratio, i.e., He⁺⁺ in diffuse events is enhanced relative to protons compared to the solar wind ratio.

Fig. 10

Counting rate profile of ∼30 keV and ∼130 keV protons during a typical upstream event. From Ipavich et al. (1981)

Fig. 11

Counting rate profiles of 30–36 keV/charge protons (solid line) and He⁺⁺ (dashed line) during an upstream event. Time is in UT on November 3, 1977. From Ipavich et al. (1981)

Close to the bow shock, anisotropies of diffuse ions are such that more particles are coming from the sunward direction. Figure 12 shows the anisotropy of ∼30 keV protons (upper panel) and of ∼60 keV protons (lower panel) (Scholer et al. 1979). The distributions to the left are as measured in the spacecraft (bow shock frame) and plotted is the intensity in eight sectors in the look direction (the Sun sector is shaded). In the shock frame the anisotropy is directed toward the shock: more particles are coming from the sunward direction than from the bow shock. The distributions to the right have been transformed by a Compton-Getting transformation into the solar wind frame (indicated by TRA). In the solar wind frame the distributions are sharply peaked from the bow shock. The anisotropy in the direction of the solar wind flow in the shock frame has been taken as strong indication that the particles are scattered by fluctuations in the solar wind. The reversal of the anisotropy in the solar wind frame is due to an intensity gradient along the magnetic field in the solar direction. Scholer et al. (1989) have reported near simultaneous observations of upstream energetic (30–40 keV) protons at a distance of 11.6 R_E along the magnetic field from the shock (ISEE 1) immediately upstream and downstream of the bow shock (AMPTE-IRM), and in the magnetosheath and the magnetosphere close to the magnetopause (AMPTE-CCE). At 11.6 R_E upstream the ions stream in the shock (spacecraft) frame in the sunward direction, with the whole forward hemisphere filled with particles. This indicates more or less free streaming along the magnetic field away from the shock. Close to the shock upstream as well as downstream the anisotropy is directed downstream. After Compton-Getting transformation into the solar wind frame the ions close to, but upstream of the shock have an upstream directed anisotropy; downstream in the magnetosheath they are isotropic in the solar wind frame. At the same time the comparison of absolute fluxes between ISEE-1 and AMPTE-IRM shows a gradient directed away from the shock; a comparison between fluxes at AMPTE-IRM and AMPTE-CCE shows that fluxes are higher in the magnetosheath near the shock than near the magnetopause. The combined anisotropy and gradient observations cannot be explained by magnetospheric escape and upstream transport of magnetospheric particles and are strong evidence for a bow shock related origin of these particles and for scattering in the upstream and downstream medium. Scholer et al. (1989) have derived from the intensity gradient and from the anisotropy measurement a mean free path for 30–40 keV protons of λ∼2.8 R_E.

Fig. 12

Anisotropies of 30 keV (M11) and 60 keV (M21) protons in the spacecraft (left part) and in the solar wind frame (right part). The sun is to the left of the figure; the intensity is plotted in the instrument look direction and the magnetic field projection into the observation plane is indicated by an arrow. From Scholer et al. (1979)

There has been extensive discussion as to what extent upstream energetic particles are bow shock related or are due to magnetospheric escape of particles accelerated within the magnetosphere. There is no doubt that the magnetosphere itself is, at times, a strong particle accelerator, and these particles can escape upstream (e.g., Sarris et al. 1976, 1978; Krimigis et al. 1978; Anagnostopoulos et al. 1986; Sarris et al. 1987). Also, energetic particles trapped within the magnetosphere can suddenly leak into the magnetosheath, escape upstream, and lead to upstream energetic particle events. From a statistical analysis of upstream events observed by ISEE-3 Scholer et al. (1981) found that there are two distinctive groups of events: the first group extends to energies well above 300 keV and is accompanied by energetic electrons (>75 keV), the second group is not accompanied by energetic electrons, and the spectrum can be very well represented by an exponential in energy. They suggested that the first group is of magnetospheric origin while the second group is due to diffusive acceleration at the bow shock. During any time both types of ions may overlap. This has been clearly shown by upstream observations of a singly-ionized magnetospheric (80 keV) oxygen burst lasting for about 15 min during a several hour lasting diffuse proton event by AMPTE-IRM (Moebius et al. 1986). The protons exhibit a bow shock directed net anisotropy while the O⁺ ions are streaming along the IMF into the sunward direction. In close coincidence with the appearance of the O⁺ burst energetic (20–207 keV) electrons have been observed, with the electrons also streaming along the IMF in the sunward direction. While the spectra of the upstream protons, of the He⁺⁺ ions, and of the ions of the CNO group can all be represented by exponentials in energy with the same e-folding energy per charge of 16 keV/charge, the spectrum of the O⁺ burst is considerably harder. At high energies (∼200 keV/charge) the O⁺ spectrum crosses the proton spectrum and the O⁺/H⁺ ratio becomes larger than 1. This is clear indication for upstream particles with two different origins: O⁺ ions (and energetic electrons) due to magnetospheric leakage and bow shock related H⁺, He⁺⁺, and ions of the CNO group.

Simultaneous observations of upstream events close to the shock by ISEE-1 and 220 R_E upstream by ISEE-3 have been reported by Scholer et al. (1980). The anisotropy close to the bow shock was characteristic for diffuse events while at 220 R_E the ions were streaming along the magnetic field. The suggestion was made that these were the same events; however scattering is limited to a region close to the shock whereas at 220 R_E energetic particles stream scatter-free and thus exhibit a large field-aligned anisotropy. Events at ISEE-3 were usually observed when the interplanetary magnetic field changed its orientation so that it was connected with the bow shock (Sanderson et al. 1981). The start and end of the events was characterized by anisotropies perpendicular to the magnetic field due to a density gradient, indicating that the events filled sheet or slab-like regions in interplanetary space. The combination of scattering limited to a region close to the bow shock and scatter-free propagation at 220 R_E may indicate the existence of a free-escape boundary somewhere upstream. On the other hand, time-dependent acceleration is also expected to result in nearly scatter-free propagation far upstream: the density of upstream particles far upstream is rather low and the time available for excitation of the low frequency waves responsible for their scattering by the particle streaming may be too short for typical magnetic field connection times to the bow shock.

Recent measurements of energetic particle events at large distances from the bow shock by such spacecraft as Wind, ACE, and STEREO have added new facts about far upstream events. Desai et al. (2000) found that in many events the high-energy portion (above ∼500 keV in total energy) of the energy spectra was dominated by heavier solar wind-like ions, such as CNO, NeS and Fe. Using earlier single parameter measurements these low energy heavy ions may have been identified wrongly as high energy protons, and many events may thus have been interpreted in terms of evidence for magnetospheric leakage. Composition of upstream events is different during solar maximum compared to solar minimum (Desai et al. 2006): during solar minimum the C/O ratio is close to the solar wind value, and during solar maximum, the ratio is closer to the value in SEP and CME driven shock events indicating pre-accelerated particles as the source material for acceleration during solar maximum.

3.2 Diffuse Ions and Diffusion

The key assumption in first-order Fermi acceleration theory is that the particles undergo diffusive transport in the upstream region. Diffusive transport from any source in the upstream direction against the streaming solar wind, i.e., balancing upstream diffusion against downstream convection, necessarily leads to an upstream density gradient determined by the diffusion coefficient parallel to the magnetic field κ and by the solar wind velocity v _sw . According to the diffusive transport equation in a steady state the density falls off exponentially with an e-folding distance L given by L=κ/v _sw . Early studies of density gradients upstream of the shock relied on single spacecraft data, and thus only statistical studies of the upstream energetic particle density profile could be carried out. For example, an e-folding distance which varied from 3.2±0.2 R_E at 10 keV to 9.3±1.0 R_E at ∼67 keV was found based on a statistical analysis of about 300 events (Trattner et al. 1994). Direct evidence for the exponential fall-off of the upstream energetic particle density has been reported by Kis et al. (2004). These authors used data obtained by the four Cluster spacecraft when the inter-spacecraft separation was relatively large (∼1.5R_E), and when the solar wind conditions stayed relatively constant so that the foreshock was sampled over a period of several hours. Figure 13 shows how the partial density of the energetic ions in the energy range 24 – 32 keV increases as the spacecraft move towards the shock over a period of about 5 hours (on the right hand side of the figure). Using a model for the bow shock location, an absolute distance of the spacecraft from the shock along the magnetic field can be inferred. Using the relative density at two of the Cluster spacecraft, the log density gradient as a function of distance from the shock is obtained. Figure 14 shows the partial density gradient in the 24–32 keV energy range versus distance from the bow shock in a log versus linear representation. Fitting a straight line results in an e-folding distance of ∼2.8R_E, somewhat smaller than e-folding distances derived previously.

Fig. 13

Data used to determine the spatial gradient in diffuse ions, and hence their scattering mean free path. From top to bottom: Solar wind velocity component v _x and magnetic field components B _x (black line/lower curve), B _y (blue line/central curve), B _z (red line/upper curve) as measured on Cluster 1, partial ion density in the 24–32 keV energy range as measured at Cluster 1 (black line/upper curve) and Cluster 3 (green line/lower curve). Also shown in the lower panel are projections of the spacecraft orbits and bow shock onto the x _gse −y _gse and x _gse −z _gse plane, respectively. From Kis et al. (2004)

Fig. 14

Average partial ion density gradient in the 24–32 keV energy range versus distance from the bow shock. From Kis et al. (2004)

Kis et al. (2004) found that the e-folding distance in the energy range 10–32 keV depends linearly on energy. This investigation has been extended to higher energies by Kronberg et al. (2009). Figure 15 shows the e-folding distance L of protons and He⁺⁺ versus energy per charge covering the low energy range from Kis et al. (2004) up to protons of ∼170–235 keV. L is almost a linear function of energy per charge (straight line). Assuming a steady state up to the highest energy this results in a diffusion coefficient κ proportional to energy per charge.

Fig. 15

The e-folding distance versus energy per charge for protons (black points) and He⁺⁺ (red points). The four lowest energy points are from Kis et al. (2004). From Kronberg et al. (2009)

3.3 ULF Waves Upstream of the Quasi-Parallel Bow Shock

The close association of compressive low frequency waves with diffuse ions was first shown by Paschmann et al. (1979). No association of waves with the field-aligned ion beams was found. This was confirmed in a detailed analysis of upstream waves by Hoppe et al. (1981). Low frequency (∼30 sec period) transverse sinusoidal waves were found in the region of intermediate ions and compressive shock-like structures are associated with the diffuse ions. These shock-like structures often break into whistler mode discrete wave packets. A typical magnetic field observation in the region of diffuse ions can be seen in Fig. 16 (Hoppe et al. 1981). Shown on the left hand side are the three vector components of the magnetic field and the magnetic field magnitude (bottom) which demonstrates the compressional character. The right hand side shows an overlay of the magnetic field z component of a discrete wave packet as measured by two spacecraft (ISEE-1, ISEE-2) separated by ∼130 km.

Fig. 16

Left: Three vector components and magnetic field magnitude during a period of diffuse ion fluxes. Right: Magnetic field z component at two spacecraft showing a discrete wave packet. From Hoppe et al. (1981)

Le and Russell (1992) have performed a statistical analysis in order to determine the forward boundary of the upstream ULF foreshock. For large (i.e., greater than 45^∘) IMF cone angles between the IMF and solar wind direction the ULF foreshock boundary is well defined and is given by the trajectory of a backstreaming ion with a velocity of ∼1.4v _sw along the interplanetary magnetic field IMF or a net guiding centre velocity of ∼1.7v _sw in the Earth’s frame. At small IMF cone angles the ULF foreshock boundary is less well defined. Typical wave power spectra in the diffuse ion region are shown in Fig. 17 from Le and Russell (1992). Terasawa (1995) has pointed out that in the region of the resonance frequency of a 40 keV proton (∼0.02 Hz) the power spectral exponent is positive, i.e., the power at the resonance frequency of He⁺⁺ of the same energy per charge (∼0.014 Hz) is smaller. The correlation between the energy density in diffuse upstream ions and the wave energy density of upstream waves has been investigated for two events by Moebius et al. (1987), and on a statistical basis by Trattner et al. (1994). The self-consistent theory of the coupling between the hydrodynamic waves and diffuse ions (Lee 1982) predicts a linear relationship between the energy density in the upstream waves W _B and the diffuse ion energy density W _p , i.e., W _B =βW _P , where the coefficient β depends on the upstream and downstream plasma densities and is proportional to the inverse of the Alfvén Mach number of the bow shock, M _A (see below). Trattner et al. (1994) have compared the measured wave energy density with that predicted by the self-consistent theory from the measured particle energy density and obtained a high correlation (correlation coefficient 0.89). They separated the power in the waves into transverse and compressive parts, and found that the transverse part is by almost an order of magnitude larger than the compressive part. This is at variance with the results reported by Paschmann et al. (1979) and Hoppe et al. (1981). The different results may be due to differences in distance from the bow shock where the measurements have been taken, i.e., compressive waves may predominantly exist closer to the shock.

Fig. 17

Magnetic field power spectra (each from 32 min magnetic field data) during a long lasting upstream diffuse particle event (from Le and Russell, 1992)

Close to the bow shock in the quasi-parallel regime very large amplitude, almost monolithic, structures are frequently observed. Figure 18 shows the magnetic field magnitude data from two spacecraft illustrating examples of this type of structure. Giacalone et al. (1993) found a correlation between the appearance of large amplitude pulsations and changes of the suprathermal particle pressure. From the temporal profile of the pressure a spatial profile relative to the large amplitude structure was deduced. The results are indicative that the pressure gradient in diffuse upstream ions may be responsible for the growth of the magnetic structures.

Fig. 18

Magnetic field magnitude time series plot showing two large amplitude magnetic structures. From Schwartz et al. (1992)

3.4 Simulation of Ion Acceleration at Quasi-parallel Shocks

The standard method to model numerically the structure of collisionless shocks is to follow trajectories of individual macro-particles in space and time and to solve simultaneously the electromagnetic equations. In the hybrid method only the ions are macro-particles; the electrons are treated as a (usually massless) fluid; the electric field is obtained from the momentum equation of the electron fluid. The advantage of this method is that temporal and spatial scales on the order of the electron scale can be neglected. The simulation can cover larger spatial systems and can be performed for longer times. On the other hand details at the electron scale, like high-frequency waves in the foot of the shock, details of the shock ramp structure, etc, cannot be resolved. Full particle simulations, where the electrons are also treated as macro-particles, have to be performed in order to resolve electron spatial and temporal scales. In this case, conventionally called particle-in-cell (PIC) simulation, a Poisson equation for the potential has to be solved in order to obtain the electric field. Since the investigation of quasi-parallel shocks involves large upstream scales, simulations of these shocks have mostly been performed with the hybrid method.

Detailed hybrid simulations of the quasi-parallel shock have shown that ions backstreaming from the shock are responsible for the generation of upstream waves which are convected back into the shock (e.g., Burgess 1989b; Scholer and Terasawa 1990; Krauss-Varban and Omidi 1991; Scholer and Burgess 1992). The question arises whether in such simulations upstream ions reach high energies, i.e., whether the self-consistent hybrid simulations do indeed result in energetic upstream ions, as predicted by diffusive shock acceleration theory. Hybrid simulations of quasi-parallel shocks have indeed resulted in energetic diffuse upstream particles. Because of computer restrictions, early hybrid simulations had to be performed with rather small numbers of ions per grid. Since the total number of diffuse ions is expected to be only a few percent of the solar wind and since the distribution function of diffuse energetic ions falls off rapidly with energy, even sampling over a large number of upstream grids did not allow the evolution of the distribution function to the higher energy range. There are two ways to overcome this numerical problem. Method A uses particle splitting: each time a particle’s energy exceeds for the first time a pre-defined energy threshold it is split into two different particles, and the contribution of the two particles to the moments are adjusted to preserve total particle number. The new particle is either placed at the same position x and the velocity v is slightly changed to $\mathbf {v}+\mathbf {\delta v}$ where $\mathbf {\delta v}$ describes a small randomly oriented vector, or the particle is placed at a random position in the same cell as the original particles. Method B uses the fact observed in simulations of quasi-parallel shocks that the majority of upstream ions originate from the outer shell in velocity space of the incident solar wind distribution. Enhancing the number of particles in this slightly suprathermal regime by some factor, and at the same time reducing correspondingly their contribution to the moments, increases the statistics of high energy upstream ions. Method A was used in a one-dimensional hybrid simulation of an exactly parallel shock with Alfvén Mach number 6.4 by Giacalone et al. (1992). These authors also superposed on the background magnetic field a spectrum of Alfvén waves. The rationale for introducing such a seed turbulence is to study the multiple interaction of the diffuse ions with the shock. Without an injected wave spectrum, the backstreaming ions must first create the resonant waves from intrinsic simulation noise before the scattering process will become efficient. Figure 19 shows upstream and downstream energy spectra in the shock frame for simulations with and without added seed waves. Shown is differential density dN/dE versus ram energy of the plasma $E_{p} = (1/2)m_{i}U_{1}^{2}$ where U ₁ is the bulk speed relative to the shock (in units of the Alfvén velocity). The high energy tail extends to 100 E _p and the downstream spectrum of the diffuse ions can be fitted in the low energy part by a power law with an exponent of −1.5. Method B was used in a one-dimensional hybrid simulation of a quasi-parallel shock with Alfv́en Mach number ∼5 by Scholer (1990). An important question in shock acceleration theory is how and why a certain part of the upstream plasma distribution is injected into a first-order Fermi acceleration process. These early simulations have already shown that a part of the ions gains initially large energies by staying at the shock and gyrating in the magnetic field in phase with a wave electric field. Figure 20 shows the trajectory of one solar wind ion in the time versus x plane (left hand side) and in time versus energy (right hand side) (Scholer 1990). Note that these simulations are usually done in the downstream rest frame, so that the shock moves from right to left in the simulation frame. The line going continuously from right to left is the position of the shock ramp. The particle stays close to the shock for an extended time period and gains a large amount of energy (∼300(v/v _A )²/2). A second point to notice is that this particle does not penetrate far downstream before being injected into an acceleration process. This has been shown by quasi-parallel shock simulations to be true for the majority of diffuse upstream ions: they are accelerated in a one-step process at the shock ramp up to about 10 times the shock ram energy, and these ions do not come from downstream of the shock overshoot (e.g., Kucharek and Scholer 1991; Trattner and Scholer 1991; Scholer et al. 1999). This single step process accelerates H⁺ and He⁺⁺ to about the same energy per charge. Figure 21 shows a histogram of number of ions (protons: solid line; He⁺⁺: dashed line) versus energy per charge when the ions cross the first time a boundary immediately (10 ion inertial lengths) upstream of the ramp. One can clearly see that the first step acceleration process leads to an ordering in energy per charge.

Fig. 19

Upstream and downstream energy spectra (differential density versus ram energy in the upstream solar wind frame) with and without added seed turbulence. From Giacalone et al. (1992)

Fig. 20

(Left) Time versus position x of a particle which gains a large amount of energy. Also shown is the position of the shock in the downstream rest frame (straight line). (Right) Time versus particle energy. From Scholer (1990)

Fig. 21

Histogram of number of ions (protons: solid line; He⁺⁺: dashed line) versus energy per charge when the ions cross the first time a boundary immediately (10 ion inertial lengths) upstream of the ramp. From Scholer et al. (1999)

The spectra shown in Fig. 19 exhibit a cut-off toward higher energies as observed at Earth’s bow shock. This can be due to two limitations of shock simulations. The particle simulation method, either as hybrid or full particle method, sets up a shock in a finite spatial system where the plasma enters from one side, say the left hand side. The shock is either produced by a piston at the right hand side so that the shock moves to the left, or it can be generated by initially imposing a shock-like solution within the box which satisfies the Rankine-Hugoniot relations. In either case accelerated ions are allowed to leave the simulation system at the upstream boundary; this upstream boundary of the simulation domain is thus called a free escape boundary (FEB). The second limitation in treating shock acceleration with particle codes is that the shock, and consequently also the acceleration process, is followed in time. One may hope that running the simulation long enough one eventually obtains the result for a steady state. The effect of a FEB on the distribution of accelerated particles can easily be seen when comparing the parallel mean free path with the distance L _FEB from the shock to the FEB: once the mean free path equals L _FEB particles are no longer scattered back to the shock and do not participate in acceleration. Giacalone et al. (1997) have solved the Parker equation for diffusive acceleration in a system with a FEB and have shown that the cut-off momentum p _c is determined by U ₁ L/κ ₁(p _c ), where κ ₁(p _c ) is the upstream diffusion coefficient and U ₁ is the upstream plasma velocity, i.e., at the bow shock the solar wind velocity U ₁=v _sw . Time dependent solutions for diffusive particle acceleration at shocks have been derived by Forman and Morfill (1979) and Axford (1981a, 1981b). The time scale τ _acc (p _c ) for acceleration of particles of momentum p _c at a planar shock is given by

$$ \tau _\mathit{acc}(p_c) = {3\over{U_1-U_2}} \biggl[{\kappa _1\over U_1}+{\kappa _2\over U_2}\biggr] , $$

(4)

where U ₁ and U ₂ are the upstream and downstream flow velocities and κ ₁ and κ ₂ are the upstream and downstream diffusion coefficients, respectively. For times smaller than τ(p _c ) the cut-off momentum is determined by time dependence and is still evolving, while for times larger than τ(p _c ) the cut-off momentum is determined by the FEB. In the simulations by Giacalone et al. (1992) the cut-off of the spectra (Fig. 19) is due to a FEB.

Figure 22 shows the ion partial densities (normalized to the upstream density) in different energy bands (Giacalone et al. 1993). At energies below ∼5E _p (E _p =ram energy) there are very few upstream accelerated particles; the partial densities begin to appear upstream for E>10E _p indicating an extraction energy threshold. At higher energies the density falls of exponentially from the shock in the upstream direction with an e-folding distance that increases with energy, as expected from steady state diffusion theory. The e-folding distance L obtained in the simulation allows determination of the diffusion coefficient or the mean free path, respectively. Figure 23 shows the mean free path versus energy determined by a fitting of the spatial profiles to exponential functions (Giacalone et al. 1993). Over a limited energy range the mean free path can be approximated by a power law λ=3(E/E _p )^1/2 L _e (E). This diffusion coefficient can be compared with the diffusion length scale obtained from quasi-linear theory. In quasi-linear theory the energy dependence of the diffusion coefficient is determined by the spectral slope of the wave power spectrum, P∝k ^−δ. From the power spectral exponent δ∼1.4 over a limited wave vector range k, Giacalone et al. (1993) have obtained an energy dependence of λ∝(E/E _p )^0.3, close to that obtained from the spatial profiles.

Fig. 22

Densities of ions with energies indicated at the left as a function of position. Numbers at the right represent the peak intensity in that particular frame. From Giacalone et al. (1993)

Fig. 23

Ion diffusion lengths calculated by fitting the partial density profiles to exponential functions versus energy. From Giacalone et al. (1993)

The FEB results naturally in an exponential-like spectral cut-off. However, a FEB is an artifact introduced in shock simulations because of the finite extent of the simulation system. In particular, it is highly problematic to assume the same distance from the shock to the free escape boundary for particles of all energies, as it is done in hybrid simulations. As outlined above, time-dependent acceleration is expected to lead to spectra with a high energy cut-off. Over a limited energy range such spectra can be represented by an exponential. Time dependent acceleration is expected at the bow shock due to the time of connection of a field line with the shock in the case of a non-radial interplanetary magnetic field. Figure 24 shows results of the temporal development of particle spectra as obtained from hybrid simulations. Plotted is the differential intensity dn/dv, where n(v) is the number density, versus E in units of ram energy in a log versus linear representation (Scholer et al. 1999). In these simulations a wave field has been initially superimposed with a k ^−1.5 spectrum and a total integrated spectral power of ϵB ² within a wavelength region ranging from 5 to 400 ion inertial lengths. In Fig. 24 the spectra are plotted in a log versus linear representation. The left hand side shows downstream spectra at a certain time ($t=600\varOmega _{c}^{-1}$ corresponding to about 600 sec at 1 AU) for different levels of superimposed total power ϵ in the fluctuations. The right hand side shows the development of spectra with time for one particular total power (ϵ=0.2) in the fluctuations. The time of connection of an interplanetary magnetic field line with the bow shock, the level of background, not self-excited turbulence, and the shock Mach number will all strongly influence the spectra of diffuse ions upstream of the bow shock.

Fig. 24

(Left) Flux distribution downstream of a M _A =4.1 shock at $t=600\varOmega _{c}^{-1}$ Different levels of initially superimposed fluctuations have been used (ϵ=0, 0.2, 0.6). (Right) Temporal development of the flux distribution at a M _A =5.4 shock with ϵ=0.2. From Scholer et al. (1999)

A simulation method which has also been widely used in shock acceleration physics, but which is different from the self-consistent macro-particle method, is the Monte Carlo method first introduced by Ellison (1981). In the Monte Carlo method the collective processes responsible for a shock in a collisionless plasma are not calculated in detail by solving the combined Vlasov equation and Maxwell equations, but instead the shock is calculated from a steady state Boltzmann equation for the distribution function with a collision operator (∂f/∂t) _coll that models the scattering due to the hydromagnetic fluctuations. More specifically, the shock is modelled by having all ions, including the ions responsible for creating the shock, scattered isotropically and elastically off a background of massive scattering centres that move with the local flow velocity. It is assumed that all particle scattering can be described with a simple expression, which relates the mean free path to the particle momentum p or rigidity R. Usually, the mean free path is taken to be proportional to some power of the rigidity, λ∝R ^α, where the rigidity R is given by R=pc/Ze (Ze=Q=particle charge). Because κ=λv/3, and since for a fluctuation power spectrum with a k ^−δ power law according to quasi-linear theory κ _∥∝v ^(3−δ), one may associate the spectral exponent α with α=2−δ. In the Monte Carlo simulation method, as in the particle plasma simulation method, the particles are followed in a spatial system of finite size. Thus the upstream boundary where the plasma enters is open and is a free escape boundary for energetic backstreaming ions. However, in contrast to the particle plasma simulation method, the Monte Carlo method calculates iteratively the steady state solutions for the velocity profile and for the particle distribution function upstream and downstream. The Monte Carlo solution is intrinsically a steady state solution and does not incorporate time-dependence. Ellison et al. (1990) have modelled by the Monte Carlo method particle observations at Earth’s bow shock during almost radial interplanetary magnetic field. Figure 25 shows Monte Carlo fits (solid lines) to observed downstream (a), upstream (b), and downstream (c) sequences of observed spectra of protons (filled and open circles), He²⁺ (triangles), and CNO. For the fits it is assumed that the mean free path is proportional to rigidity. Only the upstream velocity U ₁, the distance L to the FEB, and the observation position D _obs are then free parameters. As can be seen the Monte Carlo model fits the spectra of three different species very well. In particular, there are no adjustable parameters for the He²⁺ and C,N,O⁶⁺ fits once U ₁, L and D _obs have been determined by the proton fit. However, it should be noted that with α=1 the diffusion coefficient κ=λv/3∝mv ²/(Ze)∝E/Q becomes independent of mass and is proportional to energy per charge. With the same location of the FEB for all ions it is not surprising that the spectra of different ions are identical in energy/charge.

Fig. 25

Monte Carlo fits (solid lines) to observed downstream (a), upstream (b), and downstream (c) sequences of observed spectra of protons (filled and open circles), He²⁺ (triangles), and C,N,O⁶⁺. From Ellison et al. (1990)

A comparison of spectra obtained by hybrid simulations and by the Monte Carlo method compares favourably well when the power law dependence for the mean free path on momentum obtained from the hybrid simulation is used for the Monte Carlo simulation. Figure 26 from Ellison et al. (1993) compares downstream (left) and upstream (right) spectra obtained by the two different methods. In the downstream region the distributions obtained by the Monte Carlo method (solid lines) and by the hybrid method (dashed lines) track each other fairly well. There is an excess of suprathermal particles in the Monte Carlo result. This is probably due to the fact that the Monte Carlo does not treat injection self-consistently. In the upstream region the Monte Carlo method overemphasizes shock mediation in front of the sub-shock: already ∼5λ ₀ before the shock transition the velocity begins to decrease (λ ₀ is the mean free path of a proton with upstream flow speed in the local frame). The distribution by the Monte Carlo method at ∼0.4λ ₀ upstream (dotted curve) does not agree with the spectrum obtained by the hybrid code at the same distance. The comparison can be improved by taking a spectrum from the Monte Carlo simulation further upstream (e.g., at ∼3λ ₀ upstream). Compared to the self-consistent method the Monte Carlo method overemphasizes shock mediation and fails to describe quantitatively the injection in the suprathermal energy range, but gives quite good results for spectra and acceleration efficiencies at higher energies.

Fig. 26

(Left) Flux distributions for protons, helium, and oxygen ions downstream from the shock. The solid lines are from Monte Carlo simulation, while the dashed lines are from a hybrid simulation. (Right) Flux distributions calculated upstream from the shock. From Ellison et al. (1993)

3.5 Injection

From the early observations of field-aligned beams, intermediate ion distributions, and diffuse ions in the foreshock region it was suggested that the FAB from the quasi-perpendicular shock evolve, as the magnetic field lines convect along the shock into the quasi-parallel regime, through intermediate distributions into diffuse distributions which can then be seed particles for further Fermi acceleration (e.g., Bame et al. 1980). However, when the IMF cone angle is close to zero degrees and no suprathermal particles from the quasi-perpendicular shock can be convected into the quasi-parallel regime diffuse ions are still observed (Ellison and Moebius 1987). Furthermore, compositional measurements in FAB do not compare favourably with the composition in diffuse events, so that the FAB origin was ruled out (Ipavich et al. 1988; Fuselier and Thomsen 1992). Recently Kis et al. (2007) have reported observations of upstream ions during a time period when the spacecraft was connected due to changes of the IMF direction alternately with the quasi-perpendicular and the quasi-parallel bow shock. They found high intensity FAB in the quasi-perpendicular regime and remnants of pitch-angle scattered beams in the quasi-parallel regime together with diffuse ions, so that a contribution of FAB ions to diffuse ions under certain conditions cannot be ruled out. After the discovery that the quasi-parallel bow shock also specularly reflects solar wind ions (see Fig. 8) it was postulated that the seed particles for diffusive ion acceleration are specularly reflected ions (Fuselier 1995). These supposedly develop into gyrophase-bunched distributions and later into ring-type distributions which are eventually isotropized and can be the seed particles for subsequent Fermi acceleration. The self-consistent simulations, either hybrid or full particle simulations, have shown that diffuse ions emerge in a first acceleration process from the shock ramp so that there is no need for such a three step process, i.e., specularly reflected ions—gyrophase-bunched ions—diffuse ions. However, a wider parameter regime study, e.g., over θ _Bn , is probably required to fully evaluate the relative importance of this mechanism.

Two scatter-free models for injection of thermal solar wind ions into a shock acceleration process have been developed. The first model by Sugiyama and Terasawa (1999) relies on the consecutive motion of a particle in large-amplitude Alfvén waves upstream and downstream of the shock. In a monochromatic wave the particle velocity components can change in time, but the energy is conserved in the wave phase velocity frame and the particle moves upstream and downstream in v _⊥−v _∥ space on a circle centred at the wave phase speed. In the upstream region a circularly polarized large amplitude polarized wave has a large downstream directed phase velocity, whereas downstream the phase velocity is considerably smaller. A particle moving downstream can have its parallel velocity changed in the wave (under conservation of energy) and subsequently moves upstream. Here the energy is again conserved, but the parallel velocity changes by interaction with the wave so that eventually the velocity points upstream again. Figure 27 shows how by moving on circles in v _⊥−v _∥ space centred at the upstream and downstream phase velocities of the waves the particle successively gains perpendicular energy, while the parallel velocity changes from positive to negative values around zero, and vice versa. This is different from scattering by upstream and downstream scattering centres in that there is always a net energy gain during this process. Test particle calculations of the particle-wave interaction process in circularly and elliptically polarized large-amplitude monochromatic waves have been presented by Sugiyama et al. (2001).

Fig. 27

A particle staying near the shock surface in the upstream and downstream region. The particle moves in v _⊥−v _∥ space on circles centred at the upstream (solid lines) and downstream (broken lines) phase velocity. From Sugiyama and Terasawa (1999)

Kuramitsu and Krasnoselskikh (2005a, 2005b) also investigated particle motion in a circularly polarized monochromatic wave. However, in their model the particle stays upstream and is in cyclotron resonance with the wave ω−kv _x −Ω _c =0 where k is the wave number, ω is the wave frequency, and Ω _c is the ion cyclotron frequency. Due to the Lorentz force by the wave magnetic field the particle’s parallel velocity v _x would change and the particle would, in principle, go out of resonance, but the resonance condition can be enforced by applying a suitable electric field in the parallel x direction such that the Lorentz force in the x direction is balanced by the electric potential. The x component of the particle’s velocity then does not change and the particle gains energy by the wave electric field perpendicular to the magnetic field. The mechanism is thus called gyroresonant surfing. The electric field at the shock is given by the cross-shock potential. The form of this electric field would not result in strict enforcement of the resonance condition. However, Kuramitsu and Krasnoselskikh (2005b) have shown that for finite amplitude waves particles around the resonance condition can be trapped and in the case of large amplitude waves even non-resonant particles can be trapped. Thus the gyroresonant surfing can operate in the presence of a wider class of potential fields, i.e., also in a shock-like potential.

A different approach to the injection problem has been taken by Ellison and co-workers (e.g., Ellison and Moebius 1987; Ellison et al. 1990, 1993). These authors assumed that all particles, thermal and nonthermal, are scattered by some parameterized pitch angle diffusion process. This leads to spatial diffusion of downstream heated particles across the shock upstream, which can then be further accelerated by a Fermi mechanism. The assumption originates from the need to describe with a Monte Carlo method the shock as well the energetic particle population. Without specifying the origin of the waves responsible for the scattering, the parameters of this model can successfully be fitted to observations. Pitch-angle scattering in the low energy regime, i.e., at energies in the region where the particle velocity is comparable to the solar wind velocity, has been put on firmer theoretical grounds in terms of a quasi-linear description by Malkov and Voelk (1995). Based on this they have developed a model for the process of particle leakage of the heated downstream plasma, the upstream generation of MHD waves by this escaping beam of hot ions and the upstream pitch-angle scattering of these ions. Malkov (1998) has developed a model which treats injection and shock dissipation as an intimately connected process. The model assumes that particles from the hot downstream distribution with upstream directed velocities larger than the shock velocity escape upstream. These ions constitute a beam which excites a circularly polarized MHD wave. The wave is convected downstream and the amplitude increases by the shock compression. This has the effect that downstream the bulk of the thermal particles are trapped in the wave and are swept downstream. Part of the particles are untrapped in the large amplitude MHD wave and can escape upstream. The region of untrapped phase space in the downstream wave can be filled with trapped particles due to a postulated additional weak downstream turbulence: such weak turbulence can quickly randomize particle motion when superposed on a regular wave by phase mixing. The fraction and energy distribution of upstream escaping particles is then calculated as a function of the downstream wave amplitude. On the other hand, the beam density determines the upstream wave amplitude so that finally the beam density as well as the wave amplitude can be obtained.

Self-consistent particle simulations of quasi-parallel shocks have shown that thermal particles are indeed injected into a Fermi acceleration process without making any additional assumptions. As described earlier, these simulations set up the collisionless shock by reflecting a thermal distribution off a (right side) rigid wall. The simulation frame is then the downstream rest frame, and the shock moves to the left of the simulation regime, where a FEB is assumed. Large spatial system have to be used to run the shock for a long time and to have still a large distance to the FEB. Such large system simulations have been reported by Giacalone (2004), with distances to the FEB of 28,000 ion inertial lengths, and recently by Sugiyama (2011), with a distance of 200,000 ion inertial lengths. Hybrid simulations have shown that a large part of the particles are accelerated at the shock in a first step to considerable energies. Figure 28 shows in the upper left part from a 1-D hybrid simulation the position of the shock (in the downstream rest frame) as a function of time as a red line. The black line is the position of a solar wind proton which reaches the shock, stays at the shock for an extended period, and leaves the shock upstream. To the right is shown the particle’s energy (in units of shock ram energy) and with red and blue at times when the wave electric field is parallel or anti-parallel to the particle’s velocity. The bottom panel shows the motion of the particle in v _⊥−v _∥, where v _∥ is in the shock frame. This particle gains a high energy in a one step process which is very similar to the one described by Sugiyama and Terasawa (1999) of a particle being trapped in two waves with different phase velocities. In a 1-D hybrid simulation Kucharek and Scholer (1991) traced all solar wind ions that became diffuse upstream ions backward in time. Figure 29 shows the trajectories of these particles in x−t space in the downstream rest frame. The straight lines going to the right are the trajectories when these particles were still solar wind particles. The black area which arises from the superposition of all trajectories, is clearly separated from the downstream region to the right, i.e., no trajectory enters the white area. This demonstrates that the upstream diffuse ions are hardly due to downstream leakage.

Fig. 28

Upper left position of the shock (red line and position of a solar wind proton black line) as a function of time. Upper right: the particle’s energy (in units of shock ram energy). Red and blue are times when the wave electric field is parallel or anti-parallel to the particle’s velocity. Bottom panel: motion of the particle in v _⊥−v _∥, where v _∥ is in the shock frame. After Scholer et al. (2000)

Fig. 29

Trajectories of diffuse upstream particles obtained by a hybrid simulation of a quasi-parallel shock in the downstream rest frame in x−t space. From Kucharek and Scholer (1991)

3.6 Global Hybrid Simulations

The e-folding distance of upstream diffuse ions at Earth’s bow shock is of the same order as the size of the bow shock itself. This makes the applicability of 1-D simulations, which assume a planar shock of infinite lateral extent, questionable. Furthermore, the shock normal angle θ _Bn changes around the bow shock; the spatial scale of this change is again of the order of the e-folding distance of diffuse ions. Finally, the upstream region of the quasi-perpendicular part may have a large influence on the quasi-parallel part so that results from a pure quasi-parallel shock simulation have to be considered with caution. Omidi et al. (2005) and Blanco-Cano et al. (2006) have investigated the global structure of a curved bow shock with 2-dimensional hybrid simulations. They used a two-dimensional magnetic dipole which sits in a solar wind stream; a magnetosphere and bow shock is formed by the solar wind-dipolar field interaction. The critical parameter in these simulations is the distance between the nose of the magnetopause and the dipole centre, D _P , in units of the ion inertial length c/ω _pi of the solar wind. At 1 AU this value is for Earth’s magnetosphere ∼600. Due to restrictions in computer resources, Omidi et al. (2005) have performed 2-D simulations up to a value of D _P ∼64, i.e., the numerical system is scaled down relative to the real magnetosphere by a factor of ∼10. In these simulations, the sinusoidal parallel propagating waves and the compressional waves do not occur in the same region. For an interplanetary magnetic field that makes a 45^∘ angle with the x axis sinusoidal waves are found on field lines connected to the more oblique (θ _Bn ∼45^∘) bow shock closer to the nose while the compressional oblique propagating waves are seen more to the flank. According to Omidi et al. (2005), the parallel sinusoidal waves and the oblique compressional waves are not connected and are due to different backstreaming particle populations. It is suggested that upstream of the more oblique bow shock beams excite the sinusoidal waves by the right hand resonant beam instability, while the compressional waves in the more parallel regime are due to ring beam distributions originating from the reflection at the more parallel bow shock. Scattering of the ring beam distribution then results in more diffuse distributions (Blanco-Cano et al. 2006). Thus the 2-D global hybrid simulations support the suggestions by Fuselier (1995) that injection into the Fermi process is due to ring beam distributions originating at the quasi-parallel shock. There is clearly a discrepancy between the origin of diffuse ions as obtained from 1-D and 2-D simulations at a planar quasi-parallel shock versus 2-D global simulations, which is not yet resolved. A future challenge is that global simulations need a better spatial resolution. Omidi et al. (2005) and Blanco-Cano et al. (2006) used a resolution of one ion inertial length c/ω _pi per grid and a rather small value of D _P , and applied the results of the simulations to the Earth’s bow shock. With a realistic value of D _P , i.e., an order of magnitude larger, the shock may locally become close to planar and the results from 1-D and 2-D simulations of planar shocks may again be valid. Also 2-D simulations of quasi-parallel shocks should be carefully analyzed for the existence of backstreaming ring type distributions.

3.7 Self-consistent Theory of Diffusive Bow Shock Acceleration

Steady state diffusive acceleration theory at a planar shock predicts a spectrum at, and downstream of, the shock which is independent of the spatial diffusion coefficient. However, the dependence of the distribution function on the distance upstream (and the time in order to reach a steady state below a certain energy) depends on the spatial and momentum dependence of the diffusion coefficient. The simulations of quasi-parallel shocks have shown that the backstreaming ions excite low frequency waves, which in turn scatter the particles in pitch angle. Particles scattered through 90^∘ pitch angle are turned back toward the shock and participate in diffusive acceleration. The production of waves by the streaming of the particles relative to the solar wind, the pitch angle scattering of the particles by these waves, the resulting spatial diffusion coefficient, and diffusive acceleration by compression at the shock are intimately connected. The coupled hydromagnetic wave excitation and ion acceleration at a shock was first described by Bell (1978). Lee (1982, 1983) has derived in detail the self-consistent theory of wave excitation at the Earth’s bow shock and at interplanetary travelling shocks within the framework of quasi-linear theory. The self-consistent theory by Lee (1982, 1983) was later revised by Gordon et al. (1999). The self-consistent theory starts from a wave kinetic equation where the wave growth/damping is described by a growth rate γ, which depends on the derivative of the distribution function with respect to pitch angle. Using an integrated form of the pitch angle diffusion equation, this derivative can be expressed in terms of the pitch angle diffusion coefficient D _μμ and the spatial derivative of the distribution function along the magnetic field. The pitch angle diffusion coefficient is determined by the wave intensity. One thus ends up with a differential equation in x for the wave intensity I, which contains the spatial derivative of the distribution function ∂f ₀/∂x. The wave intensity I is written as the sum of two intensities, I=I ₊(k)+I ₋(k). Here I ₊(k) is the intensity of waves propagating in the $+\hat{e} _{b}$ direction ($\hat{e} _{b}$ is a unit vector parallel to the magnetic field in the upstream direction) with either right hand (k>0) or left hand (k<0) polarization for B ₀>0. For B ₀<0 the polarizations are reversed. Correspondingly I ₋(k) is the intensity of waves propagating in the $-\hat{e} _{b}$ direction with either left hand (k>0) or right hand (k<0) polarization for B ₀>0 and reverse polarizations for B ₀<0. This equation has to be solved together with the Parker equation for f to describe diffusive shock acceleration, which contains the spatial diffusion coefficient. The spatial diffusion coefficient is given by a μ integration of a function which contains the pitch angle diffusion coefficient. This results finally in a complicated system of integro-differential equations. In order to solve this system assumptions have to made about the boundary conditions, i.e., the wave intensities at x→∞. Since interplanetary waves are predominantly propagating outward from the Sun, Lee (1982) assumed that $I_{+}^{0}=I_{+}(k,x\rightarrow\infty )\simeq 0$, whereas $I_{-}^{0}$ is finite and represents the background intensity. Furthermore, in order to obtain the exponential spectra of diffuse ions observed at the bow shock Lee (1982) has included in the transport equation diffusion perpendicular to the magnetic field. This leads to a loss of the particles at the flanks of the bow shock where field lines do not connect anymore with the shock. Assuming this loss to be at a radial distance r=(y ²+z ²)^1/2=a and assuming the perpendicular diffusion coefficient to be independent of r, the lateral dependence of f on r can be described by J ₀(ξ ₁ r/a), where J ₀ is the Bessel function of order 0 and ξ ₁ its first zero. The perpendicular diffusion coefficient is assumed to be given by

$$ \kappa _\perp \approx {v^4\over{3\varOmega _c^2}}{1\over \kappa _\parallel} . $$

(5)

This form of κ _⊥ is based on the assumption that a particle random walks normal to the magnetic field with a step length of one gyroradius r _g =v/Ω _c for each reversal of the direction along the magnetic field, i.e., $\kappa _{\perp}=r_{g}^{2}/(\lambda v^{-1})$ with the mean free path λ=κ _∥ v/3. For an injection rate of N particles with velocity v ₀ at the shock Gordon et al. (1999) have constructed approximate analytic and numerical solutions for the wave intensity and for the ion distribution function as functions of distance from a planar shock. These solutions depend on the assumption for the k dependence of $I_{+}^{0}(k)$, the input wave spectrum far upstream. There are corrections to the wave intensity at the shock for interplanetary travelling shocks and the bow shock compared to the earlier work by Lee (1982, 1983), which are important when comparing the wave magnetic energy density with the energy density of the energetic protons. In Lee’s (1982) theory the form of the distribution function for large velocities is dominated by an exponential function $\exp [-E_{s}Q_{s}^{-1}\sigma ^{-1}]$ where E _s =(1/2)m _s v ² is the kinetic energy of an ion of species s and σ is a constant independent of species. Thus the spectra at high velocities are exponentials in energy per charge with the same e-folding energy σ. The e-folding energy σ is directly proportional to the lateral extent a of the acceleration region; for characteristic values of the shock transition σ is given by σ (keV)∼2.2a (R_E). Figure 30 shows proton (left) and He⁺⁺ (right) differential intensity spectra in a log versus linear representation at various distances in front of the shock in units of R_E; here a is assumed to be 10 R_E. The spectra of protons and He⁺⁺ are close to exponentials and are identical in shape at the shock (z=0), but exhibit a more complicated behaviour at other distances. The self-consistent theory also predicts a linear relation between the energy density in the upstream waves W _B and the total energy density in the diffuse ions W _p . Gordon et al. (1999) have re-evaluated the relation between W _B and W _p , taking also into account that the angle between the flow direction of the solar wind and the direction of the energetic particle density gradient differ around the shock.

Fig. 30

Proton (left) and He⁺⁺ (right) differential intensity spectra (from 0 to 150 keV/Q) in a log versus linear representation at various distances (0, 2, 7, 40, and 200 R_E from the shock) in front of the shock in units of R _E . From Lee (1982)

3.8 Exponential Spectra: An Assessment of Different Theories

The near exponential spectra of upstream diffuse ions with the same e-folding energy per charge of particles with different charge states is a key observation and has to be explained by any successful theory of diffusive acceleration at Earth’s bow shock.

1. The self-consistent quasi-linear theory explains the exponential spectra by perpendicular diffusion and loss to the flanks at unconnected field lines (Lee 1982). The independence of the e-folding energy per charge for ions of different mass and charge states hinges on the assumption that κ _⊥ κ _∥ is a function of energy per charge, κ _⊥ κ _∥∝(E _s /Q _s )² for each species s (see also Eichler 1981). Wibberenz et al. (1985) have analyzed parallel and perpendicular anisotropies during the rise, plateau, and decay phase observed during long-lasting diffuse upstream particle events. The perpendicular anisotropy results in a lateral extension of a=8.5 R_E, and from the intensity variation with distance from the bow shock a e-folding distance of L _e =6.5 R_E (at ∼30 keV) was derived. Since the ratio of the parallel to perpendicular diffusion coefficient is related to the ratio of the spatial scales parallel and perpendicular to the magnetic field this results in a diffusion time τ _⊥ across the distance a of τ _⊥≈1 min. According to Wibberenz et al. (1985) the very large perpendicular gradients during the onset and decay phase of the events are inconsistent with such very efficient lateral diffusion (note that with observed values of a and L _e the ratio κ _⊥ κ _∥∼0.7, i.e., diffusion is almost isotropic). Based on their observations Wibberenz et al. (1985) concluded that lateral diffusion based on the scattering law used by Lee (1982) is not the main escape mechanism determining the energy spectra.

2. The Monte Carlo model predicts exponential spectra; these are due to the assumption of a free escape boundary FEB. The identical e-folding energy per charge for different species seems to be due to the (plausible) assumption of a scattering law with a mean free path being proportional to some small power of rigidity λ∝R ^α. With α=1 the diffusion coefficient is independent of mass and charge, and proportional to energy per charge. It is not surprising that spectra of different species are identical in energy per charge (Ellison et al. 1990). In a comparison between Monte Carlo and one-dimensional hybrid code simulations Ellison et al. (1993) have used α=0.53 in the Monte Carlo simulation (derived from the hybrid simulation) and still obtain spectra of different species which are almost identical in energy per charge. However, it should be noted that also in this case the diffusion coefficients of protons and He²⁺ at the same energy per charge differ by less than a factor 1.2. The assumption of a FEB which for all particles, independent of mass, charge, and energy, is located at the same position upstream is a simplification, if not an artifact, difficult to reconcile with the whole nature of the foreshock region. More importantly, observations (e.g., Childers and Russell 1972; Le and Russell 1992) show that the power spectral exponent in the frequency range for cyclotron resonance with tens of keV per charge particles is positive, i.e., α is negative. It should be noted that this observational result is correctly described by the self-consistent theory of Lee (1982).

3. Time-dependent acceleration results naturally in exponential spectra. The time-dependence is given by the finite time of connection of a field line with the quasi-parallel bow shock. The question arises again why the e-folding energy per charge should be the same for all species. Scholer et al. (1999) found in hybrid simulations that a first step acceleration mechanism at the shock leads already to a spectral ordering in energy per charge; however, the exact mechanism leading to that ordering is unclear. Scholer et al. (1999) have argued that the first step acceleration near the shock ramp is due to the electric field of the upstream and shock produced waves when the tangential velocity of the ion and the tangential electric field are nearly in phase. If both species are trapped near the shock for the same time, He²⁺ gains twice the energy than protons, which is expected to result in an ordering of upstream spectra in terms of energy per charge.

4. Terasawa (1981) developed a model where particles are trapped by scattering within a distance L in the upstream region, but acceleration at the shock is by magnetic mirror reflection at the magnetic field increase in the shock. The argument for mirror reflection is that the mean free path near the shock is larger than the scale of the shock transition region. The spectrum is determined by the combination of acceleration by mirror reflection and trapping with a trapping coefficient proportional to the inverse of the diffusion coefficient. The relative energy increase ΔE/E due to mirroring is the same for particles of the same velocity, i.e. of the same energy per mass E/m. The relative energy increase by mirroring of particles with the same energy per charge is thus larger for particles of larger mass. On the other hand it is assumed in Terasawa (1981) that the diffusion coefficient at the same energy per charge increases with mass per charge, i.e., the trapping efficiency decreases. Both effects cancel each other and the spectral e-folding energy per charge becomes about the same for different species. We note that from Kronberg et al. (2009) the e-folding distances of protons and He²⁺ of the same energy per charge, and thus the diffusion coefficients, are about equal, i.e., there is no indication in the data that the trapping efficiency of different mass to charge particles at the same energy per charge is different.

In conclusion, the mechanism leading to exponential spectra of diffuse ions at Earth’s bow shock with the same e-folding energy per charge for different species is, after their discovery more than three decades ago, still unclear and further work is needed.

4 Concluding Remarks

The study of particle acceleration at the Earth’s bow shock is dominated, as this review demonstrates, by work done some years ago. The ISEE mission of the late 1970s and 1980s was a tremendous step forward, and results found at the period remain key to understanding the observational challenges and theoretical constraints. However, there still remain important, and in some cases fundamental, issues in this area, and we list just some of them here as pointers to future work.

1. What is the importance of scattering in the acceleration of field-aligned beams, and what is the scattering source? Recent work (e.g., Meziane et al. 2011) has revealed behaviour which seems anomalous within the simple models, but to what extent does this invalidate those models? To answer these questions two or three-dimensional shock simulations could provide answers, but the role of the shape, global morphology and finite size of the bow shock may play a role which is just as important.

2. The Earth’s bow shock is often invoked as an example which demonstrates that diffusive acceleration is viable and important. But explaining the observed exponential spectra of diffuse ions is still an open problem, with three competing explanations: free escape, time dependence and cross-field diffusion. Also, as discussed above, the exponential spectra being the same at the same E/Q is also an open issue.

3. The observations of diffuse ions seem to show that the Earth’s bow shock can efficiently take ions from the incident thermal distribution up to energies usually considered for injection into acceleration mechanisms. But what the precise mechanism is, or rather what the relative importance of different mechanisms are remain undecided. Is there a downstream “thermostat” process as suggested in models by Malkov, or is the scattering responsible at higher energies operating all the way down to thermal energies as in the Monte Carlo models of Ellison? Should individual trajectory interactions be considered as in the models of Sugiyama & Terasawa or Kurumitsu & Krasnoselskikh? Or are specular reflected ions and their subsequent phase-bunching the explanation? High time resolution observations and more realistic simulations will probably be able to begin to answer these questions.