1 Introduction

In studying the numerical solution of the linear electrostatic Vlasov dispersion equation in an unmagnetized, geneous plasma, the authors of Ref. [1] became aware of the electron acoustic mode. In addition to the well-known Langmuir and ion acoustic waves, they observed the existence of a heavily damped acoustic-like solution of the dispersion equation. Later, it was shown that in the presence of both hot and cold electrons as well as the immobile ions, one indeed obtains a weakly damped electron acoustic mode [2], the properties of which significantly differ from those of the Langmuir waves. Dubouloz et al. [3], in studying the propagation of electron acoustic solitary structures, considered a one-dimensional, unmagnetized collisionless plasma consisting of cold electrons, Maxwellian hot electrons and stationary ions.

However, in practice, the hot electrons may not follow the Maxwellian distribution. The particle distribution in space plasma deviates from the Maxwellian distribution. Intensified ion acoustic solitary waves (IASWs) have been focused basically on Boltzmann distribution of electrons. For macroscopic equilibrium systems the Boltzmann-Gibbs statistics is believed to be adequate [4, 5]. However, a Maxwellian distribution might be inconvenient in dealing with the long-range interacting systems, such as plasma and gravitational systems, where non-equilibrium stationary states exist. Indeed, astrophysical and laboratory plasma observations show that the electron distribution functions are non-Maxwellian, and complicated shapes arise showing high-energy tails. The plasma physics community has used the generalized Lorentzian kappa distribution first recognized by Lima et al. [6] by introducing an parameter q. However, in the limit \(q\rightarrow 1\), the Maxwellian nature is established. The q-nonextensive distribution approach has been used to interpret the data in various space and astrophysical environments like OGO 1 satellite observations of solar wind [7], auroral region [8], etc.

The propagation of small-but-finite amplitude waves in a plasma with one-dimensional electron acoustic model had been studied by several scientists [9,10,11,12,13]. Berthomier et al. [14] showed the existence of electron acoustic waves with two polarity potential in plasma by introducing an electron beam. It was reported that the presence of the electron beam modifies the roots of the dispersion relation. Sahu and Roychoudhury [15] as well as El-Taibany [16] studied the nonlinear propagation of EASWs in the presence of relativistic electron beam with vortex like distribution of hot electrons by employing different approaches. They found that the relativistic effects modify the existence region of solitary waves. Elwakil et al. [17] investigated electron acoustic solitons in an unmagnetized plasma consisting of stationary ions, relativistic cold electrons, nonthermal hot electrons and relativistic electron beam. They derived KdV equation to discuss the effects of relativistic electrons on the solitary wave structures. Ghosh et al. [18] studied electron acoustic solitary waves in a four-component plasma composed of warm magnetized electrons, warm electron beam and energetic multi-ion species with ions hotter than electrons and investigated its applications to boundary layers. Devanandhan et al. [19] examined the arbitrary amplitude electron acoustic solitons with electron beam in an unmagnetized plasma having stationary ions, cold electrons and kappa distributed hot electrons by employing Sagdeev pseudo-potential method. Singh et al. [20] explored the presence of positive as well as negative potential solitons in four-component unmagnetized plasma with electron beam and superthermal hot electrons. Singh et al. [21] also studied the oblique propagation of solitary waves by considering electron beam in magnetized plasma. They derived the two-dimensional Korteweg–de Vries–Zakharov–Kuznetsov (KdV-ZK) equation to study the negative potential solitary structures. It was also shown that the inclusion of obliquity and finite temperature significantly affects the solitary waves. Propagation characteristics of EA waves with beam in unmagnetized plasma having hot superthermal electrons have been investigated by Danekhar [22]. The effect of various parameters of electron beam on the physical properties of nonlinear structures was investigated using pseudo-potential method. It was found that the amplitude of the wave decreases with increasing beam speed and beam density ratio.

In plasma science, shock waves are considered as the most important tools for heating a gas to create plasma. Shocks are formed in a plasma when an initial compressional wave pulse steepens and the steepening is balanced by molecular viscosity of the particles in a medium. This leads to the wave becoming more abrupt and hence, overturn. The overturning of the wave is prevented by the momentum transfer between the faster, denser region of the wave to the slower region ahead of the wave. Molecular viscosity is a property of the medium which is responsible for the momentum exchange and causes dissipation of the wave. When the thickness of the wavefront shrinks to the collision mean free path of the particles, the steepening of wave is balanced by dissipation (via viscosity) and steady shock waves are formed. Numerous researchers have derived the KdV–Burgers equation in different plasma systems [23,24,25,26,27,28] to study shock wave structures. Dutta et al. [29] theoretically investigated the analytical and numerical perspectives of electron acoustic shock waves in collisional plasma. Electron acoustic shock waves in three-component plasma consisting of stationary ions, cold and hot electrons with kappa distribution were investigated by Sultana and Kourakis [12]. The effects of kappa distribution and kinematic viscosity on the existence of solitary waves were numerically investigated and found that kink-shaped excitations are produced with negative potential. Bansal et al. [13] examined the effects of kinematic viscosity, obliqueness and magnetic field on the electron acoustic shock waves in three-component collisionless plasma. The standard reductive perturbation method was used to derive the KdV–Burgers equation. They observed the variation of amplitude, velocity and width of the shock structures with different plasma parameters.

Before we illustrate the nonlinear evolution of electron acoustic waves, we must first write a few lines about the existence of two-electron temperature plasma, which is a requirement for electron acoustic wave propagation. Yu and Luo [30] wrote a fantastic article about the drawbacks of multi-species models as applied to the same mass species. When the two electrons are physically isolated in phase space and there is no possibility of the mixing, it was proposed that the multispecies model makes more sense. They proposed a few possibilities, including particle trapping, that could aid in the development of a reasonable multi-species model for similar species. In space plasmas, such a situation is conceivable because the particles could have originated in a particular area of space where the physical conditions were different. Such findings abound in the magnetosphere. The added benefit of assuming this scenario is that electron–electron collisions are no longer a scientific challenge since the two electron species do not belong to the same phase space distribution function.

In this work, we aim to extend the previous studies by studying the existence and main features of the nonlinear waves in four-component magnetized plasma by means of the reductive perturbation technique. The paper is organized as follows: In Sects. 2 and 3, we present the model and the basic equations. In Sect. 4, the dependence of the profile of the nonlinear structure on the configuration plasma parameters is discussed. Finally, Sect. 5 is kept for the conclusion.

2 Basic Equations and Linear Analysis

We consider a homogeneous and infinite plasma consisting of an electron beam in the presence of the magnetic field along the direction of the electron beam. We describe the cold electrons and the beam electrons by the fluid equation and assume a single nonextensive model for the plasma electrons. The constant magnetic field \(B_0\) is assumed to be in the z-direction. The fluid equations for cold electrons in such a system are given by

$$\begin{aligned}&\frac{\partial n_{c}}{\partial t} + \frac{\partial }{\partial x}( n_{c} u_{cx}) + \frac{\partial }{\partial y}( n_{c} u_{cy}) + \frac{\partial }{\partial z}( n_{c} u_{cz})= 0.\end{aligned}$$
(1)
$$\begin{aligned}\frac{\partial {u_{cx}}}{\partial t} &+ u_{cx}\frac{\partial u_{cx}}{\partial x}+u_{cy}\frac{\partial u_{cx}}{\partial y}+u_{cz}\frac{\partial u_{cx}}{\partial z}\nonumber \\&+\frac{5\alpha \left( 1+\alpha +\beta \right) ^{2/3}}{3\theta }{n_{c}}^{-1/3}\frac{\partial n_{c}}{\partial x}-\alpha \frac{\partial \phi }{\partial x}\nonumber \\ &= \eta \left( \frac{\partial ^{2}}{\partial x^2}+\frac{\partial ^{2}}{\partial y^2}+\frac{\partial ^{2}}{\partial z^2}\right) u_{cx}+ \omega _{c}{u_{cy}}\end{aligned}$$
(2)
$$\begin{aligned}\frac{\partial {u_{cy}}}{\partial t} &+ u_{cx}\frac{\partial u_{cy}}{\partial x}+u_{cy}\frac{\partial u_{cy}}{\partial y}+u_{cz}\frac{\partial u_{cz}}{\partial z}\nonumber \\&+\frac{5\alpha \left( 1+\alpha +\beta \right) ^{2/3}}{3\theta }{n_{c}}^{-1/3}\frac{\partial n_{c}}{\partial y}-\alpha \frac{\partial \phi }{\partial y} \nonumber \\&= \eta \left( \frac{\partial ^{2}}{\partial x^2}+\frac{\partial ^{2}}{\partial y^2}+\frac{\partial ^{2}}{\partial z^2}\right) u_{cy}- \omega _{c}{u_{cx}}\end{aligned}$$
(3)
$$\begin{aligned}\frac{\partial {u_{cz}}}{\partial t} &+ u_{cx}\frac{\partial u_{cz}}{\partial x}+u_{cy}\frac{\partial u_{cz}}{\partial y}+u_{cz}\frac{\partial u_{cz}}{\partial z}\nonumber \\&+\frac{5\alpha \left( 1+\alpha +\beta \right) ^{2/3}}{3\theta }{n_{c}}^{-1/3}\frac{\partial n_{c}}{\partial z}-\alpha \frac{\partial \phi }{\partial z} \nonumber \\&= \eta \left( \frac{\partial ^{2}}{\partial x^2}+\frac{\partial ^{2}}{\partial y^2}+\frac{\partial ^{2}}{\partial z^2}\right) u_{cz} \end{aligned}$$
(4)

We assume that the electron beam is moving in the z-direction, that is, in the direction of the magnetic field. In such a case, the presence of magnetic field does not affect the propagation properties of the waves. The fluid equations for the electron beam are given by

$$\begin{aligned}&\frac{\partial n_{b}}{\partial t} + \frac{\partial }{\partial z}( n_{b} u_{b})= 0.\end{aligned}$$
(5)
$$\begin{aligned}&\frac{\partial u_{b}}{\partial t} + +u_{b}\frac{\partial u_{b}}{\partial z}+\frac{3\alpha \left( 1+\alpha +\beta \right) ^{2}}{\sigma \beta ^2}{n_{b}}\frac{\partial n_{b}}{\partial z}-\alpha \frac{\partial \phi }{\partial z} = 0 \end{aligned}$$
(6)

To complete the set of dynamic equations, the Poisson’s equation,

$$\begin{aligned}\frac{\partial ^{2}\phi }{\partial x^2}&+\frac{\partial ^{2}\phi }{\partial y^2}+\frac{\partial ^{2}\phi }{\partial z^2} = \left( \frac{1+\alpha +\beta }{\alpha }\right) (n_{c}+n_b)\\ \nonumber&+n_{h}-\left( 1+\frac{1+\alpha +\beta }{\alpha }\right) \end{aligned}$$
(7)

should be supplemented.

$$\begin{aligned} \alpha = \frac{n_{ho}}{n_{co}}\quad \qquad \theta = \frac{T_h}{T_c}\end{aligned}$$
(8)
$$\begin{aligned} \beta = \frac{n_{bo}}{n_{co}}\quad \qquad \sigma = \frac{T_h}{T_b} \end{aligned}$$
(9)

Cold electron fluid velocity \(u_c\) is normalized by \(C_e = \left( K_B T_h / \alpha m\right) ^{1/2}\). \(\eta\) is the coefficient of viscosity, \(\phi\) is the electrostatic wave potential normalized by \(K_B T_h / e\), \(K_B\) is the Boltzmann’s constant. The hot electron population obeys the Tsallis distribution [6] given by

$$\begin{aligned} n_h = \left( 1+ \left( q - 1\right) \phi \right) ^{(q+1)/{2(q - 1)}} \end{aligned}$$
(10)

The parameter q called as nonextensive parameter, stands for the strength of nonextensivity of electrons. The presence of nondrifting populations allows the existence of EA wave itself and cold component does not mean \(T_c\) = 0 as EA wave will cease to exist in that case. Expand \(n_h\) in terms of \(\phi\), we get

$$\begin{aligned}\frac{\partial ^2 \phi }{\partial x^2} &+ \frac{\partial ^2 \phi }{\partial y^2} + \frac{\partial ^2 \phi }{\partial z^2}= \frac{1+\alpha +\beta }{\alpha }(n_c + n_b) + 1 \\ \nonumber&+ c_1 \phi + c_2 \phi ^2 - \left( \frac{1+\alpha +\beta }{\alpha }\right) \end{aligned}$$
(11)

where

$$\begin{aligned} c_1=\frac{q + 1}{2}\quad ,\qquad \quad ,\qquad c_2=\frac{\left( q + 1\right) \left( 3 - q\right) }{8} \end{aligned}$$

Linearizing Eqs. (1)–(4) and (11) using Fourier analysis \(exp[i(l_x x + l_y y + l_z z - \omega t)]\), we get the following dispersion relation of electron acoustic shock wave in terms of normalized wave frequency \(\omega\) and wave number k in magnetized plasma:

$$\begin{aligned}&\frac{(1-\delta )(1+{l_z}^2 {\omega _c}^2)}{[ T_c (1-\delta )^2 (1+{l_z}^2 {\omega _c}^2) -i \omega (\eta k^2 -i \omega )(\eta ^2 k^4 + \omega ^2 + {\omega _c}^2)]} \\ \nonumber&+ \frac{\delta {l_z}^2}{T_b \delta ^2 {l_z}^2 - (\omega ^2 - u_{b0} l_z)^2} + \frac{c_1 + k^2}{1+\alpha +\beta } = 0 \end{aligned}$$
(12)

In the absence of viscosity and beam parameters, we retrieve the dispersion relation of Refs. [31] and [32]. Equation (12) shows that dispersion of the EA shock waves is due to charge separation, electron Larmor frequency and magnetic field effect. We shall also highlight the fact that similar to the linear regime, the magnetic effect also plays a significant role in the nonlinear wave dispersion in order to form shock pulses in a magnetoplasma. The term \({\omega _c}^2\) emerges as a contribution of Lorentz force exerted on electrons apart from the usual acoustic type oscillation. The magnetic field exerts a force on a moving charged particle called the Lorentz force that acts in a direction perpendicular to both the direction of the magnetic field and to the direction in which the charged particle is moving and the particle’s trajectory shapes into a helix.

3 Derivation of the KdV–Burgers Equation

Now, we will derive the KdVB equation to study the finite but small amplitude electron acoustic waves with electron beam in a plasma having nonextensive distributed hot electrons and stationary ions by adopting the reductive perturbation method. Firstly, we introduce the stretched coordinates as \(\tau =\epsilon ^{3/2} t\) and \(\xi =\epsilon ^{1/2}\left( l_{x} x + l_{y} y + l_{z} z - \lambda {t}\right)\), where \(l_{x}, l_{y}, l_{z}\) are the direction cosines along the x, y and z axis so that \({l_{x}}^2 + {l_{y}}^2 + {l_{z}}^2 = 1\) and wave speed \(\lambda\) is normalized by \(C_e\). The dependent variables \(n_c,n_b, u_c,u_b\) and \(\phi\) are expanded as follows:

$$\begin{aligned} n_c=&\; \left( 1-\delta \right) +\epsilon n_{c1}+ \epsilon ^2 n_{c2}\\ +& ...u_{cx} \epsilon ^{3/2} u_{cx1}+ \epsilon ^2 u_{cx2}+...\\ \nonumber u_{cy}=&\; \epsilon ^{3/2} u_{cy1}+ \epsilon ^2 u_{cy2}+...\\ \nonumber u_{cz}=&\; \epsilon u_{cz1}+ \epsilon ^2 u_{cz2}+...\\ \nonumber n_b=&\; \delta +\epsilon n_{b1}+ \epsilon ^2 n_{b2}+...\\ \nonumber u_{b}=&\; u_{b0}+\epsilon u_{b1}+ \epsilon ^2 u_{b2}+...\\ \nonumber \phi =&\; \epsilon \phi _{1}+ \epsilon ^2 \phi _{2}+... \end{aligned}$$
(13)

Substituting Eqs. (13) into Eqs. (1)−(6) and equating the coefficients of \(\epsilon ^{3/2}\) and \(\epsilon\), we get

$$\begin{aligned}&n_{c1} = \frac{-\alpha {l_z}^2\left( 1-\delta \right) \phi _1}{\lambda ^2-T_c {l_z}^2\left( 1-\delta \right) ^2}\quad ,\qquad u_{cz1} = \frac{-\alpha {l_z} \lambda \phi _1}{\lambda ^2-T_c {l_z}^2\left( 1-\delta \right) ^2}\end{aligned}$$
(14)
$$\begin{aligned}&n_{b1} = \frac{-\alpha {l_z}^2\delta \phi _1}{\left( \lambda - u_{b0}{l_z}\right) ^2-T_b {l_z}^2\delta ^2}\quad ,\qquad u_{b1} = \frac{-\alpha {l_z}\left( \lambda - u_{b0}{l_z}\right) \phi _1}{\left( \lambda - u_{b0}{l_z}\right) ^2-T_b {l_z}^2\delta ^2} \end{aligned}$$
(15)

where

$$\begin{aligned} T_c = \frac{5\alpha \left( 1+\alpha +\beta \right) ^{2/3}}{3\theta }\quad and \qquad T_b = \frac{3\alpha \left( 1+\alpha +\beta \right) ^{2}}{\sigma \beta ^2} \end{aligned}$$

From Poisson’s equation,

$$\begin{aligned}&-\frac{\alpha {l_z}^2\left( 1-\delta \right) }{\lambda ^2-T_c {l_{z}}^2\left( 1-\delta \right) ^2}-\frac{\alpha {l_z}^2\delta }{\left( \lambda -u_{b0}{l_z}\right) ^2-T_b {l_z}^2\delta ^2}\\ \nonumber&+\frac{\alpha }{1+\alpha +\beta }c_1=0 \end{aligned}$$
(16)
Fig. 1
figure 1

Variation of \(\lambda\) with \(u_{b0}\) at \(\delta = 0.05, \theta = 100, \sigma = 20, \alpha = 3\), \(l_z = 0.7\)

Full size image

Equation (16) represents the dispersion relation of the electron acoustic shock waves with electron beam in plasma having two populations of electrons. Equation (16) has four real roots of \(\lambda\), out of which two roots (roots 1 and 2) are negative (at certain values of plasma parameters) and two are positive (Fig. 1). We consider only real positive roots for numerical computation as the negative roots imply the waves propagating in opposite direction. One of the positive roots (root 3) does not fall into the regime of electron acoustic waves [21, 33]. So, we have taken the second positive root which falls in electron acoustic range (root 4). It is to note here that by dropping the electron beam component, the above Eq. (16) reduces to that of Bansal et al. [28]. Now equating the lowest orders of \(\epsilon\) on the both sides of x and y component of momentum equation, we get

$$\begin{aligned} (1-\delta )T_c l_{x}\frac{\partial n_{c1}}{\partial \xi }= & {} l_{x}\alpha \frac{\partial \phi _1}{\partial \xi }+\omega _{c}u_{cy1}\end{aligned}$$
(17)
$$\begin{aligned} (1-\delta )T_c l_{y}\frac{\partial n_{c1}}{\partial \xi }= & {} l_{y}\alpha \frac{\partial \phi _1}{\partial \xi }-\omega _{c}u_{cx1}\end{aligned}$$
(18)
$$\begin{aligned} \lambda \frac{\partial u_{cx1}}{\partial \xi }+\omega _{c}u_{cy2}= & {} 0\end{aligned}$$
(19)
$$\begin{aligned} \lambda \frac{\partial u_{cy1}}{\partial \xi }-\omega _{c}u_{cx2}= & {} 0 \end{aligned}$$
(20)

Now, equating the coefficients of \(\epsilon ^{5/2}\) from sides of (1−6) and \(\epsilon ^2\) from both sides of (11), we obtain

$$\begin{aligned}&-\lambda \frac{\partial n_{c2}}{\partial \xi }+ l_{x} (1-\delta )\frac{\partial u_{cx2}}{\partial \xi }+ l_{y} (1-\delta )\frac{\partial u_{cy2}}{\partial \xi }\\ \nonumber&+ l_{z} (1-\delta )\frac{\partial u_{cz2}}{\partial \xi }+l_{z} \frac{\partial }{\partial \xi }(n_{c1}u_{cz1})+\frac{\partial n_{c1}}{\partial \tau }=0\end{aligned}$$
(21)
$$\begin{aligned}&-\lambda \frac{\partial u_{cz2}}{\partial \xi }-\alpha l_{z}\frac{\partial \phi _2}{\partial \xi }+l_{z}u_{cz1}\frac{\partial u_{cz1}}{\partial \xi }+\frac{\partial u_{cz1}}{\partial \tau }\\ \nonumber&+ T_c l_{z} (1-\delta )\frac{\partial n_{c2}}{\partial \xi }-\frac{T_c}{3} l_{z}n_{c1}\frac{\partial n_{c1}}{\partial \xi } - \eta _{0}\frac{\partial ^2 u_{cz1}}{\partial \xi ^2}=0\end{aligned}$$
(22)
$$\begin{aligned}&-(\lambda - u_{b0} l_z)\frac{\partial n_{b2}}{\partial \xi }+ l_{z} \delta \frac{\partial u_{bz2}}{\partial \xi }+l_{z} \frac{\partial }{\partial \xi }(n_{b1}u_{bz1})\\ \nonumber&+\frac{\partial n_{b1}}{\partial \tau }=0\end{aligned}$$
(23)
$$\begin{aligned}&-(\lambda - u_{b0} l_z)\frac{\partial u_{bz2}}{\partial \xi }-\alpha l_{z}\frac{\partial \phi _2}{\partial \xi }+l_{z}u_{bz1}\frac{\partial u_{bz1}}{\partial \xi }+\frac{\partial u_{bz1}}{\partial \tau }\\ \nonumber&+ T_b l_{z} \delta \frac{\partial n_{b2}}{\partial \xi } +T_b l_{z}n_{b1}\frac{\partial n_{b1}}{\partial \xi } =0\end{aligned}$$
(24)
$$\begin{aligned}&\frac{\partial ^2 \phi _1}{\partial \xi ^2}=\frac{1+\alpha +\beta }{\alpha }\left( n_{c2}+n_{b2}\right) + c_1\phi _2+ c_2\left( \phi _1\right) ^{2} \end{aligned}$$
(25)

Now, using Eqs. (14)−(25) and eliminating second order equations, we deduce the KdVB equation for the propagation of EASWs as

$$\begin{aligned} \frac{\partial \phi }{\partial \tau } + A \phi \frac{\partial \phi }{\partial \xi }+ B \frac{\partial ^3\phi }{\partial \xi ^3} - C\frac{\partial ^2\phi }{\partial \xi ^2}= 0 \end{aligned}$$
(26)

where \(\phi _1= \phi\). The steepening of the shock wave (nonlinearity) is expressed by the second term on the left side of the above equation, the wave widening of the wave by the third term and the dissipation characteristics of the wave by the last term of Eq. (26). A, B and C are the nonlinearity, dispersion and dissipation coefficients, respectively, given by

$$\begin{aligned} A = A_1/D \quad , \qquad B = B_1/D \quad and \qquad C = C_1/D \end{aligned}$$
(27)

where

$$\begin{aligned} D= & {} 2\alpha \left[ \frac{\lambda {l_z}^2\left( 1-\delta \right) }{\left( \lambda ^2-T_c {l_z}^2\left( 1-\delta \right) ^2\right) ^2}+ \frac{\delta {l_z}^2\left( \lambda -u_{b0} {l_z}\right) }{\left( \left( \lambda -u_{b0}{l_z}^2\right) ^2-T_b {l_z}^2\delta ^2\right) ^2}\right] \end{aligned}$$
(28)
$$\begin{aligned} A_1= & {} -\frac{2c_2\alpha }{1+\alpha +\beta }+\frac{\alpha ^2 {l_z}^4\left( 1-\delta \right) \left( -9\lambda ^2 + T_c\left( 1-\delta \right) ^2 {l_z}^2\right) }{3\left( \lambda ^2-T_c {l_z}^2\left( 1-\delta \right) ^2\right) ^3}\\ \nonumber&-\frac{\alpha ^2{l_z}^4\delta \left( 3\left( \lambda - u_{b0}{l_z}\right) ^2+T_b {l_z}^2\delta ^2\right) }{\left( \left( \lambda - u_{b0}{l_z}\right) ^2-T_b{l_z}^2\delta ^2\right) ^3}\end{aligned}$$
(29)
$$\begin{aligned} B_1= & {} \frac{\alpha }{1+\alpha +\beta } + \frac{\alpha (1- {l_z}^2)\lambda ^2\left( 1-\delta \right) \left( 1 + T_c\left( 1-\delta \right) ^2 {l_z}^2\right) }{\omega_c ^2\left( \lambda ^2-T_c {l_z}^2\left( 1-\delta \right) ^2\right) }\end{aligned}$$
(30)
$$\begin{aligned} C_1= & {} \frac{\eta _0 \lambda \alpha {l_z}^2 (1-\delta )}{\left( \lambda ^2-T_c {l_z}^2\left( 1-\delta \right) ^2\right) ^2} \end{aligned}$$
(31)

The parameter C arises purely due to the kinematic viscosity and when it is not taken into account, Eq. (26) reduces to the standard KdV equation. It should be noted that the coefficients \(A_1\), \(B_1\) and D are analogous to our plasma model of three components [28]. We are, however, expanding our previous work to four component models, which may be more general. The \(\lambda\) variable that appears in coefficients \(A_1\), \(B_1\) and D must also follow the dispersion relation given in Eq. (16). In addition, all analytical findings of Bansal et al. [28] are retrieved in the absence of beam electrons.

To find the solution of Eq. (26), we apply another transformation \(\chi = \gamma (\xi -U\tau )\) presented in terms of independent variable \(\chi\) [33,34,35]. As a result, we obtain the steady state solution as

$$\begin{aligned} \phi ={\phi _m}\left( 1-\frac{1}{4}\left[ 1+tanh\left( \frac{\xi -u_0 \tau }{\delta }\right) \right] ^2\right) \end{aligned}$$
(32)

where \({\phi _m}=\left( {12C^2}/{25AB}\right)\) , \(\gamma\) =10B/C and \(U = 6C^2/25B\) is the velocity of the new frame of reference. Here the coefficients \(\phi _m\) and \(\gamma\) represent the amplitude and width of the shock wave, respectively. It is obvious from the expression for \(\phi _m\) that the amplitude of the wave depends upon the nonlinear coefficient A, dispersion coefficient B and damping coefficient C. Equation (26) is important to investigate the effect of nonextensivity, magnetic field, beam parameters and kinematic viscosity on the characteristics of shock waves.

We note that the damping coefficient C affects both \(\phi _m\) and L. Increase in value of C results in narrower and taller shocks. Also the product \(\phi _m L^2\) is independent of C. This is reminiscent of similar relationship obeyed by KdV solitons for amplitude-width relationship. The dissipation coefficient C depends only on the kinematic viscosity \(\eta\).

4 Discussion and Results

As noted above, we have investigated nonlinear waves with electron beam in four component magnetized plasma and we are interested in small amplitude approximation. In this section, the parametric investigations are carried out at different values of real plasma parameters. Here, we will apply our results to the observed broadband electrostatic noise (BEN) emissions that were recorded as two main bursts (burst a and b) in the auroral dayside region of the Earth’s magnetosphere by the Viking satellite [3]. We will focus our attention on burst b because burst b is more intense than burst a. The chosen parameters from the observation of burst b are : cold electron density \(n_{c0}\) = 0.5 \(cm^{-3}\), beam electron density \(n_{b0}\) = 1 \(cm^{-3}\), hot electron density \(n_{h0}\) = 1.5 \(cm^{-3}\), hot electron temperature \(T_h\) = 200eV, beam electron temperature \(T_b\) = 100eV, cold electron temperature \(T_c\) = 2eV and \(\omega _c\) = 0.2. Furthermore, Eqs. (29−31) are complicated functions of plasma parameters; therefore, in order to investigate the propagation profiles of shocks, we have numerically analysed the wave potential \(\phi\) vs \(\xi\) for different values of parameters \(\eta _0\), q, \(\alpha\), \(\beta\), \(\omega _c\), \(u_{b0}\).

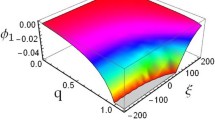
Now we present the graphical analysis of Eqs. (16, 29−31) which leads us to understand the behaviour of the phase velocity against nonextensivity, concentration of electron beam density and speed, and the behaviour of the shock potential against nonextensivity, beam parameters, kinematic viscosity, obliqueness and magnetic field. Interesting features are obtained for study of shock wave structure. Figure 2 shows the graphical representation of Eq. (16) in which the phase velocity is plotted against nonextensivity q and beam speed \(u_{b0}\). Figure 2a shows that if we increase the value of nonextensive parameter q, the phase velocity decreases. However, the opposite trend occurs with the variation of beam speed \(u_{b0}\). To observe the behaviour of the phase velocity with beam speed \(u_{b0}\), we present a two-dimensional graph of Eq. (16), which is shown in Fig. 2b.

It is evident from Eq. (29) that there exists a compressive or a rarefactive shock structure if coefficient A > 0 or A < 0, respectively. To ascertain whether A is positive or negative, we carried out a numerical investigation over the entire allowed ranges of q (i.e. 0.3 \(< q < 0.9\)) and \(\beta\)  (i.e. 0.01 \(< \beta < 0.4\)) and found that A is always negative. This means that our present plasma system can admit only rarefactive shock wave.

Fig. 2
figure 2

Variation of \(\lambda\); (a) with q, (b) with \(u_{b0}\), at \(\delta = 0.05, \theta = 100, \sigma = 20, \alpha = 3\), \(l_z = 0.7\)

Full size image

Figure 3 shows the effect of nonextensivity of electrons (q) on the dynamics of EA shock waves for q = 0.3, 0.5 and 0.9 depicted by blue solid, red dashed and green dot dashed, respectively. Other parameters are \(\delta = 0.02, \beta = 0.2, \theta = 200, \sigma = 20, \alpha = 3\), \(\eta _0 = 0.8\), \(l_z = 0.7\) and \(u_{b0}= 0.1\). It is observed that the amplitude of EA shock waves increases with increase in nonextensivity of electrons (low value of q). With increase in q, a nonlinear effect is enhanced. It makes the nonlinear coefficient bigger and reduces the amplitude of nonlinear structures. The results are similar to the one obtained by Shan et al. [32] for four component magnetized plasma. Next, for the parameters of Fig. 3, we study the influence of electron beam density via \(\beta\) on the evolution of these nonlinear electron acoustic shock waves. The value of the \(\beta\) ranges from 0.1 to 0.4, which is shown in Fig. 4. It is observed that with an increase in beam density, the shock wave amplitude decreases. This is happening due to the fact that the increment in beam number density implies the decrease of cold electrons in the given system by charge neutrality condition, which decreases the inertia of cold electrons. The latter increases the nonlinearity of the system. Thus, the EA shock wave is seen to be diminished as the beam density \(\beta\) increases. Similar findings are obtained by Singh et al. [21], where they carried out arbitrary amplitude theory of electron acoustic solitary waves in magnetized four component plasma having nonthermal electrons and electron beam.

Fig. 3
figure 3

Variation of shock profile for different values of q, q = 0.2 (solid), 0.3 (dotted), 0.5 (dashed dotted) at \(\delta = 0.05, \beta = 0.2, \theta = 100, \sigma = 20, \alpha = 2\), \(\eta _0 = 0.7\), \(l_z = 0.7\) and \(u_{b0}= 0.1\)

Full size image
Fig. 4
figure 4

Variation of soliton profile for different values of \(\beta\), \(\beta\) = 0.1 (solid), 0.3 (dotted), 0.4 (dashed dotted), at \(\delta = 0.05, \alpha = 2, \theta = 100, \sigma = 20,q = 0.3\), \(\eta _0 = 0.8\), \(l_z = 0.7\) and \(u_{b0}= 0.1\)

Full size image
Fig. 5
figure 5

Variation of soliton profile for different values of \(\alpha\), \(\alpha\) = 2 (solid), 3 (dotted), 4 (dashed dotted), at \(\delta = 0.05, \theta = 100, \beta = 0.4, q = 0.3, \sigma = 20\) and \(\eta _0 = 0.7\)

Full size image
Fig. 6
figure 6

Variation of soliton width with \(\eta _0\) , \(\eta _0\) = 0.6 (solid), 0.7 (dotted), 0.8 (dashed dotted), at \(\delta = 0.05, \alpha = 2, \theta = 100, \beta = 0.1,\sigma = 20, q = 0.3\), \(l_z = 0.7\) and \(u_{b0}= 0.1\)

Full size image
Fig. 7
figure 7

Variation of soliton profile for different values of \(\omega _c\), \(\omega _c\) = 0.2 (solid), 0.25 (dotted), 0.3 (dashed dotted), at \(\theta = 100, \alpha = 2, \sigma = 20, \beta = 0.2,\eta _0 = 0.7\), q = 0.3, \(l_z = 0.7\) and \(u_{b0}= 0.1\)

Full size image

Figure 5 examines the effects of concentration of hot electrons \(\alpha\), by giving variations \(\alpha\) = 2 (solid curve), 3 (dashed curve) and 4 (dot dashed curve), on the amplitude of EA shock waves. From the figure, it is obvious that with increase in \(\alpha\), the amplitude of the electron acoustic shock waves diminishes. With an increase in the value of \(\alpha\), there is a change in the hot electro-pressure that provides the restoring force which flourishes the nonlinearity. Thus, the EA shock waves is seen to be diminished as the ratio of hot to cold electron density ratio increases (\(\alpha\)). To investigate the effect of kinematic viscosity, a plot of EA shock wave solution \(\phi\) as a function of \(\xi\) is shown in Fig. 6 for three different values of \(\eta _0\). Here solid line is for \(\eta _0\) = 0.6, dotted line for \(\eta _0\) = 0.7 and dashed line is for \(\eta _0\) = 0.8, with \(\delta = 0.05, \alpha = 3, \theta = 200, \beta = 0.1,\sigma = 20, q = 0.3\), \(l_z = 0.7\) and \(u_{b0}= 0.1\). Clearly, the depth of potential increases with the kinematic viscosity.

It is obvious from Eq. (29) that if the dissipative term \(\eta _0\) = 0, the last term on the left-hand side goes to zero and we obtain purely solitonic structures, which means that the nonlinear term is balanced by the dispersive term. On the other hand, if the dissipative term becomes very large as compared to the nonlinear term, the shock structure will appear by balancing the effects of dissipative and dispersive terms. Lastly, we observe the effect of magnetic field (\(\omega _c\)) on the shock structure. The magnetic field exerts a force on a moving charged particle called the Lorentz force, that acts in a direction perpendicular to both the direction of the magnetic field and to the direction in which the charged particle is moving, and the particle’s trajectory shapes into a helix. The influence of variation of magnetic field strength on the properties of shock structures is presented in Fig. 7. We have plotted \(\phi\) vs \(\xi\) graphs for different values of \(\omega _c\). From the plot, it is revealed that the shock wave amplitude is significantly affected by the strength of magnetic field. An increase in magnetic field leads to increase in amplitude of EA shock waves. Thus, the magnetic field and beam parameters have a great impact on the characteristics of EA shock waves and significantly modify the shock profile.

5 Conclusionsshock structure. The magnetic

In the present work, we have studied the propagation of EA shock waves in four component magnetized plasma composed of stationary ions, cold electrons, nonextensive hot electrons and electron beam, by employing reductive perturbation method. We have derived the linear dispersion relation and studied the effects of nonextensivity and beam velocity on the phase velocity of the wave. It is noticed that these parameters have opposite effect on the phase velocity of the wave. We show that the phase velocity has four real roots, out of which two roots are negative and two are positive. We consider only the real positive roots for numerical computation, as the negative roots imply the waves propagating in opposite direction. One of the positive roots does not fall into the regime of electron acoustic waves. So we have taken the second positive root which falls in the electron acoustic range. In the nonlinear regime, we have investigated the nonlinear equation, namely KdVB equation, using the standard reductive perturbation method employing a set of stretched variables. It is observed that the nonextensivity, beam density and magnetic field play an important role in describing the behaviour of EA shock waves. An increase in beam density, kinematic viscosity and magnetic field results in increase in the amplitude, while the increase in hot electron concentration and nonextensivity leads to decrease in potential. The results are in good agreement with previous work of different scientists. The findings presented in this paper are very helpful in explaining many plasma wave phenomenon in bursts a and b and in planetary atmosphere where the presence of a warm electron beam is appropriate and meaningful. We consider that the study of phase velocity and formation of shock waves will give a clear picture of the composition and properties of plasma at such environments.