INTRODUCTION

An issue on the acceleration of solar cosmic rays (SCR) and their propagation in the interplanetary medium is one of the fundamental problems in the physics of heliosphere [4, 24, 29, 32]. Charged energetic particles is an important component of space weather; they pose a danger to space flights and influence the operation of communication and navigation systems [24, 29].

The pattern of propagation of cosmic rays (CR) in the interplanetary medium depends on the perturbation degree of the heliospheric magnetic field. If the level of the magnetohydrodynamic turbulence in the inner heliosphere is rather high, charged energetic particles may be scattered many times on their way from the Sun to the point of observations, the CR distribution function becomes almost isotropic, and the propagation of CR is described under the diffuse approximation [4, 12, 13, 29, 32]. For these solar flares, the detected intensity of CR gradually increases to the maximum and then slowly decreases; and a smooth temporal profile of the SCR intensity is observed at a given point of space [4, 18, 24, 32].

For some solar proton events with a low level of the interplanetary magnetic field turbulence, the scattering of particles was weak, while the CR transport path was comparable to an astronomical unit. During these bursts, the observed enhancement in the CR intensity was impulsive, and the particles came to the point of observations as a narrow beam [7, 9, 11, 25, 31]. The event of January 20, 2005, which is the strongest SCR burst observed for the recent half a century, is characterized by the anisotropic flux of relativistic particles at the initial stage of the burst [6, 8, 25, 26, 30]. During the initial stage of the SCR burst of January 20, 2005 (and some other events), the substantial anisotropy in the angular distribution of particles and the hard-energy spectrum of CR were observed. In length of time, the angular distribution of relativistic particles gradually became less anisotropic, and the CR energy spectrum became softer [21, 23, 31].

The diffusive description of the SCR propagation becomes incorrect for anisotropic proton events, and the kinetic equation should be used [2, 4, 12, 14]. The CR transport in the interplanetary medium was analyzed on the basis of the Fokker–Planck equation in papers [2, 12, 14, 19, 21, 22]. The kinetic equation was numerically solved, for example, in papers [1, 10, 13, 27]. The solution of the Fokker–Planck equation under the small-angle approximation was obtained in papers [2, 12]. In this approximation, the particles move mostly along the mean magnetic field (the pitch-angle θ takes small values) and are scattered through small angles. In terms of the second-approximation solution of the kinetic equation relative to the angle θ, the SCR transport was studied in papers [3, 15, 28].

In this paper, we consider the propagation of SCR injected into the interplanetary medium by an instantaneous point-like source of particles. Based on the solution of the Fokker–Planck kinetic equation, which describes the small-angle multiple scattering of particles, we analyze the evolution of the angular distribution function of particles at the initial stage of a solar proton event.

LAPLACE IMAGE OF THE DISTRIBUTION FUNCTION OF COSMIC RAYS

The kinetic equation that describes the distribution of charged energetic particles in the interplanetary magnetic fields has the following form [2, 12, 14]:

$$\frac{{\partial f}}{{\partial t}} + {v}\cos \theta \frac{{\partial f}}{{\partial r}} - \frac{{v}}{r}\sin \theta \frac{{\partial f}}{{\partial \theta }} - \frac{{v}}{{2\Lambda \sin \theta }}\frac{\partial }{{\partial \theta }}\sin \theta \frac{{\partial f}}{{\partial \theta }} = \frac{{\delta (r)\delta (t)\delta (\theta )}}{{8{{\pi }^{2}}{{r}^{2}}\sin \theta }},$$
(1)

where f(r, θ, t) is the CR distribution function, θ is the angle between the velocity vector of a particle v and the radial direction, and Λ is the CR transport path. The last term in the left side of Eq. (1) describes the scattering of charged particles on the magnetic field irregularities. We assume that the CR distribution function depends on a single spatial coordinate r. The right side of Eq. (1) contains an instantaneous source of particles located at the coordinate origin.

Let us introduce dimensionless variables

$$\rho = \frac{r}{\Lambda };{\text{ }}\tau = \frac{{{v}t}}{\Lambda }.$$
(2)

The kinetic equation (1) relative to dimensionless variables takes the following form:

$$\frac{{\partial f}}{{\partial \tau }} + \cos \theta \frac{{\partial f}}{{\partial \rho }} - \frac{{{\text{sin}}\theta }}{\rho }\frac{{\partial f}}{{\partial \theta }} - \frac{{\text{1}}}{{2\sin \theta }}\frac{\partial }{{\partial \theta }}\sin \theta \frac{{\partial f}}{{\partial \theta }} = \frac{{\delta (\rho )\delta (\tau )\delta (\theta )}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}\sin \theta }}.$$
(3)

The kinetic equation (3) can be analytically solved if the particles are scattered through small angles [2, 3, 12, 15, 28]. Let us assume that the overwhelming majority of particles move in a radial direction and the angle between the particle velocity and the radial direction is small, so that the condition θ2 ⪡ 1 is satisfied [3, 15, 28]. In the kinetic equation (3), we substitute the quantities sinθ and cos θ by θ and (1 – θ2/2), respectively. Under the considered approximation, the kinetic equation (3) takes the form

$$\frac{{\partial f}}{{\partial \tau }} + \left( {1 - \eta } \right)\frac{{\partial f}}{{\partial \rho }} - \frac{{2\eta }}{\rho }\frac{{\partial f}}{{\partial \eta }} - \frac{\partial }{{\partial \eta }}\eta \frac{{\partial f}}{{\partial \eta }} = \frac{{\delta (\rho )\delta (\tau )\delta (\eta )}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}}},$$
(4)

where

$$\eta = \frac{{{{\theta }^{2}}}}{2}.$$
(5)

Let us introduce the variable

$$\varsigma = \tau - \rho $$
(6)

and write the kinetic equation (4) for new variables by keeping the first nonvanishing terms [3]

$$\eta \frac{{\partial f}}{{\partial \varsigma }} + \frac{{\partial f}}{{\partial \rho }} - \frac{{2\eta }}{\rho }\frac{{\partial f}}{{\partial \eta }} - \frac{\partial }{{\partial \eta }}\eta \frac{{\partial f}}{{\partial \eta }} = \frac{{\delta (\rho )\delta (\varsigma )\delta (\eta )}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}}}.$$
(7)

With the Laplace transform

$$f(\rho ,\eta ,\omega ) = \int\limits_0^\infty {d\varsigma \exp ( - \omega \varsigma )f(\rho ,\eta ,\varsigma )} ,$$
(8)

we derive the following equation for the Laplace image of the CR distribution function

$$\eta \omega f + \frac{{\partial f}}{{\partial \rho }} - \frac{{2\eta }}{\rho }\frac{{\partial f}}{{\partial \eta }} - \frac{\partial }{{\partial \eta }}\eta \frac{{\partial f}}{{\partial \eta }} = \frac{{\delta (\rho )\delta (\eta )}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}}}.$$
(9)

The solution of Eq. (9) takes the form [15]

$$f(\rho ,\eta ,\omega ) = \frac{1}{{w(\rho ,\omega )}}\exp \left( { - \frac{1}{{w(\rho ,\omega )}}\frac{{\partial w(\rho ,\omega )}}{{\partial \rho }}\eta } \right),$$
(10)

where

$$w(\rho ,\omega ) = \frac{{8{{\pi }^{2}}{{\Lambda }^{3}}}}{{{{\omega }^{{3/2}}}}}\left( {\rho \sqrt \omega {\text{cosh}}\rho \sqrt \omega - {\text{sinh}}\rho \sqrt \omega } \right),$$
(11)
$$\frac{{\partial w(\rho ,\omega )}}{{\partial \rho }} = 8{{\pi }^{2}}{{\Lambda }^{3}}\rho \frac{{{\text{sinh}}\rho \sqrt \omega }}{{\sqrt \omega }},$$
(12)

and sinh z and cosh z are the hyperbolic sine and cosine of the argument z, respectively.

We note that the functions of the complex variable ω in Eqs. (11) and (12) contain no branchpoints. In fact, by expanding the hyperbolic functions in expressions (11) and (12), we obtain

$$w(\rho ,\omega ) = \frac{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{3}}}}{3}\left( {1 + \frac{{{{\rho }^{2}}\omega }}{{10}} + \frac{{{{\rho }^{4}}{{\omega }^{2}}}}{{70}} + ...} \right),$$
(13)
$$\frac{{\partial w(\rho ,\omega )}}{{\partial \rho }} = 8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}\left( {1 + \frac{{{{\rho }^{2}}\omega }}{6} + \frac{{{{\rho }^{4}}{{\omega }^{2}}}}{{120}} + ...} \right).$$
(14)

Thus, expressions (11) and (12) contain only integer powers of the variable ω.

DENSITY OF SOLAR COSMIC RAYS

The derived relationship for the Laplace image of the CR distribution function (Eq. (10)) allows us to calculate the Laplace image of the density of particles

$$N(\rho ,\omega ) = 2\pi {{f}_{0}}(\rho ,\omega ),$$
(15)

where

$${{f}_{0}}(\rho ,\omega ) = \int\limits_0^\pi {d\theta \sin \theta f(\rho ,\theta ,\omega )} .$$
(16)

If the overwhelming majority of particles are characterized by small values of the angle θ, the upper limit in formula (16) may be extended to infinity. Thus,

$${{f}_{0}}(\rho ,\omega ) = \int\limits_0^\infty {d\eta \left( {1 - \frac{\eta }{3}} \right)f(\rho ,\eta ,\omega )} ,$$
(17)

where the variable η is defined by formula (5), while the Laplace image of the CR distribution function has the form of Eq. (10). By integrating relationship (17), we obtain

$${{f}_{0}}(\rho ,\omega ) = \frac{1}{{\frac{{\partial w}}{{\partial \rho }}}} - \frac{1}{3}\frac{w}{{{{{\left( {\frac{{\partial w}}{{\partial \rho }}} \right)}}^{2}}}}.$$
(18)

The inverse Laplace transformation is defined by

$${{f}_{0}}(\rho ,\varsigma ) = \frac{1}{{2\pi i}}\int\limits_L {d\omega {{f}_{0}}(\rho ,\omega )\exp (\omega \varsigma )} ,$$
(19)

where the variable ς is defined by Eq. (6), while the integration is made along the straight line L, which is parallel to the imaginary axis and located in the right half-plane of the complex variable ω.

Let us close the integration contour by the infinite-radius arc located in the left half-plane of the complex variable ω. Note that the integral over this arc is zero. Thus, the integration over a closed contour, which is composed of the straight line L and the infinite-radius arc, is reduced to the calculation of residues at critical points of the function f0(ρ, ω) (Eq. (18)). The roots of the denominator of the function f0(ρ, ω) are on the negative part of the real axis, while the Laplace image of the function f0(ρ, ω) (Eq. (18)) on the real axis of the complex variable ω has the following form

$${{f}_{0}}(\rho ,\omega ) = \frac{1}{{8{{\pi }^{2}}{{\Lambda }^{3}}}}\left\{ {\frac{{\sqrt {\left| \omega \right|} }}{{\rho \sin \rho \sqrt {\left| \omega \right|} }} + \frac{1}{3}\frac{{\rho \cos \rho \sqrt {\left| \omega \right|} - \sin \rho \sqrt {\left| \omega \right|} }}{{{{\rho }^{2}}\sqrt {\left| \omega \right|} {{{\sin }}^{2}}\rho \sqrt {\left| \omega \right|} }}} \right\}.$$
(20)

The critical points of function (20) are determined as

$${{\omega }_{n}} = - \frac{{{{n}^{2}}{{\pi }^{2}}}}{{{{\rho }^{2}}}},$$
(21)

where n ≥ 1.

By calculating the residues of the integrand in (19) and (20) at the points ωn, we derive the following interrelation

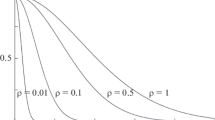
$${{f}_{0}}(\rho ,\varsigma ) = \frac{1}{{4{{\Lambda }^{3}}{{\rho }^{4}}}}\left( {1 - \frac{{2\varsigma }}{{3\rho }}} \right)\sum\limits_{n = 1}^\infty {{{{( - 1)}}^{{n + 1}}}{{n}^{2}}\exp \left( { - \frac{{{{n}^{2}}{{\pi }^{2}}}}{{{{\rho }^{2}}}}\varsigma } \right)} .$$
(22)

Figure 1 presents the spatial dependence of the function f0 (Eq. (22)) at different time moments (solid curves). The values of the dimensionless time τ are shown near the corresponding curves. We note that the CR density N (15) is proportional to the function f0. It is seen that the density is zero in a spatial range of ρ > τ. Consequently, at the moment t, the particles are within the sphere of radius r = vt; and the CR density is highest near the boundary of the area occupied by particles (Fig. 1). Over time, the spatial region occupied by particles expands, while the maximum in the CR density goes down.

Fig. 1.
figure 1

Spatial dependence of the density and anisotropy of particles at different time moments. The dimensionless quantity Λ3f0 and the anisotropy are presented by solid and dashed curves, respectively. Numbers at the curves are the values of the dimensionless time τ.

Full size image

Solid curves in Fig. 2 illustrate the time dependence of the function f0. The values of the dimensionless coordinate ρ are given at the corresponding curves. At the point ρ, the first particles appear at the time moment τ = ρ. When τ < ρ, the CR density is zero since the particles cannot reach this point of space if t < r/v. At the time moment t = r/v, when the first particles have arrived, the particle density rapidly grows to the maximum (Fig. 2). The smaller the distance to the source of particles, the higher the CR intensity maximum. Particles appear at a given point of space as a short-time pulse; after that, their density quickly vanishes (Fig. 2). It is worth noting that the considered small-angle approximation is valid only for a limited time interval after arriving the first particles to a given point of space when most of them move in a nearly radial direction.

Fig. 2.
figure 2

Time dependence of the CR density and anisotropy. Solid and dashed curves show the quantity Λ3f0 and the anisotropy, respectively. Numbers at the curves are the values of the dimensionless coordinate ρ.

Full size image

ANISOTROPY IN THE ANGULAR DISTRIBUTION OF PARTICLES

Let us consider the evolution of anisotropy in the angular distribution of SCR. The flux of particles is proportional to the following quantity:

$${{f}_{1}}(\rho ,\tau ) = \int\limits_0^\pi {d\theta \sin \theta \cos \theta f(\rho ,\theta ,\tau )} .$$
(23)

Under the small-angle approximation (θ ⪡ 1), one may extend the integration in formula (23) to infinity. By passing to the variable η (Eq. (5)), we obtain

$${{f}_{1}}(\rho ,\tau ) = \int\limits_0^\infty {d\eta \left( {1 - \frac{{4\eta }}{3}} \right)f(\rho ,\eta ,\tau )} .$$
(24)

After integrating over the angular variable in formula (24), we obtain the following interrelation for the Laplace image of the function f1:

$${{f}_{1}}(\rho ,\omega ) = \frac{1}{{\frac{{\partial w}}{{\partial \rho }}}} - \frac{4}{3}\frac{w}{{{{{\left( {\frac{{\partial w}}{{\partial \rho }}} \right)}}^{2}}}}.$$
(25)

The inverse Laplace transformation yields the following relationship:

$${{f}_{1}}(\rho ,\varsigma ) = \frac{1}{{4{{\Lambda }^{3}}{{\rho }^{4}}}}\left( {1 - \frac{{8\varsigma }}{{3\rho }}} \right)\sum\limits_{n = 1}^\infty {{{{( - 1)}}^{{n + 1}}}{{n}^{2}}\exp \left( { - \frac{{{{n}^{2}}{{\pi }^{2}}}}{{{{\rho }^{2}}}}\varsigma } \right)} .$$
(26)

The anisotropy in the angular distribution of particles is defined by the following formula [13, 18, 32]:

$$\xi (\rho ,\tau ) = 3\frac{{{{f}_{1}}(\rho ,\tau )}}{{{{f}_{0}}(\rho ,\tau )}}.$$
(27)

Taking Eqs. (22) and (26) into account, we derive the following expression for the anisotropy of the angular distribution of CR:

$$\xi (\rho ,\tau ) = 3\frac{{11\rho - 8\tau }}{{5\rho - 2\tau }}.$$
(28)

At the moment when the first particles come to a given point of space (τ = ρ), the anisotropy (Eq. (28)) is characterized by the highest value (ξ = 3). We note that interrelation (28) is approximate since it was obtained under the small-angle approximation. In the course of time, the angular distribution of CR becomes more isotropic, and the conditions for applicability of this approximation are violated.

Dashed curves in Fig. 1 illustrate the spatial dependence of the CR anisotropy (Eq. (28)) at different time moments. The CR anisotropy is strongest near the boundary of the area occupied by particles and decreases with decreasing the coordinate r (Fig. 1). It turns out that, in the range of the highest intensity of CR, the anisotropy in the angular distribution of particles is substantial and the value of the quantity ξ is close to maximal (Fig. 1).

Figure 2 presents the time dependence of the anisotropy in the angular distribution of particles at a given point of space (dashed curves). When the first particles come (τ = ρ), the CR anisotropy is strongest; then it monotonously decreases with time and becomes negative at a given point of space (Fig. 2). The negative value of the anisotropy, which corresponds to the flux of particles directed toward the source, is caused by the fact that the overwhelming majority of particles at a given time moment are already beyond the sphere of radius ρ. However, it is worth noting that the present approximation takes into consideration the particles whose motion direction slightly differs from the radial one (θ ⪡ 1).

ANGULAR DISTRIBUTION FUNCTION OF SOLAR COSMIC RAYS

The Laplace image of the CR distribution function is defined by Eq. (10), and the exponential factor in this formula is proportional to the variable η (5). Thus, the Laplace image of the CR distribution function (Eq. (10)) is characterized by the exponential dependence on the quantity θ2 ⪡ 1. By expanding relationship (10) into a series of the small quantity η, we obtain

$$f(\rho ,\eta ,\omega ) = \frac{1}{w} - \frac{\eta }{{{{w}^{2}}}}\frac{{\partial w}}{{\partial \rho }} + \frac{{{{\eta }^{2}}}}{{2{{w}^{3}}}}{{\left( {\frac{{\partial w}}{{\partial \rho }}} \right)}^{2}}.$$
(29)

In formula (29), we restrict ourselves by the component that is the squared small quantity η.

From Eqs. (11) and (12), we obtain the following expression for the Laplace image of the CR distribution function

$$\begin{gathered} f(\rho ,\eta ,\omega ) = \frac{1}{{8{{\pi }^{2}}{{\Lambda }^{3}}}}\frac{{{{\omega }^{{3/2}}}}}{{\rho \sqrt \omega {\text{cosh}}\rho \sqrt \omega - {\text{sinh}}\rho \sqrt \omega }} - \frac{1}{{8{{\pi }^{2}}{{\Lambda }^{3}}}}\frac{{\rho {{\omega }^{{5/2}}}{\text{sinh}}\rho \sqrt \omega }}{{{{{\left[ {\rho \sqrt \omega {\text{cosh}}\rho \sqrt \omega - {\text{sinh}}\rho \sqrt \omega } \right]}}^{2}}}}\eta \\ + \,\,\frac{1}{{8{{\pi }^{2}}{{\Lambda }^{3}}}}\frac{{{{\rho }^{2}}{{\omega }^{{7/2}}}{\text{sin}}{{{\text{h}}}^{2}}\rho \sqrt \omega }}{{{{{\left[ {\rho \sqrt \omega {\text{cosh}}\rho \sqrt \omega - {\text{sinh}}\rho \sqrt \omega } \right]}}^{3}}}}\frac{{{{\eta }^{2}}}}{2}. \\ \end{gathered} $$
(30)

The inverse Laplace transformation (Eq. (19)) is performed along the straight line L that is parallel to the imaginary axis. Let us close the integration contour by the infinite-radius arc located in the left half-plane of the complex variable ω. The integral over this arc is zero, and the integration over a closed contour, which is composed of the straight line L and the infinite-radius arc, is reduced to the calculation of residues at critical points of the integrand. The critical points of the function f(ω) (Eq. (30)) are in the negative part of the real axis at the points

$${{\omega }_{n}} = - \frac{{x_{n}^{2}}}{{{{\rho }^{2}}}},{\text{ }}n \geqslant {\text{1}}{\text{,}}$$
(31)

where xn are positive roots of the equation

$$x = {\text{tan}}x.$$
(32)

The Laplace image of the function f(ω) (Eq. (30)) on the real axis of the complex variable ω has the following form:

$$\begin{gathered} f(\rho ,\eta ,\omega ) = - \frac{1}{{8{{\pi }^{2}}{{\Lambda }^{3}}}}\frac{{{{{\left| \omega \right|}}^{{3/2}}}}}{{\rho \sqrt {\left| \omega \right|} \cos \rho \sqrt {\left| \omega \right|} - \sin \rho \sqrt {\left| \omega \right|} }} - \frac{1}{{8{{\pi }^{2}}{{\Lambda }^{3}}}}\frac{{\rho {{{\left| \omega \right|}}^{{5/2}}}\sin \rho \sqrt {\left| \omega \right|} }}{{{{{\left[ {\rho \sqrt {\left| \omega \right|} \cosh \rho \sqrt {\left| \omega \right|} - \sin \rho \sqrt {\left| \omega \right|} } \right]}}^{2}}}}\eta \\ - \,\,\frac{1}{{8{{\pi }^{2}}{{\Lambda }^{3}}}}\frac{{{{\rho }^{2}}{{{\left| \omega \right|}}^{{7/2}}}{{{\sin }}^{2}}\rho \sqrt {\left| \omega \right|} }}{{{{{\left[ {\rho \sqrt {\left| \omega \right|} \cos \rho \sqrt {\left| \omega \right|} - \sin \rho \sqrt {\left| \omega \right|} } \right]}}^{3}}}}\frac{{{{\eta }^{2}}}}{2}. \\ \end{gathered} $$
(33)

By calculating the residues of the integrand in (19) and (33) at the points ωn (31), we derive the following expression for the CR distribution function

$$f(\rho ,\eta ,\varsigma ) = \frac{1}{{4{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{5}}}}\left\{ { - {{\Gamma }_{1}}(\rho ,\varsigma ) + \frac{\eta }{\rho }{{\Gamma }_{2}}(\rho ,\varsigma ) + \frac{{{{\eta }^{2}}}}{{2{{\rho }^{2}}}}{{\Gamma }_{3}}(\rho ,\varsigma )} \right\},$$
(34)

where

$${{\Gamma }_{1}}(\rho ,\varsigma ) = \sum\limits_{n = 1}^\infty {\frac{{x_{n}^{3}}}{{\sin {{x}_{n}}}}\exp \left( { - \frac{{x_{n}^{2}}}{{{{\rho }^{2}}}}\varsigma } \right)} ,$$
(35)
$${{\Gamma }_{2}}(\rho ,\varsigma ) = \sum\limits_{n = 1}^\infty {\frac{{x_{n}^{3}}}{{\sin {{x}_{n}}}}\left( {5 - 2\frac{{x_{n}^{2}}}{{{{\rho }^{2}}}}\varsigma } \right)\exp \left( { - \frac{{x_{n}^{2}}}{{{{\rho }^{2}}}}\varsigma } \right)} ,$$
(36)
$${{\Gamma }_{3}}(\rho ,\varsigma ) = \frac{1}{2}\sum\limits_{n = 1}^\infty {\frac{{x_{n}^{3}}}{{\sin {{x}_{n}}}}\left( {x_{n}^{2} - 40 + 30\frac{{x_{n}^{2}}}{{{{\rho }^{2}}}}\varsigma - 4\frac{{x_{n}^{4}}}{{{{\rho }^{4}}}}{{\varsigma }^{2}}} \right)\exp \left( { - \frac{{x_{n}^{2}}}{{{{\rho }^{2}}}}\varsigma } \right)} .$$
(37)

We write the interrelation for the CR distribution function (Eqs. (34)−(37)) in the following form:

$$f(\rho ,\eta ,\varsigma ) = - \frac{{{{\Gamma }_{1}}(\rho ,\varsigma )}}{{4{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{5}}}}\left\{ {1 - \frac{\eta }{\rho }\frac{{{{\Gamma }_{2}}(\rho ,\varsigma )}}{{{{\Gamma }_{1}}(\rho ,\varsigma )}} - \frac{{{{\eta }^{2}}}}{{2{{\rho }^{2}}}}\frac{{{{\Gamma }_{3}}(\rho ,\varsigma )}}{{{{\Gamma }_{1}}(\rho ,\varsigma )}}} \right\}.$$
(38)

We assume that the particles move mostly in the radial direction (θ ⪡ 1). The variable η (Eq. (5)) is proportional to the quantity θ2. Consequently, the expression for the CR distribution function (Eq. (38)) is written within the accuracy of the quantity θ4. Within the same accuracy, we may rewrite expression (38) as

$$f(\rho ,\eta ,\varsigma ) = - \frac{{{{\Gamma }_{1}}}}{{4{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{5}}}}\Phi \left( {\frac{{{{\Gamma }_{2}}({{\Gamma }_{3}} - {{\Gamma }_{2}})}}{{{{\Gamma }_{1}}{{\Gamma }_{3}} + \Gamma _{2}^{2}}};\frac{{{{\Gamma }_{1}}({{\Gamma }_{2}} - {{\Gamma }_{3}})}}{{{{\Gamma }_{1}}{{\Gamma }_{3}} + \Gamma _{2}^{2}}};\frac{\eta }{\rho }} \right),$$
(39)

where Φ(a; c; x) is the confluent hypergeometric function.

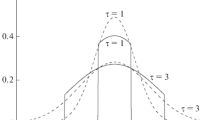
Figure 3 presents the time dependence of the distribution function (Eq. (39)) at the point ρ = 0.5. The values of the angle θ are specified at the corresponding curves. The CR distribution function in dependence on time (at a given value of the angle between the particle velocity and the radial direction) increases to the highest value and then monotonously decreases (Fig. 3). The larger the angle θ between the particle velocity and the radial direction, the lower the maximal value of the CR distribution function and the later the maximum of f (Eq. (39)) occurs at a given point of space (Fig. 3).

Fig. 3.
figure 3

Time dependence of the distribution function of particles at the point ρ = 0.5. Numbers at the curves are the corresponding values of the angle θ.

Full size image

Figure 4 presents the CR distribution function (Eq. (39)) in dependence on the angle θ at the point ρ = 1. The values of the dimensionless time τ are specified at the corresponding curves. The CR distribution function (Eq. (39)) is normalized to its value at the point θ = 0°. We note that the CR intensity at the point ρ = 1 exhibits the highest value at the time moment τ = 1.065. At the time moments τ = 1.038 and 1.119, the CR density at the point ρ = 1 is half the maximum. The curves corresponding to these time moments are also shown in Fig. 4. It is seen from the plot that, at a given point of space, the distribution of particles is most anisotropic at the beginning of the CR intensity enhancement. For example, at the point ρ = 1 and the time moment τ = 1.02, the velocity of almost all particles makes an angle smaller than 30° with the radial direction (Fig. 4). With the course of time, the angular distribution of CR gradually becomes more isotropic.

Fig. 4.
figure 4

Dependence of the CR distribution function on the angle between the particle velocity and the radial direction at the point ρ = 1. Numbers at the curves are the corresponding values of the dimensionless time τ.

Full size image

ANGULAR DISTRIBUTION OF CR UNDER THE DIFFUSION APPROXIMATION

Let us consider the SCR distribution for a long period of time passed after injecting energetic particles into the interplanetary medium. We will assume that the time passed after injecting energetic particles into the interplanetary medium substantially exceeds the time of propagation of particles to a given point of space (t ⪢ r/v) and the characteristic time of scattering (t ⪢ Λ/v). In this case, the particles have time to be scattered many times on heterogeneities of the interplanetary magnetic field, and the CR distribution function becomes close to isotropic.

Let us introduce the variable

$$\mu = \cos \theta .$$
(40)

The kinetic equation (3) may be written in the following form:

$$\frac{{\partial f}}{{\partial \tau }} + \mu \frac{{\partial f}}{{\partial \rho }} + \frac{{{\text{1}} - {{\mu }^{{\text{2}}}}}}{\rho }\frac{{\partial f}}{{\partial \mu }} - \frac{{\text{1}}}{2}\frac{\partial }{{\partial \mu }}\left( {1 - {{\mu }^{2}}} \right)\frac{{\partial f}}{{\partial \mu }} = \frac{{\delta (\rho )\delta (\tau )\delta (\mu - 1)}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}}}.$$
(41)

Let us present the CR distribution function as a sum [5, 17, 19, 20]

$$f(\rho ,\mu ,\tau ) = \frac{1}{2}{{f}_{0}}(\rho ,\tau ) + \delta f(\rho ,\mu ,\tau ),$$
(42)

where f0 is the isotropic component of the CR distribution function, and δf is a small anisotropic component. The function f0 defines the mean value of the CR distribution function

$$\left\langle f \right\rangle = \frac{{\int\limits_{ - 1}^1 {d\mu f} }}{{\int\limits_{ - 1}^1 {d\mu } }} = \frac{1}{2}{{f}_{0}},$$
(43)

while the anisotropic component satisfies the equation

$$\int\limits_{ - 1}^1 {d\mu \delta f(\rho ,\mu ,\tau ) = 0} .$$
(44)

After integrating the kinetic equation (41) with respect to μ, we derive the continuity equation

$$\frac{{\partial {{f}_{0}}}}{{\partial \tau }} + \frac{1}{{{{\rho }^{2}}}}\frac{\partial }{{\partial \rho }}{{\rho }^{2}}\int\limits_{ - 1}^1 {d\mu \mu \delta f} = \frac{{\delta (\rho )\delta (\tau )}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}}}.$$
(45)

By taking into account that the anisotropic component of the CR distribution function is small as compared to the isotropic one (δf ⪡ f0), we can obtain the following equation for the quantity δf from the kinetic equation (41) [5, 14, 20]

$$\frac{\partial }{{\partial \mu }}\left\{ {\left( {1 - {{\mu }^{2}}} \right)\left[ {\frac{{\partial \delta f}}{{\partial \mu }} - 2\frac{{\delta f}}{\rho }} \right]} \right\} = \mu \frac{{\partial {{f}_{0}}}}{{\partial \rho }}.$$
(46)

It is worth noting that the right part of Eq. (46) is proportional to the gradient of the isotropic component of the CR distribution function.

The solution of Eq. (46), which satisfies condition (44), is [5, 16]

$$\delta f(\rho ,\mu ,\tau ) = - \frac{\rho }{4}\frac{{\partial {{f}_{0}}}}{{\partial \rho }}\left\{ {\frac{{2\exp \left( {\frac{{2\mu }}{\rho }} \right)}}{{\rho {\text{sh}}\frac{2}{\rho }}} - 1} \right\}.$$
(47)

If the scattering of particles is isotropic, the CR distribution function (47) exponentially depends on the cosine of the angle between the particle velocity and the radial velocity [5, 7, 14, 16, 17, 20].

From the expression for the anisotropic component of the CR distribution function (Eq. (47)), we may calculate the quantity f1 (23) as

$${{f}_{1}}(\rho ,\tau ) = \int\limits_{ - 1}^1 {d\mu \mu \delta f(\rho ,\mu ,\tau ) = } - \frac{\rho }{4}\frac{{\partial {{f}_{0}}}}{{\partial \rho }}\left( {2{\text{coth}}\frac{2}{\rho } - \rho } \right),$$
(48)

where coth x is the hyperbolic cotangent of the argument x. If the condition ρ ⪢ 1 is satisfied, we obtain

$${{f}_{1}}(\rho ,\tau ) = - \frac{1}{3}\frac{{\partial {{f}_{0}}}}{{\partial \rho }}.$$
(49)

Applying the function f1 (Eq. (49)) to the continuity equation (45), we obtain the CR diffusion equation

$$\frac{{\partial {{f}_{0}}}}{{\partial \tau }} - \frac{1}{{3{{\rho }^{2}}}}\frac{\partial }{{\partial \rho }}{{\rho }^{2}}\frac{{\partial {{f}_{0}}}}{{\partial \rho }} = \frac{{\delta (\rho )\delta (\tau )}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}}}.$$
(50)

The solution of this equation takes the following form:

$${{f}_{0}}(\rho ,\tau ) = \frac{{{{3}^{{3/2}}}}}{{16{{\pi }^{{5/2}}}{{\Lambda }^{3}}{{\tau }^{{3/2}}}}}\exp \left( { - \frac{{3{{\rho }^{2}}}}{{4\tau }}} \right).$$
(51)

It follows from the above formula that, if τ is large, the SCR density decreases with time proportionally to τ−3/2.

Let us write an expression for the CR distribution function (Eq. (42)) normalized to the mean value (Eq. (43))

$$\frac{f}{{\left\langle f \right\rangle }} = 1 + \frac{{2\delta f}}{{{{f}_{0}}}},$$
(52)

where the anisotropic component of the CR distribution function δf is described by interrelation (47).

In Fig. 5, the CR distribution function (Eq. (52)) in dependence on the quantity μ at the point ρ = 1 is shown. The dimensionless time values τ are specified at the corresponding curves. The isotropic component of the CR distribution function f0(ρ, τ) satisfies interrelation (51). The maximum in the CR distribution function is at the μ value equal to unity (θ = 0). When μ grows, the CR distribution function monotonously increases (Fig. 5). Thus, the number of particles moving outward exceeds the number of particles moving in the opposite direction. The distribution of particles is rather anisotropic at the time moment τ = 2 and almost isotropic at τ = 10. We note that the isotropic distribution of particles corresponds to the straight line that is parallel to the abscissa (if the ordinate takes a value of unity).

Fig. 5.
figure 5

Dependence of the CR distribution function (Eq. (52)) on the quantity μ = cos θ at the point ρ =1. Numbers at the curves are the corresponding values of the dimensionless time τ.

Full size image

CONCLUSIONS

We considered the propagation of SCR in the interplanetary medium in terms of the kinetic equation describing the small-angle scattering of particles. The expression for the Laplace image of the CR distribution function was derived, and the spatial distribution of SCR was analyzed under the instantaneous injection of particles by a point-like source. It has been shown that, at the time moment t, the particles are within the sphere of a radius r = vt, while the CR density is highest near the boundary of the area occupied by particles. At the initial stage of an anisotropic burst of SCR, there is a sharp upsurge in the intensity of particles. The anisotropy in the angular distribution of SCR is strongest at the moment of the first particles’ arrival to a given point of space; in the course of time, the anisotropy monotonously decreases.

The analytical expression for the distribution function of particles was obtained under the small-angle approximation. The evolution of the angular distribution function of SCR was studied, and it has been shown that the angular distribution of particles becomes less anisotropic with time. If the time having passed after the injection of particles significantly exceeds the time of propagation of CR to the detection point and the inverse frequency of collisions, the distribution function of particles can be represented by the sum of isotropic and small anisotropic components. It has been shown that, in this case, the CR distribution function exponentially depends on the cosine of the angle between the particle velocity and the radial direction.