The Distribution Function of Solar Cosmic Rays under Prolonged Particle Injection

Abstract—The propagation of solar cosmic rays (SCR) in the interplanetary medium is considered on the basis of the Fokker–Planck kinetic equation. It is known that the SCR distribution function averaged over a solar proton event contains valuable data on the scattering process for energetic charged particles by interplanetary magnetic fields. A steady-state solution for the kinetic equation in the small-angle approximation is obtained, and the dependence of the angular distribution function of cosmic rays on the distance to the particle source is examined. This solution is applicable if the distance to the particle source is short compared to the mean free path of cosmic rays and if particles are moving primarily in the radial direction. The angular distribution of particles at large (compared to the mean free path of cosmic rays) distances to the particle source is also analyzed. An analytical expression for the distribution function of cosmic rays in the form of a sum of an isotropic component and a small anisotropic one is derived. It is demonstrated that the angular distribution of cosmic rays depends to a considerable extent on the anisotropy of their scattering. The scattering characteristics of energetic charged particles by fluctuations of interplanetary magnetic fields are estimated based on observational data for several SCR flares.

INTRODUCTION

The propagation of energetic charged particles in turbulent heliospheric magnetic fields is a topical astrophysical issue. Cosmic rays (CR) contain valuable data on the processes of acceleration of particles and their propagation in Galactic magnetic fields and the interplanetary medium. They are an important space weather factor and affect space communications and the operation of spacecraft’s onboard equipment [5, 11, 21].

Solar cosmic rays (SCR) detected by spacecraft and terrestrial detectors provide data on the acceleration processes of charged particles near the Sun and their propagation in the interplanetary medium [5, 11, 21]. The SCR angular distribution depends to a considerable extent on the scattering properties of the interplanetary medium [7, 10, 17, 19]. The SCR distribution function varies throughout a solar proton event. However, it turns out that the CR distribution function obtained by summing the corresponding quantity over the course of an SCR flare contains data on the intensity and anisotropy of energetic particles' scattering in interplanetary magnetic fields [8, 16]. It is known that the SCR distribution function averaged over the flare period is proportional to the steady-state particle distribution function [8, 16]. This remains true regardless of the temporal profile of particle injection into the interplanetary medium near the Sun [8, 16]. Thus, the solution of the steady-state kinetic equation may be used to analyze the characteristics of SCR scattering in the interplanetary magnetic field.

The SCR distributions averaged over the entire event were used in [7, 8, 16, 17] to determine the CR-scattering parameters in the interplanetary medium. Note that the obtained scattering characteristics agree well with the corresponding values determined using the temporal profiles of SCR intensity and anisotropy [19].

Multiple CR scattering in the interplanetary medium was analyzed in [2, 3, 12, 22] on the basis of the Fokker–Planck kinetic equation. The solution of the kinetic equation in the small-angle approximation, which corresponds to an instantaneous point-like particle source, was derived. If the mean free path of cosmic rays is proportional to the distance to the particle source, one may obtain an exact solution of the steady-state kinetic equation [13, 20]. The CR distribution function becomes nearly isotropic over long (compared to the inverse collision frequency) intervals of time from the moment of instantaneous particle injection, thus allowing one to derive an analytical expression for the SCR distribution function [6, 7, 14, 17].

In the present study, the steady-state kinetic equation is solved in the small-angle approximation (when the distance to the particle source is small compared to the mean free path of cosmic rays). An analytical expression for the steady-state CR distribution function away from the particle source is also derived. The parameters of particle scattering in the interplanetary medium are estimated for several SCR flares.

We start from the kinetic equation characterizing the propagation of energetic charged particles in interplanetary magnetic fields [2, 12, 13]:

$$\frac{{\partial f}}{{\partial t}} + {v}\cos \theta \frac{{\partial f}}{{\partial r}} - \frac{{v}}{r}\sin \theta \frac{{\partial f}}{{\partial \theta }} - \frac{{v}}{{2\Lambda \sin \theta }}\frac{\partial }{{\partial \theta }}\sin \theta \frac{{\partial f}}{{\partial \theta }} = \frac{{\delta (r)\delta (t)\delta (\theta )}}{{8{{\pi }^{2}}{{r}^{2}}\sin \theta }},$$

((1))

where f(r, θ, t) is the CR distribution function, v is the particle velocity, θ is the angle between the particle velocity and the radial direction, and Λ is the mean free path of cosmic rays. It is assumed that the CR distribution function depends on a single spatial coordinate r. The last term at the left-hand side of kinetic equation (1) characterizes the process of particle scattering by magnetic field nonuniformities. An instantaneous point-like particle source located at the origin of coordinates is found at the right-hand part of the kinetic equation.

Let us introduce dimensionless variables

$$\rho = \frac{r}{\Lambda },\,\,\,\,\tau = \frac{{{v}t}}{\Lambda }.$$

((2))

Equation (1) rewritten in terms of these new variables takes the following form:

$$\frac{{\partial f}}{{\partial \tau }} + \cos \theta \frac{{\partial f}}{{\partial \rho }} - \frac{{\sin \theta }}{\rho }\frac{{\partial f}}{{\partial \theta }} - \frac{1}{{2\sin \theta }}\frac{\partial }{{\partial \theta }}\sin \theta \frac{{\partial f}}{{\partial \theta }} = \frac{{\delta (\rho )\delta (\tau )\delta (\theta )}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}\sin \theta }}.$$

((3))

MULTIPLE SMALL-ANGLE PARTICLE SCATTERING

Let us examine the CR spatial distribution relying on the steady-state kinetic equation. It is known that the solutions of steady-state kinetic equations contain valuable data on the process of CR scattering in the interplanetary medium [7, 9, 10, 17]. The steady-state kinetic equation corresponding to Eq. (3) is written as

$$\cos \theta \frac{{\partial f}}{{\partial \rho }} - \frac{{\sin \theta }}{\rho }\frac{{\partial f}}{{\partial \theta }} - \frac{1}{{2\sin \theta }}\frac{\partial }{{\partial \theta }}\sin \theta \frac{{\partial f}}{{\partial \theta }} = \frac{{\delta (\rho )\delta (\theta )}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}\sin \theta }}.$$

((4))

The direction of particle motion after injection by a point-like source differs little from the radial one. Therefore, we may limit ourselves to small-angle scattering at the initial SCR flare phase. The SCR propagation was examined by solving the kinetic equations in the small-angle approximation in [2, 3, 12, 22]. Let us write kinetic equation (4) in the small-angle approximation (θ ⪡ 1):

$$\frac{{\partial {{f}_{0}}}}{{\partial \rho }} - \frac{\theta }{\rho }\frac{{\partial {{f}_{0}}}}{{\partial \theta }} - \frac{1}{{2\theta }}\frac{\partial }{{\partial \theta }}\theta \frac{{\partial {{f}_{0}}}}{{\partial \theta }} = \frac{{\delta (\rho )\delta (\theta )}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}\theta }},$$

((5))

where f₀(ρ, θ) is the CR distribution function.

Performing a change of variable

$$\eta = \frac{{{{\theta }^{2}}}}{2},$$

((6))

we obtain

$$\frac{{\partial {{f}_{0}}}}{{\partial \rho }} - \frac{{2\eta }}{\rho }\frac{{\partial {{f}_{0}}}}{{\partial \eta }} - \frac{\partial }{{\partial \eta }}\eta \frac{{\partial {{f}_{0}}}}{{\partial \eta }} = \frac{{\delta (\rho )\delta (\eta )}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}}}.$$

((7))

Introducing new variables

$$\xi = \eta {{\rho }^{2}},\,\,\,\,\zeta = \frac{{{{\rho }^{3}}}}{3},$$

((8))

we rewrite kinetic equation (7) as follows:

$$\frac{{\partial {{f}_{0}}}}{{\partial \zeta }} - \frac{\partial }{{\partial \xi }}\xi \frac{{\partial {{f}_{0}}}}{{\partial \xi }} = \frac{{\delta (\xi )\delta (\zeta )}}{{8{{\pi }^{2}}{{\Lambda }^{3}}}}.$$

((9))

Performing the Laplace transformation

$${{f}_{0}}(\omega ,\xi ) = \int\limits_0^\infty {d\zeta {{f}_{0}}(\zeta ,\xi )\exp ( - \omega \zeta ),} $$

((10))

we obtain the following equation for the Laplace transform of the CR distribution function:

$$\omega {{f}_{0}}(\omega ,\xi ) - \frac{\partial }{{\partial \xi }}\xi \frac{{\partial {{f}_{0}}(\omega ,\xi )}}{{\partial \xi }} = \frac{{\delta (\xi )}}{{8{{\pi }^{2}}{{\Lambda }^{3}}}}.$$

((11))

The change of variable

$$z = 2\sqrt {\omega \xi } $$

((12))

transforms Eq. (11) to the form

$$\frac{\partial }{{\partial z}}z\frac{{\partial {{f}_{0}}}}{{\partial z}} - z{{f}_{0}} + \frac{{\delta (z)}}{{4{{\pi }^{2}}{{\Lambda }^{3}}}} = 0.$$

((13))

Let us write the solution of this equation in the form

$${{f}_{0}}(z) = C{{K}_{0}}(z),$$

((14))

where K₀(z) is the Macdonald function. Constant C is determined from the following condition:

$$\int\limits_0^\infty {dzz{{f}_{0}}(z)} = \frac{1}{{4{{\pi }^{2}}{{\Lambda }^{3}}}}.$$

((15))

The following expression for the Laplace transform of the CR distribution function is thus obtained:

$${{f}_{0}}(\omega ,\xi ) = \frac{{{{K}_{0}}(2\sqrt {\omega \xi } )}}{{4{{\pi }^{2}}{{\Lambda }^{3}}}}.$$

((16))

Performing the inverse Laplace transformation [1], we find

$${{f}_{0}}(\zeta ,\xi ) = \frac{{\exp \left( { - \frac{\xi }{\zeta }} \right)}}{{8{{\pi }^{2}}{{\Lambda }^{3}}\zeta }}.$$

((17))

Let us rewrite this relation in terms of variables ρ and η:

$${{f}_{0}}(\rho ,\eta ) = \frac{{3\exp \left( { - \frac{{3\eta }}{\rho }} \right)}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{3}}}}.$$

((18))

The CR distribution function written in terms of variables ρ and θ takes the following form:

$${{f}_{0}}(\rho ,\theta ) = \frac{{3\exp \left( { - \frac{{3{{\theta }^{2}}}}{{2\rho }}} \right)}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{3}}}}.$$

((19))

The angular distribution of particles in a given point in space (19) is Gaussian with the mean square of angle θ proportional to distance ρ to the particle source. The preexponential factor in (19) is proportional to ρ^–3. The angular distribution of particles is narrow with a well-pronounced maximum in the radial direction (θ = 0) near the particle source and grows wider with distance from the source.

Let us write kinetic equation (4) in the next approximation in small angle θ:

$$\left( {1 - \eta } \right)\frac{{\partial f}}{{\partial \rho }} - \frac{{2\eta }}{\rho }\left( {1 - \frac{\eta }{3}} \right)\frac{{\partial f}}{{\partial \eta }} - \frac{\partial }{{\partial \eta }}\eta \frac{\partial }{{\partial \eta }} + \frac{\eta }{3}\frac{{\partial f}}{{\partial \eta }} = \frac{{\delta (\rho )\delta (\eta )}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}}}.$$

((20))

Note that variable η (6) is proportional to θ². Let us present the CR distribution function in the form

$$f(\rho ,\eta ) = {{f}_{0}}(\rho ,\eta ) + \delta f(\rho ,\eta ),$$

((21))

where function f₀(ρ, η) (18) is the solution of Eq. (7). We consider the spatial region near the particle source (i.e., assume that distance r from the source is short compared to mean free path Λ of cosmic rays). The particles then move primarily in the radial direction (are characterized by small values of η), and function δf is small compared to f₀.

Inserting relation (21) into Eq. (20), we find the following equation for δf:

$$\frac{{\partial \delta f}}{{\partial \rho }} - \frac{{2\eta }}{\rho }\frac{{\partial \delta f}}{{\partial \eta }} - \frac{\partial }{{\partial \eta }}\eta \frac{{\partial \delta f}}{{\partial \eta }} = \Phi (\rho ,\eta ),$$

((22))

where the right-hand side takes the form

$$\Phi (\rho ,\eta ) = \eta \frac{{\partial {{f}_{0}}}}{{\partial \rho }} - \frac{{2{{\eta }^{2}}}}{{3\rho }}\frac{{\partial {{f}_{0}}}}{{\partial \eta }} - \frac{\eta }{3}\frac{{\partial {{f}_{0}}}}{{\partial \eta }}.$$

((23))

Note that small quantity δf was neglected in comparison with f₀ in (23). Function f₀ (18) satisfies Eq. (7). Function δf is the solution of inhomogeneous equation (22). The terms at the right-hand side of Eq. (23) may be calculated based on the known function f₀ (18).

Let us write the equation for the Green’s function satisfying Eq. (22):

$$\frac{{\partial G}}{{\partial \rho }} - \frac{{2\eta }}{\rho }\frac{{\partial G}}{{\partial \eta }} - \frac{\partial }{{\partial \eta }}\eta \frac{{\partial G}}{{\partial \eta }} = \frac{{\delta (\rho - {{\rho }_{0}})\delta (\eta - {{\eta }_{0}})}}{{{{\rho }^{2}}}}.$$

((24))

The solution of Eq. (22) may be written as

$$\delta f(\rho ,\eta ) = \int\limits_0^\infty {d{{\rho }_{0}}\rho _{0}^{2}} \int\limits_0^\infty {d{{\eta }_{0}}G} (\rho ,{{\rho }_{0}};\eta ,{{\eta }_{0}})\Phi ({{\rho }_{0}},{{\eta }_{0}}).$$

((25))

Performing the change of variables (8), we obtain

$$\frac{{\partial G}}{{\partial \zeta }} - \frac{\partial }{{\partial \xi }}\xi \frac{{\partial G}}{{\partial \xi }} = \delta (\zeta - {{\zeta }_{0}})\delta (\xi - {{\xi }_{0}}).$$

((26))

The solution of this equation takes the form

$$G(\zeta ,{{\zeta }_{0}};\xi ,{{\xi }_{0}}) = \frac{1}{{\zeta - {{\zeta }_{0}}}}\exp \left( { - \frac{{\xi + {{\xi }_{0}}}}{{\zeta - {{\zeta }_{0}}}}} \right){{I}_{0}}\left( {\frac{{2\sqrt {\xi {{\xi }_{0}}} }}{{\zeta - {{\zeta }_{0}}}}} \right)\Theta (\zeta - {{\zeta }_{0}}),$$

((27))

where I₀(x) is the modified Bessel function and Θ(x) is the Heaviside function.

Note that variables ξ and ζ are defined by relation (8). Switching to variables ρ and η, we obtain the following relation for the Green’s function:

$$G(\rho ,{{\rho }_{0}};\eta ,{{\eta }_{0}}) = \frac{3}{{{{\rho }^{3}} - \rho _{0}^{3}}}\exp \left( { - \frac{{3({{\rho }^{2}}\eta + \rho _{0}^{2}{{\eta }_{0}})}}{{{{\rho }^{3}} - \rho _{0}^{3}}}} \right){{I}_{0}}\left( {\frac{{6\rho {{\rho }_{0}}\sqrt {\eta {{\eta }_{0}}} }}{{{{\rho }^{3}} - \rho _{0}^{3}}}} \right)\Theta (\rho - {{\rho }_{0}}).$$

((28))

Using relation (28), one may integrate in variable η₀ in (25). We use the following integral value in this integration [4]:

$$\int\limits_0^\infty {dx{{x}^{{\alpha - 1}}}\exp ( - p{{x}^{2}}){{I}_{0}}(cx)} = \frac{1}{2}{{p}^{{{{ - \alpha } \mathord{\left/ {\vphantom {{ - \alpha } 2}} \right. \kern-0em} 2}}}}\Gamma \left( {\frac{\alpha }{2}} \right)\Phi \left( {\frac{\alpha }{2};1;\frac{{{{c}^{2}}}}{{4p}}} \right),$$

((29))

where Φ is the degenerate hypergeometric function.

Integrating in η₀, we obtain

$$\begin{gathered} \delta f(\rho ,\eta ) = \frac{1}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{6}}}}\int\limits_0^\rho {d{{\rho }_{0}}({{\rho }^{3}} - \rho _{0}^{3})\exp \left( { - \frac{{3{{\rho }^{2}}\eta }}{{{{\rho }^{3}} - \rho _{0}^{3}}}} \right)} \\ \times \,\,\left\{ {\frac{{10({{\rho }^{3}} - \rho _{0}^{3})}}{{3{{\rho }^{3}}}}\Phi \left( {3;1;\frac{{3\rho _{0}^{3}\eta }}{{\rho ({{\rho }^{3}} - \rho _{0}^{3})}}} \right) - 2\Phi \left( {2;1;\frac{{3\rho _{0}^{3}\eta }}{{\rho ({{\rho }^{3}} - \rho _{0}^{3})}}} \right)} \right\}. \\ \end{gathered} $$

((30))

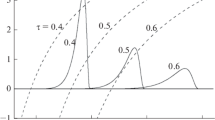
Thus, the CR distribution function is the sum of f₀(ρ, η) (18) and δf(ρ, η) (30). Figure 1 shows the dependence of the CR distribution function on angle θ between the particle velocity and the radial direction at different points in space. The values of dimensionless coordinate ρ are indicated next to the curves. It can be seen that the particle distribution near the source (ρ = 0.01) has a well-pronounced maximum in the radial direction (θ = 0). CR distribution function (18), (21), (30) is normalized to its maximum value at the given point in space (i.e., to f(ρ, 0)). As ρ increases, the angular distribution of particles becomes broader and more gently sloping (Fig. 1).

Fig. 1.

Dependence of the CR distribution function on angle θ between the particle velocity and the radial direction. The values of dimensionless coordinate ρ are indicated next to the curves.

Figure 2 shows the dependence of the CR distribution function on the dimensionless coordinate for different directions of particle motion. The values of angle θ are indicated next to the curves. It can be seen that the maximum of the spatial dependence of the CR distribution function becomes more pronounced at smaller angles θ. As θ increases, the maximum value of the CR distribution function decreases and shifts further away from the particle source (Fig. 2). The angular particle distribution becomes more isotropic as the value of ρ increases (Figs. 1, 2).

Fig. 2.

Dependence of the CR distribution function on the dimensionless coordinate for different directions of particle motion. The values of angle θ are indicated next to the curves.

The CR distribution function may be presented as an expansion in Legendre polynomials:

$$f(\rho ,\theta ) = \sum\limits_{n = 0}^\infty {\frac{{2n + 1}}{2}{{f}_{n}}(\rho ){{P}_{n}}(\cos \theta ),} $$

((31))

where

$${{f}_{n}}(\rho ) = \int\limits_0^\pi {d\theta \sin \theta {{P}_{n}}(\cos \theta )f(\rho ,\theta )} ,$$

((32))

and P_n(x) is the Legendre polynomial. The harmonics of CR distribution function (32) may be calculated based on particle distribution function (18), (21), (30).

The nth order anisotropy of the CR distribution function is defined as

$${{\xi }_{n}}(\rho ) = \frac{{{{f}_{n}}(\rho )}}{{{{f}_{0}}(\rho )}}.$$

((33))

Figure 3 presents the dependence of the CR distribution function anisotropy on the distance to the particle source. The CR anisotropy is close to unity at small values of coordinate ρ: near the source, the particles move primarily in the radial direction, and the CR distribution function has a well-pronounced maximum at θ = 0 (Fig. 1). As ρ increases, the CR angular distribution anisotropy decreases. At a given point in space, the nth order anisotropy decreases as n increases. Note that the values of ξ_n (23) are positive at any ρ (Fig. 3).

Fig. 3.

Dependence of the CR distribution function anisotropy on the distance to the particle source.

DISTRIBUTION FUNCTION OF COSMIC RAYS AWAY FROM THE PARTICLE SOURCE

Let us introduce new variable

$$\mu = \cos \theta .$$

((34))

Kinetic equation (4) is written in terms of variables ρ and μ as

$$\mu \frac{{\partial f}}{{\partial \rho }} + \frac{{1 - {{\mu }^{2}}}}{\rho }\frac{{\partial f}}{{\partial \mu }} - \frac{1}{2}\frac{\partial }{{\partial \mu }}(1 - {{\mu }^{2}})\frac{{\partial f}}{{\partial \mu }} = \frac{{\delta (\rho )\delta (\mu - 1)}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}}}.$$

((35))

Kinetic equation (35) may be rewritten as

$$\frac{1}{{{{\rho }^{2}}}}\frac{\partial }{{\partial \rho }}{{\rho }^{2}}\mu f + \frac{\partial }{{\partial \mu }}\left\{ {(1 - {{\mu }^{2}})\left( {\frac{f}{\rho } - \frac{1}{2}\frac{{\partial f}}{{\partial \mu }}} \right)} \right\} = \frac{{\delta (\rho )\delta (\mu - 1)}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}}}.$$

((36))

Integrating Eq. (36) in μ from –1 to 1, we obtain

$$\frac{1}{{{{\rho }^{2}}}}\frac{\partial }{{\partial \rho }}{{\rho }^{2}}{{f}_{1}} = \frac{{\delta (\rho )}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}}},$$

((37))

where

$${{f}_{1}}(\rho ) = \int\limits_{ - 1}^1 {d\mu \mu f(\rho ,\mu )} $$

((38))

is the first harmonic of the CR distribution function.

The solution of Eq. (37) takes the form

$${{f}_{1}}(\rho ) = \frac{1}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}}}.$$

((39))

According to (39), f₁ is inversely proportional to the squared distance from the particle source.

The CR angular distribution anisotropy decreases with distance from the particle source: the particle distribution becomes more isotropic. At large distances from the source (larger than several mean free paths of cosmic rays), the CR distribution function may be presented as a sum of isotropic component f₀(ρ) and small anisotropic component δf(ρ, μ) [6, 7, 16]:

$$f(\rho ,\mu ) = \frac{1}{2}{{f}_{0}}(\rho ) + \delta f(\rho ,\mu ),$$

((40))

where

$${{f}_{0}}(\rho ) = \int\limits_{ - 1}^1 {f(\rho ,\mu )d\mu } .$$

((41))

The anisotropic component of the CR distribution function satisfies the following equation:

$$\int\limits_{ - 1}^1 {d\mu \delta f(\rho ,\mu )} = 0.$$

((42))

Since the anisotropic component of the CR distribution function is small at large distances from the particle source (δf ⪡ f₀), it follows from kinetic equation (36) that

$$\frac{\partial }{{\partial \mu }}\left\{ {(1 - {{\mu }^{2}})\left( {\frac{{\delta f}}{\rho } - \frac{1}{2}\frac{{\partial \delta f}}{{\partial \mu }}} \right)} \right\} = - \frac{\mu }{2}\frac{{\partial {{f}_{0}}}}{{\partial \rho }}.$$

((43))

The solution of Eq. (43) is sought in the form [7, 13, 20]

$$\delta f(\rho ,\mu ) = a(\rho )\exp \left( {\frac{{2\mu }}{\rho }} \right) + b(\rho ),$$

((44))

where a(ρ) and b(ρ) are independent of μ. The solution of Eq. (43) satisfying condition (42) has the form

$$\delta f(\rho ,\mu ) = - \frac{1}{{2\sinh \frac{2}{\rho }}}\frac{{\partial {{f}_{0}}}}{{\partial \rho }}\left\{ {\exp \left( {\frac{{2\mu }}{\rho }} \right) - \frac{\rho }{2}\sinh \frac{2}{\rho }} \right\},$$

((45))

where sinhx is the hyperbolic sine of x.

Integrating relation (45) in μ with weight μ, we obtain the following expression for the first harmonic of the CR distribution function:

$${{f}_{1}}(\rho ) = - \frac{\rho }{4}\frac{{\partial {{f}_{0}}}}{{\partial \rho }}\left\{ {2\coth \frac{2}{\rho } - \rho } \right\},$$

((46))

where cothx is the hyperbolic cotangent of x. Using relation (39) for f₁, we obtain the following:

$${{f}_{0}}(\rho ) = \frac{1}{{2{{\pi }^{2}}{{\Lambda }^{3}}}}\int\limits_\rho ^\infty {\frac{{d{{\rho }_{1}}}}{{\rho _{1}^{3}\left( {2\coth \frac{2}{{{{\rho }_{1}}}} - {{\rho }_{1}}} \right)}}} .$$

((47))

It follows from (47) that f₀ is inversely proportional to ρ at large distances from the particle source (ρ ⪢ 1).

Inserting (47) into formula (45), we obtain the expression for the anisotropic component of the CR distribution function

$$\delta f(\rho ,\mu ) = \frac{{\exp \frac{{2\mu }}{\rho } - \frac{\rho }{2}\sinh \frac{2}{\rho }}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{3}}\left( {\cosh \frac{2}{\rho } - \frac{\rho }{2}\sinh \frac{2}{\rho }} \right)}},$$

((48))

where coshx is the hyperbolic cosine of x. The obtained expression demonstrates that the anisotropic component of the CR distribution function is a sum with the first term of it depending exponentially on μ and the second term being independent of μ [7, 9, 13, 20].

The dependence of the CR distribution function on angle θ is presented in Fig. 4. The values of dimensionless coordinate ρ are indicated next to the curves. Solid curves correspond to CR distribution function (40), (47), (48). Dashed curves characterize the angular particle distribution in the small-angle approximation (18), (30). The angular particle distribution near the source has a well-pronounced maximum in the radial direction (θ = 0), and the number of particles moving toward the source is negligible (dashed curves in Fig. 4). At large distances from the source, the number of particles moving toward it becomes significant, and the CR distribution function is more isotropic (solid curves in Fig. 4).

Fig. 4.

Angular particle distributions at different points in space. The values of dimensionless coordinate ρ are indicated next to the curves.

Relation (48) for the anisotropic component of the CR distribution function allows one to calculate the harmonics of the angular particle distribution

$${{f}_{n}}(\rho ) = \int\limits_{ - 1}^1 {d\mu {{P}_{n}}(\mu )\delta f(\rho ,\mu )} ,\,\,\,\,n \geqslant 1.$$

((49))

The first harmonic of the CR distribution function is given by (39). The following expressions correspond to the next three harmonics:

$${{f}_{2}}(\rho ) = \frac{{(4 + 3{{\rho }^{2}})\sinh \frac{2}{\rho } - 6\rho \cosh \frac{2}{\rho }}}{{32{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}\left( {\cosh \frac{2}{\rho } - \frac{\rho }{2}\sinh \frac{2}{\rho }} \right)}},$$

((50))

$${{f}_{3}}(\rho ) = \frac{{\left( {1 + \frac{{15}}{4}{{\rho }^{2}}} \right)\cosh \frac{2}{\rho } - \rho \left( {3 + \frac{{15}}{8}{{\rho }^{2}}} \right)\sinh \frac{2}{\rho }}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}\left( {\cosh \frac{2}{\rho } - \frac{\rho }{2}\sinh \frac{2}{\rho }} \right)}},$$

((51))

$${{f}_{4}}(\rho ) = \frac{{\left( {8 + 30{{\rho }^{2}} + \frac{{105}}{2}{{\rho }^{4}}} \right)\sinh \frac{2}{\rho } - 5\rho \left( {8 + 21{{\rho }^{2}}} \right)\cosh \frac{2}{\rho }}}{{64{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}\left( {\cosh \frac{2}{\rho } - \frac{\rho }{2}\sinh \frac{2}{\rho }} \right)}}.$$

((52))

The obtained relations provide an opportunity to calculate CR angular distribution anisotropy (33). The dependence of the CR anisotropy on the distance to the particle source is shown in Fig. 5. Solid curves correspond to the discussed case of isotropic particle scattering. It can be seen that all ξ_n values are positive and decrease as coordinate ρ increases. At large values of ρ (ρ ≳ 2), the angular particle distribution anisotropy may be represented by ξ₁ (Fig. 5), and the anisotropic component of the CR distribution function is proportional to μ = cos θ.

Fig. 5.

Dependence of the angular particle distribution anisotropy on the dimensionless coordinate. Solid and dashed curves correspond to isotropic and anisotropic (q = 5/3) scattering.

DISTRIBUTION FUNCTION OF COSMIC RAYS UNDER ANISOTROPIC PARTICLE SCATTERING

It is known that the CR scattering in the interplanetary medium is anisotropic and the scattering of particles moving perpendicularly to the magnetic field is suppressed [5, 7, 10, 13]. Let us consider the CR propagation in the radial magnetic field approximation. It is then assumed that the mean interplanetary magnetic field vector is oriented radially. Note that this approach is inapplicable at large heliocentric distances (when the spiral shape of the interplanetary magnetic field lines needs to be taken into account).

Under isotropic scattering, the angular CR diffusion coefficient is proportional to 1 – μ², and the kinetic equation has the form of Eq. (35). Let us write the steady-state kinetic equation corresponding to anisotropic scattering:

$$\mu \frac{{\partial f}}{{\partial \rho }} + \frac{{1 - {{\mu }^{2}}}}{\rho }\frac{{\partial f}}{{\partial \mu }} - \frac{\partial }{{\partial \mu }}{{D}_{{\mu \mu }}}\frac{{\partial f}}{{\partial \mu }} = \frac{{\delta (\rho )\delta (\mu - 1)}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}}},$$

((53))

where D_μμ is the coefficient of CR diffusion over angles of the particle velocity vector. This angular CR diffusion coefficient may be written as

$${{D}_{{\mu \mu }}} = \frac{{{{D}_{0}}(\mu )}}{2}(1 - {{\mu }^{2}}).$$

((54))

Note that D₀(μ) = 1 under isotropic particle scattering. Let us assume that function D₀(μ) under anisotropic particle scattering has a minimum at μ = 0.

Kinetic equation (53) may be written as

$$\frac{1}{{{{\rho }^{2}}}}\frac{\partial }{{\partial \rho }}{{\rho }^{2}}\mu f + \frac{\partial }{{\partial \mu }}\left\{ {(1 - {{\mu }^{2}})\left( {\frac{f}{\rho } - \frac{{{{D}_{0}}(\mu }}{2}\frac{{\partial f}}{{\partial \mu }}} \right)} \right\} = \frac{{\delta (\rho )\delta (\mu - 1)}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}}}.$$

((55))

Under isotropic particle scattering, D₀ is equal to unity and kinetic equation (55) is the same as Eq. (36). Let us present the CR distribution function as a sum of isotropic and anisotropic components (40). The following is obtained for the anisotropic component of the CR distribution function:

$$\frac{\partial }{{\partial \mu }}\left\{ {(1 - {{\mu }^{2}})\left( {\frac{{\delta f}}{\rho } - \frac{{{{D}_{0}}(\mu )}}{2}\frac{{\partial \delta f}}{{\partial \mu }}} \right)} \right\} = - \frac{\mu }{2}\frac{{\partial {{f}_{0}}}}{{\partial \rho }}.$$

((56))

Function G(μ) is defined as [7, 13]

$$G(\mu ) = \frac{1}{\rho }\int\limits_0^\mu {d\mu \frac{{1 - {{\mu }^{2}}}}{{{{D}_{{\mu \mu }}}}} = \frac{2}{\rho }\int\limits_0^\mu {\frac{{d\mu }}{{{{D}_{0}}(\mu )}}.} } $$

((57))

Note that function (57) is proportional to μ under isotropic scattering:

$$G(\mu ) = \frac{2}{\rho }\mu .$$

((58))

The solution of Eq. (56) is sought in the form [7, 13, 20]

$$\delta f(\rho ,\mu ) = a(\rho )\exp (G(\mu )) + b(\rho ).$$

((59))

The solution of kinetic equation (56) satisfying condition (42) has the form

$$\delta f(\rho ,\mu ) = - \frac{\rho }{2}\frac{{\partial {{f}_{0}}}}{{\partial \rho }}\frac{{\exp (G(\mu )) - \frac{1}{2}\int\limits_{ - 1}^1 {d\mu \exp (G(\mu ))} }}{{\int\limits_{ - 1}^1 {d\mu \exp (G(\mu ))} }}.$$

((60))

The formula for the first harmonic of the CR distribution function follows from relation (60):

$${{f}_{1}}(\rho ) = - \frac{\rho }{2}\frac{{\partial {{f}_{0}}}}{{\partial \rho }}\frac{{\int\limits_{ - 1}^1 {d\mu \mu \exp (G(\mu ))} }}{{\int\limits_{ - 1}^1 {d\mu \exp (G(\mu ))} }}.$$

((61))

Using relations (39) and (61), we obtain the following expression for f₀(ρ):

$${{f}_{0}}(\rho ) = \frac{1}{{4{{\pi }^{2}}{{\Lambda }^{3}}}}\int\limits_\rho ^\infty {d{{\rho }_{1}}} \frac{{\int\limits_{ - 1}^1 {d\mu \exp (G(\mu ))} }}{{\rho _{1}^{3}\int\limits_{ - 1}^1 {d\mu \mu \exp (G(\mu ))} }}.$$

((62))

Thus, the anisotropic component of the CR distribution function takes the form

$$\delta f(\rho ,\mu ) = \frac{1}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}}}\frac{{\exp (G(\mu )) - \frac{1}{2}\int\limits_{ - 1}^1 {d\mu \exp (G(\mu ))} }}{{\int\limits_{ - 1}^1 {d\mu \mu \exp (G(\mu ))} }}.$$

((63))

Note that relation (48) follows from formula (63) if the scattering is isotropic.

Let us write D₀(μ) in the form [7, 13, 15, 18]

$${{D}_{0}}(\mu ) = \frac{3}{{(4 - q)(2 - q)}}{{\left| \mu \right|}^{{q - 1}}},$$

((64))

where q is the index of power of an random magnetic field (1 ≤ q < 2). Under isotropic particle scattering, q = 1. As q increases, the scattering becomes more anisotropic. Function G(μ) (57) corresponding to D₀(μ) (64) is given by

$$G(\mu ) = \frac{2}{{3\rho }}(4 - q)\mu {{\left| \mu \right|}^{{1 - q}}}.$$

((65))

Figure 6 presents the dependence of the CR distribution function at a given point in space on μ. The CR distribution function satisfies relations (40), (62), (63), and (65). The value of the particle distribution function is normalized to the maximum value f(1). Dashed and solid curves correspond to isotropic (q = 1) and anisotropic (q = 5/3) particle scattering. The dimensionless coordinate values are indicated next to the curves. Under isotropic scattering, the dependence of the CR distribution function on μ is exponential. In the case of anisotropic scattering (solid curves in Fig. 6), the f(μ) dependence changes abruptly near μ = 0. This behavior of the angular dependence of the CR distribution function is attributable to the fact that form (64) was chosen for the angular particle diffusion coefficient.

Fig. 6.

Dependence of the CR distribution function at different points in space (see the numbers next to curves) on μ. Dashed and solid curves correspond to isotropic (q = 1) and anisotropic (q = 5/3) particle scattering.

Using relation (64) for the anisotropic component of the CR distribution function, one may calculate the harmonics of the angular particle distribution:

$${{f}_{n}}(\rho ) = \frac{1}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}}}\frac{{\int\limits_{ - 1}^1 {d\mu {{P}_{n}}(\mu )\exp (G(\mu ))} }}{{\int\limits_{ - 1}^1 {d\mu \mu \exp (G(\mu ))} }},\,\,\,\,n \geqslant 1.$$

((66))

Dashed curves in Fig. 5 illustrate the dependence of the CR anisotropy on the dimensionless coordinate under anisotropic particle scattering (q = 5/3). Note that the ξ₁ and ξ₂ values are positive, while ξ₃ and ξ₄ are negative (Fig. 5). The first-order anisotropy under anisotropic scattering differs little from the corresponding value typical of isotropic scattering. The value of ξ₂ is considerably lower in the case of anisotropic scattering (Fig. 5).

The approach based on the steady-state solution of the kinetic equation allows one to estimate both the intensity and the anisotropy of scattering of charged particles by fluctuations of the interplanetary magnetic field [7, 8, 16, 17]. The SCR scattering intensity varies significantly from one event to another. For example, the solar proton events of April 8, 1978, February 16, 1984, and October 22, 1989, were characterized by weak CR scattering in the interplanetary medium, and the mean free path of energetic particles was comparable to an astronomical unit [7, 9–11, 14, 16, 17, 19]. At the same time, many SCR flares occurred when the interplanetary magnetic field was highly turbulent; particles were scattered by field nonuniformities, and the mean free path of cosmic rays was considerably shorter than the distance to the particle source [7, 16, 19].

The obtained relations for the SCR angular distribution anisotropy provide an opportunity to estimate the mean free path of cosmic rays in the interplanetary medium and the anisotropy of particle scattering. The SCR flare of March 28, 1976, was detected by the Helios I spacecraft at a heliocentric distance of 0.495 AU [9, 16, 19]. According to observational data, the anisotropy of the angular distribution of protons with energies falling within the 4–13 MeV interval was ξ₁ = 0.22. The quantity characterizing the second harmonic of the angular particle distribution was ξ₂ = 0.05 [16]. The above relations allow one to estimate the CR scattering parameters for this flare. The obtained value of the mean free path of cosmic rays is Λ = 0.36 AU, and the parameter characterizing the scattering anisotropy is q = 1.2. Note that similar values of Λ for this flare were reported in [16, 19]. The proton event of November 19, 1981, was detected by Helios I at a heliocentric distance of 0.641 AU [16, 19]. The CR scattering in the interplanetary medium was relatively weak at the time. The following values of the SCR angular distribution anisotropy were determined: ξ₁ = 0.35 and ξ₂ = 0.06 [16]. According to our estimates, the CR scattering in the interplanetary medium was considerably anisotropic back then: parameter q, which characterizes the scattering anisotropy, was estimated at 1.8. The scattering intensity turned out to be low: mean CR free path Λ = 0.8 AU.

ANALYTICAL SOLUTION OF THE STEADY-STATE KINETIC EQUATION

Let us consider the case when the SCR scattering intensity is inversely proportional to the distance to the particle source. It is known that the steady-state kinetic equation then has an exact analytical solution [13, 20]. If the mean free path of particles is proportional to the coordinate, the CR diffusion coefficient is inversely proportional to heliocentric distance r. Let us introduce dimensionless coordinate ρ in the form

$$\rho = \frac{r}{{{{\Lambda }_{0}}}},$$

((67))

where Λ₀ is a constant. If the mean free path of particles is proportional to the heliocentric distance, the angular CR diffusion coefficient is inversely proportional to the distance. Let us write D_μμ in the following form:

$${{D}_{{\mu \mu }}} = \frac{{{{D}_{0}}(\mu )}}{{2\rho }}(1 - {{\mu }^{2}}).$$

((68))

The steady-state kinetic equation is given by (53), and dimensionless coordinate ρ is defined by (67). Inserting expression (68) for the angular diffusion coefficient into Eq. (53), we obtain

$$\mu \frac{{\partial f}}{{\partial \rho }} + \frac{{1 - {{\mu }^{2}}}}{\rho }\frac{{\partial f}}{{\partial \mu }} - \frac{1}{{2\rho }}\frac{\partial }{{\partial \mu }}{{D}_{0}}(\mu )(1 - {{\mu }^{2}})\frac{{\partial f}}{{\partial \mu }} = \frac{{\delta (\rho )\delta (\mu - 1)}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}}}.$$

((69))

The solution of Eq. (69) is sought in the form [13, 20]

$$f(\rho ,\mu ) = a(\rho )\exp (G(\mu )),$$

((70))

where

$$G(\mu ) = 2\int\limits_0^\mu {\frac{{d\mu }}{{{{D}_{0}}(\mu )}}} .$$

((71))

In the special case when D₀(μ) is defined by (69), function G(μ) takes the form

$$G(\mu ) = \frac{{2(4 - q)}}{3}\mu {{\left| \mu \right|}^{{1 - q}}}.$$

((72))

One may define function a(ρ) using relation (39) for the first harmonic of the angular particle distribution. The CR distribution function satisfying steady-state kinetic equation (69) is written as

$$f(\rho ,\mu ) = \frac{{\exp (G(\mu ))}}{{8{{\pi }^{2}}{{\Lambda }^{3}}{{\rho }^{2}}\int\limits_{ - 1}^1 {d\mu \mu \exp (G(\mu ))} }}.$$

((73))

Thus, according to formula (73), the CR distribution function is inversely proportional to the distance from the source squared, and the shape of the angular particle distribution is independent of coordinates. For example, the value of CR distribution function f(μ) normalized to its maximum value remains the same at any point in space.

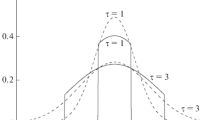
Figure 7 shows the dependence of distribution function (72), (73) on μ at different values of parameter q characterizing the particle scattering anisotropy. The CR distribution function is normalized to its maximum value f(1), and the values of q are indicated next to the curves. Under isotropic scattering (q = 1), the dependence of the CR distribution function on μ is exponential. As the scattering becomes more anisotropic, the relative number of particles moving away from the source increases. Note that the particle number changes abruptly in the region of angles near μ = 0 when the scattering is anisotropic.

Fig. 7.

Angular particle distribution under anisotropic scattering. The values of parameter q characterizing the scattering anisotropy are indicated next to the curves.

CONCLUSIONS

The steady-state kinetic equation, which characterizes the propagation of solar cosmic rays in the interplanetary medium, was solved in the small-angle approximation. The obtained solution is applicable if the distance to the particle source is short compared to the mean free path of cosmic rays and if particles are moving primarily in the radial direction. It was demonstrated that the CR angular distribution becomes more isotropic with distance from the source.

The angular particle distribution at distances from the source exceeding the mean free path of cosmic rays was also studied. The CR distribution function may be presented in this case in the form of a sum of an isotropic component and a small anisotropic one. An analytical expression for the CR distribution function was derived, and it was demonstrated that the angular particle distribution anisotropy depends to a considerable extent on the scattering anisotropy and decreases with distance from the particle source. The mean free path of cosmic rays and the parameter characterizing the anisotropy of particle scattering in the interplanetary medium were estimated based on observational data for several SCR flares detected by spacecraft.