Cosmic-Ray Distribution Function under Anisotropic Scattering of Particles by Magnetic-Field Fluctuations

Abstract

The acceleration of energetic particles and their propagation in magnetic fields of the solar wind and the Galaxy is a topical astrophysical problem. Cosmic rays (CR) affect communications and the operation of on-board spacecraft electronics and disturb the magnetosphere and the ionosphere of the Earth. The scattering of particles by magnetic-field irregularities is the primary mechanism governing the CR propagation in the interplanetary medium. If the scattering of energetic particles in the interplanetary medium is relatively inefficient (i.e., the mean free path is comparable to the heliocentric distance), a kinetic equation should be used to characterize the CR propagation. The Fokker–Planck kinetic equation is used to analyze the propagation of charged energetic particles in a magnetic field represented as a superposition of a mean uniform field and magnetic inhomogeneities of various scales. This kinetic equation corresponds to multiple small-angle scattering, and its collision integral characterizes particle diffusion in the momentum space. A system of differential equations for the spherical harmonics of the CR distribution function is obtained based on the kinetic equation. The CR transport equations are derived and solved. The evolution of the CR distribution function under anisotropic scattering of particles by magnetic-field fluctuations is examined. It is demonstrated that the angular distribution function of particles depends to a considerable extent on the degree of their scattering anisotropy. The temporal dependence of the CR distribution function is analyzed, and the parameter characterizing the scattering anisotropy is estimated.

The acceleration and propagation of charged energetic particles in the Solar System is a topical problem of physics of the heliosphere. Cosmic rays (CR) provide valuable data regarding the properties of solar-wind plasma and the electromagnetic conditions near the Sun and in the interplanetary medium. They pose a threat to spacecraft electronics and crews and penetrate into the polar regions of the terrestrial atmosphere, thus being a hazard to airliners. Cosmic rays are a factor of space weather that affects space communications and the operation of satellite equipment and disturbs the magnetosphere and the ionosphere of the Earth [25, 28, 31].

The scattering by magnetic-field irregularities is the primary mechanism governing the propagation of solar cosmic rays (SCR) in the interplanetary medium. If the CR scattering in the interplanetary medium is relatively efficient (i.e., the mean free path of particles is small compared to the heliocentric distance), a diffusion equation may be used to characterize the CR propagation. The diffusion approximation is valid when the spatial and temporal scales of variation of the CR distribution function are much larger than the mean free path and the characteristic scattering time, respectively [4, 12, 20, 22]. If the CR scattering is weak, a kinetic equation is needed to characterize the propagation of charged energetic particles [1, 4, 11, 15, 16, 22, 24]. The authors of [15, 16, 22, 24] have used the Boltzmann kinetic equation, which corresponds to arbitrary-angle particle scattering, to analyze the SCR propagation. The Fokker–Planck kinetic equation corresponds to multiple small-angle scattering, and its collision integral characterizes particle diffusion in the momentum space. This equation was used to examine the SCR propagation in the interplanetary medium in [1, 3, 5, 11, 23, 30].

If particles undergo several collisions with magnetic inhomogeneities and their distribution function becomes near-isotropic, a telegraph equation is used to characterize the CR propagation [6, 7, 12, 18]. The propagation velocity of disturbances in the telegraph equation obtained in these studies is ${v \mathord{\left/ {\vphantom {v {\sqrt 3 }}} \right. \kern-0em} {\sqrt 3 }},$ where v is the particle velocity. A modified telegraph equation, which correctly handles the small-parameter expansion of the CR distribution function, was derived in [19]. It turns out that a different “signal” velocity, which depends on the nature of particle scattering [17, 19, 29], corresponds to the modified telegraph equation. Both telegraph and hyperdiffusion equations were used in recent analyses of the SCR propagation [14, 26, 27]. The hyperdiffusion equation differs from the diffusion one in that it features higher-order derivatives of the particle density with respect to the spatial variable (e.g., the fourth coordinate derivative is present in the CR transport equation [14, 26, 27]).

The SCR distribution function contains information on the scattering properties of the interplanetary medium [8–10, 33]. It is known that the angular distribution of charged energetic particles is directly related to the characteristics of CR scattering in the interplanetary medium [8, 10, 33]. The analytical expressions for the anisotropic component of the SCR distribution function obtained in these studies were used to analyze a number of proton events. Specifically, the angular SCR distributions measured by Helios 1 and Helios 2 at a heliocentric distance of 0.5 AU were examined, and the parameters of scattering of energetic solar particles were determined [8, 33].

The present study is focused on the propagation of charged energetic particles in a magnetic field represented as a superposition of a mean uniform field and magnetic inhomogeneities of various scales. The CR transport equations (diffusion and hyperdiffusion equations and the modified telegraph equation) are derived using the Fokker–Planck kinetic equation, and their solutions are presented. The evolution of the CR distribution function under isotropic and anisotropic scattering of particles by fluctuations of the interplanetary magnetic field is examined.

KINETIC EQUATION

Let us start from the following kinetic equation characterizing the CR propagation in interplanetary magnetic fields [1, 4, 11, 13]:

$$\frac{{\partial f}}{{\partial t}} + v\mu \frac{{\partial f}}{{\partial z}} - \frac{\partial }{{\partial \mu }}{{\tilde {D}}_{{\mu \mu }}}\frac{{\partial f}}{{\partial \mu }} = \frac{1}{2}\delta (z)\delta (t),$$

((1))

where f(z, μ, t) is the CR distribution function, v is the particle velocity, z is the coordinate along a uniform regular magnetic field, and μ = cosθ (θ is the pitch angle). It is assumed that the CR distribution function depends on one spatial coordinate z. An instantaneous point-like particle source located at the origin of coordinates is found at the right-hand side of the above equation. The last term at the left-hand side of Eq. (1) characterizes the process of particle scattering by magnetic-field inhomogeneities. The diffusion of particles over pitch angles is characterized by coefficient

$${{\tilde {D}}_{{\mu \mu }}} = \frac{1}{2}{{\tilde {D}}_{0}}(\mu )(1 - {{\mu }^{2}}).$$

((2))

In the case of isotropic particle scattering, ${{\tilde {D}}_{0}}$ is independent of μ and may be written as

$${{\tilde {D}}_{0}} = \frac{v}{\Lambda },$$

((3))

where Λ is the CR free path. Note that free path Λ is related to diffusion coefficient ${{\tilde {D}}_{{\mu \mu }}}$ in the following way [20–22]:

$$\Lambda = \frac{{3v}}{8}\int\limits_{ - 1}^1 {d\mu } \frac{{{{{(1 - {{\mu }^{2}})}}^{2}}}}{{{{{\tilde {D}}}_{{\mu \mu }}}}}.$$

((4))

Let us switch to dimensionless variables

$$y = \frac{z}{\Lambda },\,\,\,\,\tau = \frac{{vt}}{\Lambda },$$

((5))

where distance y and time τ are measured in units of Λ and characteristic scattering time Λ/v, respectively. Kinetic equation (1) then takes the following form:

$$\frac{{\partial f}}{{\partial \tau }} + \mu \frac{{\partial f}}{{\partial y}} - \frac{\partial }{{\partial \mu }}{{D}_{{\mu \mu }}}\frac{{\partial f}}{{\partial \mu }} = \frac{1}{{2\Lambda }}\delta (y)\delta (\tau ),$$

((6))

where dimensionless diffusion coefficient D_μμ is given by

$${{D}_{{\mu \mu }}} = \frac{\Lambda }{v}{{\tilde {D}}_{{\mu \mu }}}.$$

((7))

SYSTEM OF EQUATIONS FOR HARMONICS OF THE CR DISTRIBUTION FUNCTION

Let us consider isotropic particle scattering by magnetic inhomogeneities. CR diffusion coefficient D_μμ then takes the form

$${{D}_{{\mu \mu }}} = \frac{1}{2}(1 - {{\mu }^{2}}).$$

((8))

The CR distribution function may be expressed as an expansion in Legendre polynomials depending on μ. If the time elapsed after particle injection is much larger than the inverse collision rate (t$\gg$ Λ/v), the particle distribution function becomes near-isotropic, and the lowest-order harmonics produce the dominant contribution to the expansion of the distribution function. An infinite system of differential equations for harmonics of the CR distribution function may be obtained based on the kinetic equation [13, 17, 32]. Let us present CR distribution function f(y, μ, τ) in the following form:

$$f(y,\mu ,\tau ) = \sum\limits_{n = 0}^\infty {\frac{{2n + 1}}{2}{{f}_{n}}(y,\tau )} {{P}_{n}}(\mu ),$$

((9))

where

$${{f}_{n}}(y,\tau ) = \int\limits_{ - 1}^1 {d\mu {{P}_{n}}(\mu )f(y,\mu ,\tau )} ,$$

((10))

and P_n(μ) is the Legendre polynomial. Multiplying kinetic equations (6) and (8) successively by 1, μ, and P₂(μ) and integrating the obtained relations in μ, we obtain the following system of equations:

$$\frac{{\partial {{f}_{0}}}}{{\partial \tau }} + \frac{{\partial {{f}_{1}}}}{{\partial y}} = \Psi (y,\tau ),$$

((11))

$$\frac{{\partial {{f}_{1}}}}{{\partial \tau }} + {{f}_{1}} + \frac{1}{3}\frac{{\partial {{f}_{0}}}}{{\partial y}} + \frac{2}{3}\frac{{\partial {{f}_{2}}}}{{\partial y}} = 0,$$

((12))

$$\frac{{\partial {{f}_{2}}}}{{\partial \tau }} + 3{{f}_{2}} + \frac{2}{5}\frac{{\partial {{f}_{1}}}}{{\partial y}} + \frac{3}{5}\frac{{\partial {{f}_{3}}}}{{\partial y}} = 0,$$

((13))

where

$$\Psi (y,\tau ) = \frac{{\delta (y)\delta (\tau )}}{\Lambda }.$$

((14))

Let us assume that the CR distribution function varies sufficiently slow $\frac{{\partial {{f}_{1}}}}{{\partial \tau }} \ll {{f}_{1}}$ and neglect second harmonic f₂ in comparison with f₀. Under these assumptions, Eq. (12) takes the form

$${{f}_{1}} = - \frac{1}{3}\frac{{\partial {{f}_{0}}}}{{\partial y}}.$$

((15))

Inserting (15) into Eq. (11), we obtain the diffusion equation for f₀:

$$\frac{{\partial {{f}_{0}}}}{{\partial \tau }} - \frac{1}{3}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{y}^{2}}}} = \Psi (y,\tau ).$$

((16))

Its solution is written as

$${{f}_{0}}(y,\tau ) = \frac{{\sqrt 3 }}{{2\Lambda \sqrt {\pi \tau } }}\exp \left( { - \frac{{3{{y}^{2}}}}{{4\tau }}} \right).$$

((17))

Neglecting the third harmonic in Eq. (13) in comparison with the first one and also neglecting $\frac{{\partial {{f}_{2}}}}{{\partial \tau }}$ in comparison with f₂, we obtain

$$3{{f}_{2}} + \frac{2}{5}\frac{{\partial {{f}_{1}}}}{{\partial y}} = 0.$$

((18))

The following CR transport equation may be derived from the system of equations (11), (12), and (18) [17]:

$$\begin{gathered} \frac{{\partial {{f}_{0}}}}{{\partial \tau }} - \frac{1}{3}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{\tau }^{2}}}} - \frac{4}{{45}}\frac{{{{\partial }^{3}}{{f}_{0}}}}{{\partial {{y}^{2}}\partial \tau }} \\ = \Psi (y,\tau ) + \frac{{\partial \Psi (y,\tau )}}{{\partial \tau }} - \frac{4}{{45}}\frac{{{{\partial }^{2}}\Psi (y,\tau )}}{{\partial {{y}^{2}}}}. \\ \end{gathered} $$

((19))

Note that this equation contains the second time derivative of f₀ and the mixed derivative with respect to y and τ. Equation (19) may be solved by applying the coordinate Fourier transform and the temporal Laplace transform. The solution has the following form [17]:

$${{f}_{0}}(y,\tau ) = \frac{{\exp ({{ - \tau } \mathord{\left/ {\vphantom {{ - \tau } 2}} \right. \kern-0em} 2})}}{{\pi \Lambda }}\int\limits_0^\infty {dk\cos ky\exp \left( { - \frac{2}{{45}}{{k}^{2}}\tau } \right)} \left\{ {{\text{cosh}}\frac{{2\tau }}{{45}}\sqrt \Gamma + \frac{{{{k}^{2}} + {{45} \mathord{\left/ {\vphantom {{45} 4}} \right. \kern-0em} 4}}}{{\sqrt \Gamma }}\sinh \frac{{2\tau }}{{45}}\sqrt \Gamma ,} \right\}$$

((20))

where

$$\Gamma (k) = {{k}^{4}} - \frac{{585}}{4}{{k}^{2}} + \frac{{2025}}{{16}},$$

((21))

and coshx and sinhx are the hyperbolic cosine and the hyperbolic sine.

If τ $\gg$ 1, Eq. (20) yields the following approximate expression for f₀:

$${{f}_{0}}(y,\tau ) = \frac{{\sqrt 3 }}{{2\Lambda \sqrt {\pi \tau } }}\exp \left( { - \frac{{3{{y}^{2}}}}{{4\tau }}} \right)\left( {1 - \frac{1}{{20\tau }} + \frac{{9{{y}^{2}}}}{{10{{\tau }^{2}}}}} \right).$$

((22))

At large values of dimensionless time τ, expression (22) for f₀ is the solution of diffusion equation (17).

Relying on CR diffusion equation (16), one may find expressions for the last two terms of Eq. (19) using the fourth derivative of function f₀ with respect to spatial coordinate y. The CR hyperdiffusion equation is obtained as a result [26, 27]:

$$\frac{{\partial {{f}_{0}}}}{{\partial \tau }} - \frac{1}{3}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{y}^{2}}}} + \frac{{11}}{{135}}\frac{{{{\partial }^{4}}{{f}_{0}}}}{{\partial {{y}^{4}}}} = \Psi (y,\tau ) - \frac{1}{3}\frac{{{{\partial }^{2}}\Psi (y,\tau )}}{{\partial {{y}^{2}}}}.$$

((23))

The solution of this equation is written as

$${{f}_{0}}(y,\tau ) = \frac{1}{{\pi \Lambda }}\int\limits_0^\infty {dk} \left( {1 + \frac{{{{k}^{2}}}}{3}} \right)\cos ky\exp \left( { - \frac{{{{k}^{2}}}}{3}\tau - \frac{{11}}{{135}}{{k}^{4}}\tau } \right),$$

((24))

Note that relation (22) follows from (24) if condition τ $\gg$ 1 is satisfied.

TELEGRAPH EQUATION FOR THE CR DENSITY

It was demonstrated in [6, 7, 12, 18] that the telegraph equation may be used to characterize the CR propagation in the interplanetary medium. Both the diffusion nature of CR transport and the characteristic features of wave propagation of particles are factored into this approach. In contrast to the diffusion equation with an infinite propagation velocity of disturbances, the telegraph equation is characterized by a finite “signal” propagation velocity that is proportional to the particle velocity. The telegraph equation for the CR density obtained in [6, 7, 12, 18] corresponds to a propagation velocity of disturbances of ${v \mathord{\left/ {\vphantom {v {\sqrt 3 }}} \right. \kern-0em} {\sqrt 3 }}$, where v is the particle velocity. If particles were injected at point z = 0 at the initial time, the solution of the telegraph equation implies that particles are distributed within $- {{vt} \mathord{\left/ {\vphantom {{vt} {\sqrt 3 }}} \right. \kern-0em} {\sqrt 3 }} < z < {{vt} \mathord{\left/ {\vphantom {{vt} {\sqrt 3 }}} \right. \kern-0em} {\sqrt 3 }}.$ at time point t. The CR density outside this spatial region is zero. The presence of the “signal” propagation velocity, which differs from the particle velocity, is the result of approximations made in the derivation of the telegraph equation.

The authors of [19] have obtained a modified telegraph equation that correctly handles the small-parameter expansion of the CR distribution function. The particle distribution function was assumed to be near-isotropic and slowly varying in time and space (i.e., the characteristic scales of its variation were assumed to be large compared to the characteristic scattering time and the mean free path of particles). Quantities $\frac{1}{{{{f}_{0}}}}\frac{{\partial {{f}_{0}}}}{{\partial y}}$ and $\frac{1}{{{{f}_{0}}}}\frac{{\partial {{f}_{0}}}}{{\partial \tau }}$ may then be regarded as small parameters [19, 29]. Thus, the modified telegraph equation correctly characterizes the CR propagation over time intervals that are considerably longer than the characteristic scattering time [19, 29].

It turns out that different CR scattering models yield different coefficients of the modified telegraph equation [17, 19, 29]. Therefore, the “signal” propagation velocity also depends on the particle-scattering model. For example, in the case of arbitrary-angle particle scattering (characterized by the Boltzmann collision integral), the modified telegraph equation has a disturbance propagation velocity of $v\sqrt {{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}} ,$ which is higher than the particle velocity [17, 19, 29]. In the case of multiple isotropic small-angle scattering (the Fokker–Planck kinetic equation), the modified telegraph equation features a “signal” propagation velocity of $v\sqrt {{5 \mathord{\left/ {\vphantom {5 {11}}} \right. \kern-0em} {11}}} ,$ which is lower than the particle velocity [17, 19, 29]. Note that, if τ $\gg$ 1, the solution of the telegraph equation is the same as the solution of the CR diffusion equation [6, 7, 12, 18, 19].

Using diffusion equation (16), one may substitute the mixed derivative in transport equation (19) with the second time derivative of f₀. The following modified telegraph equation is then obtained:

$$\frac{{\partial {{f}_{0}}}}{{\partial \tau }} - \frac{1}{3}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{y}^{2}}}} + \frac{{11}}{{15}}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{\tau }^{2}}}} = \Psi (y,\tau ) + \frac{{11}}{{15}}\frac{{\partial \psi }}{{\partial \tau }} - \frac{4}{{45}}\frac{{{{\partial }^{2}}\psi (y,\tau )}}{{\partial {{y}^{2}}}}.$$

((25))

This telegraph equation is characterized by a disturbance propagation velocity of $v\sqrt {{5 \mathord{\left/ {\vphantom {5 {11}}} \right. \kern-0em} {11}}}$ [17, 19, 29]. The solution of Eq. (25) takes the form [17]

$${{f}_{0}}(y,\tau ) = \frac{2}{{5\Lambda }}\sqrt {\frac{5}{{11}}} \exp \left( { - \frac{{15}}{{22}}\tau } \right)\left\{ { - \frac{{11}}{{15}}\frac{{{{\partial }^{2}}}}{{\partial {{\tau }^{2}}}} + \frac{4}{{11}}\frac{\partial }{{\partial \tau }} + \frac{{135}}{{88}}} \right\}{{I}_{0}}\left( {\frac{{15}}{{22}}\xi } \right)\Theta \left( {\tau - \left| y \right|\sqrt {\frac{{11}}{5}} } \right),$$

((26))

where

$$\xi = \sqrt {{{\tau }^{2}} - \frac{{11}}{5}{{y}^{2}},} $$

((27))

Θ(x) is the Heaviside step function, and I₀(x) is the modified Bessel function. Note that, according to (26), particles are distributed within $- \tau \sqrt {{5 \mathord{\left/ {\vphantom {5 {11}}} \right. \kern-0em} {11}}} \leqslant y \leqslant \tau \sqrt {{5 \mathord{\left/ {\vphantom {5 {11}}} \right. \kern-0em} {11}}} ,$ at time point τ, and their density outside this region is zero.

Performing differentiation in (26), we express f₀ as a sum of regular (f_0θ) and singular (f_0δ) parts:

$${{f}_{0}}(y,\tau ) = {{f}_{{0\theta }}}(y,\tau ) + {{f}_{{0\delta }}}(y,\tau ).$$

((28))

The regular part (f_0θ) is given by

$$\begin{gathered} {{f}_{{0\theta }}}(y,\tau ) = \frac{3}{{4\Lambda }}\sqrt {\frac{5}{{11}}} \exp \left( { - \frac{{15}}{{22}}\tau } \right)\Theta \left( {\tau - \left| y \right|\sqrt {\frac{{11}}{5}} } \right)\left\{ {\frac{{13}}{{11}}{{I}_{0}}\left( {\frac{{15}}{{22}}\xi } \right)} \right. + \left[ {\frac{\tau }{\xi } - \frac{4}{{15\xi }}\left( {1 - \frac{{{{\tau }^{2}}}}{{{{\xi }^{2}}}}} \right)} \right]{{I}_{1}}\left( {\frac{{15}}{{22}}\xi } \right) - \frac{{{{\tau }^{2}}}}{{11{{\xi }^{2}}}} \\ \times \,\,\left. {\left[ {{{I}_{0}}\left( {\frac{{15}}{{22}}\xi } \right) + {{I}_{2}}\left( {\frac{{15}}{{22}}\xi } \right)} \right]} \right\}. \\ \end{gathered} $$

((29))

The singular part of the zeroth harmonic of the particle distribution function, which is defined by the delta function and its derivative, differs from zero only at y = $\pm \tau \sqrt {{5 \mathord{\left/ {\vphantom {5 {11}}} \right. \kern-0em} {11}}} \,:$

$${{f}_{{0\delta }}}(y,\tau ) = \frac{2}{{\Lambda \sqrt {55} }}\exp \left( { - \frac{{15}}{{22}}\tau } \right)\left\{ {\left( {\frac{{11}}{4} - \frac{{15}}{{88}}\tau } \right)\delta \left( {\tau - \left| y \right|\sqrt {\frac{{11}}{5}} } \right) - \frac{{11}}{{15}}\delta {{'}}\left( {\tau - \left| y \right|\sqrt {\frac{{11}}{5}} } \right)} \right\}.$$

((30))

If the time elapsed from the moment of particle injection considerably exceeds the inverse collision rate (τ $\gg$ 1), relation (22) follows from (29). Thus, if condition τ $\gg$ 1 is satisfied, one and the same expression (22) for f₀ follows from solution (20) of CR transport equation (19), the solution of hyperdiffusion equation (23), and modified telegraph equation (25). Note that relation (22) differs from solution (17) of the diffusion equation in that it has an additional factor in brackets, which tends to unity as dimensionless time τ increases.

Figure 1 shows the spatial distribution of particles at different time points. Dimensionless coordinate y is plotted on the abscissa, and dimensionless quantity f₀, which is proportional to the particle density, is plotted on the ordinate axis. The values of dimensionless time τ are indicated next to the curves. Dashed and solid curves represent solution (17) of the diffusion equation and solution (29) of the telegraph equation. According to the diffusion equation, particles occupy an unbounded spatial region at any given time. The solid curve in Fig. 1 demonstrates that particles remain within |y| < $\sqrt {{5 \mathord{\left/ {\vphantom {5 {11}}} \right. \kern-0em} {11}}}$ at time τ = 1. This region extends with time at a characteristic rate of $v\sqrt {{5 \mathord{\left/ {\vphantom {5 {11}}} \right. \kern-0em} {11}}}$ (Fig. 1).

Fig. 1.

Spatial distribution of the particle density at different time points τ. Dashed and solid curves represent solution (17) of the diffusion equation and solution (29) of the telegraph equation, respectively.

Figure 2 shows the time dependence of f₀ at different points in space. The values of dimensionless coordinate y are indicated next to the curves. Dashed and solid curves represent solution (17) of the diffusion equation and solution (29) of the telegraph equation. In the case of diffusion propagation, particles appear at a given point in space at the time of injection at point y = 0, since an infinite disturbance propagation velocity is characteristic of the diffusion equation. In the approximation of the telegraph equation, the first particles appear at point y at time τ = $y\sqrt {{{11} \mathord{\left/ {\vphantom {{11} 5}} \right. \kern-0em} 5}}$ (Fig. 2). At larger τ values, the solution of the telegraph equation differs little from that of the diffusion equation: as time passes, the solid curves shift closer to the dashed ones (Fig. 2).

Fig. 2.

Dependence of the particle density on time τ for different values of dimensionless coordinate y. Dashed and solid curves represent solution (17) of the diffusion equation and solution (29) of the telegraph equation, respectively.

ANGULAR CR DISTRIBUTION UNDER ISOTROPIC PARTICLE SCATTERING BY MAGNETIC INHOMOGENEITIES

Let us consider an interval of time after particle injection with its length being considerably larger than the characteristic scattering time. The CR distribution function is then near-isotropic and may be written as [8, 20, 21, 33]

$$f(y,\mu ,\tau ) = \frac{1}{2}{{f}_{0}}(y,\tau ) + \delta f(y,\mu ,\tau ).$$

((31))

The first term in (31) does not depend on the particle pitch angle, and δf is a small anisotropic component of the CR distribution function. If condition

$$\int\limits_{ - 1}^1 {d\mu \delta f(y,\mu ,\tau } ) = 0,$$

((32))

is satisfied, the mean of the CR distribution function is

$$\left\langle f \right\rangle = \frac{{\int\limits_{ - 1}^1 {d\mu f} }}{{\int\limits_{ - 1}^1 {d\mu } }} = \frac{1}{2}{{f}_{0}}.$$

((33))

Let us rewrite kinetic equation (6) in the following form:

$$\frac{1}{2}\frac{{\partial {{f}_{0}}}}{{\partial \tau }} + \frac{{\partial \delta f}}{{\partial \tau }} + \frac{\mu }{2}\frac{{\partial {{f}_{0}}}}{{\partial y}} + \mu \frac{{\partial \delta f}}{{\partial y}} - \frac{1}{2}\frac{\partial }{{\partial \mu }}(1 - {{\mu }^{2}})\frac{{\partial \delta f}}{{\partial \mu }} = \frac{1}{{2\Lambda }}\delta (y)\delta (\tau ).$$

((34))

Note that coefficient D_μμ of CR diffusion over pitch angles is defined by (8) in the case of isotropic particle scattering.

Averaging Eq. (34) over μ, we obtain

$$\frac{{\partial {{f}_{0}}}}{{\partial \tau }} + \frac{\partial }{{\partial y}}\int\limits_{ - 1}^1 {d\mu \mu \delta f} = \frac{1}{\Lambda }\delta (y)\delta (\tau ).$$

((35))

The following equation is obtained by subtracting Eq. (35) from kinetic equation (34):

$$\frac{{\partial \delta f}}{{\partial \tau }} + \frac{\mu }{2}\frac{{\partial {{f}_{0}}}}{{\partial y}} + \mu \frac{{\partial \delta f}}{{\partial y}} - \frac{1}{2}\frac{\partial }{{\partial y}}\int\limits_{ - 1}^1 {d\mu \mu \delta f} - \frac{1}{2}\frac{\partial }{{\partial \mu }}(1 - {{\mu }^{2}})\frac{{\partial \delta f}}{{\partial \mu }} = 0.$$

((36))

If the time elapsed after particle injection considerably exceeds the inverse collision rate, the anisotropic component of the CR distribution function is small compared to f₀, and the particle density varies slowly in time and space [8, 21, 33]. Neglecting the first, the third, and the fourth terms in Eq. (36), we obtain the following equation for the anisotropic component of the CR distribution function:

$$\frac{\partial }{{\partial \mu }}(1 - {{\mu }^{2}})\frac{{\partial \delta {{f}^{{(1)}}}}}{{\partial \mu }} = \mu \frac{{\partial {{f}_{0}}}}{{\partial y}}.$$

((37))

In a first approximation, the expression for the anisotropic part of the distribution function is written as

$$\delta {{f}^{{(1)}}}(\mu ) = - \frac{\mu }{2}\frac{{\partial {{f}_{0}}}}{{\partial y}}.$$

((38))

It turns out that δf⁽¹⁾ is proportional to the CR density gradient and the cosine of the particle pitch angle in the case of isotropic particle scattering [8, 21, 33].

Inserting (38) into Eq. (36), we obtain an approximate relation for the anisotropic component of the CR distribution function:

$$\delta f(\mu ) = - \frac{\mu }{2}\frac{{\partial {{f}_{0}}}}{{\partial y}} + \frac{1}{6}\left( {{{\mu }^{2}} - \frac{1}{3}} \right)\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{y}^{2}}}} + \frac{\mu }{2}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial y\partial \tau }} - \frac{1}{{36}}({{\mu }^{3}} + \mu )\frac{{{{\partial }^{3}}{{f}_{0}}}}{{\partial {{y}^{3}}}}.$$

((39))

The second term at the right-hand side of Eq. (39) is an even function of μ, and the other terms are odd functions of μ.

In order to derive the CR transport equation, one needs to calculate the first harmonic of the particle distribution function:

$${{f}_{1}}(y,\tau ) = \int\limits_{ - 1}^1 {d\mu \mu f(y,\mu ,\tau } ) = \int\limits_{ - 1}^1 {d\mu \mu \delta f(y,\mu ,\tau } .$$

((40))

Integrating f₁(y, μ, τ) (39) in μ, we obtain

$${{f}_{1}}(y,\tau ) = - \frac{1}{3}\frac{{\partial {{f}_{0}}}}{{\partial y}} + \frac{1}{3}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial y\partial \tau }} - \frac{4}{{135}}\frac{{{{\partial }^{3}}{{f}_{0}}}}{{\partial {{y}^{3}}}}.$$

((41))

Inserting f₁ (41), into continuity equation (11), we obtain

$$\frac{{\partial {{f}_{0}}}}{{\partial \tau }} - \frac{1}{3}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{y}^{2}}}} + \frac{1}{3}\frac{{{{\partial }^{3}}{{f}_{0}}}}{{\partial {{y}^{2}}\partial \tau }} - \frac{4}{{135}}\frac{{{{\partial }^{4}}{{f}_{0}}}}{{\partial {{y}^{4}}}} = \Psi (y,\tau ).$$

((42))

The last two terms in (42) may be expressed through the second time derivative of f₀ using (16). The result is modified telegraph equation (25). Let us use the solution of this equation to calculate CR distribution functions (31) and (39). The CR distribution function normalized to its mean value (33) takes the form

$$\frac{{f(y,\mu ,\tau )}}{{\left\langle f \right\rangle }} = 1 - \frac{\mu }{{{{f}_{0}}}}\frac{{\partial {{f}_{0}}}}{{\partial y}} + \frac{1}{3}\left( {{{\mu }^{2}} - \frac{1}{3}} \right)\frac{1}{{{{f}_{0}}}}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{y}^{2}}}} + \frac{\mu }{{{{f}_{0}}}}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial y\partial \tau }} - \frac{1}{{18}}({{\mu }^{3}} + \mu )\frac{1}{{{{f}_{0}}}}\frac{{{{\partial }^{3}}{{f}_{0}}}}{{\partial {{y}^{3}}}}.$$

((43))

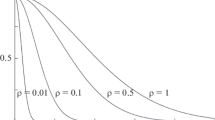
The dependence of CR distribution function (43) on μ is represented in Fig. 3. Dimensionless coordinate y = 1 and the values of τ are indicated next to the curves. Note that the isotropic particle distribution is represented by vertical line f/〈f〉 = 1. It can be seen that the angular CR distribution gets closer to the isotropic one with time. The particle distribution is highly anisotropic at time τ = 2 and almost isotropic at τ = 50 (Fig. 3). Expression (29), which is the solution of the modified telegraph equation, was used in the calculation of distribution function (43).

Fig. 3.

Dependence of the particle distribution function on μ at point y = 1 for different values of dimensionless time τ (indicated next to the curves).

ANGULAR PARTICLE DISTRIBUTION UNDER ANISOTROPIC SCATTERING

It is known that the CR scattering in the interplanetary medium is anisotropic, and the scattering of particles moving perpendicularly to the mean magnetic field is weaker [20, 22]. Let us write the CR angular diffusion coefficient in the following form:

$${{D}_{{\mu \mu }}} = \frac{1}{2}{{D}_{0}}(\mu )(1 - {{\mu }^{2}}).$$

((44))

In the case of isotropic scattering, D₀(μ) equals unity, and diffusion coefficient D_μμ is given by (8). We assume that, in the case of anisotropic scattering, function D₀(μ) has a minimum at μ = 0. Let us write the kinetic equation corresponding to anisotropic scattering:

$$\frac{{\partial \delta f}}{{\partial \tau }} + \frac{\mu }{2}\frac{{\partial {{f}_{0}}}}{{\partial y}} + \mu \frac{{\partial \delta f}}{{\partial y}} - \frac{1}{2}\frac{\partial }{{\partial y}}\int\limits_{ - 1}^1 {d\mu \mu \delta f} - \frac{1}{2}\frac{\partial }{{\partial \mu }}{{D}_{0}}(\mu )(1 - {{\mu }^{2}})\frac{{\partial \delta f}}{{\partial \mu }} = 0.$$

((45))

This equation differs from Eq. (36), which characterizes isotropic scattering, only in the last term.

Let us write D₀(μ) in the following form [8, 12, 20, 22]:

$${{D}_{0}}(\mu ) = \frac{3}{{(4 - q)(2 - q)}}{{\left| \mu \right|}^{{q - 1}}},$$

((46))

where q (1 ≤ q < 2) is the index of the spectrum of a random magnetic field. In the case of isotropic scattering, q = 1; the scattering anisotropy becomes stronger as q increases.

Figure 4 shows the dependence of coefficient D_μμ (44) and (46) of CR angular diffusion on the cosine of the particle pitch angle at different values of q. Isotropic scattering corresponds to q = 1, and the CR diffusion coefficient at q ≠ 1 is zero at μ = 0 (Fig. 4). The CR scattering intensity in the interplanetary medium is governed by free path Λ, and the scattering anisotropy depends only on q. In [8, 23, 33], CR diffusion coefficient D_μμ depends on two parameters (one of them defines the value of D_μμ at μ = 0).

Fig. 4.

Dependence of CR diffusion coefficient D_μμ (44), (46) on cosine μ of the particle pitch angle for different values of q (indicated next to the curves).

In the present study, we use both relation (46) and formula

$${{D}_{0}}(\mu ) = \gamma (1 + \beta {{\mu }^{2}}),$$

((47))

where

$$\gamma = \frac{3}{{2\beta }}\left\{ {\frac{{\beta + 1}}{{\sqrt \beta }}\arctan \sqrt \beta - 1} \right\},$$

((48))

for D₀(μ).

CR angular diffusion coefficient (44) and (48) differs from zero at μ = 0, and the scattering anisotropy is defined by one parameter β ≥ 0 (β = 0 corresponds to isotropic scattering).

Figure 5 represents the dependence of D_μμ (44) and (48) on μ for different values of β. It can be seen that the scattering anisotropy becomes stronger as β increases, while the minimum value of the CR diffusion coefficient decreases monotonically (Fig. 5).

Fig. 5.

Dependence of CR diffusion coefficient D_μμ (44), (48) on μ for different values of anisotropy parameter β (indicated next to the curves).

Using Eq. (45), we obtain the following expression for the anisotropic component of the CR distribution function:

$$\delta f(\mu ) = {{\alpha }_{1}}(\mu )\frac{{\partial {{f}_{0}}}}{{\partial y}} + {{\alpha }_{2}}(\mu )\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{y}^{2}}}} + {{\alpha }_{3}}(\mu )\frac{{{{\partial }^{3}}{{f}_{0}}}}{{\partial {{y}^{3}}}} + {{\alpha }_{4}}(\mu )\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial y\partial \tau }}.$$

((49))

CR distribution function f(y, μ,τ) is the sum of isotropic part f₀ and anisotropic part δf (δf$\ll$f₀). The expressions for α_n(μ) corresponding to relation (46) for D₀(μ) are as follows:

$${{\alpha }_{1}}(\mu ) = - \frac{{4 - q}}{6}\operatorname{sgn} \mu {{\left| \mu \right|}^{{2 - q}}},$$

((50))

$${{\alpha }_{2}}(\mu ) = \frac{{(4 - q)(2 - q)}}{9}\left\{ {\int\limits_0^{\left| \mu \right|} {d\nu {{\nu }^{{2 - q}}}\frac{{1 - {{\nu }^{{3 - q}}}}}{{1 - \nu }}} - \int\limits_0^1 {d\nu {{\nu }^{{2 - q}}}} \frac{{1 - {{\nu }^{{3 - q}}}}}{{1 + \nu }}} \right\},$$

((51))

$$\begin{gathered} {{\alpha }_{3}}(\mu ) = \frac{{(2 - q){{{(4 - q)}}^{2}}}}{{27}}\operatorname{sgn} \mu \left\{ {\int\limits_0^{\left| \mu \right|} {d\nu {{\nu }^{{2 - q}}}} \frac{{(1 - {{\nu }^{{3 - q}}})({{\nu }^{{2 - q}}} - {{{\left| \mu \right|}}^{{2 - q}}})}}{{1 - {{\nu }^{2}}}}} \right. - \frac{{(2 - q)}}{{2(3 - q)}}\int\limits_0^{\left| \mu \right|} {d\nu {{\nu }^{{1 - q}}}\frac{{{{{(1 - {{\nu }^{{3 - q}}})}}^{2}}}}{{1 - {{\nu }^{2}}}}} \\ + \,\,{{\left| \mu \right|}^{{2 - q}}}\left. {\int\limits_0^1 {d\nu {{\nu }^{{2 - q}}}\frac{{1 - {{\nu }^{{3 - q}}}}}{{1 + \nu }}} } \right\}, \\ \end{gathered} $$

((52))

$${{\alpha }_{4}}(\mu ) = \frac{{(4 - q)(2 - q)}}{{9(3 - q)}}\operatorname{sgn} \mu \int\limits_0^{\left| \mu \right|} {d\nu {{\nu }^{{1 - q}}}\frac{{1 - {{\nu }^{{3 - q}}}}}{{1 - {{\nu }^{2}}}}} .$$

((53))

Note that relations (49)–(53) transform at q = 1 into expression (39) for the anisotropic part of the CR distribution function, which corresponds to isotropic scattering. Functions α₁(μ), α₃(μ), and α₄(μ) change their sign when the sign of μ changes, and α₂(μ) is an even function of μ. If formula (47) is used to determine D₀(μ), functions α_n(μ) become rather cumbersome, and we do not list them here.

First harmonic (40) of the CR distribution function is written as

$${{f}_{1}}(y,\tau ) = - \frac{1}{3}\frac{{\partial {{f}_{0}}}}{{\partial y}} + {{\zeta }_{3}}\frac{{{{\partial }^{3}}{{f}_{0}}}}{{\partial {{y}^{3}}}} + {{\zeta }_{4}}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial y\partial \tau }},$$

((54))

where

$$\begin{gathered} {{\zeta }_{3}} = \frac{2}{{27}}(2 - q)(4 - q) \\ \times \,\,\,\left\{ { - \int\limits_0^1 {d\nu {{\nu }^{{2 - q}}}\frac{{(1 - {{\nu }^{{4 - q}}})(1 - {{\nu }^{{2 - q}}})}}{{1 - {{\nu }^{2}}}}} + \frac{1}{{3 - q}}\left[ {F(1,3 - q;4 - q; - 1)\frac{{ - 1/2F}}{2}F(1,6 - 2q;7 - 2q; - 1)} \right]} \right\}, \\ \end{gathered} $$

((55))

$${{\zeta }_{4}} = \frac{{{{{(4 - q)}}^{2}}}}{{9(5 - 2q)}},$$

((56))

and F(a, b; c; x) is the hypergeometric function. Relations (54)–(56) were obtained by integrating anisotropic component (49)–(53) of the CR distribution function in μ.

The following value of the integral was used to calculate ζ₃ (55) [2]:

$$\int\limits_0^1 {d\mu \frac{{{{\mu }^{\gamma }}}}{{1 + \mu }}} = \frac{1}{{\gamma + 1}}F(1,\gamma + 1;\gamma + 2; - 1).$$

((57))

Inserting f₁ (54)–(56) into continuity equation (11), we obtain the following CR transport equation:

$$\frac{{\partial {{f}_{0}}}}{{\partial \tau }} - \frac{1}{3}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{y}^{2}}}} + {{\zeta }_{3}}\frac{{{{\partial }^{4}}{{f}_{0}}}}{{\partial {{y}^{4}}}} + {{\zeta }_{4}}\frac{{{{\partial }^{3}}{{f}_{0}}}}{{\partial {{y}^{2}}\partial \tau }} = \psi (y,\tau ).$$

((58))

Using CR diffusion equation (16), we express the mixed derivative of f₀ through the fourth derivative of f₀ with respect to y. Hyperdiffusion equation

$$\frac{{\partial {{f}_{0}}}}{{\partial \tau }} - \frac{1}{3}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{y}^{2}}}} + \left( {{{\zeta }_{3}} + \frac{1}{3}{{\zeta }_{4}}} \right)\frac{{{{\partial }^{4}}{{f}_{0}}}}{{\partial {{y}^{4}}}} = \Psi (y,\tau ) - {{\zeta }_{4}}\frac{{{{\partial }^{2}}\Psi }}{{\partial {{y}^{2}}}}.$$

((59))

is thus obtained.

Equations (59) and (16) then yield telegraph equation

$$\frac{{\partial {{f}_{0}}}}{{\partial \tau }} - \frac{1}{3}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{y}^{2}}}} + \eta \frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{\tau }^{2}}}} = \Psi (y,\tau ) + \eta \frac{{\partial \Psi }}{{\partial \tau }} + \zeta \frac{{{{\partial }^{2}}\Psi }}{{\partial {{y}^{2}}}},$$

((60))

where

$$\eta = 3({{\zeta }_{4}} + 3{{\zeta }_{3}}),\,\,\,\,\zeta = 3{{\zeta }_{3}}.$$

((61))

Telegraph equation (60) is characterized by a disturbance propagation velocity of ${v \mathord{\left/ {\vphantom {v {\sqrt {3\eta } }}} \right. \kern-0em} {\sqrt {3\eta } }}.$ The results of calculations demonstrate that the “signal” propagation velocity corresponding to this telegraph equation decreases as the scattering anisotropy becomes stronger. For example, the disturbance propagation velocity is 0.67v for isotropic scattering and 0.55v for strongly anisotropic scattering.

The solution of telegraph equation (60) takes the form

$${{f}_{0}}(y,\tau ) = \frac{3}{{2\Lambda \sqrt {\pi \eta } }}\exp \left( { - \frac{\tau }{{2\eta }}} \right)\left\{ {3\eta \zeta \frac{{{{\partial }^{2}}}}{{\partial {{\tau }^{2}}}}} \right. + \eta \frac{\partial }{{\partial \tau }} + \left. {\left( {\frac{1}{2} - \frac{{3\zeta }}{{4\eta }}} \right)} \right\}{{I}_{0}}\left( {\frac{\xi }{{2\eta }}} \right)\Theta (\tau - \left| y \right|\sqrt {3\eta } ),$$

((62))

where

$$\xi = \sqrt {{{\tau }^{2}} - 3\eta {{y}^{2}}} .$$

((63))

Performing differentiation, we obtain an expression in the form of sum (28), where

$$\begin{gathered} {{f}_{{0\theta }}}(y,\tau ) = \frac{3}{{4\Lambda \sqrt {3\eta } }}\exp \left( { - \frac{\tau }{{2\eta }}} \right)\Theta (\tau - \left| y \right|\sqrt {3\eta } )\left\{ {\left( {1 - \frac{{3\zeta }}{{2\eta }}} \right)} \right.{{I}_{0}}\left( {\frac{\xi }{{2\eta }}} \right) + \left[ {\frac{\tau }{\xi } + \frac{{3\zeta }}{\xi }\left( {1 - \frac{{{{\tau }^{2}}}}{{{{\xi }^{2}}}}} \right)} \right] \\ \times \,\,{{I}_{1}}\left( {\frac{\xi }{{2\eta }}} \right) + \frac{{3\zeta {{\tau }^{2}}}}{{4\eta {{\xi }^{2}}}}\left. {\left[ {{{I}_{0}}\left( {\frac{\xi }{{2\eta }}} \right) + {{I}_{2}}\left( {\frac{\xi }{{2\eta }}} \right)} \right]} \right\}, \\ \end{gathered} $$

((64))

$${{f}_{{0\delta }}}(y,\tau ) = \frac{3}{{2\Lambda \sqrt {3\eta } }}\exp \left( { - \frac{\tau }{{2\eta }}} \right)\left\{ {\left( {\eta + \frac{{3\zeta }}{{4\eta }}\tau } \right)\delta (\tau - \left| y \right|\sqrt {3\eta } ) + 3\zeta \eta \delta {\text{'(}}\tau - \left| y \right|\sqrt {3\eta } )} \right\}.$$

((65))

Relation

$${{f}_{0}}(y,\tau ) = \frac{{\sqrt 3 }}{{2\Lambda \sqrt {\pi \tau } }}\exp \left( { - \frac{{3{{y}^{2}}}}{{4\tau }}} \right)\left( {1 - \frac{{\eta + 6\zeta }}{{4\tau }} + \frac{3}{4}(2\eta + 3\zeta )\frac{{{{y}^{2}}}}{{{{\tau }^{2}}}}} \right).$$

((66))

follows from (65) if τ $\gg$ 1.

At q = 1, formula (66) turns into expression (22), which corresponds to isotropic scattering.

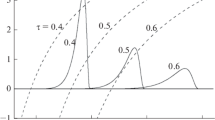
The time dependence of dimensionless quantity λf₀ is represented in Fig. 6. The values of dimensionless coordinate y are indicated next to the curves. Solid and dashed curves correspond to anisotropic (q = 5/3) and isotropic scattering. The f₀ value satisfies relation (64). In the case of anisotropic scattering, the “signal” propagation velocity is lower than that for isotropic scattering. Therefore, the particle density in a given point in space starts increasing in the anisotropic case with a certain time lag (Fig. 6). The disturbance propagation velocity for isotropic scattering is 0.67v, and the “signal” velocity at q = 5/3 is 0.57v. Solid and dashed curves become indistinguishable at large τ values; in other words, the particle density at a given point in space eventually becomes independent of the scattering anisotropy (Fig. 6).

Fig. 6.

Dependence of the particle density on time τ for different values of dimensionless coordinate y. Solid and dashed curves correspond to anisotropic (q = 5/3) and isotropic scattering.

CR distribution functions (31) and (49) takes the following form under anisotropic scattering:

$$\frac{{f(y,\mu ,\tau )}}{{\left\langle f \right\rangle }} = 1 + 2{{\alpha }_{1}}\frac{1}{{{{f}_{0}}}}\frac{{\partial {{f}_{0}}}}{{\partial y}} + 2{{\alpha }_{2}}\frac{1}{{{{f}_{0}}}}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{y}^{2}}}} + 2{{\alpha }_{3}}\frac{1}{{{{f}_{0}}}}\frac{{{{\partial }^{3}}{{f}_{0}}}}{{\partial {{y}^{3}}}} + 2{{\alpha }_{4}}\frac{1}{{{{f}_{0}}}}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial y\partial \tau }}.$$

((67))

Functions α_n(μ) (50)–(53) depend on the particle scattering anisotropy.

Figure 7 shows the dependence of normalized particle distribution function (67) on μ at point y = 1 in the case of anisotropic scattering (q = 5/3). The values of dimensionless time τ are indicated next to the curves. It can be seen that the angular CR distribution gets closer to the isotropic one with time. The dependences of the distribution function on the cosine of the pitch angle for isotropic and anisotropic scattering differ from each other. The degree of curvature of the angular dependences of the CR distribution function is higher in the case of anisotropic scattering (see Figs. 7, 3).

Fig. 7.

Dependence of particle distribution function (67) on μ at different time points τ under anisotropic scattering (q = 5/3). Dimensionless coordinate y = 1.

Figure 8 represents the dependences of the distribution function on μ for isotropic (dashed curves) and anisotropic (solid curves) scattering. Dimensionless coordinate y = 1. CR diffusion coefficient D_μμ is defined by Eq. (47); parameters β = 0 and β = 10 correspond to isotropic and anisotropic scattering, respectively. Solution (64) of the telegraph equation was used to calculate function f₀(y, τ). It is evident that the shape of curves depends on the scattering anisotropy. The dependence of the CR distribution function on μ is near-linear for isotropic scattering and has a considerable degree of curvature in the case of anisotropic scattering.

Fig. 8.

Dependence of the particle distribution function on μ at y = 1 for different time points τ. Dashed and solid curves correspond to isotropic (β = 0) and anisotropic (β = 10) scattering.

ANISOTROPY OF THE ANGULAR CR DISTRIBUTION

Let us examine the variation of the angular particle distribution with time. The CR distribution function anisotropy is given by

$$\xi (y,\tau ) = 3\frac{{{{f}_{1}}(y,\tau )}}{{{{f}_{0}}(y,\tau )}}.$$

((68))

In the case of isotropic scattering, the first harmonic of the particle distribution function is given by (41). Therefore,

$$\xi = - \frac{1}{{{{f}_{0}}}}\frac{{\partial {{f}_{0}}}}{{\partial y}} + \frac{1}{{{{f}_{0}}}}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial y\partial \tau }} - \frac{4}{{45}}\frac{1}{{{{f}_{0}}}}\frac{{{{\partial }^{3}}{{f}_{0}}}}{{\partial {{y}^{3}}}}.$$

((69))

In the diffusion approximation, f₀ satisfies relation (17), and CR anisotropy (68) varies inversely with time elapsed after particle injection.

The second-order anisotropy is written as

$${{\xi }_{2}}(y,\tau ) = 5\frac{{{{f}_{2}}(y,\tau )}}{{{{f}_{0}}(y,\tau )}},$$

((70))

where

$${{f}_{2}}(y,\tau ) = \int\limits_{ - 1}^1 {d\mu {{P}_{2}}(\mu )f(y,\mu ,\tau )} .$$

((71))

In the case of isotropic scattering,

$${{\xi }_{2}} = \frac{2}{9}\frac{1}{{{{f}_{0}}}}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{y}^{2}}}}.$$

((72))

The third-order anisotropy is given by

$${{\xi }_{3}}(y,\tau ) = 7\frac{{{{f}_{3}}(y,\tau )}}{{{{f}_{0}}(y,\tau )}}$$

((73))

and is proportional to the third harmonic of the CR distribution function

$${{f}_{3}}(y,\tau ) = \int\limits_{ - 1}^1 {d\mu {{P}_{3}}(\mu )f(y,\mu ,\tau )} .$$

((74))

Under isotropic particle scattering,

$${{\xi }_{3}} = - \frac{1}{{45}}\frac{1}{{{{f}_{0}}}}\frac{{{{\partial }^{3}}{{f}_{0}}}}{{\partial {{y}^{3}}}}.$$

((75))

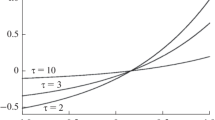
Figure 9 represents the time dependences of ξ_n at point y = 1. Dashed curves correspond to isotropic scattering. It can be seen that all ξ_n characterizing the angular CR distribution anisotropy decrease monotonically (in magnitude) with time. The value of |ξ₃| is small at any τ. At y = 1, the second harmonic of the CR distribution function is negative and much smaller in magnitude than the first harmonic. Solution (29) of the telegraph equation and expression (39) for the particle distribution function were used to calculate the CR distribution function anisotropy.

Fig. 9.

Dependence of anisotropy ξ of the angular particle distribution at point y = 1 on time τ. Solid and dashed curves correspond to anisotropic (q = 5/3) and isotropic (q = 1) scattering.

The following expression for the CR anisotropy is valid under anisotropic scattering:

$$\xi = - \frac{1}{{{{f}_{0}}}}\frac{{\partial {{f}_{0}}}}{{\partial y}} + 3{{\zeta }_{3}}\frac{1}{{{{f}_{0}}}}\frac{{{{\partial }^{3}}{{f}_{0}}}}{{\partial {{y}^{3}}}} + 3{{\zeta }_{4}}\frac{1}{{{{f}_{0}}}}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial y\partial \tau }},$$

((76))

where functions ζ₃ and ζ₄ are defined by (55) and (56).

The second-order anisotropy induced by the presence of the second harmonic in the angular particle distribution is given by

$${{\xi }_{2}} = 5\frac{1}{{{{f}_{0}}}}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{y}^{2}}}}\int\limits_0^1 {d\mu } (3{{\mu }^{2}} - 1){{\alpha }_{2}}(\mu ),$$

((77))

where function α₂(μ) satisfies relation (51).

In the case of anisotropic scattering, ξ₃ is given by

$${{\xi }_{3}} = 7\frac{1}{{{{f}_{0}}}}\frac{{\partial {{f}_{0}}}}{{\partial y}}\int\limits_0^1 {d\mu (5{{\mu }^{3}} - 3\mu ){{\alpha }_{1}}(\mu )} + 7\frac{1}{{{{f}_{0}}}}\frac{{{{\partial }^{3}}{{f}_{0}}}}{{\partial {{y}^{3}}}}\int\limits_0^1 {d\mu (5{{\mu }^{3}} - 3\mu ){{\alpha }_{3}}(\mu )} + 7\frac{1}{{{{f}_{0}}}}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial y\partial \tau }}\int\limits_0^1 {d\mu (5{{\mu }^{3}} - 3\mu ){{\alpha }_{4}}(\mu )} ,$$

((78))

where functions α_n(μ) are defined by relations (50)–(53).

Let us use solution (64) of the telegraph equation to calculate CR anisotropy (76)–(78). Solid curves in Fig. 9 represent the time dependences of ξ_n, which characterize the angular CR distribution under anisotropic scattering. Parameter q, which characterizes the scattering anisotropy, is set to 5/3. It can be seen that all ξ_n decrease (in magnitude) with time as the CR distribution function becomes more and more isotropic (Fig. 9). In contrast to the case of isotropic scattering, the value of |ξ₂| under anisotropic scattering is small. Conversely, the value of |ξ₃| becomes rather large under anisotropic scattering.

If τ $\gg$ 1, all terms except the first ones (i.e., the terms proportional to the CR density gradient) may be neglected in (76) and (78). These formulas are considerably simplified in this approximation:

$$\xi = - \frac{1}{{{{f}_{0}}}}\frac{{\partial {{f}_{0}}}}{{\partial y}},$$

((79))

$${{\xi }_{3}} = \frac{7}{3}\frac{{q - 1}}{{6 - q}}\frac{1}{{{{f}_{0}}}}\frac{{\partial {{f}_{0}}}}{{\partial y}}.$$

((80))

If the particle scattering is near-isotropic (parameter q is close to unity), ξ₃ (80) is close to zero. Thus, the ratio of ξ₃ to ξ₁ characterizes the particle scattering anisotropy. Using formulas (79) and (80), one may determine parameter q:

$$q = \frac{{7\xi - 18{{\xi }_{3}}}}{{7\xi - 3{{\xi }_{3}}}}.$$

((81))

Note that formula (81) is applicable under the condition of uniformity of a regular magnetic field. The influence of magnetic focusing on the propagation of particles in the interplanetary magnetic field was neglected in this study [4, 8–10, 20, 33].

CONCLUSIONS

A system of equations for spherical harmonics of the particle distribution function was obtained based on the Fokker–Planck kinetic equation, which characterizes the propagation of charged energetic particles in a uniform mean magnetic field. This system was used to derive the following CR transport equations: the hyperdiffusion equation, the modified telegraph equation, and the equation inclusive of the second harmonic of the angular particle distribution. Solutions of the CR transport equations corresponding to instantaneous particle injection were found. It was demonstrated that these solutions match if the time elapsed after particle injection exceeds considerably the inverse collision rate. In the extreme case of τ $\gg$ 1, the spatiotemporal CR distribution is characterized by the diffusion equation.

An analytical expression for the CR distribution function in the case of multiple scattering by magnetic-field inhomogeneities was derived. It was demonstrated that the angular particle distribution function depends to a considerable extent on the degree of scattering anisotropy. The temporal dependence of the CR distribution function was analyzed, and the parameter characterizing the scattering anisotropy was estimated.