1 INTRODUCTION

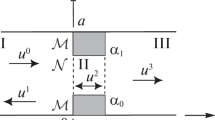
In this work, we explore the resonant properties of a semi-infinite rectangular waveguide with metal walls in the presence of a transverse diaphragm at some distance from the flange being a transverse metal wall (Fig. 1).

Fig. 1
figure 1

Diaphragm in a semi-infinite rectangular waveguide.

Full size image

As it is known [1, 2], in a waveguide, homogeneous along the longitudinal axis and filled with a homogeneous isotropic linear medium, any electromagnetic field can be presented as a sum of its eigen waves propagating or damping in different directions along the waveguide axis. At the same time, there can be only the limited number of propagating waves carrying energy.

If the cross-wall (without the diaphragm) is run by the propagating eigen wave of waveguide, which came from infinity, then a reflected eigen wave of the same polarization and with the same number appears, but moving in the opposite direction. This pair of waves can be considered as a single standing wave, which can be interpreted as an eigen wave of cylindrical resonator with an open infinitely distant section. It is easy to see that such eigen waves exist at any frequency of harmonic electromagnetic oscillations, at which the waveguide has at least one propagating eigen wave.

If there is heterogeneity inside the waveguide (in our case, it is a thin conductive diaphragm), then a diffracted field appears, which in joint of a sum with together with the incoming wave can be considered as eigen wave of the disturbed semi-infinite waveguide. It is clear that the frequencies of such eigen waves form a continuous spectrum also. In single-mode case, the disturbance will be noticeable only in the near zone (near the diaphragm).

Diaphragms in waveguides are widely used in waveguide equipment when designing mode converters, communication elements, filters and other nodes. There are approximate formulas for calculating them in the technical reference literature. Simple models of the diffraction process of electromagnetic waves by diaphragms and by some other heterogeneities (the theory of equivalent chains) are built in the lectures by J. Schwinger [3]. Rigorous method of semi-conversion (the method of the Riemann–Hilbert problem) for calculating fields in waveguides with inductive and capacitive diaphragms and the numerical results obtained by it are presented in the books of V. P. Shestopalov [4] (Chapters IV, V), [5] (§ 10). These books have an extensive bibliography.

In recent years, during the study of the resonant properties of diaphragms in waveguides, a method of equivalent circuits [6] and a method of moments [7] are used, as well as more rigorous method of integral equations [8, 9]. In the ‘‘connection of volumes through the hole’’ problems, the integral equations on the hole are usually constructed using Green’s functions (see, for example, [10]). In this work, the method of integral-series identities (ISI) is used to reduce the paired series functional equations (PSFE) of diffraction problems by the diaphragms to regular infinite sets of linear algebraic equations (ISLAE) [11].

Comparison of numerical results with experimental data can be found in the works [12, 13]. The works [12, 14, 15] are dedicated to diaphragms of finite thickness. Various inverse problems for waveguides with diaphragms are also actively investigated (see, for example, [16, 17]). When solving the problem of diffraction by the diaphragm before flange, you need to look for an electromagnetic field in two adjacent areas: in the semi-infinite part I of the structure in the form of a series of outgoing to infinity eigen waves and in the area II between the diaphragm and the flange in the form of a series of standing waves that satisfy the boundary conditions on the flange. It is expected (and this is confirmed by the computational experiment) that the amplitudes of standing waves can increase sharply at the frequency of oscillations close to some resonant values.

Our purpose is to find frequencies (or, that is almost the same, wave numbers being the coefficients in the Helmholtz equation) when approaching to which there is a sharp increase of modules of coefficients of field decomposition in area II (at least, only of one of the coefficients). Such frequencies and corresponding to them wave numbers will be called resonant. As in the work [18], the computational experiment is based on the multiple solving of the truncated ISLAE for the frequency value of the excitatory wave that runs on the diaphragm in the case when the frequency changes with a small step.

Area II is a resonator with a hole in the metal wall. Therefore, for small sizes of holes in the diaphragm, we should expect that the resonant frequencies we are looking for will be close to the real eigen frequencies of the closed resonator. But if there is a hole in its wall, the values of eigen resonator frequencies become complex (if the energy of the electromagnetic field goes through the hole).

Resonators with holes in the walls are often considered in the theory of wave diffraction as ‘‘trap-like’’ areas. A. A. Arsenyev’s work notes that ‘‘from a physical point of view it is clear’’ that the characteristics of the field within the ‘‘trap-like’’ will be great if the frequency of the excitatory wave is close to eigen resonator frequencies. The resonant nature of the problem of scattering on the body with the ‘‘trap-like’’ is explained (it is a hypothesis) by the presence of poles in the scattering matrix or at the Green function in the vicinity of their eigen frequencies [20, 21]. Similar effects are observed in the study of scattering of acoustic waves. Resonant scattering of waves on acoustic resonators with a hole is studied in the works R.A. Gadylshin [22, 23].

In this work, a two-dimensional case that is the problem of diffraction of TE-wave by the diaphragm before stub in a place waveguide is studied in detail. The results of computing experiments are presented. Various resonant effects are discussed when the frequency of the excitatory wave changes. The three-dimensional problem of the electromagnetic wave diffraction by the diaphragm in the rectangular waveguide is then considered. It is shown that the problem-solving algorithm is simplified when the diaphragm is inductive or capacitive.

2 TWO-DIMENSIONAL DIFFRACTION PROBLEM

Let us consider the two-dimensional problem of diffraction of TE-polarized wave by the diaphragm before flange in a semi-infinite place waveguide \(0<x<a\), \(z<c\). The diaphragm is located in a plane \(z=0\) (see Fig. 2). Let’s denote by \({\mathcal{N}}=(\alpha,\beta)\) a part of the segment \([0,a]\), corresponding to a hole, and by \(\mathcal{M}\) the rest of the segment.

Fig. 2
figure 2

Diaphragm in a semi-infinite place waveguide.

Full size image

It is assumed that there are no free currents and charges, the medium is homogeneous and isotropic, the electromagnetic field harmonically depends on time, this dependence has the form of \(e^{-i\omega t}\), and does not depend on the coordinates of \(y\). Potential functions of TE-polarized eigen waves have the form

$$\varphi_{n}(x)e^{\pm i\gamma_{n}z},\quad\varphi_{n}(x)=\sqrt{2/a}\sin\frac{\pi nx}{a},\quad\gamma_{n}=\sqrt{\kappa^{2}-(\pi n/a)^{2}},\quad n=1,2,\dots,$$

where \(\textrm{Re}\gamma_{n}>0\) or \(\textrm{Im}\gamma_{n}>0\). The sign \(+\) corresponds to waves of positive orientation (propagating to the right or damping to the right), and the sign \(-\) corresponds to waves of negative orientation (propagating to the left or damping to the left). The wave number \(\kappa\) is directly proportional to the frequency of electromagnetic oscillations.

For the brevity of the speech, let’s say ‘‘wave’’ instead of ‘‘potential function’’.

Let eigen TE-wave \(u^{0}(x,z)=\varphi_{l}(x)e^{i\gamma_{l}z}\) run from the \(z<0\) area to the diaphragm. We will look for the wave reflected to the left in the form \(u^{1}(x,z)=\sum_{n=1}^{+\infty}a_{n}\varphi_{n}(x)e^{-i\gamma_{n}z},\) and we will look for the wave reflected to the right in the form \(u^{2}(x,z)=\sum_{n=1}^{+\infty}b_{n}\varphi_{n}(x)\bigl{(}e^{i\gamma_{n}z}-e^{2i\gamma_{n}c}e^{-i\gamma_{n}z}\bigr{)}.\) For such a wave, a boundary condition on the flange is fulfilled, and this potential function is limited at \(n\to+\infty\).

Let’s write down the boundary conditions on the metal \({\mathcal{M}}=\{0<x<\alpha\}\cup\{\beta<x<a\}\):

$$\varphi_{l}(x)+\sum_{n=1}^{+\infty}a_{n}\varphi_{n}(x)=0,$$
(1)
$$\sum_{n=1}^{+\infty}b_{n}\bigl{(}1-e^{2i\gamma_{n}c}\bigr{)}\varphi_{n}(x)=0,$$
(2)

and the conjugation conditions on the hole \({\mathcal{N}}=\{\alpha<x<\beta\}\):

$$\varphi_{l}(x)+\sum_{n=1}^{+\infty}a_{n}\varphi_{n}(x)=\sum_{n=1}^{+\infty}b_{n}\bigl{(}1-e^{2i\gamma_{n}c}\bigr{)}\varphi_{n}(x),$$
(3)
$$\gamma_{l}\varphi_{l}(x)-\sum_{n=1}^{+\infty}a_{n}\gamma_{n}\varphi_{n}(x)=\sum_{n=1}^{+\infty}b_{n}\gamma_{n}\bigl{(}1+e^{2i\gamma_{n}c}\bigr{)}\varphi_{n}(x).$$
(4)

We denote by

$$I_{nm}=\int\limits_{\mathcal{M}}\varphi_{n}(t)\varphi_{m}(t)dt,\quad J_{nm}=\int\limits_{\mathcal{N}}\varphi_{n}(t)\varphi_{m}(t)dt.$$

All these integrals are easy to calculate.

Theorem 1. The two-dimensional problem of diffraction of TE-polarized electromagnetic wave by the diaphragm in a semi-infinite waveguide is reduced to ISLAE

$$b_{k}\gamma_{k}-\sum_{n=1}^{+\infty}b_{n}\bigl{(}1-e^{2i\gamma_{n}c}\bigr{)}\sum_{m=1}^{+\infty}\frac{\gamma_{m}}{1-e^{2i\gamma_{m}c}}J_{nm}I_{mk}=\gamma_{l}J_{lk},\quad k=1,2,\dots .$$
(5)

Proof. It follows from (1), (2) and (3) that equality (2) is fulfilled on both \(\mathcal{N}\), and \(\mathcal{M}\). Then

$$1+a_{l}=b_{l}\bigl{(}1-e^{2i\gamma_{l}c}\bigr{)},\quad a_{n}=b_{n}\bigl{(}1-e^{2i\gamma_{n}c}\bigr{)},\quad n\neq l.$$
(6)

We exclude the unknown \(a_{n}\) from (4) and then we get on \(\mathcal{N}\)

$$\sum_{n=1}^{+\infty}b_{n}\gamma_{n}\varphi_{n}(x)=\gamma_{l}\varphi_{l}(x).$$
(7)

To regularize the PSFE (2), (7), we use an integral-series identity (ISI)

$$\int\limits_{0}^{a}\biggl{(}\sum_{n=1}^{+\infty}b_{n}\bigl{(}1-e^{2i\gamma_{n}c}\bigr{)}\varphi_{n}(t)\biggr{)}K(t,x)dt=\sum_{n=1}^{+\infty}b_{n}\gamma_{n}\varphi_{n}(x),\quad 0<x<a,$$

here \(K(t,x)=\sum_{m=1}^{+\infty}\frac{\gamma_{m}}{1-e^{2i\gamma_{m}c}}\varphi_{m}(t)\varphi_{m}(x)\) (it is assumed that \(\gamma_{m}c\neq\pi j\)). From ISI, with the account (2), we will get on \(\mathcal{M}\)

$$\sum_{n=1}^{+\infty}b_{n}\gamma_{n}\varphi_{n}(x)=\sum_{n=1}^{+\infty}b_{n}\bigl{(}1-e^{2i\gamma_{n}c}\bigr{)}\sum_{m=1}^{+\infty}\frac{\gamma_{m}}{1-e^{2i\gamma_{m}c}}\varphi_{m}(x)J_{nm}.$$
(8)

Finally, we will project (7) and (8) on \(\varphi_{k}(x)\) and get ISLAE (5). \(\Box\)

3 COMPUTING EXPERIMENT

We will look for approximate solutions of ISLAE (5) by the truncation method. Let us replace (5) by the set of linear algebraic equations (SLAE)

$$\gamma_{k}b_{k}-\sum_{n=1}^{N}b_{n}\bigl{(}1-e^{2i\gamma_{n}c}\bigr{)}\sum_{m=1}^{M}\frac{\gamma_{m}}{1-e^{2i\gamma_{m}c}}J_{nm}I_{mk}=\gamma_{l}I_{lk},\quad k=1,\,\dots,N.$$
(9)

Let’s limit ourselves to the case when the truncation parameters are equal, let \(M=N\). As the computing experiment has shown, it is enough to take \(N=30\) for the internal convergence of the truncation method. As a wave incoming on the diaphragm, we will consider the first mode of the waveguide (\(l=1\)).

Let’s choose the following parameters of the waveguide and of the diaphragm: \(a=1.1\), \(c=1.3\), \(\alpha=0.5\), \(\beta=0.6\) (in dimensionless amounts). We will look for solutions SLAE (9) by Gauss method with the selection of the lead element on the column with double accuracy (double) of arithmetic of real numbers. The dependence of modules of coefficients \(b_{1}\) and \(b_{3}\) on the spectral parameter of \(\kappa\) is shown in Fig. 3.

Fig. 3
figure 3

The dependence of the coefficient modules \(b_{1}\) and \(b_{3}\) on the parameter \(\kappa\).

Full size image

This dependency has a resonant nature, or more precisely, the coefficient module \(b_{1}\) has three local extremes at a segment \([3.5,8.5]\), which correspond to the wave numbers \({\approx}3.7355\), \({\approx}5.5985\), and \({\approx}7.7645\). These values are close to the eigen wave numbers \(\kappa_{1,1}\approx 3.7412,\kappa_{1,2}\approx 5.6140\), and \(\kappa_{1,3}\approx 7.7921\) of a two-dimensional rectangular resonator without a hole.

With the hole in the diaphragm which is symmetrical relative to the axis of waveguide, the following phenomenon is observed: \(b_{n}\) with the odd numbers are zeros for the even number of the running wave (\(b_{n}\) with the even numbers are zeros for the odd numbers). This is not the case if the diaphragm hole is asymmetrical.

As the size of the hole in the diaphragm increases, the resonant frequency values decrease (Fig. 4) and the resonant curve becomes more stretched.

Fig. 4
figure 4

Resonant frequency dependency on hole sizes.

Full size image

The coefficients \(a_{n}\) are calculated by the coefficients \(b_{n}\) by the formulas (6). The dependence of the modules of the coefficients \(a_{1}\) and \(a_{3}\) on the parameter \(k\) in the neighborhood of eigen frequency \(\kappa_{1,1}\) is presented in Fig. 5. We note that \(a_{n}\approx b_{n}\) for \(n\geq 3\).

Fig. 5
figure 5

Modules of coefficients \(a_{1}\) and \(a_{3}\) in the neighborhood \(\kappa_{1,1}\).

Full size image

In one-mode case (only one eigen wave of waveguide transfers energy) the first reflected mode should bring back all the energy of the wave that came from infinity. Therefore, at any value of \(k\), the exact value \(|a_{1}|=1\). When debugging a computer program, it is advisable to check two other limit cases. If the diaphragm completely overlaps the waveguide, then it follows from (1), (2) that \(a_{1}=-1\), all other coefficients are zero. If there is no diaphragm (\(\alpha=0,\beta=a\)), then it follows from (3), (4) that \(b_{1}=1,a_{1}=-e^{2i\gamma_{1}c}\), and all other coefficients are zeros. In the neighborhood of other eigen frequencies, the dependence of the desired values on the frequency of oscillations is also resonant (Fig. 6).

Fig. 6
figure 6

Modules of coefficients \(a_{1}\) and \(a_{3}\) in the neighborhood \(\kappa_{1,2}\).

Full size image

Let’s examine how the spectral parameter \(\kappa\) depends on the conditioned number of the matrix \(A\) of SLAE coefficients (9)

$$\textrm{cond}A=||A||\cdot||A^{-1}||,\quad||A||=\sqrt{\sum_{k=1}^{N}\sum_{j=1}^{N}|A_{kj}|^{2}}$$

(the norm of Frobenius is used). This dependence is also resonant. For example, in the neighborhood of the resonant value of parameter \(3.7355\) (diaphragm hole is \([0.5,0.6]\)) the maximum value cond A exceeds \(22000\).

Let’s balance the equations in SLAE (9). Let us divide each equation by the largest in-module coefficient for unknowns. Then the conditioned number will be significantly reduced, but the solution of the SLAE does not change. But after balancing, it becomes possible to study the dependence on the parameter \(\kappa\) of the values of the determinant of the matrix of the SLAE coefficients, now the modules of these values in the neighborhood of the resonant point are no more than one. Before balancing, they had an order of \(10^{45}\) or more. When approaching the resonant values of \(\kappa\), the determinant of coefficients matrix sharply tends to zero. Thus, the resonant values of the parameter \(\kappa\) can be found: 1) when solving the SLAE (9); 2) when calculating the conditioned number of the matrix of its coefficients; 3) when analyzing the values of the determinant of this matrix.

The third method is consistent with the fact that resonant (complex) eigen resonator frequencies with a hole in the wall should be the roots of the characteristic equation \(\textrm{det}A=0\). When formulating a problem on eigen frequencies of such a resonator, you need to formulate physically correctly a boundary condition on the hole. In our case, this condition is reduced to the fact that the energy goes away through the hole in the flat waveguide attached to the resonator. Then non-zero solutions of the homogeneous diffraction problem are the eigen waves of structure consisting of the resonator and the waveguide.

Another effect of resonant nature is observed in an exceptional case, when \(\gamma_{n_{0}}c=\pi j\) for some \(n_{0}\) and \(j\). In this case \(\kappa^{2}=\kappa^{2}_{n_{0},j}=(\pi n_{0}/a)^{2}+(\pi j/c)^{2}\) are eigen wave number values of resonator without a hole. The resonance is observed only for values of \(\textrm{cond}A\) and of \(\textrm{det}A\), the solution of SLAE (9) remains stable. For example, if \(\kappa=\kappa_{1,1}\), that is \(\gamma_{1}c=\pi\), then \(e^{2i\gamma_{1}c}=1\). The PSFE (7), (8) has an obvious solution \(b_{1}=1,b_{n}=0,n\neq 1\). Therefore, \(a_{1}=-1\). The interesting thing is that in this exceptional case, this solution does not depend on the size of the hole in the diaphragm.

The resonance of the values of \(\textrm{cond}A\) and of \(\textrm{det}A\) is based on the fact that in an exceptional case, in the ISLAE (5) and in its truncation (9) the denominator of one of the terms \(1-e^{2i\gamma_{m}c}\) in the internal sum turns to zero. This effect does not appear for the second version of ISLAE

$$d_{k}\bigl{(}1-e^{2i\gamma_{k}c}\bigr{)}-\sum_{n=1}^{+\infty}d_{n}\gamma_{n}\sum_{m=1}^{+\infty}\frac{1-e^{2i\gamma_{m}c}}{\gamma_{m}}I_{nm}J_{mk}=\bigl{(}e^{2i\gamma_{l}c}-1\bigr{)}I_{lk},\quad k=1,2,\dots$$
(10)

relatively unknown \(d_{l}=b_{l}-1\), \(d_{n}=b_{n}\), \(n\neq l\). ISLAE (10) is obtained from PSFE (7), (8) by the second ISI

$$\int\limits_{0}^{a}\biggl{(}\sum_{n=1}^{+\infty}d_{n}\gamma_{n}\varphi_{n}(t)\biggr{)}\biggl{(}\sum_{m=1}^{+\infty}\frac{1-e^{2i\gamma_{m}c}}{\gamma_{m}}\varphi_{m}(t)\varphi_{m}(x)\biggr{)}dt=\sum_{n=1}^{+\infty}d_{n}\bigl{(}1-e^{2i\gamma_{n}c}\bigr{)}\varphi_{n}(x).$$

4 THREE-DIMENSIONAL DIFFRACTION PROBLEM

The three-dimensional problem of diffraction of the electromagnetic wave by the diaphragm before flange in a rectangular waveguide is explored in a similar way.

Let the diaphragm with a hole \(\mathcal{N}\) and \({\mathcal{M}}={\mathcal{S}}\backslash{\mathcal{N}}\) be located in the cross-section of the waveguide \({\mathcal{S}}=[0,a]\times[0,b]\) on the plane \(z=0\) (Fig. 7). The flange lies in the plane \(z=c\).

Fig. 7
figure 7

Diaphragm in a rectangular waveguide.

Full size image

Let an electromagnetic wave with longitudinal components (potential functions) run from the left on a hole \(E^{0}_{z}=e_{0}e^{i\gamma_{m_{0}n_{0}}z}s^{a}_{m_{0}}(x)s^{b}_{n_{0}}(y),\) \(H^{0}_{z}=h_{0}e^{i\gamma_{m_{0}n_{0}}z}c^{a}_{m_{0}}(x)c^{b}_{n_{0}}(y).\) Here and beyond the following designations are used: \(\gamma_{mn}=\sqrt{\kappa^{2}-\delta_{mn}}\) is a longitudinal propagation constant, \(\kappa\) is a wave number, \(\delta_{mn}=(\pi m/a)^{2}+(\pi n/b)^{2}\),

$$s^{a}_{m}(x)=\sqrt{2/a}\sin\frac{\pi m}{a}x,\quad s^{b}_{n}(y)=\sqrt{2/b}\sin\frac{\pi n}{b}y,\quad m,n=1,2,\dots,$$
$$c^{a}_{m}(x)=\sqrt{2/a}\cos\frac{\pi m}{a}x,\quad c^{b}_{n}(y)=\sqrt{2/b}\cos\frac{\pi n}{b}y,\quad m,n=0,1,\dots$$

The longitudinal components of the wave reflected in the \(z<0\) area will be searched in the form of

$$E^{I}_{z}=\sum_{m,n=1}^{+\infty}a_{mn}e^{-i\gamma_{mn}z}s^{a}_{m}(x)s^{b}_{n}(y),\quad H^{I}_{z}=\sum_{m,n=(0)}^{+\infty}c_{mn}e^{-i\gamma_{mn}z}c^{a}_{m}(x)c^{b}_{n}(y),$$

expression \(m,n=(0)\) means that the summation indices do not turn to zero at the same time. The longitudinal components of the standing wave in the domain \(0<z<c\) will be searched in the form of

$$E^{II}_{z}=\sum_{m,n=1}^{+\infty}b_{mn}s^{a}_{m}(x)s^{b}_{n}(y)\bigl{(}e^{2i\gamma_{mn}c}e^{-i\gamma_{mn}z}+e^{i\gamma_{mn}z}\bigr{)},$$
$$H^{II}_{z}=\sum_{m,n=(0)}^{+\infty}d_{mn}c^{a}_{m}(x)c^{b}_{n}(y)\bigl{(}e^{i\gamma_{mn}z}-e^{2i\gamma_{mn}c}e^{-i\gamma_{mn}z}\bigr{)},$$

these functions, as in the two-dimensional case, are limited when \(m,n\to+\infty\).

We will record the boundary conditions and the conjugation conditions when \(z=0\). On \(\mathcal{M}\) should be turned to zero limit values \(\partial E_{z}/\partial z\) and \(H_{z}\):

$$e_{0}\gamma_{m_{0}n_{0}}s^{a}_{m_{0}}(x)s^{b}_{n_{0}}(y)-\sum_{m,n=1}^{+\infty}a_{mn}\gamma_{mn}s^{a}_{m}(x)s^{b}_{n}(y)=0,$$
(11)
$$h_{0}c^{a}_{m_{0}}(x)c^{b}_{n_{0}}(y)+\sum_{m,n=(0)}^{+\infty}c_{mn}c^{a}_{m}(x)c^{b}_{n}(y)=0,$$
(12)
$$\sum_{m,n=1}^{+\infty}b_{mn}\gamma_{mn}\bigl{(}1-e^{2i\gamma_{mn}c}\bigr{)}s^{a}_{m}(x)s^{b}_{n}(y)=0,$$
(13)
$$\sum_{m,n=(0)}^{+\infty}d_{mn}\bigl{(}1-e^{2i\gamma_{mn}c}\bigr{)}c^{a}_{m}(x)c^{b}_{n}(y)=0.$$
(14)

On \(\mathcal{N}\) the values \(\partial E_{z}/\partial z,H_{z},\partial H_{z}/\partial z\) and \(E_{z}\) should be continuous:

$$e_{0}\gamma_{m_{0}n_{0}}s^{a}_{m_{0}}(x)s^{b}_{n_{0}}(y)-\sum_{m,n=1}^{+\infty}a_{mn}\gamma_{mn}s^{a}_{m}(x)s^{b}_{n}(y)$$
$${}=\sum_{m,n=1}^{+\infty}b_{mn}\gamma_{mn}\bigl{(}1-e^{2i\gamma_{mn}c}\bigr{)}s^{a}_{m}(x)s^{b}_{n}(y),$$
(15)
$$h_{0}c^{a}_{m_{0}}(x)c^{b}_{n_{0}}(y)+\sum_{m,n=(0)}^{+\infty}c_{mn}c^{a}_{m}(x)c^{b}_{n}(y)=\sum_{m,n=(0)}^{+\infty}d_{mn}\bigl{(}1-e^{2i\gamma_{mn}c}\bigr{)}c^{a}_{m}(x)c^{b}_{n}(y),$$
(16)
$$h_{0}\gamma_{m_{0}n_{0}}c^{a}_{m_{0}}(x)c^{b}_{n_{0}}(y)-\sum_{m,n=(0)}^{+\infty}c_{mn}\gamma_{mn}c^{a}_{m}(x)c^{b}_{n}(y)$$
$${}=\sum_{m,n=(0)}^{+\infty}d_{mn}\gamma_{mn}\bigl{(}1+e^{2i\gamma_{mn}c}\bigr{)}c^{a}_{m}(x)c^{b}_{n}(y),$$
(17)
$$e_{0}s^{a}_{m_{0}}(x)s^{b}_{n_{0}}(y)+\sum_{m,n=1}^{+\infty}a_{mn}s^{a}_{m}(x)s^{b}_{n}(y)=\sum_{m,n=1}^{+\infty}b_{mn}\bigl{(}1+e^{2i\gamma_{mn}c}\bigr{)}s^{a}_{m}(x)s^{b}_{n}(y).$$
(18)

Theorem 2. The problem of diffraction of the electromagnetic wave on the diaphragm in a semi-infinite rectangular waveguide is reduced to two independent ISLAE

$$b_{jk}-\sum_{m,n=1}^{+\infty}b_{mn}\gamma_{mn}\bigl{(}1-e^{2i\gamma_{mn}c}\bigr{)}\sum_{p,q=1}^{+\infty}\frac{1}{\gamma_{pq}\bigl{(}1-e^{2i\gamma_{pq}c}\bigr{)}}J^{sasb}_{mpnq}I^{sasb}_{pjqk}$$
$${}=e_{0}J^{sasb}_{m_{0}jn_{0}k},\quad j,k=1,2,\dots$$
(19)
$$\gamma_{jk}d_{jk}-\sum_{m,n=(0)}^{+\infty}d_{mn}\bigl{(}1-e^{2i\gamma_{mn}c}\bigr{)}\sum_{p,q=(0)}^{+\infty}\frac{\gamma_{pq}}{1-e^{2i\gamma_{pq}c}}J^{cacb}_{mpnq}I^{cacb}_{pjqk}$$
$${}=h_{0}\gamma_{m_{0}n_{0}}J^{cacb}_{m_{0}jn_{0}k},\quad j,k=(0),1,\dots$$
(20)

where

$$J^{sasb}_{mpnq}=\int\limits_{\mathcal{N}}s^{a}_{m}(x_{1})s^{a}_{p}(x_{1})s^{b}_{n}(y_{1})s^{b}_{q}(y_{1})dx_{1}dy_{1},\quad I^{sasb}_{mpnq}=\int\limits_{\mathcal{M}}s^{a}_{m}(x_{1})s^{a}_{p}(x_{1})s^{b}_{n}(y_{1})s^{b}_{q}(y_{1})dx_{1}dy_{1},$$
$$J^{cacb}_{mpnq}=\int\limits_{\mathcal{N}}c^{a}_{m}(x_{1})c^{a}_{p}(x_{1})c^{b}_{n}(y_{1})c^{b}_{q}(y_{1})dx_{1}dy_{1},\quad I^{cacb}_{mpnq}=\int\limits_{\mathcal{M}}c^{a}_{m}(x_{1})c^{a}_{p}(x_{1})c^{b}_{n}(y_{1})c^{b}_{q}(y_{1})dx_{1}dy_{1}.$$

Proof. It is easy to see that the boundary conditions and the conjugation conditions form two independent groups of equations: (11), (13), (15) and (18) for TM-polarized waves and (12), (14), (16) and (17) for TE-polarized waves. We convert these equations into ISLAE by integral-series identities.

In the case of TM-polarized waves, from (11), (13) and (15) it follows that (15) fulfills at \(\mathcal{S}\). Then \(a_{m_{0}n_{0}}=-b_{m_{0}n_{0}}\bigl{(}1-e^{2i\gamma_{m_{0}n_{0}}c}\bigr{)}+e_{0},\) \(a_{mn}=-b_{mn}\bigl{(}1-e^{2i\gamma_{mn}c}\bigr{)},m,n\not=m_{0},n_{0}.\) We eliminate \(a_{mn}\) from the equation (18) and we get

$$\sum_{m,n=1}^{+\infty}b_{mn}s^{a}_{m}(x)s^{b}_{n}(y)=e_{0}s^{a}_{m_{0}}(x)s^{b}_{n_{0}}(y),\quad(x,y)\in{\mathcal{N}}.$$
(21)

For \((x,y)\in{\mathcal{S}}\), there is an integral-series identity (ISI)

$$\int\limits_{\mathcal{S}}\Bigl{(}\sum_{m,n=1}^{+\infty}b_{mn}\gamma_{mn}\bigl{(}1-e^{2i\gamma_{mn}c}\bigr{)}s^{a}_{m}(x_{1})s^{b}_{n}(y_{1})\Bigr{)}K_{-1}(x_{1},y_{1},x,y)dx_{1}dy_{1}=\sum_{m,n=1}^{+\infty}b_{mn}s^{a}_{m}(x)s^{b}_{n}(y),$$

where

$$K_{-1}(x_{1},y_{1},x,y)=\sum_{p,q=1}^{+\infty}\frac{1}{\gamma_{pq}\bigl{(}1-e^{2i\gamma_{pq}c}\bigr{)}}s^{a}_{p}(x_{1})s^{b}_{q}(y_{1})s^{a}_{p}(x)s^{b}_{q}(y).$$

From the ISI, by (13) it follows that on \(\mathcal{M}\)

$$\sum_{m,n=1}^{+\infty}b_{mn}s^{a}_{m}(x)s^{b}_{n}(y)=\sum_{m,n=1}^{+\infty}b_{mn}\gamma_{mn}\bigl{(}1-e^{2i\gamma_{mn}c}\bigr{)}\sum_{p,q=1}^{+\infty}\frac{1}{\gamma_{pq}\bigl{(}1-e^{2i\gamma_{pq}c}\bigr{)}}J^{sasb}_{mpnq}s^{a}_{p}(x)s^{b}_{q}(y).$$
(22)

We project a paired equation (21) (on the hole) and (22) (on the metal) on \(s^{a}_{j}(x)s^{b}_{k}(y)\) and get ISLAE (19).

Similarly, in the case of TM-polarized waves from (12), (14) and (16) it follows that (16) fulfills at \(\mathcal{S}\). Then \(c_{m_{0}n_{0}}=d_{m_{0}n_{0}}\bigl{(}1-e^{2i\gamma_{m_{0}n_{0}}c}\bigr{)}-h_{0},\) \(c_{mn}=d_{mn}\bigl{(}1-e^{2i\gamma_{mn}c}\bigr{)},m,n\not=m_{0},n_{0}.\) We exclude \(c_{mn}\) out of the equation and then we get

$$\sum_{m,n=(0)}^{+\infty}d_{mn}\gamma_{mn}c^{a}_{m}(x)c^{b}_{n}(y)=h_{0}\gamma_{m_{0}n_{0}}c^{a}_{m_{0}}(x)c^{b}_{n_{0}}(y),\quad(x,y)\in\mathcal{N.}$$
(23)

For \((x,y)\in{\mathcal{S}}\), there is an integral-series identity

$$\int\limits_{\mathcal{S}}\Bigl{(}\sum_{m,n=(0)}^{+\infty}d_{mn}\bigl{(}1-e^{2i\gamma_{mn}c}\bigr{)}c^{a}_{m}(x_{1})c^{b}_{n}(y_{1})\Bigr{)}K_{1}(x_{1},y_{1},x,y)dx_{1}dy_{1}=\sum_{m,n=(0)}^{+\infty}d_{mn}\gamma_{mn}c^{a}_{m}(x)c^{b}_{n}(y),$$

where \(K_{1}(x_{1},y_{1},x,y)=\sum_{p,q=(0)}^{+\infty}\frac{\gamma_{pq}}{1-e^{2i\gamma_{pq}c}}c^{a}_{p}(x_{1})c^{b}_{q}(y_{1})c^{a}_{p}(x)c^{b}_{q}(y).\) From the ISI, by (14) we get on \(\mathcal{M}\)

$$\sum_{m,n=(0)}^{+\infty}d_{mn}\gamma_{mn}c^{a}_{m}(x)c^{b}_{n}(y)=\sum_{m,n=(0)}^{+\infty}d_{mn}\bigl{(}1-e^{2i\gamma_{mn}c}\bigr{)}\sum_{p,q=(0)}^{+\infty}\frac{\gamma_{pq}}{1-e^{2i\gamma_{pq}c}}J^{cacb}_{mpnq}c^{a}_{p}(x)c^{b}_{q}(y).$$
(24)

We project a paired equation (23) (on the hole) and (24) (on the metal) on \(c^{a}_{j}(x)c^{b}_{k}(y)\) and get ISLAE (20). \(\Box\)

Note that functions \(s^{a}_{m}(x)s^{b}_{n}(y),c^{a}_{m}(x)c^{b}_{n}(y)\) form orthonormal function sets on \(\mathcal{S}\). So \(I^{sasb}_{mpnq}=\delta_{mp}\delta_{nq}-J^{sasb}_{mpnq}\), \(I^{cacb}_{mpnq}=\delta_{mp}\delta_{nq}-J^{cacb}_{mpnq}\), here \(\delta_{jk}\) is Kronecker symbol.

If the diaphragm hole has a rectangular shape, \({\mathcal{N}}=[\alpha_{0},\alpha_{1}]\times[\beta_{0},\beta_{1}]\), then all integrals over \(\mathcal{N}\) and over \(\mathcal{M}\) in ISLAE (19), (20) can be easily expressed through integrals

$$J^{sa}_{mp}=\int\limits_{\alpha_{0}}^{\alpha_{1}}s^{a}_{m}(x_{1})s^{a}_{p}(x_{1})dx_{1},\quad J^{sb}_{nq}=\int\limits_{\beta_{0}}^{\beta_{1}}s^{b}_{n}(y_{1})s^{b}_{q}(y_{1})dy_{1},$$
$$J^{ca}_{mp}=\int\limits_{\alpha_{0}}^{\alpha_{1}}c^{a}_{m}(x_{1})c^{a}_{p}(x_{1})dx_{1},\quad J^{cb}_{nq}=\int\limits_{\beta_{0}}^{\beta_{1}}c^{b}_{n}(y_{1})c^{b}_{q}(y_{1})dy_{1}.$$

Let, for example, \(b>a\). Then the diaphragm in the Fig. 8a) is inductive and diaphragm in the Fig. 8b) is capacitive. In these two particular cases, ISLAE (19) and (20) become significantly easier.

Fig. 8
figure 8

Inductive and capacitive diaphragms in a rectangular waveguide.

Full size image

Corollary 1. The problem of diffraction of the electromagnetic wave on the inductive diaphragm is reduced to two independent ISLAE

$$b_{m_{0}k}-\sum_{n=1}^{\infty}b_{m_{0}n}\gamma_{m_{0}n}\bigl{(}1-e^{2i\gamma_{m_{0}n}c}\bigr{)}\sum_{q=1}^{\infty}\frac{1}{\gamma_{m_{0}q}\bigl{(}1-e^{2i\gamma_{m_{0}q}c}\bigr{)}}J^{sb}_{nq}I^{sb}_{qk}=e_{0}J^{sb}_{n_{0}k},\quad k=1,2,\dots$$
$$\gamma_{m_{0}k}d_{m_{0}k}-\sum_{n=(0)}^{\infty}d_{m_{0}n}\bigl{(}1-e^{2i\gamma_{m_{0}n}c}\bigr{)}\sum_{q=(0)}^{\infty}\frac{\gamma_{m_{0}q}}{1-e^{2i\gamma_{m_{0}q}c}}J^{cb}_{nq}I^{cb}_{qk}=h_{0}\gamma_{m_{0}n_{0}}J^{cb}_{n_{0}k},\quad k=(0),1,\dots$$

If the lower limit of the index change is \((0)\), then it is zero if \(m_{0}\neq 0\) and is a unit if \(m_{0}=0\). Really, in the case of the inductive diaphragm, the equations (21) and (22) (and ones considered above, including ISI) should be fulfilled when \(x\in[0,a]\). Due to the orthonormality of the functions \(s^{a}_{j}(x)\) on \([0,a]\), these equations split into independent pairs of equations, which are obtained as equalities of the coefficients at \(s^{a}_{j}(x)\). Only a pair of equations with the number \(j=m_{0}\) has a non-trivial solution, and the first ISLAE corresponds to it in the statement of the Corollary 1.

The second ISLAE is obtained from the equations (23) and (24) on the basis of the orthonormality of the functions \(c^{a}_{j}(x)\) on \([0,a]\).

A similar statement takes place in the case of a capacitive diaphragm.

Corollary 2. The problem of diffraction of the electromagnetic wave by the capacitive diaphragm is reduced to two independent ISLAE

$$b_{jn_{0}}-\sum_{m=1}^{\infty}b_{mn_{0}}\gamma_{mn_{0}}\bigl{(}1-e^{2i\gamma_{mn_{0}}c}\bigr{)}\sum_{p=1}^{\infty}\frac{1}{\gamma_{pn_{0}}\bigl{(}1-e^{2i\gamma_{pn_{0}}c}\bigr{)}}J^{sa}_{mp}I^{sa}_{pj}=e_{0}J^{sa}_{m_{0}j},\quad j=1,2,\dots$$
$$\gamma_{jn_{0}}d_{jn_{0}}-\sum_{m=(0)}^{\infty}d_{mn_{0}}\bigl{(}1-e^{2i\gamma_{mn_{0}}c}\bigr{)}\sum_{p=(0)}^{\infty}\frac{\gamma_{pn_{0}}}{1-e^{2i\gamma_{pn_{0}}c}}J^{ca}_{mp}I^{ca}_{pj}=h_{0}\gamma_{m_{0}n_{0}}J^{ca}_{m_{0}j},\quad j=(0),1,\dots$$

5 RESONANT FREQUENCIES IN THE 3D CASE

We will look for an approximate solution of ISLAE (19) by the truncation method. Consider SLAE

$$b_{jk}-\sum_{m,n=1}^{N}b_{mn}\gamma_{mn}\bigl{(}1-e^{2i\gamma_{mn}c}\bigr{)}\sum_{p,q=1}^{N}\frac{1}{\gamma_{pq}\bigl{(}1-e^{2i\gamma_{pq}c}\bigr{)}}J^{sa}_{mp}J^{sb}_{nq}I^{sa}_{pj}I^{sb}_{qk}=e_{0}J^{sa}_{m_{0}j}J^{sb}_{n_{0}k},$$
$$j,k=1,2,\dots,N,$$
(25)

where \(N\) is a truncation parameter. As the computing experiment has shown, it’s enough to set \(N=40\).

Let’s choose the following values of the original data: the number of the running wave \(m_{0}=1\), \(n_{0}=1\), the amplitude \(e_{0}=1\), the waveguide size \(a=1.1\), \(b=1.8\), \(c=1.3\) and diaphragm windows \(\alpha_{0}=0.4\), \(\alpha_{1}=0.5\), \(\beta_{0}=0.4\), \(\beta_{1}=0.5\) (square resonant window).

As the computing experiment has shown, the dependence of standing wave decomposition modules in area II on the spectral parameter of \(\kappa\) (frequency of the running wave) has a resonant nature. Resonances are observed at the frequency of the running wave, close to eigen frequencies of the rectangular resonator without a hole in the wall.

Resonant curves for coefficients \(b_{1,1}\) and \(b_{1,3}\) are presented on the Fig. 9. The three extremes for the \(b_{1,1}\) coefficient correspond to frequencies close to eigen frequencies \(\kappa_{1,1,1}\approx 4.128\), \(\kappa_{1,1,2}\approx 5.879\), \(\kappa_{1,1,3}\approx 7.985\) of the resonator without a hole, and extremes for \(b_{1,3}\) coefficient are observed at frequencies close to \(\kappa_{1,2,1}\approx 5.116\), \(\kappa_{1,2,2}\approx 6.610\), \(\kappa_{1,2,3}\approx 8.538\).

Fig. 9
figure 9

Resonant curves for coefficients \(b_{1,1}\) and \(b_{1,3}\).

Full size image

Similar results were obtained in the case of TM-polarization of the field.

6 CONCLUSION

In the work the diffraction problems of the electromagnetic wave by the diaphragm in a semi-infinite place waveguide and rectangular waveguides are reduced to infinite sets of linear algebraic equations relative to decomposition coefficients by eigen field waves in the region between the diaphragm and the flange. The computing experiment has shown that the dependence of the desired coefficients on the frequency of the excitatory wave is resonant. At small diaphragm size, resonant frequencies are close to eigen frequencies of rectangular resonators without a hole.