The Branch-and-Bound Algorithm for the Traveling Salesman Problem is Not a Direct Algorithm

Abstract—

This article considers the concept of a linear separation direct algorithm introduced by V.A. Bondarenko in 1983. The concept of a direct algorithm is defined using the solution graph of a combinatorial optimization problem. The vertices of this graph are all feasible solutions of the problem. Two solutions are called adjacent if there are input data for which these and only these solutions are optimal. A key feature of direct algorithms is that their complexity is bounded from below by the clique number of the solution graph. In 2015–2018, there were five articles published, the main results of which are estimates of the clique numbers of polyhedron graphs associated with various combinatorial optimization problems. The thesis that the class of direct algorithms is broad and includes many classical combinatorial algorithms, including the branch-and-bound algorithm for the traveling salesman problem proposed by J.D.C. Little, K.G. Murty, D.W. Sweeney, and C. Karel in 1963, was the main motivation for these articles. We show that this algorithm is not a direct algorithm. Earlier, in 2014, the author of this article showed that the Hungarian algorithm for the assignment problem is not a direct algorithm. Therefore, the class of direct algorithms is not as broad as previously assumed.

INTRODUCTION

In 2015–2018, several articles [1–5] were published, the main results of which are estimates of clique numbers of polyhedron graphs associated with various combinatorial optimization problems. The main motivation for such estimates was the following thesis [5]: “It is known that this value characterizes the time complexity in a broad class of algorithms based on linear comparisons.” Namely, we are talking about the class of direct algorithms first introduced in [6]. As a proof of this thesis, works [2, 3] stated that this class includes sorting algorithms, a greedy algorithm, dynamic programming, and the branch-and-bound method¹. The proofs that these algorithms (as well as the Edmonds’ algorithm for the matching problem) are direct algorithms were first published in thesis [7] (see also [8]). In 2014, it was shown in [9] that the Kuhn–Munkres algorithm for the assignment problem (and with it the Edmonds’ algorithm) does not belong to this class. There we also described a method of modifying algorithms that is often used in practice, which takes them out of the class of direct algorithms. Below, we will prove that the classical branch-and-bound algorithm for the traveling salesman problem [10, 11] also does not belong to this class. It will thus be shown that Theorem 2.6.3 from [7] (Theorem 3.6.6 from [8]) cannot be proved in the initial formulation. This leads to the conclusion that the class of direct algorithms is not as broad as previously assumed.

The article is organized as follows. Section 1 presents a pseudocode of the classical branch-and-bound algorithm for the traveling salesman problem. Section 2 introduces the basic notions of the concept of direct algorithms and two key definitions: the direct algorithm and the “direct” algorithm. Section 3 shows that the classical branch-and-bound algorithm for the traveling salesman problem is not a direct algorithm and Section 4 shows that it is not a “direct” algorithm.

1 BRANCH-AND-BOUND ALGORITHM FOR THE TRAVELING SALESMAN PROBLEM

Consider a complete orgraph $G = (V,A)$ with a set of vertices $V = [n] = \{ 1,2, \ldots ,n\}$ and arcs $A = \left\{ {\left. {(i,j)} \right|i,j \in V,\,\,i \ne j} \right\}$. Each arc $(i,j) \in A$ is assigned a number ${{c}_{{ij}}} \in \mathbb{Z}$, called an arc length. The length of a subset $H \subseteq A$ is the total length of its arcs: ${\text{len}}(H) = \sum\nolimits_{(i,j) \in H} {{c}_{{ij}}}$. The traveling salesman problem consists in finding $H^{*} \subseteq A$, which is a Hamiltonian circuit in $G$ and has a minimal length of ${\text{len}}(H^{*})$.

For ease of further discussion, let us put the numbers ${{c}_{{ij}}}$ in the matrix $C = ({{c}_{{ij}}})$. We assign to the diagonal elements ${{c}_{{ii}}}$ the maximum possible lengths, ${{c}_{{ii}}}: = \infty$, in order to exclude their effect on the operation of the algorithm, and we assume that $\infty - b = \infty$ for any number $b \in \mathbb{Z}$. We denote by ${\text{I}}(M)$ the set of matrix row indices $M$, and by ${\text{J}}(M)$ we denote the set of matrix column indices $M$. At the beginning of the algorithm operation, ${\text{I}}(C) = {\text{J}}(C) = V$. We denote by $M(S,T)$ the submatrix of the matrix $M$ that lies at the intersection of rows $S \subseteq {\text{I}}(M)$ and columns $T \subseteq {\text{J}}(M)$.

The algorithm itself was described in detail in [11, Section 4.1.6] and [10]. We give only its pseudocode, Algorithm 1. Separately, Algorithm 2 describes the process of reducing matrix rows and columns, and Algorithm 3 describes the way of selecting such a zero element of a matrix that, when replaced by infinity, maximizes the sum of matrix reductions.

Algorithm 1. Branch-and-bound method for the traveling salesman problem
Global: Hamiltonian circuit Hopt of minimal length; its length is lopt. Before      the algorithm was launched, lopt := ∞.
Input : distance matrix M; the set of arcs Arcs required to be included in the circuit;        the current sum of all reductions sum. At the very beginning of the algorithm operation, M ∶= C,      Arcs ∶= ∅, sum ∶= 0
1 Procedure BranchBound (M, Arcs, sum)
		/* Reduce the matrix M							$*/$
2		Reduction (M, sum)
3		if sum ≥ lopt then
4				terminate the current instance of the procedure
		/* Choose the optimal zero element of the matrix M							$*/$
5		(i, j) := ChooseArc (M)
		/* Examine cases in which the circuit contains the arc (i, j)							$*/$
6		if |I| = 3 then
				/* Find a single Hamiltonian circuit					$*/$
7				H := HamiltonCycle(Arcs $\cup$ {(i, j)})
8				if len(H) < lopt then
9						Hopt := H
10						lopt := len(H)
11		else
				/* Remove the ith row and jth column					$*/$
12				Mnew := M(I(M) \ {i}, J(M) \ {j})
				/* Find the forbidden arc					$*/$
13				(l, k) := ForbiddenArc (Arcs, (i,j))
14				Mnew[l,k] := ∞
15				BranchBound (Mnew, Arcs $\cup$ {(i, j)}, sum)
		/* Examine cases in which the circuit does not have the arc (i, j)							$*/$
16		M[i,j] := ∞
17		BranchBound (M, Arcs, sum)
18 Function HamiltonCycle (Arcs)
19		Find a Hamiltonian circuit which contains all arcs from Arcs.
20 Function ForbiddenArc (Arcs, (i, j))
21		Find a pair of vertices l and k which are the end and the beginning of the largest (by inclusion)  path in Arcs containing (i, j).

Algorithm 2. Reducing the rows and columns of a matrix
Input   : matrix M; the current sum of all reductions sum.
Output     : reduced matrix M; modified sum.
1 Procedure Reduction (M, sum)
		/* Reduce the rows of the matrix M							$*/$
2		for i ∈ I(M) do
3				m := ∞
				/* Find m = m(i) = minj ∈ J(M) M[i,j]					$*/$
4				for i ∈ J(M) do
5						if m > M[i,j] then m := M[i,j]
6				sum := sum + m
7				for j ∈ J(M) do M[i,j] := M[i,j] − m
		/* Reduce columns of the matrix M							$*/$
8		for j ∈ J(M) do
9				m := ∞
10				for i ∈ I(M) do
11						if m > M[i,j] then m := M[i,j]
12				sum := sum + m
13				for i ∈ I(M) do M[i,j] := M[i,j] − m

Algorithm 3. Arc selection
Input   : matrix M.
Output     : the arc (i*, j*) whose lower Hamiltonian circuit length estimate is maximum when forbidden.
1 Function ChooseArc(M)
2		w := −1
3		for i ∈ I(M) do
4				for j ∈ J(M) do
5						if M[i,j] = 0 then
6								m := ∞
								/*  Find m = mint  M[i,t]			$*/$
7								for t ∈ J(M)\ {j} do
8										if m > M[i,t] then m := M[i,t]
9								k := ∞
								/*  Find k = mint  M[t,j]			$*/$
10								for t ∈ I(M)\ {i} do
11										if k > M[t,j] then k := M[t,j]
								/*  Compare m + k with the current record w			$*/$
12								if m + k > w then
13										w := m + k
14										(i*, j*) := (i, j)

2 DIRECT ALGORITHMS

In presenting the basics of the theory of direct algorithms, we follow [7] (see also [8]).

For the purpose of unifying the description, the arc-length matrix $C$ will hereafter be called an input data vector² or simply an input. The solution of the traveling salesman problem, i.e., the Hamiltonian circuit $H \subseteq A$, will be represented as a 0/1-vector ${\mathbf{x}} = ({{x}_{{ij}}})$ with the same dimensionality as $C$. The coordinates of this vector ${{x}_{{ij}}} = 1$, for $(i,j) \in H$, and ${{x}_{{ij}}} = 0$ otherwise. We denote by $X$ the set of all 0/1"-vectors x corresponding to the Hamiltonian circuits in the orgraph $G$ under consideration. Therefore, given a fixed input $C$, the traveling salesman problem is to find a solution ${\mathbf{x}}^{*} \in X$ such that $\left\langle {{\mathbf{x}}^{*},C} \right\rangle \leqslant \left\langle {{\mathbf{x}},C} \right\rangle$ $\forall {\mathbf{x}} \in X$. Hereafter, we call such a solution ${\mathbf{x}}{\kern 1pt}^{*}$ optimal with respect to input C. Following [7, Definition 1.1.2], the set of all such optimization problems formed by a fixed set of feasible solutions $X$ (in the case of the traveling salesman problem, $X$ is uniquely defined by the number of vertices of the orgraph $G$) and all possible input vectors $C$ will be called a problem $X$. Two feasible solutions ${\mathbf{x}},{\mathbf{y}} \in X$ of the problem $X$ are called adjacent if the vector $C$ is found such that they and only they are optimal with respect to $C$. The subset $Y \subseteq X$ is called a clique if any pair ${\mathbf{x}},{\mathbf{y}} \in Y$ is adjacent.

The convex hull ${\text{conv}}(X)$ is called a polyhedron of the problem $X$. Since $X$ is a subset of the vertices of the unit cube in the traveling salesman problem, $X$ coincides with the set of vertices of the polyhedron ${\text{conv}}(X)$. In this terminology, two solutions ${\mathbf{x}},{\mathbf{y}} \in X$ are adjacent if and only if the corresponding vertices of the polyhedron ${\text{conv}}(X)$ are adjacent [7]. It is known [12] that all vertices of the traveling salesman polyhedron are pairwise adjacent for $n < 6$, where $n$ is the number of vertices of the orgraph $G$ in which the optimal Hamiltonian circuit needs to be found.

Direct algorithms belong to the class of linear separation algorithms, which can be conveniently represented as linear decision trees.

Definition 1 ([7, Definition 1.3.1]). A linear decision tree of the problem $X \subset {{\mathbb{Z}}^{m}}$ is an oriented tree that has the following properties:

(a) Every node except one, called the root, has exactly one arc; there are no arcs entering the root.

(b) For every node, there are either two arcs coming out of it, or there are no such arcs at all; in the first case, the node is called an inner node and in the second one, an outer node, or a leaf.

(c) Some vector $B \in {{\mathbb{Z}}^{m}}$ is associated with some inner nodes.

(d) Each leaf corresponds to an element from $X$ (several leaves can correspond to the same element of the set $X$).

(e) Each arc $d$ corresponds to a number ${\text{sgn}}d$, either $1$ or $- 1$; two arcs coming from the same node have different values.

(f) For each circuit $W = {{B}_{1}}{{d}_{1}}{{B}_{2}}{{d}_{2}} \ldots {{B}_{k}}{{d}_{k}}{\mathbf{x}}$ connecting the root and the leaf (the notation of the circuit lists vectors ${{B}_{i}}$ corresponding to its nodes; the arc ${{d}_{i}}$ exits a node ${{B}_{i}}$, $i \in [k]$), and for any input $C$ from the inequalities $\left\langle {{{B}_{i}},C} \right\rangle {\text{sgn}}{{d}_{i}} \geqslant 0$, $i \in [k]$, it follows that the solution ${\mathbf{x}}$ is optimal with respect to $C$.

Therefore, within the theory of linear separation algorithms, attention is paid only to those operations in which conditions $\left\langle {B,C} \right\rangle \geqslant 0$ are tested, where $C$ is the vector of input data. For example, in line 5 of Algorithm 2, the inequality $\infty > {{C}_{{11}}}$ is tested in the very first step of the loop; in the second step, the condition ${{C}_{{11}}} > {{C}_{{12}}}$ is tested, etc. In functions HamiltonCycle and ForbiddenArc of Algorithm 1, from the point of view of linear separation algorithms, nothing interesting happens, because no comparisons with elements of the input data vector are performed.

The operation of the linear separation algorithm for a fixed input data vector $C$ is some circuit ${{B}_{1}}{{d}_{1}}{{B}_{2}}{{d}_{2}} \ldots {{B}_{m}}{{d}_{m}}{\mathbf{x}}$ connecting the root ${{B}_{1}}$ and some leaf ${\mathbf{x}}$ of the corresponding linear decision tree. The leaf in our case is a Hamiltonian circuit (more precisely, its characteristic vector) which it is optimal with respect to $C$.

Let $B$ be some internal node in the linear decision tree of the algorithm, and $X$ be the set of all feasible solutions (the set of labels of all leaves). Denote by ${{X}_{B}}$, ${{X}_{B}} \subseteq X$, the set of labels of all leaves of this tree preceded by the node $B$, and by $X_{B}^{ + }$ and $X_{B}^{ - }$ we denote subsets of the set ${{X}_{B}}$ corresponding to two arcs exiting from $B$. Obviously, ${{X}_{B}} = X_{B}^{ + } \cup X_{B}^{ - }$. Denote by $R_{B}^{ - } = X_{B}^{ + }{\kern 1pt} \backslash {\kern 1pt} X_{B}^{ - }$ the set of labels that are discarded in the case of transition along the negative arc. By analogy, let us define the set of labels $R_{B}^{ + } = X_{B}^{ - }{\kern 1pt} \backslash {\kern 1pt} X_{B}^{ + }$ that are discarded when passing through a “positive” arc.

Definition 2 ([7, Definition 1.4.2]). A linear decision tree is called a direct tree if for any internal node $B$ and for any clique $Y \subseteq X$ the inequality

$$\min \left\{ {\left| {R_{B}^{ + } \cap Y} \right|,\left| {R_{B}^{ - } \cap Y} \right|} \right\} \leqslant 1.$$

(1)

It follows directly from the definition that the height of a direct tree (i.e., the number of comparisons used by the algorithm in the worst case) for the problem $X$ cannot be less than $\omega (X) - 1$, where $\omega (X)$ is the clique number of the set $X$ [7, Theorem 1.4.3].

If we want to prove that some algorithm is not a direct algorithm, it is sufficient to specify a clique $Y$ consisting of four solutions and a node $B$ such that $\left| {R_{B}^{ + } \cap Y} \right| = \left| {R_{B}^{ - } \cap Y} \right| = 2$.

For each ${\mathbf{x}} \in X$, let us define the initial data cone

$$K({\mathbf{x}}) = \left\{ {\left. {C\,} \right|\left\langle {{\mathbf{x}},C} \right\rangle \leqslant \left\langle {{\mathbf{y}},C} \right\rangle ,\,\,\forall {\mathbf{y}} \in X} \right\}.$$

That is, $K({\mathbf{x}})$ consists of all vectors $C$ such that ${\mathbf{x}}$ is optimal with respect to $C$.

Definition 3 ([7, Definition 1.4.4]). A linear decision tree is called a “direct” tree if every circuit ${{B}_{1}}{{d}_{1}}{{B}_{2}}{{d}_{2}} \ldots {{B}_{k}}{{d}_{k}}{\mathbf{x}}$ connecting the root and the leaf satisfies the following conditions:

(*) For any ${\mathbf{y}} \in X$ adjacent to ${\mathbf{x}}$, there is a number $i \in [k]$ such that the conditions $\left\langle {{{B}_{i}},C} \right\rangle {\text{sgn}}{{d}_{i}} > 0$ and $C \in K({\mathbf{y}})$ are incompatible.

(**) For any $i \in [k]$, from the incompatibility of the conditions

$$\left\langle {{{B}_{i}},C} \right\rangle {\text{sgn}}{{d}_{i}} > 0\,\,{\text{and}}\,\,C \in K({\mathbf{y}})$$

for ${\mathbf{y}}$ adjacent to ${\mathbf{x}}$, and from the solidity of the cone

$$K({\mathbf{x}}) \cap \left\{ {\left. {C\,} \right|\left\langle {{{B}_{i}},C} \right\rangle {\text{sgn}}{{d}_{i}} \leqslant 0} \right\}$$

it follows that the branch starting at the node ${{B}_{i}}$ with the arc $- {{d}_{i}}$ has at least one leaf labeled ${\mathbf{x}}$.

“Direct” trees are united with direct trees by the fact that their height is also bounded from below by the quantity $\omega (X) - 1$ [7, Theorem 1.4.5].

In order to prove that Algorithm 1 is not a “direct” algorithm, we restrict ourselves to testing condition (*) of this definition. Namely, we specify a very particular input vector $C{\kern 1pt} *$ that uniquely defines some circuit ${{B}_{1}}{{d}_{1}}{{B}_{2}}{{d}_{2}} \ldots {{B}_{k}}{{d}_{k}}{\mathbf{x}}$. Next, we choose ${\mathbf{y}} \in X$ adjacent to ${\mathbf{x}}$, for which conditions $\left\langle {{{B}_{i}},C} \right\rangle {\text{sgn}}{{d}_{i}} > 0$ and $C \in K({\mathbf{y}})$ are compatible for any $i \in [k]$. Let us emphasize that we need to test the compatibility of conditions $\left\langle {{{B}_{i}},C} \right\rangle {\text{sgn}}{{d}_{i}} > 0$ and $C \in K({\mathbf{y}})$ separately for each $i \in [k]$, regardless of the results of other comparisons. That is, for each $i \in [k]$, it is sufficient to specify ${{C}_{i}}$ such that $\left\langle {{{B}_{i}},{{C}_{i}}} \right\rangle {\text{sgn}}{{d}_{i}} > 0$ and ${{C}_{i}} \in K({\mathbf{y}})$.

3 ALGORITHM 1 IS NOT “DIRECT”

Consider the traveling salesman problem in a complete orgraph on five vertices. The set of feasible solutions $X$ of such a problem consists of 24 0/1-vectors corresponding to the Hamiltonian circuits in that orgraph. All 24 solutions are pairwise adjacent [12].

Assume that the elements of the arc length matrix $C \in {{\mathbb{Z}}^{{5 \times 5}}}$ satisfy the following conditions:

$$\begin{gathered} {{c}_{{12}}} \leqslant {{c}_{{13}}},\,\,\,\,{{c}_{{12}}} \leqslant {{c}_{{14}}},\,\,\,\,{{c}_{{12}}} \leqslant {{c}_{{15}}}, \\ {{c}_{{21}}} \leqslant {{c}_{{23}}},\,\,\,\,{{c}_{{21}}} \leqslant {{c}_{{24}}},\,\,\,\,{{c}_{{21}}} \leqslant {{c}_{{25}}}, \\ {{c}_{{31}}} > {{c}_{{32}}},\,\,\,\,{{c}_{{32}}} > {{c}_{{34}}},\,\,\,\,{{c}_{{34}}} > {{c}_{{35}}}. \\ \end{gathered} $$

(2)

At the very beginning of the operation of the algorithm under consideration, this matrix is reduced (Algorithm 2). We limit our discussion to the row reduction stage. Successive comparisons result in selecting the smallest element in the first row (in this case, ${{c}_{{12}}}$) and subtracting it from all its elements. Then the minimum element in the second line is selected, which is ${{c}_{{21}}}$, and the minimum element in the third line is ${{c}_{{35}}}$. Then the algorithm proceeds to test the following inequality

$${{c}_{{41}}} > {{c}_{{42}}}$$

(3)

(the comparison $\infty > {{c}_{{41}}}$ is used in the algorithm only for brevity and does not contain any information). The corresponding node of the linear decision tree of the algorithm is denoted by $B$. It is clear that the algorithm enters this tree node if and only if conditions (2) are satisfied for the input vector $C$.

Consider the characteristic vectors of the four Hamiltonian circuits:

$$\begin{gathered} {\mathbf{x}} = \left( {\begin{array}{*{20}{c}} {}&0&0&1&0 \\ 0&{}&0&0&1 \\ 1&0&{}&0&0 \\ 0&1&0&{}&0 \\ 0&0&1&0&{} \end{array}} \right),\,\,\,\,{\mathbf{y}} = \left( {\begin{array}{*{20}{c}} {}&0&0&0&1 \\ 0&{}&1&0&0 \\ 1&0&{}&0&0 \\ 0&1&0&{}&0 \\ 0&0&0&1&{} \end{array}} \right), \\ {\mathbf{z}} = \left( {\begin{array}{*{20}{c}} {}&0&1&0&0 \\ 0&{}&0&0&1 \\ 0&1&{}&0&0 \\ 1&0&0&{}&0 \\ 0&0&0&1&{} \end{array}} \right),\,\,\,\,{\mathbf{w}} = \left( {\begin{array}{*{20}{c}} {}&0&0&0&1 \\ 0&{}&0&1&0 \\ 0&1&{}&0&0 \\ 1&0&0&{}&0 \\ 0&0&1&0&{} \end{array}} \right). \\ \end{gathered} $$

It is easy to test that the input vectors

$$\begin{gathered} {{C}_{x}} = \left( {\begin{array}{*{20}{c}} {}&0&6&1&6 \\ 0&{}&6&6&1 \\ 3&2&{}&1&0 \\ 6&0&6&{}&6 \\ 6&6&0&6&{} \end{array}} \right),\,\,\,\,{{C}_{y}} = \left( {\begin{array}{*{20}{c}} {}&0&6&6&1 \\ 0&{}&1&6&6 \\ 3&2&{}&1&0 \\ 6&0&6&{}&6 \\ 6&6&6&0&{} \end{array}} \right), \\ {{C}_{z}} = \left( {\begin{array}{*{20}{c}} {}&0&1&6&6 \\ 0&{}&6&6&1 \\ 6&3&{}&1&0 \\ 0&6&6&{}&6 \\ 6&6&6&0&{} \end{array}} \right),\,\,\,\,{{C}_{w}} = \left( {\begin{array}{*{20}{c}} {}&0&6&6&1 \\ 0&{}&6&1&6 \\ 6&3&{}&1&0 \\ 0&6&6&{}&6 \\ 6&6&0&6&{} \end{array}} \right) \\ \end{gathered} $$

satisfy conditions (2), and for each ${\mathbf{t}} \in \{ {\mathbf{x}},{\mathbf{y}},{\mathbf{z}},{\mathbf{w}}\}$ and for any ${\mathbf{s}} \in X{\kern 1pt} \backslash {\kern 1pt} \{ {\mathbf{t}}\}$ the inequality $\left\langle {{\mathbf{t}},{{C}_{t}}} \right\rangle = 5 < \left\langle {{\mathbf{s}},{{C}_{t}}} \right\rangle$ is satisfied. Hence, all four vectors are included in the set of labels ${{X}_{B}}$ of all the leaves of the tree of the algorithm preceded by the node $B$.

Let us show that ${\mathbf{z}}$ and ${\mathbf{w}}$ are part of the set of labels $R_{B}^{ + }$ discarded if inequality (3) is satisfied, and ${\mathbf{x}}$ and ${\mathbf{y}}$ are part of the set of labels $R_{B}^{ - }$ discarded if inequality (3) is not satisfied.

Assume that conditions (2) and inequality (3) are satisfied for the input matrix $C$. Then $\left\langle {{\mathbf{z}},C} \right\rangle > \left\langle {{\mathbf{z}}{\kern 1pt} ',C} \right\rangle$ for

$${\mathbf{z}}{\kern 1pt} ' = \left( {\begin{array}{*{20}{c}} {}&0&1&0&0 \\ 1&{}&0&0&0 \\ 0&0&{}&0&1 \\ 0&1&0&{}&0 \\ 0&0&0&1&{} \end{array}} \right).$$

Similarly, $\left\langle {{\mathbf{w}},C} \right\rangle > \left\langle {{\mathbf{w}}{\kern 1pt} ',C} \right\rangle$ for

$${\mathbf{w}}{\kern 1pt} ' = \left( {\begin{array}{*{20}{c}} {}&0&0&0&1 \\ 1&{}&0&0&0 \\ 0&0&{}&1&0 \\ 0&1&0&{}&0 \\ 0&0&1&0&{} \end{array}} \right).$$

Therefore, ${\mathbf{z}},{\mathbf{w}} \in R_{B}^{ + }$.

Assume that conditions (2) are satisfied for $C$, but inequality (3) is not satisfied. Then $\left\langle {{\mathbf{x}},C} \right\rangle > \left\langle {{\mathbf{x}}{\kern 1pt} ',C} \right\rangle$ for

$${\mathbf{x}}{\kern 1pt} ' = \left( {\begin{array}{*{20}{c}} {}&1&0&0&0 \\ 0&{}&0&0&1 \\ 0&0&{}&1&0 \\ 1&0&0&{}&0 \\ 0&0&1&0&{} \end{array}} \right),$$

and $\left\langle {{\mathbf{y}},C} \right\rangle > \left\langle {{\mathbf{y}}{\kern 1pt} ',C} \right\rangle$ for

$${\mathbf{y}}{\kern 1pt} ' = \left( {\begin{array}{*{20}{c}} {}&1&0&0&0 \\ 0&{}&1&0&0 \\ 0&0&{}&0&1 \\ 1&0&0&{}&0 \\ 0&0&0&1&{} \end{array}} \right).$$

Hence, ${\mathbf{z}},{\mathbf{w}} \in R_{B}^{ + }$.

Therefore, condition (1) for a given node $B$ is not satisfied, and Algorithm 1 is not a direct algorithm.

4 ALGORITHM 1 IS NOT “DIRECT”

When analyzing Algorithm 1 as a linear decision tree, we only encounter inequalities of the following kind:

$$\left\langle {{{B}^{ + }},C} \right\rangle - \left\langle {{{B}^{ - }},C} \right\rangle > 0,$$

(4)

where $C \in {{\mathbb{Z}}^{{{{n}^{2}}}}}$ is the input vector,

$$\begin{gathered} {{B}^{ + }},{{B}^{ - }} \in {{\{ 0,1\} }^{{{{n}^{2}}}}},\,\,\,\,\left\langle {{{B}^{ + }},{{B}^{ - }}} \right\rangle = 0 \\ {\text{and}}\,\,\left\langle {{{B}^{ + }},{\mathbf{1}}} \right\rangle = \left\langle {{{B}^{ - }},{\mathbf{1}}} \right\rangle > 0, \\ \end{gathered} $$

(5)

${\mathbf{1}}$ is the all-ones vector. In other words, condition (5) means that the sets of unit coordinates for ${{B}^{ + }}$ and ${{B}^{ - }}$ are equal and do not overlap. For each such inequality and for some feasible solution of ${\mathbf{y}} \in X \subset {{\{ 0,1\} }^{{{{n}^{2}}}}}$, we need to check that there exists $C \in K({\mathbf{y}})$ for which this inequality holds. This analysis is greatly simplified if we use the following criterion.

Lemma 1. Let ${\mathbf{y}} \in {{\{ 0,1\} }^{{{{n}^{2}}}}}$ be the characteristic vector of some Hamiltonian circuit in a complete orgraph $G = ([n],A)$ . If conditions (5) and $\left\langle {{{B}^{ + }},{\mathbf{y}}} \right\rangle \leqslant 2$ are satisfied, then inequality (4) and condition $C \in K({\mathbf{y}})$ are compatible.

Proof. Let

$$S = \left\{ {\left. {(i,j) \in {{{[n]}}^{2}}\,} \right|{{y}_{{ij}}} = 1\,\,{\text{and}}\,\,B_{{ij}}^{ + } = 0} \right\}.$$

It follows from condition $\left\langle {{{B}^{ + }},{\mathbf{y}}} \right\rangle \leqslant 2$ that $\left| S \right| \geqslant n - 2$. Assume

$$C: = {\mathbf{4}} - {{B}^{ - }}$$

and, after that, ${{C}_{{ij}}}: = 0$ for $(i,j) \in S$.

Then $\left\langle {{{B}^{ + }},C} \right\rangle = \left\langle {{{B}^{ + }},{\mathbf{4}} - {{B}^{ - }}} \right\rangle = \left\langle {{{B}^{ + }},{\mathbf{4}}} \right\rangle$ and $\left\langle {{{B}^{ - }},C} \right\rangle \leqslant \left\langle {{{B}^{ - }},{\mathbf{4}} - {{B}^{ - }}} \right\rangle = \left\langle {{{B}^{ + }},{\mathbf{4}}} \right\rangle - \left\langle {{{B}^{ - }},{{B}^{ - }}} \right\rangle$ (since ${{B}^{ + }}$ and ${{B}^{ - }}$ satisfy condition (5)). Hence, inequality (4) for such $C$ will be satisfied.

Let us now show that $\left\langle {{\mathbf{y}},C} \right\rangle < \left\langle {{\mathbf{x}},C} \right\rangle$ for any ${\mathbf{x}} \in X{\kern 1pt} \backslash {\kern 1pt} {\mathbf{y}}$.

Obviously, $\left\langle {{\mathbf{y}},C} \right\rangle = \left( {n - \left| S \right|} \right) \times 4 \leqslant 8$.

Let ${\mathbf{x}} \in X$. Note that if $\left\langle {{\mathbf{y}},{\mathbf{x}}} \right\rangle \geqslant n - 2$, then ${\mathbf{x}} = {\mathbf{y}}$, because any Hamiltonian circuit in an orgraph on $n$ vertices is uniquely defined by any of its $n - 2$ arcs. Hence, $\left\langle {{\mathbf{x}},C} \right\rangle \geqslant 3 \times 3 = 9$ for any ${\mathbf{x}} \in X{\kern 1pt} \backslash {\kern 1pt} {\mathbf{y}}$.

In particular, the conditions of the lemma are satisfied if ${{B}^{ + }}$ has no more than two units.

Therefore, assume $n = 4$ and consider the following input vector (we substitute infinity with a space):

$$C{\kern 1pt} *: = \left( {\begin{array}{*{20}{c}} {}&0&2&1 \\ 2&{}&0&2 \\ 1&2&{}&0 \\ 0&1&2&{} \end{array}} \right).$$

(6)

It is clear that the only optimal solution is the following vector

$${\mathbf{x}}: = \left( {\begin{array}{*{20}{c}} {}&1&0&0 \\ 0&{}&1&0 \\ 0&0&{}&1 \\ 1&0&0&{} \end{array}} \right)$$

and its corresponding circuit $\{ (1,2),(2,3),(3,4),(4,1)\}$. It is easy to test that the set of all feasible solutions $X$ consists of six pairwise adjacent vectors. Assume

$${\mathbf{y}}: = \left( {\begin{array}{*{20}{c}} {}&0&0&1 \\ 0&{}&1&0 \\ 1&0&{}&0 \\ 0&1&0&{} \end{array}} \right).$$

Note that ${\mathbf{y}}$ is the second (after ${\mathbf{x}}$) by optimality with respect to $C{\kern 1pt} *$. This fact greatly simplifies further testing of corresponding comparisons.

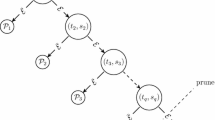
In general, the working scheme of the algorithm for a given input $C{\kern 1pt} *$ is shown in Fig. 1.

Fig. 1.

General scheme of Algorithm 1 for the input given by formula (6).

First of all, let us consider which inequalities are tested at the first run of the BranchBound procedure with input $C{\kern 1pt} *$. When reducing the first row of the matrix $C{\kern 1pt} *$ (row 5 of Algorithm 2), the inequalities $\infty > {{C}_{{12}}}$, ${{C}_{{13}}} > {{C}_{{12}}}$, and ${{C}_{{14}}} > {{C}_{{12}}}$ are tested (and satisfied). Further on, we will not consider inequalities in which the sum (or difference) of elements of the initial matrix is compared to infinity, because they are always satisfied and compatible with any feasible solution. Note that the listed inequalities satisfy the conditions of Lemma 1, because $\left\langle {{{B}^{ + }},{\mathbf{1}}} \right\rangle = 1$. Hence, they are compatible with the condition $C \in K({\mathbf{y}})$.

When the first row is reduced, its cells $M[1,j]$, $j \in [4]$, contain differences ${{C}_{{1j}}} - {{C}_{{12}}}$, and the variable sum takes the value of ${{C}_{{12}}}$.

When the second row is reduced, the inequalities ${{C}_{{21}}} > {{C}_{{23}}}$ and ${{C}_{{24}}} > {{C}_{{23}}}$ are tested. According to Lemma 1, they are consistent with the condition $C \in K({\mathbf{y}})$.

When the second row is reduced, in its cells $M[2,j]$, $j \in [4]$, there are differences ${{C}_{{2j}}} - {{C}_{{23}}}$, and the variable sum takes the value ${{C}_{{12}}} + {{C}_{{23}}}$.

When the last two rows are reduced, the situation is exactly the same. When the reduction of the rows is finished

$$sum = {{C}_{{12}}} + {{C}_{{23}}} + {{C}_{{34}}} + {{C}_{{41}}},$$

$$M = \left( {\begin{array}{*{20}{c}} {}&0&{{{C}_{{13}}} - {{C}_{{12}}}}&{{{C}_{{14}}} - {{C}_{{12}}}} \\ {{{C}_{{21}}} - {{C}_{{23}}}}&{}&0&{{{C}_{{24}}} - {{C}_{{23}}}} \\ {{{C}_{{31}}} - {{C}_{{34}}}}&{{{C}_{{32}}} - {{C}_{{34}}}}&{}&0 \\ 0&{{{C}_{{42}}} - {{C}_{{41}}}}&{{{C}_{{43}}} - {{C}_{{41}}}}&{} \end{array}} \right).$$

Next, when the first column is reduced, the inequalities $M[2,1] > M[3,1]$ and $M[3,1] > M[4,1]$ are tested. We know that $M[2,1] = {{C}_{{21}}} - {{C}_{{23}}}$, $M[3,1] = {{C}_{{31}}} - {{C}_{{34}}}$, $M[4,1] = {{C}_{{41}}} - {{C}_{{41}}} = 0$. Hence, the inequalities ${{C}_{{21}}} - {{C}_{{23}}} > {{C}_{{31}}} - {{C}_{{34}}}$ and ${{C}_{{31}}} - {{C}_{{34}}} > 0$ are tested. Each of them satisfies the conditions of Lemma 1.

When we reduce the remaining three columns, the situation repeats. The value of sum does not change when the columns are reduced, because each column already contains zeros.

After that, the sum $\geqslant$ lopt condition is tested in Algorithm 1. However, lopt $= \infty$. Therefore, the algorithm proceeds to calculate the function ChooseArc.

The first zero element is $M[1,2]$. After that, the comparisons are performed $\infty > M[1,3]$ and $M[1,3] > M[1,4]$ in row 8 of Algorithm 3. In this case, after the previous reduction step, we have $M[1,3] = {{C}_{{13}}} - {{C}_{{12}}}$ and $M[1,4] = {{C}_{{14}}} - {{C}_{{12}}}$. Obviously, the inequality ${{C}_{{13}}} - {{C}_{{12}}} > {{C}_{{14}}} - {{C}_{{12}}}$ satisfies the conditions of Lemma 1. In this step, $m: = {{C}_{{14}}} - {{C}_{{12}}}$ is assigned. Next, in line 11 of Algorithm 3, comparisons $\infty > M[3,2]$ and $M[3,2] > M[4,2]$ are performed. In this step, $M[3,2] = {{C}_{{32}}} - {{C}_{{34}}}$ and $M[4,2] = {{C}_{{42}}} - {{C}_{{41}}}$. The conditions of Lemma 1 are satisfied again. In this step, $k: = {{C}_{{42}}} - {{C}_{{41}}}$ is assigned. Next, the comparison $m + k > - 1$ or, what is the same, ${{C}_{{14}}} - {{C}_{{12}}} + {{C}_{{42}}} - {{C}_{{41}}} > - 1$ is performed. Obviously, this inequality is compatible with the condition $C \in K({\mathbf{y}})$. The variable $w$ is populated with the value of the expression ${{C}_{{14}}} - {{C}_{{12}}} + {{C}_{{42}}} - {{C}_{{41}}}$.

The second zero element is $M[2,3]$. By analogy, let us list only nontrivial comparisons. The inequality $M[2,1] \leqslant M[2,4]$ or ${{C}_{{21}}} - {{C}_{{23}}} \leqslant {{C}_{{24}}} - {{C}_{{23}}}$ is obviously compatible with the condition $C \in K({\mathbf{y}})$. The inequality $M[1,3] \leqslant M[4,3]$ is also compatible. Next, in row 12 the inequality $m + k > w$ is tested or, given the previous steps,

$${{C}_{{21}}} - {{C}_{{23}}} + {{C}_{{13}}} - {{C}_{{12}}} > {{C}_{{14}}} - {{C}_{{12}}} + {{C}_{{42}}} - {{C}_{{41}}}.$$

Obviously, it satisfies the conditions of Lemma 1. After this step

$$w = {{C}_{{21}}} - {{C}_{{23}}} + {{C}_{{13}}} - {{C}_{{12}}}.$$

The third zero element is $M[3,4]$. The inequality $M[3,1] < M[3,2]$ or ${{C}_{{31}}} - {{C}_{{34}}} < {{C}_{{32}}} - {{C}_{{34}}}$ is obviously compatible with the condition $C \in K({\mathbf{y}})$. The inequality $M[1,4] < M[2,4]$ is also compatible. The condition $m + k < w$ is as follows

$${{C}_{{14}}} - {{C}_{{12}}} + {{C}_{{31}}} - {{C}_{{34}}} < {{C}_{{21}}} - {{C}_{{23}}} + {{C}_{{13}}} - {{C}_{{12}}}$$

and is also compatible with the condition $C \in K({\mathbf{y}})$.

The fourth zero element is $M[4,1]$. It is easy to test that $M[4,2] < M[4,3]$ and $M[3,1] < M[2,1]$ are compatible with the condition $C \in K({\mathbf{y}})$. The condition $m + k < w$ is as follows

$${{C}_{{31}}} - {{C}_{{34}}} + {{C}_{{42}}} - {{C}_{{41}}} < {{C}_{{21}}} - {{C}_{{23}}} + {{C}_{{13}}} - {{C}_{{12}}}$$

and is also compatible.

At this point, we are still in the first instance of the BranchBound procedure. After the implementation of the function ChooseArc described above, the arc $(i,j) = (2,3)$ is selected (the sum $m + k$ turned out to be the largest for it), the second row and the third column are removed from the matrix $M$, and the arc $(3,2)$ becomes forbidden. The following matrix is fed to the input of the second instance of the procedure BranchBound

$$C': = \left( {\begin{array}{*{20}{c}} {}&0&{}&1 \\ {}&{}&{}&{} \\ 1&{}&{}&0 \\ 0&1&{}&{} \end{array}} \right)$$

(the empty row and the empty column are left for the ease of reading). It is clear that nothing new happens when it is reduced, because each row and each column contains zeros. When the function ChooseArc is called in line 12, the following comparisons $m + k > w$ are carried out.

$${{C}_{{14}}} - {{C}_{{12}}} + {{C}_{{42}}} - {{C}_{{41}}} > - 1.$$

Obviously, this inequality is compatible with the condition $C \in K({\mathbf{y}})$. Next, the following inequality holds

$${{C}_{{31}}} - {{C}_{{34}}} + {{C}_{{14}}} - {{C}_{{12}}} \leqslant {{C}_{{14}}} - {{C}_{{12}}} + {{C}_{{42}}} - {{C}_{{41}}},$$

which satisfies the conditions of Lemma 1. The following comparison

$${{C}_{{31}}} - {{C}_{{34}}} + {{C}_{{42}}} - {{C}_{{41}}} \leqslant {{C}_{{14}}} - {{C}_{{12}}} + {{C}_{{42}}} - {{C}_{{41}}}$$

is also compatible with $C \in K({\mathbf{y}})$.

Thus, after calling the function $(1,2)$ in the second instance of BranchBound, the arc $(1,2)$ is selected. A Hamiltonian circuit with the arcs $(2,3)$ and $(1,2)$ is uniquely defined. The following assignment is performed

$$lopt: = {{C}_{{12}}} + {{C}_{{23}}} + {{C}_{{34}}} + {{C}_{{41}}}.$$

The algorithm then proceeds to consider cases in which the circuit contains the arc $(2,3)$ but does not contain $(1,2)$. The third instance of BranchBound is started with the matrix

$$C'': = \left( {\begin{array}{*{20}{c}} {}&{}&{}&1 \\ {}&{}&{}&{} \\ 1&{}&{}&0 \\ 0&1&{}&{} \end{array}} \right).$$

In the reduction, the two ones are replaced by zeros. No “discarding” comparisons are carried out. The value of the variable sum is incremented by $M\,[1,4] = {{C}_{{14}}} - {{C}_{{12}}}$ and by $M[4,2] = {{C}_{{42}}} - {{C}_{{41}}}$. The current instance of the procedure terminates on row 3 after testing the inequality sum $\geqslant$ lopt:

$$({{C}_{{14}}} - {{C}_{{12}}}) + ({{C}_{{42}}} - {{C}_{{41}}}) > 0.$$

Note that a valid solution ${\mathbf{y}}$ is completely discarded by the algorithm at this very step (taking into account the previously tested inequality ${{C}_{{31}}} > {{C}_{{34}}}$). Nevertheless, this inequality satisfies the conditions of Lemma 1 and, hence, together with the condition $C \in K({\mathbf{y}})$.

Along with the third instance of the procedure BranchBound, the second instance of this procedure is also terminated. The algorithm proceeds to execute the next to last row in the first instance. In this instance

$$sum = {{C}_{{12}}} + {{C}_{{23}}} + {{C}_{{34}}} + {{C}_{{41}}}.$$

In order to analyze cases, in which the circuit does not have the arc $(2,3)$, we call a fourth instance of the procedure with the following matrix

$$C{\kern 1pt} ''': = \left( {\begin{array}{*{20}{c}} {}&0&2&1 \\ 2&{}&{}&2 \\ 1&2&{}&0 \\ 0&1&2&{} \end{array}} \right).$$

When reducing the second row, the comparison $M[2,1] \leqslant M[2,4]$ is performed, and when reducing the third column, $M[1,3] \leqslant M[4,3]$. Obviously, neither of them discards the entire cone $K({\mathbf{y}})$. The value is increased by $({{C}_{{21}}} - {{C}_{{23}}}) + ({{C}_{{13}}} - {{C}_{{12}}})$.

Finally, the comparison sum $\geqslant$ lopt completes this fourth instance of the procedure and the entire algorithm in general. This comparison is as follows

$$({{C}_{{21}}} - {{C}_{{23}}}) + ({{C}_{{13}}} - {{C}_{{12}}}) \geqslant 0$$

and is also compatible with the condition $C \in K({\mathbf{y}})$.

Thus, condition (*) from Definition 3 is not satisfied for this algorithm.