1 Introduction

The bilevel assignment problem (BAP) is a class of assignment problems [6] that models two autonomous (conflicting or collaborative) decision makers, namely, the leader and the follower, who act in a bilevel hierarchy [12] . Each decision maker controls a distinct set of edges. The leader acts first by choosing a subset of its edges; consequently, the follower completes the assignment process. The edges selected by the leader and the follower are required to form a perfect matching. The decision makers pursue their own individual objectives. Therefore, the leader decides by considering the follower’s reaction, i.e., an optimal solution to the lower-level optimization problem. In general, BAP belongs to a family of discrete bilevel (hierarchical) optimization problems, see surveys in [8, 18] and the references therein.

Formally, let \(G = (U \cup V , E)\) be a balanced bipartite graph with \(|U|=|V|=n\). The edge set E is partitioned into two disjoint subsets \(E_{\ell }\) and \(E_f\), i.e., \(E_{\ell } \cap E_f = \emptyset \) and \(E_{\ell } \cup E_f = E\), which are controlled by the leader and the follower, respectively. Let \(|E_{\ell }| = m_{\ell }\) and \(|E_f| = m_f\). For all \(i \in U\), define

$$\begin{aligned} V_{\ell }^{(i)} = \{ j \in V : (i,j) \in E_{\ell } \}\quad \text {and} \quad V_{f}^{(i)} = \{ j \in V : (i,j) \in E_{f} \}. \end{aligned}$$

Likewise, we define \(U_{\ell }^{(j)}\) and \(U_{f}^{(j)}\) for all \(j \in V\). Then BAP is formulated as follows:

$$\begin{aligned} \text {[BAP]} \quad \min _{\mathbf {x}} \quad&g_{\ell }(\mathbf {x}, \mathbf {y}) \end{aligned}$$
(1a)
$$\begin{aligned} \text {s.t.} \ \&\min _{\mathbf {y}} \quad g_{f}(\mathbf {y}) \end{aligned}$$
(1b)
$$\begin{aligned}&\ \text {s.t.} \ \ \sum _{j \in V_{\ell }^{(i)}} x_{ij} + \sum _{j \in V_{f}^{(i)}} y_{ij} = 1 \quad \quad \forall i \in U, \end{aligned}$$
(1c)
$$\begin{aligned}&\qquad \ \sum _{i \in U_{\ell }^{(j)}} x_{ij} + \sum _{i \in U_{f}^{(j)}} y_{ij} = 1 \quad \quad \forall j \in V, \end{aligned}$$
(1d)
$$\begin{aligned}&\qquad \ y_{ij} \in \{0,1\} \quad \quad \quad \forall (i,j) \in E_{f}, \end{aligned}$$
(1e)
$$\begin{aligned}&\qquad \ x_{ij} \in \{0,1\} \quad \quad \quad \forall (i,j) \in E_{\ell }, \end{aligned}$$
(1f)

where \(g_{\ell } : \{ 0,1 \}^{m_{\ell }+m_f} \rightarrow {\mathbb {R}}\) and \(g_{f}: \{ 0,1 \}^{m_f} \rightarrow {\mathbb {R}}\).

For a given feasible decision \(\mathbf {x}\) of the leader, the lower-level optimization problem (1b)–(1e) may have alternative optimal solutions. If the follower always implements the most (least) favorable solution for the leader, then we refer to the obtained problem as the optimistic (pessimistic) bilevel program. In the remainder of the paper we make the following assumptions:

  • A1: Optimistic case of BAP is considered.

  • A2: There exists a perfect matching in \(G(U \cup V, E)\).

Assumption A1 is typical in the bilevel (hierarchical) optimization literature [8]. Assumption A2 is technical in order to ensure the existence of a feasible solution in BAP.

In conventional assignment problems, e.g., the linear sum assignment problem, there exists a single decision maker who fully controls the assignment processes [6, 20]. In BAP there are two autonomous decision makers. Specifically, one player, namely, the leader, whose perspective is modeled in BAP, has an advantage of acting first and, hence, influencing the decision of the other player, i.e., the follower. Naturally, BAP can be generalized for the case of multiple followers. In fact, for any assignment problem with the centralized decision-making process one can envision its generalized version in the bilevel framework. Thus, BAP is particularly appropriate for modeling a decentralized assignment process with a bilevel hierarchy of independent decision makers.

In this paper we focus on the objective functions considered by Gassner and Klinz [12], namely, linear sum and linear bottleneck functions, formally defined for the leader as:

$$\begin{aligned} \begin{aligned} g_{\ell }(\mathbf {x},\mathbf {y})&= \sum _{(i,j) \in E_{\ell }} d_{ij} x_{ij} + \sum _{(i,j) \in E_f} d_{ij} y_{ij} \ \ \text {and}\\ g_{\ell }(\mathbf {x},\mathbf {y})&= \max \Big \{ \max _{(i,j) \in E_{\ell }} \{ d_{ij} x_{ij} \}, \max _{(i,j) \in E_f} \{d_{ij} y_{ij}\} \Big \}, \end{aligned} \end{aligned}$$
(2)

respectively, where \(\mathbf {d} \in {\mathbb {R}^{m_{\ell }+m_{f}}_{+}}\). Similarly, for the follower we have:

$$\begin{aligned} g_f(\mathbf {y}) = \sum _{(i,j) \in E_f} c_{ij} y_{ij} \quad \text {and} \quad g_f(\mathbf {y}) = \max _{(i,j) \in E_f} \big \{ c_{ij} y_{ij} \big \}, \end{aligned}$$
(3)

where \(\mathbf {c} \in {\mathbb {R}_{+}^{m_{f}}}\). In [12] the authors establish that, in contrast to the single-level linear sum and linear bottleneck assignment problems, all variants of BAP are NP-hard when the leader’s and the follower’s objective functions are in either a linear sum or a bottleneck form, except for the optimistic case when both decision makers have linear bottleneck objective functions (see Table 1). These results are not surprising and, in fact, in line with similar results on the theoretical computational complexity of bilevel linear programs, which cannot be solved in polynomial time unless \(P = NP\) [9].

Table 1 BAP complexity for the optimistic case/pessimistic case [12]
Full size table

This paper is focused on developing exact solution methods for BAP. To the best of our knowledge, this research direction has not been addressed in the literature. In particular, the contributions presented in this paper are as follows.

(i) We introduce a combinatorial branch-and-bound approach for solving BAP (see Sect. 2.2), in which the branching process is based on imposing and forbidding assignments for the follower’s edges in each node of the B&B tree as well as pruning nodes of the B&B tree that do not provide feasible solutions. The lower bounds are constructed using a single-level relaxation by removing the follower’s objective function. The proposed method is also tailored for BAP, where the follower’s objective function is in either linear sum or linear bottleneck form (Sect. 2.3).

(ii) We describe an equivalent single-level mixed integer programming (MIP) reformulation of BAP when the follower’s objective is a linear sum function (Sect. 3.1).

(iii) We show that BAP admits polynomial time solution algorithms in some restricted cases (Sect. 3.2). In particular, we first describe BAPs with the special structure of the leader’s and the follower’s objective functions that admits reduction to a single-level problem. Second, we consider two classes of BAP, where the leader’s set of feasible actions is polynomially bounded.

(iv) Finally, we provide an extensive computational study demonstrating the performance of the developed algorithms (Sect. 4) and conclude the paper highlighting possible directions for future work (Sect. 5).

2 Combinatorial branch-and-bound algorithm

Ranking assignments according to the objective function value is a well-studied topic in the literature [7, 19, 21]. A typical application arises when the decision maker has to solve an assignment problem with constraints that are difficult to specify formally. In this case an optimal assignment can be found by enumerating suboptimal assignments until a solution satisfying the complicating constraints is found. Similarly, BAP can be viewed as an assignment problem in which a feasible assignment needs to satisfy the optimality criteria of the lower-level problem and, hence, can be solved using one of the ranking algorithms. The downside of this somewhat naïve approach is that the rank of the assignment for which optimality of the lower-level problem is satisfied, can be exponentially large. Nevertheless, this observation motivates our combinatorial branch-and-bound (B&B) algorithm for solving BAP, which we describe in detail next.

2.1 Preliminaries

A matching \(\mu \) in \(G(U\cup V,E)\) is a subset of edges such that each vertex is incident to at most one member of \(\mu \). A matching is perfect if every vertex in \(U\cup V\) is incident to exactly one edge in \(\mu \). Let \((\mathbf {{x}}, \mathbf {{y}}) \in \{0,1\}^{m_{\ell } + m_f}\) be a feasible solution to (1c)–(1f), which induces a perfect matching \(\mu (\mathbf {{x}},\mathbf {{y}}) = \{ (i,j) \in E_{\ell } \cup E_f : {x}_{ij} = 1 \text { or } {y}_{ij} = 1 \}\) in G. Also, let \(\mu _f(\mathbf {{y}}) = \{ (i,j) \in E_f : {y}_{ij} = 1 \}\subseteq \mu (\mathbf {{x}},\mathbf {{y}})\), which is also a matching in G; however, it is not necessarily perfect. Define \({\mathcal {M}}(G)\) to be the set of all perfect matchings (assignments) in G, i.e.,

$$\begin{aligned} {\mathcal {M}}(G) = \Big \{ \mu (\mathbf {x}, \mathbf {y})\subseteq E_{\ell } \cup E_f\ : \ (1c)-(1f) \ \text{ hold } \ \Big \}. \end{aligned}$$

For a given feasible leader’s solution \(\mathbf {x}\), we have the follower’s reaction set defined as:

$$\begin{aligned} {\mathcal {R}}(\mathbf {x}) = \mathop {\hbox {argmin}}\limits _{\mathbf {y}} \Big \{ g_f(\mathbf {y}) : \mu ({\mathbf {x}},{\mathbf {y}})\in {\mathcal {M}}(G) \Big \}. \end{aligned}$$

Next, denote by \({\mathcal {F}}(G)\) the set of all perfect matchings in G that correspond to feasible solutions of BAP:

$$\begin{aligned} {\mathcal {F}}(G) = \Big \{ \mu (\mathbf {x}, \mathbf {y}) \in {\mathcal {M}}(G): \ \mathbf {y} \in {\mathcal {R}}(\mathbf {x}) \Big \}. \end{aligned}$$

Thus, \({\mathcal {F}}(G) \subseteq {\mathcal {M}}(G)\), and the optimistic case of BAP can be reformulated as:

$$\begin{aligned} \min \limits _{\mathbf {x}, \mathbf {y}} \Big \{ g_{\ell }(\mathbf {x}, \mathbf {y}) : \mu (\mathbf {x}, \mathbf {y}) \in {\mathcal {F}}(G) \Big \}. \end{aligned}$$

2.2 General algorithm

The B&B algorithm keeps a list of assignment problems obtained by ignoring the follower’s objective function along with imposing and forbidding some of the follower’s edges. Each such problem corresponds to an unfathomed node of the search tree. In particular, the root node represents all possible perfect matchings in the bipartite graph G. In the following we discuss the details of each step of the algorithm separately and conclude the subsection by presenting the outline of the approach.

Let \({\mathcal {E}}\) and \(\bar{{\mathcal {E}}}\) be two disjoint subsets of the follower’s edges, i.e., \({\mathcal {E}} \cup \bar{{\mathcal {E}}} \subseteq E_f\) and \({\mathcal {E}} \cap \bar{{\mathcal {E}}} = \emptyset \). Define \({\mathcal {P}}\) to be a nonempty subset of \({\mathcal {M}}(G)\) of the form

$$\begin{aligned} {\mathcal {P}} = \Big \{ \mu \in {\mathcal {M}}(G) : \mu \cap {\mathcal {E}} = {\mathcal {E}}\text { and } \mu \cap \bar{{\mathcal {E}}} = \emptyset \Big \}, ~ \end{aligned}$$
(4)

where for each matching \(\mu \in {\mathcal {P}}\) it is required that edges in \({\mathcal {E}}\) are contained in \(\mu \), i.e., \({\mathcal {E}}\subseteq \mu \), while edges in \(\bar{{\mathcal {E}}}\) are excluded from \(\mu \). Then for notational brevity we re-write (4) as

$$\begin{aligned} {\mathcal {P}} = \big \{{\mathcal {E}};\bar{{\mathcal {E}}}\big \}, \end{aligned}$$

where \({\mathcal {E}}\) and \(\bar{{\mathcal {E}}}\) are often referred to as the sets of imposed and forbidden edges, respectively; see, e.g., [6].

Within our branch-and-bound algorithm each node of the search tree is associated with a subset of perfect matchings \({\mathcal {P}}\). Hence, we define a single level-relaxation of BAP with respect to \({\mathcal {P}}\) as:

$$\begin{aligned} \big [\text {AP}({\mathcal {P}})\big ]\quad \quad \min _{\mathbf {x},\mathbf {y}} \quad \Big \{ g_{\ell }(\mathbf {x}, \mathbf {y}) : \mu (\mathbf {x}, \mathbf {y}) \in {\mathcal {P}} \Big \}, \end{aligned}$$

which is obtained by removing the follower’s objective function and enforcing that each matching should belong to \({\mathcal {P}}\). The root node of the B&B tree corresponds to \({\mathcal {P}}^0=\{ \emptyset ; \emptyset \}\). Note that \({\mathcal {P}}^0={\mathcal {M}}(G)\). Thus, \(\text {AP}({\mathcal {M}}(G))\) is simply a single-level relaxation of BAP.

Bounding. Let \((\bar{\mathbf {x}},\bar{\mathbf {y}})\) be an optimal solution to \(\text {AP}({\mathcal {P}})\). Clearly, \(g_{\ell }(\bar{\mathbf {x}}, \bar{\mathbf {y}})\) serves as a lower bound for BAP at the B&B node associated with \({\mathcal {P}}\). If \(\bar{\mathbf {y}} \in {\mathcal {R}}(\bar{\mathbf {x}})\), then \((\bar{\mathbf {x}}, \bar{\mathbf {y}})\) is a feasible solution to (1), and \(g_{\ell }(\bar{\mathbf {x}}, \bar{\mathbf {y}})\) is an upper bound on the optimal value of BAP. Otherwise (i.e., \(\bar{\mathbf {y}} \notin {\mathcal {R}}(\bar{\mathbf {x}})\)), one can always find another \(\widetilde{\mathbf {y}} \in {\mathcal {R}}(\bar{\mathbf {x}})\) such that \((\bar{\mathbf {x}}, \widetilde{\mathbf {y}})\) is a feasible solution to (1), which also results in a valid upper bound given by \(g_{\ell }(\bar{\mathbf {x}}, \widetilde{\mathbf {y}})\). Moreover, the following result holds:

Proposition 1

For a given \((\bar{\mathbf {x}},\bar{\mathbf {y}}) \in \{0,1\}^{m_{\ell } + m_f}\), if \(\bar{\mathbf {y}} \notin {\mathcal {R}}(\bar{\mathbf {x}})\), then \(\bar{\mathbf {y}}\) cannot belong to any feasible solution of BAP, i.e., the following inequality is valid:

$$\begin{aligned} \sum _{e \in \mu _f(\bar{\mathbf {y}})} y_e \le |\mu _f(\bar{\mathbf {y}})| - 1 \end{aligned}$$

or, equivalently,

$$\begin{aligned} {\mathcal {F}}(G) \subseteq {\mathcal {M}}(G) {\setminus } \Gamma (\bar{\mathbf {y}}) \end{aligned}$$
(5)

where \(\Gamma (\bar{\mathbf {y}}) = \Big \{ \mu \in {\mathcal {M}}(G) : \mu _f(\bar{\mathbf {y}}) \subseteq \mu \Big \}.\)

Next, we discuss our branching technique that induces \(\Gamma (\mathbf {y})\) as one of the branches, which is immediately pruned.

Branching. Murthy [19] describes an algorithm for determining a ranked set of solutions to the assignment problem using partitioning with respect to a minimum cost assignment. Our branching technique follows the same idea. However, we branch with respect to the follower’s matching, which allows us to create a fewer number of branches and prune a larger set of perfect matchings.

Formally, let \(\mu \in {\mathcal {P}} = \big \{{\mathcal {E}};\bar{{\mathcal {E}}}\big \}\) be a perfect matching obtained by solving AP(\({\mathcal {P}}\)) and \(\mu _f \subseteq \mu \) be the corresponding follower’s matching, i.e., \(\mu _f = \mu \cap E_f\). If \(\mu _f {\setminus } {\mathcal {E}}\) is a nonempty subset of edges, i.e.,

$$\begin{aligned} \mu _f {\setminus } {\mathcal {E}}= \Big \{ (t_1,s_1), \ldots , (t_q,s_q)\Big \} \end{aligned}$$

for some integer \(q\ge 1\), then \({\mathcal {P}}\) can be partitioned with respect to \(\mu _f\) as the union of subsets \({\mathcal {P}}_1, {\mathcal {P}}_2, \ldots \) and \({\mathcal {P}}_{q+1}\) that are mutually disjoint, where

$$\begin{aligned}&{\mathcal {P}}_1=\Big \{{\mathcal {E}}; \bar{{\mathcal {E}}} \cup {(t_1, s_1)} \Big \},\\&{\mathcal {P}}_2= \Big \{{\mathcal {E}}\cup {(t_1, s_1)}; \bar{{\mathcal {E}}} \cup {(t_2, s_2)} \Big \},\\&{\mathcal {P}}_3= \Big \{{\mathcal {E}}\cup {(t_1, s_1)}\cup {(t_2, s_2)}; \bar{{\mathcal {E}}} \cup {(t_3, s_3)} \Big \},\\&\vdots \\&{\mathcal {P}}_q= \Big \{{\mathcal {E}}\cup {(t_1, s_1)}\cup {(t_2, s_2)}\cup \ldots \cup (t_{q-1},s_{q-1}); \bar{{\mathcal {E}}} \cup {(t_q, s_q)} \Big \},\\&{\mathcal {P}}_{q+1}= \Big \{{\mathcal {E}}\cup (t_1,s_1) \cup (t_2,s_2) \cup \ldots \cup (t_{q},s_{q}); \bar{{\mathcal {E}}}\Big \}, \end{aligned}$$

or, equivalently, \({\mathcal {P}}_v=\big \{{\mathcal {E}}_v;\bar{{\mathcal {E}}}_v\big \}, v=1,\ldots ,q+1\), and

$$\begin{aligned} {\mathcal {E}}_v\!=\!{\mathcal {E}}\cup \big \{(t_i,s_i)\ | \ i=1,\ldots ,v{-}1\big \}\quad \text{ and }\quad \bar{{\mathcal {E}}}_v\!=\!\bar{{\mathcal {E}}}\cup (t_v,s_v),\; v=1,\ldots ,q+1, \end{aligned}$$
(6)

where it is assumed that \((t_{q+1},s_{q+1})=\emptyset \). Then

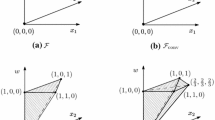
$$\begin{aligned} {\mathcal {P}} = \cup _{v =1}^{q+1}{\mathcal {P}}_v. \end{aligned}$$

For a given \((\bar{\mathbf {x}},\bar{\mathbf {y}}) \in \{0,1\}^{m_{\ell } + m_f}\), if \(\bar{\mathbf {y}} \notin {\mathcal {R}}(\bar{\mathbf {x}})\), then we define \(\mu _f = \mu _f(\bar{\mathbf {y}})\) and create q new nodes of the B&B tree with the corresponding sets of imposed and forbidden edges given by \({{\mathcal {E}}}_v\) and \(\bar{{\mathcal {E}}}_v\), respectively, for each \(v=1,\ldots ,q\). Note that \({\mathcal {P}}_{q+1} = \Gamma (\bar{\mathbf {y}})\). Thus, based on Proposition 1, \({\mathcal {P}}_{q+1}\) is pruned immediately. Figure 1 provides an illustration of the branching process.

Fig. 1
figure 1

An illustration of q new nodes created for given matching \(\{ (t_1,s_1), \ldots , (t_q,s_q)\} \)

Full size image

Algorithm Outline. For a node \({\mathcal {N}}^{\nu }\) of the B&B tree, let \(z^\nu \) denote the optimal value of the corresponding assignment problem AP(\({\mathcal {P}}^\nu \)), where \({\mathcal {P}}^\nu =\big \{{\mathcal {E}}^\nu ;\bar{{\mathcal {E}}}^\nu \big \}\). The root node \({\mathcal {N}}^0\) is associated with \({\mathcal {P}}^0=\{ \emptyset ; \emptyset \}\), i.e., \({\mathcal {P}}^0={\mathcal {M}}(G)\). Let \({\mathcal {Q}}\) be a set of unprocessed nodes (i.e., nodes that have not been pruned nor branched on) of the B&B tree, and \(z_u\) be the current upper bound on the optimal value \(z^*\). Next, using this notation we provide the pseudo-code of our algorithm.

Algorithm 1. Combinatorial branch-and-bound algorithm to solve BAP

  • Step 0: (Initialization) Create a node \({\mathcal {N}}^0\), let \({\mathcal {E}}^0=\bar{{\mathcal {E}}}^0=\emptyset \) and \({\mathcal {P}}^0=\{ \emptyset ; \emptyset \}\). Initialize list \({\mathcal {Q}} \leftarrow \left\{ {\mathcal {N}}^0\right\} \) and the global upper bound \(z_u= +\infty \).

  • Step 1: (Node selection) If \({\mathcal {Q}} = \emptyset \), terminate with the optimal objective function value \(z_u\); otherwise, select and delete node \({\mathcal {N}}^\eta \) from \({\mathcal {Q}}\).

  • Step 2: (Bounding) Solve \(AP({\mathcal {P}}^{\eta })\) for node \({\mathcal {N}}^\eta \). Denote by \((\mathbf {x}^\eta , \mathbf {y}^\eta )\) and \(z^\eta \) its optimal solution and the objective function value, respectively.

  • Step 3: (Pruning)

    1. (3a)

      If \(z^\eta \ge z_u\) , go to Step 1.

    2. (3b)

      If \(\mathbf {y}^\eta \in {\mathcal {R}}(\mathbf {x}^\eta )\), then let \(z_u = z^\eta \) and go to Step 1.

    3. (3c)

      If \(\mathbf {y}^\eta \notin {\mathcal {R}}(\mathbf {x}^\eta )\), then find \(\widetilde{\mathbf {y}} \in {\mathcal {R}}({\mathbf {x}}^\eta )\) and update (if necessary) the global upper bound. Go to Step 4.

  • Step 4: (Branching) From \({\mathcal {P}}^\eta =\{ {\mathcal {E}}^\eta ; \bar{{\mathcal {E}}}^\eta \}\) construct \({\mathcal {P}}^\eta _1=\{ {\mathcal {E}}_1^\eta ; \bar{{\mathcal {E}}}_1^\eta \}, \ldots , {\mathcal {P}}^\eta _{q}=\{ {\mathcal {E}}_q^\eta ; \bar{{\mathcal {E}}}_q^\eta \}\) with respect to \(\mu _f(\mathbf {y}^\eta )\) using (6). Add the corresponding new nodes \({\mathcal {N}}^\eta _1, \ldots , {\mathcal {N}}^\eta _q\) to \({\mathcal {Q}}\) and go to Step 1.

In Step 0, the algorithm initializes the root node by \({\mathcal {E}}=\bar{{\mathcal {E}}}=\emptyset \). In Step 1, a node \({\mathcal {N}}^\eta \) is chosen from \({\mathcal {Q}}\) according to some node selection rule. Step 2 solves AP(\({\mathcal {P}}^\eta \)). Step 3a checks whether the considered node is promising based on the obtained solution of AP(\({\mathcal {P}}^\eta \)) and the current value of the global upper bound. If this is the case, then Step 3b verifies whether the follower’s solution \(\mathbf {y}^\eta \) is optimal for the lower-level problem. Specifically, if it is optimal, then the algorithm updates the global upper bound. Otherwise, in Step 4 the algorithm branches by creating new nodes of the search tree using to the follower’s matching \(\mu _f(\mathbf {y}^\eta )\).

Generally speaking, our combinatorial branch-and-bound algorithm can handle any 0–1 function, e.g., polynomials, for the leader’s and the follower’s objective functions of the form:

$$\begin{aligned} g(\mathbf {z})= \sum _{S\subseteq E} p_S\prod _{e \in S} z_e \end{aligned}$$
(7)

where \(\prod _{e \in \emptyset } z_e =1, p_S \in {\mathbb {R}}\) and \(z_e\in \{0,1\}\) for all \(S \subseteq E\). Note that any pseudo-boolean function can be uniquely represented in form (7) [5].

The performance of our B&B approach is affected by the tractability of AP(\({\mathcal {P}}\)) in Step 2 and the efficiency of checking whether the obtained follower’s solution is optimal for the lower-level optimization problem in Step 3b. Clearly, all of the above depend on the types of the leader’s and the follower’s objective functions considered. Next, we describe implementation issues for the objective functions given by (2) and (3) as well as several enhancements that improve the overall performance of the algorithm.

2.3 Implementation and enhancements

If \(g_{\ell }(\mathbf {x}, \mathbf {y})\) is in either a linear sum or linear bottleneck form (2), then AP(\({\mathcal {M}}(G)\)) is polynomially solvable as it reduces to the linear sum assignment problem (LSAP) or linear bottleneck assignment problem (LBAP), respectively [6]. In order to solve AP(\({\mathcal {P}}\)) for general \({\mathcal {P}} = \big \{{\mathcal {E}};\bar{{\mathcal {E}}}\big \}\) one simple approach is to set \(d_{ij} = +\infty \) for all \((i,j) \in \bar{{\mathcal {E}}}\) and remove the vertices in the set \(\{i \in V, j \in U \ | \ \exists (i,j) \in {{\mathcal {E}}}\}\) from G together with their incident edges. Then the obtained problem becomes either LSAP or LBAP, which can be solved efficiently using known algorithms.

Given a solution of AP(\({\mathcal {P}}\)), one way to check its optimality with respect to the follower’s objective is to solve the lower-level optimization problem (1b)–(1e) for a given leader’s decision and compare the objective function values. Also, the number of branches created in Step 4 depends on the size of the follower’s matching, and based on Proposition 1 we prune one of those branches. However, if optimality of the current solution can be verified with less effort than solving the lower-level problem and/or branching can be done with respect to a smaller size matching, then the overall solution time can be improved. In the following, we discuss how to achieve these goals for BAPs with the follower’s objective function in either a linear sum or a linear bottleneck form.

In the literature (see, e.g., [6]), primal approaches for LSAP and LBAP often start with a perfect matching (i.e., a feasible solution) and incrementally improve the objective function value by finding an alternating cycle with respect to the current perfect matching until it reaches the global optimum. Recall that an alternating cycle with respect to some perfect matching \(\mu \) is a cycle, the edges of which are alternately in \(\mu \) and not in \(\mu \), and swapping the edges in \(\mu \) with edges not in \(\mu \) results in a better feasible solution [6]. Next, we exploit alternating cycles to strengthen our result from Proposition 1 as follows:

Proposition 2

For a given \((\bar{\mathbf {x}},\bar{\mathbf {y}}) \in \{0,1\}^{m_{\ell } + m_f}\), if there exists an alternating cycle with respect to \(\mu _f(\bar{\mathbf {y}})\), say \(C_{\mu _f(\bar{\mathbf {y}})}\), then let \(S = \mu _f(\bar{\mathbf {y}}) \cap C_{\mu _f(\bar{\mathbf {y}})}\), and the following inequality is valid:

$$\begin{aligned} \sum _{e \in S} y_e \le |S| - 1. \end{aligned}$$

or, equivalently,

$$\begin{aligned} {\mathcal {F}}(G) \subseteq {\mathcal {M}}(G) {\setminus } \Gamma (S), \end{aligned}$$

where \(\Gamma (S) = \Big \{ \mu \in {\mathcal {M}}(G) : S \subseteq \mu \Big \}.\)

Note that \(2 \le |S| \le |\mu _f(\mathbf {y})|\) and \(\Gamma (\mu _f(\mathbf {y})) \subseteq \Gamma (S)\). Proposition 2 implies that the problem of checking optimality of the lower-level optimization problem reduces to the problem of finding an alternating cycle. If an alternating cycle does not exist, then the current solution is optimal. Otherwise, an alternating cycle is used to create a fewer number of branches and prune a larger set of perfect matchings than the earlier approach based on Proposition 1. Observe that one should prefer finding smaller sets S, as it results in larger sets \(\Gamma (S)\).

We use the labeling algorithm in [3] for LSAP and the threshold algorithm in [11] for LBAP to construct set S. Specifically, for the threshold algorithm let \(\mathbf {y}\) be a follower’s decision and \(t = \max _{(i,j) \in E_f}\{c_{ij} y_{ij}\}\). If there exists a matching, say \(\mu _f(\mathbf {y}')\), that saturates the same set of vertices saturated by \(\mu _f(\mathbf {y})\), with edges that cost strictly less than t, then \(\mathbf {y}\) is not optimal for the lower-level optimization problem. Thus, if we denote \(S = \mu _f(\mathbf {y}) {\setminus } \mu _f(\mathbf {y}')\), then a similar result to Proposition 2 holds here.

3 Special cases

3.1 MIP formulation

For a general bilevel optimization problem, if the lower-level problem is convex and the regularity conditions are satisfied, then one standard solution method is based on reformulating the original bilevel problem as a single-level mixed integer program by exploiting the Karush-Kuhn-Tucker (KKT) optimality conditions [8]. Next, we follow this approach to present an MIP reformulation of BAPs with the follower’s objective function (1b) in a linear sum form, i.e., \(g_f(\mathbf {y}) = \sum _{(i,j) \in E_f} c_{ij} y_{ij}\).

Note that in this case the lower-level problem is LSAP. Its constraint matrix is known to be totally unimodular and the integrality restrictions can be relaxed. Thus, the lower-level problem becomes a simple linear program (LP), which can be represented in terms of its dual as follows:

$$\begin{aligned} \max _{\varvec{\lambda }, \varvec{\gamma }} \quad&\sum _{i \in U} \Bigg (1 - \sum _{j \in V_{\ell }^{(i)}} x_{ij}\Bigg ) \lambda _i + \sum _{j \in V} \Bigg (1 - \sum _{i \in U_{\ell }^{(j)}} x_{ij}\Bigg ) \gamma _j \end{aligned}$$
(8a)
$$\begin{aligned} \text {s.t.} \quad&\lambda _i + \gamma _j \le c_{ij} \qquad (i,j) \in E_f. \end{aligned}$$
(8b)

Consequently, BAP can be equivalently rewritten as:

$$\begin{aligned} \min \limits _{\varvec{\lambda },\varvec{\gamma },\mathbf {x},\mathbf {y}} \quad&g_{\ell }(\mathbf {x},\mathbf {y}) \end{aligned}$$
(9a)
$$\begin{aligned} \text {s.t.} \quad&\sum _{j \in V_{\ell }^{(i)}} x_{ij} + \sum _{j \in V_{f}^{(i)}} y_{ij} = 1 \quad \quad \quad \forall i \in U, \end{aligned}$$
(9b)
$$\begin{aligned}&\sum _{i \in U_{\ell }^{(j)}} x_{ij} + \sum _{i \in U_{f}^{(j)}} y_{ij} = 1 \quad \quad \quad \forall j \in V, \end{aligned}$$
(9c)
$$\begin{aligned}&\lambda _i + \gamma _j \le c_{ij} \quad \quad \quad \forall (i,j) \in E_f, \end{aligned}$$
(9d)
$$\begin{aligned}&\sum _{(i,j) \in E_f} c_{ij} y_{ij} = \sum _{i = 1}^n \Bigg (1 {-} \sum _{j \in V_{\ell }^{(i)}} x_{ij}\Bigg ) \lambda _i + \sum _{j = 1}^n \Bigg (1 {-} \sum _{i \in U_{\ell }^{(j)}} x_{ij}\Bigg ) \gamma _j, \end{aligned}$$
(9e)
$$\begin{aligned}&x_{ij} \in \{0,1\} \quad \quad \quad \forall (i,j) \in E_{\ell }, \end{aligned}$$
(9f)
$$\begin{aligned}&y_{ij} \in \{0,1\} \quad \quad \quad \forall (i,j) \in E_{f}, \end{aligned}$$
(9g)

where (9e) ensures optimality of the lower-level problem by the LP strong duality property.

The MIP formulation given by (9) is nonlinear due to the presence of nonlinear terms of the form \(x_{ij}\lambda _i\) and \(x_{ij}\gamma _j\) in constraint (9e). However, since \(x_{ij}\) is binary, it can be easily linearized using a standard Big-M method, see, e.g., [13]. We compare the performances of our B&B algorithm and an off-the-shelf MIP solver in Sect. 4 for instances with the follower’s linear sum objective.

3.2 Polynomially solvable classes

In this section we describe several classes of BAP that can be solved efficiently. First, we exploit the following simple observation. If for all feasible leader’s decisions both the leader’s and follower’s objective function values coincide (up to a constant summand), i.e., \(g_{\ell }(\hat{\mathbf {x}}, \mathbf {y}) = g_f(\mathbf {y})+const\), for all feasible \(\hat{\mathbf {x}}\), then the follower’s objective function can be omitted and BAP reduces to a single-level assignment problem. Furthermore, for linear sum objective functions in BAP there exist more general sufficient conditions:

Proposition 3

If there exists \(k \in {\mathbb {R}}\) such that \(d_{ij} = c_{ij} + k\) for all \((i,j) \in E_f\), then BAP with the leader’s and follower’s linear sum objective functions reduces to LSAP.

Proposition 4

If there exists \(k \in {\mathbb {R}}_{>0}\) such that \(d_{ij} = k\cdot c_{ij}\) for all \((i,j) \in E_f\), then BAP with the leader’s and follower’s linear sum objective functions reduces to LSAP.

The proofs of these results can be derived using the assignment constraints (1c)–(1d) and the single-level relaxation of BAP. Specifically, one can show that if \((\bar{\mathbf {x}},\bar{\mathbf {y}})\) is an optimal solution of \(\text {AP}({\mathcal {P}}^0)\), then \(\bar{\mathbf {y}} \in {\mathcal {R}}(\bar{\mathbf {x}})\) for the classes of BAP considered in Propositions 3 and 4. A similar in spirit result for BAP with bottleneck objective functions is given by:

Proposition 5

Suppose there exists an ordering of edges in \(E_f\) given by \((i_1,j_1), (i_2,j_2), \ldots , (i_{m_f},j_{m_f})\) such that \(c_{i_1,j_1}\le c_{i_2,j_2}\le \ldots \le c_{i_{m_f},j_{m_f}}\) and \(d_{i_1,j_1}\le d_{i_2,j_2}\le \ldots \le d_{i_{m_f},j_{m_f}}\). Then BAP with the leader’s and follower’s linear bottleneck objective functions reduces to LBAP.

The latter result follows from the fact the optimal objective function value of LBAP is exactly equal to one of the edge’s cost coefficients and its optimal assignment depends only on the relative order of the coefficients but not on their actual numerical values.

Finally, we note the results of Propositions 3–5 hold under the assumption that the leader’s and the follower’s objective functions are in the same form (specifically, either both in a linear sum or both in a linear bottleneck form). In the next section we explore computationally test instances with the objectives’ coefficients as in Proposition 3 (referred to as strongly-correlated instances) for BAPs, where the leader’s and the follower’s objectives are not in the same form.

If the leader’s feasible set of actions is relatively small, then one solution approach for BAP is to solve the follower’s problem for each leader’s feasible solution and pick the one that returns the most favorable objective function value for the leader. In general, there are \(O(2^{m_\ell })\) possible leader’s decisions. However, this number can be reduced depending on the graph topology. For example, consider the case when all leader’s edges emanate from exactly one node, which implies that the number of feasible leader’s action is bounded by \(O(m_\ell )\).

Formally, given a feasible leader’s solution \(\hat{\mathbf {x}}\), define

$$\begin{aligned} U_f(\hat{\mathbf {x}}) = \{ i \in U : \forall j \in V^{(i)}_{\ell }, \hat{x}_{ij} = 0 \}\quad \text {and}\quad V_f(\hat{\mathbf {x}}) = \{ j \in V : \forall i \in U^{(j)}_{\ell }, \hat{x}_{ij} = 0 \}, \end{aligned}$$

i.e., all vertices of G that are not assigned by the leader. Note that \(U_f(\hat{\mathbf {x}}) \subseteq U, V_f(\hat{\mathbf {x}}) \subseteq V\) and \(|U_f(\hat{\mathbf {x}})| = |V_f(\hat{\mathbf {x}})|\). For all \(i \in U_f(\hat{\mathbf {x}})\), define \(V_{f}^{(i)}(\hat{\mathbf {x}}) = \{ j \in V_f(\hat{\mathbf {x}}) : (i,j) \in E_{f} \}\). Likewise, we define \(U_{f}^{(j)}(\hat{\mathbf {x}})\) for all \(j \in V_f(\hat{\mathbf {x}})\). Denote \(E_f(\hat{\mathbf {x}}) = \{ (i,j) \in E_f : i \in U_f(\hat{\mathbf {x}}), j \in V_f(\hat{\mathbf {x}}) \}\), where \(E_f(\hat{\mathbf {x}})\subseteq E_f\). Then evaluating the leader’s objective function \(g_{\ell }(\hat{\mathbf {x}},\mathbf {y})\) requires solution of the follower’s problem:

$$\begin{aligned}{}[\text {BAP}(\hat{\mathbf {x}})] \quad \min _{\mathbf {y}} \quad&g_{\ell }(\hat{\mathbf {x}},\mathbf {y}) \end{aligned}$$
(10a)
$$\begin{aligned} \text {s.t.} \quad&\min _{\mathbf {y}} \ g_{f}(\mathbf {y}) \end{aligned}$$
(10b)
$$\begin{aligned}&\text {s.t.} \quad \sum _{j \in V_f^{(i)}(\hat{\mathbf {x}})} y_{ij} = 1 \quad \forall i \in U_f(\hat{\mathbf {x}}),\end{aligned}$$
(10c)
$$\begin{aligned}&\ \qquad \sum _{i \in U_f^{(j)}(\hat{\mathbf {x}})} y_{ij} = 1 \quad \forall j \in V_f(\hat{\mathbf {x}}), \end{aligned}$$
(10d)
$$\begin{aligned}&\ \qquad y_{ij} \in \{0,1\} \quad \forall (i, j)\in E_f(\hat{\mathbf {x}}). \end{aligned}$$
(10e)

Observe that problem (10b)–(10e) is a single-level assignment problem that can be solved by an appropriate method depending on \(g_{f}(\cdot )\); the objective of (10a) ensures that if there are multiple optimal solutions for the follower, then we select the most favorable one for the leader, which is consistent with Assumption A1, i.e., the optimistic case for BAP. Naturally, the pessimistic case can be handled by replacing minimization with maximization in (10a).

Any ranking algorithm [6] can be used to solve (10) by enumerating over all optimal solutions for (10b)–(10e). However, this approach may be computationally expensive as the number of such solutions can be exponentially large. In the following we show that if the follower’s objective is in either linear sum or linear bottleneck form, then problem (10) can be solved efficiently as long as its single-level relaxation obtained by removing (10b) is also efficiently solvable. This also implies that if \(m_\ell \) is fixed then these classes of BAP are polynomially solvable. It is interesting to contrast this observation with the result in [17], where it is shown that if the number of variables controlled by the follower is constant, then bilevel linear programs are polynomially solvable.

3.2.1 Follower’s objective: linear sum

For \(g_{f}(\mathbf {y}) = \sum _{(i,j) \in E_f(\hat{\mathbf {x}})} c_{ij} y_{ij} \), let \((\varvec{\lambda },\varvec{\gamma })\) be a dual optimal solution to (10b)–(10e). Define \(E(\varvec{\lambda },\varvec{\gamma }) = \{ (i,j)\in E_f(\hat{\mathbf {x}}): \lambda _i + \gamma _j = c_{ij}, i \in U_f(\hat{\mathbf {x}}), j \in V_f(\hat{\mathbf {x}}) \}\). The following result from [10] characterizes all optimal solutions of LSAP:

Lemma 1

A feasible solution \(\mathbf {y}\) is optimal to (10b)–(10e) if and only if \(\mu _f(\mathbf {y}) \subseteq E(\varvec{\lambda },\varvec{\gamma })\).

Consequently, problem (10) can be solved using the following two-step procedure. First, we solve LSAP given by (10b)–(10e); specifically, we need to obtain a dual optimal solution. Second, we re-define the leader’s cost coefficients for edges in \(E_f(\hat{\mathbf {x}})\) as:

$$\begin{aligned} d'_{ij} = \left\{ \begin{array}{l l} d_{ij} &{} \quad \text {if }(i,j) \in E(\varvec{\lambda },\varvec{\gamma }),\\ \infty &{} \quad \text {otherwise}; \end{array} \right. \end{aligned}$$

and solve a single-level relaxation of (10) by removing the follower’s objective in (10b). Clearly, by Lemma 1 the obtained solution is optimal for (10).

Note that this procedure does not depend on a type of the leader’s objective. Furthermore, one interesting observation links the above result to another class of assignment problems, namely, singly constrained LSAP (SC-LSAP) [1, 16]. Suppose \(g_{\ell }(\mathbf {y}) = \sum _{(i,j) \in E_f} d_{ij} y_{ij}\). Then, (10) is reformulated as the following IP:

$$\begin{aligned}&\min _\mathbf{y } \ \sum _{(i,j) \in E_f} d_{ij} y_{ij} \end{aligned}$$
(11a)
$$\begin{aligned}&\text {s.t.} \quad \sum _{(i,j) \in E_f} c_{ij} y_{ij} \le c^*, \end{aligned}$$
(11b)
$$\begin{aligned}&\ \qquad \sum _{j \in V_f^{(i)}(\hat{\mathbf {x}})} y_{ij} = 1 \quad \forall i \in U_f(\hat{\mathbf {x}}), \end{aligned}$$
(11c)
$$\begin{aligned}&\ \qquad \sum _{i \in U_f^{(j)}(\hat{\mathbf {x}})} y_{ij} = 1 \quad \forall j \in V_f(\hat{\mathbf {x}}), \end{aligned}$$
(11d)
$$\begin{aligned}&\qquad \ y_{ij} \in \{0,1\} \quad \forall (i,j)\in E_f(\hat{\mathbf {x}}) , \end{aligned}$$
(11e)

where

$$\begin{aligned} c^* = \min \big \{ \sum _{(i,j) \in E_f} c_{ij} y_{ij}: (11c)-(11e) \big \}. \end{aligned}$$
(12)

If equation (12) is not required to be satisfied, i.e., one considers a general class of SC-LSAPs, then the problem is known to be NP-hard. However, in our case (12) holds, which implies that (11)–(12) forms a polynomially solvable class of SC-LSAPs. We refer the reader to [16] for other examples of efficiently solvable classes of SC-LSAP.

3.2.2 Follower’s objective: linear bottleneck

Characterizing the set of alternative optimal solutions for LBAP is rather straightforward as one should simply omit all edges with their costs greater than the optimal value of LBAP. Formally, denote by \(c^*\) the optimal objective function value of (10b)–(10e) with \(g_{f}(\mathbf {y}) = \max _{(i,j) \in E_f(\hat{\mathbf {x}})} \{c_{ij} y_{ij}\} \). Similar to the previous section, we redefine the leader’s cost coefficients for edges in \(E_f(\hat{\mathbf {x}})\) as:

$$\begin{aligned} d'_{ij} = \left\{ \begin{array}{l l} \infty &{} \quad \text {if }c_{ij} > c^*,\\ d_{ij} &{} \quad \text {otherwise.} \end{array} \right. \end{aligned}$$

Then solving single-level relaxation of (10) by removing the follower’s objective in (10b) yields the optimal solution to the problem (10) with the follower’s bottleneck objective function.

4 Computational experiments

4.1 Preliminaries

In our computational study we focus on four classes of BAP, where the leader’s and the follower’s objective functions are in either a linear sum or a linear bottleneck form. We refer to the resulting optimization problems as Sum-Sum, Bottleneck-Sum, Sum-Bottleneck and Bottleneck-Bottleneck, where for each problem the first and second terms correspond to the considered types of the leader’s and the follower’s objective functions, respectively.

Our test instances are constructed as follows. The leader’s and follower’s cost matrices are generated with varying degrees of correlation:

  • un-correlated: \(d_j\sim U[1,100]\) and \(c_j \sim U[1,100]\),

  • weakly-correlated: \(d_j \sim U[1,100]\) and \(c_j = \max \{ 0 , \ d_j + U[-10,10] \}\),

  • strongly-correlated: \(d_j \sim U[1,100]\) and \(c_j = d_j + 10\),

where U denotes a coefficient generated according to a uniform distribution over the specified interval. We consider test instances with complete bipartite graphs G, i.e., \(m_{\ell } + m_f = n^2\), where \(n\in \{25, \ 50,\ 75,\ 100,\ 150,\ 200,\ 250,\ 300\}\). The number of edges controlled by the follower (\(m_f\)) is assumed to be some fraction, say \(\rho \), of the total number of edges in G and modeled using a Bernoulli distribution, i.e., \(m_f \approx \rho n^2\), where \(\rho \) varies over \(\{0.1, \ 0.2, \ 0.3, \ldots , \ 0.9\}\). We generate 5 instances for each \(n, \rho \) and degree of correlation. Our test instances are available online [4].

In the computational experiments, we consider three different algorithmic approaches:

  1. (i)

    CPLEX 12.4 applied to the linearized version of MIP (9) (only for the Sum-Sum and Bottleneck-Sum problems);

  2. (ii)

    the general branch-and-bound (B&B) algorithm described in Sect. 2.2 (see Algorithm 1); and

  3. (iii)

    its improved version referred to as IB&B that uses the algorithmic enhancements described in Sect. 2.3.

The algorithms in our study are coded in C++, compiled using Microsoft Visual Studio 2010. For solving the linear sum assignment problem, the dlib open source library is used [14]. All experiments (with CPLEX as well as our B&B and IB&B algorithms) are performed on a single thread of a Windows 7 PC with 3.6GHz CPU and 32GB of RAM. Note that in our implementation of the branch-and-bound algorithms (i.e., B&B and IB&B), in Step 1 nodes are selected according to the breadth-first rule.

4.2 Results and discussion

Our computational results are summarized in Tables 2, 3, 4, 5, and 6. The reported average running times are in seconds. The time limit is set to 3600 seconds. If an algorithm does not find an optimal solution within the time limit, we report the obtained average optimality gap. The superscripts over average time and gap values indicate the number of instances for each type of possible outcome (note that the superscript is dropped if its value is exactly 5). For example, consider an un-correlated class of test instances of the Sum-Sum problem in Table 2, where \(n=25\) and \(\rho = 0.6\). CPLEX solves four instances to optimality with average running time of 276 seconds, and for one instance it does not find an optimal solution within the time limit and the optimality gap is 5.6 %. On the other hand, B&B solves three instances to optimality with average running time 112 seconds, while for the remaining two instances the average gap is 26.8 %. Finally, IB&B solves all instances to optimality with average running time of 1 second. The best result for a given test instance is in bold. An entry of “-” in our tables indicates that the corresponding algorithm can not find a feasible integer solution within the time limit for any of the instances in the considered class. Note that for strongly-correlated instances (Table 6), the results for the Sum-Sum and Bottleneck-Bottleneck problems are not presented; recall that they are polynomially solvable as shown in Sect. 3.2.

Table 2 Results for un-correlated instances with the follower’s objective function in a linear sum form
Full size table
Table 3 Results for un-correlated instances with the follower’s objective function in a linear bottleneck form
Full size table
Table 4 Results for weakly-correlated instances with the follower’s objective function in a linear sum form
Full size table
Table 5 Results for weakly-correlated instances with the follower’s objective function in a linear bottleneck form
Full size table
Table 6 Results for strongly-correlated instances
Full size table

As one would expect, the computational difficulty of the problem decreases with the degree of correlation (between the leader’s and follower’s cost coefficients), i.e., the un-correlated test instances seems to be the most challenging ones, while the strongly-correlated are much easier to solve. For example, compare the performance of IB&B for the Bottleneck-Sum problem with \(n=100, \rho = 0.6\) and different degrees of correlation given in Tables 2, 4 and 6. None of the un-correlated instances can be solved within the time limit and the average optimality gap is 90.8 %, while four out of five weakly-correlated instances can be solved with the average runtime of 112 seconds and one instance has the optimality gap of 33.3 %. All strongly-correlated instances can be solved within 7 seconds on average. These observations are rather intuitive because the leader’s and the follower’s objectives are more in line when the degree of correlation increases, which results in a better quality of bounds obtained via a single-level relaxation of BAP.

Another intuitive observation is that the computational difficulty of the problem typically increases with \(\rho \). It can be attributed to the fact that larger values of \(\rho \) result in larger-sized follower’s reaction sets, which evidently make BAP more challenging.

Regarding the algorithms developed in this paper, IB&B turns out to be the best approach among the considered solutions methods in almost all cases (except for some un-correlated instances discussed below). Specifically, IB&B either reaches the optimal solution faster or has a tighter optimality gap at the time limit than B&B and CPLEX. Advantages of IB&B in comparison to B&B are rather clear due the nature of the proposed enhancement described in Sect. 2.3. Moreover, the smaller values in the column \(\# nodes\) (i.e., the number of nodes in the search tree) for IB&B provides another supporting argument for its superior performance. As a side note, we should mention that these values are reported only for instances that are solved within the time limit.

Finally, we note that for some un-correlated instances CPLEX obtains better results than IB&B, in particular, see Table 2 with \(n=25\) and \(\rho \in \{0.8,0.9\}, n=50\) and \(\rho \in \{0.6,0.7,0.9\}, n=75\) and \(\rho \in \{0.4,0.5,0.6\}\) as well as \(n=100\) and \(\rho \in \{0.3,0.4\}\). As mentioned above, for un-correlated instances the lower bound computed by ignoring the follower’s objective can be arbitrarily loose as there is no correlation between the leader’s and the follower’s cost coefficients. This hinders the performance of IB&B. However, as the number of edges controlled by the follower increases, see instances in Table 2 for \(n=100\) and \(\rho \ge 0.5\), IB&B is able to find a better quality feasible solution than CPLEX, which improves the tightness of IB&B’s optimality gaps. We attribute this observation to the fact that IB&B constructs feasible solutions at every node of the search tree (see Step 3(c) of Algorithm 1).

5 Concluding remarks

In this paper we describe exact solution methods for the bilevel assignment problem. Our approach is based on a branch-and-bound framework and tailored to exploit structural properties of the assignment problem and specific classes of the considered objective functions. Our extensive computational experiments (including comparisons with an off-the-shelf MIP solver) demonstrate both advantages and limitations of the developed algorithms. Furthermore, the bilevel assignment problem is known to be NP-hard. Thus, we also describe some polynomially solvable classes of the problem.

One possible direction of the future research is to relax assumption A1 and extend our solution methods for the pessimistic case of the bilevel assignment problem. Also, it would be interesting to consider bilevel extensions of other well-known classes of assignment problems, e.g., multi-index assignment problems [2, 15]. Finally, we note that our combinatorial branch-and-bound framework can potentially handle (perhaps, with some modifications) more general types of BAP than those considered in this paper, e.g., other types of objective functions, unbalanced assignments, or problems where some of the edges can be controlled by both the leader and the follower. We believe such generalizations provide a number of interesting research directions.